Testing the Feasibility of an Agent-Based Model for Hydrologic Flow Simulation
Abstract
1. Introduction
- Implementing ABM systems to model flood disasters intelligently and expeditiously.
- Agent-based modeling for hydrologic flow simulation in a tropical basin context.
- Potential to contribute to tropical water resource management and well-being.
2. Antecedents and Similar Work
2.1. A Briefing on Agent-Based Modeling
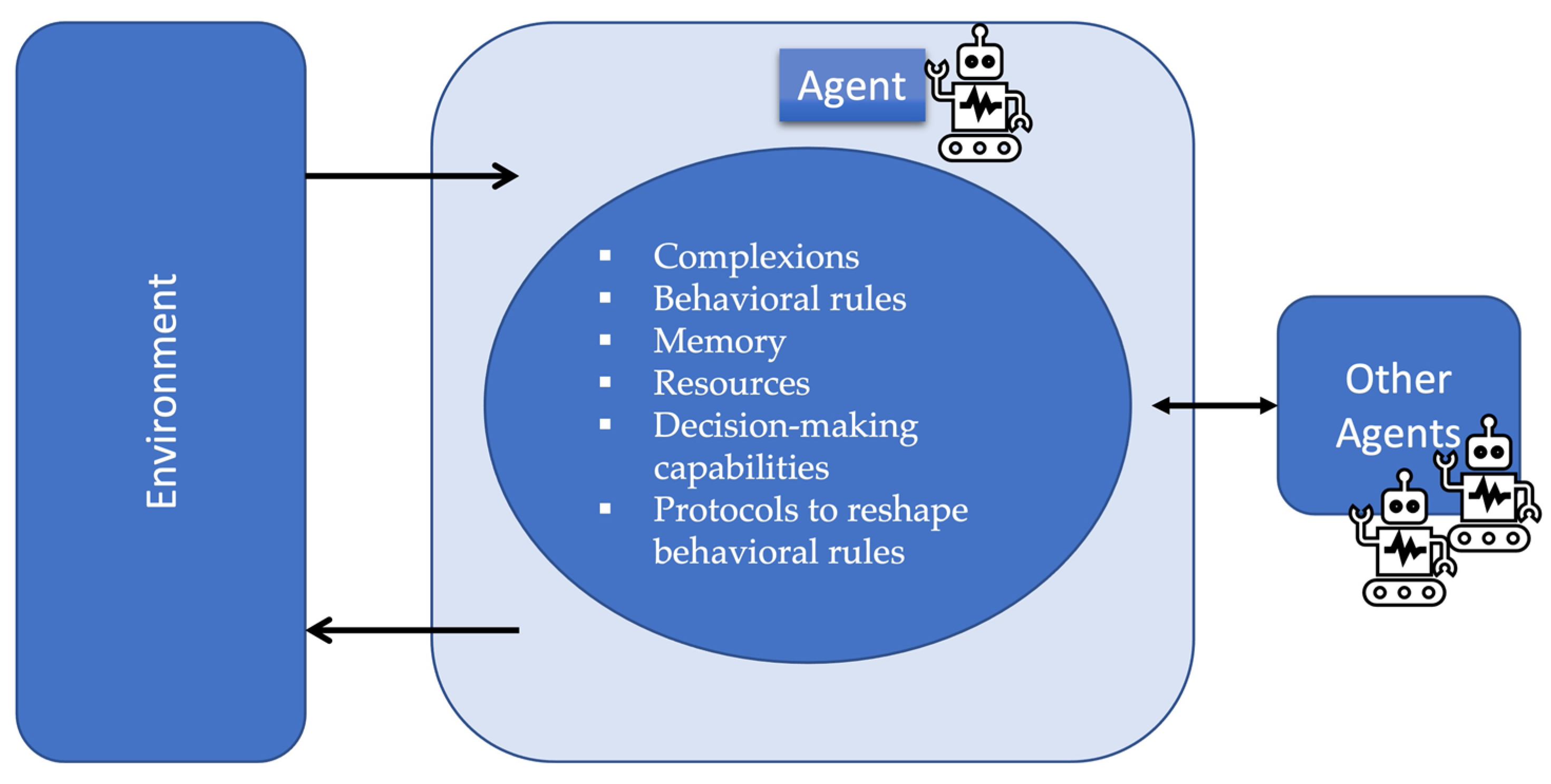
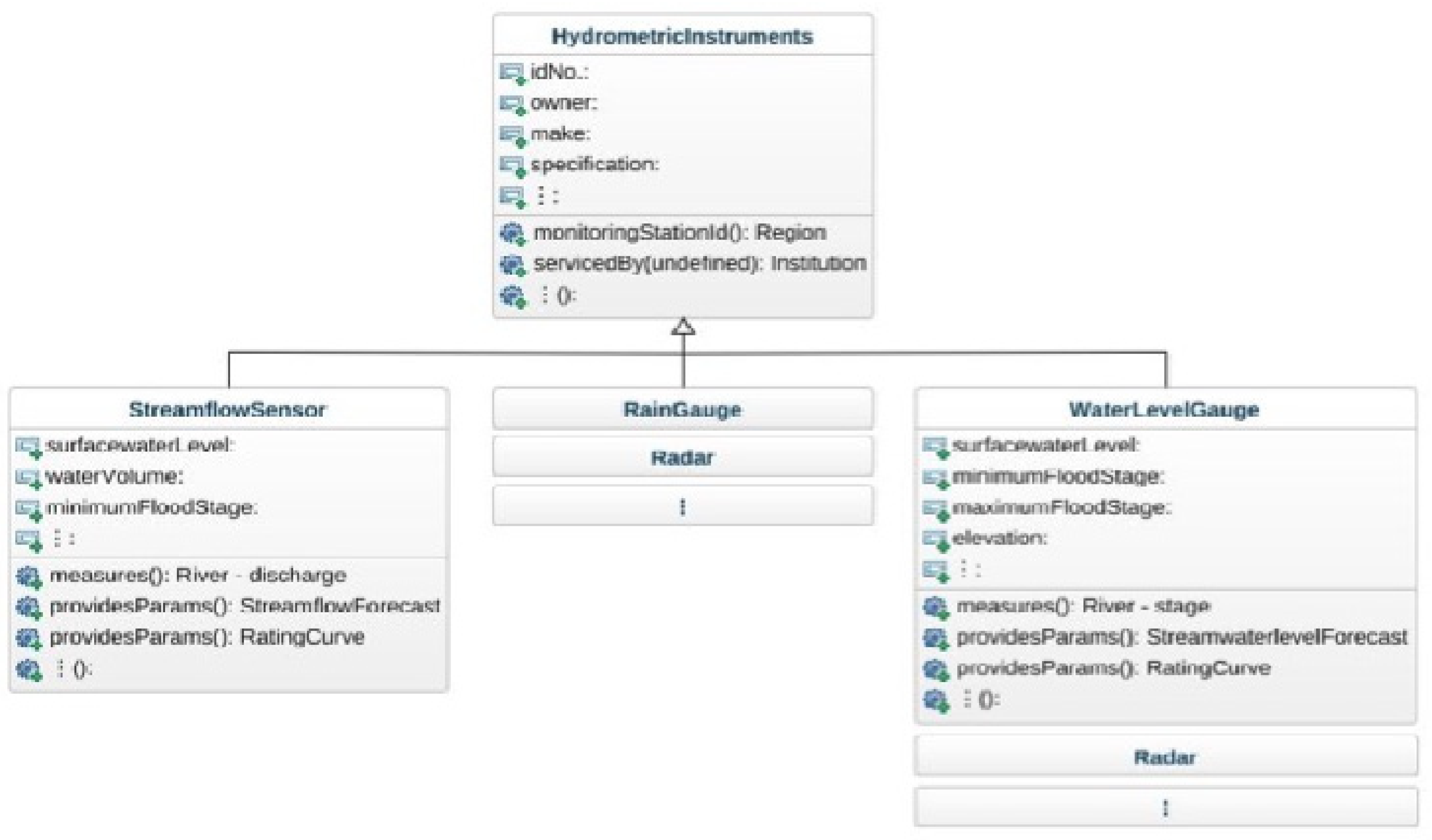
2.1.1. Domain Model Ontology
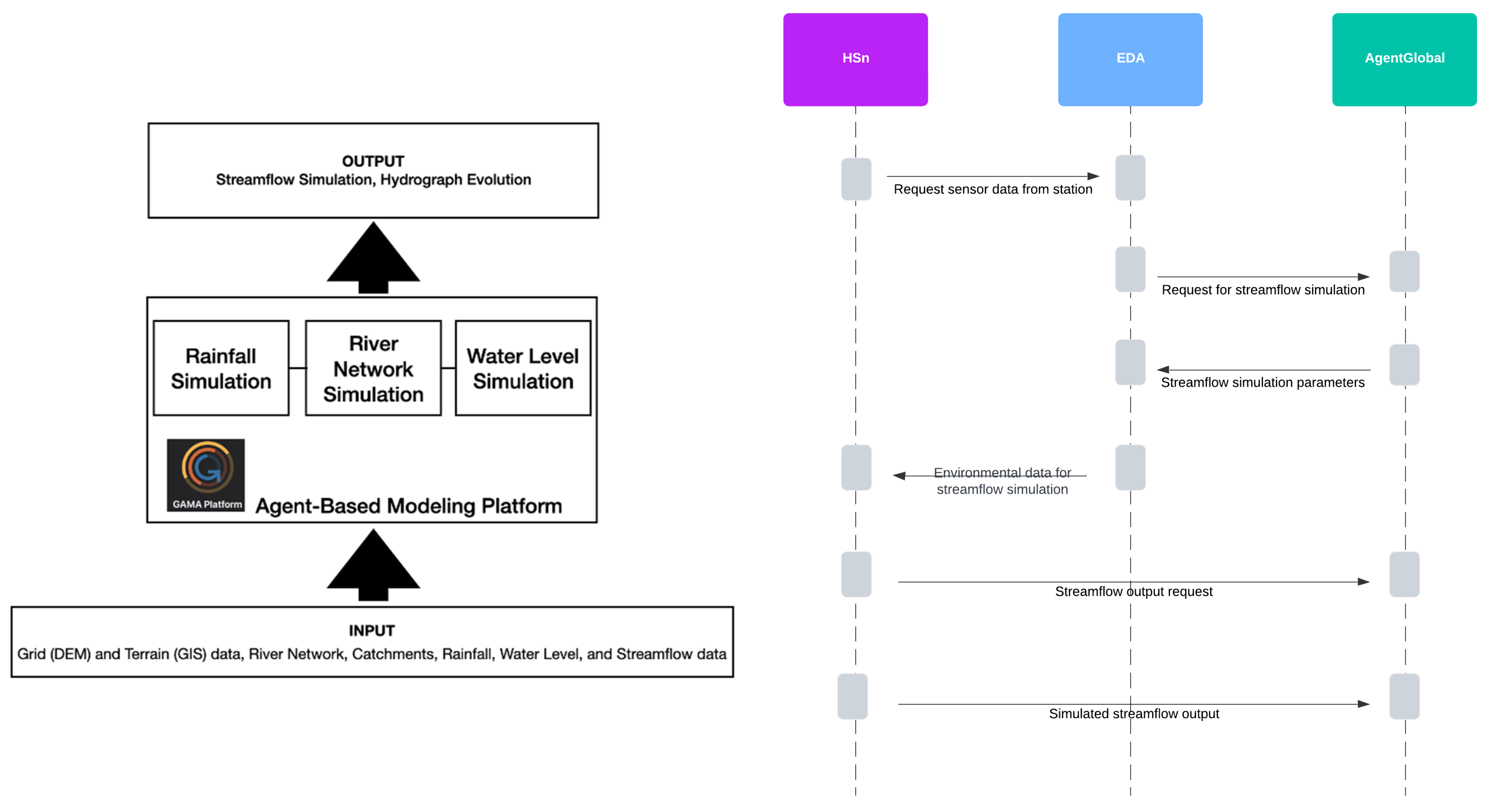
2.1.2. ABM Framework for Flow Simulation
2.2. Some Applications of ABM in Streamflow Simulation
3. Materials and Methods
3.1. Study Area
3.2. Soil Type Description
3.3. Land Use Description
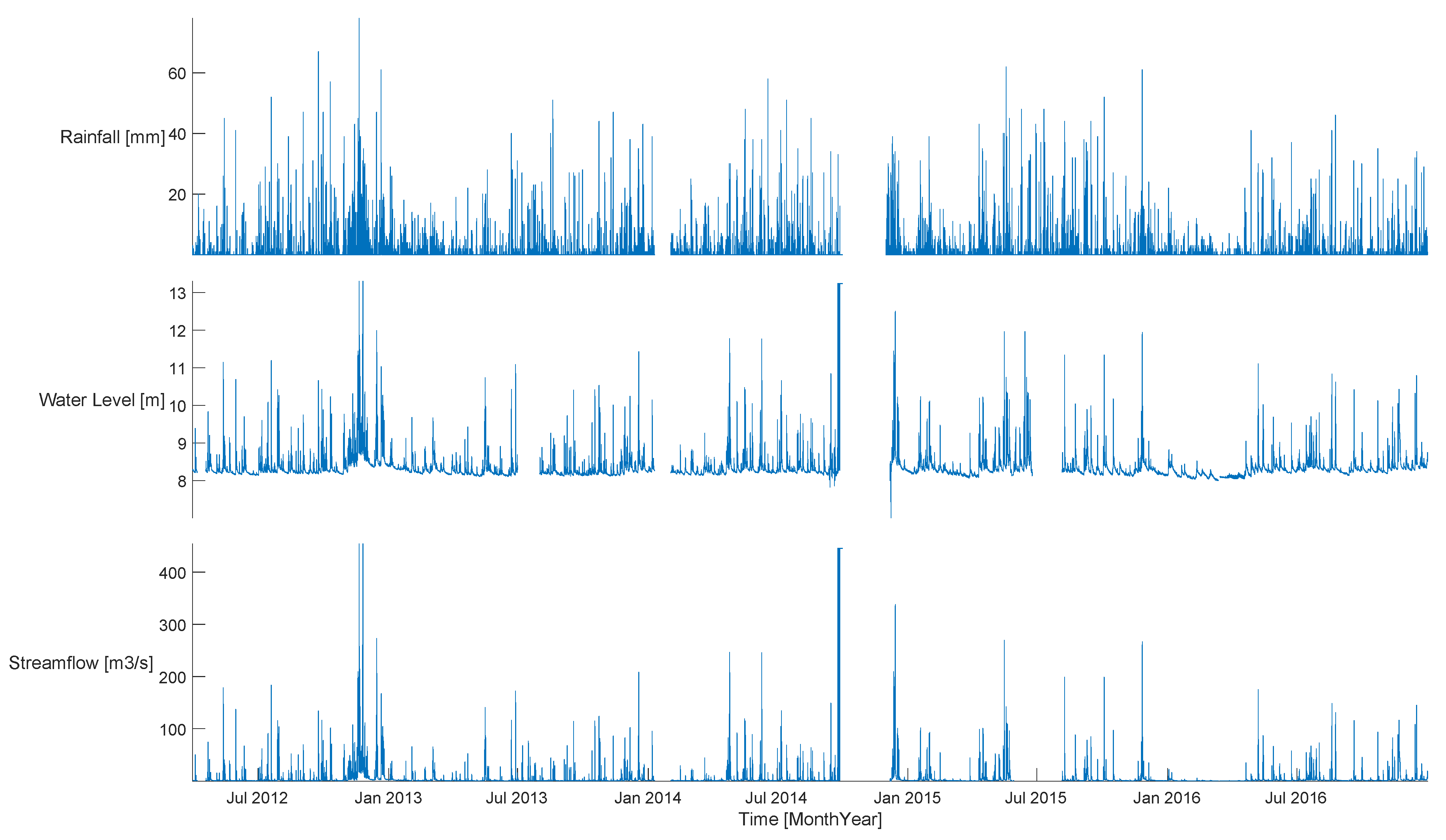
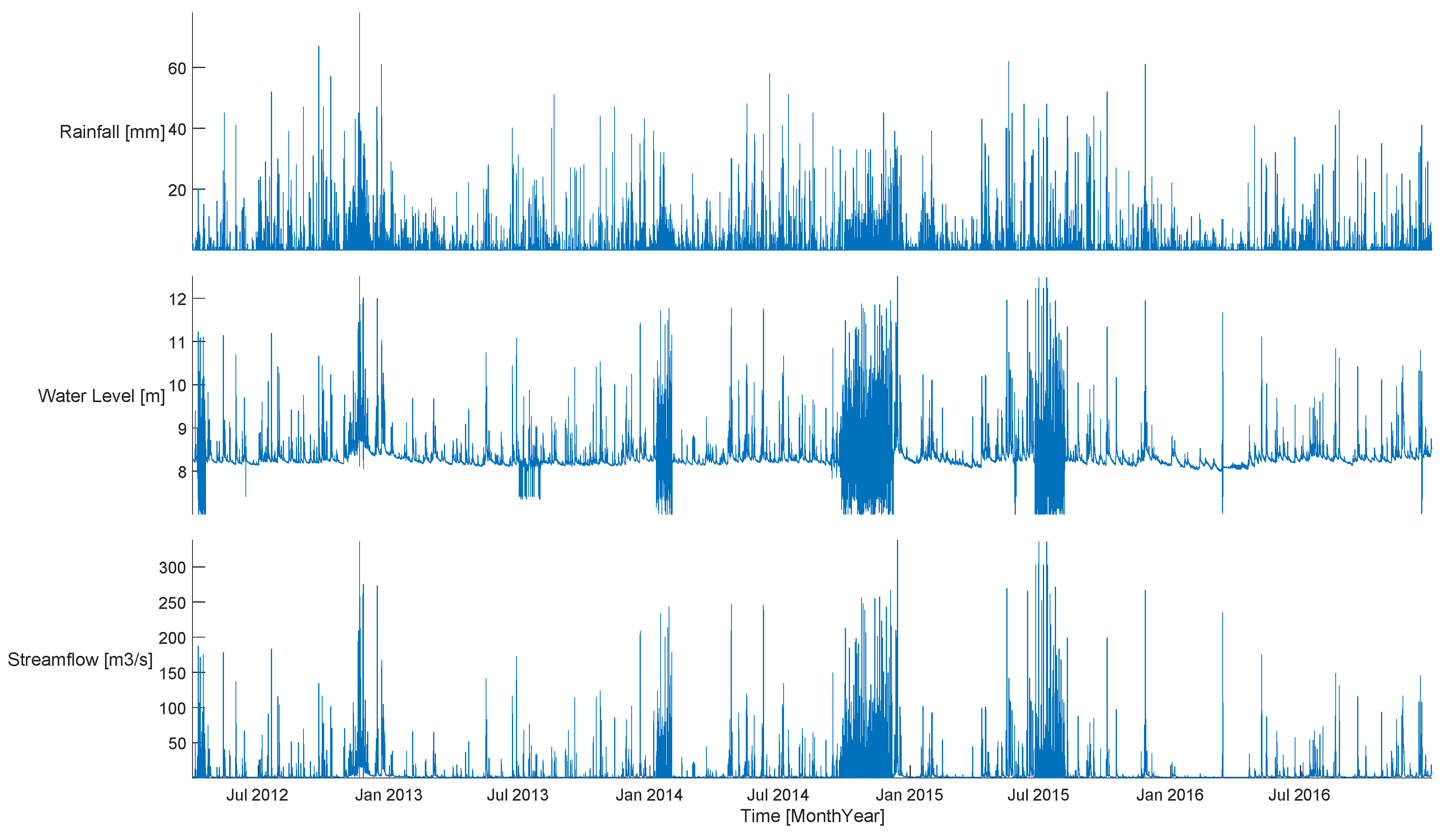
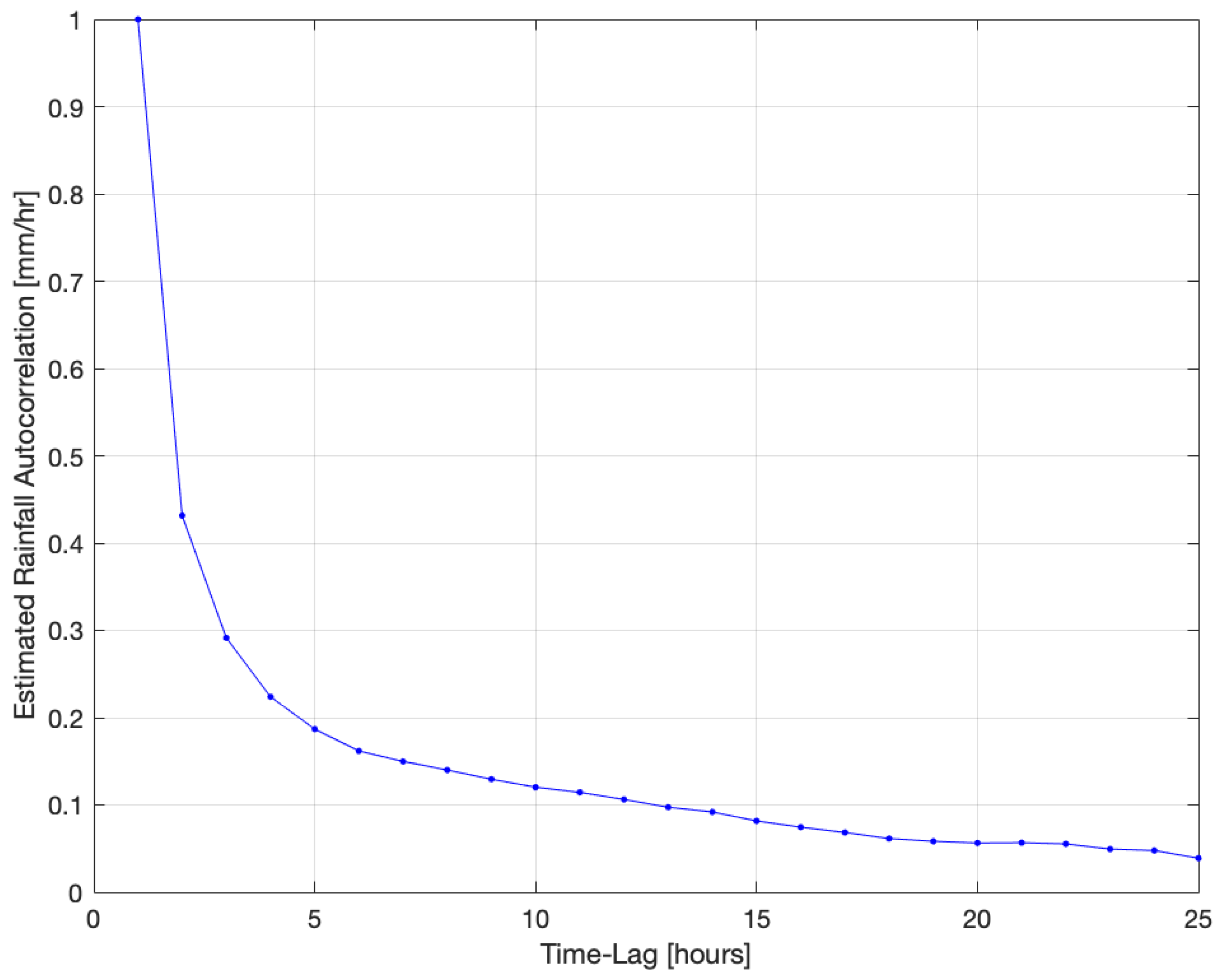
3.4. Rainfall Data Description
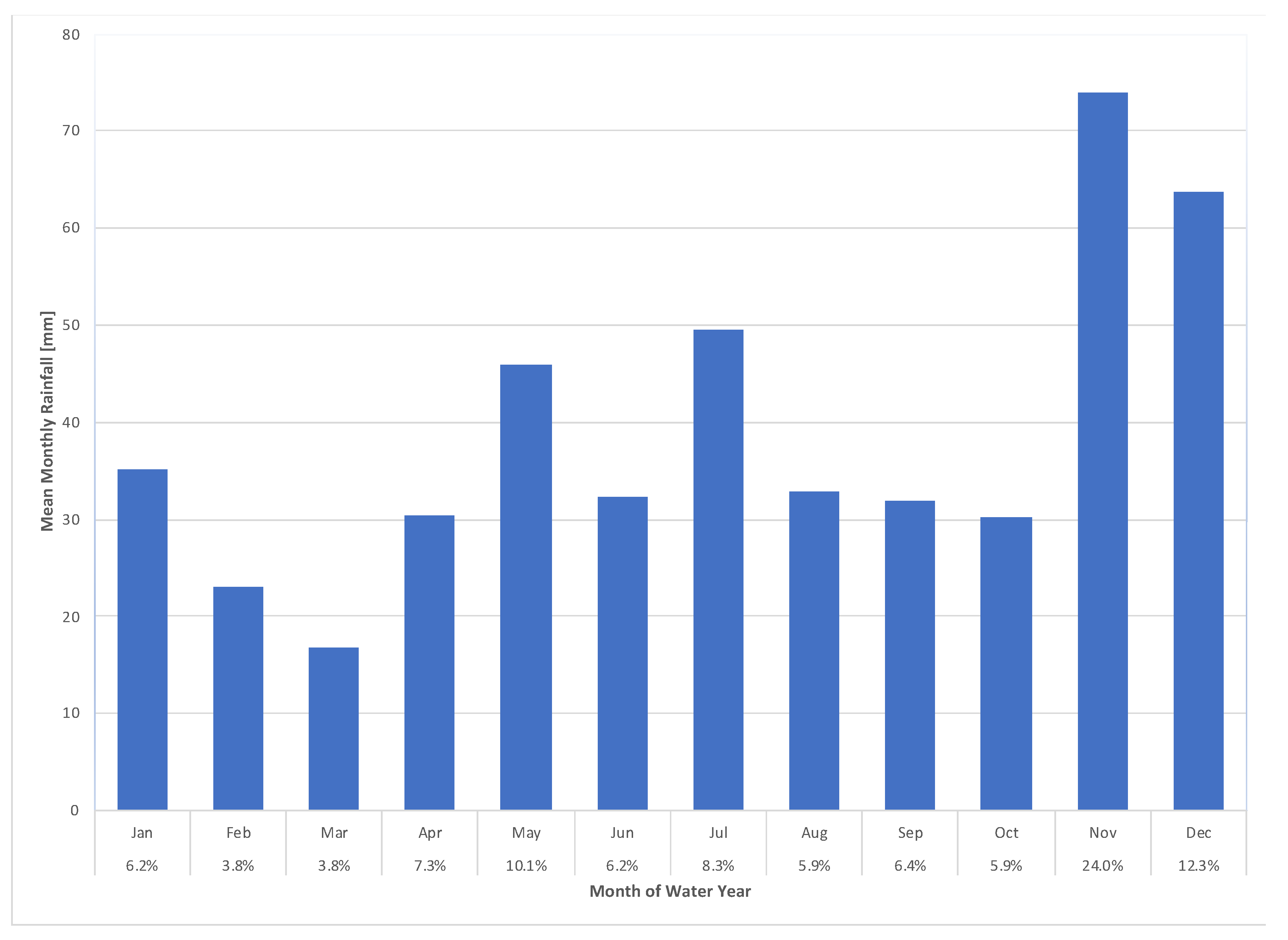
Rainfall Distribution
3.5. Streamflow and Water Level Data Description
3.5.1. Water Level
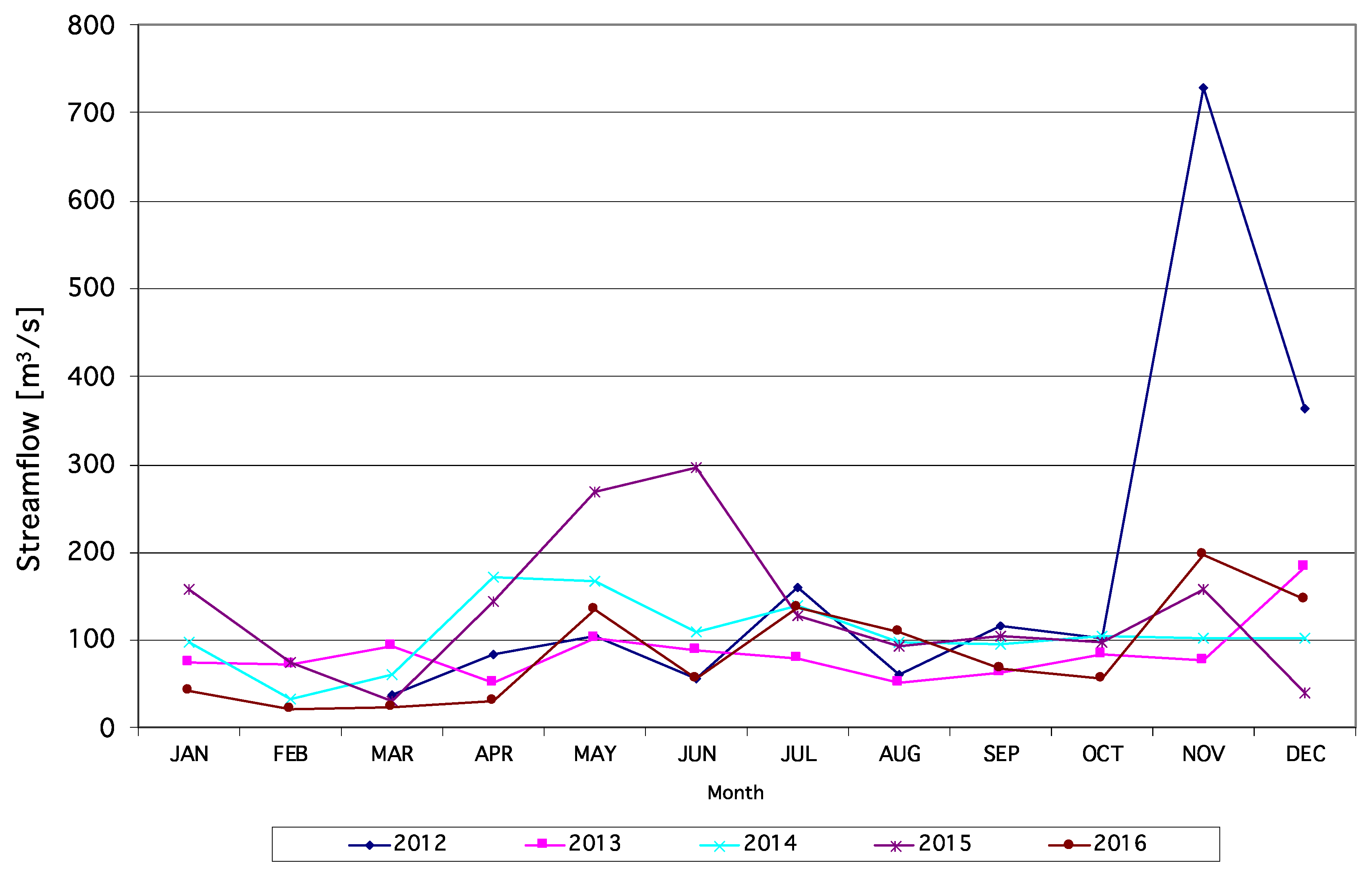
3.5.2. Streamflow Distribution
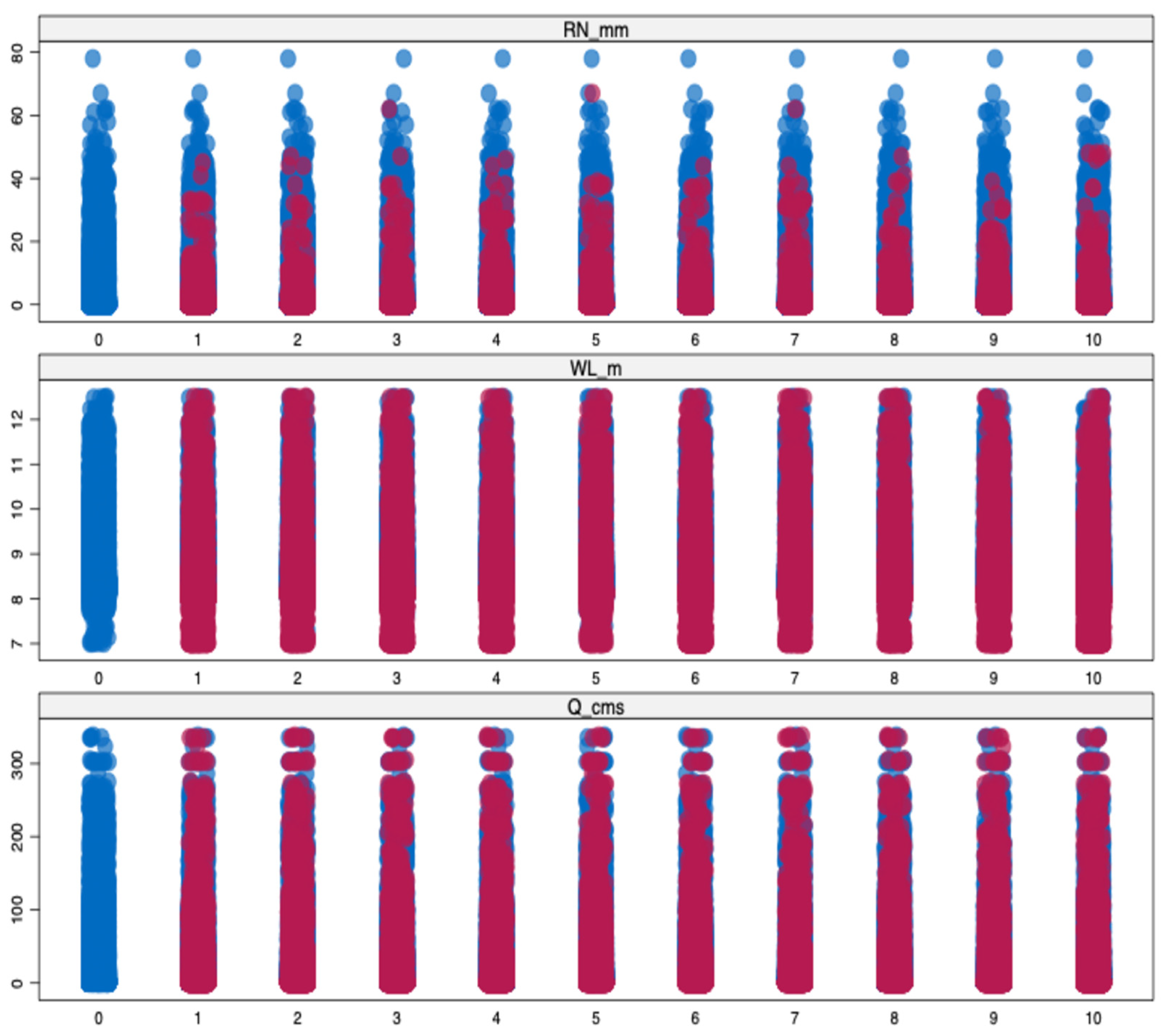
3.6. Hydrologic Record Reconstruction
Data Reconstruction Results
4. ABM Experimental Setting
4.1. Hydrologic Information Extraction
4.2. Storm Episode Selection
- 1.
- Storm Depth: The storms under consideration must be so intense as to cause flooding. However, because genuine hydro-records are now sparse, knowledge that might correlate precise streamflow data to the timing of a future flood might be challenging to acquire; so, it is assumed that only the documented maximum heights produced floodwaters.
- 2.
- Storm Duration:
- For a downpour to be replicated as a storm event, it must be visible in the hydrologic dataset.
- Preceding and antecedent flow conditions must be sufficiently low to be assigned to the base flow during these times, disregarding the antecedent soil moisture.
- The extent of flood days is verified using residents’ and precipitation records.
- 3.
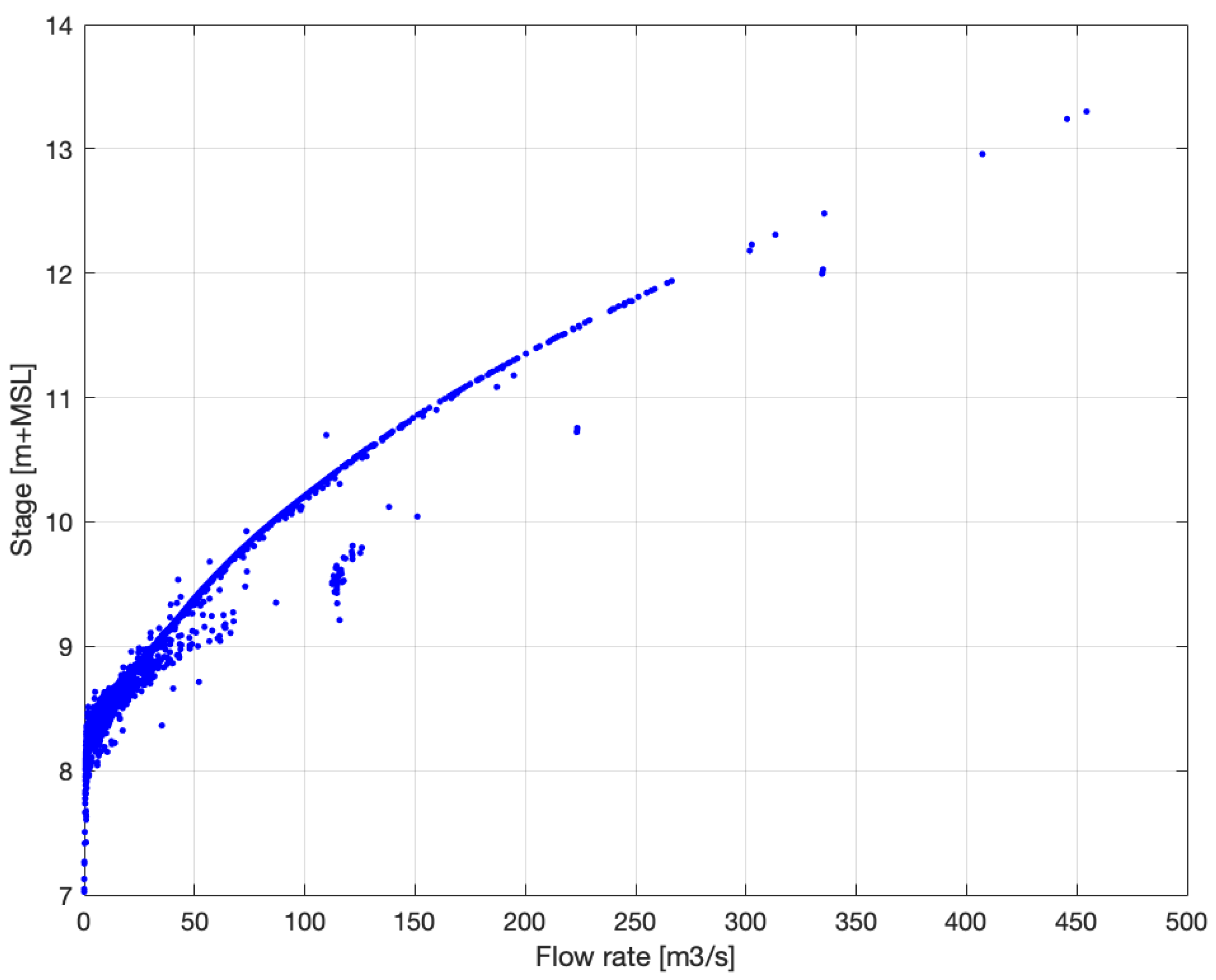
- Storm Period: Using the given data, linking storms to the computed rating curve shown in Figure 10 should be possible. This ensures that the modeling approach is accurate and matches the river’s present hydraulics (i.e., channel shape).
- 4.
- Data Accuracy: Because the hydrologic database stores all its data electronically, outliers, inconsistent records, data gaps, and missing values can produce errors in the results. Therefore, each instance of the hydrograph should be related to the dynamics of active physical processes.
- Rainstorm intensity
- Rainstorm duration
- Air temperature
- Wind speed
- Kind of soil type
- Land usage
- The slope of the basin
- Riverbank (slope)
- Channel configuration
- Geospatial and climate differences
- The amount of vegetation and the proportion of impervious surfaces
4.3. ABM-Driven Streamflow Simulation
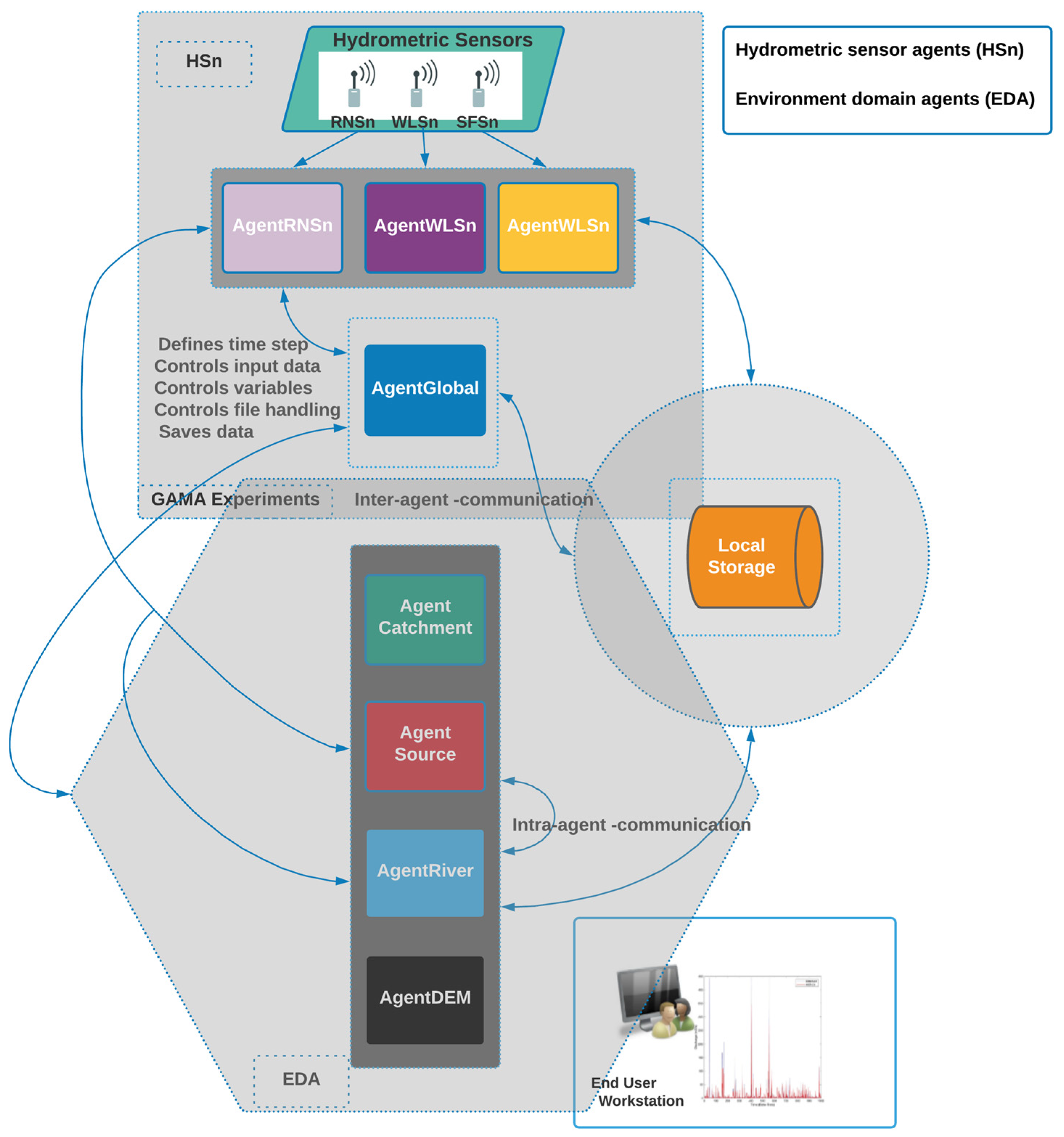
4.3.1. ABM Environment Selection
- Hydrometric sensor agents (HSn): Due to technical constraints, the hydrometric station’s three sensors collect data from simulated document files. Future efforts will pursue real-time data tests.
- The role of the rainfall sensor agent (AgentRNSn) is to record, aggregate, and provide river agent sources with real-time incoming rain data readings.
- The water level sensor agent’s (AgentWLSn) job collects, aggregates, and provides the river agent with real-time incoming river surface–water level data.
- The role of the streamflow sensor agent (AgentSFSn) is to receive, aggregate, and provide the river agent with real-time inflow flow data on discharge derived from field flow meter sensor data.
| Algorithm 1. Hydrometric Sensor Agents (HSn). Details of the pseudocode for initializing and defining the roles of hydrometric sensor agents within the agent-based model. |
| 1: Agent HydrometricSensor: 2: type: Rainfall, WaterLevel, Streamflow 3: data source: SimulatedDocumentFiles 4: for Every time step,… do 5: BehaviorCollect data(): 6: for behaviorcollect data(): do 7: if type == Rainfall then 8: AgentRNSn.collect rainfall data() 9: behavior collect rainfall data(): 10: data = read data from simulated file() 11: aggregate data(data) 12: provide data to river agent(data) 13: else if type == WaterLevel: then 14: AgentWLSn.collect water level data() 15: behavior collect water level data(): 16: data = read data from simulated file() 17: aggregate data(data) 18: provide data to river agent(data) 19: else if type == Streamflow: then 20: AgentSFSn.collect streamflow data() 21: behavior collect streamflow data(): 22: data = read data from simulated file() 23: aggregate data(data) 24: provide data to river agent(data) 25: end if 26: end for 27: end for |
- Environment domain agents (EDA): The catchment environment comprises four agents in addition to the default global agent created by GAMA. See Algorithm 2 for an overview of the script.
- Catchment agent (AgentCatchment): The static agent simulates the Medio River catchment with specific parameters for the area, catchment hierarchy, nearby sub-catchments, drainage outlet, main channel, rivers, and monitoring stations. These characteristics help determine the gradient behavior of the catchment and enable interaction with the river agent for water transport and exchange.
- Water source agent (AgentSource): The hydrologic agent manages river flow by adjusting the water supply based on flow and precipitation data at the start of the simulation. Source agents are linked to river inlets and are directed to supply a predetermined quantity of water based on the input volume, flow, and precipitation data.
- River network agent (AgentRiver): The river agent is distributed among sub-catchment locations and moves water within the catchment. It calculates the volume of water in a river using information from the precipitation series. Water exchange between river reach segments in neighboring catchments is influenced by precipitation volume and frequency, resulting in flow routing. According to Neitsch [86] et al., the AgentRiver manages water flow in the river systems by computing flow rates and estimating water levels. This is achieved by overseeing the global agent and responding to the requests.
- Terrain elevation agent (AgentDEM): The “agentified” DEM is a unique form of an agent class with a grid structure. It is a static agent with no mobility during the simulation time. It represents the catchment terrain elevation and is responsible for the overall gradient profile.
| Algorithm 2. Define Environment Domain Agents (EDA). Presents the pseudocode for initializing and defining the actions of the environment domain agents. These include the catchment agent, which simulates the Medio River catchment and interacts with the river agent; the water source agent, which manages river flow; the river network agent, which distributes water and calculates volumes within the catchment; and the terrain elevation agent, which represents the catchment terrain and gradient profile. |
|
- Global agent (AgentGlobal): Defined in the Algorithm in Algorithm 3, the global species in GAMA is an automatically created agent representing the entire environment. It describes all variables, parameters, actions, and behaviors that regulate the world and oversees and manages all other agents within the system. It also archives the data generated during the simulations, acting as a supervisory agent.
| Algorithm 3. Define Global Agent (AgentGlobal). This algorithm outlines the pseudocode for the global agent, which is an automatically created entity in the GAMA platform that represents the entire simulation environment. |
|
4.3.2. ABM Platform Feature Engineering and Input Parameters
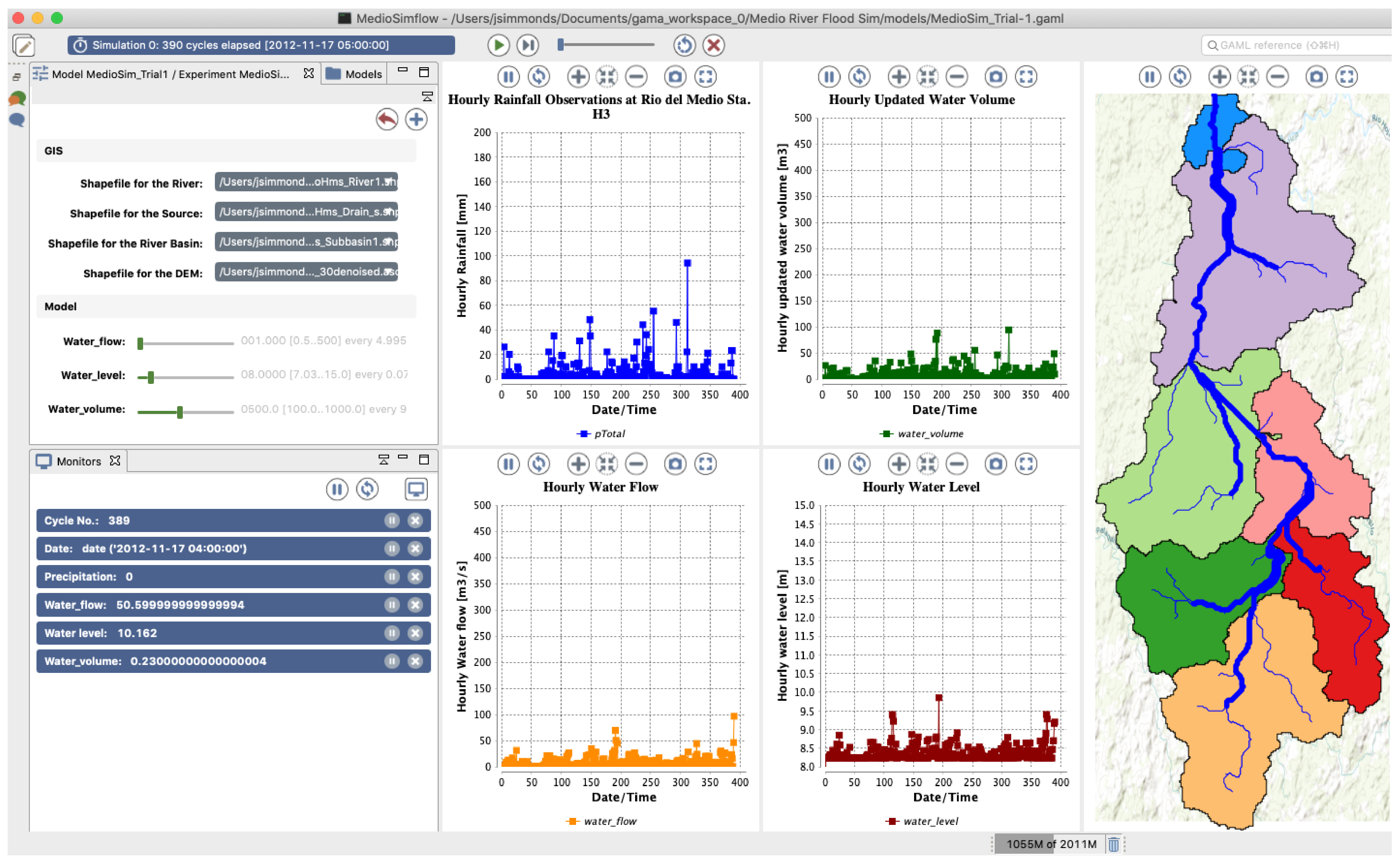
- Base Map: The model simulates the Medio River Catchment using a section of the Donoso District in Colon City selected from OpenStreetMap. This area was imported into QGIS as a shapefile and utilized in the GAMA platform to replicate the catchment area shown in Figure 15.
- Precipitation: The modeling experiment includes essential precipitation and hydrometric components: observed 1-h interval time-series data for streamflow inundations in the Medio River, lateral flows, and flood waves from nearby rivers. These flood waves contribute to intense flooding along the stream banks and floodplain regions. Additionally, the dataset includes time-series data for observed streamflow and surface water height.
5. Results
5.1. ABM: Dry-Run Flow Simulation
5.2. ABM: Calibration Setup
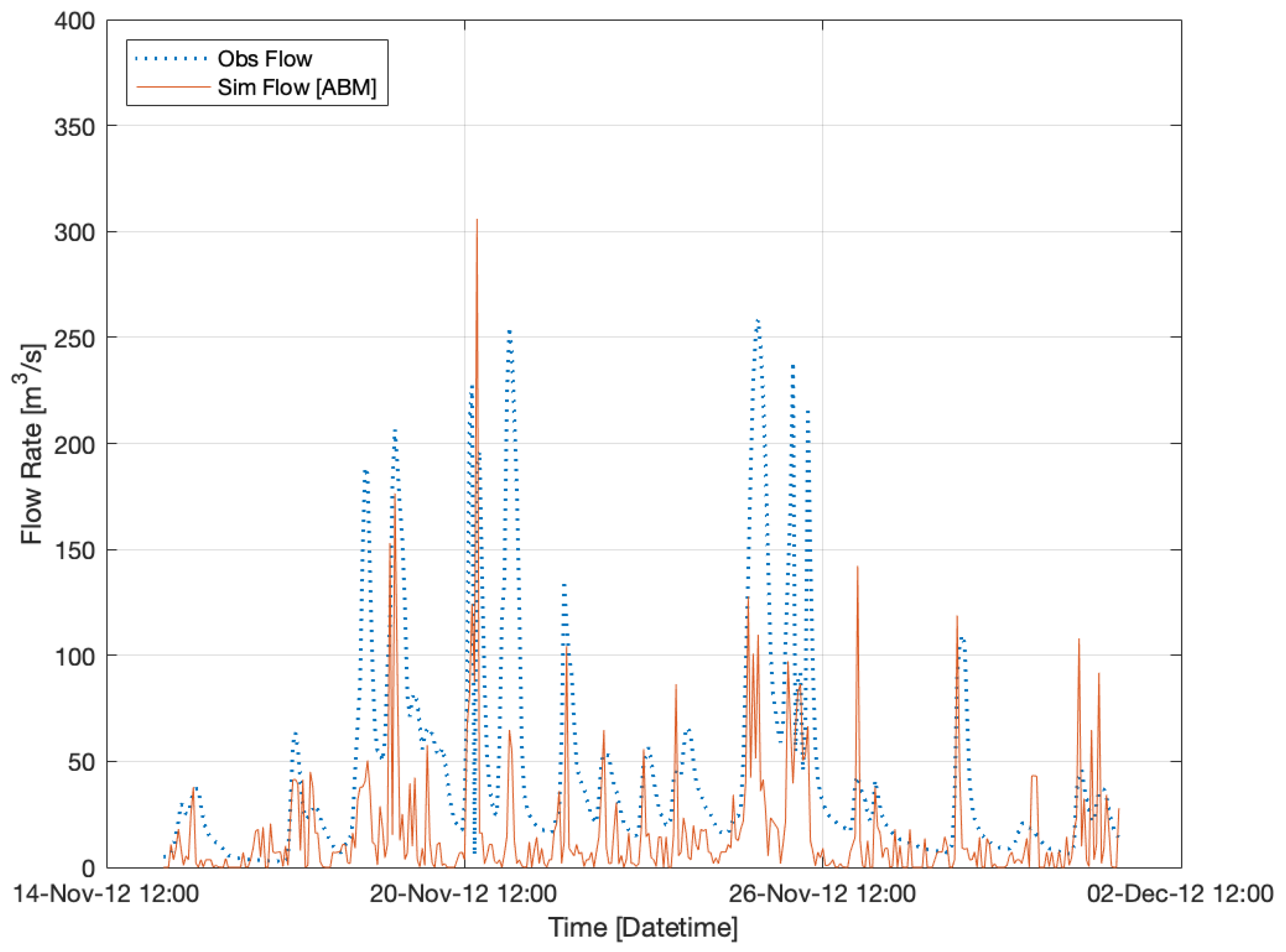
5.2.1. ABM: Calibration, Comparing Scenario-Based Simulation
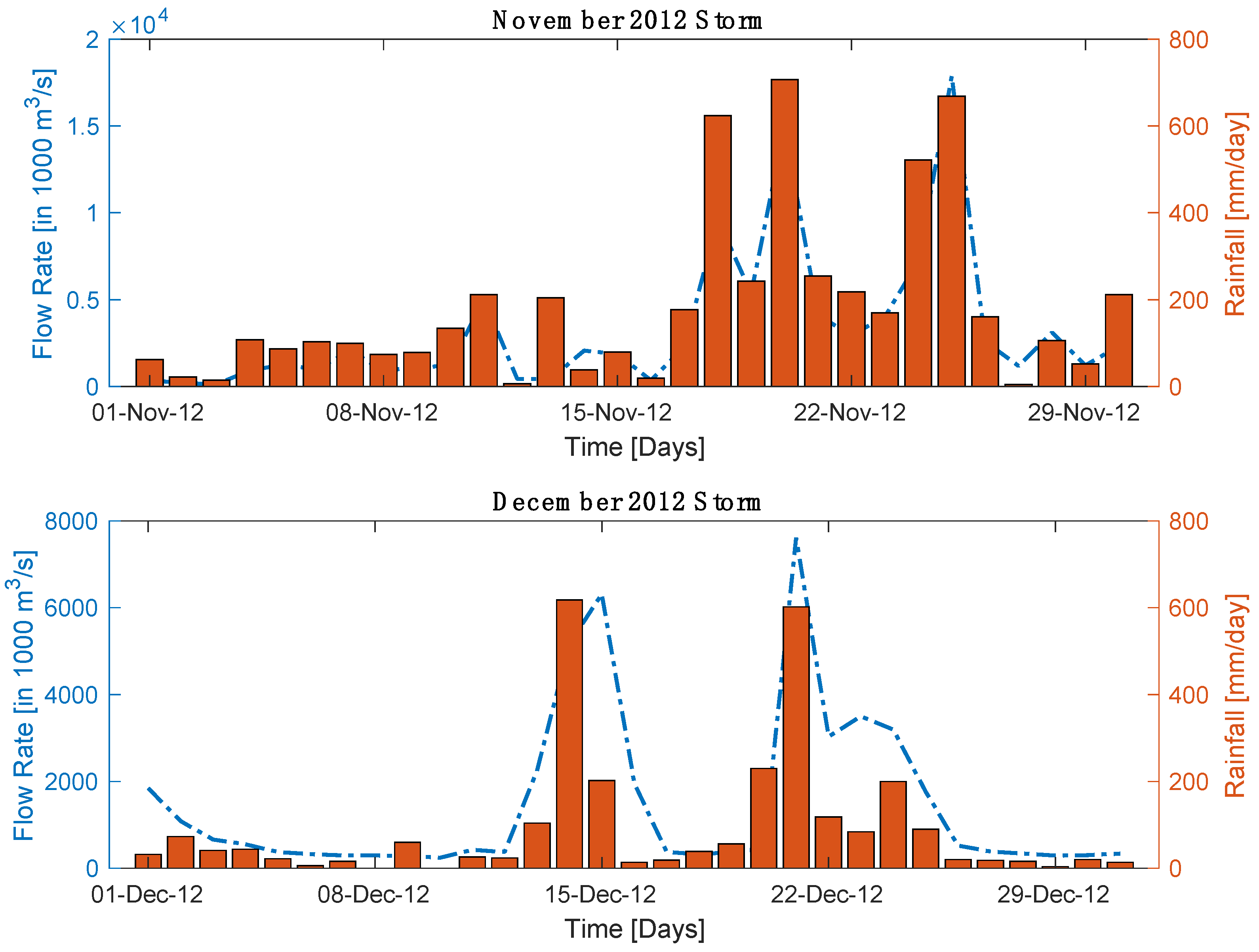
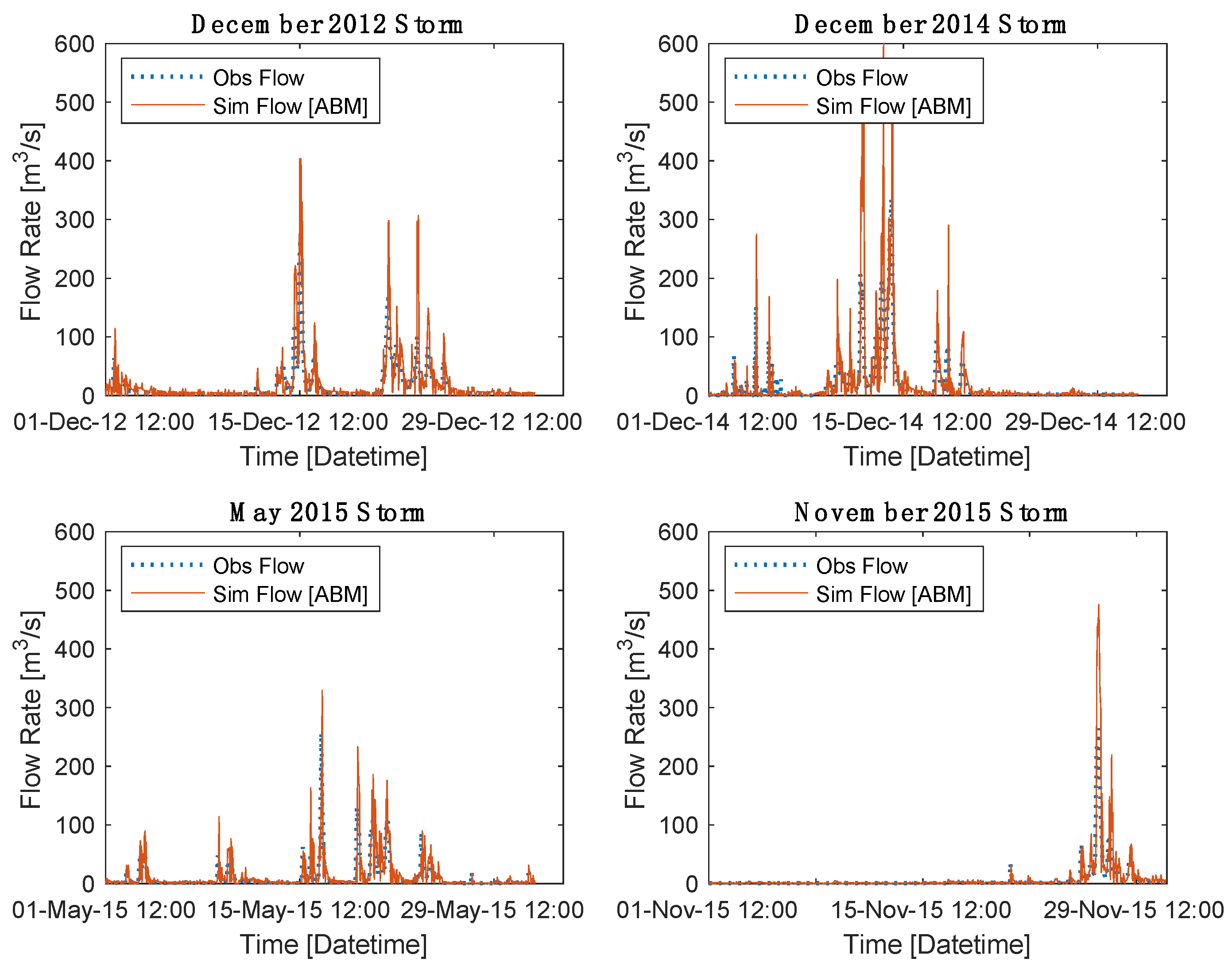
5.2.2. ABM: Validation, Comparing Single Storm-Based Simulation
- Data with a high degree of variability
- Distinctive data distribution shape
- Lack of linearity
- Exceptions
- The sample’s features are distinct
- F-measures
6. Discussion
7. Conclusions
- Enhanced forecasting and control of flooding incidents.
- 2.
- Improved comprehension of how water interacts with different processes.
- 3.
- Use in Studies on the Impact of Climate Change
- 4.
- Integration with Infrastructure Development and Urban Planning.
8. Future Work Plans
- -
- Incorporating more complex hydrological processes, such as adding meteorological variables, groundwater interactions, and riverbed processes, into the model to increase accuracy.
- -
- Testing the model on different tropical river basins with varying characteristics, such as topography, geology, and vegetation cover, to assess its applicability and generalizability.
- -
- Incorporating uncertainty and sensitivity analysis to identify the most critical parameters and variables that affect the model’s outputs.
- -
- Creating an on-demand tracking system to continually update the model inputs and outputs for flooding projections and early notification systems may be helpful.
- -
- Collaborating with stakeholders, such as local communities, water managers, and policymakers, to integrate their perspectives and knowledge into the model’s development and implementation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FloodList Database. 2022. Available online: https://floodlist.com/ (accessed on 19 July 2022).
- Eckstein, D.; Künzel, V.; Schäfer, L. Global Climate Risk Index 2021: Who Suffers Most from Extreme Weather Events; Germanwatch: Bonn, Germany, 2021; pp. 2000–2019. [Google Scholar]
- Adikari, Y.; Yoshitani, J. Global Trends in Water-Related Disasters: An Insight for Policymakers; World Water Assessment Programme Side Publication Series, Insights; The United Nations, UNESCO: Paris, France; International Centre for Water Hazard and Risk Management (ICHARM): Tsukuba, Japan, 2009; pp. 1–24. [Google Scholar]
- Wieriks, K.; Vlaanderen, N. Water-related disaster risk reduction: Time for preventive action! Position paper of the High Level Experts and Leaders Panel (HELP) on water and disasters. Water Policy 2015, 17 (Suppl. S1), 212–219. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A review on hydrological models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Abdulkareem, J.; Pradhan, B.; Sulaiman, W.; Jamil, N. Review of studies on hydrological modelling in Malaysia. Model. Earth Syst. Environ. 2018, 4, 1577–1605. [Google Scholar] [CrossRef]
- Jain, S.K.; Mani, P.; Jain, S.K.; Prakash, P.; Singh, V.P.; Tullos, D.; Kumar, S.; Agarwal, S.P.; Dimri, A.P. A Brief review of flood forecasting techniques and their applications. Int. J. River Basin Manag. 2018, 16, 329–344. [Google Scholar] [CrossRef]
- Pandi, D.; Kothandaraman, S.; Kuppusamy, M. Hydrological models: A review. Int. J. Hydrol. Sci. Technol. 2021, 12, 223–242. [Google Scholar] [CrossRef]
- Peel, M.C.; McMahon, T.A. Historical development of rainfall-runoff modeling. Wiley Interdiscip. Rev. Water 2020, 7, e1471. [Google Scholar] [CrossRef]
- Sitterson, J.; Knightes, C.; Parmar, R.; Wolfe, K.; Avant, B.; Muche, M. An Overview of Rainfall-Runoff Model Types; U.S. Environmental Protection Agency: Washington, DC, USA, 2018. [Google Scholar]
- Abudu, S.; Cui, C.-L.; King, J.P.; Abudukadeer, K. Comparison of performance of statistical models in forecasting monthly streamflow of Kizil River, China. Water Sci. Eng. 2010, 3, 269–281. [Google Scholar]
- Kan, G.; He, X.; Li, J.; Ding, L.; Hong, Y.; Zhang, H.; Liang, K.; Zhang, M. Computer aided numerical methods for hydrological model calibration: An overview and recent development. Arch. Comput. Methods Eng. 2019, 26, 35–59. [Google Scholar] [CrossRef]
- Veiga, V.B.; Hassan, Q.K.; He, J. Development of flow forecasting models in the Bow River at Calgary, Alberta, Canada. Water 2014, 7, 99–115. [Google Scholar] [CrossRef]
- Wang, W. Stochasticity, Nonlinearity and Forecasting of Streamflow Processes; IOS Press: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Wang, W.; Vrijling, J.; Van Gelder, P.H.; Ma, J. Testing for nonlinearity of streamflow processes at different timescales. J. Hydrol. 2006, 322, 247–268. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, X.; Qin, H. A data-driven model based on Fourier transform and support vector regression for monthly reservoir inflow forecasting. J. Hydro-Environ. Res. 2018, 18, 12–24. [Google Scholar] [CrossRef]
- Ji, J.; Choi, C.; Yu, M.; Yi, J. Comparison of a data-driven model and a physical model for flood forecasting. WIT Trans. Ecol. Environ. 2012, 159, 133–142. [Google Scholar]
- Khatibi, R.; Ghorbani, M.A.; Kashani, M.H.; Kisi, O. Comparison of three artificial intelligence techniques for discharge routing. J. Hydrol. 2011, 403, 201–212. [Google Scholar] [CrossRef]
- Shrestha, R.R.; Nestmann, F. Physically based and data-driven models and propagation of input uncertainties in river flood prediction. J. Hydrol. Eng. 2009, 14, 1309–1319. [Google Scholar] [CrossRef]
- Borshchev, A.; Filippov, A. From system dynamics and discrete event to practical agent based modeling: Reasons, techniques, tools. In Proceedings of the 22nd International Conference of the System Dynamics Society, Oxford, England, 25–29 July 2004; Citeseer: Princeton, NJ, USA, 2004. [Google Scholar]
- Chan, S. Complex adaptive systems. In ESD.83 Research Seminar in Engineering Systems; MIT: Cambridge, MA, USA, 2001. [Google Scholar]
- Heath, B.L. The History, Philosophy, and Practice of Agent-Based Modeling and the Development of the Conceptual Model for Simulation Diagram. Ph.D. Thesis, Wright State University, Dayton, OH, USA, 2010. [Google Scholar]
- Mckie, D. Complexity—The Emerging Science at the Edge of Order and Chaos—Waldrop, M.M. Media Cult. Soc. 1994, 16, 693–698. [Google Scholar] [CrossRef]
- Agre, P.; Rosenschein, S.J. Computational Theories of Interaction and Agency; Mit Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Steinbacher, M.; Raddant, M.; Karimi, F.; Camacho Cuena, E.; Alfarano, S.; Iori, G.; Lux, T. Advances in the agent-based modeling of economic and social behavior. SN Bus. Econ. 2021, 1, 99. [Google Scholar] [CrossRef] [PubMed]
- Axtell, R.L.; Farmer, J.D. Agent-based modeling in economics and finance: Past, present, and future. J. Econ. Lit. 2022, 60, 1–101. [Google Scholar]
- Niazi, M.; Hussain, A. Agent-based computing from multi-agent systems to agent-based models: A visual survey. Scientometrics 2011, 89, 479–499. [Google Scholar] [CrossRef]
- Macal, C.M.; North, M.J. Tutorial on agent-based modeling and simulation part 2: How to model with agents. In Proceedings of the 2006 Winter Simulation Conference, Monterey, CA, USA, 3–6 December 2006; Volume 1–5, pp. 73–83. [Google Scholar]
- Macal, C.M. Tutorial on Agent-Based Modeling and Simulation: Abm Design for the Zombie Apocalypse. In Proceedings of the 2018 Winter Simulation Conference (Wsc), Gothenburg, Sweden, 9–12 December 2018; pp. 207–221. [Google Scholar]
- Macal, C.M.; North, M.J. Tutorial on agent-based modelling and simulation. J. Simul. 2010, 4, 151–162. [Google Scholar] [CrossRef]
- Taylor, S.J.E.; Anagnostou, A.; Kiss, T.; Terstyanszky, G.; Kacsuk, P.; Fantini, N. A Tutorial on Cloud Computing for Agent-Based Modeling & Simulation with Repast. In Proceedings of the 2014 Winter Simulation Conference (Wsc), Savannah, GA, USA, 7–10 December 2014; pp. 192–206. [Google Scholar]
- Macal, C.M.; North, M.J. Tutorial on agent-based modeling and simulation. In Proceedings of the Winter Simulation Conference, Orlando, FL, USA, 4 December 2005; IEEE: Piscataway, NJ, USA, 2005. [Google Scholar]
- De Almeida Falbo, R. SABiO: Systematic Approach for Building Ontologies. In Proceedings of the Onto.Com/odise@Fois. 2014, Rio de Janeiro, Brazil, 21 September 2014. [Google Scholar]
- De Nicola, A.; Missikoff, M.; Navigli, R. A software engineering approach to ontology building. Inf. Syst 2009, 34, 258–275. [Google Scholar] [CrossRef]
- Uschold, M.; Gruninger, M. Ontologies: Principles, methods and applications. Knowl. Eng. Rev. 1996, 11, 93–136. [Google Scholar] [CrossRef]
- Uschold, M.; King, M. Towards a Methodology for Building Ontologies; AIAI-TR 183; Artificial Intelligence Applications Institute, University of Edinburgh: Edinburgh, UK, 1995; 13p. [Google Scholar]
- Guarino, N. Formal Ontology in Information Systems: Proceedings of the First International Conference (FOIS’98), June 6–8, Trento, Italy; Frontiers in Artificial Intelligence and Applications; IOS Press: Amsterdam, The Netherlands, 1998; 337p. [Google Scholar]
- Noy, N.F.; McGuinness, D.L. Ontology Development 101: A Guide to Creating Your First Ontology. 2001. Available online: http://protege.stanford.edu/publications (accessed on 18 June 2024).
- Shurville, S. Model driven architecture and ontology development. Interact. Learn. Environ. 2007, 15, 96–99. [Google Scholar]
- Neches, R.; Fikes, R.; Finin, T.; Gruber, T.; Patil, R.; Senator, T.; Swartout, W.R. Enabling Technology for Knowledge Sharing. AI Mag. 1991, 12, 36–56. [Google Scholar]
- Agresta, A.; Fattoruso, G.; Pollino, M.; Pasanisi, F.; Tebano, C.; De Vito, S.; Di Francia, G. An Ontology Framework for Flooding Forecasting. In Computational Science and Its Applications–ICCSA 2014: 14th International Conference, Guimarães, Portugal, June 30–July 3, 2014, Proceedings, Part IV; Springer International Publishing: Cham, Switzerland, 2014; Volume 8582, pp. 417–428. [Google Scholar]
- Sermet, Y.; Demir, I. Towards an information centric flood ontology for information management and communication. Earth Sci Inf. 2019, 12, 541–551. [Google Scholar] [CrossRef]
- Wang, C.; Chen, Z.Q.; Chen, N.C.; Wang, W. A Hydrological Sensor Web Ontology Based on the SSN Ontology: A Case Study for a Flood. Isprs Int. J. Geo-Inf. 2018, 7, 2. [Google Scholar] [CrossRef]
- Nikraz, M.; Caire, G.; Bahri, P.A. A methodology for the analysis and design of multi-agent systems using JADE. Int. J. Comput. Syst. Sci. Eng. 2006, 21, 1–40. [Google Scholar]
- Amouroux, E.; Chu, T.-Q.; Boucher, A.; Drogoul, A. GAMA: An environment for implementing and running spatially explicit multi-agent simulations. In Proceedings of the Pacific Rim International Conference on Multi-Agents, Bangkok, Thailand, 21–23 November 2007; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Taillandier, P.; Gaudou, B.; Grignard, A.; Huynh, Q.-N.; Marilleau, N.; Caillou, P.; Philippon, D.; Drogoul, A. Building, composing and experimenting complex spatial models with the GAMA platform. GeoInformatica 2019, 23, 299–322. [Google Scholar] [CrossRef]
- Simmonds, J.; Gómez, J.A.; Ledezma, A. The role of agent-based modeling and multi-agent systems in flood-based hydrological problems: A brief review. J. Water Clim. Change 2020, 11, 1580–1602. [Google Scholar] [CrossRef]
- Brouwers, L.; Boman, M. A computational agent model of flood management strategies. In Regional Development: Concepts, Methodologies, Tools, and Applications; IGI Global: Hershey, PA, USA, 2012; pp. 522–534. [Google Scholar]
- Anantsuksomsri, S.; Tontisirin, N. Agent-based modeling and disaster management. J. Archit./Plan. Res. Stud. (JARS) 2013, 10, 1–14. [Google Scholar]
- Coates, G.; Hawe, G.; Wright, N.; Ahilan, S. Agent-based modelling and inundation prediction to enable the identification of businesses affected by flooding. WIT Trans. Ecol. Environ. 2014, 184, 13–22. [Google Scholar]
- Berglund, E.Z. Using agent-based modeling for water resources planning and management. J. Water Resour. Plan. Manag. 2015, 141, 04015025. [Google Scholar] [CrossRef]
- Yang, L.E.; Scheffran, J.; Süsser, D.; Dawson, R.; Chen, Y.D. Assessment of flood losses with household responses: Agent-based simulation in an urban catchment area. Environ. Model. Assess. 2018, 23, 369–388. [Google Scholar] [CrossRef]
- Condro, A.A.; Widagdo, I.B. Katara: Model hidrologi berbasis agen (agent-based modelling) untuk analisis banjir di das ciliwung. J. Meteorol. Klimatol. Dan Geofis. 2019, 4, 1–7. [Google Scholar] [CrossRef]
- Shirvani, M.; Kesserwani, G.; Richmond, P. Agent-based simulator of dynamic flood-people interactions. J. Flood Risk Manag. 2019, 14, e12695. [Google Scholar] [CrossRef]
- Huber, L.; Bahro, N.; Leitinger, G.; Tappeiner, U.; Strasser, U. Agent-Based Modelling of a Coupled Water Demand and Supply System at the Catchment Scale. Sustainability 2019, 11, 6178. [Google Scholar] [CrossRef]
- Farias, G.P.; Leitzke, B.; Born, M.; Aguiar, M.S.d.; Adamatti, D.F. Water Resources Analysis: An Approach based on Agent-Based Modeling. RITA 2020, 27, 81–95. [Google Scholar] [CrossRef]
- Strahler, A.N. Hypsometric (area-altitude) analysis of erosional topography. Geol. Soc. Am. Bull. 1952, 63, 1117–1142. [Google Scholar] [CrossRef]
- MPSA. Environmental Impact Assessment Study; MPSA: Bloomington, IN, USA, 2010. [Google Scholar]
- Mockus, V. National Engineering Handbook; US Soil Conservation Service: Washington, DC, USA, 1964; Volume 4. [Google Scholar]
- Wieder, W.; Boehnert, J.; Bonan, G.; Langseth, M. Regridded Harmonized World Soil Database v1.2; ORNL DAAC: Oak Ridge, TN, USA, 2014. [Google Scholar]
- Sene, K. Flood Warning. In Flash Floods; Springer: Berlin/Heidelberg, Germany, 2013; pp. 169–198. [Google Scholar]
- Simmonds, J.; Gómez, J.A.; Ledezma, A. Data Preprocessing to Enhance Flow Forecasting in a Tropical River Basin. In Proceedings of the Engineering Applications of Neural Networks: 18th International Conference, EANN 2017, Athens, Greece, 25–27 August 2017; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Little, R.J.; Rubin, D.B. Statistical Analysis with Missing Data; John Wiley & Sons: Hoboken, NJ, USA, 2019; Volume 793. [Google Scholar]
- Wilkinson, L. Statistical methods in psychology journals: Guidelines and explanations. Am. Psychol. 1999, 54, 594. [Google Scholar] [CrossRef]
- Bodner, T.E. Missing data: Prevalence and reporting practices. Psychol. Rep. 2006, 99, 675–680. [Google Scholar] [CrossRef] [PubMed]
- Peugh, J.L.; Enders, C.K. Missing data in educational research: A review of reporting practices and suggestions for improvement. Rev. Educ. Res. 2004, 74, 525–556. [Google Scholar] [CrossRef]
- Rubin, D. Inference and missing data. Biometrika 1976, 63, 581–592. [Google Scholar] [CrossRef]
- Gao, Y.; Merz, C.; Lischeid, G.; Schneider, M. A review on missing hydrological data processing. Environ. Earth Sci. 2018, 77, 47. [Google Scholar] [CrossRef]
- Hamzah, F.B.; Hamzah, F.M.; Razali, S.M.; Samad, H. A comparison of multiple imputation methods for recovering missing data in hydrological studies. Civ. Eng. J. 2021, 7, 1608–1619. [Google Scholar] [CrossRef]
- Hamzah, F.B.; Mohamad Hamzah, F.; Mohd Razali, S.F.; El-Shafie, A. Multiple imputations by chained equations for recovering missing daily streamflow observations: A case study of Langat River basin in Malaysia. Hydrol. Sci. J. 2022, 67, 137–149. [Google Scholar] [CrossRef]
- Umar, N.; Gray, A. Comparing single and multiple imputation approaches for missing values in univariate and multivariate water level data. Water 2023, 15, 1519. [Google Scholar] [CrossRef]
- Lopucki, R.; Kiersztyn, A.; Pitucha, G.; Kitowski, I. Handling missing data in ecological studies: Ignoring gaps in the dataset can distort the inference. Ecol. Model. 2022, 468, 109964. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- van Buuren, S.; Groothuis-Oudshoorn, K. Mice: Multivariate Imputation by Chained Equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef]
- Jang, J.-H. An advanced method to apply multiple rainfall thresholds for urban flood warnings. Water 2015, 7, 6056–6078. [Google Scholar] [CrossRef]
- Blanc, J.; Hall, J.; Roche, N.; Dawson, R.; Cesses, Y.; Burton, A.; Kilsby, C. Enhanced efficiency of pluvial flood risk estimation in urban areas using spatial–temporal rainfall simulations. J. Flood Risk Manag. 2012, 5, 143–152. [Google Scholar] [CrossRef]
- Cheng, C.S.; Li, Q.; Li, G.; Auld, H. Climate change and heavy rainfall-related water damage insurance claims and losses in Ontario, Canada. J. Water Resour. Prot. 2012, 4, 49–62. [Google Scholar] [CrossRef]
- Hurford, A.; Parker, D.; Priest, S.; Lumbroso, D. Validating the return period of rainfall thresholds used for E xtreme R ainfall A lerts by linking rainfall intensities with observed surface water flood events. J. Flood Risk Manag. 2012, 5, 134–142. [Google Scholar] [CrossRef]
- Priest, S.J.; Parker, D.J.; Hurford, A.P.; Walker, J.; Evans, K. Assessing options for the development of surface water flood warning in England and Wales. J Environ. Manag. 2011, 92, 3038–3048. [Google Scholar] [CrossRef] [PubMed]
- Słownik, W. International Meteorological Vocabulary, 1992; WMO/OMM/IMGW: Geneva, Switzerland, 1992; p. 182. [Google Scholar]
- Lam, H.; Lam, C.Y.; Wass, S.; Dupuy, C.; Chavaux, F.; Kootval, H. Guidelines on Cross-Border Exchange of Warnings; WMO/OMM/IMGW: Geneva, Switzerland, 2003; p. 182. [Google Scholar]
- Sofiati, I.; Nurlatifah, A. The prediction of rainfall events using WRF (weather research and forecasting) model with ensemble technique. In Proceedings of IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019. [Google Scholar]
- Dunkerley, D. Rain event properties in nature and in rainfall simulation experiments: A comparative review with recommendations for increasingly systematic study and reporting. Hydrol. Process. Int. J. 2008, 22, 4415–4435. [Google Scholar] [CrossRef]
- Dunkerley, D.L. How do the rain rates of sub-event intervals such as the maximum 5-and 15-min rates (I5 or I30) relate to the properties of the enclosing rainfall event? Hydrol. Process. 2010, 24, 2425–2439. [Google Scholar] [CrossRef]
- Mendham, P.; Clarke, T. Macsim: A simulink enabled environment for multi-agent system simulation. IFAC Proc. Vol. 2005, 38, 325–329. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Champaign, IL, USA, 1949. [Google Scholar]
- Crooks, A.; Castle, C.; Batty, M. Key challenges in agent-based modelling for geo-spatial simulation. Comput. Environ. Urban Syst. 2008, 32, 417–430. [Google Scholar] [CrossRef]
- Crooks, A.T.; Heppenstall, A.J. Introduction to agent-based modelling. In Agent-Based Models of Geographical Systems; Springer: Berlin/Heidelberg, Germany, 2011; pp. 85–105. [Google Scholar]
- Klügl, F. A validation methodology for agent-based simulations. In Proceedings of the 2008 ACM Symposium on Applied Computing, Fortaleza, Brazil, 16–20 March 2008. [Google Scholar]
- Parry, H.R. Agent-based modeling, large-scale simulations. In Complex Social and Behavioral Systems: Game Theory and Agent-Based Models; Springer: Berlin/Heidelberg, Germany, 2020; pp. 913–926. [Google Scholar]
- Taillandier, P.; Vo, D.-A.; Amouroux, E.; Drogoul, A. GAMA: A simulation platform that integrates geographical information data, agent-based modeling and multi-scale control. In Proceedings of the Principles and Practice of Multi-Agent Systems: 13th International Conference, PRIMA 2010, Kolkata, India, 12–15 November 2010; Revised Selected Papers 13. Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Vo, D.-A.; Drogoul, A.; Zucker, J.-D. An operational meta-model for handling multiple scales in agent-based simulations. In Proceedings of the 2012 IEEE RIVF International Conference on Computing & Communication Technologies, Research, Innovation, and Vision for the Future, Ho Chi Minh City, Vietnam, 27 February–1 March 2012; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar]
- Khu, S.T.; Madsen, H. Multiobjective calibration with Pareto preference ordering: An application to rainfall-runoff model calibration. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Ngo, T.A.; See, L. Calibration and validation of agent-based models of land cover change. In Agent-Based Models of Geographical Systems; Springer: Berlin/Heidelberg, Germany, 2011; pp. 181–197. [Google Scholar]
- Rogers, A.; Von Tessin, P. Multi-objective calibration for agent-based models. In Proceedings of the 5th Workshop on Agent-Based Simulation, Lisbon, Portugal, 3–5 May 2004. [Google Scholar]
- Canessa, E.; Chaigneau, S. Calibrating agent-based models using a genetic algorithm. Stud. Inform. Control 2015, 24, 79–90. [Google Scholar] [CrossRef]
- Cockrell, C.; An, G. Genetic Algorithms for model refinement and rule discovery in a high-dimensional agent-based model of inflammation. bioRxiv 2019, 790394. [Google Scholar]
- Espinosa, O.B. A genetic algorithm for the calibration of a micro-simulation model. arXiv 2012, arXiv:1201.3456. [Google Scholar]
- Boes, J.; Migeon, F. Self-organizing multi-agent systems for the control of complex systems. J. Syst. Softw. 2017, 134, 12–28. [Google Scholar] [CrossRef]
- Caillou, P. Automated multi-agent simulation generation and validation. In Proceedings of the Principles and Practice of Multi-Agent Systems: 13th International Conference, PRIMA 2010, Kolkata, India, 12–15 November 2010; Revised Selected Papers 13. Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Lomuscio, A.; Qu, H.; Raimondi, F. MCMAS: An open-source model checker for the verification of multi-agent systems. Int. J. Softw. Tools Technol. Transf. 2017, 19, 9–30. [Google Scholar] [CrossRef]
- Oliveros, M.M.; Nagel, K. Automatic calibration of agent-based public transit assignment path choice to count data. Transp. Res. Part C Emerg. Technol. 2016, 64, 58–71. [Google Scholar] [CrossRef]
- Drchal, J.; Čertický, M.; Jakob, M. Data driven validation framework for multi-agent activity-based models. In Proceedings of the Multi-Agent Based Simulation XVI: International Workshop, MABS 2015, Istanbul, Turkey, 5 May 2015; Revised Selected Papers 16. Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Liu, Z.; Rexachs, D.; Epelde, F.; Luque, E. A simulation and optimization based method for calibrating agent-based emergency department models under data scarcity. Comput. Ind. Eng. 2017, 103, 300–309. [Google Scholar] [CrossRef]
- Duda, P.; Hummel, P.; Donigian, A., Jr.; Imhoff, J. BASINS/HSPF: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1523–1547. [Google Scholar] [CrossRef]
- Fonseca, A.; Ames, D.P.; Yang, P.; Botelho, C.; Boaventura, R.; Vilar, V. Watershed model parameter estimation and uncertainty in data-limited environments. Environ. Model. Softw. 2014, 51, 84–93. [Google Scholar] [CrossRef]
- Doyle, W.H.; Miller, J.E. Calibration of a Distributed Routing Rainfall-Runoff Model at Four Urban Sites Near Miami, Florida; US Geological Survey, Water Resources Division, Gulf Coast Hydroscience: Reston, VA, USA, 1980; Volume 80. [Google Scholar]
- Shade, P.J. Hydrology and Sediment Transport, Moanalua Valley; US Geological Survey: Oahu, HI, USA, 1984; Volume 84. [Google Scholar]
- Goodwin, L.D.; Leech, N.L. Understanding correlation: Factors that affect the size of R. J. Exp. Educ. 2006, 74, 249–266. [Google Scholar] [CrossRef]
- Gutierrez, J.C.T.; Adamatti, D.S.; Bravo, J.M. A new stopping criterion for multi-objective evolutionary algorithms: Application in the calibration of a hydrologic model. Comput. Geosci. 2019, 23, 1219–1235. [Google Scholar] [CrossRef]
- Herman, M.R.; Hernandez-Suarez, J.S.; Nejadhashemi, A.P.; Kropp, I.; Sadeghi, A.M. Evaluation of multi-and many-objective optimization techniques to improve the performance of a hydrologic model using evapotranspiration remote-sensing data. J. Hydrol. Eng. 2020, 25, 04020006. [Google Scholar] [CrossRef]
- He, Q.; Molkenthin, F. Improving the integrated hydrological simulation on a data-scarce catchment with multi-objective calibration. J. Hydroinformatics 2021, 23, 267–283. [Google Scholar] [CrossRef]
- Althoff, D.; Rodrigues, L.N. Goodness-of-fit criteria for hydrological models: Model calibration and performance assessment. J. Hydrol. 2021, 600, 126674. [Google Scholar] [CrossRef]

| Observation Points | Period | No. Annual Records | Approximate Distance from the Coast [km] | Altitude [m.a.s.l] | Average Yearly Precipitation [mm] |
|---|---|---|---|---|---|
| Cocle del Norte | 1966–Sep 2008 | 43 | 0.0 | 2.0 | 4989 |
| San Lucas | 1966–2008 | 43 | 10.0 | 30.0 | 4716 |
| Boca de Toabré | 1966–2008 | 43 | 20.0 | 30.0 | 4413 |
| Coclesito | 1966–1998 | 33 | 30.0 | 60.0 | 3171 |
| Station H3 | 2012–2016 | 5 | 16.0 | 89.0 | 1151 |
| Station H4 1 | 2012–2016 | 5 | 9.4 | 44.0 | - |
| Return Period | Yearly Precipitation [mm] | |||||
|---|---|---|---|---|---|---|
| Cocle del Norte | San Lucas | Boca de Toabré | Coclesito | Station H3 | Station H4 2 | |
| Number Years of Record | 33 | 40 | 39 | 33 | 5 | 5 |
| Highest Recorded | 8836 | 6715 | 6239 | 5195 | 1406 | - |
| Average | 4989 | 4716 | 4416 | 3171 | 1151 | - |
| Lowest Recorded | 3164 | 3420 | 2990 | 2491 | 864 | - |
| Major Type of Soil Inclusions and Associated Soils | |||
|---|---|---|---|
| Grade | 1 | 2 | 3 |
| Land-Categories (FAO 90) | Haplic Nitosols | Haplic Acrisols | Vitric Andisols |
| Highland Granule | Medium | Medium | Medium |
| Depth of Land Source (cm) | 100 | 100 | 100 |
| Type of Catchment (0–0.5% slope) | Moderately Well | Moderately Well | Moderately Well |
| HIGHLAND (“Sand Fraction”) (%) | 45 | 48 | 66 |
| HIGHLAND (“Silt Fraction”) (%) | 24 | 23 | 29 |
| HIGHLAND (“Clay Fraction”) (%) | 31 | 29 | 5 |
| HIGHLAND “USDA” Granule Categories | clay loam | sandy clay loam | sandy loam |
| Hydrologic Year (HY) | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2012 | - | - | 38.8 | 84.1 | 104.0 | 55.5 | 159.1 | 60.1 | 115.5 | 103.1 | 729.5 | 364.4 |
| 2013 | 75 | 72 | 94.1 | 50.4 | 102.3 | 89.6 | 79.6 | 50.5 | 63.5 | 82.9 | 75.9 | 183.9 |
| 2014 | 98 | 32 | 60.0 | 170.7 | 166.8 | 109.6 | 139.2 | 96.9 | 94.6 | 104.1 | 102.1 | 102.1 |
| 2015 | 158 | 75 | 30.6 | 143.1 | 268.8 | 296.7 | 128.2 | 94.1 | 104.9 | 97.0 | 157.3 | 39.3 |
| 2016 | 41 | 22 | 24.9 | 31.2 | 135.6 | 57.2 | 137.2 | 108.8 | 67.7 | 56.7 | 197.7 | 147.3 |
| Mean Monthly Streamflow for 5 Years of Record | 93.2 | 50.1 | 49.7 | 95.9 | 155.5 | 121.7 | 128.6 | 82.1 | 89.2 | 88.8 | 252.5 | 167.4 |
| Standard Deviation | 48.9 | 27.2 | 28.2 | 59.6 | 68.6 | 100.4 | 29.7 | 25.3 | 22.8 | 19.8 | 270.8 | 122.6 |
| Maximum Flow | 157.7 | 75.0 | 94.1 | 170.7 | 268.8 | 296.7 | 159.1 | 108.8 | 115.5 | 104.1 | 729.5 | 364.4 |
| Minimum Flow | 41.5 | 21.5 | 24.9 | 31.2 | 102.3 | 55.5 | 79.6 | 50.5 | 63.5 | 56.7 | 75.9 | 39.3 |
| Variable | No. of Variables with Missing Data | |||
|---|---|---|---|---|
| No. of Instances | RN [mm] | Q [m3/s] | WL [m] | |
| 147,086 | 1 | 1 | 1 | 0 |
| 95 | 0 | 1 | 1 | 1 |
| 2977 | 1 | 1 | 0 | 1 |
| 2579 | 1 | 0 | 1 | 1 |
| 5778 | 1 | 0 | 0 | 2 |
| 8241 | 0 | 0 | 0 | 3 |
| Total of missing | 8336 | 16,598 | 16,996 | 41,930 |
| Classification of Precipitation | Rainfall Quantity | |
|---|---|---|
| Classification I [mm·h−1] | Classification II [mm·d−1] | |
| Light precipitation | 1–5 | 5–20 |
| Average precipitation | 5–10 | 20–50 |
| Intense precipitation | 10–20 | 50–100 |
| Very intense precipitation | >20 | >100 |
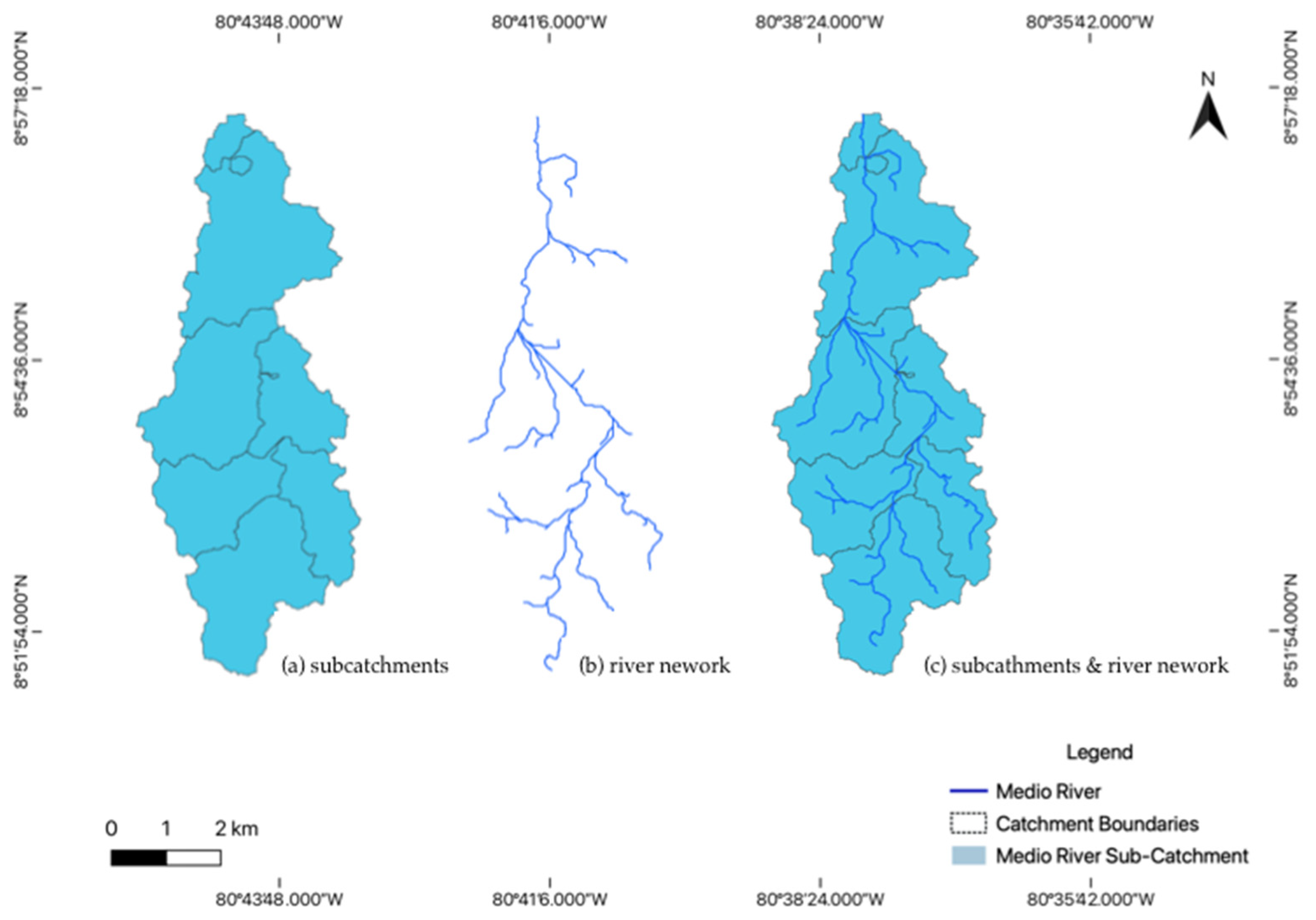
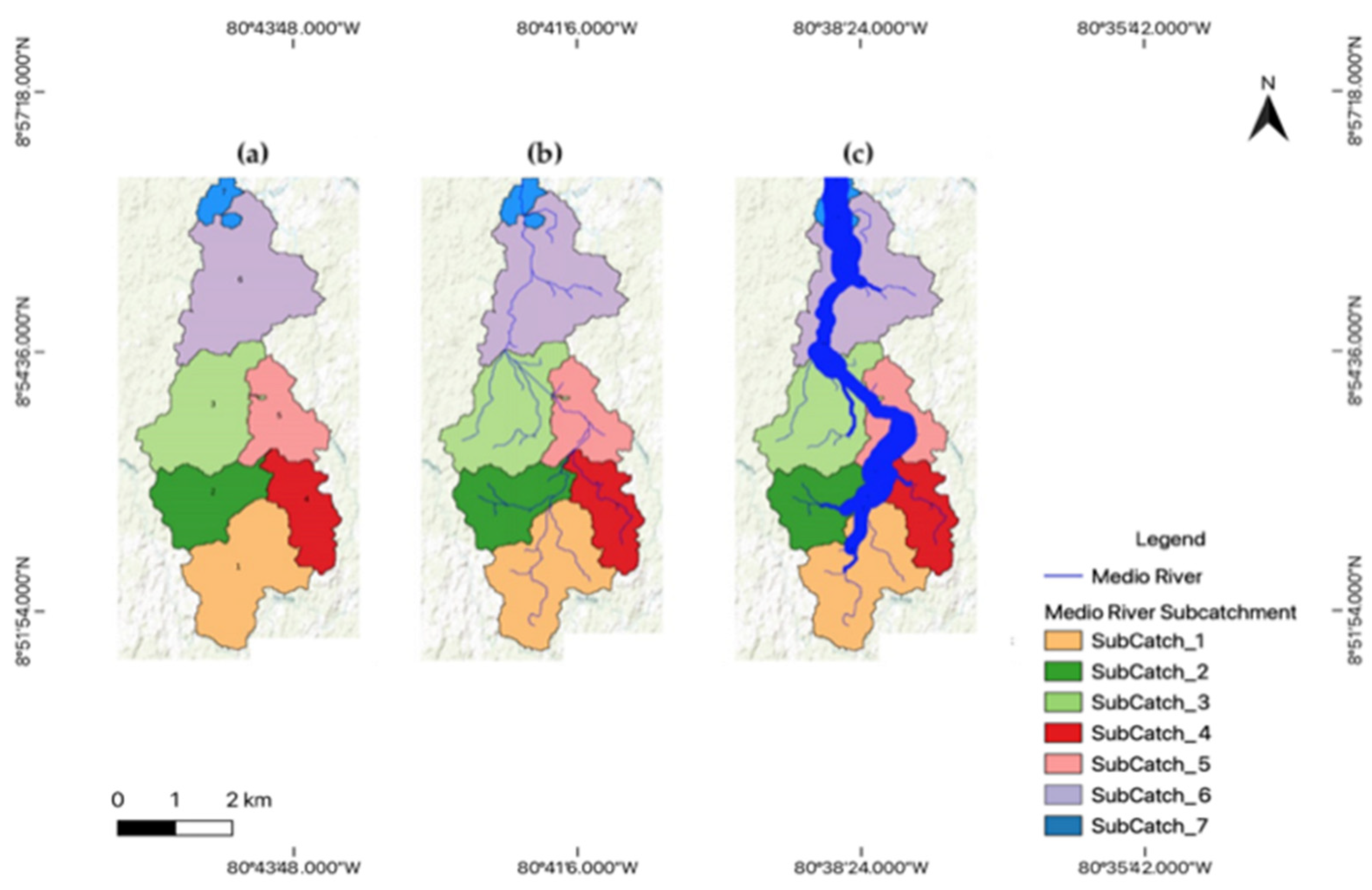
| Subcatchment_ID | Area [km2] | ≈Order | Catchment Outlet_ID |
|---|---|---|---|
| 1 | 9.9 | 3 | 4 |
| 2 | 6.3 | 2 | 4 |
| 3 | 9.6 | 3 | 4 |
| 4 | 4.9 | 1 | 8 |
| 5 | 5.3 | 1 | 8 |
| 6 | 12.8 | 2 | 8 |
| 7 | 1.3 | 1 | 8 |
| Calibration Scenario | Cor. Coef. [r] | Coef. of Det. [R2] | RMSE [m3/s] | Percent. Error in Qpk [%] | ABM Sim. Qpk [m3/s] |
|---|---|---|---|---|---|
| 1 | 0.78 | 0.60 | 42.3 | 80.0 | 465.5 |
| 2 | 0.80 | 0.65 | 230.2 | 84.6 | 1675.9 |
| 3 | 0.79 | 0.63 | 40.3 | 80.8 | 465.5 |
| 4 | 0.80 | 0.64 | 43.9 | 80.5 | 466.7 |
| Validation Scenario | Cor. Coef. [r] | Coef. of Det. [R2] | RMSE [m3/s] | Percent. Error in Qpk [%] | Obs. Qpk [m3/s] | ABM Sim. Qpk [m3/s] |
|---|---|---|---|---|---|---|
| December 2012 | 0.86 | 0.74 | 25.1 | 51.7 | 266.4 | 404.0 |
| December 2014 | 0.79 | 0.62 | 41.7 | 88.7 | 335.5 | 633.3 |
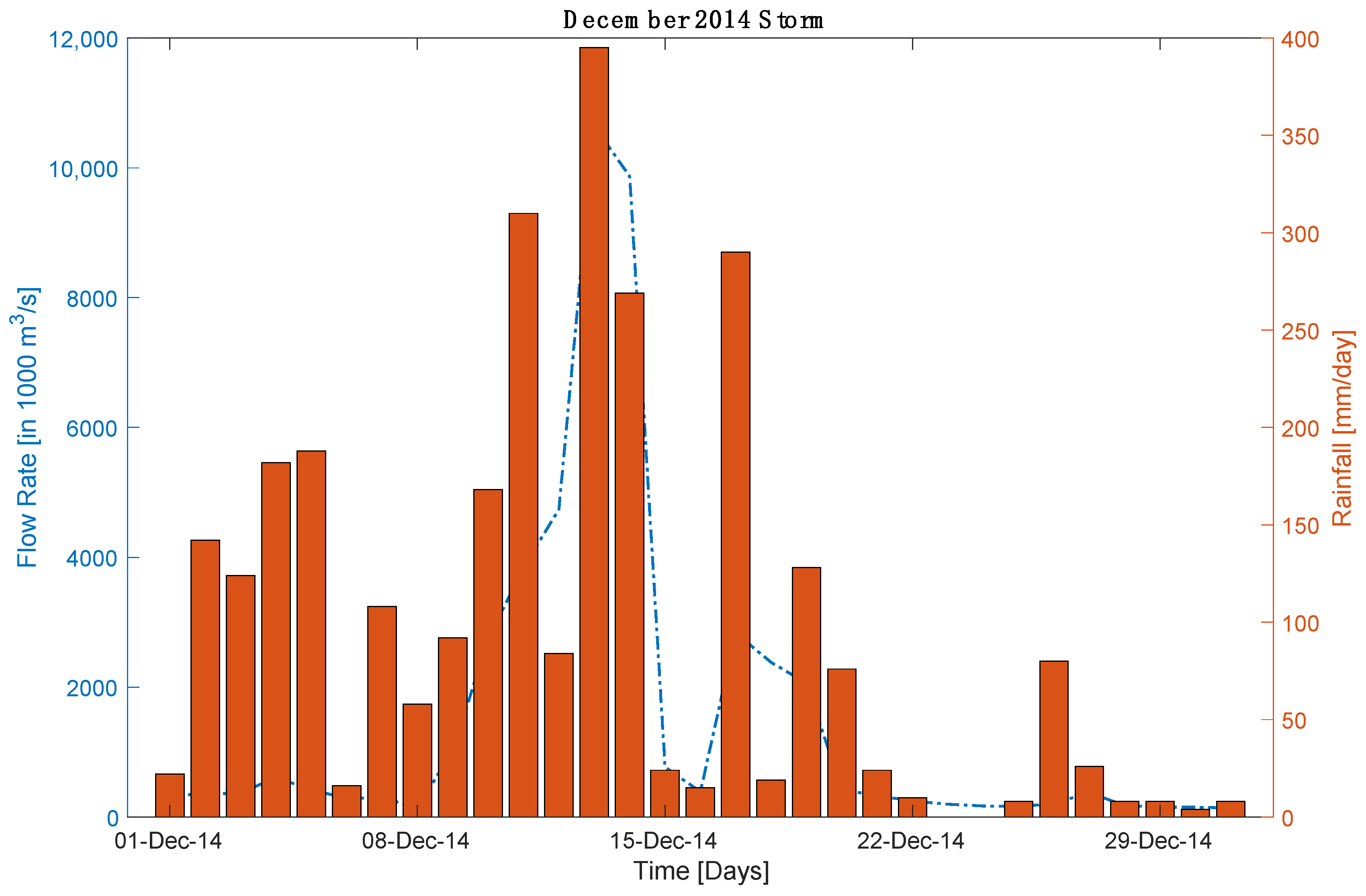
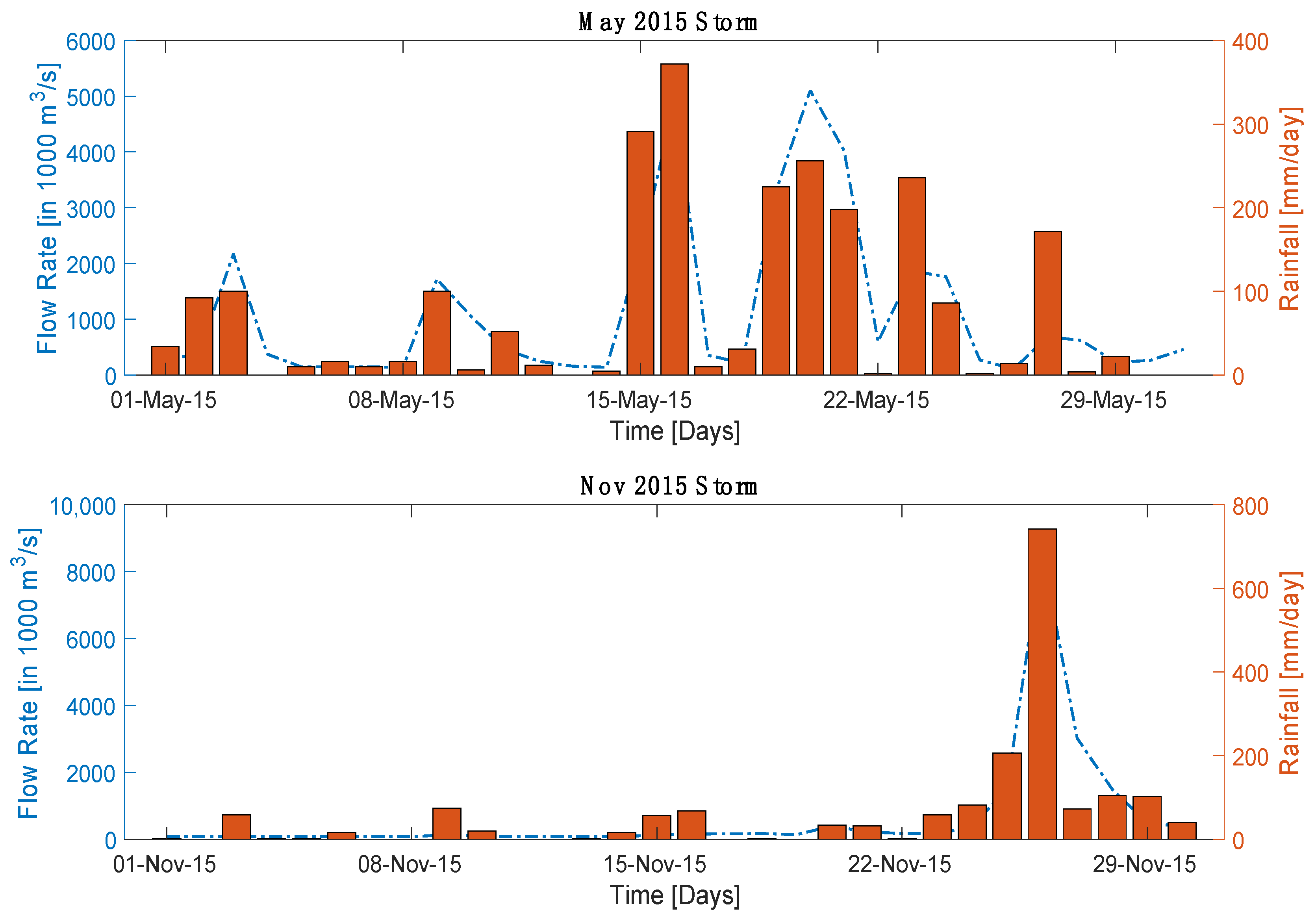
| May 2015 | 0.76 | 0.58 | 20.1 | 28.1 | 257.1 | 329.3 |
| November 2015 | 0.90 | 0.82 | 23.0 | 80.0 | 264.3 | 475.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simmonds, J.; Gómez, J.A.; Ledezma, A. Testing the Feasibility of an Agent-Based Model for Hydrologic Flow Simulation. Information 2024, 15, 448. https://doi.org/10.3390/info15080448
Simmonds J, Gómez JA, Ledezma A. Testing the Feasibility of an Agent-Based Model for Hydrologic Flow Simulation. Information. 2024; 15(8):448. https://doi.org/10.3390/info15080448
Chicago/Turabian StyleSimmonds, Jose, Juan Antonio Gómez, and Agapito Ledezma. 2024. "Testing the Feasibility of an Agent-Based Model for Hydrologic Flow Simulation" Information 15, no. 8: 448. https://doi.org/10.3390/info15080448
APA StyleSimmonds, J., Gómez, J. A., & Ledezma, A. (2024). Testing the Feasibility of an Agent-Based Model for Hydrologic Flow Simulation. Information, 15(8), 448. https://doi.org/10.3390/info15080448







