New Test to Detect Clustered Graphical Passwords in Passpoints Based on the Perimeter of the Convex Hull
Abstract
1. Introduction
2. Preliminaries
2.1. Passpoints
2.2. Known Tests to Detect Clustered Graphical Passwords in Passpoints
3. Our Contribution: New Test to Detect Clustered Graphical Passwords in Passpoints
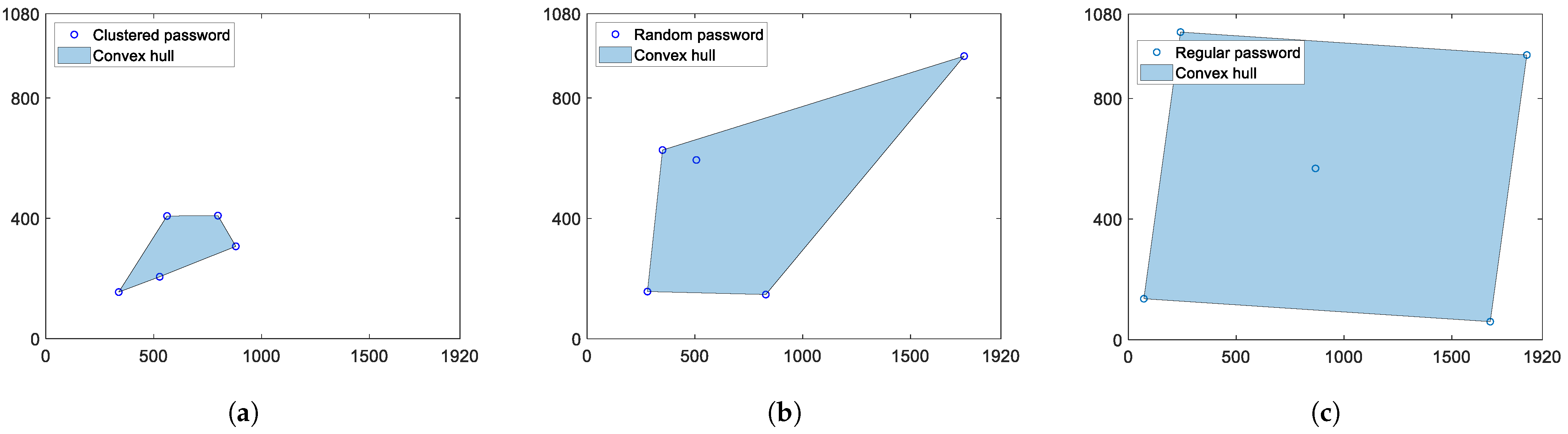
3.1. Our Hypothesis
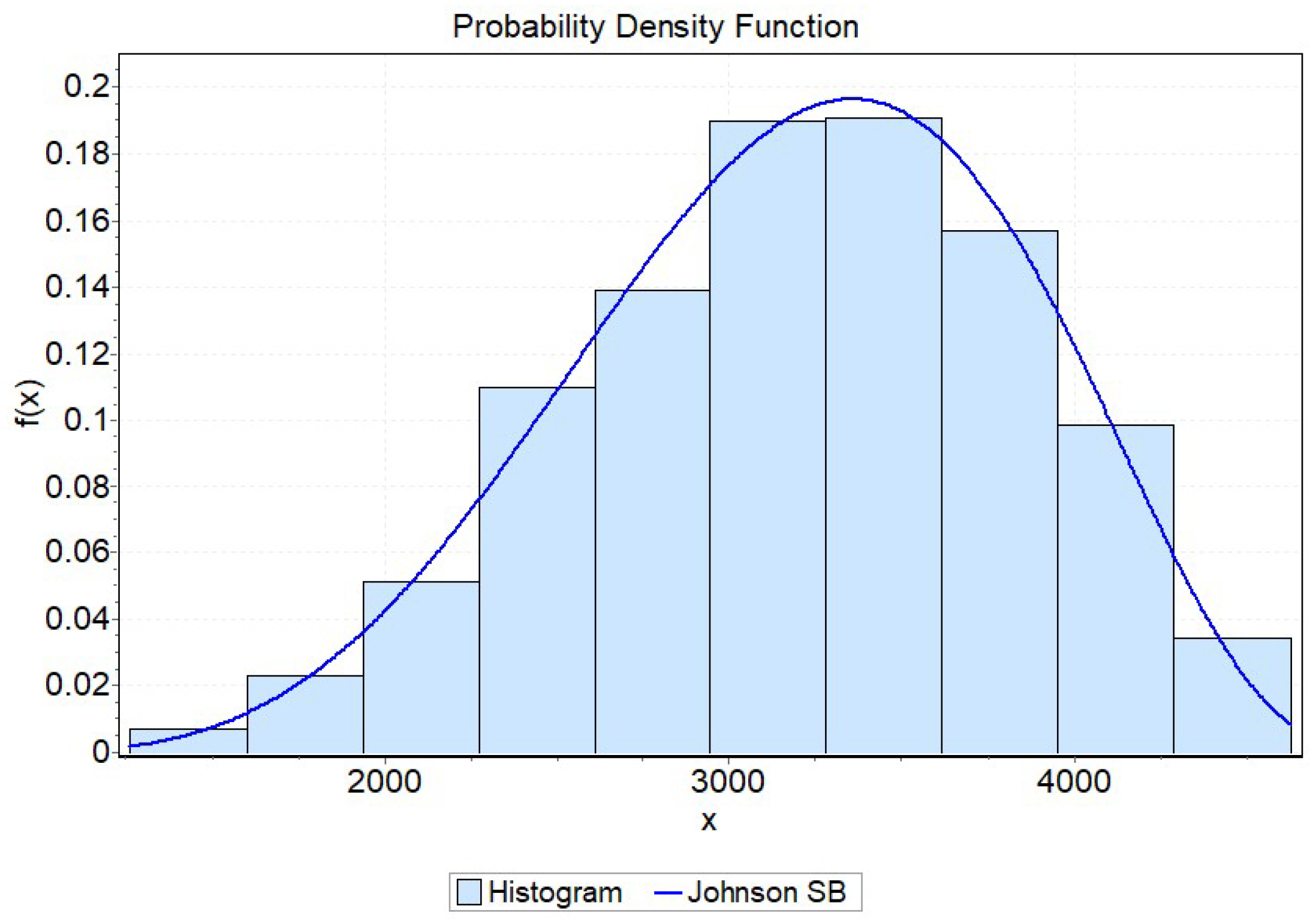
3.2. Estimate of the Probability Distribution of the Perimeter of the Convex Hull
3.3. Hypothesis Test Based on the Perimeter of the Convex Hull
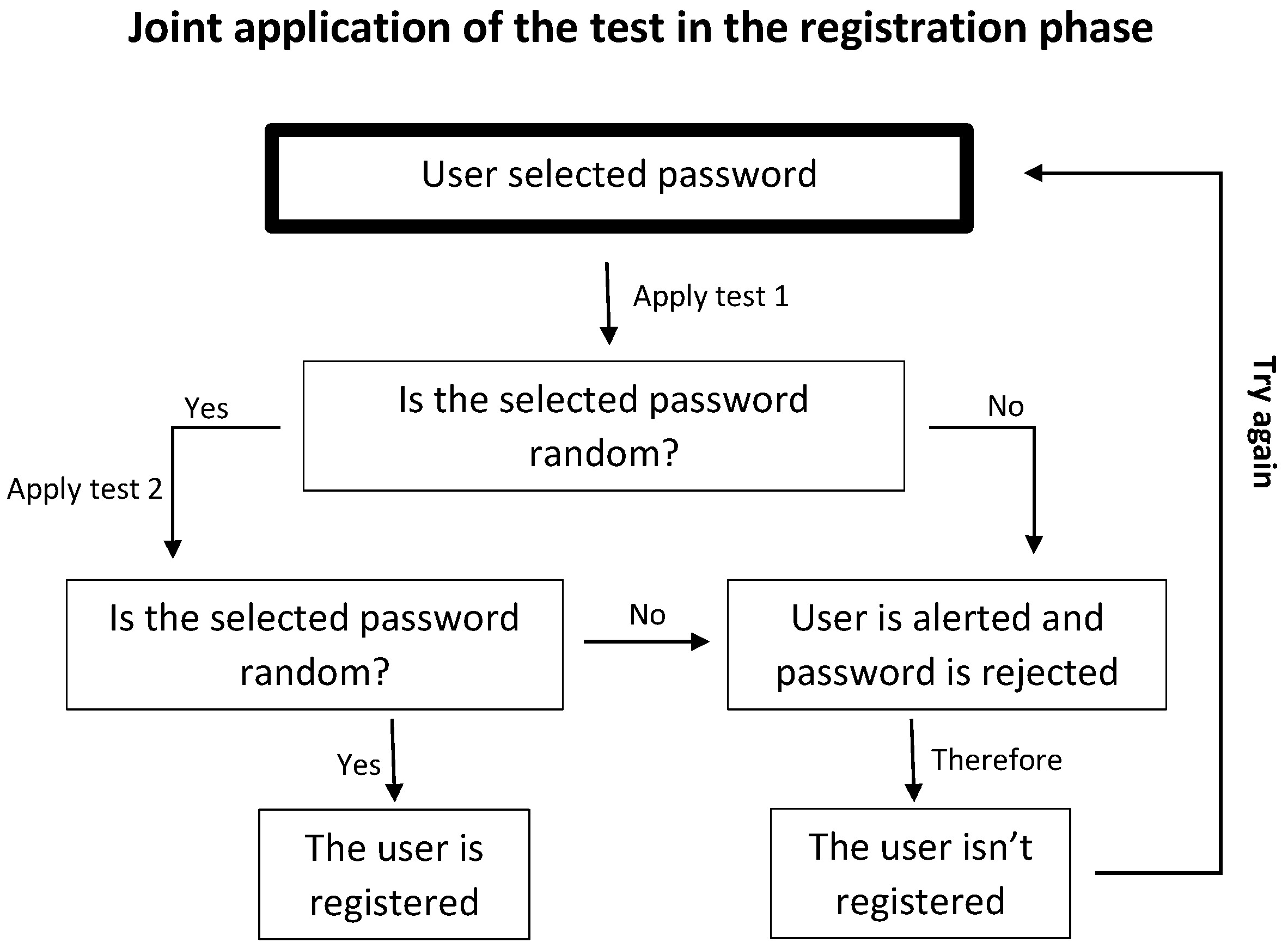
3.3.1. Definition of the Proposed Test
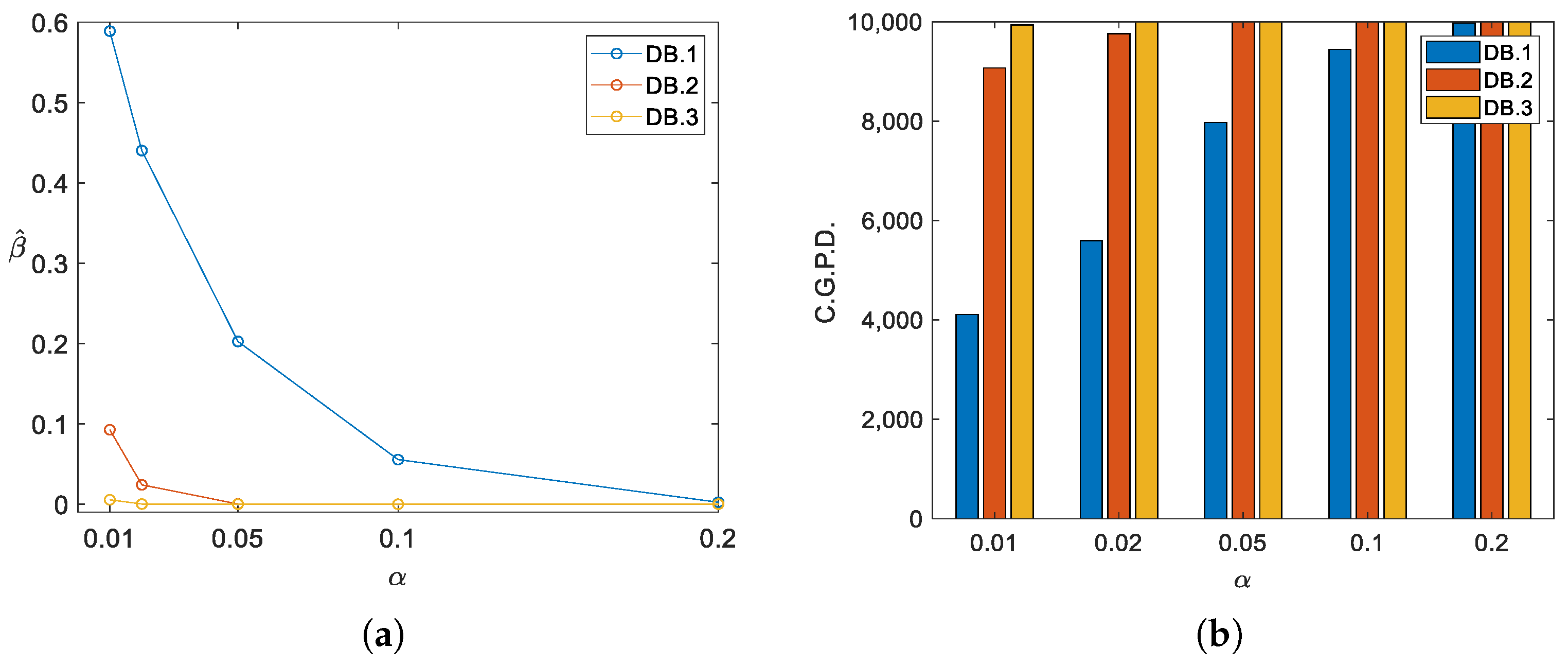
3.3.2. Evaluation of the Effectiveness of the Proposed Test
4. Comparison with Other Tests in the Literature
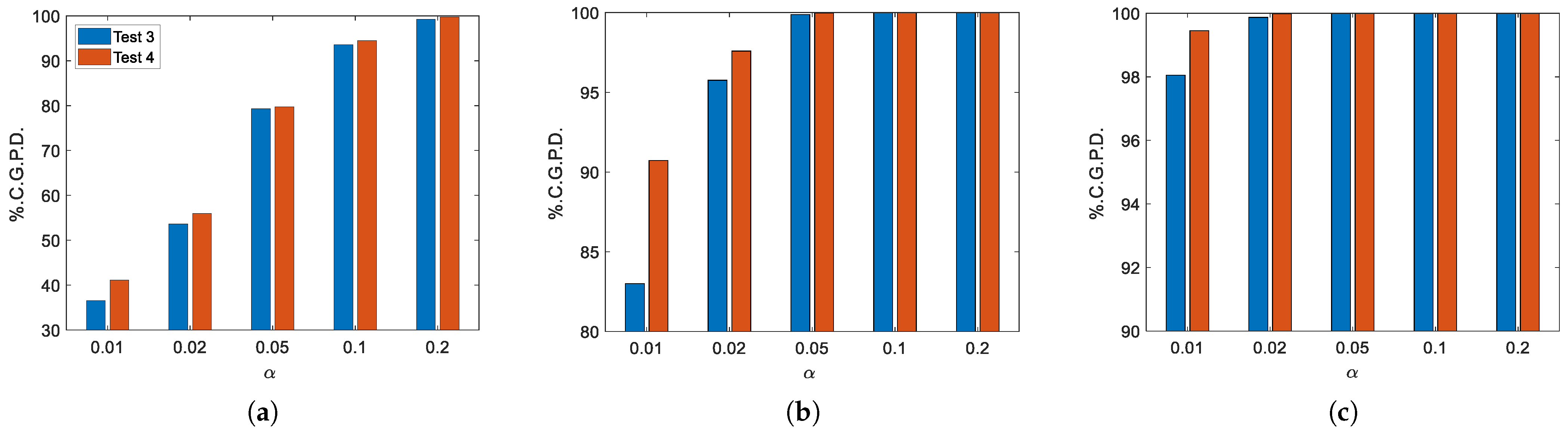
4.1. Effectiveness
4.2. Efficiency
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- David, L.; Wool, A. An explainable online password strength estimator. In Computer Security–ESORICS 2021: 26th European Symposium on Research in Computer Security, Darmstadt, Germany, 4–8 October 2021; Proceedings, Part I 26; Springer International Publishing: Cham, Switwerland, 2021; pp. 285–304. [Google Scholar] [CrossRef]
- Awan, K.; Ud Din, I.; Almogren, A.; Kumar, N.; Almogren, A. A Taxonomy of Multimedia-based Graphical User Authentication for Green Internet of Things. ACM Trans. Internet Technol. (TOIT) 2021, 22, 1–28. [Google Scholar] [CrossRef]
- Nosenko, A.; Cheng, Y.; Chen, H. Password and Passphrase Guessing with Recurrent Neural Networks. Inf. Syst. Front. 2023, 25, 549–565. [Google Scholar] [CrossRef]
- Rando, J.; Perez-Cruz, F.; Hitaj, B. PassGPT: Password Modeling and (Guided) Generation with Large Language Models. In European Symposium on Research in Computer Security; Springer Nature: Cham, Switzerland, 2023. [Google Scholar]
- Itti, L.; Koch, C. Computational modelling of visual attention. Nat. Rev. Neurosci. 2001, 2, 194–203. [Google Scholar] [CrossRef] [PubMed]
- Wiedenbeck, S.; Waters, J.; Birget, J.; Brodskiy, A.; Memon, N. PassPoints: Design and longitudinal evaluation of a graphical password system. Int. J. -Hum.-Comput. Stud. 2005, 63, 102–127. [Google Scholar] [CrossRef]
- Rodriguez Valdés, O.; Legón, C.; Socorro Llanes, R. Seguridad y usabilidad de los esquemas y técnicas de autenticación gráfica. Rev. Cuba. Cienc. Inform. 2018, 12, 13–27. [Google Scholar]
- Legón, C.; Socorro, R.; Navarro, P.; Rodríguez, O.; Borrego, E. Nuevo modelo probabilístico en autenticación gráfica. Ing. Electrón. Autom. Y Comun. 2019, 40, 92–104. [Google Scholar]
- Herrera-Macías, J.; Legón-Pérez, C.; Suárez-Plasencia, L.; Piñeiro-Díaz, L.; Rojas, O.; Sosa-Gómez, G. Test for detection of weak graphic passwords in passpoint based on the mean distance between points. Symmetry 2021, 13, 777. [Google Scholar] [CrossRef]
- Suárez-Plasencia, L.; Legón-Pérez, C.; Herrera-Macías, J.; Socorro-Llanes, R.; Rojas, O.; Sosa-Gómez, G. Weak PassPoint Passwords Detected by the Perimeter of Delaunay Triangles. Secur. Commun. Netw. 2022, 2022, 3624587. [Google Scholar] [CrossRef]
- Herrera-Macías, J.; Suárez-Plasencia, L.; Legón-Pérez, C.; Piñeiro-Díaz, L.; Rojas, O.; Sosa-Gómez, G. Effectiveness of some tests of spatial randomness in the detection of weak graphical passwords in passpoint. In Proceedings of the International Conference on Computer Science and Health Engineering, Virtual Event, 26 November 2020; pp. 173–183. [Google Scholar]
- Macías, J.; Plasencia, L.; Pérez, C.; Gomez, G. Comparación y combinación de dos test efectivos en la detección de contraseñas gráficas no aleatorias en Passpoints. Rev. Cuba. Cienc. Inform. 2023, 17, 78. [Google Scholar]
- Suárez-Plasencia, L.; Herrera-Macías, J.; Legón-Pérez, C.; Sosa-Gómez, G.; Rojas, O. Detection of DIAG and LINE Patterns in PassPoints Graphical Passwords Based on the Maximum Angles of Their Delaunay Triangles. Sensors 2022, 22, 1987. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Klette, R. Euclidean Shortest Paths. In Euclidean Shortest Paths: Exact or Approximate Algorithms; Springer: London, UK, 2011; pp. 3–29. [Google Scholar] [CrossRef]
- Preparata, F.; Shamos, M. Computational Geometry: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Mark, D.; Otfried, C.; Marc, V.; Mark, O. Computational Geometry Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- ORourke, J. Computational Geometry in C; Cambridge University Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Rockafellar, R. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- de Berg, M.; van Kreveld, M.; Overmars, M.; Schwarzkopf, O. Computational Geometry: Algorithms and Applications, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Candela, C.; Sepúlveda, L.; Chavarro, J.; Meneses, C.; Sanabria, J.; Arcila, O. Implementación de algoritmos para calcular el Convex Hull. Entre Cienc. Ing. 2022, 16, 27–34. [Google Scholar] [CrossRef]
- Gamby, A.; Katajainen, J. A faster convex-hull algorithm via bucketing. In Proceedings of the International Symposium on Experimental Algorithms, Kalamata, Greece, 24–29 June 2019; pp. 473–489. [Google Scholar]
- Gamby, A.; Katajainen, J. Convex-hull algorithms: Implementation, testing, and experimentation. Algorithms 2018, 11, 195. [Google Scholar] [CrossRef]
- Keith, A.; Ferrada, H.; Navarro, C. Accelerating the Convex Hull Computation with a Parallel GPU Algorithm. In Proceedings of the 2022 41st International Conference of the Chilean Computer Science Society (SCCC ), Santiago, Chile, 21–25 November 2022; pp. 1–7. [Google Scholar]
- Tabacman, M. Implementing and Visualizing Algorithms for Computing Convex Hulls in the Plane; University of Minnesota: Minneapolis, MN, USA, 2021. [Google Scholar]
- Efron, B. The convex hull of a random set of points. Biometrika 1965, 52, 331–343. [Google Scholar] [CrossRef]
- Groeneboom, P. Limit theorems for convex hulls. Probab. Theory Relat. Fields 1988, 79, 327–368. [Google Scholar] [CrossRef]
- Khamdamov, I.; Chay, Z.; Sharipova, L. The limit distribution of the perimeter of a convex hull generated by a Poisson point process in a convex polygon. Vestn. Tomsk. Gos. Univ. Mat. Mekhanika 2022, 44–57. [Google Scholar] [CrossRef]
- McRedmond, J.; Wade, A. The convex hull of a planar random walk: Perimeter, diameter, and shape. Electron. J. Probab. 2018, 23, 1–24. [Google Scholar] [CrossRef]
- McRedmond, J.; Fergal, W. Convex Hulls of Random Walks; Durham University: Durham, UK, 2019. [Google Scholar]
- NIST Special Publication 800-63B; Digital Identity Guidelines. Authentication and Lifecycle Management. NIST Special Publication: Gaithersburg, MD, USA, 2017. [CrossRef]
- Ray, P. Ray’s scheme: Graphical password-based hybrid authentication system for smart hand-held devices. J. Inf. Eng. Appl. 2012, 2, 1–12. [Google Scholar]
- Dirik, A.; Memon, N.; Birget, J. Modeling user choice in the PassPoints graphical password scheme. In Proceedings of the 3rd Symposium on Usable Privacy and Security, Pittsburgh, PA, USA, 18–20 July 2007; pp. 20–28. [Google Scholar]
- Van Oorschot, P.; Salehi-Abari, A.; Thorpe, J. Purely automated attacks on passpoints-style graphical passwords. IEEE Trans. Inf. Forensics Secur. 2010, 5, 393–405. [Google Scholar] [CrossRef]
- Zhu, B.; Wei, D.; Yang, M.; Yan, J. Security implications of password discretization for click-based graphical passwords. In Proceedings of the 22nd International Conference On World Wide Web, Rio de Janeiro, Brazil, 13–17 May 2013; pp. 1581–1591. [Google Scholar]
- Floch, J.; Marcon, E.; Puech, F. Spatial distribution of points. In Handbook of Spatial Analysis: Theory and Application with R; Loonis, V., Bellefon, M.P., Eds.; Eurostat: Paris, France, 2018; pp. 77–111. [Google Scholar]
- Chiasson, S.; Forget, A.; Biddle, R.; Oorschot, P. User interface design affects security: Patterns in click-based graphical passwords. Int. J. Inf. Secur. 2009, 8, 387–398. [Google Scholar] [CrossRef]
- Pogoda, P.; Ochał, W.; Orzeł, S. Performance of Kernel estimator and Johnson SB function for modeling diameter distribution of black alder (Alnus glutinosa (L.) Gaertn.) stands. Forests 2020, 11, 634. [Google Scholar] [CrossRef]
| Significance Level | First Clustering Level | Second Clustering Level | Third Clustering Level |
|---|---|---|---|
| 0.2 | 9922 | 10,000 | 10,000 |
| 0.1 | 9358 | 10,000 | 10,000 |
| 0.05 | 7931 | 9987 | 10,000 |
| 0.02 | 5365 | 9576 | 9987 |
| 0.01 | 3652 | 8300 | 9805 |
| Goodness-of-Fit Test | Kolmogorov–Smirnov | Chi-Square | Anderson–Darling |
|---|---|---|---|
| p-value | 0.98139 | Accepted | 0.79775 |
| Accepted for each | 5/5 | 5/5 | 5/5 |
| Image Size | ||||
|---|---|---|---|---|
| (Theoretical) | of | DB.2 |
|---|---|---|
| 0.2 | 0.2029 | |
| 0.1 | 0.1019 | |
| 0.05 | 0.0535 | |
| 0.02 | 0.0234 | |
| 0.01 | 0.0136 |
| Significance Level | Critical Region | () DB.3.1 | () DB.3.2 | () DB.3.3 |
|---|---|---|---|---|
| 0.2 | −1.282 1.282 | 0.0024 | 0 | 0 |
| 0.1 | −1.645 1.645 | 0.0555 | 0 | 0 |
| 0.05 | −1.960 1.960 | 0.2026 | 0.0003 | 0 |
| 0.02 | −2.326 2.326 | 0.4402 | 0.0241 | 0.0002 |
| 0.01 | −2.575 2.575 | 0.5889 | 0.0927 | 0.0055 |
| Significance Level | Critical Region | () DB.3.1 | () DB.3.2 | () DB.3.3 |
|---|---|---|---|---|
| 0.2 | −1.282 1.282 | ↓0.0054 | 0 | 0 |
| 0.1 | −1.645 1.645 | ↓0.0087 | 0 | 0 |
| 0.05 | −1.960 1.960 | ↓0.0043 | ↓0.0010 | 0 |
| 0.02 | −2.326 2.326 | ↓0.0233 | ↓0.0241 | ↓0.0011 |
| 0.01 | −2.575 2.575 | ↓0.0459 | ↓0.0773 | ↓0.0140 |
| Minimum Time | Average Time | Maximum Time | |
|---|---|---|---|
| Test 1 | 0.001 | 0.006 | 0.084 |
| Test 3 | 0.001 | 0.045 | 0.155 |
| Test 4 | 0.017 | 0.033 | 0.110 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herrera-Macías, J.A.; Suárez-Plasencia, L.; Legón-Pérez, C.M.; Sosa-Gómez, G.; Rojas, O. New Test to Detect Clustered Graphical Passwords in Passpoints Based on the Perimeter of the Convex Hull. Information 2024, 15, 447. https://doi.org/10.3390/info15080447
Herrera-Macías JA, Suárez-Plasencia L, Legón-Pérez CM, Sosa-Gómez G, Rojas O. New Test to Detect Clustered Graphical Passwords in Passpoints Based on the Perimeter of the Convex Hull. Information. 2024; 15(8):447. https://doi.org/10.3390/info15080447
Chicago/Turabian StyleHerrera-Macías, Joaquín Alberto, Lisset Suárez-Plasencia, Carlos Miguel Legón-Pérez, Guillermo Sosa-Gómez, and Omar Rojas. 2024. "New Test to Detect Clustered Graphical Passwords in Passpoints Based on the Perimeter of the Convex Hull" Information 15, no. 8: 447. https://doi.org/10.3390/info15080447
APA StyleHerrera-Macías, J. A., Suárez-Plasencia, L., Legón-Pérez, C. M., Sosa-Gómez, G., & Rojas, O. (2024). New Test to Detect Clustered Graphical Passwords in Passpoints Based on the Perimeter of the Convex Hull. Information, 15(8), 447. https://doi.org/10.3390/info15080447








