Exploring the Depths of the Autocorrelation Function: Its Departure from Normality
Abstract
1. Introduction
2. Theoretical Background
2.1. Autocorrelation Functions (ACF)
2.2. Sum of Sample Autocorrelation Functions (SACF)
2.3. Diagnosis of White Noise (WN)
- 1.
- If , then is distributed, with and .
- 2.
- If is distributed, we have , and .
3. Theoretical Results
3.1. Contradiction with Theorems 1 and 2
3.2. Asymptotic Normality
4. Simulation Results for WN
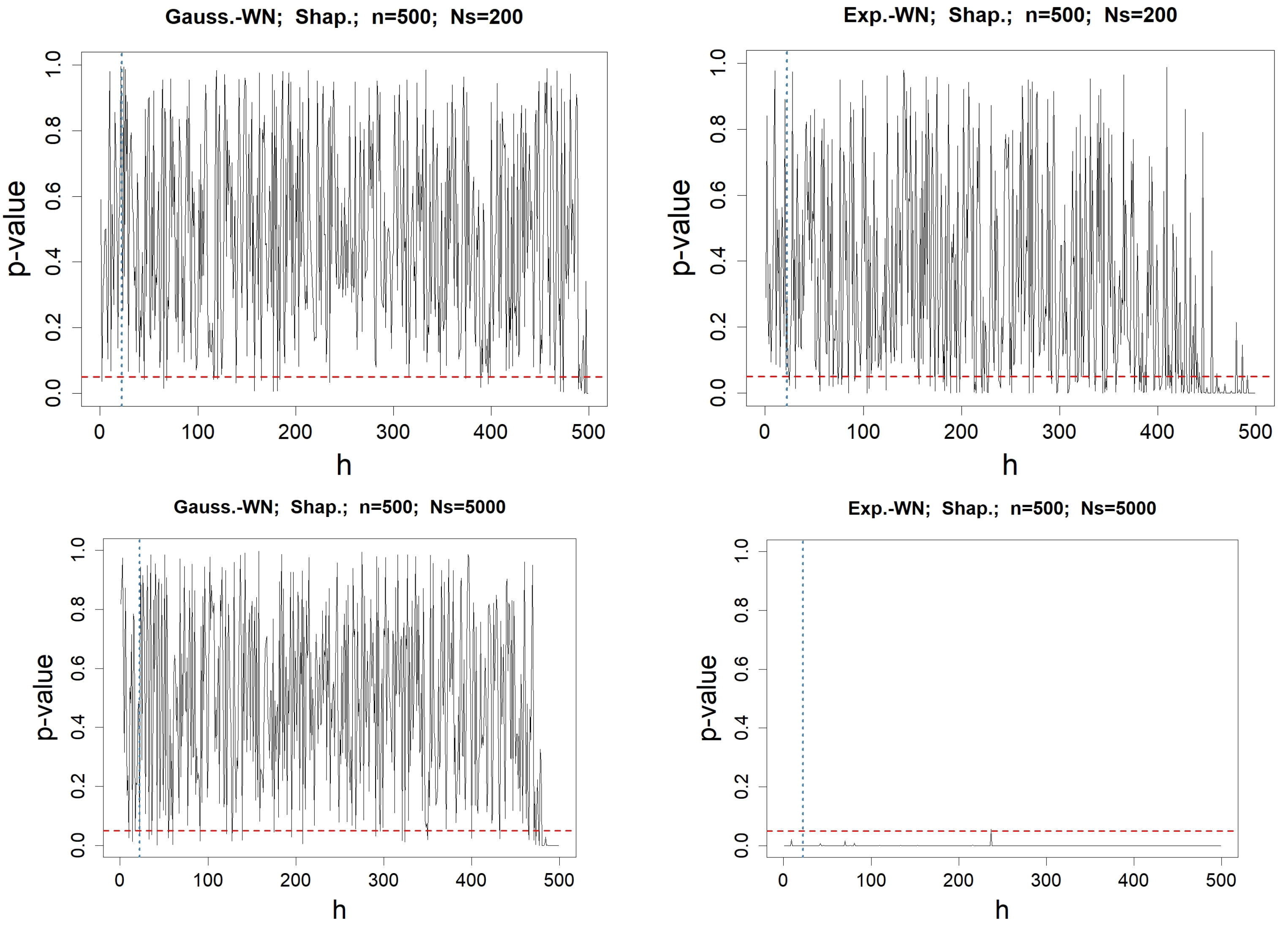
4.1. Check for the Normality of at a Fixed Lag h
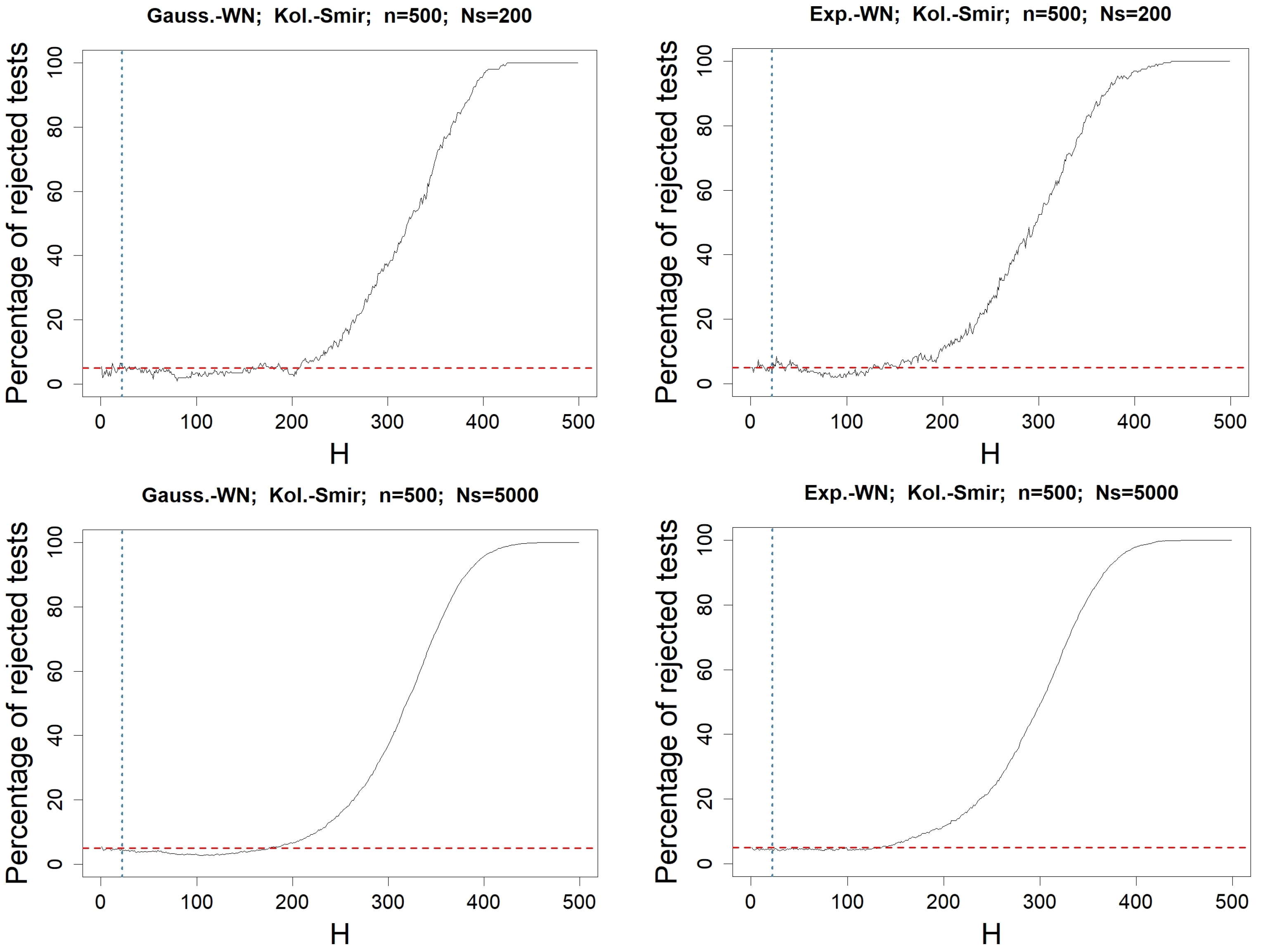
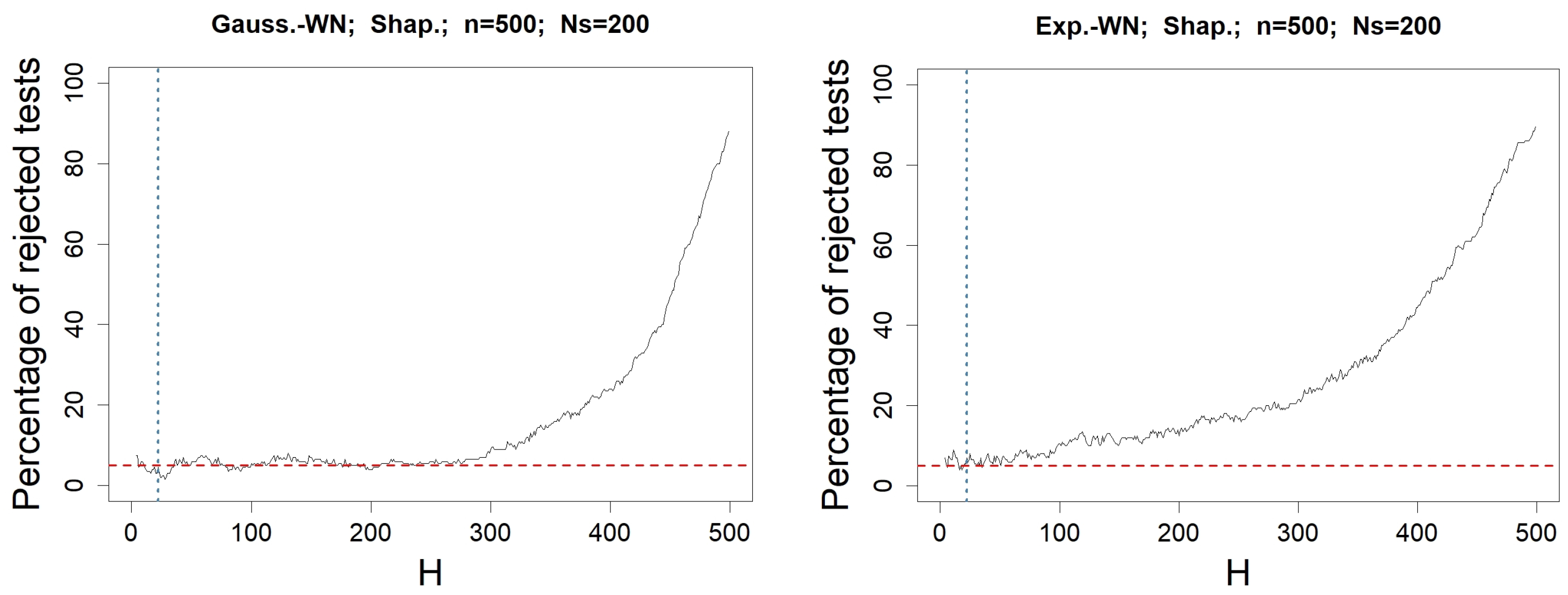
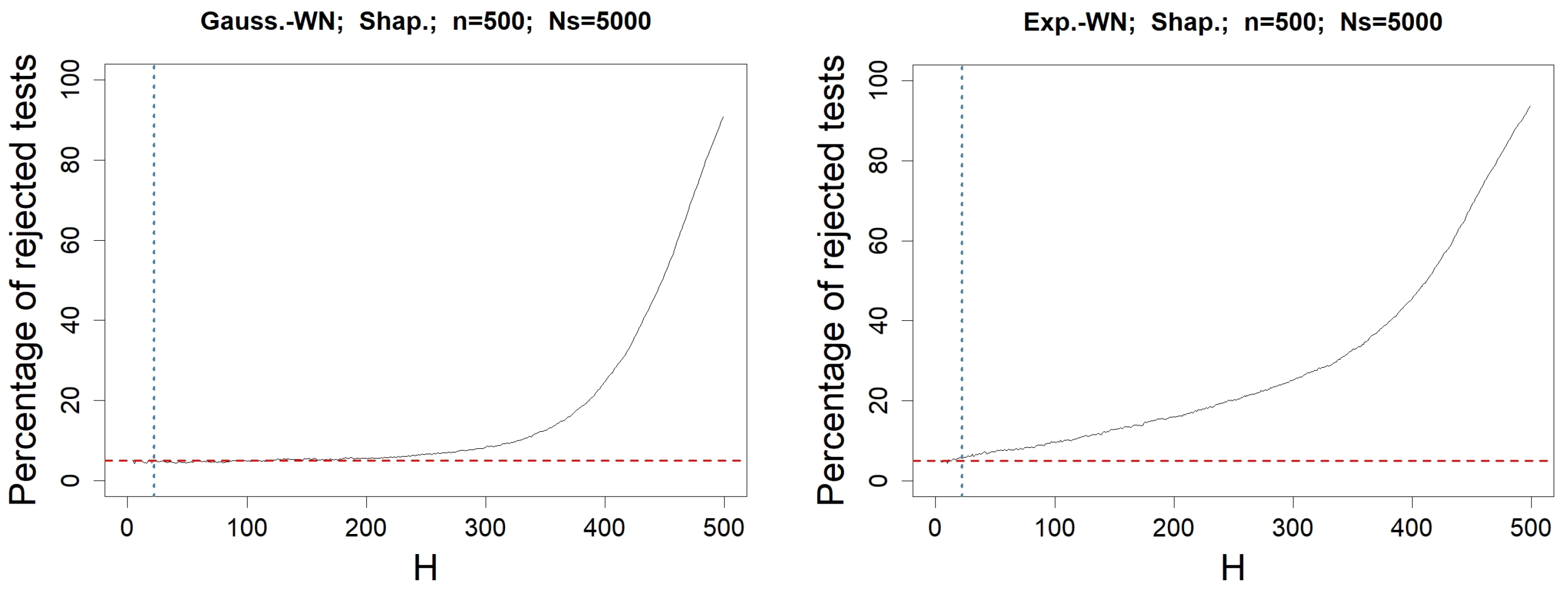
4.2. Check for
4.3. Check for
5. Simulation Results for Residuals
5.1. Well-Specified Models
5.2. Misspecified Models
5.3. Check for the Normality of at a Fixed Lag h
5.4. Check for the Normality of at a Fixed Lag H
5.5. Check for
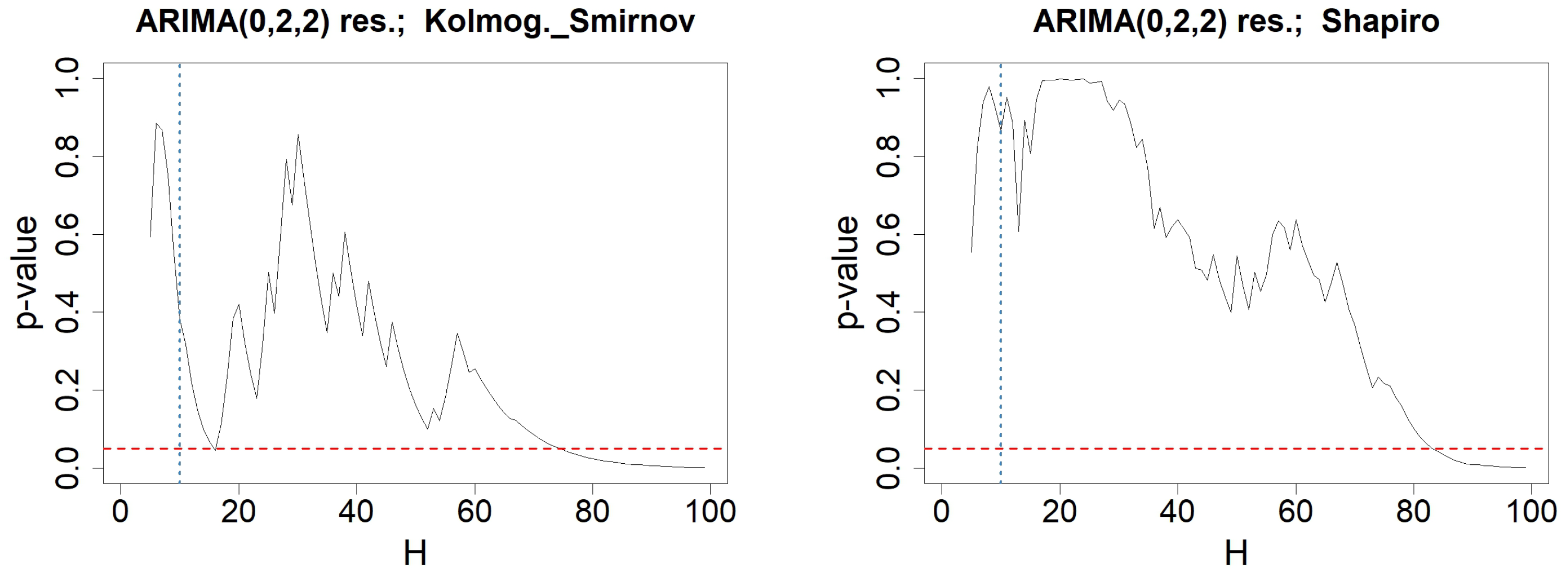
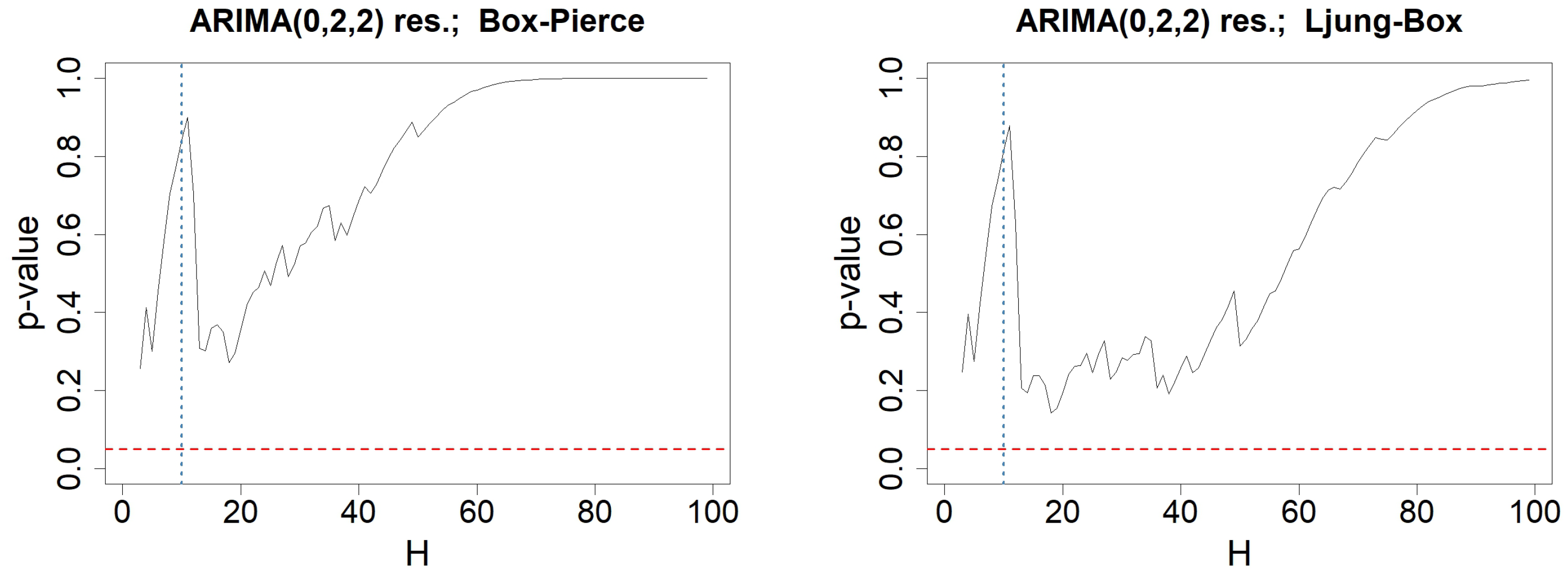
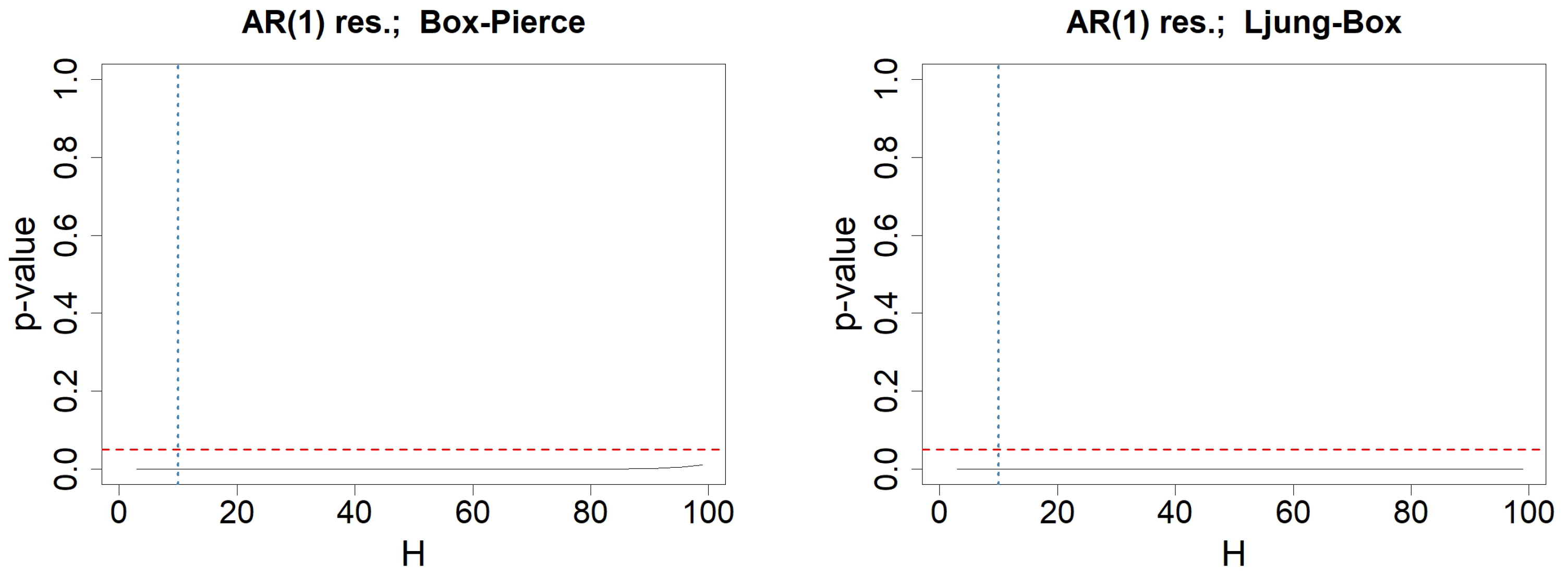
6. Illustration Using an Economic Data Set
7. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
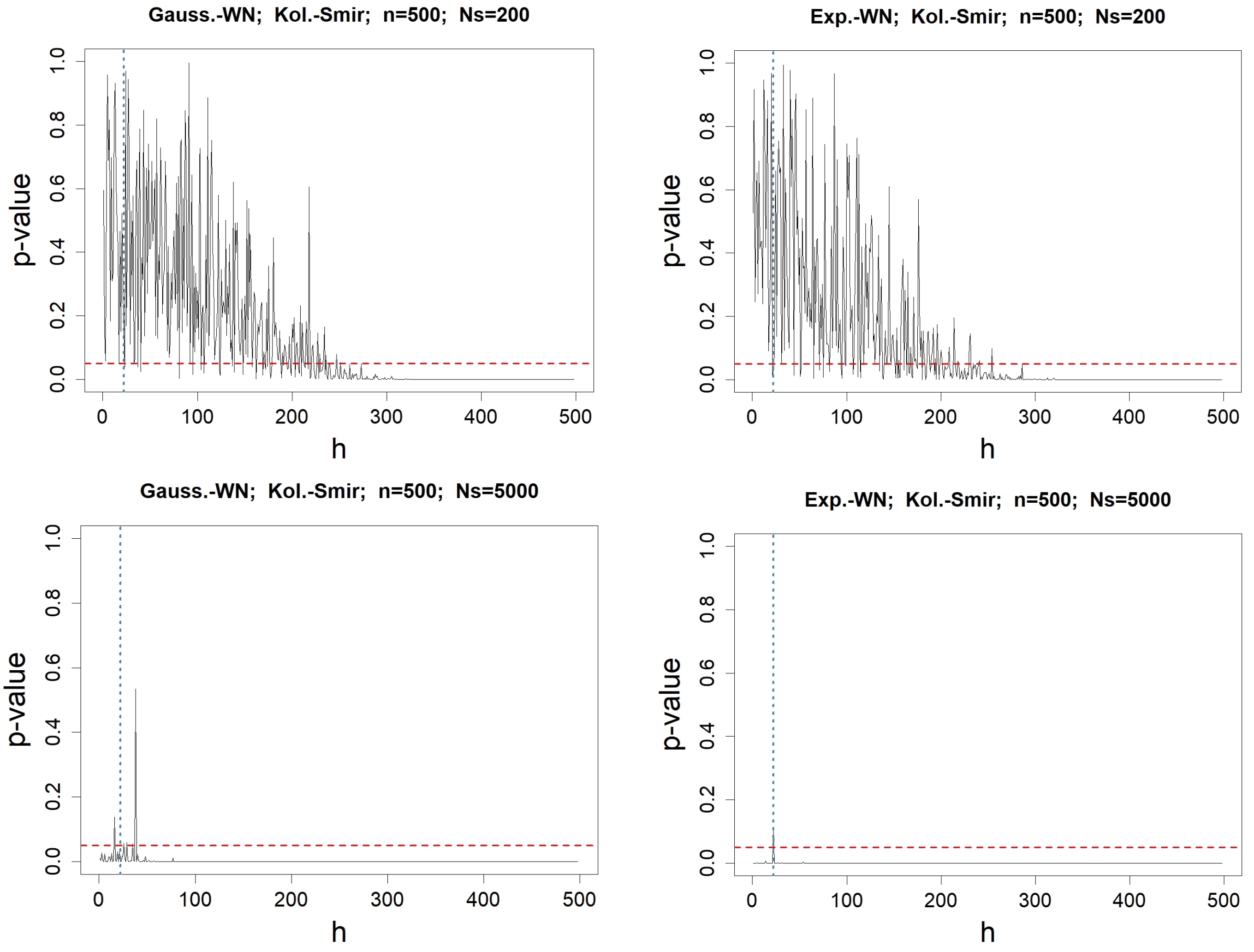
Appendix A. Reliability of Portmanteau Tests for WN

Appendix B. Reliability of Portmanteau Tests for Residuals of a Mis-Specified Model
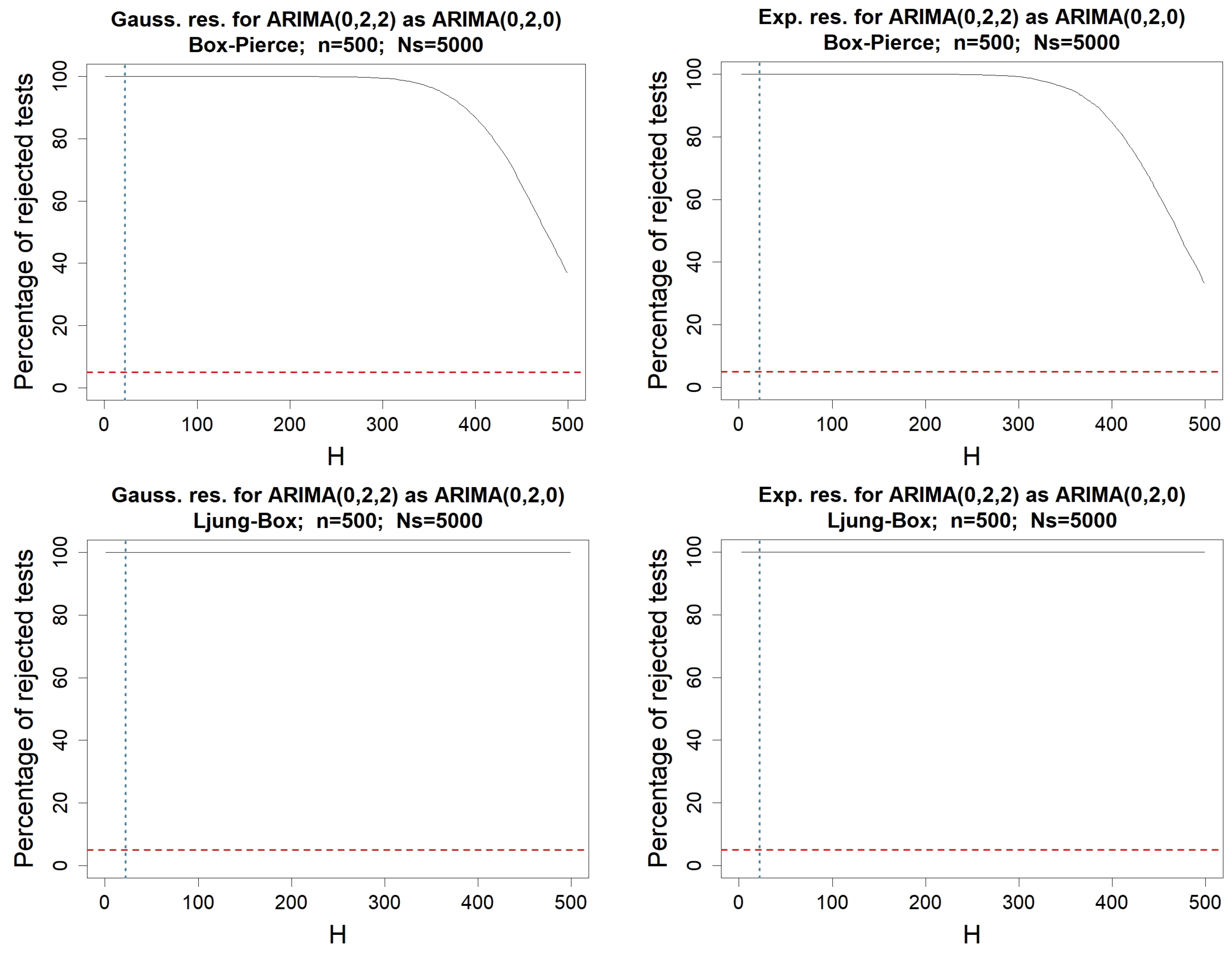
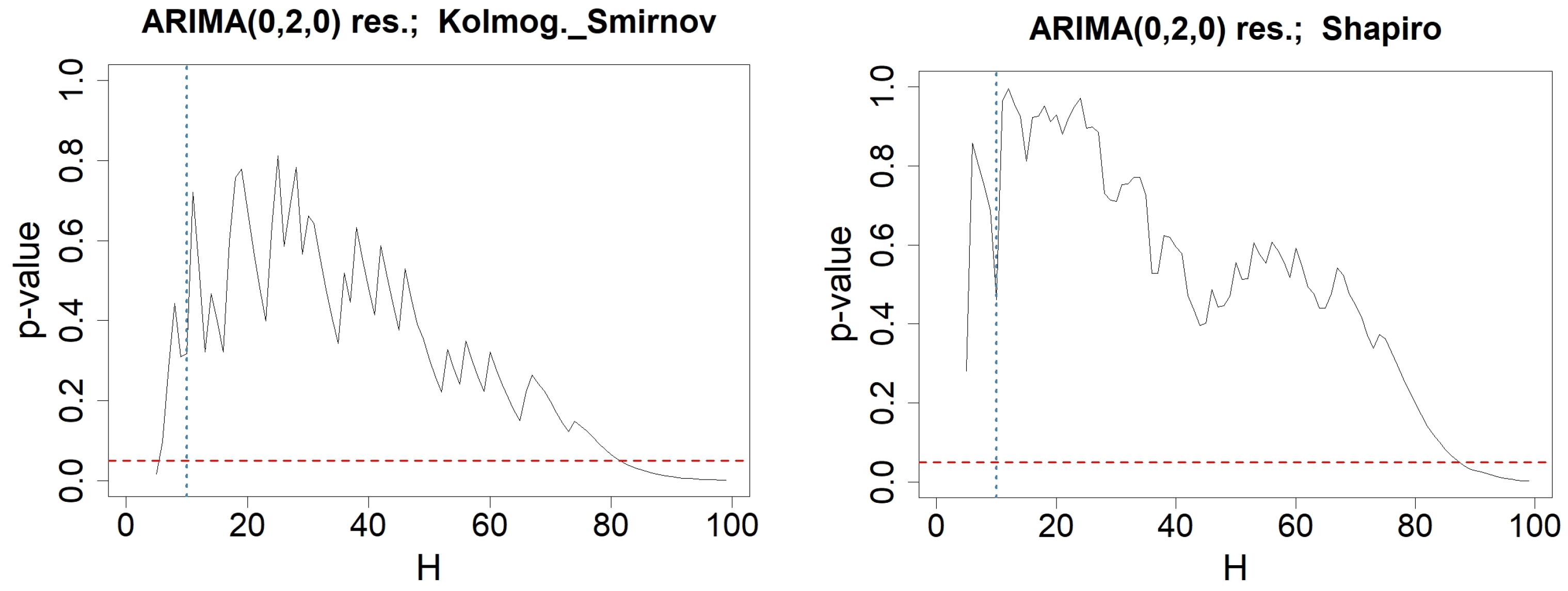
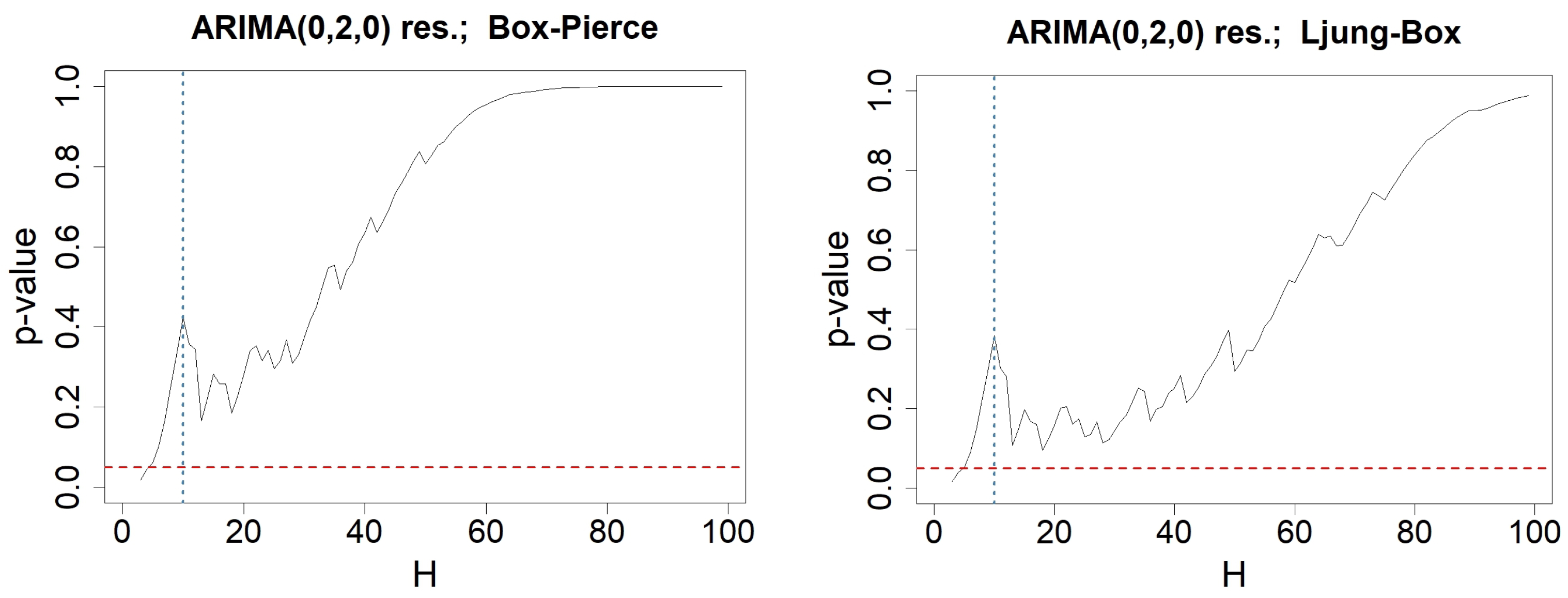
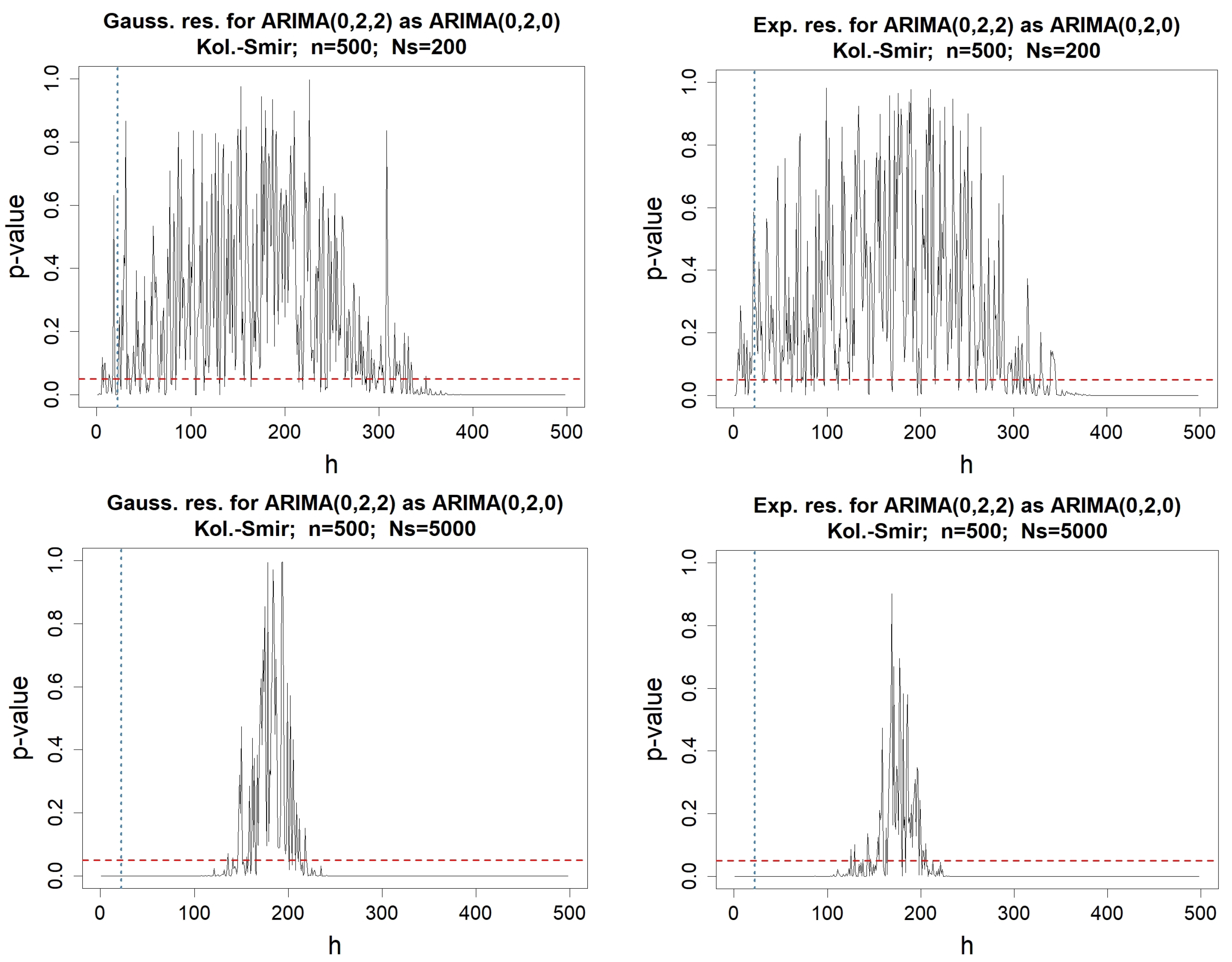
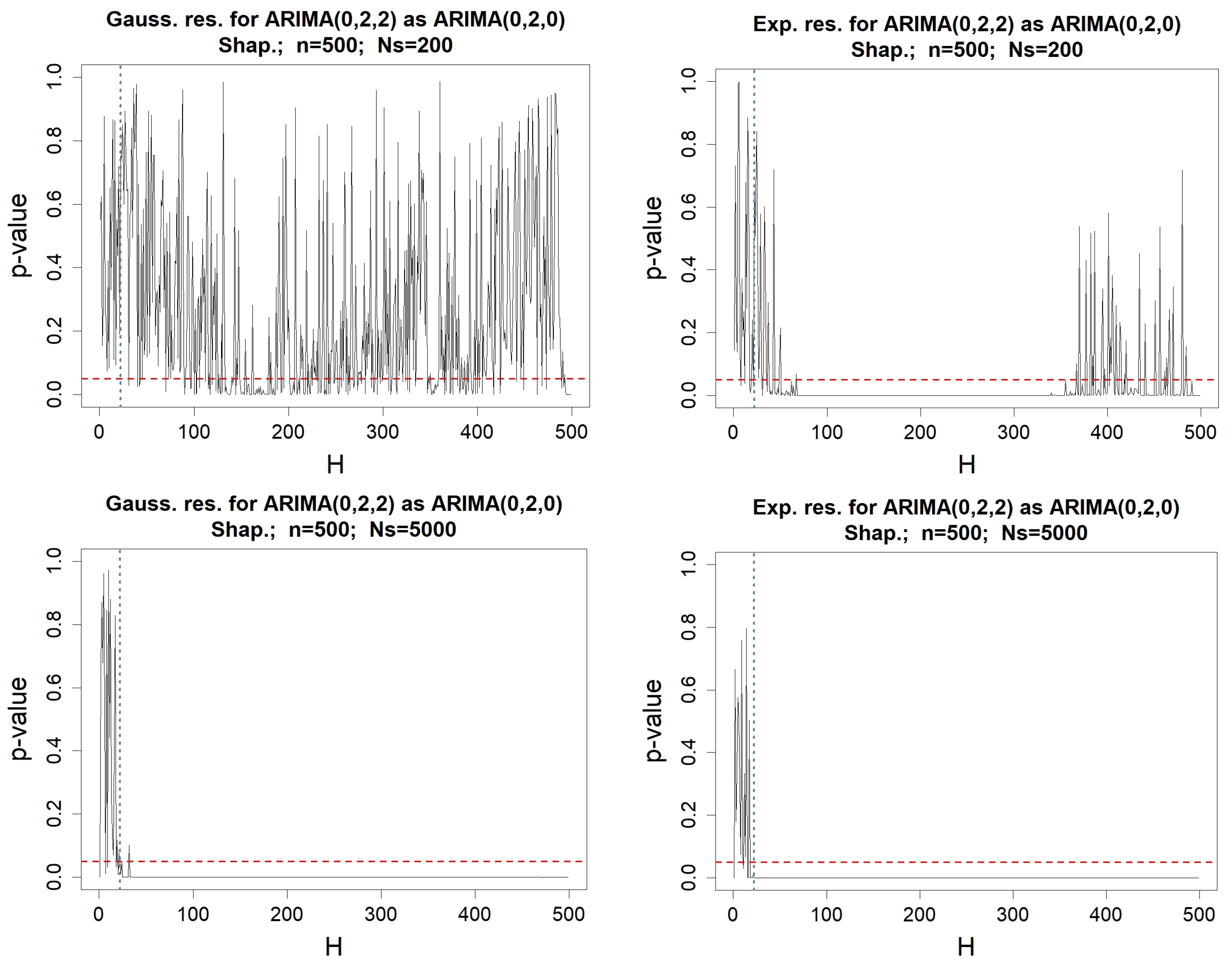
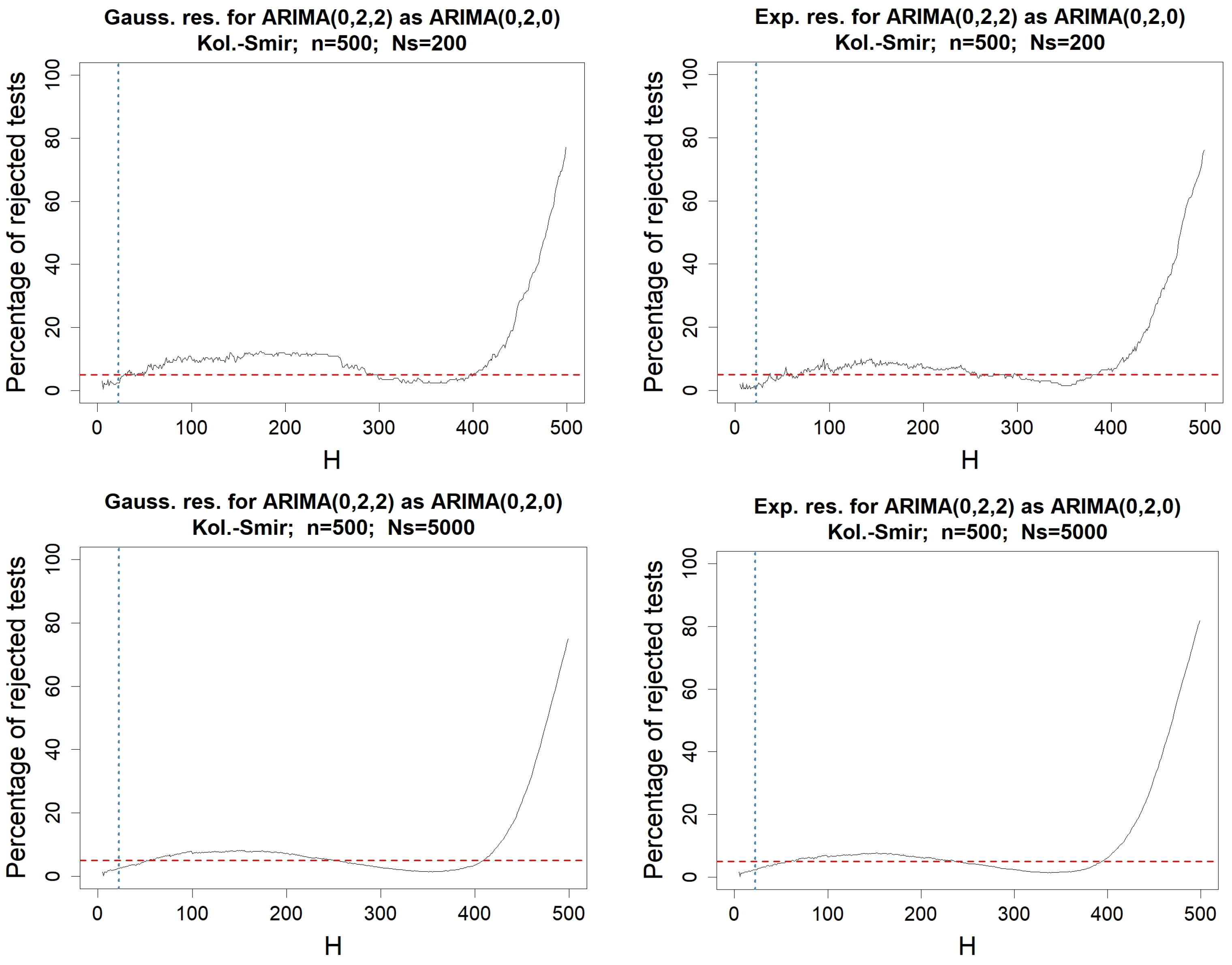
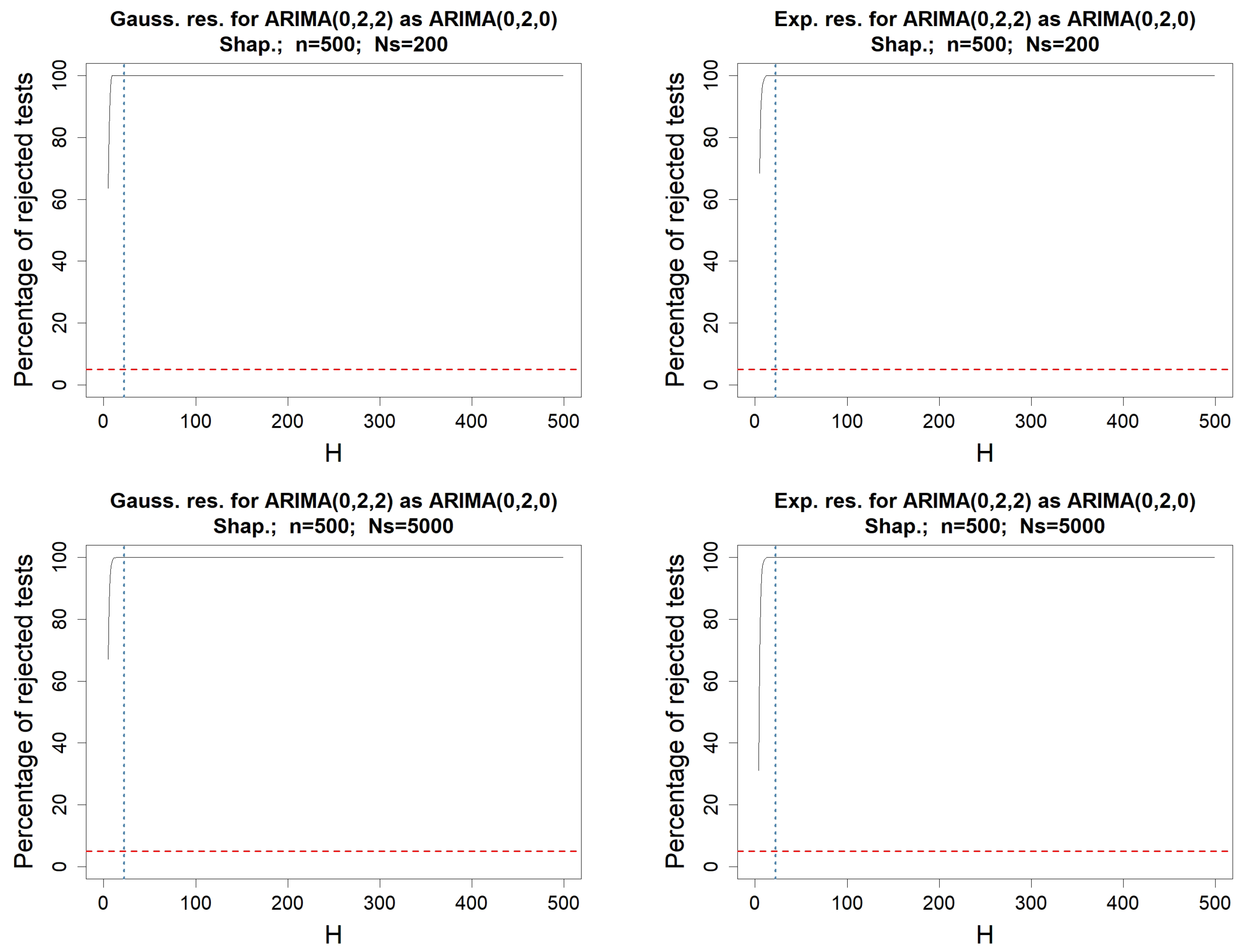
Appendix C. Testing-Procedures for Money Stock Modeled by an ARIMA(0,2,0)

| Model | RMSE | MAPE |
|---|---|---|
| ARIMA(0,2,2) | 0.095 | 0.122 |
| ARIMA(0,2,0) | 0.141 | 1.649 |
| AR(1) | 0.255 | 3.156 |
References
- Elsaraiti, M.; Musbah, H.; Merabet, A.; Little, T. Time Series Analysis of Electricity Consumption Forecasting Using ARIMA Model. IEEE Green Technol. Conf. 2021, 259–262. [Google Scholar] [CrossRef]
- Nelson, C.R.; Plosser, C.I. Trends and Random Walks in Macroeconomic Time Series: Some Evidence and Implications. J. Monet. Econ. 1982, 10, 139–162. [Google Scholar] [CrossRef]
- Ogunlana, S.O.; Oyebisi, T.O. Modelling and Forecasting Nigerian Electricity Demand Using Univariate Box-Jenkins Approach. J. Energy Technol. Policy 2013, 3, 84–91. [Google Scholar]
- Pena, D.; Rodriguez, J. Forecasting Traffic Flow by Using Time Series Models. Transp. Rev. 2001, 21, 293–317. [Google Scholar]
- Tsay, R. Analysis of Financial Time Series, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- Teyssière, G.; Kirman, A. Microeconomic models for long memory in the volatility of financial time series. Physics A 2002, 370, 26–31. [Google Scholar]
- Arunachalam, V.; Jaafar, A. Forecasting Dengue Incidence in Penang, Malaysia: A Comparison of ARIMA and GARCH Models. Am. J. Trop. Med. Hyg. 2011, 85, 827–833. [Google Scholar]
- Glass, G.V.; Willson, V.L.; Gottman, J.M. Design and Analysis of Time-Series Experiments. Annu. Rev. Psychol. 1975, 26, 609–653. [Google Scholar]
- Luis, C.O.; Francisco, G.S.; Jose, M.S. Forecasting of Emergency Department Admissions. Healthc. Manag. Sci. 2012, 15, 215–224. [Google Scholar]
- Campbell, J.Y.; Perron, P. An Empirical Investigation of the Relations between Climate Change and Agricultural Yield: A Time Series Analysis of Maize Yield in Nigeria. J. Agric. Environ. Sci. 2004, 5, 217–230. [Google Scholar]
- Zheng, X.; Basher, R.E. Structural Time Series Models and Trend Detection in Global and Regional Temperature Series. J. Clim. 1999, 12, 2347–2358. [Google Scholar] [CrossRef]
- Box, G.; Pierce, D. Distribution of Residual Autocorrelations in Autoregressive-Integrated Moving Average Time Series Models. J. Am. Statist. Assoc. 1970, 65, 1509–1526. [Google Scholar] [CrossRef]
- Brockwell, P.; Davis, R. Time Series: Theory and Methods, 2nd ed.; Springer: New York, NY. USA, 1991. [Google Scholar]
- Brockwell, P.J.; Davis, R.A. Introduction to Time Series and Forecasting; STS; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Chatfield, C. The Analysis of Time Series: An Introduction; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Hamilton, J.D. Time Series Analysis. Econom. Rev. 1994, 13, 147–192. [Google Scholar]
- Hassani, H. Sum of the sample of autocorrelation function. Random Oper. Stoch. Eqs. 2009, 17, 125–130. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice. Int. J. Forecast. 2018, 34, 587–590. [Google Scholar]
- Ljung, G.; Box, G. On a Measure of a Lack of Fit in Time Series Models. Biometrika 1978, 65, 297–303. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Jennings, C.L.; Kulahci, M. Introduction to Time Series Analysis and Forecasting; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Priestley, M.B. Spectral Analysis and Time Series. J. Time Ser. Anal. 1981, 2, 85–106. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications: With R Examples; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Wei, W.W.S. Time Series Analysis Univariate and Multivariate Methods, 2nd ed.; Addison Wesley: New York, NY, USA, 2006. [Google Scholar]
- Bisaglia, L.; Gerolimetto, M. Testing for Time Series Linearity Using the Autocorrelation Function. Stat. Methods Appl. 2009, 18, 23–50. [Google Scholar]
- Boutahar, M.; Royer-Carenzi, M. Identifying trends nature in time series using autocorrelation functions and stationarity tests. Int. J. Econ. Econom. 2024, 14, 1–22. [Google Scholar] [CrossRef]
- Kendall, M.G. Time-Series; Oxford University Press: Oxford, UK, 1976. [Google Scholar]
- McLeod, A.I.; Zhang, Y. Partial Autocorrelation Parameterization for Seasonal ARIMA Models. Int. J. Forecast. 2006, 22, 661–673. [Google Scholar]
- Granger, C.W.J.; Joyeux, R. An Introduction to Long-Memory Time Series Models and Fractional Differencing. J. Time Ser. Anal. 1980, 1, 15–29. [Google Scholar] [CrossRef]
- Hassani, H.; Yarmohammadi, M.; Mashald, L. Uncovering hidden insights with long-memory-proscess detection: An in-depth overview. Risks 2023, 11, 113. [Google Scholar] [CrossRef]
- Hosking, J. Asymptotic distribution of the sample mean, autocovariances, autocorrelations of long-memory time series. J. Econom. 1996, 73, 261–284. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Koutsoyiannis, D. Climacogram versus Autocovariance and Power Spectrum in Stochastic Modelling for Markovian and Hurst-Kolmogorov Processes. Stoch. Environ. Res. Risk Assess. 2015, 15, 1649–1669. [Google Scholar] [CrossRef]
- Liu, S.; Xie, Y.; Fang, H.; Du, H.; Xu, P. Trend Test for Hydrological and Climatic Time Series Considering the Interaction of Trend and Autocorrelations. Water 2022, 14, 3006. [Google Scholar] [CrossRef]
- Phojanamongkolkij, N.; Kato, S.; Wielicki, B.A.; Taylor, P.C.; Mlynczak, M.G. A Comparison of Climate Signal Trend Detection Uncertainty Analysis Methods. J. Clim. 2014, 27, 3363–3376. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, S.; Fang, H.; Wang, J. Global Autocorrelation Test Based on the Monte Carlo Method and Impacts of Eliminating Nonstationary Components on the Global Autocorrelation Test. Stoch. Environ. Res. Risk Assess. 2020, 34, 1645–1658. [Google Scholar] [CrossRef]
- Belmahdi, B.; Louzazni, M.; El Bouardi, A. One month-ahead forecasting of mean daily global solar radiation using time series models. Optik 2020, 219, 165207. [Google Scholar] [CrossRef]
- Gostischa, J.; Massolo, A.; Constantine, R. Multi-species feeding association dynamics driven by a large generalist predator. Front. Mar. Sci. 2021, 8, 739894. [Google Scholar] [CrossRef]
- Yang, Y.; Qin, S.; Liao, S. Ultra-chaos of a mobile robot: A higher disorder than normal-chaos. Chaos. Solitons Fractals 2023, 167, 113037. [Google Scholar] [CrossRef]
- Bai, M.; Zhou, Z.; Chen, Y.; Liu, J.; Yu, D. Accurate four-hour-ahead probabilistic forecast of photovoltaic power generation based on multiple meteorological variables-aided intelligent optimization of numeric weather prediction data. Earth Sci. Inform. 2023, 16, 2741–2766. [Google Scholar] [CrossRef]
- Orlando, G.; Bufalo, M. Empirical evidences on the interconnectedness between sampling and asset returns’s distributions. Risks 2021, 9, 88. [Google Scholar] [CrossRef]
- Wang, X.; Yang, J.; Yang, F.; Wang, Y.; Liu, F. Multilevel residual prophet network time series model for prediction of irregularities on high-speed railway track. J. Transp. Eng. Part Syst. 2023, 149, 04023012. [Google Scholar] [CrossRef]
- Li, W. Diagnostic Checks in Time Series; Monographs on Statistices and Applied Probability; Chapman & Hall: New York, NY, USA, 2004; Volume 102. [Google Scholar]
- Box, G.; Jenkins, G.; Reinsel, G.C. Time Series Analysis: Forecasting and Control, 3rd ed.; Prentice Hall: Englewood Clifs, NJ, USA, 1994. [Google Scholar]
- Shapiro, S.; Wilk, M. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Dallal, G.; Wilkinson, L. An analytic approximation to the distribution of lilliefors’ test for normality. Am. Stat. 1986, 40, 294–296. [Google Scholar] [CrossRef]
- Kolmogorov, A. Sulla determinazione empirica di una legge di distribuzione. G. Ist. Ital. Attuari 1933, 4, 83–91. [Google Scholar]
- Smirnov, N. Table for estimating the goodness of fit of empirical distributions. Ann. Math. Statist. 1948, 19, 279–281. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Dickey, D.A.; Fuller, W.A. Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root. Econometrica 1981, 49, 1057–1072. [Google Scholar] [CrossRef]
- Phillips, P.C.B.; Perron, P. Testing for a unit root in time series regression. Biometrika 1988, 75, 335–346. [Google Scholar] [CrossRef]
- Hassani, H.; Yeganegi, M. Sum of squared ACF and the Ljung-Box statistic. Physica A 2019, 520, 80–86. [Google Scholar] [CrossRef]
- Anderson, O. The box-jenkins approach to time series analysis. RAIRO 1977, 11, 3–29. [Google Scholar] [CrossRef]
- Hassani, H.; Yeganegi, M. Selecting optimal lag order in Ljung-Box test. Physica A 2020, 541, 123700. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassani, H.; Royer-Carenzi, M.; Mashhad, L.M.; Yarmohammadi, M.; Yeganegi, M.R. Exploring the Depths of the Autocorrelation Function: Its Departure from Normality. Information 2024, 15, 449. https://doi.org/10.3390/info15080449
Hassani H, Royer-Carenzi M, Mashhad LM, Yarmohammadi M, Yeganegi MR. Exploring the Depths of the Autocorrelation Function: Its Departure from Normality. Information. 2024; 15(8):449. https://doi.org/10.3390/info15080449
Chicago/Turabian StyleHassani, Hossein, Manuela Royer-Carenzi, Leila Marvian Mashhad, Masoud Yarmohammadi, and Mohammad Reza Yeganegi. 2024. "Exploring the Depths of the Autocorrelation Function: Its Departure from Normality" Information 15, no. 8: 449. https://doi.org/10.3390/info15080449
APA StyleHassani, H., Royer-Carenzi, M., Mashhad, L. M., Yarmohammadi, M., & Yeganegi, M. R. (2024). Exploring the Depths of the Autocorrelation Function: Its Departure from Normality. Information, 15(8), 449. https://doi.org/10.3390/info15080449







