Abstract
Integrated photonic chips leverage the recent developments in integrated circuit technology, along with the control and manipulation of light signals, to realize the integration of multiple optical components onto a single chip. By exploiting the power of light, integrated photonic chips offer numerous advantages over traditional optical and electronic systems, including miniaturization, high-speed data processing and improved energy efficiency. In this review, we survey the current status of quantum computation, optical neural networks and the realization of some algorithms on integrated optical chips.
1. Introduction
1.1. Background and Motivation
The rapid development of technology has given rise to two fields that hold the potential to significantly reshape the landscape of computation: quantum computing and machine learning. Quantum computing (QC) is a computational paradigm that leverages the principles of quantum mechanics to perform complex computations more efficiently than classical computers, particularly for specific problem domains [1]. Quantum computing has attracted much interest over the past decade due to possible quantum advantages in solving computationally complex problems using various models, including the qubit model on trapped ion systems [2,3] and super-conducting systems [4,5], measurement-based quantum computing [6,7], and Gaussian boson sampling (GBS) on a photonic platform [8]. Researchers have identified several quantum algorithms that outperform their classical counterparts, including Shor’s algorithm for integer factorization [9] and Grover’s algorithm for unstructured search [10]. By exploiting the quantum nature of multiple photons, such as quantum superposition, interference and entanglement, some quantum algorithms have been put forward to offer the potential to reduce computational time for problems in machine learning [11,12], chemistry [13,14] and other areas [15].
In parallel, machine learning (ML) has emerged as a type of artificial intelligence that can process large amounts of data and learn patterns from this data. This approach enables more accurate results in predicting outcomes without being explicitly programmed to do so. This technology is used in a wide range of applications, including recommendation systems, image recognition and autonomous vehicles [16,17].
The integration of quantum computing and machine learning can possibly unlock new opportunities and challenges for various application domains, such as healthcare and medical diagnosis, finance and risk assessment, telecommunications and networking, smart cities and transportation, environmental monitoring and climate modeling, etc. By combining the computational advantages of quantum computing with machine learning, this integrated approach has the potential to transform the way machine learning models are developed, trained and deployed.
Although quantum computing has been systematically studied from different perspectives, there are few existing reviews focusing on quantum computing and machine learning on an integrated photonics platform. However, in comparison with other physical platforms, such as superconducting and trapped-ion systems, photonic systems operate at room temperature and are generally less susceptible to lossy errors. Therefore, the photonic systems are worthy of exploration for quantum computing and quantum machine learning. In addition, the integrated platforms have the advantages of ultracompact size, high-density integration and high programmability, which make them more appealing for realizing a large-scale programmable quantum microprocessor. We thus provide a detailed review on the intersection of quantum computing and machine learning from the perspective of the integrated photonics platform. It is the hope of the authors that this comprehensive review will allow researchers to understand the status and challenges of quantum computing on silicon photonics platforms and, thus, inspire and contribute to their further development.
1.2. Objective and Scope of the Review
The objective of this review is to provide an integrative understanding of quantum computing and machine learning, exploring their fundamental principles, state-of-the-art techniques and emerging applications. Our aims are as follows:
- Discuss the current state of research in quantum computing and machine learning;
- Present case studies and experimental results that demonstrate the potential to integrate quantum computing;
- Examine the challenges and opportunities associated with integrating these technologies;
- Outline future directions and open research questions in this rapidly evolving field.
In this review, we aim to provide a comprehensive understanding of the principles, techniques and emerging applications of the integration of quantum computing and machine learning. We discuss the current state of research based on integrated photonic platforms in this rapidly evolving field, identify the challenges and opportunities associated with integrating these technologies and outline future directions and open research questions.
1.3. Organization of the Review
This review is organized into eight sections, and the structure is as follows:
- Section 2 provides an overview of the quantum mechanics principles and QC basics, including quantum superposition, quantum entanglement, quantum measurements, qubit, quantum gates and circuits and quantum algorithms and complexity;
- Section 3 provides an overview of quantum algorithms and complexity in terms of quantum machine learning and quantum optimization algorithms;
- Section 4 introduces the fundamental devices in integrated quantum photonic and typical quantum operations;
- Section 5 explores state-of-the-art chip-based quantum computing approaches and techniques;
- Section 6 highlights challenges and open issues in chip-based quantum computing, including quantum limitations and resource constraints, noise and error mitigations, model and data heterogeneity, standardization, interoperability and ethics and legal considerations;
- Section 7 outlines future directions and open research questions, such as quantum circuit optimization;
- Section 8 concludes the review by summarizing its key points and discussing the potential impact of quantum-assist computing in the field of machine learning.
2. Quantum Mechanics Principles and Quantum Computing Basics
2.1. Quantum Mechanics Principles
Quantum computing essentially harnesses some unique properties of quantum mechanics to gain a speedup for some specific computational problems compared to similar tasks on classical computers [18]. One such feature of quantum theory is superposition. Quantum superposition is a unique property of quantum mechanics [1] that allows a quantum state to be in multiple states at the same time until it is measured. This phenomenon is related to the wave-like nature of quantum particles, such as electrons or photons, which allows them to occupy different positions, energies or other properties at the same time. Mathematically, a quantum system’s state is represented by a vector in a complex Hilbert space, and the superposition principle implies that any linear combination of these basis vectors is also a valid state for the system. Superposition is crucial for understanding the behavior of quantum systems and is a key concept underlying many quantum phenomena, such as the so-called “quantum parallelism” and quantum entanglement.
Quantum entanglement is another unique phenomenon, in which the states of two or more qubits become intertwined, such that the state of one qubit cannot be described independently of the state of the other(s) [19]. Quantum entanglement gives rise to non-classical correlations. This property arises due to the superposition principle and has profound implications for quantum computing. Entangled qubits can be created through operations like the controlled-NOT (CNOT) gate and can be utilized to perform complex, correlated operations on multiple qubits simultaneously. Quantum entanglement may provide more efficient computation and communication, as well as novel protocols for secure information exchange and distributed computing [20], although the latter statement has never been rigorously proven.
Quantum measurement, also known as the “measurement problem”, is a key concept in quantum mechanics that describes the process of observing or measuring a quantum system [21]. Due to the superposition principle, a quantum system can exist in multiple states simultaneously until a measurement is performed. Upon measurement, the quantum system collapses into one of the possible states, with probabilities determined by the squared magnitudes of the coefficients associated with each state. This collapse is inherently probabilistic, and the outcome cannot be predicted with certainty. Quantum measurement challenges our classical understanding of how physical systems behave, and it is still a topic of ongoing research and debate.
2.2. Quantum Computing Basics
The fundamental unit of quantum computing is the quantum bit, or qubit, which, unlike classical bits, can represent not only 0 and 1 but also a superposition of both states [22]. Mathematically, a qubit can be described as a linear combination of its basis states and as
where and are complex numbers satisfying . This unique property allows quantum computers to process a vast amount of information simultaneously by encoding multiple possibilities in a single qubit, thus enabling them to solve problems that are intractable for classical computers [23].
Quantum gates are the fundamental operations used to manipulate the states of qubits in a controlled manner [24]. Unlike classical gates, which operate on bits, quantum gates operate on qubits and are represented as unitary matrices. Some common quantum gates include the Pauli-X, -Y and -Z gates, the Hadamard gate and the CNOT gate. These gates can be combined to form quantum circuits, which can then be used to implement quantum algorithms. Notably, quantum gates are reversible, meaning that they can transform a quantum state back to its original state, and the inverse of a quantum gate can easily be computed [25].
2.3. Quantum Computing with Linear Optics
A qubit is often encoded in photonics using a single photon with two optical modes. These modes can encompass various degrees of freedom, including time, polarization, frequency and orbital angular momentum [26,27,28]. This survey specifically concentrates on path encodings of a photon. To represent a qubit, it is common to use two waveguides, where the upper waveguide indicates a logical state of when a single photon is present and the lower waveguide represents a logical state of . Likewise, this definition can be extended to encompass the encoding of d-dimensional qubits when the photon can occupy d distinct waveguides (, , ⋯, ).
In linear photonic quantum information processing, the core operation is multipartite entangled states, considered as resources of quantum communication and computation. Due to the absence of nonlinearities, the generation of entanglement in photonics inherently relies on probabilistic methods [29]. A photonic implementation of a C-Phase two-qubit gate using interferometers is depicted in Figure 1b, whose scheme is developed in Refs. [30,31]. The interferometer in this setup has six modes and comprises three beam splitters with a transmissivity of 1/3. The two input qubits correspond to two photons that enter the four spatial modes of the interferometer. Specifically, the first qubit is associated with the top two spatial modes, while the second qubit is associated with the bottom two spatial modes. To ensure the proper definition of qubits in the output, only those output scenarios where one photon occupies the top two spatial modes and the other photon occupies the bottom two spatial modes are selectively considered, disregarding all other possible output results. The selective process, called post-selection, is a probabilistic way of generating entangled output configuration. It is easy to see that the success probability of the C-Phase is 1/9. Another basic requirement in quantum computation is the generation of multiple pairs of entangled photons, which is core to realizing graph states and error-protected qubits [32]. Figure 1c shows a simple scheme to produce an entangled qubit–pair source. Four coherently pumped spiral waveguides (1.5 cm long) initially have two pairs of maximally entangled photons. These photons are then spatially separated using integrated filters of asymmetric Mach–Zehnder interferometers (AMZIs) and Mach–Zehnder interferometers (MZIs). The entangled source is produced through the waveguide crossers. With these two simple examples, two key elements are identified in linear optical quantum computing: quantum interference in the linear optical circuits and post-selection. The measurements represent non-unitary operations, and such effective interaction is often called measurement-induced nonlinearity. However, this probabilistic post-selection limits the gate numbers and cascaded layers, which further limits the performance of universal quantum computation.
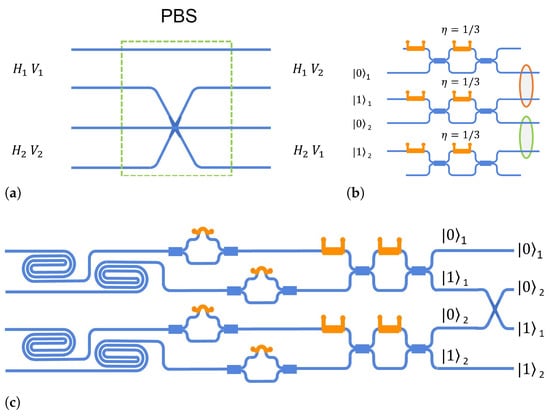
Figure 1.
Schematic of the integrated units performing gates and states. (a) On-chip polarizing beam splitter. (b) Probabilistic C-Phase entangling gate. (c) Bell state .
The detection system is a multi-channel superconducting single-photon detector. It can absorb an amount of energy equivalent to a single photon and convert it into an electrical signal in the superconducting circuit. Then, the signal is amplified and processed by the time tagger to measure the coincidence count.
3. Quantum Machine Learning
Quantum computing uses entanglement, superposition and interference to perform certain tasks significantly faster than classical computing, sometimes exponentially. In fact, although such speedups have been observed for a well-designed problem, for data science, achieving such speedups is still uncertain, even at a theoretical level. This is precisely one of the main goals in building quantum machine learning (QML) [33]. QML algorithms for universal quantum computers have been proposed and small-scale demonstrations have been implemented. Relaxing the requirement of universality, quantum machine learning for NISQ processors has emerged as a rapidly advancing field that may provide a plausible route towards practical quantum-enhanced machine learning systems. From the aspect of machine learning models, machine learning algorithms are classified into the three categories: supervised learning, unsupervised learning, reinforcement learning. From the aspect of quantum data encoding, the quantum machine learning is classified into discrete variable quantum computing and continuous variable quantum computing, as shown in Figure 2.
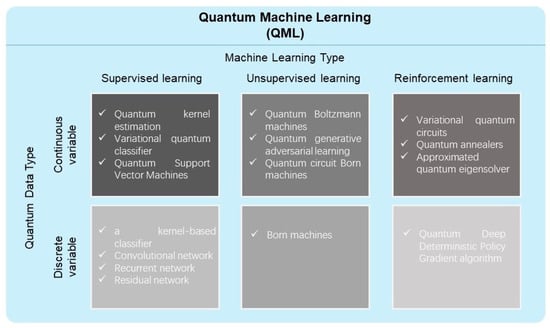
Figure 2.
Summary of various quantum machine learning tasks.
In Table 1, we present a comprehensive summary of quantum machine learning algorithms along with their diverse applications across various platforms. The subsequent section provides a succinct yet informative introduction to these quantum neural networks, shedding light on their unique attributes and applications within the quantum computing landscape.

Table 1.
Summary for quantum machine learning algorithms.
3.1. Quantum Neural Networks
For a classical neural network model, artificial neural networks (ANNs) are comprised of an input layer, one or more hidden layers and an output layer. The connections between layers have two parts: the linear part and the nonlinear part, as shown in Figure 3a. The linear part can be expressed by a vector–matrix multiplier. The nonlinear activation function is a nonlinear function. As a comparison, quantum neural networks (QNNs) combine the architecture of traditional neural networks with principles of quantum computing, thereby establishing a novel paradigm for data processing. QNNs are usually represented as variational circuits, which are parameterized quantum circuits that are optimized using classical optimization techniques (Figure 3b). The power of quantum neural networks is also an important open question, attracting significant attention. Currently, quantum neural networks have demonstrated their quantum advantage in specific tasks, as evidenced by recent studies [44,45].
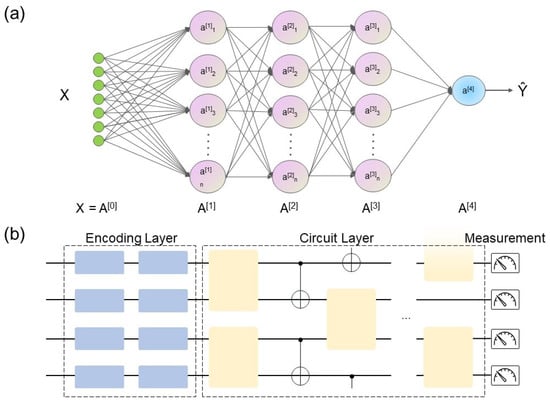
Figure 3.
The structure of classical neural networks and Variational Quantum Classifier.
3.2. Variational Quantum Classifier
Variational Quantum Classifier (VQC) [46] is a type of quantum machine learning algorithm that leverages the principles of quantum computing to perform classification tasks on data. VQC is built on the concept of variational circuits. The goal of a VQC is to find the optimal parameters that minimize a cost function, which typically represents the difference between the predicted output and the actual output for a given dataset. As shown in Figure 3, the structure of VQC consists of three parts, including the encoding layer, circuit layer and measurement, which correspond to the input layer, hidden layer and output layer of classical neural networks, respectively. The VQC algorithm can be broken down into the following steps:
- Data encoding: The classical data are encoded into a quantum state using a quantum feature map. This process translates the input features into a higher-dimensional Hilbert space, where quantum effects can be exploited for classification;
- Variational circuit: The parameterized quantum circuit, often referred to as the ansatz, processes the encoded quantum data. The circuit’s parameters are adjusted through the optimization process to minimize the cost function;
- Measurement: The output of the variational circuit is measured, collapsing the quantum state into a classical probability distribution. This measurement provides the predictions for the input data.
- Optimization: A classical optimization algorithm, such as gradient descent, is used to update the parameters of the variational circuit based on the cost function. This iterative process continues until the cost function converges to a minimum value, which signifies the best possible classification performance;
- Evaluation: Once the optimal parameters are found, the VQC can be evaluated on unseen data for classification tasks. Overall, the research on VQC has provided insights into the theoretical foundations and practical applications of this algorithmic approach. VQC is frequently utilized to build a QNN, which is a counterpart to the conventional neural network.
Variational Quantum Classifiers are promising for a variety of machine learning applications, particularly in cases where quantum advantages may lead to improved performance compared to classical ML algorithms.
3.3. Quantum Convolutional Neural Networks (QCNN)
QCNN [34] is an area of research that explores the potential of quantum computing to accelerate the training and inference of neural networks. Ref. [9] proposes a quantum version of the convolutional neural network (CNN), which is a widely used architecture in classical machine learning. The authors show that QCNN can achieve better performance than classical CNNs on certain image recognition tasks.
3.4. Quantum Long Short-Term Memory
Ref. [35] extends the classical LSTM into the quantum realm by replacing the classical neural networks in the LSTM cells with VQCs, which would play the roles of both feature extraction and data compression. In Ref. [36], the researchers demonstrate that a long short-term memory (LSTM) neural network can successfully learn to model quantum experiments by correctly predicting output state characteristics for given setups without the necessity of computing the states themselves.
3.5. Quantum Generative Adversarial Network (QGAN)
QGAN [37] is an emerging area of research that aims to apply the principles of quantum computing to the field of generative modeling. Refs. [37,38] introduce the notion of QGAN, where the data consist either of quantum states or of classical data, and the generator and discriminator are equipped with quantum information processors.
3.6. Quantum Transfer Learning
Ref. [39] extends the concept of transfer learning, widely applied in modern machine learning algorithms, to the emerging context of hybrid neural networks composed of classical and quantum elements. This paper proposes different implementations of hybrid transfer learning, but we focus mainly on the paradigm in which a pre-trained classical network is modified and augmented by a final variational quantum circuit.
3.7. Quantum Reinforcement Learning
Early versions of quantum reinforcement learning (RL) were based on the Grover algorithm, which resulted in a quadratic speedup compared to classical versions [47,48]. However, these methods could only be used for tasks with discrete action and state spaces. Subsequently, with the development of quantum neural networks, the QRL algorithm was extended to continuous space, rendering it more compatible with contemporary NISQ devices [40,41].
3.8. Hybrid Classical–Quantum Neural Network
Although there are many quantum analogs of the classical DNN, NISQ will be the only quantum devices that can be used in the near-term, where only a limited number of qubits without error-correcting can be used. For this reason, Ref. [42] introduces the quantum deep neural network (QDNN), which is a composition of multiple quantum neural network layers (QNNLs). Unlike other approaches of quantum analogs of DNNs, QDNN still keeps the advantages of the classical DNN such as the non-linear activation, the multi-layer structure and the efficient backpropagation training algorithm. The inputs and the outputs of the QDNN are both classical, which makes the QDNN more practical. Ref. [43] proposes a hybrid quantum–classical neural network architecture where each neuron is a variational quantum circuit.
4. Integrated Quantum Photonic Platforms
Recent years have seen remarkable strides in integrated photonic quantum technology. Figure 4 presents a timeline highlighting pivotal milestones, from the first implementation of two-photon quantum interference on an integrated photonic chip in 2008 [49] to the recent breakthroughs in large-scale quantum computing [50]. Currently, various optical platforms have been developed, primarily including silicon-on-insulator (SOI) [51,52,53,54,55], silica (SiO2) [49,56,57,58], silicon nitride (Si3N4) [59,60], lithium niobate (LN) [61,62] and others. An integrated photonic platform necessitates integrating essential photonic functional components like light sources, manipulation and detectors. Leveraging well-established manufacturing processes, the silicon-based photonic platform enables the integration of these essential functionalities onto a single chip, courtesy of its high-confinement silicon waveguides, high integration density, compatibility with metal-oxide-semiconductor (CMOS) fabrication techniques and scalability for mass production. The SOI platform, in particular, has reached a relatively mature stage of integration, showing consistent rapid advancements and promising potential for further development.
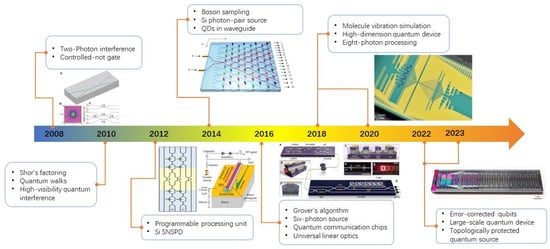
Figure 4.
Timeline of key demonstrations of integrated quantum photonics. Thees technologies include on-chip interference and CNOT gate [49], Shor’s algorithm [63], quantum walk [64], high visibility interference [65], on-chip SNSPD [54], boson sampling [66], on-chip QD source [67], Grover’s search algorithm [68], measurement of 6-photon on chip [69], quantum communication [70,71], universal linear optics [72], molecular vibronic dynamics [73], high-dimension quantum device [74], 8-photon processing [75], error-corrected qubits [76], large-scale quantum device [50] and topologically protected quantum source [77].
4.1. Fundamental Devices
A silicon-based photonic chip typically comprises devices such as waveguides, beam splitters, optical couplers and modulators. In this section, a concise overview is provided.
4.1.1. Waveguides
The optical waveguide serves as a fundamental component in a quantum photonic chip, and the integration of optical elements onto a single chip is achieved through the fabrication of optical waveguides. Common optical waveguides include strip and ridge waveguides, used, respectively, for passive and active optical devices. The characteristics of waveguides are determined by the materials used and the manufacturing techniques employed. Presently, owing to continuous technological advancements, photon absorption and losses in silicon-based waveguides have reached notably low levels [78]. Among these platforms, silicon-on-insulator (SOI) has emerged as a highly favored integrated quantum optics platform due to its compatibility with CMOS manufacturing techniques.
4.1.2. Beam Splitters
An optical beam splitter functions by dividing an incoming light beam into two or more separate beams, thereby distributing the input light across multiple output paths. The most widely employed beam splitter structure is the multimode interferometer (MMI). Other alternatives, such as directional couplers and Y-branch couplers, also exist. A typical photonic beam splitter is shown in Figure 5. It is a multi-mode interferometer (MMI) with specially designed interference length and multi-mode area that splits the photon into a superposition state. For a 50:50 beam splitter, its transformation matrix can be written as

Figure 5.
Multi-mode interferometer to split the light passively with a fixed ratio of 1:1.
The advantage of the MMI lies in its less stringent manufacturing requirements, exhibiting robustness against manufacturing errors. In 2012, the first on-chip MMI was experimentally demonstrated [79], followed by the design of optimized splitters to further enhance performance and reduce device size [80,81].
4.1.3. Phase Shifters
In addition to the MMI, the phase shifter is another component required for constructing a linear optical interferometer. A photonic phase shifter (PS) is shown in Figure 6. It is simply a waveguide with a TiN resistor fused to it. A current can flow through it using the Digital-to-Analogue Converter (DAC), and the latter generates heat and changes the refractive index of the surrounding waveguide. The changes in the optical path induce a phase difference . Its transformation matrix is written as
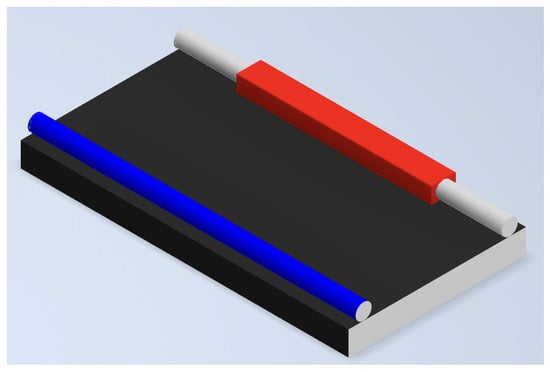
Figure 6.
Phase shifter to induce relative phase change between two arms.
In dual encoding, if the PS moves to the lower arm of the waveguide, its transformation matrix is adjusted accordingly so that the element becomes .
4.1.4. Modulator
A photonic modulator is a core device of integrated quantum photonics that enables encoding information onto optical signals for various applications in quantum information processing. The plasma dispersion (PD) effect is utilized in silicon-based modulators to achieve electro-optic modulation. By controlling the density of free carriers through an applied electric field, the phase or amplitude of light passing through the material can be modulated. In particular, silicon-based electro-optic modulators manipulate carrier density in their active regions to leverage this effect for modulation purposes. The commonly used optical structure for modulators is the Mach–Zehnder interferometer (MZI), which consists of the beam splitters and the phase shifters, as previously introduced. It enables the manipulation of photons with arbitrary splitting ratios and phase differences. The unit for MZI is formed by two beam splitters and two tunable phase shifts, and its transformation can be written as
According to Eular’s formula, the matrix elements in Equation (4) can be simplified to
Therefore, the can be written as
The splitting ratio is determined by the inner PS angle, , to be , and the phase difference between two output ports is . When the PS position is changed to add the at the front of the MZI structure, its transformation matrix can then be expressed as
The transformation matrices of BS and PS both satisfy the definition of a Unitary matrix, given by
and it is obvious that is also a Unitary matrix.
An N-mode integrated quantum photonic circuit is composed of several MZI structures, and it can form a complicated Unitary matrix, as shown in Figure 7. The nth MZI between modes i and j is denoted as . Its transformation matrix can be represented as an Identity matrix with four matrix elements replaced by , which is expressed as
where and . Therefore, the Unitary matrix of this N-mode photonic circuit can be represented as the product of MZI transform matrices in the designed orders as

Figure 7.
Typical schematic of an N-mode photonic integrated circuit to represent an arbitrary Unitary matrix. The final Unitary matrix form is the product of the matrices for each MZI component.
4.1.5. Coupler
An optical coupler is used to efficiently couple light in and out of optical waveguides on a chip. Its design aims to facilitate the transmission of light signals between the chip and external optical components. Edge couplers are typically implemented at the periphery or sidewall of a chip, facilitating the ingress or egress of light into/from the waveguide, thereby offering notable advantages such as enhanced efficiency and expanded bandwidth. However, it presents challenges in terms of fabrication processes. Over the past decade, researchers have extensively studied edge couplers and proposed various structural transformations, including edge couplers based on inverse taper with different nonlinear profiles [82] or consisting of double-tip inverse taper [83]. Grating coupling utilizes a grating structure to couple the light signal into the chip at a vertical angle. It offers advantages such as compact size and flexible coupling positions, but also has limitations like lower efficiency and narrower bandwidth. Currently, there are ongoing expansions in the applications of grating couplers, such as two-dimensional grating couplers [84] and polarization-splitting grating couplers [85].
4.2. Main Components
By utilizing the aforementioned fundamental devices, it becomes feasible to achieve silicon-based photonic quantum chips, thereby enabling applications such as large-scale quantum computing and quantum simulation. All of these applications require functionalities encompassing photon generation, manipulation and detection. In this paper, we provide a comprehensive introduction to each of these pivotal components.
4.2.1. Photon Source
Photon sources find extensive use across various applications, including boson sampling, quantum computing, quantum communication, etc. Depending on their application, there exist three primary techniques for preparing quantum light sources: spontaneous parametric down-conversion (SPDC), stimulated four-wave mixing (SFWM) and quantum dots. The first two methods of single-photon sources are probabilistic in nature, employing nonlinear processes to generate inherently correlated photon pairs. These methods excel in photon production while preserving high indistinguishability between photons. However, the generation of photon pairs through these two approaches involves a probabilistic approach, with a trade-off between generation probability and multi-photon purity. For quantum dot photon sources, the main mechanism is based on the emission of semiconductor material. A pair of carriers, called the exciton, is excited by the injected laser pulse in the quantum dot. The decay of the exciton then emits a single photon via the spontaneous emission process. This is a deterministic single-photon source that each laser pulse would generate, theoretically, only one photon each time. There have been reports that the best single-photon source has reached the detection efficiency of 0.5 for each laser pulse, considering all the collection efficiency, system loss and detection efficiency. However, the single-photon source also possesses its own drawbacks; for instance, it requires a critical working environment, with ultra-low temperature and high-vacuum chambers. It is difficult to maintain the indistinguishability of photons generated from separated quantum dots, and people usually take active de-multiplexing technologies to separate a single-photon source as a multi-photon source. Quantum dot can only generate single photons; it is unable to generate other non-classical quantum states such as the squeeze state, which is another fundamental resource for quantum photonic computing.
In this review, we focus on the nonlinear material that induces an optical conversion process called spontaneous four-wave mixing (SFWM). It would absorb two pump photons and generate a pair of signal and idler photons. This process is widely used for heralded single-photon source, entangled photon pair and squeezed quantum light source with low phase or amplitude noise beneath the standard quantum limit.
Based on the difference between signal and idler photon, the process can be divided into two categories: the non-degenerated SFWM as seen in Figure 8a, in which the two photons generated have the different wavelengths, and the degenerated SFWM as seen in Figure 8b, where the two photons have the identical wavelength. From the pump laser point of view, the non-degenerated SFWM is also called the single-pump scheme, as it only requires a single laser pulse to create the photon pair. The degenerated SFWM is called the dual-pump scheme, as the experimental set-up requires two laser pulses working simultaneously to create the photon pair.
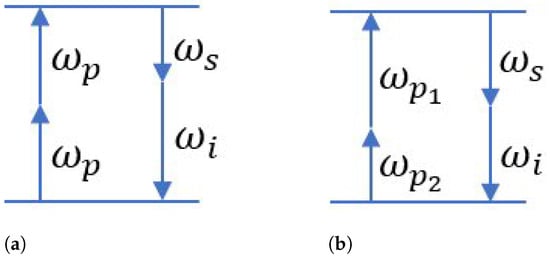
Figure 8.
(a) Non-degenerated and (b) degenerated spontaneous four-wave mixing process to generate photon pairs on chips by absorbing two pump photons.
The relation between pump frequency and generated photon frequency satisfies the laws of energy conservation and momentum conservation:
where k is called the wavevector. In waveguide modes, the momentum conservation is also called the phase-matching condition; these wavevectors are the propagation constant and is the effective index of the corresponding frequency decided by the material nonlinear property.
To realize the photon generation, the main problem is to achieve the phase-matching condition. Assuming the non-degenerated SFWM condition of and neglecting other nonlinear effects, the difference of propagation constant can be expressed as
By taking the Taylor expansion of , the phase-matching condition can be expressed as
where is expanded in . Due to the limitation of energy conservation law , the difference of frequency can be written as . Therefore, can be simplified as
where the higher order of terms is ignored. The second-order derivative, , is known as the group velocity dispersion (GVD) of the waveguide. By selecting the point where , can be achieved to meet the phase-matching condition.
By considering the higher-order terms for the derivative of propagation constant [86], the phase-matching condition can be written as
If the waveguide is designed to make and assume opposite signs and the magnitude is appropriately adjusted, phase matching can be achieved.
When the pump photon and generated photon are propagating in different modes, their propagation constants are unrelated to each other [87]. The phase-matching condition can thus be written as
If the propagation constant difference matching with the group velocity is found, the phase matching can be realized.
Finally, the waveguide parameter can be modulated periodically with quasi-phase-matching conditions [88], which are simplified as
where is the periodicity of poling designed to match .
For the simple case of , the approximation is taken, and the energy conservation in the wavelength domain is expressed as
The probability of the two-photon state is decided by the energy conservation and phase-matching condition, with expression given by
This is interpreted as the distribution of two-photon state at mode s and i, and the probability amplitude is called the Joint Spectra Amplitude (JSA). The latter is dictated by the law of energy conservation and phase matching, and it can be expressed as
where is the complex amplitude of the pump at the frequency . Usually, the pump spectrum is assumed to be a Gaussian distribution with a bandwidth decided by pump filter or laser property. is defined as
where it is determined by the phase-matching condition. L is the interaction length of waveguide. is the real measured probability of the photon pair and is called the Joint Spectra Intensity (JSI).
Taking all these factors into consideration, the state can be expressed as
where is called the squeeze operator on the mode n, and is the squeeze parameter, determined by the material nonlinearity, interaction length, pump energy density and so on. Depending on whether the squeeze parameter condition is filtered or resonated SFWM, the output state is given by
and, by writing , the state in photon number basis is expressed as
The probabilities for detecting n photons at mode s or mode i are the same, which can be expressed as
Following Equation (22), a maximum entangled two-photon state from an SFWM process can be written as
with different modes from 1 to n. And it is known that the state describing a composition system is decomposed as
where and are orthonormal basis states called Schmidt modes. The Schmidt coefficients are the “weights” of each subsystem satisfying . The degree of factorizability is called the Schmidt number K and is defined as
The photon purity P of this state is defined as
where represents and , indicating a perfectly pure two-photon state. If is measured, it means the state also contains other degrees of entangled photon pairs. For a maximally entangled state with the condition that and , , which indicates that the state has almost no purity (maximally mixed) and is not suitable for a heralded single-photon source.
In the weak pump regime, the multi-photon probability is relatively low and the purity P can be directly estimated as
where is called the second-order correlation. It is an experimentally measurable value that describes the statistics of photon pair correlations. From the reference [89], the can be written as
where is the probability of measuring coincidence counts at the delay time of and is the probability of measuring signal photon at the detector.
With the heralded photon measured, the remaining photon state can be used as a single-photon state, and the purity of this heralded single photon describes the quantity of single-photon against the multi-photon emission. It can be written as
where and are the probabilities of measuring coincidence count at the delay time of and is the probability of measuring signal photon.
The noise of the measured photon counts is estimated by coincidence to accidental ratio (). Coincidence counts between signal and idler photons from the same pair of photon generation are desired counts, while the spurious coincidence between time uncorrelated different pairs or other noises are called the accidental coincidences. The is defined as
where is the overall coincidence between signal channel and idler channel and is the accidental coincidence.
Currently, there are multiple platforms available for integrating SFWM, including UV-writing silica waveguides [69], Si [53,87] and SoI [90] platforms. To enhance the brightness of light sources and the purity of single-photon states, people have proposed long spiralled waveguides and microring resonators. Furthermore, to tackle the problem of non-deterministic photon production in parametric methods, various techniques such as time [91] or spatial [92] multiplexing have been implemented to enhance their performance.
4.2.2. Manipulation
Various degrees of freedom of photons such as path, polarization, frequency, spatial and temporal modes, etc., can be utilized for encoding quantum states. In particular, on silicon-based photonic chips, it is already possible to achieve encoding and manipulation of photon quantum states using multiple degrees of freedom. For instance, the path information of photons within parallel-transmitting multiple waveguides enables path-encoded quantum states. Different combinations of on-chip MZIs and phase shifters allow for arbitrary manipulation of path-encoded quantum states. As mentioned earlier, the optical circuit composing several MZIs are universal, meaning that the circuits can be programmed to achieve any Unitary evolution of quantum states encoded in m paths. There has been a study showing that an arbitrary Unitary circuit can be decomposed by MZIs with specific orders. Two of the main decomposition schemes are the Triangle Circuit [93] and the Square Circuit [94].
Compared to other encoding methods, the advantages of path encoding lie in its straightforward design, enabling high-precision programmable control. Moreover, it is currently extensively employed in the design of large-scale integrated silicon-photonics quantum chips.
4.2.3. Single-Photon Detector
Photon detection is the process of converting photon signals into electrical signals, which is a crucial step in quantum information processing that is aimed at retrieving information about quantum states. Single-photon detectors mainly include avalanche photodiodes (APDs) and superconducting nanowire single-photon detectors (SNSPD). Most APDs can operate at room temperature, but they exhibit low detection efficiency. At present, SNSPD is the most-studied device due to its advantages such as high detection efficiency, low time jitter, high signal-to-noise ratio, etc.
5. Recent Advances in Chip-Based Quantum-Assist Computational Works
With the progressive maturation of silicon-based integration technology, significant strides have been made in large-scale silicon quantum experiments, resulting in continuous enhancement of information processing capabilities and driving the advancement of optical quantum computing systems. In this section, we provide a comprehensive overview of recent advancements in silicon quantum photonics pertaining to the fields of quantum computing and machine learning.
In the early stages, experiments based on integrated silicon chips primarily focused on demonstrating fundamental gates for universal computation. For instance, work [49] implemented single-qubit and two-qubit gates using path encoding on an integrated chip. Following this, a demonstration was conducted using two integrated CNOT gates to execute the Shor factorization algorithm on an integrated waveguide silica-on-silicon chip [63]. However, these two examples implemented the unheralded CNOT scheme and and did not require auxiliary photons. A landmark achievement was the first implementation of the heralded quantum logic gates on a single SiO2 chip in 2015 [72]. This was also the first universal linear optical circuit to be realized on a silicon-based integrated chip, which is constructed by a cascade of 15 MZIs across 6 modes. Meanwhile, large-scale programmable integrated photonics quantum computing is gradually flourishing. In 2018, Qiang et al. achieved the first universal two-qubit silicon-based photonic quantum computing chip using large-scale silicon-based integrated optical technology [95]. This work realized the generation of entangled photons, photon state preparation, manipulation and measurement on a single chip. This laid the foundation for the feasibility of large-scale, high-precision, programmable photonic quantum computation using silicon-based photonic chip technology.
With the advent of the noisy intermediate-scale quantum (NISQ) era, various platforms have emerged as choices to showcase quantum advantages in this period, and silicon-based quantum optical platforms are also important candidates. Currently, silicon-based photonic quantum computing has been widely applied in areas such as quantum neural networks [96], variational algorithms [97] and coherent Ising machines [98]. In particular, neural networks stands as a crucial area in current quantum computing research. Here, we focus on optical neural networks that utilize the principle of optical coherence to perform linear matrix operations in photonics circuits [93,94]. In 2017, Shen et al. proposed an on-chip integrated optical neural network constructed by a cascaded array of 56 programmable MZIs, where the parameters of this neural network were real numbers [99]. This work successfully conducted experiments using a two-layer fully connected neural network to solve the vowel recognition task. However, due to the influence of noise, the accuracy was only 76.6%. In 2021, work [100] developed fully connected complex-valued neural networks based on an integrated silicon photonics platform. The optical neural networks presented here are capable of processing information in both phase and magnitude, resulting in significantly improved computational speed and energy efficiency. Simultaneously, various optical neural networks with Fourier transform and convolution structures have also been proposed [101,102]. However, these approaches are limited by space consumption and the difficulty in real-time programming. To tackle these challenges, work [103] proposed an integrated diffractive optical network utilizing silicon chips with integrated ultracompact diffractive cells and programmable MZIs. This scheme enables parallel Fourier transformation and convolution operations. What originally required a linear matrix calculation using N2 cascaded MZIs has now been reduced to using two ultracompact diffractive cells and N MZIs. This significantly minimizes the size of integrated photonic chips and reduces energy consumption. The effective training of these photon neural networks is another crucial issue that deserves attention. A gradient-free training scheme was proposed in Ref. [104], which is an efficient, physics-agnostic and closed-loop protocol for training optical neural networks on chip. In addition to the aforementioned neural networks, silicon-based optical chips can also be utilized for the implementation of machine learning models such as quantum autoencoders [105]. Moreover, photonic neural networks are specifically tailored for addressing diverse machine learning tasks, encompassing prediction of molecular properties [106] and classification of financial data [107].
Boson sampling is also an important computational task [108]. It is widely known that sampling from a distribution that is obtainable by photons propagating through a linear optical network becomes classically intractable as the photon number increases, which suggests that a photonic experiment implementing a Unitary evolution of input photons can be a viable candidate to demonstrate quantum advantage [109]. At present, the experimental demonstration of boson sampling is mainly based on integrated photon platforms [66,110,111,112,113,114,115]. Recently, Paesani et al., achieved the generation of an eight-photon state and implemented the Gaussian boson sampling algorithm on a silicon-based photonic chip [75]. Another set of the latest results is from Wang et al., who realized a large-scale programmable silicon-based photonic chip based on graph theory, integrating approximately 2500 components in a single device [50]. This work demonstrates multi-photon high-dimensional quantum entanglement preparation and programmable boson sampling for specialized quantum computing. In addition, the application of photon sampling problems has been extensively studied in the fields of graph theory [116,117,118,119,120] and quantum simulation [121,122].
Furthermore, utilizing quantum algorithms for molecular simulation is an intriguing research direction. Typically, phase estimation [9] or variational quantum eigensolvers [97] are employed to find the eigenvalues and eigenvectors of a Hamiltonian. Both these algorithms have been implemented on silicon-based devices [123,124]. Recently, an experimental realization of a combined scheme that incorporates these two algorithms has demonstrated remarkable fidelity, exceeding 99% in approximating ground- and excited-state eigenvalues [125].
6. Challenges and Open Issues
6.1. Quantum Hardware Limitations and Resource Constraints
- (1)
- Limited qubits:
- a.
- Scalability: Scaling up the number of qubits in a quantum computer is a significant challenge due to the need for error correction and fault tolerance;
- b.
- System size: The limited number of qubits impacts the size and complexity of quantum federated learning algorithms that can be executed, hindering the ability to solve larger problems;
- c.
- Resource-efficient algorithms: Designing quantum algorithms that are resource-efficient in terms of qubits; gates can help mitigate these limitations.
- (2)
- Coherence time:
- a.
- Quantum gate operations: The short coherence time limits the number of quantum gate operations that can be performed before the quantum state becomes decoherent, impacting the complexity of quantum federated learning algorithms;
- b.
- Qubit materials and designs: Investigating novel qubit materials and designs that exhibit longer coherence times can help overcome the limitations posed by decoherence in quantum computations;
- c.
- Environmental noise: Reducing the impact of environmental noise on quantum hardware can help extend coherence times and improve the performance of quantum algorithms;
- d.
- Dynamical decoupling: Exploring dynamical decoupling techniques, which involve applying a sequence of control pulses to mitigate the effects of noise, can contribute to the preservation of quantum states during computations.
- (3)
- Connectivity:
- a.
- Topology: Quantum hardware architectures may have different qubit connectivity topologies, which can impact the performance of quantum algorithms, including quantum federated learning;
- b.
- Hardware-aware algorithms: Developing hardware-aware algorithms that consider qubit connectivity can help optimize the implementation of quantum federated learning on various quantum devices.
6.2. Noise and Error Mitigation
- (1)
- Error correction:
- a.
- Fault-tolerant quantum computation: Developing fault-tolerant quantum computation techniques, which allow for the execution of quantum algorithms despite the presence of errors, is crucial for the practical implementation of quantum federated learning;
- b.
- Resource overhead reduction: Investigating methods to reduce the resource overhead associated with quantum error correction, such as optimized encoding schemes and error-correction-friendly quantum circuit designs, can enable the efficient integration of error correction into quantum federated learning algorithms.
- (2)
- Error-aware training:
- a.
- Noise extrapolation: Techniques such as Richardson extrapolation and zero-noise extrapolation can be used to estimate and mitigate the impact of noise on quantum federated learning algorithms;
- b.
- Error-aware training: Developing error-aware training techniques that incorporate noise models into the learning process can help enhance the performance of quantum federate learning algorithms in noisy environments.
Addressing these challenges and open issues in greater detail will help drive significant advancements in the field of quantum machine learning. Ongoing research and development efforts will be essential for overcoming these obstacles and realizing the full potential of quantum-enhanced federated learning in various applications and industries.
7. Open Opportunities and Future Directions
Integrated photonics is a rapidly evolving field with several open opportunities and future directions. Some key areas include the following:
- (1)
- Higher Integration Technologies:
- a.
- Increased complexity: Developing more complex integrated photonics circuits with higher component counts to enable advanced functionalities;
- b.
- Multi-functional chips: Designing chips that serve multiple purposes, integrating various components on a single platform.
- (2)
- Novel Materials and Components with Explorative New Materials: Researching novel materials with unique optical properties to enhance device performance. In addition, it is possible to explore the implementation of heterogeneous integrated photonic chips based on multiple material systems;
- (3)
- Machine Learning Assistance Using machine learning technologies: Combining machine learning algorithms with integrated optical devices can improve the performance of quantum machines.
8. Conclusions
Integrated photonic quantum technologies provides a new pathway for quantum computing and machine learning, harnessing the innate properties of photons to achieve rapid information processing and transmission. The silicon-based photon platform exhibits significant promise in this domain, as evidenced by our comprehensive review summarizing the latest advancements. Furthermore, we highlight some opportunities and challenges faced by integrated photonic quantum technology currently, seeking to offer novel perspectives for future advancements in this field. With ongoing technological progress, we firmly anticipate that integrated chip technology will assume an increasingly pivotal role across diverse applications.
Author Contributions
The paper has been conceptualized by H.Z. (Huihui Zhu), L.C.K. and A.L. The review of techniques and methodologies were performed by H.Z. (Huihui Zhu), H.L., W.L., Y.Z., H.Z. (Hui Zhang) and S.W., numerical checks were carried out by H.Z. (Huihui Zhu), S.W., W.L. and H.Z. (Hui Zhang) and validation was performed by X.W. and Y.Z. The final manuscript was written by H.Z. (Huihui Zhu), H.L. and S.W., with review and editing by X.W., L.C.K. and A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Education, Singapore and the National Research Foundation, Singapore. We also acknowledge generous support under NRF2022-QEP2-02-P16.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data supporting this study’s findings are available from the corresponding authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Wright, K.; Beck, K.M.; Debnath, S.; Amini, J.; Nam, Y.; Grzesiak, N.; Chen, J.S.; Pisenti, N.; Chmielewski, M.; Collins, C.; et al. Benchmarking an 11-qubit quantum computer. Nat. Commun. 2019, 10, 5464. [Google Scholar] [CrossRef]
- Kielpinski, D.; Monroe, C.; Wineland, D.J. Architecture for a large-scale ion-trap quantum computer. Nature 2002, 417, 709–711. [Google Scholar] [CrossRef] [PubMed]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Clarke, J.; Wilhelm, F.K. Superconducting quantum bits. Nature 2008, 453, 1031–1042. [Google Scholar] [CrossRef] [PubMed]
- Asavanant, W.; Shiozawa, Y.; Yokoyama, S.; Charoensombutamon, B.; Emura, H.; Alexander, R.N.; Takeda, S.; Yoshikawa, J.I.; Menicucci, N.C.; Yonezawa, H.; et al. Generation of time-domain-multiplexed two-dimensional cluster state. Science 2019, 366, 373–376. [Google Scholar] [CrossRef] [PubMed]
- Larsen, M.V.; Guo, X.; Breum, C.R.; Neergaard-Nielsen, J.S.; Andersen, U.L. Deterministic generation of a two-dimensional cluster state. Science 2019, 366, 369–372. [Google Scholar] [CrossRef] [PubMed]
- Kruse, R.; Hamilton, C.S.; Sansoni, L.; Barkhofen, S.; Silberhorn, C.; Jex, I. Detailed study of Gaussian boson sampling. Phys. Rev. A 2019, 100, 032326. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; IEEE: Piscataway, NJ, USA, 1994; pp. 124–134. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Schuld, M.; Killoran, N. Quantum machine learning in feature Hilbert spaces. Phys. Rev. Lett. 2019, 122, 040504. [Google Scholar] [CrossRef] [PubMed]
- Cerezo, M.; Verdon, G.; Huang, H.Y.; Cincio, L.; Coles, P.J. Challenges and opportunities in quantum machine learning. Nat. Comput. Sci. 2022, 2, 567–576. [Google Scholar] [CrossRef]
- Lanyon, B.P.; Whitfield, J.D.; Gillett, G.G.; Goggin, M.E.; Almeida, M.P.; Kassal, I.; Biamonte, J.D.; Mohseni, M.; Powell, B.J.; Barbieri, M.; et al. Towards quantum chemistry on a quantum computer. Nat. Chem. 2010, 2, 106–111. [Google Scholar] [CrossRef]
- Abrams, D.S.; Lloyd, S. Simulation of many-body Fermi systems on a universal quantum computer. Phys. Rev. Lett. 1997, 79, 2586. [Google Scholar] [CrossRef]
- Zhang, S.; Li, L. A brief introduction to quantum algorithms. CCF Trans. High Perform. Comput. 2022, 4, 53–62. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- El Naqa, I.; Murphy, M.J. What Is Machine Learning? Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Verstraete, F.; Wolf, M.M.; Ignacio Cirac, J. Quantum computation and quantum-state engineering driven by dissipation. Nat. Phys. 2009, 5, 633–636. [Google Scholar] [CrossRef]
- Zhonglin, B. Quantum-Mechanical Description of Physical Reality Shall Be Considered Complete. Int. J. Phys. 2022, 10, 174–181. [Google Scholar]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]
- Davies, E. Information and quantum measurement. IEEE Trans. Inf. Theory 1978, 24, 596–599. [Google Scholar] [CrossRef]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. phys 2018, 21, 6–7. [Google Scholar]
- Vos, J. Quantum Computing in Action; Simon and Schuster: New York, NY, USA, 2022. [Google Scholar]
- Hayashi, M.; Ishizaka, S.; Kawachi, A.; Kimura, G.; Ogawa, T. Introduction to Quantum Information Science; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Zhong, Y.; Chang, H.S.; Bienfait, A.; Dumur, É.; Chou, M.H.; Conner, C.R.; Grebel, J.; Povey, R.G.; Yan, H.; Schuster, D.I.; et al. Deterministic multi-qubit entanglement in a quantum network. Nature 2021, 590, 571–575. [Google Scholar] [CrossRef]
- Barreiro, J.T.; Wei, T.C.; Kwiat, P.G. Beating the channel capacity limit for linear photonic superdense coding. Nat. Phys. 2008, 4, 282–286. [Google Scholar] [CrossRef]
- O’brien, J.L.; Furusawa, A.; Vučković, J. Photonic quantum technologies. Nat. Photonics 2009, 3, 687–695. [Google Scholar] [CrossRef]
- Wang, X.L.; Cai, X.D.; Su, Z.E.; Chen, M.C.; Wu, D.; Li, L.; Liu, N.L.; Lu, C.Y.; Pan, J.W. Quantum teleportation of multiple degrees of freedom of a single photon. Nature 2015, 518, 516–519. [Google Scholar] [CrossRef]
- Tokunaga, Y.; Yamamoto, T.; Koashi, M.; Imoto, N. Simple experimental scheme of preparing a four-photon entangled state for the teleportation-based realization of a linear optical controlled-NOT gate. Phys. Rev. A 2005, 71, 030301. [Google Scholar] [CrossRef]
- Ralph, T.C.; Langford, N.K.; Bell, T.; White, A. Linear optical controlled-NOT gate in the coincidence basis. Phys. Rev. A 2002, 65, 062324. [Google Scholar] [CrossRef]
- Hofmann, H.F.; Takeuchi, S. Quantum phase gate for photonic qubits using only beam splitters and postselection. Phys. Rev. A 2002, 66, 024308. [Google Scholar] [CrossRef]
- Vigliar, C.; Paesani, S.; Ding, Y.; Adcock, J.C.; Wang, J.; Morley-Short, S.; Bacco, D.; Oxenløwe, L.K.; Thompson, M.G.; Rarity, J.G.; et al. Error-protected qubits in a silicon photonic chip. Nat. Phys. 2021, 17, 1137–1143. [Google Scholar] [CrossRef]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef]
- Oh, S.; Choi, J.; Kim, J. A tutorial on quantum convolutional neural networks (QCNN). In Proceedings of the 2020 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Republic of Korea, 21–23 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 236–239. [Google Scholar]
- Chen, S.Y.C.; Yoo, S.; Fang, Y.L.L. Quantum long short-term memory. In Proceedings of the ICASSP 2022-2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 8622–8626. [Google Scholar]
- Adler, T.; Erhard, M.; Krenn, M.; Brandstetter, J.; Kofler, J.; Hochreiter, S. Quantum Optical Experiments Modeled by Long Short-Term Memory. Photonics 2021, 8, 535. [Google Scholar] [CrossRef]
- Lloyd, S.; Weedbrook, C. Quantum generative adversarial learning. Phys. Rev. Lett. 2018, 121, 040502. [Google Scholar] [CrossRef] [PubMed]
- Dallaire-Demers, P.L.; Killoran, N. Quantum generative adversarial networks. Phys. Rev. A 2018, 98, 012324. [Google Scholar] [CrossRef]
- Mari, A.; Bromley, T.R.; Izaac, J.; Schuld, M.; Killoran, N. Transfer learning in hybrid classical-quantum neural networks. Quantum 2020, 4, 340. [Google Scholar] [CrossRef]
- Jerbi, S.; Gyurik, C.; Marshall, S.; Briegel, H.; Dunjko, V. Parametrized quantum policies for reinforcement learning. Adv. Neural Inf. Process. Syst. 2021, 34, 28362–28375. [Google Scholar]
- Wu, S.; Jin, S.; Wen, D.; Han, D.; Wang, X. Quantum reinforcement learning in continuous action space. arXiv 2020, arXiv:2012.10711. [Google Scholar]
- Zhao, C.; Gao, X.S. Qdnn: Deep neural networks with quantum layers. Quantum Mach. Intell. 2021, 3, 15. [Google Scholar] [CrossRef]
- Arthur, D. A hybrid quantum-classical neural network architecture for binary classification. arXiv 2022, arXiv:2201.01820. [Google Scholar]
- Abbas, A.; Sutter, D.; Zoufal, C.; Lucchi, A.; Figalli, A.; Woerner, S. The power of quantum neural networks. Nat. Comput. Sci. 2021, 1, 403–409. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Arunachalam, S.; Temme, K. A rigorous and robust quantum speed-up in supervised machine learning. Nat. Phys. 2021, 17, 1013–1017. [Google Scholar] [CrossRef]
- Blance, A.; Spannowsky, M. Quantum machine learning for particle physics using a variational quantum classifier. J. High Energy Phys. 2021, 2021, 212. [Google Scholar] [CrossRef]
- Dunjko, V.; Taylor, J.M.; Briegel, H.J. Advances in quantum reinforcement learning. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 282–287. [Google Scholar]
- Dong, D.; Chen, C.; Li, H.; Tarn, T.J. Quantum reinforcement learning. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2008, 38, 1207–1220. [Google Scholar] [CrossRef] [PubMed]
- Politi, A.; Cryan, M.J.; Rarity, J.G.; Yu, S.; O’Brien, J.L. Silica-on-Silicon Waveguide Quantum Circuits. Science 2008, 320, 646–649. [Google Scholar] [CrossRef] [PubMed]
- Bao, J.; Fu, Z.; Pramanik, T.; Mao, J.; Chi, Y.; Cao, Y.; Zhai, C.; Mao, Y.; Dai, T.; Chen, X.; et al. Very-large-scale integrated quantum graph photonics. Nat. Photonics 2023, 17, 573–581. [Google Scholar] [CrossRef]
- Takesue, H.; Tokura, Y.; Fukuda, H.; Tsuchizawa, T.; Watanabe, T.; Yamada, K.; Itabashi, S.i. Entanglement generation using silicon wire waveguide. Appl. Phys. Lett. 2007, 91, 201108. [Google Scholar] [CrossRef]
- Bonneau, D.; Engin, E.; Ohira, K.; Suzuki, N.; Yoshida, H.; Iizuka, N.; Ezaki, M.; Natarajan, C.M.; Tanner, M.G.; Hadfield, R.H.; et al. Quantum interference and manipulation of entanglement in silicon wire waveguide quantum circuits. New J. Phys. 2012, 14, 045003. [Google Scholar] [CrossRef]
- Silverstone, J.W.; Bonneau, D.; Ohira, K.; Suzuki, N.; Yoshida, H.; Iizuka, N.; Ezaki, M.; Natarajan, C.M.; Tanner, M.G.; Hadfield, R.H.; et al. On-chip quantum interference between silicon photon-pair sources. Nat. Photonics 2014, 8, 104–108. [Google Scholar] [CrossRef]
- Pernice, W.H.; Schuck, C.; Minaeva, O.; Li, M.; Goltsman, G.; Sergienko, A.; Tang, H. High-speed and high-efficiency travelling wave single-photon detectors embedded in nanophotonic circuits. Nat. Commun. 2012, 3, 1325. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Feng, L.T.; Zhou, Z.Y.; Chen, Y.; Wu, H.; Li, M.; Gao, S.M.; Guo, G.P.; Guo, G.C.; Dai, D.X.; et al. Generation of multiphoton quantum states on silicon. Light Sci. Appl. 2019, 8, 41. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Shao, L.; Zhang, S.X.; Yi, X.; Wiersig, J.; Wang, L.; Gong, Q.; Lončar, M.; Yang, L.; Xiao, Y.F. Chaos-assisted broadband momentum transformation in optical microresonators. Science 2017, 358, 344–347. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Cao, Q.T.; Wang, Z.; Liu, Y.x.; Qiu, C.W.; Yang, L.; Gong, Q.; Xiao, Y.F. Symmetry-breaking-induced nonlinear optics at a microcavity surface. Nat. Photonics 2019, 13, 21–24. [Google Scholar] [CrossRef]
- Li, M.; Li, C.; Chen, Y.; Feng, L.T.; Yan, L.; Zhang, Q.; Bao, J.; Liu, B.H.; Ren, X.F.; Wang, J.; et al. On-chip path encoded photonic quantum Toffoli gate. Photonics Res. 2022, 10, 1533–1542. [Google Scholar] [CrossRef]
- Lu, X. Chip-integrated visible-telecom entangled photon pair source for quantum communication. In Proceedings of the Photonics for Quantum 2019, New York, NY, USA, 23–25 January 2019; SPIE: Bellingham, WA, USA, 2021; Volume 11917, p. 119170Z. [Google Scholar]
- Zhang, X.; Bell, B.A.; Mahendra, A.; Xiong, C.; Leong, P.H.W.; Eggleton, B.J. Integrated silicon nitride time-bin entanglement circuits. Opt. Lett. 2018, 43, 3469–3472. [Google Scholar] [CrossRef]
- Höpker, J.P.; Bartnick, M.; Meyer-Scott, E.; Thiele, F.; Krapick, S.; Montaut, N.; Santandrea, M.; Herrmann, H.; Lengeling, S.; Ricken, R.; et al. Towards integrated superconducting detectors on lithium niobate waveguides. arXiv 2017, arXiv:1708.06232. [Google Scholar]
- Jin, H.; Liu, F.M.; Xu, P.; Xia, J.L.; Zhong, M.L.; Yuan, Y.; Zhou, J.W.; Gong, Y.X.; Wang, W.; Zhu, S.N. On-Chip Generation and Manipulation of Entangled Photons Based on Reconfigurable Lithium-Niobate Waveguide Circuits. Phys. Rev. Lett. 2014, 113, 103601. [Google Scholar] [CrossRef]
- Politi, A.; Matthews, J.C.F.; O’Brien, J.L. Shor’s Quantum Factoring Algorithm on a Photonic Chip. Science 2009, 325, 1221. [Google Scholar] [CrossRef]
- Peruzzo, A.; Lobino, M.; Matthews, J.C.; Matsuda, N.; Politi, A.; Poulios, K.; Zhou, X.Q.; Lahini, Y.; Ismail, N.; Wörhoff, K.; et al. Quantum walks of correlated photons. Science 2010, 329, 1500–1503. [Google Scholar] [CrossRef]
- Laing, A.; Peruzzo, A.; Politi, A.; Verde, M.R.; Halder, M.; Ralph, T.C.; Thompson, M.G.; O’Brien, J.L. High-fidelity operation of quantum photonic circuits. Appl. Phys. Lett. 2010, 97, 211109. [Google Scholar] [CrossRef]
- Crespi, A.; Osellame, R.; Ramponi, R.; Brod, D.J.; Galvao, E.F.; Spagnolo, N.; Vitelli, C.; Maiorino, E.; Mataloni, P.; Sciarrino, F. Integrated multimode interferometers with arbitrary designs for photonic boson sampling. Nat. Photonics 2013, 7, 545–549. [Google Scholar] [CrossRef]
- Arcari, M.; Söllner, I.; Javadi, A.; Hansen, S.L.; Mahmoodian, S.; Liu, J.; Thyrrestrup, H.; Lee, E.H.; Song, J.D.; Stobbe, S.; et al. Near-unity coupling efficiency of a quantum emitter to a photonic crystal waveguide. Phys. Rev. Lett. 2014, 113, 093603. [Google Scholar] [CrossRef] [PubMed]
- Ciampini, M.A.; Orieux, A.; Paesani, S.; Sciarrino, F.; Corrielli, G.; Crespi, A.; Ramponi, R.; Osellame, R.; Mataloni, P. Path-polarization hyperentangled and cluster states of photons on a chip. Light Sci. Appl. 2016, 5, e16064. [Google Scholar] [CrossRef]
- Spring, J.B.; Mennea, P.L.; Metcalf, B.J.; Humphreys, P.C.; Gates, J.C.; Rogers, H.L.; Söller, C.; Smith, B.J.; Kolthammer, W.S.; Smith, P.G.; et al. Chip-based array of near-identical, pure, heralded single-photon sources. Optica 2017, 4, 90–96. [Google Scholar] [CrossRef]
- Wang, J.; Bonneau, D.; Villa, M.; Silverstone, J.W.; Santagati, R.; Miki, S.; Yamashita, T.; Fujiwara, M.; Sasaki, M.; Terai, H.; et al. Chip-to-chip quantum photonic interconnect by path-polarization interconversion. Optica 2016, 3, 407–413. [Google Scholar] [CrossRef]
- Sibson, P.; Erven, C.; Godfrey, M.; Miki, S.; Yamashita, T.; Fujiwara, M.; Sasaki, M.; Terai, H.; Tanner, M.G.; Natarajan, C.M.; et al. Chip-based quantum key distribution. Nat. Commun. 2017, 8, 13984. [Google Scholar] [CrossRef]
- Carolan, J.; Harrold, C.; Sparrow, C.; Martín-López, E.; Russell, N.J.; Silverstone, J.W.; Shadbolt, P.J.; Matsuda, N.; Oguma, M.; Itoh, M.; et al. Universal linear optics. Science 2015, 349, 711–716. [Google Scholar] [CrossRef] [PubMed]
- Sparrow, C.; Martín-López, E.; Maraviglia, N.; Neville, A.; Harrold, C.; Carolan, J.; Joglekar, Y.N.; Hashimoto, T.; Matsuda, N.; O’Brien, J.L.; et al. Simulating the vibrational quantum dynamics of molecules using photonics. Nature 2018, 557, 660–667. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Paesani, S.; Ding, Y.; Santagati, R.; Skrzypczyk, P.; Salavrakos, A.; Tura, J.; Augusiak, R.; Mančinska, L.; Bacco, D.; et al. Multidimensional quantum entanglement with large-scale integrated optics. Science 2018, 360, 285–291. [Google Scholar] [CrossRef] [PubMed]
- Paesani, S.; Ding, Y.; Santagati, R.; Chakhmakhchyan, L.; Vigliar, C.; Rottwitt, K.; Oxenløwe, L.K.; Wang, J.; Thompson, M.G.; Laing, A. Generation and sampling of quantum states of light in a silicon chip. Nat. Phys. 2019, 15, 925–929. [Google Scholar] [CrossRef]
- Zhang, H.; Wan, L.; Paesani, S.; Laing, A.; Shi, Y.; Cai, H.; Luo, X.; Lo, G.Q.; Kwek, L.C.; Liu, A.Q. Encoding Error Correction in an Integrated Photonic Chip. PRX Quantum 2023, 4, 030340. [Google Scholar] [CrossRef]
- Ren, R.J.; Lu, Y.H.; Jiang, Z.K.; Gao, J.; Zhou, W.H.; Wang, Y.; Jiao, Z.Q.; Wang, X.W.; Solntsev, A.S.; Jin, X.M. Topologically protecting squeezed light on a photonic chip. Photonics Res. 2022, 10, 456–464. [Google Scholar] [CrossRef]
- Poot, M.; Schuck, C.; Song Ma, X.; Guo, X.; Tang, H.X. Design and characterization of integrated components for SiN photonic quantum circuits. Opt. Express 2016, 24, 6843–6860. [Google Scholar] [CrossRef]
- Sheng, Z.; Wang, Z.; Qiu, C.; Li, L.; Pang, A.; Wu, A.; Wang, X.; Zou, S.; Gan, F. A compact and low-loss MMI coupler fabricated with CMOS technology. IEEE Photonics J. 2012, 4, 2272–2277. [Google Scholar] [CrossRef]
- Ding, Y.; Ou, H.; Peucheret, C. Wideband polarization splitter and rotator with large fabrication tolerance and simple fabrication process. Opt. Lett. 2013, 38, 1227–1229. [Google Scholar] [CrossRef]
- Huang, J.; Yang, J.; Chen, D.; He, X.; Han, Y.; Zhang, J.; Zhang, Z. Ultra-compact broadband polarization beam splitter with strong expansibility. Photon. Res. 2018, 6, 574–578. [Google Scholar] [CrossRef]
- Ren, G.; Chen, S.; Cheng, Y.; Zhai, Y. Study on inverse taper based mode transformer for low loss coupling between silicon wire waveguide and lensed fiber. Opt. Commun. 2011, 284, 4782–4788. [Google Scholar] [CrossRef]
- Wang, J.; Xuan, Y.; Lee, C.; Niu, B.; Liu, L.; Liu, G.N.; Qi, M. Low-loss and misalignment-tolerant fiber-to-chip edge coupler based on double-tip inverse tapers. In Proceedings of the 2016 Optical Fiber Communications Conference and Exhibition (OFC), Anaheim, CA, USA, 20–24 March 2016; pp. 1–3. [Google Scholar]
- Taillaert, D.; Chong, H.; Borel, P.I.; Frandsen, L.H.; De La Rue, R.M.; Baets, R. A compact two-dimensional grating coupler used as a polarization splitter. IEEE Photonics Technol. Lett. 2003, 15, 1249–1251. [Google Scholar] [CrossRef]
- Sun, P.; Van Vaerenbergh, T.; Hooten, S.; Beausoleil, R. Adjoint optimization of polarization-splitting grating couplers. Opt. Express 2023, 31, 4884–4898. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Kuyken, B.; Roelkens, G.; Baets, R.; Osgood, R.M., Jr.; Green, W.M. Bridging the mid-infrared-to-telecom gap with silicon nanophotonic spectral translation. Nat. Photonics 2012, 6, 667. [Google Scholar] [CrossRef]
- Paesani, S.; Borghi, M.; Signorini, S.; Maïnos, A.; Pavesi, L.; Laing, A. Near-ideal spontaneous photon sources in silicon quantum photonics. Nat. Commun. 2020, 11, 2505. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Zhu, S. Quasi-phase-matching engineering of entangled photons. AIP Adv. 2012, 2, 053807. [Google Scholar] [CrossRef]
- Signorini, S.; Pavesi, L. On-chip heralded single photon sources. AVS Quantum Sci. 2020, 2, 041701. [Google Scholar] [CrossRef]
- Kultavewuti, P.; Zhu, E.Y.; Xing, X.; Qian, L.; Pusino, V.; Sorel, M.; Aitchison, J.S. Polarization-entangled photon pair sources based on spontaneous four wave mixing assisted by polarization mode dispersion. Sci. Rep. 2017, 7, 5785. [Google Scholar] [CrossRef] [PubMed]
- Kaneda, F.; Kwiat, P.G. High-efficiency single-photon generation via large-scale active time multiplexing. Sci. Adv. 2019, 5, eaaw8586. [Google Scholar] [CrossRef]
- Collins, M.J.; Xiong, C.; Rey, I.H.; Vo, T.D.; He, J.; Shahnia, S.; Reardon, C.; Krauss, T.F.; Steel, M.; Clark, A.S.; et al. Integrated spatial multiplexing of heralded single-photon sources. Nat. Commun. 2013, 4, 2582. [Google Scholar] [CrossRef]
- Reck, M.; Zeilinger, A.; Bernstein, H.J.; Bertani, P. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 1994, 73, 58–61. [Google Scholar] [CrossRef]
- Clements, W.R.; Humphreys, P.C.; Metcalf, B.J.; Kolthammer, W.S.; Walmsley, I.A. Optimal design for universal multiport interferometers. Optica 2016, 3, 1460–1465. [Google Scholar] [CrossRef]
- Qiang, X.; Zhou, X.; Wang, J.; Wilkes, C.M.; Loke, T.; O’Gara, S.; Kling, L.; Marshall, G.D.; Santagati, R.; Ralph, T.C.; et al. Large-scale silicon quantum photonics implementing arbitrary two-qubit processing. Nat. Photonics 2018, 12, 534–539. [Google Scholar] [CrossRef]
- Steinbrecher, G.R.; Olson, J.P.; Englund, D.; Carolan, J. Quantum optical neural networks. Npj Quantum Inf. 2019, 5, 60. [Google Scholar] [CrossRef]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 4213. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, Y.; Aihara, K.; Leleu, T.; Kawarabayashi, K.i.; Kako, S.; Fejer, M.; Inoue, K.; Takesue, H. Coherent Ising machines—optical neural networks operating at the quantum limit. NPJ Quantum Inf. 2017, 3, 49. [Google Scholar] [CrossRef]
- Shen, Y.; Harris, N.C.; Skirlo, S.; Prabhu, M.; Baehr-Jones, T.; Hochberg, M.; Sun, X.; Zhao, S.; Larochelle, H.; Englund, D.; et al. Deep learning with coherent nanophotonic circuits. Nat. Photonics 2017, 11, 441–446. [Google Scholar] [CrossRef]
- Zhang, H.; Gu, M.; Jiang, X.; Thompson, J.; Cai, H.; Paesani, S.; Santagati, R.; Laing, A.; Zhang, Y.; Yung, M.; et al. An optical neural chip for implementing complex-valued neural network. Nat. Commun. 2021, 12, 457. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.; Sitzmann, V.; Dun, X.; Heidrich, W.; Wetzstein, G. Hybrid optical-electronic convolutional neural networks with optimized diffractive optics for image classification. Sci. Rep. 2018, 8, 12324. [Google Scholar] [CrossRef]
- Lin, X.; Rivenson, Y.; Yardimci, N.T.; Veli, M.; Luo, Y.; Jarrahi, M.; Ozcan, A. All-optical machine learning using diffractive deep neural networks. Science 2018, 361, 1004–1008. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Zou, J.; Zhang, H.; Shi, Y.; Luo, S.; Wang, N.; Cai, H.; Wan, L.; Wang, B.; Jiang, X.; et al. Space-efficient optical computing with an integrated chip diffractive neural network. Nat. Commun. 2022, 13, 1044. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Thompson, J.; Gu, M.; Jiang, X.D.; Cai, H.; Liu, P.Y.; Shi, Y.; Zhang, Y.; Karim, M.F.; Lo, G.Q.; et al. Efficient On-Chip Training of Optical Neural Networks Using Genetic Algorithm. ACS Photonics 2021, 8, 1662–1672. [Google Scholar] [CrossRef]
- Zhang, H.; Wan, L.; Haug, T.; Mok, W.; Kim, M.S.; Kwek, L.C.; Liu, A.Q. On-Chip Quantum Autoencoder for Teleportation of High-Dimensional Quantum States. In Proceedings of the 2022 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 15–20 May 2022; pp. 1–2. [Google Scholar]
- Lau, J.; Zhang, H.; Wan, L.; Shi, L.; Lee, C.K.; Kwek, L.; Liu, A. Predicting Molecular Properties Using Photonic Chip-Based Machine Learning Approach. In Proceedings of the 2022 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 15–20 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–2. [Google Scholar]
- Lin, H.; Zhang, H.; Wan, L.; Karim, M.; Cai, H.; Kwek, L.; Liu, A. Quantum Photonic Chip for Binary Classification of Financial Data. In Proceedings of the 2022 IEEE Photonics Conference (IPC), Vancouver, BC, Canada, 13–17 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–2. [Google Scholar]
- Aaronson, S.; Arkhipov, A. The Computational Complexity of Linear Optics. In Proceedings of the STOC’11, Forty-Third Annual ACM Symposium on Theory of Computing, San Jose, CA, USA, 6–8 June 2011; pp. 333–342. [Google Scholar] [CrossRef]
- Clifford, P.; Clifford, R. The Classical Complexity of Boson Sampling. In Proceedings of the SODA’18, Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–10 January 2018; pp. 146–155. [Google Scholar]
- Giordani, T.; Flamini, F.; Pompili, M.; Viggianiello, N.; Spagnolo, N.; Crespi, A.; Osellame, R.; Wiebe, N.; Walschaers, M.; Buchleitner, A.; et al. Experimental statistical signature of many-body quantum interference. Nat. Photonics 2018, 12, 173–178. [Google Scholar] [CrossRef]
- Carolan, J.; Meinecke, J.D.; Shadbolt, P.J.; Russell, N.J.; Ismail, N.; Wörhoff, K.; Rudolph, T.; Thompson, M.G.; O’brien, J.L.; Matthews, J.C.; et al. On the experimental verification of quantum complexity in linear optics. Nat. Photonics 2014, 8, 621–626. [Google Scholar] [CrossRef]
- Spagnolo, N.; Vitelli, C.; Bentivegna, M.; Brod, D.J.; Crespi, A.; Flamini, F.; Giacomini, S.; Milani, G.; Ramponi, R.; Mataloni, P.; et al. Experimental validation of photonic boson sampling. Nat. Photonics 2014, 8, 615–620. [Google Scholar] [CrossRef]
- Broome, M.A.; Fedrizzi, A.; Rahimi-Keshari, S.; Dove, J.; Aaronson, S.; Ralph, T.C.; White, A.G. Photonic Boson Sampling in a Tunable Circuit. Science 2013, 339, 794–798. [Google Scholar] [CrossRef]
- Tillmann, M.; Dakić, B.; Heilmann, R.; Nolte, S.; Szameit, A.; Walther, P. Experimental boson sampling. Nat. Photonics 2013, 7, 540–544. [Google Scholar] [CrossRef]
- Spring, J.B.; Metcalf, B.J.; Humphreys, P.C.; Kolthammer, W.S.; Jin, X.M.; Barbieri, M.; Datta, A.; Thomas-Peter, N.; Langford, N.K.; Kundys, D.; et al. Boson Sampling on a Photonic Chip. Science 2013, 339, 798–801. [Google Scholar] [CrossRef]
- Zhu, H.H.; Chen, H.S.; Li, S.Y.; Chen, T.; Cai, H.; Chin, L.P.; Zhang, X.D.; Liu, A.Q. A Gaussian Boson Sampling for Graph Computation. In Proceedings of the CLEO: QELS_Fundamental Science, Washington, DC, USA, 7–12 May 2023; Optica Publishing Group: Washington, DC, USA, 2023; p. FM3A.1. [Google Scholar] [CrossRef]
- Wan, L.; Zhu, H.; Wang, B.; Zhang, H.; Kwek, L.C.; Liu, A.Q. A Boson Sampling Chip for Graph Perfect Matching. In Proceedings of the CLEO: QELS_Fundamental Science 2022, San Jose, CA, USA, 15–20 May 2022; Optica Publishing Group: Washington, DC, USA, 2022; p. FF2I.6. [Google Scholar] [CrossRef]
- Schuld, M.; Brádler, K.; Israel, R.; Su, D.; Gupt, B. Measuring the similarity of graphs with a Gaussian boson sampler. Phys. Rev. A 2020, 101, 032314. [Google Scholar] [CrossRef]
- Arrazola, J.M.; Bromley, T.R. Using Gaussian Boson Sampling to Find Dense Subgraphs. Phys. Rev. Lett. 2018, 121, 030503. [Google Scholar] [CrossRef] [PubMed]
- Brádler, K.; Dallaire-Demers, P.L.; Rebentrost, P.; Su, D.; Weedbrook, C. Gaussian boson sampling for perfect matchings of arbitrary graphs. Phys. Rev. A 2018, 98, 032310. [Google Scholar] [CrossRef]
- Huh, J.; Guerreschi, G.G.; Peropadre, B.; McClean, J.R.; Aspuru-Guzik, A. Boson sampling for molecular vibronic spectra. Nat. Photonics 2015, 9, 615–620. [Google Scholar] [CrossRef]
- Banchi, L.; Fingerhuth, M.; Babej, T.; Ing, C.; Arrazola, J.M. Molecular docking with Gaussian boson sampling. Sci. Adv. 2020, 6, eaax1950. [Google Scholar] [CrossRef]
- Paesani, S.; Gentile, A.A.; Santagati, R.; Wang, J.; Wiebe, N.; Tew, D.P.; O’Brien, J.L.; Thompson, M.G. Experimental Bayesian Quantum Phase Estimation on a Silicon Photonic Chip. Phys. Rev. Lett. 2017, 118, 100503. [Google Scholar] [CrossRef]
- Wang, J.; Paesani, S.; Santagati, R.; Knauer, S.; Gentile, A.A.; Wiebe, N.; Petruzzella, M.; O’brien, J.L.; Rarity, J.G.; Laing, A.; et al. Experimental quantum Hamiltonian learning. Nat. Phys. 2017, 13, 551–555. [Google Scholar] [CrossRef]
- Santagati, R.; Wang, J.; Gentile, A.A.; Paesani, S.; Wiebe, N.; McClean, J.R.; Morley-Short, S.; Shadbolt, P.J.; Bonneau, D.; Silverstone, J.W.; et al. Witnessing eigenstates for quantum simulation of Hamiltonian spectra. Sci. Adv. 2018, 4, eaap9646. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).