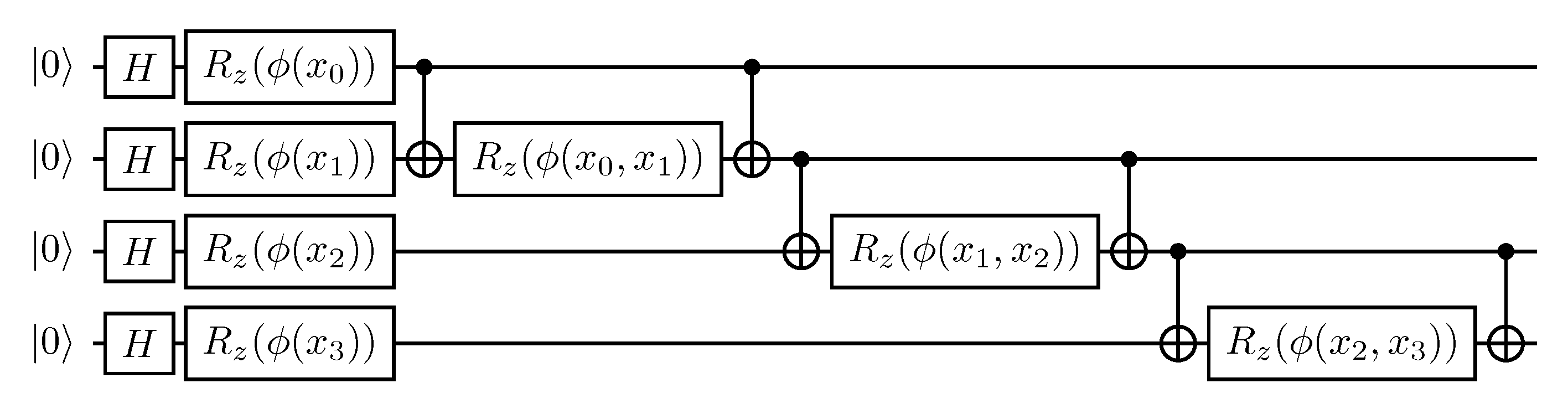1. Introduction
Quantum computing, as an evolving sub-discipline within computer science, amalgamates various research fields, including physics, mathematics, and computer science, among many others. The course of technological advancement has divided the field into two distinct approaches: gate-based quantum computation and adiabatic quantum computation. Although these approaches are theoretically equivalent, their practical utilization diverges significantly. Gate-based quantum computation is studied for a more general-purpose application, whereas adiabatic computation is primarily employed for quantum annealing, an optimization process aimed at determining the minimum of a cost function.
Quantum machine learning (QML) stands as a heavily studied sub-discipline within the framework of quantum computation, it being popular within both the gate-based and adiabatic paradigms. This article focuses on the Support Vector Machine (SVM) model and describes how these two divergent quantum computing approaches seek to implement it. We propose a novel approach to model this problem, combining both technologies.
Our model is based on the observation that the two quantum approaches for the Quantum Support Vector Machine (QSVM) focus on two different parts of the classical approach. Gate-based computation aims to leverage quantum properties to discover a useful kernel for the high-dimensional Hilbert space. On the other hand, the annealing model focuses on optimization that comes after computing the kernel matrix. These are two separate but complementary components of the Support Vector Machine model. The combination of these approaches, if correctly applied, provides advantages over the classical method, as well as each approach on its own.
The following sections perform an in-depth analysis of the current advancements in Quantum Support Vector Machines. It begins with an exposition on classical SVM, then delves into an investigation of the distinct approaches employed in computing QSVM.
1.1. Classical Support Vector Machines
An SVM is a supervised machine learning algorithm designed for both classification and regression tasks. It operates on a dataset , where represents a point in d-dimensional space, serving as a feature vector, and denotes the target label assigned to . We will focus on the classification task and learning a binary classifier that assigns a class label to a given data point . For clarity, we designate the class as ’positive’ and the class as ’negative’.
The training of an SVM entails solving the quadratic programming (QP) problem:
with
For a set of
N coefficients
, where
C denotes a regularization parameter and
represents the kernel function of the Support Vector Machine [
1,
2], the resulting coefficients
establish a
-dimensional decision boundary that partitions
into two regions corresponding to the predicted class label. The decision boundary is defined by points associated with
, commonly referred to as the support vectors of the SVM. Prediction for an arbitrary point
can be accomplished by
where
b can be estimated by formula [
2]:
Geometrically, the decision function corresponds to the signed distance between the point x and the decision boundary. Consequently, the predicted class label for x as determined by the trained Support Vector Machine is given by .
The problem formulation can be equivalently expressed as a convex quadratic optimization problem [
3], indicating its classification among the rare minimization problems in machine learning that possess a globally optimal solution. It is crucial to note that while the optimal solution exists, it is dataset-specific and may not necessarily generalize optimally across the entire data distribution.
Kernel-based SVMs exhibit exceptional versatility as they can obtain nonlinear decision boundaries denoted by
. This is achieved through the implicit mapping of feature vectors into higher-dimensional spaces [
4]. Importantly, the computational complexity does not escalate with this higher dimensionality, as only the values of the kernel function
are involved in the problem specification. This widely recognized technique is commonly referred to as the “kernel trick” and has been extensively explored in the literature [
1,
2].
The selection of the kernel function significantly influences the outcomes, with radial basis function kernels (RBF) [
3] generally serving as the search starting point for the right kernel of a Support Vector Machine problem. An RBF kernel is distinguished by the property that
can be expressed as a function of the distance
[
1]. The Gaussian kernel, often referred as “The RBF kernel”, is the most prevalent RBF kernel and is represented as
Here, the value of the hyperparameter
is typically determined through a calibration procedure before the training phase [
5].
The SVM are very susceptible to the choice of the hyper-parameters, like or C, and different assignments can radically change the result of the optimization.
2. Materials and Methods
In the outlined quantum computing landscape, we introduced two distinct architectures for employing Support Vector Machines in classification tasks. Both models, still in their early stages, warrant further thorough investigation and testing.
Quantum Annealer Support Vector Machines (QaSVM) demonstrate partial efficacy in addressing the problem, yet encounter challenges in precisely determining the optimal hyperplane. Additionally, QaSVM relies on a classical kernel trick to compute the component of the formulation.
Conversely, Quantum gate-based Support Vector Machines (QgSVM) exhibit impressive data manipulation capabilities. However, they currently lack the readiness to handle the optimization aspect of the SVM algorithm. Present-day quantum technology does not possess the computational power necessary for intricate optimization problems. Consequently, the optimization step necessitates an approximate approach, achieved either through an ansatz (transitioning from QgSVM to a Quantum Neural Network, QNN model) or by resorting to classical optimization methods.
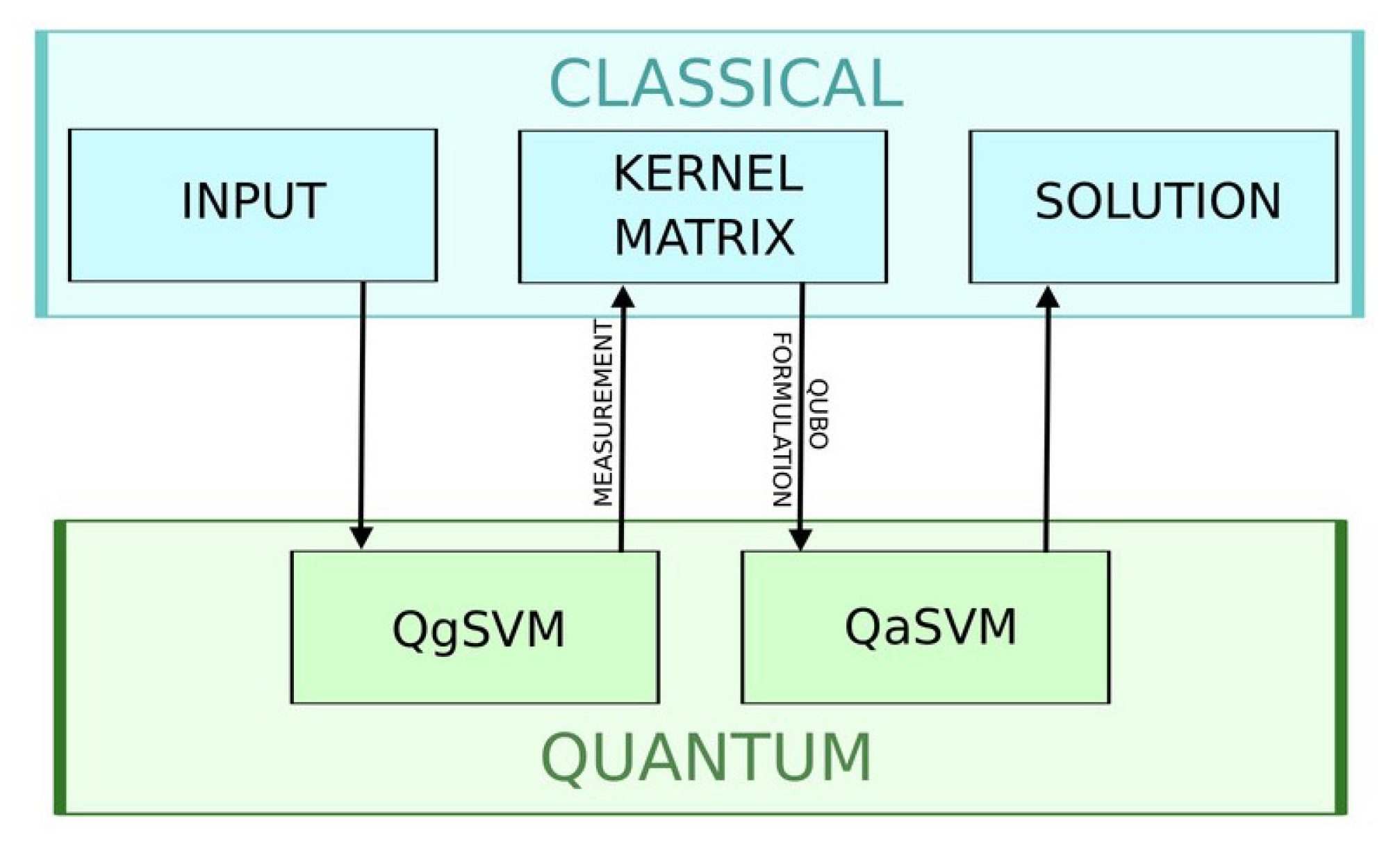
Our proposed approach involves a fusion of the quantum annealing and gate-based models, establishing a connection through a classical channel. The core idea is to capitalize on the strengths of each approach: annealing excels in optimization but lacks a dedicated kernel method, while the gate-based model performs well with the kernel trick but faces challenges in optimization.
Building upon our previous discussions, we recognize the ability to derive the Kernel Matrix from a quantum feature map within the gate-based architecture. Once the Kernel matrix is defined, we employ a standard procedure to reformulate the problem into a Quadratic Unconstrained Binary Optimization (QUBO) format, achieved by discretizing the continuous variables of a quantum computing problem. Subsequently, the QUBO formulation is encoded into the annealer, enabling the extraction of minima, as previously described. The illustrated process, as depicted in
Figure 1, allows the attainment of results for even challenging problems, leveraging the combined advantages of both quantum technologies.
2.2. From Classical to Quantum Kernel
As previously discussed, the Gaussian kernel is the most used radial basis function (RBF) kernel. It facilitates the computation of the similarity between each pair of points in a higher-dimensional space while circumventing explicit calculations. Once an RBF kernel is selected, the similarities between each pair of points are computed and stored in a kernel matrix. Due to the symmetry of the distance function, it naturally follows that both the kernel matrix and, subsequently, are symmetric as well.
In our proposal, we assume that the kernel is a Quantum Kernel. This approach allows us to leverage the exponentially higher dimension of the Hilbert space to separate the data effectively.
For the sake of simplicity, in the experiment we propose as a proof of concept, we employ the simple algorithm of the quantum inner product to compute the similarity between two vectors in the Hilbert space (
Figure 2). Consider two points
and
along with their respective feature maps
A and
B, such that
and
on a
M qubit register. Our objective is to derive the similarity
s between the two through the quantum inner product:
where |
k〉 and
are, respectively, the
kth standard basis vector and its coefficient. It is evident that if
, then
is equal to 1, while if they are orthogonal to each other, the result will be 0. This behavior describes a similarity metric in a high-dimensional space, precisely what we sought to integrate into our Quantum Support Vector Machine.
The final step to complete the QgSVM involves determining two feature maps, A and B, capable of encoding the data in the Hilbert space. To obtain the quantum inner product between vectors, we employ the same feature map technique for both A and B. Additionally, given that each vector for all possesses the same number of features , it follows that the number of qubits in every circuit used for gate-based computation depends solely on and the chosen feature map technique.
In our study, we opt for one of the widely employed feature map techniques known as the Pauli expansion circuit [
17]. The Pauli expansion circuit, denoted as
U, serves as a data encoding circuit that transforms input data
, where
N represents the feature dimension, as
Here,
S represents a set of qubit indices describing the connections in the feature map,
is a set containing all these index sets, and
. The default data mapping is
This technique offers various degrees of freedom, including the choice of the Pauli gate, the number of circuit repetitions, and the type of entanglement. In our implementation, we select a second-order Pauli-Z evolution circuit, a well-known instance of the Pauli expansion circuit readily available in libraries such as Qiskit [
20]. A more detailed formulation will be provided in the next subsection.
Our decision to use this specific feature map aligns with prior research by Havlicek et al. [
17], where they leverage a Pauli Z expansion circuit to train a Quantum gate-based Support Vector Machine (QgSVM). It is essential to note that this choice is arbitrary and the feature map can be substituted with a variety of circuits. One important constraint applied to the feature map circuits is that, in a real-world implementation, they must encode data in a manner not easily simulated by classical computers. This requirement is necessary, though not sufficient, for achieving a quantum advantage.
Given that the focus of this paper is on proposing a new methodology rather than experimentally proving quantum advantage, we opted to simulate the quantum gate-based environment on classical hardware during the experimental phase.
2.4. Experiments
Our experiments serve as a demonstration of the viability of the proposed methodology. All experiments involve binary classification problems conducted on pairs of classes from the MNIST dataset [
22], following preprocessing. Due to the limited capabilities of current quantum computers and simulations, and to maintain simplicity for demonstration purposes, we applied Principal Component Analysis (PCA) [
23] to each image, considering only the first two principal components as input to the model (
Table 1 reports the explained variance). The resulting values are then mapped into the range
to fully exploit the properties of the Quantum gate-based Support Vector Machine (QgSVM). Simultaneously, the labels are adapted to the Quantum Annealer-based Support Vector Machine (QaSVM) standard, where
.
We present four different experiments utilizing class pairs 0–9, 3–8, 4–7 and 5–6; referred to as MN09, MN38, MN47, and MN56, respectively. In each experiment, we selected 500 data points with balanced classes and divided them into a training set (300 data points) and a test set (200 data points), each with two features (referred to as ).
The experiments are divided into three phases: hyperparameter tuning, training, and testing.
Hyperparameter Tuning: Initially, a 4-fold Monte Carlo cross-validation is performed on the training set for hyperparameter tuning. The optimized hyperparameters include
K,
B, and
from Equation (
8). While an exhaustive search on the hyperparameter space is beyond the scope of this work, additional information and results on the effect of hyperparameter tuning can be found in [
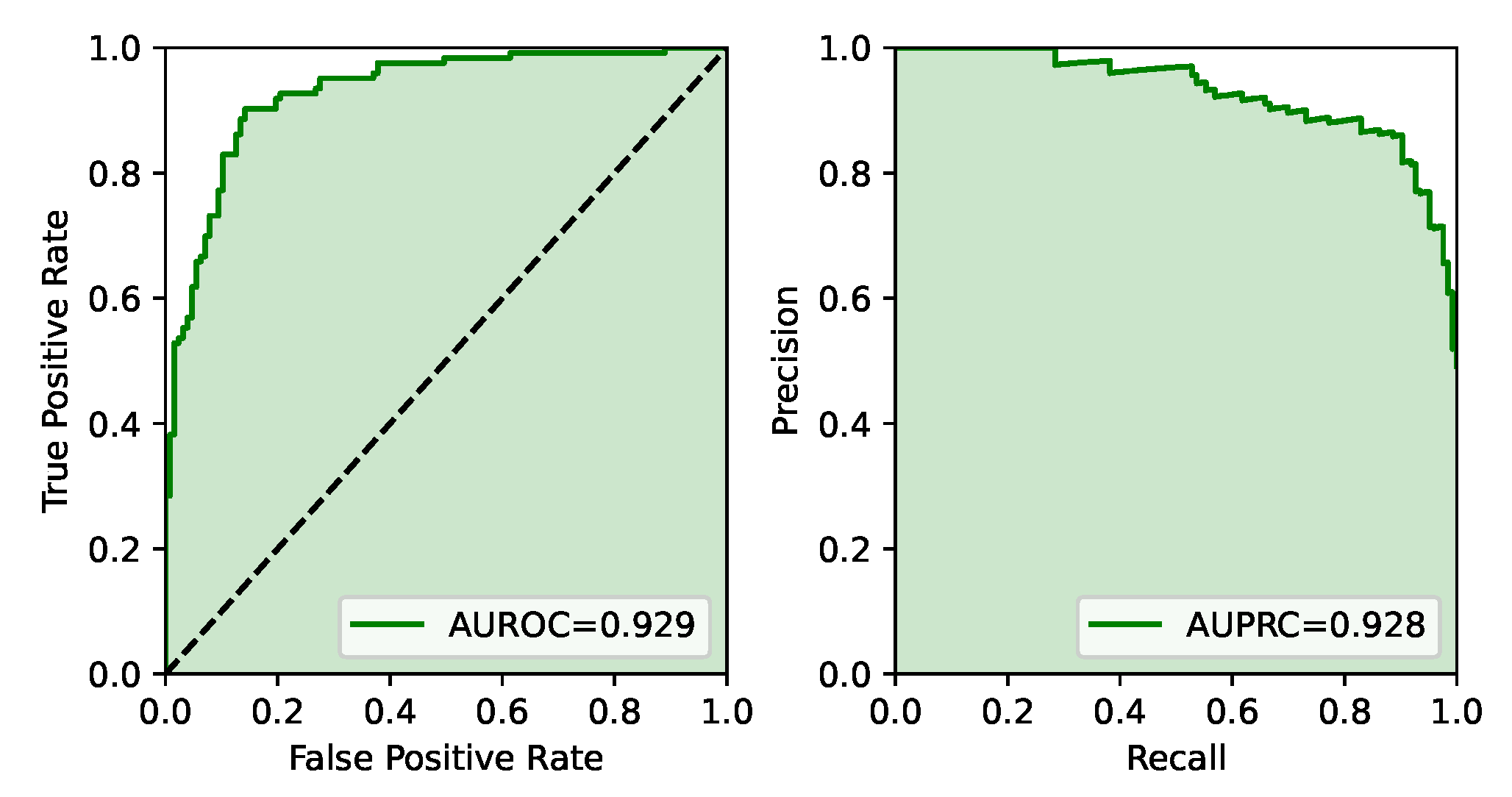
9]. To assess the performance of each model, we compute the Area Under the Receiver Operating Characteristic curve (AUROC) and the Area Under the Precision–Recall curve (AUPCR), as shown in
Figure 4.
Training: Once the optimal hyperparameters are determined, we instantiate the best model for each dataset and train it on the entire training set. Following the original proposal by Willsch et al. [
9], and to address the challenge of limited connectivity in the annealing hardware, the entire training set is divided into six small, disjoint subsets (referred to as folds), each containing approximately 50 samples. The approach involves constructing an ensemble of quantum weak Support Vector Machines, with each classifier trained on one of the subsets.
This process unfolds in two steps. First, for each fold, the top twenty solutions (qSVM
where
is the index of the best solutions) obtained from the annealer are combined by averaging their respective decision functions. Since the decision function is linear in the coefficients, and the bias for each fold
l, denoted as
, is computed from
using Equation (
4), this step effectively produces a single classifier with an effective set of coefficients given by
and bias given by
Second, an average is taken over the six subsets. It is important to note that the data points
are unique for each
l. The complete decision function is expressed as
where
L is the number of folds and
. Similar to the formulation showed before, the decision for the class label of a point
is determined by
.
Testing: After the training concludes, we test the models on the 200 data points of the test set. Similar to the training phase, a total of 6 weak SVMs, each resulting from the combination of the 20 annealer’s solutions, are utilized to determine the class of the data point.
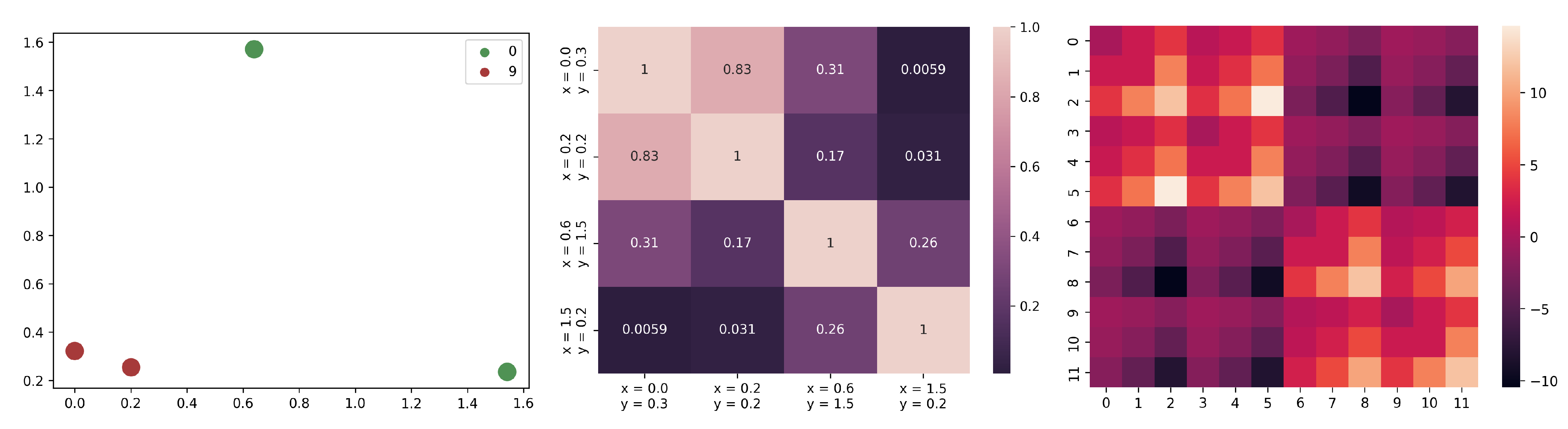
A visual representation of the process can be found in
Figure 5, while in
Appendix C a toy example with the visualization of the kernel and QUBO matrix can be found.
4. Discussion
The results obtained from our Hybrid Quantum Support Vector Machine (Hybrid QSVM) showcase great promise across various aspects. Remarkably, we achieved favorable outcomes using only two features derived through Principal Component Analysis (PCA) while harnessing both quantum gate-based technology (simulated) and quantum annealing (real hardware).
As previously mentioned, our experimental focus was not centered on seeking the optimal model or comparing its performance against classical approaches. Instead, our primary goal was to experimentally validate the viability of our proposed approach. We deliberately invested minimal effort in performance optimization, aside from a modest hyperparameter tuning step that surpassed the naive approach. Consequently, these results serve as a baseline for potential future enhancements to the model.
During the tuning phase, we concentrated solely on hyperparameters related to the annealing component of the algorithm (specifically, B, K, and ), without delving into the gate-based part. This decision is motivated by three main factors.
Firstly, the existing literature on Quantum gate-based Support Vector Machines (QgSVM) is more developed compared to Quantum annealing Support Vector Machines (QaSVM), making exploration of the latter more pertinent from a research standpoint.
Secondly, we had access to real annealing hardware through the D-Wave Leap program [
24]. Although access to real gate-based hardware is possible through the IBM Quantum Initiative, leveraging both technologies concurrently was impractical due to extended wait times in the hardware queues. Moreover, given our constraint of limiting each data point to two features, a two-qubit gate-based quantum hardware was sufficient for simulating the quantum kernel, further simplifying the process.
Third, and directly linked to the point above, we considered that an easy-to-simulate quantum kernel cannot surpass classical performance. This means that one of the reasons why the QgSVM in our experiment performed sub-optimally is because we could not access hard-to-simulate quantum hardware. For this reason, optimizing its hyperparameters was deemed futile. The same applies to the circuit design, we decided to keep it fixed for the whole experimental phase, since any 2-qubit circuit (with depth within reason) can be simulated.
It is essential to clarify that the three reasons outlined above pertain to the experimental setup and not the specific model’s performance on the datasets. While tuning different hyperparameters or exploring more values of the already optimized ones might enhance performance on specific datasets, it deviates from the primary objective of this paper.
When talking about the goal of this proposal and the advantages it brings, we need to highlight that the quantum annealer is on the verge of addressing industrial optimization challenges [
24]. Simultaneously, the inherent variational nature of the QgSVM positions it favorably for the Noisy Intermediate-scale Quantum (NISQ) era. The convergence of these two approaches is nearing completion, offering several potential benefits. QgSVM can leverage the exponentially large Hilbert space
to more effectively capture similarities and distances between points than classical kernel tricks. This allows it to distinguish between points that are traditionally considered challenging. Moreover, the quantum annealer’s speed surpasses classical optimization methods, providing a solution quicker.
Recent studies on Quantum gate-based Support Vector Machines (QgSVM) have highlighted certain theoretical limitations under specific assumptions. In [
25], the authors connect the exponential dimension of the feature space to a limitation in the model’s ability to generalize. One proposed solution, discussed both theoretically [
26] and empirically [
27], involves introducing a new hyperparameter to regulate the bandwidth.
We argue that our proposal can further enhance the generalization ability of QgSVM. Building on the findings from the original QaSVM study [
9], we know that Quantum annealing Support Vector Machines can outperform the single classifier obtained by classical SVM optimization in the same computational problem, and this can be directly translated to an improvement on the QgSVM since its optimization is done classically. This improvement stems from the ensembling technique used and the intrinsic ability of the annealer to generate a distribution of solutions close to optimal, thereby enhancing generalization (similar results can be found in [
28,
29] for different annealing machine learning models). Moreover, since our proposal is not tied to a specific implementation, it can employ various strategies to mitigate the limitations of QgSVM like the one discussed above.
Future work in this direction could involve a theoretical analysis of these features.
5. Conclusions
In the realm of quantum computing, the conventional approach involves selecting one technology and working within its framework, often neglecting the potential synergies that could arise from mixing different quantum technologies to harness their respective strengths. In this paper, we propose a novel version of Quantum Support Vector Machines (QSVM) that capitalizes on the advantages of both gate-based quantum computation and quantum annealing.
Our proposal positions itself within the context of Quantum Support Vector Machines (QSVM) from both technological points of view improving on both techniques. We enhance the generalization ability of standard QgSVM through the ensemble technique and leverage the intrinsic capability of Quantum annealing Support Vector Machines (QaSVM) to generate a distribution of suboptimal solutions during optimization within constant annealing time.
The ensemble method, similarly to its classical counterpart, not only enhances generalization but also reduces the computation time of the kernel matrix and the accesses to the quantum computer. For a dataset
X with
n samples and
features, the full kernel matrix is composed of
elements, implying
calls to the (gate-based) quantum computer where
s is the number of shots needed to accuratly compute the similarity score. Among other important factors [
30],
s is strongly linked to the dimensionality of the Hilbert space [
26] that in turn depends on the kernel implementation and
. Our ensemble of
m Kernels quadratically reduces the needed number of accesses to
while only needing
accesses to the quantum annealer. In this context,
m becomes a new hyperparameter and its value is highly dependant on the specific problem and the implementation in question.
To conclude, we can summarize our contribution in three points.
First, we introduce a method that combines quantum technologies, leveraging the complementarity between gate-based quantum computation and quantum annealing in the context of Support Vector Machines. While previous research has touched on the integration of these approaches for solving large-size Ising problems [
31], to the best of our knowledge, our work is the first to explore this fusion in the context of classification problems.
Second, we provide experimental validation of our approach. Notably, the annealing component of our experiments is conducted on real quantum hardware, demonstrating the feasibility of our methodology in the early era of Noisy Intermediate-Scale Quantum (NISQ) computation.
Third, we establish a baseline result for future hybrid technology approaches, particularly on one of the most widely used datasets in classical machine learning.
Future work in this area is straightforward. As quantum technologies advance, our approach should undergo testing on quantum hardware to validate its capabilities. Additionally, there is a need for more extensive hyperparameter tuning to achieve optimal results. We recommend exploring and proposing different quantum kernel methods based on the characteristics of the data to further enhance performance. Simultaneously, a rigorous proof of the generalization power of our model is essential to prove the positive interaction of the technologies in a more rigorous manner.
It is crucial to note that the implementation of our methodology is not rigidly tied to the specific formulations described here. Rather, it adapts to the state of the art for each technology. The core of our proposal lies in the fusion of approaches, allowing for flexibility as advancements occur in individual technologies.
Quantum machine learning (QML) currently stands as a focal point of research, offering the potential to revolutionize various applications through the utilization of quantum computational power and innovative algorithmic models like Variational Algorithms. Similar to any scientific field, as it expands, new limitations come to light. However, simultaneously, researchers develop techniques to overcome and mitigate these restrictions. Despite the increasing attention, the field is still in its early stages, necessitating further exploration to unveil its practical benefits.