Quantum Convolutional Long Short-Term Memory Based on Variational Quantum Algorithms in the Era of NISQ
Abstract
1. Introduction
2. Preliminaries
2.1. Long Short-Term Memory
2.2. Convolutional Long Short-Term Memory
3. Related Work
3.1. Amplitude Encoding
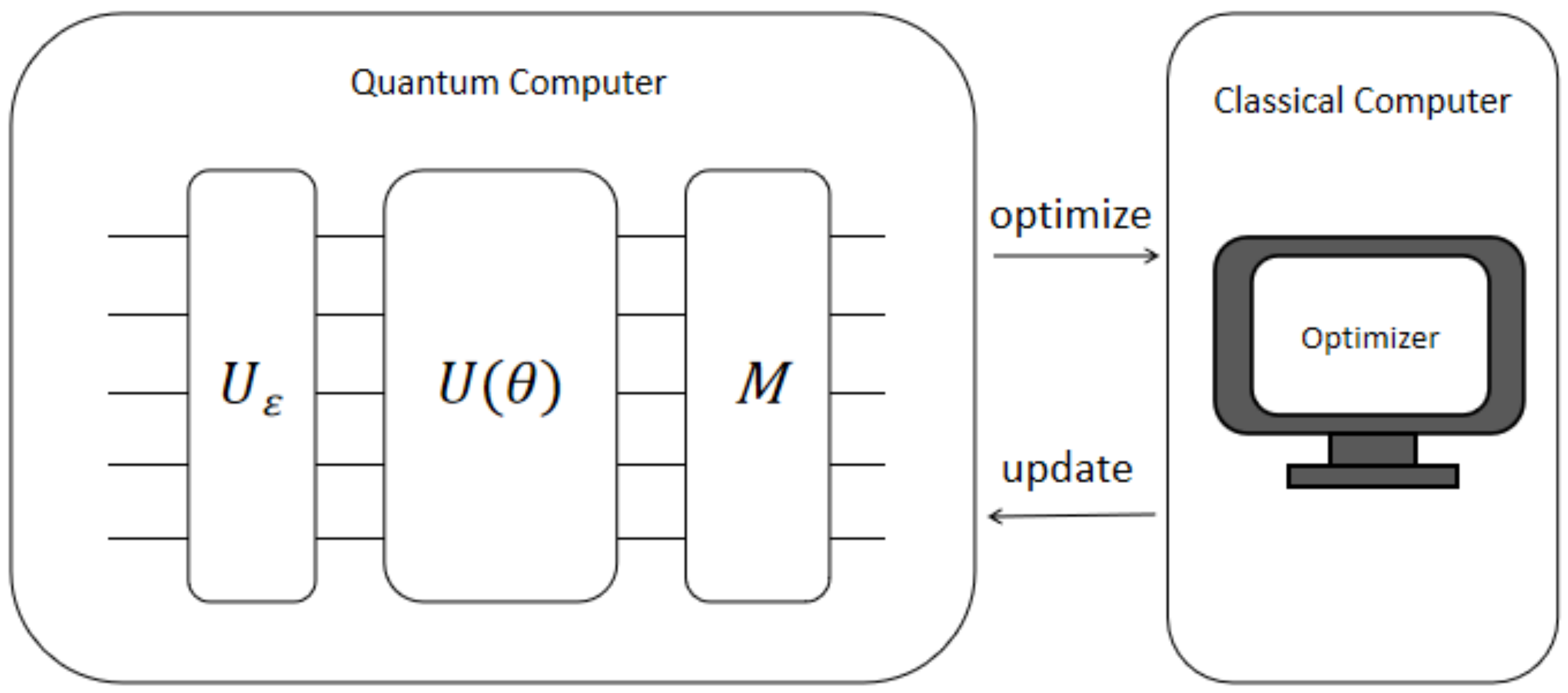
3.2. Variational Quantum Circuits
3.3. Incoherent Noise
4. Model
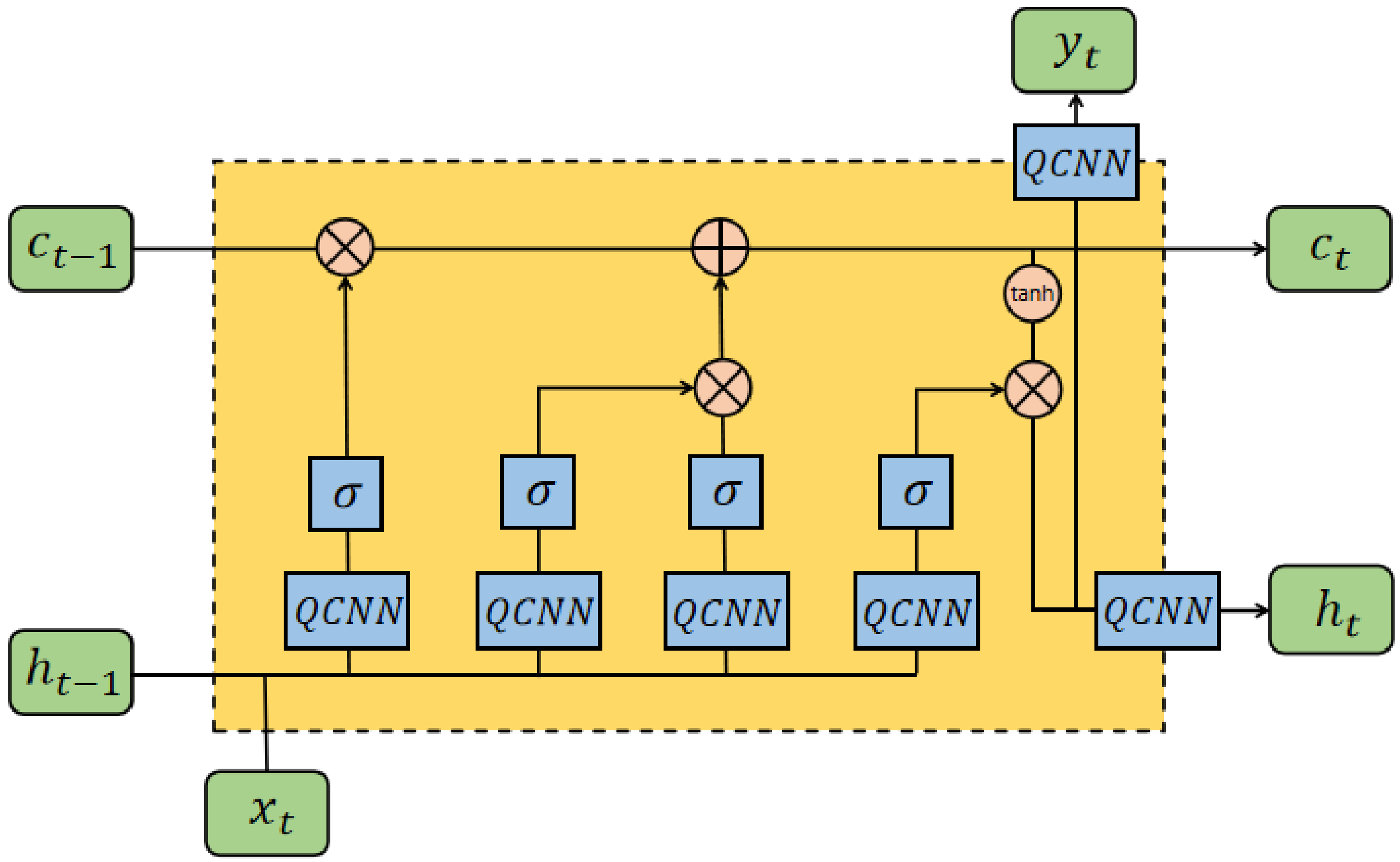
4.1. Quantum Convolutional Long Short-Term Memory
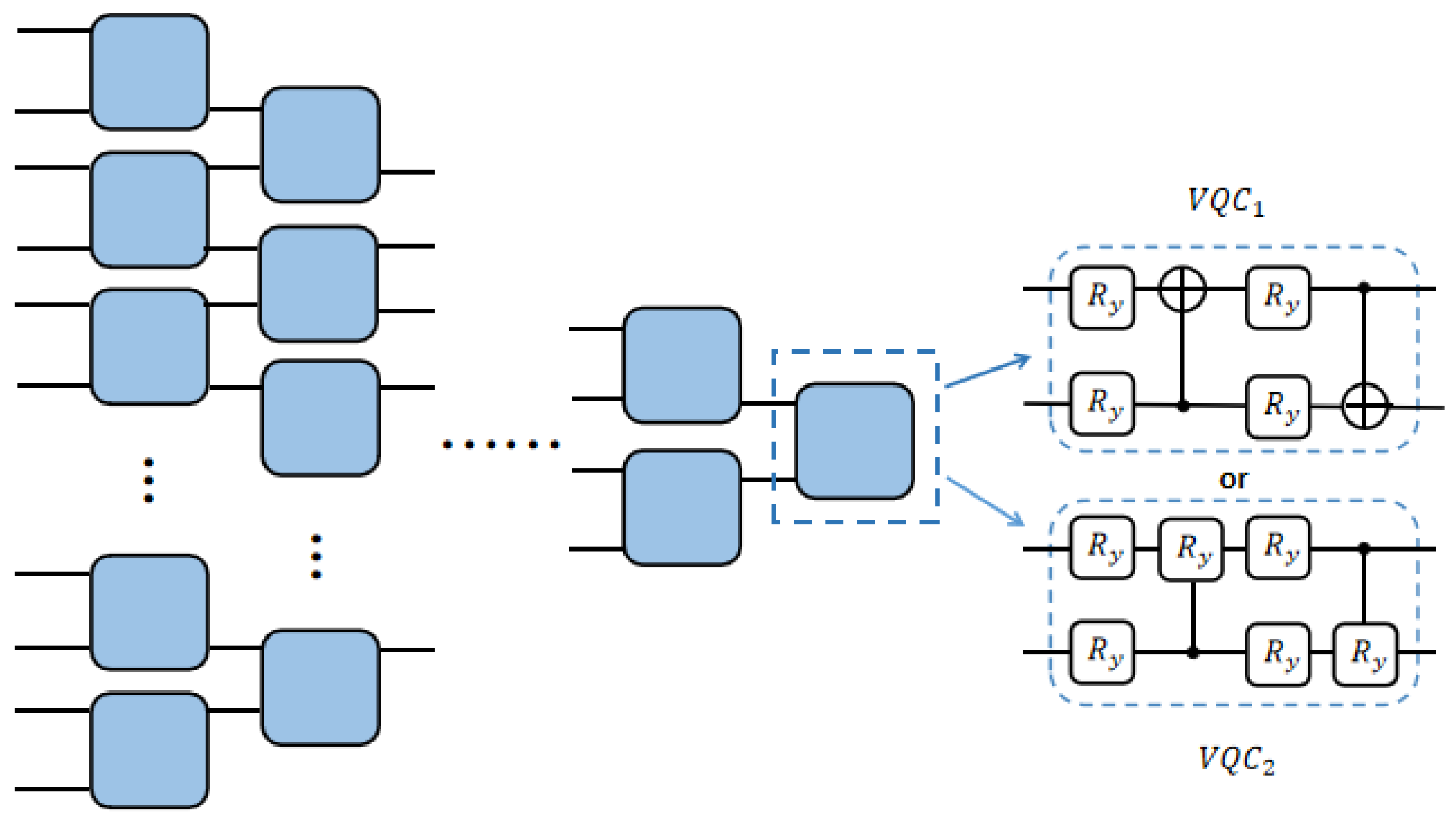
4.2. Quantum Convolutional Circuit Structure
5. Experiments
5.1. Experimental Setup
5.2. Noiseless Simulations
5.3. Noisy Simulations
6. Results
6.1. Noiseless
6.2. Noisy
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Karpathy, A.; Fei-Fei, L. Deep visual-semantic alignments for generating image descriptions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the 30th International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 16–21 June 2013; pp. 1310–1318. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Bengio, Y.; Goodfellow, I.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Srivastava, N.; Mansimov, E.; Salakhudinov, R. Unsupervised learning of video representations using lstms. In Proceedings of the 32nd International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015. [Google Scholar]
- Xu, K.; Ba, J.; Kiros, R.; Cho, K.; Courville, A.; Salakhudinov, R.; Bengio, Y. Show, attend and tell: Neural image caption generation with visual attention. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Gers, F.A.; Schmidhuber, E. LSTM recurrent networks learn simple context-free and context-sensitive languages. IEEE Trans. Neural Netw. 2001, 12, 1333–1340. [Google Scholar] [CrossRef] [PubMed]
- Eck, D.; Schmidhuber, J. A first look at music composition using lstm recurrent neural networks. Ist. Dalle Molle Studi Sull Intell. Artif. 2002, 103, 48–56. [Google Scholar]
- Wang, S.; Jiang, J. Learning natural language inference with LSTM. arXiv 2015, arXiv:1512.08849. [Google Scholar]
- Monner, D.; Reggia, J.A. A generalized LSTM-like training algorithm for second-order recurrent neural networks. Neural Netw. 2012, 25, 70–83. [Google Scholar] [CrossRef] [PubMed]
- Krause, B.; Lu, L.; Murray, I.; Renals, S. Multiplicative LSTM for sequence modelling. arXiv 2016, arXiv:1609.07959. [Google Scholar]
- Chen, Q.; Zhu, X.; Ling, Z.; Wei, S.; Jiang, H.; Inkpen, D. Enhanced LSTM for natural language inference. arXiv 2016, arXiv:1609.06038. [Google Scholar]
- Cao, Z.; Zhu, Y.; Sun, Z.; Wang, M.; Zheng, Y.; Xiong, P.; Tian, L. Improving prediction accuracy in LSTM network model for aircraft testing flight data. In Proceedings of the 2018 IEEE International Conference on Smart Cloud (SmartCloud), New York, NY, USA, 21–23 September 2018. [Google Scholar]
- Wang, Y.; Zhu, S.; Li, C. Research on multistep time series prediction based on LSTM. In Proceedings of the 2019 3rd International Conference on Electronic Information Technology and Computer Engineering (EITCE), Xiamen, China, 18–20 October 2019. [Google Scholar]
- Edholm, G.; Zuo, X. A Comparison between Aconventional LSTM Network and Agrid LSTM Network Applied on Speech Recognition; KTH Royal Institute of Technology: Stockholm, Sweden, 2018. [Google Scholar]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. An introduction to quantum machine learning. Contemp. Phys. 2015, 56, 172–185. [Google Scholar] [CrossRef]
- Lloyd, S.; Mohseni, M.; Rebentrost, P. Quantum algorithms for supervised and unsupervised machine learning. arXiv 2013, arXiv:1307.0411. [Google Scholar]
- Havenstein, C.; Thomas, D.; Chandrasekaran, S. Comparisons of performance between quantum and classical machine learning. SMU Data Sci. Rev. 2018, 1, 11. [Google Scholar]
- Chen, S.Y.C.; Yoo, S.; Fang, Y.L.L. Quantum long short-term memory. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022. [Google Scholar]
- Yulita, I.N.; Purwani, S.; Rosadi, R.; Awangga, R.M. A quantization of deep belief networks for long short-term memory in sleep stage detection. In Proceedings of the 2017 International Conference on Advanced Informatics, Concepts, Theory, and Applications (ICAICTA), Denpasar, Indonesia, 16–18 August 2017. [Google Scholar]
- Khan, S.Z.; Muzammil, N.; Zaidi, S.M.H.; Aljohani, A.J.; Khan, H.; Ghafoor, S. Quantum long short-term memory (qlstm) vs. classical lstm in time series forecasting: A comparative study in solar power forecasting. arXiv 2023, arXiv:2310.17032. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Torlai, G.; Melko, R.G. Machine-learning quantum states in the NISQ era. Annu. Rev. Condens. Matter Phys. 2020, 11, 325–344. [Google Scholar] [CrossRef]
- Huang, H.L.; Xu, X.Y.; Guo, C.; Tian, G.; Wei, S.J.; Sun, X.; Long, G.L. Near-term quantum computing techniques: Variational quantum algorithms, error mitigation, circuit compilation, benchmarking and classical simulation. Sci. China Phys. Mech. Astron. 2023, 66, 250302. [Google Scholar] [CrossRef]
- Cerezo, M.; Arrasmith, A.; Babbush, R.; Benjamin, S.C.; Endo, S.; Fujii, K.; Coles, P.J. Variational quantum algorithms. Nat. Rev. Phys. 2021, 3, 625–644. [Google Scholar] [CrossRef]
- Lubasch, M.; Joo, J.; Moinier, P.; Kiffner, M.; Jaksch, D. Variational quantum algorithms for nonlinear problems. Phys. Rev. A 2020, 101, 010301. [Google Scholar] [CrossRef]
- Jones, T.; Endo, S.; McArdle, S.; Yuan, X.; Benjamin, S.C. Variational quantum algorithms for discovering Hamiltonian spectra. Phys. Rev. A 2019, 99, 062304. [Google Scholar] [CrossRef]
- Zhao, A.; Tranter, A.; Kirby, W.M.; Ung, S.F.; Miyake, A.; Love, P.J. Measurement reduction in variational quantum algorithms. Phys. Rev. A 2020, 101, 062322. [Google Scholar] [CrossRef]
- Bonet-Monroig, X.; Wang, H.; Vermetten, D.; Senjean, B.; Moussa, C.; Bäck, T.; O’Brien, T.E. Performance comparison of optimization methods on variational quantum algorithms. Phys. Rev. A 2023, 107, 032407. [Google Scholar] [CrossRef]
- Sakib, S.N. SM Nazmuz Sakib’s Quantum LSTM Model for Rainfall Forecasting; OSF Preprints: Peoria, IL, USA, 2023. [Google Scholar]
- Beaudoin, C.; Kundu, S.; Topaloglu, R.O.; Ghosh, S. Quantum Machine Learning for Material Synthesis and Hardware Security. In Proceedings of the 41st IEEE/ACM International Conference on Computer-Aided Design, San Diego, CA, USA, 30 October–3 November 2022. [Google Scholar]
- Parcollet, T.; Morchid, M.; Linarès, G.; De Mori, R. Bidirectional quaternion long short-term memory recurrent neural networks for speech recognition. In Proceedings of the 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2019), Brighton, UK, 12–17 May 2019. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Witless Bay, NL, Canada, 2015; p. 28. [Google Scholar]
- Mateo-García, G.; Adsuara, J.E.; Pérez-Suay, A.; Gómez-Chova, L. Convolutional long short-term memory network for multitemporal cloud detection over landmarks. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2019), Yokohama, Japan, 28 July–2 August 2019. [Google Scholar]
- Kosana, V.; Madasthu, S.; Teeparthi, K. A novel hybrid framework for wind speed forecasting using autoencoder-based convolutional long short-term memory network. Int. Trans. Electr. Energy Syst. 2021, 31, e13072. [Google Scholar] [CrossRef]
- Sudhakaran, S.; Lanz, O. Learning to detect violent videos using convolutional long short-term memory. In Proceedings of the 2017 14th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Lecce, Italy, 29 August–1 September 2017. [Google Scholar]
- Paiva, E.; Paim, A.; Ebecken, N. Convolutional neural networks and long short-term memory networks for textual classification of information access requests. IEEE Lat. Am. Trans. 2021, 19, 826–833. [Google Scholar] [CrossRef]
- Gandhi, U.D.; Malarvizhi Kumar, P.; Chandra Babu, G.; Karthick, G. Sentiment analysis on twitter data by using convolutional neural network (CNN) and long short term memory (LSTM). In Wireless Personal Communications; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1–10. [Google Scholar]
- LaRose, R.; Coyle, B. Robust data encodings for quantum classifiers. Phys. Rev. A 2020, 102, 032420. [Google Scholar] [CrossRef]
- Gao, S.; Yang, Y.G. New quantum algorithm for visual tracking. Phys. A Stat. Mech. Its Appl. 2023, 615, 128587. [Google Scholar] [CrossRef]
- Huang, S.Y.; An, W.J.; Zhang, D.S.; Zhou, N.R. Image classification and adversarial robustness analysis based on hybrid quantum–classical convolutional neural network. Opt. Commun. 2023, 533, 129287. [Google Scholar] [CrossRef]
- Bar, N.F.; Yetis, H.; Karakose, M. An efficient and scalable variational quantum circuits approach for deep reinforcement learning. Quantum Inf. Process. 2023, 22, 300. [Google Scholar] [CrossRef]
- Kim, R. Implementing a Hybrid Quantum-Classical Neural Network by Utilizing a Variational Quantum Circuit for Detection of Dementia. arXiv 2023, arXiv:2301.12505. [Google Scholar]
- Gong, L.H.; Pei, J.J.; Zhang, T.F.; Zhou, N.R. Quantum convolutional neural network based on variational quantum circuits. Opt. Commun. 2024, 550, 129993. [Google Scholar] [CrossRef]
- Ren, W.; Li, Z.; Huang, Y.; Guo, R.; Feng, L.; Li, H.; Li, X. Quantum generative adversarial networks for learning and loading quantum image in noisy environment. Mod. Phys. Lett. B 2021, 35, 2150360. [Google Scholar] [CrossRef]
- Error, M.S. Mean Squared Error; Springer: Boston, MA, USA, 2010; p. 653. [Google Scholar]
- Jia, X.; De Brabandere, B.; Tuytelaars, T.; Gool, L.V. Dynamic filter networks. In Proceedings of the Advances in Neural Information Processing Systems 29 (NIPS 2016), Barcelona, Spain, 5–10 December 2016; pp. 667–675. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
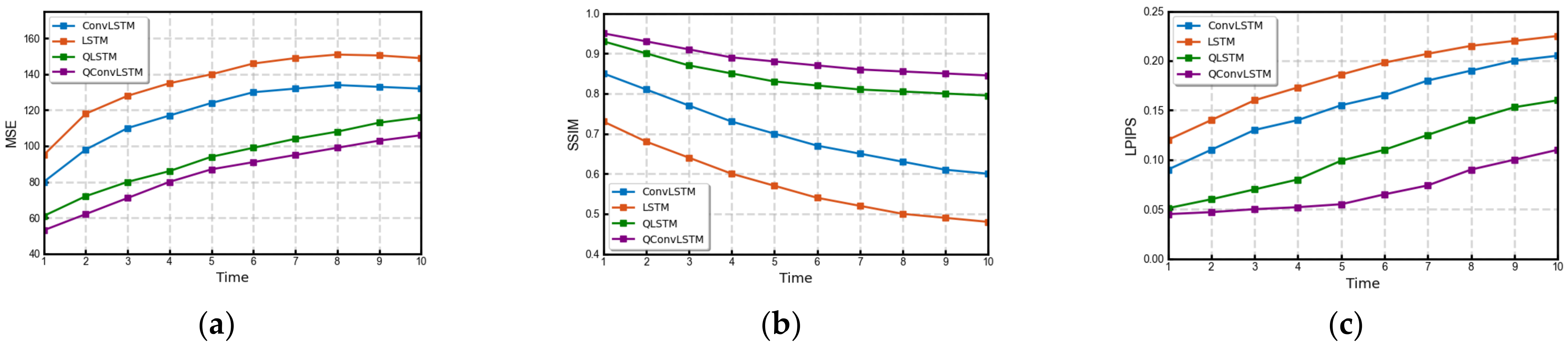
| Model | MSE | SSIM | LPIPS |
|---|---|---|---|
| () | () | () | |
| LSTM | 132.7 | 0.687 | 0.174 |
| ConvLSTM | 113.4 | 0.758 | 0.162 |
| QLSTM | 87.2 | 0.843 | 0.095 |
| QConvLSTM | 64.8 | 0.861 | 0.083 |
| Environment | MSE | SSIM | LPIPS |
|---|---|---|---|
| () | () | () | |
| Noiseless | 64.8 | 0.861 | 0.083 |
| Bit flip | 64.1 | 0.859 | 0.084 |
| Phase flip | 65.0 | 0.857 | 0.081 |
| Bit–phase flip | 65.9 | 0.853 | 0.085 |
| Depolarizing | 66.1 | 0.850 | 0.089 |
| Layers | MSE | SSIM | LPIPS |
|---|---|---|---|
| () | () | () | |
| 1 Layer | 67.5 | 0.783 | 0.092 |
| 2 Layers | 64.8 | 0.861 | 0.083 |
| 3 Layers | 64.9 | 0.863 | 0.081 |
| Structure | MSE | SSIM | LPIPS |
|---|---|---|---|
| () | () | () | |
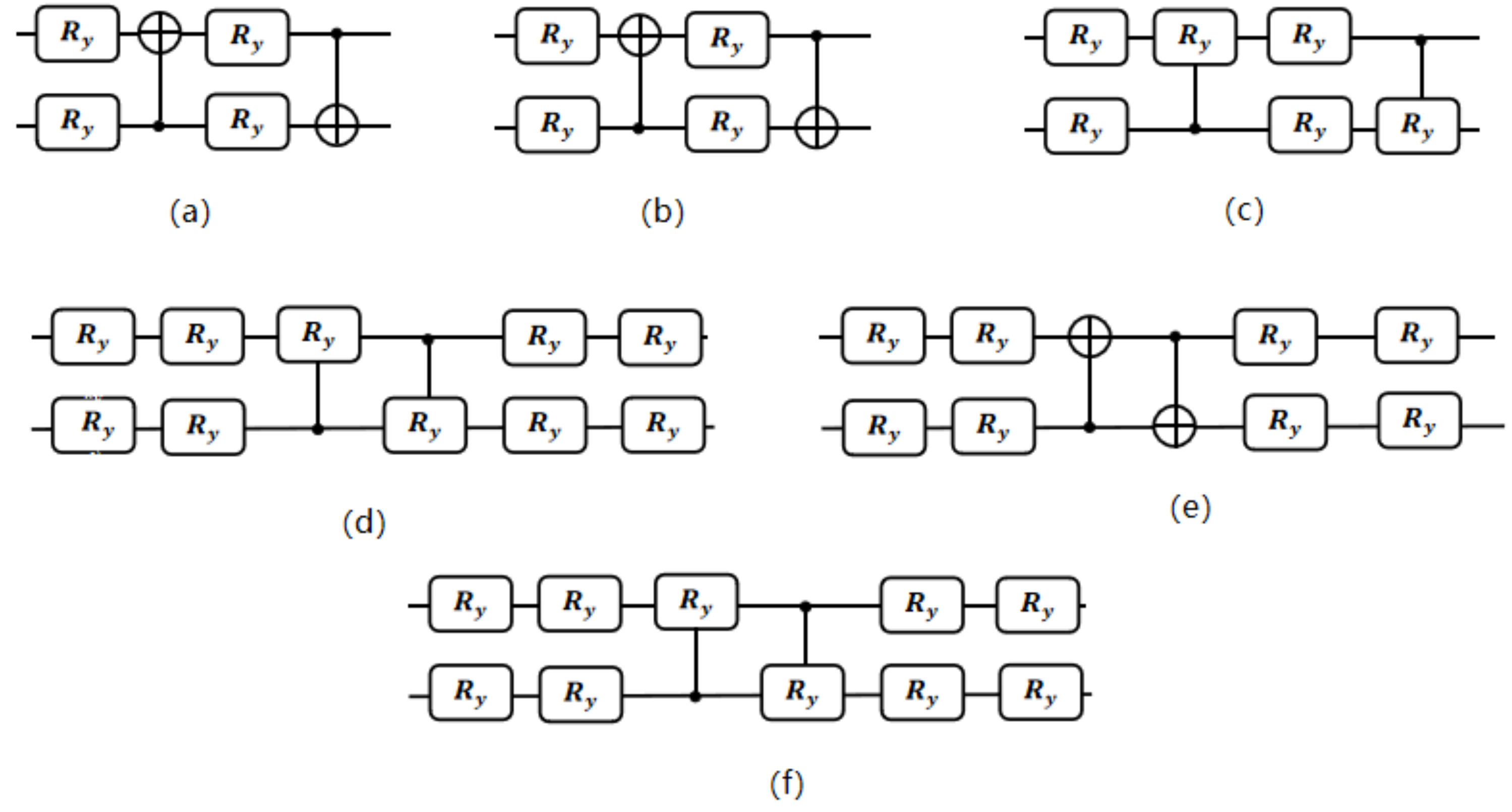
| VQC (a) | 65.9 | 0.805 | 0.095 |
| VQC (b) | 65.2 | 0.832 | 0.089 |
| VQC (c) | 64.8 | 0.861 | 0.083 |
| VQC (d) | 65.3 | 0.846 | 0.092 |
| VQC (e) | 65.7 | 0.827 | 0.094 |
| VQC (f) | 65.4 | 0.836 | 0.092 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Yu, W.; Zhang, C.; Chen, Y. Quantum Convolutional Long Short-Term Memory Based on Variational Quantum Algorithms in the Era of NISQ. Information 2024, 15, 175. https://doi.org/10.3390/info15040175
Xu Z, Yu W, Zhang C, Chen Y. Quantum Convolutional Long Short-Term Memory Based on Variational Quantum Algorithms in the Era of NISQ. Information. 2024; 15(4):175. https://doi.org/10.3390/info15040175
Chicago/Turabian StyleXu, Zeyu, Wenbin Yu, Chengjun Zhang, and Yadang Chen. 2024. "Quantum Convolutional Long Short-Term Memory Based on Variational Quantum Algorithms in the Era of NISQ" Information 15, no. 4: 175. https://doi.org/10.3390/info15040175
APA StyleXu, Z., Yu, W., Zhang, C., & Chen, Y. (2024). Quantum Convolutional Long Short-Term Memory Based on Variational Quantum Algorithms in the Era of NISQ. Information, 15(4), 175. https://doi.org/10.3390/info15040175








