Abstract
A graph is a widely used and effective data structure in many applications; it describes the relationships among nodes or entities. Currently, most semi-supervised or unsupervised graph neural network models are trained based on a very basic operation called negative sampling. Usually, the purpose of the learning objective is to maximize the similarity between neighboring nodes while minimizing the similarity between nodes that are not close to each other. Negative sampling can reduce the time complexity by sampling a small fraction of the negative nodes instead of using all of the negative nodes when optimizing the objective. However, sampling of the negative nodes may fail to deliver stable model performance due to the uncertainty in the sampling procedure. To avoid such disadvantages, we provide an efficient Non-Sampling Graph Neural Network (NS-GNN) framework. The main idea is to use all the negative samples when optimizing the learning objective to avoid the sampling process. Of course, directly using all of the negative samples may cause a large increase in the model training time. To mitigate this problem, we rearrange the origin loss function into a linear form and take advantage of meticulous mathematical derivation to reduce the complexity of the loss function. Experiments on benchmark datasets show that our framework can provide better efficiency at the same level of prediction accuracy compared with existing negative sampling-based models.
1. Introduction
Over the past few years, learning from graph-structured data has seen rapid growth, since a graph is an efficient means to represent the information of nodes and their relationships. Graph neural networks (GNN) are deep learning methods applied on graphs. One of the key motivations of GNN models lies in the long-term history of developing effective graph representation methods. To learn the features from the graph-structured data, DeepWalk [1] used random walk to extract features from the graph. More recently, researchers have made efforts in develop graph neural network (GNN) models. GNN learning can be classified as supervised learning, semi-supervised learning or unsupervised learning. Supervised learning models assume the availability of a supervisor, who classifies the training examples into different classes and utilizes the class information of each instance in the training process, whereas unsupervised learning models identify the class information heuristically and semi-supervised learning models lie between supervised learning and unsupervised learning; only a few training instances have class information in the training process.
In recent years, many efforts have been made to develop unsupervised learning models for GNN, and an increasing number of GNN models have been shown to be effective [2,3]. In unsupervised learning, we do not have access to the label information for each node during the training process. To differentiate between positive and negative nodes, most current unsupervised learning models rely on a basic operation known as negative sampling. This process randomly selects some disconnected nodes from the target node to serve as negative samples (in contrast to the nodes that are connected to the target nodes, which are treated as positive samples). Although negative sampling enhances the training efficiency, it can also destabilize the model training. This is because the sampled negative nodes may differ in various runs, as has been demonstrated in previous studies [4].
Inspired by recent progress in non-sampling recommendation and factorization machines [5,6,7,8], we develop a non-sampling approach to train a GNN. More specifically, we propose a Non-Sampling Graph Neural Network (NS-GNN) framework that can be applied to train unsupervised GNN models. This framework allows us to take all of the positive and negative nodes into consideration and eliminate negative sampling from the training process. A natural problem that arises when using all samples for training is the training efficiency, since, for each node, the number of negative nodes (i.e., nodes not connected to this node) is huge. To mitigate this problem, we first adopt a linear activation function in the loss function, which is shown to be effective in many tasks [9,10]. Next, we provide a mathematical derivation to reformulate the loss function, which enables us to achieve better computational efficiency without compromising the accuracy. To evaluate the performance of our NS-GNN framework, we apply the framework to three GNN models, namely GraphSage-mean, GraphSage-pool [11] and a graph convolution network [12]. Experimental results show that, in most cases, the framework achieves better computational efficiency with the same level of prediction accuracy.
Regarding the remainder of this paper, we first introduce the related work in Section 2. Then, in Section 2, we introduce our NS-GNN framework in detail. In Section 3, we show how to apply the framework to different GNN models. We discuss the experiment results in Section 4 and conclude the work in Section 5.
2. Materials and Methods
In this section, we introduce the related works and our method.
2.1. Related Work
Graph neural networks (GNNs) [13] are a powerful tool in machine learning, particularly when learning from data structured in graphs. Graphs, with nodes representing entities and edges illustrating relationships, form a significant part of many data-driven fields, from social networks to transportation and e-commerce.
Machine learning models are traditionally used for structured or unstructured data (such as tabular data, images, and text) and often fall short when it comes to graph data. For instance, while a convolutional neural network (CNN) [14] is excellent for grid-like data (e.g., images), it does not capture the irregular structures and relational information inherent in graph data.
GNNs extend the principles of deep learning to graph data, transforming the way in which we handle complex interrelated data and providing breakthroughs in various applications, such as social networks [15,16,17], natural language processing [18,19,20,21], computer vision [22,23,24,25] and recommendation [26,27,28]. The introduction of GNNs addressed these challenges by introducing a method that can learn directly from graph data, preserving and leveraging the inherent relational information. With this capability, GNNs represent a significant advancement in machine learning, particularly when dealing with intricate relational data.
Recently, a growing number of GNN models have been developed. For example, DeepWalk [1] learns node embeddings for the graph by random walk to simulate the expectation in the training corpus. A graph convolutional network (GCN) [12] uses a Laplacian matrix to transmit the node feature information from the neighbor nodes to the target node. The GCN follows the neighborhood aggregation scheme, where each node gathers features from its neighboring nodes, creating an aggregated feature. This feature is then passed through a transformation, generally a simple linear transformation, followed by a non-linear activation function such as ReLU. In essence, the GCN leverages the graph’s topology and the nodes’ features to learn a function that generates powerful node embeddings, beneficial for tasks such as node classification and link prediction.
While GCNs provide a strong foundation, they treat each neighboring node equally during aggregation, which might not always be the optimal strategy. Graph Attention Networks (GATs) [29] introduce an attention mechanism to tackle this issue. Attention mechanisms allow models to assign different degrees of importance to different nodes in the aggregation process, making them more adaptive to the input data. A GAT computes the attention coefficients between a node and its neighbors, which are then used to weight the contribution of each neighbor during aggregation. The attention coefficients are learned in such a way as to maximize the model’s performance on the downstream task, making GATs quite powerful for many graph-based learning tasks.
Unlike traditional GNNs, which are transductive and generate embeddings for only the nodes seen during training, GraphSAGE [11] is an inductive method. It can create embeddings for new nodes or entirely new graphs, unseen during training, by leveraging node feature information. GraphSAGE achieves this by learning a function that generates a node’s embedding by sampling and aggregating features from its local neighborhood. By defining the aggregation function and the neural network parameters, GraphSAGE can produce a node-level embedding capable of capturing the graph’s structure and the nodes’ features. Compared to GCNs, GraphSAGE splits the whole graph into several small batches, which increases the node convergence to a large extent, but the training time of one epoch in GraphSAGE is slower than that of the GCN since the embedding utilization in GraphSAGE is smaller [30]. Graph Isomorphism Networks (GINs) [31] were introduced to tackle the limitations of previous GNNs, which were unable to distinguish between certain types of graphs, a property known as distinguishing graph isomorphism. GINs, with their unique aggregation scheme, can capture the complete structural information of graphs, enabling them to discern different graph structures. GINs use a multilayer perceptron (MLP) in the update step, which gives them the power to capture complex patterns in the graph data. MLP’s versatility, along with the unique aggregation mechanism, makes GINs quite expressive and powerful for graph-structured data.
Overall, graph neural networks represent a broad area with various types of models and applications. For a more comprehensive review of GNNs and their applications, readers may refer to some recent surveys, such as [32,33,34,35].
In the following sections, we begin by introducing the notations utilized throughout this paper. Subsequently, we provide background information on GNNs and present our non-sampling approach (NS-GNN). Initially, we outline the general framework, followed by a detailed explanation of how the NS-GNN approach enhances the computational efficiency. Furthermore, a dedicated subsection discusses the application of the NS-GNN framework across various GNN models.
2.2. Preliminaries and Notations
A graph G is often defined as a tuple , where V denotes the set of nodes (or vertices), and E denotes the set of edges. Each edge is a pair indicating a relationship or connection between nodes u and v. An essential aspect of graph data is that the data points (i.e., nodes) are not isolated but interconnected in complex and often meaningful ways.
Traditional machine learning models, from linear regression and decision trees to more sophisticated models such as convolutional neural networks (CNNs) and recurrent neural networks (RNNs), were not designed to handle this type of relational data. While adaptations and pre-processing techniques (such as graph feature extraction [36]) have been employed, these often lead to sub-optimal results or the loss of valuable information.
GNNs offer an alternative approach by directly operating on the graph structure. They use the graph’s topology and node features to learn a function that generates a robust node-level representation or embedding.
A typical GNN model operates in an iterative message-passing framework. The steps involved are as follows.
- Message Passing or Propagation: Each node in the graph sends out message to its neighboring nodes [13]. This information could be the node’s original feature vector or a transformed version of it. Mathematically, the message from node u to node v at the iteration can be written as a function M of their features and and node embedding vectors :
- Aggregation: Each node aggregates the messages received from its neighbors. Let us denote the set of neighbors of node u as [12]. The aggregation step can be represented as an aggregation function A over the messages from the neighbor nodes:
- Update: Each node updates its feature vector based on the aggregated message. This update can be modeled as an update function U:
With the help of message-passing, aggregation and update functions, GNN models can learn the structure and the context of the model. These functions facilitate the exchange, accumulation and evolution of information across the nodes of the graph. The message-passing function serves as a communication method, ensuring the spread of local node information throughout the network. The aggregation function, on the other hand, plays a critical role in gathering information, allowing each node to draw knowledge from its neighbor nodes. Then, the GNN model will use this aggregated information to refine each node’s features, leading to more robust and informative representations that ensure the structural and contextual aspects of the graph [12]. These three functions make sure GNNs to effectively learn from graph-structured data, setting them apart from traditional machine learning models.
2.3. Problem Formalization
In this section, we provide an abstract formalization of unsupervised learning for GNNs, which is used in the remaining parts of the paper. Table 1 introduces the basic notations that are used in this paper. Given a graph , the purpose of unsupervised learning is to train a scoring function , which is able to distinguish the neighbor nodes of node u, which is , and the nodes that are not neighbours of u, which are . Therefore, the goal of an unsupervised learning model is to minimize the difference between the neighbor nodes (or positive nodes) and maximize the difference between the nodes that are not connected to each other (or negative nodes) [36]. Based on these definitions, the loss function of an unsupervised learning model can be formulated as
where the term represents the loss of the positive nodes and the term represents the loss of the negative nodes, and is a monotonic activation function, which is usually the log-sigmoid function . The purpose of the loss is to maximize the similarity of the connected nodes ( term) and minimize the similarity of disconnected nodes ( term).

Table 1.
Summary of the notations in this work.
2.4. Non-Sampling Graph Neural Network
If we wish to develop a non-sampling GNN framework, we need to take all of the negative samples into consideration, i.e., the term in Equation (4) should sum over all nodes . We first equivalently rewrite Equation (4) in the following form:
where the term denotes the sum over all nodes. From this equation, we can see that the time complexity for the calculation of the loss function is huge. More specifically, the time complexity of is , where d is the size of the dimension. Therefore, the time complexity of the calculation of the whole loss function is . If we apply this method to real-world datasets, the computational time would be unrealistic. As a result, we require an efficient method of reformulating the loss function through mathematical derivations. We provide further details in the subsequent sections.
2.5. Improving Time Efficiency
To improve the time efficiency, the first step is to identify the most time-consuming part. In practice, most graphs are sparse, meaning that each node in the graph has only a few neighboring nodes. As a result, the calculation of the term in Equation (5) is feasible, but the calculation of the term would dominate the time complexity since it sums over all node pairs. As a result, we need to decompose the term and seek more efficient implementations of Equation (5).
However, if the activation function is non-linear, it is very difficult for us to decompose and simplify the term.
To solve this problem, similar to recent advances in graph neural network research [9], we adopt a linear activation function. More specifically, since itself is already a monotonic increasing function and it is decomposable, we use to replace (in particular, ) in the loss function. In the experiments, it is found that the model can provide the same level of prediction accuracy with such substitution but better efficiency. In this case, the loss function can be reformulated as
Since the time complexity of calculating is very high, we examine the term. The term can be represented as the following:
where and are the node embeddings of node u and node v, and and represent the i-th element of the corresponding embedding vector. By manipulating the inner product, can be rewritten as the following:
From the above equation, we can see that and are separated from each other and we can disentangle the parameters in and rearrange them in an more efficient way. Then, we apply Equation (8) into Equation (6) and obtain the final loss function as
Algorithm 1 is the pseudocode of our method. As mentioned before, contributes the most significantly to the complexity of the loss function. However, through the operation applied above, we are able to decrease this complexity, which can be a crucial step when dealing with large-scale problems. Initially, the complexity of the loss function was . In practice, this could lead to prohibitively long computation times, especially when dealing with large datasets and high-dimensional embeddings. After applying our operation, the complexity has been reduced to . This is a significant improvement: the computational time now scales linearly with the size of the vocabulary |V|. In practical terms, this reduction in complexity means that our algorithms will run faster, enabling us to deal with larger datasets, more complex models and more sophisticated applications. Furthermore, the reduced computational requirements make the approach more accessible, as it can now be implemented on hardware with fewer resources. The loss function can be applied over existing graph representation learning methods such as GCN [12] and GraphSAGE [11] to improve the efficiency of these models, compared with training the loss based on negative sampling methods.
| Algorithm 1 Efficient Calculation of Loss Function |
|
3. Results
In this section, we list the experimental results and evaluate both the efficiency and accuracy of the Non-Sampling Graph Neural Network (NS-GNN) framework.
3.1. Experimental Setup
We first introduce the datasets, baseline methods, evaluation metrics and parameter settings.
We conduct our experiments on three benchmark datasets for graph neural network research, which are NELL, PubMed and Cora. Some statistical details of these three datasets are shown in Table 2.

Table 2.
Basic statistics of the datasets.
NELL [37]: The NELL dataset is extracted from the knowledge graph introduced in [37]. We follow the same pre-processing scheme as described for GCNs in [12]. The dataset consists of 55,864 relation nodes and 9891 entity nodes.
PubMed [38]: The PubMed dataset includes 19,717 scientific publications on diabetes from the PubMed database. Each publication in the dataset is described by a term frequency–inverse document frequency (TF/IDF) weighted word vector in a dictionary consisting of 500 unique words.
Cora [39]: The Cora dataset consists of 2708 scientific publications classified into one of seven classes. The citation network consists of 5429 links. Each publication in the dataset is described by a 0/1-valued word vector indicating the absence/presence of the corresponding word from the dictionary.
3.2. Baselines Methods
We apply the NS-GNN framework to the following frequently used graph neural network models for comparison.
- GCN [12]: The graph convolutional neural network (GCN) model uses convolutions to learn the representations of the nodes in the graph under a neural network architecture.
- GraphSAGE [11]: This is an inductive learning graph neural network framework that can use node feature information to generate embeddings for unseen vertices.
All of the models are implemented by PyTorch, an open-source library. Moreover, we use the baselines implemented by Pytorch geometric [40], which is an open-source toolkit for graph neural networks.
3.3. Evaluation Metrics
For each model, we first use unsupervised learning to learn the embedding of each node in the graph. In the next step, we split the whole dataset into a training set, validation set and testing test. Then, we use the embedding learned from the unsupervised learning and adopt a logistic regression over the training set to train the classifier and use the validation set to avoid overfitting. We then test the learned classifier on the testing set.
For each dataset, there are multiple classes, and each node in the graph only belongs to one of these classes. In the testing set, we use our trained model to perform the classification and compare the predicted label with the ground-truth label. Then, we report the accuracy of the prediction result, which is defined as
3.4. Parameter Settings
For every model, we establish an embedding dimension default size of . This numerical value is not randomly selected; rather, it is determined from a number of previous studies, initial experiments and computational limitations. This ensures the optimal equilibrium between intricacy and manageability. Nevertheless, acknowledging the potential significance of this parameter, we perform an ablation study, methodically altering the size of the embedding dimension to comprehend its effect on our models’ performance.
All of the NS-GNN models undergo normalization to circumvent the issue of overfitting. This method reduces the magnitude of the weight vectors without changing their direction, helping to prevent extreme weight values and maintain the model’s capacity to generalize from training to unseen data. However, for the negative sampling-based baselines, we skip this normalization step. The decision to do so stems from our observations that the sigmoid loss function, which we employ in these cases, tends to produce better experimental results without normalization.
4. Discussion
In this section, we discuss the results of our method.
4.1. Computational Efficiency
We apply the NS-GNN framework to the GCN, GraphSAGE-mean and GraphSAGE-max models, where GraphSAGE-mean is the GraphSAGE model under the mean-pooling aggregation function, while GraphSAGE-max is the GraphSAGE model under the max-pooling aggregation function. We use NS-X to denote the model in which we apply our non-sampling framework to model X. For a fair comparison, all results are run on a single NVIDIA Geforce 2080Ti GPU. The operating system is Ubuntu 16.04 LTS. For all models, the dimension is set as 64 and the number of training epochs is 50. The experimental results regarding the accuracy and running time for each dataset are shown in Table 3.

Table 3.
Experimental results regarding accuracy, efficiency and speedup.
We can see that, compared to the baselines, in most cases, our NS-GNN framework achieves better training efficiency than the corresponding baseline. For example, if we apply NS-GNN to GraphSAGE under the max-pooling aggregation function (GraphSAGE-max) on the PubMed dataset, the training time is 13.1 s, while the original negative-sampling based model requires 68.1 s. Acceleration is performed around 5 times. For other models and datasets, our non-sampling framework also achieves better efficiency and the speedup ranges from 1.09 times to 4.8 times.
4.2. Classification Accuracy
In this section, we discuss the classification performance of the NS-GNN framework. We compare the prediction accuracy of the three sampling-based models, GraphSAGE-mean, GraphSAGE-max and GCN, with their corresponding non-sampling versions.
As seen in Table 3, our framework outperforms the baselines in terms of prediction accuracy in most cases. The reason that NS-GNN can deliver superior performance in less time under linear activation is that sampling-based models only consider a portion of the negative samples in the dataset. However, our NS-GNN framework can take all of the negative samples in the dataset into consideration, which largely offsets the influence of using linear activation while achieving better efficiency.
Another interesting observation from Table 3 is that the NS-GNN framework has better performance on NELL and PubMed than Cora. This is because NELL and PubMed possess significantly more nodes and edges compared to the other dataset. When dealing with large graphs, the benefits of using our non-sampling training framework become more pronounced. This is because the negative sampling approach can only consider a small fraction of the negative nodes, while our non-sampling framework can incorporate all negative nodes for training, thereby utilizing more comprehensive information from the graph.
4.3. Influence of Embedding Dimension
In Figure 1, we show the accuracy of the NS-GNN framework under different embedding dimensions d. In most cases, models will demonstrate better performance with larger dimensions d. However, a larger dimension will also result in a longer model training time. Therefore, we need to achieve a trade-off between the performance and training time. As we can see in Figure 2, in most cases, the performance becomes relatively stable around dimension 50–100. As a result, we recommend an embedding dimension in this range for the best trade-off.
Figure 1.
An illustration of the GNN model. The left side features a sample of a graph, while the right side depicts the process of message passing and aggregation.
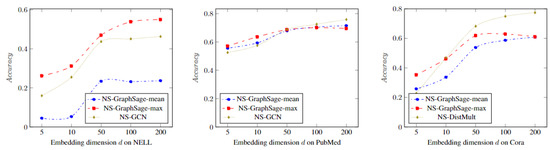
Figure 2.
Performance in terms of accuracy under different embedding dimensions d.
5. Conclusions
In this paper, we propose the Non-Sampling Graph Neural Network (NS-GNN), a novel non-sampling training framework for graph neural networks (GNNs) that fully leverages all the negative samples within a dataset during model training. Our rigorous experiments on three diverse datasets illustrate that this framework can markedly enhance the training efficiency while maintaining a comparable level of classification accuracy.
The exploration of decomposable non-linear activation functions is not only pivotal to the NS-GNN framework but also holds considerable potential to benefit other types of models beyond GNNs. One particularly promising application lies in the domain of knowledge graphs, where these activation functions could help to extract and represent more complex relationships among entities. Furthermore, in the context of pre-trained language models, these functions could enhance their ability to understand and generate language, thereby contributing to improvements in a myriad of natural language processing tasks.
Simultaneously, we also foresee the potential of these activation functions in various other fields, such as collaborative filtering for recommendation systems, anomaly detection in time-series data or even bio-informatics, where the methods used for GNNs have started to exhibit significant benefits.
Alongside these exciting prospects, it is essential to continue applying the NS-GNN framework against other contemporary graph neural network models, across different datasets and tasks. This will allow us to further understand the strengths, limitations and potential improvements that can be made to our proposed model.
In conclusion, this study marks the beginning of a long and promising journey in the exploration and development of the Non-Sampling Graph Neural Network framework. We look forward to further exploring this exciting area and pushing the boundaries of what GNNs can achieve.
Author Contributions
Conceptualization, J.J., Z.L. and Y.Z.; methodology, J.J. and S.X.; software, J.J. and Z.L.; validation, J.J. and Z.L.; formal analysis, J.J. and Y.G.; investigation, J.J. and J.T.; writing—original draft preparation, J.J., Z.L., Y.G. and Y.Z.; writing—review and editing, J.J., S.X., J.T. and Y.Z.; supervision, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available datasets were analyzed in this study. Data can be found at https://github.com/pyg-team/pytorch_geometric (accessed on 11 July 2023).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GNN | Graph Neural Network |
| NS-GNN | Non-Sampling Graph Neural Network |
| GAT | Graph Attention Network |
| GCN | Graph Convolutional Network |
References
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Yang, L.; Gu, J.; Wang, C.; Cao, X.; Zhai, L.; Jin, D.; Guo, Y. Toward Unsupervised Graph Neural Network: Interactive Clustering and Embedding via Optimal Transport. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; pp. 1358–1363. [Google Scholar]
- Henaff, M.; Bruna, J.; LeCun, Y. Deep convolutional networks on graph-structured data. arXiv 2015, arXiv:1506.05163. [Google Scholar]
- Wang, M.; Gong, M.; Zheng, X.; Zhang, K. Modeling dynamic missingness of implicit feedback for recommendation. Adv. Neural Inf. Process. Syst. 2018, 31, 6669. [Google Scholar]
- Rendle, S. Factorization machines. In Proceedings of the 2010 IEEE International Conference on Data Mining, Sydney, Australia, 13–17 December 2010; pp. 995–1000. [Google Scholar]
- Chen, C.; Zhang, M.; Zhang, Y.; Ma, W.; Liu, Y.; Ma, S. Efficient heterogeneous collaborative filtering without negative sampling for recommendation. Proc. AAAI Conf. Artif. Intell. 2020, 34, 19–26. [Google Scholar] [CrossRef]
- Li, Z.; Ji, J.; Fu, Z.; Ge, Y.; Xu, S.; Chen, C.; Zhang, Y. Efficient Non-Sampling Knowledge Graph Embedding. In Proceedings of the Web Conference 2021, Online, 12–23 April 2021; pp. 1727–1736. [Google Scholar]
- Chen, C.; Zhang, M.; Ma, W.; Liu, Y.; Ma, S. Efficient non-sampling factorization machines for optimal context-aware recommendation. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 2400–2410. [Google Scholar]
- Wu, F.; Souza, A.; Zhang, T.; Fifty, C.; Yu, T.; Weinberger, K. Simplifying graph convolutional networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6861–6871. [Google Scholar]
- Katharopoulos, A.; Vyas, A.; Pappas, N.; Fleuret, F. Transformers are rnns: Fast autoregressive transformers with linear attention. In Proceedings of the International Conference on Machine Learning, Vienna, Austria, 12–17 July 2020; pp. 5156–5165. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2017, arXiv:1609.02907. [Google Scholar]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2008, 20, 61–80. [Google Scholar] [CrossRef] [PubMed]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Chen, J.; Ma, T.; Xiao, C. FastGCN: Fast Learning with Graph Convolutional Networks via Importance Sampling. arXiv 2018, arXiv:1801.10247. [Google Scholar]
- Yang, L.; Liu, Z.; Dou, Y.; Ma, J.; Yu, P.S. Consisrec: Enhancing gnn for social recommendation via consistent neighbor aggregation. In Proceedings of the 44th international ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 11–15 July 2021; pp. 2141–2145. [Google Scholar]
- Liu, Y.; Zeng, K.; Wang, H.; Song, X.; Zhou, B. Content matters: A GNN-based model combined with text semantics for social network cascade prediction. In Proceedings of the Advances in Knowledge Discovery and Data Mining: 25th Pacific-Asia Conference, PAKDD 2021, Virtual Event, 11–14 May 2021; Proceedings, Part I.. Springer: Berlin/Heidelberg, Germany, 2021; pp. 728–740. [Google Scholar]
- Yao, L.; Mao, C.; Luo, Y. Graph convolutional networks for text classification. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 29–31 January 2019; Volume 33, pp. 7370–7377. [Google Scholar]
- Wu, L.; Chen, Y.; Ji, H.; Liu, B. Deep learning on graphs for natural language processing. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 11–15 July 2021; pp. 2651–2653. [Google Scholar]
- Schlichtkrull, M.S.; Cao, N.D.; Titov, I. Interpreting Graph Neural Networks for {NLP} with Differentiable Edge Masking. In Proceedings of the International Conference on Learning Representations, Virtual Event, 3–7 May 2021. [Google Scholar]
- Wu, L.; Chen, Y.; Shen, K.; Guo, X.; Gao, H.; Li, S.; Pei, J.; Long, B. Graph neural networks for natural language processing: A survey. Found. Trends® Mach. Learn. 2023, 16, 119–328. [Google Scholar] [CrossRef]
- Wang, X.; Ye, Y.; Gupta, A. Zero-shot recognition via semantic embeddings and knowledge graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6857–6866. [Google Scholar]
- Pradhyumna, P.; Shreya, G. Graph neural network (GNN) in image and video understanding using deep learning for computer vision applications. In Proceedings of the 2021 Second International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 4–6 August 2021; pp. 1183–1189. [Google Scholar]
- Shi, W.; Rajkumar, R. Point-gnn: Graph neural network for 3d object detection in a point cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1711–1719. [Google Scholar]
- Han, K.; Wang, Y.; Guo, J.; Tang, Y.; Wu, E. Vision GNN: An Image is Worth Graph of Nodes. Proc. Adv. Neural Inf. Process. Syst. 2022, 35, 8291–8303. [Google Scholar]
- Wu, C.; Wu, F.; Cao, Y.; Huang, Y.; Xie, X. FedGNN: Federated Graph Neural Network for Privacy-Preserving Recommendation. arXiv 2021, arXiv:2102.04925. [Google Scholar]
- Gao, C.; Wang, X.; He, X.; Li, Y. Graph neural networks for recommender system. In Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining, Virtual Event, 21–25 February 2022; pp. 1623–1625. [Google Scholar]
- Wu, S.; Tang, Y.; Zhu, Y.; Wang, L.; Xie, X.; Tan, T. Session-based recommendation with graph neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 346–353. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2018, arXiv:1710.10903. [Google Scholar]
- Chiang, W.L.; Liu, X.; Si, S.; Li, Y.; Bengio, S.; Hsieh, C.J. Cluster-gcn: An efficient algorithm for training deep and large graph convolutional networks. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 257–266. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How Powerful are Graph Neural Networks? In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Kefato, Z.T.; Girdzijauskas, S. Self-supervised graph neural networks without explicit negative sampling. arXiv 2021, arXiv:2103.14958. [Google Scholar]
- Tam, P.; Song, I.; Kang, S.; Ros, S.; Kim, S. Graph Neural Networks for Intelligent Modelling in Network Management and Orchestration: A Survey on Communications. Electronics 2022, 11, 3371. [Google Scholar] [CrossRef]
- Zhuge, W.; Nie, F.; Hou, C.; Yi, D. Unsupervised single and multiple views feature extraction with structured graph. IEEE Trans. Knowl. Data Eng. 2017, 29, 2347–2359. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, JMLR Workshop and Conference Proceedings, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Sen, P.; Namata, G.; Bilgic, M.; Getoor, L.; Galligher, B.; Eliassi-Rad, T. Collective classification in network data. AI Mag. 2008, 29, 93. [Google Scholar] [CrossRef]
- McCallum, A.K.; Nigam, K.; Rennie, J.; Seymore, K. Automating the construction of internet portals with machine learning. Inf. Retr. 2000, 3, 127–163. [Google Scholar] [CrossRef]
- Fey, M.; Lenssen, J.E. Fast Graph Representation Learning with PyTorch Geometric. arXiv 2019, arXiv:1903.02428. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).