Abstract
Knowledge graphs are graph-based data models which can represent real-time data that is constantly growing with the addition of new information. The question-answering systems over knowledge graphs (KGQA) retrieve answers to a natural language question from the knowledge graph. Most existing KGQA systems use static knowledge bases for offline training. After deployment, they fail to learn from unseen new entities added to the graph. There is a need for dynamic algorithms which can adapt to the evolving graphs and give interpretable results. In this research work, we propose using new auction algorithms for question answering over knowledge graphs. These algorithms can adapt to changing environments in real-time, making them suitable for offline and online training. An auction algorithm computes paths connecting an origin node to one or more destination nodes in a directed graph and uses node prices to guide the search for the path. The prices are initially assigned arbitrarily and updated dynamically based on defined rules. The algorithm navigates the graph from the high-price to the low-price nodes. When new nodes and edges are dynamically added or removed in an evolving knowledge graph, the algorithm can adapt by reusing the prices of existing nodes and assigning arbitrary prices to the new nodes. For subsequent related searches, the “learned” prices provide the means to “transfer knowledge” and act as a “guide”: to steer it toward the lower-priced nodes. Our approach reduces the search computational effort by 60% in our experiments, thus making the algorithm computationally efficient. The resulting path given by the algorithm can be mapped to the attributes of entities and relations in knowledge graphs to provide an explainable answer to the query. We discuss some applications for which our method can be used.
1. Introduction
Over the past few decades, attempts have been made to provide human-like commonsense reasoning to systems by acquiring vast knowledge about any domain. Humans are intuitively good at dealing with uncertainties and making meaningful inferences from incomplete, missing, and unstructured information. On the other hand, machines need precise information typically stored in a structured database and queried using a parsing strategy or well-defined rules. It is hard to rely on traditional relational data stores, as the massive influx of unstructured data and real-world information continuously evolve.
In recent years, knowledge graphs (KGs) have emerged as a flexible representation using the graph-based data model. They capture and integrate factual knowledge from diverse sources of data at a large scale in a way that machines conduct reasoning and inference over the graphs for downstream tasks such as question answering, making useful recommendations, etc., [1].
The knowledge graph allows for postponing the schema definition, thus letting the data evolve more flexibly [2]. A typical data unit in knowledge graphs is stored as entity–relationship–entity triplets, representing entities as nodes and relationships as the edges in a graph. The nodes are modeled to contain the knowledge or facts about the entities in the form of entity attributes. However, most existing systems used in answering a question over the knowledge graphs rely on static knowledge bases (KBs to train the knowledge graph question-answering (KGQA) model. These systems are trained offline with specific datasets and then deployed online to handle user queries. After deployment, they fail to learn from unseen new entities added to the graph. Thus, the problem faced by the knowledge graphs is the need for dynamic algorithms which can continuously learn and adapt to evolving data [3].
Another challenge is the explainability and interpretation of the results when a query is posed to these evolving graphs. Question answering in knowledge graphs requires reasoning over multiple edges to arrive at the right answer and should have a tractable path to explain the new behavior [4,5]. A full explanation of the answer helps the users in their interaction with the system. For example, a query such as, “Which paper author Amanda published in SIGIR conference?” needs multihop reasoning of the form, and to deduce the answer. Given the nature of this domain, if more papers, conferences, or authors are added in the future, the inference mechanisms need to be adaptable to the changes and interpretable to trace the new paths.
The state-of-the-art embedding-based neural network models for answering semantic queries consider only the candidate answer entities. They learn embeddings conditioned on neighboring entities and relations while being oblivious to the query relations and path. These methods help deduce the new facts but need more interpretation and logical reasoning of the answer [6]. The alternative approach uses path-based methods including path ranking algorithms (PRAs) based on random walk [7], DeepPath [8] etc. These methods are highly interpretable but suffer from large search space issues [9]. Moreover, they consider only a static snapshot and fail to learn from dynamically changing knowledge graphs [10].
In this paper, we propose using the auction algorithms recently introduced in the paper [11], to perform question answering in knowledge graphs. These algorithms are dynamic and can adapt to the changing environments in real time, making them suitable for offline and online training. They can help knowledge graphs to address the challenges of adaptability and interpretability.
The main auction path construction (APC) algorithm, to be discussed in Section 3, computes paths (not necessarily the shortest) connecting an origin node to one or more destination nodes in a directed graph and uses node prices to guide the search for the path. The prices are initially chosen arbitrarily and are dynamically updated using a set of rules to be described later. When new entities are added or removed from the graph, the algorithm can dynamically adapt to the changing structure by reusing the prices for existing nodes and allocating arbitrary prices to the new nodes. The prices provide the means to “transfer knowledge”. The prices from previous searches can be used as initial prices for subsequent related searches, resulting in faster computation.
The auction algorithms provide full traceable paths and not just the single entity answer score. The full path can give the user a logical inference for the queries requiring multihop reasoning. Thus, the final answer constructed using our method is interpretable and provides an explainable answer. In particular, we can leverage the knowledge graph path relations, entity metadata, and attributes to add semantic information to the paths constructed by the auction algorithms.
The main contributions of the paper are as follows:
- We propose a new method using auction algorithms for question answering in knowledge graphs.
- We show that knowledge graphs can take advantage of the dynamic nature of auction algorithms.
- Our results show that the computational efficiency of the search can be improved by reusing the prices that have been learned from previous queries.
- Lastly, we leverage the entity metadata and path relations to construct an interpretable answer from the resulting path given by auction algorithms.
2. Related Work
In this section we review the path-finding approaches currently used in knowledge graphs, and we contrast them with our proposed approach that is based on auction algorithms.
2.1. Embedding-Based Methods
The popular methods used in knowledge graphs for tasks like question answering, knowledge base completion, link prediction, relation extraction, etc., are embedding-based models [12]. Low-dimensional vectors called graph embeddings represent the entities and relations for these tasks. The embedding models learn a scoring function in latent embedding space based on the co-occurrence of words in the text to manifest the semantics of the original graph. The higher score is used to determine the plausibility of facts [6]. The top-ranked entities are chosen as the predicted answers. These models learn subtle patterns in data, but they lack generic forms of reasoning. The predicted answers given by the model are a single entity and do not provide any explanation to the user. For instance, the embedding-based model is trained on individual facts such as (Irving Cummings, wasBornIn, New York City) and (New York City, isLocatedin, United States). The model can leverage the logical patterns and compute a score to possibly deduce that (Irving Cummings, isCitizenOf, United States). However, it fails to explain or offer any inference path evidence supporting the answer. This black-box style makes the reasoning process less interpretable and hampers the users from interacting with the system [9].
Palmonari et al. [13] suggested performing complex logical queries over embedding models to deal with explainability. Bhowmik et al. [10] used an inductive learning framework to learn representations and find reasoning paths between entities.
Secondly, the embedding-based methods are used to answer factoid-based questions, and they need to improve at answering multihop queries. Most works extract a subgraph to answer the question in parts and later augment the answers [14]. Ren et al. [15] added a query synthesizer tree to parse the multihop query in parts. A multihop KBQA was proposed by Saxena et al. [4] to fill the gaps. They embedded all the entities instead of only using neighborhood entities, and the answers were chosen by finding the similarity score between the question and relations.
2.2. Path-Based Methods
Another approach used for question-answering tasks in knowledge graphs is path based. This approach relies on the conventional graph traversal methods such as A*, Dijkstra, and minimum spanning tree, which use statistical characteristics such as adjacency matrix, degree, closeness, Eigenvector, PageRank, and connectivity [7,8,9,16,17]. The inference process is highly interpretable, but these methods suffer from scalability issues and high computation costs, as they rely on enumerating all possible paths [9].
All these methods consider the static snapshot of the knowledge graph and only learn the representation of the known entities they have seen before during the offline training. The models are unaware of the emerging entities and fail to keep up with the changes in the graph to answer new questions [5,9]. They thus may not be well-suited for an evolving knowledge graph [10].
2.3. Auction Algorithms
Auction algorithms are fundamentally based on mathematical ideas of duality and convex optimization and are inspired by economic equilibrium processes. They have a long history, starting with the original proposal [18], which aimed to solve the classical problem of assignment of objects to persons through a competitive bidding mechanism that resembles a real-life auction. Over time, the original auction algorithm [18] was extended to solve a wide variety of network optimization problems with linear and convex costs (see the tutorial survey [19] and the book [20]). Among others, auction algorithms have been used widely in optimal transport applications [21,22,23] and have been applied to the training of machine learning models [24,25,26].
One paper [27] considered the classical shortest path problem and proposed an adaptation of the original auction algorithm, which bears similarity with the path construction algorithms recently proposed in [11] and used in the present paper. The more recent algorithms are different in one respect, which is critical for application in knowledge graphs. They allow arbitrary initial prices, making them faster and more suitable for dynamic environments involving a changing knowledge graph topology and queries. In particular, this property allows for the reuse of prices from one query to another similar query through an ongoing “price learning” process which can significantly improve computational efficiency, and our computational experiments have also confirmed this. Thus, the “learned prices” can improve computational efficiency, and contrary to the Dijkstra-like path-based algorithms, they can adapt well to an evolving knowledge graph environment and continuously learn as new entities emerge.
3. Auction Algorithms Description
In this section, we will discuss the use of auction algorithms for constructing paths from a given origin to one or more destinations in knowledge graphs. In this work, we used two variations of auction algorithms. The first variation is a path construction algorithm recently proposed in [11] called auction path construction (APC), and the second is its extension called the auction weighted path construction algorithm (AWPC).
Auction algorithms use a price mechanism to guide the search for a solution. The algorithms efficiently emulate the search process, guided by some rules for price updates that we will describe shortly. Intuitively, the algorithms can be visualized in terms of a mouse moving in a graph-like maze to reach the destination. The mouse advances from high-price to low-price nodes, going from a node to a downstream neighbor node only if that neighbor has a lower price (or equal price under some conditions). It backtracks when it reaches a node whose downstream neighbors have higher prices. In such a case, it suitably increases the price of that node, thus marking the node as less desirable for future exploration and finding alternative paths to the destination.
3.1. Auction Path Construction (APC) Algorithm
We first provide some terminology before describing the algorithms mathematically.
3.1.1. Background and Terminology
A knowledge graph consists of a set of entities E, a set of relations R, and attributes I. The entities are represented as the nodes, and the relations as the edges connecting the nodes. The attributes are the metadata associated with each edge and contain the facts about the corresponding entities. For any edge, , the node is called the downstream neighbor of . A node is called a deadend if it has no downstream neighbors.
At the typical iteration, the algorithm maintains a path P = that starts at the origin node , ends at some node , and is such that is an edge, and is an edge for all .
Once the destination becomes the terminal node of the path, the algorithm terminates. The path is either extended by adding a new node or contracted by deleting its terminal node. The decision to extend or contract is based on a set of variable ones per node, called prices. Each node e is assigned a scalar price . The prices are initially chosen arbitrarily, and the algorithm maintains and updates the prices according to some rules. To describe these rules, we introduce some terminology. Under the current set of prices, each edge is classified as follows:
- (a)
- (b)
- (c)
The prices can be seen as a measure of the desirability of revisiting and advancing from that node in the future. Low-price nodes are viewed as more desirable.
When the algorithm starts with a path of the nondegenerate form , a contraction removes the terminal node from P to obtain the new path , while an extension adds a node to obtain a new path . The predecessor of the node in path P is denoted by . If , then . If the terminal node of P is not a deadend, then the downstream neighbor of with minimal price is denoted by and is called the successor of :
If multiple downstream neighbors of have a minimal price, the algorithm arbitrarily designates one of these neighbors as . The algorithm also uses a positive scalar to regulate the size of price changes. For auction path construction (APC), we use , but the value of can play an essential role in the weighted version of the algorithm (AWPC).
3.1.2. Formal Definition
Given the current path P = , the algorithm chooses a min-price successor node and updates the price by keeping track of the node prices of the predecessor, and successor, , such that the following downhill path property is always maintained.
Downhill Path Property: All the edges of the path P = maintained by the APC algorithm are level or downhill. Moreover, the last edge of P is downhill following an extension to .
In particular, given the current path P and a set of node prices, the algorithm changes P and the price of its terminal nodes according to following cases (see Figure 1):
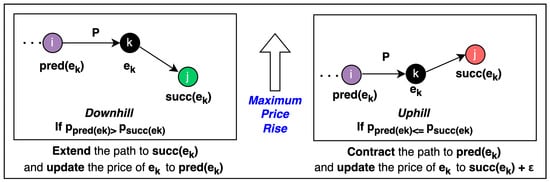
Figure 1.
Figure showing the price update and raising the price to the maximum possible level. In case of extension, the algorithm maintains the maximum possible level making the predecessor arc level. In the case of a contraction, it raises the price of to the maximum possible level, making the arc uphill.
- (a)
- Set the price to , and extend P to .
- (b)
- and node is deadend: Set the price to ∞ (or a very high number for practical purposes), and contract P to .
- (c)
- and node is not deadend. Then, the following two cases are considered.
- (i)
- If , then extend P to and set to any price level that makes the arc level or downhill and the arc downhill. For example, setThis raises the price to the maximum possible level, making the arc level.
- (ii)
- If , then contract P to and raise the price of to the price of plus . This makes the arc uphill and the arc downhill.
The algorithm terminates once the destination becomes the terminal node of P. The significance of the downhill path property is that when an extension occurs, a cycle cannot be created in the sense that the terminal node is different from all the predecessor nodes, on the path P. The reason for this is that the downhill path property implies that following an extension, we have
showing that the terminal node following an extension cannot be equal to any of the preceding nodes of P.
3.1.3. Multiple Destinations or Multiple Origins
The algorithm can be generalized to handle a single origin but not multiple destinations. A list containing the destinations that have yet to be reached is maintained. Once a destination is reached by the path P, it is removed from the destination list. The algorithm continues to run until it has reached all the destinations. Similarly, for the multiple-origin problem, the algorithm is used to construct a tree of paths from all the origins by concatenating the respective paths.
To illustrate APC with an example, consider the five-node graph shown in Figure 2a, with initial prices (0, 3, 0, 0, 0). For this example, the origin is node 1, with three destinations: nodes 2, 4, and 5. The algorithm terminates after it has reached all the destinations. Figure 2 shows the successive iterations of the algorithm. The algorithm maintains a path and updates prices as per the defined rules. The path for each destination can be stored, and finally, the algorithm terminates after it has reached all the destinations. This example shows the single application of the algorithm. If the algorithm is applied to multiple searches, then at the end of each search, the infinite price should be set to a finite value, such as the minimum price of the upstream neighbors of the respective node.
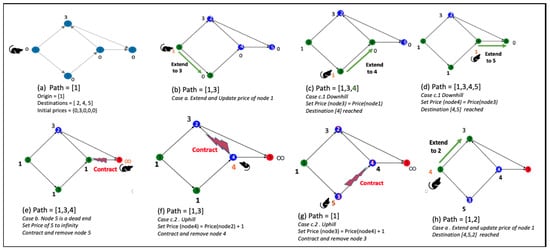
Figure 2.
The figure shows the APC traversal on a five-node graph. The initial prices are arbitrarily chosen as . The origin node is given as , with three destination nodes . The algorithm chooses to extend or contract and update the price as per the given rules. The prices after the update in each iteration are shown against each node in the figure.
3.2. Auction Weighted Path Construction (AWPC) Algorithm
The generalization of the APC algorithm is the auction weighted path construction (AWPC) algorithm. It uses a weight for every edge , which measures the desirability of including an edge, , into the path. In particular, the length of a path is defined as the sum of the weights of its edges. The edge weights can act as a bias toward producing paths with a smaller length. The paths generated by the AWPC algorithm have relatively short lengths but do not guarantee they are the shortest.
Extending the terminology of APC, under the current set of prices and weights, the edge is called:
- (a)
- ;
- (b)
- ;
- (c)
- .
The AWPC algorithm maintains a directed path that starts at the origin and consists of distinct nodes. The path is either the degenerate path , or it ends at some node , which is called the terminal node of P. Similarly to APC, each node is assigned an initial arbitrarily chosen scalar price . In addition to prices, AWPC also maintains edge weights for every edge . The edge weights are used to introduce a bias. The algorithm tends to converge faster in case of smaller values of edge weights. In this work, we simulated experiments with different edge weights such as (0, 1, 2, 3, 6). As shown later in Results Section 5, our experimental findings supported this. APC is the special case of AWPC where for all edges .
The AWPC algorithm starts with the degenerate path and some initial prices. Each iteration starts with a path P and a scalar price for each node . At the end of the iteration, a new path is obtained from P through a contraction or an extension, as explained earlier in APC. Here, the amount of the price rise is also determined by a scalar parameter . The path and prices are updated at every iteration according to the following cases:
- (a)
- Set the price to , and extend P to .
- (b)
- and node is deadend : Set the price to ∞ (or a very high number for practical purposes), and contract P to .
- (c)
- and node is not deadend. Then, the following two cases are considered.
- (i)
- If , then extend P to and set to any price level that makes the arc level and the arc downhill. For example, setThis raises the price to the maximum possible level, making the arc level.
- (ii)
- If , then contract P to and raise the price of to . This makes the arc uphill and the arc downhill.
The algorithm terminates when the destination becomes the terminal node of P. A more detailed discussion of the AWPC rules, properties, and performance guarantees is given in the paper [11].
Role of the Parameter
A positive is used to regulate the size of the price rise. The choice of does not affect the path produced by the APC algorithm (for ease of calculation, its value was chosen as = 1). In AWPC, provides a trade-off between the ability of the algorithm to produce a minimal length path and its convergence rate (see the paper [11]). As the value of becomes small, the path quality improves, but at the same time, the small value of tends to slow down the algorithm.
For an illustration, consider the four-node graph shown in Figure 3a. In this example, the origin node is s, and the destination node is t. We assume that AWPC starts with and with all initial prices equal to 0. Consider first the case where . Then, using the rules of the algorithm, the trajectory of the path will be an extension from s to 1, followed by an extension from 1 to the destination t, thus producing the nonshortest path (s, 1, t). On the other hand, if , the algorithm will extend the path from s to 1 and then contract back to s. It will then extend the path to 2 and perform a final extension to t, resulting in the shortest path (s, 2, t); see Figure 3b. Thus, if , the algorithm produces the nonshortest path (s, 1, t) faster, and if , it produces the shortest path (s, 2, t) more slowly. This behavior is characteristic of the role of in providing a trade-off between the ability of the algorithm to construct paths with near-minimum lengths and its rate of convergence. For further explanation and a theoretical analysis, see [11]. In this paper, we have kept the value of at 1 for all of our experiments.
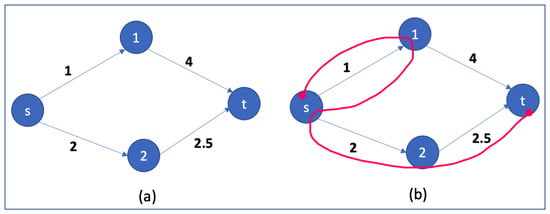
Figure 3.
The figure shows the AWPC traversal on a four-node graph. The initial prices are arbitrarily chosen as and edge weights as (a). The origin node is given as , with the destination node as . The algorithm chooses to extend or contract and update the price per the given rules. The path chosen by AWPC for is shown in (b).
4. Question Answering in Knowledge Graphs
In this section, we will present our approach for answering the queries over a knowledge graph using auction algorithms. We demonstrate the use of auction path construction (APC) and the variant with weighted version auction weighted path construction (AWPC).
4.1. Problem Statement
A knowledge graph, , as described in Section 3.1.1, is a set of entities, relations, and attributes. Knowledge graph applications include data mining tasks, such as discovering new facts or answering questions. All such tasks requires the prediction of the link, , between the head (or origin) entity, , and the tail (or destination) entity, . The link is either the edge, , which can be denoted as relation r at a single hop, , or it can be a multihop path, such as .
In either case, we can model this problem as constructing the path between the origin and the destination entities using the auction path construction algorithm, as described in the previous section.
4.2. Method
We follow a step-wise method to answer the queries by traversing directly through the knowledge graph. We first parse the query to extract the entities. We then map the entities to find the closest matching entity in the knowledge graph and obtain the attributes of each entity from the entity metadata in the knowledge graph. In the subsequent step, we use the auction path construction algorithm to acquire the path from the source to the destination entity. In the final step, we construct an answer by mapping the attributes of all the entities in the path. Figure 4 illustrates the process for single and multiple destination queries. Our method does not require structured query processing languages or training a model on a static knowledge base to answer the questions. The step-wise process is explained in detail below.
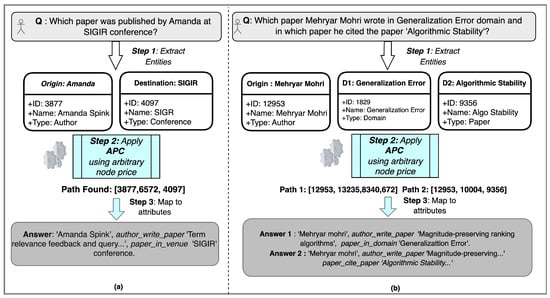
Figure 4.
The figure illustrates the step-wise method to answer queries. (a) The single destination query and (b) the query with two parts, i.e., multiple destinations.
- Parsing the Query: In the first step, the user query is semantically parsed to extract the entities. The entities can be extracted using any state-of-the-art parsing or entity extraction techniques [28] such as natural language processing (NLP)-based named-entity recognition (NER) methods [29]. Different techniques such as rule-based [30], ontology-based methods [31], and learning-based methods [32] can be used for extracting the entities from a query. The choice of the named-entity extraction method for knowledge graphs largely depends on the domain and if the given dataset has a well-defined schema.In this work, we used a dictionary-based look-up method to match the entities [33]. First, the entities are extracted using the spaCy-based named-entity recognition (NER) [34]. Then, using the named-entity linking, we look for the closest matching entity in the knowledge base (KB). Alternatively, a custom lexical matcher can be used [35]. After extraction of the entities, the information from the metadata of the knowledge graph is used to map the entities to the corresponding nodes.For example, as shown in Figure 4a, in a knowledge graph based on a triple dataset, KG20C [36] for the query, “Which paper was published by Amanda at SIGIR conference?”, the entities extracted using spaCy are, (“paper”, “Amanda”, “SIGIR”, “conference”). The closest matching entities in KB are (“Amanda” and “SIGIR”). The metadata in KB has each entity’s attributes, entity ID, name, and type. We fetch the attributes for the candidate entities, “Amanda” and “SIGIR”. Here, the entity ID is the corresponding node number in the graph, (“Amanda”:3877) and (“SIGIR”:4097).We must also determine the origin and destination entities to construct the path. Most knowledge graph question-answering (KGQA) systems use semantic parsing to detect the occurrence and order of entities in the question [37]. In some KGQA systems, the entity extraction models are trained on a question-answer dataset to understand the query pattern [9]. More sophisticated methods use a predefined query template [38]. In this work, for simplicity, we have used the order of occurrence of entities to determine the origin and destination entities. In the case of multiple entities, we consider the first as the origin and the rest as multiple destinations, as shown in the query in Figure 4b. In this paper, we do not elaborate further on each method used in this step, as our work focuses on demonstrating the use of the APC in knowledge graphs.
- Path construction using APC (or AWPC): In the second step, the triple dataset of a knowledge graph is modeled into a directed graph with nodes and edges. The nodes from step 1 can be denoted as the origin and destination nodes in the graph, and for instance, if the auction path construction algorithm (APC) is used to construct the path between them. The initial prices for all the nodes in E can be chosen arbitrarily or reused from previous searches. If the weighted version of the algorithm (AWPC) is used, then the edges in R should also be given initial edge weights to introduce a bias.The algorithm starts at the origin node. It follows the rules defined in Section 3.1.2 to navigate through the graph structure and update the path and node prices at each iteration. The algorithm terminates and returns to the final path once it reaches the single (or all) destination(s). The resulting path is essentially the set of final nodes with lower prices chosen by the algorithm while auctioning from the origin to the destination node.For the above query example, as shown in Figure 4a, the path given by APC is . This set of nodes in the final path can now be used to provide an explainable answer to the query.
- Mapping attributes to build an interpretable answer: In the final step, we use the attributes I for each entity in E, given as the metadata in knowledge graphs. These attributes can add semantic meaning to the path generated by APC. The edges are mapped to the corresponding relations, and the type and entity names are added from the attributes to construct the final answer.Referring to our example in Figure 4a, for the path, , the attributes for each node and relations for each edge in the path are mapped to construct the final answer as shown in below Figure 5. The prices learned by the algorithm in this search can be used as the starting prices for the following query.
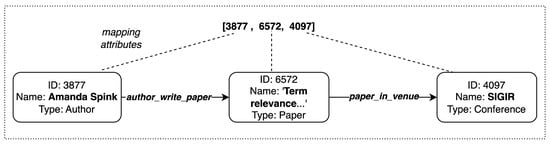 Figure 5. The figure illustrates the mapping of path nodes to entity attributes and edge relations to build an explainable answer.
Figure 5. The figure illustrates the mapping of path nodes to entity attributes and edge relations to build an explainable answer.
4.2.1. Prices as a “Learning Experience”
The node prices play a significant role in the search process. The node prices act as a “guide” for the algorithm and “steer” it toward nodes with lower prices, which are more likely to be part of the solution. APC provides the flexibility to use arbitrary prices. Initially, zeros or random values can be used as the starting prices for the nodes in the graph. In successive runs, prices from the previous run can be reused. Reusing the prices is similar to learning from previous experiences. For subsequent similar queries, the “experience” in terms of “learned prices” helps produce the path faster, making the algorithm computationally efficient. Eventually, the algorithm can learn favorable starting prices to generate paths faster.
4.2.2. Ability of APC to Adapt to an “Evolving KG”
Given the dynamic and incomplete nature of the knowledge graphs, newly emerging relations and entities are added, and redundant ones are removed, resulting in constant changes in the graph structure. The auction algorithms are well-suited to this kind of dynamic environment. They are flexible as the node prices are initially assigned arbitrary values and updated dynamically as per the rules defined in Section 3. The algorithms navigate the graph from higher-price to low-price nodes. When new nodes or edges are added or removed from the graph, the existing nodes can reuse the prices from previous searches, and the newly added nodes are given arbitrary prices. We simulated the experiments by dynamically adding new nodes in the knowledge graph. Our results show that the algorithms adapt well to the environment changes. While assigning arbitrary prices to newly added nodes, a good strategy is to allocate prices in the range of prices of existing nodes.
4.2.3. Edge Weights as per “Query Semantics”
Another significant parameter in the search process is the arc length (or edge weight) used in the auction weighted path construction (AWPC), the weighted version of APC as described in Section 3.2. The edge weights act as a bias and aim to provide a path with near-minimal total length. The arcs with smaller lengths tend to give shorter paths, and thus the algorithm should converge faster. Once the relations from a query are semantically extracted, the edge weights can be assigned as per the semantic meaning. The relation (or edges) with a strong match with the query are given “0” weights, and all the other edges are given higher values of weights. By adding this bias, the algorithm looks for lower-length paths similar to the relation in the query. Thus, we are highly likely to obtain more accurate and faster results with shorter paths, making it computationally more efficient.
5. Evaluation
5.1. Dataset
We used two benchmark datasets, KG20C [36] and YAGO3-10 [39], to showcase the application of APC in knowledge graphs for question answering. The first dataset, KG20C, was constructed from the Microsoft Academic Graph dataset [40] by extracting the information from high-quality computer science papers published in the top 20 conferences. KG20C is a standard benchmark dataset used for several tasks in knowledge graphs such as graph embedding, link prediction, recommendation systems, and question answering about high-quality papers [41,42]. It is a triple dataset with five intrinsic entity types, Paper, Author, Affiliation, Venue, and Domain. The five intrinsic relation types defined between these entities are , , , , . The entity attributes contain the metadata as entity ID, name, and type. The statistical details of KG20C are in Table 1.

Table 1.
KG20C Triple dataset stats.
Another dataset, YAGO3-10, is a benchmark dataset for knowledge base completion. It is a subset of YAGO3 (which is an extension of YAGO (Yet Another Great Ontology) [43]). YAGO3 contains entities related to people, universities, cities, organizations, and artworks and their canonical relations. YAGO3-10 has 123,182 entities, 37 relations, and 1,179,040 triples. Most triples describe attributes of places and persons such as citizenship, gender, and profession, for instance, the city a person was born in, which city is located in which country, which player played for a team, which singer sang which song, etc.
5.2. Experiments and Results
In this section, we present our experiments and results. First, we discuss the protocol for evaluating and measuring the effectiveness of the proposed method. Then, we provide the experiment setup and the result analysis and discussion.
5.2.1. Evaluation Protocol
The research question is whether APC (and AWPC) algorithms are suitable for application in knowledge graphs. To answer this question, we ran multiple simulations to test the algorithm’s behavior in different settings. The primary objectives for this work are to evaluate the accuracy of the method, adaptability of the knowledge graph to the dynamic environment , and interpretability of the answer. The other important factors are computational efficiency and support for multihop and multidestination queries. Each objective is described below:
- Prediction Accuracy—Did the algorithm predict the answers the same or close to the ground truth?
- Adaptability to Evolving Knowledge Graph—Can the algorithm adapt dynamically when new entities and relations are added to the graph?
- Explainable Reasoning Paths—Does the algorithm give traceable and explainable reasoning paths? Can users make proper inferences from the answers provided by the system?
- Computational Efficiency—How many iterations (or steps) does the algorithm take to provide the final answer? The number of iterations is analogous to the algorithm’s run time complexity and can be used to show computational efficiency.
- Support for Multihop Queries—Can the algorithm answer the queries with multiple hops or longer paths?
- Queries with Multiple Destinations—Can the algorithm answer the questions with two or more parts combined? For example, a query such as, “Which paper author published in this conference and where does he work?” has two destinations.
5.2.2. Experimental Setup
We conducted simulations with eight different parameter settings. For each simulation, we used around 50 queries, a mix of single and multihop type questions with single or multiple destinations. Table 2 shows the experimental settings for different prices and edge weights as well as the corresponding observations for each experiment for the KG20C dataset.

Table 2.
Experimental Setup.
The first four simulations were run using APC with different initial price settings. The algorithm was relatively stable, and the resulting paths matched the ground truth with the initial price set as “0”. We then reused the “learned” prices and observed that the number of iterations reduced by 60% while the resulting paths remained the same. We also stress-tested the algorithm by assigning random prices between 100 and 1000. The iteration count went very high, and most of the paths remained the same, but it chose longer paths for some queries. Reusing these prices gave relatively stable results, and the iterations reduced significantly. For APC, the second experiment achieved the best results regarding computational efficiency.
Further experiments were conducted using the weighted version (AWPC). We kept the variations in price settings the same as those in the first four runs and repeated the first four experiments for different edge weights. We conducted experiments with different combinations of edge weights such as (0, 1, 2, 3, 6) and random weights between and −10 and 10. The edge weights were used to add the bias; the algorithm converges faster with lower edge weights. Our experimental results also supported it. In Table 2, we reported the significant observations for each experiment.
For AWPC, the edge weights were set to “0” to validate whether the results matched the first four price settings using APC. In the next run, we set the edge weights to “1”. The paths remained the same, and iterations were higher or the same as in those in (2). Then, the algorithm became unstable with random weights between −10 and 10. Iterations increased almost twice, but there was not much change in the paths.
When the query is parsed, suppose the relation can be extracted and matched with a predefined pattern. If it is possible to state which relation in the query matches which of the relations in knowledge graph metadata, then we can preassign the edge weights as per the match. We experimented by assigning edge weights as per the query semantics. In the first set, the edges with strong match were given “0” weights, and the remaining edges (weak) were set to “1”, denoted as (S:0, W:1). In the second setting, the relations were classified as a strong, medium, and weak match. For example, in the query, “Which author may cite this paper?”, the relation, is a strong match, whereas is medium, and all other relations are weak. The strong match edges were given “0” weights, medium “3”, and weak “6”, denoted as (S:0, M:3, W:6). When the prices were reused from the initial price of “0”, the resulting paths were the same or shorter, and the iterations were the less or same as (2). In this case, the algorithm yielded the best results compared to all the other settings. Intuitively, we can therefore say that the algorithm can do a semantic-based search and tends to progress in a meaningful direction if the parameters are chosen wisely.
5.2.3. Result Analysis
We now discuss the results from the above experiments and analyze if the objectives of the evaluation protocol were satisfied by the method.
Prediction Accuracy: The resulting paths from each query matched the ground truth. The different node-prices and edge-weights settings given in Table 2 only affected the number of iterations taken by the algorithm to provide the final answer, to be discussed shortly.
Adaptability to Evolving Knowledge Graph: To test the algorithm’s adaptability to changing knowledge graphs, we conducted the following experiments.
- We started with a small subgraph of 12 entities from the KG20C dataset and ran around ten queries. The node prices were initially set to “0”. The prices were then reused for the subsequent queries. Similar experiments were conducted by initializing random prices and edge weights settings as described in Table 2.
- In the second simulation, 40 new entities were added to the knowledge graph. The prices of existing nodes were reused, and the newly added nodes were given arbitrary prices. In this step, 20 queries were run on a total of 52 nodes.
- In the third simulation, the remaining entities and relations were added, and 50 queries for each setting (as given in Table 2) were run on the large graph with entities. The prices from previous searches were reused for existing nodes. The number of iterations increased slightly for a few queries but eventually decreased after the prices were reused in successive runs.
The results from each simulation show that the algorithm dynamically adapted to the newly added nodes. The final answers from all the resulting paths matched the ground truth. A critical observation in a larger graph was that if the origin in the following query is too far from the previous question, the number of iterations may increase and stabilize after it starts reaching the reasonable learned prices. Thus, the algorithm continuously learns and adapts to evolving knowledge graphs.
Explainable Reasoning Paths: Explainability refers to the ability of a system to explain the results and the reasoning process to the users, such that they can know the whys and hows of the decision-making process [44].
APC returns a complete path between the entities in question. The paths are traceable and can be inferred by mapping the entity attributes as shown in Figure 6. The need for explainable reasoning paths can be demonstrated using the second query example from the KG20C dataset, “Has Mehryar worked in the Matrix Decomposition domain?” From the explanation given in the answer, we can see no direct yes-or-no answer to this question. The author has not worked directly in the domain, but technically, he has referred to some work that cited another work in the said domain. In such cases, the user would want to know the complete answer and infer the degree of association of the author with that domain. In cases where no path exists, the algorithm will explore all the nodes and raise an exception saying that paths do not exist.
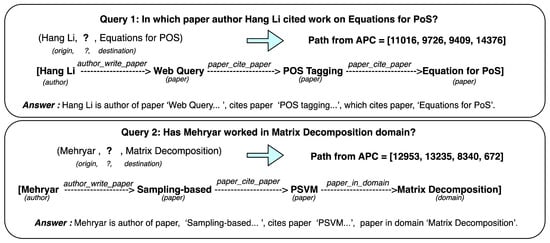
Figure 6.
Explainable paths given by our method in question answering for KG20C dataset.
Computational Efficiency: Table 3 shows the number of iterations for a few sample queries from the KG20C dataset with different prices and edge weight (EW) settings, as discussed in experiments 6, 7, 8(a), and 8(b) in Table 2. We can see from the results that the number of iterations reduces significantly by reusing the prices for similar queries. It also shows the effect of bias introduced due to different values of edge weights in the cases where the edge weights were assigned as per the relations extracted from query semantics. The edges with strong matching relations were given “0” initial weights, the medium relations “3”, and the weak relations “6”. The first query with edge weight settings per query semantics had only 76 iterations, which is much fewer than the random weights. The number of iterations dropped to 2 and 3 in the second and the third queries on reusing the prices, respectively, which is a significant computational improvement.

Table 3.
Number of Iterations for sample queries.
Support for Multihop Queries: Most of the queries used in our experiments require multihop reasoning. For example, the query, “In which paper author Fredric cited the paper on Equations for PoS?” needs a multihop inference of the form, (Fredric, , ?), (?, , Equations for PoS). The APC is able to provide a full traceable path and support the queries with multihop reasoning.
Queries with Multiple Destinations: Figure 3b shows the example of a query with multiple destinations. Both the APC and AWPC algorithms support the queries with multiple destinations. They work the same as does a single destination, but a list of all the destinations is maintained and the algorithm continues to run until it has reached all the destinations. This is described in Section 3.1.3.
To validate our approach, we ran the queries on another dataset, YAGO3-10, using the same settings. Figure 7 and Figure 8 show the explainable paths generated for sample queries on the YAGO3-10 dataset using our method.
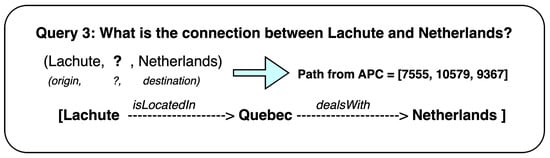
Figure 7.
Explainable paths for the query made to the YAGO3-10 dataset.
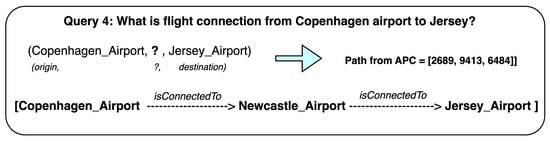
Figure 8.
Explainable path from another query from the YAGO3-10 dataset.
The complete implementation code for both the APC and AWPC algorithms for single and multiple destination queries and a summary of all the experiment results are available on GitHub [45].
We further show the comparison of our approach with state-of-the-art methods. Table 4 shows the comparison of our method (using APC) with the multirelational embedding (MEI) embedding methods used on the KG20C dataset to answer semantic queries [36]. The semantic queries answered by this work are single-hop factoid questions such as, “Who may write this paper?”, “What paper does this author have?”, and not multihop questions such as, “Which paper does this author have in that conference?”. Moreover, these methods only give a single candidate score as the answer but not the explainable paths. Our method can support single and multihop questions and queries with multiple destinations. The predictions are the same as the ground truth, and the search using APC returns an explainable reasoning path for all the queries.

Table 4.
Comparison of APC with the Embedding Method.
We also compared our method with the Dijkstra algorithm. Both auction and Dijkstra can be used for finding paths from source to destination, and both have polynomial time complexity. However, auction has two advantages. First, it tends to be faster, mainly because it aims to find any path (which is not guaranteed to be the shortest) rather than the shortest path, as is the case with Dijkstra. Secondly, the auction algorithm generates the prices for future queries, whereas the Dijkstra provides no such information. Table 5 below shows the results of some sample queries from KG20C for Dijkstra and auction. The path was the same for most of the queries, but in some queries shown in Table 5, the path returned by Dijkstra differed from that by auction and gave a shorter path. Dijkstra starts fresh for each query enumerating all possible paths. It does not have a learning mechanism from pasts searches, making it computationally expensive as the knowledge graph grows.

Table 5.
Comparison of the APC with the Dijkstra Algorithm.
The above experiments and results show that APC (and AWPC) meets the evaluation criteria. Thus, the potential of auction algorithms can be explored for various tasks in knowledge graphs. A summary of the experimental results against each evaluation objective is shown in Table 6.

Table 6.
Summary of Experiments and Results.
6. Discussion
We discussed the need for dynamic algorithms in evolving knowledge graphs that can continuously learn from adding new information and provide explainable answers. To this end we proposed using a recently proposed class of auction algorithms that maintain and update node prices, while constructing low-price paths. The prices from the previous searches can be used as a learning experience for related searches, making it computationally efficient. We used two benchmark datasets in knowledge graphs, KG20C and YAGO3-10, to show that the resulting paths given by auction are highly interpretable and explainable. The algorithm can answer single and multihop questions with one or more destinations. We also compared our method with the Dijkstra shortest path algorithm, showing that both could give explainable paths. However, auction can learn from previous searches. The most significant advantage of the auction algorithm is its capability to arbitrarily assign the initial prices and dynamically update the prices independent of new nodes added to the graph. This property makes auction suitable for continuous learning in a dynamic knowledge graph environment.
The auction algorithms can also be used in application contexts to provide recommendations and design flow graphs. One of the applications can be in customer contact centers where the customers call the agents to get help on their bills, payment methods, products, WIFI service, call plans, etc. These agents can be human or virtual assistants. Once the call intent or the named entities are extracted from the customer query and given the endpoints, the algorithm can provide the full path to the troubleshooting steps for the agents to resolve customer tickets quickly.
There are certain limitations that we plan to improve upon in future work. For example, in open-ended questions such as “Who may write this paper?”, the algorithm will search for all the “author” nodes in the graph. It may make the search inefficient at the run time for a huge graph. Furthermore, it will provide multiple answers to the user, which may not be a desirable situation. To address these types of scenarios, link prediction embedding methods can be used first to predict the destination candidate. Then, the auction algorithms can be used to provide explainable paths.
7. Conclusions
This work proposes the use of auction algorithms for question answering over knowledge graphs. We show that these algorithms can adapt to changing conditions by dynamically updating node prices and have the ability to learn the proper values of prices using past experience. In particular, the learned prices can be reused efficiently for similar future searches. Our method leverages the entity attributes and path relations to construct interpretable answers from the resulting paths generated by the auction algorithms for multihop queries.
In this work, we have used two variations of auction algorithms, auction path construction (APC) and auction weighted path construction (AWPC), which have the key properties of allowing arbitrary starting prices. Other variants of auction algorithms, such as reverse path, distributed, and multiple node price rise, can be further explored (such variations are given in the paper [11] and the book [20]). Moreover, a neural network model can be trained to learn near-optimal starting prices and to reoptimize these prices when significant changes occur in the network’s structure.
Author Contributions
Conceptualization, G.A. and D.B.; methodology, G.A.; software, G.A.; validation, G.A. and D.B.; formal analysis, G.A.; investigation, G.A.; resources, G.A.; data curation, G.A.; writing—original draft preparation, G.A.; writing—review and editing, G.A., D.B. and H.L; visualization, G.A.; supervision, D.B. and H.L.; project administration, H.L.; funding acquisition, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This material is based upon work supported by the National Science Foundation under grant no. 2114789. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| KG | knowledge graph |
| KGQA | knowledge graph question-answering system |
| KB | knowledge base |
| NER | named entity recognition |
| NLP | natural language processing |
References
- Kejriwal, M. Domain-Specific Knowledge Graph Construction; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Hogan, A.; Blomqvist, E.; Cochez, M.; d’Amato, C.; Melo, G.D.; Gutierrez, C.; Kirrane, S.; Gayo, J.E.L.; Navigli, R.; Neumaier, S.; et al. Knowledge graphs. ACM Comput. Surv. CSUR 2021, 54, 1–37. [Google Scholar]
- Chen, Z.; Wang, Y.; Zhao, B.; Cheng, J.; Zhao, X.; Duan, Z. Knowledge graph completion: A review. IEEE Access 2020, 8, 192435–192456. [Google Scholar] [CrossRef]
- Saxena, A.; Tripathi, A.; Talukdar, P. Improving multi-hop question answering over knowledge graphs using knowledge base embeddings. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 4498–4507. [Google Scholar]
- Geng, S.; Fu, Z.; Tan, J.; Ge, Y.; De Melo, G.; Zhang, Y. Path Language Modeling over Knowledge Graphsfor Explainable Recommendation. In Proceedings of the ACM Web Conference 2022, Lyon, France, 25–29 April 2022; pp. 946–955. [Google Scholar]
- Rossi, A.; Barbosa, D.; Firmani, D.; Matinata, A.; Merialdo, P. Knowledge graph embedding for link prediction: A comparative analysis. ACM Trans. Knowl. Discov. Data TKDD 2021, 15, 1–49. [Google Scholar] [CrossRef]
- Lao, N.; Mitchell, T.; Cohen, W. Random walk inference and learning in a large scale knowledge base. In Proceedings of the 2011 Conference on Empirical Methods in Natural Language Processing, Edinburgh, UK, 27–31 July 2011; pp. 529–539. [Google Scholar]
- Xiong, W.; Hoang, T.; Wang, W.Y. Deeppath: A reinforcement learning method for knowledge graph reasoning. arXiv 2017, arXiv:1707.06690. [Google Scholar]
- Lan, Y.; He, G.; Jiang, J.; Jiang, J.; Zhao, W.X.; Wen, J.R. Complex knowledge base question answering: A survey. IEEE Trans. Knowl. Data Eng. 2022. [Google Scholar] [CrossRef]
- Bhowmik, R.; Melo, G.D. Explainable link prediction for emerging entities in knowledge graphs. In Proceedings of the International Semantic Web Conference, Athens, Greece, 2–6 November 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 39–55. [Google Scholar]
- Bertsekas, D.P. New Auction Algorithms for Path Planning, Network Transport, and Reinforcement Learning. arXiv 2022, arXiv:2207.09588. [Google Scholar]
- Nguyen, D.Q. An overview of embedding models of entities and relationships for knowledge base completion. arXiv 2017, arXiv:1703.08098. [Google Scholar]
- Palmonari, M.; Minervini, P. Knowledge graph embeddings and explainable AI. Knowl. Graphs Explain. Artif. Intell. Found. Appl. Chall. 2020, 47, 49. [Google Scholar]
- Bao, J.; Duan, N.; Yan, Z.; Zhou, M.; Zhao, T. Constraint-based question answering with knowledge graph. In Proceedings of the COLING 2016, the 26th International Conference on Computational Linguistics: Technical Papers, Osaka, Japan, 11–16 December 2016; pp. 2503–2514. [Google Scholar]
- Ren, H.; Dai, H.; Dai, B.; Chen, X.; Yasunaga, M.; Sun, H.; Schuurmans, D.; Leskovec, J.; Zhou, D. Lego: Latent execution-guided reasoning for multi-hop question answering on knowledge graphs. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 8959–8970. [Google Scholar]
- Das, R.; Dhuliawala, S.; Zaheer, M.; Vilnis, L.; Durugkar, I.; Krishnamurthy, A.; Smola, A.; McCallum, A. Go for a walk and arrive at the answer: Reasoning over paths in knowledge bases using reinforcement learning. arXiv 2017, arXiv:1711.05851. [Google Scholar]
- Fu, Z.; Xian, Y.; Gao, R.; Zhao, J.; Huang, Q.; Ge, Y.; Xu, S.; Geng, S.; Shah, C.; Zhang, Y.; et al. Fairness-aware explainable recommendation over knowledge graphs. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual, 25–30 July 2020; pp. 69–78. [Google Scholar]
- Bertsekas, D.P. A Distributed Algorithm for the Assignment Problem; Lab. for Information and Decision Systems Working Paper; MIT: Cambridge, MA, USA, 1979. [Google Scholar]
- Bertsekas, D.P. Auction algorithms for network flow problems: A tutorial introduction. Comput. Optim. Appl. 1992, 1, 7–66. [Google Scholar] [CrossRef]
- Bertsekas, D. Network Optimization: Continuous and Discrete Models; Athena Scientific: Nashua, NH, USA, 1998; Volume 8. [Google Scholar]
- Dieci, L.; Walsh, J.D., III. The boundary method for semi-discrete optimal transport partitions and Wasserstein distance computation. J. Comput. Appl. Math. 2019, 353, 318–344. [Google Scholar] [CrossRef]
- Merigot, Q.; Thibert, B. Optimal transport: Discretization and algorithms. In Handbook of Numerical Analysis; Elsevier: Amsterdam, The Netherlands, 2021; Volume 22, pp. 133–212. [Google Scholar]
- Peyré, G.; Cuturi, M. Computational optimal transport: With applications to data science. Found. Trends Mach. Learn. 2019, 11, 355–607. [Google Scholar] [CrossRef]
- Lewis, M.; Bhosale, S.; Dettmers, T.; Goyal, N.; Zettlemoyer, L. Base layers: Simplifying training of large, sparse models. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 6265–6274. [Google Scholar]
- Bicciato, A.; Torsello, A. GAMS: Graph Augmentation with Module Swapping. In Proceedings of the ICPRAM, Virtual, 3–5 February 2022; pp. 249–255. [Google Scholar]
- Clark, A.; de Las Casas, D.; Guy, A.; Mensch, A.; Paganini, M.; Hoffmann, J.; Damoc, B.; Hechtman, B.; Cai, T.; Borgeaud, S.; et al. Unified scaling laws for routed language models. In Proceedings of the International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022; pp. 4057–4086. [Google Scholar]
- Bertsekas, D.P. An auction algorithm for shortest paths. SIAM J. Optim. 1991, 1, 425–447. [Google Scholar] [CrossRef]
- Goyal, A.; Gupta, V.; Kumar, M. Recent named entity recognition and classification techniques: A systematic review. Comput. Sci. Rev. 2018, 29, 21–43. [Google Scholar] [CrossRef]
- Grishman, R.; Sundheim, B.M. Message understanding conference-6: A brief history. In Proceedings of the COLING 1996 Volume 1: The 16th International Conference on Computational Linguistics, Copenhagen, Denmark, 5–9 August 1996. [Google Scholar]
- Chiticariu, L.; Krishnamurthy, R.; Li, Y.; Reiss, F.; Vaithyanathan, S. Domain adaptation of rule-based annotators for named-entity recognition tasks. In Proceedings of the 2010 Conference on Empirical Methods in Natural Language Processing, Online, 9–11 October 2010; pp. 1002–1012. [Google Scholar]
- Karkaletsis, V.; Fragkou, P.; Petasis, G.; Iosif, E. Ontology based information extraction from text. In Knowledge-Driven Multimedia Information Extraction and Ontology Evolution: Bridging the Semantic Gap; Springer: Berlin/Heidelberg, Germany, 2011; pp. 89–109. [Google Scholar]
- Al-Moslmi, T.; Ocaña, M.G.; Opdahl, A.L.; Veres, C. Named entity extraction for knowledge graphs: A literature overview. IEEE Access 2020, 8, 32862–32881. [Google Scholar] [CrossRef]
- Nadeau, D.; Sekine, S. A survey of named entity recognition and classification. Lingvisticae Investig. 2007, 30, 3–26. [Google Scholar] [CrossRef]
- Vasiliev, Y. Natural Language Processing with Python and spaCy: A Practical Introduction; No Starch Press: San Francisco, CA, USA, 2020. [Google Scholar]
- Srihari, R.K.; Li, W.; Cornell, T.; Niu, C. Infoxtract: A customizable intermediate level information extraction engine. Nat. Lang. Eng. 2008, 14, 33–69. [Google Scholar] [CrossRef]
- Tran, H.N.; Takasu, A. Exploring scholarly data by semantic query on knowledge graph embedding space. In International Conference on Theory and Practice of Digital Libraries; Springer: Berlin/Heidelberg, Germany, 2019; pp. 154–162. [Google Scholar]
- Yih, S.W.t.; Chang, M.W.; He, X.; Gao, J. Semantic parsing via staged query graph generation: Question answering with knowledge base. In Proceedings of the Joint Conference of the 53rd Annual Meeting of the ACL and the 7th International Joint Conference on Natural Language Processing of the AFNLP, Beijing, China, 26–31 July 2015. [Google Scholar]
- Bast, H.; Haussmann, E. More accurate question answering on freebase. In Proceedings of the 24th ACM International on Conference on Information and Knowledge Management, Melbourne, Australia, 18–23 October 2015; pp. 1431–1440. [Google Scholar]
- Mahdisoltani, F.; Biega, J.; Suchanek, F. YAGO3: A knowledge base from multilingual wikipedias. In Proceedings of the 7th Biennial Conference on Innovative Data Systems Research, CIDR Conference, Asilomar, CA, USA, 13–16 January 2014. [Google Scholar]
- Sinha, A.; Shen, Z.; Song, Y.; Ma, H.; Eide, D.; Hsu, B.J.; Wang, K. An overview of microsoft academic service (mas) and applications. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 243–246. [Google Scholar]
- Tran, H.N.; Takasu, A. Multi-Partition Embedding Interaction with Block Term Format for Knowledge Graph Completion. arXiv 2020, arXiv:2006.16365. [Google Scholar]
- Tran, H.N.; Takasu, A. MEIM: Multi-partition Embedding Interaction beyond Block Term Format for Efficient and Expressive Link Prediction. arXiv 2022, arXiv:2209.15597. [Google Scholar]
- Suchanek, F.M.; Kasneci, G.; Weikum, G. Yago: A core of semantic knowledge. In Proceedings of the 16th International Conference on World Wide Web, Banff, AB, Canada, 8–12 May 2007; pp. 697–706. [Google Scholar]
- Hoffman, R.R.; Mueller, S.T.; Klein, G.; Litman, J. Metrics for explainable AI: Challenges and prospects. arXiv 2018, arXiv:1812.04608. [Google Scholar]
- Agrawal, G. Auction Path Construction Algorithms in Knowledge Graphs. 2023. Available online: https://github.com/garima0106/KG-Auction.git (accessed on 12 June 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).