Multicriteria Approach for Design Optimization of Lightweight Piezoelectric Energy Harvesters Subjected to Stress Constraints
Abstract
1. Introduction
2. Multi-Objective Genetic Algorithms
2.1. NSGA-II and NSGA-III
2.2. GDE3
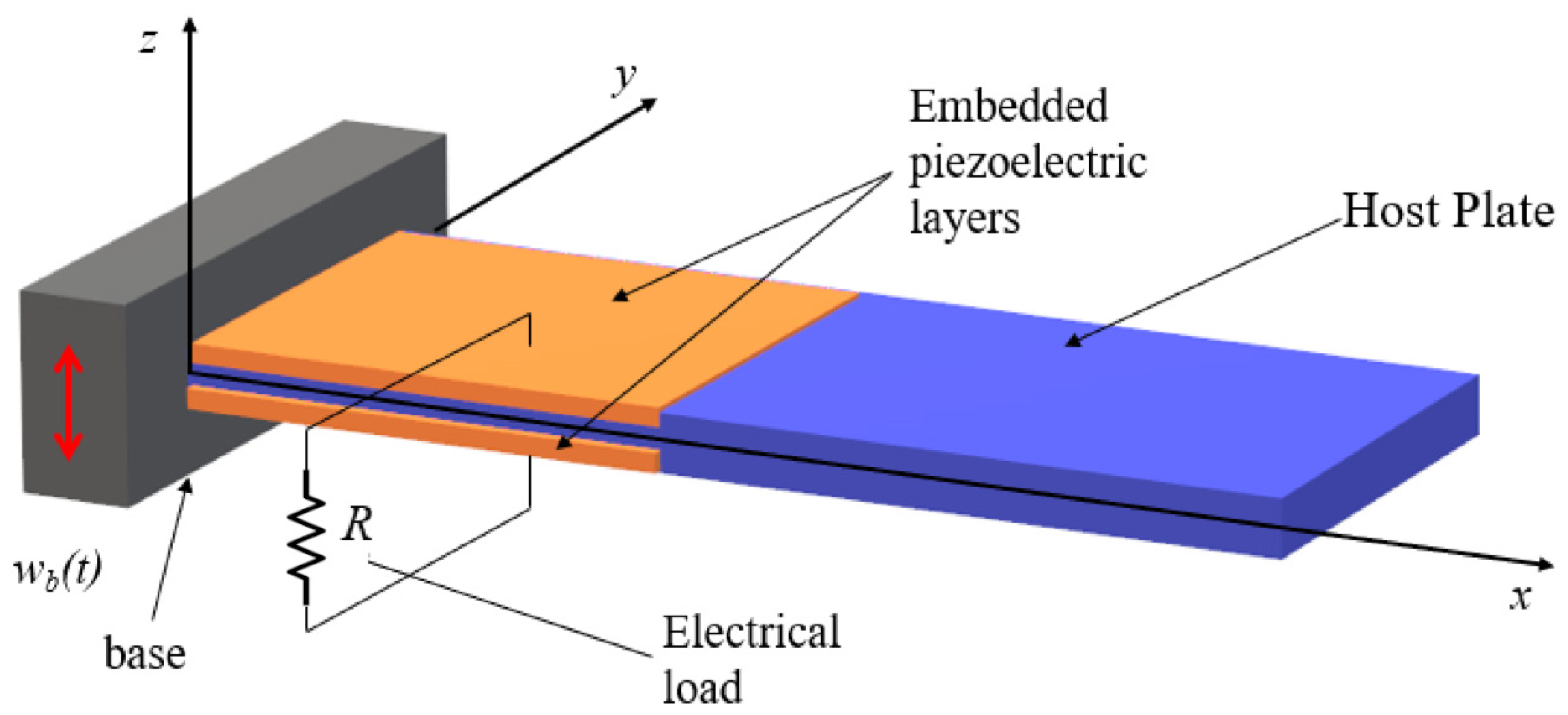
3. Mathematical Model of a Piezoelectric Energy Harvester
3.1. Mechanical Displacements and Strains
3.2. Constitutive Relations
3.3. Finite Element Discretization
3.4. Variational Formulation
3.5. Coupled Electromechanical Equations of the PEH
3.6. Solution of the Coupled Electromechanical System
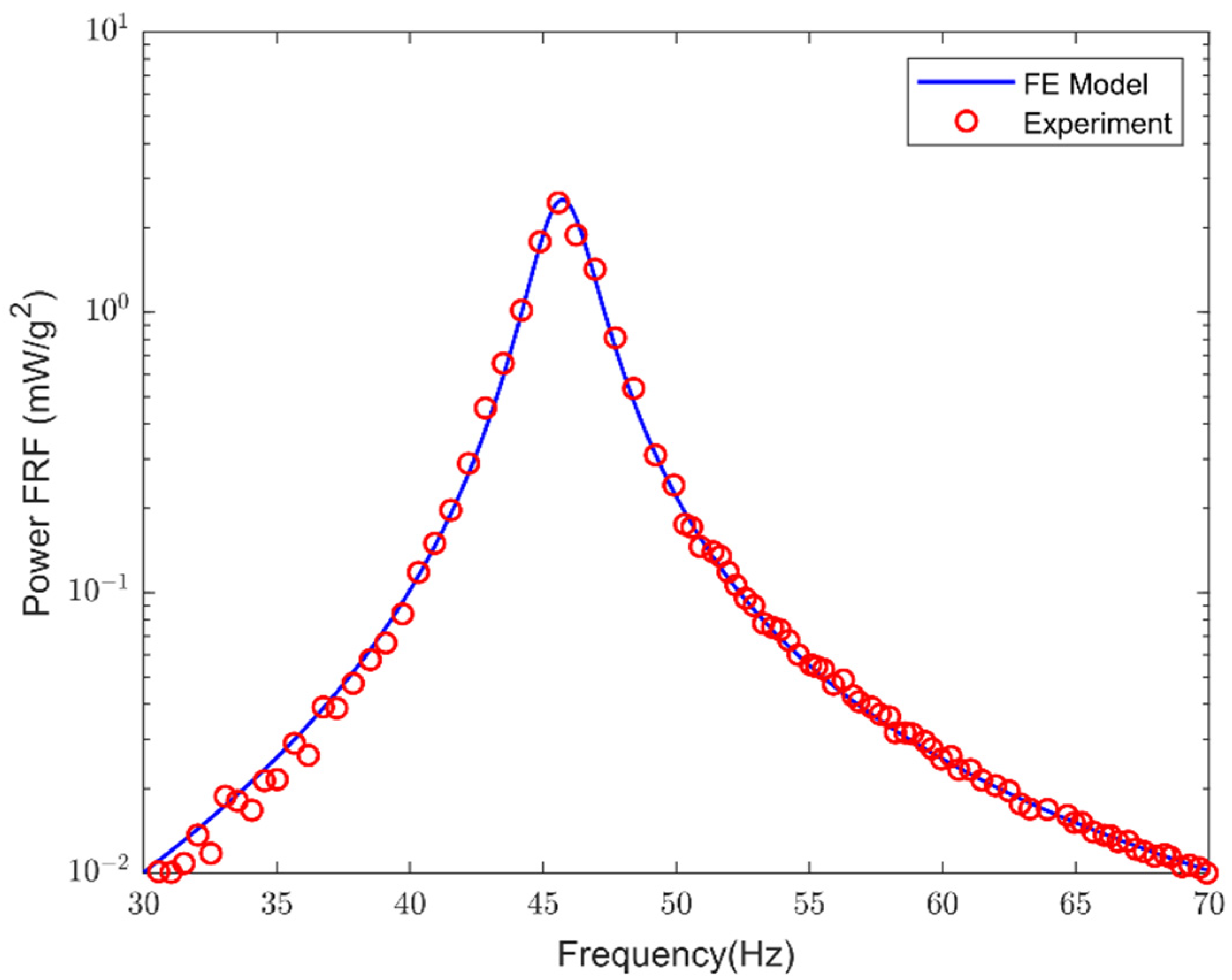
3.7. Verification of the FE Model
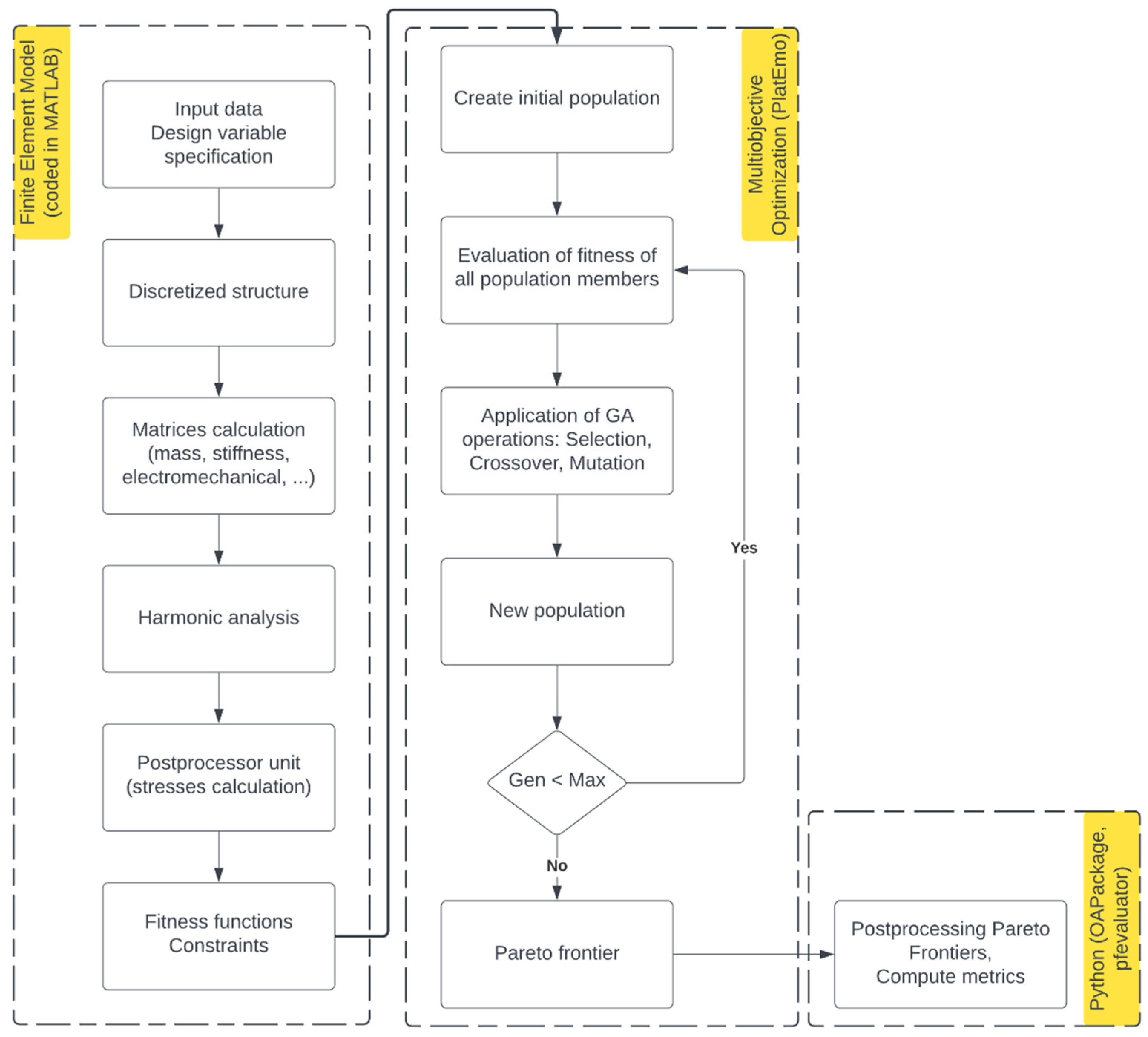
4. Design Optimization of PEH
Formulation of the Optimization Problem
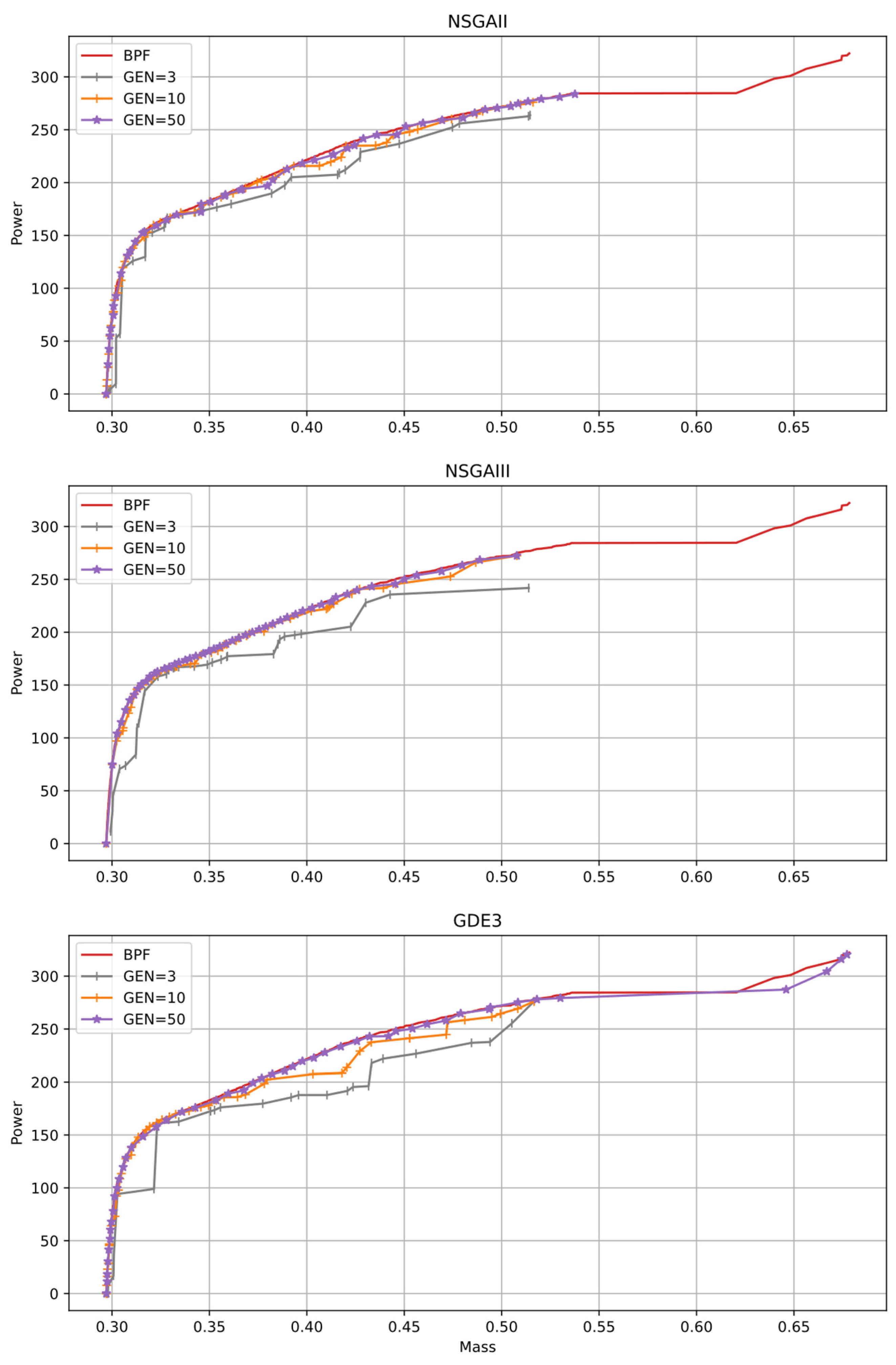
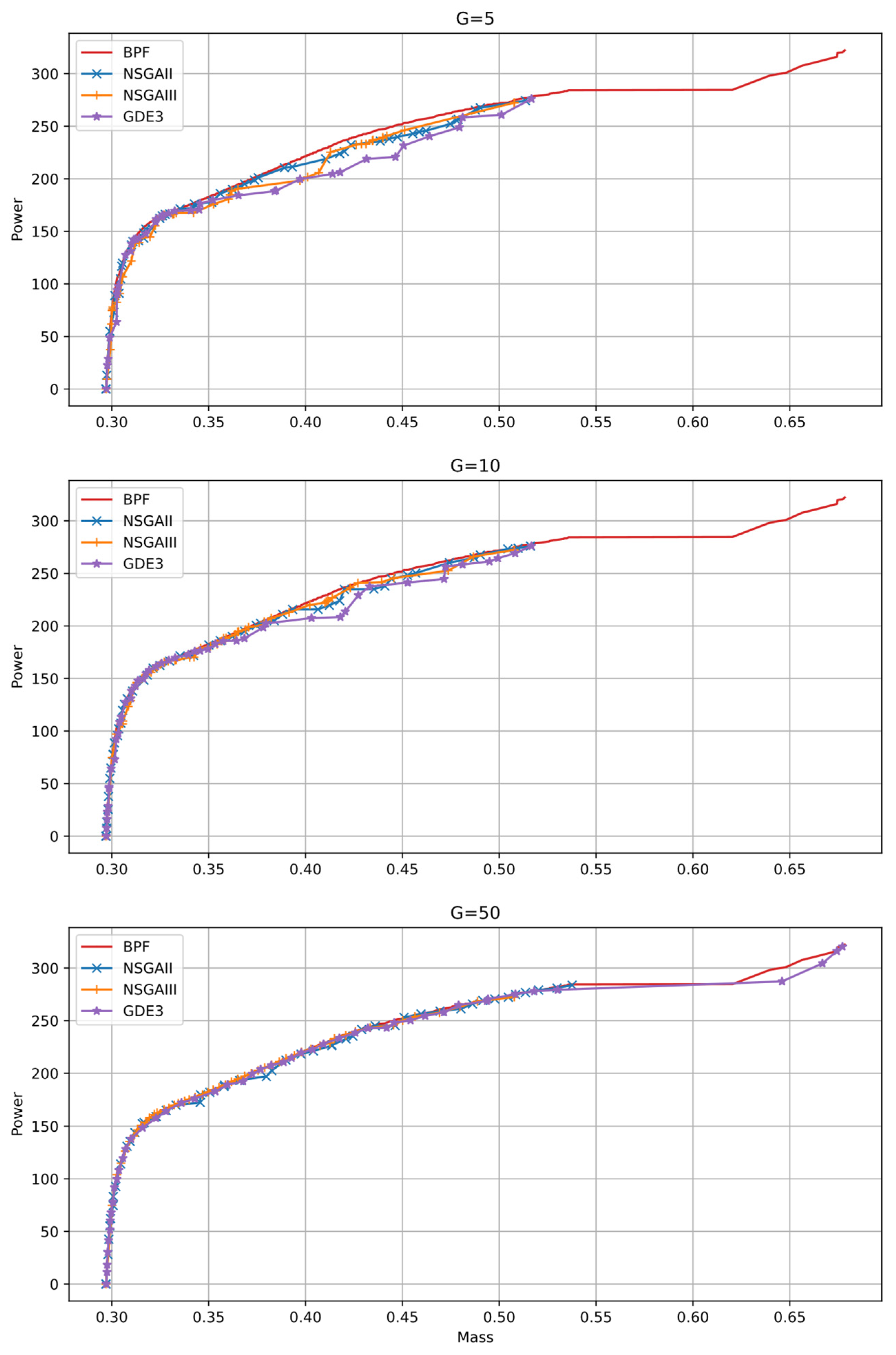
5. Optimization Results
5.1. Metrics
5.2. Solutions of the Multi-Objective Optimization Problem
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, H.S.; Kim, J.-H.; Kim, J. A Review of Piezoelectric Energy Harvesting Based on Vibration. Int. J. Precis. Eng. Manuf. 2011, 12, 1129–1141. [Google Scholar] [CrossRef]
- Sarker, M.R.; Julai, S.; Sabri, M.F.M.; Said, S.M.; Islam, M.M.; Tahir, M. Review of Piezoelectric Energy Harvesting System and Application of Optimization Techniques to Enhance the Performance of the Harvesting System. Sens. Actuators A Phys. 2019, 300, 111634. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, Y.; Zheng, H.; Ramakrishna, S. Piezoelectric Materials for Flexible and Wearable Electronics: A Review. Mater. Des. 2021, 211, 110164. [Google Scholar] [CrossRef]
- Mokhtari, F.; Spinks, G.M.; Fay, C.; Cheng, Z.; Raad, R.; Xi, J.; Foroughi, J. Wearable Electronic Textiles from Nanostructured Piezoelectric Fibers. Adv. Mater. Technol. 2020, 5, 1900900. [Google Scholar] [CrossRef]
- Yao, M.; Li, L.; Wang, Y.; Yang, D.; Miao, L.; Wang, H.; Liu, M.; Ren, K.; Fan, H.; Hu, D. Mechanical Energy Harvesting and Specific Potential Distribution of a Flexible Piezoelectric Nanogenerator Based on 2-D BaTiO3-Oriented Polycrystals. ACS Sustain. Chem. Eng. 2022, 10, 3276–3287. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. A Distributed Parameter Electromechanical Model for Cantilevered Piezoelectric Energy Harvesters. J. Vib. Acoust. 2008, 130, 041002. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An Experimentally Validated Bimorph Cantilever Model for Piezoelectric Energy Harvesting from Base Excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Paknejad, A.; Rahimi, G.; Farrokhabadi, A.; Khatibi, M.M. Analytical Solution of Piezoelectric Energy Harvester Patch for Various Thin Multilayer Composite Beams. Compos. Struct. 2016, 154, 694–706. [Google Scholar] [CrossRef]
- De Marqui Junior, C.; Erturk, A.; Inman, D.J. An Electromechanical Finite Element Model for Piezoelectric Energy Harvester Plates. J. Sound Vib. 2009, 327, 9–25. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, A.; Kumar, R.; Vaish, R.; Chauhan, V.S. Finite Element Analysis of Vibration Energy Harvesting Using Lead-Free Piezoelectric Materials: A Comparative Study. J. Asian Ceram. Soc. 2014, 2, 139–143. [Google Scholar] [CrossRef][Green Version]
- Khazaee, M.; Rosendahl, L.; Rezania, A. A Comprehensive Electromechanically Coupled Model for Non-Uniform Piezoelectric Energy Harvesting Composite Laminates. Mech. Syst. Signal Process. 2020, 145, 106927. [Google Scholar] [CrossRef]
- Park, J.; Lee, S.; Kwak, B.M. Design Optimization of Piezoelectric Energy Harvester Subject to Tip Excitation. J. Mech. Sci. Technol. 2012, 26, 137–143. [Google Scholar] [CrossRef]
- Nabavi, S.; Zhang, L. MEMS Piezoelectric Energy Harvester Design and Optimization Based on Genetic Algorithm. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–4. [Google Scholar]
- Foutsitzi, G.; Gogos, C.; Magklaras, A.; Antoniadis, N. Multi-Objective Design Optimization of Piezoelectric Energy Harvesting System for Unmanned Aerial Vehicles. In Proceedings of the 2021 6th South-East Europe Design Automation, Computer Engineering, Computer Networks and Social Media Conference (SEEDA-CECNSM), Preveza, Greece, 24 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Upadrashta, D.; Yang, Y.; Tang, L. Material Strength Consideration in the Design Optimization of Nonlinear Energy Harvester. J. Intell. Mater. Syst. Struct. 2015, 26, 1980–1994. [Google Scholar] [CrossRef]
- King, R.A.; Deb, K.; Rughooputh, H.C. Comparison of NSGA-II and SPEA2 on the Multiobjective Environmental/Economic Dispatch Problem. Afr. J. Online 2010, 16, 485–511. [Google Scholar]
- El-Abbasy, M.S.; Elazouni, A.; Zayed, T. Finance-Based Scheduling Multi-Objective Optimization: Benchmarking of Evolutionary Algorithms. Autom. Constr. 2020, 120, 103392. [Google Scholar] [CrossRef]
- Gambier, A.; Badreddin, E. Multi-Objective Optimal Control: An Overview. In Proceedings of the 2007 IEEE International Conference on Control Applications, Singapore, 1–3 October 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 170–175. [Google Scholar]
- Campos Ciro, G.; Dugardin, F.; Yalaoui, F.; Kelly, R. A NSGA-II and NSGA-III Comparison for Solving an Open Shop Scheduling Problem with Resource Constraints. IFAC-PapersOnLine 2016, 49, 1272–1277. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Computat. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Matnei Filho, R.A.; Vergilio, S.R. A Multi-Objective Test Data Generation Approach for Mutation Testing of Feature Models. J. Softw. Eng. Res. Dev. 2016, 4, 4. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Computat. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Kukkonen, S.; Lampinen, J. GDE3: The Third Evolution Step of Generalized Differential Evolution. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, Scotland, UK, 2–5 September 2005; IEEE: Piscataway, NJ, USA, 2005; Volume 1, pp. 443–450. [Google Scholar]
- Rostami, S.; Neri, F.; Gyaurski, K. On Algorithmic Descriptions and Software Implementations for Multi-Objective Optimisation: A Comparative Study. SN Comput. Sci. 2020, 1, 247. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004; ISBN 978-0-8493-1592-3. [Google Scholar]
- Rohatgi, A. WebPlotDigitizer; Pacifica, CA, USA. 2021. Available online: https://automeris.io/WebPlotDigitizer (accessed on 29 March 2022).
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB Platform for Evolutionary Multi-Objective Optimization [Educational Forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Nguyen, T.; Nguyen, T.; Nguyen, B.M.; Nguyen, G. Efficient Time-Series Forecasting Using Neural Network and Opposition-Based Coral Reefs Optimization. IJCIS 2019, 12, 1144. [Google Scholar] [CrossRef]
- Eendebak, P.; Vazquez, A. OApackage: A Python Package for Generation and Analysis of Orthogonal Arrays, Optimal Designs and Conference Designs. JOSS 2019, 4, 1097. [Google Scholar] [CrossRef]
- Yen, G.G.; He, Z. Performance Metric Ensemble for Multiobjective Evolutionary Algorithms. IEEE Trans. Evol. Computat. 2014, 18, 131–144. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Beam length (mm) | 50.8 |
| Beam width (mm) | 31.8 |
| Substructure thickness (mm) | 0.14 |
| Piezoelectric thickness (mm) | 0.26 (each) |
| Substructure Young’s modulus, [GPa] | 105 |
| Substructure Poisson’s ratio, | 0.35 |
| ] | 9000 |
| Rayleigh coefficient α [rad/s] | 14.65 |
| Rayleigh coefficient β [s/rad] | 10−5 |
| ] | 7800 |
| Tip mass [kg] | 0.012 |
| [GPa] | 70 |
| [GPa] | 24.5 |
| [GPa] | 21.8 |
| [GPa] | 22.8 |
| ] | 15.97 |
| [nF/m] | 11.0 |
| Short-Circuit | Open-Circuit | |
|---|---|---|
| Analytical | 45.7 | 48.2 |
| Experimental | 45.6 | 48.4 |
| Present FE | 45.7 | 48.3 |
| Parameter | Value |
|---|---|
| [GPa] | 70 |
| 0.34 | |
| ] | 2750 |
| Rayleigh coefficient α [rad/s] | 21.28 |
| Rayleigh coefficient β [s/rad] | 10−5 |
| GD | IGD | MPFE | MS | HV | ||
|---|---|---|---|---|---|---|
| NSGA-II | Mean | 0.0863 | 0.2380 | 8.3296 | 0.7398 | 38,026.42 |
| SD | 0.0073 | 0.0508 | 2.5134 | 0.0349 | 722.97 | |
| Best | 0.0737 | 0.3158 | 5.3478 | 0.7652 | 38,566.79 | |
| NSGA-III | Mean | 0.0576 | 0.4174 | 35.4863 | 0.7307 | 37,782.24 |
| SD | 0.0067 | 0.0223 | 2.5286 | 0.0264 | 600.21 | |
| Best | 0.0518 | 0.4405 | 32.3415 | 0.7623 | 38,477.20 | |
| GDE3 | Mean | 0.0870 | 0.1121 | 6.3600 | 0.9743 | 41,234.90 |
| SD | 0.0124 | 0.0265 | 1.2441 | 0.0295 | 1227.58 | |
| Best | 0.0740 | 0.1769 | 4.8380 | 1.0000 | 42,357.87 |
| Power | Mass | Algorithm | |||
|---|---|---|---|---|---|
| 283.46553 | 0.53482 | 0.62928 | 0.34647 | 310.01575 | NSGA-III |
| 284.36259 | 0.53595 | 0.62587 | 0.35000 | 325.36746 | NSGA-II |
| 310.98901 | 0.66365 | 0.99147 | 0.33902 | 63.05137 | GDE3 |
| 320.36665 | 0.67724 | 0.99596 | 0.35000 | 69.58982 | GDE3 |
| 322.27086 | 0.67842 | 0.99905 | 0.35000 | 76.01130 | GDE3 |
| Power | Mass | Algorithm | |||
|---|---|---|---|---|---|
| 165.71184 | 0.32666 | 0.24316 | 0.11184 | 139.61471 | NSGA-II |
| 165.57695 | 0.32656 | 0.22207 | 0.12203 | 160.53703 | NSGA-III |
| 165.27248 | 0.32619 | 0.20690 | 0.12934 | 190.74535 | GDE3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foutsitzi, G.; Gogos, C.; Antoniadis, N.; Magklaras, A. Multicriteria Approach for Design Optimization of Lightweight Piezoelectric Energy Harvesters Subjected to Stress Constraints. Information 2022, 13, 182. https://doi.org/10.3390/info13040182
Foutsitzi G, Gogos C, Antoniadis N, Magklaras A. Multicriteria Approach for Design Optimization of Lightweight Piezoelectric Energy Harvesters Subjected to Stress Constraints. Information. 2022; 13(4):182. https://doi.org/10.3390/info13040182
Chicago/Turabian StyleFoutsitzi, Georgia, Christos Gogos, Nikolaos Antoniadis, and Aris Magklaras. 2022. "Multicriteria Approach for Design Optimization of Lightweight Piezoelectric Energy Harvesters Subjected to Stress Constraints" Information 13, no. 4: 182. https://doi.org/10.3390/info13040182
APA StyleFoutsitzi, G., Gogos, C., Antoniadis, N., & Magklaras, A. (2022). Multicriteria Approach for Design Optimization of Lightweight Piezoelectric Energy Harvesters Subjected to Stress Constraints. Information, 13(4), 182. https://doi.org/10.3390/info13040182







