Abstract
Contemporary information-sharing environments such as Facebook offer a wide range of social and practical benefits. These environments, however, may also lead to privacy and security violations. Moreover, there is usually a trade-off between the benefits gained and the accompanying costs. Due to the uncertain nature of the information-sharing environment and the lack of technological literacy, the layperson user often fails miserably in balancing this trade-off. In this paper, we use game theory concepts to formally model this problem as a “game”, in which the players are the users and the pay-off function is a combination of the benefits and costs of the information-sharing process. We introduce a novel theoretical framework called Online Information-Sharing Assistance (OISA) to evaluate the interactive nature of the information-sharing trade-off problem. Using these theoretical foundations, we develop a set of AI agents that attempt to calculate a strategy for balancing this trade-off. Finally, as a proof of concept, we conduct an empirical study in a simulated Facebook environment in which human participants compete against OISA-based AI agents, showing that significantly higher utility can be achieved using OISA.
1. Introduction
While the use of digital applications and the Internet continues to increase worldwide [1,2,3], it also introduces significant risks to both privacy and security, threatening to violate individual data ownership [4]. For example, sensitive personal information that might be disclosed when making e-commerce purchases can later potentially be used improperly [5,6,7,8,9], private health data may leak when using wearable e-health technologies [10,11], and users’ behavioral patterns may be disclosed through Internet of Things (IoT) applications [12]. The protection of privacy and security is considered essential to liberal society, and for individual autonomy, these are considered basic human rights [13,14] that are extensively regulated by governments and intragovernmental organizations, e.g., the EU’s General Data Protection Regulation (GDPR) [15,16].
Protecting privacy and security is not a trivial task, and contains an inherent trade-off between the benefits derived from sharing data and the resultant costs [17,18]. Online purchasing, for example, is beneficial in terms of cost reduction and convenience, but it may involve both a loss of privacy (e.g., disclosing one’s shopping list) and security issues (e.g., disclosing one’s credit card details).
Information-sharing (or information-exchange) is defined as “the act of people, companies, and organizations passing information from one to another, especially electronically” [19], and can be considered as a characteristic of modern human society and behavior [20]. As beneficial as information-sharing currently is, it also raises concerns about privacy and security, thereby affecting the likelihood of using information-sharing services [21,22]. Individuals in online information-sharing environments are often helpless in managing and controlling their own privacy and security, usually due to the lack of technological literacy, the stochastic nature of the problem (it is probabilistic rather than deterministic, making it more difficult to perceive), and cognitive laziness [23]. As suggested by prospect theory, the uncertainty resulting from sharing the information causes people to act with bounded rationality, meaning they may not behave in an optimal manner [24]. However, the broad discussion in the literature on privacy and security in the information-sharing domain relates mainly to the involvement of machines, e.g., blocking intrusions to a network [25] or developing strategies for decisions taken by firewall algorithms [26]. The current theories are limited when dealing with scenarios in which actual human factors are involved.
To bridge this gap, we introduce a novel framework, the “Online Information-Sharing Assistance” (OISA), based on concepts from the field of game theory [27], a broadly applicable methodology in the social sciences [28]. Combining game theory and user behavior on social networks is a promising research direction that has gained popularity in the last few years. Alvari et al. [29] used game theory to detect overlapping communities on social networks for the purpose of building efficient recommendation systems and improving business opportunities. Wahab et al. [30] modeled the multi-cloud community formation problem as a trust-based, hedonic coalition formation game. However, forming a coalition is not common on many online information-sharing platforms such as Facebook because it requires secured authentication and trust [31,32]. Guo et al. [33] applied a game theory framework to handle disinformation on social networks. In our study, we deal with another issue inherent to information-sharing environments, namely how to effectively share information while considering the trade-off between the benefits and the resultant costs. Using game theory concepts, the information-sharing process can be modeled as a “game” in which the decision-makers are the players, who act according to the rules of the information-sharing environment (usually based on the platform used, e.g., Facebook) and whose pay-off function is a combination of the benefits (e.g., social benefits) and the costs (e.g., privacy violation) of information-sharing. An adequate approximate solution can, thus, be formulated in the form of a game theory strategy to be used in the online environment. For example, in the Facebook Online Social Network (OSN) environment, a user may click on the “like” button associated with a post published by another Facebook user. This choice will increase the probability of future posts appearing on both users’ feeds [34]. In that case, the benefit for the user could be attaining a higher rate of publicity of future posts, which is usually the main motivation when publishing a post online [35]. Liking a post, however, can also lead to the violation of privacy, e.g., by enabling a third party to accurately deduce a range of highly sensitive personal attributes of the user [36]. In this example, OISA can be used to decipher optional strategies adopted by Facebook users to provide them with recommendations that assist them in improving their utility. Recommendation agents are prevalent today and aim to support complicated decisions, for example agents that assist travelers’ calls concerning the COVID-19 pandemic [37].
Using OISA, we will represent information-sharing environments as a formal mathematical model. We will thereby encapsulate purely mathematical factors (e.g., the probability distribution of shared data to be disclosed) and “soft” human factors (e.g., cognitive burden or privacy disclosure costs) to create an approximate real-life model that represents the cost–benefit trade-off resulting from using an information-sharing platform.
In this paper, we formally introduce OISA and empirically prove in a simulated Facebook environment that the OISA agent performs significantly better than a human. The novelty of OISA is twofold: (1) it is a first step towards bridging the gap between existing mathematical theories and the reality of information-sharing; (2) OISA constitutes the basis for creating a smart AI agent that will be able to assist users in navigating the potential benefits vs. privacy and security threats of OSN.
2. Related Work
Several solutions have been proposed for balancing various utilities against potential privacy and security costs, e.g., when targeting advertisements based on users’ collected data [38,39], publishing data [40,41,42], using location-based applications [43,44] or e-health platforms [45], applying IoT technologies [46,47], and when directly sharing information [48,49,50,51,52,53]. However, many users find it increasingly hard to balance this trade-off in practice, which leads to failures in protecting their privacy and security [54,55,56,57]. Several reasons may account for this difficulty. First, understanding the complicated relationships between the actions taken in a digital space and their real-world consequences requires technological literacy [58,59], which is usually limited [60] and hard to acquire [61]. Indeed, this has been considered a matter worthy of societal attention [62,63,64]. Second, the rules of information disclosure are dynamic and change frequently [65]. Third, because many users naturally tend toward cognitive laziness, they are often nudged to choose the defaults that reflect the preferences of the service provider more than their own [66,67]. Fourth, the nature of the data-sharing process itself is often uncertain, e.g., Facebook users do not always know to whom their posts will eventually be exposed [68]. Thus, there is a significant gap between the actual privacy and security consequences of using technological applications and the users’ knowledge, expectations, and control of these consequences. This phenomenon poses a real problem for many users [69,70,71].
More specifically, the following approaches have been proposed: (1) Using a classical game theory approach [72]. This approach is limited to financial scenarios and is not fully applicable to the domain of privacy and security, where games do not have a zero-sum nature. (2) Using game theory as a mathematical tool to simplify difficult problems [73]. This approach focuses on reducing computations and does not provide a solution to the privacy and security trade-off game. (3) Relying on the distributed nature of cyber defense systems, where coalitions are established [74] or secret-sharing occurs, involving multi-party computation [75]. The coalition assumptions are usually unrealistic in the information-sharing domain (e.g., on Facebook) because users usually do not coordinate their information-sharing actions. (4) Seeking consensus on a privacy level [76], assuming that users negotiate their privacy. As in the case of coalitions, this assumption is unrealistic for most online activities. (5) Using privacy-preserving methodologies, such as adding artificial noise to the dataset [77]. These methodologies are relevant to protecting databases, but not to online decision-making. (6) Abstracting a simplified model, e.g., by discretizing data-sharing levels OSNs to optimal, undershared, overshared, and hybrid states [78]. While this solution enables the introduction of an elegant mathematical model, it is not viable for realistic problems. Hu et al. [79] applied a game theory model based on multi-party access control to elicit privacy concerns in OSN settings. However, they did not address the iterative decisions that need to be made within each action.
Taken together, the existing literature has established some important theoretical grounds for tackling privacy and security issues using game theory [80,81]. However, a rigorous and comprehensive investigation is still required for applying game theory solutions to privacy and security problems in the online information-sharing domain.
3. Increasing Information-Sharing Utility Methodology
3.1. Model
The first step required for representing any trade-off on an information-sharing platform in an accurate and realistic way is generating a formal mathematical model of the information-sharing environment itself. All information-sharing platforms include a finite set of agents, acting in a collaborative space as the underlying condition for the sharing operation. Agent is associated with a group, , which is defined to be a subset of (i.e., ). All agents who are a part of ’s group (i.e., might influence and vice versa. An agent can be a part of more than one agent’s group. If agent is not a part of ’s group, i.e., , it does not have any direct influence on , nor does have a direct influence on it. Each agent has a channel through which it communicates and shares information with its group members. Using this channel, agent can perform any operation out of a finite set of operations, which we denote as . To maintain generality, we define the action of “doing nothing” as a valid operation, meaning .
The timeline used in this model is defined to be discrete rather than continuous. In practice, this is achieved by implementing an action during an interval of time (of length ); an agent can perform only one operation per interval. Each operation is denoted by , where is the chosen operation index, is the agent who performed the operation, and is the interval of time in which the operation was performed. While this approach enables the implementation of a viable agent, it does not detract from the generality of the methodology, because by minimizing the time interval (T), we are practically dealing with a continuous timeline scenario. In any given interval, agent is only aware of its choice of operation, and has a set of probabilities regarding the other agents’ choices, where () corresponds to . Note that those probabilities are dynamic and might change from one time interval to another based on previous experience and resulting world states. Omitting agent , we denote all other agents’ chosen operations in a certain interval as Once an operation is completed, it can have several possible outcomes (realizations). Each combination of ’s chosen operation, , and might be realized in a few possible ways, each leading to a different world state . Realization has a probability to be the actual one. We denote to be a function that maps each combination as a specific world state. Thus, an agent is faced with uncertainty on two levels: (1) the opponent agents’ choice of operation (); (2) the potential combinations of the chosen operations ().
Due to the stochastic nature of the problem, while choosing an operation, the agent must consider all possible world states and their probabilities to calculate the expectancy of both the benefits and costs that result from the chosen operation. Since the limitations of currently available solutions mainly stem from unrealistic assumptions or abstractions of the information-sharing world, we introduce a novel framework called online information-sharing assistance (OISA) that inherently considers and faithfully represents the interactive nature of the information-sharing trade-offs, aiming to consider major costs and pay-offs for generating “bottom line” utility. As described in the following section, OISA provides a formal, close-to-reality representation of the information-sharing costs and benefits considering both the soft and rigid factors included in the interaction, offers a comprehensive game theory representation of the interaction itself, and enables the generation of smart AI-based agents who can help the users improve their performance.
3.2. Information-Sharing Benefits and Costs
Each possible operation might benefit the agent performing it, e.g., by providing a social benefit. We denote the myopic benefit function as , where is the agent who performed the operation, is the interval of time in which the operation was performed, and is the operation index out of the set . The function is myopic in the sense that it only measures the benefit gained in the interval following the one in which the operation is performed. The overall benefit function is additive, obtained by summing the benefits earned in each interval, i.e., . On the other hand, as a consequence of performing an operation, an agent may also incur some costs, e.g., the burden of the operation (amount of time spent and cognitive efforts). We denote the myopic cost as (myopic in the sense that it only measures the cost in the interval in which the operation is performed) and the overall cost as , where are defined as in the benefit function. In addition, for any operation, the agent risks losing some privacy or security, e.g., when disclosing information to a malicious actor who can exploit that information. We denote the future privacy or security losses at time resulting from operation () as . The accumulative privacy and security loss by operation is given by , where is the finite time interval of the interaction. The overall privacy loss function is additive and obtained by summing the privacy loss in every time interval, i.e., . We consider the operation as a neutral operation that does not cost anything, does not cause privacy loss, and does not benefit the agent in any way, i.e., . Each of the above-mentioned calculations (cost, benefit, and privacy loss) is made based on: (1) the users’ personal preferences and characteristics, e.g., “how much time does it take for the user to share a piece of information?” “how much does sharing this information improve their popularity?”, or “how much privacy did the user lose due to sharing this information?”; (2) the user’s chosen action and its possible realizations; (3) other users’ actions (with the proper probabilities) and their possible realizations.
An example of a classic privacy threat may be an unwilling leakage of sensitive information to undesired entities, while a classic security threat may be using social engineering to tempt a user to click on a harmful web link or URL. Notably, while it is often hard to distinguish between privacy and security costs, our scheme does not require such a distinction; we will, thus, accommodate both cost types in one holistic model in order to produce a single bottom line utility. Hence, as a generalization, we use the same units to measure both the benefits and the costs, which enables us to calculate the degree to which an agent performed well (produced utility) throughout the entire interaction. To this end, we use the function to calculate the bottom line utility of agent from the interaction.
3.3. Game Theoretical Representation
In OISA, as in real life, we assume that users’ interactions are not sequential; indeed, users may be required to choose their operations before knowing what the other users have chosen to do. An efficient way to represent scenarios in which a participant must choose an action under uncertainty is using a game tree, a directed graph whose nodes are positions in the game and whose edges, also called branches, are possible moves [82]. The pay-offs resulting from choosing a certain path through the tree appear next to the terminal node of that path. In case of uncertainty, which can result either from not knowing what the opponent’s choice of operation will be or from the possible realizations of the performed operations, the probabilities are indicated next to the branches representing each case. Figure 1 depicts a tree representation of an example taken from a specific agent’s () point of view. In this example, there are two agents and three possible operations, i.e., and . A circle represents an operation taken by an agent, and a rectangle represents a world state. The probabilities for each possible world state are the result of multiplying all possible realizations of all relevant operations and are displayed next to each branch.
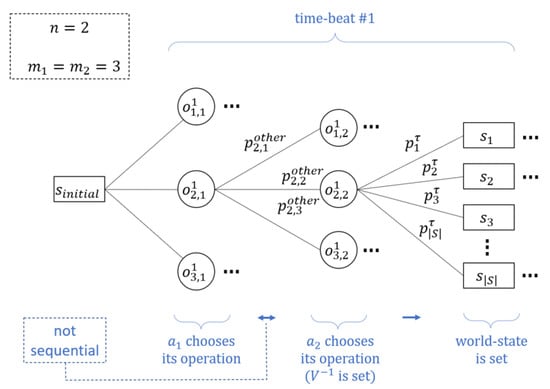
Figure 1.
A tree representation of an example case.
We define a satisfactory solution to be a series of decisions that maximize or significantly increase a specific user’s bottom line utility (we do not seek equilibrium for the entire game). The naive way for an agent to optimize its operation is to scan all possible routes of the tree and choose the one that yields the highest utility (brute force). A complete game tree starts at the initial position and contains all possible moves from each position. For simplicity, we assume that there are possible operations at any given time interval for each of the agents ( ) and that each combination spans world states. The resulting tree complexity is , where is the tree depth. This can be concretized by observing the massive tree in Figure 1, which describes a relatively simple case with only two agents and three possible operations. Hence, finding the agent’s best strategy by using brute force is inherently difficult, and given both the time limit imposed by the online environment and the limited computational resources (e.g., a PC) it is practically impossible. Thus, in the next subsection we will present three heuristic search algorithms that aim to provide a sufficient solution to the problem given the described constraints.
3.4. Heuristic Search Algorithms
As the strategy space of the problem increases rapidly, a brute force algorithm, which indeed computes all possible scenarios, would be highly time-consuming and unsuitable for the online environment. Hence, we introduce three heuristic algorithms inspired by well-known search algorithms: the simulated annealing (SA), hill climbing (HC), and Monte Carlo tree search (MCTS) algorithms.
Algorithm 1 is a modification of the simulated annealing (SA) algorithm [83], a probabilistic technique for approximating the global optimum of a given function. It does not search the tree deeply for possible decisions. Rather, SA is a metaheuristic for approximating global optimization in a large discrete search space. The algorithm receives the pre-set quota of intervals, the node from which the search begins, and the index of the relevant agent as an input. In each interval, the algorithm only examines the direct children of its current state and tries to improve its current utility. First, it randomly chooses one node out of the current state’s direct children (the number of the node’s direct children is equal to the number of possible operations at that specific state). Then, if the utility received from choosing that node is positive, the agent performs the operation leading to this node. Otherwise, based on the negative utility difference and the interval number (the higher the interval number is, the lower the probability of the agent selecting negative values), the agent calculates a probability () by which it decides between two alternatives: (1) randomly choosing another node and checking whether it improves the utility; (2) performing the operation that leads to the less preferable node. The latter option was added to encourage some exploration and prevent convergence to a local maximum. The iterative process is executed until a selection is made. Note that this algorithm is limited to a range of rounds because when then .
| Algorithm 1. Local search, probabilistic first choice |
 |
Algorithm 2 is a modification of the hill climbing (HC) algorithm [84], a local search algorithm that continuously moves in the direction of increasing elevation to find the peak of the mountain or best solution to the problem. It terminates when no neighbor remains or when the utility reaches the given threshold . HC is considered a greedy local search function as it only looks to its immediate neighbor state and not beyond that.
| Algorithm 2. Local search, next best choice |
 |
The algorithm receives the pre-set quota of rounds, the node from which the search begins, the index of the relevant agent, and the threshold as an input. Here also, in each round the algorithm only examines the direct children of its current state and tries to improve its current utility. Due to being a greedy algorithm, it only chooses nodes that result in a better utility than the one where it is currently located. The threshold is used to reduce the processing time if a “reasonable” result is reached. The reasonability boundaries can also be set dynamically (although this was not done in the version discussed in this paper).
Algorithm 3 is a modification of the Monte Carlo tree search (MCTS) [85], a best-first search technique that uses stochastic simulations. The algorithm builds a tree of possible future game states according to the following mechanism: selection, expansion, simulation, and backpropagation. This is also a greedy algorithm, meaning the operation that is chosen to be executed in the actual game is the one corresponding to the child with the greatest potential based on the simulations. The algorithm receives the pre-set quota of rounds, node from which the search begins, depth of search, number of repetitions, and index of the relevant agent. For each possible operation that might be selected, the algorithm randomly selects a quantity of tree paths spanning from the selected operation. The path that yields the maximal utility indicates the utility that may be gained by this operation. As mentioned above, the chosen operation is the one with the maximal utility.
| Algorithm 3. Random paths tree search |
 |
4. Empirical Study
In this section, we provide an empirical evaluation of an OISA AI-based agent when interacting with humans.
4.1. Experimental Environment
To empirically evaluate OISA, we chose to use the Facebook OSN. Facebook is one of the most popular OSNs worldwide [86,87], making it suitable both as a conceptual selection representative of an information-sharing platform and for recruiting participants for the experiment. We define the finite set of agents, , as the general population of Facebook users, while the subset () contains agents that can potentially interact with each other. In the experiments, we focused on four major types of operations that are among the most popular: (1) publishing a post; (2) liking a post, which has two possible alternatives, namely an (a) unsafe post, e.g., containing a URL (a post containing a URL may expose the user to an attack such as ransomware, meaning it has a relatively higher cost, although it may also contain significant benefits, e.g., referencing an interesting legitimate website) or a (b) safe post; (3) sending a friend request; (4) accepting a friend request (the two latter operations address the need for an agent to increase its potential exposure). Note that extending the experimental framework to include more operations is straightforward.
To illustrate the computational complexity of using a brute force technique, we introduce a case study with ten possible actions from which each agent can choose: two available posts that can be published, three safe posts and one unsafe post that can be “liked”, two pending friend requests that can be accepted, and two users to which a friend request can be sent. The number of agents interacting in the described case study is 5 and the depth of the tree that we are interested in examining is 3. The number of combinations to be tested is, meaning . From the resulting complexity, it is easy to see that the brute force approach demands an enormous calculation force, which is impractical in an online environment.
To demonstrate this computationally, we conducted a series of simulations of applying brute force with different machines (parameterized by the amount of internal memory or RAM) and the optimization level (parameterized by the searching depth in the tree). The results of the simulations are depicted in Figure 2, in which it is apparent that the performance time increases exponentially when the tree depth grows, and that achieving reasonable performances requires a relatively strong machine that is not available to the public.
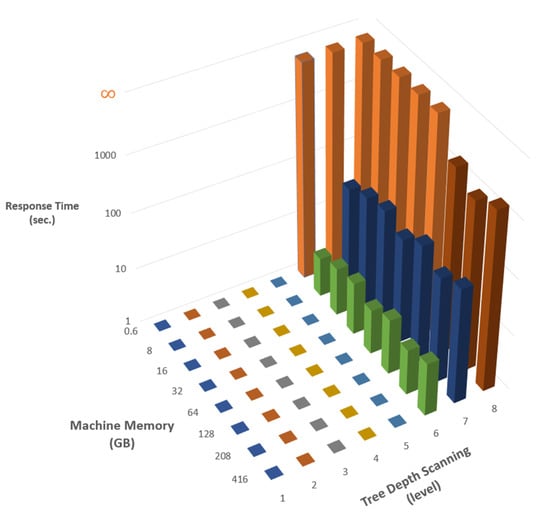
Figure 2.
Simulation of brute force performances (given in seconds) for various machines (measured by their amount of memory) and the level of optimization (measured as the depth of the search tree). The red blocks, which reach the level, mark tasks that never reach an end.
4.2. Experimental Framework
For our experiments, we built a Facebook simulator that captures the essence of the Facebook application. To this end, both the layout of our Facebook simulator and the functionality it offers users are similar to the actual Facebook application. For example, participants using the simulator can publish a post, like posts published by other participants, offer friendship to other participants, and other functions. The simulator provides a fully controlled environment, which enables us to test the performance of the human participants vs. the AI agents. Furthermore, due to the artificiality of this managed environment, we can provide incentives for the users to maximize their utilities and challenge the AI agents. The interaction between the users has a set number of discrete time intervals (called rounds) that are each limited to a pre-set discrete value. During the first round, each participant (player) is introduced to all other participants in the experiment (using their chosen nicknames for privacy preserving). For each round, users are asked to choose one operation out of those available (as mentioned above, doing nothing is also an acceptable choice). Next to each operation, users are shown a description of its benefit, cost, and privacy or security loss. Thus, they are fully informed regarding their choices. In these controlled experiments, the values were provided and were identical for all participants. However, in real life, the values (tangibly) can be collected and evaluated for each user [88], and each agent can be configured accordingly. The OISA model is general enough to accommodate different values. This simplifying assumption of identical costs and benefits does not detract from the validity of the results to be presented, but rather it strengthens them, because all performances can only be improved by adjusting the costs, benefits, and privacy loss based on the personal preferences of each user. Once we consider each user’s personal preferences, we will be able to predict the cost and benefit values each action carries for a specific agent, meaning we will be able to improve the results achieved so far. Throughout the game, the appropriate adjustments to the users’ total accumulated points are made (adding the benefits earned and subtracting the costs and privacy losses). For this setting, we set to be an aggregation of , , and and to be a given set of acceptable probabilities measured on Facebook. The goal of the player is to accumulate as many points as possible during the game.
4.3. Experimental Design
To measure the effectiveness of OISA, we conducted a set of experiments in which each includes a group of humans and an AI-based agent. The human participants were unaware of the fact that one of the participants is an AI-based agent, so this had no implications for their behavior throughout the experiments. Each user, human or not, is interested in maximizing its own utility from the interaction. The tangible values of all costs, benefits, and privacy losses (measured in game points) were fully relayed to the participants both in the instructions and in real time (by presenting the value on the screen). In each experiment, several participants were asked to log in to the Facebook simulator in the same time slot. Once logged in, the participants were: (a) informed about the experiment and asked to provide their consent; (b) asked to go through a short training, which also included a short quiz to ensure that they fully understood the game; (c) take part in the interactive information-sharing Facebook simulation; (d) asked to fill in a demographic survey, as well as answer questions regarding satisfaction. Throughout the experiment, all players’ actions were logged.
The participants were recruited through the crowdsourcing platform Amazon Mechanical Turk (MTurk) and among engineering students in their final year of studies. MTurk has proven to be a well-established method for data collection in tasks that require human intelligence (known as “human intelligence tasks” or HIT) [89]. To prevent a carryover effect, a “between-subjects” design was used, assigning each participant to one experiment only. The compensation included a payment of $4.50 for carrying out the HIT on MTurk. Participation was anonymous, and the participants were required to be at least 18 years old and have some experience with Facebook. The research was approved by the institutional ethics committee.
Both the Facebook simulator and the AI agent were programmed in Python. We developed the server side by using the Django web framework, the database by using PostgreSQL, the HTTP server by using Apache, and the user interface by using Bootstrap plus CSS and JS. Google Cloud was used to host the virtual machine on which the server side was implemented. We applied two types of non-human agents. The first type, a “monkey agent”, is an arbitrary agent that uses a uniform distribution to choose an operation randomly out of the entire decision space, i.e., . The second type, an “AI agent”, is a smart agent that implements one of the algorithms described in Section 3.4. The threshold for the HC agent was , and the MCTS agent was implemented with and .
We conducted 45 successful experiments with a total of valid participants; each included between three and five human participants and one non-human agent. Each experiment lasted approximately 40 min. Of all the participants, 53% were females and 47% were males; 46% were 18–25 years old and 47% were 26–30 years old; 27% had a bachelor’s degree, 67% had a high school diploma or higher, and 6% had no diploma at all. Most participants (63%) were employees, 13% were self-employed, and 34% were unemployed; 76% of the participants reported that they use Facebook at least once a day, while the rest used it less frequently; 34% reported that they were “very” concerned about privacy and security, 32% were “somewhat” concerned, and 34% were “a little” or “not at all” concerned. However, only 2% of the participants responded that Facebook is a safe environment.
4.4. Results
For convenience, the utility in all experiments was linearly normalized to values between 0 and 100. The performances of all participants (humans, monkey agent, SA, HC, and MCTS) are depicted in Figure 3. Overall, the utility score of the human participants () was significantly higher than that of the monkey agent (); . This finding is important because it demonstrates that the human participants indeed made efforts to maximize their utility. Despite these apparent efforts, the utility of all AI agents for SA (), HC (), and MCTS (100 replications only) with () was almost twice as high as that of the human participants, with , , and , respectively (applying Welch’s t-test). These results indicate that AI has a significantly better ability to manage cost–benefit trade-offs in this environment.
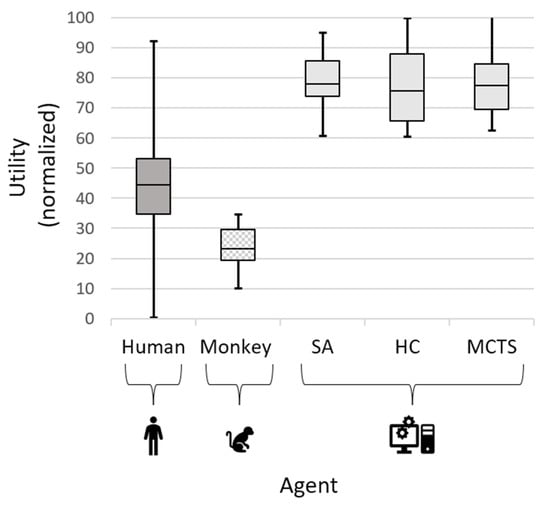
Figure 3.
Human vs. AI agent performance.
Plotting the differences in performance between the human participants and the AI agent over the number of rounds through the simulation, as depicted in Figure 4, reveals that these differences are not uniform over rounds, including instances (e.g., round 14) in which the human participants performs better than the AI agent. These fluctuations reflect the strategic approach taken by the AI agent, which sometimes prefers to sacrifice utility so as to increase it more significantly in future rounds.
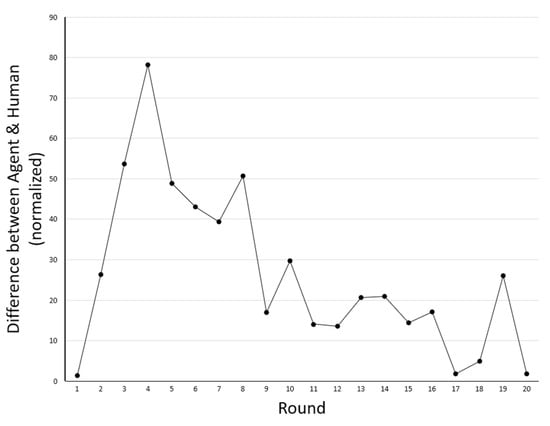
Figure 4.
The difference between the utility achieved by the AI agent and the human participants in successive rounds of the Facebook simulation. The values (which are all positive) indicate that the AI agent gained a higher utility value.
To evaluate the effect of the presence of different AI agents in the simulation, i.e., the extent to which humans in the system are influenced by different “opponent” strategies, the average human performances were calculated for each group of experiments using the same type of agent. Figure 5. depicts the findings of this evaluation. The rhombuses indicate the average human performances (not normalized) for each group, while the whiskers indicate the standard deviation. The ANOVA analysis shows that the type of AI agent has a significant effect on the humans’ performance ). These findings are quite surprising, since as mentioned above the human participants were unaware of the fact that one of the participants was an AI-based agent. One possible explanation for the differences in the utilities gained may be the reciprocal nature of the interactions in social networks.
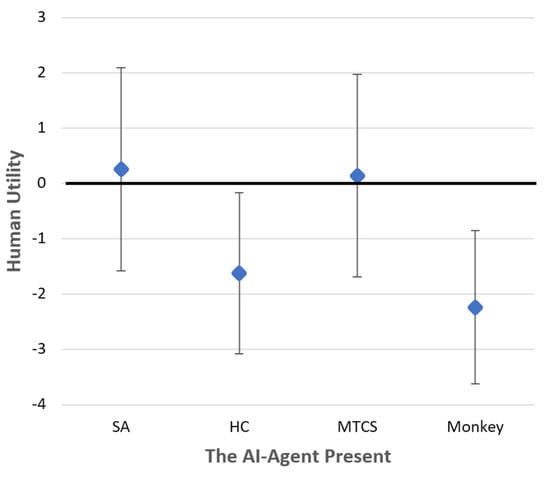
Figure 5.
The effect of the different AI agents’ presence on human performance.
The different algorithms yield different levels of utility, while a deeper investigation showed that the algorithm can be dynamically selected throughout the process to fine-tune the optimization. An ANOVA analysis showed significant correlations between the utility and the numbers of likes and friendship offers. We drew a Bayesian decision tree based on these factors and distilled a decision layout, shown in Table 1, to dynamically select the algorithm. The numbers of likes and friendship offers were classified according to their quantiles and are represented as low, med, or high, respectively, for . “Not applicable” (N/A) indicates a combination that did not appear in the experimental study. This refinement, however, should be investigated empirically in further research.

Table 1.
Algorithm selection layout.
5. Discussion
In this study, we introduced OISA, a methodology to improve decision-making when sharing information. OISA addresses the inherent trade-off between the benefits and the costs in information-sharing by (1) formally representing all realistic factors of the information-sharing process, (2) modeling the problem as a game using a game theory concept, and (3) applying relevant custom heuristic search algorithms. Our empirical study () showed that OISA AI agents perform significantly better than human agents, meaning that AI can be harnessed to handle this delicate task.
To enable OISA to act as an assistant, the values of the benefits and the costs of privacy must be quantified. The sensitivity level, which directly derived the privacy concern, may vary from one data item to another [90]. Naturally, these values are approximated and are achievable [91]. Moreover, the OISA approach is based on calculus theory (pure risk–benefit analysis), even though the psychological idea of bounded rationality [92] contends that people do not necessarily make decisions rationally, e.g., as described by prospect theory [24]. Rational decisions line up with the calculus theory; however, in reality in many cases, people deviate from rationality [93]. In this paper, we assumed that users deviated from optimality not because of an underlying desire, but because of limitations such as those discussed in the introduction.
The OISA strategy relies on real-time analysis. Based on the results of this research, the representation of information-sharing environments as a formal mathematical model can also be considered as an offline strategy. In this approach, we propose training the machine offline and producing a decision layout to be used online. This strategy, which requires further research, might reduce the heuristic nature of OISA. In addition, the OISA AI agent was tested as competing with the human user. However, its actual purpose is to assist the user. Thus, another study is required to test the user acceptance of OISA agents as a mechanism that makes recommendations.
The proposed model relies on actions taken by the user to balance their trade-off only. However, a user may also consider other users’ interests, for example based on agreement technologies [94,95] or collaborative strategies [96]. This approach may be included in further research to extend the OISA model.
Author Contributions
Conceptualization, methodology, software, validation, resources, data curation, writing—original draft preparation, writing—review and editing, visualization, supervision, project administration, and funding acquisition, R.S.H. and S.A.; formal analysis S.A.; investigation R.S.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ariel Cyber Innovation Center in conjunction with the Israel National Cyber directorate in the Prime Minister’s Office, grant number RA2000000281.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of Ariel University (authorization number: AU-ENG-RH-20200401, date of first approval 1/APR/2020, extended on 31/MAY/2021).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- ITUNews. New ITU Statistics Show More than Half the world Is Now Using the Internet. 2018. Available online: https://news.itu.int/itu-statistics-leaving-no-one-offline/ (accessed on 6 December 2018).
- Romansky, R. A survey of digital world opportunities and challenges for user’s privacy. Int. J. Inf. Technol. Secur. 2017, 9, 97–112. [Google Scholar]
- Dwivedi, Y.K.; Rana, N.P.; Jeyaraj, A.M.; Clement, M.; Williams, M.D. Re-examining the unified theory of acceptance and use of technology (UTAUT): Towards a revised theoretical model. Inf. Syst. Front. 2019, 21, 719–734. [Google Scholar] [CrossRef]
- Asswad, J.; Marks, J.G. Data Ownership: A Survey. Information 2021, 12, 465. [Google Scholar] [CrossRef]
- Gurung, A.; Raja, M. Online privacy and security concerns of consumers. Inf. Comput. Secur. 2016, 24, 348–371. [Google Scholar] [CrossRef]
- Marriott, H.R.; Williams, M.D.; Dwivedi, Y.K. Risk, privacy and security concerns in digital retail. Mark. Rev. 2017, 17, 337–365. [Google Scholar] [CrossRef]
- Rotman, D. Are You Looking At Me? Social Media and Privacy Literacy, IDEALS. Available online: http://hdl.handle.net/2142/15339 (accessed on 26 January 2022).
- Brenda, J. Understanding Ecommerce Consumer Privacy from the Behavioral Marketers’ Viewpoint. Ph.D. Thesis, Walden University, Minneapolis, MN, USA, 2019. [Google Scholar]
- Steinke, G. Data privacy approaches from US and EU perspectives. Telemat. Inform. 2002, 19, 193–200. [Google Scholar] [CrossRef]
- Bellekens, X.; Hamilton, A.; Seeam, P.; Nieradzinska, K.; Franssen, Q.; Seeam, A. Pervasive eHealth services a security and privacy risk awareness survey. In Proceedings of the 2016 International Conference On Cyber Situational Awareness, Data Analytics And Assessment (CyberSA), London, UK, 13–14 June 2016. [Google Scholar] [CrossRef]
- Price, W.N.; Cohen, I.G. Privacy in the age of medical big data. Nat. Med. 2019, 25, 37–43. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, L.; Yin, G.; Li, L.; Zhao, H. A survey on security and privacy issues in Internet-of-Things. IEEE Internet Things J. 2017, 4, 120–1258. [Google Scholar] [CrossRef]
- Regan, P.M. Privacy as a common good in the digital world. Inf. Commun. Soc. 2002, 5, 382–405. [Google Scholar] [CrossRef]
- Mokrosinska, D. Privacy and Autonomy: On Some Misconceptions Concerning the Political Dimensions of Privacy. Law Philos. 2018, 37, 117–143. [Google Scholar] [CrossRef]
- Dorraji, S.E.; Barcys, M. Privacy in digital age: Dead or alive? Regarding the new EU data protection regulations. Soc. Technol. 2014, 4, 306–317. [Google Scholar] [CrossRef]
- Li, H.; Yu, L.; He, W. The impact of GDPR on global technology development. J. Glob. Inf. Technol. Manag. 2019, 22, 1–6. [Google Scholar] [CrossRef]
- Min, J.; Kim, B. How are people enticed to disclose personal information despite privacy concerns in social network sites? The calculus between benefit and cost. J. Assoc. Inf. Sci. Technol. 2015, 66, 839–857. [Google Scholar] [CrossRef]
- Kung, S. A compressive privacy approach to generalized information bottleneck and privacy funnel problems. J. Frankl. Inst. 2018, 355, 1846–1872. [Google Scholar] [CrossRef]
- Cambridge Dictionary (Online). Information Exchange. Available online: https://dictionary.cambridge.org/dictionary/english/information-exchange (accessed on 22 March 2022).
- Talja, S.; Hansen, P. Information sharing. In New Directions in Human Information Behavior; Spink, A., Cole, C., Eds.; Springer: Dordrecht, The Netherlands, 2006; Volume 8, pp. 113–134. [Google Scholar] [CrossRef]
- Baruh, L.; Secinti, E.; Cemalcilar, Z. Online privacy concerns and privacy management: A meta-analytical review. J. Commun. 2017, 67, 26–53. [Google Scholar] [CrossRef]
- Olson, J.S.; Grudin, J.; Horvitz, E. A study of preferences for sharing and privacy. In Proceedings of the CHI’05 Extended Abstracts on Human Factors in Computing Systems, New York, NY, USA, 2–7 April 2005; pp. 1985–1988. [Google Scholar] [CrossRef]
- Puaschunder, J. A Utility Theory of Privacy and Information Sharing. In Encyclopedia of Information Science and Technology, 5th ed.; IGI Global: Hershey, PA, USA, 2021; pp. 428–448. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect Theory: An analysis of decision under risk. Econom. J. Econom. Soc. 1979, 47, 263–292. [Google Scholar] [CrossRef]
- Modi, C.; Patel, D.; Borisaniya, B.; Patel, H.; Patel, A.; Rajarajan, M. A survey of intrusion detection techniques in cloud. J. Netw. Comput. Appl. 2013, 36, 42–57. [Google Scholar] [CrossRef]
- Gouda, M.G.; Liu, A.X. Structured firewall design. Comput. Netw. 2007, 51, 1106–1120. [Google Scholar] [CrossRef]
- Newton, J. Evolutionary game theory: A renaissance. Games 2018, 9, 31. [Google Scholar] [CrossRef]
- Myerson, R.B. On the value of game theory in social science. Ration. Soc. 1992, 4, 62–73. [Google Scholar] [CrossRef]
- Alvari, H.; Hashemi, S.; Hamzeh, A. Detecting Overlapping Communities in Social Networks by Game Theory and Structural Equivalence Concept. In Artificial Intelligence and Computational Intelligence; Deng, H., Miao, D., Lei, J., Wang, F.L., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 620–630. [Google Scholar] [CrossRef]
- Wahab, O.A.; Bentahar, J.; Otrok, H.; Mourad, A. Towards Trustworthy Multi-Cloud Services Communities: A Trust-Based Hedonic Coalitional Game. IEEE Trans. Serv. Comput. 2018, 11, 184–201. [Google Scholar] [CrossRef]
- Phan, C. Coalition Information Sharing. In Proceedings of the MILCOM 2007—IEEE Military Communications Conference, Orlando, FL, USA, 29–31 October 2007; pp. 1–7. [Google Scholar] [CrossRef]
- Myers, K.; Ellis, T.; Lepoint, T.; Moore, R.A.; Archer, D.; Denker, G.; Lu, S.; Magill, S.; Ostrovsky, R. Privacy technologies for controlled information sharing in coalition operations. In Proceedings of the Symposium on Knowledge System for Coalition Operations, Los Angeles, LA, USA, 6–8 November 2017. [Google Scholar]
- Guo, Z.; Cho, J. Game Theoretic Opinion Models and Their Application in Processing Disinformation. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Kuchta, M.; Vaskova, L.; Miklosik, A. Facebook Explore Feed: Perception and Consequences of the Experiment. Rev. Socionetwork Strateg. 2019, 14, 93–107. [Google Scholar] [CrossRef]
- Vishwanath, A.; Xu, W.; Ngoh, Z. How people protect their privacy on Facebook: A cost-benefit view. J. Assoc. Inf. Sci. Technol. 2018, 69, 700–709. [Google Scholar] [CrossRef]
- Bhagat, S.; Saminathan, K.; Agarwal, A.; Dowsley, R.; De Cock, M.; Nascimento, A. Privacy-Preserving User Profiling with Facebook Likes. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 5298–5299. [Google Scholar] [CrossRef]
- Nilashi, M.; Asadi, S.; Minaei-Bidgoli, B.; Abumalloh, R.A.; Samad, S.; Ghabban, F.; Ahani, A. Recommendation agents and information sharing through social media for coronavirus outbreak. Telemat. Inform. 2021, 61, 101597. [Google Scholar] [CrossRef] [PubMed]
- Wattal, S.; Telang, R.; Mukhopadhyay, T.; Boatwright, P. Examining the personalization-privacy tradeoff—An empirical investigation with email advertisements. In Carnegie Mellon University Journal Contribution; Carnegie Mellon University: Pittsburgh, PA, USA, 2005. [Google Scholar] [CrossRef]
- Rafieian, O.; Yoganarasimhan, H. Targeting and privacy in mobile advertising. Marketing Science. 2020, 40, 193–394. [Google Scholar] [CrossRef]
- Rastogi, V.; Suciu, D.; Hong, S. The boundary between privacy and utility in data publishing. In Proceedings of the 33rd International Conference on Very Large Data Bases, Vienna, Austria, 23–27 September 2007; pp. 531–542. [Google Scholar]
- Zhang, D. Big data security and privacy protection. In Proceedings of the 8th International Conference on Management and Computer Science (ICMCS 2018), Shenyang, China, 10–12 August 2018. [Google Scholar] [CrossRef]
- Kalantari, K.; Sankar, L.; Sarwate, A.D. Robust Privacy-Utility Tradeoffs Under Differential Privacy and Hamming Distortion. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2816–2830. [Google Scholar] [CrossRef]
- Price, B.A.; Adam, K.; Nuseibehm, B. Keeping ubiquitous computing to yourself: A practical model for user control of privacy. Int. J. Hum.-Comput. Stud. 2005, 63, 228–253. [Google Scholar] [CrossRef]
- Gutierrez, A.; O’Leary, S.; Rana, N.P.; Dwivedi, Y.K.; Calle, T. Using privacy calculus theory to explore entrepreneurial directions in mobile location-based advertising: Identifying intrusiveness as the critical risk factor. Comput. Hum. Behav. 2019, 95, 295–306. [Google Scholar] [CrossRef]
- Zhang, A.; Lin, X. Towards secure and privacy-preserving data sharing in e-health systems via consortium blockchain. J. Med. Syst. 2018, 42, 140. [Google Scholar] [CrossRef]
- Sun, Y.; Yin, L.; Sun, Z.; Tian, Z.; Du, X. An IoT data sharing privacy preserving scheme. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Toronto, ON, Canada, 6–9 July 2020. [Google Scholar] [CrossRef]
- Sharma, S.; Chen, K.; Sheth, A. Toward practical privacy-preserving analytics for IoT and cloud-based healthcare systems. IEEE Internet Comput. 2018, 22, 42–51. [Google Scholar] [CrossRef]
- Kenneally, E.; Claffy, K. An internet data sharing framework for balancing privacy and utility. In Proceedings of the Engaging Data: First International Forum on the Application and Management of Personal Electronic Information, Cambridge, MA, USA, 12–13 October 2009. [Google Scholar]
- Bhumiratana, B.; Bishop, M. Privacy aware data sharing: Balancing the usability and privacy of datasets. In Proceedings of the 2nd International Conference on PErvasive Technologies Related to Assistive Environments, Corfu, Greece, 9–13 June 2009. [Google Scholar] [CrossRef]
- Hirschprung, R.; Toch, E.; Schwartz-Chassidim, H.; Mendel, T.; Maimon, O. Analyzing and optimizing access control choice architectures in online social networks. ACM Trans. Intell. Syst. Technol. 2017, 8, 1–22. [Google Scholar] [CrossRef]
- Beam, M.A.; Child, J.T.; Hutchens, M.J.; Hmielowski, J.D. Context collapse and privacy management: Diversity in Facebook friends increases online news reading and sharing. New Media Soc. 2018, 20, 2296–2314. [Google Scholar] [CrossRef]
- Garcia, D.; Goel, M.; Agrawal, A.K.; Kumaraguru, P. Collective aspects of privacy in the Twitter social network. EPJ Data Sci. 2018, 7, 3. [Google Scholar] [CrossRef]
- Choi, B.; Wu, Y.; Yu, J.; Land, L. Love at first sight: The interplay between privacy dispositions and privacy calculus in online social connectivity management. J. Assoc. Inf. Syst. 2018, 19, 124–151. [Google Scholar] [CrossRef]
- Madejskiy, M.; Johnson, M.; Bellovin, S.M. The Failure of Online Social Network Privacy Settings; Columbia University Computer Science Technical Reports, CUCS-010-11; Columbia University: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Acquisti, A. Privacy in electronic commerce and the economics of immediate gratification. In Proceedings of the 5th ACM Conference on Electronic Commerce, New York, NY, USA, 17–20 May 2004. [Google Scholar] [CrossRef]
- Isaak, J.; Hanna, M.J. User data privacy: Facebook, Cambridge Analytica, and privacy protection. Computer 2018, 51, 56–59. [Google Scholar] [CrossRef]
- Wisniewski, P.; Lipford, H.; Wilson, D. Fighting for my space: Coping mechanisms for SNS boundary regulation. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, New York, NY, USA, 5–10 May 2012. [Google Scholar] [CrossRef]
- Desimpelaere, L.; Hudders, L.; Van de Sompel, D. Knowledge as a strategy for privacy protection: How a privacy literacy training affects children’s online disclosure behaviour. Comput. Hum. Behav. 2020, 110, 106382. [Google Scholar] [CrossRef]
- Korneeva, E.; Cichy, P.; Salge, T.O. Privacy Risk Perceptions and the Role of Evaluability, Framing and Privacy Literacy. Acad. Manag. Proc. 2019, 2019, 18986. [Google Scholar] [CrossRef]
- Pingo, Z.; Narayan, B. Privacy Literacy and the Everyday Use of Social Technologies. In Proceedings of the European Conference on Information Literacy, Oulu, Finland, 18–27 September 2018; p. 18. [Google Scholar] [CrossRef]
- Spiering, A. Improving Cyber Security Safety Awareness Education at Dutch Elementary Schools. Available online: https://openaccess.leidenuniv.nl/bitstream/handle/1887/64565/Spiering_A_2018_CS.docx?sequence=2 (accessed on 22 March 2022).
- Furnell, S.; Moore, L. Security literacy: The missing link in today’s online society? Comput. Fraud Secur. 2014, 5, 12–18. [Google Scholar] [CrossRef]
- Masur, P.K. How online privacy literacy supports self-data protection and self-determination in the age of information. Media Commun. 2020, 8, 258–269. [Google Scholar] [CrossRef]
- Harborth, D.; Pape, S. How Privacy Concerns, Trust and Risk Beliefs, and Privacy Literacy Influence Users’ Intentions to Use Privacy-Enhancing Technologies: The Case of Tor. ACM SIGMIS Database DATABASE Adv. Inf. Syst. 2020, 51, 51–69. [Google Scholar] [CrossRef]
- Andrew, H. Facebook’s Implementing New Rules and Processes to Stop the Spread of Harmful Content. Available online: https://www.socialmediatoday.com/news/facebooks-implementing-new-rules-and-processes-to-stop-the-spread-of-harmf/552481/ (accessed on 22 March 2022).
- Craciun, G. Choice defaults and social consensus effects on online information sharing: The moderating role of regulatory focus. Comput. Hum. Behav. 2018, 88, 89–102. [Google Scholar] [CrossRef]
- Anaraky, R.G.; Knijnenburg, B.P.; Risius, M. Exacerbating mindless compliance: The danger of justifications during privacy decision making in the context of Facebook applications. AIS Trans. Hum.-Comput. Interact. 2020, 12, 70–95. [Google Scholar] [CrossRef]
- Maxwell, G. How Will the Latest Facebook Algorithm Change. Available online: https://www.falcon.io/insights-hub/industry-updates/social-media-updates/facebook-algorithm-change/ (accessed on 22 March 2022).
- Trepte, S.; Teutsch, D.; Masur, P.K.; Eicher, C.; Fischer, M.; Hennhöfer, A.; Lind, F. Do people know about privacy and data protection strategies? Towards the: Online Privacy Literacy Scale”(OPLIS). In Reforming European Data Protection Law; Gutwirth, S., Leenes, R., de Hert, P., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 333–365. [Google Scholar] [CrossRef]
- Bartsch, M.; Dienlin, T. Control your Facebook: An analysis of online privacy literacy. Comput. Hum. Behav. 2016, 56, 147–154. [Google Scholar] [CrossRef]
- Brough, A.R.; Martin, K.D. Critical roles of knowledge and motivation in privacy research. Curr. Opin. Psychol. 2020, 31, 11–15. [Google Scholar] [CrossRef] [PubMed]
- Qu, Y.; Yu, S.; Gao, L.; Zhou, Z.; Peng, S. A hybrid privacy protection scheme in cyber-physical social networks. IEEE Trans. Comput. Soc. Syst. 2018, 5, 773–784. [Google Scholar] [CrossRef]
- Gupta, A.; Cedric, L.; Basar, T. Optimal control in the presence of an intelligent. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010. [Google Scholar] [CrossRef]
- Wu, H.; Wang, W. A game theory based collaborative security detection method for Internet of Things systems. IEEE Trans. Inf. Forensics Secur. 2018, 13, 1432–1445. [Google Scholar] [CrossRef]
- Katz, J. Bridging game theory and cryptography: Recent results and future directions. In Proceedings of the Theory of Cryptography Conference, New York, NY, USA, 19–21 March 2008. [Google Scholar] [CrossRef]
- Ding, K.; Zhang, J. Multi-Party Privacy Conflict Management in Online Social Networks: A Network Game Perspective. IEEE/ACM Trans. Netw. 2020, 28, 2685–2698. [Google Scholar] [CrossRef]
- Kotra, A. A Game Theoretic Approach Applied in k-Anonymization for Preserving Privacy in Shared Data. Ph.D. Thesis, University of Nevada, Reno, NV, USA, 2020. [Google Scholar]
- Liu, F.; Pan, L.; Yao, L. Evolutionary Game Based Analysis for User Privacy Protection Behaviors in Social Networks. In Proceedings of the 2018 IEEE Third International Conference on Data Science in Cyberspace (DSC), Guangzhou, China, 18–21 June 2018; pp. 274–279. [Google Scholar] [CrossRef]
- Hu, H.; Ahn, G.; Zhao, Z.; Yang, D. Game theoretic analysis of multiparty access control in online social networks. In Proceedings of the 19th ACM Symposium on Access Control Models and Technologies, New York, NY, USA, 25–27 June 2014; pp. 93–102. [Google Scholar] [CrossRef]
- Do, C.T.; Tran, N.H.; Hong, C.; Kamhoua, C.A.; Kwiat, K.A.; Blasch, E.; Ren, S.; Pissinou, N.; Iyengar, S.S. Game theory for cyber security and privacy. ACM Comput. Surv. (CSUR) 2017, 50, 1–37. [Google Scholar] [CrossRef]
- Manshaei, M.H.; Zhu, Q.; Alpcan, T.; Bacşar, T.; Hubaux, J. Game theory meets network security and privacy. ACM Comput. Surv. (CSUR) 2013, 45, 1–39. [Google Scholar] [CrossRef]
- Tsuruoka, Y.; Yokoyama, D.; Chikayama, T. Game-tree search algorithm based on realization probability. Icga J. 2002, 25, 145–152. [Google Scholar] [CrossRef]
- Van Laarhoven, P.J.; Aarts, E.H. Simulated annealing. In Simulated Annealing: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2010; Volume 37, pp. 7–15. [Google Scholar]
- Selman, B.; Gomes, C.P. Hill-climbing search. Encycl. Cogn. Sci. 2006, 81, 82. [Google Scholar] [CrossRef]
- Coulom, R. Efficient selectivity and backup operators in Monte-Carlo tree search. In Proceedings of the International Conference on Computers and Games, Turin, Italy, 29–31 May 2006; pp. 72–83. [Google Scholar] [CrossRef]
- Karl. The 15 Biggest Social Media Sites and Apps. 2022. Available online: https://www.dreamgrow.com/top-15-most-popular-social-networking-sites/ (accessed on 17 January 2022).
- Statista. Leading Countries Based on Facebook Audience Size as of January 2022. Available online: https://www.statista.com/statistics/268136/top-15-countries-based-on-number-of-facebook-users/ (accessed on 17 January 2022).
- Hirschprung, R.; Toch, E.; Bolton, F.; Maimon, O. A methodology for estimating the value of privacy in information disclosure systems. Comput. Hum. Behav. 2016, 61, 443–453. [Google Scholar] [CrossRef]
- Paolacci, G.; Chandler, J.; Ipeirotis, P.G. Running experiments on Amazon Mechanical Turk. Judgm. Decis. Mak. 2010, 5, 411–419. [Google Scholar]
- Xiao, Y.; Li, H. Privacy preserving data publishing for multiple sensitive attributes based on security level. Information 2020, 11, 166. [Google Scholar] [CrossRef]
- Huberman, B.A.; Adar, E.; Fine, L.R. Valuating privacy. IEEE Secur. Priv. 2005, 3, 22–25. [Google Scholar] [CrossRef]
- Sent, E.M. Rationality and bounded rationality: You can’t have one without the other. Eur. J. Hist. Econ. Thought 2018, 25, 1370–1386. [Google Scholar] [CrossRef]
- Fernandes, T.; Pereira, N. Revisiting the privacy calculus: Why are consumers (really) willing to disclose personal data online? Telemat. Inform. 2021, 65, 101717. [Google Scholar] [CrossRef]
- Kekulluoglu, D.; Kokciyan, N.; Yolum, P. Preserving privacy as social responsibility in online social networks. ACM Trans. Internet Technol. (TOIT) 2018, 18, 1–22. [Google Scholar] [CrossRef]
- Rajtmajer, S.; Squicciarini, A.; Such, J.M.; Semonsen, J.; Belmonte, A. An ultimatum game model for the evolution of privacy in jointly managed content. In Decision and Game Theory for Security; Rass, S., An, B., Kiekintveld, C., Fang, F., Schauer, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 112–130. [Google Scholar] [CrossRef]
- Lampinen, A.; Lehtinen, V.; Lehmuskallio, A.; Tamminen, S. We’re in it together: Interpersonal management of disclosure in social network services. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Vancouver, BC, Canada, 7–12 May 2011; pp. 3217–3226. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).