Secure Sensitive Data Sharing Using RSA and ElGamal Cryptographic Algorithms with Hash Functions
Abstract
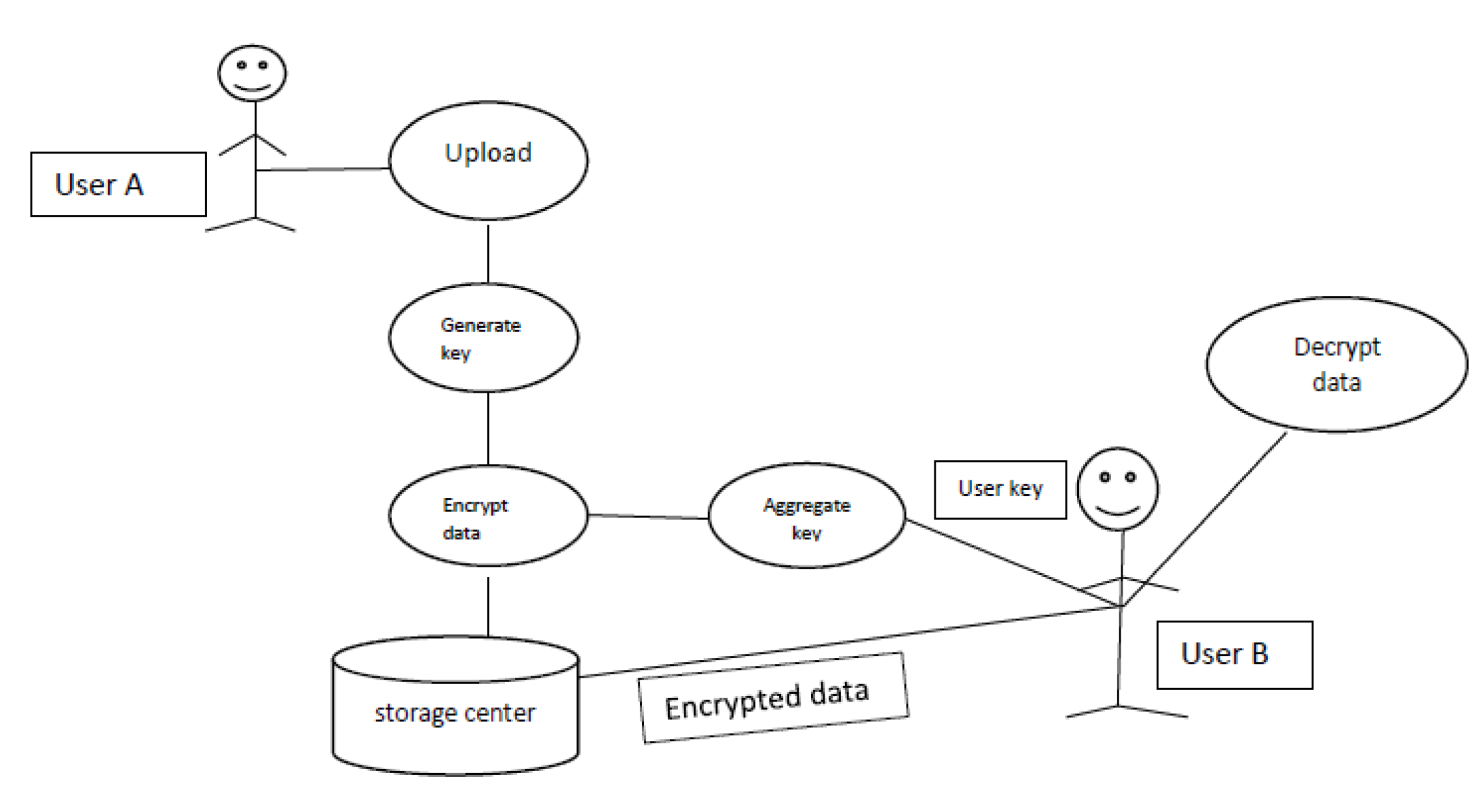
:1. Introduction
Review of Literature
2. Materials and Methods
2.1. The RSA Algorithm
2.1.1. Key Generation
- Randomly choose two huge, unique primes p and q.
- Compute the modulus n, n = p ∗ q and the phi function Ø(n) = (p − 1) ∗ (q − 1).
- Choose a random integer e, such that 0 < e < Ø(n).
- Compute d = e−l mod Ø(n).
- The private key is given as (d, n) and the public key as (e, n).
2.1.2. Encryption and Decryption
- Encryption is carried out with the aid of the public key (e, n).
- C = Me mod n.
- The secret key is used for decryption (d, n).
- M = Cd mod n.
2.2. Signing and Verification
- Calculate the hash h = H(M) of the message M.
- The signature S is given as S = Hd mod n.
- Calculate the hash H of the message M.
- Compute H′ = Se mod n.
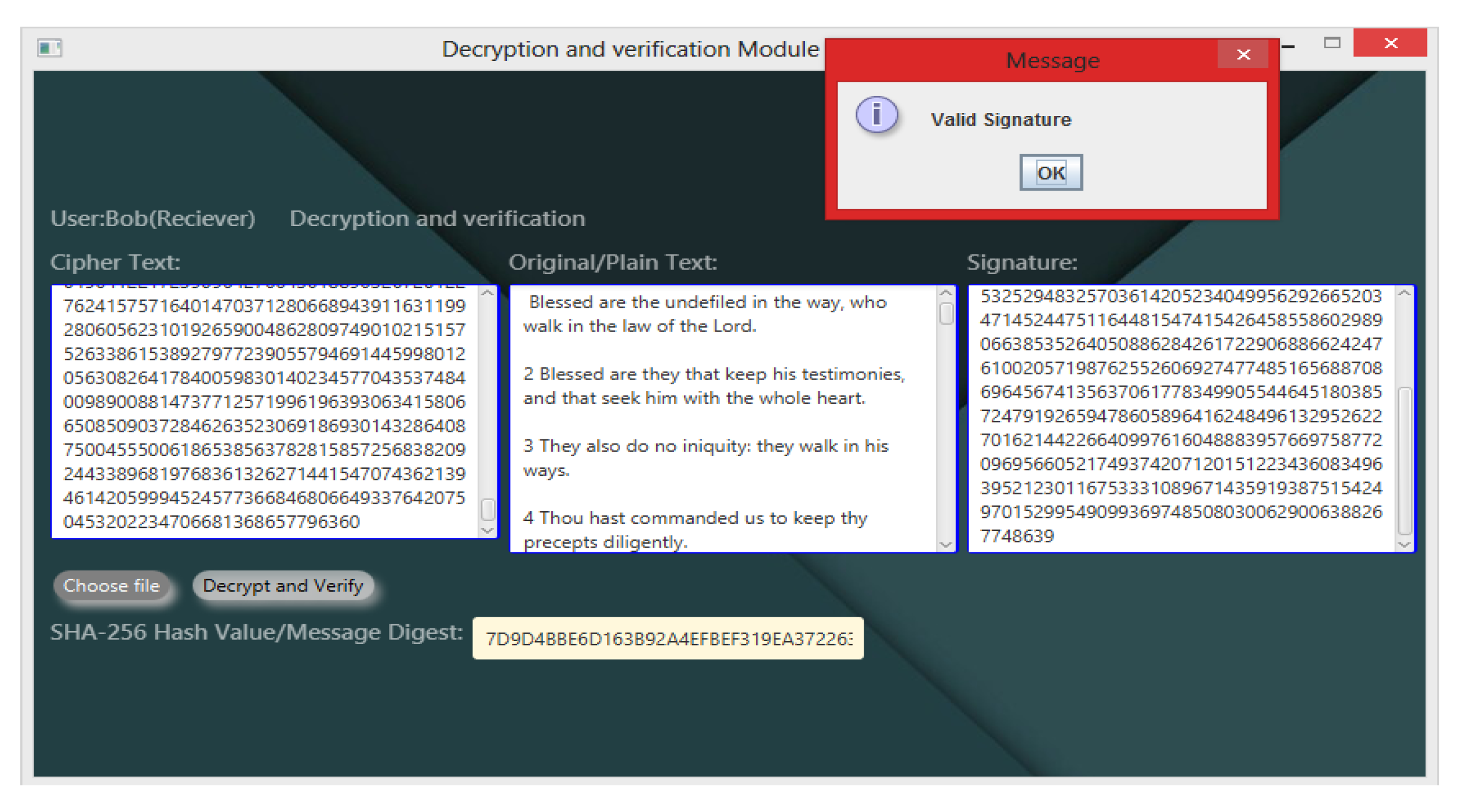
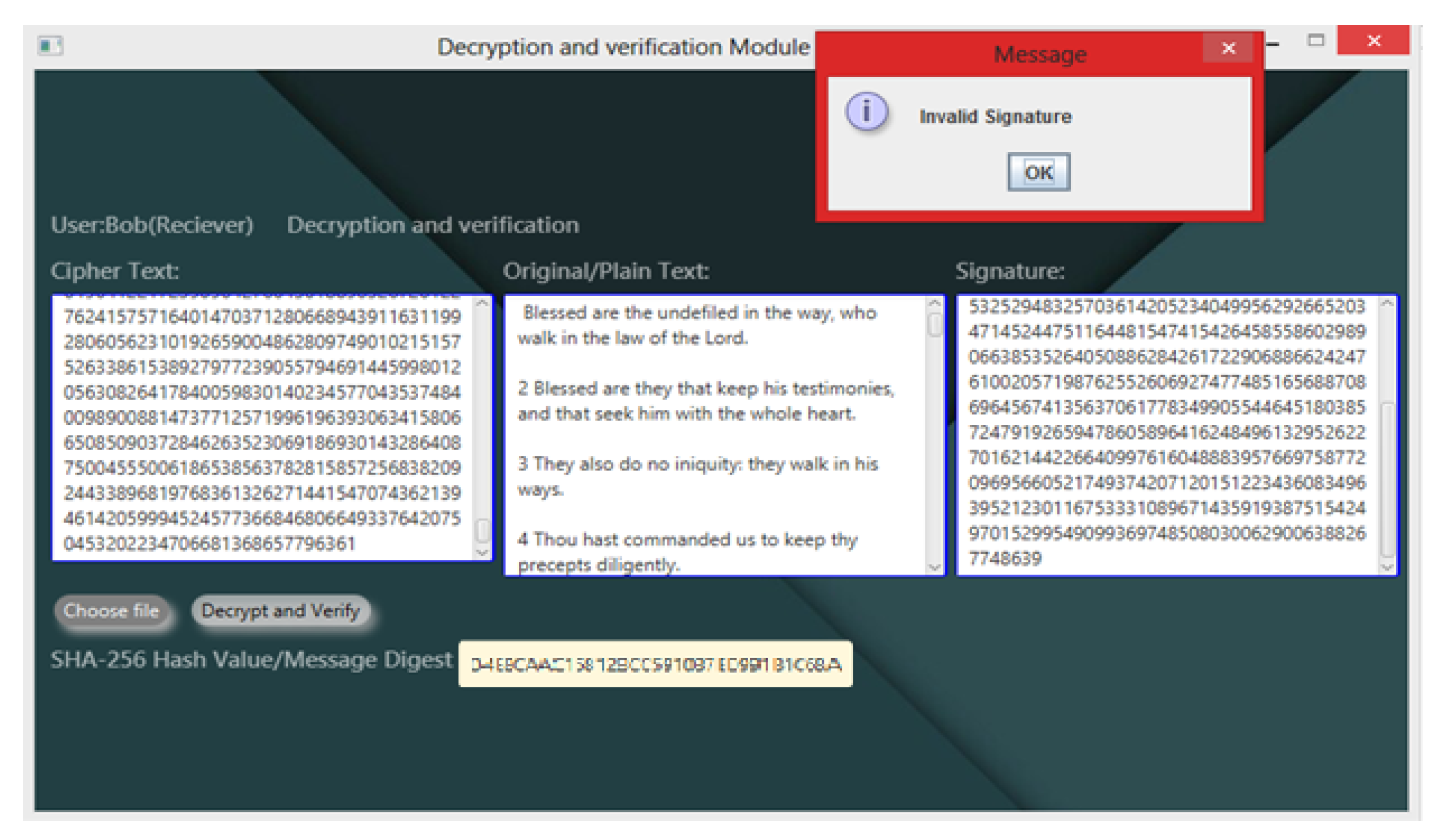
- If H == H′, then the signature is valid.
2.3. The ElGamal Algorithm
2.3.1. Key Generation
- Generate a large random prime number (p).
- Choose a generator number (a).
- Choose an integer (x) less than (p − 2), as the secret number.
- Compute (d), where d = ax mod p.
- The private key is given as (x) and the public key as (p, a, d).
2.3.2. Encryption and Decryption
- Choose an integer k such that 1 < k < p − 2.
- Compute y, y = ak mod p.
- Compute z, z = (dk ∗ m) mod p.
- The ciphertext is given as C = (y, z).
- The receiver obtains the ciphertext C = (y, z).
- Next, r is computed as follows: r = yp−1−x mod p.
2.3.3. Signature Generation
- Choose a random integer K with 1 ≤ K ≤ (p − 1) and gcd(K, p − 1) = 1.
- Compute the temporary key: h = ak mod p.
- Compute K − 1 the inverse of K mod (p − 1).
- Compute the value s = K−1(m − xh) mod (p − 1).
- The signature is (h, s).
- The hash m for the message M;
- V1 = am mod p;
- V2 = dh hS mod p;
- The signature is valid if V1 = = V2.
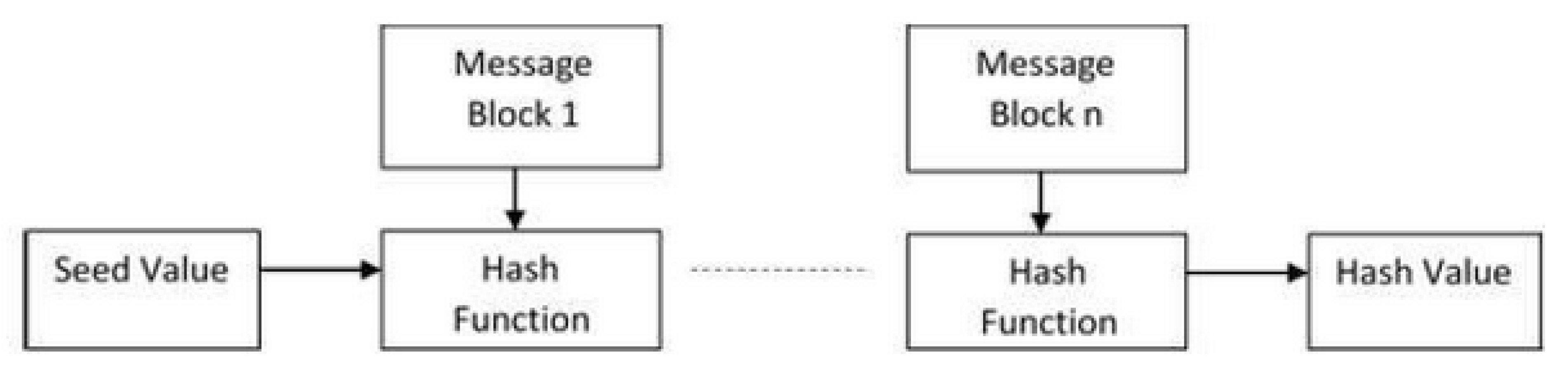
2.4. The SHA-256 Hash Function
The SHA-256 Algorithm
- Append a single bit, whose value is set to 1, to the input x.
- Compute the smallest r such that (b + r) mod 512 = 448. Append r-1 bits, whose values are set to 0, to the result of step 1.
- Compute the 64-bit value b mod 2^64 and append this value to the result of step 2.
- This yields a string of length that must be a multiple, m, of 512 bits and, thus, may be represented as 16*m 32-bit blocks.
3. Results
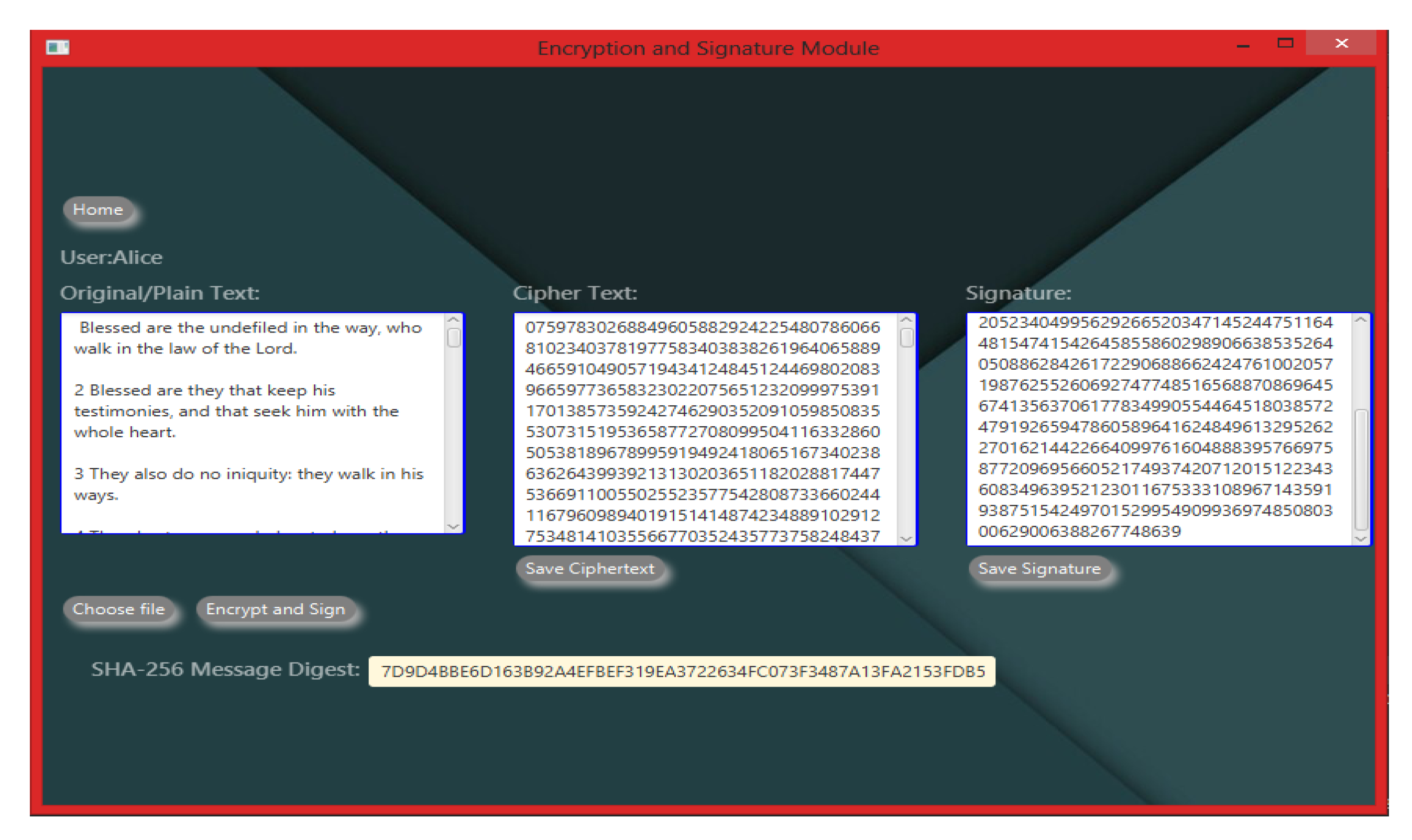
- Encryption of files using RSA and ElGamal algorithms;
- Signature generation and verification for text files;
- Decryption of information using the RSA and ElGamal algorithms;
- Generation of message digest for information/data;
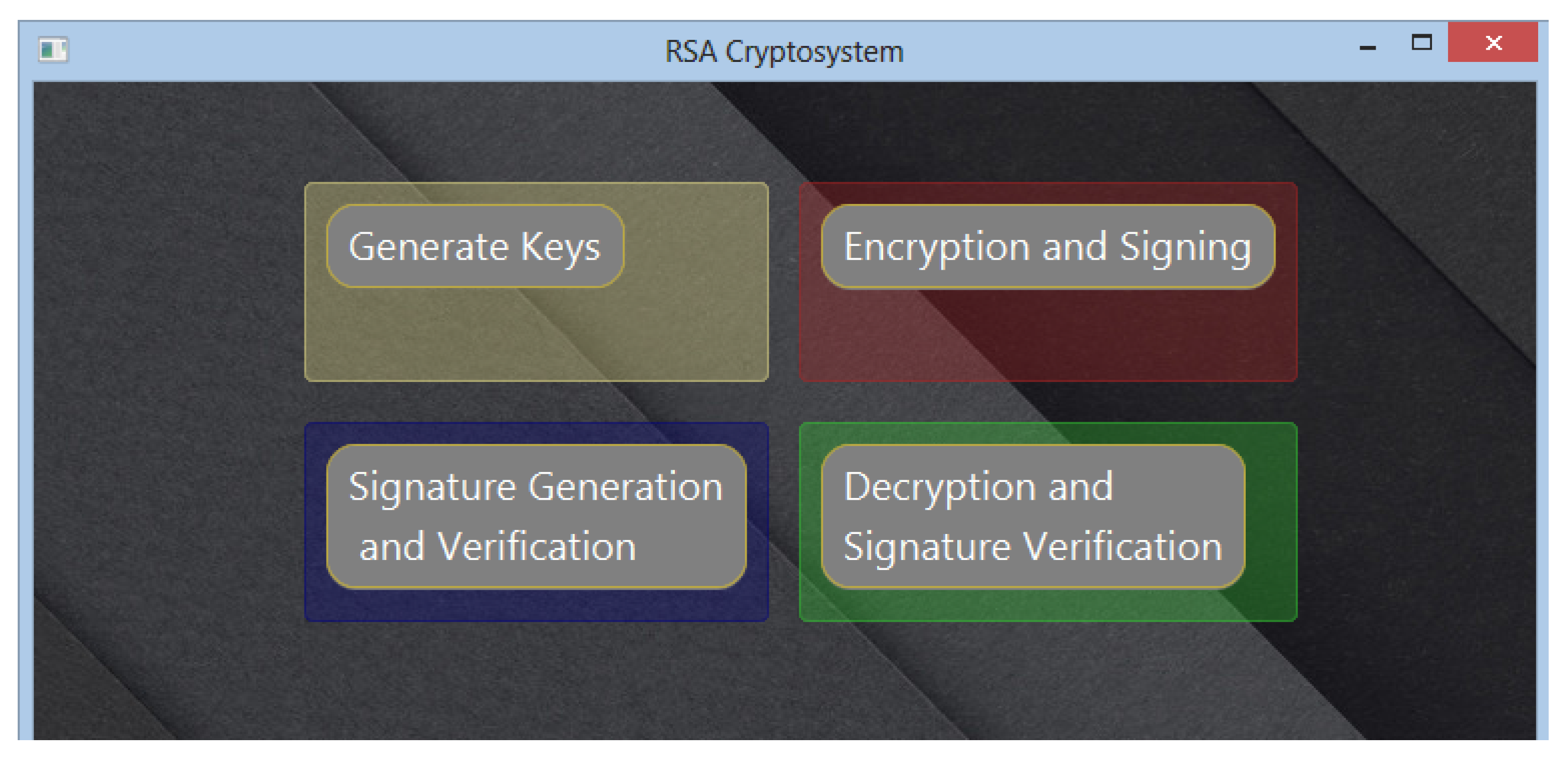
- GUI interface for easy interaction with the system;
- Auto-generation of private and public keys for encryption, signing, and decryption;
- Provision of interface for the selection of files or documents to be signed or encrypted. See Figure 5.
3.1. Result Analysis
3.1.1. Encryption
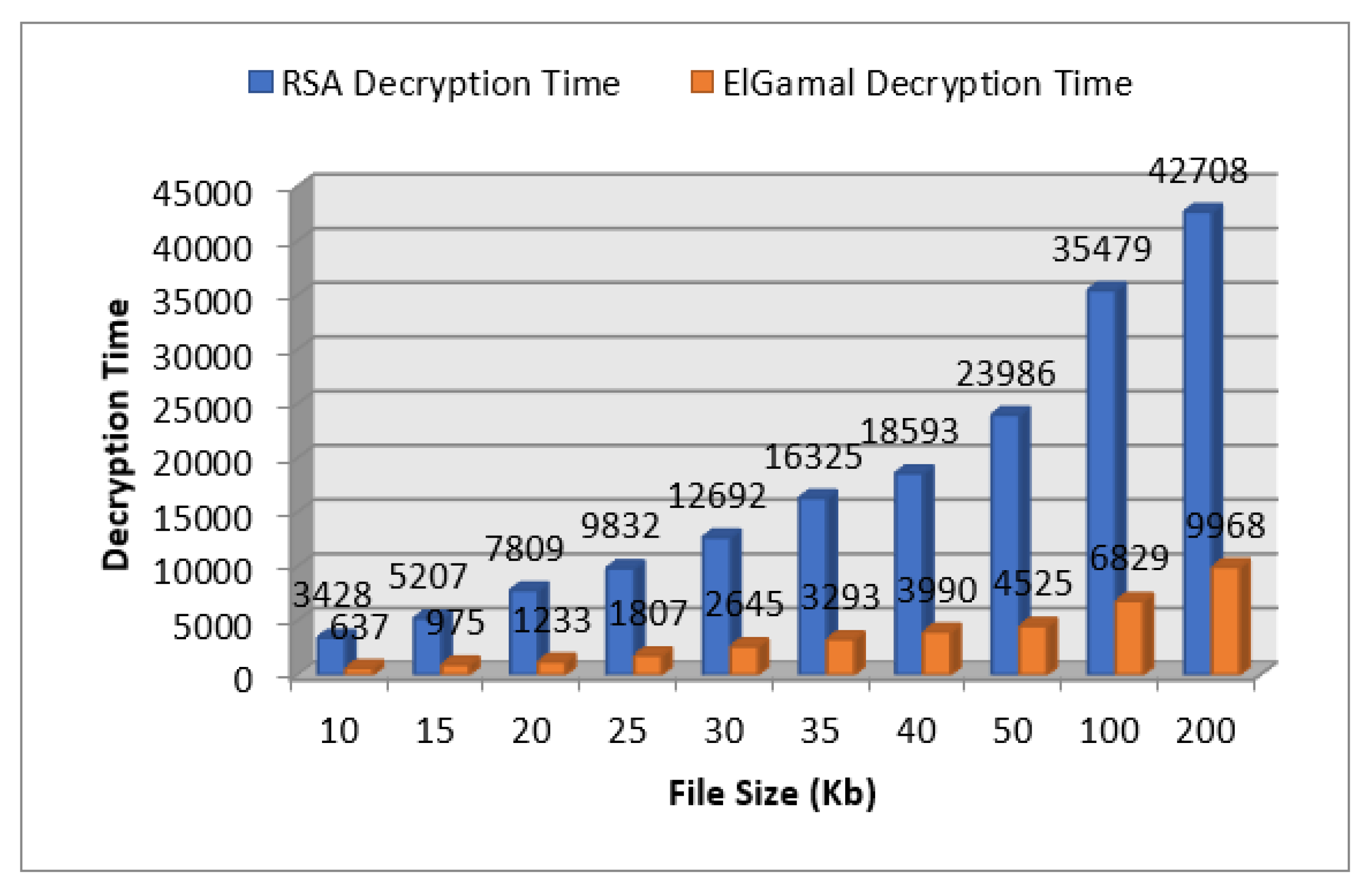
3.1.2. Decryption
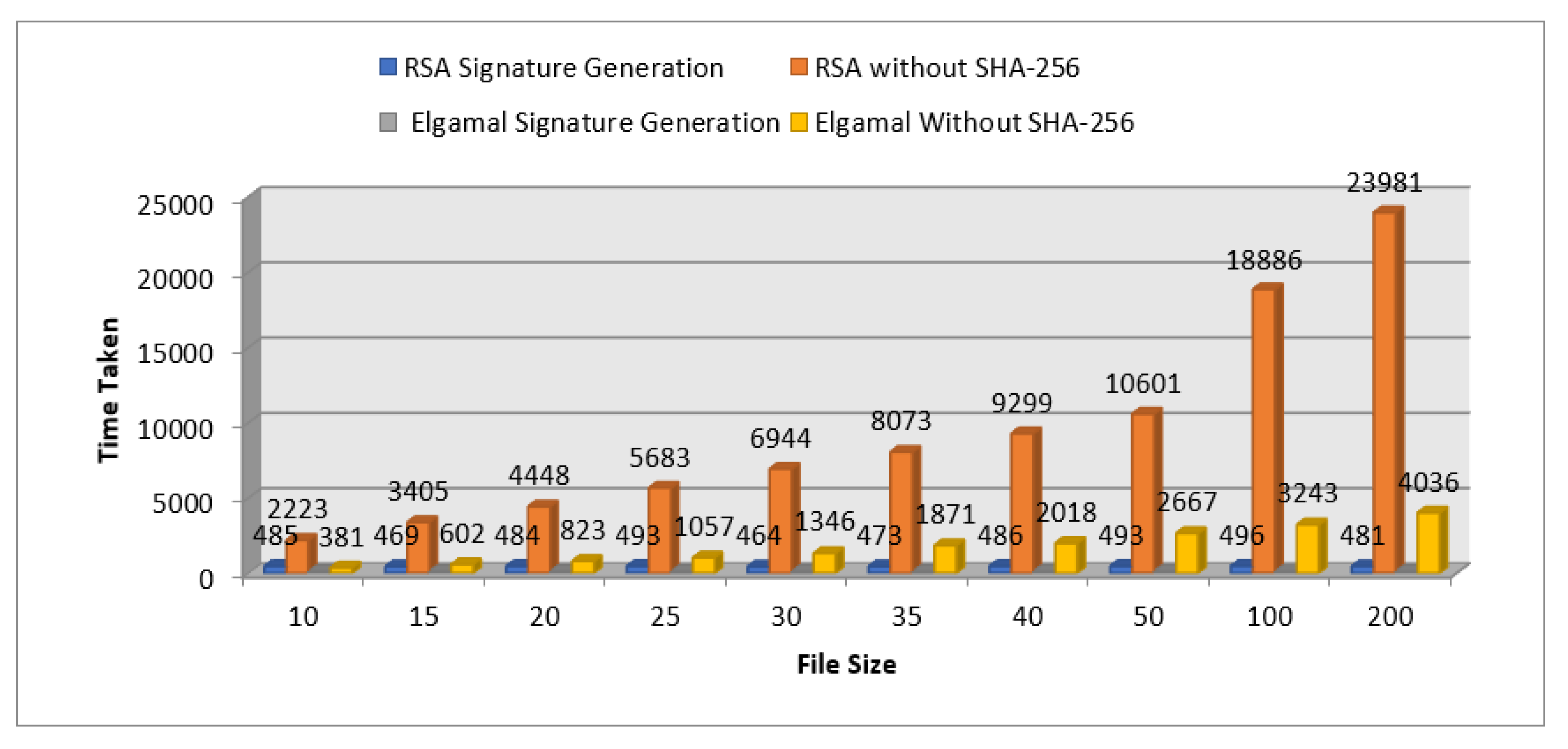
3.1.3. Signature Generation
3.1.4. Signature Verification
4. Discussion
Findings and Comparison with Existing Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gunduz, M.Z.; Das, R. Cyber-security on smart grid: Threats and potential solutions. Comput. Netw. 2020, 169, 107094. [Google Scholar] [CrossRef]
- Saxena, N.; Choi, B.J.; Lu, R. Authentication and Authorization Scheme for Various User Roles and Devices in Smart Grid. IEEE Trans. Inf. Forensics Secur. 2015, 11, 907–921. [Google Scholar] [CrossRef]
- Misbha, A.; Baswal, K.; Simha, M.N.; Abujam, R.; C.M., S. GUPTDOC AN ENTERPRISE PORTAL FOR CRYPTING WITH AES. Int. Res. J. Eng. Technol. 2017, 4, 1309–1311. [Google Scholar]
- Emmanuel, A.A.; Okeyinka, A.E.; Adebiyi, M.O.; Asani, E.O. A Note on Time and Space Complexity of RSA and ElGamal Cryptographic Algorithms. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 143–147. [Google Scholar] [CrossRef]
- Chandra, S.; Paira, S.; Alam, S.S.; Sanyal, G. A comparative survey of Symmetric and Asymmetric Key Cryptography. In Proceedings of the 2014 International Conference on Electronics, Communication and Computational Engineering (ICECCE), Hosur, India, 17–18 November 2014; pp. 83–93. [Google Scholar] [CrossRef]
- Sejfuli-Ramadani, N. The Role and the Impact of Digital Certificate and Digital Signature in Improving Security During Data Transmission. Eur. J. Sustain. Dev. Res. 2017, 2, 116–120. [Google Scholar]
- Winter, C.; Berchtold, W.; Hollenbeck, J.N. Securing physical documents with digital signatures. In Proceedings of the 2019 IEEE 21st International Workshop on Multimedia Signal Processing (MMSP), Kuala Lumpur, Malaysia, 18 November 2019; pp. 1–6. [Google Scholar]
- Zhang, H.; Yuan, Z.; Wen, Q.Y. A Digital Signature Schemes Without Using One-way Hash and Message Redundancy and Its Application on Key Agreement. In Proceedings of the 2007 IFIP International Conference on Network and Parallel Computing Workshops (NPC 2007), Dalian, China, 18–21 September 2007; pp. 873–878. [Google Scholar] [CrossRef]
- Chang, C.C.; Chang, Y.F. A novel three-party encrypted key exchange protocol. Comput. Stand. Interfaces 2004, 26, 471–476. [Google Scholar] [CrossRef]
- Burr, W. Cryptographic hash standards: Where do we go from here? IEEE Secur. Priv. 2006, 4, 88–91. [Google Scholar] [CrossRef]
- Acharya, K.; Sajwan, M.; Bhargava, S. Analysis of Cryptographic Algorithms for Network Security. Int. J. Comput. Appl. Technol. Res. 2014, 3, 130–135. [Google Scholar] [CrossRef]
- Saleh, E.; Meinel, C. HPISecure: Towards Data Confidentiality in Cloud Applications. In Proceedings of the 2013 13th IEEE/ACM International Symposium on Cluster, Cloud, and Grid Computing, Delft, Netherlands, 13–16 May 2013; pp. 605–609. [Google Scholar] [CrossRef]
- Mell, P.; Grance, T. The NIST definition of cloud computing. NIST Spec. Publ. 2011, 800, 145. [Google Scholar]
- Abiodun, M.K.; Awotunde, J.B.; Ogundokun, R.O.; Misra, S.; Adeniyi, E.A.; Arowolo, M.O.; Jaglan, V. Cloud and Big Data: A Mutual Benefit for Organization Development. J. Phy. Conf. Ser. 2021, 1767, 012020. [Google Scholar] [CrossRef]
- Hwang, J.J.; Chuang, H.K.; Hsu, Y.C.; Wu, C.H. A Business Model for Cloud Computing Based on a Separate Encryption and Decryption Service. In Proceedings of the 2011 International Conference on Information Science and Applications, Jeju, Korea, 26–29 April 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Chandra, D.G.; Prakash, R.; Lamdharia, S. A Study on Cloud Database. In Proceedings of the 2012 Fourth International Conference on Computational Intelligence and Communication Networks, Mathura, India, 3–5 November 2012; pp. 513–519. [Google Scholar]
- Haque, E.; Zobaed, S.; Islam, M.U.; Areef, F.M. Performance Analysis of Cryptographic Algorithms for Selecting Better Utilization on Resource Constraint Devices. In Proceedings of the 2018 21st International Conference of Computer and Information Technology (ICCIT), Dhaka, Bangladesh, 21–23 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Dijesh, P.; Babu, S.; Vijayalakshmi, Y. Enhancement of e-commerce security through asymmetric key algorithm. Comput. Commun. 2020, 153, 125–134. [Google Scholar] [CrossRef]
- Hamza, A.H.; Al-Alak, S.M.K. Evaluation key generator of multiple asymmetric methods in wireless sensor networks (WSNs). J. Phys. Conf. Ser. 2021, 1804, 012096. [Google Scholar] [CrossRef]
- Bharany, S.; Sharma, S.; Badotra, S.; Khalaf, O.I.; Alotaibi, Y.; Alghamdi, S.; Alassery, F. Energy-Efficient Clustering Scheme for Flying Ad-Hoc Networks Using an Optimized LEACH Protocol. Energies 2021, 14, 6016. [Google Scholar] [CrossRef]
- Kaur, K.; Bharany, S.; Badotra, S.; Aggarwal, K.; Nayyar, A.; Sharma, S. Energy-efficient polyglot persistence database live migration among heterogeneous clouds. J. Supercomput. 2022, 1–30. [Google Scholar] [CrossRef]
- Bharany, S.; Sharma, S.; Bhatia, S.; Rahmani, M.K.I.; Shuaib, M.; Lashari, S.A. Energy Efficient Clustering Protocol for FANETS Using Moth Flame Optimization. Sustainability 2022, 14, 6159. [Google Scholar] [CrossRef]
- Steichen, M.; Fiz Pontiveros, B.; Norvill, R.; Shbair, W. Blockchain-Based, Decentralized Access Control for IPFS. In Proceedings of the 2018 IEEE International Conference on Blockchain (Blockchain-2018), Halifax, NS, Canada, 30 July–3 August 2018; pp. 1499–1506. [Google Scholar]
- Gaby, G.; Chandra, L.; Enderson, T. Towards Secure Interoperability between Heterogeneous Blockchains using Smart Contracts. In Proceedings of the Future Technologies Conference (FTC), Vancouver, BC, Canada, 15–16 November 2017; pp. 73–81. [Google Scholar]
- Bharany, S.; Sharma, S.; Khalaf, O.I.; Abdulsahib, G.M.; Al Humaimeedy, A.S.; Aldhyani, T.H.H.; Maashi, M.; Alkahtani, H. A Systematic Survey on Energy-Efficient Techniques in Sustainable Cloud Computing. Sustainability 2022, 14, 6256. [Google Scholar] [CrossRef]
- Nizamuddin, N.; Salah, K.; Azad, M.A.; Arshad, J.; Rehman, M. Decentralized document version control using ethereum blockchain and IPFS. Comput. Electr. Eng. 2019, 76, 183–197. [Google Scholar] [CrossRef]
- Bharany, S.; Kaur, K.; Badotra, S.; Rani, S.; Kavita; Wozniak, M.; Shafi, J.; Ijaz, M.F. Efficient Middleware for the Portability of PaaS Services Consuming Applications among Heterogeneous Clouds. Sensors 2022, 22, 5013. [Google Scholar] [CrossRef]
- Guo, R.; Shi, H.; Zhao, Q.; Zheng, D. Secure Attribute-Based Signature Scheme With Multiple Authorities for Blockchain in Electronic Health Records Systems. IEEE Access 2018, 6, 11676–11686. [Google Scholar] [CrossRef]
- Bharany, S.; Badotra, S.; Sharma, S.; Rani, S.; Alazab, M.; Jhaveri, R.H.; Gadekallu, T.R. Energy efficient fault tolerance techniques in green cloud computing: A systematic survey and taxonomy. Sustain. Energy Technol. Assess. 2022, 53, 102613. [Google Scholar] [CrossRef]
- Dias, J.P.; Reis, L.; Ferreira, H.S.; Martins, Â. Blockchain for access control in e-health scenarios. arXiv 2018, arXiv:1805.12267. [Google Scholar]
- Bharany, S.; Sharma, S.; Frnda, J.; Shuaib, M.; Khalid, M.I.; Hussain, S.; Iqbal, J.; Ullah, S.S. Wildfire Monitoring Based on Energy Efficient Clustering Approach for FANETS. Drones 2022, 6, 193. [Google Scholar] [CrossRef]
- Fukumitsu, M.; Hasegawa, S.; Iwazaki, J.; Sakai, M.; Takahashi, D. A proposal of a secure P2P-type storage scheme by using the secret sharing and the blockchain. In Proceedings of the 2017 IEEE 31st International Conference on Advanced Information Networking and Applications (AINA), Taipei, Taiwan, 27–29 March 2017; pp. 803–810. [Google Scholar]
- Pãnescu, A.T.; Manta, V. Smart Contracts for Research Data Rights Management over the Ethereum Blockchain Network. Sci. Technol. Libr. 2018, 37, 235–245. [Google Scholar] [CrossRef]
- Dai, M.; Zhang, S.; Wang, H.; Jin, S. A Low Storage Room Requirement Framework for Distributed Ledger in Blockchain. IEEE Access 2018, 6, 22970–22975. [Google Scholar] [CrossRef]
- Nizamuddin, N.; Hasan, H.; Salah, K.; Iqbal, R. Blockchain-Based Framework for Protecting Author Royalty of Digital Assets. Arab. J. Sci. Eng. 2019, 44, 3849–3866. [Google Scholar] [CrossRef]




| S/N | Author | Methods | Result | Limitations |
|---|---|---|---|---|
| 1 | Zhang et al. [8] | Digital signature algorithm | The authors proposed DSA to mitigate fraudulent assault. | Only digital signature was used. |
| 2 | Burr [10] | SHA-1 and SHA-2 | The study concluded that realistic threats to SHA-2 hash functions remain impossible in the next decades. | The study only protects the integrity of data but does not properly secure the data. |
| 3 | Acharya et al. [11] | Analyzed some well-known cryptographic algorithms | The study noted that the power of cryptography is in the key selection. | The study lacks a proper way to ensure complete data security. |
| 4 | Saleh and Meinel [12] | HPISecure was used to secure the HTTP client. | The study recommends using a coordinator for key management. | The drawback of this research is that the client must install the program on each computer where it will be used. |
| 5 | Haque et al. [17] | AES, RC4, Blowfish, CAST, 3DES, Twofish, DSA, and ElGamal | The effectiveness of an algorithm depends on execution time and lower memory usage requirement. | The study only compares the computational time of the selected algorithms. |
| 6 | Dijesh et al. [18] | Multilayer encryption algorithm RSA and Fernet cipher encryption algorithms | The method used to decrease fraudulent activities easily and effectively over the internet. | The study recommends a more efficient algorithm to secure online transactions. |
| 7 | Hamza and Al-Alak [19] | KCMA for key generation (ECC, RSA, ElGamal) with SHA-1 and SHA-2 | SHA-2 was the best as compared with XOR. | The study only compares the key generation of encryption algorithms with the hashing function. |
| S/N | File Size (Kb) | RSA | ElGamal |
|---|---|---|---|
| Encryption Time (ms) | Encryption Time (ms) | ||
| 1 | 10 | 95 | 3520 |
| 2 | 15 | 256 | 4340 |
| 3 | 20 | 312 | 6689 |
| 4 | 25 | 476 | 7311 |
| 5 | 30 | 499 | 7834 |
| 6 | 35 | 561 | 8372 |
| 7 | 40 | 606 | 9161 |
| 8 | 50 | 1094 | 13,215 |
| 9 | 100 | 2136 | 19,359 |
| 10 | 200 | 4229 | 44,689 |
| Size (Kb) | RSA | ElGamal | |
|---|---|---|---|
| Decryption Time (ms) | Decryption Time (ms) | ||
| 1 | 10 | 3428 | 637 |
| 2 | 15 | 5207 | 975 |
| 3 | 20 | 7809 | 1233 |
| 4 | 25 | 9832 | 1807 |
| 5 | 30 | 12,692 | 2645 |
| 6 | 35 | 16,325 | 3293 |
| 7 | 40 | 18,593 | 3990 |
| 8 | 50 | 23,986 | 4525 |
| 9 | 100 | 35,479 | 6829 |
| 10 | 200 | 42,708 | 9968 |
| File Size (Kb) | RSA Signature Generation | RSA without SHA-256 | ElGamal Signature Generation | ElGamal without SHA-256 | |
|---|---|---|---|---|---|
| Time Taken (ms) | Time Taken (ms) | Time Taken (ms) | Time Taken (ms) | ||
| 1 | 10 | 485 | 2223 | 136 | 381 |
| 2 | 15 | 469 | 3405 | 139 | 602 |
| 3 | 20 | 484 | 4448 | 145 | 823 |
| 4 | 25 | 493 | 5683 | 138 | 1057 |
| 5 | 30 | 464 | 6944 | 147 | 1346 |
| 6 | 35 | 473 | 8073 | 134 | 1871 |
| 7 | 40 | 486 | 9299 | 136 | 2018 |
| 8 | 50 | 493 | 10,601 | 146 | 2667 |
| 9 | 100 | 496 | 18,886 | 131 | 3243 |
| 10 | 200 | 481 | 23,981 | 136 | 4036 |
| File Size (KB) | RSA Signature Verification Time Taken (ms) | RSA without SHA-256 (ms) | ElGamal Signature Verification (ms) | ElGamal without SHA-256 (ms) | |
|---|---|---|---|---|---|
| 1 | 10 | 15 | 63 | 177 | 827 |
| 2 | 15 | 15 | 66 | 189 | 1281 |
| 3 | 20 | 12 | 69 | 189 | 1630 |
| 4 | 25 | 14 | 76 | 194 | 2057 |
| 5 | 30 | 15 | 77 | 165 | 2718 |
| 6 | 35 | 15 | 82 | 167 | 3152 |
| 7 | 40 | 19 | 87 | 188 | 3770 |
| 8 | 50 | 15 | 98 | 190 | 4234 |
| 9 | 100 | 21 | 103 | 179 | 5141 |
| 10 | 200 | 25 | 122 | 199 | 6089 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adeniyi, E.A.; Falola, P.B.; Maashi, M.S.; Aljebreen, M.; Bharany, S. Secure Sensitive Data Sharing Using RSA and ElGamal Cryptographic Algorithms with Hash Functions. Information 2022, 13, 442. https://doi.org/10.3390/info13100442
Adeniyi EA, Falola PB, Maashi MS, Aljebreen M, Bharany S. Secure Sensitive Data Sharing Using RSA and ElGamal Cryptographic Algorithms with Hash Functions. Information. 2022; 13(10):442. https://doi.org/10.3390/info13100442
Chicago/Turabian StyleAdeniyi, Emmanuel A., Peace Busola Falola, Mashael S. Maashi, Mohammed Aljebreen, and Salil Bharany. 2022. "Secure Sensitive Data Sharing Using RSA and ElGamal Cryptographic Algorithms with Hash Functions" Information 13, no. 10: 442. https://doi.org/10.3390/info13100442
APA StyleAdeniyi, E. A., Falola, P. B., Maashi, M. S., Aljebreen, M., & Bharany, S. (2022). Secure Sensitive Data Sharing Using RSA and ElGamal Cryptographic Algorithms with Hash Functions. Information, 13(10), 442. https://doi.org/10.3390/info13100442








