Abstract
In natural language generation, word ordering is the task of putting the words composing the output surface form in the correct grammatical order. In this paper, we propose to apply general learning-to-rank algorithms to the task of word ordering in the broader context of surface realization. The major contributions of this paper are: (i) the design of three deep neural architectures implementing pointwise, pairwise, and listwise approaches for ranking; (ii) the testing of these neural architectures on a surface realization benchmark in five natural languages belonging to different typological families. The results of our experiments show promising results, in particular highlighting the performance of the pairwise approach, paving the way for a more transparent surface realization from arbitrary tree- and graph-like structures.
1. Introduction
Natural language generation (NLG) is the computational process of producing natural language from a formal structure representing some information. The input structure can be of varying format, composition, and level of abstraction. Indeed, NLG systems exist that take input structures ranging from numeric tables to syntactic trees, to abstract representations of meaning. NLG is, conceptually, the inverse process to natural language understanding (NLU), where the input is well-defined as a text or speech segment. Just as the input to NLG, the output of NLU may vary in terms of complexity and scope of the analysis, but in general it is a data structure containing several types of semantic information. For instance, the classical Montague semantic analysis produces predicate–argument recursive structures expressing subject–predicate–object relations [1]. Another example, one that uses statistics for merging substructures, is abstract meaning representation (AMR), where the final structure is a directed acyclic graph [2]. In contrast, modern commercial dialog systems, such as Google Dialogflow, often produce simpler, non-recursive semantics structures (https://cloud.google.com/dialogflow/es/docs/basics, accessed on 17 August 2021).
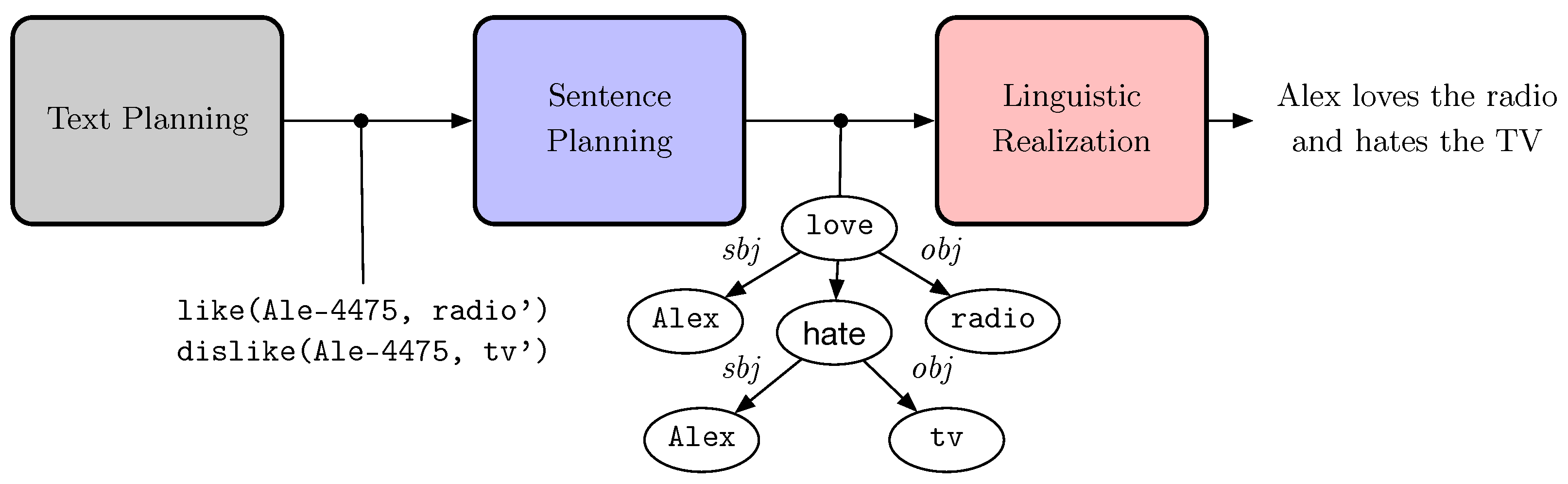
In NLG, the level of abstraction and the format of the input depend on several factors, including specific goals and application scenarios. Among the semantic formalisms that have been used in literature as input to NLG models, we find subject–predicate–object triples deriving from the Semantic Web [3], AMR structure [4], discourse representation graphs [5], and tables [6,7]. From a historical perspective, NLG has been approached in several different ways, either tackling single subtasks or attempting at solving the NLG problem in its entirety from input to surface form. Reiter and Dale [8] defined the de facto standard pipeline of NLG tasks, which paved the way for most NLG works thus far. The classical macro-steps of the standard NLG pipeline are text planning, sentence planning, and linguistic realization (Figure 1), each composed of a number of subtasks.
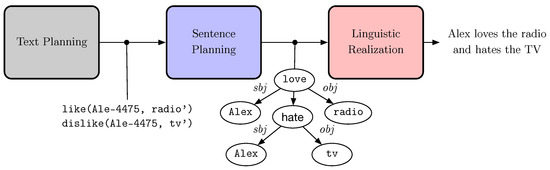
Figure 1.
The standard NLG three macro-steps architecture.
At a high level, text planning starts from (numeric or symbolic) data to produce structures containing rhetoric information. Sentence planning uses this intermediate structure for producing predicate–arguments and lexical information. Finally, linguistic realization uses the information produced in the previous steps to generate correct and fluent output in a target natural language. The three macro-steps of NLG can be approached with different models that can be based on rules or on statistics [9].
Surface realization (SR) is one of the main tasks involved in the linguistic realization. SR focuses on the final stage of the pipeline, involving the production of natural language sentences and longer documents from formal abstract representations. The input to the SR step is assumed to come from an external source or from a previous step of the pipeline, and it contains all the necessary information to create the final natural language output. Generating a correct and fluent output in a target natural language is the main responsibility of the SR component. Many subtasks can take place to support SR. Among these, for instance, we find morphological inflection (producing the correct word forms from input lemmas and syntax) and word ordering (putting the words in the right syntactic order). Word ordering is particularly important towards a successful SR, because an incorrect word order could lead to an unintelligible “word salad”, from which the meaning is not recoverable.
Word ordering is also the main focus of this article, where the problem is approached by means of ranking algorithms in a supervised machine learning framework. We build on top of the work that led to the participation to two editions of the Surface Realization Shared Task [10,11,12] (SRST), organized in the context of the Multilingual Surface Realization Workshop. In particular, we concentrate on the task of word order prediction. In the present work, the attention is focused on the application of neural learning-to-rank approaches to the word-ordering problem. We extensively test this approach on a multilingual benchmark for SR from syntactic dependency structures.
The three editions of SRST consider the surface realization of universal dependency (UD) trees, i.e., syntactic structures where the words of a sentence are linked by labeled directed arcs [13]. In particular, UD represents natural language syntax with trees where each node is a word. The labels on the arcs indicate the syntactic relation holding between each word and its dependent words. Table 1 shows an example of the UD tree in CONNL format. Besides syntactic relations, UD trees are typically augmented with lexical and morphological information, such as the part of speech, gender, number, and other features at the word level (For details on the annotation of universal dependencies see the documentation on the project’s website: http://universaldependencies.org/guidelines.html, accessed on 17 August 2021) Indeed, many approaches proposed in SRST exploit the tree format of the input and, especially in the last edition, achieved superb results [12].

Table 1.
Universal dependency tree for the Italian sentence “Numerose sue opere contengono prodotti chimici tossici.” (“Many of his works contain toxic chemicals.”).
In this paper we follow a different direction: in order to have a more general algorithm for word ordering, we do not exploit the tree format of the input, instead, we apply a more general learning-to-rank approach. In [14], a method based on splitting the SR task into word order and morphology realization is applied to structures encoding formal representations of the meaning of natural language sentences. In particular, the meaning representations are discourse representation graphs [5], a lossless transformation of discourse representation structures (DRS) from discourse representation theory [15]. DRSs are recursive structures, whereas DRGs encode the same meaning “flattened” into a non-recursive structure, which is more apt to be employed in supervised machine learning contexts. DRGs are directed acyclic graphs (DAG). The learning-to-rank method of Basile [14], as well as the one we propose in this work, can be applied without further adaptation to this kind of structures.
Contributions and Outline
In this paper, we explore the role of ranking algorithms with respect to word ordering, and, by extension, to natural language generation. The two main new contributions are:
- We formalize three deep neural models implementing pointwise, pairwise, and listwise learning-to-rank approaches to word ordering, with varying network architectures. These methods represent the neural evolution of existing methods from the literature.
- We compare the performances between the three neural learning-to-rank algorithms in the context of surface realization. In particular, we present the results of an experimentation carried out on five languages from different typological families.
Note that some ideas expressed in this paper have been previously presented in some workshop papers [14,16,17,18]. The idea to use the ListNet algorithm for a word-ordering task has been originally proposed in [14] in the context of realization from formal logical structures. This idea has been adapted to the context of the realization from an (unordered) dependency tree in [16]. Both these works adopt a simple shallow neural implementation (i.e., an architecture with no hidden layer) of ListNet. In later works, the same identical shallow neural architecture of [16] has been optimized for Italian [17] and tried on some other languages [18]. To summarize, in this paper we employ deep neural architectures (i.e., with at least one hidden layer) and experiment with pointwise, pairwise, and listwise algorithms, whereas all the previous work proposed (i) only a shallow neural architecture, and (ii) experimented only with the listwise algorithm.
The rest of the paper is organized as follows. In Section 2 we describe the state-of-the-art and recent advancements in word ordering as part of the surface realization task; Section 3 describes our proposed methodology, that is a neural-network-based system implementing three distinct ranking algorithms; Section 4 describes a number of experiments on the proposed neural architecture; Section 5 closes the paper by summing up the current state of our research and discussing future development.
2. Related Work
The primary goal of this paper is the application of ranking algorithms to the task of word ordering. We first discuss the main ranking algorithms related to our approach (Section 2.1), then we report the main approaches to word ordering from the NLG literature (Section 2.2).
2.1. Algorithms for Ranking
The learning-to-rank task is ubiquitous in information retrieval. It may be informally defined as learning the ordering of the items in a list of n documents, each representing a relevant object in the application at hand, such as a web page or a job candidacy. More formally, a dataset is given where each is a feature vector and s are the labels representing the position of a document in the query . The task is then to learn a function f that computes a partial order of the documents.
Ranking algorithms may be derived from well-known classifiers such as support vector machines (SVMs) [19] and decision trees [20]. Furthermore, ranking algorithms may be categorized according to how many documents are considered during the cost function computation. Pointwise methods consider each document individually in a setting that is similar to classification. Various algorithms may be employed here, such as logistic regression [21] and boosting [22]. Pairwise methods consider instead pairs of documents that are compared to learn which of the two is the more relevant for the query at hand (see, e.g., RankNet [23] and Cao et al.’s adaptation of SVM to information retrieval [19]). Lastly, listwise algorithms are able to consider the whole list of documents in the query during the computation of the cost function [24,25]. Listwise rankers are commonly thought to be superior to pairwise and pointwise methods, but the evaluation of the loss function and their cost function is often prohibitively expensive to compute (see, e.g., the discussion in Cao et al. [24]); however, Köppel et al. have recently found that the pairwise neural method RankNet may be generalized to be competitive with listwise rankers in terms of performance and efficiency [26]. We discuss how to implement listwise, pairwise, and pointwise rankers in a neural network in Section 3.2.1, Section 3.2.2 and Section 3.2.3, respectively.
2.2. The Word-Ordering Task in NLG
The order of words into a sentence has a fundamental importance for communicating the correct meaning from the speaker to the hearer. A trivial example are the simple sentences Mary loves John and John loves Mary, which have the same three words but have a total different meaning. Moreover, the studies on the complexity of natural languages consider the word order as a fundamental linguistic feature for modeling the syntax of a specific language [27].
The task of word ordering has a long history in NLG [9]. Surface realizers can order words by using both rule-based and statistical approaches, and these general approaches can be mixed in several ways. The constraints on the word order can be encoded formally in the production rules of a generative grammar [28,29] or as more general symbolic constraints in the form of programming language constructions [30], and many different generative grammar formalisms have been proposed to model the natural languages generative power (e.g., [31]). In all these approaches, very often the (generative or programming) rules have been manually designed; however, in the case of generative rules encoded into grammars, a number of studies tried to learn them from large treebanks datasets, i.e., from collections of syntactically annotated sentences [32,33].
A different approach has been applied by the HALogen system [34], which propose a two-step process. In the first overgeneration step, HALogen builds a very large number of possible sentences by using several (hundreds) general hand-written rules. In the second ranking step, HALogen scores all the generated sentences by using n-grams models. Another statistical approach with syntax has been adopted by [35], where a discriminative “learning-guided search framework, based on best-first search” has been applied. They consider different kind of syntactic constraints on the bag of words in input. When these constraints can be formulated as a dependency tree, their system works as a tree linearizer.
More recently, the neural tsunami in NLP [36] shocked the field of NLG too, and a number of works related to the task of neural surface generation have been proposed. In the specific case of (neural) large language models, the generation of free texts in response to arbitrary prompts raised a big hype in the whole artificial intelligence community [37]. More specifically, a number of neural architecture have been proposed for the specific task of word ordering assuming different input formats [38].
In order to shed light on the performances of word ordering and morphology inflection from syntactically specified structures, in the last years the NLG community organized four editions of the surface realization shared task (SRST), initially for English [39] and later on multilingual corpora [10,11,12]. The SRSTs concentrate on the NLG subtask of surface realization and so they contain two distinct subtasks: word ordering and morphology inflection.
The main idea in these shared tasks was to use real data annotated with dependency syntax deriving from treebanks. While the first edition proposed English input data produced converting the Penn Treebank, the last three editions used multilingual input data produced by the Universal Dependency (UD) project (https://universaldependencies.org/, accessed on 17 August 2021). In particular, the organizers of the SRSTs [10,11,12] formalize the task of word ordering as the production of a sequence of words starting from an unordered typed dependency tree. So, the participants could use the original morphological and syntactic annotation of each word with the exception of the information on the (real) position of the word in the sentence. Moreover, the organizers of SRSTs proposed both deep and shallow lines of the task. In the the deep version, the task assumes as input an abstract representation of original universal dependency treebank of the UD project. In contrast, the shallow version of the task assumes, as input, exactly the original version of the treebank: an example of this format is reported in Table 1. Note that, in the remaining part of this paper, we consider only the shallow version of SRST.
The third edition of SRST reported very good results from various participants [12]. In particular, the system described in [40] produced impressive results by using a Tree-LSTM neural architecture that modeled the local word reordering task as a travel salesman problem. In the following Section, we will report the results of [40] as the state-of-the-art for evaluating the results of the neural word-ordering system proposed in this paper, which is an elaboration of the DipInfo-Unito Realizer that participated to the second and third edition of SRSTs [16,18].
3. Predicting Word Ordering with General Ranking Algorithms
The recursive nature of the natural languages allows for the application of recursive techniques and algorithms in the field of NLP. For instance, in the case of the parsing task, most of the classical algorithms (e.g., the CYK parsing algorithm) are based on the fact that the complete syntactic tree of a sentence can be derived by composing together small subtrees. This can be seen as an application of the well-known algorithmic design paradigm of divide-and-conquer. We apply the same divide-and-conquer paradigm in the context of NLG. We formulate the task of predicting the correct order of words in a sentence in terms of reordering the subtrees in its syntactical structure. At a high level, the algorithm works in three steps:
- Splitting the unordered tree into single-level unordered subtrees.
- Predicting the local word order for each subtree by using a ranking algorithm.
- Recomposing the single-level ordered subtrees into a single multi-level ordered tree to obtain the global word order.
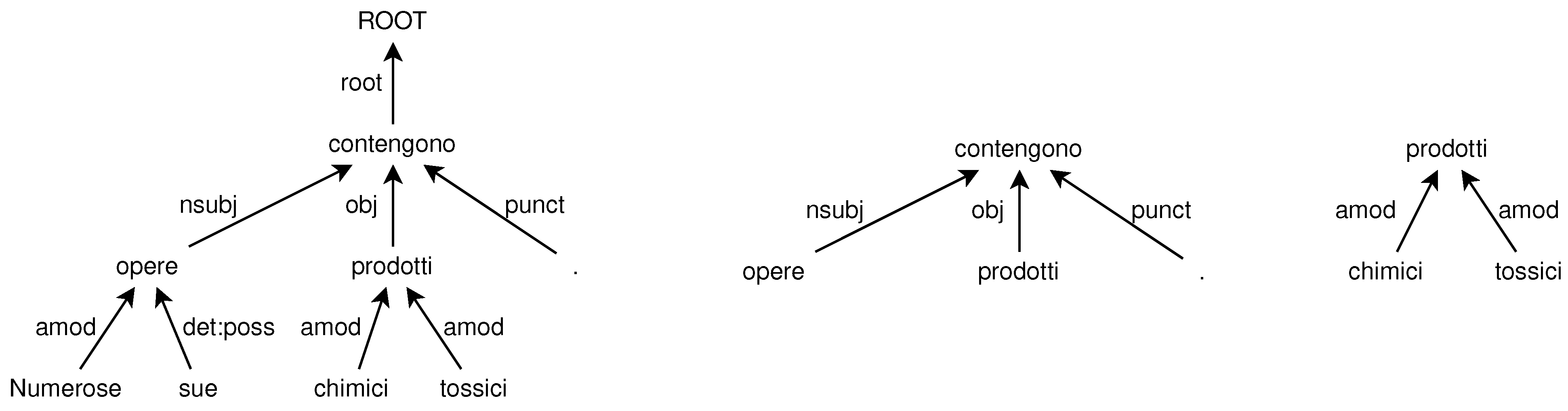
The first step splits the input UD tree into several single-level unordered trees composed by a head (the root) and all its dependents (the children), similarly to [41]. An example is shown in Figure 2 where the (unordered) tree representing the Italian sentence “Numerose sue opere contengono prodotti chimici tossici.” (left side of the figure) is broken into subtrees limited to one-level dependencies (two of such subtrees, as examples, are shown in the right side of the figure). The head and the dependents of each subtree form an unordered list of lexical items. We leverage the flat structure of the subtrees to extract structures that are suitable as input to the learning-to-rank approach we propose, carried out by the next step of the pipeline.
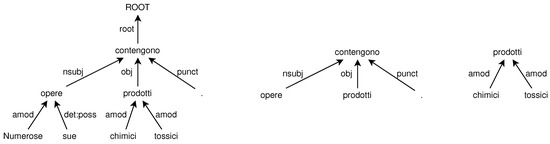
Figure 2.
Tree corresponding to the Italian sentence “Numerose sue opere contengono prodotti chimici tossici.” (“Many of his works contain toxic chemicals.”), on the left, and two subtrees extracted from the main tree, on the right.
The second step of the algorithm predicts the relative order of the head and the dependents of each subtree with a learning-to-rank approach, detailed in the rest of this section.
The third step of the word-ordering algorithm reconstructs the global order (at the sentence level) from the local order of the single-level trees. Note that this approach works under the hypothesis of projectivity. The current approach cannot predict the correct word order for non-projective sentences. If the local reordering of the one-level tree with root h and children produces an order of nodes , the hypothesis of projectivity implies that in the global word order the position of all the children of the node will be after the position of the node and before the position of the node . Under this hypothesis, the node global order (O) of a k-level tree rooted in h and with children can be written in terms of the local order as:
where is the permutation learned by the ranking algorithm from the training set and parametrized over the feature set.
The rest of this section described the central step of the algorithm in greater detail, organized as follows: first we give some details on the conversion of the lexical items belonging to a subtree into vectors (Section 3.1); then, we describe the three ranking algorithms experimented in this paper, namely a listwise (Section 3.2.1), a pairwise (Section 3.2.2), and a pointwise (Section 3.2.3) approach.
3.1. Feature Encoding
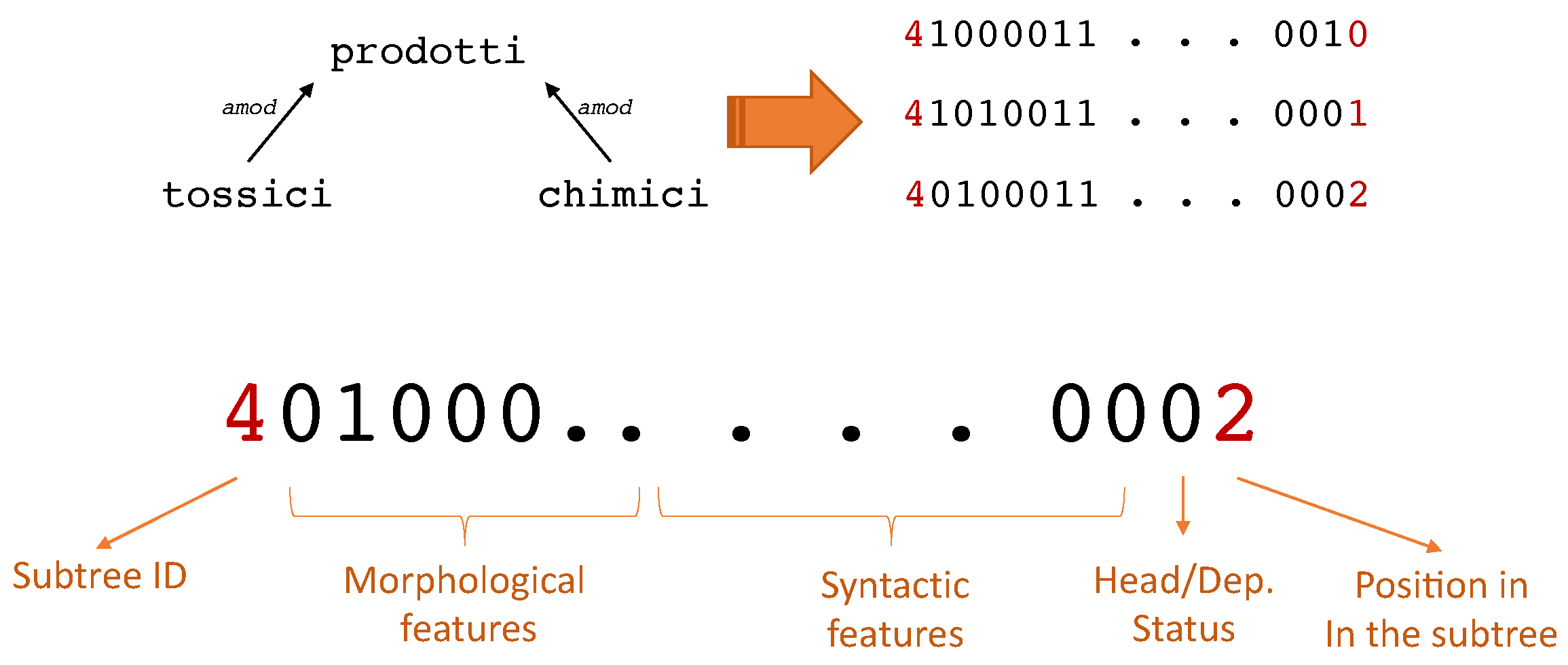
A key step of the algorithm for word-ordering concerns the way in which we encode the words in a subtree as a sequence of numerical features. We manually engineer the features that will be used by the ranking learning algorithms: each individual subtree is converted into a sequence of vectors representing each word in a subtree (Figure 3). The number of vectors is therefore equal to the number of the children nodes, plus one vector representing the parent node. We identify three kinds of features, namely morphological, syntactic, and positional.
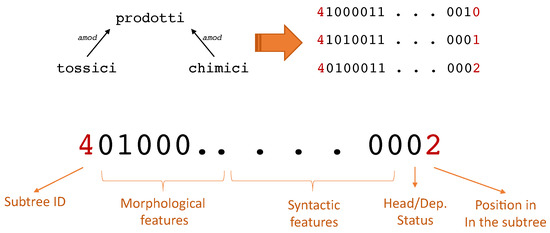
Figure 3.
The conversion of a subtree into a sequence of vectors.
The morphology is modeled by several word-level features encoded as one-hot vectors: the universal POS tag, the treebank-specific POS tag, and the treebank-specific morphological features. It is worth mentioning that treebank-specific morphological features are specific properties of the language under analysis. Consequently features vectors change in length depending on the language being analyzed. For instance, the Italian treebank contains a boolean feature (clitic) representing particles related to the reflexive nature of some syntactic relations (https://universaldependencies.org/treebanks/it_isdt/it_isdt-feat-Clitic.html, accessed on 17 August 2021). This feature is represented with one bit in the feature vector. Another example for Italian is the person feature, which assumes three distinct numeric values, namely 1, 2, or 3 and is consequently represented by two bits in the morpphological part of the feature vector. Other languages need not model these attributes nor do they need to model them with the same number of attributes.
For the representation of the lexical items, we implement two different encodings. Function words, such as articles, pre/post-positions, and conjunctions, are encoded as one-hot bag-of-words vectors since they belong to a closed class of items. In contrast, content words (nouns, verbs, adjectives, and adverbs) are represented by language-specific, pre-trained word embeddings. In particular, we employ the multilingual model fastText [42], which encodes words as 64-dimensional vectors with real values between 0 and 1. Moreover, fastText uses sub-word information, allowing us to encode out-of-vocabulary terms, e.g., misspelled words in the treebanks.
For the syntactic part of the encoding, we again use one-hot representations of the dependency relations connecting the dependents to the head. Note that multilingual UD representation allows for a rich taxonomy of dependencies relations (https://universaldependencies.org/u/overview/syntax.html#the-taxonomy-of-typed-dependencies, accessed on 17 August 2021), but each treebank uses only a limited portion of this taxonomy. For instance, since the Italian treebank uses only 45 different dependency relations, the syntactic part of a token from this treebank will be encoded as one-hot sequence of 45 bits.
The feature vector is completed with (1) the head/dependent status of the word in the subtree, (2) the identifier of the subtree, and (3) the position of the word in the sub-sentence corresponding to the subtree. The head/dependent status of the word, that is, the information about whether the word is the parent of the single-level subtree or it is a child, is encoded as a boolean feature in one bit of the feature vector. Both the identifier and the position of the word related to the subtree are encoded as integers. These last two features are not directly fed in input to the neural network, but they are both used to compute the loss function that guides the learning of the network.
We report the lengths of the different language encoding vectors in Table 2. Notably, the significantly different length of the Chinese feature vectors is due to the one-hot encoding of function words, which constitute a larger closed class in this language. Moreover, we note that the different lengths of the syntactic features encoding is due to the different number of syntactic relations used by each treebank, which itself is a choice that is both subjective (being related to the preferences of the annotators) and objective (due to the characteristics of the language).

Table 2.
The lengths of vector encoding for the five languages studied. Note that each treebank has a different number of morphological and syntactic features.
An implementation of the feature encoding for the word-ordering module of our architecture is available online (https://github.com/alexmazzei/ud2ln/blob/master/ud2HVR-NO21.py, accessed on 17 August 2021).
3.2. Neural Implementation of Ranking Algorithms
In the following, we describe the three neural ranking algorithms we employ in this work. To fully test the capabilities of ranking algorithms in the field of NLG and surface realization in particular, we chose one representative from each of the main families of ranking methodologies. Thus, in the following we describe ListNet [24], a listwise neural ranker, DirectRanker [26], a pairwise method, and a simple pointwise neural ranker.
3.2.1. Neural Listwise
We employ the listwise learning-to-rank algorithm ListNet [24]. The limited cardinality of the lists to rank makes it advantageous to use a listwise approach without an unmanageable increase in the computation load. In this application, each “list” is a linearized subtree as described in Section 3.1.
ListNet is a generalized version of the pairwise learning-to-rank algorithm RankNet [23]. ListNet employs a listwise loss function based on the top-one probability, i.e., the probability of an element being the first one in the ranking. The top-one probability model approximates the permutation probability model that assigns a probability to each possible permutation of an ordered list. This approximation is necessary to keep the problem tractable by avoiding the exponential explosion of the number of permutations. Formally, the top-one probability of an object j is defined as
where is the probability of the permutation given a list of scores which are functions of the position of the elements in the list [23]. In other words, the top-one probability is the sum of the probabilities of all the possible permutations of n objects (denoted as ) in which j is the first element.
However, we use a formulation which is equivalent, but more efficient to compute:
where is the score of the j-th element of a list, and is an increasing and strictly positive function [23]. We use the exponential function for this purpose.
Considering two permutations of the same list y and z (in the case of the SR task, the predicted order and the reference order), their distance is computed using cross-entropy. The cross-entropy-based distance measure and the top-one probabilities of the list elements are used to compute the loss function:
where is a regularization term and is the set of parameters of the network. Note that ListNet does not need a special mechanism (such as recursion or sequence windowing) to handle variable-length sequences. Each word in a sentence (list) is assigned a top-one probability value, which is compared to the ground truth ordering. The loss function can then be minimized via stochastic gradient descent.
To provide a concrete example, we consider one of the subtrees from the syntax tree in Table 1, in particular, the one rooted at the noun prodotti with two adjectives as children: chimici and tossici. Linearizing the tree as explained in the beginning of this section, we obtain the list of three tokens prodotti chimici tossici, whose order is given as ground truth by the global word order. Employing scores that are the opposite of the position of the word in the list, that is, the i-th word in a list of n words has score , the three words in the example have the scores: 3 (prodotti), 2 (chimici), and 1 (tossici), respectively. Their respective top-one probability, according to the formula are ∼0.09 (prodotti), ∼0.24 (chimici), and ∼0.66 (tossici).
In previous work dealing with SR [14], a linear neural network model was employed in conjunction with the listwise loss defined above. Here, we opt for a more general approach that employs multiple hidden layers and non-linearities as their activation function. We describe the details of our software implementation and hyperparameter search strategy in Section 4.3.
3.2.2. Neural Pairwise
We include experiments that employ the pairwise ranking method DirectRanker [26]. As discussed previously, a pairwise learning-to-rank strategy performs a comparison between two documents, returning its belief on which one is the most relevant one. We chose to use a DirectRanker model, which has been shown to be competitive with listwise approaches on relevance and computation time. The DirectRanker relies on a siamese network architecture with shared parameters, similarly to RankNet [23]. A pair of documents is selected from the dataset and the more relevant one—which we assume in the following to be —is fed into the top network. In our setting, the more relevant document is the word appearing first in the sentence at hand. After feature extraction, the two documents’ neural features are subtracted to one another and fed into the last layer, which employs a single neuron with an antisymmetric, sign-conserving activation function and no bias term. The main idea here is to use the single output neuron to learn the difference in relevance between the two terms: A positive output represents the decision that the first document is more relevant; a negative output represents the opposite. It can be proven that this architecture defines a binary relation that is transitive, reflexive, and antisymmetric. Thus, it is able to learn a total quasiorder on the input feature space. For more details and a proof of this property we refer the reader to the original work by Köppel et al. [26].
A DirectRanker model may be trained via stochastic gradient descent over a loss function, which is computed as the mean squared error between the model output and the difference between relevance labels .
in which we also include a regularization term [26]. To better understand how the DirectRanker works, let us come back to the running example of the syntax subtree in Figure 1, which contains the list of tokens prodotti chimici tossici. Here, the pairwise loss may be computed over any ordered pair of tokens. The full list of possible pair is (prodotti, chimici), (prodotti, tossici), (chimici, tossici), and the relative are . Indeed, all these possible pairs can be used in the training of the network and this is one of the strengths of this approach: it is easy to generate many training samples starting from relatively few sequences.
3.2.3. Neural Pointwise
We also experimented with a neural pointwise method, i.e., a neural network that uses a single example as input . This method simply performs a regression task over each label which is the position of the word in a linearized subtree. We thus employed a mean squared error loss computed between the network output and the position label.
where a regularization term is also included. In our running example, which focuses on the subtree prodotti chimici tossici, the network is simply trying to predict , respectively. This method is simplistic, as it is possible (and even expected) that the same word can appear in a different subtree with a different position and thus a different label; however, we include the method in our experimentation so we can compare its performance with the more complex listwise and pairwise approaches.
4. Experiments
We tested our approach on five languages, namely English (EN), Spanish (ES), Italian (IT), Chinese (ZH), and Hindi (HI), in order to cover different typological families of languages. Note that Italian and Spanish are both neo-latin languages, but we decided to use both in our experiments in order to compare our findings with previous results [16]. In Table 3, we report some data on the treebank used in the experiments.

Table 3.
The five treebanks for English, Spanish, Hindi, Italian, and Chinese that have been used in the experimentation.
We ran the word-ordering systems on two GNU/Linux boxes, one sporting 4 Xeon CPUs (E5 family) running at 3.30 GHz for a total of 16 cores and 128 GB of RAM, and one virtualized box using 24 Xeon (Skylake) cores, 32 GB of RAM, and two NVIDIA Tesla T2 GPUs (16 GB of VRAM each). Part of the experiments have been run on the HPC4AI cloud infrastructure at the University of Torino [43].
We implemented the neural rankers using the TensorFlow library [44], version 2.3.1. Our implementation of all relevant steps in the experimentation may be found at https://github.com/Pibborn/neural-sr, accessed on 17 August 2021.
4.1. Pipelines
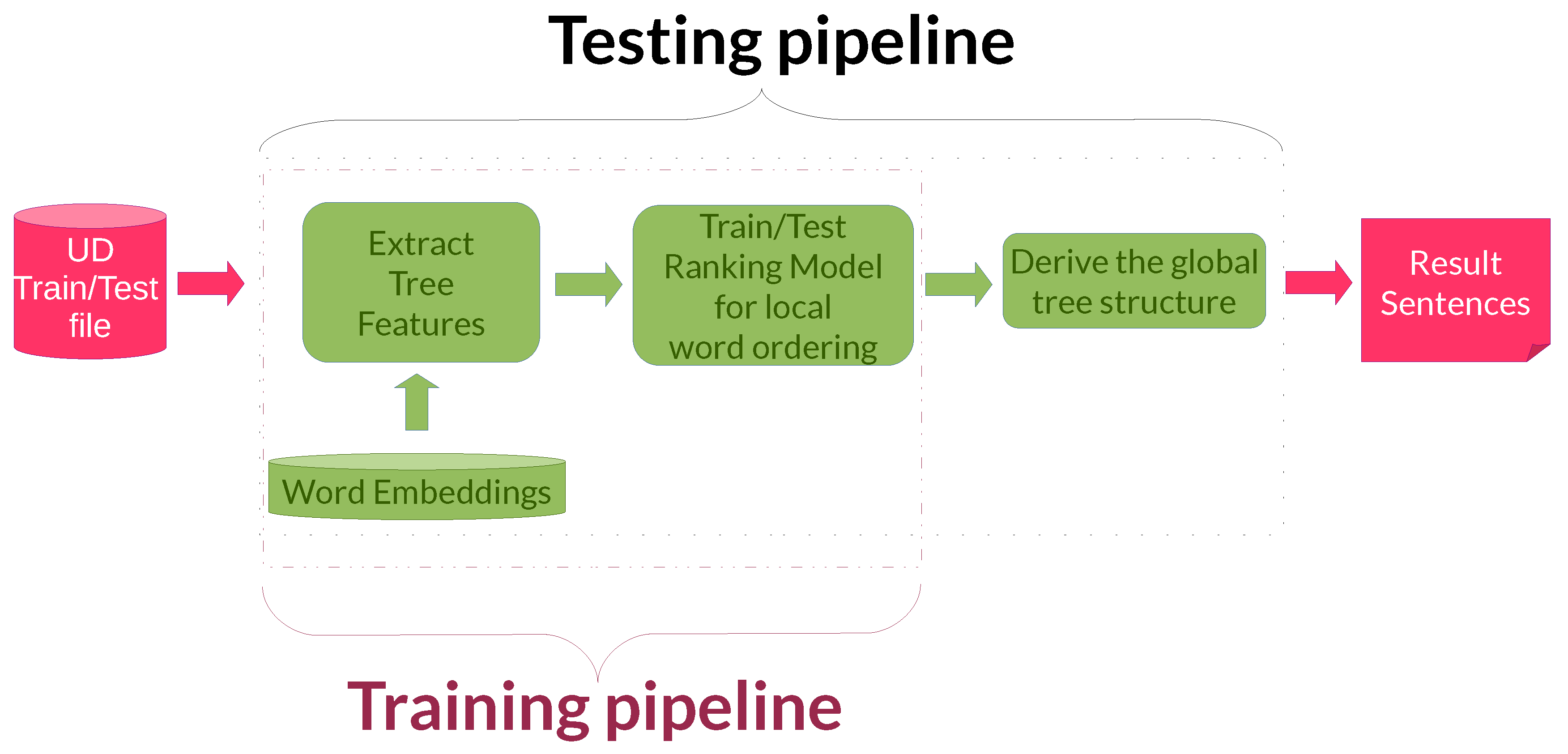
In contrast to the legacy system that inspired this work [16], the training and testing pipelines are very similar (see Figure 4). Indeed, in the experiments described in this paper we concentrate only on the word-ordering task and, as a consequence, we do not need to merge transformations arising from different subtasks.
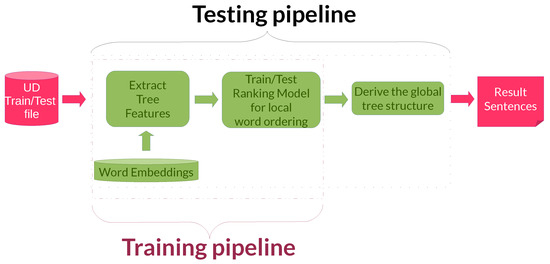
Figure 4.
The training and testing pipelines.
In the training pipeline, we created a specific file starting from the UD treebank training files. This file contains the vector representation of the features (word embeddings or one-hot encodings for function words, plus the representation of morphological features, see Section 3.1) and it is used to create the word order model by using the neural network architectures described in Section 3. The training phase produces a neural ranking model by considering only the local order of the various subtrees. In contrast, the final evaluation in the testing phase will be based uniquely on the produced sentence, that is, on the final reassembled complete tree.
We applied this training/testing pipeline separately for each of the tested languages.
4.2. Datasets
In order to investigate about the syntactic information contained in the universal dependency format and its appropriateness for the word-ordering task, we focused on information derived from the Universal Dependency project [13], with the only exception of the pre-compiled embeddings we used for the open-class words. Note that the rules of SRST 2018 and 2019 would not have allowed us to use external resources to train the surface realizer; however, embeddings and neural language models are among a small number of lexical resources which are explicitly allowed.
The task organizers provided twenty training files and twenty development files, derived from version 2.2 of the UD dataset for the eleven languages included in the shallow track. In particular, they provided modified versions of the original treebanks, where the information about the original word order was replaced by a random ordering and the original UD feature set was enriched with a new feature, namely the original_id containing the original position of the word in the sentence. For a number of specific parts of speech (e.g., punctuation), a feature lin is added, containing the original relative position of the word with respect to its head. Note that the lin feature, in contrast to the original_id feature, is present in the test file too. The idea behind the lin feature is to provide more information on word ordering for flat structures, as for instance in the case of conjunction, where there is no linguistic preference for a specific permutation (e.g., “…cats and dogs” versus “…dogs and cats”). In the following experiments, the lin feature was not employed. Rather, we employed version of the UD treebank files in their original form, since they contain both the gold local and global word order.
4.3. Hyperparameter Search
Our experimentation includes a hyperparameter search step, which we perform for each individual model (pointwise, pairwise, and listwise) and language treebank over an independent validation set. Specifically, we use the 60/20/20 (train/validation/test) split provided by the authors of the treebanks. Our search strategy employs a Bayesian black-box optimization algorithm, which optimizes the Kendall’s tau metric [45]:
where I is the indicator function returning 1 when its argument is true and 0 otherwise, sgn is the sign function, and range over the integers between 1 and the length n of the sequence. In practice, Kendall’s tau metric can be thought of as counting the number of concordant pairs in the rankings, subtracting the number of discordant pairs, and dividing by the binomial coefficient .
To compute the number of concordant pairs over a sentence, the neural ranker is first employed to obtain a list of position predictions where n is the number of words in the sentence at hand. These predictions are compared with the ground-truth ordering . Then, the pairs are formed. Two pairs and (with ) are concordant if it is true that or ; otherwise, the two pairs are discordant. Kendall’s tau metric can be thought of as a ranking correlation metric, where a perfect ranking obtains a score of 1 and the inverse ranking obtains a score of −1.
For performance reasons, during the hyperparameter search we opted to employ a subset of each training split (50,000 words) and a relatively short training time (60 epochs). This enabled us to perform a deeper search in hyperparameter space by shortening the computation time for each hyperparameter combination. Our best performing models for each language corpus were then trained on the full training split for 200 epochs. We report the list of hyperparameters searched in Table 4, and our best hyperparameters for each language corpus in Table 5. We relied on the Bayesian optimization strategy implemented in the Weights and Biases platform [46].

Table 4.
The list of hyperparameters considered in our search strategy. The learning rate is the stochastic gradient descent initial learning rate and is included as a [min; max] range; the same notation is used for the regularization parameter, noted as in Section 3.2.1, Section 3.2.2 and Section 3.2.3. Our strategy could also employ one of the four reported architectures in their hidden layers. Lastly, sigmoid and rectified linear units were considered as the activation functions for each hidden layer.

Table 5.
The best hyperparameters for each methodology and corpus found by our search strategy.
4.4. Results
Table 6 reports the scores of the systems presented in this paper, along with the official scores of the top-ranking systems from the shared task. The scores are computed in terms of three automatic metrics: BLUE, NIST, and DIST [10]. Moreover, the Subposition accuracy is a metric counting the number of exact positions computed in the single subtrees, and as a consequence can be computed only for methods based on ordering the single subtrees. The yellow lines report the best scores obtained for each specific language in the various editions of SRST [10,12], in particular: ADAPT (20b) is bidirectional recurrent neural network with long short term memory augmented the WikiText 103 and CNN stories corpora [12]; IMS (20a), (20b) is a bidirectional Tree-LSTM encoder architecture word ordering as a traveling salesman problem, that uses a biaffine attention model to calculate the bigram scores [40]; Tilburg-MT18 is a word ordering algorithm based on the neural machine translation paradigm [10]. Moreover, DipInfo-UniTo18 is the neural implementation of the listwise algorithm originally proposed in [16] and optimized in [17]. Note that all these scores have been computed by considering the output of both the (i) word ordering and (ii) morphology tasks, in contrast to our output that considers (i) the only word-ordering task.

Table 6.
The scores of the neural ranker system for English, Chinese, Hindi, Italian, and Spanish languages, in terms of the automatic metrics BLUE, NIST, and DIST and subposition accuracy.
An analysis of the results follows. All the ranking algorithms exhibit lower performance with respect to the state-of-the-art; however, note that our research is motivated by the generality of the ranking algorithms, that can be applied to different kinds of NLG input. In contrast, most of the state-of-the-art systems are specialized on the tree structure of universal dependency formalism, following the structure of the SR shared tasks.
Not surprisingly, the evaluation metrics are quite related to each other. Indeed, the simple subposition accuracy seems to be a good indicator of the performance of the global word ordering.
Another consideration arises from the comparison of the results in Table 6 with the dataset sizes in Table 3, suggesting that the performance of the various ranking algorithms does not correlate with the dataset size. We speculate that there are other linguistic features influencing the performance, e.g., average length of the sentences, or the complexity of the lexicon. Moreover, it seems that the length of input vectors does affect the final performance, as shown by the scores for Chinese, which is similar to other languages, while the vector representations for this language are significantly longer.
By comparing the performance of the proposed approaches, we see how the pairwise algorithm yields generally better results with respect to the listwise and the pointwise approaches. A possible explanation concerns the necessity of a larger dataset for a more complex algorithm. Another speculation is related to the linguistics of dependency relations, which models syntax as binary relations between words. In this view, the pairwise approach could capture the word order constraints arising from syntax more naturally. The performance of the pointwise approach is subpar with respect with the other approaches, which is not surprising considering that this algorithm has access to less information at the training time. The distance in terms of performance between the pairwise and the listwise approach is reduced when the size of the training data is larger, e.g., in the case of Spanish. This is because the inner working of the pairwise algorithm is akin to a data augmentation step, whose positive impact is less relevant in presence of more actual data; however, the pairwise approach fails to overcome the listwise approach in one case, namely Italian, where the effect of significant overfitting seems to be observed, which will be object of further investigation in future work.
Finally, we note the performance improvement of the current neural, multi-layer implementation of the listwise approach with respect to the original single-layer version proposed in [17].
5. Conclusions and Future Work
In this paper, we described a number of approaches to the task of word ordering in the broader context of natural language generation, and in particular the surface realization step. The approaches are based on the learning-to-rank paradigm, and we compare their performance among one another and with the state-of-the-art defined by the Surface Realization Shared Task competitions [10,11,12].
The proposed methods, while not reaching state-of-the-art performance, improve upon previous work with similar approaches [17,18]. More importantly, our methodology aims at creating transparent NLG pipelines, as opposed to end-to-end systems, where the outcome of each step can be analyzed and improved and. In particular, the main motivation of our research is the generality of ranking algorithms that, in contrast with most of state-of-the-art word orders, can be applied to very general input structures. We believe that two results of our research are important from an applicative point of view. First, we proved that it is straightforward to apply the learning-to-rank paradigm for word ordering. Following our design, one can easily implement a new NLG realizer for a new kind of input, even beyond unordered dependency trees as is the standard in most of the current state-of-the-art approaches. Second, we experimentally showed that the performances of pairwise and listwise approaches vary greatly depending on the dataset at hand and therefore their appropriateness should be evaluated on the specific language and training set.
We remark that the primary goal of this paper is to compare the performances of the pointwise, pairwise, and listwise neural algorithms for word ordering. These algorithms have different computational and model complexities and their performances are bound to be related to the size of the training set as well as to language specific linguistic features. To this regard, it is interesting to point out that the performances seem to be similarly good for the five languages we tested but that, with the available data, it would be a stretch to try to predict how the system would work on an unseen language. This is especially true for languages such as Japanese that do not belong to the four families of language studied in this paper.
The experimentation on five different treebanks showed that, quite surprisingly, the pairwise algorithm outperforms the listwise algorithm for English, Hindi, and Chinese; however, this picture is different for Spanish and Italian: for Spanish there is no difference in the performances of pairwise and listwise and for Italian the listwise performs better than pairwise. Since the Spanish treebank is the larger one with respect to the number of words, we can speculate that the advantage in performances of the pairwise model with respect to the listwise model decreases with the size of the training set; however, this hypothesis does not explain the behavior of the two models on the Italian treebank, where the overfitting phenomenon seen during the training could be related to specific treebank features (e.g., the semantic/pragmatic domain). In future work, we plan to repeat the experiments on different treebanks with the aim to correlate the performances of the ranking algorithms with the specific linguistic characteristics of the language families, as morphological inflection (e.g., agglutinative) or basic declarative sentence word ordering (e.g., SVO). The objective of this study would be to uncover correlations allowing one to predict in advance the performances of a specific ranking algorithm on a specific language family.
With respect to the problem of generalizing our approach to account for non-projective structure, we intend to develop our work in two directions. First, decomposing the original dependency tree into structures with a wider domain of locality. By following the direction by [31], we plan to model the prediction of local order with more complex structures. Second, as pointed out in ([14], Chapter 7), learning the global order of the words rather (or in addition to) their local order; however, learning the word order globally may impact the transparency of the system; therefore, a careful balance between performance and explainability must be achieved. On the other hand, global order may alleviate the problem of non-projective sentences, which is currently an issue with the local ordering approach.
Author Contributions
Conceptualization, A.M., M.C., R.E. and V.B.; Data curation, A.M.; Formal analysis, A.M., M.C., R.E. and V.B.; Investigation, A.M., M.C., R.E. and V.B.; Methodology, A.M., M.C., R.E. and V.B.; Software, A.M., M.C. and R.E.; Supervision, R.E.; Visualization, A.M. and V.B.; Writing—original draft, A.M., M.C., R.E. and V.B.; Writing—review & editing, A.M., M.C., R.E. and V.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not Applicable, the study does not report any data.
Acknowledgments
This work has been partially supported by the HPC4AI project funded by Regione Piemonte (POR FESR 2014-20-INFRA-P).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Montague, R. Universal Grammar; Wiley: Hoboken, NJ, USA, 1970; Volume 1974, pp. 222–246. [Google Scholar]
- Banarescu, L.; Bonial, C.; Cai, S.; Georgescu, M.; Griffitt, K.; Hermjakob, U.; Knight, K.; Koehn, P.; Palmer, M.; Schneider, N. Abstract meaning representation for sembanking. In Proceedings of the 7th Linguistic Annotation Workshop and Interoperability with Discourse, Sofia, Bulgaria, 8–9 August 2013; pp. 178–186. [Google Scholar]
- Gardent, C.; Shimorina, A.; Narayan, S.; Perez-Beltrachini, L. The WebNLG Challenge: Generating Text from RDF Data. In Proceedings of the 10th International Conference on Natural Language Generation, Santiago de Compostela, Spain, 4–7 September 2017; pp. 124–133. [Google Scholar] [CrossRef]
- Damonte, M.; Cohen, S.B. Structural Neural Encoders for AMR-to-text Generation. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, MN, USA, 2–7 June 2019; pp. 3649–3658. [Google Scholar] [CrossRef]
- Basile, V.; Bos, J. Aligning Formal Meaning Representations with Surface Strings for Wide-coverage Text Generation. In Proceedings of the 14th European Workshop on Natural Language Generation, Sofia, Bulgaria, 8–9 August 2013; p. 1. [Google Scholar]
- Chen, W.; Chen, J.; Su, Y.; Chen, Z.; Wang, W.Y. Logical Natural Language Generation from Open-Domain Tables. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 7929–7942. [Google Scholar] [CrossRef]
- Anselma, L.; Di Lascio, M.; Mana, D.; Mazzei, A.; Sanguinetti, M. Content Selection for Explanation Requests in Customer-Care Domain. In Proceedings of the 2nd Workshop on Interactive Natural Language Technology for Explainable Artificial Intelligence, Dublin, Ireland, 15–18 December 2020; pp. 5–10. [Google Scholar]
- Reiter, E.; Dale, R. Building Natural Language Generation Systems; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Gatt, A.; Krahmer, E. Survey of the State of the Art in Natural Language Generation: Core tasks, applications and evaluation. J. Artif. Intell. Res. 2018, 61, 65–170. [Google Scholar] [CrossRef]
- Mille, S.; Belz, A.; Bohnet, B.; Graham, Y.; Pitler, E.; Wanner, L. The First Multilingual Surface Realisation Shared Task (SR’18): Overview and Evaluation Results. In Proceedings of the First Workshop on Multilingual Surface Realisation, Melbourne, Australia, 19 July 2018; pp. 1–12. [Google Scholar] [CrossRef]
- Mille, S.; Belz, A.; Bohnet, B.; Graham, Y.; Wanner, L. The Second Multilingual Surface Realisation Shared Task (SR’19): Overview and Evaluation Results. In Proceedings of the 2nd Workshop on Multilingual Surface Realisation (MSR 2019), Hong Kong, China, 3 November 2019; pp. 1–17. [Google Scholar] [CrossRef]
- Mille, S.; Belz, A.; Bohnet, B.; Castro Ferreira, T.; Graham, Y.; Wanner, L. The Third Multilingual Surface Realisation Shared Task (SR’20): Overview and Evaluation Results. In Proceedings of the Third Workshop on Multilingual Surface Realisation, Barcelona, Spain (Online), 12 December 2020; pp. 1–20. [Google Scholar]
- Nivre, J.; de Marneffe, M.; Ginter, F.; Goldberg, Y.; Hajic, J.; Manning, C.D.; McDonald, R.T.; Petrov, S.; Pyysalo, S.; Silveira, N.; et al. Universal Dependencies v1: A Multilingual Treebank Collection. In Proceedings of the Tenth International Conference on Language Resources and Evaluation LREC 2016, Portorož, Slovenia, 23–28 May 2016. [Google Scholar]
- Basile, V. From Logic to Language: Natural Language Generation from Logical Forms. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 2015. [Google Scholar]
- Kamp, H. A Theory of Truth and Semantic Representation. In Truth, Interpretation and Information; Groenendijk, J., Janssen, T.M., Stokhof, M., Eds.; FORIS: Dordrecht, The Netherlands; Cinnaminson, NJ, USA, 1984; pp. 1–41. [Google Scholar]
- Basile, V.; Mazzei, A. The DipInfo-UniTo system for SRST 2018. In Proceedings of the First Workshop on Multilingual Surface Realisation, Melbourne, Australia, July 2018; pp. 65–71. Available online: https://aclanthology.org/W18-3609/ (accessed on 17 August 2021).
- Basile, V.; Mazzei, A. Neural Surface Realization for Italian. In Proceedings of the Fifth Italian Conference on Computational Linguistics (CLiC-it 2018), Berlin, Germany, 8 July 2018; pp. 1–6. [Google Scholar]
- Mazzei, A.; Basile, V. The DipInfoUniTo Realizer at SRST’19: Learning to Rank and Deep Morphology Prediction for Multilingual Surface Realization. In Proceedings of the 2nd Workshop on Multilingual Surface Realisation (MSR 2019), Hong Kong, China, 3 November 2019; pp. 81–87. [Google Scholar] [CrossRef]
- Cao, Y.; Xu, J.; Liu, T.Y.; Li, H.; Huang, Y.; Hon, H.W. Adapting Ranking SVM to Document Retrieval. In Proceedings of the 29th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Seattle, WA, USA, 6–11 August 2006; pp. 186–193. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 1189–1232. [Google Scholar]
- Cooper, W.S.; Gey, F.C.; Dabney, D.P. Probabilistic Retrieval Based on Staged Logistic Regression. In Proceedings of the 15th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Copenhagen, Denmark, 21–24 June 1992; pp. 198–210. [Google Scholar]
- Li, P.; Burges, C.J.C.; Wu, Q. McRank: Learning to Rank Using Multiple Classification and Gradient Boosting. In Advances in Neural Information Processing Systems; NIPC: Vancouver, BC, Canada, 2007; pp. 897–904. [Google Scholar]
- Burges, C.; Shaked, T.; Renshaw, E.; Lazier, A.; Deeds, M.; Hamilton, N.; Hullender, G. Learning to Rank Using Gradient Descent. In Proceedings of the 22nd International Conference on Machine Learning, New York, NY, USA, 16–20 June 2005; pp. 89–96. [Google Scholar] [CrossRef]
- Cao, Z.; Qin, T.; Liu, T.Y.; Tsai, M.F.; Li, H. Learning to Rank: From Pairwise Approach to Listwise Approach. In Proceedings of the 24th International Conference on Machine Learning, New York, NY, USA, 19–24 June 2007; pp. 129–136. [Google Scholar] [CrossRef]
- Xu, J.; Li, H. AdaRank: A boosting algorithm for information retrieval. In Proceedings of the SIGIR 2007: Proceedings of the 30th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Amsterdam, The Netherlands, 23–27 July 2007; pp. 391–398. [Google Scholar]
- Köppel, M.; Segner, A.; Wagener, M.; Pensel, L.; Karwath, A.; Kramer, S. Pairwise Learning to Rank by Neural Networks Revisited: Reconstruction, Theoretical Analysis and Practical Performance. In Proceedings of the Machine Learning and Knowledge Discovery in Databases-European Conference, ECML PKDD 2019, Würzburg, Germany, 16–20 September 2019. [Google Scholar]
- Chomsky, N. Syntactic Structures; Mouton and Co.: The Hague, The Netherlands, 1957. [Google Scholar]
- Robin, J. An overview of surge: A reusable comprehensive syntactic realization component. In INLG’96 Demonstrations and Posters; Association for Computational Linguistics: Herstmonceux Castle, Sussex, UK, 1996; pp. 1–4. [Google Scholar]
- White, M.; Steedman, M.; Baldridge, J.; Kruijff, G. OpenCCG: The OpenNLP CCG Library. 2008. Available online: https://sourceforge.net/projects/openccg/ (accessed on 17 August 2021).
- Gatt, A.; Reiter, E. SimpleNLG: A realisation engine for practical applications. In Proceedings of the 12th European Workshop on Natural Language Generation, Athens, Greece, 30–31 March 2009. [Google Scholar]
- Joshi, A.; Rambow, O. A formalism for dependency grammar based on tree adjoining grammar. In Proceedings of the Conference on Meaning-Text Theory; MTT: Paris, France, 2003; pp. 207–216. [Google Scholar]
- Callaway, C.B. Evaluating Coverage for Large Symbolic NLG Grammars. In Proceedings of the Eighteenth International Joint Conference on Artificial Intelligence, Acapulco, Mexico, 9–15 August 2003; pp. 811–817. [Google Scholar]
- White, M.; Rajkumar, R.; Martin, S. Towards broad coverage surface realization with CCG. In Proceedings of the Workshop on Using Corpora for NLG: Language Generation and Machine Translation, Copenhagen, Denmark, 11 September 2007; pp. 22–30. [Google Scholar]
- Langkilde-Geary, I. A Foundation for General-Purpose Natural Language Generation: Sentence Realization Using Probabilistic Models of Language; University of Southern California: Los Angeles, CA, USA, 2003. [Google Scholar]
- Zhang, Y.; Clark, S. Discriminative Syntax-Based Word Ordering for Text Generation. Comput. Linguist. 2015, 41, 503–538. [Google Scholar] [CrossRef]
- Manning, C.D. Last Words: Computational Linguistics and Deep Learning. Comput. Linguist. 2015, 41, 701–707. [Google Scholar] [CrossRef]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. arXiv 2020, arXiv:2005.14165. [Google Scholar]
- Hasler, E.; Stahlberg, F.; Tomalin, M.; de Gispert, A.; Byrne, B. A Comparison of Neural Models for Word Ordering. In Proceedings of the 10th International Conference on Natural Language Generation, Santiago de Compostela, Spain, 4–7 September 2017; pp. 208–212. [Google Scholar] [CrossRef]
- Belz, A.; White, M.; Espinosa, D.; Kow, E.; Hogan, D.; Stent, A. The First Surface Realisation Shared Task: Overview and Evaluation Results. In Proceedings of the 13th European Workshop on Natural Language Generation, Nancy, France, 28–31 September 2011; pp. 217–226. [Google Scholar]
- Yu, X.; Tannert, S.; Vu, N.T.; Kuhn, J. Fast and Accurate Non-Projective Dependency Tree Linearization. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 1451–1462. [Google Scholar] [CrossRef]
- Bohnet, B.; Björkelund, A.; Kuhn, J.; Seeker, W.; Zarrieß, S. Generating non-projective word order in statistical linearization. In Proceedings of the 2012 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning, Jeju Island, Korea, 12–14 July 2012; pp. 928–939. [Google Scholar]
- Joulin, A.; Grave, E.; Bojanowski, P.; Mikolov, T. Bag of Tricks for Efficient Text Classification. arXiv 2016, arXiv:1607.01759. [Google Scholar]
- Available online: http://alpha.di.unito.it/storage/papers/2018_hpc4ai_ACM_CF.pdf (accessed on 17 August 2021).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: http://tensorflow.org (accessed on 17 August 2021).
- Kendall, M.G. A New Measure of Rank Correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Biewald, L. Experiment Tracking with Weights and Biases. 2020. Available online: http://wandb.com (accessed on 17 August 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).