Abstract
Yield prediction for tomatoes in greenhouses is an important basis for making production plans, and yield prediction accuracy directly affects economic benefits. To improve the prediction accuracy of tomato yield in Chinese-style solar greenhouses (CSGs), a wavelet neural network (WNN) model optimized by a genetic algorithm (GA-WNN) is applied. Eight variables are selected as input parameters and the tomato yield is the prediction output. The GA is adopted to optimize the initial weights, thresholds, and translation factors of the WNN. The experiment results show that the mean relative errors (MREs) of the GA-WNN model, WNN model, and backpropagation (BP) neural network model are 0.0067, 0.0104, and 0.0242, respectively. The results root mean square errors (RMSEs) are 1.725, 2.520, and 5.548, respectively. The EC values are 0.9960, 0.9935, and 0.9868, respectively. Therefore, the GA-WNN model has a higher prediction precision and a better fitting ability compared with the BP and the WNN prediction models. The research of this paper is useful from both theoretical and technical perspectives for quantitative tomato yield prediction in the CSGs.
1. Introduction
Tomatoes represent enormous economic value for producers across the world, and they also offer numerous health benefits for consumers [1]. Tomatoes are one of the main crops that are cultivated in Chinese-style solar greenhouses (CSGs) in China. In 2016, China became one of the world’s leading produce sources, and Chinese tomato production accounted for 7% of the world’s production [2]. In order to adapt to the supply and demand relationship in the global tomato market, an accurate production forecasting model which can adjust the cost input according to the market demand is required. Furthermore, such a model can provide an important theoretical and technical basis for the quantitative prediction of tomato yields in CSGs.
The application of artificial neural networks (ANNs) to prediction models has received considerable attention in various fields. The advantage of an ANN is that it does not need to know functional relationships in advance, allowing the development of models based on the intrinsic relationships between variables [3]. ANNs use a nonlinear mapping structure basis of the human brain for support learning. Their powerful processing ability was proven with various real-world applications [4]. The soft sensing of ANN techniques was widely applied to develop models for predicting different crop indicators, such as yield, growth, and other biophysical processes [5,6]. Salazar et al. used a Levenberg–Marquardt algorithm with ANN to train and verify weights and perform bias adjustment and the ideal fresh fruit production result was obtained [7]. An ANN model was established to predict eight regression factors for pepper fruit yields by employing a large number of genotypes, and the results indicate that ANN with an 8:10:1 architecture achieved high accuracy [8]. BP neural networks are also widely applied in the field of yield forecasting. The approach combined thermal camera technology with a BP neural network prediction model that was used to predict winter wheat yields and was accurate enough to meet production requirements [9]. Another wheat yields predictive model that used two remotely-sensed variables based on the BP neural network was constructed for the Guanzhong Plain, China [10]. Coke yield was predicted by a BP neural network combined with industrial production data [11].
However, BP neural networks cannot converge to a global minimum. Furthermore, they sometimes have slow convergence speeds. To avoid the shortcomings of falling into a local minimum with gradient descent learning algorithms, a wavelet neural network with a faster convergence speed was proposed [12,13]. The WNN model was established for forecasting basin sediment yield [14]. The results show that the hybrid model, compared with the traditional BP model, has high accuracy for the simulation of the basin sediment yield. The application of precise fertilization based on a WNN increased maize production, reducing production costs and agricultural pollution simultaneously [15]. A genetic algorithm [16] combined with a WNN has better robustness and a better function approximation ability. A traffic prediction model was proposed based on a WNN that was optimized by a genetic algorithm [17]. A predictive model for the entry percentage into expressway service areas based on the analysis of explanatory variables was constructed using a WNN and genetic algorithm [18]. It reflected that the GA-WNN model had an excellent fitting ability and a better prediction precision.
In the process of agricultural greenhouse production, tomato yields are affected by the interactions of various factors. The relationships between ambient parameters, fertilizers, and yields are very complicated. It is difficult to quantify the strongly non-linear characteristic with the traditional analytic method. Inspired by [18], the main objective here is to apply a GA-WNN model for the prediction of tomato yields in CSGs. The main contributions of this paper are summarized as follows:
- (1)
- In this paper, a basic model of yield prediction was applied to describe the non-linear relationship between tomato yield and environmental factors and eight variables are selected as input parameters for the yield predictive model. However, the parameters cannot accurately acquire in the basic model of yield prediction. Therefore, the accuracy of the basic model of yield prediction is difficult to meet actual needs.
- (2)
- To the best of the author’s knowledge, the GA-WNN model has not been used for tomato yield forecasting so far. This model takes advantage of the automatic search ability and probability optimization ability in the global space of the genetic algorithm. In this paper, GA optimizes the dilation and translation factor, thresholds, and the initial weight of the wavelet neural network. Then, in the prediction of tomato yield, this model can obtain the optimal network dilation factor, translation factor and weight. The accuracy of the models was reflected by the MRE, RMSE, EC, the predicted average and the predicted standard deviation. The results of the simulations show that the GA-WNN model is more robust and offers a better function approximation ability, which is useful from theoretical and technical perspectives for quantitative tomato yield prediction in CSGs.
2. Materials
The test site considered here is located in the scientific research and experimental base of the Shenyang Agricultural University in Liaoning Province, China (41.48° N, 123.24° E, 42 m a.s.l.). The region is characterized by a temperate continental monsoon climate. The annual sunshine is about 2800 h, the average annual rainfall is between 600 and 800 mm, the annual average temperature is 6.20 to 9.70 °C, and the average frost-free period is 155 to 180 days. The experiment was carried out in a Liaoshen Type III solar greenhouse built in an east–west orientation. The greenhouse was 60 m long and 12 m wide [19]. The heights of the northern wall and northern roof were 3 and 5.5 m, respectively. The cover on the southern roof was made from a 0.00012-m-thick polyvinyl chloride (PVC) film [20], and a rainproof quilt was used to maintain the temperature in the greenhouse. The percentages of sand, silt, and clay in the test soil were 37.6%, 40.7%, and 21.3%, respectively. The water field capacity was 0.26 g/cm3. Some nutrients in the soil are shown in Table 1. The experimental tomato cultivar was “Fenguan No. 1”, which was planted at spacings of 40 × 40 cm, with 35 plants in each row.

Table 1.
The part of the nutrients in the experimental soil.
3. Basic Model of Yield Prediction
The growth and development of greenhouse tomatoes are related to varieties and environmental factors. Therefore, when establishing a basic model of yield prediction, it is necessary to consider the interaction of various growth stages and the role of related influencing factors at each stage. In [21], a basic model of yield prediction was established in crop growth. The calculation process is as Equation (1).
where —Basic development function. The calculation equation is .
—Basic development coefficient. According to the value, it can be distinguished whether the crops are early- or late-maturing varieties.
—Development rate. Development time is expressed as the reciprocal of value.
—Developmental process. When the value is an integer, it means that the current growth and development stage has just ended, otherwise it means the transition period between the two stages. According to the value, the date and time of each growth stage of the crop can be obtained.
where indicates that the crop is growing at stage .
—Growth rate.
—Completion time of specific growth stage.
—Influence function of temperature factor.
—Influence function of the temperature difference between day and night.
—Influence function of lighting time.
—The influence function of water, fertilizer and seeding depth. The calculation equation of is .
—Influence function of fertilizer factor.
—Influence function of the moisture factor.
—Influence function of seeding depth factor.
During the establishment of the mechanism model, it is necessary to determine the functions based on the actual data collected and the interrelationship between each growth stage. The above analysis fully considers the effects of light, moisture, effective accumulated temperature and fertilizer effect on the growth stage of the tomatoes. When the CO2 concentration is suitable for tomato growth, the nonlinear model of tomato growth and development is expressed by Equation (3).
—Average temperature of tomato’s current growth stage.
—Lower temperature limit for tomato development.
—Upper temperature limit for tomato development.
—Average length of each day.
—The longest day of the current tomato growth stage.
—The shortest day of the current tomato growth stage.
—The influence index of temperature on the tomato growth process.
—The influence index of light intensity on the tomato growth process.
—The relationship between sowing depth and germination rate.
—Average CO2 concentration in the greenhouse.
—Critical value of CO2 concentration.
—CO2 concentration factor.
The key influencing factors for the yield prediction model were found by the growth model, i.e., the ambient temperature, humidity, irrigation amount, nitrogen fertilizer, phosphorus fertilizer, potassium fertilizer, CO2 concentration, and light intensity. It should be noted that the crop growth model is not suitable for the tomato yield prediction model. The main reason is that the parameters of the growth model cannot accurately acquire. Furthermore, critical factors such as and can only be obtained by practice and experiment. Therefore, the degree of accuracy for the yield prediction using a crop growth model cannot meet actual demand.
4. Methodology
4.1. BP Neural Network
BP neural network is a multi-layer feedforward network, which can be trained using an error backpropagation learning algorithm. BP neural network has the advantages of strong nonlinear mapping ability, high precision, and better versatility. The BP neural network contains an input signal layer , a hidden layer and an output layer . The weight between the input layer and the hidden layer is . The weight from the hidden layer to the output layer is [22]. The functions are S-type functions that have continuously differentiable properties. The value of the training sample is assigned to vector group , and the vector groups and are calculated from vector group . The output layer equations are given by Equations (4) and (5):
It can obtain the maximum number of iterations by adjusting the weight of each layer. Then, calculate the network layer output error. The total output error is recorded as per Equation (6):
If is less than the set value, the training will end. If is greater than the set value, the training will continue.
4.2. Wavelet Neural Network
In the wavelet neural network model, the major advantages of the WNN model lie in its excellent performance in non-stationary signal analysis and non-linear mapping [23]. It can effectively solve the problem of BP neural network easily falling into local minimal and slow convergence speed. In the WNN model, the mother wavelet function is shown in Equation (7).
The wavelet basis function is obtained by the dilation factor and translation factor of the parent wavelet function as shown in Equation (8):
where and are dilation factor and translation factor in the node in the hidden layer. By adjusting the weight, dilation factor, and translation factor of the model many times, the prediction accuracy and stability were improved to realize a better prediction ability. The output layer equations are given by Equation (9):
By modifying and adjusting the parameters in the above equations, the model found higher prediction accuracy.
4.3. GA-WNN
In the GA-WNN model, GA can optimize the dilation and translation factor, thresholds, and the initial weight of the wavelet neural network. It can provide optimal dilation and translation factor, thresholds, and the initial weight for the model. These are based on that GA is used to adopt a random search method that can directly operate on the structural object. This method uses a probabilistic optimization method to realize automatic search in the global space [24]. The GA-WNN model of yield prediction is presented as follows:
- (1)
- Coding: Firstly, groups of chromosomes are generated randomly. Secondly, these chromosomes correspond to the dilation and translation factor, the connection weight, and the neuron threshold of the wavelet neural network. Thirdly, the crossover and mutation probability are initialized, respectively. Subsequently, the initial population number and the total genetic algebra are given in advance, respectively.
Z chromosomes were randomly generated to represent the initial population P and each chromosome was encoded with a real number. The corresponding relation is shown by Equation (10):
where is the weights between the input layer and the hidden layer. Moreover, is the connection weight between the hidden layer and the output layer. and are the dilation and translation factors, respectively. is the threshold value in the output layer.
- (2)
- Setting fitness function: Use a wavelet neural network to calculate the error function value of the input sample. Calculate the fitness value of the chromosome corresponding to the reciprocal of the error. Then, sequence the fitness value respectively.
In this paper, the fitness value is calculated by Equations (11) and (12):
where is the error function, S is the number of input samples, is the expected output value of sample s () corresponding to the ith node, and represents its actual value.
Sort the fitness value of each individual in ascending order. Probability of the ith the individual was calculated by the Equations (13) and (14):
where stands for the odds of choosing the best individual, is the quantity of individual fitness values.
- (3)
- Selection: The formula for calculating the cumulative selection probability of the chromosome is . is a random ascending sequence in the interval of 0–1, When , the chromosome corresponds to the maximum fitness function value. Then, inherit this value directly to the next generation.
- (4)
- Cross-mutation: Set crossover probability and mutation probability . If the performance of the training data is not good, we should return the selection process.
- (5)
- Decoding: Decode the final result where the values are the optimal initial weight, threshold and translation factor of the wavelet neural network prediction model.
The GA-WNN construction process is shown in Figure 1.
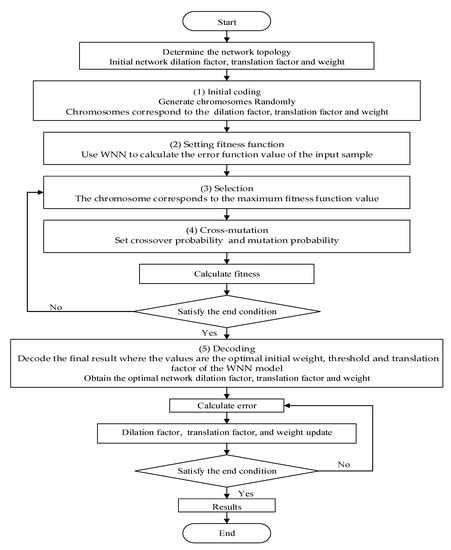
Figure 1.
GA-WNN model construction process.
5. Results and Analysis
5.1. Evaluation Parameters
We adopted the mean relative error (MRE), the evaluation index (EC), and root mean square error (RMSE) as evaluation parameters. In this paper, the MRE, EC, and RMSE values were used to verify the validity of the tomato yield prediction model.
In the evaluation of the greenhouse tomato yield prediction model, the absolute error was obtained by subtracting the actual measured value from the predicted yield for the current year according to Equation (15):
The relative error is defined as the ratio of the absolute error of the measurement to the actual measurement. The average relative error is taken as the mean relative error (MRE), which can reflect the percentage of prediction error in the total error. MRE is calculated as Equation (16):
The RMSE is obtained by averaging the sum of the squares of all errors and performing a square root operation (Equation (17)):
EC is obtained by the predicted value and actual measurement value in Equation (18). When the EC value is greater than 0.95, the predictions are considered satisfactory predictions [25].
where is the absolute error, is the predicted value, is the actual measurement value, the unit is , and is the sample number.
5.2. Collection and Processing of Historical Data
The experimental data were obtained from the Shenyang Agricultural University Scientific Research Base. The experimental data included ambient parameter data and the data regarding tomato production in the greenhouse from March 2010 to December 2018 (Table 2). The ambient parameter data include temperature, light intensity, humidity, and CO2 concentration data. The CSGs use automatic water and fertilizer machines for fertilization and irrigation.

Table 2.
Ambient parameters and production data.
In the experiment, tomatoes generally were harvested four to six times during the growing season. Tomato yield data could be obtained for past years by accumulating the production data for each harvest in the last year. However, some abnormal data were generated in the measurement process because of the ambient parameter data, which seriously affects the prediction accuracy when establishing the greenhouse tomato yield prediction model. It was necessary to preprocess the collected raw ambient parameter data to ensure better prediction accuracy. There were certain rules for performing data preprocessing which are given are as follows:
- (1)
- During the measurement of the ambient parameter data, it should be noted that some data may exceed normal values or not match the current environmental conditions due to the improper use of measuring instruments or incorrect sensor settings. Incorrect data should be eliminated and new data should be used via linear interpolation instead of the incorrect data.
- (2)
- In order to ensure model prediction accuracy and function convergence speed, the data need to be normalized to finally obtain input data for the prediction model [26,27]. A linear function conversion method was used to normalize the data (Equation (19)):where is the measured value of the instrument, and are the maximum and minimum values of the same parameter data, and is the normalized value. Through the above formula, the data were normalized to values within the range of 0–1. In this way, the dynamic range of the data was reduced and the model prediction accuracy was improved.
5.3. Analysis of BP Neural Network Model and Results
In BP neural network model, the neurons in the input layer are the eight feature parameters, i.e., the ambient temperature, humidity, irrigation amount, nitrogen fertilizer, phosphorus fertilizer, potassium fertilizer, CO2 concentration, and light intensity and the neuron in the output layer is the tomato yield. The momentum coefficient of the BP neural network model herein was set to 0.85, the learning rate was set to 0.09, the maximum training time was set to 1000, and the maximum allowable error was set to 0.01. In this model, if the number of hidden layer nodes is small, the prediction accuracy will be reduced. If the number of nodes is too large, then the training speed of the model will slow down. The number of hidden layer nodes can be obtained by continuous trial and training. The method for judging the number of hidden layer nodes is given by Equation (20):
where is the quantity of nodes in the hidden layer, is the quantity of nodes in the input layer, is the quantity of nodes in the output layer, and is any constant from 0 to 10. The optimal quantity of hidden layer nodes was obtained by training the network repeatedly. The results are shown in Table 3. The yield prediction results are shown in Figure 2.

Table 3.
Influence of the node number in different hidden layers on the network prediction error.
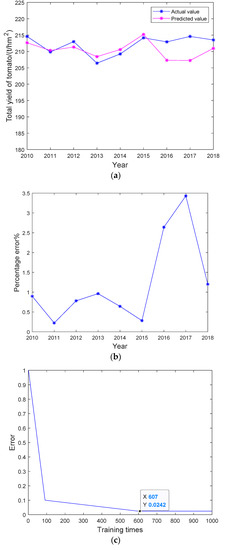
Figure 2.
(a) Comparison chart of predicted values and actual values. (b) Error percentage curve. (c) BP neural network training process.
As can be seen from Table 3, the optimal quantity of hidden layer nodes was 5. Through calculation, the absolute error of the test samples in 2016 was 5.6213 t·hm−2 and the relative error was 2.64%. The absolute error of the 2017 test samples was 7.3607 t·hm−2 and the relative error is 3.43%. The absolute error of the 2018 test samples was 2.562 t·hm−2 and the relative error is 1.20%. The mean relative error (MRE) of the BP neural network prediction model was 2.42%. Furthermore, in BP neural network model, the average production was 213.678 t·hm−2, the predicted average result was 208.497 t·hm−2 and the predicted standard deviation was 1.731. The EC was 0.9868, and the root mean square error (RMSE) was 5.548. After 607 iterations, the error reached a minimum and the prediction effect as optimal. However, it was found that the RMSE of the BP neural network prediction model was slightly too high. Therefore, the model accuracy needs to be improved.
5.4. Analysis of the WNN Model and Results
In the WNN model, the momentum coefficient was set to 0.85, the learning rate was set to 0.09, and the maximum allowable error was set to 0.01. The optimal number of hidden layer nodes can ensure prediction accuracy and the compactness of the structure. The calculation equations for the number of hidden layer nodes are given as per Equations (21) and (22):
where is the quantity of nodes in the hidden layer, is the quantity of nodes in the input layer, is the quantity of nodes in the output layer, and is any constant within the range of 0–10. The optimal quantity of hidden layer nodes was obtained by training the network repeatedly (Table 4). The yield prediction results are shown in Figure 3.

Table 4.
Influence of different hidden layer node numbers on prediction error.
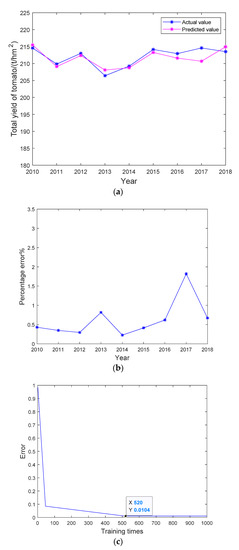
Figure 3.
(a) Comparison chart of predicted value and actual value. (b) Error percentage curve. (c) WNN training process.
As can be seen from Table 4, the optimal quantity of hidden layer nodes was 6. Through calculation, the absolute error for the test samples in 2016 was 1.320 t·hm−2 and the relative error was 0.62%. The absolute error for the 2017 test samples was 3.906 t·hm−2 and the relative error was 1.82%. The absolute error for the 2018 test samples was 1.431 t·hm−2 and the relative error was 0.67%. The mean relative error (MRE) for the WNN model was 1.04%. Moreover, in the WNN model, the average production was 213.678 t·hm−2, the predicted average result was 212.419 t·hm−2 and the predicted standard deviation was 1.794. The EC was 0.9935, and the root mean square error (RMSE) was 2.520. After 520 iterations, the error reached a minimum and the prediction effect was optimal. Compared with the BP neural network, the WNN model had better forecast accuracy, but the RMSE was still higher. Therefore, the model needs further improvement.
5.5. Analysis of the GA-WNN Model and Results
In the GA-WNN model, the size of the initial population was 85, the crossover probability was 0.5, and the mutation probability was 0.05. The data from 2010 to 2015 were selected as the training set for the model and the data from 2016 to 2018 were used as the test set to verify the prediction ability of the model. The size of the initial population was 85, the crossover probability was 0.5, and the mutation probability was 0.05. The yield prediction results are shown in Figure 4.
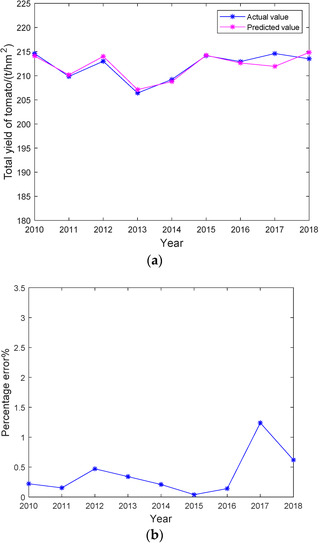
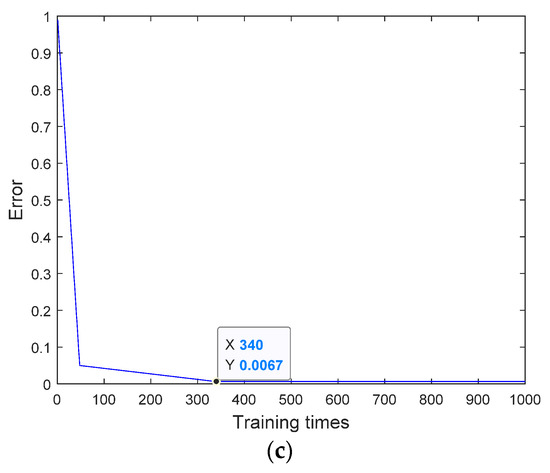
Figure 4.
(a) Comparison chart of predicted value and actual value. (b) Error percentage curve. (c) GA-WNN training process.
Through calculation, the absolute error for the test samples in 2016 was 0.298 t·hm−2 and the relative error was 0.14%. The absolute error for the 2017 test samples was 2.661 t·hm−2 and the relative error was 1.24%. The absolute error for the 2018 test samples was 1.324 t·hm−2 and the relative error was 0.62%. The mean relative error (MRE) of the GA-WNN model was 0.67%. In addition, in the GA-WNN model, the average production was 213.678 t·hm−2, the predicted average result was 213.133 t·hm−2 and the predicted standard deviation was 1.234. The EC was 0.9960, and the root mean square error (RMSE) was 1.725. After 340 iterations, the error reached a minimum and the prediction effect was optimal. The EC value was the highest with the GA-WNN model among the others considered here, which shows that the model can effectively predict greenhouse tomato yields.
6. Discussion
This section compares the predicted values produced by the three models with the actual values (Figure 5). The MRE, RMSE, EC, and convergent iterations are used to compare and analyze the prediction results from the three models (Table 5).
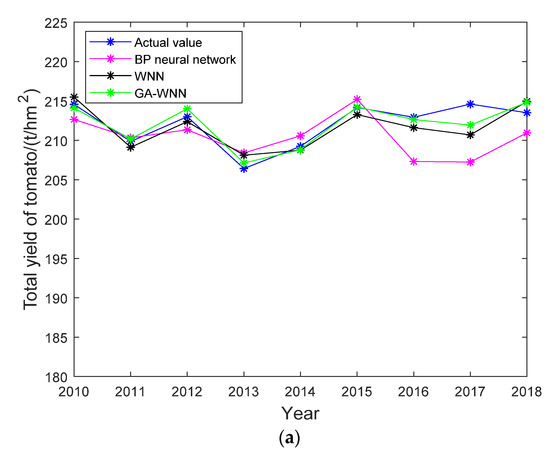
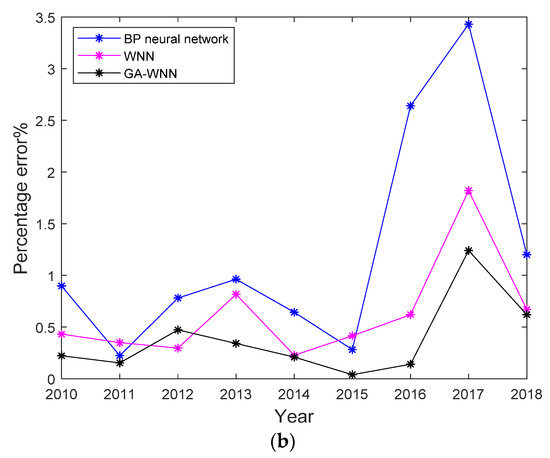
Figure 5.
(a) Comparison of predicted and measured values. (b) Error percentage curve.

Table 5.
Comparison of the results of the three prediction methods.
From the above results, it can be seen that the prediction results obtained by the GA-WNN model were the closest to the actual measured values. The mean relative errors (MREs) of the GA-WNN model, WNN model, and BP neural network model were 0.0067, 0.0104, and 0.0242, respectively. The results indicate that the GA-WNN model has the highest prediction accuracy. After 340 iterations, the GA-WNN model had the smallest error. The four evaluation indicators for the GA-WNN prediction model were better than those for the BP neural network model and WNN model. The experiments show that the GA-WNN model is reasonable and feasible for predicting greenhouse tomato yields.
Three models for predicting tomato yield were discussed here. The GA-WNN model integrates the advantages of a genetic algorithm for global searching. Therefore, the method had better prediction ability of neural network by GA algorithm. The GA-WNN model could quickly and accurately predict tomato yields in CSGs. According to the prediction results for the GA-WNN model, a corresponding management plan for sowing, irrigation, and fertilization can be formulated. At the same time, the ambient parameters such as the temperature and humidity can be regulated to the best conditions for crop growth.
7. Conclusions
This study has collected and recorded ambient parameters and yield data during the growth of tomatoes in a CSG for nine consecutive years. The main ambient parameters affecting the growth and yield of greenhouse tomatoes were determined through a basic model of yield prediction. A BP neural network, WNN, and GA-WNN were applied to predict greenhouse tomato yields. The results show that the GA-WNN model has a higher prediction precision and a better fitting ability compared with the BP and the WNN prediction models. The GA-WNN model has an important role in the reasonable planning of crop species and planting plans in CSGs. It also has an important role in the regulation and management of local tomato supply and demand balances. This model provides a theoretical basis for the prediction of greenhouse tomato yields and has a high practical application value. Furthermore, GA-WNN model provides theoretical support and technical guidance for the prediction of other crop yield.
Author Contributions
Y.W., R.X., Y.Y. and T.L. conceived and designed the experiments. Y.W., R.X. and Y.Y. performed the experiments. R.X. and Y.Y. analyzed the data. Y.W. and T.L. supervised the experiment. R.X. and Y.Y. wrote the manuscript. Y.W. and T.L. reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (NSFC) (61673281, 32001415, 61903264) and the Natural Science Foundation of Liaoning Province (2019-KF-03-01).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Acknowledgments
The authors sincerely thank the National Natural Science Foundation of China for their financial support. We gratefully acknowledge the assistance of Qingyun Yuan, Dapeng Zhang Nannan Zhang in revised manuscript. We are also grateful to reviewers for their recommendations to improve the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Leoni, C. Focus on lycopene. Acta Hort. 2003, 797, 25–36. [Google Scholar] [CrossRef]
- FAO. Statistical Database. Available online: http://faostat3.fao.org/home/E (accessed on 10 February 2016).
- Meirelles, G.; Manzi, D.; Brentan, B.; Goulart, T.; Luvizotto, E.J. Calibration Model for Water Distribution Network Using Pressures Estimated by Artificial Neural Networks. Water Resour. Manag. 2017, 31, 4339–4351. [Google Scholar]
- Shabani, A.; Ghaffary, K.A.; Sepaskhah, A.R.; Kamgar-Haghighi, A.A. Using the artificial neural network to estimate leaf area. Sci. Hortic. 2017, 216, 103–110. [Google Scholar]
- López-Aguilar, K.; Benavides-Mendoza, A.; González-Morales, S.; Juárez-Maldonado, A.; Chiñas-Sánchez, P.; Morelos-Moreno, A. Artificial Neural Network Modeling of Greenhouse Tomato Yield and Aerial Dry Matter. Agriculture 2020, 10, 97. [Google Scholar]
- Rohani, A.; Abbaspourfard, M.H.; Abdolahpour, S. Prediction of tractor repair and maintenance costs using Artificial Neural Network. Expert Syst. Appl. 2011, 38, 8999–9007. [Google Scholar]
- Salazar, R.; Dannehl, D.; Schmidt, U.; López, I.; Rojano, A. A dynamic artificial neural network for tomato yield prediction. Acta Hortic. 2017, 1154, 83–90. [Google Scholar]
- Gholipoor, M.; Nadali, F. Fruit yield prediction of pepper using artificial neural network. Sci. Hortic. 2019, 250, 249–253. [Google Scholar] [CrossRef]
- Hu, Z.F.; Zhang, L.D.; Wang, Y.X.; Shamaila, Z.; Zeng, A.J.; Song, J.L.; Liu, Y.J.; Wolfram, S.; Joachim, M.; He, X.K. Application of BP Neural Network in Predicting Winter Wheat Yield Based on Thermography Technology. Spectrosc. Spectr. Anal. 2013, 33, 1587–1592. [Google Scholar]
- Yin, G.H.; Gu, J.; Liu, Z.X.; Hao, L.; Tong, N. Analysis of Grain Yield Prediction Model in Liaoning Province. In Advances in Future Computer and Control Systems; Jin, D., Lin, S., Eds.; Springer: Berlin, Germany, 2012; Volume 159, pp. 355–360. [Google Scholar]
- Zhang, J.Q.; Zhang, W.B.; He, Y.T.; Yan, Y. Predicting the amount of coke deposition on catalyst pellets through image analysis and soft computing. Meas. Sci. Technol. 2016, 27, 114006. [Google Scholar]
- Lu, Z.J.; Zhu, L.; Pei, H.P. The model of chlorophyll-a concentration forecast in the West Lake based on wavelet analysis and BP neural networks. Acta Ecol. Sin. 2008, 28, 4965–4973. [Google Scholar]
- Fang, J.; Zhang, Z. Prediction of human blood pressure based on wavelet analysis and BP neural network. Comput. Syst. Appl. 2017, 26, 157–161. [Google Scholar]
- Li, S.X.; Yao, C.A.; Wen, J.; Huang, X.; Shao, X.H. Forecasting of Basin Sediment Yield Based on Wavelet-BP Neural Network. In Proceedings of the International Asia Conference on Informatics in Control, Automation and Robotics (CAR), Wuhan, China, 6–7 March 2010; pp. 96–99. [Google Scholar]
- Yd, A.; Zfa, B.; Yp, A.; Yz, A.; Hy, A.; Xla, B. Precision fertilization method of field crops based on the wavelet-bp neural network in China. J. Clean. Prod. 2019, 246, 118735. [Google Scholar]
- Yang, X.H.; Liu, X.P.; Liu, H.S.; Guo, Y.; Xu, S.P. Research based on the neural network of simulated annealing and genetic algorithm in the precise fertilization. Guangdong Agric. Sci. 2012, 39, 60–69. [Google Scholar]
- Peng, Y.N.; Xiang, W.L. Short-term traffic volume prediction using GA-BP based on wavelet denoising and phase space reconstruction. Phys. A Stat. Mech. Its Appl. 2020, 549, 14. [Google Scholar] [CrossRef]
- Shen, X.Y.; Zhang, F.; Lv, H.T.; Liu, J.; Liu, H.X. Prediction of Entering Percentage into Expressway Service Areas Based on Wavelet Neural Networks and Genetic Algorithms. IEEE Access 2019, 7, 54562–54574. [Google Scholar] [CrossRef]
- Zhang, D.P.; Zhang, T.Y.; Ji, J.W. Estimation of Solar Radiation for Tomato Water Requirement Calculation in Chinese-Style Solar Greenhouses Based on Least Mean Squares Filter. Sensors 2019, 20, 155. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tong, G.; Christopher, D.M.; Li, B. Numerical modelling of temperature variations in a Chinese solar greenhouse. Comput. Electron. Agric. 2009, 68, 129–139. [Google Scholar] [CrossRef]
- Chen, X.L.; Zhang, X.F.; Luo, X.L.; Liu, J.G.; Yao, Y.S. Study of dynamic simulation model of maize growth in northeast China. J. Jilin Agric. Univ. 2012, 34, 242–247. [Google Scholar]
- Yang, Y.; Wang, J.; Weng, H.; Hou, J.; Gao, T. Research on Online Correction of SOC Estimation for Power Battery Based on Neural Network. In Proceedings of the IEEE Advanced Information Technology, Electronic and Automation Control Conference, Xi’an, China, 12–14 October 2018. [Google Scholar]
- Zhang, J. Wavelet neural network for function learning. IEEE Trans. Signal Process. 1995, 43, 1485–1497. [Google Scholar] [CrossRef]
- Chaves, P.; Chang, F.J. Intelligent reservoir operation system based on evolving artificial neural networks. Adv. Water Resour. 2008, 31, 926–936. [Google Scholar] [CrossRef]
- Ouyang, L.; Zhu, F.; Xiong, G.; Zhao, H.; Wang, F.; Liu, T. Short-Term Traffic Flow Forecasting Based on Wavelet Transform and Neural Network. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017. [Google Scholar]
- Guo, Z.X.; Wong, W.K.; Li, M. Sparsely connected neural network-based time series forecasting. Inf. Sci. 2012, 193, 54–71. [Google Scholar] [CrossRef]
- Wong, W.K.; Guo, Z.X.; Leung, S.Y.S. Partially connected feedforward neural networks on apollonian networks. Phys. A Stat. Mech. Its Appl. 2010, 389, 5298–5307. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).