On Training Knowledge Graph Embedding Models
Abstract
1. Introduction
- We provide a comprehensive analysis of training loss functions as used in several state-of-the-art KGE models in Section 3. We also preform an empirical evaluation of different KGE models with different loss functions and we show the effect of these losses on the KGE models predictive accuracy.
- We study negative sampling strategies and we examine their effects on the accuracy and scalability of KGE models.
- We study the effects of changes in the different hyperparameters and their effects on the accuracy and scalability of KGE models during the training process.
2. Background
2.1. Loss Functions in Learning to Rank
- Pairwise approach. The loss is defined as the summation of the differences between the predicted score of an element and the scores of other elements with a smaller labels’ value. The formula is as follows:where the function can be the hinge function as in Translating Embeddings model [1] or the exponential function as in RankBoost [20].
- Listwise approach. The loss is defined as a comparison between the rank permutation probabilities of model scores and values of actual labels [21]. Let be an increasing and strictly positive function. We define the probability of an object being ranked on the top (a.k.a. top one probability), given the scores of all the objects as:where is the score of object i, . The listwise loss can then be defined as:where is a model-dependent loss and is a labelling function which returns the true label of x. Possible examples include cross-entropy in ListNet [21] or likelihood loss as in ListMLE [22].
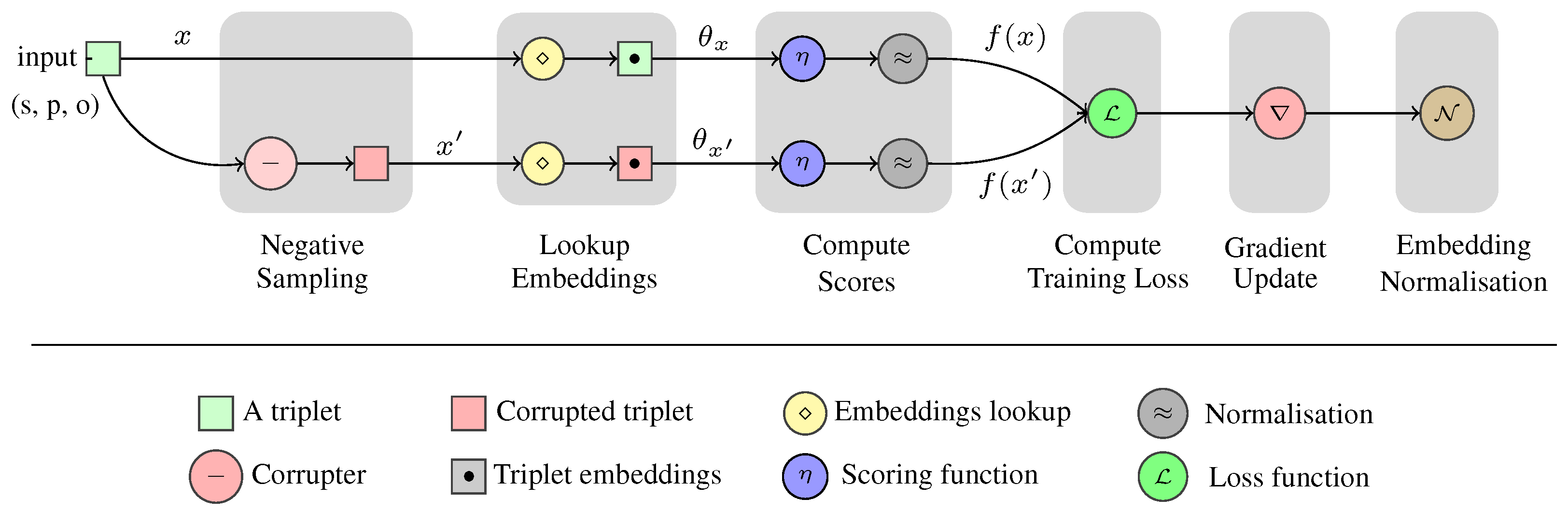
2.2. Knowledge Graph Embedding Process
2.2.1. Negative Sampling
2.2.2. Embedding Interactions
- Distance-based embeddings’ interactions
- Factorisation-based embedding interactions
2.3. Ranking Evaluation Metrics
- Mean Average Precision (MAP). MAP is a ranking measure that evaluates the quality of a rank depending on the whole rank of its true (relevant) elements. First, we need to define Precision at position k (denoted as ):where and is an indicator function that is equal to 1 when x is a relevant element and 0 otherwise.The Average Precision (AP) is defined by:where n is the total number of objects associated with query q, and is the number of objects with label one. The MAP is then defined as the mean of AP over all queries Q:
- Mean Reciprocal Rank (MRR). The Reciprocal Rank (RR) is a statistical measure used to evaluate the response of ranking models depending on the rank of the first correct answer. The MRR is the average of the reciprocal ranks of results for different queries in Q. Formally, MRR is defined as:where is the highest ranked relevant item for query . Values of RR and MRR have a maximum of 1 for queries with true items ranked first, and get closer to 0 when the first true item is ranked in lower positions. Therefore, we can define the MRR error as . This error starts from 0 when the first true item is ranked first, and increases towards 1 for less successful rankings.
- Hits@k. This metric represents the number of correct elements predicted among the top-k elements in a rank, where we use Hits@1, Hits@3 and Hits@10. This metric indicates that the model’s probability of ranking a relevant (true) fact in the top-k element scores in the rank.
2.4. Experimental Evaluation
- ●
- Benchmarking Datasets. In our experiments, we use five knowledge graph benchmarking datasets:
- PSE: a poly-pharmacy side-effects dataset [33] containing facts about drug combinations and their related side-effects. The dataset was introduced by Zitnik et al. [33] to study modelling poly-pharmacy side-effects using knowledge graph embedding models. Since the dataset is significantly larger than the available standard benchmark we use it to study the effects of hyperparameters and accuracy of the knowledge graph embedding models.
- ●
- Evaluation Protocol. We evaluate the KGE models using a unified protocol that assesses their performance in the task of link prediction. Let X be the set of facts, i.e., triples; be the embeddings of entities E, and be the embeddings of relations R. The KGE evaluation protocol works in three steps:
- (1)
- Corruption: For each , x is corrupted times by replacing its subject and object entities with all the other entities in E. The corrupted triples can be defined as:where and . These corruptions effectively provide negative examples for the supervised training and testing process due to the Local Closed World Assumption [34], frequently adopted for knowledge graph mining tasks.
- (2)
- Scoring: Both original triples and corrupted instances are evaluated using a model-dependent scoring function. This process involves looking up embeddings of entities and relations, and computing scores depending on these embeddings.
- (3)
- Evaluation: Each triple and its corresponding corruption triples are evaluated using the RR ranking metric as a separate query, where the original triples represent true objects and their corruptions false ones. It is possible that corruptions of triples may contain positive instances that exist among training or validation triples. In our experiments, we alleviate this problem by filtering out positive instances in the triple corruptions. Therefore, MRR and Hits@k are computed using the knowledge graph original triples and non-positive corruptions only [1].
3. Loss Functions in KGE Models
3.1. KGE Pointwise Losses
- Pointwise square error loss (SE). It is a pointwise ranking loss function used in RESCAL [4]. It models training losses with the objective of minimising the squared difference between model predicted scores for triples and their true labels:The optimal score for true and false facts is 1 and 0, respectively. A nice to have characteristic of the SE loss is that it does not require configurable training parameters, shrinking the search space of hyperparameters compared to other losses (e.g., the margin parameter of the hinge loss).
- Pointwise hinge loss. Hinge loss can be interpreted as a pointwise loss, where the objective is to generally minimise the scores of negative facts and maximise the scores of positive facts to a specific configurable value. This approach is used in HolE [9], and it is defined as:where is an abbreviation for pointwise to clarify the type of the loss, if x is true and otherwise, and denotes the function. This effectively generates two different loss slopes for positive and negative scores as shown in Figure 2. Thus, the objective resembles a pointwise loss that minimises negative scores to reach , and maximises positives scores to reach .
- Pointwise logistic loss. The ComplEx [8] model uses a logistic loss, which is a smoother version of pointwise hinge loss without the configurable margin parameter. Logistic loss uses a logistic function to minimise the negative triples score and maximise the positive triples score. This is similar to hinge loss, but uses a smoother linear loss slope defined as:where is the true label of fact x, which is equal to 1 for positive facts and equal to otherwise.
3.2. KGE Pairwise Losses
- Pairwise hinge loss. Hinge loss is a linear learning to rank loss that can be implemented in both a pointwise or pairwise loss settings. In both, the TransE [1] and DistMult [7] models the hinge loss is used in its pairwise form and defined as follows:where the term is an abbreviation for pairwise, is the set of true facts, is the set of false facts, and is a configurable margin that separates positive from negative facts.
- Pairwise logistic loss. Logistic loss can also be interpreted as pairwise margin based loss following the same approach as in hinge loss. The loss is then defined as:where the objective is to minimise the marginal difference between negative and positive scores with a smoother linear slope than hinge loss as shown in Figure 3.
3.3. KGE Multi-Class Losses
- Binary cross entropy loss (BCE). The authors of the ConvE model [14] proposed a new binary cross entropy multi-class loss to model the training error of KGE models in link prediction. In this setting, the whole vocabulary of entities is used to train each positive fact such that for a triple , all facts with and are considered false. The BCE loss can be defined as follows:where is the true label of triplet . Despite the extra computational cost of this approach, it allowed ConvE to generalise over a larger sample of negative instances, therefore surpassing other approaches in accuracy [14].
- Negative-log softmax loss (NLS). In a recent work, Lacroix et al. [15] introduced a soft-max regression loss to model training error of the ComplEx model as a multi-class problem. In this approach, the objective for each triple is to minimise the following loss:where is the model score for the triple , and , , and . This resembles a log-loss of the soft-max value of the positive triple compared to all possible object and subject corruptions where the objective is to maximise positive fact scores and minimise all other scores. This approach achieved significant improvement to the prediction accuracy of ComplEx model over all benchmark datasets when used with the 3-nuclear norm regularisation of embeddings [15].
3.4. Effects of Training Objectives on Accuracy
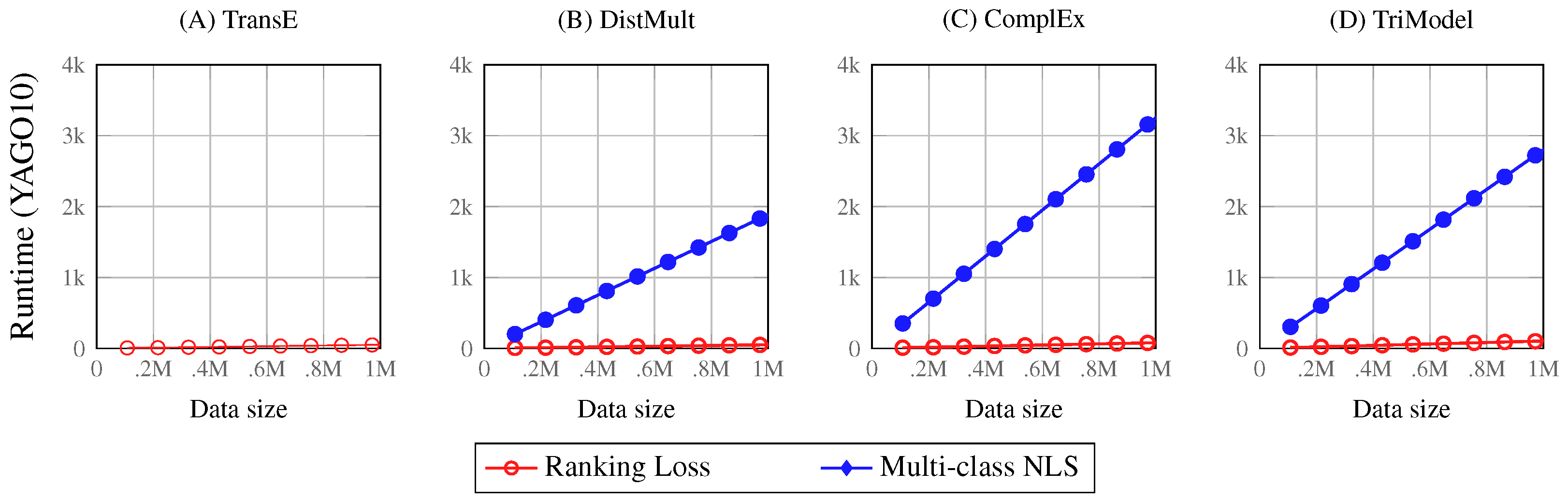
3.5. Effects of Training Objectives on Scalability
4. KGE Training Hyperparameters
4.1. Training Hyperparameters Effects on KGE Scalability
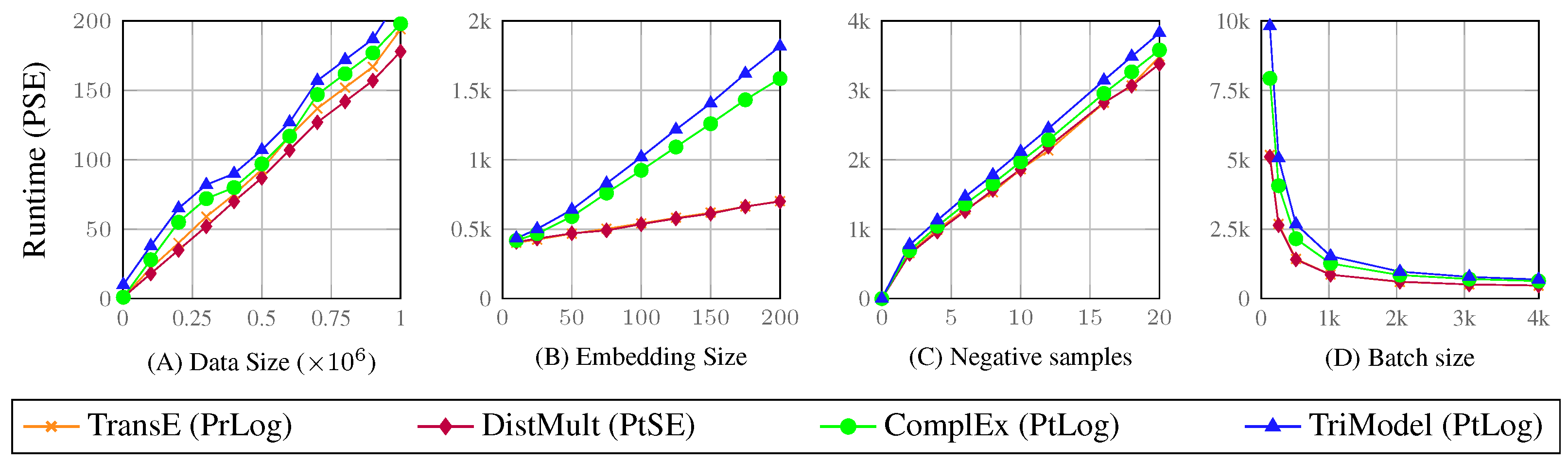
Analysis of the Predictive Scalability Experiments
- The results confirm that KGE models have linear time complexity as shown in Figure 5 where the models’ runtime grows linearly corresponding to increase of both data size and embedding vector sizes.
- The results also confirm that models such as the TriModel and Complex model which have more than one embedding vector for each entity, and relations require more training time compared to models with only one embedding vector.
- The results also show that the training batch size has a significant effect on the training runtime, therefore, using larger batch sizes are suggested to significantly decrease the training runtime of the training of KGE models.
4.2. Training Hyperparameters’ Effects on KGE Accuracy
- Changes on the embedding vectors’ size have the biggest effect on the predictive accuracy of KGE models. Thus, we suggest to carefully select this parameter by searching through a larger search space, which can help with ensuring that the models can reach their best representations of the knowledge graph.
- The increased number of training iterations can sometimes have a negative effect on the outcome predictive accuracy. Thus, we suggest using early stopping techniques to decide when to stop model training before accuracy starts to decrease.
- Both the number of negative samples and batch sizes showed a small effect on the predictive accuracy of KGE models. Thus, this parameter can either be assigned fixed values or be found using a small search spaces to help decrease the hyperparameters search space, and thus the hyperparameters’ tuning runtime.
5. Discussion
5.1. The Compromise between Scalability and Accuracy
5.2. The Relationship between Datasets and Embedding Interaction Functions
5.3. Compatibility between Scoring and Loss Functions
5.4. Limitations of Knowledge Graph Embedding Models
- Lack of interpretability. In knowledge graph embedding models, the learning objective is to model nodes and edges of the graph using low-rank vector embeddings that preserve the graph’s coherent structure. The embedding learning procedure operates mainly by transforming noise vectors to useful embeddings using gradient decent optimisation on a specific objective loss. These procedures, however, work as a black box that is hard to interpret compared to other association rule mining and graph traversal approaches that can be interpreted based on the features they use.
- Sensitivity to data quality. KGE models generate vector representations of entities according to their prior knowledge. Therefore, the quality of this knowledge affects the quality of the generated embeddings.
- Hyperparameter sensitivity. The outcome predictive accuracy of KGE embeddings is sensitive to their hyperparameters [16]. Therefore, minor changes in these parameters can have significant effects on the outcome predictive accuracy of KGE models. The process of finding the optimal parameters of KGE models is traditionally achieved through an exhausting brute-force parameter search. As a result, their training may require rather time-consuming grid search procedures to find the right parameters for each new dataset.
5.5. Future Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bordes, A.; Usunier, N.; García-Durán, A.; Weston, J.; Yakhnenko, O. Translating Embeddings for Modeling Multi-relational Data. In Proceedings of the Neural Information Processing Systems (NIPS) 2013, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 2787–2795. [Google Scholar]
- Wang, Z.; Zhang, J.; Feng, J.; Chen, Z. Knowledge Graph Embedding by Translating on Hyperplanes. In Proceedings of the AAAI Conference on Artificial Intelligence 2014, Quebec City, QC, Canada, 27–31 July 2014; pp. 1112–1119. [Google Scholar]
- Nie, B.; Sun, S. Knowledge graph embedding via reasoning over entities, relations, and text. Future Gener. Comp. Syst. 2019, 91, 426–433. [Google Scholar] [CrossRef]
- Nickel, M.; Tresp, V.; Kriegel, H. A Three-Way Model for Collective Learning on Multi-Relational Data. In Proceedings of the 28th International Conference on International Conference on Machine Learning, Washington, DC, USA, 28 June–2 July 2011; pp. 809–816. [Google Scholar]
- Bordes, A.; Glorot, X.; Weston, J.; Bengio, Y. A semantic matching energy function for learning with multi-relational data—Application to word-sense disambiguation. Mach. Learn. 2014, 94, 233–259. [Google Scholar] [CrossRef]
- Nickel, M.; Tresp, V.; Kriegel, H. Factorizing YAGO: Scalable machine learning for linked data. In Proceedings of the 21st international conference on World Wide Web 2012, Lyon, France, 16–20 April 2012; pp. 271–280. [Google Scholar]
- Yang, B.; Yih, W.; He, X.; Gao, J.; Deng, L. Embedding Entities and Relations for Learning and Inference in Knowledge Bases. In Proceedings of the International Conference on Learning Representations (ICLR) 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex Embeddings for Simple Link Prediction. In Proceedings of the International Conference on Machine Learning 2016, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 2071–2080. [Google Scholar]
- Nickel, M.; Rosasco, L.; Poggio, T.A. Holographic Embeddings of Knowledge Graphs. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, ZA, USA, 12–17 February 2016; pp. 1955–1961. [Google Scholar]
- Wang, Q.; Mao, Z.; Wang, B.; Guo, L. Knowledge Graph Embedding: A Survey of Approaches and Applications. IEEE Trans. Knowl. Data Eng. 2017, 29, 2724–2743. [Google Scholar] [CrossRef]
- Mohamed, S.K.; Novácek, V.; Vandenbussche, P.; Muñoz, E. Loss Functions in Knowledge Graph Embedding Models. In DL4KG@ESWC—CEUR Workshop Proceedings, Proceedings of the 16th European Semantic Web Conference, Portoroz, Slovenia, 2 June 2019; CEUR-WS.org: Aachen, Germany, 2019; Volume 2377, pp. 1–10. [Google Scholar]
- Hayashi, K.; Shimbo, M. On the Equivalence of Holographic and Complex Embeddings for Link Prediction. In Proceedings of the Association for Computational Linguistics, Vancouver, BC, Canada, 30 July–4 August 2017; pp. 554–559. [Google Scholar]
- Trouillon, T.; Nickel, M. Complex and Holographic Embeddings of Knowledge Graphs: A Comparison. arXiv 2017, arXiv:1707.01475. [Google Scholar]
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2D Knowledge Graph Embeddings. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Lacroix, T.; Usunier, N.; Obozinski, G. Canonical Tensor Decomposition for Knowledge Base Completion. arXiv 2018, arXiv:1806.07297. [Google Scholar]
- Kadlec, R.; Bajgar, O.; Kleindienst, J. Knowledge Base Completion: Baselines Strike Back. In Proceedings of the Rep4NLP@ACL. Association for Computational Linguistics, Vancouver, BC, Canada, 28 April 2017; pp. 69–74. [Google Scholar]
- Mohamed, S.K.; Novácek, V. Link Prediction Using Multi Part Embeddings. In Lecture Notes in Computer Science, Proceedings of the European Semantic Web Conference, Portorož, Slovenia, 2–6 June 2019; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11503, pp. 240–254. [Google Scholar]
- Hitchcock, F.L. The expression of a tensor or a polyadic as a sum of products. J. Math. Phys. 1927, 6, 164–189. [Google Scholar] [CrossRef]
- Cossock, D.; Zhang, T. Statistical Analysis of Bayes Optimal Subset Ranking. IEEE Trans. Inf. Theory 2008, 54, 5140–5154. [Google Scholar] [CrossRef]
- Freund, Y.; Iyer, R.D.; Schapire, R.E.; Singer, Y. An Efficient Boosting Algorithm for Combining Preferences. J. Mach. Learn. Res. 2003, 4, 933–969. [Google Scholar]
- Cao, Z.; Qin, T.; Liu, T.; Tsai, M.; Li, H. Learning to rank: From pairwise approach to listwise approach. In Proceedings of the 24th International Conference on Machine Learning 2007, Corvallis, OR, USA, 13–15 April 2007; Volume 227, pp. 129–136. [Google Scholar]
- Xia, F.; Liu, T.; Wang, J.; Zhang, W.; Li, H. Listwise approach to learning to rank: Theory and algorithm. In Proceedings of the International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; Volume 307, pp. 1192–1199. [Google Scholar]
- Chen, W.; Liu, T.; Lan, Y.; Ma, Z.; Li, H. Ranking Measures and Loss Functions in Learning to Rank. Adv. Neural Inf. Process. Syst. 2009, 22, 315–323. [Google Scholar]
- Yang, B.; Yih, W.; He, X.; Gao, J.; Deng, L. Learning Multi-Relational Semantics Using Neural-Embedding Models. arXiv 2015, arXiv:1411.4072. [Google Scholar]
- Liu, T. Learning to Rank for Information Retrieval; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Mitchell, T.; Cohen, W.; Hruschka, E.; Talukdar, P.; Yang, B.; Betteridge, J.; Carlson, A.; Dalvi, B.; Gardner, M.; Kisiel, B.; et al. Never-ending learning. Commun. ACM 2018, 61, 103–115. [Google Scholar] [CrossRef]
- Gardner, M.; Mitchell, T.M. Efficient and Expressive Knowledge Base Completion Using Subgraph Feature Extraction. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015; pp. 1488–1498. [Google Scholar]
- Miller, G.A. WordNet: A Lexical Database for English. Commun. ACM 1995, 38, 39–41. [Google Scholar] [CrossRef]
- Bollacker, K.D.; Evans, C.; Paritosh, P.; Sturge, T.; Taylor, J. Freebase: A collaboratively created graph database for structuring human knowledge. In Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, 10–12 June 2008; pp. 1247–1250. [Google Scholar]
- Toutanova, K.; Chen, D.; Pantel, P.; Poon, H.; Choudhury, P.; Gamon, M. Representing Text for Joint Embedding of Text and Knowledge Bases. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015; pp. 1499–1509. [Google Scholar]
- Mahdisoltani, F.; Biega, J.; Suchanek, F.M. YAGO3: A Knowledge Base from Multilingual Wikipedias. In Proceedings of the 7th Biennial Conference on Innovative Data Systems Research 2014, Asilomar, CA, USA, 4–7 January 2015. [Google Scholar]
- Bouchard, G.; Singh, S.; Trouillon, T. On approximate reasoning capabilities of low-rank vector spaces. In Proceedings of the AAAI Spring Syposium on Knowledge Representation and Reasoning (KRR): Integrating Symbolic and Neural Approaches, Palo Alto, CA, USA, 23–25 March 2015. [Google Scholar]
- Zitnik, M.; Agrawal, M.; Leskovec, J. Modeling polypharmacy side effects with graph convolutional networks. Bioinformatics 2018, 34, i457–i466. [Google Scholar] [CrossRef] [PubMed]
- Nickel, M.; Murphy, K.; Tresp, V.; Gabrilovich, E. A review of relational machine learning for knowledge graphs. Proc. IEEE 2016, 104, 11–33. [Google Scholar] [CrossRef]
- Nguyen, D.Q.; Nguyen, T.D.; Nguyen, D.Q.; Phung, D. A Novel Embedding Model for Knowledge Base Completion Based on Convolutional Neural Network. In Proceedings of the 16th Annual Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL-HLT), New Orleans, LA, USA, 1–6 June 2018; pp. 327–333. [Google Scholar]

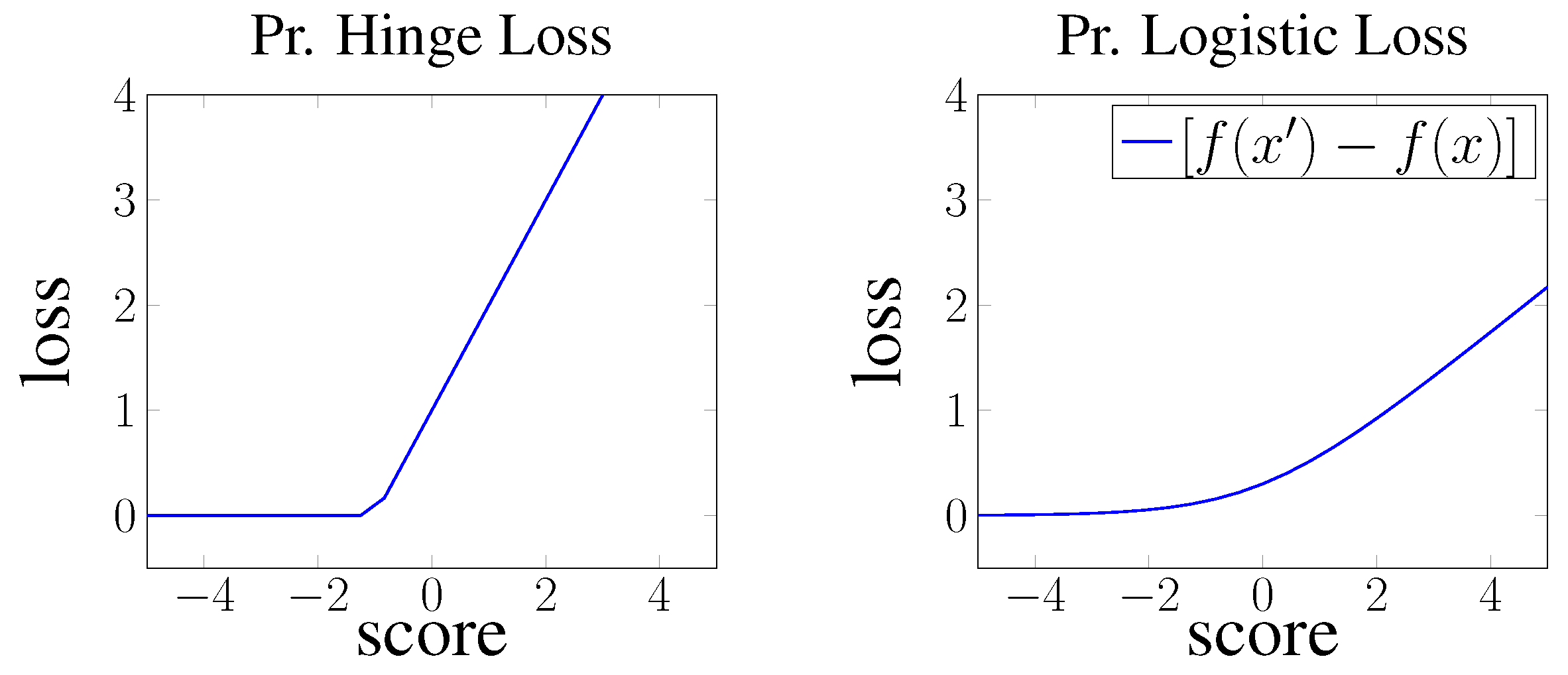

| Dataset | Entity Count | Relation Count | Train | Valid | Test |
|---|---|---|---|---|---|
| NELL239 | 48K | 239 | 74K | 3K | 3K |
| WN18RR | 41K | 11 | 87K | 3K | 3K |
| FB15k-237 | 15K | 237 | 272K | 18K | 20K |
| YAGO10 | 123K | 37 | 1M | 5K | 5K |
| PSE | 32K | 967 | 3.7M | 459K | 459K |
| Model | Loss | NELL239 | WN18RR | Fb15k-237 | |||||
|---|---|---|---|---|---|---|---|---|---|
| MRR | H10 | MRR | H10 | MRR | H10 | ||||
| Ranking Loss | TransE | Pr | * Hinge | 0.28 | 0.43 | 0.20 | 0.47 | 0.27 | 0.43 |
| Logistic | 0.27 | 0.43 | 0.21 | 0.48 | 0.26 | 0.43 | |||
| Pt | Hinge | 0.19 | 0.32 | 0.12 | 0.34 | 0.12 | 0.25 | ||
| Logistic | 0.17 | 0.31 | 0.11 | 0.31 | 0.01 | 0.23 | |||
| SE | 0.01 | 0.02 | 0.00 | 0.00 | 0.01 | 0.01 | |||
| DistMult | Pr | Hinge | 0.20 | 0.32 | 0.40 | 0.45 | 0.10 | 0.16 | |
| Logistic | 0.26 | 0.40 | 0.39 | 0.45 | 0.19 | 0.36 | |||
| Pt | * Hinge | 0.25 | 0.41 | 0.43 | 0.49 | 0.21 | 0.39 | ||
| Logistic | 0.28 | 0.43 | 0.43 | 0.50 | 0.20 | 0.39 | |||
| SE | 0.31 | 0.48 | 0.43 | 0.50 | 0.22 | 0.40 | |||
| ComplEx | Pr | Hinge | 0.24 | 0.38 | 0.39 | 0.45 | 0.20 | 0.35 | |
| Logistic | 0.27 | 0.43 | 0.41 | 0.47 | 0.19 | 0.35 | |||
| Pt | Hinge | 0.21 | 0.36 | 0.41 | 0.47 | 0.20 | 0.39 | ||
| * Logistic | 0.14 | 0.24 | 0.36 | 0.39 | 0.13 | 0.28 | |||
| SE | 0.35 | 0.52 | 0.47 | 0.53 | 0.22 | 0.41 | |||
| Multi-class losses | CP | MC | BCE | - | - | - | - | - | - |
| NLS | - | - | 0.08 | 0.12 | 0.22 | 0.42 | |||
| DistMult | MC | BCE | - | - | 0.43 | 0.49 | 0.24 | 0.42 | |
| NLS | 0.39 | 0.55 | 0.43 | 0.50 | 0.34 | 0.53 | |||
| ComplEx | MC | BCE | - | - | 0.44 | 0.51 | 0.25 | 0.43 | |
| NLS | 0.40 | 0.58 | 0.44 | 0.52 | 0.35 | 0.53 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, S.K.; Muñoz, E.; Novacek, V. On Training Knowledge Graph Embedding Models. Information 2021, 12, 147. https://doi.org/10.3390/info12040147
Mohamed SK, Muñoz E, Novacek V. On Training Knowledge Graph Embedding Models. Information. 2021; 12(4):147. https://doi.org/10.3390/info12040147
Chicago/Turabian StyleMohamed, Sameh K., Emir Muñoz, and Vit Novacek. 2021. "On Training Knowledge Graph Embedding Models" Information 12, no. 4: 147. https://doi.org/10.3390/info12040147
APA StyleMohamed, S. K., Muñoz, E., & Novacek, V. (2021). On Training Knowledge Graph Embedding Models. Information, 12(4), 147. https://doi.org/10.3390/info12040147






