A Brief Analysis of Key Machine Learning Methods for Predicting Medicare Payments Related to Physical Therapy Practices in the United States

Abstract

Background and objectives: Machine learning approaches using random forest have been effectively used to provide decision support in health and medical informatics. This is especially true when predicting variables associated with Medicare reimbursements. However, more work is needed to analyze and predict data associated with reimbursements through Medicare and Medicaid services for physical therapy practices in the United States. The key objective of this study is to analyze different machine learning models to predict key variables associated with Medicare standardized payments for physical therapy practices in the United States. Materials and Methods: This study employs five methods, namely, multiple linear regression, decision tree regression, random forest regression, K-nearest neighbors, and linear generalized additive model, (GAM) to predict key variables associated with Medicare payments for physical therapy practices in the United States. Results: The study described in this article adds to the body of knowledge on the effective use of random forest regression and linear generalized additive model in predicting Medicare Standardized payment. It turns out that random forest regression may have any edge over other methods employed for this purpose. Conclusions: The study provides a useful insight into comparing the performance of the aforementioned methods, while identifying a few intricate details associated with predicting Medicare costs while also ascertaining that linear generalized additive model and random forest regression as the most suitable machine learning models for predicting key variables associated with standardized Medicare payments.

1. Introduction

Investigators have used various methods and techniques to analyze results in healthcare delivery. While many of these studies have involved methods such as ANOVA and MANOVA, regression, and more recently deep learning techniques [1,2,3], there has been a dearth of literature on the use of random forests [4] and other ensemble learning methods [5] for analyzing health and medical data when compared to other machine learning algorithms. The goal of the current study was to compare traditional regression techniques with the random forest approach and assess the differences in predicting payments to Medicare beneficiaries. Here, we would like to point out that Medicare is defined by Rajaram and Bilimoria [6] as “a federal program that provides health insurance coverage to people aged 65 years or older and younger people with permanent disabilities.” Based on this aforementioned comparison the broader research goals targeted by this study are as follows: (a) increasing the information available to the health informaticians on Medicare payments with respect to physical therapy practices in the United States [7,8], and (b) analyzing the computational techniques available to the researchers in deciphering the necessary information that can assist in the development of a knowledge base for decision making purposes [1].

As such, the specific research objectives of the study are as follows: (a) analyze the utility of random forest in predicting the total standardized Medicare payment by a variety of variables that include the proxy for number of new patients, and number of Medicare beneficiaries, (b) identify variables that can be used to predict Medicare payments, (c) more broadly, add to the body of knowledge on the usage of random forest and other methods used in the study [2] for the purpose of implementing machine learning techniques in health informatics, and (d) analyze linear generalized additive model (GAM) [9] as a method which exists between parametric and non-parametric methods on Medicare payments. Here, the authors would like to define standardized Medicare payment as [10] “a process to remove the area and policy-based payment differentials allowing for a more accurate comparison of resource use between providers and across geographic region.” This definition is presented based on the study provided by O’Donnell et al. [10]. The investigators involved in this study have attempted to identify critical variables that effect standardized Medicare payments. It is important to note that “total standardized payment” refers to standardized payments with respect to all services provided by the healthcare provider. Assessing and reducing hospital readmissions has become a key element in improving healthcare delivery [11].

An important motivation towards carrying out this important study is the increase in healthcare costs tied to Medicare payments. Hospital readmissions are defined as, “admission to a hospital within a given time period after an original admission (often time defined within 30 days).” The recent changes in policies by Centers for Medicare and Medicaid Service (CMS) [12] have incentivized outpatient care to decrease patient readmission rates. As such, ascertaining the risk of readmission for each patient with high accuracy is an important step to decrease readmission rates. One method to accomplish this goal is comparing various predictive models to calculate risk of readmissions among patients being discharged to determine the most accurate model. Here, it is important to mention that Futoma, Morris, and Lucas [11] used a dataset of 3.3 million hospital admissions obtained from New Zealand Ministry of Health and examined hospital readmissions. The readmission was treated as a binary classification problem between high or low chance of readmission. Here, it is important to note that hospital readmissions are tied to Medicare payments for healthcare providers and therefore, the investigators have decided to discuss this topic here. Here, it is important to note that the research study is focused on Medicare standardized payments for physical therapies using machine learning approaches.

In this article we first provide the reader a brief background information on the research methods used for the study. This is followed by the description of the dataset and an overview of the research process. This is followed by a description of the individual methods employed and their associated results. A discussion on the results obtained along with the limitations of the experiment is presented and finally the authors conclude with a brief description of the core contributions and direction of future research work.

2. Background

In this section the authors attempt to explore the usefulness and applicability of the individual machine learning methods explored for achieving the aforementioned research objectives.

2.1. Summarizing Previous Work Conducted in Using Random Forest Analysis for Predicting Medicare Payments

Based on the existing literature, few key methods were identified as critical in predicting a few important variables associated with Medicare costs. Here, it is to be noted that random forest [4] has the possibility of helping ontology development [13] that will be useful in developing knowledge bases for decision support systems [3,14,15]. Selecting the correct regression method for predicting an outcome is an important step in medical decision making. Random forest is one method that has been used in the medical field for classification and predictive tasks, although, it is an under used method. Torgo [16] provided an overview of decision trees, random forest, and their uses in classification, diagnosis, and prediction. Here, the author presents different induction methods for trees and the domains where they are the most effective. Furthermore, Podgorelec, Kokol, Stiglic, and Rozman [3] present how decision trees are used and compare the approach with other prediction models. It is important to mention that Khalilia et al. [17] analyzed the healthcare cost and utilization report (HCUP) to predict disease risk of individuals based on medical diagnosis history. The dataset presented 8 million records with both clinical and non-clinical records. The diseases considered were cancer, heart disease, diabetes, hypertension, osteoporosis, and other related diseases. Additionally, the random forest learning method showed promising results as compared to support vector machines (SVM) bagging and boosting for receiver operating characteristic (ROC) and area under curve (AUC). Denis Arnold [9] in their work on linguistics applied both random forest and generalized additive models (GAM), including the linear model. A key observation made here was that random forest was a good method for analyzing variable importance while GAMs were effective in modelling non-linear interactions. The current study employs random forest techniques because they rely on several decision trees to make predictions which helps to prevent the issue of overfitting models which is common in decision tree regression [18,19].

2.2. Decision Tree Regression

Loh [15] illustrated the effectiveness of decision trees in predicting continuous variables. This study focused on modern methods of regression tree algorithms, specifically those that can partition data with linear splits and other sophisticated partition models. It is worth mentioning that these methods can be applied to all types of statistical models and distribution types. The findings in this paper delineate the strengths and potential pitfalls of random forest models. Specifically, while this analysis was effective in predictive capacity, there were limitations in the handling of missing values and covariates for longitudinal data. Single tree methods were also less capable in terms of accuracy compared to new ensemble methods that combine different techniques of predictive analysis. However, this study provided a foundation for the work presented in this article by showcasing the strengths of decision tree regressions and showing its effectiveness in continuous variable predictive analysis. It is worthwhile noting that Williams and Wan [20] described how decision tree regression and random forest models can be effectively used for evaluating clinical practices and their associated decision-making process to improve healthcare services provided by the healthcare providers.

2.3. K-Nearest Neighbors

It is important to note that Zhang et al. [21] in their work considered K-nearest neighbors (KNN) because of its simplicity and power of classification. Here, the investigators formulated the idea that it was impractical to assign the K-value to all test samples by using a cross-validation method. They proposed a K decision tree to learn optimal K-values during the training and then kTree would output the optimal K-value for each test sample and this resulted in greater accuracy as compared to traditional KNN methods. K* tree enabled to conduct KNN classification by applying a subset of training records for the leaf nodes rather than considering all the training samples. Thus, the importance of K-value was illustrated in the work and we drew inspiration to apply different K-values for unscaled all variable dataset and unscaled select variable dataset. An important study presented by Cherif [22] proposed a way to improve the performance of KNN by clustering and attribute selection for breast cancer diagnosis. This optimization led to an improved performance in the use of KNN with an F-measure of 94%. In the present work, the authors have derived motivation from this study. KNN has been used by removing top three variables which exhibit a high correlation with the dependent variable.

2.4. Linear Generalized Additive Model

Linear GAM is a type of semi-parametric methods that is based on the generalized linear models [23]. The smooth functions of the model are designed to capture the non-linear relations between the independent and the dependent variables. Ilseven and Gol applied various methods for predicting monthly electricity demand with a high level of accuracy [24]. They considered methods like multiple linear regression (MLR), linear GAM, multivariate adaptive regression splines (MARS), KNN, classification and regression trees (CART), neural networks (NN) and support vector machines (SVM) methods over metrics like mean absolute percentage error (MAPE), mean absolute error (MAE), and Root Mean Square Error (RMSE). It is important to note that some of the critical findings of this study have motivated the authors to use Linear GAM and RMSE in performing the required analysis.

2.5. Comparison with Other Key Related Works

At this point the investigators would like to illustrate a few other projects that have attempted to perform similar analyses.

Table 1. Comparison of research projects and analysis methods.

Research Study	Analysis Techniques	Results
This Project	Multiple linear regression vs. decision tree vs. random forest	Random forest and decision tree analysis outperformed multiple linear regression in predicting Medicare physical therapy payments.
Loh 2014 [15]	Decision tree analysis	Decision tree analysis was effective in use for continuous variable prediction (baseball player salaries).
Long 1993 [14]	Decision tree analysis vs. logistic regression	Logistic regression slightly outperforms decision tree analysis for predicting acute cardiac ischemia classification.
Futoma 2015 [11]	Logistic regression, logistic regression with multi-step variable selection, penalized logistic regression, random forest, and support vector machine	Random forests were superior in predicting readmission rates compared to other methods of predictive analysis.

provides a comparison of the various analysis methods used through literature in the field of medical sciences.

3. Materials and Methods

3.1. Description of the Dataset Used for Experimentation

The dataset used in the study consists of twenty-five independent variables as indicated in

Table 2. Linear relationship of training variables with the predicted feature.

Index	Alias Name	Feature Name	Correlation
27	TotalPayment	Total Medicare Standardized Payment Amount	1.000000
7	PatientProxy	Proxy for # of new patients	0.796309
3	#MedicareBeneficiaries	Number of Medicare Beneficiaries	0.747528
5	MedicareBenefit	Medicare standardized amount benefit	0.474725
2	HCPCS	Number of HCPCS	0.335347
6	PhysicalAgentPercentage	Physical agent percentage	0.205529
8	BeneficiaryAge	Average Age of Beneficiaries	0.175424
9	HCCBeneficiary	Average HCC Risk Score of Beneficiaries	0.170843
14	RiskAdjustedCost	Standardized Risk-Adjusted Per Capita Medicare Costs	0.135006
17	MedicareBenefitPopulation	Percent Medicare Fee-For-Service(FFS) benefit pop 2014	0.130285
18	AverageAgeFee	Medicare FFS Benefit Average Age Fee for Service 2014	0.128929
20	AverageHCCScoreFee	Medicare FFS Benefit Avg HCC Score Fee for Service 2014	0.120106
23	OldInDeepPoverty	Percent of persons 65 or older in Deep Poverty 2014	0.080313
19	FemaleMedicareBenefit	Percent of Medicare FFS Benefit Female 14	0.064783
13	LargeMetroArea	Large metro area	0.012649
12	NonMetroArea	Non-metropolitan area or missing (9 counties missing)	0.012599
21	MedicareBeneficiaryforMedicaid	Percent Medicare Beneficiary Eligible for Medicaid 14	0.002792
11	SmallMetroArea	Small metro area	−0.000148
22	MedianHouseholdIncome2014	Median Household Income 2014	−0.008139
10	MiSizedMetroArea	Mid-sized metro area	−0.024261
1	ReportingDPTDegree	Reporting DPT degree	−0.048336
16	PhysicalTherapistsPer10000	Physical Therapists per 10,000 pop 2009	−0.068251
15	PrimaryCarePer10000	Primary care Physicians per 10,000 pop 2014	−0.081168
24	PhysicalTherapsistsPerBeneficiary	Physical Therapists per beneficiaries ratio	−0.084612
4	ChargeToAllowedAmount	Charge to allowed amount ratio	−0.098310
0	Female	Female gender	−0.175792

and examines the total Medicare amount paid by individuals given certain non-personally identifiable information as the independent variable. The investigators created a machine learning model to take the twenty-five predictor variables as input and predict the total standardized Medicare amount to be paid. The dataset had data points for total annual dollar payments to 40,662 physical therapists. In the dataset, one of the feature variables contained non-numeric values; therefore, it was converted to a bit vector of size four owing to four unique values contained within it. In addition, this dataset was used as the 2014 Medicare Provider Utilization and Payment Data [25] that had the necessary information in relation to procedures and services provided to individuals covered under Medicare by physical therapists. This dataset encompassed variables and associated data that had critical information on the dollar amount spent for individuals covered under Medicare and the type of services used with respect to physical therapy. The choice of this dataset for this study was made based on the idea that the associated results could be critical in identifying the factors that affect the total Medicare standardized payment which happens to be the dependent variable for the study addressed in this article. It is important to mention here that Gurupur et al. [8] have previously worked on the 2014 Medicare Provider Utilization and Payment Data focusing on predictive analysis using deep learning techniques. The same dataset was used in this project for the purpose of comparing statistical techniques; thereby, expanding on the body of knowledge of predictive analytics. It contains data on physical therapy patients and amounts paid to the physical therapists in each case. In this dataset, the Healthcare Common Procedure Coding System (HCPCS) is an important part.

Termed as the “curse of dimensionality” by Bellman [19], machine learning is computationally very expensive, and the time complexity increases as the number of variables increases. As a result, this study attempts to demonstrate that classical approaches such as random forest are a viable option for particular datasets where the number of variables is relatively large. In general practice, a paradigm should be chosen [26] only after significant statistical analysis of the given dataset often with an input from a domain expert who can point out certain non-correlated or unimportant variables which can be directly removed. It is important to note that in this dataset some feature values followed a very close linear trend with respect to the feature to be predicted, thus a MLR [8] approach was selected for comparison with the decision tree method. With regards to this phenomenon, Zuckermann et al. [27] depict the calculation of percentage probabilities of a patient being readmitted within the time specified time period. Here, the classification problem starts resembling a continuous variable prediction problem as there are a hundred labels that can be applied to the probability from 0 to 100 percent. Then based on the percentage and a predetermined threshold a decision is made regarding if the patient will be readmitted or not. In addition, investigators have used decision trees to capture more complex relationships among variables in the dataset. This project aims to take lessons learned from these projects to compare random forest to MLR analysis to comprehend the strengths and limitations of random forest within the context of total Medicare payment for physical therapists. Sci-kit learn a library provided for Python programming language was used for normalization and modelling machine learning algorithms used in the analysis. The versions were Python 3.5.2 scikit-learn 0.19.1, the Pandas 0.23.1, and Numpy 1.14.5 on hardware Intel^® Core™i5-7200 U CPU @ 2.50 GHz.

Here, the investigators would like to point the following key motivational factors that led to the choice of this dataset: (i) the dataset was well suited to fulfill the core objectives of the study, and (ii) any work performed on the dataset can be scaled for the prediction of Medicare payments for non-physical therapy practices.

3.2. Data Pre-Processing

The general workflow (shown in Figure 1) of our approach is divided into three parts: (a) identify the selected predictor variables, (b) the location feature was converted from string values to bit vectors using one-hot encoding, and (c) the dataset was divided into training set and test set by implementing a 60:40 ratio. The training set was used to train MLR models and the resulting models were used on the test dataset to obtain results. Thus, a training set containing 60% of the training values and a test set containing 40% of testing values was used for all the models under consideration. The results of the study are detailed in the following section. All the different values that a single nominal feature could take were mapped to a corresponding bit value, thus capturing the uniqueness of each string. To select the necessary variables the variables that impacted the predictor variable to the greatest extent was first identified. This was followed by the application of MinMaxScaler to the predictor variable to normalize the values.

4. Results

4.1. Results of Data Pre-Processing

To test the best model for the problem, various combinations of the pre-processing steps and training models were compared. Performing this comparison helped the investigators find the best results and comprehend the significance of various steps involved in a machine learning pipeline. Interestingly, the difference in the RMSE for the selected feature training and the training performed on all variables did deliver significantly different results. An RMSE of 15,349.55 was observed for the MLR model using all variables and a RMSE of 32,172.84 was observed for the model using selected variables dataset. This was substantially different from the random forest results, where RMSE of 3739.26 was observed for the model using all variables and root mean error of 30,685.62 was observed for analysis involving the selected feature dataset. The R² value for the MLR model with all variables was observed to be 0.82 and the value derived from random forest regression was equal to 0.99. Table 2 shows the correlation between the selected independent variables and the dependent variable. It is important to point out that values closer to 1 are highly correlated. This correlational analysis is performed using Pearson’s R. The linear relationship of the top correlated variables is visualized in Figure 2 using scatter plots.

The dataset was further used to build two separate sets of training and testing datasets based on the correlation of the variables. The first data set, termed as the “complete dataset”, contained all the variables; the second data set, termed as the “selected variables dataset”, contained all variables expect the three highly correlated variables depicted in Table 2 in bold. The complete dataset contained 25 variables, including the abovementioned three variables.

A situation when all the variables in the unscaled dataset was considered led the authors to analyze the factors of correlation. Pearson’s correlation [28] was considered as it provided useful ways of measuring linear association between the variables in the dataset. A value of 1 indicated good correlation; 0, no correlation; −1, negative correlation. The Panda library from Python was used to develop a script to graphically plot the correlation among variables for the entire dataset as shown in Figure 3. The color codes were filled to indicate relative correlation between all the variables. A dark red indicated high degree of correlation; dark blue of negative correlation and intermediate colors showed the variations among the extremes. Figure 3 indicates weak correlation between variables. The presence of weak correlation may not be very conclusive; to work on it further, we may need to apply it to a model. This helped the investigators draw insights into the relatively poorer performance of MLR model using metrics such as RMSE and R². Another useful insight could be provided by the metric “Mean Absolute Error (MAE)” which investigates mean of absolute errors.

4.2. Multiple Linear Regression Results

Some of the variables in the dataset are linearly related, therefore a linear regression model was built using the scikit-learn library [1] for Python. The dataset was divided into two sets. One part was used to train the regression model and the second part was used to test the final trained model to check for accuracy. The data were split in a 60:40 ratio with 60% of the data used for training which was about 24,397 data points. Rest of the 40% of the data were used for testing and this was applied to all methods.

The resulting model was used to predict the testing data set and the predictions were stored and plotted against the actual values. The following parameters values were used. Fit intercept was set to true and Normalize was set to False since we had already scaled the data in two of the four MLR models tested. Number of jobs was set to None since we did not use any parallelization for training the models.

Table 3. Performance of multiple linear regression, linear generalized additive, decision tree, random forest and K-nearest neighbors in terms of root mean square error and R².

Model and Type	Dataset	Root Mean Square Error	R2 Score
Multiple linear regression (parametric)	All variables and unscaled data	15,349.55	0.83
Multiple linear regression (parametric)	Selected variables and unscaled data	32,172.84	0.24
Linear generalized additive model (semiparametric)	All variables and unscaled data	13,469.41	0.87
Linear generalized additive model (semiparametric)	Selected variables and unscaled data	31,057.77	0.29
Decision tree regression (nonparametric)	All variables and unscaled data	8204.61	0.95
Decision tree regression (nonparametric)	Selected variables and unscaled data	32,587.74	0.22
Random forest regression (nonparametric)	All variables and unscaled data	3739.26	0.99
Random forest regression (nonparametric)	Selected variables and unscaled data	30,685.62	0.30
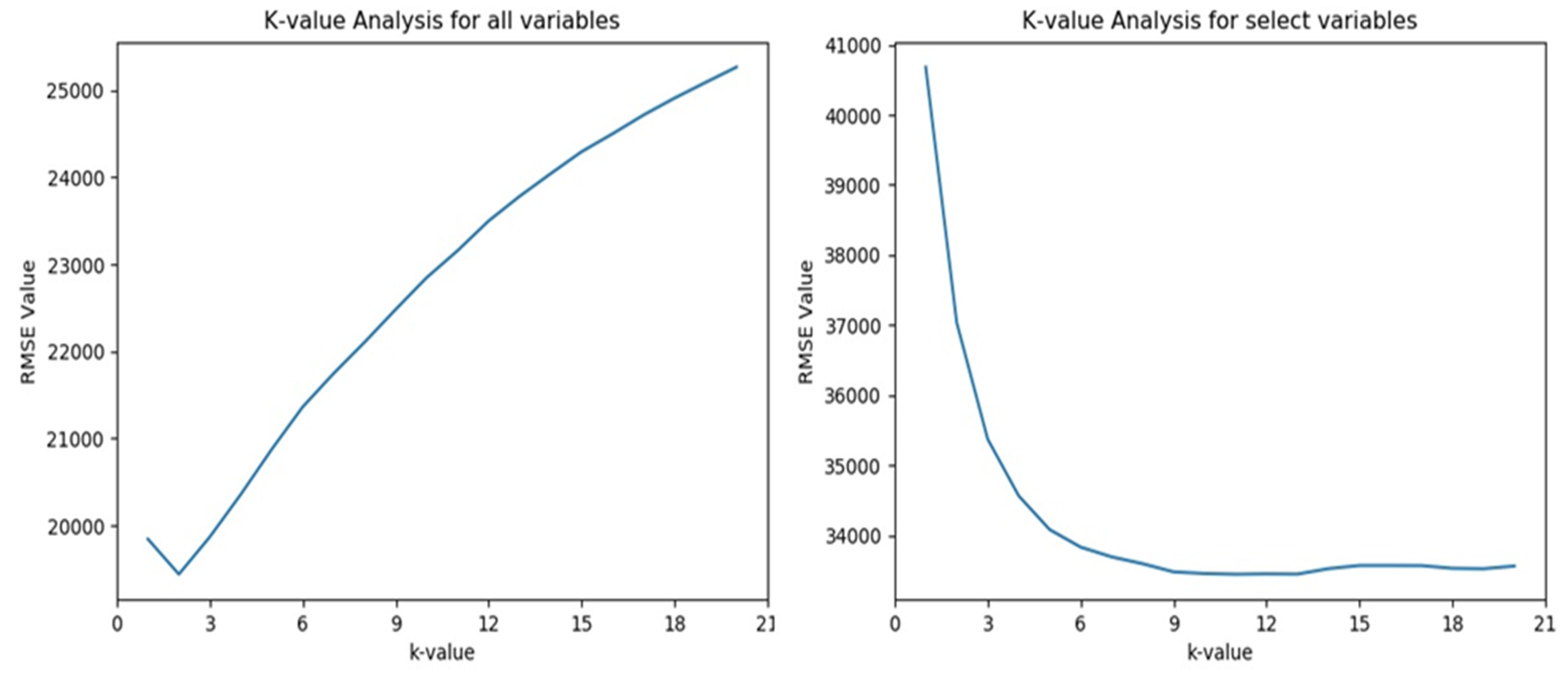
K-nearest neighbors (nonparametric)	All variables and unscaled data	19,438	0.72
K-nearest neighbors (nonparametric)	Selected variables and unscaled data	33,445.64	0.17

shows the root mean squared values and the R² values of all our MLR models. Figure 4 includes relationship between the predicted model and the original values for the MLR model. The graph plots the original values and the predicted values against each other, most of the points lie near the straight diagonal running in the middle, which indicates a good performance.

Figure 5 shows the performance of the MLR model on dataset with selected variables, i.e., with the top predictor variables removed from the dataset. Figure 5 illustrates that the points are drifting from the diagonal line for unscaled selected variables thereby establishing the need for using all the variables in the dataset. This clearly shows that at times there is a performance penalty in terms of accuracy when a few selected independent variables are used for analysis.

4.3. Decision Tree Regression Analysis and Results

The MLR model was also compared with the decision tree regression (DTR) model. DTR uses a greedy algorithm called classification and regression tree algorithm (CART) to grow a decision tree. The representation of the CART model is a binary tree. A node represents a single input variable X and a split point on that variable. The leaf nodes of the tree contain the value of the predicted/dependent variable. Once created, a tree can be navigated with a new instance of data following each branch with the splits until a final prediction is made. Thus, a decision tree splits the input space recursively. A greedy approach is used to divide the space called recursive binary splitting. This is a numerical procedure where all the values are lined up and different split points are tried and tested using a cost function. The split that minimizes the cost is selected [29]. The cost function for the regression model is the mean squared error or absolute mean error depending on the dataset in use. The critical part of the DTR is the splitting algorithm is described in [14].

4.4. Application of Decision Tree Regression

DTR can capture complex non-linear relations between different variables [11]. Therefore, it was a computational model used for testing. The scikit-learn library used for this analysis includes a decision tree regressor class. A few parameters of the class were changed, and others were not owing to the nature of the problem being analyzed. The major attribute included maximum depth which defines the depth of the constructed tree. This was varied and the resulting RMSE scores were plotted against the maximum depth. The minimum sample split defines the minimum number of samples in the internal node before a split can occur. If the number of samples exceed the minimum sample split, the node is further divided into two. This was set to two for this study since the output is a continuous variable as opposed to a classification variable. Minimum sample leaf defines the number of samples in the leaf node. Its value was set to one for the aforementioned reasons. Maximum variables identify the number of variables to examine before splitting an internal node, while all variables were used for decision tree analysis. Here, it is important to note that the parameter criterion defines the loss function and its value was set to the mean square error whose role is to minimize L2 loss function. Table 3 shows the root mean squared errors and R² values for all the DTR models. To find the optimal value for the tree depth, the RMSE score was plotted against varying tree depths, as depicted in Figure 6. Figure 4 presents the predicted values versus the original values for the optimal model on all variable’s dataset. Most of the points lie near the diagonal in the center indicating higher accuracy in prediction, whereas Figure 5 represents the predicted values of the model on the dataset with top predictors removed. As can be seen from Table 3, the performance of the DTR model has displayed a higher level of performance in terms of predictability when compared to the linear model that involved MLR on the test dataset.

After observing the near-root level split nodes in Figure 7, we can make a few conclusions regarding the importance of certain variables in the decision making when predicting the Medicare physical therapy payments. Here, it is important to inform the readers that the value of X associated in the parenthesis is the same as the value in the index table in Table 2. The three-level decision tree was observed, and the split nodes now were “Average age of beneficiaries”, “Number of Medicare Beneficiaries” and “Medicare standard amount benefit”. The first major split is on the variable “Average age of beneficiaries.” This feature is important because it sets an upper limit to our predicted variable, meaning that the maximum value of this variable is directly proportional to the maximum value of the predicted variable. This correlation was easily found by analyzing the decision splits in tree model used in the study. A similar analysis was carried out on factors affecting differences in Medicare reimbursements for physicians’ services by [7]. However, it is important to point out that they did not use machine learning methods [30].

4.5. Random Forest Analysis and Results

Decision Trees work well for correlating and predicting for non-linear data; however, the deeper the level of the nodes are, the higher the chance of overfitting. This means that the model starts fitting to the details of the data instead of the general properties of the data distribution. Random Forest overcomes this shortcoming by combining models to reduce overfitting. This method is termed as “bagging.” Bagging [16] makes use of an ensemble of parallel estimators each of which over-fits the data and averages the results to find a better model. As observed in the results of this study, this method was very effective. To test the optimal number of trees to use and the effect of number of trees on the performance of the random forest algorithm, the model was tested with a sequence of different number of trees plotted against the RMSE values and R² values as depicted in Figure 8. The variable importance of all the splits on variables (tree depth) was also seen as compared to decision tree regression in (Figure 6). It is important to note that the R² in case of random forest regression was computed by correlating the observed scores with the predictions generated by the random forest model.

The test results of random forest study were trained on unscaled data and all variables, and finally on unscaled and selected variables. The following major parameter values were chosen for the models: (a) criterion was set as MSE (same as decision tree model), and number of trees was set to 500, (b) random state was set to 0 this is the seed used by the random number generator used by the Random Forest, and (c) all the parameters had the same value as the decision tree model. Figure 4 includes a plot of the original values and the predicted values of the random forest model. Figure 5 represents the predicted values of the random forest model with the top predictors removed. Table 3 shows the R² scores of the predicted values for each type of dataset. The random forest regressor performed the best out of all the models tested. Specifically, using all variables the random forest regression had an R² value of 0.99 when compared to the decision tree with a value of 0.95, the MLR model with an R² value of 0.83 and Linear GAM model with an R² value of 0.87.

4.6. K-Nearest Neighbors Analysis and Results

It is observed that KNN is one of the simplest machine learning algorithms available for regression analysis. It is known to work well for large training datasets. KNN is a non-parametric regression that can handle many predictor variables. The value of K or the number of neighbors affects the bias-variance tradeoff. A low value of K results in low bias but high variance and on the contrary a larger value of k may result in a lesser variable fit. The optimal K-value for the dataset with all variables and for the dataset with selected variables is illustrated in Figure 9. The optimal is the one with the smallest RMSE value. Thus, from the analysis we choose k = 2 for further study action on unscaled and all variables and a k = 11 for unscaled and selected K-nearest neighbors model was trained on unscaled all variables and unscaled with selected variables. The value of K was chosen as 2 as illustrated in Figure 9. The measured vs. predicted values was as illustrated in Figure 4 and Figure 5. For the study for all variables KNN could achieve an R² value of 0.72 and for the study with top correlated variables removed KNN’s performance was the poorest among all models considered and it was indicated as an unfit model for the considered data with an R² of 0.17. A low value for R² indicates that the model is not highly recommended for more accurate predictions.

4.7. Analysis of Linear Generalized Additive Model

The Linear GAM was implemented using the gridsearch() method from Python version 3.5.2, which performs a search over parameter space for optimal parameters. The feature functions use splines to model non-linear relations. The number of splines we considered were 25 and 11 models from logscales ranging from 1 × 10⁻³ to 1 × 10³ were set to logspace to find the best smoothing which may either be linear or non-linear features. The above parameters resulted in optimal value for R² and were thus considered for application to the linear GAM which resulted in a R² of 0.87 for all variables and R² 0.29 for selected variables. The measured vs. predicted values for all variables and select variable dataset is as illustrated in Figure 4 and Figure 5. Here, it is important to note that Linear GAM has performed better than methods such as multiple linear regression. An important theoretical observation here could be that the linear GAM model works well for datasets where variables have minimum co-linearity. This claim might need further investigation with similar other datasets. While the study illustrates the use of random forest regression in analyzing datasets where variables have minimum correlation, it also identifies the possibility of the weakness of the K-nearest neighbors method. It was evident that the degree of correlation to the dependent variable was further reduced when the top three predictor variables identified in Table 2 were removed. This removal of top predictor variables resulted in an instability in correlation and had an impact on the performance of the K-nearest neighbors analysis.

5. Discussion

5.1. Discussion on Efficiency and Computational Time for the Methods Applied

The novelty of the experimentation illustrated in this article is that there is very little information available on the predicting power of the methods discussed on Medicare and especially on total Medicare standardized payment.

As the size of data grows, it becomes imperative to measure the computational time efficiency. The computational time efficiency analysis is as illustrated in

Table 4. Computational time analysis.

Analysis Technique	Computational Time (ms)
Multiple linear regression	63.558
Decision tree	532.042
Random forest	288,897.591
K-nearest neighbor	950.597
Linear GAM	1134.083

. It can be easily visualized that MLR model outperformed decision trees [31] and random forest, KNN and linear GAM models by 88.05%, 99.97%, 93.31% and 94.39%, respectively. This analysis shows that MLR models could have a positive role for big data applications where computational time efficiency could be one of the important criteria. This leads to the idea of exploring additional data samples in the area of population health and its impact on improving the accuracy of random forest regression as compared to more advanced deep learning algorithms [14,32], where more samples can help in accurate predictions [33]. This study provides a key contribution not only in terms of the accuracy of three different types of machine learning methods but also provides key insight into their associated computational time. The evaluation of computational time is a key factor with large and ever-increasing size of data associated with population health.

Table 3 provides a comparison between different methods used in terms of accuracy. The authors used MLR and random forest on selected variables and the complete dataset to predict the total Medicare payment amount for the physical therapists. Mean absolute error (MAE) and R² were computed for the test dataset. The MAE of the MLR model was close to 24% of the mean of the dependent variable. A model is considered good if MAE could be a value close to 10%. Thus, MLR with its R² of 0.79 and MAE of 24% had a lower performance as compared to decision trees whose R² was 0.97 and MAE was approximately 5%. The R² for linear GAM model was found to be 0.87 and MAE turned out to be 21.43%. The R² for random forest was 0.99 and MAE close to 2%. The R² for K-nearest neighbors was 0.72 and MAE close to 26.60%, which indicated the highest deviation from the mean and among all models in the study. This clearly corroborated the concept that random forests were more suitable for data which were not highly correlated.

5.2. Limitations and Future Work

This analytic report has several potential limitations. First, predictive modeling approach could be assisted by a theoretically informed framework that could guide the development of precise and valid statistical models. For instance, a transdisciplinary perspective enables the investigator to identify the relative importance of predictor variables such as the contextual, ecological, organizational, and personal factors influencing in the variability in readmission rates [34]. Secondly, from a broader perspective, the comparative analysis of decision tree regression was not compared with other correlation analytic techniques such as ANOVA and neural network analysis. Traditionally, MLR has been employed for health care, but in Seligman et al. [35], it was found that feed forward neural networks outperformed linear regression, penalized regressions, random forests, when analyzing the effect of social and economic factors on health issues like systolic blood pressure, body mass index, waist circumference, and telomere length. Therefore, it would be interesting to apply neural network models in future studies. Thirdly, the investigators limited the study to the dataset readily available for the purpose of this study. Thus, the generalizability of the results is limited. Future research could include longitudinal panel data to be analyzed by selected variables guided by specific theoretical frameworks. Thus, predictive models for health services use could be replicated and verified. Gurupur et al. [8] created a binary valued prediction variable using the total payment amount and the median amount and demonstrated the power of deep learning methods [13] in classification, whereas the investigators involved in this study were more interested in using the dataset to predict the exact value of the total payment amount using relatively simpler methods that require less computation and even try to cut down the number of variables required to make these predictions.

6. Conclusions

A key finding of this research is the analysis of linear GAM and random forest regression in addition to other methods employed for experimentation. Linear GAM is a fairly newer method and this article expands on the body of knowledge in terms of its application on Medicare reimbursements. The key contributions of the study discussed in this article are as follows: (i) comparison between linear GAM and random forest regression for analyzing CMS data, (ii) demonstration of hyper-parameter tuning to minimize bias-variance and testing for CMS data for random forest regression, and (iii) an overall comparison of the machine learning methods for prediction on CMS data.

Furthermore, this research provides a multidimensional view of predicting standardized payments for Medicare. This can potentially lead to further investigations of theoretical importance involving the synthesis or development of deep learning networks, directed acyclic graphs, and structural equation models. Therefore, the described study will serve as a precursor for more advanced studies involving machine learning on Medicare payments. As aforementioned, there is a possibility that decision tree regression can be used in synthesizing knowledge bases [20,32,36,37,38] used in the development of expert systems. The investigators will be advancing the work illustrated in this article in this direction applying various correlational and predictive analysis in implementing knowledge curation that furthers the science of decision support systems [26]. In addition, in future studies, the interplay of statistical variable optimization and deep learning [39] Regression could be deployed for accurately predicting medical healthcare affordability for larger size datasets which would help clinical practitioners. Lastly, the emergence of the adversarial machine has opened a new chapter to adversarial attacks to machine learning algorithms and these challenges need to be addressed in our future studies [40,41].