Study of Transformed η^ζ Networks via Zagreb Connection Indices

Abstract

A graph is a tool for designing a system’s required interconnection network. The topology of such networks determines their compatibility. For the first time, in this work we construct subdivided ${\eta }^{\zeta }$ network $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ and discussed their topology. In graph theory, there are a variety of invariants to study the topology of a network, but topological indices are designed in such a way that these may transform the graph into a numeric value. In this work, we study $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ via Zagreb connection indices. Due to their predictive potential for enthalpy, entropy, and acentric factor, these indices gain value in the field of chemical graph theory in a very short time. ${\eta }^{\zeta }\mathsf{\Gamma }$ formed by $\zeta$ time repeated process which consists ${\eta }^{\zeta }$ copies of graph $\mathsf{\Gamma }$ along with $\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\left|V\left(\mathsf{\Gamma }\right)\right|\zeta {\eta }^{\zeta -1}$ edges which used to join these ${\eta }^{\zeta }$ copies of $\mathsf{\Gamma }$. The free hand to choose the initial graph $\mathsf{\Gamma }$ for desired network $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ and its relation with chemical networks along with the repute of Zagreb connection indices enhance the worth of this study. These computations are theoretically innovative and aid topological characterization of $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$.

1. Introduction

Graph theory may use to design desired interconnection networks and provides its topology. Furthermore, interlink computer science, chemistry and mathematics for practical usage. This area of study has their worth as a separate field named Chem-informatics, a combination of chemistry, information science, and mathematics. In this discipline QSAR/QSPR relationship, bioactivity, and classification of chemical compounds are examined.

It is a new area of research that has captivated the interest of researchers. It creates a relationship between the structure of organic compounds and their physio-chemical properties using several helpful graph invariants and chemical graph of underlying compound. A chemical graph is a representation of a chemical compound’s structural formula using graph theory, consists vertices in place of atoms and edges for chemical bonds.

The theoretical analysis of underlying substance molecular graphs via graph invariants might assist in the QSPR/QSAR investigations. The use of topological descriptors of chemical structure in the study of structure-property interactions is common now a days, particularly in QSPR/QSAR investigations. There are many graph invariants which used to characterize interconnection networks for desired investigations in computer science and chemistry. However, in the QSPR/QSAR analysis, topological indices play an important role as they depict chemical substances’ physio-chemical properties. Topological indices are the graph invariants which may used to reduce the practical work at some extent through prediction of desired property of related structure via topology of the graph [1,2]. Harry Winner was the first who used the topology of chemical graph for prediction of bolling point in 1947 [3]. Later on, in 1972 and 1975, Gutman with their collaborator introduces

$$M_1\left(\mathsf{\Gamma }\right)=\sum _{uv\in E\left(\mathsf{\Gamma }\right)}(d_u+d_v),M_2\left(\mathsf{\Gamma }\right)=\sum _{uv\in E\left(\mathsf{\Gamma }\right)}(d_u\times d_v)$$

indices in there work of $\pi -$ electron energy of hydrocarbons [4,5]. In [6], another version of Zagreb indices named Hyper Zagreb index introduced as

$$HM\left(\mathsf{\Gamma }\right)=\sum _{uv\in E\left(\mathsf{\Gamma }\right)}{(d_u+d_v)}^2.$$

Recently, Ali and Trinajstic [7] used modified version of Zagreb indices named first Zagreb connection index which based on connection numbers ${\tau }_u$ associated with the vertices of graph as

$$Z{C}_1\left(\mathsf{\Gamma }\right)=\sum _{s\in V\left(\mathsf{\Gamma }\right)}{\tau }_u^2.$$

The connection numbers ${\tau }_u$ is the total of distinct vertices which are at distance two from the fixed vertex $u\in \mathsf{\Gamma }$. In [8], modified first Zagreb connection index studied which is defined as

$$Z{C}_1^{*}\left(\mathsf{\Gamma }\right)=\sum _{s\in V\left(\mathsf{\Gamma }\right)}\left(d_u{\tau }_u\right)=\sum _{uv\in E\left(\mathsf{\Gamma }\right)}({\tau }_u+{\tau }_v).$$

The second Zagreb connection index is

$$Z{C}_2\left(\mathsf{\Gamma }\right)=\sum _{uv\in E\left(\mathsf{\Gamma }\right)}{\tau }_u\times {\tau }_v.$$

Refs. [7,9,10,11,12] justify the applicability of these indices through correlation with entropy and acentric factor. For the first time in this work we construct subdivided network as $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ and discussed its topology. One can extend applications of these networks by using fuzzy graphs techniques as used in [13,14,15]. Furthermore, We determined closed form formulas for $Z{C}_1,Z{C}_2$ and $Z{C}_1^{*}$ of $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ when ${\eta }^{\zeta }\mathsf{\Gamma }$ generated by the single vertex graph $\mathsf{\Gamma }$ and extend our finding up to a large class generated by any graph $\mathsf{\Gamma }$. As applications, we computed $Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right),$ $Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)$ and $Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)$ when $\mathsf{\Gamma }$ represents a specific family of graphs. The research work [16,17,18,19,20,21,22,23,24] on Zagreb connection indices and the correlation of these indices with acentric factor, enthalpy and entropy along with the formation of with chemical networks by ${\eta }^{\zeta }\mathsf{\Gamma }$ assure applicability of this work.

2. Material and Method

We adopted techniques as used in [25,26,27,28,29,30] for edges and vertex partition. We admits subdivision technique for the desired network $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$. We used notation for graph, edge set, vetex set, order, size and degree of vertex $s\in \mathsf{\Gamma }$ as $\mathsf{\Gamma },V\left(\mathsf{\Gamma }\right),E\left(\mathsf{\Gamma }\right)$, $\left|V\left(\mathsf{\Gamma }\right)\right|=n_{\mathsf{\Gamma }},\left|E\left(\mathsf{\Gamma }\right)\right|=e_{\mathsf{\Gamma }}$ and $d_s$, respectively.

${\eta }^{\zeta }$ Network

${\eta }^{\zeta }\mathsf{\Gamma }$ network formed by $\zeta$ time repeated process using Cartesian product. It consists ${\eta }^{\zeta }$ copies of graph $\mathsf{\Gamma }$ along with $\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\left|V\left(\mathsf{\Gamma }\right)\right|\zeta {\eta }^{\zeta -1}$ edges which used to join these ${\eta }^{\zeta }$ copies of $\mathsf{\Gamma }$ as ${\eta }^{\zeta }\left(\mathsf{\Gamma }\right)=\eta \left({\eta }^{\zeta -1}\mathsf{\Gamma }\right)=\eta \left(\eta \left({\eta }^{\zeta -2}\mathsf{\Gamma }\right)\right)=\eta \left(\eta \left(\eta \left(\left({\eta }^{\zeta -3}\mathsf{\Gamma }\right)\right)\right)\right),\dots ,$$\underset{\underset{(\zeta -1)\mathrm{times}}{⏟}}{\eta \left(\eta \right(\eta (\dots (\eta }\left(\eta \mathsf{\Gamma }\right))\dots ))),$$\underset{\underset{\left(\zeta \right)\mathrm{times}}{⏟}}{\eta \left(\eta \right(\eta (\dots (\eta }\left(\mathsf{\Gamma }\right))\dots )))$. The new edges which join these copies joined corresponding vertices of all the copies. The total vertices and edges are $|V\left({\eta }^{\zeta }\mathsf{\Gamma }\right)|={\eta }^{\zeta }{n}_{\mathsf{\Gamma }}$ and $|E\left({\eta }^{\zeta }\mathsf{\Gamma }\right)|={\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{\zeta -1}$, respectively. The ${\eta }^{\zeta }\mathsf{\Gamma }$ for $\eta =2$ and $\zeta =0,3,4$ when $\mathsf{\Gamma }$ is a single vertex graph shown in Figure 1.

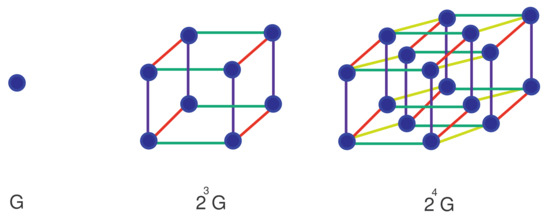
Figure 1. ${\eta }^{\zeta }\mathsf{\Gamma }$ for $\eta =2$ and $\zeta =0,3,4$ when $\mathsf{\Gamma }$ is a single vertex graph.

3. Molecular Networks Identical with ${\mathit{\eta }}^{\mathit{\zeta }}\mathsf{\Gamma }$

The importance of ${\eta }^{\zeta }\mathsf{\Gamma }$ may estimates by its relation with chemical networks as shown in Figure 2.

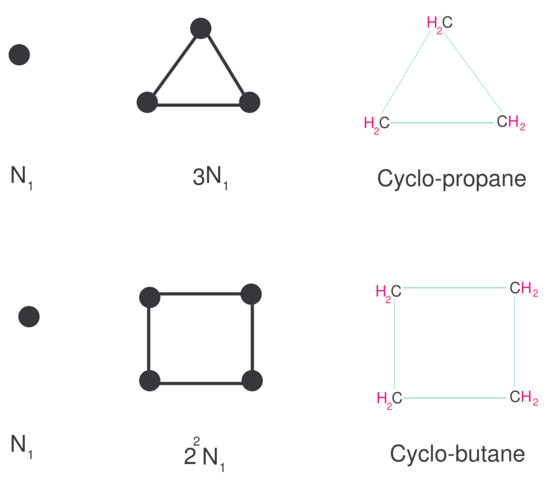
Figure 2. ${\eta }^{\zeta }\mathsf{\Gamma }$ as organic compounds.

Carbon Nanotube $TU{C}_4(m,3)$ as $3P_n$

Carbon nanotube $TU{C}_4(m,3)$ is identical with the graph formed by $P_t$ as $3P_t$, shown in Figure 3.

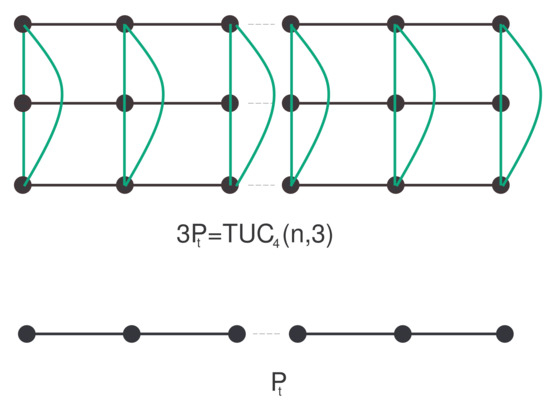
Figure 3. $3P_t$ as carbon nanotube $TU{C}_4(n,3)$.

Cyclo-butane is also identical with $2P_2$.

4. Subdivided Network $\mathit{S}\left({\mathit{\eta }}^{\mathit{\zeta }}\mathsf{\Gamma }\right)$ When $\mathsf{\Gamma }$ Consist Only One Vertex

Subdivided graph obtained by inserting new vertex at each edge, i.e., let $uv\in \mathsf{\Gamma }$ and x be the new vertex and replace each edge $uv\in \mathsf{\Gamma }$ with two edges $ux$ and $xv$ to form subdivided graph $S\left(\mathsf{\Gamma }\right)$. In a similar way, we obtain $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ shown in Figure 4 for $\eta =2$ and $\zeta =2,3$ when $\mathsf{\Gamma }$ is a single vertex graph. There are $|V\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)|=\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{\zeta -1}+{\eta }^{\zeta }$ and $|E\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)|=2\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{\zeta -1}$ vertices and edges of $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$, respectively.

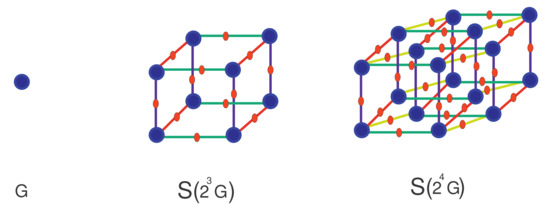
Figure 4. $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ for $\zeta =2,3$ when $\mathsf{\Gamma }$ is a single vertex graph.

Theorem 1.

Let Γ be the graph with $n_{\mathsf{\Gamma }}=1$. Then $Z{C}_1,Z{C}_2$ and $Z{C}_1^{*}$ of $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ are

$$\begin{array}{ccc}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& {\eta }^{\zeta -1}{\eta }^2{(\zeta +1)}^2(\eta +4\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta )\hfill \\ \hfill Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& 2{\eta }^2\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{\zeta -1}{(\zeta +1)}^2\hfill \\ \hfill Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& 6\eta \left(\genfrac{}{}{0pt}{}{\zeta }{2}\right){\eta }^{\zeta -1}(\zeta +1).\hfill \end{array}$$

Proof. 

Let $n_{\mathsf{\Gamma }}=1$, $|V\left({\eta }^{\zeta }\mathsf{\Gamma }\right)|={\eta }^{\zeta },|E\left({\eta }^{\zeta }\mathsf{\Gamma }\right)|=\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{\zeta -1},\left|V\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)\right|=\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{\zeta -1}+{\eta }^{\zeta }$ and $|E\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)|=2\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{\zeta -1}$. The construction of $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ implies $d_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(v\right)\in \{2,\eta (\zeta +1)\}$ and connection numbers ${\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(v\right)\in \{\eta (\zeta +1),2\eta (\zeta +1)\}$ of $v\in S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$. These findings enabled us to find $Z{C}_1(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right),$

$$Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=\sum _{v\in V\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)}{\left({\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(v\right)\right)}^2$$

$$\begin{array}{c}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=\sum _{v\in V\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}{\left(\eta (\zeta +1)\right)}^2+\sum _{u\in V(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\backslash V\left({\eta }^{\zeta }\mathsf{\Gamma }\right))}{\left(2\eta (\zeta +1)\right)}^2\end{array}$$

In case $n_{\mathsf{\Gamma }}=1$ the total number of vertices of ${\eta }^{\zeta }\mathsf{\Gamma }$ are ${\eta }^{\zeta }$, i.e., $|V\left({\eta }^{\zeta }\mathsf{\Gamma }\right)|={\eta }^{\zeta }$ and $|V\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)\backslash V\left({\eta }^{\zeta }\mathsf{\Gamma }\right)|=\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{\zeta -1}$.

$$\begin{array}{c}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)={\eta }^{\zeta }{\eta }^2{(\zeta +1)}^2+4{\eta }^2\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{\zeta -1}{(\zeta +1)}^2\end{array}$$

$$\begin{array}{c}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)={\eta }^{\zeta -1}{\eta }^2{(\zeta +1)}^2(\eta +4\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta )\end{array}$$

(1)

Now for $Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)$,

$$Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=\sum _{uv\in E\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)}{\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(u\right){\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(v\right).$$

For each edge $uv\in E\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)$ the end vertex connection number is $({\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(u\right),$${\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(v\right))=(\eta (\zeta +1),2\eta (\zeta +1))$ and $|E\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)|=2\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{\zeta -1}$. So,

$$\begin{array}{c}\hfill Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=\sum _{uv\in E\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)}\left(\eta (\zeta +1)\right)\left(2\eta (\zeta +1)\right)\end{array}$$

$$\begin{array}{c}\hfill Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=2\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{\zeta -1}2{\eta }^2{(\zeta +1)}^2\end{array}$$

$$\begin{array}{c}\hfill Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=2{\eta }^2\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{\zeta -1}{(\zeta +1)}^2.\end{array}$$

(2)

Now for $Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)$,

$$Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=\sum _{uv\in E\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)}({\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(u\right)+{\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(v\right))$$

Now again, for each edge $uv\in S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ the end vertex connection number $({\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(u\right),$${\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(v\right))=(\eta (\zeta +1),2\eta (\zeta +1))$ and $|E\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)|=2\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{\zeta -1}$. So,

$$\begin{array}{c}\hfill Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=\sum _{uv\in E\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)}(\eta (\zeta +1)+2\eta (\zeta +1))\end{array}$$

$$\begin{array}{c}\hfill Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=2\left(\genfrac{}{}{0pt}{}{\zeta }{2}\right)\zeta {\eta }^{\zeta -1}\left(3\eta (\zeta +1)\right)\end{array}$$

$$\begin{array}{c}\hfill Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=6m\left(\genfrac{}{}{0pt}{}{\zeta }{2}\right){\eta }^{\zeta -1}(\zeta +1).\end{array}$$

(3)

Equation (1) completes the proof. □

5. $\mathit{S}\left({\mathit{\eta }}^{\mathit{\zeta }}\mathsf{\Gamma }\right)$ When $\mathsf{\Gamma }$ Is Any ${\mathit{n}}_{\mathsf{\Gamma }}$-Vertex Simple Connected Graph

There are $|V\left({\eta }^{\zeta }\mathsf{\Gamma }\right)|={\eta }^{\zeta }\left|V\left(\mathsf{\Gamma }\right)\right|$ vertices and $|E\left({\eta }^{\zeta }\mathsf{\Gamma }\right)|={\eta }^{\zeta }|E\left(\mathsf{\Gamma }\right)|+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\left|V\left(\mathsf{\Gamma }\right)\right|\zeta {\eta }^{\zeta -1}$ edges of ${\eta }^{\zeta }\mathsf{\Gamma }$ for any graph $\mathsf{\Gamma }$. The degree of each vertex $u\in \mathsf{\Gamma }$ is $d_u+\eta (\zeta +2)$ [31]. In this section we defined subdivided graph $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ and computed $Z{C}_1,Z{C}_2$ and $Z{C}_1^{*}$ of $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$. The $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ for $\mathsf{\Gamma }=C_6$, $\eta =2$ and $\zeta =2$ shown in Figure 5.

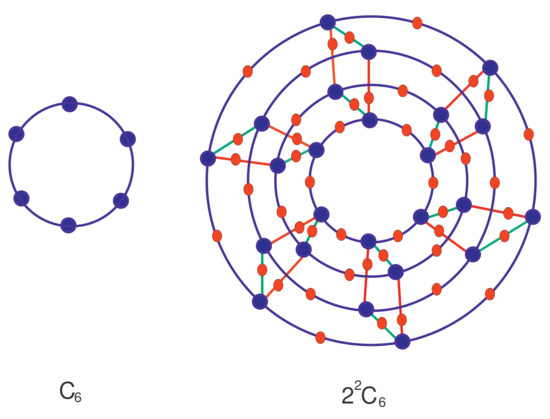
Figure 5. $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ for $\mathsf{\Gamma }=C_6$, $\eta =2$ and $\zeta =2$.

Theorem 2.

The $Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)$ for any graph Γ is

$$\begin{array}{ccc}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& {\eta }^{\zeta }{n}_{\mathsf{\Gamma }}[M_1\left(\mathsf{\Gamma }\right)+{\eta }^2{(\zeta +1)}^2{n}_{\mathsf{\Gamma }}+4\eta (\zeta +1)e_{\mathsf{\Gamma }}]+({\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)})\hfill \\ & & [HM\left(\mathsf{\Gamma }\right)+4{\eta }^2{(\zeta +1)}^2{e}_{\mathsf{\Gamma }}+4\eta (\zeta +1)M_1\left(\mathsf{\Gamma }\right)].\hfill \end{array}$$

Proof. 

The connection number of vertices $v\in \mathsf{\Gamma }$ is ${\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(v\right)$, $|V\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)|={\eta }^{\zeta }{n}_{\mathsf{\Gamma }}+{\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)}$ and $|E\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)|=2{\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+2\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)}$. The $Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)$ is

$$Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=\sum _{v\in V\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)}{\left({\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(v\right)\right)}^2$$

$$\begin{array}{ccc}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& {\eta }^{\zeta }{n}_{\mathsf{\Gamma }}\sum _{v\in V\left(\mathsf{\Gamma }\right)}{(d_v+\eta (\zeta +1))}^2\hfill \\ & +& ({\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)})\sum _{uv\in E\left(\mathsf{\Gamma }\right)}(d_u+\eta (\zeta +1)\hfill \\ & +& d_v{+\eta (\zeta +1))}^2\hfill \end{array}$$

$$\begin{array}{ccc}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& {\eta }^{\zeta }{n}_{\mathsf{\Gamma }}\sum _{v\in V\left(\mathsf{\Gamma }\right)}[d_v^2+{\eta }^2{(\zeta +1)}^2+2d_v\eta (\zeta +1)]+({\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)})\hfill \\ & & \sum _{uv\in E\left(\mathsf{\Gamma }\right)}[{(d_u+d_v)}^2+4{\eta }^2{(\zeta +1)}^2+4(d_u+d_v)\eta (\zeta +1)]\hfill \end{array}$$

$$\begin{array}{ccc}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& {\eta }^{\zeta }{n}_{\mathsf{\Gamma }}[\sum _{v\in V\left(\mathsf{\Gamma }\right)}{d}_v^2+{\eta }^2{(\zeta +1)}^2\sum _{v\in V\left(\mathsf{\Gamma }\right)}1\hfill \\ & +& 2\eta (\zeta +1)\sum _{v\in V\left(\mathsf{\Gamma }\right)}{d}_v]+({\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)})\hfill \\ & & [\sum _{uv\in E\left(\mathsf{\Gamma }\right)}{(d_u+d_v)}^2+4{\eta }^2{(\zeta +1)}^2\sum _{uv\in E\left(\mathsf{\Gamma }\right)}1+4\eta (\zeta +1)\sum _{uv\in E\left(\mathsf{\Gamma }\right)}(d_u+d_v)]\hfill \end{array}$$

$$\begin{array}{ccc}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& {\eta }^{\zeta }{n}_{\mathsf{\Gamma }}[M_1\left(\mathsf{\Gamma }\right)+{\eta }^2{(\zeta +1)}^2{n}_{\mathsf{\Gamma }}+4\eta (\zeta +1)e_{\mathsf{\Gamma }}]+({\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)})\hfill \\ & & [HM\left(\mathsf{\Gamma }\right)+4{\eta }^2{(\zeta +1)}^2{e}_{\mathsf{\Gamma }}+4\eta (\zeta +1)M_1\left(\mathsf{\Gamma }\right)].\hfill \end{array}$$

□

Theorem 3.

Let Γ be the simple connected graph with $\left|V\left(\mathsf{\Gamma }\right)\right|=n_{\mathsf{\Gamma }}\ge 2$. Then

$$\begin{array}{ccc}\hfill Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& [{\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)}][HM\left(\mathsf{\Gamma }\right)+4\eta (\zeta +1)M_1\left(G\right)+4{\eta }^2{(\zeta +1)}^2{e}_{\mathsf{\Gamma }}].\hfill \end{array}$$

Proof. 

Let $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ be the sub divided graph of ${\eta }^{\zeta }\mathsf{\Gamma }$ for any graph $\mathsf{\Gamma }$. The $|V\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)|={\eta }^{\zeta }{n}_{\mathsf{\Gamma }}+{\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)}$ and $|E\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)|=2{\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+2\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)}$.

$$Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=\sum _{uv\in E\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)}{\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(u\right){\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(v\right)$$

$$\begin{array}{ccc}\hfill Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& ({\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)})\sum _{uv\in E\left(\mathsf{\Gamma }\right)}[(d_u+\eta (\zeta +1))(d_u+d_v+2\eta (\zeta +1))\hfill \\ & +& (d_v+\eta (\zeta +1))(d_u+d_v+2\eta (\zeta +1))]\hfill \end{array}$$

$$\begin{array}{ccc}\hfill Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& ({\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)})\hfill \\ & & \sum _{uv\in E\left(\mathsf{\Gamma }\right)}[{(d_u+d_v)}^2+4\eta (\zeta +1)(d_u+d_v)+4{\eta }^2{(\zeta +1)}^2]\hfill \end{array}$$

$$\begin{array}{ccc}\hfill Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& [{\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)}][\sum _{uv\in E\left(\mathsf{\Gamma }\right)}{(d_u+d_v)}^2+4\eta (\zeta +1)\sum _{uv\in E\left(\mathsf{\Gamma }\right)}(d_u+d_v)\hfill \\ & +& 4{\eta }^2{(\zeta +1)}^2\sum _{uv\in E\left(\mathsf{\Gamma }\right)}1]\hfill \end{array}$$

$$\begin{array}{ccc}\hfill Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& [{\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)}][HM\left(\mathsf{\Gamma }\right)+4\eta (\zeta +1)M_1\left(G\right)+4{\eta }^2{(\zeta +1)}^2{e}_{\mathsf{\Gamma }}].\hfill \end{array}$$

□

Theorem 4.

For any graph Γ

$$\begin{array}{c}\hfill Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=[{\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)}][3M_1\left(\mathsf{\Gamma }\right)+6\eta (\zeta +1)e_{\mathsf{\Gamma }}].\end{array}$$

Proof. 

Let $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ be the sub divided graph of ${\eta }^{\zeta }\mathsf{\Gamma }$ for any graph $\mathsf{\Gamma }$. The $|V\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)|={\eta }^{\zeta }{n}_{\mathsf{\Gamma }}+{\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)}$ and $|E\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)|=2{\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+2\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)}$.

$$Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=\sum _{uv\in E\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)}({\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(u\right)+{\tau }_{S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)}\left(v\right))$$

$$\begin{array}{ccc}\hfill Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& ({\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)})\hfill \\ & & \sum _{uv\in E\left(\mathsf{\Gamma }\right)}[(d_u+\eta (\zeta +1))+(d_u+d_v+2\eta (\zeta +1))\hfill \\ & +& (d_v+\eta (\zeta +1))+(d_u+d_v+2\eta (\zeta +1))]\hfill \end{array}$$

$$\begin{array}{c}\hfill Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=[{\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)}]\sum _{uv\in E\left(\mathsf{\Gamma }\right)}[3(d_u+d_v)+6\eta (\zeta +1)]\end{array}$$

$$\begin{array}{c}\hfill Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=[{\eta }^{\zeta }{e}_{\mathsf{\Gamma }}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n_{\mathsf{\Gamma }}\zeta {\eta }^{(\zeta -1)}][3M_1\left(\mathsf{\Gamma }\right)+6\eta (\zeta +1)e_{\mathsf{\Gamma }}].\end{array}$$

□

6. Applications of Computed Results as Zagreb Connection Indices of $\mathit{S}\left({\mathit{\eta }}^{\mathit{\zeta }}{\mathit{C}}_{\mathit{n}}\right)$ and $\mathit{S}\left({\mathit{\eta }}^{\mathit{\zeta }}{\mathit{k}}_{\mathit{m}}\right)$

Corollary 1.

The $Z{C}_1\left(S\left({\eta }^{\zeta }{C}_n\right)\right)$ is

$$\begin{array}{c}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=n^2{\eta }^{(\zeta -1)}{[2+\eta (\zeta +1)]}^2[5\eta +4\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta ].\end{array}$$

Proof. 

Let $\mathsf{\Gamma }=C_n$ of order n and size m, $n=m$. Replacing $M_1\left(C_n\right)=4n$ and $HM\left(C_n\right)=16n$ in Theorem 2 we get,

$$\begin{array}{ccc}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& {\eta }^{\zeta }n[4n+{\eta }^2{(\zeta +1)}^{2}n+4\eta (\zeta +1)n]+({\eta }^{\zeta }n+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)n\zeta {\eta }^{(\zeta -1)})\hfill \\ & & [16n+4{\eta }^2{(\zeta +1)}^{2}n+16\eta (\zeta +1)n]\hfill \end{array}$$

$$\begin{array}{c}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=n^2[4+{\eta }^2{(\zeta +1)}^2+4\eta (\zeta +1)][5{\eta }^{\zeta }+4\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{(\zeta -1)}]\end{array}$$

$$\begin{array}{c}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=n^2{\eta }^{(\zeta -1)}{[2+\eta (\zeta +1)]}^2[5\eta +4\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta ].\end{array}$$

□

Corollary 2.

The $Z{C}_2\left(S\left({\eta }^{\zeta }{C}_n\right)\right)$ is

$$\begin{array}{ccc}\hfill Z{C}_2\left(S\left({\eta }^{\zeta }{C}_n\right)\right)& =& 4n^2[{\eta }^{\zeta }+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{(\zeta -1)}][4+4\eta (\zeta +1)+{\eta }^2{(\zeta +1)}^2].\hfill \end{array}$$

Proof. 

Replacing $M_1\left(C_n\right)=4n$ and $HM\left(C_n\right)=16n$ in Theorem 3 we get,

$$\begin{array}{ccc}\hfill Z{C}_2\left(S\left({\eta }^{\zeta }{C}_n\right)\right)& =& 4n^2[{\eta }^{\zeta }+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta {\eta }^{(\zeta -1)}][4+4\eta (\zeta +1)+{\eta }^2{(\zeta +1)}^2].\hfill \end{array}$$

□

Corollary 3.

The $Z{C}_1^{*}\left(S\left({\eta }^{\zeta }{C}_n\right)\right)$ is

$$\begin{array}{c}\hfill Z{C}_1^{*}\left(S\left({\eta }^{\zeta }{C}_n\right)\right)=6n^2{\eta }^{(\zeta -1)}[\eta +\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta ][2+\eta (\zeta +1)].\end{array}$$

Proof. 

Replacing $M_1\left(C_n\right)=4n$ in Theorem 3 we get,

$$\begin{array}{c}\hfill Z{C}_1^{*}\left(S\left({\eta }^{\zeta }{C}_n\right)\right)=6n^2{\eta }^{(\zeta -1)}[\eta +\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)\zeta ][2+\eta (\zeta +1)].\end{array}$$

□

Corollary 4.

Let $\mathsf{\Gamma }=k_m$ a complete graph of order m. Then

$$\begin{array}{ccc}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& m{\eta }^{\zeta }[\frac{m{(m-1)}^3}{2}+m{\eta }^2{(\zeta +1)}^2+2m(m-1)\eta (\zeta +1)]\hfill \\ & +& (\frac{m(m-1){\eta }^{\zeta }}{2}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)m\zeta {\eta }^{(\zeta -1)})\hfill \\ & & [2m{(m-1)}^3+2m(m-1){\eta }^2{(\zeta +1)}^2+2m{(m-1)}^3\eta (\zeta +1)]\hfill \end{array}$$

$$\begin{array}{ccc}\hfill Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& [\frac{m(m-1)}{2}{\eta }^{\zeta }+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)m\zeta {\eta }^{(\zeta -1)}][2m{(m-1)}^3+2m{(m-1)}^3\eta (\zeta +1)\hfill \\ & +& 2m(m-1){\eta }^2{(\zeta +1)}^2]\hfill \end{array}$$

$$\begin{array}{c}\hfill Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=[\frac{m(m-1)}{2}{\eta }^{\zeta }+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)m\zeta {\eta }^{(\zeta -1)}][\frac{3m{(m-1)}^3}{2}+3\eta (\zeta +1)m(m-1)].\end{array}$$

Proof. 

Let complete graph $\mathsf{\Gamma }=k_m$ of order m. Replacing $M_1\left(k_m\right)=\frac{m{(m-1)}^3}{2}$ and $HM\left(\mathsf{\Gamma }\right)=2m{(m-1)}^3$ in the Theorem 2, we get required result as,

$$\begin{array}{ccc}\hfill Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& m{\eta }^{\zeta }[\frac{m{(m-1)}^3}{2}+m{\eta }^2{(\zeta +1)}^2+2m(m-1)\eta (\zeta +1)]\hfill \\ & +& (\frac{m(m-1){\eta }^{\zeta }}{2}+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)m\zeta {\eta }^{(\zeta -1)})\hfill \\ & & [2m{(m-1)}^3+2m(m-1){\eta }^2{(\zeta +1)}^2+2m{(m-1)}^3\eta (\zeta +1)].\hfill \end{array}$$

(4)

Now using Theorem 3 and values of $M_1\left(k_m\right)$ and $HM\left(\mathsf{\Gamma }\right)$ we get the following result,

$$\begin{array}{ccc}\hfill Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)& =& [\frac{m(m-1)}{2}{\eta }^{\zeta }+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)m\zeta {\eta }^{(\zeta -1)}][2m{(m-1)}^3+2m{(m-1)}^3\eta (\zeta +1)\hfill \\ & +& 2m(m-1){\eta }^2{(\zeta +1)}^2].\hfill \end{array}$$

(5)

From Theorem 4 and values of $M_1\left(k_m\right)$ and $HM\left(\mathsf{\Gamma }\right)$, we get,

$$\begin{array}{c}\hfill Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)=[\frac{m(m-1)}{2}{\eta }^{\zeta }+\left(\genfrac{}{}{0pt}{}{\eta }{2}\right)m\zeta {\eta }^{(\zeta -1)}][\frac{3m{(m-1)}^3}{2}+3\eta (\zeta +1)m(m-1)].\end{array}$$

(6)

Equations (4)–(6) completes the proof.

□

7. Future Work

In future, the study of $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ can be done via the following methods:

• Study of $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ via degree based topological indices.
• Study of $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ via eccentricity based topological indices.
• Study of $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ via distance based topological indices.
• One can compute the energies of $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$.

8. Conclusions

For the first time in this work we construct subdivided graph of ${\eta }^{\zeta }\mathsf{\Gamma }$ network as $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$. We also discussed its topology and find closed form formulas for total number of edges and vertices. In Theorem 1, we determined $Z{C}_1\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right),Z{C}_2\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)$ and $Z{C}_1^{*}\left(S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)\right)$ for single vertex graph $\mathsf{\Gamma }$. In Theorems 2–4 we extend our work for $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$ when $\mathsf{\Gamma }$ is any graph. In Corollaries 1–4 we compute result for uni-cyclic graph $C_n$ and complete graph $K_m$ as an application of our computed results. Finally, we proposed some open problems for future work on $S\left({\eta }^{\zeta }\mathsf{\Gamma }\right)$.