Graph Analysis Using Fast Fourier Transform Applied on Grayscale Bitmap Images
Abstract
:1. Introduction
2. Identifying Graph Morphisms
3. Sub-Graph Representation Using a Bitmap Image
- Bitmap image can be used regardless of the target morphism graph calculation.
- The same bitmap image generation rules applied for the same sub-graphs must give the same results, including the same size.
- There are many image comparison methods developed and available for use.
- It is possible to generate bitmap images for vertices using a given threshold.
4. Image Comparison Algorithm
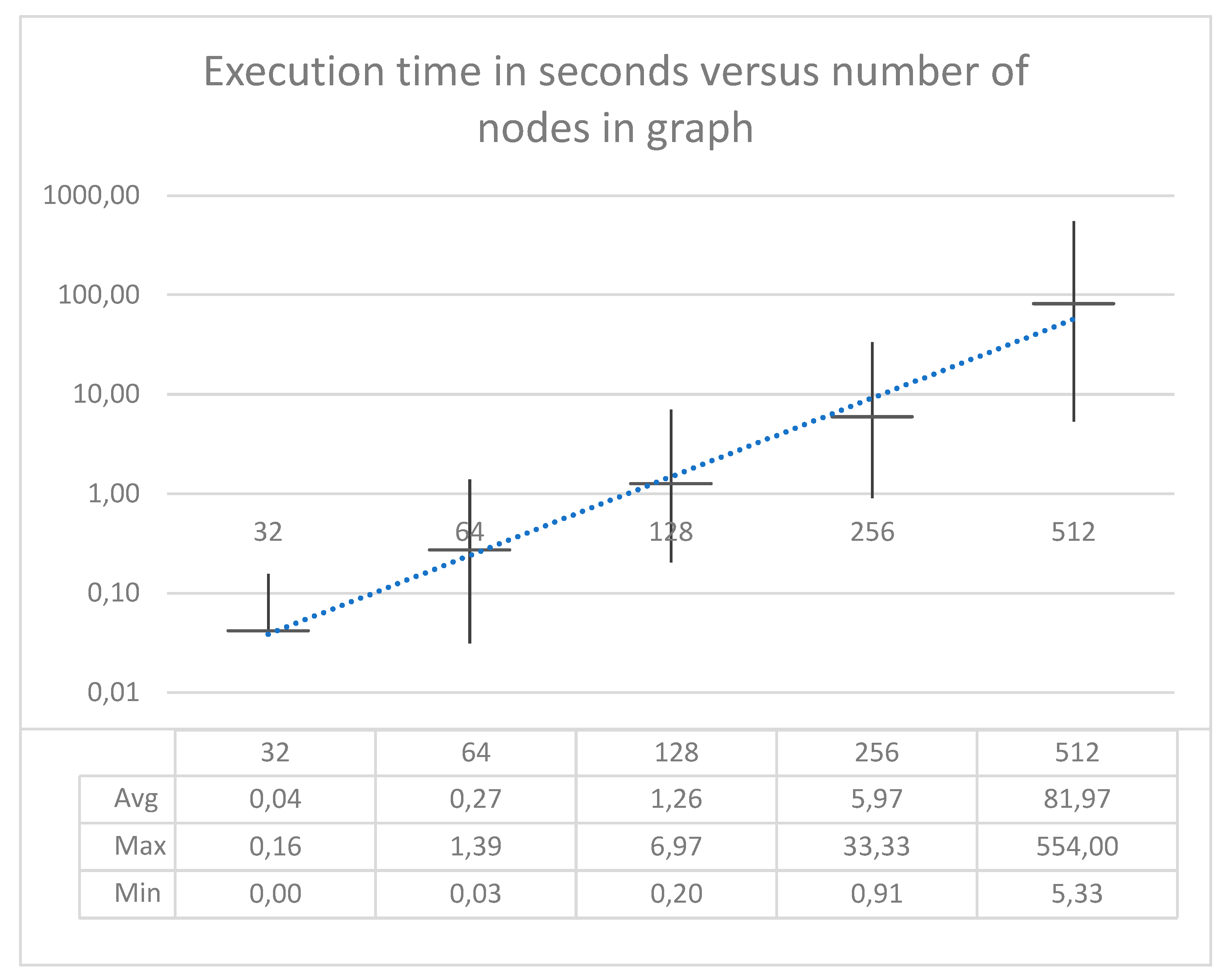
5. Proof-of-Concept Implementation
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, H.-L.; Tang, J.-H. Team structure and team performance in IS development: A social network perspective. Inf. Manag. 2004, 41, 335–349. [Google Scholar] [CrossRef]
- Avesani, P.; Bazzanella, C.; Perini, A.; Susi, A. Supporting the Requirements Prioritization Process. A Machine Learning Approach. Available online: https://www.researchgate.net/profile/Anna-Perini-2/publication/221390930_Supporting_the_Requirements_Prioritization_Process_A_Machine_Learning_approach/links/00463519e064cd7643000000/Supporting-the-Requirements-Prioritization-Process-A-Machine-Learning-approach.pdf (accessed on 28 October 2021).
- Wu, W.; Xiao, Y.; Wang, W.; He, Z.; Wang, Z. K-Symmetry Model for Identity Anonymization in Social Networks. In Proceedings of the 13th International Conference on Extending Database Technology, Lausanne, Switzerland, 22–26 March 2010; pp. 111–122. [Google Scholar]
- Leung, C.W.; Lim, E.-P.; Lo, D.; Weng, J. Mining Interesting Link Formation Rules in Social Networks. In Proceedings of the 19th ACM International Conference on Information and Knowledge Management, Toronto, Canada, 26–30 October 2010; pp. 209–218. [Google Scholar]
- Gacitua-Decar, V.; Pahl, C. Structural Process Pattern Matching Based on Graph Morphism Detection. Int. J. Softw. Eng. Knowl. Eng. 2017, 27, 153–189. [Google Scholar] [CrossRef]
- Szanto, A. Defuse the News: Predicting Misinformation and Bias in News on Social Networks via Content-Blind Learning. Available online: https://dash.harvard.edu/bitstream/handle/1/38811538/SZANTO-SENIORTHESIS-2018.pdf?sequence=3&isAllowed=y (accessed on 28 October 2021).
- Bonchi, F.; Castillo, C.; Gionis, A.; Jaimes, A. Social Network Analysis and Mining for Business Applications. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–37. [Google Scholar] [CrossRef]
- Shiau, W.-L.; Dwivedi, Y.K.; Yang, H.S. Co-citation and cluster analyses of extant literature on social networks. Int. J. Inf. Manag. 2017, 37, 390–399. [Google Scholar] [CrossRef] [Green Version]
- Ullmann, J.R. An Algorithm for Subgraph Isomorphism. J. ACM 1976, 23, 31–42. [Google Scholar] [CrossRef] [Green Version]
- Jiang, C.; Coenen, F.; Zito, M. A survey of frequent subgraph mining algorithms. Knowl. Eng. Rev. 2013, 28, 75–105. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Yan, X.; Zhu, F.; Han, J. GApprox: Mining Frequent Approximate Patterns from a Massive Network. In Proceedings of the Seventh IEEE International Conference on Data Mining (ICDM 2007), IEEE, Omaha, NE, USA, 28–31 October 2007; pp. 445–450. [Google Scholar] [CrossRef]
- Wang, X.; Huan, J.; Smalter, A.; Lushington, G.H. G-Hash: Towards Fast Kernel-Based Similarity Search in Large Graph Databases. In Graph Data Management: Techniques and Applications; Sakr, S., Pardede, E., Taniar, D., Eds.; Advances in data mining and database management; IGI Global: Hershey, PA, USA, 2012; pp. 176–213. [Google Scholar] [CrossRef]
- Yan, X.; Yu, P.S.; Han, J. Graph Indexing. In Proceedings of the 2004 ACM SIGMOD International Conference on Management of Data-SIGMOD ’04, Paris, France, 14–16 June 2004; ACM Press: New York, NY, USA, 2004; p. 335. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, J. RAM: Randomized Approximate Graph Mining. In Scientific and Statistical Database Management; Ludäscher, B., Mamoulis, N., Eds.; Springer : Berlin/Heidelberg, Germany, 2008; pp. 187–203. [Google Scholar] [CrossRef]
- Yuan, Z.; Li, F.; Zhang, P.; Chen, B. Description of shape characteristics through Fourier and wavelet analysis. Chin. J. Aeronaut. 2014, 27, 160–168. [Google Scholar] [CrossRef] [Green Version]
- Burrus, C.S. Fast Fourier Transforms. OpenStax CNX. 2012. Available online: http://cnx.org/contents/82e6ba6f-b828-42ef-9db1-8de4b448b869@22.1 (accessed on 28 October 2021).
- Mantoro, T.; Alfiah, F. Comparison Methods of DCT, DWT and FFT Techniques Approach on Lossy Image Compression. In Proceedings of the 2017 International Conference on Computing, Engineering, and Design (ICCED), Kuala Lumpur, Malaysia, 23–25 November 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Ye, Y.; Bruzzone, L.; Shan, J.; Bovolo, F.; Zhu, Q. Fast and Robust Matching for Multimodal Remote Sensing Image Registration. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9059–9070. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Chen, J.; Li, X.; Li, W.; Yuan, W. An Image Matching Method Based on Fourier and LOG-Polar Transform. Sens. Transducers 2014, 169, 61. [Google Scholar]
- Scellato, S. NetworkX: Network Analysis with Python. 2010. Available online: https://www.cl.cam.ac.uk/~cm542/teaching/2010/stna-pdfs/stna-lecture8.pdf (accessed on 28 October 2021).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, J.; Leskovec, J. Community-Affiliation Graph Model for Overlapping Network Community Detection. In Proceedings of the 2012 IEEE 12th International Conference on Data Mining, Brussels, Belgium, 10–13 December 2012; IEEE: Manhattan, NY, USA; pp. 1170–1175. [Google Scholar] [CrossRef]
- Junttila, T.; Kaski, P. Engineering an Efficient Canonical Labeling Tool for Large and Sparse Graphs. In Proceedings of the Ninth Workshop on Algorithm Engineering and Experiments (ALENEX), New Orleans, LA, USA, 6 January 2007. [Google Scholar]
- Isaacs, R. Infinite Families of Nontrivial Trivalent Graphs Which Are Not Tait Colorable. Am. Math. Mon. 1975, 82, 221–239. [Google Scholar] [CrossRef]
- Majeed, A.; Rauf, I. Graph Theory: A Comprehensive Survey about Graph Theory Applications in Computer Science and Social Networks. Inventions 2020, 5, 10. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baszuro, P.; Swacha, J. Graph Analysis Using Fast Fourier Transform Applied on Grayscale Bitmap Images. Information 2021, 12, 454. https://doi.org/10.3390/info12110454
Baszuro P, Swacha J. Graph Analysis Using Fast Fourier Transform Applied on Grayscale Bitmap Images. Information. 2021; 12(11):454. https://doi.org/10.3390/info12110454
Chicago/Turabian StyleBaszuro, Pawel, and Jakub Swacha. 2021. "Graph Analysis Using Fast Fourier Transform Applied on Grayscale Bitmap Images" Information 12, no. 11: 454. https://doi.org/10.3390/info12110454
APA StyleBaszuro, P., & Swacha, J. (2021). Graph Analysis Using Fast Fourier Transform Applied on Grayscale Bitmap Images. Information, 12(11), 454. https://doi.org/10.3390/info12110454






