Capacity Analysis of Lattice Reduction Aided Equalizers for Massive MIMO Systems
Abstract
1. Introduction
- This study provides a mathematical calculation to find the capacity gain of the MMSE receiver over the ZF receiver.
- It highlights the impact of the channel correlation on the capacity.
- An expression to established the capacity gain due to lattice reduction-aided receivers over the linear counterpart is derived.
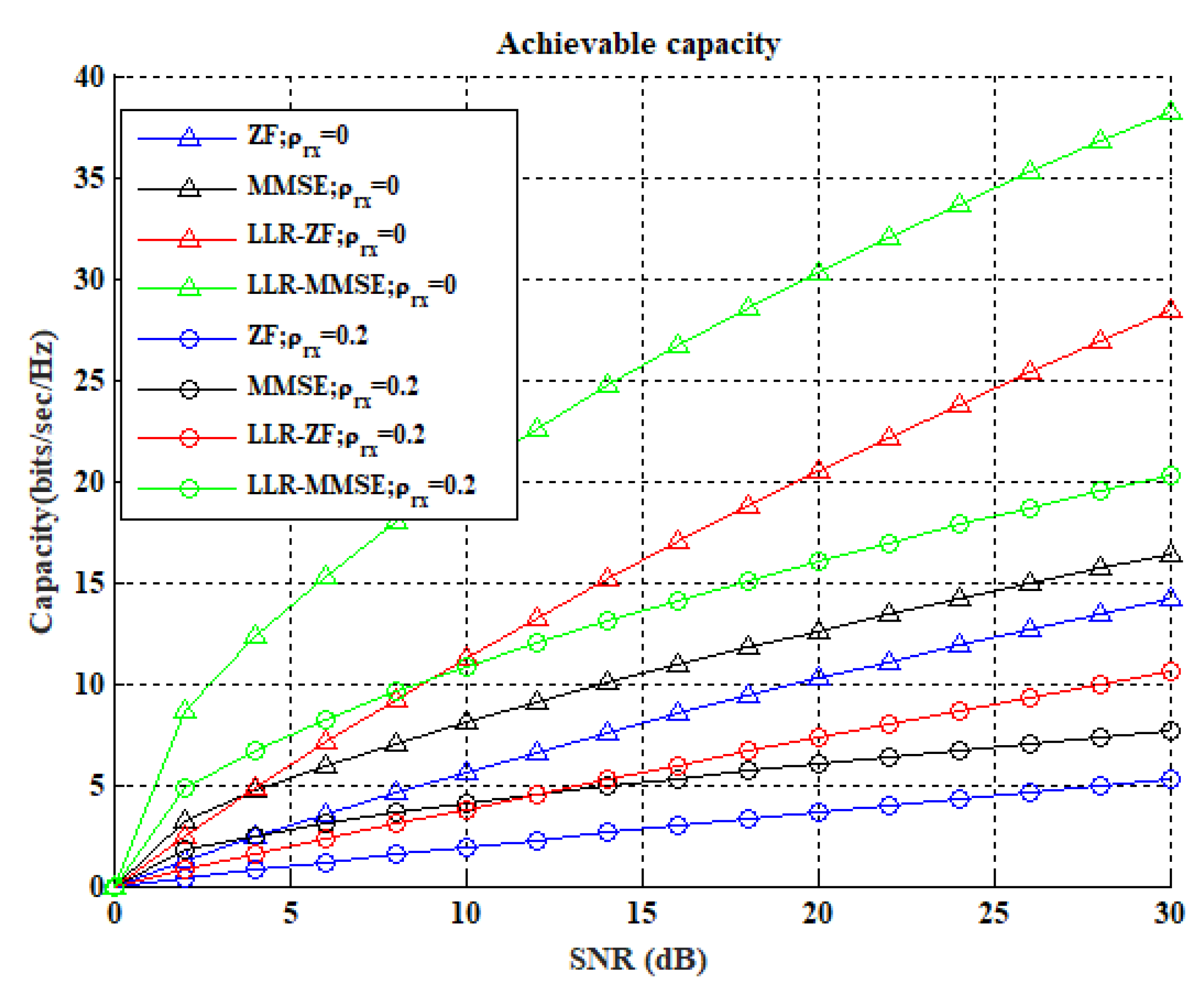
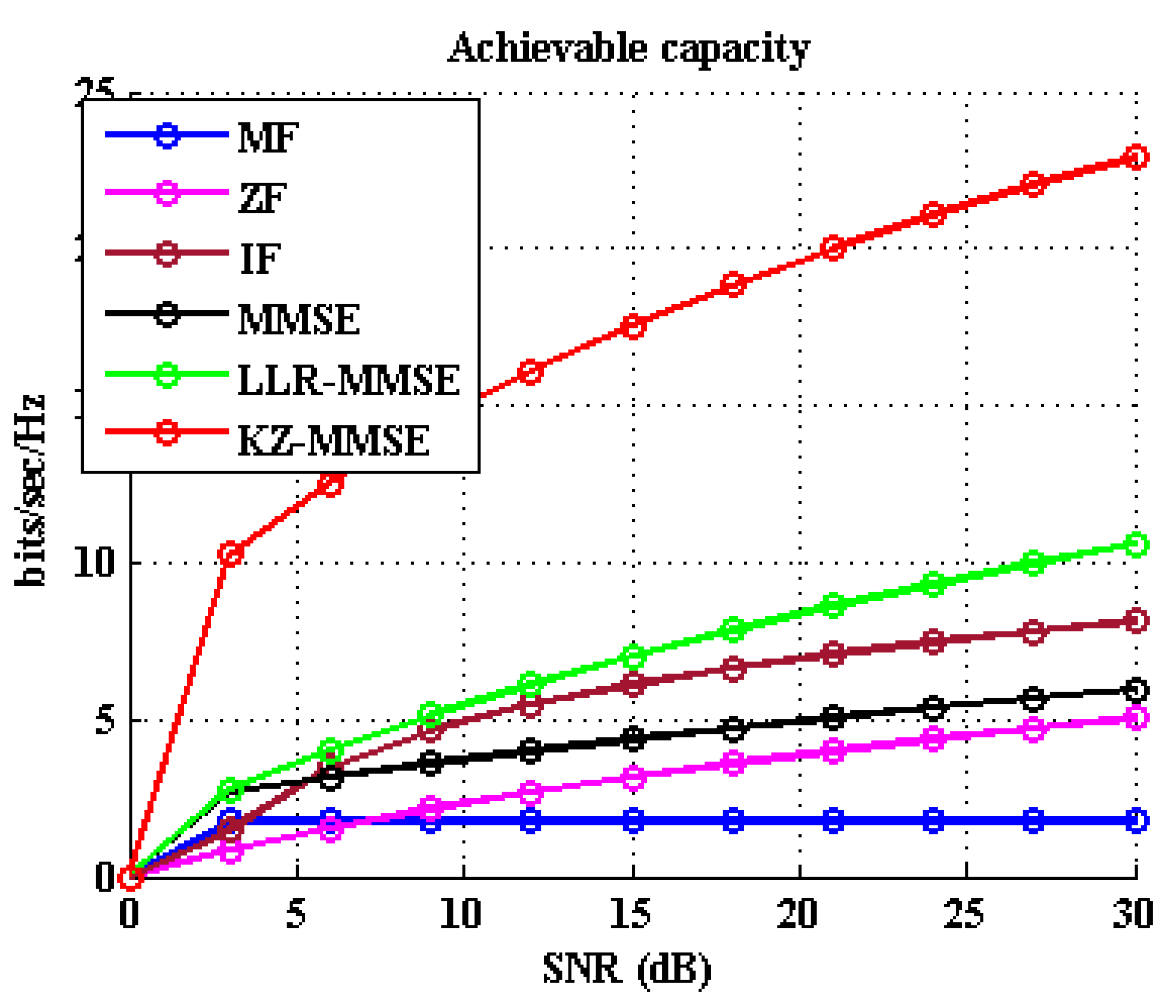
- The lattice reduction-aided receivers are shown to perform much better than the conventional linear receiver in terms of capacity gain in a massive MIMO system. It shows that the lattice reduction-aided receivers perform much better than LLL-enabled IF receiver.
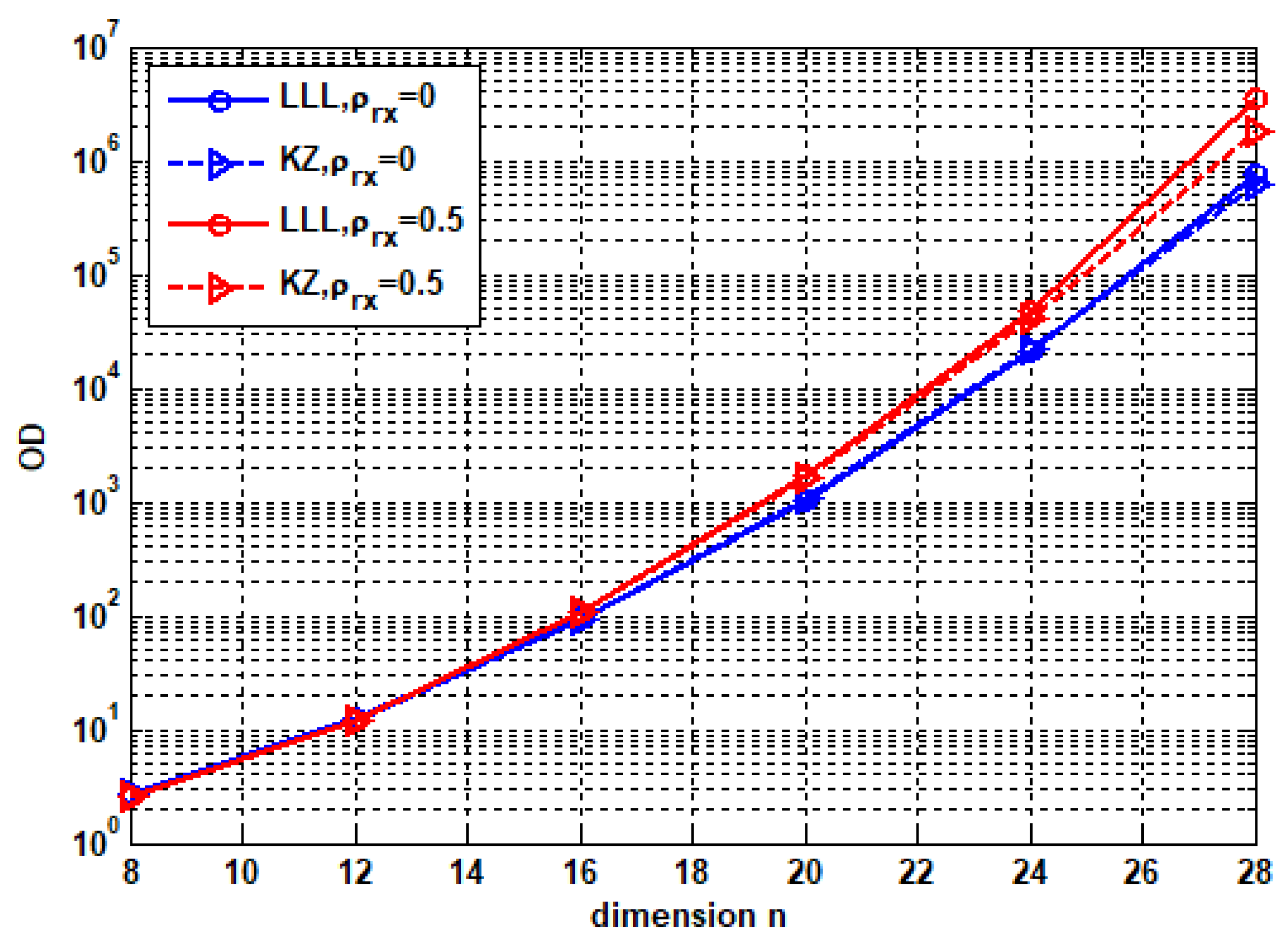
- The achievable capacity corresponding to LLL- and KZ-based lattice reduction-aided receivers are compared, establishing that KZ-aided receivers perform much better.
2. Related Work
3. Receivers
3.1. MF
3.2. ZF
3.3. MMSE
3.4. IF
3.5. LR-Aided Receiver
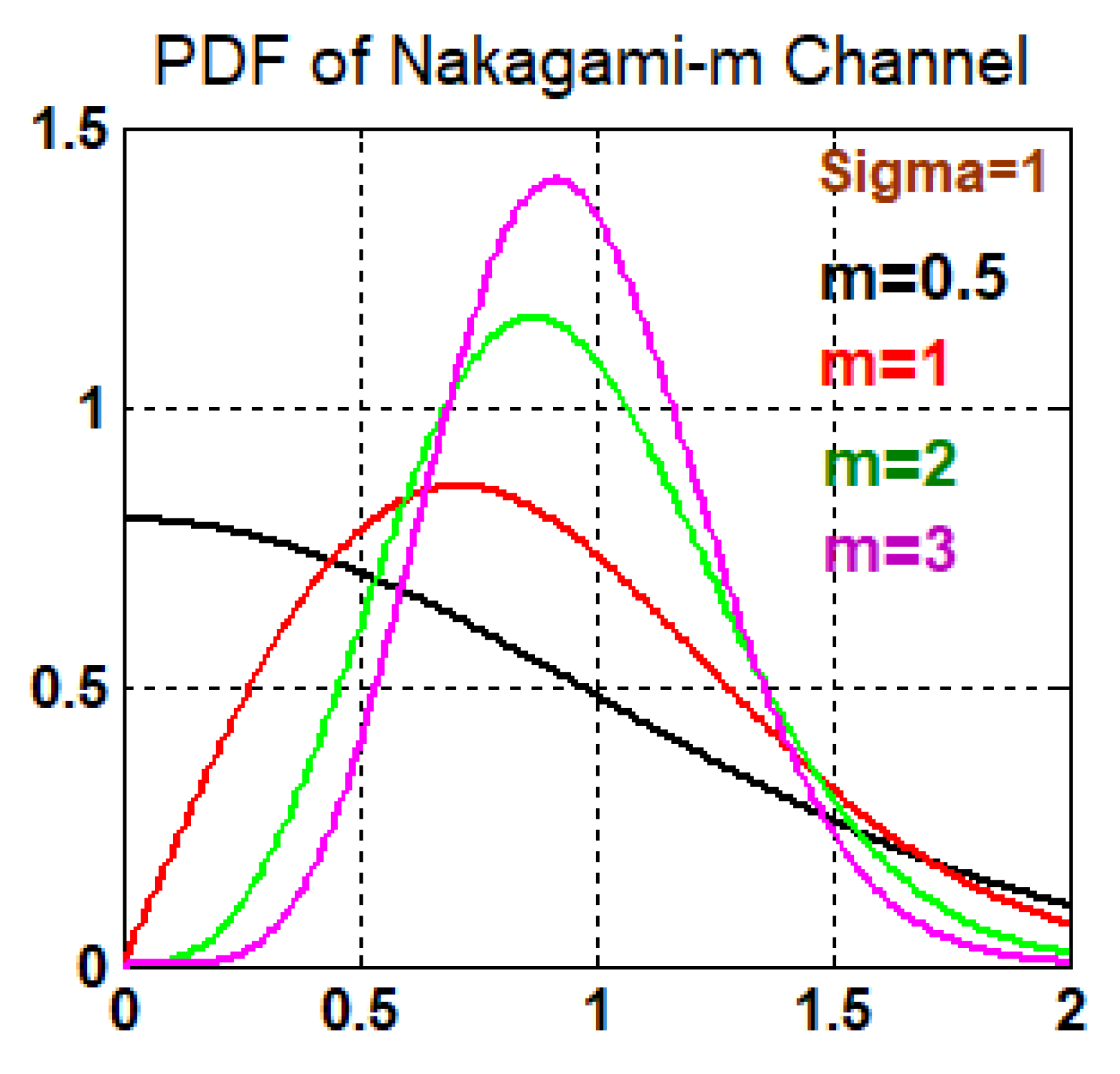
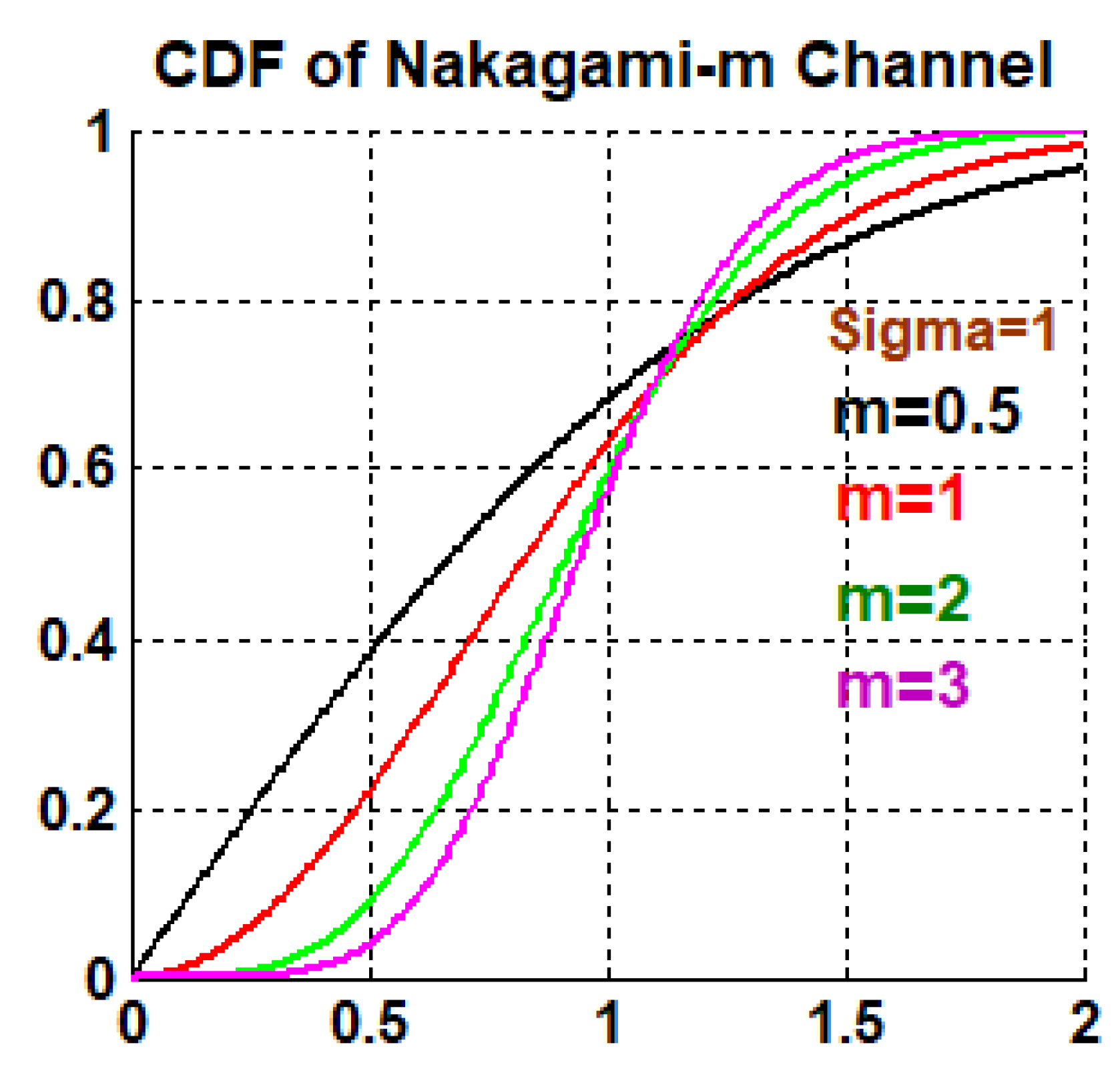
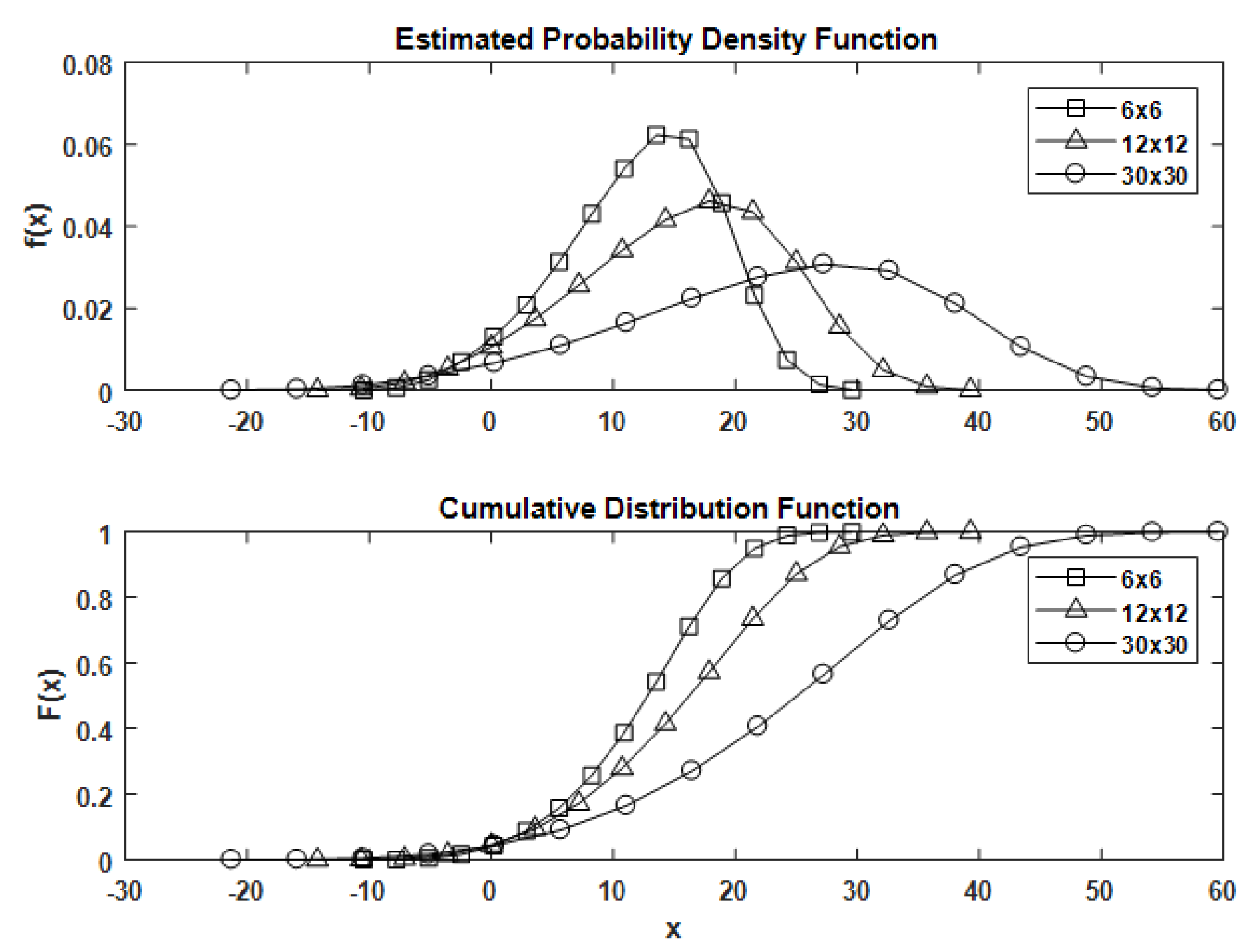
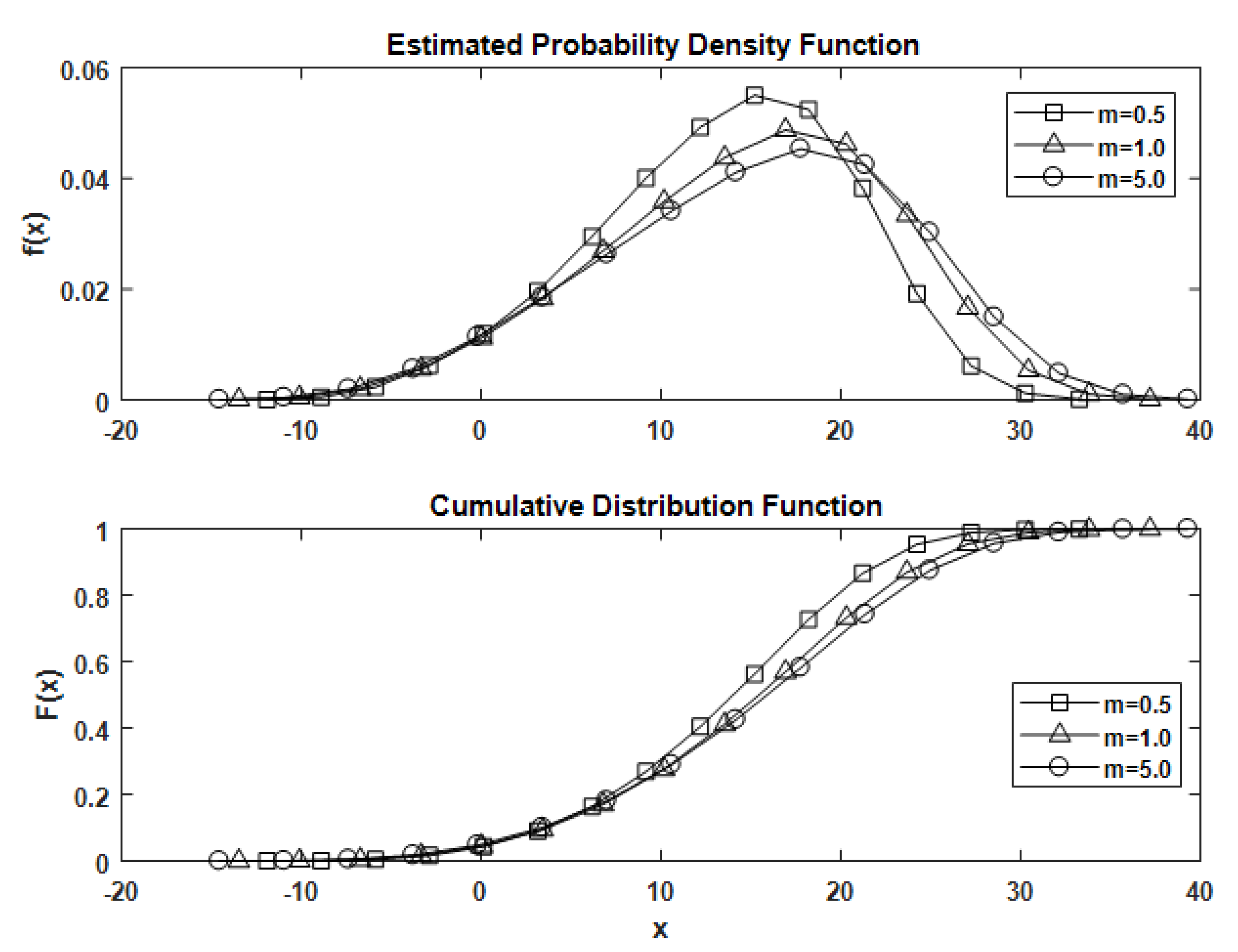
4. Nakagami-m Channel
5. Mathematical Analysis
5.1. Impact of Channel Correlation on the Capacity
5.2. Improvement in Channel Capacity: LR-Aided Receiver
5.3. Comparison between LLL and KZ Lattice Reduction
- (a)
- represents the shortest nonzero vector of lattice L.
- (b)
- , for .
- (c)
- If represents the orthogonal projection of L on the orthogonal complement spanned by , then the projections of yield a KZ basis of .
- (a)
- , for .
- (b)
- , for .
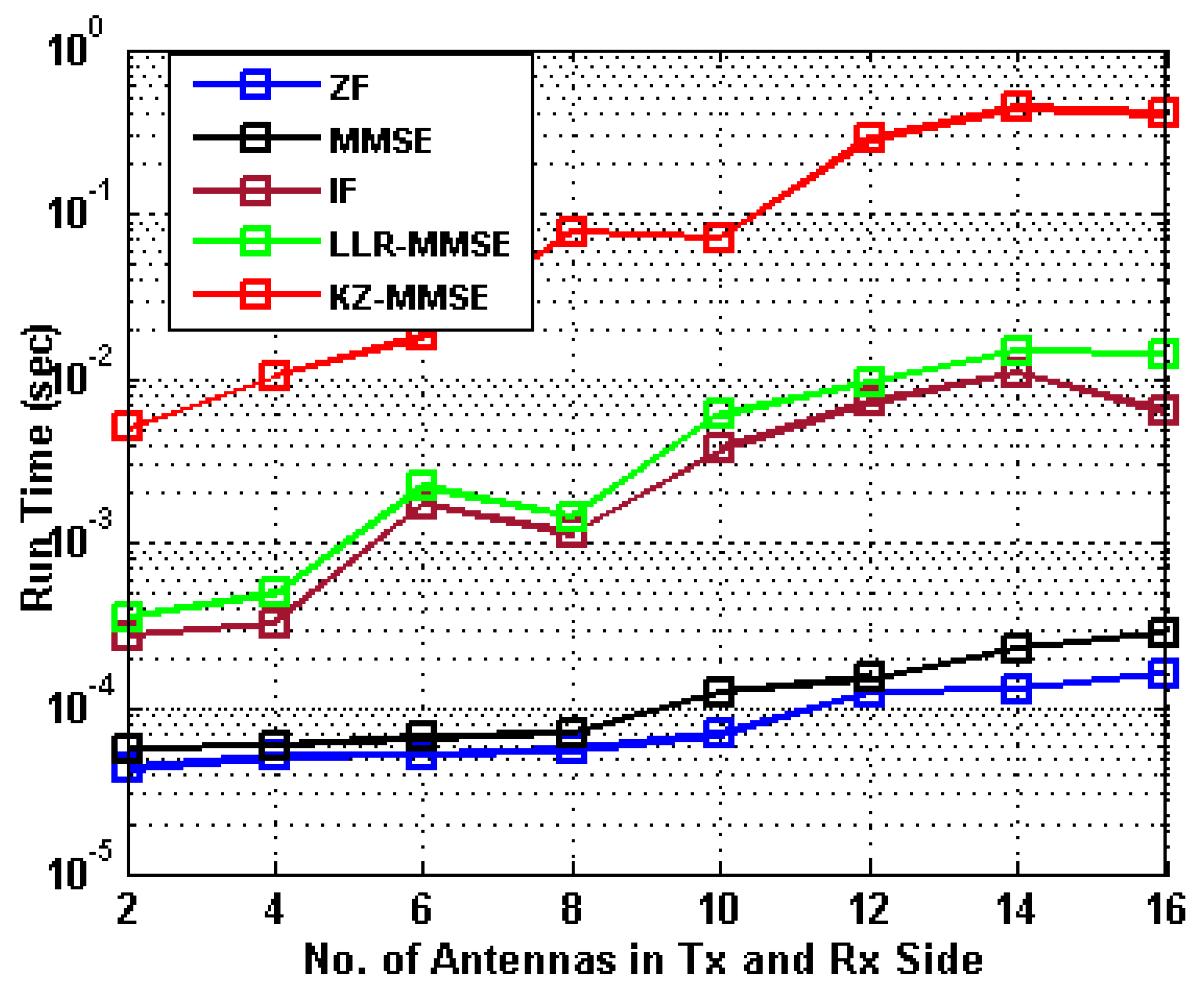
6. Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jiavana, K.F.K.; Malarvizhi, S. Lattice reduction aided pre-processor for large scale MIMO detection. Microprocess. Microsyst. 2019, 71, 102851. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Larsson, E.G.; Marzetta, T. Energy and spectral efficiency of very large multiuser MIMO systems. IEEE Trans. Commun. 2013, 61, 1436–1449. [Google Scholar]
- Rusek, F.; Persson, D.; Kiong, B.L.; Larsson, E.; Marzetta, T.L.; Edfors, O.; Tufvesson, F. Scaling up MIMO: Opportunities and challenges with very large arrays. IEEE Signal Process. Mag. 2013, 30, 40–60. [Google Scholar] [CrossRef]
- Yang, C.; Markovic, D. A 2.89 mW 50GOPS 16 × 16 16-core MIMO sphere decoder in 90 nm CMOS. In Proceedings of the ESSCIRC, Athens, Greece, 14–18 September 2009; pp. 344–347. [Google Scholar]
- Sheikh, F.; Balatsoukas-Stimming, A.; Chen, C.-H. High throughput lattice reduction for large-scale MIMO systems based on Seysen’s algorithm. In Proceedings of the IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016. [Google Scholar]
- Guenach, M. Novel lattice reduction algorithms: Precoder reduction and vector perturbation tradeoffs. IEEE Commun. Lett. 2018, 22, 1628–1631. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Z.; Wang, C.; Zhong, C. Performance analysis of MF Receiver in noncooperative cellular networks with distributed massive MIMO. In Proceedings of the International Workshop on High Mobility Wireless Communications (HMWC), Shanghai, China, 1–3 November 2013; pp. 146–150. [Google Scholar]
- Ma, X.; Kong, Y. Capacity analysis of lattice reduction aided equalizers for MIMO systems. In Proceedings of the IEEE Military Communications Conference (MILCOM), Tampa, FL, USA, 26–28 October 2015; pp. 866–871. [Google Scholar]
- Yang, S.; Hanzo, L. Fifty Years of MIMO Detection: The Road to Large-Scale MIMOs. IEEE Commun. Surv. Tutor. 2015, 17, 1941–1988. [Google Scholar] [CrossRef]
- Lee, J.; Toumpakaris, D.; Jang, E.W.; Lou, H.-L. DFE-Based Receiver Implementation for MIMO Systems Employing Hybrid ARQ. In Proceedings of the IEEE GLOBECOM (2008), New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–5. [Google Scholar]
- Sur, S.N.; Bera, R.; Maji, B. Decision Feedback Equalization for MIMO Systems. Intell. Comput. Appl. Adv. Intell. Syst. Comput. 2015, 343, 205–212. [Google Scholar]
- Sur, S.N.; Bera, R.; Maji, B. Decision Feedback Equalization for Large Scale MIMO System. In Proceedings of the 3rd International Conference on Foundations and Frontiers In Computer, Communication and Electrical Engineering (C2E2—2016), West Bengal, India, 15–16 January 2016. [Google Scholar]
- Kofidis, E.; Rontogiannis, A.A. Adaptive BLAST deci-sion-feedback equalizer for MIMO-FBMC/OQAM systems. In Proceedings of the 21st Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Istanbul, Turkey, 26–29 September 2010; pp. 841–846. [Google Scholar]
- Lin, B.; Choi, J. Low Complexity MIMO Detection; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Wubben, D.; Seethaler, D.; Jalden, J.; Matz, G. Lattice reduction. IEEE Signal Process. Mag. 2011, 28, 70–91. [Google Scholar] [CrossRef]
- Yang, S.; Lv, T.; Hanzo, L. Semidefinite Programming Re-laxation Based Virtually Antipodal Detection for MIMO Systems Using Gray-Coded High-Order QAM. IEEE Trans. Veh. Technol. 2013, 62, 1667–1677. [Google Scholar] [CrossRef]
- Sur, S.N.; Bera, R.; Maji, B. A Review on MIMO Based V2V Communication. In Advances in Electronics, Communication and Computing; Lecture Notes in Electrical Engineering; Springer: Singapore, 2018; Volume 443, pp. 333–340. [Google Scholar]
- Husseina, A.H.; Enany, A.M.; Selim, M.M.; Nasr, M.E. BER Performance Enhancement of MIMO Systems Using Hybrid Detection Techniques Based on Sphere Decoding. Am. Sci. Res. J. Eng. Technol. Sci. 2020, 63, 7–21. [Google Scholar]
- Barbero, L.; Thompson, J. Fixing the complexity of the sphere decoder for MIMO detection. IEEE Trans. Wirel. Commun. 2008, 7, 2131–2142. [Google Scholar] [CrossRef]
- Qi, X.F.; Holt, K. A Lattice-Reduction-Aided Soft Demapper for High-Rate Coded MIMO-OFDM Systems. IEEE Signal Process. Lett. 2007, 14, 305–308. [Google Scholar] [CrossRef]
- Halak, B.; El-Hajjar, M.; Hassanein, A. Hardware efficient architecture for element-based lattice reduction aided k-best detector for MIMO systems. J. Sens. Actuator Netw. 2018, 7, 22. [Google Scholar] [CrossRef]
- Yao, H.; Wornell, G.W. Lattice-reduction-aided detectors for MIMO communication systems. In Proceedings of the Global Telecommunications Conference (GLOBECOM’02), Taipei, Taiwan, 17–21 November 2002; Volume 1, pp. 424–428. [Google Scholar]
- Kim, H.; Park, J.; Lee, H.; Kim, J. Near-ML MIMO Detection Algorithm With LR-Aided Fixed-Complexity Tree Searching. Proc. IEEE Commun. Lett. 2014, 18, 2221–2224. [Google Scholar] [CrossRef]
- Lenstra, A.K.; Lenstra, H.W., Jr.; Lovasz, L. Factoring polynomials with rational coefficients. Math. Ann. 1982, 261, 515–534. [Google Scholar] [CrossRef]
- Seysen, M. Simultaneous reduction of a lattice basis and its reciprocal basis. Combinatorica 1993, 13, 363–376. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, W.; Swami, A. Lattice-reduction aided equalization for OFDM systems. IEEE Trans. Wirel. Commun. 2009, 8, 1608–1613. [Google Scholar]
- Zhou, Q.; Ma, X. Element-based lattice reduction algorithms for large MIMO detection. IEEE J. Sel. Areas Commun. 2013, 31, 274–286. [Google Scholar] [CrossRef]
- Kim, H.; Lee, H.; Koo, J.; Kim, J. Low-complexity lattice reduction algorithm for MIMO detectors with tree searching. EURASIP J. Wirel. Commun. Netw. 2017, 1, 1–11. [Google Scholar] [CrossRef]
- Agrell, E.; Eriksson, T.; Vardy, A.; Zeger, K. Closest point search in lattices. IEEE Trans. Inf. Theory 2002, 48, 2201–2214. [Google Scholar] [CrossRef]
- Wen, J.; Chang, X.-W. On the KZ Reduction. IEEE Trans. Inf. Theory 2018, 65, 1921–1935. [Google Scholar] [CrossRef]
- Gan, Y.; Ling, C.; Mow, W. Complex lattice reduction algorithm for low-complexity full-diversity MIMO detection. IEEE Trans. Signal Process. 2009, 57, 2701–2710. [Google Scholar]
- Jiang, H.; Du, S. Complex Korkine-Zolotareff Reduction Algorithm for Full-Diversity MIMO Detection. IEEE Commun. Lett. 2013, 17, 381–384. [Google Scholar] [CrossRef]
- Ling, C. On the Proximity Factors of Lattice Reduction-Aided Decoding. IEEE Trans. Signal Process. 2011, 59, 2795–2808. [Google Scholar] [CrossRef]
- Lyu, S.; Ling, C. Boosted KZ and LLL Algorithms. IEEE Trans. Signal Process. 2017, 65, 4784–4796. [Google Scholar] [CrossRef]
- Lv, H.; Li, J. A novel hybrid fix-LLL lattice reduction algorithm for MIMO detection system. IEEJ Trans. Electr. Electron. Eng. 2017, 12, 372–378. [Google Scholar] [CrossRef]
- Mussi, A.M.; Costa, B.F.; Abrao, T. Efficient Lattice Reduction Aided Detectors Under Realistic MIMO Channels. Wirel. Pers. Commun. 2017, 95, 947–978. [Google Scholar] [CrossRef]
- Xiao, Z.; Zhao, J.; Liu, T.; Geng, L.; Zhang, F.; Tong, J. On the energy efficiency of massive MIMO systems with low-resolution ADCs and lattice reduction aided detectors. Symmetry 2020, 12, 406. [Google Scholar] [CrossRef]
- Zhan, J.; Nazer, B.; Erez, U.; Gastpar, M. Integer-forcing linear receivers. IEEE Trans. Inf. Theory 2014, 60, 7661–7685. [Google Scholar] [CrossRef]
- Chen, L.; Xing, Z.; Li, Y.; Qiu, S. Efficient MIMO Pre-processor With Sorting-Relaxed QR Decomposition and Modified Greedy LLL Algorithm. IEEE Access 2020, 8, 54085–54099. [Google Scholar] [CrossRef]
- Poor, H.V.; Verdu, S. Probability of error in MMSE multiuser detection. IEEE Trans. Inf. Theory 1997, 43, 858–871. [Google Scholar] [CrossRef]
- Li, P.; Paul, D.; Narasimhan, R.; Cioffi, J. On the distribution of SINR for the MMSE MIMO receiver and performance analysis. IEEE Trans. Inf. Theory 2006, 52, 271–286. [Google Scholar]
- Shin, H.; Lee, J. On the Error Probability of Binary and M-ary Signals in Nakagami-m Fading Channels. IEEE Trans. Commun. 2004, 52, 536–539. [Google Scholar] [CrossRef]
- Tang, L.; Hongbo, Z. Analysis and Simulation of nakagami fading channel with Matlab. In Proceedings of the Asia-Pacific Conference on Environmental Electromagnetic CEEM’2003, Hangzhou, China, 4–7 November 2003; pp. 490–494. [Google Scholar]
- Nakagami, M. The m-distribution, a general formula of intensity distribution of rapid fading. In Statistical Methods in Radio Wave Propagation; Hoffman, W.G., Ed.; Pergamum: Oxford, UK, 1960; pp. 3–36. [Google Scholar]
- Sur, S.N.; Bera, R.; Maji, B. Capacity Analysis of MIMO in Non-Uniform Nakagami Channel with Linear Receiver. IETE J. Res. 2017, 63, 795–804. [Google Scholar] [CrossRef]
- Zhong, C.; Matthaiou, M.; Huang, A.; Zhang, Z. On the sum rate of MIMO Nakagamim fading channels with linear receivers. IEEE Trans. Wirel. Commun. 2012, 11, 3651–3659. [Google Scholar] [CrossRef]
- Sur, S.N.; Bera, S.; Bera, R.; Maji, B. Capacity Analysis of Lattice reduction Aided Detection in Massive-MIMO systems. In Proceedings of the URSI Asia-Pacific Radio Science Conference (AP-RASC), New Delhi, India, 9–15 March 2019; pp. 1–4. [Google Scholar]
- Gruber, P.M.; Lekkerkerker, C.G. Geometry of Numbers; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar]
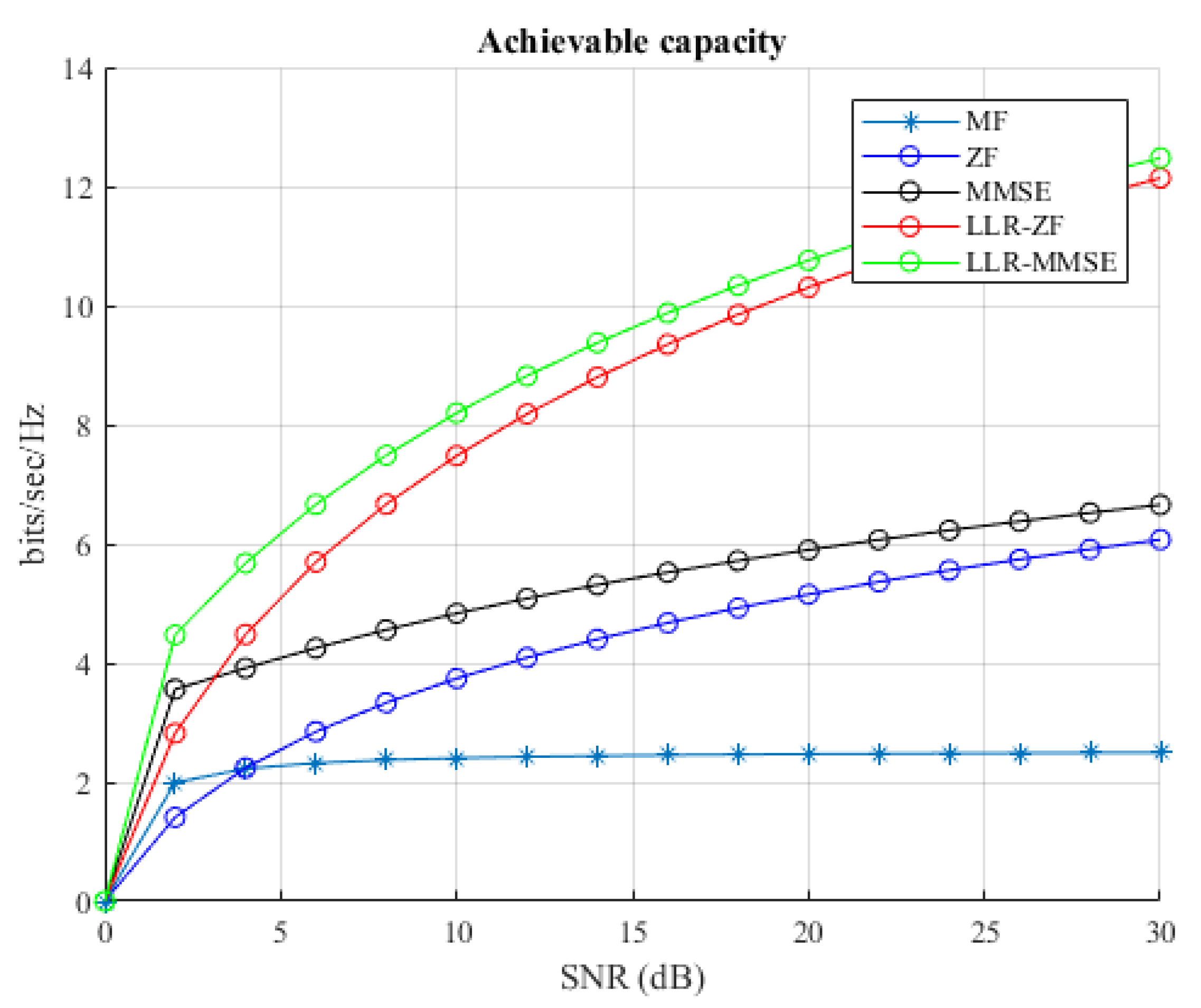
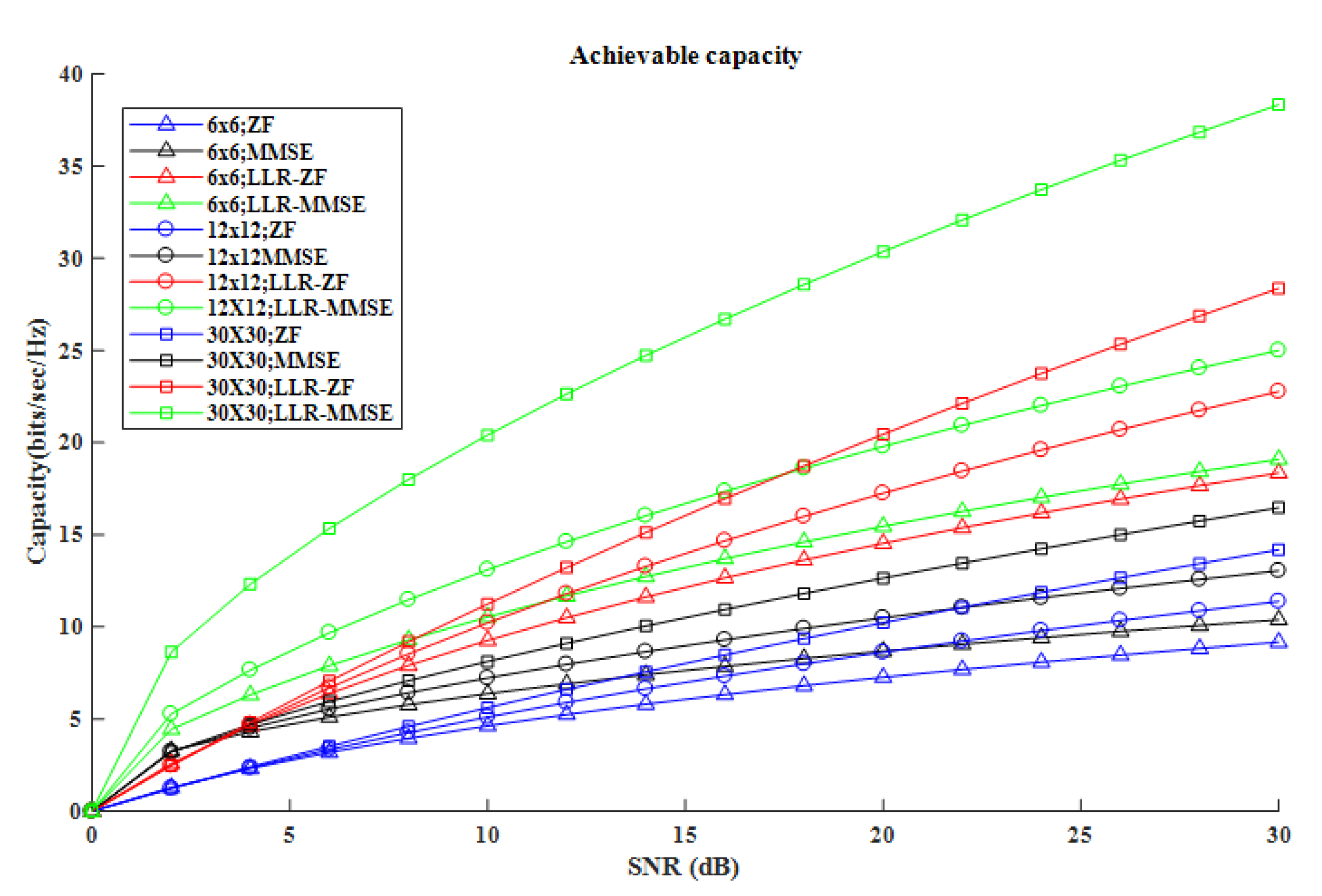

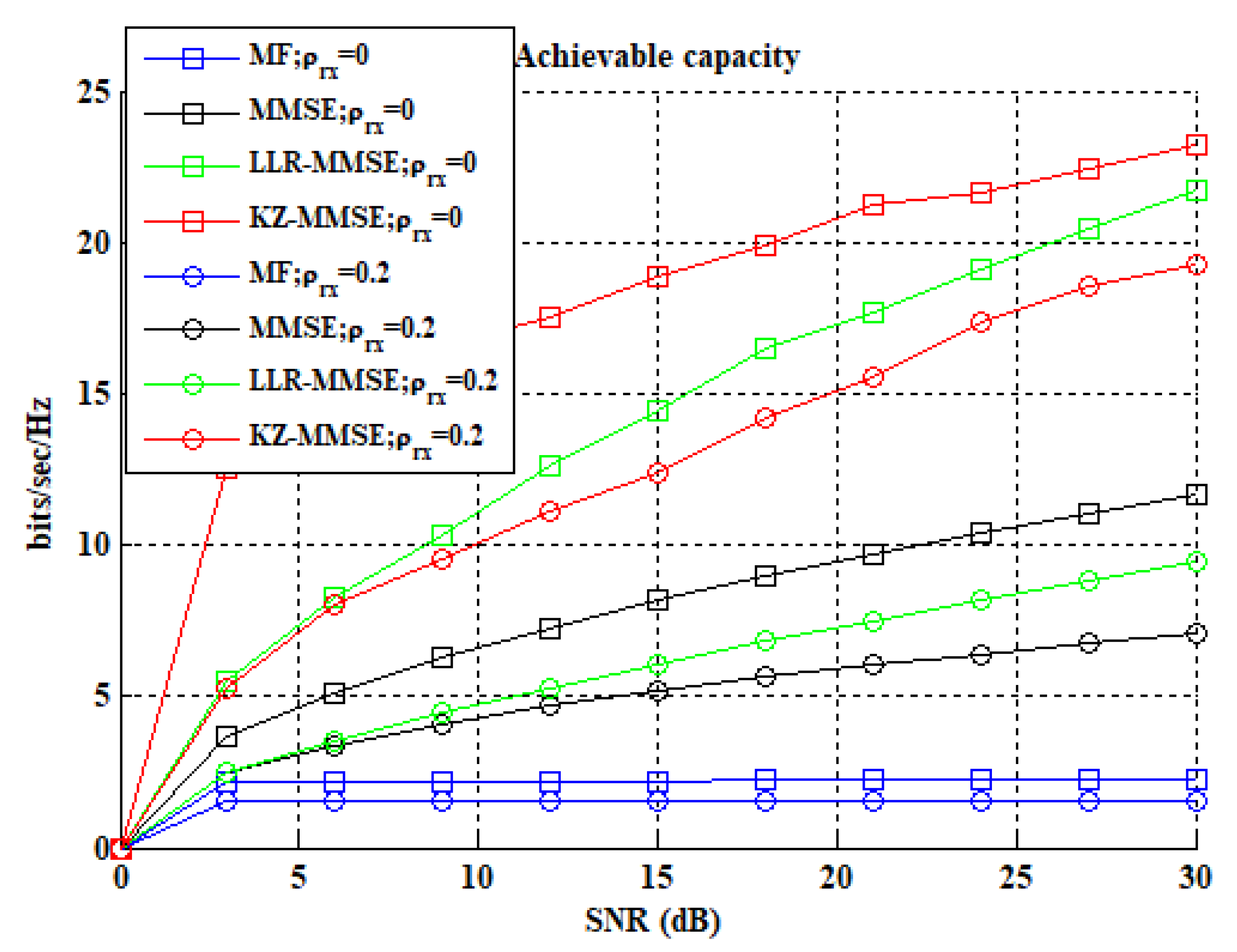
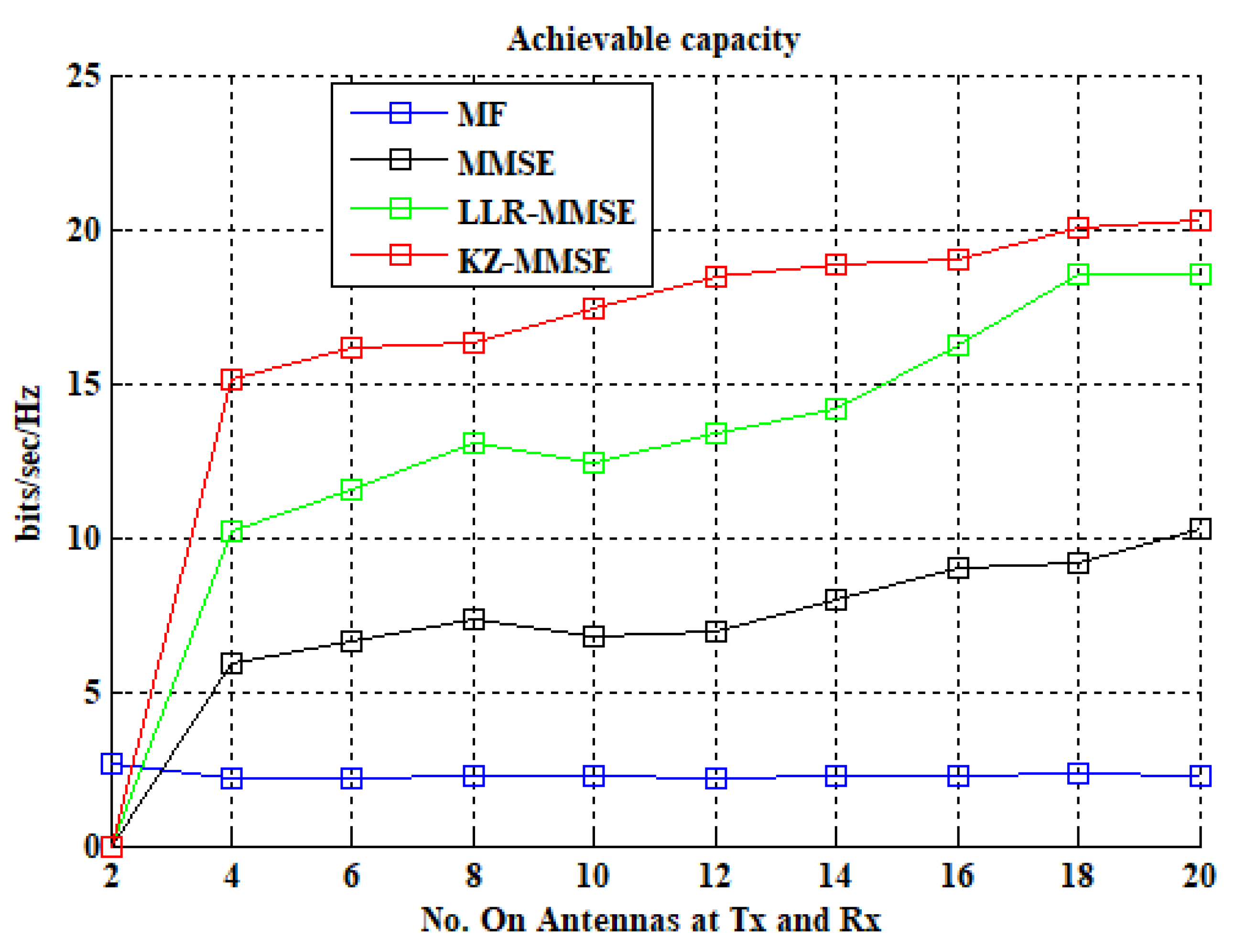

| Receiver | Capacity (Bits/S/Hz) | |||
|---|---|---|---|---|
| = 0 | = 0.2 | |||
| System | SNR = 3 dB | SNR = 30 dB | SNR = 3 dB | SNR = 30 dB |
| MF | 2.17 | 2.22 | 1.531 | 1.533 |
| MMSE | 3.709 | 11.66 | 2.453 | 7.051 |
| LLR-MMSE | 5.519 | 21.73 | 2.455 | 9.425 |
| KZ-MMSE | 12.57 | 23.23 | 5.264 | 19.26 |
| Capacity (Bits/S/Hz) | |||
|---|---|---|---|
| Antenna Configuration | |||
| ME | 2.189 | 2.273 | 2.293 |
| MMSE | 5.897 | 6.779 | 10.25 |
| LLR-MMSE | 10.16 | 12.45 | 18.52 |
| KZ-MMSE | 15.14 | 17.42 | 20.29 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sur, S.N.; Bera, R.; Kumar Bhoi, A.; Shaik, M.; Marques, G. Capacity Analysis of Lattice Reduction Aided Equalizers for Massive MIMO Systems. Information 2020, 11, 301. https://doi.org/10.3390/info11060301
Sur SN, Bera R, Kumar Bhoi A, Shaik M, Marques G. Capacity Analysis of Lattice Reduction Aided Equalizers for Massive MIMO Systems. Information. 2020; 11(6):301. https://doi.org/10.3390/info11060301
Chicago/Turabian StyleSur, Samarendra Nath, Rabindranath Bera, Akash Kumar Bhoi, Mahaboob Shaik, and Gonçalo Marques. 2020. "Capacity Analysis of Lattice Reduction Aided Equalizers for Massive MIMO Systems" Information 11, no. 6: 301. https://doi.org/10.3390/info11060301
APA StyleSur, S. N., Bera, R., Kumar Bhoi, A., Shaik, M., & Marques, G. (2020). Capacity Analysis of Lattice Reduction Aided Equalizers for Massive MIMO Systems. Information, 11(6), 301. https://doi.org/10.3390/info11060301







