A Blockchain Voting System Based on the Feedback Mechanism and Wilson Score

Abstract

A blockchain voting system based on the feedback mechanism and Wilson score is proposed to solve the problem of the malicious votes behavior. Firstly, the relatively accurate supporting rate and ranking for candidates are obtained using the Wilson score. Secondly, different feedback coefficients are calculated according to the above parameters. Finally, the account points are adjusted according to the feedback coefficients. The feedback mechanism is designed in the voting smart contract, and the smart contract is deployed on the blockchain to ensure the enforcement of the feedback mechanism. A fully functional smart contract is designed and briefly verified in this paper. The experiment is conducted under the K-out-of-L type of weighted voting. Experimental results show that the Wilson score can accurately modify the candidates’ supporting rates, and the feedback mechanism can effectively suppress malicious votes.

1. Introduction

With the development of cryptography and Internet technology, electronic voting (E-voting) has gradually become a popular research direction. The concept of electronic voting appeared in 1981. In nearly forty years of development, security and privacy have always been the focus of electronic voting research. Aiming at the security of electronic voting, many researchers propose a large number of secure electronic voting schemes using various technologies such as informatics and cryptography. In 1992, A Fujioka and others proposed a new type of electronic voting protocol that uses the blind signature technology to improve the security of the voting system [1]. In 2001, Magkos and others proposed a large-scale voting scheme, which is based on an anonymous channel to improve the anonymity of voting users [2]. In recent years, the blockchain technology has been used in electronic voting. Blockchain was originally derived from the concept of decentralized cryptocurrencies. Recently, many other applications of blockchain have also emerged in some non-financial fields. In 2015, Zhao and others developed a new type of voting system on the Bitcoin blockchain [3]. In 2017, McCorry and others wrote a simple voting agreement as a smart contract, which runs on the Ethereum blockchain [4]. With the help of the blockchain platform and smart contracts, security of the voting system data can be better guaranteed. Most blockchain voting systems also consider the privacy of users, thereby increasing the anonymity of the voting process [2,3,5,6].

There are many situations where voting is used in daily life. For example, the traditional voting schemes are applied for public elections in a democratic country, which are widely participated and have great economic and political influence. In addition, there are many other voting situations in which the voting results will not have a wide social impact. For example, a movie activity organizer wants to investigate the popularity of candidate movies, or a talent show wants to determine the ranking of the contestants through voting by audience. In these latter voting situations, the purpose of the voting initiator is to collect opinions from the audience. There are also often some voters who want to increase the approval rate of non-mainstream candidates by casting more votes. This behavior goes against the original intention of holding the voting. This paper defines this behavior as malicious votes, and the voting users who perform malicious votes are defined as malicious users.

According to the above analysis, the existed research of most blockchain voting systems is mainly to improve the privacy and security of users. However, as the anonymity of electronic voting users increases, it is not easy for the system to locate the address of the malicious user. If there are malicious voting behaviors in the system, it will be difficult to punish these operations. Therefore, the blockchain voting system needs a way to restrict the behavior of users.

This paper proposes a feedback mechanism based on the blockchain weighted voting system. In the proposed design, the account points are adjusted according to the candidate’s ranking and the candidate’s support rate. The Wilson score is used to calculate the candidate support rate in the voting to obtain the candidate’s support rate and ranking to ensure the accuracy of the feedback mechanism. Furthermore, the voting process and feedback mechanism are written in the smart contract where the feedback coefficient and the Wilson score coefficient are set up. Experimental results and analysis show that the proposed feedback mechanism can effectively suppress malicious votes behavior, and the designed voting system based on this feedback mechanism can obtain more appropriate candidate support rates.

2. Related Information and Related Work

2.1. Blockchain and Smart Contract

Blockchain emerged in 2008 as the underlying technology of Bitcoin [7]. Blockchain is essentially a decentralized distributed storage database. When a user registers an account in the Bitcoin system, they will obtain a private key randomly assigned by the system. The user’s public key is calculated from the private key through elliptic curve cryptography (ECC). The asymmetric encryption method formed by the public key–private key is the basis for digital signature encryption of the data on the blockchain. In the blockchain system, the hash operation participates in the calculation of the user’s address and the calculation of the summary of each transaction in the system. In addition, the blockchain system uses data structures such as Merkel trees to store data, and uses the consensus mechanism between distributed nodes to update data. Therefore, blockchain has the characteristics of decentralization and security. The immutability of blockchain internal data, consensus mechanisms, and good incentives ensure the operation of the blockchain system.

Bitcoin is a trading system based on utxo (unspent transaction output). Only transactions are recorded on the Bitcoin blockchain, and there is no concept of account on it. The system design is too simple to connect with many practical applications in reality. Unlike the Bitcoin system, Ethereum is a Turing complete open source platform for building decentralized applications [8]. It allows anyone to build and use decentralized applications using the blockchain technology on the platform. There is a smart contract type account in Ethereum, which can be used to expand the application of the Ethereum blockchain. A smart contract is a collection of code and data that is stored in a specific address on the Ethereum blockchain. Smart contracts can be understood as contracts that can be automatically executed on the blockchain and written in code. An important feature of smart contracts is Turing completeness. Turing completeness enables the script system to solve all computable problems. All logical operations that can be done by general programming languages can be implemented in smart contracts, and the combination of smart contracts and blockchain has more mandatory properties than general programming languages.

2.2. Wilson Score

In this paper, the voting smart contract is designed as a points-weighted voting. Each candidate can be given a number of yes votes and a number of negative votes. In the voting support rate statistics of candidates, the score of every candidate cannot be calculated simply by the number of yes votes/(yes votes + negative votes). If a candidate has a large sample of voters, the drawbacks of this algorithm are not obvious, but once the number of samples is too small, there will be errors in the confidence interval. In the points-weighted voting system, if the support rate of candidates is calculated according to the above algorithm, the cost of malicious voting will be very low. Therefore, this paper uses the Wilson score ranking algorithm to modify the voter support rate of candidates. The Wilson confidence interval calculation formula is as follows [9]:

$$\frac{\overline{p}+\frac{1}{2n}{Z}_{1-\alpha /2}^2\pm Z_{1-\alpha /2}\sqrt{\frac{\overline{p}(1-\overline{p})}{n}+\frac{Z_{1-\alpha /2}^2}{{4n}^2}}}{1+\frac{1}{n}{Z}_{1-\alpha /2}^2}.$$

(1)

In Formula (1), $\overline{p}$ represents the initial support rate of a candidate, and n refers to the size of the sample of the candidate. Z_1−α/2 is a constant, which represents the Z statistic corresponding to a certain confidence level (it can be obtained by looking up the statistics table). Through the calculation formula of the Wilson confidence interval, the lower bound of the Wilson confidence interval can be obtained, and the expression is as follows:

$$\frac{\overline{p}+\frac{1}{2n}{Z}_{1-\alpha /2}^2-Z_{1-\alpha /2}\sqrt{\frac{\overline{p}(1-\overline{p})}{n}+\frac{Z_{1-\alpha /2}^2}{{4n}^2}}}{1+\frac{1}{n}{Z}_{1-\alpha /2}^2}.$$

(2)

It can be seen from Formula (2) that when n is large enough, the lower bound will gradually tend to $\overline{p}$. On the contrary, the lower bound will be much smaller than $\overline{p}$ if n is small. Therefore, the lower bound of the Wilson interval can be taken as the final support rating S.

2.3. Related Work

In practical applications, the security of electronic voting is the primary factor, so the privacy protection in the electronic voting protocol has attracted more and more attention from researchers in many countries. Japanese scholars Fujioka, Okamoto, and Ohta gave the definition of security requirements for electronic voting. At the same time, they proposed the famous FOO electronic voting protocol (FOO is an abbreviation of the authors’ name). Many famous electronic voting systems are designed based on this scheme, such as the Sensus system of the University of Washington [10] and the EVOX system of the Massachusetts Institute of Technology [11]. The Sensus system is an actual electronic voting system designed by researchers at the University of Washington based on the FOO protocol. It meets the security requirements proposed by the FOO protocol. Even if the electoral institutions collude with each other, this system can also protect the privacy of voters. Voters can verify whether their votes are counted correctly. If their votes are not counted correctly, they can anonymously question the correctness of the election results. The EVOX system developed by MIT researchers is also based on the FOO protocol. The completion of the electronic voting process requires five stages: the preparation stage, the authorization stage, the anonymization stage, the collection stage, and the vote-counting stage. This voting process also greatly increases the anonymity of voters.

In addition to traditional electronic voting, some recent voting systems tend to be combined with the blockchain technology. In the voting system based on the blockchain technology, research on user privacy and security is also a hot topic. Reference [5] built an electronic voting system on Bitcoin blockchain, which allows candidates to vote while maintaining the privacy of individual voting. The disadvantage of this method is its low scalability. Building a voting smart contract on the blockchain can improve the efficiency of the voting process, and the voting contract can be used in multiple directions. Smart contracts simplify the voting process through third-party solutions. Na et al. proposed a chat system based on blockchain in which users can vote, and this system guarantees the anonymity of the users’ voting and chatting process [12]. In the voting protocol designed by Kshetri et al., each user is only allowed to spend one time for weighted voting. Although this method can simply restrict users from voting maliciously within the system, in practice, users who want to vote maliciously can always have multiple user accounts [13]. According to the survey in [14], since 2018, among all blockchain voting systems, the number of smart contracts built on the Ethereum platform has been the most largest. Yavuz et al. used the Ethereum platform to build a voting program for Android system, but its functions were too simple [15]. In some other blockchain platforms, there are also some practical application cases of the voting system, such as a simplified voting method of Quantum blockchain [16]. On the Hyperledger platform, Zhang et al. proposed a voting system that protects user privacy. This system can detect and correct the ballot, but it cannot verify the fairness of the ballot [17]. There are also many voting systems on the blockchain [6,18,19,20,21,22], which are designed to protect the privacy of voting users.

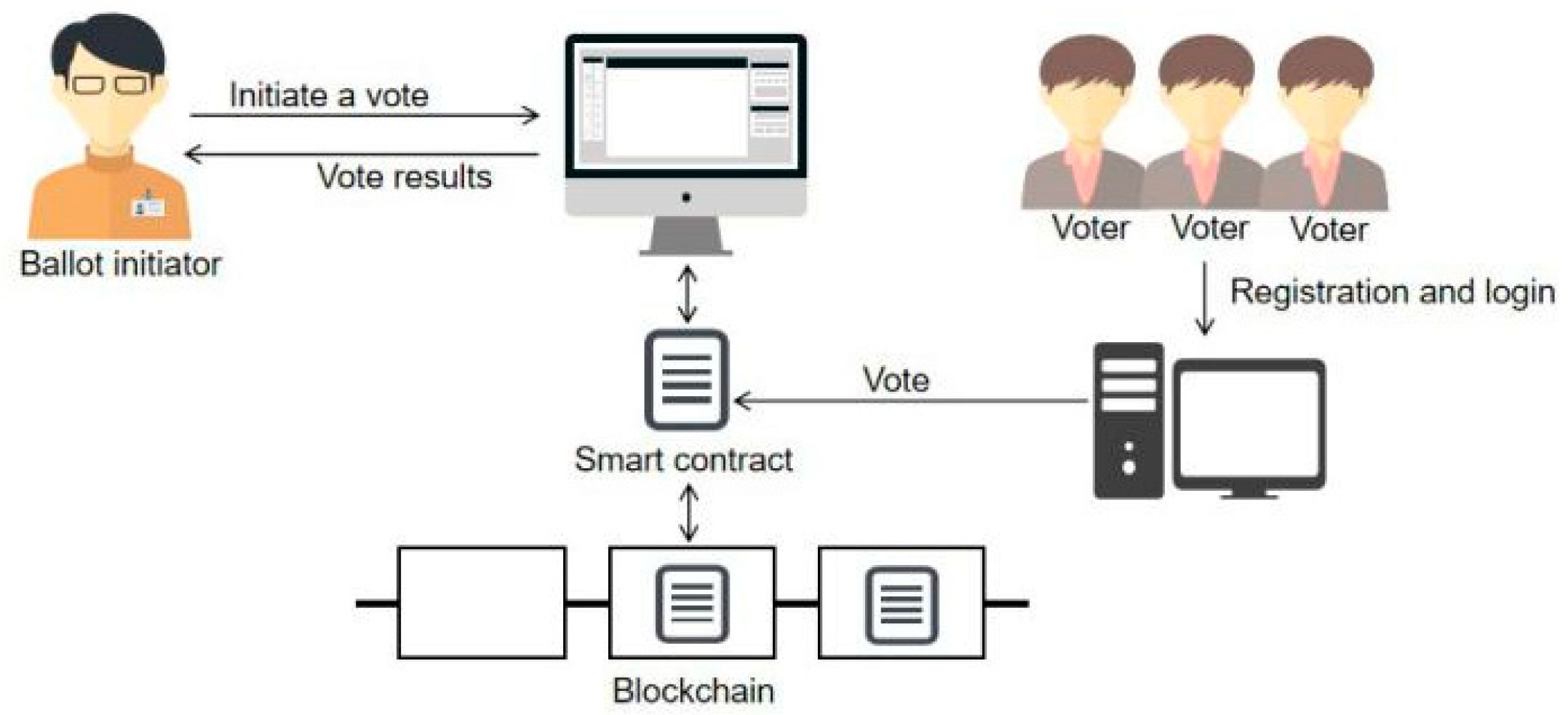
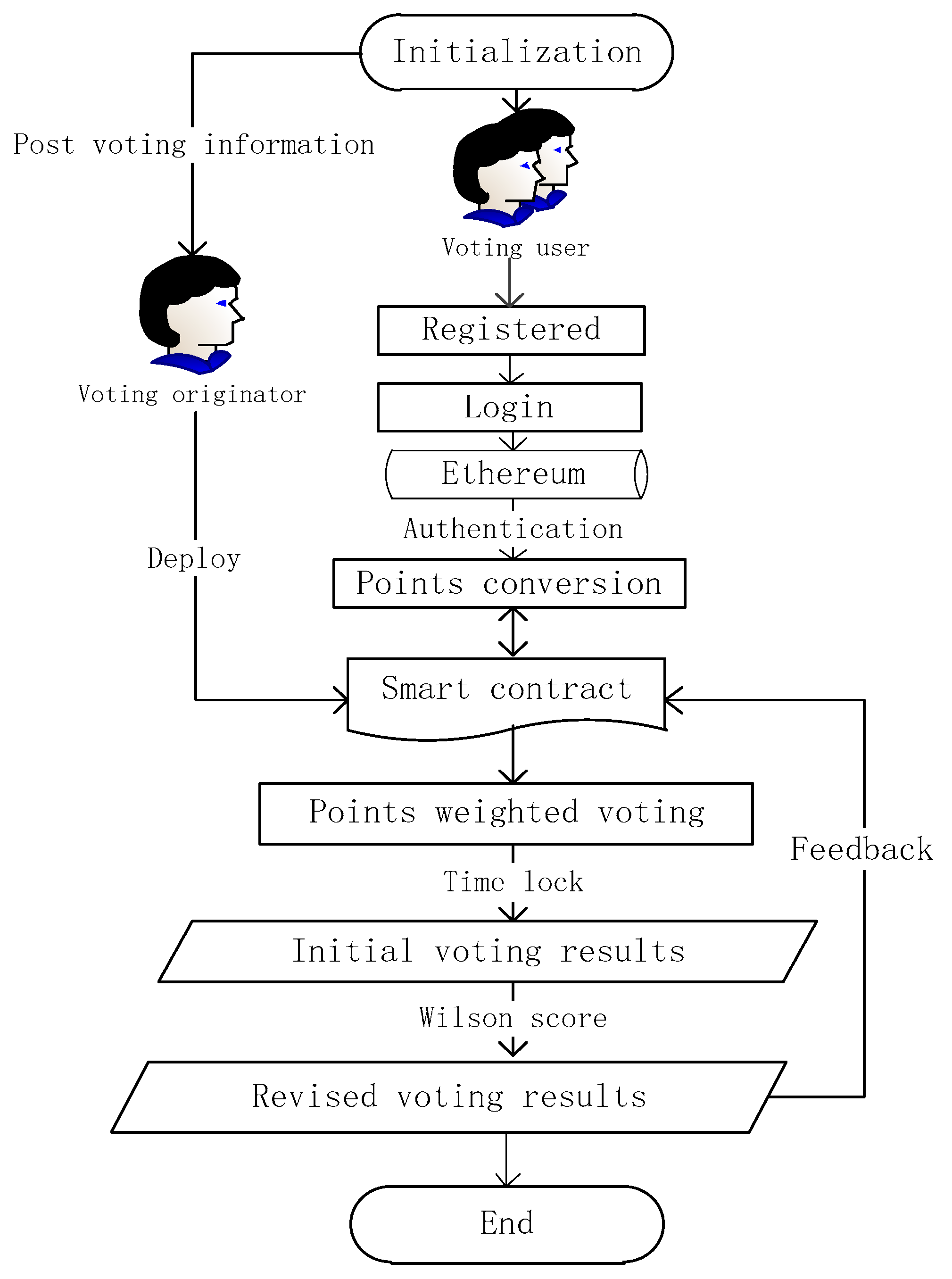
3. Voting System

The electronic voting system realizes the election process through the supporting of software and hardware. The election process generally includes registration, certification, voting, statistics, and other steps. In a blockchain voting system, the initiator of a vote writes the information about the vote into a smart contract and publishes it on the blockchain before the formal vote. Then, voters can learn about voting information in the smart contract. The registration and login process of the users in blockchain voting system is generally completed when users log in the blockchain, and the voting process is carried out in the form of sending a transaction into the smart contract account. The general blockchain voting process is shown in Figure 1.

The blockchain voting system designed in this paper is aimed at points-weighted voting. We have added a feedback mechanism to the basic blockchain voting process and designed a complete voting process. The smart contract we designed is actually a decentralized application. For the convenience of research, the smart contract introduced in this paper is built on the Ethereum private chain. This smart contract with the feedback mechanism can also be extended to the Ethereum consortium chain or other blockchain systems. Every vote requires a new smart contract. In a smart contract, we define α as the voting point conversion rate coefficient. The voting point conversion rate α represents the proportion of ether converted into voting points, which can be set according to the specific situation of each vote. For example, when α = 1, 1 ether can be converted into 1 voting point. In the voting system designed in this paper, voting points are only used to give yes votes. Voting points can be converted to ether after the end of the voting process and continue to circulate on the Ethereum private chain. When voters give yes votes for their prefer candidates, they will get negative votes, and the amount of negative votes is the same as the amount of yes votes they have used. Negative votes are only used to express the displeasure of the voters and will not be returned to the voter’s account after the voting is over. The voting process designed in this paper is shown in Figure 2.

In the voting process, the voting user is represented by V_i, and i is the index corresponding to each voting user. The candidate is represented by C_j, and j is the index corresponding to each candidate. A complete voting process is divided into two sections:

System initialization section:

Step1:

The voting initiator publishes voting details on the website, including the information of candidates (C₁, C₂, …, C_j, …), the voting time limit, and the voting point conversion rate α.

Step2:

Voting initiators register and log in to the Ethereum private chain, build, and deploy smart contracts.

User voting section:

Step1:

Users register and log in to participate in the voting smart contracts of the Ethereum private chain.

Step2:

The system performs a simple certification for the users participating in the voting to confirm that they are eligible to vote. The certification here is mainly to prevent some simple network attacks and re-entry attacks on smart contracts. This step is to expand the voting system in actual applications. In our experiment, we assume that all voting users are eligible. Then, the system generates voters (V₁, V₂, …, V_i, …).

Step3:

After the voting users have verified their voting qualifications, they can transfer ether to the smart contract account to obtain voting points, and the conversion rate of points is α.

Step4:

The smart contract works. When users participate in voting, each candidate can give yes votes and negative votes.

Step5:

The voting result is locked when the voting is closed. After that, the number of votes and samples of the candidates will be counted, and the initial support rate $\overline{p}$ of the candidate will be calculated by the number of votes ($\overline{p}$= yes votes/ (yes votes + negative votes)).

Step6:

The system calculates the data in step 5 by using the Wilson score algorithm to obtain the candidate’s final score S, and it obtains the feedback coefficient β through S.

Step7:

The smart contract feedback takes effect. Through the feedback coefficient β, the user’s voting points can be adjusted. The points can be converted to the user’s ether (conversion rate is α) and continue to circulate on the blockchain.

4. Feedback Mechanism

This section introduces the details of the voting system designed in this paper, including the realization principle of the feedback step and the algorithm of the feedback coefficient.

Most of the blockchain voting schemes are implemented in the form of transactions, and transactions are often accompanied by the value transfer, so the voting results are also a reflection of the benefits of users. In conventional points-weighted voting schemes, the benefits of voters are only related to the voting results. When a candidate wins the vote, the voters who support it may gain a sense of psychological happiness and self-identity. We can regard these psychological changes as a part of the voting benefits. In addition, when the voting organizer wants the default voting winner or a candidate team wants to get some economic and social benefits from the vote, it will provide the perverse incentive to vote for the expected winner, and not the candidate that the user legitimately wants to win. Therefore, when there are no restrictions, users can obtain voting benefits through the malicious voting behavior.

To prevent the malicious voting behavior, we can add a reverse adjustment factor to voting benefits. For example, in points-weighted voting, when the candidate the user expects wins, the system will deduct some voting points in the user’s account. According to the voting system designed in this way, voting users will consider two factors in the voting process when voting, which is the value of voting points and the value of voting results.

According to the above analysis, it is feasible to constrain the voting behavior by deducting some voting points. We refer to the points deducted as commissions. Considering the weight in points-weighted voting, it is better that the calculation of commissions is related to the user’s initial voting points and the voting results. In the voting process designed in this paper, all voting points are locked in the smart contract. In order to punish malicious users, the commission is designed in the form of total voting points × β (β is related to S, and the symbol × stands for the multiplication sign in this paper).

In order to determine the feasibility of the system and set the approximated range of β value, we conducted a survey on some users who participated in K-out-of-L voting. In this paper, the candidates are selected as candidate films for the 2020 Hundred Flowers Awards. The voters of the survey are 180 students from Shanghai Film School of Shanghai University. We stipulate that each voting user has initial 100 points (all must be used) to vote for the preferred movie, and another 100 points can be used to vote against the unsatisfactory movie. The top three are selected as winning candidates (three out of ten). At the same time, we inform voters that we will deduct some voting points as commissions after voting.

We assume three situations where the value of voting points is different.

(1)

The points are worthless. The points have no economic value, but the points returned to voters after deducting the commissions can be used to participate in the next similar vote.

(2)

The points have a lower value. One voting point can be exchanged for 0.1 yuan, and the points returned to voters after deducting the commissions can be used to participate in the next similar vote, or they can be exchanged for cash.

(3)

The points have a higher value. One voting point can be exchanged for 1 yuan. The points returned to voters after deducting the commissions can be used to participate in the next similar vote, or they can be exchanged for cash.

After determining three different initial conditions, we will ask voters to answer the following two questions.

(1)

If the option you voted for finally wins, how many points are you willing to pay as commission (0 means you are not willing to pay any commission).

(2)

If the option you voted is ultimately unsuccessful, how many points are you willing to pay as commission (0 means you are not willing to pay any commission).

We define the voters who voted for the winning candidates as the winning voter (VW) and the voters who voted for the unsuccessful candidates as the losing voters (VL). After statistics and calculation of experimental data, the statistics table of the survey is shown in

Table 1. Statistical table of survey of voting users.

Points Value	VW	R∈(0%,20%] in VW	VL
Higher	45.6%	89.02%	13.89%
Lower	63.3%	85.09%	26.67%
Worthless	81.1%	86.99%	36.11%

.

Table 1 records the proportion of the voters who are willing to pay commissions in VW and VL in the three cases where the value of points is higher, lower, and worthless. R represents the proportion of the commissions in the initial points that users used. The third column in Table 1 is the proportion of people in VW who is willing to pay the fee R ∊ (0%, 20%].

It can be seen that with the gradual decrease in the value of points, voting users are more willing to pay voting commissions. In the case where the points have no actual value, more than 80% of the winning voters VW are willing to pay the voting fees. In addition, 86.99% of the VW who are willing to pay for voting commission prefer the commission ratio to be between 0 and 20%. The survey of VL shows that when the value of points is high, 13.89% of users are willing to pay commission; when the value of the points is low, 26.67% of the users are willing to pay commission; when the points are worthless, 36.11% of the users are willing to pay commission. This means that in each of the three cases, more than 60% of VL are unwilling to pay commissions.

Based on the analysis of the data in Table 1, we make feedback rules as follows. According to the result of the vote, the winning user will pay commission, while the losing user will pay no fee. The feedback coefficient β can be set in a reasonable range (such as 5–20%), so as to not only ensure the system feedback process but also improve users’ enthusiasm for voting.

In K-out-of-L voting, the feedback algorithm is set as follows. First, the system counts the sample number n_j and the initial support rate $\overline{p}$_j of each candidate C_j, and it calculates the S_j of the candidate. Then, the candidate C_j is ranked according to S_j, and the top K candidates are defined as winning candidates, and the last (L−K) candidates are losing candidates. Finally, the system calculates the β value of the winning candidate, traverses the voting information of V_i among the winning candidates, and returns (1 − β) × the number of yes vote points to the voters’ account. Then, the system traverses the voting information of V_i among the unsuccessful candidates, and it returns all the yes votes. The specific steps are as follows.

Step 1: The number of votes for each candidate, the initial support rate $\overline{p}$_j, and the number of samples n_j are calculated after voting. For candidate j, the initial voting support rate $\overline{p}$_j is calculated by the number of yes votes/(yes votes + negative votes). The sample number n_j of candidate j is the number of voters that give yes votes for candidate j in the system.

Step 2: The system calculates the lower bound of the Wilson interval according to Algorithm 1 to obtain the Wilson score S_j of each candidate.

Taking the 95% confidence level as an example, the Z_1−ɑ/2 statistic is 1.96.

Algorithm 1: Lower bound of the Wilson score confidence interval

1. Input $\overline{p}$j, nj, Z1-ɑ/2 (abbreviated as Z)   2. Output Sj   3. BEGIN   4. Z ← 1.96   5. FOR EACH j:   6. IF n == 0   7. RETURN 0   8. ELSE Sj ← ($\overline{p}$ j+ Z × Z/(2 × nj) −Z × Math.sqrt(($\overline{p}$j × (1 − $\overline{p}$j) + Z × Z/(4 × nj))/nj))/(1 + Z × Z/nj)   9. RETURN Sj   10. END IF   11. END FOR

Step 3: The candidates (C₁, C₂, …, C_j, …) are re-ranked according to the value of S_j, the top K positions among the re-ranked candidates are selected as the winning options, and the Boolean value B_j of the voting results of these candidates is marked as true.

Step 4: The system calculates the feedback coefficient β_j of the winning option after ranking by Algorithm 2.

Algorithm 2: Feedback coefficient algorithm

1. Input Sj, Bj, Cj   2. Output βj   3. BEGIN   4. FOR EACH j:   5. IF Bj == true   6. VAR a ← (1 − Sj)/2   7. IF a < 0.05 THEN   8. βj ← 0.05   9. ELSE IF a > 0.20 THEN   10. βj ← 0.20   11. ELSE βj ← a   12. END IF   13. END FOR   14. RETURN βj

Step 5: All voting points of the unsuccessful candidates will be returned to the voters according to the source. For the voting points obtained by the winning candidates, the system will deduct the commissions of (1 − β_j) × total number of votes, and the remaining points of β_j × total number of votes are returned to the voters according to the source.

5. Experiment Analysis

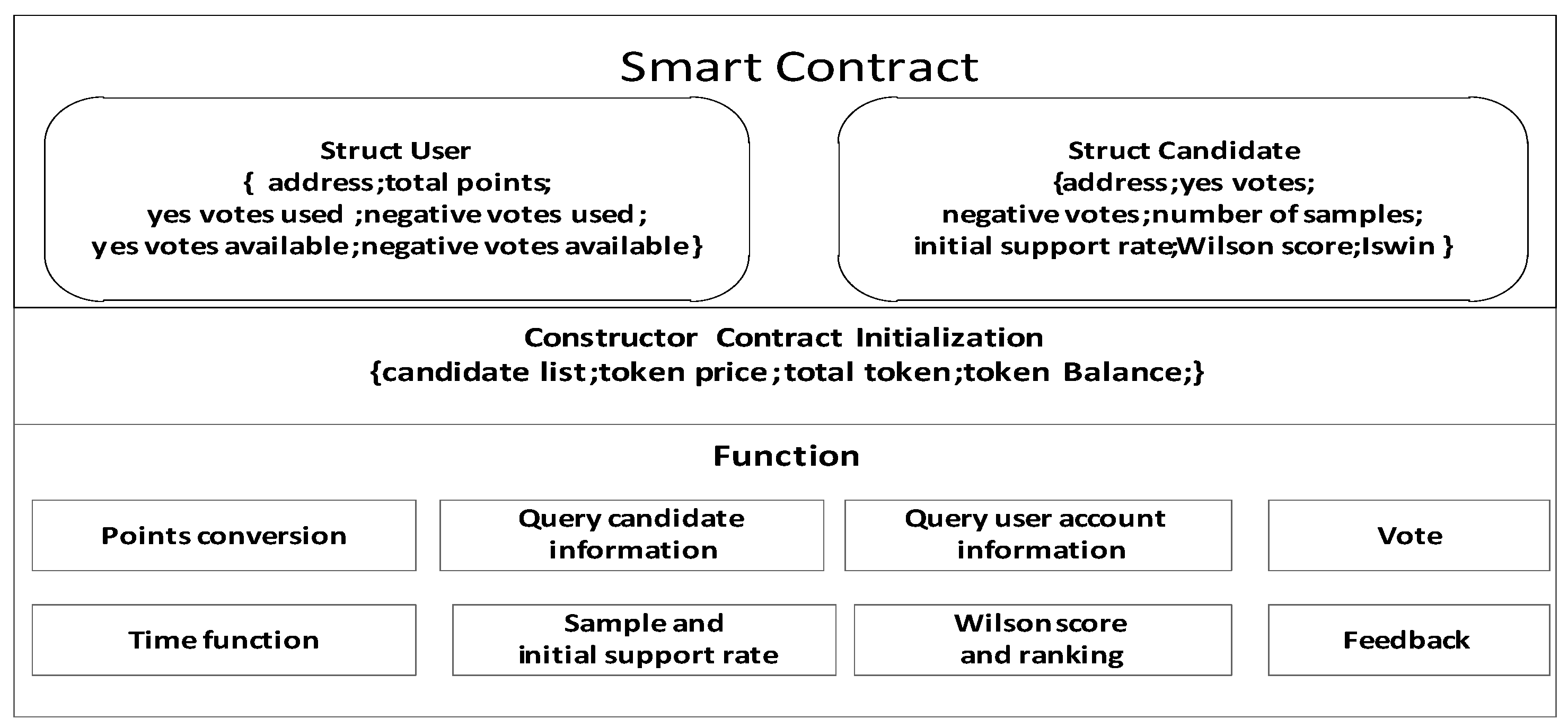
5.1. Smart Contract Function

In this section, we introduced the functions required by the smart contract and deployed the smart contract. The smart contract is tested in the Solidity Remix IDE integrated development environment. The smart contract uses the Solidity language. The Solidity Remix IDE provides an online compilation environment for the Solidity smart contract. In the JavaScript VM framework, five account addresses with a balance of 100 ether are initialized, which facilitates the deployment, compilation, and testing of smart contracts. The smart contract structure is shown in Figure 3.

The above methods are deployed and tested in the Solidity Remix IDE environment. The result is shown in Figure 4.

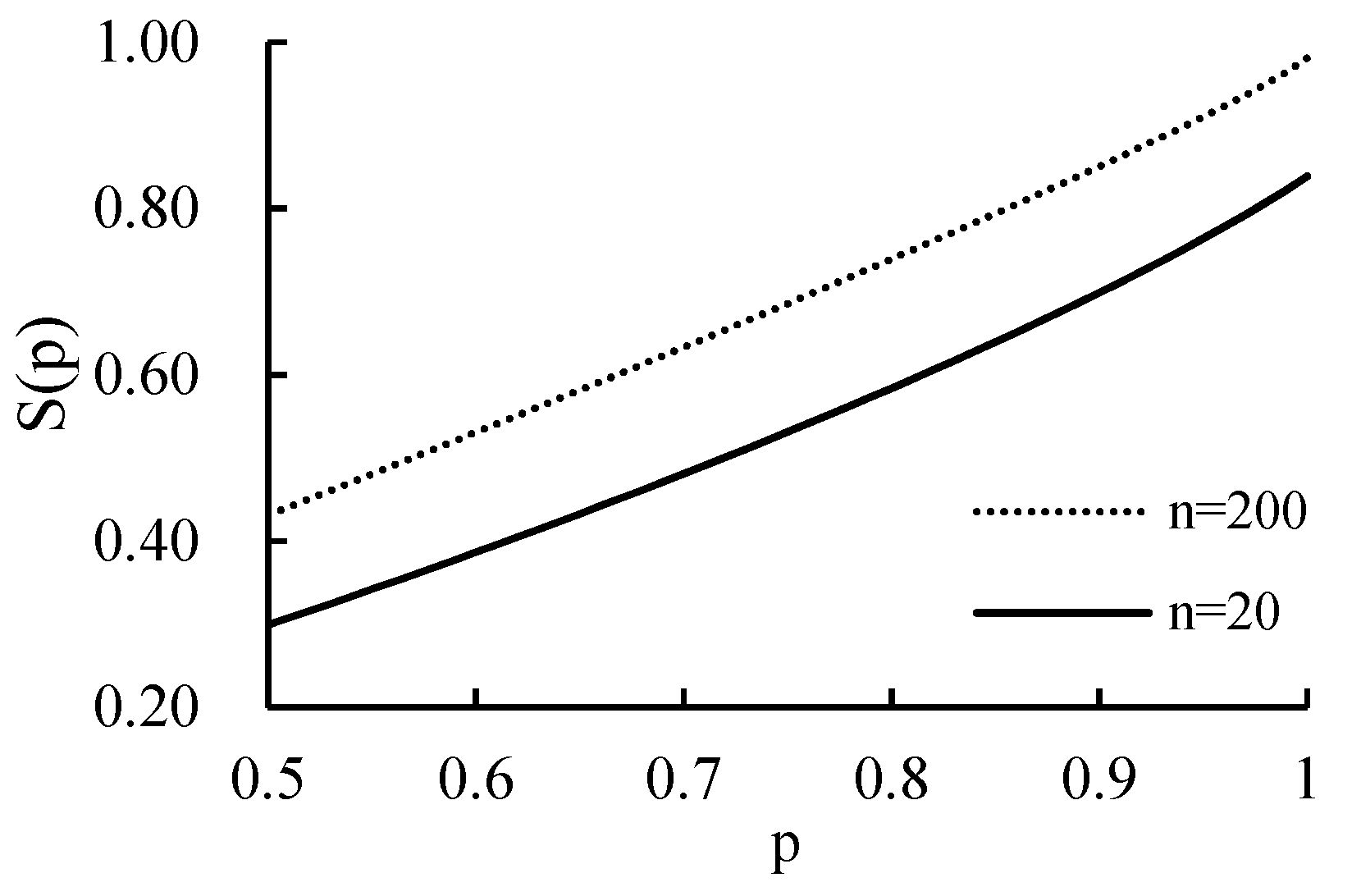
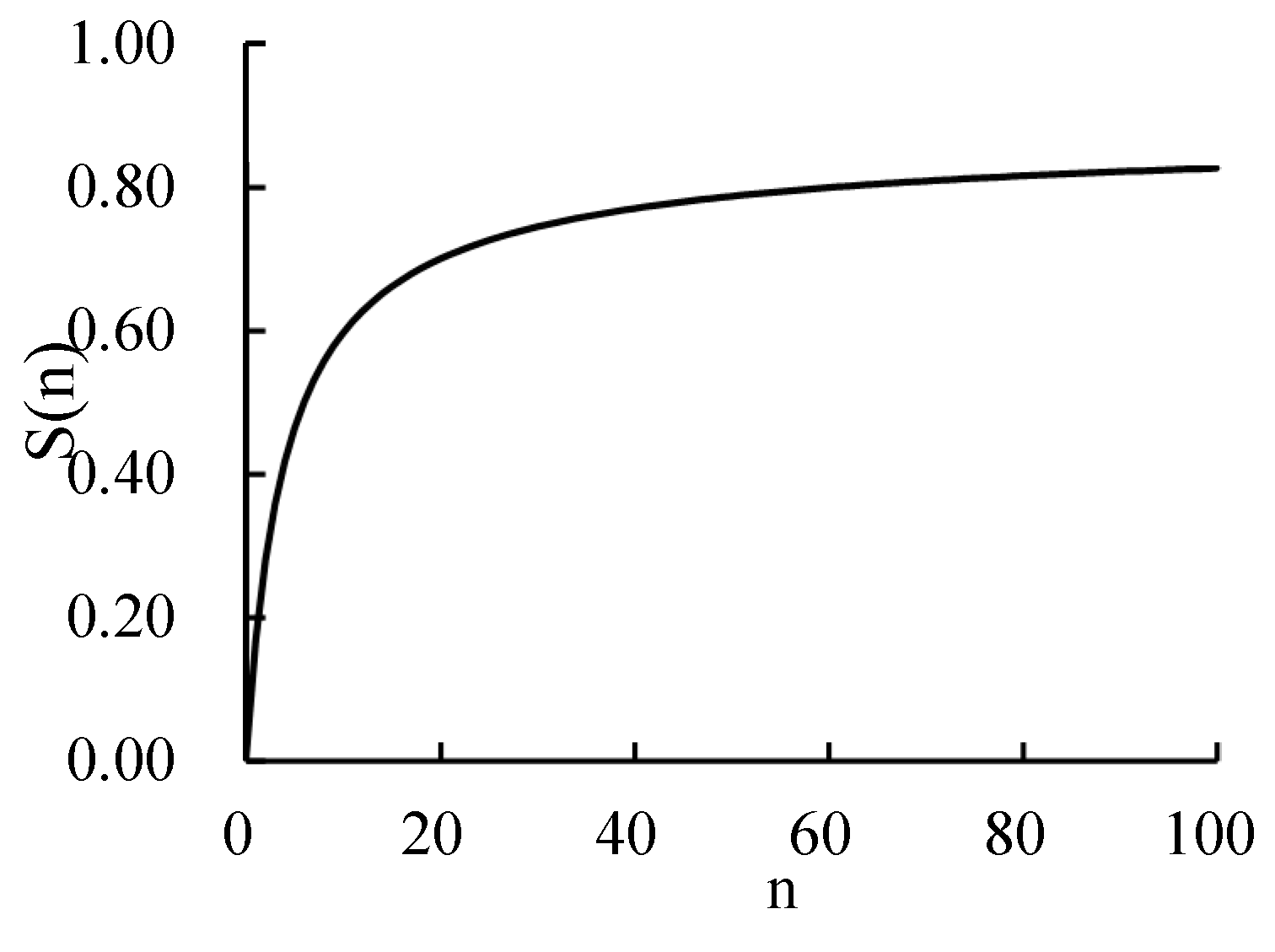
5.2. Wilson Score Analysis

In the two cases of the same approval rate with different sample sizes and the same sample size with different approval rates, we use the method proposed in this paper to modify the initial support rate by the Wilson score.

As shown in Figure 5, when the number of samples is 20 and 200, the curve of the Wilson score with the initial support rate approximates a straight line, indicating that the Wilson score is approximately proportional to the initial support rate. The size of the sample size has little effect on the speed of the Wilson score changing with the initial support rate.

We set the initial approval rate to be 90% and observe that the Wilson score changes with the number of samples, as shown in Figure 6. When the number of samples is less than 20, as the number of samples increases, the Wilson score changes significantly. For the number of samples between 20 and 40, the growth of the Wilson score slows down, but it is still more obvious. If the number of samples is between 40 and 80, the Wilson score increases more slowly. When the number of samples exceeds 80, as the number of samples increases, the Wilson score only slightly increases. The above analysis indicates that the Wilson score has a large correction range for the support rate of low-sample candidates. As the number of samples increases, the Wilson score gradually approaches the initial support rate. Therefore, the Wilson score is applicable to the feedback mechanism in this paper.

5.3. Case Analysis

In this chapter, we will make a case analysis on the survey data of the 2020 Hundred Flowers Awards mentioned in Section 4. The vote statistics are shown in

Table 2. 2020 Hundred Flowers Award favorite questionnaire.

Movie Names	n	$\overline{\mathit{p}}$	S
My People, My Country	157	73.67%	0.6627
Dying to Survive	160	90.15%	0.8455
Ne Zha	178	86.35%	0.8053
The Wandering Earth	172	54.04%	0.4659
The Captain	142	40.90%	0.3316
Better Days	125	85.40%	0.7816
Sheep Without A Shepherd	98	74.75%	0.6533
The Bravest	85	34.77%	0.2551
The Climbers	76	7.50%	0.0342
Project Gutenberg	66	87.68%	0.7763

.

In Table 2 and

Table 3. Ranking comparison table.

Ranking	Initial	$\overline{\mathit{p}}$	Final	S
1	Dying to Survive	90.15%	Dying to Survive	0.8455
2	Project Gutenberg	87.68%	Ne Zha	0.8053
3	Ne Zha	86.35%	Better Days	0.7816
4	Better Days	85.40%	Project Gutenberg	0.7763
5	Sheep Without A Shepherd	74.75%	My People, My Country	0.6627
6	My People, My Country	73.67%	Sheep Without A Shepherd	0.6533
7	The Wandering Earth	54.04%	The Wandering Earth	0.4659
8	The Captain	40.90%	The Captain	0.3316
9	The Bravest	34.77%	The Bravest	0.2551
10	The Climbers	7.50%	The Climbers	0.0342

, we evaluated the performance of our proposal to use the Wilson score to calculate the vote support rate. In Table 2, $\overline{p}$ is a benchmarking data to evaluate the Wilson score S. By comparing $\overline{p}$ and S, we can see that the Wilson score effectively evaluates the approval rate of candidates with fewer samples. It can be found that the higher the sample size of a candidate, the smaller the change in its original support rate by the Wilson score. For the top three candidates, their Wilson scores are all above 0.6 and below 0.9, which means that the feedback coefficient β is between 5% and 20%. The feedback coefficient does not reach the maximum or minimum of feedback, indicating that the feedback algorithm design is relatively reasonable.

In Table 3, the initial ranking and final ranking are two benchmarking variables to evaluate the ranking changes brought about by the Wilson score. It can be seen that the Wilson score effectively evaluates the candidate’s confidence interval based on the number of samples n and the initial support rate $\overline{p}$. In addition, the Wilson score also has a reasonable correction to the ranking of candidates.

In order to test the rationality of the feedback mechanism, we conduct malicious cost analysis on ten candidates. In

Table 4. The analysis of malicious user cost.

Movie Names	Nc	Fc	Nk	Fk
Dying to Survive	0	0	0	0
Ne Zha	1168	90	0	0
Better Days	1964	152	0	0
Project Gutenberg	843	65	38	4
My People, My Country	5226	404	2204	241
Sheep Without A Shepherd	4131	319	1712	187
The Wandering Earth	11,278	871	6099	666
The Captain	11,215	866	6291	687
The Bravest	16,792	1297	9063	990
The Climbers	61,858	4778	33,862	3699

, Nc represents the number of votes required for a single user to control the option to become the first place, and Fc represents the commissions required to complete the above operation. Nk represents the number of votes required for a single user to control the option to become the top three, and Fk represents the commissions required to complete the above operation.

It can be seen from Table 4 that when a single user wants to control the voting results, the number of votes that needs to be cast is very large compared to 100 (the initial votes number) and the proportion of commissions is high as well. In addition, the number of votes can be kept private during the voting time through some cryptography techniques. This will not affect the trust mechanism of the smart contract, so that the cost of a single malicious user will become very huge. The feedback mechanism proposed in this paper can well restrain users’ behavior of swiping tickets.

6. Conclusions

This paper proposes a blockchain voting feedback mechanism based on the Wilson score to achieve effective constraints on the malicious voting behavior. Experiments are carried out for the K-out-of-L type of points-weighted voting, and the Wilson score is used to modify the initial support rate of each candidate. Experimental results confirm the applicability of the Wilson score and the feasibility of the feedback mechanism. Experimental results also show that the Wilson score improves the accuracy of voting results, and the feedback mechanism greatly increases the cost of malicious users.

Blockchain was born from digital currency, which itself is the product of decentralization and economic decentralization. In the blockchain system, smart contracts that are truly value-related are more meaningful. This article proposes a new feedback idea in the blockchain voting system, which is to restrict voting behavior through voting results, so that the cost and risk of voting can be quantified. At the same time, this idea can be extended to other types of blockchain voting systems, and other blockchain applications. This scheme is also scalable, because everyone can be the initiator of the vote (as long as the vote can attract enough users to participate in). Then, for the handling of the commissions, we can choose to feedback to the voting users, or it can be used as the initial fund of a project. According to this direction, the voting contract can be also used as a crowdfunding contract.