Penalty-Enhanced Utility-Based Multi-Criteria Recommendations
Abstract
1. Introduction
2. Related Work
2.1. Multi-Criteria Recommendations
2.2. Utility-Based Recommendation Models
3. Preliminary: Utility-Based Multi-Criteria Recommendations
3.1. Utility-Based Model (UBM)
3.2. Optimization
| Algorithm 1: Workflow in PSO. |
 |
4. Penalty-Enhanced Utility-Based Multi-Criteria Recommendation Model
4.1. Issue of Over-/Under-Expectations
4.2. Penalty-Enhanced Models (PEMs)
5. Experiments and Results
5.1. Data Sets and Evaluations
- TripAdvisor data: This data was crawled by Jannach, et al. [33]. The data was collected through a Web crawling process which collects users’ ratings on hotels located in 14 global metropolitan destinations, such as London, New York, Singapore, etc. There are 22,130 ratings given by 1502 users and 14,300 hotels. Each user gave at least 10 ratings which are associated with multi-criteria ratings on seven criteria: value for the money, quality of rooms, convenience of the hotel location, cleanliness of the hotel, experience of check-in, overall quality of service and particular business services.
- Yahoo!Movie data: This data was obtained from YahooMovies by Jannach, et al. [33]. There are 62,739 ratings given by 2162 users on 3078 movies. Each user left at least 10 ratings which are associated with multi-criteria ratings on four criteria: direction, story, acting and visual effects.
- SpeedDating data: It was available on Kaggle (https://www.kaggle.com/annavictoria/speed-dating-experiment). There are 8378 ratings given by 392 users. It is a special data for reciprocal people-to-people recommendations, while the “items” to be recommended are the users too. Each user will rate his or her dating partner in six criteria: attractiveness, sincerity, intelligence, fun, ambition, and shared interests.
- ITMLearning data: It was collected for the educational project recommendations [34], while the authors used the filtering strategy to alleviate the over-/under-expectations. There are 3306 ratings given by 269 users on 70 items. Each rating entry is also associated with three criteria: app (how students like the application of the project), data (the ease of data preprocessing in the project) and ease (the overall ease of the project).
- The matrix factorization (MF) is the biased matrix factorization model [25] by using the rating matrix <User, Item, Ratings> only without considering multi-criteria ratings.
- The linear aggregation model (LAM) [4] is a standard aggregation-based multi-criteria recommendation method which predicts the multi-criteria ratings independently and uses a linear aggregation to estimate a user’s overall rating on an item.
- The UBM model which is the original utility-based multi-criteria recommendation model without handling the over-/under-expectation issues.
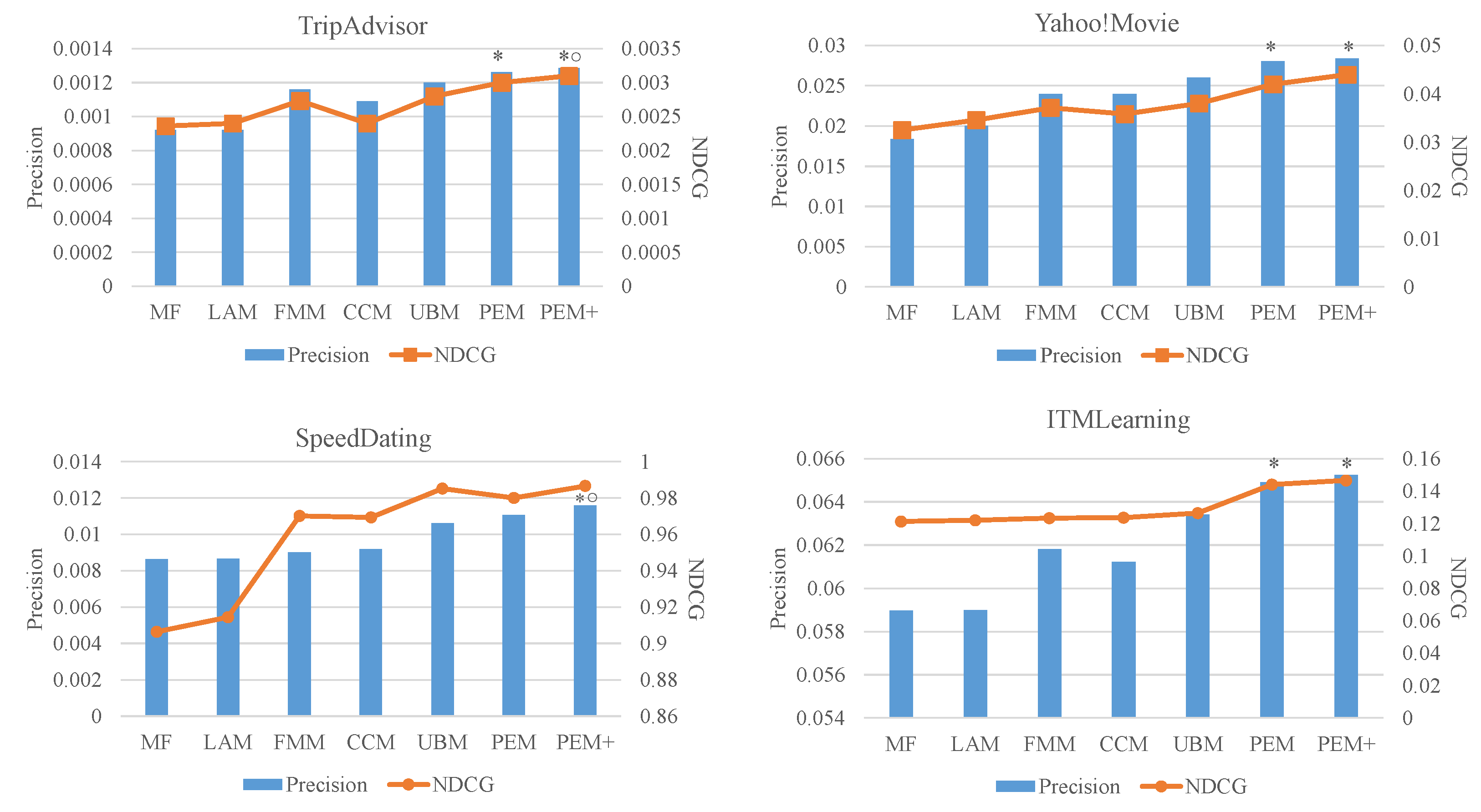
5.2. Results and Findings
6. Conclusions and Future Work
Funding
Conflicts of Interest
Abbreviations
| CCM | Criteria Chain Model |
| DCG | Discounted Cumulative Gain |
| FMM | Flexible Mixture Model |
| LAM | Linear Aggregation Model |
| MCRS | Multi-Criteria Recommender Systems |
| MF | Matrix Factorization |
| MOEA | Multi-Objective Evolutionary Algorithms |
| NDCG | Normalized Discounted Cumulative Gain |
| PEM | Penalty-Enhanced Model |
| PSO | Particle Swarm Optimization |
| UBM | Utility-Based Model |
References
- Bawden, D.; Robinson, L. The dark side of information: Overload, anxiety and other paradoxes and pathologies. J. Inf. Sci. 2009, 35, 180–191. [Google Scholar] [CrossRef]
- Alexandridis, G.; Siolas, G.; Stafylopatis, A. ParVecMF: A paragraph vector-based matrix factorization recommender system. arXiv 2017, arXiv:1706.07513. [Google Scholar]
- Alexandridis, G.; Tagaris, T.; Siolas, G.; Stafylopatis, A. From Free-text User Reviews to Product Recommendation using Paragraph Vectors and Matrix Factorization. In Companion Proceedings of the 2019 World Wide Web Conference; Association for Computing Machinery: New York, NY, USA, 2019; pp. 335–343. [Google Scholar]
- Adomavicius, G.; Kwon, Y. New recommendation techniques for multicriteria rating systems. IEEE Intell. Syst. 2007, 22, 48–55. [Google Scholar] [CrossRef]
- Zheng, Y. Utility-based multi-criteria recommender systems. In Proceedings of the 34th ACM/SIGAPP Symposium on Applied Computing, Limasso, Cyprus, 8–12 April 2019; pp. 2529–2531. [Google Scholar]
- Liu, T.Y. Learning to Rank for Information Retrieval; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Balakrishnan, S.; Chopra, S. Collaborative ranking. In Proceedings of the Fifth ACM International Conference on Web Search and Data Mining, Seattle, WA, USA, 8–12 February 2012; pp. 143–152. [Google Scholar]
- Zheng, Y.; Ghane, N.; Sabouri, M. Personalized Educational Learning with Multi-Stakeholder Optimizations. In Proceedings of the Adjunct ACM Conference on User Modelling, Adaptation and Personalization, Larnaca, Cyprus, 9–12 June 2019. [Google Scholar]
- Manouselis, N.; Costopoulou, C. Experimental analysis of design choices in multiattribute utility collaborative filtering. Int. J. Pattern Recognit. Artif. Intell. 2007, 21, 311–331. [Google Scholar] [CrossRef]
- Sahoo, N.; Krishnan, R.; Duncan, G.; Callan, J. Research Note—The Halo Effect in Multicomponent Ratings and Its Implications for Recommender Systems: The Case of Yahoo! Movies. Inf. Syst. Res. 2012, 23, 231–246. [Google Scholar] [CrossRef]
- Zheng, Y. Criteria Chains: A Novel Multi-Criteria Recommendation Approach. In Proceedings of the 22nd International Conference on Intelligent User Interfaces, Limassol, Cyprus, 13–16 March 2017; pp. 29–33. [Google Scholar]
- Burke, R. Hybrid recommender systems: Survey and experiments. User Model. User-Adapt. Interact. 2002, 12, 331–370. [Google Scholar] [CrossRef]
- Schafer, J.B.; Frankowski, D.; Herlocker, J.; Sen, S. Collaborative filtering recommender systems. In The Adaptive Web; Springer: Berlin/Heidelberg, Germany, 2007; pp. 291–324. [Google Scholar]
- Ekstrand, M.D.; Riedl, J.T.; Konstan, J.A. Collaborative Filtering Recommender Systems. Available online: https://dl.acm.org/doi/10.1561/1100000009 (accessed on 23 November 2020).
- Pazzani, M.J.; Billsus, D. Content-based recommendation systems. In The Adaptive Web; Springer: Berlin/Heidelberg, Germany, 2007; pp. 325–341. [Google Scholar]
- Lops, P.; De Gemmis, M.; Semeraro, G. Content-based recommender systems: State of the art and trends. In Recommender Systems Handbook; Springer: Berlin/Heidelberg, Germany, 2011; pp. 73–105. [Google Scholar]
- Zhao, W.X.; Li, S.; He, Y.; Wang, L.; Wen, J.R.; Li, X. Exploring demographic information in social media for product recommendation. Knowl. Inf. Syst. 2016, 49, 61–89. [Google Scholar] [CrossRef]
- Burke, R. Knowledge-based recommender systems. Encycl. Libr. Inf. Syst. 2000, 69, 175–186. [Google Scholar]
- Tarus, J.K.; Niu, Z.; Mustafa, G. Knowledge-based recommendation: A review of ontology-based recommender systems for e-learning. Artif. Intell. Rev. 2018, 50, 21–48. [Google Scholar] [CrossRef]
- Guttman, R.H. Merchant Differentiation through Integrative Negotiation in Agent-Mediated Electronic Commerce. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1998. [Google Scholar]
- Zihayat, M.; Ayanso, A.; Zhao, X.; Davoudi, H.; An, A. A utility-based news recommendation system. Decis. Support Syst. 2019, 117, 14–27. [Google Scholar] [CrossRef]
- Li, Z.; Fang, X.; Bai, X.; Sheng, O.R.L. Utility-based link recommendation for online social networks. Manag. Sci. 2017, 63, 1938–1952. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Lacerda, A.; Veloso, A.; Ziviani, N. Pareto-efficient hybridization for multi-objective recommender systems. In Proceedings of the Sixth ACM Conference on Recommender Systems, Dublin, Ireland, 9–13 September 2012. [Google Scholar]
- Ribeiro, M.T.; Ziviani, N.; Moura, E.S.D.; Hata, I.; Lacerda, A.; Veloso, A. Multiobjective pareto-efficient approaches for recommender systems. ACM Trans. Intell. Syst. Technol. 2014, 5, 1–20. [Google Scholar]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Valizadegan, H.; Jin, R.; Zhang, R.; Mao, J. Learning to Rank by Optimizing NDCG Measure. Available online: https://dl.acm.org/doi/10.5555/2984093.2984304 (accessed on 23 November 2020).
- Donmez, P.; Svore, K.M.; Burges, C.J. On the local optimality of LambdaRank. In Proceedings of the 32nd International ACM SIGIR Conference on Research and Development in Information Retrieval, Boston, MA, USA, 19–23 July 2009; pp. 460–467. [Google Scholar]
- Yeh, J.Y.; Lin, J.Y.; Ke, H.R.; Yang, W.P. Learning to rank for information retrieval using genetic programming. In Proceedings of the SIGIR 2007 Workshop on Learning to Rank for Information Retrieval (LR4IR 2007), Amsterdam, The Netherlands, 23–27 July 2007. [Google Scholar]
- Ujjin, S.; Bentley, P.J. Particle swarm optimization recommender system. In Proceedings of the 2003 IEEE Swarm Intelligence Symposium, SIS’03 (Cat. No. 03EX706), Indianapolis, IN, USA, 26 April 2003; pp. 124–131. [Google Scholar]
- Zheng, Y.; Burke, R.; Mobasher, B. Recommendation with differential context weighting. In Proceedings of the International Conference on User Modeling, Adaptation, and Personalization, Rome, Italy, 10–14 June 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 152–164. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Jannach, D.; Zanker, M.; Fuchs, M. Leveraging multi-criteria customer feedback for satisfaction analysis and improved recommendations. Inf. Technol. Tour. 2014, 14, 119–149. [Google Scholar] [CrossRef]
- Zheng, Y. Personality-Aware Decision Making In Educational Learning. In Proceedings of the 23rd International Conference on Intelligent User Interfaces, Tokyo, Japan, 7–11 March 2018; p. 58. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1945–1950. [Google Scholar]
- Sierra, M.R.; Coello, C.A.C. Improving PSO-based multi-objective optimization using crowding, mutation and ϵ-dominance. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Guanajuato, Mexico, 9–11 March 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 505–519. [Google Scholar]
- Pizzato, L.; Rej, T.; Chung, T.; Koprinska, I.; Kay, J. RECON: A reciprocal recommender for online dating. In Proceedings of the Fourth ACM Conference on Recommender Systems, Barcelona, Spain, 26–30 September 2010; pp. 207–214. [Google Scholar]
- Zheng, Y.; Dave, T.; Mishra, N.; Kumar, H. Fairness In Reciprocal Recommendations: A Speed-Dating Study. In Proceedings of the Adjunct ACM Conference on User Modelling, Adaptation and Personalization, Singapore, 8–11 July 2018. [Google Scholar]
- Adomavicius, G.; Mobasher, B.; Ricci, F.; Tuzhilin, A. Context-Aware Recommender Systems. AI Mag. 2011, 32, 67–80. [Google Scholar] [CrossRef]
- Adomavicius, G.; Tuzhilin, A. Context-aware recommender systems. In Recommender Systems Handbook; Springer: Berlin/Heidelberg, Germany, 2011; pp. 217–253. [Google Scholar]
- Agreste, S.; De Meo, P.; Ferrara, E.; Piccolo, S.; Provetti, A. Trust networks: Topology, dynamics, and measurements. IEEE Internet Comput. 2015, 19, 26–35. [Google Scholar] [CrossRef]
- Lee, J.; Noh, G.; Oh, H.; Kim, C.k. Trustor clustering with an improved recommender system based on social relationships. Inf. Syst. 2018, 77, 118–128. [Google Scholar] [CrossRef]
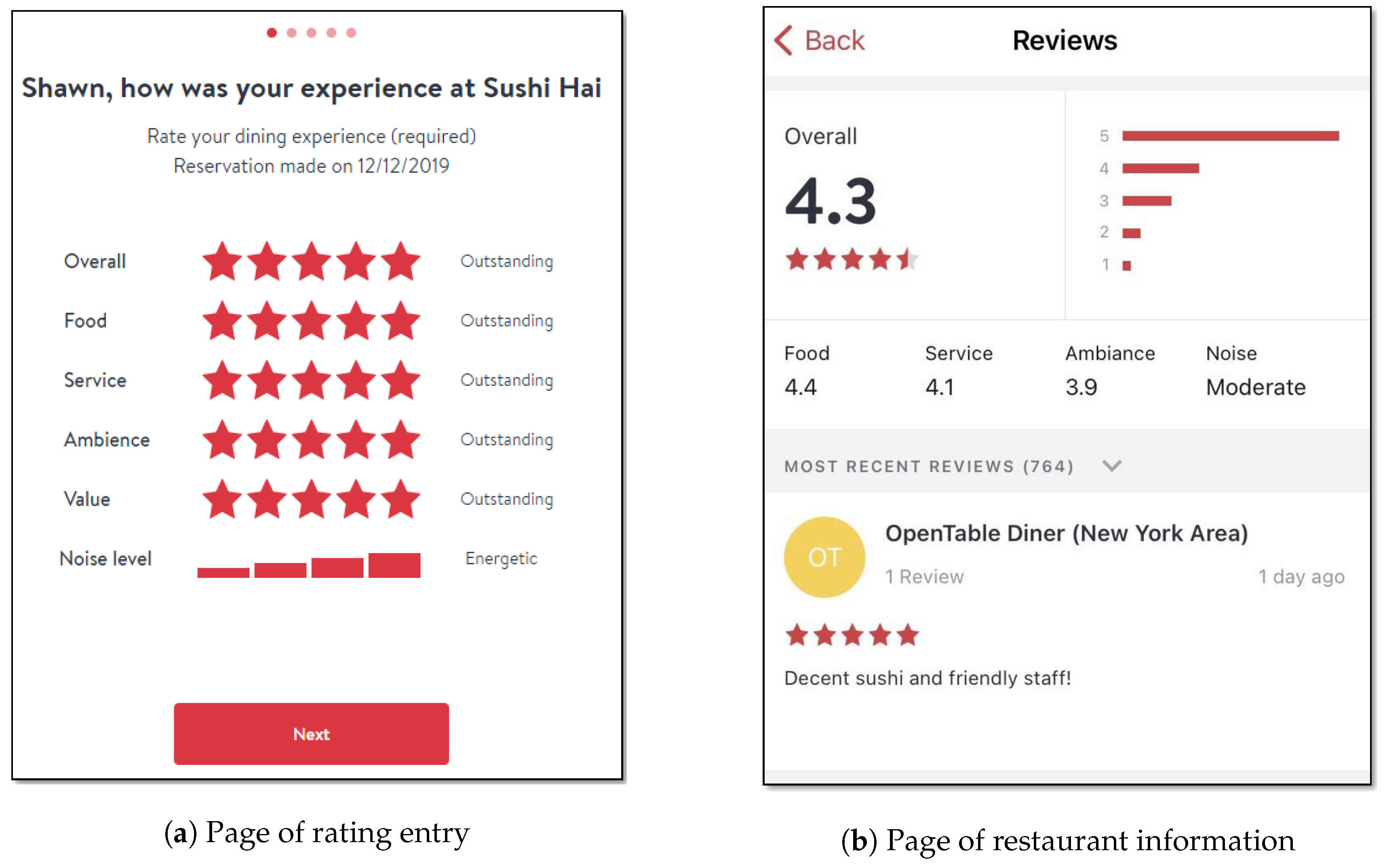
| User | Item | Rating | Food | Service | Value |
|---|---|---|---|---|---|
| 4 | 4 | 3 | 4 | ||
| 3 | 3 | 3 | 3 | ||
| ? | ? | ? | ? |
| User | Item | Food | Service | Value | Ambiance |
|---|---|---|---|---|---|
| u | 2 | 2 | 2 | 2 | |
| u | 4 | 4 | 4 | 4 | |
| u | 1 | 4 | 2 | 1 | |
| u’s expectation | 3 | 3 | 3 | 3 | |
| TripAdvisor | Yahoo!Movie | SpeedDating | ITMLearning | |
|---|---|---|---|---|
| UBM | 0.0028 | 0.038 | 0.9852 | 0.1264 |
| PEM | 0.003 (7.14%) * | 0.042 (10.5%) * | 0.98 (−0.5%) | 0.1441 (14%) * |
| PEM+ | 0.0031 (10.7%) * ∘ | 0.044 (15.8%) * ∘ | 0.9866 (0.14%) | 0.1466 (15.9%) * ∘ |
| TripAdvisor | 0.124 | −0.022 |
| Yahoo!Movie | 0.574 | −0.985 |
| SpeedDating | −0.29 | 0.02 |
| ITMLearning | 0.324 | −0.165 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y. Penalty-Enhanced Utility-Based Multi-Criteria Recommendations. Information 2020, 11, 551. https://doi.org/10.3390/info11120551
Zheng Y. Penalty-Enhanced Utility-Based Multi-Criteria Recommendations. Information. 2020; 11(12):551. https://doi.org/10.3390/info11120551
Chicago/Turabian StyleZheng, Yong. 2020. "Penalty-Enhanced Utility-Based Multi-Criteria Recommendations" Information 11, no. 12: 551. https://doi.org/10.3390/info11120551
APA StyleZheng, Y. (2020). Penalty-Enhanced Utility-Based Multi-Criteria Recommendations. Information, 11(12), 551. https://doi.org/10.3390/info11120551





