K-Means Clustering-Based Electrical Equipment Identification for Smart Building Application
Abstract
1. Introduction
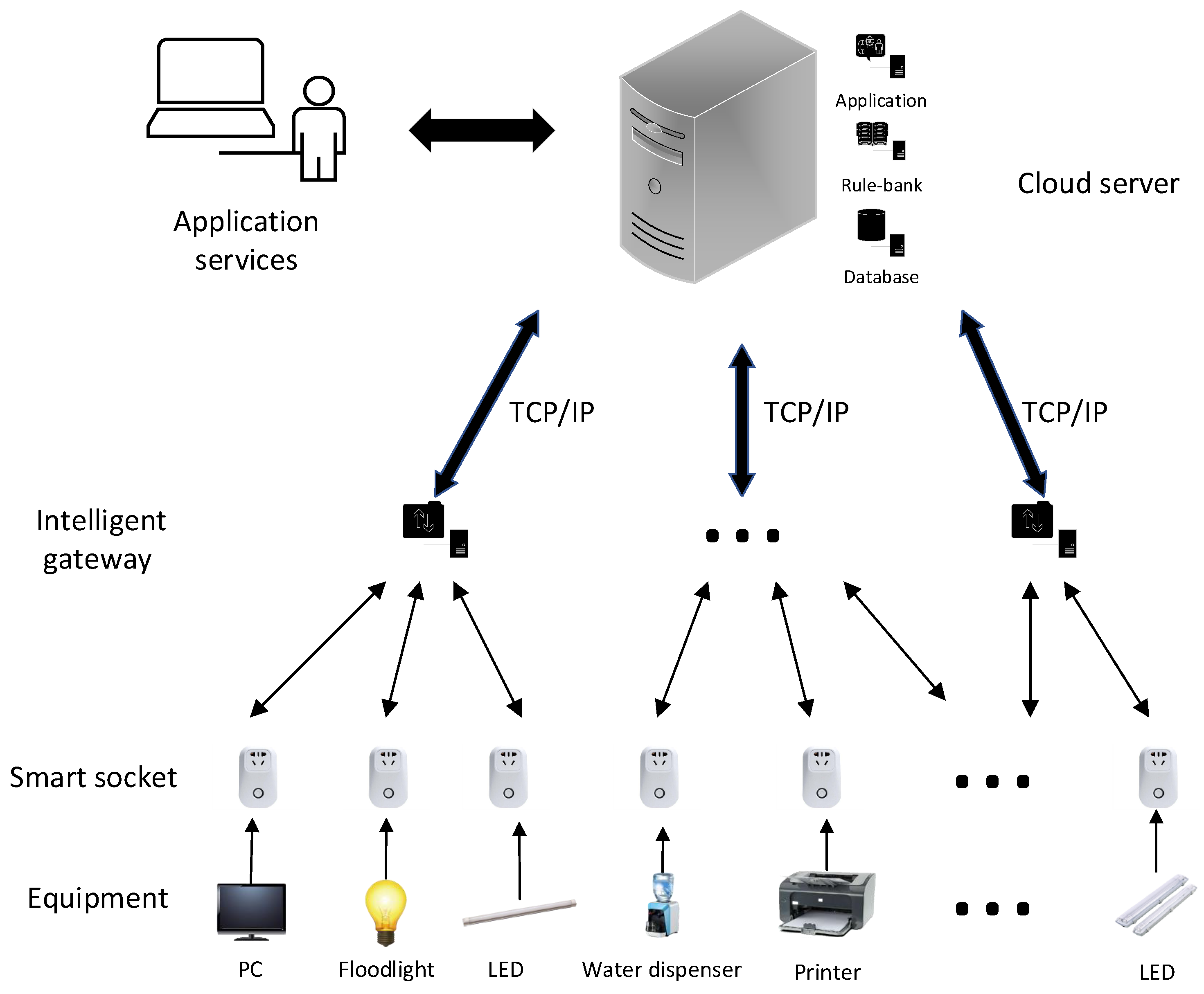
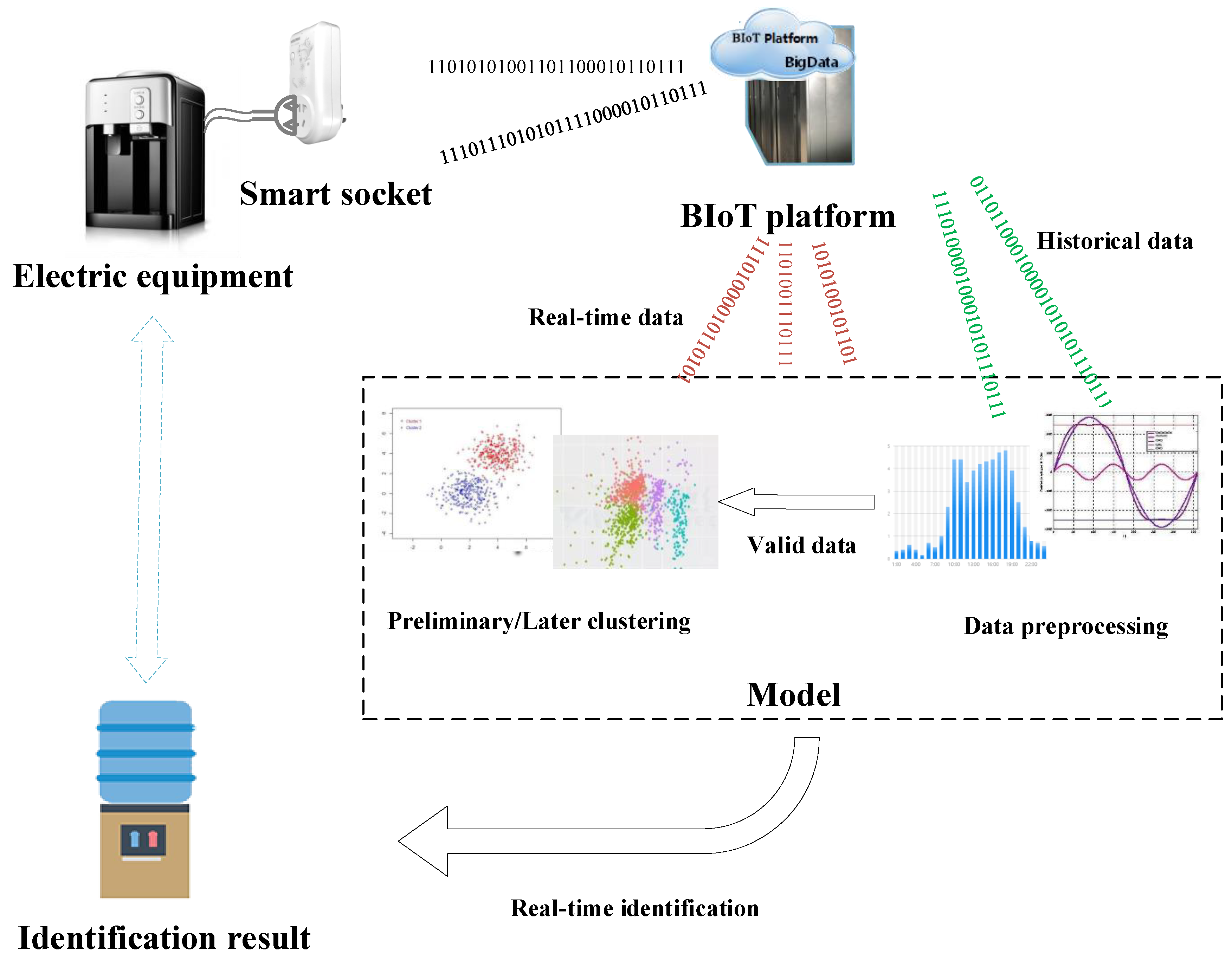
2. Analysis of BIoT Platform and Electrical Equipment
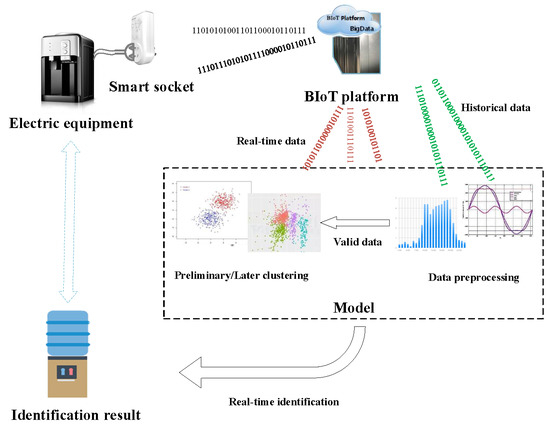
2.1. BIoT Platform and Data Collection
2.2. Analysis of Equipment Characteristics
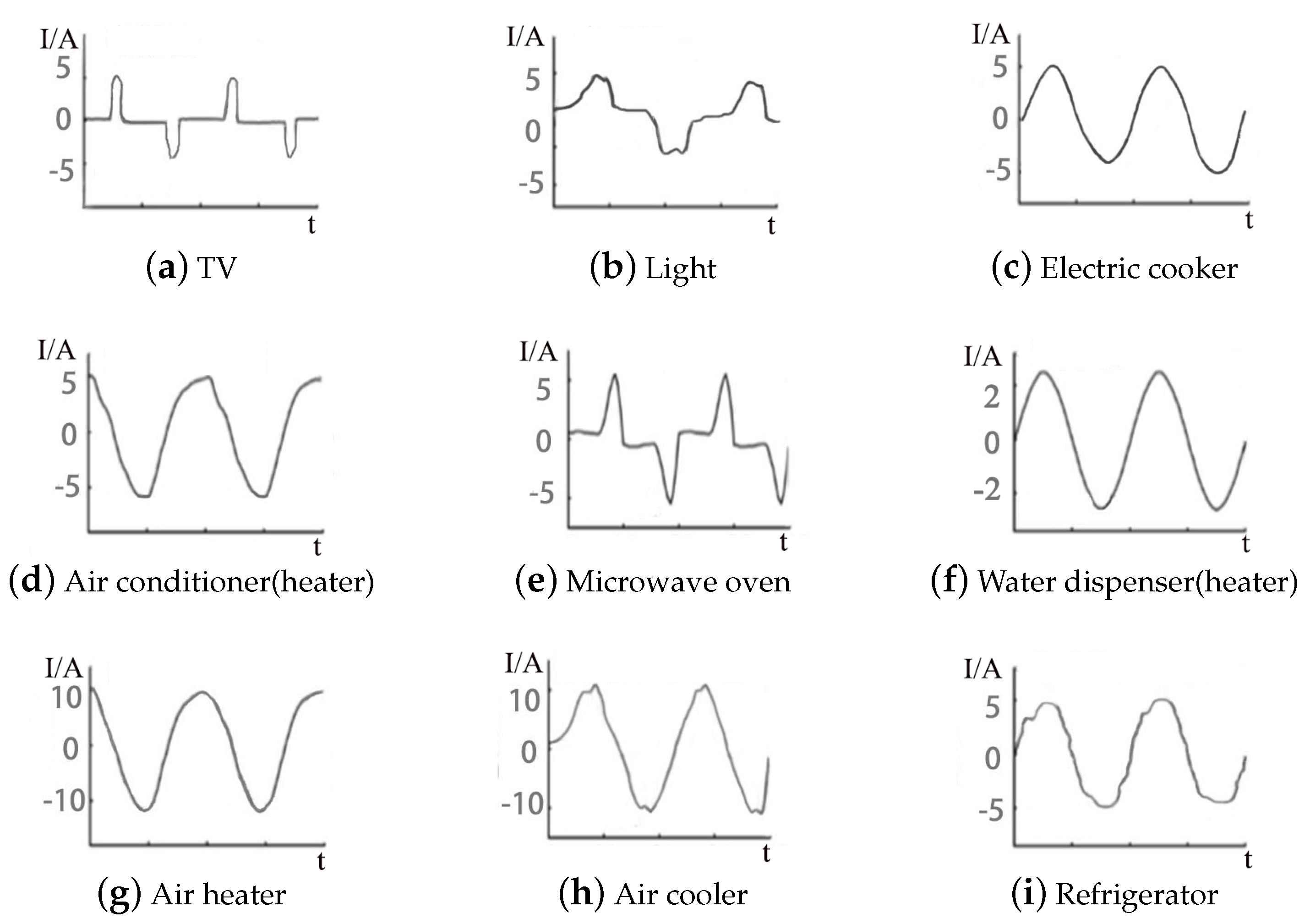
2.2.1. Analysis of Load Characteristics
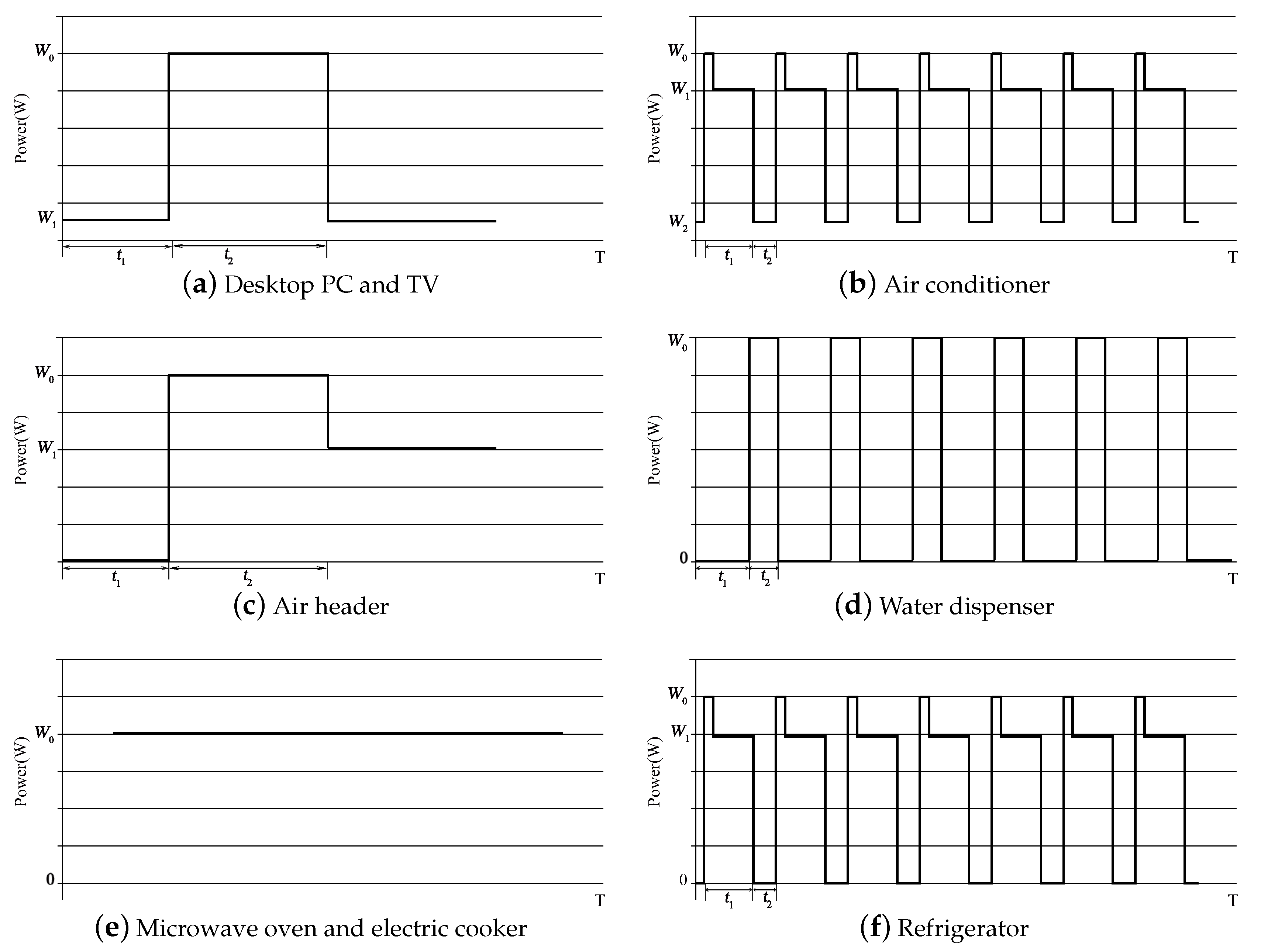
2.2.2. Analysis of Power and Working Characteristics
2.3. Feature Extraction
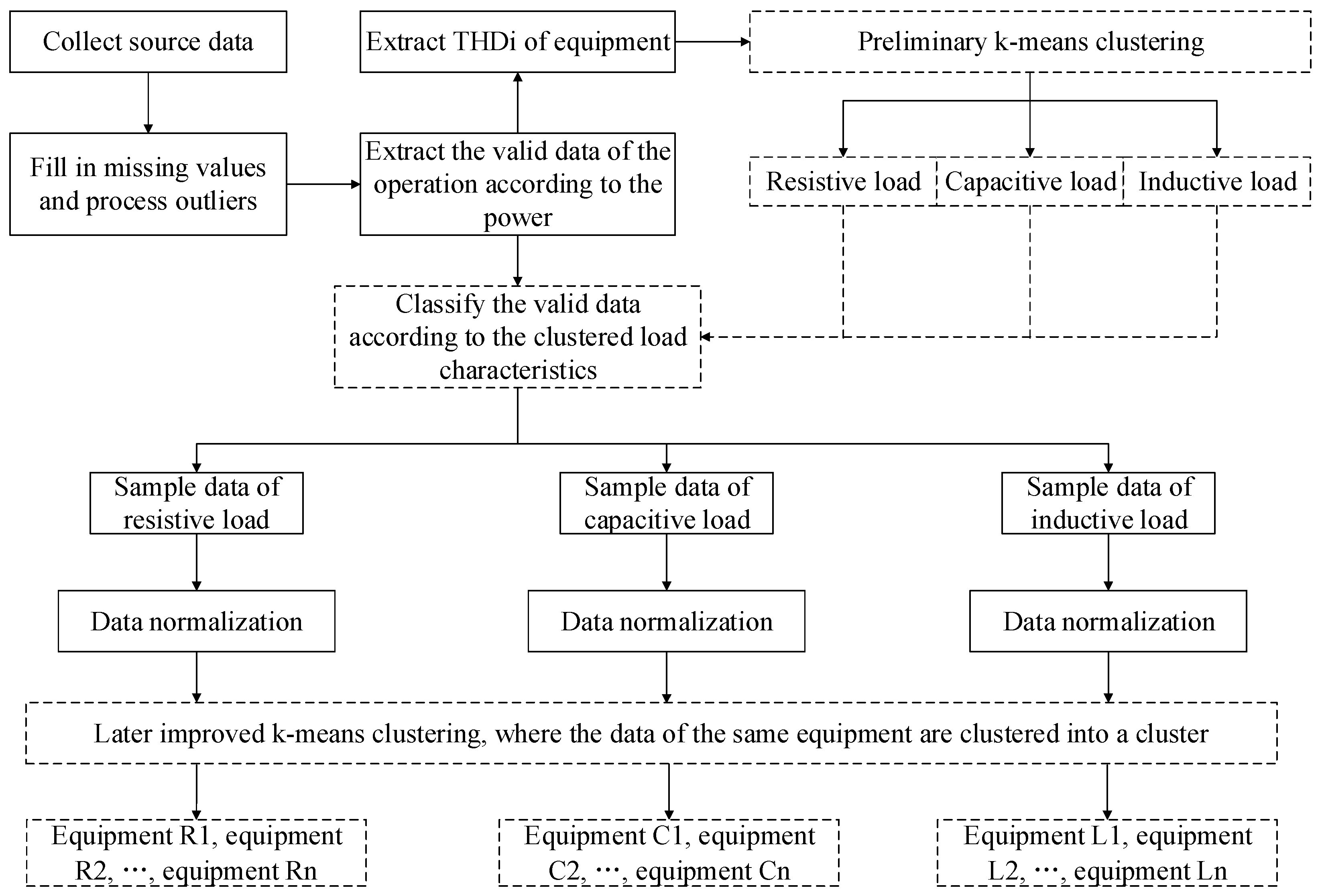
3. Proposed Method
3.1. Data Preprocessing
3.1.1. Extraction
3.1.2. Data Normalization
3.2. Construction of Equipment Identification Model
- (1)
- Preliminary clustering: Preliminary clustering uses the data of the equipment harmonic index and divides the equipment valid data on the basis of the clustering results. The electrical characteristics of equipment cannot be fully reflected from the harmonics. The divided sample data are clustered by later k-means, and an improved similarity measurement method is proposed.
- (2)
- Later clustering: The sample data of equipment with the same type are divided by improved k-means clustering. By comparing the source data with the current waveforms and power models of the above mentioned common electrical equipment, the equipment type labels at the centroid are marked, and the clustering results are evaluated to complete the establishment of the equipment identification model.
3.2.1. Preliminary Clustering
3.2.2. Later Clustering
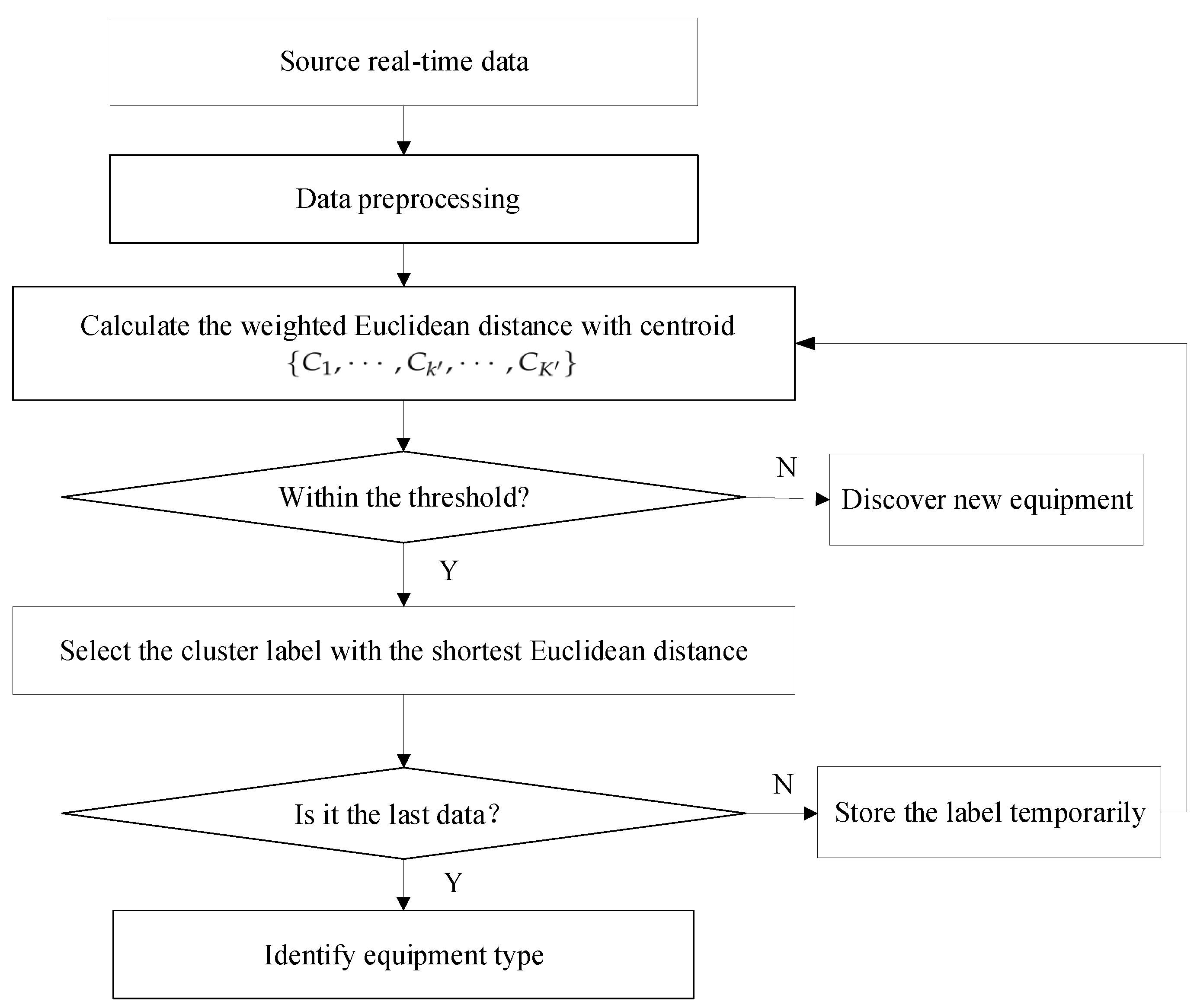
3.3. Real-Time Equipment Identification
4. Case Studies
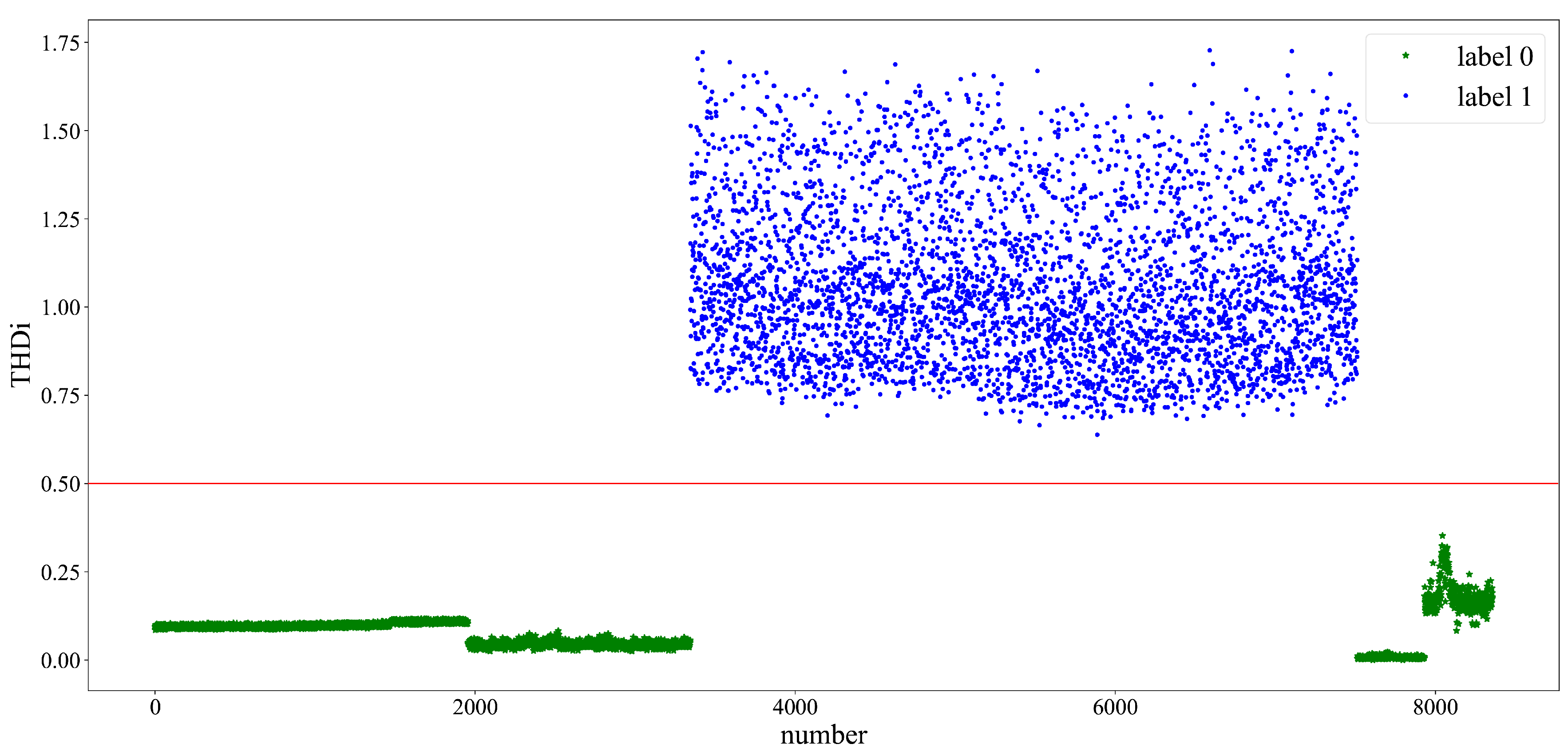
4.1. Description of Dataset
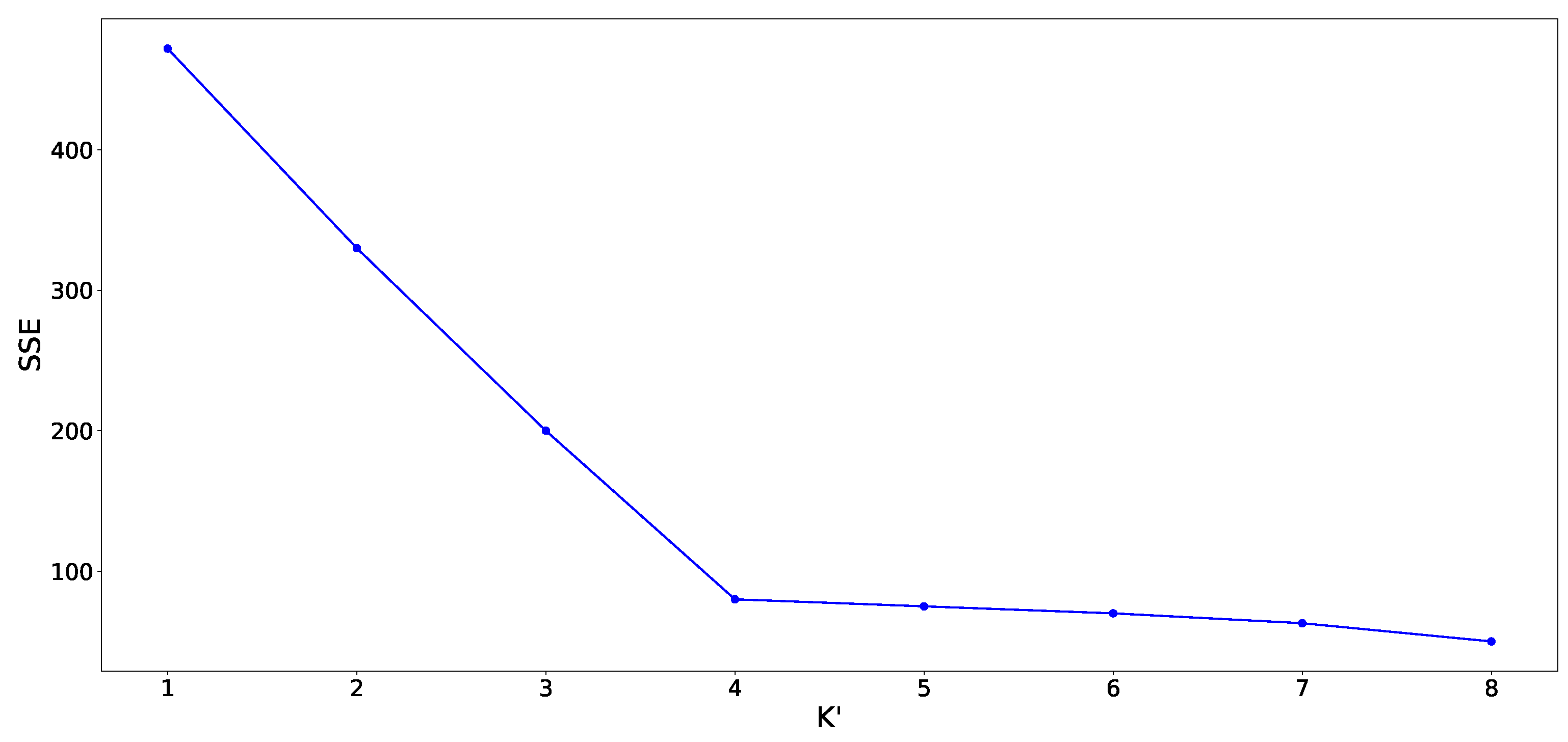
4.2. Model Training
4.3. Identification Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Deng, X.; Peng, J.; Peng, X.; Mi, C. An intelligent outlier detection method with one class support tucker machine and genetic algorithm towards big sensor data in internet of things. IEEE Trans. Ind. Electron. 2018, 66, 4672–4683. [Google Scholar] [CrossRef]
- Villari, M.; Celesti, A.; Fazio, M.; Puliafito, A. A secure self-identification mechanism for enabling iot devices to join cloud computing. In Internet of Things. IoT Infrastructures; Springer: Cham, Switzerland, 2015; pp. 306–311. [Google Scholar]
- Zhiying, F.; Wenhu, T.; Qinghua, W. Users’consumption behavior clustering method considering longitudinal randomness of load. Electr. Power Autom. Equip. 2018, 38, 39–44. [Google Scholar]
- Bauerle, F.; Miller, G.; Nassar, N.; Nassar, T.; Penney, I. Context sensitive smart device command recognition and negotiation. In Internet of Things. User-Centric IoT; Springer: Cham, Switzerland, 2015; Volume 150, pp. 314–330. [Google Scholar]
- Jia, M.; Komeily, A.; Wang, Y.; Srinivasan, R.S. Adopting internet of things for the development of smart buildings: A review of enabling technologies and applications. Autom. Constr. 2019, 101, 111–126. [Google Scholar] [CrossRef]
- Tu, Y.; Zhang, Z.; Li, Y.; Wang, C.; Xiao, Y. Research on the internet of things device recognition based on rf-fingerprinting. IEEE Access 2019, 7, 37426–37431. [Google Scholar] [CrossRef]
- Rashid, K.M.; Louis, J. Times-series data augmentation and deep learning for construction equipment activity recognition. Adv. Eng. Inform. 2019, 42, 100944. [Google Scholar] [CrossRef]
- Huang, Y.; Zhan, J.; Luo, C.; Wang, L.; Wang, N.; Zheng, D.; Fan, F.; Ren, R. An electricity consumption model for synthesizing scalable electricity load curves. Energy 2019, 169, 674–683. [Google Scholar] [CrossRef]
- Arif, A.; Wang, Z.; Wang, J.; Mather, B.; Bashualdo, H.; Zhao, D. Load modeling—A review. IEEE Trans. Smart Grid 2018, 9, 5986–5999. [Google Scholar] [CrossRef]
- Rashid, H.; Singh, P.; Stankovic, V.; Stankovic, L. Can non-intrusive load monitoring be used for identifying an appliance’s anomalous behaviour? Appl. Energy 2019, 238, 796–805. [Google Scholar] [CrossRef]
- Mohd Rosdi, N.A.; Nordin, F.H.; Ramasamy, A.K. Identification of electrical appliances using non-intrusive magnetic field and probabilistic neural network (PNN). In Proceedings of the 2014 IEEE International Conference on Power and Energy (PECon), Kuching, Malaysia, 1–3 December 2014; pp. 47–52. [Google Scholar]
- Hou, R.; Pan, M.; Zhao, Y.; Yang, Y. Image anomaly detection for iot equipment based on deep learning. J. Vis. Commun. Image Represent. 2019, 64, 102599. [Google Scholar] [CrossRef]
- Chicco, G.; Ilie, I.-S. Support vector clustering of electrical load pattern data. Power Syst. IEEE Trans. 2009, 24, 1619–1628. [Google Scholar] [CrossRef]
- Chen, G.; Chen, J.; Zi, Y.; Pan, J.; Han, W. An unsupervised feature extraction method for nonlinear deterioration process of complex equipment under multi dimensional no-label signals. Sens. Actuators A Phys. 2018, 269, 464–473. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, L.; Chen, X.; Niu, J. Facial landmark automatic identification from three dimensional (3D) data by using hidden markov model (HMM). Int. J. Ind. Ergon. 2017, 57, 10–22. [Google Scholar] [CrossRef]
- Mets, K.; Depuydt, F.; Develder, C. Two-stage load pattern clustering using fast wavelet transformation. IEEE Trans. Smart Grid 2016, 7, 2250–2259. [Google Scholar] [CrossRef]
- Ran, L.; Li, F.; Smith, N.D. Multi-resolution load profile clustering for smart metering data. IEEE Trans. Power Syst. 2016, 31, 4473–4482. [Google Scholar]
- Quek, Y.; Woo, W.; Logenthiran, T. DC equipment identification using k-means clustering and KNN classification techniques. In Proceedings of the IEEE Region 10 Annual International Conference (TENCON), Singapore, 22–25 November 2016; pp. 777–780. [Google Scholar]
- Chen, G.; Liu, Y.; Ge, Z. K-means bayes algorithm for imbalanced fault classification and big data application. J. Process Control 2019, 81, 54–64. [Google Scholar] [CrossRef]
- Dinesh, C.; Nettasinghe, B.W.; Godaliyadda, R.I.; Ekanayake, M.P.B.; Ekanayakem, J.; Wijayakulasooriya, J.V. Residential appliance identification based on spectral information of low frequency smart meter measurements. IEEE Trans. Smart Grid. 2016, 7, 2781–2792. [Google Scholar] [CrossRef]
- Ghosh, S.; Chatterjee, A.; Chatterjee, D. Improved non-intrusive identification technique of electrical appliances for a smart residential system. IET Gener. Transm. Distrib. 2019, 13, 695–702. [Google Scholar] [CrossRef]
- Jagtap, H.P.; Bewoor, A.K. Development of an algorithm for identification and confirmation of fault in thermal power plant equipment using condition monitoring technique. Procedia Eng. 2017, 181, 690–697. [Google Scholar] [CrossRef]
- Yuan, Y.; Peng, L. Wireless Device Identification Based on Improved Convolutional Neural Network Model. In Proceedings of the 2018 IEEE 18th International Conference on Communication Technology (ICCT), Chongqing, China, 8–11 October 2018; pp. 683–687. [Google Scholar]
- Peng, W.; Li, C.; Zhang, G.; Yi, J. Interval type-2 fuzzy logic based transmission power allocation strategy for lifetime maximization of wsns. Eng. Appl. Artif. Intell. 2020, 87, 103269. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, D.; Xiao, X.; Li, Y.; Xu, F. Review and development tendency of research on 2∼150 khz supraharmonics. Power Syst. Technol. 2018, 42, 353–365. [Google Scholar]
- Zhou, M.; You, X.; Wang, C.; Li, Q. Harmonic analysis of selected harmonic elimination pulse width modulation. Trans. China Electrotech. Soc. 2013, 28, 11–20. [Google Scholar]
- Yazdani-Asrami, M.; Gholamian, S.A.; Mirimani, S.M.; Adabi, J. Experimental investigation for power loss measurement of superconducting coils under harmonic supply current. Measurement 2019, 132, 324–329. [Google Scholar] [CrossRef]
- Liu, Q.; Kamoto, K.M.; Liu, X.; Sun, M.; Linge, N. Low-complexity non-intrusive load monitoring using unsupervised learning and generalized appliance models. IEEE Trans. Consum. Electron. 2019, 65, 28–37. [Google Scholar] [CrossRef]
- Lin, S.; Zhao, L.; Liu, Q.; Li, D.; Fu, Y. A nonintrusive load identification method based on quadratic 0-1 programming. Power Syst. Prot. Control 2016, 44, 85–91. [Google Scholar]
- Yang, L.; Ban, X.; Chen, Z.; Guo, H. A new data preprocessing technique based on feature extraction and clustering for complex discrete temperature data. Procedia Comput. Sci. 2018, 129, 78–80. [Google Scholar] [CrossRef]
- Meng, F.; Xu, X.; Gao, L.; Man, Z.; Cai, X. Dual passive harmonic reduction at dc link of the double-star uncontrolled rectifier. IEEE Trans. Ind. Electron. 2019, 66, 3303–3309. [Google Scholar] [CrossRef]
- Jain, S.; Shukla, S.; Wadhvani, R. Dynamic selection of normalization techniques using data complexity measures. Expert Syst. Appl. 2018, 106, 252–262. [Google Scholar] [CrossRef]
- Qi, J.; Yu, Y.; Wang, L.; Liu, J.; Wang, Y. An effective and efficient hierarchical k-means clustering algorithm. Int. J. Distrib. Sens. Netw. 2017, 13. [Google Scholar] [CrossRef]
- Li, B.; Fan, Z.-T.; Zhang, X.-L. Robust dimensionality reduction via feature space to feature space distance metric learning. Neural Netw. 2019, 112, 1–14. [Google Scholar] [CrossRef]
- Bu, F.; Chen, J.; Zhang, Q.; Tian, S.; Ding, J.; Zhu, B. A controllable refined recognition method of electrical load pattern based on bilayer iterative clustering analysis. Dianwang Jishu/Power Syst. Technol. 2018, 42, 903–910. [Google Scholar]
- Kwedlo, W. A clustering method combining differential evolution with the k-means algorithm. Pattern Recognit. Lett. 2011, 32, 1613–1621. [Google Scholar] [CrossRef]
- Liu, Z.; Xiao, S.L.; Chen, J. Household load identification method based on feature similarity. J. Chongqing Univ. Technol. Nat. Sci. 2018, 187, 174–180. [Google Scholar]
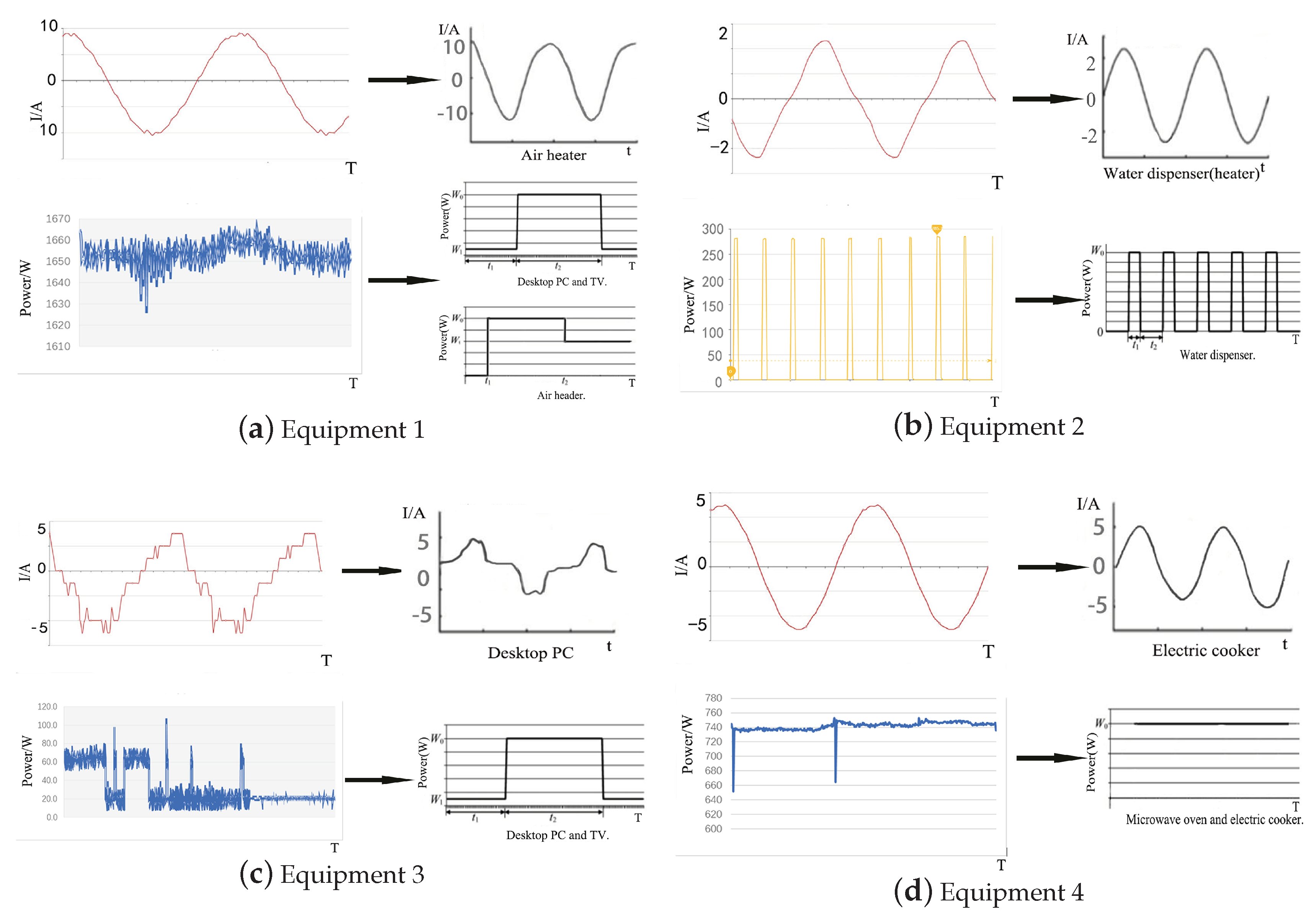
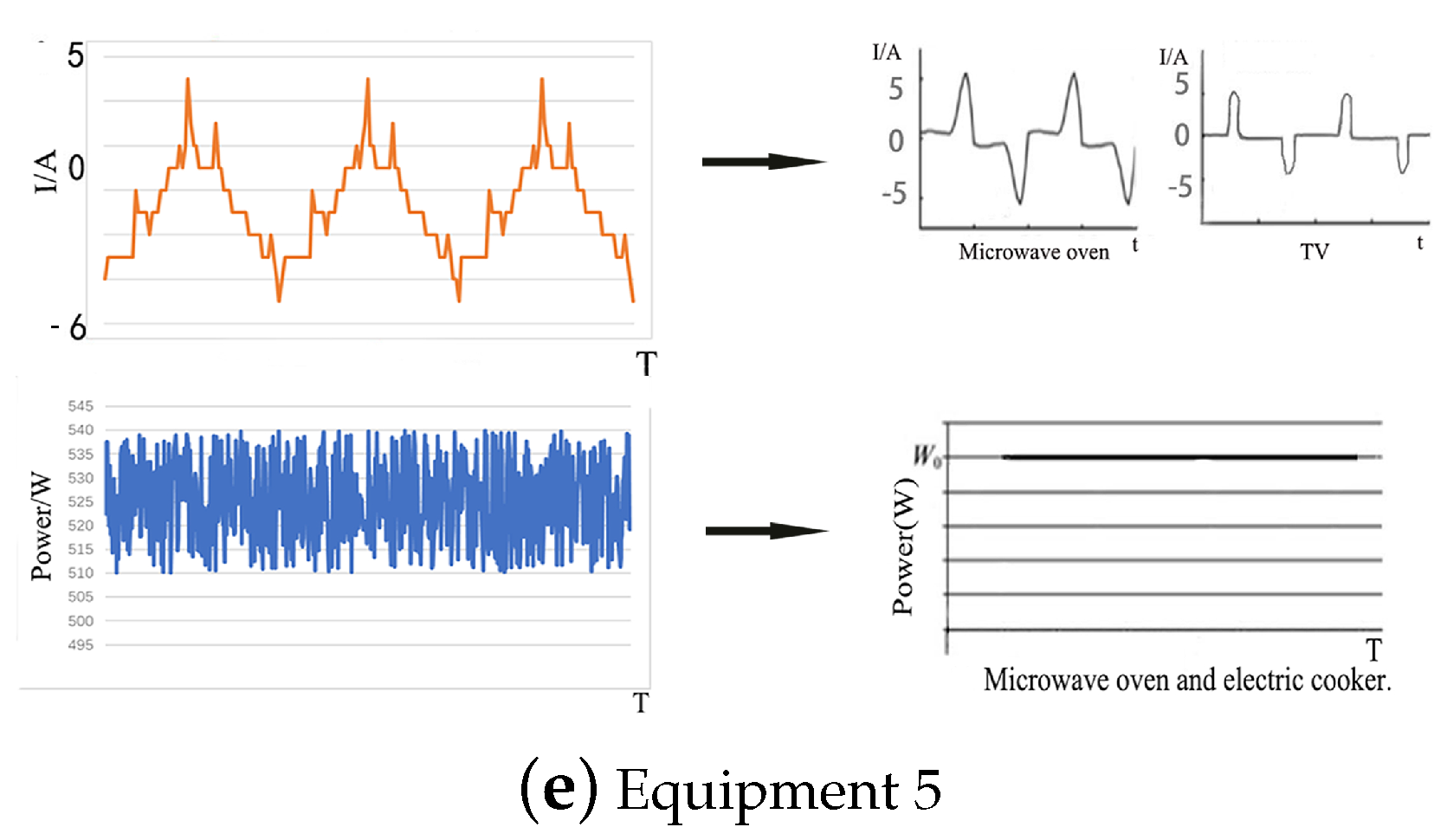
| Load Characteristics | Harmonics | Power | Example |
|---|---|---|---|
| Resistive load | Absent | Generally larger | Water dispenser |
| Capacitive load | Larger | Not too large | Desktop computer |
| Inductive load | Large | Irregular | Air conditioner |
| Operation Status | Characteristics | Example | Work Time | |
|---|---|---|---|---|
| Self-varying multiple-state switching operation | Specific time use | It can automatically switch between multiple states in normal operation, and each state has a fixed step size and constant power. | Electric cooker | 11:00–13:00 and 17:00–19:00 |
| Uncertain time use | Each state will have an uncertain step size due to human intervention, but the power is constant. | Air conditioner and water dispenser | - - - - | |
| Long-term use | The normal operation will automatically switch the operation state, and the power and time period of each state are fixed. | Refrigerator | Whole day | |
| Man- controlled multiple-state switching operation | Specific time use | When the state changes, the power changes accordingly and is constant in a specific state. | 1. Range hood and 2. water heater | 1. 11:00–13:00 and 17:00–19:00 2. 19:00–8:00 (next day) |
| Uncertain time use | Man Controls the transition between multiple states during normal operation. | Notebook and desktop PC | - - - - | |
| Stateless switching operation | Specific time use | Only one each of the running state and fixed power are present in normal operation. | 1. LED and 2. microwave oven | 1. 18:00–23:00 2. 11:00–13:00 and 17:00–19:00 |
| Uncertain time use | Generally, only one each of operating state and fixed power are present. | TV and air heater | - - - - | |
| Equipment Name | Equipment 1 | Equipment 2 | Equipment 3 | Equipment 4 | Equipment 5 |
|---|---|---|---|---|---|
| Quantity of source data | 1955 | 3070 | 4555 | 419 | 533 |
| Quantity of valid data | 1955 | 1389 | 4169 | 419 | 425 |
| No. | FHG | SHG | THG | ... | Power(W) | Time |
|---|---|---|---|---|---|---|
| 1 | 5.41 | 0.03 | 0.43 | ... | 1665.1 | 2019/1/1 8:18:16 |
| 2 | 5.38 | 0.00 | 0.38 | ... | 1663.4 | 2019/1/1 8:19:44 |
| 3 | 5.36 | 0.00 | 0.39 | ... | 1667.5 | 2019/1/1 8:20:12 |
| 4 | 5.35 | 0.00 | 0.41 | ... | 1661.5 | 2019/1/1 8:21:07 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 8356 | 2.5 | 0.00 | 0.33 | ... | 540.3 | 2019/1/26 11:18:50 |
| 8357 | 2.54 | 0.00 | 0.35 | ... | 539.8 | 2019/1/26 11:19:45 |
| FHG is the fundamental wave. | ||||||
| SHG is the 2-order harmonics. | ||||||
| THG is the 3-order harmonics. | ||||||
| ... is the 4-order to 32-order harmonics. | ||||||
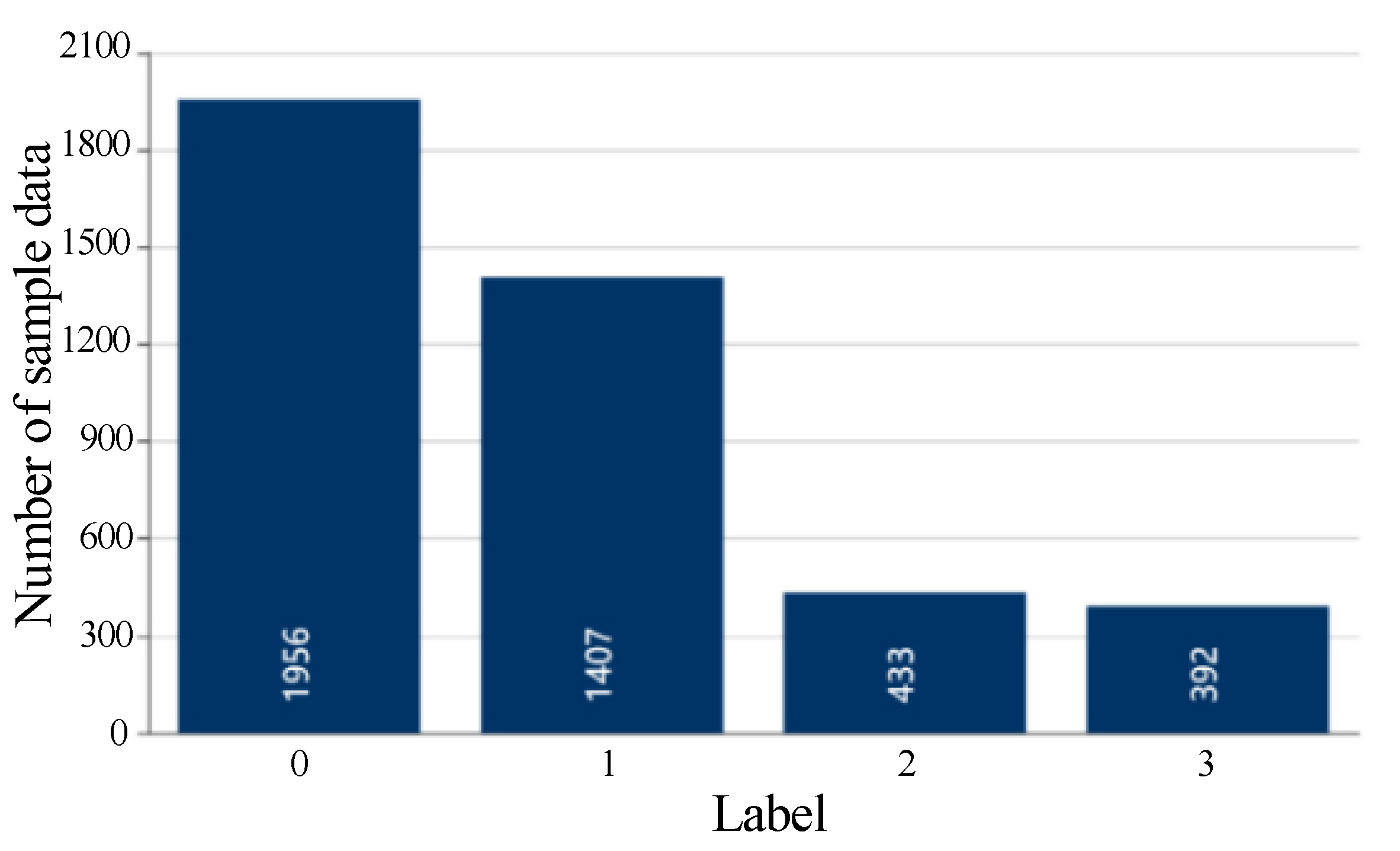
| Cluster Label | Quantity | Threshold | Centroid Power | Equipment Type (Number) | Accuracy | |
|---|---|---|---|---|---|---|
| 0 | 1956 | 0.0092 | 0.0276 | 1653.89 | 1 (1956) | 99.45% |
| 1 | 1407 | 0.0114 | 0.0341 | 293.61 | 2 (1398), 5 (9) | |
| 2 | 433 | 0.0041 | 0.0124 | 735.62 | 4 (419), 5 (14) | |
| 3 | 392 | 0.0022 | 0.0067 | 521.04 | 5 (392) |
| Cluster Label | Cluster Centroid Vector | |||
|---|---|---|---|---|
| 0 | 0.9845 | 0.0851 | 0.0016 | ... |
| 1 | 0.0314 | 0.0005 | 0.0254 | ... |
| 2 | 0.1681 | 0.0003 | 0.0025 | ... |
| 3 | 0.0008 | 0.0003 | 0.0003 | ... |
| Cluster Label | Quantity | Threshold | Equipment Type (Number) | Accuracy | |
|---|---|---|---|---|---|
| 0 | 1962 | 0.0582 | 0.1745 | 1 (1956), 5 (6) | 96.54% |
| 1 | 1432 | 0.0484 | 0.1453 | 2 (1398), 5 (34) | |
| 2 | 505 | 0.0671 | 0.2014 | 4 (419), 5 (86) | |
| 3 | 289 | 0.0613 | 0.1838 | 5 (289) |
| Equipment Sample Set | Equipment Type |
|---|---|
| Equipment 1 | Air heater |
| Equipment 2 | Water dispenser |
| Equipment 3 | Desktop computer |
| Equipment 4 | Electric cooker |
| Equipment 5 | Microwave oven |
| No. | FHG | SHG | THG | ... | Power (W) |
|---|---|---|---|---|---|
| 1 | 0.92 | 0.01 | 0.02 | ... | 294.2 |
| 2 | 0.91 | 0.01 | 0.00 | ... | 290.0 |
| 3 | 0.93 | 0.00 | 0.00 | ... | 292.1 |
| 4 | 0.89 | 0.00 | 0.41 | ... | 293.3 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 22 | 0.87 | 0.00 | 0.00 | ... | 293.5 |
| 23 | 0.96 | 0.00 | 0.00 | ... | 291.9 |
| Label | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Distance | 0.8141 | 0.0089 | 0.1468 | 0.0561 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Li, Y.; Deng, X. K-Means Clustering-Based Electrical Equipment Identification for Smart Building Application. Information 2020, 11, 27. https://doi.org/10.3390/info11010027
Zhang G, Li Y, Deng X. K-Means Clustering-Based Electrical Equipment Identification for Smart Building Application. Information. 2020; 11(1):27. https://doi.org/10.3390/info11010027
Chicago/Turabian StyleZhang, Guiqing, Yong Li, and Xiaoping Deng. 2020. "K-Means Clustering-Based Electrical Equipment Identification for Smart Building Application" Information 11, no. 1: 27. https://doi.org/10.3390/info11010027
APA StyleZhang, G., Li, Y., & Deng, X. (2020). K-Means Clustering-Based Electrical Equipment Identification for Smart Building Application. Information, 11(1), 27. https://doi.org/10.3390/info11010027