Abstract
The purpose of this study is to ascertain whether implementation difficulty can be used in a slot allocation model as a new mechanism for slightly weakening grandfather rights; according to which, a linear integer programming model is designed to compare and analyze displacement, implementation difficulty and priority with different weights. Test results show that the implementation difficulty can be significantly reduced without causing excessive displacement and disruption of existing priorities, by weight setting while declared capacity is cleared. In addition to this, whether the movements are listed in order of descending priority or not have great impact on displacement and implementation difficulty within the slot allocation model. Capacity is surely a key factor affecting displacement and implementation difficulties. This study contributes to propose a new mechanism for slightly weakening grandfather right, which can help decision makers to upgrade slot allocation policies.
1. Introduction
Most of the busiest airports worldwide experience serious congestion and delay problems, such as Beijing Capital International Airport (PEK), Shanghai Pudong International Airport (PVG), and Guangzhou Baiyun International Airport (CAN) [1]. The existing imbalance between supply and demand for air transport services forces all aviation stakeholders to drastically rethink airport capacity and its utilization while readdressing the issue of experienced or anticipated capacity shortages [2]. Results of past research have proven that demand management could provide significant benefits at busy airports worldwide by permitting large delay reductions through limited interference with airline competitive scheduling [3] or even by a small substantial increase in declared capacity [4]. However, the latter, aiming to build new capacity, are capital intensive solutions which require significant implementation time, and thus are often subject to heated political debates. The need for an immediate relief to seriously congested airports calls for short to medium-term, demand-side solutions that are based on the optimum allocation and use of available airport capacity [5]. To control over-capacity scheduling, the most common demanding management schemes fall into two categories: (i) approaches introducing market-driven or pure economic instruments (e.g., slot trading, auctions, congestion pricing), which aim to allocate capacity among competing users by considering real market (or approximations of) valuations of access to congested airport facilities [6,7,8,9,10,11,12]; (ii) efforts aiming to improve the efficiency by using administrative allocation mechanism [2,3,4,5,13,14,15,16,17,18,19].
In order to control the excessive demand of airports, Chinese Civil Aviation (CAA) has enacted slot regulation since 2010, but a satisfactory effect has not been achieved. Consequently, the new slot regulation of CAA similar to that of International Air Transport Association (IATA) is introduced in April 2018. Although flight delay in the Chinese airport has been improved after the implementation of these slot management methods, the unreasonable slot structure still exists [20,21,22,23]. As the analysis of these articles indicated, the typical characteristics of slot structure in large Chinese airports are that the departure of flights is concentrated in the morning while the arrival of flights are in the evening, which is shown in Figure 1.
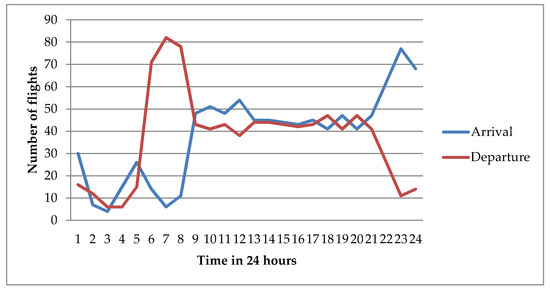
Figure 1.
The typical slot structure of PEK airport from July to September in 2017.
Because of this unreasonable schedule, the problems of low punctuality rate of lights in the morning and evening rush hours are doomed. Why is the application for all flights in the slot allocation process meeting the declared capacity constraints, but still having to be delayed while operating in large Chinese airports? One of the key reasons behind this is that slot allocation does not take into account the actual implementation difficulties. This is a typical case where peak hours are misused. The inefficiency of slot allocation (over-use or lower use) also exists in other countries. The fundamental principle of the slot allocation process of IATA is the grandfather right, i.e., the right of an airline to keep a slot of the preceding equivalent season. This right is granted if and only if such a slot was used at least 80% of the time (use-it-or-lose-it rule). However, this procedure is far from being efficient. Indeed, as reported by Airports Council International (ACI) Europe, unsatisfied/ unaccommodated demand, overbidding, late return of unwanted slots, flights operated significantly and repeatedly off slot time (“off slot”), and failure to operate allocated slots (the so-called “no shows”), are all factors pointing or contributing to the inefficient allocation and use of an already insufficient resource [4,24,25]. Picard et al. [26] found that, compared to public airports, private airports may restrain their supply of peak slots strictly below their capacity levels when they serve airlines that compete with the same destinations. Almost all airports in China are public owned, so this will hardly happen in China. Therefore, the “off slot” is the focus of our attention.
The slot scheduling problem may provide a solution to the optimum utilization of available capacity by displacing flights from time intervals where demand exceeds capacity to time intervals where capacity exceeds demand. However, it may produce solutions that are not acceptable or even practical at all. This is because the displacement of a flight to an undesirable slot may have a detrimental effect on the feasibility of the entire flight schedule of the airline’s network or the commercial viability of the flight. As a result, certain slots may not be attractive enough to be actually operated by the assigned airport users, a fact that may lead to waste of a really scarce resource [16]. At present, this situation is very common in China’s airports. Most specifically, the current schedule does not take into account actual implementation difficulties. Although the scheduled slot is constrained by capacity, it cannot be implemented in actual operation, resulting in the accumulation and propagation of delays [27]. Acquiring the appropriate slots at two congested airports like PEK and PVG is extraordinarily difficult given the scarce capacity at both airports. This difficulty is common, as Debbage [25] has pointed out for many years, but surprisingly it has not yet been clearly integrated into any slot allocation model. Although the network-based slot allocation model has emerged in recent years [15,19], which explicitly considers the problem of flight time matching at hinge airports, it is still subject to priority constraints. It is conceivable that if a new entrant is to operate such a competitive route, the priority of his application will be less than that of other applications with grandfather rights when the application slot is limited coincidentally by capacity. This application may be adjusted or rejected, and other applications with grandfather rights may not have this difficulty but still occupy a scarce slot. This is obviously unreasonable because it will increase the cost of new entrants on this route, which in turn affects the welfare of passengers on this route, although the new entrant may obtain this slot through secondary market transactions. Therefore, incorporating implemented difficulties into CAA rules seems to be one of the promising solutions to the over-concentration of departure flights in the morning and arrival flights in the evening in China. In this article, we do not try to solve all the problems caused by the integration of implementation difficulties. We only discuss whether introducing difficulty in our model and algorithmic framework based on the administrative allocation mechanism of CAA will affect the total displacement and priority. Assuming that our approach can hedge some of the implementation difficulties caused by the grandfather right by introducing implementation difficulties without causing excessive displacement and disruption of existing priorities, it will be a win-win situation for airports and airlines operating at the airport. The comment from Gillen et al. [28], Levine [29] that “an imperfect solution is superior to a naive application of first-best theory” seems appropriate.
The remainder of this paper is organized as follows. Section 2 is the related work of difficulty in slot allocation. Section 3 formulates the model, including the technical aspects of capturing the CAA regulation and difficulty in optimizing the allocation of slots. Section 4 is the iterative linear integer programming algorithms based on data-splitting for proposed model. Section 5 presents tests and simulation results. Section 6 is the summary of the study with implications for future research.
2. Related Work of Difficulty in Slot Allocation
As far as we know, no one has clearly defined the implementation difficulty of slot displacement. Recently, Zografos et al. [16] modeled acceptability by using maximum acceptable deviation. An airline’s tolerance in accepting a slot offered by the airport coordination authority can be expressed by a maximum acceptable deviation () from the requested time interval (). If the slot allocated to a given request (m ∈ M) is not aligned with this tolerance limit (i.e., the slot assigned for this movement lies before time or after time ), then the corresponding slot assignment is called “violated slot assignment”. The number of violated slot assignments constitutes an aggregate measure of the dissatisfaction of airlines for the allocation of slots at a schedule coordinated airport. The work of Zografos et al. [16] focused on how to improve acceptability, but we focus on how to reduce implementation difficulties. In recent years, Zografos [30] has performed a detail review of fairness and constructed a fairness metric based on ratio by schedule and ratio by required. Fairness can improve acceptability, but fairness is meaningless until feasibility is solved, so it is beyond the scope of our discussion. We are only discussing how to reduce implementation difficulty because of the concentration of morning departures and evening arrivals within the CAA slot allocation framework similar to IATA.
Just as Zografos et al. [16] pointed out that most existing models of flight scheduling typically do not consider acceptability of slot schedules. The more difficult the slot displacement is, the less likely the flight will accept the displacement. On the contrary, the less difficult the slot displacement is, the more likely the flight will accept it. Therefore, instead of slot allocation acceptability, implementation difficulty is proposed in this study, which is constructed into the model and examined together with slot displacement and priority. Although acceptability and difficulty are two aspects of the feasibility problem, difficulties can better reflect the nature of the feasibility problem. Because acceptability has no uniform standard and is designated by airlines themselves, it is impossible to judge and compare its rank. But the degree of difficulty is measurable and comparable. In addition, since difficulty and acceptance are two aspects of a problem, the problem of acceptance constraints can be reduced to the problem of unconstrained difficulty minimization by dual theory [31]. By setting the objective function as the difficulty instead of acceptability constraints in model of Zografos et al. [16], the number of constraints will be greatly simplified, the calculation time will be saved and the calculation efficiency will be improved. Therefore, in a sense, modeling with difficulty has advantages over modeling with acceptability.
Of course, the fundamental way to reduce the implementation difficulties is to improve the runway capacity, airspace capacity, and precisely integrate the slot allocation system with the air traffic management system. Even extending the single airport slot allocation model to a multi-airport slot allocation model will be useful to reduce implementation difficulties. It can also be achieved by adjusting the slot structure through economic means. But these solutions depend on systematic and comprehensive demand and capacity management, which is time-consuming. On the contrary, considering the implementation difficulty in slot allocation can produce an immediate effect, which means the reduction of the implementation difficulties under the certain technical conditions is the key element to conquer. Although the solution we proposed is one of all solutions, even imperfect solutions, no one has tried, so it is worth making the attempt. Therefore, we tentatively assume that in airport operation, when the declared capacity is cleared (the existing technical conditions and equipment deployment remain unchanged), the slot coordinator (manager) and airlines (operator) are very willing to find a new slot displacement mechanism that can not only ensure small displacement change, but also effectively reduce the implementation difficulties.
Especially by encouraging new entrants to open up some new competitive routes, and the arrival time (departure time) of flights running on these routes coincides within the early departure peak (arrival peak) of these airports. Therefore, some inefficient departure flights (departure peak) and arrival flights (arrival peak) are squeezed into other periods, which not only reduce the implementation difficulties, but also have important significance for balancing arrival and departure and improving the unreasonable slot structure in these airports.
The key question is whether there is opportunity to reduce implementation difficulty while not increasing displacement. At the same time, other issues need to be carefully considered, such as: with our algorithm, is it possible for high priority movement to have a lower probability of being displaced? Can priority be considered as the cost of displacing the unit time to ensure that the high priority movement has a low probability of being displaced (HPLA)? What are the differences in performance indicators when priority is fed into a computer program in priority order or in the order of morning to night (final slot-table presentation) when priority is considered as the cost of displacing the unit time? All of these questions that have not been investigated in previous articles will be discussed and answered within this study. If there are clear answers to these questions, it is feasible to introduce difficulty performance objectives into the model to reduce implementation difficulty.
The main contribution of this paper is three-fold. The first is that the difficulty index of slot displacement for quantifying implementation difficulties of each movement is proposed. Secondly, a multi-objectives linear integer programming model and algorithm are developed to minimize the total compound cost of slot allocation. Thirdly, we found that the implementation difficulty can be significantly reduced without causing excessive displacement and disruption of existing priorities, by weight setting while declared capacity is cleared. By encouraging new entrants to develop competitive routes in favorable periods and squeezing inefficient or low priority applications into non-peak periods, implementation difficulties caused by the concentration of morning departure flights and evening arrival flights at typical busy airports in China can be reduced. Then, the current unreasonable slot structure will be gradually changed and optimized. This is a new mechanism for weakening grandfather rights.
3. Proposed Slot Displacement Models
Before describing the model, notations are stated as follows:
: Priority of movement .
: Flight implementation difficulties
: Flight difficulty index of one displacement unit
: Interval that movement required. A movement corresponds to an application.
: Interval that movement is scheduled.
: Seats of flights corresponding movement .
: The average flight elapse time of movement , to (arrival flight) or from (departure flight) this airport.
: Coordination level parameters of this airport (main coordinator, auxiliary coordinated airport and uncoordinated airport; 7, 4, 1).
: Coordination level parameters of associated airports.
: {0, 1}, if movement is scheduled at interval, = 1, otherwise, = 0.
: Hourly capacity constraint;
: 15-min capacity constraint;
: 5-min capacity constraint;
: Corridor capacity constraints, .
: Movement plans to operate on day of a series day, usually series day expressed as [1,2,3,4,5,6,7]. is set mandatorily as 1, which means the same flight operating in one day has two movement number, such as and .
: The amount of the kind of capacity consumed by movement . In our model, may be hourly capacity, 15-min capacity, 5-min capacity, or corridor capacity. In our model, the amount of each capacity consumed by a movement is 1, which means all of ,, and are set as 1.
: Number of seats.
: Displacement, absolute value of difference between and . The displacement value is related to the interval used as slot, the application time, and the final planned time. The coordination time interval represents the unit of time (e.g., 5-min, 15-min, 60-min) used as the basis for capacity determination and slot allocation. Usually each time interval contains multiple slots. A movement corresponds to a takeoff or landing activity. A slot refers specifically to the interval occupied by one movement. The following example further illustrates the meaning of interval, slot and displacement.
Assuming that the operator of flight AF125 submitted an application for departure, and the required departure time is 9:14. When the interval is set as one hour, there is 24 slots within a day, and is 9 ( is located at 9th interval). When the interval is set as 15 min, there are 96 slots within a day, and turns to 37. When the interval is set as 5 min, there are 288 slots within a day, and is 111.
In the process of slot allocation, if the departure application of flight AF125 is scheduled at 11:14 ( is 11) when the interval is set as one hour, then the displacement () of is 2, which is showed in Figure 2. Similarly, it can be inferred that the displacement of this application is 8 when the interval is set as 15 min, and that is 24 when interval is set as 5 min. If Flight AF125 is scheduled before 9:14, the displacement may be negative or zero, and thus an absolute value symbol is added to the displacement.
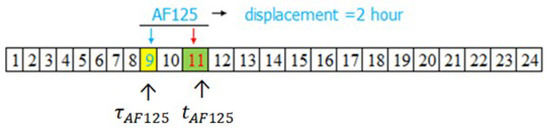
Figure 2.
Displacement of when interval is set as an hour.
We are motivated by the idea that the less difficult it is to adjust slot, the easier it will be accepted; the more difficult it is to adjust slot, the harder it will be accepted. Therefore, the problem of acceptability is transformed into the problem of minimizing the difficulty of slot displacement subject to the priority rule stipulated by CAA slot regulations and other operational constraints.
3.1. Difficulty Index and Difficulty of Displacement
Difficulty index, is inversely proportional to elapse time , and is proportional to slot displacement. Because elapse time increases with the range of flight distance as shown in Figure 3, the longer the flight distance is, the more time the aircraft will be shortened or increased by adjusting its speed during flight. This means that long-haul flights can receive larger slot adjustments than short-haul flights. Changing flight time by adjusting speed is not only considered as a technology to schedule, but also utilized to support other technical methods, such as four dimension trajectory [32,33,34,35], conflict detection and resolution [36,37,38], airborne technology [39], and air flow management [40,41,42,43,44]. These technical methods in turn make changing flight time by adjusting speed more mature and feasible. Therefore, difficulty index is inversely proportional to elapse time.
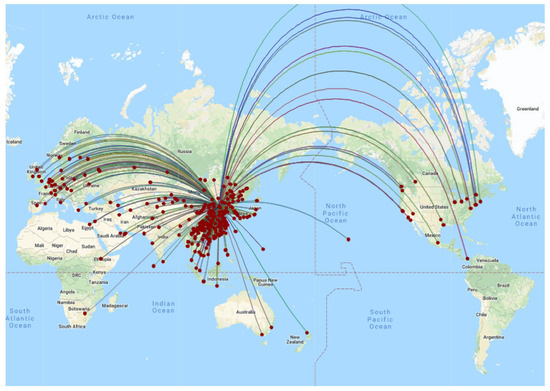
Figure 3.
Air route network connected with PEK in 2018.
Difficulty index is subject to the coordination level of the connected airport. The larger the number of the coordination level of the connected airport, the more difficult the slot coordination is. On the contrary, the smaller the number, the easier the slot coordination is. Implementing difficulty index is the difficulty of displacing a unit interval.
Flight implementation difficulties index and difficulty brought by difficulty expressed as follows:
The peak departure time in Figure 1 is around 7:00–8:00. It is almost impossible to balance the arrival and departure of flights in PEK airport by domestic flights, which have to take off at 5:00–6:00 in domestic cities and are not in line with people’s travel habits. However, if international long-haul flights are introduced, the problem will be solved easily. The flight time of domestic flights is generally less than 150 min, and the number of seats is mostly more than 180. This will make of domestic flights larger than that of international long-haul flights. Therefore, it is necessary to curb the impact of the greater difficulty index of domestic flights. The purpose of is to reduce the possibility of excessive difficulty index of domestic flights.
Whether the local airport and airport connected with it are coordinated airport and the coordination level of them exert great impact on the implementation difficulty index, consequentially, the is utilized. A graph of functions and are shown in Figure 4. The characteristics of these two functions happen to meet our requirements. This makes the difficulty index, , grow slowly with the growth of and relatively sharply with the growth of .
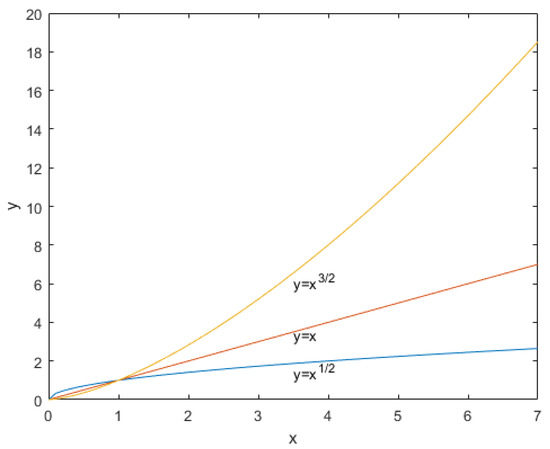
Figure 4.
Characteristics of value changes of functions and .
When the priority of a movement is greater than the difficulty index ( > ), priority plays a key role. On the contrary, when < , the difficulty index plays a key role. We tested formula (1) and found that the average value of the difficulty index of all flights is about 42% of the average value of priority allocation (). This is an ideal numerical range which makes the slot allocation generally tend to adjust low priority flights.
3.2. Standardized Priority
The CAA slot regulations enforced the requirement of different priorities assigned to various types of slot requests. This is achieved through a sequential approach that first allocates a historic series of slots, then is followed by the “change to historic” series of slots, next by new entrant slots, and finally by the remaining slots. The CAA slot regulations clearly stipulate that priority should be determined from high to low according to the product of allocation cardinality and time efficiency allocation coefficient of aviation enterprises. We standardize the calculated priority values so that the four types of priority are distributed within a clearly distinguishable range showed as in Table 1.

Table 1.
Range of standardized priority.
In reality, priority determines the priority of slot selection. Similarly, in model computing, priority determines which movement can enter the model earlier and get the preferred slot. This is called High-Priority First (HPF).
3.3. Comprehensive Displacement Cost
As mentioned before, cost of one movement in most traditional slot allocation models [4,13,24] is as follows:
In expression (3), is the interval displacement when required interval is replaced with scheduled interval .
When priority is considered as the cost of displacing the unit time, cost of one movement can be presented as follows:
In our model, we integrate cost of displacement, difficulties and priorities as a whole in order to facilitate calculation and comparison. At the same time, three weight factors () are introduced artificially for the same reason. The comprehensive displacement cost of a movement, displaced from required interval to scheduled interval , could be expressed as follows:
We call the comprehensive displacement cost factor with the consideration of implementation difficulties and priority. It is an important find that is a constant, which makes it possible to solve it by Linear Integer Programming (LIP).
3.4. Displacement Model for all Flights
The objective function (7) minimizes the overall comprehensive displacement cost of all flights. Constraint (8) stipulates that every movement must be allocated to one interval. Constraint (9) specifies that total movement consumption cannot exceed capacity, for each constraint, day and interval. Constraint (10) ensures that this model can be solved by integer programming method. There is no detailed description of the coefficient matrix in previous papers. Thus, in the next section, we will elaborate the proposed approach.
4. LIP for Slot Displacement Models
In order to limit the flow of corridors, it is necessary to determine which corridor should be allocated to each flight. Firstly, the courses of all flights from the airport to the linked airport are calculated. Then, the courses for arrival or departure are sorted descending. If there are corridors for arrival (or departure), then the arrival (or departure) courses are classified into categories.
In general, the number of corridors for arrival is equal to the number of corridors for departure. Each corridor entrance must meet the capacity constraints. All movement is classified according to the number of corridors and assigned evenly to corridors before executing LIP. By designing the variable , the relationship matrix of movement and corridors is constructed as shown in Table 2. The sum of each column must be 1, that is, each movement must be assigned to a corridor . The sum of each row is limited by the capacity of the corridor in every interval. This makes it easy to solve the capacity constraints of the corridor with linear programming, but with the increase of the number of flights and the number of corridors, the dimension of the constraints increases rapidly.

Table 2.
Relationship matrix of movement i and corridors e.
Considering that the flight execution cycle is usually at least once a week, and that most flights operate every day, in order to reduce the computing time with the proposed approach, it is possible to determine the calendar days with the same set of requests, and then represent these as a single calendar day. In order to keep the accumulated rolling volume of flights from exceeding the hourly capacity, we consider three kinds of capacities in brackets (hourly capacity, 15-min capacity and 5-min capacity) to prevent this from happening. For preventing memory overflow, these three capacities are arranged separately and in the order of hourly capacity, 15-min capacity and 5-min capacity sequentially; that is to say, the other two are not active in the arrangement of the third capacity. Because of the fact that 5-min capacity has the greatest impact on the uniform distribution of time, the check of 5-min capacity is put at the end. When the proposed algorithm is used for a 5-min check, the dimension of the constraint is too large, and sometimes the memory is insufficient to execute. So, we activate constraints of runway capacity and corridors capacity in batches according to the order of priority. The corresponding capacity is updated after each batch of arrangement. The following is the procedure of iterative linear integer programming Algorithm 1 based on data-splitting.
| Algorithm 1. Iterative linear integer programming algorithms based on data-splitting. |
| Priority calculation For i = 1:7
|
Table 3 is an example of description of the coefficient matrix in detail in the objective function and constrains within hours. The coefficient matrices (, and ) of the third column in Table 3 are derived from the equation corresponding to the fourth column in Table 3 and used in the linear integer programming.

Table 3.
Coefficient matrix and detailed expression when interval is based on hour.
5. Testing and Results
Many previous papers have made intensive study on specific performance of the slot allocation model, and significant conclusions have been drawn. The primary performance criterion of the slot allocation problem [4,24,45] is the minimization of a delay-based cost function, which is expressed either in the form of typical operational delay or the “schedule delay” concept [46]. Operational delay is usually expressed in terms of the expected arrival/departure delays and total passenger delays. “Schedule delay” is the same as displacement described in Section 3 of this article. In addition to allocation efficiency considerations (usually expressed in terms of delays), fairness and equity [30,47,48], access and competition, as well as environmental objectives [49] have been also proposed by researchers. Employing a game-theoretic framework of airline frequency competition, Vaze and Barnhart [11] showed that small reductions in allocated airport capacity can reduce delays and improve airline profitability. Computational results in [47] suggest that, under a wide range of current and hypothetical scheduling settings, ignoring inter-airline equity can lead to highly inequitable outcomes, but under a wide range of realistic and hypothetical scenarios, inter-airline equity can be achieved at small efficiency losses. Performance objectives in article [16] include the minimization of the total schedule displacement (total ‘cost’ of schedule delay) and minimization of the maximum schedule displacement. Test results of [16] suggest that substantial improvements in schedule acceptability metrics are achieved without sacrificing a lot in terms of scheduling efficiency. The comparison between NGFR (Non Grandfathered Rights) and GFR (Grandfathered Rights) scenarios of [16] demonstrates clearly the strong impact of GFR on potential schedule acceptability for airlines. Performance objectives in article [16] is the most relevant to our work.
The purpose of the test is to observe the impact of changing the weights setting on performance. Meanwhile it aims to investigate following questions.
- (1)
- Whether there is opportunity to reduce implementation difficulty while not to increase too much displacement.
- (2)
- With our algorithm, is it possible for high priority movement to have a lower probability of being displaced?
- (3)
- Can priority be considered as the cost of displacing the unit time to ensure that the high priority movement has a low probability of being displaced (HPLA)?
- (4)
- What are the differences in performance indicators when priority is fed into a computer program in priority order or in the order of morning to night (final slot-table presentation) when priority is considered as the cost of displacing the unit time?
If these questions are answered affirmatively, then displacement, difficulty and priority in the slot allocation process will be effectively controlled by the weights setting.
5.1. Performances Compare with Different Weight Factors of Evaluation Objectives
Weights setting and results with different weights of objective functions are showed in Table 4.

Table 4.
Performance compare with different weight factors of evaluation objectives.
➢ For question 1: Whether there is opportunity to reduce implementation difficulty while not to increase too much displacement?
According to results in Table 4, we found that there is a contradictory relationship between displacement and difficulty, and still cannot answer the first question. So, we leave it to next part.
➢ For question 2: With our algorithm, is it possible for high priority movement to have a lower probability of being displaced?
Displacement and difficulty of slot allocation and weights are set as [0,1,0] (test 1 in Table 4) as shown in Figure 5 and Figure 6. In this case, the slot with small priority (late entering procedure) has more probability of being displaced, and the amount of slot displacement and its displaced probability will increase significantly with priority decreasing. While weights are set as [0,1,0] in test 2, displacement and difficulty of each slot allocation are shown in Figure 7 and Figure 8. In this case, as the priority is decreasing, the displaced probability of a movement has the same trend as in test 1, but the difference is that even if the priority is high, there is a certain probability of being displaced greatly. In test 1, the average slot displacement is relatively small, but the average difficulty of the slot displacement is greater than in test 2. This means just using displacement or difficulty as an objective cannot guarantee priority well enough.
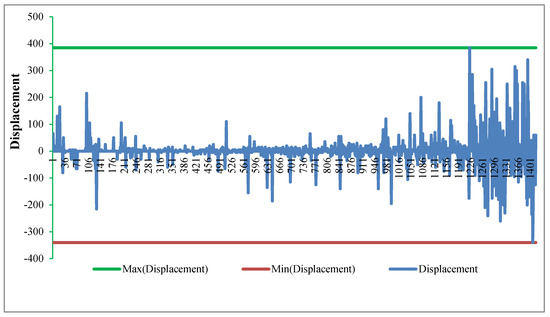
Figure 5.
Displacement of required slot while objective function not including difficulty cost.
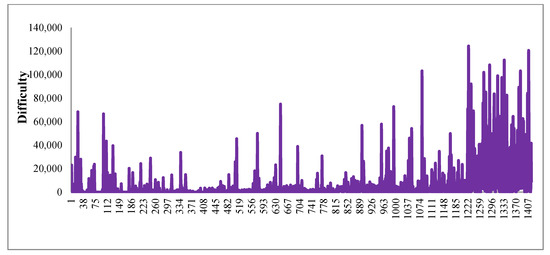
Figure 6.
Difficulty of every slot allocation while objective function not including difficulty cost.
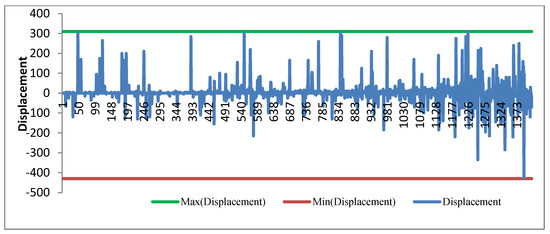
Figure 7.
Displacement while weights set as [0,1,0] in test 2.
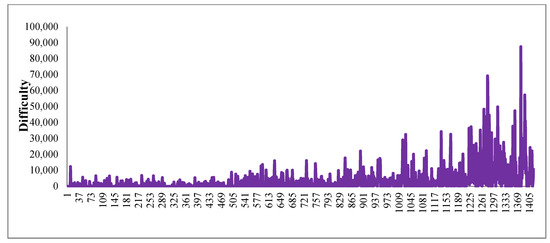
Figure 8.
Difficulty of every slot allocation while weights set as [0,1,0] in test 2.
Comparing Figure 5 and Figure 7, we found the number of applications with large displacement in Figure 7 (using difficulty as objective function only, weights setting as [0,1,0] in test 1) is more than that in Figure 5 (using displacement as objective function only, weights setting as [1,0,0] in test 2). Comparing Figure 6 and Figure 8, we found that the number of applications with hard difficulty in Figure 6 (using difficulty as objective function only, weights setting as [0,1,0]) is more than that in Figure 8 (using displacement as objective function only, weights setting as [1,0,0]). When weights are set as [0,0,1], both displacement and difficulty, showed in Figure 9 and Figure 10, are gradually increased with decreasing priority.
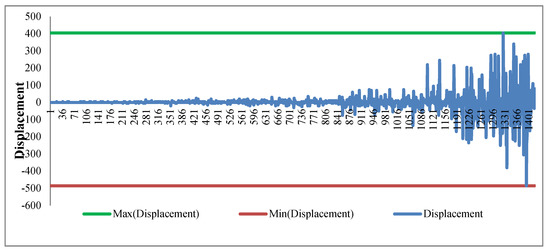
Figure 9.
Displacement of required slot while weights set as [0,0,1] in test 3.
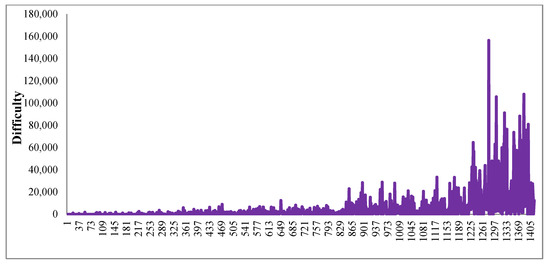
Figure 10.
Difficulty of every slot allocation while weights set as [0,0,1] in test 3.
According to Figure 5, Figure 7, Figure 9 and Figure 11, although the number of applications with large displacement is different with weights setting, the displacement probability of high priority movement is always low. On the contrary, even if the priority of an application is high, the displacement amount and the probability of being adjusted are high if it is fed later in the process. Obviously, the determinant of the amount of displacement and the probability of being adjusted is the order of the feeding process. Interestingly, from Figure 6, Figure 8, Figure 10 and Figure 12, we find that the same is true for the determinant of difficulty and the probability of difficulty increasing.
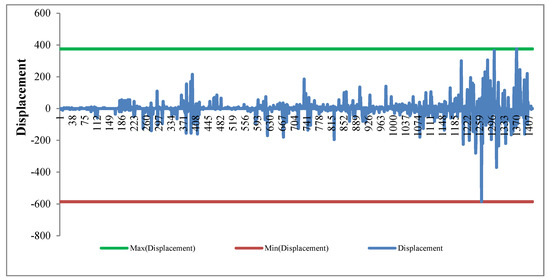
Figure 11.
Displacement while weights set as [0,0.5,0.5] in test 8.
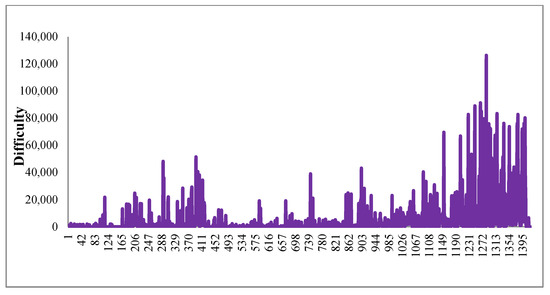
Figure 12.
Difficulty of every slot allocation while weights set as [0,0.5,0.5] in test 8.
Therefore, we conclude that no matter how the weight is set, the application with high priority will have a lower probability of being adjusted as long as movements are sent to the process according to the priority order, but the amount of displacement will vary with the weight setting. The same is true for difficulty.
➢ For question 3: Can priority is considered as the cost of displacing the unit time to ensure that the high priority movement has a low probability of being displaced (HPLA)?
According to Figure 9 and Figure 10, we found when priority is the solely evaluation objective (weights setting as [0,1,0] in test 3 showed in Table 4), both difficulty and amount of displacement will increase gradually with priority decreasing (Figure 9 and Figure 10). This means that making priority an objective is a good way to ensure priority, even if the displacement or difficulty is not so excellent.
So, according to investigation of question 2&3, we found three of these evaluation objectives should be included in the slot model.
➢ For question 4: What are the differences in performance indicators when priority is fed into a computer program in priority order or in the order of morning to night (final slot-table presentation) when priority is considered as the cost of displacing the unit time?
Comparing data of test 8 and test 6 in Table 4, we found that when other conditions remain unchanged, if the application is fed to the process without application sorting, the average difficulty will increase, but the average displacement remains almost unchanged. This means that the effect of sorting or not on difficulty is greater than that on displacement.
Comparing data of test 8 and test 6 (or data of test 10 and test 1) in Table 4, if movements are not listed according to the descent order of priority (In Figure 13, priority fluctuates as movements are fed to program according to required slot ), total difficulty is greater than that while movements are listed according to the descent order of priority. This means that if movements are not listed (and fed to program) according to the descent order of priority, difficulty will increase.
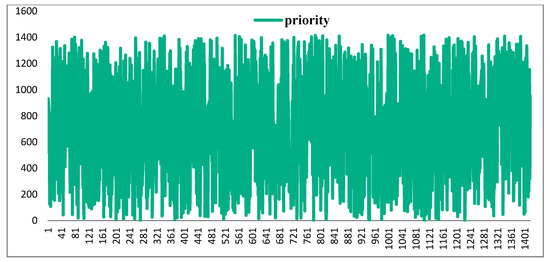
Figure 13.
Priority while weights set as [0,0.5,0.5] in test 8.
From Figure 11 (test 8), movements listed later in inputting data have more probability of being displaced and being displaced greater (and more hard difficulty, Figure 12) than a movement ahead of the list. It is very obvious that when a movement listed at the end of the roster, the remaining capacity becomes less and less, the probability of being displaced becomes larger and larger, and the difficulty becomes harder and harder.
➢ Another found
According to data of test 4–6, 9, 11–12 in Table 4, when difficulty and priority exist simultaneously in evaluation objectives while movements are sorted according to priority, the changes of the weight of these two objectives mainly affect the change of difficulty while the average displacement amount remains almost unchanged. This may imply that priority doesn’t have much of an effect on displacement, but does have an effect on difficulty while movements are sorted according to priority.
According to data test 7 in Table 4, due to the fact that the limited capacity (limited capacity equal to minimum in [78,20×4,7×12], which is 78) is smaller than that (minimum in [88,23×4,12] is 84) in other tests, the average displacement amount and the displacement difficulty are significantly increased. This comparing result implies that capacity is the key factor affecting the displacement.
5.2. Analysis of the Correlation between Average Displacement and Average Difficulty
The following formula of Pearson correlation coefficient is used to calculate the correlation coefficients of average displacement and average difficulty with the same capacity setting [88,23,7].
Three columns in Table 4 (excluding test 7, because the capacity of this test is different from others) are extracted to Table 5, and then all rows are ranked according to the average displacement in ascending order. The first column is index of test. After calculating with formula 11 and Table 5, the results show that there is a negative correlation between mean displacement and average difficulty with correlation coefficient = −0.54. That is, one decreases while another one increases. If the average difficulty is sensitive to the average displacement, there is an opportunity to increase the average displacement a little to achieve a significant reduction in the average difficulty. Therefore, we need to test the sensitivity of the average difficulty to the average displacement.

Table 5.
Data sorting according to average displacement.
The following formula is used to test the sensitivity of average difficulty to average displacement.
Using the data in Table 5, we obtained the following sensitivity coefficients, = −408.20. This shows that the average difficulty is very sensitive to the average displacement. The average displacement only needs to increase a small amount, which can greatly reduce the implementation difficulty.
6. Discussion and Conclusions
The test results show that the average difficulty is very sensitive to the average displacement. This means the average displacement only needs to increase by a small amount, which can greatly reduce the implementation difficulty. It is worthwhile to increase some amount of slot displacement appropriately in return for a significant reduction in average execution difficulty. Especially when the number of seats on some regional flights is small, the air elapse time is large, or when the linked airports are uncoordinated, it is reasonable to make more displacement for these flights.
Priority cost also should be included in the objectives to guarantee priority, but it is not suitable to give priority cost too much weight because too much weight will lead to increased difficulty. Furthermore, “lower displacement for movements with higher priority” has been guaranteed by that high priority list ahead of data table. Therefore, airlines should pay more attention to “the position in the list” and not priority itself. When applications are not listed according to priority, great differences in priorities make displacement become more difficult. For the management department of slot allocation, it is an effective way to ensure “lower displacement for movements with higher priority” by inputting programs in priority order.
The test results show implementation difficulties, displacement and priority can be trade-off by suitable weights setting, which means that when the publication capacity is fixed, by setting the weight, the displacement and difficulty will be balanced, and the grandfather rights owned by some inefficient flights could be weakened by introducing implementation difficulties into performance evaluation objectives.
In summary, by introducing performance evaluation objectives of implementation difficulty and priority, the implementation difficulty will be effectively reduced without causing excessive displacement and disruption of existing priorities. Moreover, the application with high priority will not be greatly affected if it is put into the procedure according to the priority order. Only when the number of applications is close to saturation (later in the process of slot allocation) should it affect these applications with high priority. This means that by introducing the difficulty performance objective, the implementation difficulty of some applications caused by grandfather rights can be partially eliminated, and the application with high priority will not be damaged, which will help new entrants to develop competitive routes at favorable slots and squeeze inefficient or lower priority applications into off-peak periods. As a result, it will reduce the possibility of new entrants getting the required slot in secondary market transactions with higher cost, while guaranteeing the satisfaction of passengers. Finally, the introduction of the new mechanism seems likely to be at the expense of some slot adjustments; however, it will make all flights run smoother, make all flights have their suitable slot, reduce the overall implementation difficulty, and also help to further cut the peak, fill the valley, and gradually improve the current slot structure.
The real-time applicability of our method is that at airports like Beijing Capital International Airport, the main base airlines have a number of ineffective slots, which seriously hinder the application of some new entrant carriers for new significant routes. Through our approach, the difficulty of implementation can be reduced, and grandfather rights can be weakened according to the strategic needs of the airport. At the same time, peak cutting and valley filling will be done to optimize the slot structure of these airports.
The main limitation of the study is that priority is produced by simulation because of a limitation of available data. This implies that the relationship of implementation difficulty and priority requires further research. We believe that with the improvement of technical methods and awareness of slot allocation, it is promising to make slot allocation more scientific and reasonable by investigating new slot performance evaluation objectives, suitable weights setting and other constraints in future research.
Author Contributions
Conceptualization, Z.Y.; Methodology, Z.Y.; Software, Z.Y.; Validation, Z.Y.; Formal Analysis, Z.Y.; Investigation, Z.Y.; Resources, Y.L.; Data Curation, Z.Y.; Writing-Original Draft Preparation, Z.Y.; Writing-Review & Editing, Z.Y., J.B. and X.Z.; Visualization, Z.Y.; Supervision, Z.Y.; Project Administration, Z.Y.; Funding Acquisition, Z.Y. and Y.L.
Funding
This study is supported by the National Natural Science Foundation of China (71571182), the National Natural Science Youth Foundation of China (61603396), the National Natural Science Foundation of China and the Civil Aviation Grant (U1633124) and the research projects of the social science, humanity on Young Fund of the ministry of Education of China (14YJC630185).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wu, W.; Zhang, H.; Wei, W. Optimal design of hub-and-spoke networks with access to regional hub airports: A case for the Chinese regional airport system. Transp. A Transp. Sci. 2018, 14, 330–345. [Google Scholar] [CrossRef]
- Zografos, K.G.; Madasz, M.A.; Salourasx, Y. A decision support system for total airport operations management and planning. J. Adv. Transp. 2013, 47, 170–189. [Google Scholar] [CrossRef]
- Jacquillat, A.; Odoni, A.R. An Integrated Scheduling and Operations Approach to Airport Congestion Mitigation. Oper. Res. 2015, 63, 1390–1410. [Google Scholar] [CrossRef]
- Zografos, K.G.; Salouras, Y.; Madas, M.A. Dealing with the efficient allocation of scarce resources at congested airports. Transp. Res. Part C Emerg. Technol. 2012, 21, 244–256. [Google Scholar] [CrossRef]
- Zografos, K.G.; Madas, M.A.; Androutsopoulos, K.N. Increasing airport capacity utilisation through optimum slot scheduling: Review of current developments and identification of future needs. J. Sched. 2017, 20, 3–24. [Google Scholar] [CrossRef]
- Basso, L.J.; Zhang, A.M. Pricing vs. slot policies when airport profits matter. Transp. Res. B Methodol. 2010, 44, 381–391. [Google Scholar] [CrossRef]
- Verhoef, E.T. Congestion pricing, slot sales and slot trading in aviation. Transp. Res. B Methodol. 2010, 44, 320–329. [Google Scholar] [CrossRef]
- Zhang, A.M.; Zhang, Y.M. Airport capacity and congestion pricing with both aeronautical and commercial operations. Transp. Res. B Methodol. 2010, 44, 404–413. [Google Scholar] [CrossRef]
- Czerny, A.I.; Zhang, A.M. Airport congestion pricing and passenger types. Transp. Res. B Methodol. 2011, 45, 595–604. [Google Scholar] [CrossRef]
- Le, L.; Donohue, G.; Hoffman, K.; Chen, C.H. Optimum airport capacity utilization under congestion management: A case study of New York LaGuardia airport. Transp. Plan Technol. 2008, 31, 93–112. [Google Scholar] [CrossRef]
- Vaze, V.; Barnhart, C. Modeling Airline Frequency Competition for Airport Congestion Mitigation. Transp. Sci. 2012, 46, 512–535. [Google Scholar] [CrossRef]
- Grunewald, E. Incentive-based Slot Allocation for Airports. Transp. Res. Procedia 2016, 14, 3761–3770. [Google Scholar] [CrossRef]
- Jacquillat, A.; Odoni, A.R. Congestion Mitigation at John F. Kennedy International Airport in New York City: Potential of Schedule Coordination. Transp. Res. Rec. 2013, 2400, 28–36. [Google Scholar] [CrossRef]
- Pyrgiotis, N.; Odoni, A. On the Impact of Scheduling Limits: A Case Study at Newark Liberty International Airport. Transp. Sci. 2016, 50, 150–165. [Google Scholar] [CrossRef]
- Ribeiro, N.A.; Jacquillat, A.; Antunes, A.P.; Odoni, A.R.; Pita, J.P. An optimization approach for airport slot allocation under IATA guidelines. Transp. Res. B Methodol. 2018, 112, 132–156. [Google Scholar] [CrossRef]
- Zografos, K.G.; Androutsopoulos, K.N.; Madas, M.A. Minding the gap: Optimizing airport schedule displacement and acceptability. Transp. Res. Part A Policy Pract. 2018, 114, 203–221. [Google Scholar] [CrossRef]
- Jacquillat, A.; Odoni, A.R. Endogenous control of service rates in stochastic and dynamic queuing models of airport congestion. Transp. Res. Part E Logist. Transp. Rev. 2015, 73, 133–151. [Google Scholar] [CrossRef][Green Version]
- Jacquillat, A.; Odoni, A.R. A roadmap toward airport demand and capacity management. Transp. Res. Part A Policy Pract. 2018, 114, 168–185. [Google Scholar] [CrossRef]
- Benlic, U. Heuristic search for allocation of slots at network level. Transp. Res. Part C Emerg. Technol. 2018, 86, 488–509. [Google Scholar] [CrossRef]
- Li, X.; Chen, X.; Li, D.; Wei, D. Classification and characteristics of flights taking off and landing waveforms. Flight Dyn. 2016, 34, 90–94. [Google Scholar]
- Sun, C.L.; Su, X. Analysis & Optimization of Beijing Capital Airport’s flight waves. China Civ. Aviat. 2013, 30–31. [Google Scholar]
- Hu, M.; Yi, T.; Ren, Y. Optimization of airport slot based on improved Hungarian algorithm. Appl. Res. Comput. 2019, 1–7. [Google Scholar]
- Huang, J.; Wang, J. A comparison of indirect connectivity in Chinese airport hubs: 2010 vs. 2015. J. Air Transp. Manag. 2017, 65, 29–39. [Google Scholar] [CrossRef]
- Corolli, L.; Lulli, G.; Ntaimo, L. The time slot allocation problem under uncertain capacity. Transp. Res. Part C Emerg. Technol. 2014, 46, 16–29. [Google Scholar] [CrossRef]
- Debbage, K.G. Airport runway slots: Limits to growth. Ann. Tour. Res. 2002, 29, 933–951. [Google Scholar] [CrossRef]
- Picard, P.M.; Tampieri, A.; Wan, X. Airport capacity and inefficiency in slot allocation. Int. J. Ind. Organ. 2019, 62, 330–357. [Google Scholar] [CrossRef]
- Ahmadbeygi, S.; Cohn, A.; Guan, Y.; Belobaba, P. Analysis of the potential for delay propagation in passenger airline networks. J. Air Transp. Manag. 2008, 14, 221–236. [Google Scholar] [CrossRef]
- Gillen, D.; Jacquillat, A.; Odoni, A.R. Airport demand management: The operations research and economics perspectives and potential synergies. Transp. Res. Part A Policy Pract. 2016, 94, 495–513. [Google Scholar] [CrossRef]
- Levine, M.E. Airport congestion: When theory meets reality. Yale J. Reg. 2009, 26, 37. [Google Scholar]
- Zografos, K. A Bi-objective Efficiency-Fairness Model for Scheduling Slots at Congested Airports. Transp. Res. Part C Emerg. Technol. 2019, 102, 336–350. [Google Scholar] [CrossRef]
- Ogryezak, W. Symmetric duality theory for linear goal programming. Optimization 1988, 19, 373–396. [Google Scholar] [CrossRef]
- Brooker, P. Simple Models for Airport Delays During Transition to a Trajectory-Based Air Traffic System. J. Navig. 2009, 62, 555–570. [Google Scholar] [CrossRef]
- Han, F.; Wong, B.L.W.; Gauhrodger, S. Improving future air traffic punctuality: “pinch-and-pull” target windows. Aircr. Eng. Aerosp. Technol. 2010, 82, 207–216. [Google Scholar] [CrossRef]
- Richard, O.; Constans, S.; Fondacci, R. Computing 4D near-optimal trajectories for dynamic air traffic flow management with column generation and branch-and-price. Transp. Plan. Technol. 2011, 34, 389–411. [Google Scholar] [CrossRef]
- Tang, X.M.; Han, Y.X. 4d Trajectory Estimation for Air Traffic Control Automation System Based on Hybrid System Theory. Promet Traffic Transp. 2012, 24, 91–98. [Google Scholar] [CrossRef]
- Cafieri, S.; D’Ambrosio, C. Feasibility pump for aircraft deconfliction with speed regulation. J. Glob. Optim. 2017, 71, 501–515. [Google Scholar] [CrossRef]
- Durand, N.; Allignol, C.; Barnier, N. A Ground Holding Model for Aircraft Deconfliction. In Proceedings of the 29th Digital Avionics Systems Conference, Salt Lake City, UT, USA, 3–7 October 2010. [Google Scholar]
- Han, Y.X.; Huang, X.Q.; Zhang, Y. Traffic system operation optimization incorporating buffer size. Aerosp. Sci. Technol. 2017, 66, 262–273. [Google Scholar] [CrossRef]
- Jackson, M.R.C.; Sharma, V.; Haissig, C.M.; Elgersma, M. Airborne Technology for Distributed Air Traffic Management. Eur. J. Control 2005, 11, 464–477. [Google Scholar] [CrossRef]
- Wang, T.C.; Li, Y.J. Optimal Scheduling and Speed Adjustment in En Route Sector for Arriving Airplanes. J. Aircr. 2011, 48, 673–682. [Google Scholar] [CrossRef]
- Rey, D.; Rapine, C.; Fondacci, R.; El Faouzi, N.E. Minimization of Potential Air Conflicts Through Speed Regulation. Transp. Res. Rec. 2012, 2300, 59–67. [Google Scholar] [CrossRef]
- Rosenow, J.; Fricke, H.; Luchkova, T.; Schultz, M. Impact of optimised trajectories on air traffic flow management. Aeronaut. J. 2019, 123, 157–173. [Google Scholar] [CrossRef]
- Haraldsdottir, A.; Scharl, J.; Berge, M.E.; Coats, M.L.; King, J. Performance analysis of arrival management with 3D paths and speed control. In Proceedings of the 2007 IEEE/AIAA 26th Digital Avionics Systems Conference, Dallas, TX, USA, 21–25 October 2007. [Google Scholar]
- Rezaee, A.; Izadpanah, S. An Optimized, Mathematical-Based Flight Performance Planning. In Proceedings of the 2009 International Conference on Computer Technology and Development, Kota Kinabalu, Malaysia, 13–15 November 2009. [Google Scholar] [CrossRef]
- Koesters, D. Airport scheduling performance—An approach to evaluate the airport scheduling process by using scheduled delays as quality criterion. In Proceedings of the Air Transport Research Society (ATRS) Annual World Conference, Berkeley, CA, USA, 21–23 June 2007. [Google Scholar]
- Swaroop, P.; Zou, B.; Ball, M.O.; Hansen, M. Do more US airports need slot controls? A welfare based approach to determine slot levels. Transp. Res. Part B Methodol. 2012, 46, 1239–1259. [Google Scholar] [CrossRef]
- Jacquillat, A.; Vaze, V. Interairline Equity in Airport Scheduling Interventions. Transp. Sci. 2018, 52, 941–964. [Google Scholar] [CrossRef]
- Castelli, L.; Pellegrini, P.; Pesenti, R. Airport slot allocation in Europe: Economic efficiency and fairness. Int. J. Revenue Manag. 2011, 6, 28–44. [Google Scholar] [CrossRef]
- Ranieri, A.; Alsina, N.; Castelli, L.; Bolic, T.; Herranz, R. Airport slot allocation: Performance of the current system and options for reform. In Proceedings of the 3rd SESAR Innovation Days, Stockholm, Sweden, 26–28 November 2013. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).