Multi-PQTable for Approximate Nearest-Neighbor Search
Abstract
1. Introduction
- We propose a product quantization table (PQTable) algorithm on the basis of the PQ algorithm, according to the ability of the Hash Table to quickly find the required content. This algorithm can implement a non-exhaustive approximate nearest-neighbor search algorithm, aiming at quickly and accurately retrieving the vector candidate sets in a large-scale dataset.
- We also propose a multi-PQTable query strategy for ANN search. Besides, we generate several nearest-neighbor vectors for each sub-compressed vector of the query vector to reduce the failure rate and improve the recall in image retrieval.
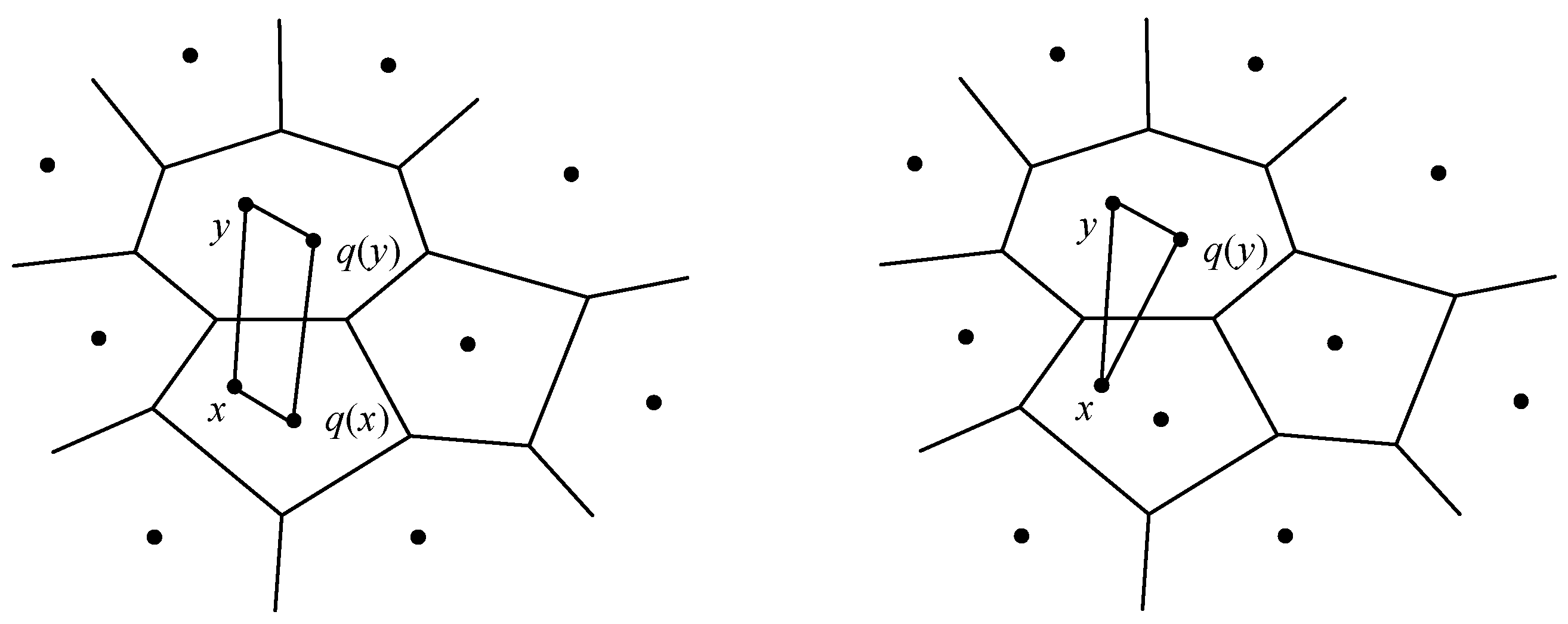
2. Product Quantization
- (1)
- Uniformly split the vector X into M distinct sub-vectors uj(x), 1 ≤ j ≤ M. The dimension of the sub-vector is D* and D* = D/M, where D is a multiple of M. Therefore, the vector X can be seen as a series of sub-vectors, and .
- (2)
- Each sub-vector is quantized and compressed by the K-means algorithm, and the corresponding codebook set Cj is obtained.
- (3)
- The Codebook C of the vector X is the Cartesian product generated from all the set Cj, and C = C1 × C2 × ⋯ × CM.
3. Multi-PQTable for ANN Search
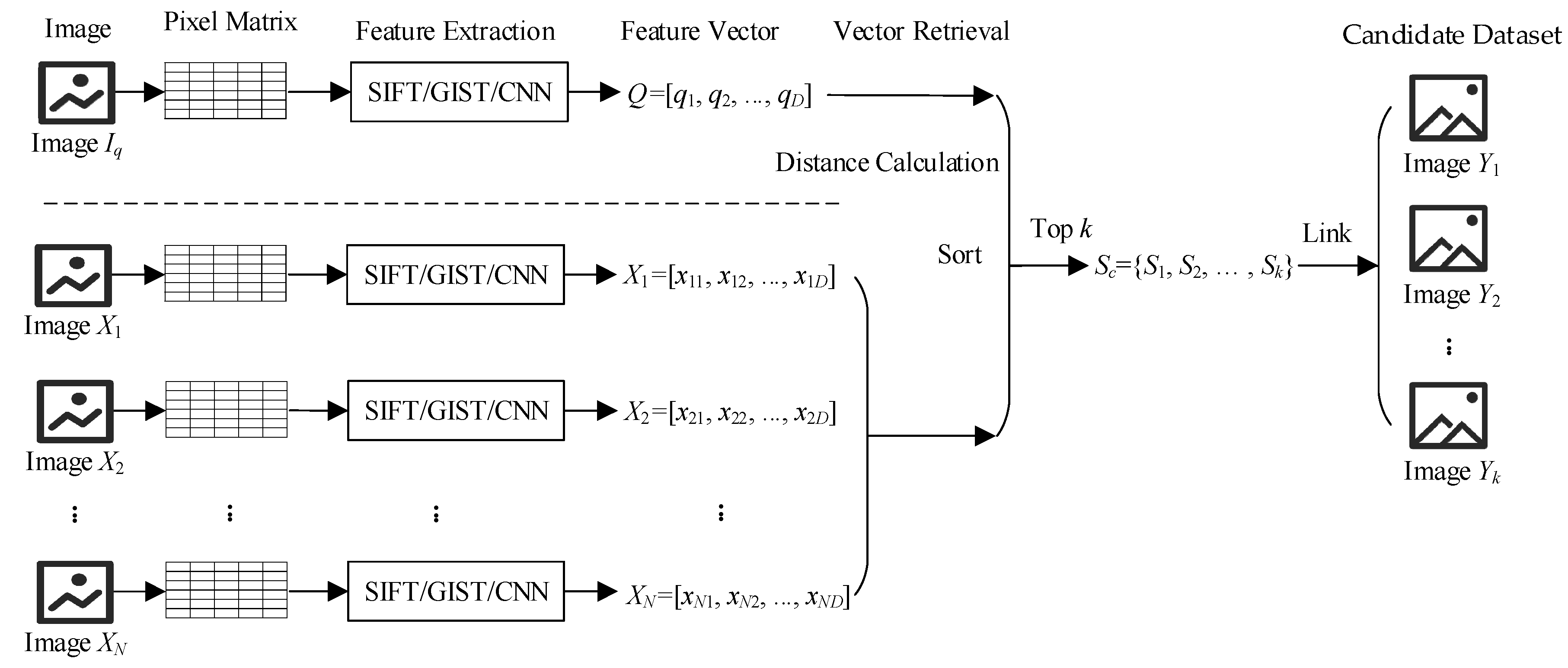
3.1. Problem Description
- (1)
- Extract the features for the query image Iq and for the image dataset I by feature extraction tools such as SIFT, GIST, CNN, and so on. Correspondingly obtain the image feature vector Q = [q1, q2, …, qn] and the image feature dataset X = {X1, X2, …, XN}, where Q is the feature vector of the query image Iq, Xi = [xi1, xi2, …, xiD], and D is the dimension of the feature vector.
- (2)
- Obtain the top-k vector candidate subsets Sc = {S1, S2, …, Sk} through calculating and sorting according to the query vector Q.
- (3)
- Correspondingly obtain the top-k image candidate sub-dataset Y = {Y1, Y2, …, Yk} via the linking relationship between the vectors and the images.
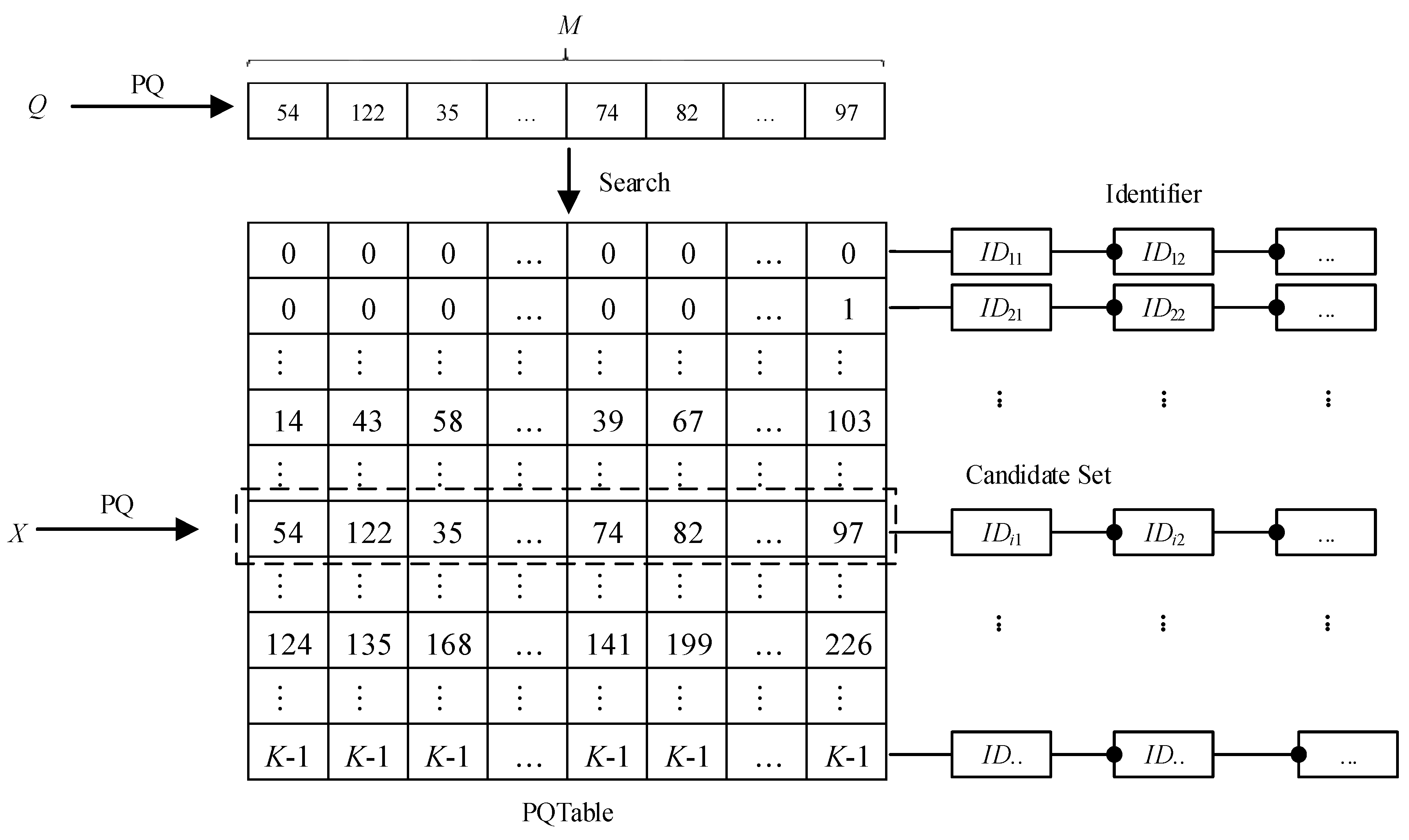
3.2. PQTable Algorithm
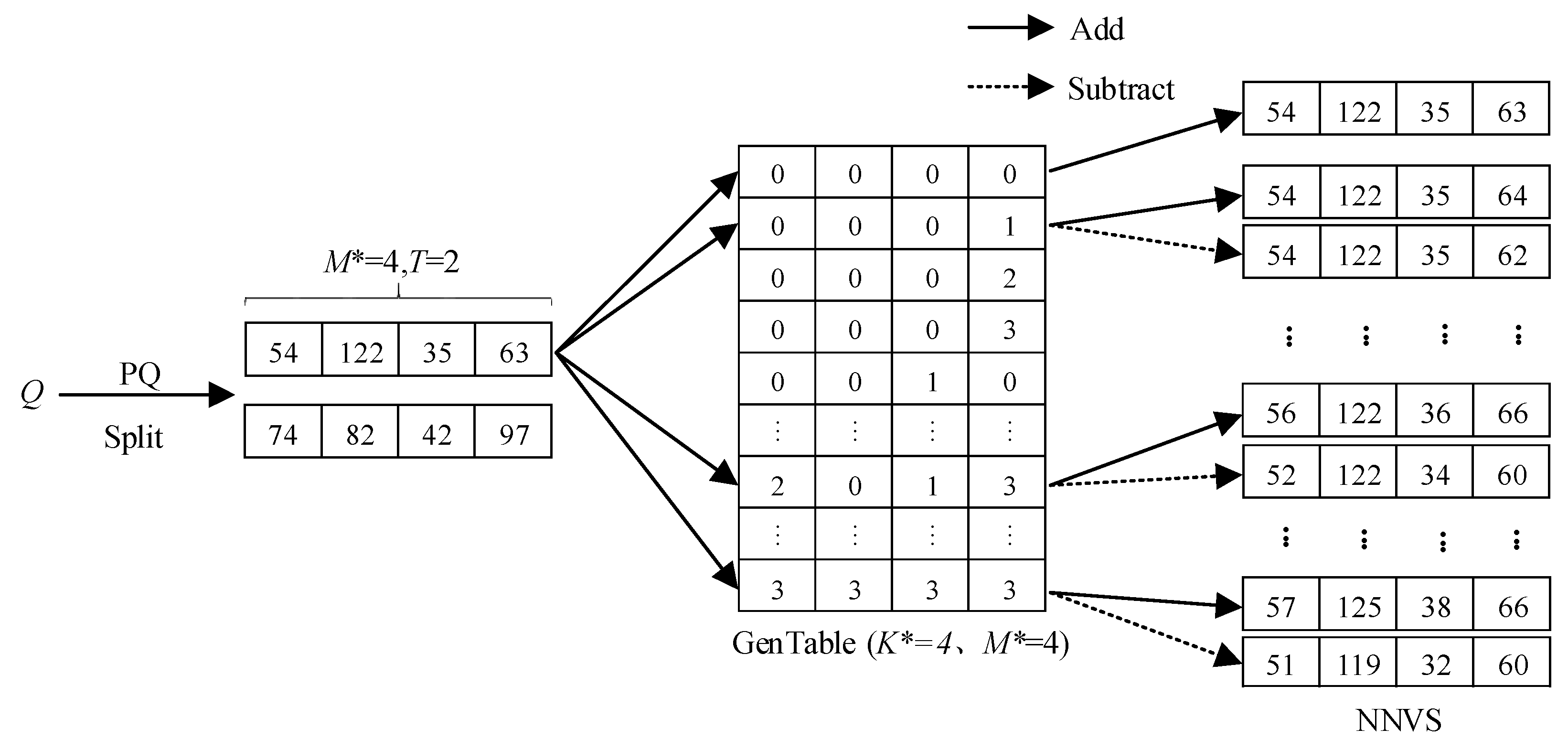
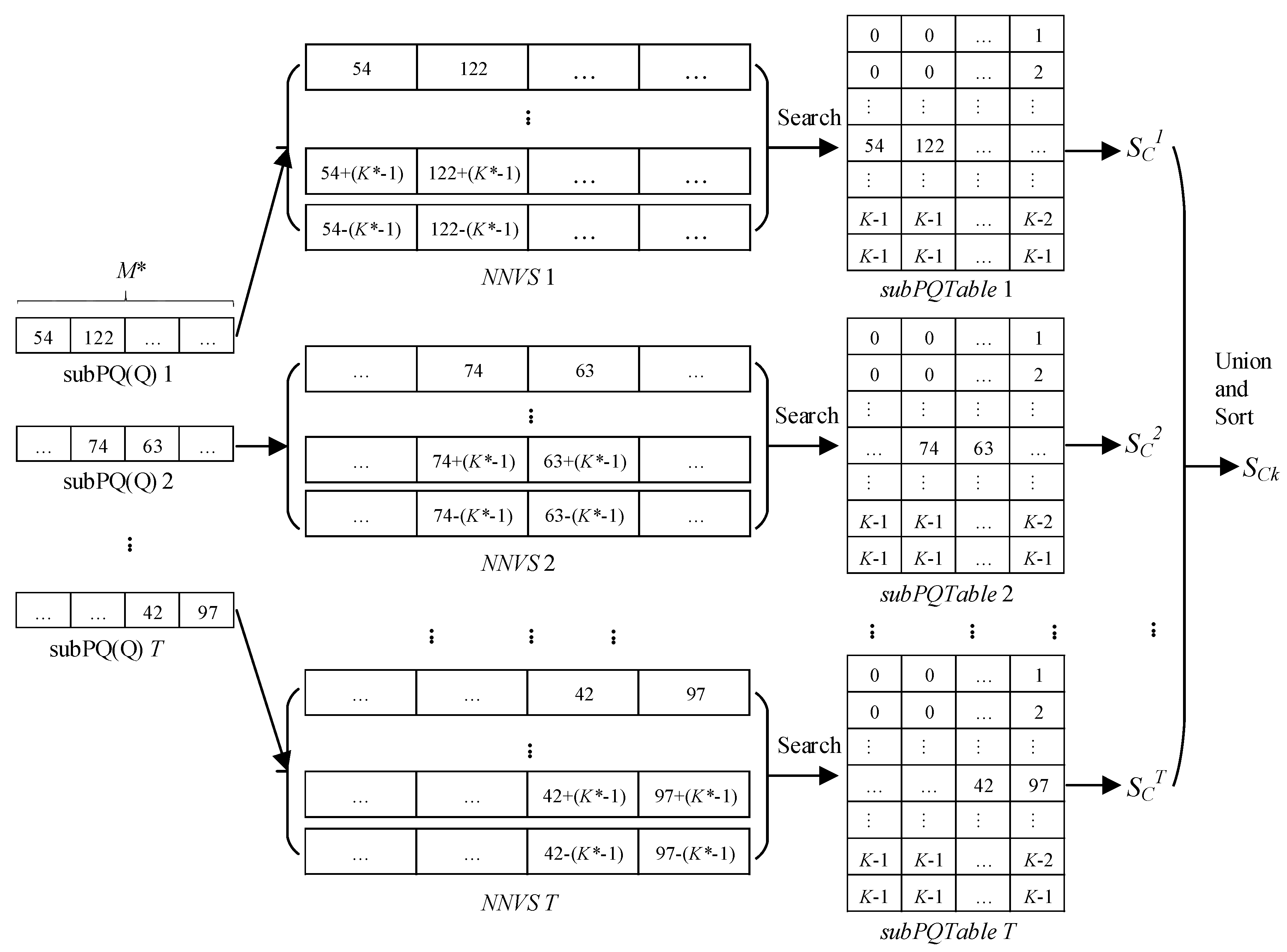
3.3. Multi-PQTable Query Strategy
- (1)
- Creating a generator table. We define K* − 1 as the largest parameter and create a two-dimensional generator table with a size of U × V, where K is a positive integer, and K* << K, U = K*M*, V = M*, M* = M/T. We sequentially fill the table with integers from 0 to K* − 1 and get a generator table (GenTable).
- (2)
- Generating several nearest-neighbor vectors. Each subPQ(Q)t is added and subtracted to every row data in the GenTable. Then, we can get the corresponding nearest-neighbor vector set (NNVS).
- (3)
- Filtering the elements in nearest-neighbor vectors. We validate each vector in the NNVS and filter out the vectors whose elements are less than zero. Finally, we get the final NNVS.
| Algorithm 1: Generating Nearest-Neighbor Vector Set (genNNVS). | |
| Input: | |
| GenTable[U][V], subPQ[V] | |
| Output: | |
| NNVS | |
| 1: | for i <= U do |
| 2: | Flag = true; |
| 3: | for j <= V do |
| 4: | V0[j] = subPQ [j] + GenTable[i][ j]; |
| 5: | V1[j] = subPQ [j] − GenTable[i][j]; |
| 6: | if V1[j] < 0 then |
| 7: | flag = false; |
| 8: | end if |
| 9: | end for |
| 10: | NNVS add V0; |
| 11: | if flag == true then |
| 12: | NNVS add V1; |
| 13: | end if |
| 14: | end for |
| Algorithm 2: The Approximate Nearest-Neighbor (ANN) Search Algorithm based on the Multi-PQTable | |
| Input: | |
| k, Q, GenTable[U][V], subPQTables = {subPQTable1, subPQTable2, …, subPQTableT} | |
| Output: | |
| SCk | |
| 1: | PQ(Q); |
| 2: | subPQs = {subPQ1[V], subPQ2[V], …, subPQT[V]}; |
| 3: | while t <= T do |
| 4: | t = t + 1; |
| 5: | NNVSt = genNNVS(GenTable[U][V], subPQt[V]); |
| 6: | foreach vector ∈ NNVS do |
| 7: | IDs←search vector in subPQTablest; |
| 8: | sc←obtain the vector set through IDs; |
| 9: | SCt = SCt∪sc; |
| 10: | end foreach |
| 11: | SC = SC∪SCt; |
| 12: | end while |
| 13: | SCk = SC; |
| 14: | size←get size of SC; |
| 15: | if size > k then |
| 16: | SCk←calculate similarity and sort; |
| 17: | end if |
4. Experiments and Analysis
4.1. Experimental Settings
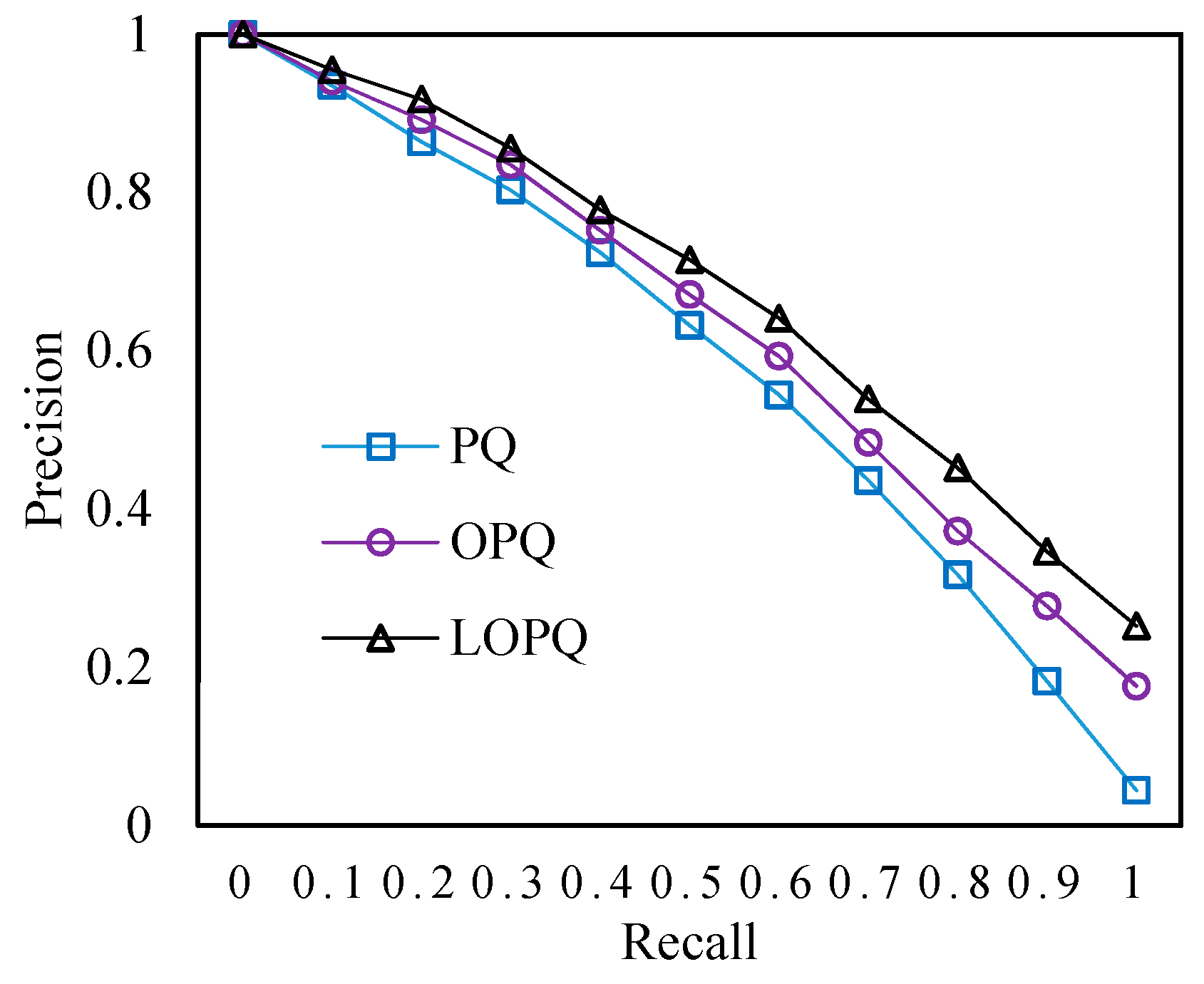
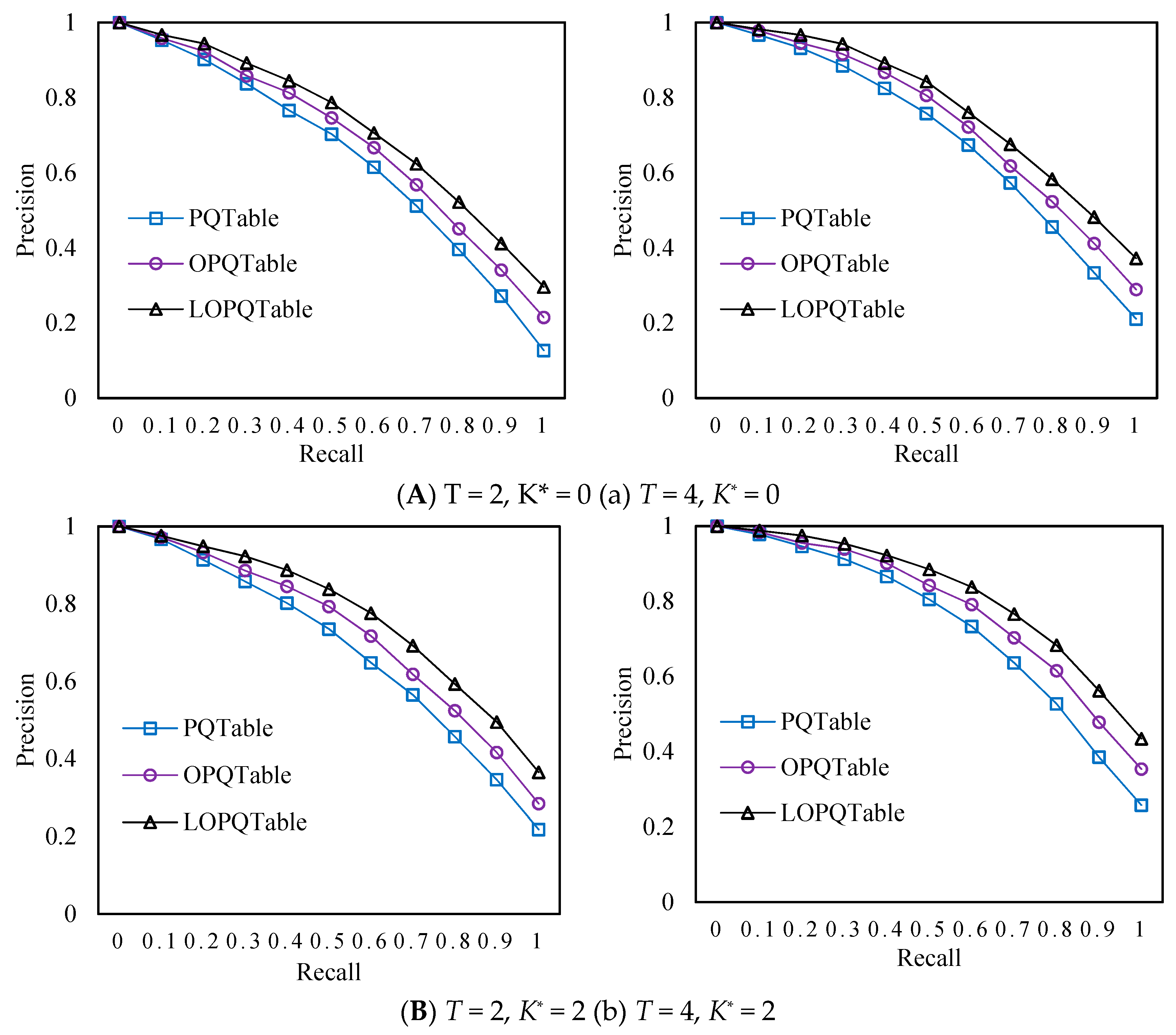
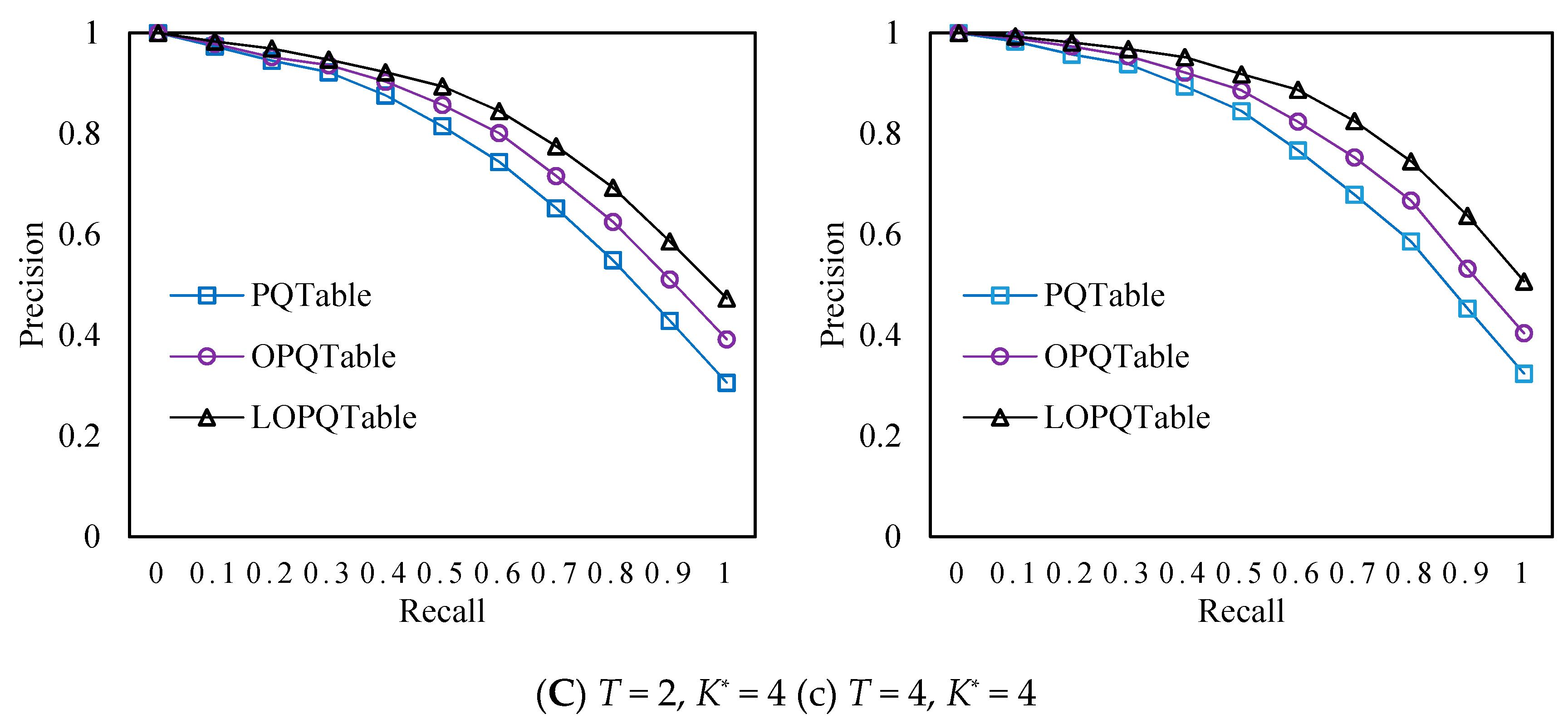
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Figat, J.; Kornuta, T.; Kasprzak, W. Performance Evaluation of Binary Descriptors of Local Features. In Proceedings of the International Conference on Computer Vision and Graphics, Warsaw, Poland, 15–17 September 2014; pp. 187–194. [Google Scholar]
- Bay, H.; Tuytelaars, T.; Gool, L.V. SURF: Speeded Up Robust Features. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2006; pp. 404–417. [Google Scholar]
- Boulkenafet, Z.; Komulainen, J.; Hadid, A. Face Antispoofing Using Speeded-Up Robust Features and Fisher Vector Encoding. IEEE Signal Process. Lett. 2017, 24, 141–145. [Google Scholar]
- Oliva, A.; Torralba, A. Modeling the Shape of the Scene: A Holistic Representation of the Spatial Envelope. Int. J. Comput. Vis. 2001, 42, 145–175. [Google Scholar] [CrossRef]
- Oliva, A.; Torralba, A. Building the gist of a scene: The role of global image features in recognition. Prog. Brain Res. 2006, 155, 23–36. [Google Scholar] [PubMed]
- Sánchez, J.; Redolfi, J. Exponential family Fisher vector for image classification. Pattern Recognit. Lett. 2015, 59, 26–32. [Google Scholar] [CrossRef]
- Jégou, H.; Douze, M.; Schmid, C.; Pérez, P. Aggregating local descriptors into a compact image representation. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Amato, G.; Bolettieri, P.; Falchi, F.; Gennaro, C. Large Scale Image Retrieval Using Vector of Locally Aggregated Descriptors. In International Conference on Similarity Search & Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sun, P.X.; Lin, H.T.; Luo, T. Learning discriminative CNN features and similarity metrics for image retrieval. In Proceedings of the IEEE International Conference on Signal Processing, Communications and Computing, Hong Kong, China, 5–8 August 2016. [Google Scholar]
- Fu, R.; Li, B.; Gao, Y.; Wang, P. Content-based image retrieval based on CNN and SVM. In Proceedings of the IEEE International Conference on Computer and Communications, Chengdu, China, 14–17 October 2016; pp. 638–642. [Google Scholar]
- Melekhov, I.; Kannala, J.; Rahtu, E. Siamese network features for image matching. In Proceedings of the International Conference on Pattern Recognition, Cancun, Mexico, 4–8 December 2016; pp. 378–383. [Google Scholar]
- Appalaraju, S.; Chaoji, V. Image Similarity Using Deep CNN and Curriculum Learning. arXiv 2017, arXiv:1709.08761. [Google Scholar]
- Li, Y.; Miao, Z.; Wang, J.; Zhang, Y. Deep binary constraint hashing for fast image retrieval. Electron. Lett. 2018, 54, 25–27. [Google Scholar] [CrossRef]
- Hoffer, E.; Ailon, N. Deep Metric Learning Using Triplet Network. In Similarity-Based Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2015; pp. 84–92. [Google Scholar]
- Schroff, F.; Kalenichenko, D.; Philbin, J. FaceNet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 815–823. [Google Scholar]
- Liu, Y.; Chao, H. Scene Classification via Triplet Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 220–237. [Google Scholar] [CrossRef]
- Kumar, Y.S.; Pavithra, N. KD-Tree approach in sketch based image retrieval. In Proceedings of the International Conference on Mining Intelligence and Knowledge Exploration, Hyderabad, India, 9–11 December 2015; pp. 247–258. [Google Scholar]
- Kao, B.; Lee, S.D.; Lee, F.K.; Cheung, D.W.; Ho, W.S. Clustering Uncertain Data Using Voronoi Diagrams and R-Tree Index. IEEE Trans. Knowl. Data Eng. 2010, 22, 1219–1233. [Google Scholar]
- Viet, H.H.; Anh, D.T. M-tree as an index structure for time series data. In Proceedings of the International Conference on Computing, Management and Telecommunications, Ho Chi Minh City, Vietnam, 21–24 January 2013; pp. 146–151. [Google Scholar]
- Wieschollek, P.; Wang, O.; Sorkine-Hornung, A.; Lensch, H. Efficient Large-scale Approximate Nearest Neighbor Search on the GPU. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2017; pp. 2027–2035. [Google Scholar]
- Amsaleg, L. Locality sensitive hashing: A comparison of hash function types and querying mechanisms. Pattern Recognit. Lett. 2010, 31, 1348–1358. [Google Scholar]
- Abdulhayoglu, M.A.; Thijs, B. Use of locality sensitive hashing (LSH) algorithm to match Web of Science and Scopus. Scientometrics 2018, 116, 1229–1245. [Google Scholar] [CrossRef]
- Jégou, H.; Douze, M.; Schmid, C. Product Quantization for Nearest Neighbor Search. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 117–128. [Google Scholar] [CrossRef]
- Ge, T.; He, K.; Ke, Q.; Sun, J. Optimized Product Quantization for Approximate Nearest Neighbor Search. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2946–2953. [Google Scholar]
- Ge, T.; He, K.; Ke, Q.; Sun, J. Optimized Product Quantization. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 744–755. [Google Scholar] [CrossRef]
- Kalantidis, Y.; Avrithis, Y. Locally Optimized Product Quantization for Approximate Nearest Neighbor Search. Available online: http://openaccess.thecvf.com/content_cvpr_2014/papers/Kalantidis_Locally_Optimized_Product_2014_CVPR_paper.pdf (accessed on 15 May 2018).
- Martinez, J.; Hoos, H.H.; Little, J.J. Stacked Quantizers for Compositional Vector Compression. arXiv 2014, arXiv:1411.2173. [Google Scholar]
- Wang, J.; Li, Z.; Du, Y.; Qu, W. Stacked Product Quantization for Nearest Neighbor Search on Large Datasets. In Proceedings of the IEEE Trustcom, Tianjin, China, 23–26 August 2016; pp. 787–795. [Google Scholar]
- Babenko, A.; Lempitsky, V. Additive Quantization for Extreme Vector Compression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 931–938. [Google Scholar]
- Yuan, X.; Liu, Q.; Long, J.; Hu, L.; Wang, Y. Deep Image Similarity Measurement based on the Improved Triplet Network with Spatial Pyramid Pooling. Information 2019, 10, 129. [Google Scholar] [CrossRef]
- Hu, F.; Zhu, Z.; Mejia, J.; Tang, H.; Zhang, J. Real-time indoor assistive localization with mobile omnidirectional vision and cloud GPU acceleration. AIMS Electron. Electr. Eng. 2017, 1, 74–99. [Google Scholar] [CrossRef]
- Bing, Z.; Xin-xin, Y.A. A content-based parallel image retrieval system. In Proceedings of the International Conference on Computer Design and Applications (ICCDA), Qinhuangdao, China, 25–27 June 2010; pp. 332–336. [Google Scholar]


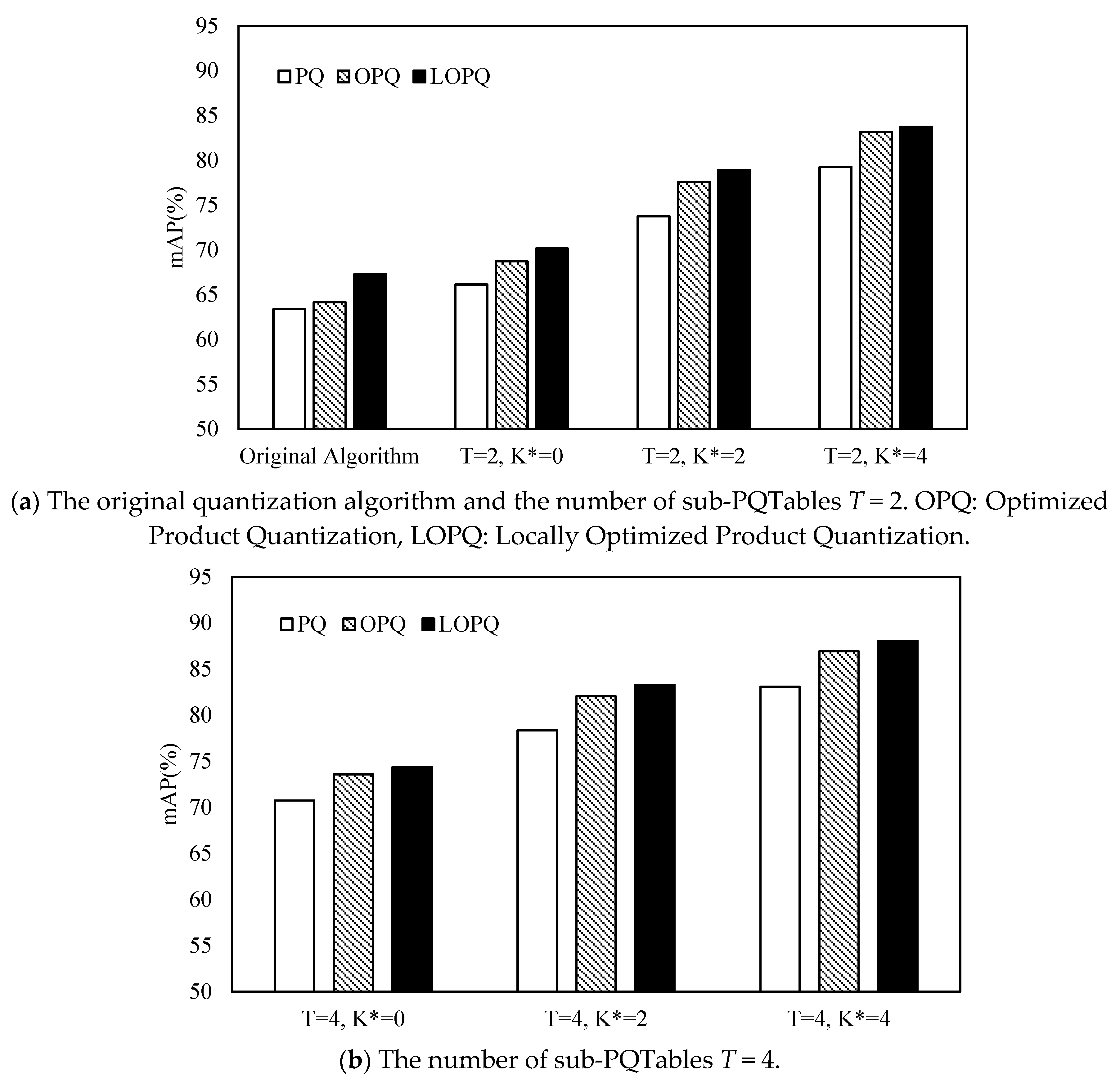


| No. | Parameter Settings | Average Retrieval Time (×103/ms) | ||
|---|---|---|---|---|
| PQ | OPQ | LOPQ | ||
| 1 | Original Algorithm | 14.29 | 14.23 | 14.16 |
| 2 | T = 2, K* = 0 | 45.93 | 45.86 | 45.77 |
| 3 | T = 2, K* = 2 | 63.56 | 62.95 | 62.84 |
| 4 | T = 2, K* = 4 | 217.69 | 198.31 | 197.92 |
| 5 | T = 4, K* = 0 | 0.004 | 0.002 | 0.003 |
| 6 | T = 4, K* = 2 | 0.012 | 0.008 | 0.009 |
| 7 | T = 4, K* = 4 | 0.21 | 0.16 | 0.17 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, X.; Liu, Q.; Long, J.; Hu, L.; Wang, S. Multi-PQTable for Approximate Nearest-Neighbor Search. Information 2019, 10, 190. https://doi.org/10.3390/info10060190
Yuan X, Liu Q, Long J, Hu L, Wang S. Multi-PQTable for Approximate Nearest-Neighbor Search. Information. 2019; 10(6):190. https://doi.org/10.3390/info10060190
Chicago/Turabian StyleYuan, Xinpan, Qunfeng Liu, Jun Long, Lei Hu, and Songlin Wang. 2019. "Multi-PQTable for Approximate Nearest-Neighbor Search" Information 10, no. 6: 190. https://doi.org/10.3390/info10060190
APA StyleYuan, X., Liu, Q., Long, J., Hu, L., & Wang, S. (2019). Multi-PQTable for Approximate Nearest-Neighbor Search. Information, 10(6), 190. https://doi.org/10.3390/info10060190





