Next Article in Journal / Special Issue
5-Hydroxymethylfurfural (5-HMF) Production from Hexoses: Limits of Heterogeneous Catalysis in Hydrothermal Conditions and Potential of Concentrated Aqueous Organic Acids as Reactive Solvent System
Previous Article in Journal
Assessing the Relationship Between Hazard Mitigation Plan Quality and Rural Status in a Cohort of 57 Counties from 3 States in the Southeastern U.S.
Previous Article in Special Issue
Continuous-Flow Processes in Heterogeneously Catalyzed Transformations of Biomass Derivatives into Fuels and Chemicals
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Challenges
Volume 3
Issue 2
10.3390/challe3020194
challenges-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Particle Handling Techniques in Microchemical Processes

by
Brian S. Flowers
and
Ryan L. Hartman
*
Department of Chemical and Biological Engineering, The University of Alabama, Box 870203, Tuscaloosa, AL 35487-0203, USA
*
Author to whom correspondence should be addressed.
Challenges 2012, 3(2), 194-211; https://doi.org/10.3390/challe3020194
Submission received: 27 July 2012 / Accepted: 14 August 2012 / Published: 22 August 2012
(This article belongs to the Special Issue Challenges in Chemical Processes)
Browse Figures
Versions Notes

Abstract

:
The manipulation of particulates in microfluidics is a challenge that continues to impact applications ranging from fine chemicals manufacturing to the materials and the life sciences. Heterogeneous operations carried out in microreactors involve high surface-to-volume characteristics that minimize the heat and mass transport resistances, offering precise control of the reaction conditions. Considerable advances have been made towards the engineering of techniques that control particles in microscale laminar flow, yet there remain tremendous opportunities for improvements in the area of chemical processing. Strategies that have been developed to successfully advance systems involving heterogeneous materials are reviewed and an outlook provided in the context of the challenges of continuous flow fine chemical processes.

1. Introduction

The field of microfluidics has grown extensively over the last decade, interfacing problems in biology, chemistry, and materials science to name a few [1,2,3,4,5,6,7,8,9,10]. A major challenge that continues to limit this exciting field is the ability to perform operations involving particles in microfluidic devices [11]. Heterogeneous systems of relevance to microfluidics are becoming increasingly common. A lack of technological approaches or fundamental understanding of how to deal with particulate matter in microscale laminar flow often leads to devices that clog, significantly reducing device life-cycles, or worse, rendering them inoperable. Advancing the ability to control particles in microfluidics [2,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41] promises to create new areas of research and discovery with microsystems.
There are numerous microfluidic problems where solids are encountered yet limit the discovery of new science and engineering insights. Performing synthetic chemistry in microreactors can improve the selectivity and the yield while simultaneously elucidating the kinetic information needed to scale-up from the laboratory to an industrial process [42,43,44]. The majority of reactions relevant to the preparation of fine chemicals, however, involve the use of solid reagents, catalysts, products, and by-products. The manipulation of cells and biomolecules in microfluidics also demands control strategies for heterogeneous matter [6,20,45,46,47,48]. Microfluidic cell culturing can offer improvements on the nutrient conditions and hence cell yield, therapy, and response [49,50]. Devices have been engineered small enough to constrain a single cell, revealing deeper understanding of individual cellular mechanics [51,52]. Healthcare diagnostics and purification devices also take advantage of micro-scale flows to enhance the selectivity of biofluid separations, which can be used to isolate and purify proteins, cells, and lipids among others [53,54]. The microfluidic synthesis of inorganic crystals, another example of the flow and reaction of solids in micro-scales, can generate advanced nanomaterials for applications in catalysis, material science, and healthcare [5,10,55,56,57,58,59,60,61]. There exists the potential for device clogging in each of the aforementioned systems. Understanding the differences between the particle interaction mechanisms that constrain fluid flow is critical to exploiting microfluidics for research discovery and the development of devices that improve society.
There are important design considerations to be made when engineering microfluidic devices that will encounter particles. The mechanism(s) of device clogging depends on the nature of the particle-to-particle and particle-to-device interactions. Investing time up front to identify the dominant interactions can mitigate or prevent device failure. Techniques that can be applied to manage solids generally fall into one of two categories: active or passive particle manipulation. A combined understanding of the clogging mechanism(s) with the appropriate engineering strategy can ensure the flow of new knowledge.
This mini-review summarizes the fundamental concepts that one might consider when encountering solids in microfluidic systems, while the theme of chemical manufacturing is emphasized. Clogging mechanisms are described and examples drawn from the literature highlighted to demonstrate the basic concepts. A toolbox of engineering strategies to manage solids is presented, including advancements in both active and passive particle manipulation techniques. Finally, current limitations are discussed and opportunities for future advancements are delineated.

2. Particles Encountered in Microreactors

The synthetic methodologies applied in the preparation of pharmaceuticals and fine chemicals commonly involve solids in the form of reagents, catalysts, inorganic by-products, and organic products [62,63]. The coupling of aromatic molecules to prepare useful intermediates and final products presents virtually unlimited pathways and methodologies that involve the use of solids. Palladium-catalyzed bond forming reactions, for example, have found broad utility in the preparation of pharmaceuticals, natural products, and specialty materials [64,65,66]. This ubiquitous class of transition-metal catalyzed reactions commonly involves the use of starting materials that are introduced as solids into chemical reactors. As part of the catalytic cycle, palladium precipitates as a colloid (e.g., palladium black) and insoluble inorganic halide salts are formed as by-products. The example of palladium-catalyzed amination is one of many methodologies in pharmaceuticals and fine chemicals that involve substrates, catalyst, and by-products that become insoluble during chemical transformations.
Microfluidic devices also find utility in operations involving insoluble biomolecules, cells, and the synthesis of nanocrystals. The continuous separation of blood cells from lipids [19,20,22] or operations involving proteins [67,68] creates the potential for adhesion and/or agglomeration. The microfluidic synthesis of inorganic nanocrystals (e.g., CdSe nanoparticles) [58,61,69] has also been demonstrated to improve material properties, yet the continuous production creates the potential for reactor accumulation.
Microreactors can be used to accurately and rapidly extract the intrinsic kinetic information needed to scale-up microfluidic processes from the laboratory to intermediary and full production. Strategies are therefore needed to take advantage of microreactors for continuing discovery and development. Choosing the appropriate strategy depends on the chemistry and the physics of particle interactions that lead to clogging events.

3. Particle Formation, Stability, and Accumulation Considerations

3.1. Nucleation Theory

The root of the clogging problem in microfluidics begins with events that take place at the molecular scale, while keeping in mind that much larger scales of tens-to-hundreds of microns ultimately result in device failures. If the thermodynamics predict reactive particle formation, then nucleation theory is the appropriate starting point to understand how to control particles in microfluidics [15,34,35,36,70]. The solubility product of each compound should be estimated for a given reaction solvent and the corresponding supersaturation ratio, the driving force for nucleation, approximated. Precipitation can be anticipated when supersaturation exists, where the primary rate of nucleation is dependent on the induction time; the time from when supersaturated conditions have been achieved to the appearance of the first detectable nucleus. It is common for nucleation kinetic predictions to vary by orders of magnitude due to heterogeneous nucleation and other molecular level variations. The presence of impurities, the reactor surface characteristics, axial and radial concentration and temperature gradients, and molecular interactions between compounds can all influence the prediction of the nucleation kinetics. If a reasonable estimate for the induction time has been experimentally validated, then a quantity useful in evaluating the potential for reactor fouling is the ratio of the induction time, tind, relative to the time necessary for a molecule to flow from the entrance to the exit of a reactor (i.e., the residence time τ), α, which can be expressed as [62]:
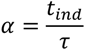
Challenges 03 00194 i001
Such a dimensionless quantity is, as a worst case, useful for reducing the risk of particle accumulation on continuous reactor surfaces. In continuous operation, the large surface-to-volume ratios of microreactors are exposed to infinite residence time. Evaluation of Equation (1) can offer insight, from a heterogeneous nucleation perspective, on whether or not production goals can be met before any material accumulation begins. Classical nucleation theory and extensive models derived from it have been developed for inorganic and organic crystallization [71,72,73,74].

3.2. Particle Inertia

A reasonable starting point once bulk particles grow to a critical size (or in the absence of particle growth) is the consideration of inertial forces, which influence the motions of particles in microscale laminar flow. Stokes number, the ratio of the viscous to the inertial forces acting on a flowing particle, written as [75]
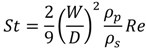
Challenges 03 00194 i002
can be estimated to approximate the potential for particle-to-wall interactions. When St < 1, particles do not spend enough time in the vicinity of a microchannel wall to undergo inertial impaction. When St > 1, particle trajectories along streamlines are modified and collisions with microreactor walls possible. When the inertial forces are favorable for impaction, or the onset of crystal growth on reactor surfaces takes place, estimation of the constriction rate, rc, gives the ratio of the constriction rate to the convective transport rate through the reactor and in the axial direction, written as
Challenges 03 00194 i003
Equation (3) is useful to approximate the accumulation time scale relative to the residence time, which similar to Equation (1) can help to identify a process window in which the accumulation influences production. Comprehensive understanding of each materials class, crystalline or amorphous and organic or inorganic, is needed to most appropriately engineer continuous reactors that undergo steady-state operation while manufacturing microfluidic products.

3.3. Colloidal Attraction and Repulsion Physics

Colloidal attraction and repulsion theory describes the significance of sub-micron particle interaction energies and their role on aggregate formation and/or wall deposition. Consider two colloidal particles flowing along laminar streamlines in a microfluidic device (i.e., Reynolds number (Re) < 1000) and in the axial direction (i.e., the z-direction) according to Figure 1. Neglecting body forces such as gravity, an assumption that generally holds for sub-micron particles, approximates the settling time relative to the axial particle motion through the microfluidic device to be large. Thus, particle-to-particle, particle-to-wall, and hydrodynamic interactions represent the dominant forces acting on each particle, as illustrated in Figure 1.
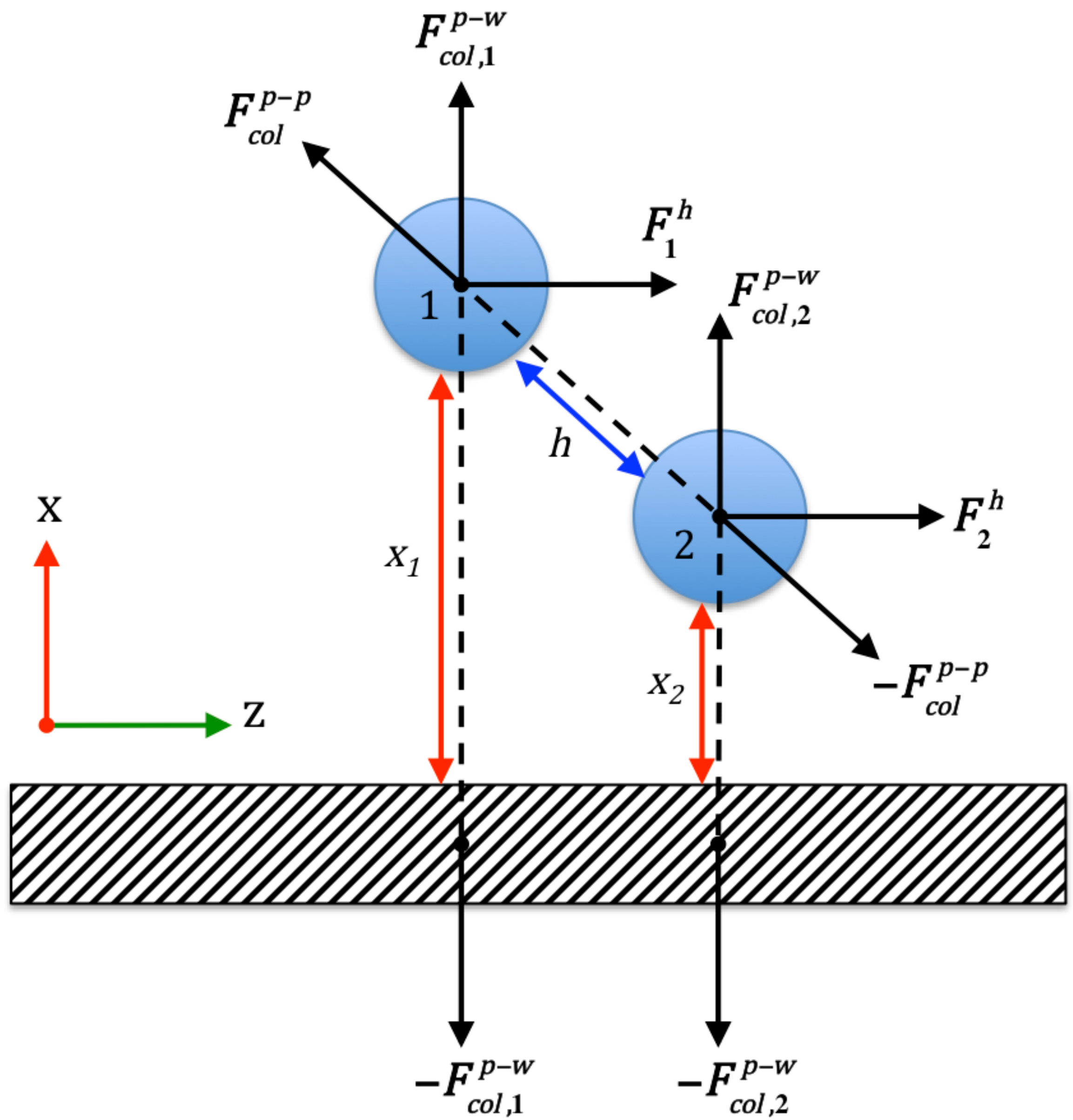
Challenges 03 00194 g001 1024
Figure 1. Colloidal and hydrodynamic forces acting on two spheres in laminar flow near the surface of a microfluidic device.
Figure 1. Colloidal and hydrodynamic forces acting on two spheres in laminar flow near the surface of a microfluidic device.
Challenges 03 00194 g001
The total particle-to-particle colloidal force, Fcolp-p, is made up of three components with the first being van der Waals attraction for particles of identical surface chemistry, VA(h), [76,77]
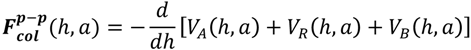
Challenges 03 00194 i004
The particle-to-particle colloidal force is also a function of the electrostatic interaction energy, VR(h), [75] and the Born interaction energy, VB(h) [78]. Each of the three interaction energies are influenced by the interparticle distance, h, and the particle diameters, a. When particle-to-wall attraction or repulsion exists, quite possible in complex synthesis routes that often involve ionic species, the particle-to-wall colloidal force should be considered, Fcolp-w, expressed in terms of the electrostatic free energy (GR) [79] and the free energy of adhesion (GA) [80], by
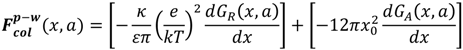
Challenges 03 00194 i005
where κ is the Debye parameter, ε the permittivity, k Boltzmann constant, e the electronic charge, T the temperature, and x0 the minimum equilibrium distance between the particle and the wall. Here, note that the particle-to-wall separation distance, x, influences the magnitude of the force, and thus only particles flowing near the reactor wall are expected to encounter such an energy field. Although our example is a simplified scenario, estimation of the magnitudes of the particle-to-particle and the particle-to-wall interaction forces yields important information for the design of continuous reactor operating conditions. As an example, the ratio of the interparticle and the particle-to-wall colloidal attraction magnitudes,
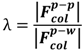
Challenges 03 00194 i006
offers mechanistic understanding of the potential solids handling challenges. When λ > 1, aggregation may take place, leading to microscopic blockages. When λ < 1, there exists the potential for the accumulation of particles on surfaces. In a system of particles, Equation (6) can be expressed as the sum of the particle-to-particle and particle-to-wall attractive interactions. A force balance in equilibrium and without gravitational forces can be rearranged as
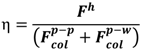
Challenges 03 00194 i007
One observes that η< −1 when the net hydrodynamic force acting on a particle exceeds the colloidal forces. For η > −1 values, low Reynolds number flow for instance, colloidal particle forces can generate agglomerates or accumulate on microreactor surfaces. The relationship of Equation (7), however, yields a deeper understanding when a comparison of the important time scales is made. When α< 1, defining the work time for each force reveals the expression,
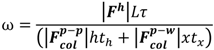
Challenges 03 00194 i008
The hydrodynamic work time relative to the colloidal attraction work time, ω, only considering particle attraction, describes the probability of either aggregation or wall accumulation in terms of the overall residence time. For example, when λ ~ 1 and tx >> th (or the distance x >> h), then ωw = (|Fh|Lτ)/(|Fcolp-w|xtx) and ωw values < 1 imply that particles are transported axially throughout a microreactor before accumulation has had enough time to occur. Similarly, when λ~1 and th >> tx (or the distance h >> x), then ωp = (|Fh|Lτ)/(|Fcolp-p|hth) and ωp values < 1 imply that particles are transported axially throughout a microreactor before aggregation has had enough time to occur. Such a relationship is critical in understanding when particle aggregates that remain in the bulk flow exit a microreactor in time to eliminate any pressure losses. Additional theoretical models relating particle aggregation physics can be applied to predict the growth rates for a population of suspended particles.

3.4. Bridging, Constriction, and Random Detachment

Three fundamentally different mechanisms, (1) bridging, (2) constriction, or (3) random detachment, can result in pressure losses during the micro-to-meso-scale laminar flow of particulates. A combination of any of the three mechanisms can propagate when chemical reactions occur. Each of the three mechanisms may also arise in the absence of particle formation or growth.
Particle motions tracking lamellae are possible when the net hydrodynamic forces are greater than the colloidal and inertial forces (i.e., η < −1, ω < 1, and St < 1). A reduction in the cross-sectional flow path under such conditions can lead to the simultaneous arrival of particles at the constriction point, and in turn generate bridging events; a statistical or velocity controlled phenomenon depending on the operating regime [76,81]. Bridging can also occur in the absence of reduced cross-sections. As shown in Figure 2a, bridging constrains fluid flow (not considering attraction or repulsion) for channel width-to-particle size aspect ratios, D/a < 10. The bridging, also shown in the microreactor image of Figure 2b for NaCl formation, is imminent when St > 1, η > −1, and ω > 1. Under such conditions particles traveling near the reactor wall deposit, forming dendrites that eventually bridge.
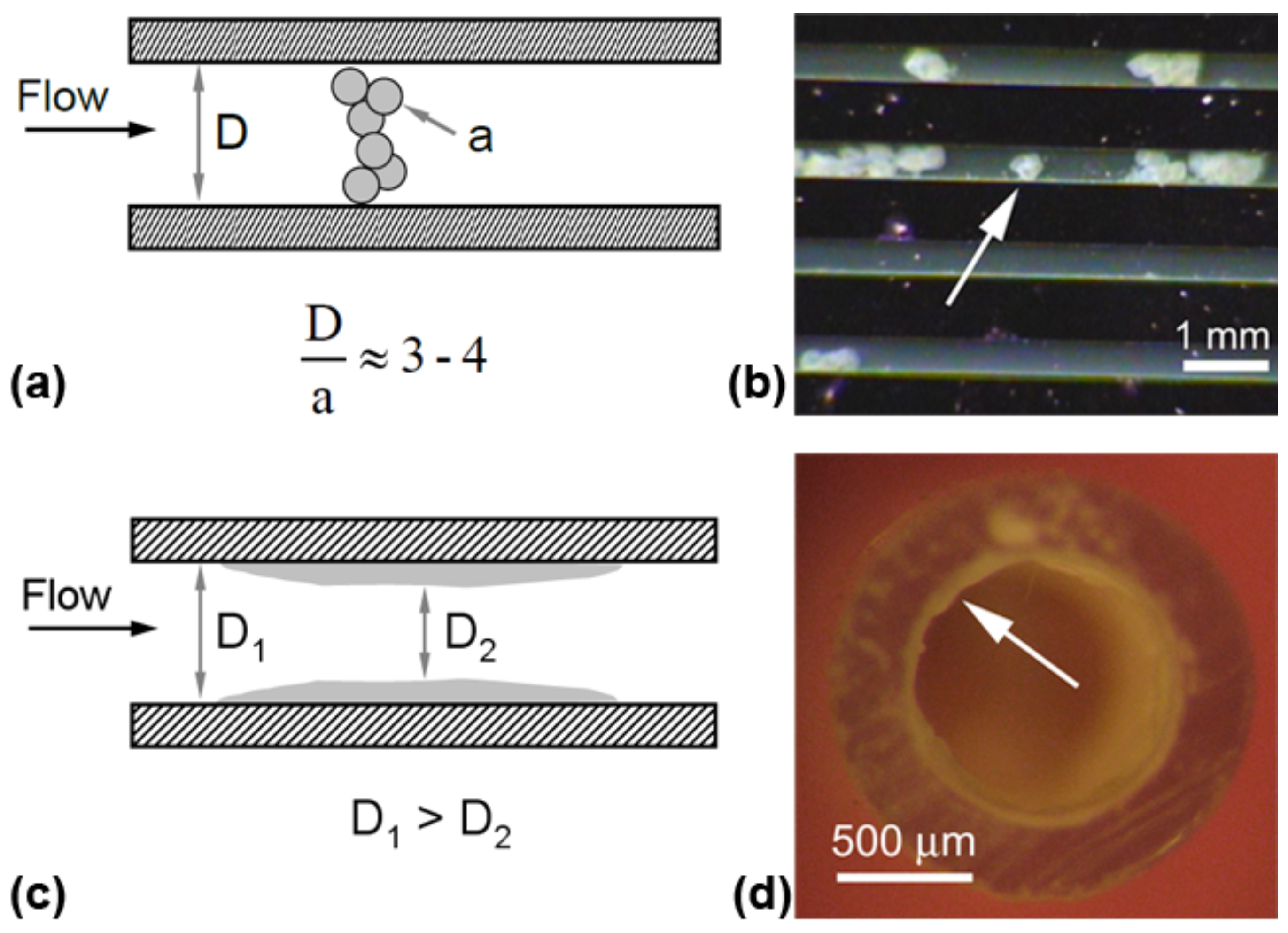
Challenges 03 00194 g002 1024
Figure 2. Example plugging mechanisms that occur in micro-scale laminar flow. (a) Particle bridging constrains fluid flow when the aspect ratio of the channel width to the particle sizes is about 3–7. (b) The bridging of NaCl crystals in a microreactor has been observed to occur while performing palladium-catalyzed bond forming reactions. (c) The microreactor cross-section is reduced, or constricted, when wall deposition or nucleation occurs, which also has been observed during (d) reactive NaCl precipitation in fluoropolymer capillaries. (Reprinted with permission from Reference [35] Copyright 2010 American Chemical Society).
Figure 2. Example plugging mechanisms that occur in micro-scale laminar flow. (a) Particle bridging constrains fluid flow when the aspect ratio of the channel width to the particle sizes is about 3–7. (b) The bridging of NaCl crystals in a microreactor has been observed to occur while performing palladium-catalyzed bond forming reactions. (c) The microreactor cross-section is reduced, or constricted, when wall deposition or nucleation occurs, which also has been observed during (d) reactive NaCl precipitation in fluoropolymer capillaries. (Reprinted with permission from Reference [35] Copyright 2010 American Chemical Society).
Challenges 03 00194 g002
Fluid flow may also be constrained when microreactor cross-sections diminish with time, [82] illustrated in Figure 2(c,d). The constriction occurs when particles deposit on surfaces or when nucleation followed by growth takes place. In either scenario, wall build-ups present a challenge to continuous production in microfluidic systems because process shutdowns are needed to remediate accumulated material. The random detachment of the accumulated material, another potential challenge, is virtually unpredictable yet can generate macroscopic blockages that severely limit fluid flow.

4. Techniques to Control Particle Transport

When particle-to-particle or particle-to-wall attraction exists, nano-to-micro-scale phenomena, the bridging or constrictions of microfluidic flow paths are imminent. The nucleation and growth of clusters in the bulk or on device surfaces, a molecular scale problem, can result in the bridging or the constriction as well. Either mechanism, from the molecular to the micro-scale, requires the conception of engineering techniques to control particle transport. Such techniques generally fit into one of two categories: (1) passive particle manipulation or (2) active particle manipulation.

4.1. Passive Particle Manipulation

Passive techniques are those that do not impose any external forces beyond the steady-state energy required to commence and sustain fluid flow. Hydrodynamic flow focusing, an example of passive particle manipulation, has been demonstrated as an effective technique to order micron-sized particles in microfluidics. The streaming of particle suspensions (e.g., polystyrene microspheres) is made possible via flow through spiral geometries that establish Dean flow [83]. The existence of hydrodynamic force vectors tangential to the flow cross-section enables centerline particle equilibrium (i.e., the ratio of the inertial lift to the drag force magnitudes is optimized), and thus the longitudinal ordering and lateral flow focusing of random particles is possible [83]. The Dean number, expressed as
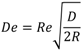
Challenges 03 00194 i009
estimates the existence of cross-sectional velocity components where R is the radius of microchannel curvature. In straight microchannels, De = 0, indicating the absence of a drag force due to the transverse Dean flows [83]. The magnitude of the transverse Dean flow increases, as seen in Equation (9), with a decreasing radius of curvature, and thus the microchannel geometry can be microfabricated to spatially position particles of different momentums [47]. A challenge with passive flow focusing, however, is its ability to manage particle concentrations encountered in fine chemical production when particle-to-particle and particle-to-wall attraction exists (i.e., η > −1, and ω > 1). Furthermore, particle momentum can lead to migration across streamlines, creating particle-to-particle and particle-to-wall collisions.
The isolation of particles that tend to agglomerate or stick to surfaces has been accomplished by the encapsulation of reactions within dispersed droplets, as highlighted in Figure 3(a,b). Protein crystals (Figure 3a), [67] or other insoluble compounds such as polymers (Figure 3b), [38,39] are limited in their interaction with microchannel surfaces in the presence of an immiscible barrier between the phases. Interestingly, immiscible gas-liquid interfaces [84,85,86] have been demonstrated as possible separation techniques; micron-sized particles accumulate at the lower surface-free-energy interfaces (see Figure 3c) [87,88,89]. In a system of excess particles, shown in Figure 3d, armored bubbles form when liquid-liquid immiscible interfaces are occupied entirely by particulates [90,91]. Establishing the equilibrium illustrated in Figure 3d is possible when the colloidal forces are stabilized, which depends on the ionic strength of the liquid media; an important design consideration and a challenge to control in complex heterogeneous reaction pathways exposed to convective forces.
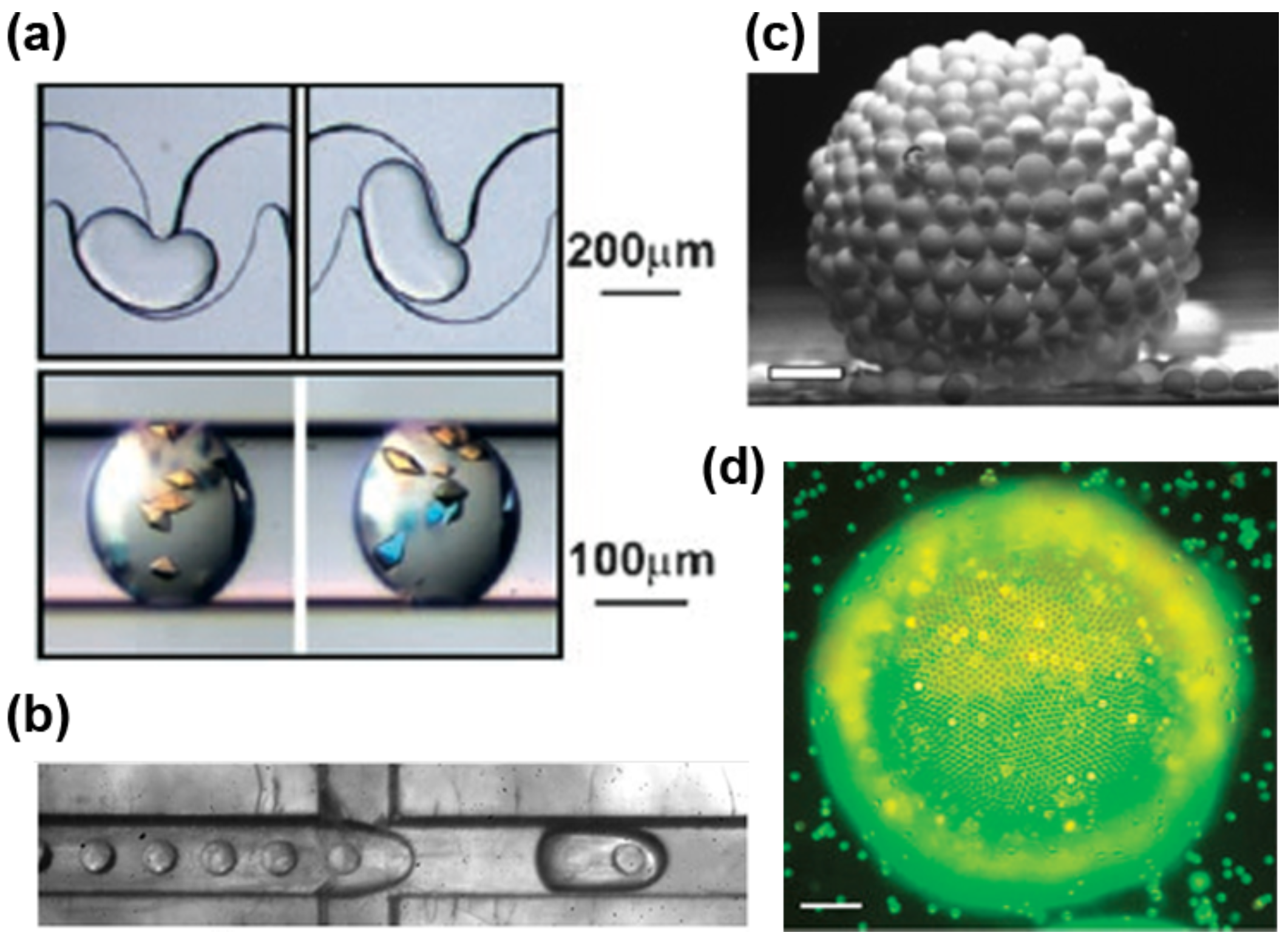
Challenges 03 00194 g003 1024
Figure 3. Examples of passive techniques engineered to control particles in microscale laminar flow. Immiscible liquid-liquid flows enable the encapsulation of solids within dispersed droplets and thereby limit the particle-to-wall interactions, shown for (a) protein crystals (Reprinted with permission from Reference [67] Copyright 2005 American Chemical Society) and (b) polymers (Copyright Wiley-VCH Verlag GmbH & Co. KGaA, reproduced with permission) [39]. Immiscible interfaces also provide lower surface free energy sites for particles to accumulate, thus (c) collecting particles at gas-liquid interfaces (scale bar = 400 μm) (Reprinted with permission from Reference [88] Copyright 2006 American Chemical Society)and/or (d) creating armored bubbles is possible (scale bar = 60 μm) (Reprinted by permission from Macmillan Publishers Ltd: Nature Materials [90], copyright 2005).
Figure 3. Examples of passive techniques engineered to control particles in microscale laminar flow. Immiscible liquid-liquid flows enable the encapsulation of solids within dispersed droplets and thereby limit the particle-to-wall interactions, shown for (a) protein crystals (Reprinted with permission from Reference [67] Copyright 2005 American Chemical Society) and (b) polymers (Copyright Wiley-VCH Verlag GmbH & Co. KGaA, reproduced with permission) [39]. Immiscible interfaces also provide lower surface free energy sites for particles to accumulate, thus (c) collecting particles at gas-liquid interfaces (scale bar = 400 μm) (Reprinted with permission from Reference [88] Copyright 2006 American Chemical Society)and/or (d) creating armored bubbles is possible (scale bar = 60 μm) (Reprinted by permission from Macmillan Publishers Ltd: Nature Materials [90], copyright 2005).
Challenges 03 00194 g003

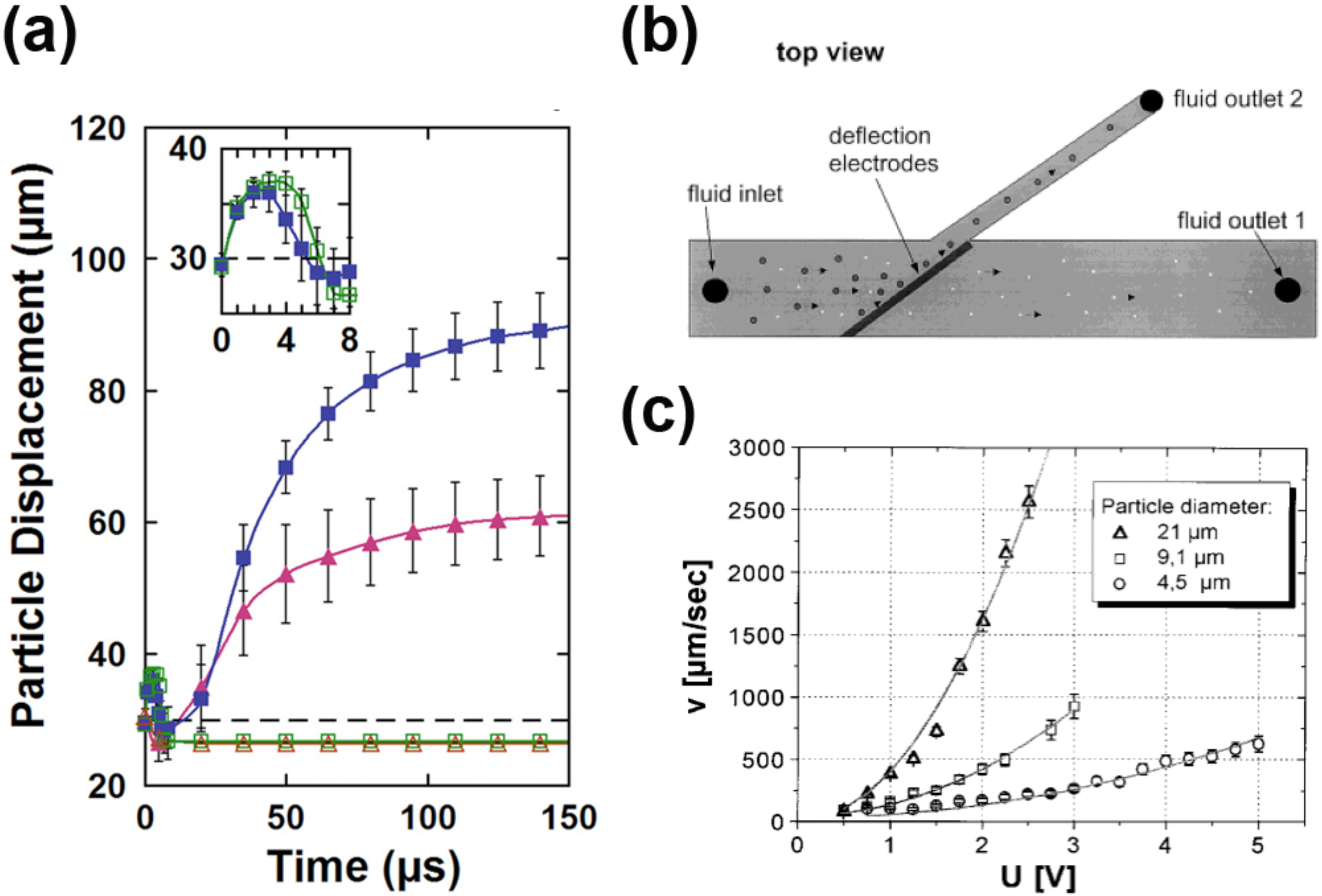
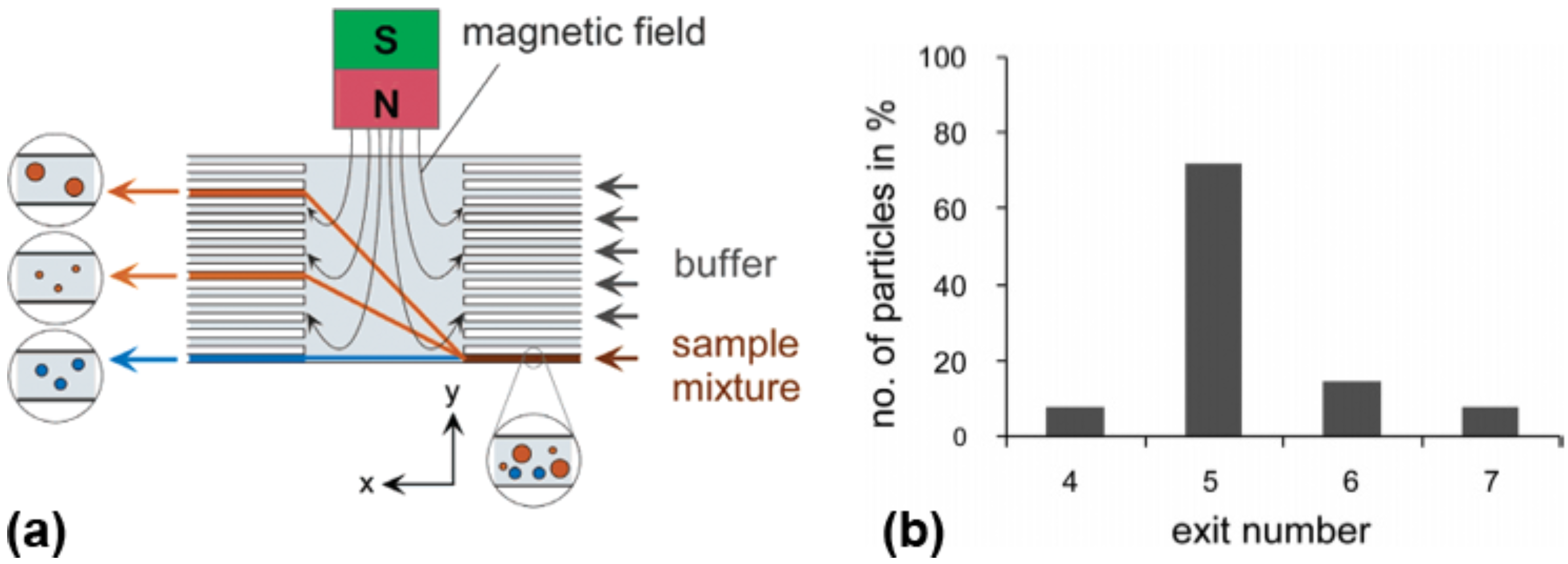
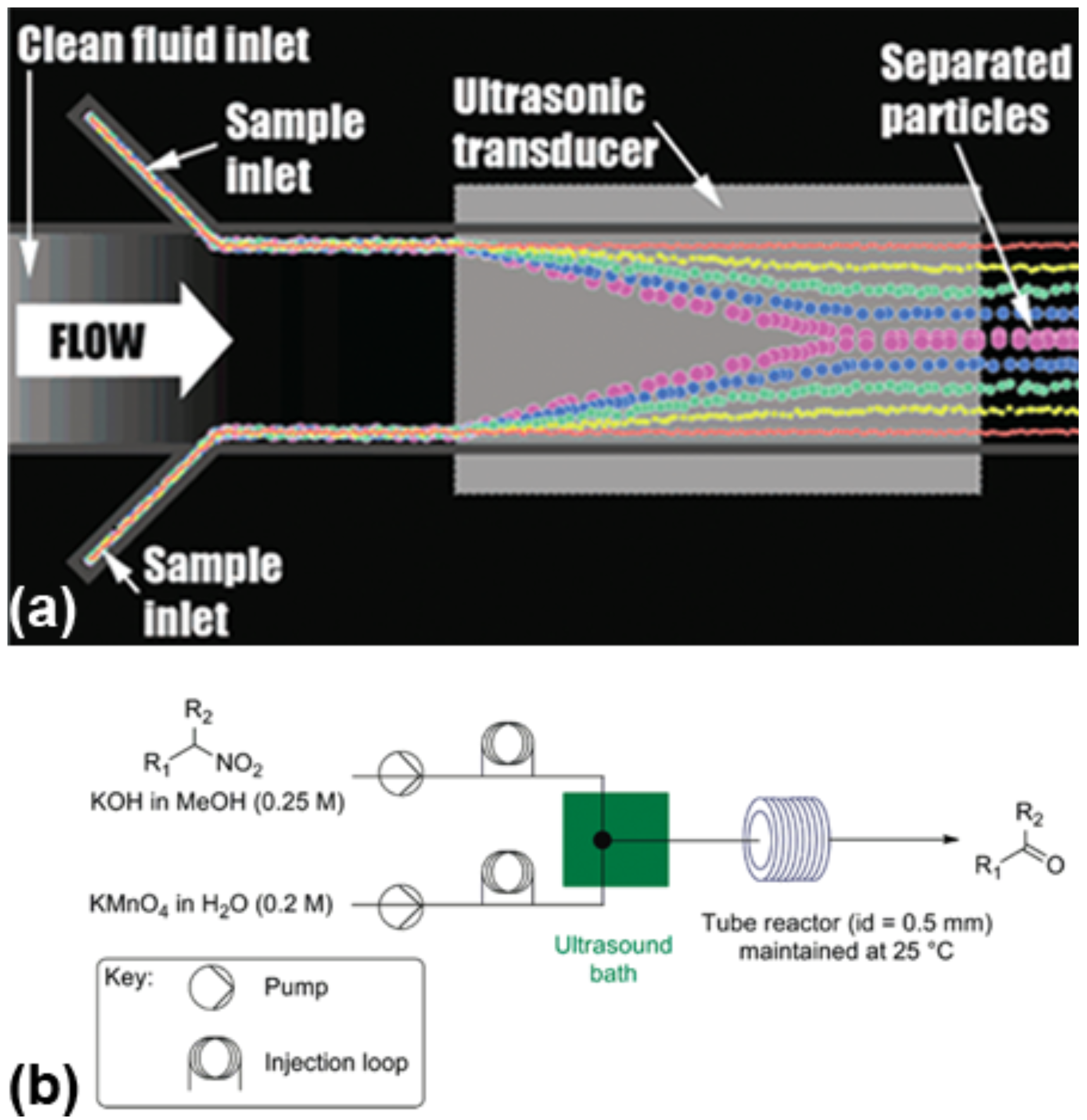
4.2. Active Particle Manipulation

Active particle techniques involve external forces beyond the steady-state energy required to commence and sustain fluid flow. Pulse flow could be considered an active particle manipulation technique and has been exploited to engineer dry powder injections within microfluidic devices [31]. For D/a aspect ratios that do not bridge, inert gas has been used to carry dry pharmaceutical powders within microscale devices [31]. The working principle allows the formation of a fluidized particle bed in microfluidics when particle-to-particle attractive interactions do not exist [31].
The use of light and electron gradients also represents active particle manipulation techniques. For example, optical particle displacement has been accomplished by generating bubbles with sufficiently intense laser light [92]. Single and tandem bubbles generated by infrared and green lasers displaced particles such as polystyrene microspheres [92]. As shown in Figure 4a, particles were displaced tens-of-microns and within microseconds [92]. Optical force switching, another active technique utilizing light, has been engineered for the microfluidic separation of mammalian cells [93]. The diminishing light intensity with increasing cross-sectional dimensions presents a challenge, in general, for scaling up optical particle control techniques, especially when considering fine chemical manufacturing. Dielectrophoretic particle separations and cell isolations are also possible when an electric field is imposed upon a system of charged particles traveling through a microfluidic device. The governing principles that establish a force balance for the steady-state separation of particles have previously been described [41,94]. As seen in the schematic of Figure 4b, the fabrication of devices with deflection electrodes enables particle sorting where the threshold velocity for the displacement of different sized latex microspheres scales with the voltage amplitude (Figure 4c) [94].
Challenges 03 00194 g004 1024
Figure 4. (a) Laser light driven particle displacements made possible through the generation of single and tandem bubbles (Reprinted with permission from [92]. Copyright 2010, American Institute of Physics). (b) Dielectrophoretic particle sorting by the microfabrication of deflection electrodes. (c) The threshold velocity for the displacement of different sized latex microspheres scales with the voltage amplitude. (Copyright Wiley-VCH Verlag GmbH & Co. KGaA, reproduced with permission) [94].
Figure 4. (a) Laser light driven particle displacements made possible through the generation of single and tandem bubbles (Reprinted with permission from [92]. Copyright 2010, American Institute of Physics). (b) Dielectrophoretic particle sorting by the microfabrication of deflection electrodes. (c) The threshold velocity for the displacement of different sized latex microspheres scales with the voltage amplitude. (Copyright Wiley-VCH Verlag GmbH & Co. KGaA, reproduced with permission) [94].
Challenges 03 00194 g004
Magnetism, another active technique, also enables the separation of particulates in microfluidics [2,24,30,32,33,95,96]. When particles flow by a magnetic field (see Figure 5a), the magnetically induced velocity vector, umag, is described by the magnetic force, Fmag, exerted on the particle relative to the viscous drag force, Fvis, by [30]
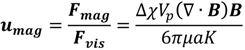
Challenges 03 00194 i010
where Δχ is the magnetic susceptibility difference between the particle and the liquid medium, Vp the particle volume, B the externally applied magnetic flux density, ∇B the flux density gradient, μ the liquid viscosity, and K the permeability of a vacuum [30]. One can infer from Equation (10) that magnetically driven particle motions occur when the magnitude of the magnetic force exceeds the viscous force. Equation (10) additionally illustrates the critical dependence of magnetically driven particle separations on the particle radius, a, and the magnetic characteristics of the particle (i.e., Δχ by χp). There exists potential for magnetic separations in fine chemical and some inorganic crystal manufacturing. Aggregates (i.e., agglomerates) behave as larger particle sizes in a magnetic field, and thus the continuous, laminar separation of the aggregates is possible [30]. In practice, a distribution of particle sizes (superparamagnetic particles, e.g., Dynabeads), shown in Figure 5b, were deflected each corresponding to the parallel outlets of Figure 5b [30]. Scaling up magnetic particle separations for the continuous flow manufacturing of many microfluidic processes remains a challenge as the viscous force magnitude increases with Re and the delivery of adequate magnetic fields, a capital cost consideration, requires design innovations.
Challenges 03 00194 g005 1024
Figure 5. (a) Microfluidic separation of superparamagnetic particles in the presence of a magnetic field. (b) The collection of particles exiting the device enables the isolation of the fraction of particles deflected by magnetism.(Reprinted with permission from Reference [30] Copyright 2004 American Chemical Society).
Figure 5. (a) Microfluidic separation of superparamagnetic particles in the presence of a magnetic field. (b) The collection of particles exiting the device enables the isolation of the fraction of particles deflected by magnetism.(Reprinted with permission from Reference [30] Copyright 2004 American Chemical Society).
Challenges 03 00194 g005
It is also readily known that acoustic waves displace particles traveling along lamellae [18,20,21,22,23,25,26,27,97,98,99,100,101,27,97]. High frequency (e.g., MHz) acoustic standing waves force particles to pressure nodes in laminar flow, which has been demonstrated for the separation of red blood cells from lipids [23,25,26,102]. A particle traveling through an acoustic standing wave experiences a primary force, Fa1, described by
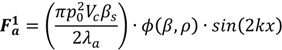
Challenges 03 00194 i011
where p0 is the acoustic pressure amplitude, Vc the particle volume, λa the acoustic wavelength, k the wavenumber, and x the distance from a pressure node. The primary force is considered significant when a phase difference parameter, φ, expressed as
Challenges 03 00194 i012
is non-zero [23,25,26,102]. The terms ρi and βi are the density and compressibility of the solvent (s) and the particle (p), respectively.When particle diameters are less than half the wavelength, the acoustic streaming of suspended particles is possible on-chip, shown in Figure 6a, by integrating ultrasonic transducers with microfluidic devices. Secondary forces, also significant when a concentrated system of particles scatters acoustic standing waves, have been described in a more detailed review [22].
Acoustic waveforms in the range of kHz, for example ultrasonic cleaning equipment, have been demonstrated as effective in carrying out microchemical transformations that generate solids [15,35,64]. On-chip ultrasound has been engineered to manage the NaCl formation during palladium-catalyzed bond forming reactions [13]. As an example, the by-product MnO2 formed during the Nef oxidation leads to flow-induced clogging, which can be prevented using ultrasound (shown in Figure 6b) [103]. Overall, the integration of acoustics with microreactors has tremendous potential that fosters a need for scale-up innovations.
Challenges 03 00194 g006 1024
Figure 6. (a) The separation of microparticles via acoustic streaming in microfluidics (Reprinted with permission from [25]. Copyright 2007 American Chemical Society). (b) Performing solids forming reactions, such as the nef oxidation, in the presence of ultrasound has been shown to mitigate flow-induced clogging (Reprinted with permission from [103]. Copyright 2010 American Chemical Society).
Figure 6. (a) The separation of microparticles via acoustic streaming in microfluidics (Reprinted with permission from [25]. Copyright 2007 American Chemical Society). (b) Performing solids forming reactions, such as the nef oxidation, in the presence of ultrasound has been shown to mitigate flow-induced clogging (Reprinted with permission from [103]. Copyright 2010 American Chemical Society).
Challenges 03 00194 g006
Advancements continue to be made towards the innovation of new techniques for solids handling in microreactors. Continuous-stirred tank reactors and mechanically agitated flow cells [104] have been demonstrated as effective methods to carry out particle forming reactions. Nevertheless, the design of solids handling reactors only represents part of the challenge; an entire chemical process is made up of many different unit operations each where solids in continuous flow could be problematic.

5. Outlook and Challenges

The thermodynamic and the kinetic conditions that make solids formation probable necessitate understanding of the relative time scales in continuous flow microreactors. Such understanding is also needed when particles undergo laminar flow through microfluidic devices. Engineering techniques to control particles, whether generated or not, requires the consideration of particle-to-particle and particle-to-wall attraction and repulsion. Overcoming particle-to-wall attraction that results in accumulation is possible through the evaluation of the force magnitudes acting on each particle. Minimizing particle aggregation leading to macroscopic blockages is possible by assessing particle-to-particle attraction in relationship to the residence time throughout a microreactor. The analogy is particularly useful in the design of continuous microreactors for chemical processes.
A number of creative passive and active techniques have been engineered for the manipulation of particles in microscale laminar flow, which have the potential to impact chemical processing. The integration of such techniques, however, is not without challenges. The majority of passive techniques do not solve the problem of particle aggregation or wall accumulation due to attraction. Similarly, scaling up active techniques introduces design challenges in terms of the imposed forces relative to the viscous and inertial forces. There remains tremendous opportunity for new approaches, building on existing solids handling strategies, to ensure that continuous microfluidic processes do not require remediation.

References

  1. Ottino, J.M.; Wiggins, S. Introduction: Mixing in microfluidics. Philos. Trans. R. Soc. A 2004, 362, 923–935. [Google Scholar] [CrossRef]
  2. Pamme, N. Magnetism and microfluidics. Lab Chip 2006, 6, 24–38. [Google Scholar] [CrossRef]
  3. Stone, H.A.; Stroock, A.D.; Ajdari, A. Engineering flows in small devices: Microfluidics toward a lab-on-a-chip. Ann. Rev. Fluid Mech. 2004, 36, 381–411. [Google Scholar] [CrossRef]
  4. Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef]
  5. Marre, S.; Jensen, K.F. Synthesis of micro and nanostructures in microfluidic systems. Chem. Soc. Rev. 2010, 39, 1183–1202. [Google Scholar] [CrossRef]
  6. El-Ali, J.; Sorger, P.K.; Jensen, K.F. Cells on chips. Nature 2006, 442, 403–411. [Google Scholar]
  7. Hartman, R.L.; Jensen, K.F. Microchemical systems for continuous-flow synthesis. Lab Chip 2009, 9, 2495–2507. [Google Scholar] [CrossRef]
  8. Jensen, K.F. Microreaction engineering—Is small better? Chem. Eng. Sci. 2001, 56, 293–303. [Google Scholar] [CrossRef]
  9. Atencia, J.; Beebe, D.J. Controlled microfluidic interfaces. Nature 2005, 437, 648–655. [Google Scholar] [CrossRef]
  10. Krishnadasan, S.; Brown, R.J.C.; Demello, A.J.; Demello, J.C. Intelligent routes to the controlled synthesis of nanoparticles. Lab Chip 2007, 7, 1434–1441. [Google Scholar] [CrossRef]
  11. Mukhopadhyay, R. When microfluidic devices go bad—How does fouling occur in microfluidic devices, and what can be done about it? Anal. Chem. 2005, 77, 429–432. [Google Scholar]
  12. Horie, T.; Sumino, M.; Tanaka, T.; Matsushita, Y.; Ichimura, T.; Yoshida, J. Photodimerization of maleic anhydride in a microreactor without clogging. Org. Proc. Res. Dev. 2010, 14, 405–410. [Google Scholar] [CrossRef]
  13. Kuhn, S.; Noel, T.; Gu, L.; Heider, P.L.; Jensen, K.F. A Teflon microreactor with integrated piezoelectric actuator to handle solid forming reactions. Lab Chip 2011, 11, 2488–2492. [Google Scholar]
  14. Nagasawa, H.; Mae, K. Development of a new microreactor based on annular microsegments for fine particle production. Ind. Eng. Chem. Res. 2006, 45, 2179–2186. [Google Scholar] [CrossRef]
  15. Noel, T.; Naber, J.R.; Hartman, R.L.; McMullen, J.P.; Jensen, K.F.; Buchwald, S.L. Palladium-catalyzed amination reactions in flow: Overcoming the challenges of clogging via acoustic irradiation. Chem. Sci. 2011, 2, 287–290. [Google Scholar]
  16. Poe, S.L.; Cummings, M.A.; Haaf, M.R.; McQuade, D.T. Solving the clogging problem: Precipitate-forming reactions in flow. Angew. Chem. Int. Ed. 2006, 45, 1544–1548. [Google Scholar]
  17. Pribyl, M.; Snita, D.; Marek, M. Nonlinear phenomena and qualitative evaluation of risk of clogging in a capillary microreactor under, imposed electric field. Chem. Eng. J. 2005, 105, 99–109. [Google Scholar] [CrossRef]
  18. Bengtsson, M.; Laurell, T. Ultrasonic agitation in microchannels. Anal. Bioanal. Chem. 2004, 378, 1716–1721. [Google Scholar] [CrossRef]
  19. Evander, M.; Johansson, L.; Lilliehorn, T.; Piskur, J.; Lindvall, M.; Johansson, S.; Almqvist, M.; Laurell, T.; Nilsson, J. Noninvasive acoustic cell trapping in a microfluidic perfusion system for online bioassays. Anal. Chem. 2007, 79, 2984–2991. [Google Scholar]
  20. Hawkes, J.J.; Barber, R.W.; Emerson, D.R.; Coakley, W.T. Continuous cell washing and mixing driven by an ultrasound standing wave within a microfluidic channel. Lab Chip 2004, 4, 446–452. [Google Scholar] [CrossRef]
  21. Hawkes, J.J.; Coakley, W.T. Force field particle filter, combining ultrasound standing waves and laminar flow. Sens. Act. B Chem. 2001, 75, 213–222. [Google Scholar] [CrossRef]
  22. Laurell, T.; Petersson, F.; Nilsson, A. Chip integrated strategies for acoustic separation and manipulation of cells and particles. Chem. Soc. Rev. 2007, 36, 492–506. [Google Scholar]
  23. Nilsson, A.; Petersson, F.; Jonsson, H.; Laurell, T. Acoustic control of suspended particles in micro fluidic chips. Lab Chip 2004, 4, 131–135. [Google Scholar] [CrossRef]
  24. Pamme, N. Continuous flow separations in microfluidic devices. Lab Chip 2007, 7, 1644–1659. [Google Scholar] [CrossRef]
  25. Petersson, F.; Aberg, L.; Sward-Nilsson, A.M.; Laurell, T. Free flow acoustophoresis: Microfluidic-based mode of particle and cell separation. Anal. Chem. 2007, 79, 5117–5123. [Google Scholar] [CrossRef]
  26. Petersson, F.; Nilsson, A.; Holm, C.; Jonsson, H.; Laurell, T. Continuous separation of lipid particles from erythrocytes by means of laminar flow and acoustic standing wave forces. Lab Chip 2005, 5, 20–22. [Google Scholar] [CrossRef]
  27. Petersson, F.; Nilsson, A.; Jonsson, H.; Laurell, T. Carrier medium exchange through ultrasonic particle switching in microfluidic channels. Anal. Chem. 2005, 77, 1216–1221. [Google Scholar]
  28. Dittrich, P.S.; Tachikawa, K.; Manz, A. Micro total analysis systems. Latest advancements and trends. Anal. Chem. 2006, 78, 3887–3907. [Google Scholar]
  29. Pamme, N.; Koyama, R.; Manz, A. Counting and sizing of particles and particle agglomerates in a microfluidic device using laser light scattering: Application to a particle-enhanced immunoassay. Lab Chip 2003, 3, 187–192. [Google Scholar] [CrossRef]
  30. Pamme, N.; Manz, A. On-chip free-flow magnetophoresis: Continuous flow separation of magnetic particles and agglomerates. Anal. Chem. 2004, 76, 7250–7256. [Google Scholar] [CrossRef]
  31. Vilkner, T.; Shivji, A.; Manz, A. Dry powder injection on chip. Lab Chip 2005, 5, 140–145. [Google Scholar] [CrossRef]
  32. Pamme, N.; Wilhelm, C. Continuous sorting of magnetic cells via on-chip free-flow magnetophoresis. Lab Chip 2006, 6, 974–980. [Google Scholar] [CrossRef]
  33. Rodriguez-Villarreal, A.I.; Tarn, M.D.; Madden, L.A.; Lutz, J.B.; Greenman, J.; Samitier, J.; Pamme, N. Flow focussing of particles and cells based on their intrinsic properties using a simple diamagnetic repulsion setup. Lab Chip 2011, 11, 1240–1248. [Google Scholar]
  34. Hartman, R.L. Managing solids in microreactors for the upstream continuous processing of fine chemicals. Org. Proc. Res. Dev. 2012. [Google Scholar]
  35. Hartman, R.L.; Naber, J.R.; Zaborenko, N.; Buchwald, S.L.; Jensen, K.F. Overcoming the challenges of solid bridging and constriction during Pd-catalyzed C-N bond formation in microreactors. Org. Proc. Res. Dev. 2010, 14, 1347–1357. [Google Scholar] [CrossRef]
  36. Kuhn, S.; Hartman, R.L.; Sultana, M.; Nagy, K.D.; Marre, S.; Jensen, K.F. Teflon-coated silicon microreactors: Impact on segmented liquid-liquid multiphase flows. Langmuir 2011, 27, 6519–6527. [Google Scholar]
  37. Honda, T.; Miyazaki, M.; Nakamura, H.; Maeda, H. Controllable polymerization of N-carboxy anhydrides in a microreaction system. Lab Chip 2005, 5, 812–818. [Google Scholar] [CrossRef]
  38. Li, W.; Pharn, H.H.; Nie, Z.; MacDonald, B.; Guenther, A.; Kumacheva, E. Multi-step microfluidic polymerization reactions conducted in droplets: The internal trigger approach. J. Am. Chem. Soc. 2008, 130, 9935–9941. [Google Scholar]
  39. Marcati, A.; Serra, C.; Bouquey, M.; Prat, L. Handling of polymer particles in microchannels. Chem. Eng. Tech. 2010, 33, 1779–1787. [Google Scholar] [CrossRef]
  40. Yamada, M.; Seki, M. Hydrodynamic filtration for on-chip particle concentration and classification utilizing microfluidics. Lab Chip 2005, 5, 1233–1239. [Google Scholar] [CrossRef]
  41. Kralj, J.G.; Lis, M.T.W.; Schmidt, M.A.; Jensen, K.F. Continuous dielectrophoretic size-based particle sorting. Anal. Chem. 2006, 78, 5019–5025. [Google Scholar]
  42. Hessel, V. Novel process windows—Gate to maximizing process intensification via flow chemistry. Chem. Eng. Technol. 2009, 32, 1655–1681. [Google Scholar] [CrossRef]
  43. Kockmann, N.; Gottsponer, M.; Roberge, D.M. Scale-up concept of single-channel microreactors from process development to industrial production. Chem. Eng. J. 2011, 167, 718–726. [Google Scholar] [CrossRef]
  44. Roberge, D.M.; Zimmermann, B.; Rainone, F.; Gottsponer, M.; Eyholzer, M.; Kockmann, N. Microreactor technology and continuous processes in the fine chemical and pharmaceutical industry: Is the revolution underway? Org. Proc. Res. Dev. 2008, 12, 905–910. [Google Scholar] [CrossRef]
  45. Adamo, A.; Jensen, K.F. Microfluidic based single cell microinjection. Lab Chip 2008, 8, 1258–1261. [Google Scholar] [CrossRef]
  46. Huh, D.; Gu, W.; Kamotani, Y.; Grotberg, J.B.; Takayama, S. Microfluidics for flow cytometric analysis of cells and particles. Physiol. Meas. 2005, 26, R73–R98. [Google Scholar] [CrossRef]
  47. Kuntaegowdanahalli, S.S.; Bhagat, A.A.S.; Kumar, G.; Papautsky, I. Inertial microfluidics for continuous particle separation in spiral microchannels. Lab Chip 2009, 9, 2973–2980. [Google Scholar] [CrossRef]
  48. Salieb-Beugelaar, G.B.; Simone, G.; Arora, A.; Philippi, A.; Manz, A. Latest developments in microfluidic cell biology and analysis systems. Anal. Chem. 2010, 82, 4848–4864. [Google Scholar] [CrossRef]
  49. Bruzewicz, D.A.; McGuigan, A.P.; Whitesides, G.M. Fabrication of a modular tissue construct in a microfluidic chip. Lab Chip 2008, 8, 663–671. [Google Scholar] [CrossRef]
  50. Marcy, Y.; Ishoey, T.; Lasken, R.S.; Stockwell, T.B.; Walenz, B.P.; Halpern, A.L.; Beeson, K.Y.; Goldberg, S.M.D.; Quake, S.R. Nanoliter reactors improve multiple displacement amplification of genomes from single cells. PLoS Genet. 2007, 3, 1702–1708. [Google Scholar]
  51. Kortmann, H.; Blank, L.M.; Schmid, A. Single Cell Analytics: An Overview. In High Resolution Microbial Single Cell Analytics; Muller, S., Bley, T., Eds.; Springer-Verlag Berlin: Berlin, Germany, 2011; Volume 124, pp. 99–122. [Google Scholar]
  52. Schmid, A.; Kortmann, H.; Dittrich, P.S.; Blank, L.M. Chemical and biological single cell analysis. Curr. Opin. Biotechnol. 2010, 21, 12–20. [Google Scholar] [CrossRef]
  53. Jaggi, R.D.; Sandoz, R.; Effenhauser, C.S. Microfluidic depletion of red blood cells from whole blood in high-aspect-ratio microchannels. Microfluid. Nanofluid. 2007, 3, 47–53. [Google Scholar]
  54. Pommer, M.S.; Zhang, Y.T.; Keerthi, N.; Chen, D.; Thomson, J.A.; Meinhart, C.D.; Soh, H.T. Dielectrophoretic separation of platelets from diluted whole blood in microfluidic channels. Electrophoresis 2008, 29, 1213–1218. [Google Scholar] [CrossRef]
  55. Chabert, M.; Viovy, J.L. Microfluidic high-throughput encapsulation and hydrodynamic self-sorting of single cells. Proc. Natl. Acad. Sci. USA 2008, 105, 3191–3196. [Google Scholar] [CrossRef]
  56. Dorvee, J.R.; Sailor, M.J.; Miskelly, G.M. Digital microfluidics and delivery of molecular payloads with magnetic porous silicon chaperones. Dalton Trans. 2008, 721–730. [Google Scholar]
  57. Hung, L.H.; Choi, K.M.; Tseng, W.Y.; Tan, Y.C.; Shea, K.J.; Lee, A.P. Alternating droplet generation and controlled dynamic droplet fusion in microfluidic device for CdS nanoparticle synthesis. Lab Chip 2006, 6, 174–178. [Google Scholar] [CrossRef]
  58. Nakamura, H.; Yamaguchi, Y.; Miyazaki, M.; Maeda, H.; Uehara, M.; Mulvaney, P. Preparation of CdSe nanocrystals in a micro-flow-reactor. Chem. Commun. 2002, 2844–2845. [Google Scholar]
  59. Edel, J.B.; Fortt, R.; de Mello, J.C.; de Mello, A.J. Microfluidic routes to the controlled production of nanoparticles. Chem. Commun. 2002, 1136–1137. [Google Scholar]
  60. Khan, S.A.; Jensen, K.F. Microfluidic synthesis of titania shells on colloidal silica. Adv. Mat. 2007, 19, 2556–2560. [Google Scholar] [CrossRef]
  61. Yen, B.K.H.; Gunther, A.; Schmidt, M.A.; Jensen, K.F.; Bawendi, M.G. A microfabricated gas-liquid segmented flow reactor for high-temperature synthesis: The case of CdSe quantum dots. Angew. Chem. Int. Ed. 2005, 44, 5447–5451. [Google Scholar] [CrossRef]
  62. Hartman, R.L. Managing solids in microreactors for the upstream continuous processing of fine chemicals. Org. Proc. Res. Dev. 2012. [Google Scholar]
  63. Roberge, D.M.; Ducry, L.; Bieler, N.; Cretton, P.; Zimmermann, B. Microreactor technology: A revolution for the fine chemical and pharmaceutical industries? Chem. Eng. Technol. 2005, 28, 318–323. [Google Scholar] [CrossRef]
  64. Noel, T.; Buchwald, S.L. Cross-coupling in flow. Chem. Soc. Rev. 2011, 40, 5010–5029. [Google Scholar] [CrossRef]
  65. Surry, D.S.; Buchwald, S.L. Biaryl phosphane ligands in palladium-catalyzed amination. Angew. Chem. Int. Ed. 2008, 47, 6338–6361. [Google Scholar]
  66. Suzuki, A. Cross-coupling reactions of organoboranes: An easy way to construct C–C bonds (Nobel Lecture). Angew. Chem. Int. Ed. 2011, 50, 6722–6737. [Google Scholar] [CrossRef]
  67. Chen, D.L.; Gerdts, C.J.; Ismagilov, R.F. Using microfluidics to observe the effect of mixing on nucleation of protein crystals. J. Am. Chem. Soc. 2005, 127, 9672–9673. [Google Scholar]
  68. Koc, Y.; de Mello, A.J.; McHale, G.; Newton, M.I.; Roach, P.; Shirtcliffe, N.J. Nano-scale superhydrophobicity: Suppression of protein adsorption and promotion of flow-induced detachment. Lab Chip 2008, 8, 582–586. [Google Scholar] [CrossRef]
  69. Marre, S.; Park, J.; Rempel, J.; Guan, J.; Bawendi, M.G.; Jensen, K.F. Supercritical continuous-microflow synthesis of narrow size distribution quantum dots. Adv. Mater. 2008, 20, 4830–4834. [Google Scholar] [CrossRef]
  70. Kockmann, N.; Kastner, J.; Woias, P. Reactive particle precipitation in liquid microchannel flow. Chem. Eng. J. 2008, 135, S110–S116. [Google Scholar] [CrossRef]
  71. Mullin, J.W. Crystallization, 3rd ed; Butterworth Heinemann: Oxford, UK, 1997. [Google Scholar]
  72. Slaughter, D.W.; Doherty, M.F. Calculation of solid-liquid equilibrium and crystallization paths for melt crystallization processes. Chem. Eng. Sci. 1995, 50, 1679–1694. [Google Scholar] [CrossRef]
  73. Winn, D.; Doherty, M.F. Modeling crystal shapes of organic materials grown from solution. Aiche J. 2000, 46, 1348–1367. [Google Scholar] [CrossRef]
  74. Zhang, Y.C.; Sizemore, J.P.; Doherty, M.F. Shape evolution of 3-dimensional faceted crystals. Aiche J. 2006, 52, 1906–1915. [Google Scholar] [CrossRef]
  75. Russel, W.B.; Saville, D.A.; Schowalter, W.R. Colloidal Dispersions; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
  76. Ramachandran, V.; Fogler, H.S. Plugging by hydrodynamic bridging during flow of stable colloidal particles within cylindrical pores. J. Fluid Mech. 1999, 385, 129–156. [Google Scholar] [CrossRef]
  77. Schenkel, J.H.; Kitchener, J.A. A test of the Derjaguin-Verwey-Overbeek theory with a colloidal suspension. Trans. Faraday Soc. 1960, 56, 161–173. [Google Scholar] [CrossRef]
  78. Feke, D.L.; Prabhu, N.D.; Mann, J.A.; Mann, J.A. A formulation of the short-range repulsion between spherical colloidal particles. J. Phys. Chem. 1984, 88, 5735–5739. [Google Scholar] [CrossRef]
  79. Bowen, R.W.; Sharif, A.O. Adaptive finite-element solution of the nonlinear Poisson-Boltzmann equation: A charged spherical particle at various distances from a charged cylindrical pore in a charged planar surface. J. Colloid Interface Sci. 1997, 187, 363–374. [Google Scholar] [CrossRef]
  80. Bhattacharjee, S.; Sharma, A. Lifshitz-van der waals energy of spherical-particles in cylindrical pores. J. Colloid Interface Sci. 1995, 171, 288–296. [Google Scholar] [CrossRef]
  81. Wyss, H.M.; Blair, D.L.; Morris, J.F.; Stone, H.A.; Weitz, D.A. Mechanism for clogging of microchannels. Phys. Rev. E Stat. Nonlin. Soft. Matter Phys. 2006, 74. [Google Scholar]
  82. Ramachandran, V.; Fogler, H.S. Multilayer deposition of stable colloidal particles during flow within cylindrical pores. Langmuir 1998, 14, 4435–4444. [Google Scholar] [CrossRef]
  83. Di Carlo, D.; Irimia, D.; Tompkins, R.G.; Toner, M. Continuous inertial focusing, ordering, and separation of particles in microchannel. Proc. Natl. Acad. Sci. USA 2007, 104, 18892–18897. [Google Scholar]
  84. Gunther, A.; Jensen, K.F. Multiphase microfluidics: From flow characteristics to chemical and materials synthesis. Lab Chip 2006, 6, 1487–1503. [Google Scholar] [CrossRef]
  85. Gunther, A.; Jhunjhunwala, M.; Thalmann, M.; Schmidt, M.A.; Jensen, K.F. Micromixing of miscible liquids in segmented gas-liquid flow. Langmuir 2005, 21, 1547–1555. [Google Scholar] [CrossRef]
  86. Gunther, A.; Khan, S.A.; Thalmann, M.; Trachsel, F.; Jensen, K.F. Transport and reaction in microscale segmented gas-liquid flow. Lab Chip 2004, 4, 278–286. [Google Scholar] [CrossRef]
  87. Wang, F.K.; Chon, C.H.; Li, D.Q. Particle separation by a moving air-liquid interface in a microchannel. J. Colloid Interface Sci. 2010, 352, 580–584. [Google Scholar] [CrossRef]
  88. Subramaniam, A.B.; Abkarian, M.; Mahadevan, L.; Stone, H.A. Mechanics of interfacial composite materials. Langmuir 2006, 22, 10204–10208. [Google Scholar] [CrossRef]
  89. Subramanian, R.S.; Larsen, R.J.; Stone, H.A. Stability of a flat gas-liquid interface containing nonidentical spheres to gas transport: Toward an explanation of particle stabilization of gas bubbles. Langmuir 2005, 21, 4526–4531. [Google Scholar] [CrossRef]
  90. Subramaniam, A.B.; Abkarian, M.; Stone, H.A. Controlled assembly of jammed colloidal shells on fluid droplets. Nat. Mater. 2005, 4, 553–556. [Google Scholar] [CrossRef]
  91. Subramaniam, A.B.; Mejean, C.; Abkarian, M.; Stone, H.A. Microstructure, morphology, and lifetime of armored bubbles exposed to surfactants. Langmuir 2006, 22, 5986–5990. [Google Scholar] [CrossRef]
  92. Lautz, J.; Sankin, G.; Yuan, F.; Zhong, P. Displacement of particles in microfluidics by laser-generated tandem bubbles. Appl. Phys. Lett. 2010, 97, 183701–183701-3. [Google Scholar]
  93. Wang, M.M.; Tu, E.; Raymond, D.E.; Yang, J.M.; Zhang, H.C.; Hagen, N.; Dees, B.; Mercer, E.M.; Forster, A.H.; Kariv, I.; et al. Microfluidic sorting of mammalian cells by optical force switching. Nat. Biotechnol. 2005, 23, 83–87. [Google Scholar]
  94. Durr, M.; Kentsch, J.; Muller, T.; Schnelle, T.; Stelzle, M. Microdevices for manipulation and accumulation of micro- and nanoparticles by dielectrophoresis. Electrophoresis 2003, 24, 722–731. [Google Scholar] [CrossRef]
  95. Gijs, M.A.M. Magnetic bead handling on-chip: New opportunities for analytical applications. Microfluid. Nanofluid. 2004, 1, 22–40. [Google Scholar]
  96. Lu, L.H.; Ryu, K.S.; Liu, C. A magnetic microstirrer and array for microfluidic mixing. J. Microelectromech. Syst. 2002, 11, 462–469. [Google Scholar] [CrossRef]
  97. Challis, R.E.; Povey, M.J.W.; Mather, M.L.; Holmes, A.K. Ultrasound techniques for characterizing colloidal dispersions. Rep. Prog. Phys. 2005, 68, 1541–1637. [Google Scholar] [CrossRef]
  98. Lilliehorn, T.; Simu, U.; Nilsson, M.; Almqvist, M.; Stepinski, T.; Laurell, T.; Nilsson, J.; Johansson, S. Trapping of microparticles in the near field of an ultrasonic transducer. Ultrasonics 2005, 43, 293–303. [Google Scholar] [CrossRef]
  99. Mason, W.P. Physical Acoustics; Academic Press: New York, NY, USA, 1982. [Google Scholar]
  100. Poesio, P.; Ooms, G. Formation and ultrasonic removal of fouling particle structures in a natural porous material. J. Pet. Sci. Eng. 2004, 45, 159–178. [Google Scholar] [CrossRef]
  101. Spengler, J.; Jekel, M. Ultrasound conditioning of suspensions—Studies of streaming influence on particle aggregation on a lab- and pilot-plant scale. Ultrasonics 2000, 38, 624–628. [Google Scholar] [CrossRef]
  102. Laurell, T.; Petersson, F.; Nilsson, A. Chip integrated strategies for acoustic separation and manipulation of cells and particles. Chem. Soc. Rev. 2007, 36, 492–506. [Google Scholar]
  103. Sedelmeier, J.; Ley, S.V.; Baxendale, I.R.; Baumann, M. KMnO(4)-mediated oxidation as a continuous flow process. Org. Lett. 2010, 12, 3618–3621. [Google Scholar]
  104. Browne, D.L.; Deadman, B.J.; Ashe, R.; Baxendale, I.R.; Ley, S.V. Continuous flow processing of slurries: Evaluation of an agitated cell reactor. Org. Proc. Res. Dev. 2011, 15, 693–697. [Google Scholar]

Share and Cite

MDPI and ACS Style

Flowers, B.S.; Hartman, R.L. Particle Handling Techniques in Microchemical Processes. Challenges 2012, 3, 194-211. https://doi.org/10.3390/challe3020194

AMA Style

Flowers BS, Hartman RL. Particle Handling Techniques in Microchemical Processes. Challenges. 2012; 3(2):194-211. https://doi.org/10.3390/challe3020194

Chicago/Turabian Style

Flowers, Brian S., and Ryan L. Hartman. 2012. "Particle Handling Techniques in Microchemical Processes" Challenges 3, no. 2: 194-211. https://doi.org/10.3390/challe3020194

APA Style

Flowers, B. S., & Hartman, R. L. (2012). Particle Handling Techniques in Microchemical Processes. Challenges, 3(2), 194-211. https://doi.org/10.3390/challe3020194

Article Metrics

Back to TopTop