Abstract
Within the context of anthropogenic warming, rainfall oscillations may induce especially important societal impacts worldwide. In this article, we propose to study potential underlying mechanisms related to precipitation changes on a planetary scale by taking advantage of the recent theory of Rossby waves of long periods winding around subtropical gyres, the Gyral Rossby Waves (GRWs). The stable oxygen isotopic compositions of speleothems are used to regionalize and reconstruct the evolution of long-term rainfall oscillation during the Holocene. The method applied here consists in estimating the wavelet power of dated series of stable oxygen isotopic composition (δ18O) in speleothems within period bands representative of subharmonic modes. Our findings highlight: (1) hydrological processes resulting from friction between the North Equatorial Current (NEC) and the North Equatorial Counter Current (NECC) to explain the weakening of ENSO activity in mid-Holocene, and (2) the quasi-resonance of the equatorward migration of the summer Inter Tropical Convergence Zone (ITCZ) during the Holocene, because of the progressive decrease of the thermal gradient between the low and high latitudes of the gyres. The results of this study suggest that the spatial and temporal variations in the amplitude of the rainfall oscillations are related both on the acceleration/deceleration phases of the western boundary currents and on the shrinkage of the Hadley cell. The latitudinal shift of the summer ITCZ in response to changes in the thermal gradient is of the utmost importance in predicting the expansion of deserts resulting from anthropogenic warming.
1. Introduction
1.1. State of the Art
Studies on the impacts of long-term rainfall oscillation upon biodiversity and human populations at the planetary scale, but also on the evolution of the current climate at a secular scale, are so far needed for a good appreciation of the correlated anthropogenic effects. Although outstanding progress has been made over the past half century in understanding how climate responds to external and internal forcing, many questions remain unanswered. This is the case, for example, of the role played by subtropical gyres on a planetary scale or of the drivers of long-term evolution of ENSO activity and rainfall oscillation, as well as migration of the summer inter-tropical convergence zone (ITCZ) at the centennial timescale.
Studies focused on these open issues demand novel approaches to clarify the contribution of natural cycles in the current context of anthropogenic warming, but also for a better understanding of the impact of human activities on the natural dynamics of the climate system. Following on from the various works on the interannual rainfall oscillation, whether it is related to ENSO [1,2,3] or the Interdecadal Pacific Oscillation [4], this study focuses on the evolution of long-term ENSO activity and rainfall oscillation on a planetary scale throughout the Holocene. The variability observed in both South America and Asia in contrast to a remarkably stable trend in other regions like Europe may embed the existence of other underlying mechanisms driving such climate changes.
1.2. Rainfall Oscillation
The nearly periodic interannual variability of precipitations is widespread. The two main causes of such variations are the El Niño Southern Oscillation (ENSO) and the sea surface temperature (SST) anomalies along the subtropical gyres [5].
El Niño events originate in the tropical Pacific. Two coupled baroclinic wave systems behave like quasi-stationary waves, one being annual and the other quadrennial [6,7,8]. The annual wave is a first baroclinic-mode, fourth meridional-mode Rossby wave resonantly forced by easterlies. In the second system, a Kelvin wave causes the transfer of warm waters from the western Pacific to cold waters in the eastern Pacific, which induces strong evaporative processes accompanied by high air pressure in the western Pacific and low air pressure in the eastern Pacific. Although ENSO causes global changes in temperature and rainfall, the tropical regions are those mainly impacted. This occurs both during the warm phase of El Niño and the cold phase of La Niña induced by the westward recession of the quadrennial wave, which favors upwelling off the Peruvian and Chilean coasts. Although the average period of ENSO is 4 years, it varies between 1.5 years and 7 years.
At mid-latitudes, the rainfall oscillation mainly results from SST anomalies where the western boundary currents leave the continents to reenter the tropical gyres. 1/2-, 1-, 4-, and 8-year period westward propagating Rossby waves embedded in the wind-driven current of the gyres are paced according to the warm water amount transferred by the western boundary currents from the low to the high latitudes of the gyres [9]. A powerful feedback that results from the difference in temperature between the low and high latitudes of the gyres causes the western boundary currents to accelerate/decelerate, which deepens or rises the thermocline around the gyres. In turn, the oscillation of the thermocline reinforces the modulation of the polar and radial currents of the gyres.
The correlation between inter-hemispheric and large-scale anomalies of precipitation to variations in insolation during the Holocene have been observed and described in previous studies [10,11,12]. However, changes in the forcing are too small to explain the observed climate variations as simple linear responses. The climate response necessarily implies amplifying phenomena of solar and orbital forcing.
1.3. Subtropical Gyres
Controlling the temperature gradient profile around the gyres, that is, evaporative processes, GRWs induce the formation of low- or, on the contrary, high-pressure systems. Ocean-atmosphere interactions are even more sensitive in the high latitudes of the gyres as they influence the trajectory of the polar jet streams. When accelerating, western boundary currents can channel subtropical cyclones by merging the two low pressure systems formed from the tropical depression and the extra-tropical depression over the positive SST anomaly, as occurred in 2005 when Hurricane Katrina made landfall. Rainfall oscillation has a considerable economic and societal impact, due to the episodes of drought or flood that may follow, superimposing on the effects of anthropogenic warming.
Long-period Rossby waves embedded in the wind-driven anticyclonic polar current propagate cyclonically around the gyres. Multi-frequency Rossby waves overlap. Sharing the same modulated polar current, they behave like coupled oscillators with inertia forced by the variations in solar irradiance. Consequently, these Gyral Rossby Waves (GRWs) are resonantly forced by solar and orbital cycles in subharmonic modes [13,14,15]. This means that the periods of resonance are deduced from each other by recurrence, which supposes an adjustment between the apparent wavelength of the GRWs, i.e., the circumference of the gyres, and the latitude of their centroids. The first mode , the mean period of which is = 64 years, corresponds to one turn of GRWs in the North and South Atlantic and in the Indian Ocean. The following modes are deduced recursively: , where the integer subharmonic number is 2 or 3 to ensure the stability of the system of oscillators. GRWs travel around the North and South Pacific gyres in = 128 years that is the second subharmonic mode.
1.4. The Speleothems, Witnesses of the Evolution of Precipitation
The present work intends to quantify the amplitude of precipitation variations during the Holocene in different regions of the globe to highlight the evolution of large-sale atmospheric circulation. This study is based on the use of speleothems available in the database developed within the framework of the Speleothem Isotopes Synthesis and AnaLysis (SISAL) project. The method consists in taking advantage of the stable oxygen isotopic composition (δ18O) in the calcite/aragonite of cave concretions, which involves processes that control equilibrium and kinetic fractionation of oxygen isotopes in water and carbonate species.
Because of the observed correlation between the decrease in rainfall δ18O values and the increase in the amount of rain [16], the so-called “amount effect” [17,18,19], precipitation amount can be deduced from δ18O measurements in speleothems.
2. Materials and Methods
2.1. Methodological Approach
Speleothems allow the reconstruction of the history of precipitation and have raised much interest since the 1970s. However, the proper interpretation of speleothem δ18O as paleoclimate and paleoenvironmental proxies remains complex because of site-specific cave processes such as infiltration, flow routing, drip seasonality and saturation state, and cave microclimate, among others [20]. On the other hand, the magnitude of the amount effect at a particular site is not constant because it depends on the initial mass of water vapor in the air parcel, sea surface temperature, and cloud microclimate dynamics [19]. Therefore, the calibration curve is obtained from a large sampling to be as representative as possible.
The method applied in this study consists in taking advantage of the greatest number of available speleothems to obtain results representative of various regions of the globe. Indeed, a continuous and accurate representation of the amplitude of rainfall oscillation throughout the Holocene requires many overlapping speleothems. In addition, all the speleothems which do not satisfy the conditions required for obtaining quantitative results have to be removed, either because of their discontinuity and/or insufficient temporal resolution or else due to their inadequate timespan to carry out a frequency analysis. However, the main difficulty is to test the degree of reliability of the information contained in the speleothem, i.e., the extent to which it widely affects the observed variations in calcite δ18O composition related to rain or to changes in the functioning of the karst system and its epikarst. For this reason, we tested the consistency of each speleothem with the variations in δ18O composition in ice cores representative of global temperature. Only those speleothems showing coherence greater than 0.5 were considered, disregarding the phase difference, by accepting some shifts in the dating. The coherence is estimated in period bands representative of subharmonic modes.
Considering that variations in δ18O composition within particular period bands is not restrictive, because those bands are joint so that the information is available in a wide band, the upper limit filters out drifts reflecting slow modifications in the functioning of the karst system. All these precautions being taken, several hundred speleothems allow measuring the precipitation amount accurately. In areas where many speleothems are available, the regionalized amplitudes of rainfall oscillation can be averaged along with a standard deviation from which an estimation error is deduced by assuming the measurements to be independent of each other and belonging to the same statistical population. Since we are looking for a trend representative of a large region to describe the evolution of the general atmospheric circulation during the Holocene, we do not consider the peculiarities of the rainfall patterns related to the site locations regardless of their altitude, their distance from the sea, or their continental response.
This amounts to admitting that the calibration curve proposed by [21] is applied worldwide. In this case, the δ18O composition of precipitation mainly depends on the salinity and temperature of the ocean, where evaporative processes occurred. Indeed, where rainfall pattern is not controlled by open waters, the transfer of water vapor until it precipitates over the site can be considered as a conservative process regarding δ18O composition. This is justified by the fact that, once the water vapor precipitates over the continent, being partially intercepted by the canopy, infiltrated in the soils, or being in the form of runoff, the residual water layer that wets the surface dries up. In this case, the fractionation that occurs while water is evaporating does not modify the initial conditions when the entire layer of water has been evaporated.
2.2. Ocean Stratification
The rainfall oscillation is closely conditioned by the ocean stratification that results in baroclinic waves propagating along the pycnoclines. The stratification of the oceans is followed with the greatest attention in the context of global warming. Seawater density changes with depth and thereby impacts the vertical exchanges of heat, carbon, dissolved oxygen, and nutrients [22]. Furthermore, ocean stratification reflects the warming/cooling of subsurface seawater, with consequences on the large-scale ocean circulation. Within this work, we consider the vertical oscillation of the stratification that results in the phase of GRWs.
Ocean stratification is quantified by density change with depth, i.e., by the vertical distribution of temperature and salinity, in addition to pressure. Representing the squared buoyancy frequency of the oceans versus the depth down to 2000 m, Li et al. [22] shed new light on the evolution of ocean stratification (Figure 1). This study adopts the recently improved temperature and salinity estimates to better quantify long-term changes of stratification in the upper 2000 m of the world’s oceans over the past half century. This allows a full quantification of the spatial structure of changes in stratification, which overcomes previous systematic biases associated with sampling. The study also adopted an improved metric of stratification, providing a true estimate of ocean stratification and its changes over time (Figure 2).
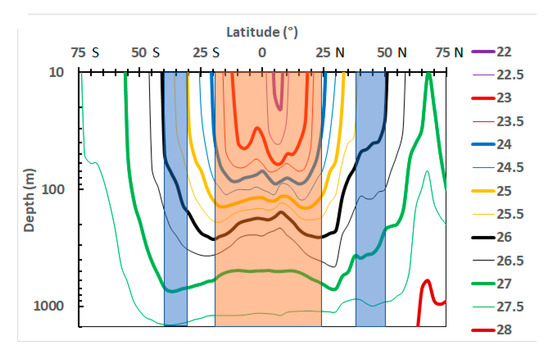
Figure 1.
Isopycnals in the world ocean: ( = potential density) is represented with 0.5 kg intervals. Zonal blue bands intersect the gyres in their part furthest from the equator; the zonal pink band intersects the gyres in their part closest to the equator [22].
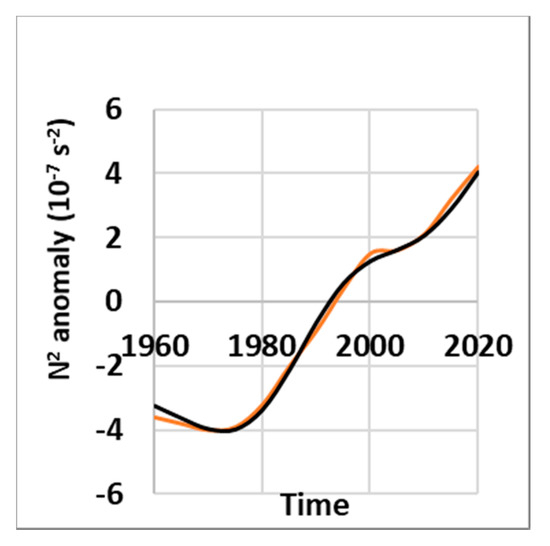
Figure 2.
Time evolution of the 0–2000 m ocean stratification changes. Red curves represent the observed anomalies, black curves the weighted sum of 128-, 64-, and 32-year period sinusoids whose parameters associated to each mode are 4.9, 0.9, 0.5 for the amplitude and 1972, 1960, and 1979 for the dates defining the phase.
2.3. Data
The database is developed within the framework of the Speleothem Isotopes Synthesis and AnaLysis (SISALv2) project [23].
The δ18O composition in the ice core is obtained within the Greenland Ice Core Project (GRIP) [24].
2.4. Wavelet Power, Coherence, and Phase Difference
The wavelet transforms of a series is defined as the convolution of with a scaled and translated function :
where is the complex conjugate of , is the wavelet scale (a real number), is the time increment, and is the length of the series [25].
Within this work, the Morlet wavelet function is used, that is:
that consists of a plane wave modulated by a Gaussian ( is a nondimensional time parameter, = 6). The wavelet power spectrum is and the amplitude , the dimension of which is that of the series .
Given two time series and , with wavelet transforms and , the cross-wavelet spectrum is and the cross-wavelet power . The coherence is defined as the square of the cross-spectrum normalized by the individual power spectra, which measures the cross-correlation between two time series as a function of frequency. The phase difference is , which measures the time shift between the two series and . and represent the imaginary and real parts of .
2.5. Filtering
A wavelet-filtered time series is obtained by summing over a subset of the scales the sum of the wavelet functions between scales and :
where = 0.776 and .
2.6. Examples
The approach is illustrated by the processing of three speleothems, namely, in the SISAL nomenclature:
- entity 142 (COMNISPA II), site 58 (Spannagel cave), latitude 47.08° N, longitude 11.67° E, elevation 2310 m, geology marble, rock age Jurassic, Jens Fohlmeister [26];
- entity 366 (S3), site 170 (Defore cave), latitude 17.1667° N, longitude 54.0833° E, elevation 150 m, geology limestone, rock age unknown, Drew Lorrey [27];
- entity 285 (BA03_highres), site 116 (Bukit Assam cave), latitude 4.03° N, longitude 114.8° E, elevation 150 m, geology unknown, rock age unknown, Jun Hu [28].
2.6.1. Speleothems Reflecting Long-Period Rainfall Oscillation
In Figure 3, the speleothem (entity 366) represents the calcite δ18O composition in the speleothem versus the age, a 780-year annually resolved speleothem from south Oman. Data are filtered in bands characteristic of the first three subharmonic modes. The amplitudes of the three components are comparable (Figure 3b). The raw data from speleothem can be reconstructed adequately if it is filtered in the broad band 48–576 years when the short periods are ignored (Figure 3a).
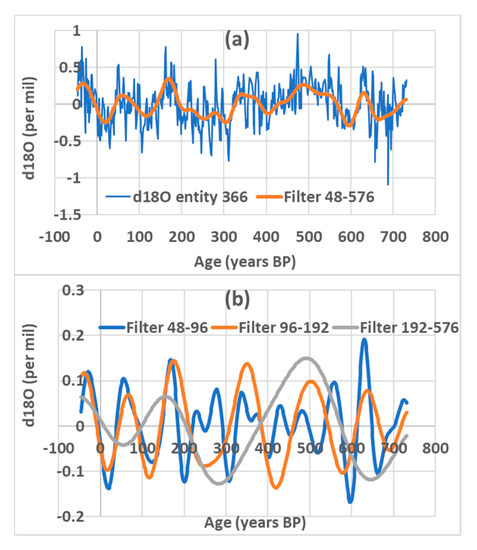
Figure 3.
Filtering in subharmonic modes the speleothem (entity 366). (a) The raw data and filtered in the broad band 48–576 years (sum of components in (b)); (b) speleothems are filtered in the characteristic bands 48–96, 96–192, and 192–576 years.
In Figure 4, the speleothem (entity 142) represents the calcite δ18O composition in the speleothem versus the age, from a mid-European paleosite, covering the period of 11 ka up to the present. Data are filtered in bands characteristic of the first five subharmonic modes. As shown in Figure 4a, correct reconstruction of the speleothem would require the addition of higher subharmonic modes (low frequencies are missing). However, this information could not be used within this study because too few speleothems would be suitable for subharmonic numbers greater than 5.
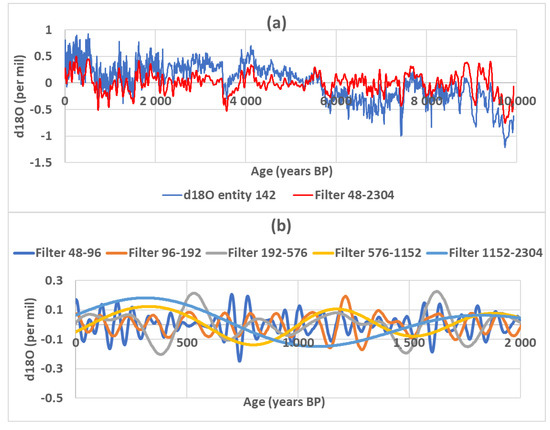
Figure 4.
Filtering in subharmonic modes the speleothem (entity 142). (a) The raw data and filtered in the broad band 48–576 years; (b) speleothems are filtered in the characteristic bands 48–96, 96–192, 192–576, 576–1152, and 1152–2304 years.
In Figure 5, the amplitude of the speleothem (entity 142) is supposed to be stationary within the three regions in which it is averaged. This assumption allows processing incomplete sections of speleothems such as those observed between 8000 and 12,000 years BP.
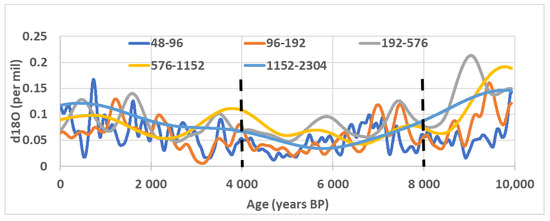
Figure 5.
Amplitude of the speleothem (entity 142) decomposed in subharmonic modes. The limits of the regions in which the components are averaged are indicated.
In Figure 6, the reduced signals are supposed to be stationary within the three periods of the Holocene in which amplitudes, coherence, and phase difference are averaged (this assumption allows considering speleothems within a time period shorter than the time intervals of the Holocene). In the present case, this assumption is clearly questionable because of the inflection of the coherence and the discontinuity of the phase difference which occur over 400 years BP. This probably reveals a time shift between the speleothem and the reference. The average coherence and phase difference are 0.87 and 38°, respectively. In this case, the mean coherence remains sufficiently high for the speleothem to be selected in order to contribute to the estimation of the amplitude and of the phase difference of the rainfall oscillation assigned to the subharmonic mode and the first region (0–4000 years BP).
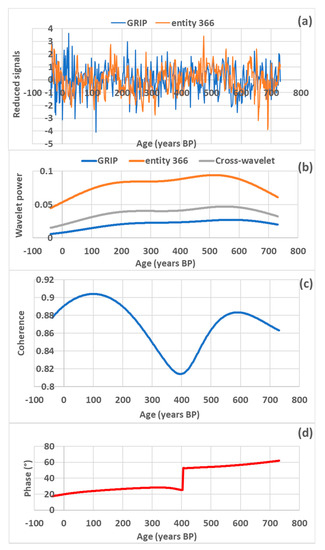
Figure 6.
Coherence and phase difference, within the band 192–576 years, of the speleothem (entity 366) relative to the δ18O composition from GRIP ice core records. Signals are reduced (divided by the standard deviation). (a) Raw signals; (b) wavelet power spectra and cross-wavelet spectrum; (c) coherence; (d) phase difference.
2.6.2. Speleothems Reflecting the Contribution of ENSO to Total Precipitation
Located in the tropical Pacific band, the sites from which the speleothems originate are subject to variable precipitation patterns. A precise estimate of the mean contribution of ENSO to precipitation is obtained from the ratio of the standard deviation of the δ18O signal filtered in the band 2–7 years characteristic of ENSO, on the standard deviation of the same signal filtered in the band 0–7 years which reflects both the annual and pluriannual precipitation.
Figure 7 shows the sequences for estimating the ratio whose evolution is to be represented during the Holocene from relevant speleothems. Here, δ18O concentration in the speleothem in Borneo (entity 285) is used to demonstrate the method. This speleothem is a long sequence spanning from 2386 to 8317 years BP with interruptions, the resolution being 0.25 years. Here, the first part of the speleothem is utilized.
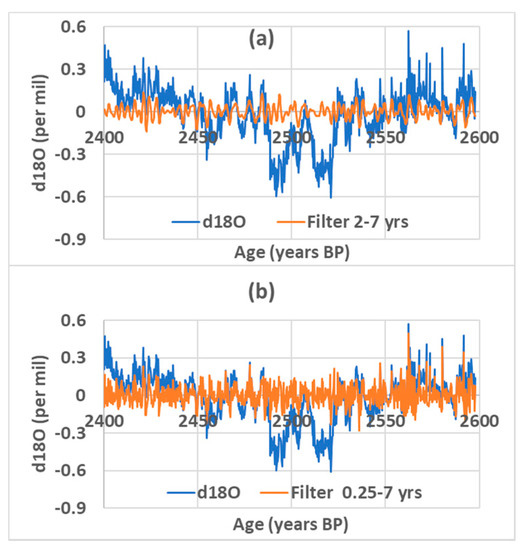
Figure 7.
δ18O in speleothem (entity 285). (a) Raw and filtered in the 2–7-year band; (b) raw and filtered in the 0.25–7-year band.
2.7. The Scope of the Study
Speleothems allow precise estimation of the rainfall oscillation amplitude throughout the Holocene over three time periods—0–4000 (late Holocene), 4000–8000 (mid-Holocene), and 8000–12,000 years (early Holocene)—in seven regions located in Western and Central Europe, Asia, Southeast Asia, New Zealand, as well as North, Central, and South America. The analysis refers to the first five subharmonic modes, , , , , and , whose respective periods are the subharmonic number multiplied by 64, that is, 64, 128, 256, 768, and 1536 years. The corresponding period bands are 48–96, 96–192, 192–576, 576–1152, and 1152–2304 years so that they cover a broadband extending from 48 to 2304 years (http://climatorealist.neowordpress.fr/subharmonic-modes/, accessed on 5 August 2021).
Regarding ENSO, subharmonic modes , , and are used (mean periods are 12,288 years, 24,576 years, and 49,152 years).
3. Results
3.1. Seven Regions to Result in the Climatic Response of Speleothems
To represent the climatic impact resulting in each subharmonic mode of the oscillation of the ocean stratification, seven regions are selected, which contain enough sites for an accurate analysis of ocean−atmosphere interactions (Figure 8).
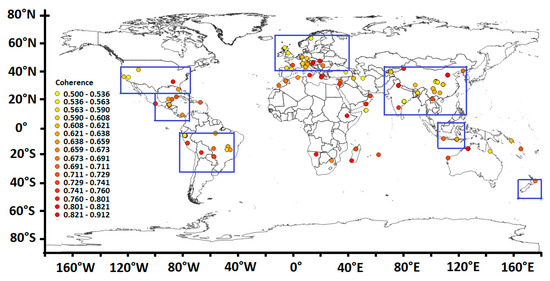
Figure 8.
The seven regions selected from sites for which the climatic response according to the different subharmonic modes is observed. They are Western and Central Europe (15° W, 40° E) × (65° N, 40° N), Asia (66° E, 124° E) × (43° N, 10° N), Southeast Asia (106° E, 123° E) × (5° N, 15° S), New Zealand (163° E, 180° E) × (38° S, 50° S), Southern North America (125° W, 75° W) × (42° N, 26° N), Central America (100° W, 76° W) × (25° N, 7° N), and Central South America (82° W, 42° W) × (3° S, 33° S). The coherence between the speleothems and the paleorecord higher than 0.5 is represented for the subharmonic mode (average period = 128 years). The paleorecord is the δ18O composition in the ice core records available in the Greenland Ice Core Project (GRIP).
3.2. Variations in the δ18O Composition of Speleothems from the Seven Regions for the First Five Subharmonic Modes
Amplitudes of rainfall oscillation are presented in Table 1 and Figure 9. Jointly, the phase difference is estimated in relation with the δ18O composition from GRIP ice core records. It represents a few tens of degrees at most, depending on the number of speleothems involved as well as their representativity. Therefore, the rainfall oscillation can always be considered nearly in phase with the paleorecord used as the time reference, whatever the subharmonic mode.

Table 1.
For every subharmonic mode, variations in the δ18O composition in speleothems (per mil) representing the amplitude of rainfall oscillation averaged over the speleothems representative for each region (M), the standard deviation of the mean (S.D.), and the number of speleothems (N).
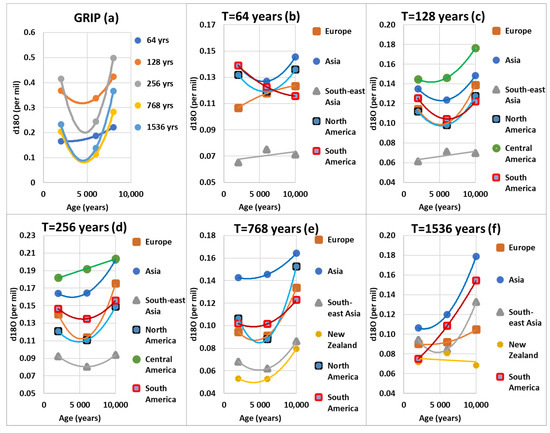
Figure 9.
Used as a paleorecord versus the subharmonic modes, amplitude of δ18O variations throughout the Holocene. (a) In GRIP ice core record; (b–f) in speleothems located in the seven regions. Mean periods are T = 64 (b), 128 (c), 256 (d), 768 (e), and 1536 (f) years.
The Figure 9a shows the amplitude of oscillation variations according to the subharmonic modes of the five GRWs winding around the subtropical gyres. Because of the paleorecord used as the reference, amplitudes of the five gyres are not differentiated. They are high in early Holocene due to the enhanced temperature gradient between the high and low latitudes of the gyres, decreasing in the mid-Holocene and then increasing again in the late Holocene, reflecting the acceleration/deceleration of the western boundary currents.
3.2.1. Subharmonic Mode (Band 48–96 Years, = 64 Years)
Despite the small number of speleothems with enough time resolution for this subharmonic mode, the amplitude of rainfall oscillation seems to reflect the amplitude of GRWs everywhere throughout the Holocene (Figure 9a,b). Moreover, the amplitudes are similar in the different regions, ranging from nearly 0.10 to 0.15 per mil δ18O (42 to 63 mm/yr), except for Southeast Asia that remains exceptionally low at about 0.07 per mil δ18O (29 mm/yr).
3.2.2. Subharmonic Mode (Band 96–192 Years, = 128 Years)
The amplitudes are high in the early Holocene, decreasing in the mid-Holocene and then rising again in the late Holocene but without reaching the initial level. They shift within a similar range over distinct regions except for Central America and, to a lesser extent, Asia, which is slightly higher. The amplitude in Southeast Asia is still exceptionally low. Apart from New Zealand, all regions are represented within this subharmonic mode because most of the speleothems convey sufficient resolution, covering an adequate time interval for the frequency analysis (at least 128 × 2 = 256 years).
3.2.3. Subharmonic Mode (Band 192–576 Years, = 256 Years)
Although a similar trend is depicted throughout the Holocene, a wider range of amplitudes is shown for different regions (Figure 9d), spanning from 0.09 to 0.21 per mil δ18O (38 to 88 mm/yr).
3.2.4. Subharmonic Mode (Band 576–1152 Years, = 768 Years)
Figure 9e is like the previous one, with the absence of Central America but the appearance of New Zealand whose amplitude is exceptionally low at nearly 0.06 per mil δ18O (25 mm/yr). By contrast, the value reached by North America is high at the beginning of the Holocene.
3.2.5. Subharmonic Mode (Band 1152–2304 Years, = 1536 Years)
As in North America for the mode, an amplifying phenomenon of the amplitude occurs in early Holocene for the mode , mainly in South America and Asia (Figure 9f). The amplitude of the oscillation that is 0.16 or 0.18 per mil δ18O (67 or 76 mm/yr) in early Holocene is almost divided by two during that period, reaching 0.08 or 0.11 per mil δ18O (34 to 46 mm/yr) nowadays.
3.3. Variations in δ18O Concentration in Speleothems According to the Latitude
Figure 10 shows the amplitude of rainfall oscillation (δ18O per mil) versus the latitudes from which the location of summer ITCZ are deduced. In North America, the summer ITCZ was positioned over 37° N at 10,000 years BP (Figure 10c) to shift to 21° N at 2000 years BP (Figure 10a), the same location of the ITCZ in mid-Holocene, albeit less accurate (Figure 10b). In South America, the summer ITCZ was 25° S at 10,000 years BP (Figure 10f) with a shift to 4° S at 2000 years BP (Figure 10d). Here again, the intermediate value lacks precision due to the scarcity of speleothems. As for Asia, the summer ITCZ was placed over 42° N at 10,000 years BP (Figure 10i) with a shift to 25° N at 2000 years BP (Figure 10g). However, equatorward migration of the summer ITCZ was slower than in the previous two cases as it was still ongoing in the mid-Holocene when the summer ITCZ was located over 34° N.
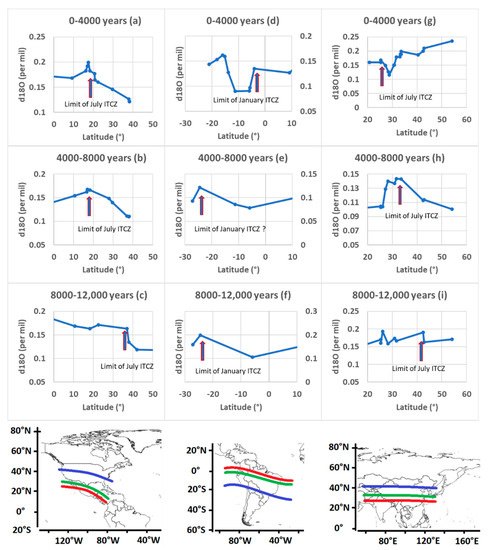
Figure 10.
Graphs represent the amplitude of rainfall oscillation ( per mil) according to the latitudes of deduced location of summer ITCZ. The limit is located where the amplitude drops when following it from the equator—(a–c) refer to North America, (d–f) to the South America. For a given latitude, all the available speleothems are considered. Subharmonic modes are ( = 256 years) in (a–c), ( = 128 years) in (d), and ( = 1536 years) in (e,f). Figures (g–i) refer to Asia. For a given latitude, the speleothems included in the band (66° E, 124° E) are considered. Subharmonic modes are ( = 256 years) in (g) and ( = 1536 years) in (h,i). The maps below the graphics represent the migration of summer ITCZ during the Holocene (in blue, green, and red from the beginning of the Holocene to the end).
The oscillation amplitude is high in Asia over the region located between 43° N and 10° N, regardless of the subharmonic mode. This region is dominated by widespread and persistent subtropical high-pressure cells and the associated circulation patterns that propitiate the formation of low- to mid-latitude arid zones in Asia [29]. This probably makes that region very sensitive to changes in monsoon circulation.
The tropical Southeast Asia region is not subject to rainfall oscillation. However, the increased amplitude in the early Holocene observed for the subharmonic mode suggests an encroachment of the January ITCZ over that region located between 5° N and 15° S (Figure 10f).
Despite being also located inside the Hadley cell, the Central American region experiences strong rainfall oscillation for all subharmonic modes because of the quasi-permanent encroachment of the ITCZ in July. It is therefore the latitudinal oscillation of the July ITCZ which seems to operate for all subharmonic modes, tuned to the different periods.
3.4. Variations in δ18O Concentration in Speleothems in the Tropical Pacific
Sixteen high resolution speleothems are available at five sites (Figure 11). At site 60, the speleothem covers the period −53 to 393 years, −57 to 251 years at site 204, −60 to 527 years at site 181, 2387 to 8317 years with five discontinuities at site 116, and 247 to 1965 years at site 107 divided into seven intervals.
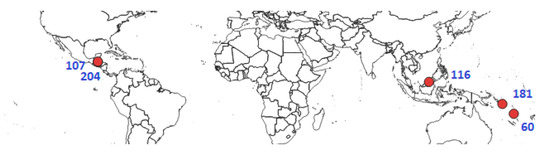
Figure 11.
The five sites from which the speleothems originate: 116 (Bukit Assam cave, 6 speleothems) [28], 60 (Taurius cave, 1 speleothem) [30], 181 (Forestry cave, 1 speleothem) [31], 107 (Yok Balum cave, 1 speleothem) [32], and 204 (Xibalba cave, 7 speleothems) [33].
Sites 181 and 60 are in the tropical South Pacific convergence zone. δ18O in Borneo rainfall (site 116) is a robust proxy of regional convective intensity and precipitation amount, both of which are directly influenced by ENSO activity. These three sites, being located to the west of the tropical basin, are negatively correlated with the ENSO: precipitation decreases during ENSO. East of the tropical basin, the sites 107 and 204, located in the convection zone, are positively correlated with ENSO.
Figure 12 reinforces the decrease in ENSO activity in the middle of the Holocene, a result widely accepted by the scientific community nowadays. However, the precision of the measurement results allows a straightforward interpretation from the decomposition into subharmonic modes of δ18O concentration in the GRIP ice core record used as a paleo proxy of the amplitude of GRWs.
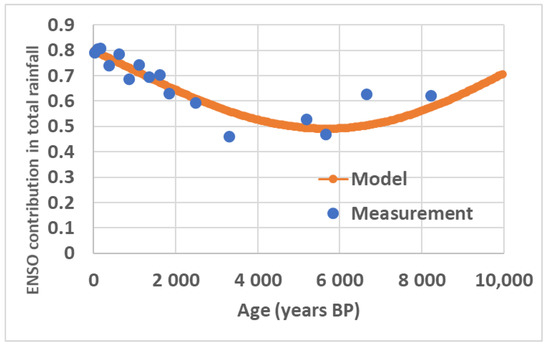
Figure 12.
ENSO contribution to precipitation deduced from speleothems and the model—that is, δ18O concentration in the GRIP ice core filtered within the band 9216–73,728 Ka (union of subharmonic modes , , and ), and multiplied by a constant to produce an adimenstional variable. This constant is a negative real number adjusted so that the quadratic sum of the deviations between the measurements and the model is minimal.
4. Discussion
4.1. Decomposition in Subharmonic Modes
The prominent role of the five subtropical gyres is clearly highlighted in Figure 1. Indeed, the variations in potential density and are deepest within a zonal band framed by the limit closest to the pole of the subtropical gyres (within the blue bands) and the ocean stratification increase for the upper 150 m occurs within the pink band, reaching almost 5 10−7 s−2 yr−1 [22].
The decomposition in subharmonic modes of the anomaly in the world ocean allows a full quantification of the spatial and temporal structure of changes in stratification. The anomalies observed in Figure 2 exhibit the oscillation of the pycnoclines in the subharmonic modes, which are fitted in the weighted sum of 128-, 64-, and 32-year-period sinusoids. This hypothesis is supported by the coherence of the oscillations of and that of SST anomalies observed around the North Atlantic gyre [34], whose amplitudes are maximum in 1969 and 1958 calendar years according to the 128- and 64-year period subharmonic modes. This supports the hypothesis according to which the five subtropical gyres are nearly in phase. The errors reflect small variations in the phase (the time lags compared to the sunspot number within the bands characteristic of subharmonic modes) observed around the North Atlantic gyre.
The 128-year period subharmonic mode is dominant because the evolution of the 0–2000 m ocean stratification changes in the global ocean is dominated by the Pacific Ocean for which the subharmonic mode is of particular importance since the GRWs make one turn around the north and south subtropical gyres. Furthermore, this mode is resonantly forced by the year-period Gleissberg cycle of the Sun. The 32-year period subharmonic mode cannot be highlighted accurately because a 20-year moving average is applied to the observed anomalies. The short time interval of observation does not allow highlighting higher subharmonic modes.
4.2. δ18O Concentration According to the Regions
The modes and show the direct influence of variations in SST of ocean gyres because the amplitude of rainfall oscillation seems to follow a similar change when compared with the amplitude of GRWs reflected by δ18O variability in the GRIP ice core records for this time period (Figure 9a,c).
The location of the summer ITCZ has a considerable influence on the precipitation pattern, depending on the position of the tropical sites, as they may be situated inside the range of the annual ITCZ migratory precipitation belt or not. As the summer ITCZ migrates to tropical and subtropical latitudes during the respective hemisphere’s summer season, the same holds for baroclinic instabilities [35].
4.2.1. Regions Located Outside the Hadley Cell
The evolution of the amplitude of the precipitation oscillation in areas outside the Hadley cell throughout the Holocene recalls the amplitude of GRWs, regardless of the subharmonic modes. This is what occurs in Europe and in New Zealand by reflecting the alternation of synoptic high- and low-pressure systems stimulated and guided by the polar jet streams at the rate of the acceleration/deceleration of the western boundary currents, the Gulf Stream for Europe, and the Eastern Australian Current for New Zealand. Such behavior has also been reported in [9] regarding the 8-yr period rainfall oscillation, as extra-tropical cyclones and anticyclones are formed from SST anomalies at the high latitudes of the subtropical gyres (the Cape Hatteras for Europe, South Eastern Australia, and Tasmania for New Zealand) where the western boundary current leaves the continental margin to re-enter the subtropical gyre.
The amplitude of rainfall oscillation is ruled by the ocean-atmosphere coupling, as well as by the location and orography of continents. Thereby, the deep continental penetration of depressions across Europe to Asia benefits from a low relief north of the Alps and the Himalayas. On the other hand, the amplitude of oscillation is low in New Zealand because of its geographical position, isolated in the Pacific Ocean.
4.2.2. Regions Located Close to the Hadley Cell
These mechanisms also occur in North and South America as well as in Asia. However, unlike the two previous regions, the summer ITCZ overlap on these three regions in the early Holocene results in a high amplitude of oscillation. The maximum sensitivity to the latitudinal migration of summer ITCZ is obtained from subharmonic modes for which the variation is steepest as occurs with the mode n4 for North America and n5 for South America and Asia. A strong decrease in amplitude indicates that summer ITCZ withdraws from the region by shifting equatorward, which drastically reduces rainfall oscillation within this region. This phenomenon seems to have a resonant character because it occurs for specific subharmonic modes. This quasi-resonance suggests a latitudinal oscillation of summer ITCZ according to the period of the mode.
As represented in Figure 10, the amplitude of rainfall oscillation according to the latitude allows for locating the ITCZ in North and South America as well as in Asia by taking advantage of the quasi-resonance. This is made possible because of the considerable availability of speleothems.
4.3. The Atlantic Multidecadal Oscillation and the Subharmonic Mode
The Atlantic Multidecadal Oscillation (AMO) has been the subject of relevant studies on the evolution of atmospheric circulation over the Atlantic during the Holocene [35]. This oscillatory climate variation had been attributed to changes in the Atlantic Meridional Overturning Circulation and could not be explained only from AMOC.
These observations suggest that the role of AMOC at the multidecadal scale would be overestimated, even for the North Atlantic. The ubiquity of rainfall oscillation instead reinforces the hypothesis that ocean stratification would actually play a major role in climate variability at all time scales. The driver of ocean circulation around the five subtropical gyres would result from the oscillation of the pycnoclines which generates both a modulated polar and radial current whose velocity is added to that of the steady wind-driven current. As multifrequency GRWs oscillate in subharmonic modes, the amplitude of rainfall oscillation is significant in all characteristic period bands. In this context, AMO would appear as a particular event of climate variability, both at spatial and frequency scales. Therefore, the thermohaline circulation would turn out to behave more as an overflow than as a driver of surface ocean circulation. The findings rather suggest that it is the resonant orbital forcing of GRWs resulting from the ocean stratification, mainly due to the variations in the eccentricity, that would ultimately act as a driver. Indeed, the forcing period sharply coincides with the natural period of the GRWs for the subharmonic mode since the Mid-Pleistocene Transition (MPT). Due to the coupling of the GRWs, energy is transferred to lower subharmonic modes, possibly forced by the solar and orbital variations of shorter periods.
4.4. Latitudinal Shift of the Summer Intertropical Convergence Zone
The displacement of the summer ITCZ has been mainly studied in the North Atlantic [36]. From the observation of AMO, the internal ocean variability and its influence on climate has been investigated precisely in the North Atlantic through the last 8000 years [37]. Based on spectral analyses of high-resolution climate proxy records from the region bounding the North Atlantic, it has been shown that the summer ITCZ was located north of its present position during the North Hemisphere summer and a zonal atmospheric circulation dominated.
Based on observations over the Holocene [38,39,40], the Last Glacial Maximum [41,42,43], or the last three glacial cycles [44], the widely accepted idea is that the average position of summer ITCZ has varied since the Last Glacial Maximum in response to changing climate boundary conditions. The reasons for this migration are the subject of debate.
Figure 10 shows that the shift in the summer ITCZ occurred in much the same way in North and South America, as well as in Asia—that is, nearly 16° in North America, 20° in South America, and 17° in Asia. Equatorward shift of the summer ITCZ occurred rapidly in the early Holocene and has not changed much since.
As suggested in [38], the present study argues in favor of the idea that the summer ITCZ has migrated latitudinally on a global scale. Furthermore, as observed in North and South America, the shift presumably occurred symmetrically in both hemispheres as has been documented in tropical Africa from marine sediment cores [38].
The quasi-resonance of the summer ITCZ shift for subharmonic modes and suggests that the width of the Hadley cell responds to changes in SST distribution resulting from the resonant forcing of GRWs around the subtropical gyres. To understand why the ITCZ was further north in early Holocene, one must imagine the sequence of transformations that lead from the current position to the conditions that have prevailed.
In early Holocene, the extension of the polar caps increases the thermal gradient between the high and low latitudes of the subtropical gyres. This has the effect of increasing the amplitude of GRWs [34]. During the phase of acceleration of the western boundary currents, baroclinic growth rates are exacerbated, which pushes the latitude of baroclinic instability onset (and therefore the edge of the Hadley cell) to a location that is farther equatorward where the wind shear and the factor of in the Phillips’ criterion ( is the Coriolis parameter, the gradient of the Coriolis parameter) are less [38].
Thus, the increase in the thermal gradient favors the poleward migration of the summer ITCZ as well as the subtropical gyres due to the poleward displacement of trade winds and the wind-driven currents. According to the dispersion relation of GRWs, the cyclonic phase velocity of Rossby waves, which only depends on the latitude of the centroid of the gyres, reduces. On the other hand, the anticyclonic wind-driven currents of the gyres reduce as well because of the weakening of trade winds. However, the apparent velocity of Rossby waves embedded into the wind-driven current of the gyres may be altered, which supposes the adjustment of the mean radius of the gyres to preserve the resonance parameters. Indeed, GRWs should complete one turn in 64 years in the North and South Atlantic and in the Indian Ocean, and 128 years in the North and South Pacific [13].
These successive transformations show how the ITCZ migrated equatorward until it reached an equilibrium position fixed by the current thermal gradient. The asymmetry of the summer ITCZ over Asia, which lies far north of the equator, reflects the absence of a subtropical gyre in the Northern Indian Ocean to push the latitude of baroclinic instability onset closer to the equator.
This clearly highlights the vulnerability of the regions exposed to the narrowing of the Hadley cell because of the melting of the ice caps that is reducing the thermal gradient between the low and high latitudes of the gyres. In arid regions bordering deserts, the shifting of moisture flow out of these regions has important implications for probable changes induced by global warming.
4.5. Evolution of ENSO Activity during the Holocene
Evolution of ENSO activity during the Holocene strengthens the interpretation given from δ18O concentrations in short-lived individual Globigerinoides ruber in a sediment core sampled from the eastern equatorial Pacific near the Galapagos Islands [15]. The negative correlation between the ENSO activity and the amplitude of GRWs (Figure 12) means that geostrophic forces act on the North Equatorial Counter Current (NECC) to enable a reduction of the ENSO activity when the modulated polar current of the North Pacific gyre accelerates while being anticyclonic. Then, the modulated component of the North Equatorial Current (NEC) at the lowest latitudes of the North Pacific gyre accelerates as it flows west, which slows down the NECC by friction and, consequently, the South Equatorial Current (SEC) to which it is coupled. Indeed, while flowing in opposite directions, the modulated components of the NECC and the SEC are at the nodes of the annual quasi-stationary wave in the tropical Pacific, belonging that way to a single dynamical system [6]. However, the SEC is also at the node of the quadrennial quasi-stationary wave of the tropical Pacific that is the driver of ENSO. A weakening of the SEC induces a reduction of the ENSO activity.
In Figure 12, the amplitudes of the GRWs for the subharmonic modes to (mean periods T = 12.3, 24.6, and 49.2 Ka) suggest that the friction between the North Pacific gyre and the NECC is quasi-resonant since it acts as a low pass filter: the highest subharmonic mode is probably beyond , which is difficult to prove numerically. However, subharmonic modes lower than have no significant impact. It is thus that the modulated currents of the coupled annual and quadrennial waves behave as strongly inertial oscillators by involving geostrophic forces on the whole tropical basin scale.
5. Conclusions
Evolution of long-period rainfall oscillation during the Holocene is highlighted from the wavelet power of dated series in speleothems within period bands representative of subharmonic modes. Depending on the period, long-term rainfall oscillation is observed at all latitudes, with an amplitude that varies greatly from region to region. The main cause of variability seems to arise from the latitudinal shift of the summer ITCZ, and the most affected regions are those bordering the Hadley cell.
The use of the different subharmonic modes as markers of the oscillation is a generalization of what is widely practiced with AMO that corresponds to the first subharmonic mode and which, again, is ubiquitous and should not be considered as a peculiarity of the Atlantic Ocean. Moreover, large-scale representation of long-term rainfall oscillation points to the stratification of the oceans as a driver of rainfall variability, while AMOC would turn out to be rather a consequence of stratification.
Another aspect of this work is that it reinforces the notion concerning the equatorward displacement of the summer ITCZ since the early Holocene by taking advantage of the quasi-resonance of the latitudinal shift according to subharmonic modes. The main driver is the thermal gradient between the low and high latitudes of the subtropical gyres. The gradual retreat of the pack ice during the Holocene reduced this thermal gradient, and consequently, the amplitude of GRWs for all subharmonic modes, before raising from the mid-Holocene. This reduction in amplitude made the evaporative processes less efficient during the phase of acceleration of the western boundary currents, which favored the narrowing of the Hadley cell nearly symmetrically with respect to the equator. The asymmetry of the summer ITCZ over Asia, which lies far north of the equator, reflects the absence of a subtropical gyre in the Northern Indian Ocean to push the latitude of the edge of the Hadley cell closer to the equator.
Finally, this work concerns the evolution of ENSO activity during the Holocene. This activity has weakened in the mid-Holocene, which strengthens previous results. Here, the involved hydrological processes are interpreted based on the friction between the NEC and the NECC. Friction only operates for subharmonic modes greater than , which suggests a quasi-resonant transfer of energy between the North Pacific gyre and the annual and quadrennial waves of the tropical Pacific by involving geostrophic forces at the basin scale.
To conclude, the theory of GRWs sheds new light on the driving mechanisms of ENSO as well as rainfall oscillation and how the position of the summer ITCZ responds to the thermal gradient with important implications for predicting the extension of deserts because of anthropogenic warming. However, the investigations based on the use of speleothems remain imprecise where the density of measurements is low. In particular, the method does not apply to the African continent outside the Mediterranean strip. Except for Europe, few speleothems are available north of latitude 40° N and south of latitude 40° S, which precludes the study of the movement of the polar front during the Holocene.
Future research could focus on the exploration of the Last Glacial Maximum always by seeking to enhance the information delivered by speleothems.
Author Contributions
L.P.: original draft contribution; J.-L.P.: methodology, writing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The study did not use new data.
Acknowledgments
The authors warmly thank the anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sadekov, A.Y.; Ganeshram, R.S.; Pichevin, L.; Berdin, R.; McClymont, E.; Elderfield, H.; Tudhope, A.W. Palaeoclimate reconstructions reveal a strong link between El Niño-Southern Oscillation and Tropical Pacific mean state. Nat. Commun. 2013, 4, 2692. [Google Scholar] [CrossRef] [Green Version]
- Barr, C.; Tibby, J.; Leng, M.J.; Tyler, J.; Henderson, A.C.G.; Overpeck, J.T.; Simpson, G.L.; Cole, J.E.; Phipps, S.J.; Marshall, J.C.; et al. Holocene El Niño–Southern Oscillation variability reflected in subtropical Australian precipitation. Sci. Rep. 2019, 9, 1627. [Google Scholar] [CrossRef]
- Qian, J. Multi-scale climate processes and rainfall variability in Sumatra and Malay Peninsula associated with ENSO in boreal fall and winter. Int. J. Clim. 2019, 40, 4171–4188. [Google Scholar] [CrossRef]
- Porter, S.E.; Mosley-Thompson, E.; Thompson, L.G.; Wilson, A.B. Reconstructing an Interdecadal Pacific Oscillation Index from a Pacific Basin–Wide Collection of Ice Core Records. J. Clim. 2021, 34, 3839–3852. [Google Scholar] [CrossRef]
- Reißig, S.; Nürnberg, D.; Bahr, A.; Poggemann, D.; Hoffmann, J. Southward Displacement of the North Atlantic Subtropical Gyre Circulation System During North Atlantic Cold Spells. Paleoceanogr. Paleoclimatol. 2019, 34, 866–885. [Google Scholar] [CrossRef]
- Pinault, J.-L. Long Wave Resonance in Tropical Oceans and Implications on Climate: The Pacific Ocean. Pure Appl. Geophys. Pageoph 2016, 173, 2119–2145. [Google Scholar] [CrossRef]
- Pinault, J.-L. Anticipation of ENSO: What teach us the resonantly forced baroclinic waves. Geophys. Astrophys. Fluid Dyn. 2016, 110, 518–528. [Google Scholar] [CrossRef]
- Pinault, J.-L. The Anticipation of the ENSO: What Resonantly Forced Baroclinic Waves Can Teach Us (Part II). J. Mar. Sci. Eng. 2018, 6, 63. [Google Scholar] [CrossRef] [Green Version]
- Pinault, J.-L. Regions Subject to Rainfall Oscillation in the 5–10 Year Band. Climate 2018, 6, 2. [Google Scholar] [CrossRef] [Green Version]
- Deininger, M.; McDermott, F.; Cruz, F.W.; Bernal, J.P.; Mudelsee, M.; Vonhof, H.; Millo, C.; Spötl, C.; Treble, P.C.; Pickering, R.; et al. Inter-hemispheric synchroneity of Holocene precipitation anomalies controlled by Earth’s latitudinal insolation gradients. Nat. Commun. 2020, 11, 5447. [Google Scholar] [CrossRef] [PubMed]
- Brahim, Y.A.; Wassenburg, J.A.; Cruz, F.; Sifeddine, A.; Scholz, D.; Bouchaou, L.; Dassie, E.; Jochum, K.P.; Edwards, R.L.; Cheng, H. Multi-decadal to centennial hydro-climate variability and linkage to solar forcing in the Western Mediterranean during the last 1000 years. Sci. Rep. 2018, 8, 17446. [Google Scholar] [CrossRef] [PubMed]
- Novello, V.F.; Vuille, M.; Cruz, F.; Stríkis, N.M.; de Paula, M.S.; Edwards, R.L.; Cheng, H.; Karmann, I.; Jaqueto, P.; Trindade, R.; et al. Centennial-scale solar forcing of the South American Monsoon System recorded in stalagmites. Sci. Rep. 2016, 6, 24762. [Google Scholar] [CrossRef] [PubMed]
- Pinault, J.-L. Resonantly Forced Baroclinic Waves in the Oceans: Subharmonic Modes. J. Mar. Sci. Eng. 2018, 6, 78. [Google Scholar] [CrossRef] [Green Version]
- Pinault, J.-L. Resonant Forcing of the Climate System in Subharmonic Modes. J. Mar. Sci. Eng. 2020, 8, 60. [Google Scholar] [CrossRef] [Green Version]
- Pinault, J.-L. Resonantly Forced Baroclinic Waves in the Oceans: A New Approach to Climate Variability. J. Mar. Sci. Eng. 2020, 9, 13. [Google Scholar] [CrossRef]
- Dansgaard, W. Stable isotopes in precipitation. Tellus 1964, 16, 438–468. [Google Scholar] [CrossRef]
- Rozanski, K.; Araguás-Araguás, L.; Gonfiantini, R. Isotopic patterns in modern global precipitation. In Climate Change in Continental Isotopic Records; Swart, P.K., Lohmann, K.L., McKenzie, J., Savin, S., Eds.; American Geophysical Union: Washington, DC, USA, 1993; pp. 1–37. [Google Scholar]
- Bony, S.; Risi, C.; Vimeux, F. Influence of convective processes on the isotopic composition (δ18O andδD) of precipitation and water vapor in the tropics: 1. Radiative-convective equilibrium and Tropical Ocean–Global Atmosphere–Coupled Ocean-Atmosphere Response Experiment (TOGA-COARE) simulations. J. Geophys. Res. Space Phys. 2008, 113, 19305. [Google Scholar] [CrossRef]
- Risi, C.; Bony, S.; Vimeux, F. Influence of convective processes on the isotopic composition (δ18O andδD) of precipitation and water vapor in the tropics: 2. Physical interpretation of the amount effect. J. Geophys. Res. Space Phys. 2008, 113, 19306. [Google Scholar] [CrossRef]
- Lachniet, M.S. Climatic and environmental controls on speleothem oxygen-isotope values. Quat. Sci. Rev. 2009, 28, 412–432. [Google Scholar] [CrossRef]
- Lachniet, M.S.; Patterson, W.P. Use of correlation and multiple stepwise regression to evaluate the climatic controls on the stable isotope values of Panamanian surface waters. J. Hydrol. 2006, 324, 115–140. [Google Scholar] [CrossRef]
- Li, G.; Cheng, L.; Zhu, J.; Trenberth, K.E.; Mann, M.E.; Abraham, J.P. Increasing ocean stratification over the past half-century. Nat. Clim. Chang. 2020, 10, 1116–1123. [Google Scholar] [CrossRef]
- Comas-Bru, L.; Atsawawaranunt, K.; Harrison, S.; SISAL Working Group Members. SISAL (Speleothem Isotopes Synthesis and AnaLysis Working Group) Database Version 2.0.; Dataset; University of Reading: Reading, UK, 2020. [Google Scholar] [CrossRef]
- GRIP Members. Climate Instability during the Last Interglacial Period Recorded in the GRIP Ice Core. Nature 1993, 364, 203–207. Available online: https://www.ncei.noaa.gov/pub/data/paleo/icecore/greenland/summit/grip/isotopes/gripd18o.txt (accessed on 5 August 2021). [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef] [Green Version]
- Fohlmeister, J.; Vollweiler, N.; Spötl, C.; Mangini, A. COMNISPA II: Update of a mid-European isotope climate record, 11 ka to present. Holocene 2012, 23, 749–754. [Google Scholar] [CrossRef]
- Burns, S.J. A 780-year annually resolved record of Indian Ocean monsoon precipitation from a speleothem from south Oman. J. Geophys. Res. 2002, 107, ACL-9. Available online: https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2001JD001281 (accessed on 5 August 2021). [CrossRef] [Green Version]
- Chen, S.; Hoffmann, S.S.; Lund, D.C.; Cobb, K.M.; Emile-Geay, J.; Adkins, J.F. A high-resolution speleothem record of western equatorial Pacific rainfall: Implications for Holocene ENSO evolution. Earth Planet. Sci. Lett. 2016, 442, 61–71. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Guo, Q.; Guo, Z.; Yin, Z.-Y.; Dong, B.; Smith, R. Where were the monsoon regions and arid zones in Asia prior to the Tibetan Plateau uplift? Natl. Sci. Rev. 2015, 2, 403–416. [Google Scholar] [CrossRef]
- Partin, J.W.; Quinn, T.M.; Shen, C.-C.; Emile-Geay, J.; Taylor, F.W.; Maupin, C.R.; Lin, K.; Jackson, C.; Banner, J.L.; Sinclair, D.J.; et al. Multidecadal rainfall variability in South Pacific Convergence Zone as revealed by stalagmite geochemistry. Geology 2013, 41, 1143–1146. [Google Scholar] [CrossRef] [Green Version]
- Kennett, D.J.; Breitenbach, S.F.M.; Aquino, V.V.; Asmerom, Y.; Awe, J.; Baldini, J.U.; Bartlein, P.; Culleton, B.J.; Ebert, C.; Jazwa, C.; et al. Development and Disintegration of Maya Political Systems in Response to Climate Change. Science 2012, 338, 788–791. [Google Scholar] [CrossRef] [Green Version]
- Maupin, C.R.; Partin, J.W.; Shen, C.-C.; Quinn, T.M.; Lin, K.; Taylor, F.W.; Banner, J.L.; Thirumalai, K.; Sinclair, D.J. Persistent decadal-scale rainfall variability in the tropical South Pacific Convergence Zone through the past six centuries. Clim. Past 2014, 10, 1319–1332. [Google Scholar] [CrossRef] [Green Version]
- Winter, A.; Zanchettin, D.; Miller, T.; Kushnir, Y.; Black, D.; Lohmann, G.; Burnett, A.; Haug, G.H.; Estrella-Martínez, J.; Breitenbach, S.F.M.; et al. Persistent drying in the tropics linked to natural forcing. Nat. Commun. 2015, 6, 7627. [Google Scholar] [CrossRef] [PubMed]
- Pinault, J.-L. Modulated Response of Subtropical Gyres: Positive Feedback Loop, Subharmonic Modes, Resonant Solar and Orbital Forcing. J. Mar. Sci. Eng. 2018, 6, 107. [Google Scholar] [CrossRef] [Green Version]
- van Hengstum, P.; Donnelly, J.P.; Fall, P.L.; Toomey, M.R.; Albury, N.A.; Kakuk, B. The intertropical convergence zone modulates intense hurricane strikes on the western North Atlantic margin. Sci. Rep. 2016, 6, 21728. [Google Scholar] [CrossRef] [PubMed]
- Arbuszewski, J.A.; Demenocal, P.; Cléroux, C.; Bradtmiller, L.; Mix, A. Meridional shifts of the Atlantic intertropical convergence zone since the Last Glacial Maximum. Nat. Geosci. 2013, 6, 959–962. [Google Scholar] [CrossRef]
- Knudsen, M.F.; Seidenkrantz, M.-S.; Jacobsen, B.H.; Kuijpers, A. Tracking the Atlantic Multidecadal Oscillation through the last 8,000 years. Nat. Commun. 2011, 2, 178. [Google Scholar] [CrossRef]
- Haug, G.H.; Hughen, K.A.; Sigman, D.M.; Peterson, L.C.; Röhl, U. Southward Migration of the Intertropical Convergence Zone Through the Holocene. Science 2001, 293, 1304–1308. [Google Scholar] [CrossRef]
- Chiang, J.C.H.; Bitz, C.M. Influence of high latitude ice cover on the marine Intertropical Convergence Zone. Clim. Dyn. 2005, 25, 477–496. [Google Scholar] [CrossRef]
- Donohoe, A.; Marshall, J.; Ferreira, D.; McGee, D. The relationship between ITCZ location and cross equatorial atmospheric heat transport; from the seasonal cycle to the Last Glacial Maximum. J. Clim. 2013, 26, 3597–3618. [Google Scholar] [CrossRef]
- Collins, J.A.; Schefuß, E.; Heslop, D.; Mulitza, S.; Prange, M.; Zabel, M.; Tjallingii, R.; Dokken, T.M.; Huang, E.; Mackensen, A.; et al. Interhemispheric symmetry of the tropical African rainbelt over the past 23,000 years. Nat. Geosci. 2010, 4, 42–45. [Google Scholar] [CrossRef]
- Baker, P.A.; Seltzer, G.O.; Fritz, S.C.; Dunbar, R.B.; Grove, M.J.; Tapia, P.M.; Cross, S.L.; Rowe, H.D.; Broda, J.P. The History of South American Tropical Precipitation for the Past 25,000 Years. Science 2001, 291, 640–643. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chiang, J.C.H.; Biasutti, M.; Battisti, D.S. Sensitivity of the Atlantic Intertropical Convergence Zone to Last Glacial Maximum boundary conditions. Paleoceanography 2003, 18, 1094. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, M.W.; Spero, H.J. Meridional shifts in the marine ITCZ and the tropical hydrologic cycle over the last three glacial cycles. Paleoceanography 2011, 26, 1206. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).