Energy Spectra of Ensemble of Nonlinear Capillary Waves on a Fluid

Abstract

The problem of spectral description of the nonlinear capillary waves on the fluid surface is discussed. Usually, three-wave nonlinear interactions are considered as a major factor determined by the energy spectrum of these waves in the kinetic wave turbulent regime. We demonstrate that four-wave interactions should be taken into account. In this case, there are two possible scenarios for the transfer of energy over the wave spectrum: kinetic and dynamic. The first is described by the averaged stochastic interaction of waves using the kinetic equation, while the second is described by dynamic equations written for discrete modes. In this article, we compare the time scales, spectral shapes, and other properties of both energy cascades, allowing them to be identified in an experiment.

1. Introduction

It is a well-known fact that internal waves in the ocean manifest on the sea surface via their interaction with short gravity and capillary waves, e.g., [1,2,3]. The description of the wind ripple is a very difficult task due to its strong nonlinearity, breaking effects and wind interaction. Moreover, even if capillary waves are not bounded and have small amplitudes, their dynamics are not completely understood, and a lot of laboratory experiments have been recently conducted aiming to gain more insight, for instance [4,5,6,7] and many others. Two recent reviews should be mentioned in this context. In the first of them [8], the existing methods for the experimental study of capillary waves are considered, and a novel technical device is proposed that provides high measurement accuracy and allows the study of elasticity, surface tension and wavelength. The theoretical approach in this review is limited to linear waves. The second review [9] is devoted to nonlinear gravitational-capillary waves, in which the effects of nonlinearity, dissipation, and the finite size of the wave system are studied experimentally and theoretically. Both surveys are provided with an extensive bibliography.

Due to the new possibilities of experimental studies of capillary waves, the need for more detailed theoretical studies has also increased, which would allow a deeper understanding of the newly available measurement data. Capillary waves that appear on the surface of a liquid are found both in large natural reservoirs and in various technical systems, such as electrolytic solutions, oil films, trapping bubbles, rupture of a gas thread, etc., which determines their particular importance and necessity of deep theoretical study. In this work, we restrict ourselves to the study of nonlinear capillary waves.

Theoretically, the first analysis of nonlinear interaction of capillary waves was conducted in pioneer work by Zakharov and Filonenko [10]. In this paper, the kinetic equation for three-wave interactions of capillary waves is first written out, and its stationary solution is found in the form of the power energy spectrum. The kinetic wave turbulence theory is based on a number of assumptions, the main of them being as follows: (I) weak nonlinearity (nonlinearity is small but non-zero and defined by a small parameter ε << 1; (II) randomness of phases (all waves interact with each other stochastically); (III) infinite-box limit L/λ → ∞, where L is the size of the system and λ is characteristic wavelength; (IV) existence of an inertial interval in the wavenumber space (k₀, k₁), where energy input and dissipation are balanced; (V) locality of interactions in k-space (only waves with wavelengths of the same order do interact; (VI) interactions are locally isotropic (no dependence on direction); (VII) at initial moment energy is distributed among an infinite number of modes. Under these and other assumptions, wave kinetic equations have stationary solutions in the form of energy power spectra E_k~k^−ν, ν > 0 [11], with k being the length of the wave vector k. These spectra are called kinetic spectra or K-spectra.

In the case when the dispersion function depends only on one dimensional parameter, say the gravity constant g for water surface gravity waves or surface tension σ for capillary waves, one can compute ν using dimensional analysis, without solving the corresponding kinetic equation. For example, for a direct cascade we have:

ν = 2α + d − 6 + (5 − 3α − d)/(N − 1)

(1)

where α is defined by the form of dispersion function $\mathsf{\omega }~k^{\mathsf{\alpha }}$, d is the space dimension of the system and N is the minimal number of waves constituting a resonance interaction.

As it was mentioned above, for kinetic wave turbulence theory to occur, a number of assumptions must hold, some of which are not easily verified in a laboratory. However, the advantage, in this case, is that the knowledge of dispersion function in a wave system immediately yields the explicit form of energy distribution over the scales.

On the other hand, if we abandon any one of these assumptions, the form of energy distribution will be changed drastically. For instance, in the realistic laboratory set up, narrow frequency band excitation is used. In this case, not a statistically described K-cascade is observed but a D-cascade formed by a set of distinct modes first introduced in [12]; this process is described by dynamic equations [13]. The spectrum of the D-cascade can be computed deterministically by the increment chain equation method; its form depends on the excitation parameters [14]. During the formation of a D-cascade spectrum, broadening occurs in such a way that after 10 steps of the D-cascade, more than 1000 non-cascading modes become excited, thus forming a distributed energy state and later possibly a K-cascade.

In this paper, we analyze the spectra formed in K- and D-cascades of the capillary waves and give some clues for understanding whether a K-cascade or a D-cascade is observed in an experiment.

2. Three-Wave Interactions of Capillary Waves

As was mentioned above, kinetic wave turbulence theory is developed for initially distributed systems and is based on a number of assumptions. One of the main steps while developing a corresponding wave kinetic equation is to determine the minimal possible resonance in the wave system under consideration. Capillary waves are usually regarded as a three-wave system, while three-wave resonance conditions for capillary water waves have infinitely many solutions. However, there are important properties of the resonance solutions that should be checked before deciding whether a wave system may be regarded as a three-wave system or also four-wave interactions should be taken into account. These properties (I)–(VII) have been listed in the Introduction. Below, in this section, we study the properties for three-wave resonant interactions of capillary water waves aiming to check the properties (I)–(VII).

2.1. Space Dimension and Wavevector’s Coordinates

Three-wave resonance conditions for capillary water waves with dispersion function $\mathsf{\omega }=\mathsf{\sigma }{k}^{3/2}$ read

$$k_1^{3/2}+k_2^{3/2}=k_3^{3/2},\hspace{1em}{k}_1+k_2=k_3$$

(2)

and characteristic behavior of the ensemble of waves depends on whether the characteristic lengths of the wave vectors are comparable with the size of the interaction domain or not. In the first case, the interaction should be regarded in the bounded domain and correspondingly, the wavevector coordinates should be integers. Otherwise, the interaction domain is infinite, and coordinates are described by real numbers. Another important characteristic of the ensemble evolution is the dimensions of the wavevector. Accordingly, there are following cases to study.

Case 1. Wavevectors $k_j\in {\overrightarrow{Z}}^d$ have integer coordinates (1, 2, 3, e.g., wave interactions in a bounded domain are regarded) and d is arbitrary. In this case, Equation (2) has no solution for arbitrary dimension d of the wave vectors [15].

Case 2. Wavevectors $k_j\in R^1$ have real coordinates and d = 1. In this case,

$$k_1^{3/2}+k_2^{3/2}={(k_1+k_2)}^{3/2}\Rightarrow k_1=0\hspace{0.17em}\mathrm{or}\hspace{0.17em}{k}_2=0,$$

(3)

and one can see immediately that for all positive $k_j$, the right-hand side of Equation (3) is always greater than its left-hand side if both $k_j\ne 0$. If $k_1=k,\hspace{0.17em}{k}_2=ck,$ with some constant 1 ≤ c ≤ 10 (cf. V), absolute resonance width

$${\Delta }_A=\left|{\mathsf{\omega }}_1+{\mathsf{\omega }}_2-{\mathsf{\omega }}_3\right|=\left|k^{3/2}+c^{3/2}{k}^{3/2}-{[(c+1)k]}^{3/2}\right|\to$$

(4)

$${\Delta }_A=k^{3/2}\left|1+c^{3/2}-{(c+1)}^{3/2}\right|>\frac{3\sqrt{c}}{2}{k}^{3/2}$$

(5)

is rapidly growing function of k when $k_j\to \infty$ (cf. III). In particular, if $k_1=\hspace{0.17em}{k}_2=k,$ ${\Delta }_A\approx 0.82k^{3/2}$.

Case 3. Wavevectors $k_j\in R^2$ have real coordinates, d = 2, and all three wavevectors are collinear. This case can obviously be reduced to the previous one by an appropriate rotation of coordinate axes.

Case 4. Wavevectors $k_j\in R^2$ are real valued and non-collinear. One might argue that if in this case, a great amount of almost collinear wavevectors form approximate triads with small resonance width, we still can expect manifestation of a three-wave kinetic regime in laboratory experiments in the form of power energy spectrum $E_{k,3}~k^{-7/2}$. This case has been studied numerically, and the results are as follows.

2.2. Resonance Width

Absolute resonance width ${\Delta }_A$ explicitly depends on $k_1$, and considering if it is “small” or “large”, the value of $k_1$ should, of course, be taken into account. It is intuitively clear that for larger vectors, larger resonance width is tolerable, and vice versa. Relative resonance width ${\Delta }_R$, allowing to distinguish between various wave turbulent regimes, might be introduced in a number of ways, e.g., [16,17] and others; the problems with introducing a general cumulative function ${\Delta }_R$ are discussed in [12], Chapter 6.

To perform a numerical study of solutions of Equation (2), for a pair of two-dimensional wave vectors $k_1=(m_1,n_1)$, $k_2=(m_2,n_2)$, we define relative resonance width as absolute resonance of a proportional pair with norm 1, understanding by the norm of a pair of two-dimensional vectors that of the corresponding vector in $R^4$: $\Vert (k_1,k_2)\Vert =\sqrt{m_1^2+n_1^2+m_2^2+n_2^2}$ so that

$${\Delta }_R=\left|\left({\left({\tilde{m}}_1^2+{\tilde{n}}_1^2\right)}^{3/4}+{\left({\tilde{m}}_2^2+{\tilde{n}}_2^2\right)}^{3/4}-{\left({\left({\tilde{m}}_1+{\tilde{m}}_2\right)}^2+{\left({\tilde{n}}_1+{\tilde{n}}_2\right)}^2\right)}^{3/4}\right)\hspace{0.17em}\right|$$

(6)

where ${\tilde{m}}_j=m_j/\Vert (k_1,k_2)\Vert$ and ${\tilde{n}}_j=n_j/\Vert (k_1,k_2)\Vert$ with j = 1,2.

2.3. Wavenumbers and Angles

Our first series of numerical simulations served to cast a first glance at distribution of wavevectors satisfying Equation (2) in the k-space, primarily, if they are distributed evenly over the computation domain or concentrated in some restricted subdomains. Calculations were performed on $Z^d$ grid fragments $-50<m_1,n_1,m_2,n_2<50$ or $0<m_1,n_1,m_2,n_2<100$.

Exact resonances (with ${\Delta }_R=0$) are achieved for pairs ($k_1,\hspace{0.17em}0$) and ($0,\hspace{0.17em}{k}_2$) only (cf. Case 1), while for all other pairs ($k_1,\hspace{0.17em}{k}_2$), approximate interactions may take place. In Figure 1, left panel, all wavevectors $k_1,\hspace{0.17em}{k}_2$ with non-negative coordinates taking part in approximate interactions are shown, and their distribution appears to be fairly even. However, if one of the wavevectors, say $k_1$, has non-negative coordinates, all $k_2$ interacting with such (Figure 1b) are distributed in k-space quite irregularly, leaving the third quadrant and the most part of the first quadrant completely empty. Irregularity becomes even more striking if we consider interacting pairs where both $k_1,\hspace{0.17em}{k}_2$ have non-negative coordinates (Figure 1c). The most part of the domain consists of wavevectors not participating in interactions, while interacting vectors are contained in narrow triangles along the axes. Moreover, a simple check shows that wavevectors from the lower triangle only interact with vectors from the upper triangle and vice versa; this is shown in the Figure 1a.

2.4. Norms of Wavevectors

To characterize the ratios of norms of interacting vectors and angles between them, for each solution, we computed the ratio of the vector norms $k_1/\hspace{0.17em}{k}_2$ and the corresponding angle ($k_1\wedge k_2$) (see Figure 2).

It can be seen immediately that the solution set is highly anisotropic—angles between interacting wavevectors all belong to the narrow band between 75° and 87°, i.e., interacting wavevectors are almost perpendicular. Norms of the interacting wavevectors can differ by more than 2 orders (Figure 2a)—the maximal ratio found in our solution set is $k_1/k_2$ = 101.8. For more than 10% of all the solutions, $k_1/k_2$ > 10. Restricting our attention to interactions of wavevectors with norms of the same order makes angle anisotropy even more pronounced (Figure 2b); all angles now lie between 75° and 81°, i.e., the bandwidth becomes twice smaller. Standard averaging by angles spectra [15] obviously cannot give any reliable information in this case.

2.5. Resonance Curves

The solution distribution irregularities demonstrated above have an elegant explanation. Indeed, let us notice two simple properties of the resonance set of wavevectors satisfying Equation (2). If a pair $(k_1,k_2)$ is a solution, then every $(c{k}_1,c{k}_2)$ is also a solution for any $c\in R$, and every rotated pair is also a solution. Therefore, it is enough to compute all vectors $k_2$ producing resonant interactions with some given $k_1$, say $k_1$ = (0, 1), to obtain a clear view of the whole resonant interaction set. 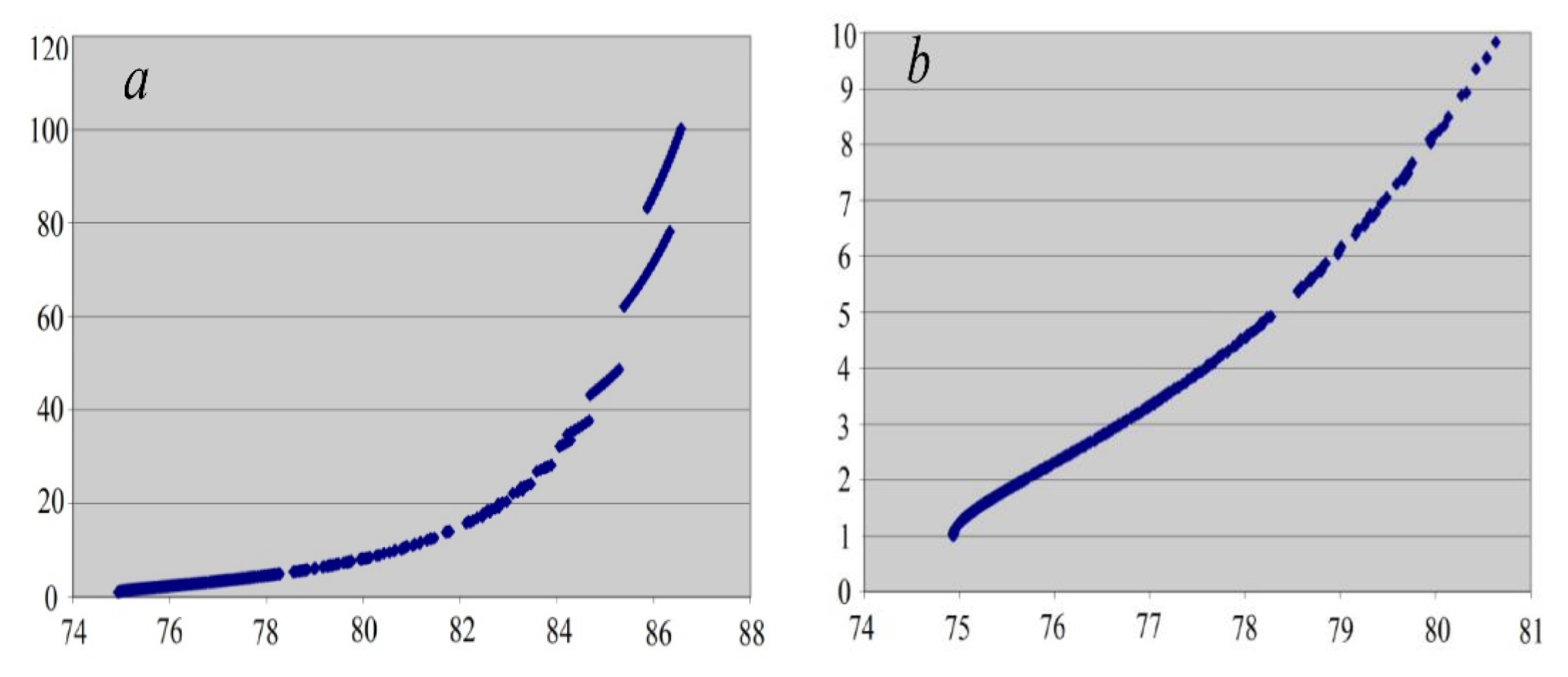Indeed, all resonance partners of $k_1$ = (0, 1) constitute a smooth curve, as shown in Figure 3. This curve, as a function n(m), starts with a flat region $n~m^{3/2}$ (Figure 3a), then becomes steeper and for m → ∞ has asymptotic $n~m^{1/2}$ (Figure 3b).

Notice that the two asymptotic regions lie a few magnitudes of 10 apart and cannot be illustratively presented in one figure, so we proceed with a schematic representation (Figure 4).

The tangent to the curve drawn from (0, 0) gives $k_2$ with the minimal angle to $k_1$ ~ 74.9. We also see that the unit vector can interact both with vectors of arbitrarily small and arbitrarily large norms $\hspace{0.17em}{k}_2$. Notice that both for $\hspace{0.17em}{k}_2\to 0$ and $\hspace{0.17em}{k}_2\to \infty$, the angle between $k_1$ and $k_2$ $\to \pi /2$. Now, any vector k ∈ R can be produced by stretch and rotation of our unit vector, and its resonance curve is obtained by stretching the curve of the unit vector (with the same coefficient) and rotation (by the same angle). If two vectors interact resonantly, then each of them lies on the resonance curve of another (Figure 4b). We may conclude with confidence that conditions for a three-wave kinetic regime to occur are decidedly violated.

A K-spectrum relies on the broad excitation, and in a usual laboratory experiment or numerical simulation, we have to deal with narrow frequency band excitation. The standard assumption of the kinetic theory is that starting with one excited frequency, a necessary Gaussian distribution will be established. The transition from one-mode excitation to the broad excitation is described by dynamic energy cascade formed by the set of distinct modes and can be computed by the increment chain equation method (ICEM) [13]. How to apply it for the case of capillary waves is shown in the next section.

3. Dynamic Energy Cascade of Capillary Waves

The model of the dynamic energy cascade—D-cascade—generation was first proposed in [12]; the physical mechanism underlying the formation of a D-cascade is modulation instability. The phenomenon of modulation instability has been encountered in various fields and is known under different names, such as parametric instability in classical mechanics, Suhl instability of spin waves, Oraevsky–Sagdeev decay instability of plasma waves, modulation instability in nonlinear optics, Benjamin–Feir instability in deep water waves, etc.

Modulation instability is the physical phenomenon that can be described as the decay of a carrier wave $\hspace{0.17em}{\mathsf{\omega }}_0$ into two side-bands $\hspace{0.17em}{\mathsf{\omega }}_1,\hspace{0.17em}{\mathsf{\omega }}_2$:

$$\hspace{0.17em}{\mathsf{\omega }}_1+\hspace{0.17em}{\mathsf{\omega }}_2=2{\mathsf{\omega }}_0,k_1+\hspace{0.17em}{k}_2=2k_0+\mathsf{\theta },$$

(7)

$$\hspace{0.17em}{\mathsf{\omega }}_1={\mathsf{\omega }}_0+\Delta \mathsf{\omega },\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathsf{\omega }}_2={\mathsf{\omega }}_0-\Delta \mathsf{\omega },\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<\Delta \mathsf{\omega }<<1.$$

(8)

A wave train with initial real amplitude A, wavenumber $k=\left|\overrightarrow{k}\right|$ and frequency $\hspace{0.17em}\mathsf{\omega }$ is modulationally unstable if

$$0\le \Delta \mathsf{\omega }/Ak\mathsf{\omega }\le \sqrt{2}.$$

(9)

Equation (9) described the so-called instability interval for the wave systems with a small nonlinearity of the order of ε~0.1 to 0.2, as first obtained in [17]. It is also established for gravity surface waves that the most unstable modes in this interval satisfy the condition

$$\Delta \mathsf{\omega }/Ak\mathsf{\omega }=1.$$

(10)

The essence of the increment chain equation method is the use of Condition (10) for computing the frequencies of the cascading modes. In the first step of the D-cascade, an excited wave with frequency $\hspace{0.17em}{\mathsf{\omega }}_0$ is regarded as the carrier mode. The distance to the next cascading mode $\hspace{0.17em}\Delta \mathsf{\omega }=\left|{\mathsf{\omega }}_0-{\mathsf{\omega }}_1\right|$ with frequency $\hspace{0.17em}{\mathsf{\omega }}_0$ is chosen in such a way that Condition (10) is satisfied; it is called the maximum increment condition.

In the next step of the D-cascade, the mode with frequency $\hspace{0.17em}{\mathsf{\omega }}_1$ is regarded as a carrier mode for the next step of the D-cascade, and so on. This procedure can easily be written out as a recursive relation between neighboring cascading modes:

$$\hspace{0.17em}\sqrt{p_n}{A}_n=A({\mathsf{\omega }}_n\pm {\mathsf{\omega }}_n{A}_n{k}_n)$$

(11)

Here, the notation $\hspace{0.17em}{p}_n$ is chosen for the fraction of energy transported from the cascading mode $\hspace{0.17em}{A}_n$ to the cascading mode $\hspace{0.17em}{A}_{n+1},$ i.e., $A_{n+1}=\hspace{0.17em}\sqrt{p_n}{A}_n.$ Equation (11) describes two chain equations: one chain equation with “+” for a direct D-cascade with $\hspace{0.17em}{\mathsf{\omega }}_n<{\mathsf{\omega }}_{n+1}$ and another chain equation with “-” for an inverse D-cascade with $\hspace{0.17em}{\mathsf{\omega }}_n>{\mathsf{\omega }}_{n+1}$. All computations below are given for a direct D-cascade. Computations for the inverse cascade are quite similar; they are omitted.

Theoretically, $\hspace{0.17em}{p}_n=p_n(A_0,{\mathsf{\omega }}_0,n)$ is a function of the excitation parameters $A_0,{\mathsf{\omega }}_0$ and the step n. However, as in a lot of experiments, it is established that $\hspace{0.17em}{p}_n$ depends only on the excitation parameters and does not depend on the step n. All the formulae below are given for this case. Accordingly, the notation p is used instead of the notation $\hspace{0.17em}{p}_n$. This means that $\hspace{0.17em}{A}_{n+1}=\sqrt{p}{A}_n=p^{n/2}{A}_0$, and as energy $\hspace{0.17em}{E}_n~A_n^2$, it follows $\hspace{0.17em}{E}_n~p^n{A}_0^2$, i.e., the energy spectrum of the D-cascade has an exponential form as in experimental data for capillary waves, e.g., [6,7].

Taking the Taylor expansion of the RHS of the chain equation and regarding only the two first terms of the resulting infinite series, one can derive a very simple ordinary differential equation describing stationary amplitudes of the cascading modes satisfying Condition (10):

$$\sqrt{p}{A}_n\approx A_n+{A^{\prime }}_n{\mathsf{\omega }}_n{A}_n{k}_n\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{A^{\prime }}_n=\frac{\sqrt{p}-1}{{\mathsf{\omega }}_n{k}_n}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow$$

(12)

$$A({\mathsf{\omega }}_n)=(\sqrt{p}-1){\displaystyle \int \frac{d{\mathsf{\omega }}_n}{{\mathsf{\omega }}_n{k}_n}+C({\mathsf{\omega }}_0,A_0)}$$

(13)

where $\hspace{0.17em}{\mathsf{\omega }}_0,\hspace{0.17em}{A}_0$ are excitation parameters.

The maximum increment condition for the weakly nonlinear capillary waves with ε ~ 0.1–0.2 differs from Equation (10) by the constant coefficient 1/24:

$$\left(\Delta \mathsf{\omega }\right)/\left(\frac{1}{24}\mathsf{\omega }Ak\right)=1$$

(14)

as was first shown in [17]. As for capillary waves $\mathsf{\omega }(k)~k^{3/2}$, one obtains easily, e.g., for direct D-cascade that

$$(\sqrt{p}-1)\approx \frac{1}{24}{A^{\prime }}_n{\mathsf{\omega }}_n^{5/3}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow$$

(15)

$$E{({\mathsf{\omega }}_n)}^{(Dir)}~{\left[\frac{(1-\sqrt{p})}{16}{\mathsf{\omega }}_n^{-2/3}+C^{(Dir)}\right]}^2$$

(16)

where $C^{(Dir)}=A_0-\frac{1-\sqrt{p}}{16}{\mathsf{\omega }}_0^{-2/3}.$

4. Discussion

We have demonstrated above that for describing K-spectrum of the system of capillary waves with distributed initial state, we have to take into account four-wave resonances, i.e., take N = 4 in Equation (1). As energy spectra depend on a number of parameters, it would be interesting to see how different their shapes are. For comparing energy spectra $\hspace{0.17em}{E}_k$ and $\hspace{0.17em}{E}_n$, it is convenient to rewrite $\hspace{0.17em}{E}_n$ as $\hspace{0.17em}{E}_n=b^{-n}{E}_0$ with b = 1/p, b > 1. Thus, we have to compare functions $\hspace{0.17em}{\mathsf{\gamma }}_1\cdot b^{-x}$ and $\hspace{0.17em}{\mathsf{\gamma }}_2\cdot x^{-a}$, where the magnitudes of parameters $\hspace{0.17em}a,\hspace{0.17em}b,\hspace{0.17em}{\mathsf{\gamma }}_1,\hspace{0.17em}{\mathsf{\gamma }}_2$ are defined by the specific wave system. As for a, b > 1

$$\hspace{0.17em}\underset{x\to \infty }{\lim }(x^a/b^x)=0,$$

(17)

$\hspace{0.17em}{E}_k>E_n$ in the long run. However, for some combinations of parameters and in some finite domains in k-space, the opposite relation can take place, $\hspace{0.17em}{E}_k<E_n$. The spectra $\hspace{0.17em}{E}_k$ and $\hspace{0.17em}{E}_n$ might be quite close and even coincide for some k (see Figure 5, left panel).

As the formation of the D-cascade is accompanied by the spectrum broadening, at some moment of time, the phases become stochastic, s-wave resonant interactions may appear and the kinetic regime may be developed (shown schematically in Figure 5, right panel).

Our conclusions concerning four-wave interactions and spectrum broadening by generating discrete harmonics. the formation of a D-cascade is supported by the experimental data in [4,6], where experiments were performed in cylindrical containers with distilled water that were shaken vertically at different frequencies. Diameters of containers varied from 10 to 20 cm, monochromatic excitation in the range of 0.5 to 3500 Hz was used and the surface perturbations are detected using the reflection of laser beam of 5 mm diameter off the water surface.

Indeed, the evidence of strong four-wave coupling in nonlinear capillary waves has been identified in [4] by computing tricoherence as

$${\mathsf{\tau }}^2={\left|\langle F_1{F}_2{F}_3{F}_{1+2-3}^{*}\rangle \right|}^2/\langle {\left|F_1{F}_2{F}_3\right|}^2\rangle \langle {\left|F_{1+2-3}\right|}^2\rangle ,$$

where $\hspace{0.17em}{F}_j$ is the Fourier component of the surface elevation at the frequency $\hspace{0.17em}{\omega }_j$. In general, tricoherence $\hspace{0.17em}{\tau }^2$ can change from 0 (no phase coupling) to 1 (coherent phases); in experiments reported in [4], the level of tricoherence $\hspace{0.17em}{\tau }^2>0.5$ has been observed for a wide range on the initial data, while bicoherence drops below < 0.2 under the spectrum broadening.

It was also observed in these experiments that the total energy of $\hspace{0.17em}{E}_{tot}$ of the system is contained in a zero-frequency band and a set of discrete modes forming the D-cascade at lower forcing. The kinetic cascade occurs first at frequencies about 220 Hz, and its energy grows (with an increase in the forcing frequency) from $\hspace{0.17em}0.01E_{tot}$ to $\hspace{0.17em}0.23E_{tot}$, while energy contained in the dynamic cascade decreases from $0.82E_{tot}$ to $0.46E_{tot}.$

There is another fact that is easily checked in an experiment. As it follows from the difference in the magnitudes of the small parameters for two cascades, a dynamical cascade is formed much faster compared to a kinetic one. In particular, for capillary water waves with the dispersion function ${\mathsf{\omega }}^2=\mathsf{\sigma }{k}^3/p$, the density $\mathsf{\rho }={10}^3{\mathrm{kg}/\mathrm{m}}^3$ and the coefficient of surface tension $\mathsf{\sigma }=72.75\cdot {10}^{-3}\mathrm{kg}\cdot {\mathrm{m}/\mathrm{s}}^2$, it is easy to compute the corresponding characteristic times. Indeed, say for wavelength 1 mm, we have: wave period is 0.0022 s; time scale for the D-cascade formation is 0.22 s and time scale for four-wave K-cascade is 2200 s, which is approximately 37 min. An experiment reported in [4,6] lasted no more than 15–20 min each (personal communication, Michael Shats).

The main characteristics that allow distinguishing between kinetic and dynamic cascades that can be easily observed in experimental data are summarized in

Table 1. Main characteristics of K-cascade and D-cascade.

Property	$\hspace{0.17em}{\mathit{E}}_{\mathit{k}}$	$\hspace{0.17em}{\mathit{E}}_{\mathit{n}}$
Coherent phases	no	yes
Dependence on the excitation parameters	no	yes
Local interactions	yes	no
Existence of inertial interval	yes	not important
Small parameter	$~{10}^{-2}$	$~{10}^{-1}$

below.

The understanding of differences between dynamic and kinetic cascades is of the utmost importance for the correct interpretation of the experimental observations. Thus, in [5], weak turbulence of capillary waves in Helium has been studied, and the formation of a local maximum of the wave-spectrum near a viscous cut-off was observed (under periodic driving force) and correctly attributed to the discrete regime (interactions are non-local).

On the other hand, the authors conclude that “n the inertial range, the dependence of the peak amplitudes on frequency is described well by a power law function $\hspace{0.17em}{I}_{\mathsf{\omega }}~{\mathsf{\omega }}^{-m}$ with the index $\hspace{0.17em}m\approx 3.7$. This is in agreement with the weak turbulence theory, which gives the value m = 21/6″ [5] (p.032001-3). As 21/6 = 3.5, the observed and predicted indexes differ by about 6%. It would be worth checking phase coherence in these data in order to understand whether this discrepancy is due to the available accuracy of measurements or a dynamic cascade is observed and not a kinetic one.

As the form of a D-cascade and a K-cascade might be pretty similar for some parameters of initial excitation, the main characteristic that should checked while estimating the measured data are time scales for the cascade formation, as explained in detail in [18].

5. Conclusions

In the system of weakly nonlinear capillary waves, two types of energy cascades are theoretically predicted: K-cascade, formed by three-wave resonances in a system with a distributed initial state, and D-cascade, formed by four-wave resonances of a special form, in the systems with narrow frequency band excitation. As we have shown above,

(1)

A K-cascade among capillary waves cannot be formed by three-wave resonant interactions; four-wave resonant interactions should be regarded instead. Accordingly, a K-cascade of capillary waves is formed at the time scale $1/{\mathsf{\epsilon }}^4$ with $\mathsf{\epsilon }~{10}^{-2}$.

(2)

A D-cascade is always formed at the time scale $1/{\mathsf{\epsilon }}^2$ with $\mathsf{\epsilon }~{10}^{-1}$, i.e., it develops much faster than a K-cascade; known laboratory experiments with capillary waves confirm the time scale of the D-cascade, e.g., [4,6,7].

(3)

The absence of three-wave resonances of capillary waves has also been noticed in numerical simulations [19,20] and was coined by the term “frozen turbulence”. This has been attributed to the interplay of two facts: the discretization of the numerical scheme and the absence of exact three-wave resonances among capillary waves with integer wave numbers, as first proven in [14]. It was observed that capillary waves demonstrate “fluxless modes, there is virtually no energy absorption associated with high-wavenumbers damping in this case” ([20], p. 107).

(4)

Speaking very generally, if dispersion function $\hspace{0.17em}\mathsf{\omega }(k)$ has a decay type, this only means that three-wave resonance conditions

$$\hspace{0.17em}\mathsf{\omega }(k_1)+\mathsf{\omega }(k_2)=\mathsf{\omega }(k_3),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{k}_1+k_2=k_3$$

(18)

may have solutions with real $\hspace{0.17em}{k}_j$, even an infinite number of solutions. However, this does not necessarily mean that these solutions possess the properties necessary for the deduction of the wave kinetic equation. In particular, if $\hspace{0.17em}\mathsf{\omega }(k)~k^{\mathsf{\gamma }},\gamma >1$, then both properties formulated in Section 2 hold and the geometry of resonances can be outlined in terms of resonance curves similar to those shown in Figure 4.

The results presented in this paper are obtained for an ensemble of free nonlinear capillary waves formed from initial monochromatic disturbance. The next step will be an analysis of the ensemble of capillary waves in present of current induced by the internal waves.