1. Introduction
Almost all modeling of the dynamic processes occurring in the coastal zone of the sea begin with estimates of the wave parameters. When approaching the shore and with decreasing water depth, the waves transform, becoming steeper and more asymmetrical, and then breaking. The process of wave breaking is characterized by significant losses of their energy. Changes in the steepness of waves and their asymmetry, occurring both due to linear and nonlinear processes and due to breaking, lead to a change in the higher statistical moments of wave motion, which determine the magnitude and the direction of sediment flow in the coastal zone [
1].
There are a number of models that describe, with high accuracy, the linear and nonlinear transformation of waves over the real bottom topography in the coastal zone. However, dissipation processes have been much less studied. There is no generally accepted and well-tested model of wave energy dissipation in the surf zone or an accurate physical description of changes in wave properties during the dissipation process [
2]. In general wave models can be divided in to phase resolving and phase averaged. The first usually are solved using hydrodynamic equations in the time domain, and the second represent the wave spectrum evolution in the frequency domain based on the wave action balance equation (for example, SWAN (Simulating WAves Nearshore) model). Some phase resolving wave models are solved by spectral methods in the frequency domain that are less time-consuming in modeling as compared to the time domain simulation. Spectral method modeling results in the complex amplitudes of wave harmonics (deterministic models [
3,
4,
5]) or the modulus of complex amplitudes and biphases (stochastic models [
6]). Together with the modeling of the spectrum itself, phase-resolving models allow using the inverse Fourier transform to determine the free surface elevations and the velocity field.
The main difficulty in accurate representation and modeling wave breaking in phase-resolving models is to account for the spatio-temporal occurrence of breaking events in combination with the type of wave breaking. Recent investigations confirm that models can reproduce the overall behavior of wave breaking dissipation, but this does not necessarily mean that the process itself is modeled with physically accuracy [
7]. In spectral-type models, the main challenge is to describe the effect of wave energy dissipation due to breaking on the frequency structure of waves and wave spectrum shape [
4].
To assess the effect of wave breaking on the amplitudes of wave harmonics and wave spectrum shape, two approaches are now used:
(1) the wave breaking does not change the shape of the spectrum, but only reduces the spectral density of waves by the same factor for all frequencies, so-called independent wave energy dissipation [
8,
9,
10];
(2) the spectral density during wave breaking decreases, depending on the square of the frequency [
4,
11].
The use of the uniform wave energy dissipation coefficient for modeling in spectral phase-resolving models showed a fairly good agreement between the model and experimental results [
10,
12]. The concept of uniform or frequency-independent (or uniform) energy dissipation is often used in modeling the evolution of spectra in phase-averaged models, for example, SWAN. Spectral shapes in shallow water areas are modified by triad wave interaction equations in phase-averaged spectral wave models.
The combination of the two approaches offers an empirical formula that assumes a partial dependence of the dissipation coefficient on the square of the frequency: during wave breaking in one frequency range of the first and lowest harmonics the energy decreases uniformly, but in the high-frequency range it has quadratic dependence on the frequency [
4,
13]. The quadratic type of the dependence was shown theoretically using the equations of the eddy viscosity model [
11]. There are some other frequency dependencies of energy dissipation; for example, the dependence on the fourth power of frequency was demonstrated in [
14].
By comparing laboratory experimental data and modeling, it was found that in the case of using a finite-difference model of eddy viscosity for modeling breaking waves, the dependence of the rate of dissipation of wave energy on frequency is inversely proportional to the spectral density for waves with a random phase. However, this dependence does not hold for wave groups. It was noted that, apparently, wave groups on the whole are subject to dissipation to a greater extent than waves, equivalent in spectral parameters without a group structure [
15].
Based on the data of two field experiments, it was shown that in the outer part of the surf zone, the dissipation of wave energy is practically independent of frequency, and in the inner part of the surf zone, there is either a partially quadratic or selective (at frequencies of the second and third harmonics) dependence of the wave energy dissipation on frequency. It was noted that the type of frequency dependence of the dissipation of wave energy inside the surf zone is determined by the wave asymmetry and the bottom slope [
16]. Increased values of energy dissipation at frequencies of the second and third harmonics were also obtained in laboratory experiments described in [
17].
Comparison of the simulation results with the data of laboratory and field experiments [
12] showed that the exact form of the frequency dependence of energy dissipation is not so important for calculating and modeling wave spectra. However, by comparing the simulation results with experimental data, it was shown that the exact form of the frequency dependence of energy dissipation has a significant effect on the values of the higher wave statistical moments obtained from the elevations of the free surface, which is of great importance for assessing the processes of sediment transport (for example, [
14,
18]).
Analysis of waves breaking in the surf zone showed that the energy losses observed in the wave spectrum are primarily the result of nonlinear transfer from the spectral peak to higher frequencies, and therefore energy dissipation occurs mainly in the high-frequency part of the spectrum [
19]. This indicates that nonlinear processes can play a more significant role in the transformation of the wave spectrum than processes caused by collapse. As studies of recent years have shown, nonlinear processes of wave transformation largely determine the processes of breaking. For example, the different frequency composition of breaking waves (amplitudes of higher harmonics and the phase shift between them) leads to the breaking of waves of different types, which is determined by the conditions of wave transformation, for example, the conditions of “shallowness” of water [
20]. It was shown that the breaking index, which relates the height of the breaking waves to the depth of breaking, depends on the nonlinear processes of wave transformation before breaking, and new formulas have been proposed for its determination [
21,
22]. However, how different formulas for the breaking index affect the frequency dependence of the dissipation of wave energy during breaking has been insufficiently studied, which is still relevant both for physical processes and for model applications.
When studying the change in the shape of the spectrum of breaking waves by comparing the field data of two experiments and the data of numerical modeling without taking into account dissipation, it was revealed that the breaking compensates the processes of linear and nonlinear transformation of waves “fitting” the spectrum to a universal form [
16].
This means that the dissipative term depends partly on the nonlinear term, how it is modeled, and what the accuracy is. Recently, according to the data of field and laboratory experiments, it was shown that waves breaking by different types have different nonlinear properties and spectral composition, namely, a different ratio between the amplitudes of the first and second harmonics and the phase shift between them [
20,
22]. This suggests that with the same method of simulating nonlinearity, the dissipative term can have a different structure for waves breaking with different types.
Thus, it can be stated that, when describing dissipation processes, there is no unified approach and universal dependence for energy dissipation during wave breaking on frequency or a clear physical description of changes in wave spectrum during their breaking under the influence of dissipative and nonlinear processes. Meanwhile, modeling is now the main method for studying the dynamics of the coastal zone. When simulating the process of breaking waves, it is important to understand how accurately the processes are simulated and how applicable the parameters are of the models offered by default.
The main purpose of this work is to study the necessary dissipation term and the dependence of the dissipation of the spectral energy of waves breaking by different types on the spectral frequency at the modeling wave spectrum by phase-resolving and phase-averaged models, with recommendations on default nonlinear terms. The problem will be solved based on the comparison of data of a field experiment and on numerical simulations for more frequently used models.
3. Discussion of Results
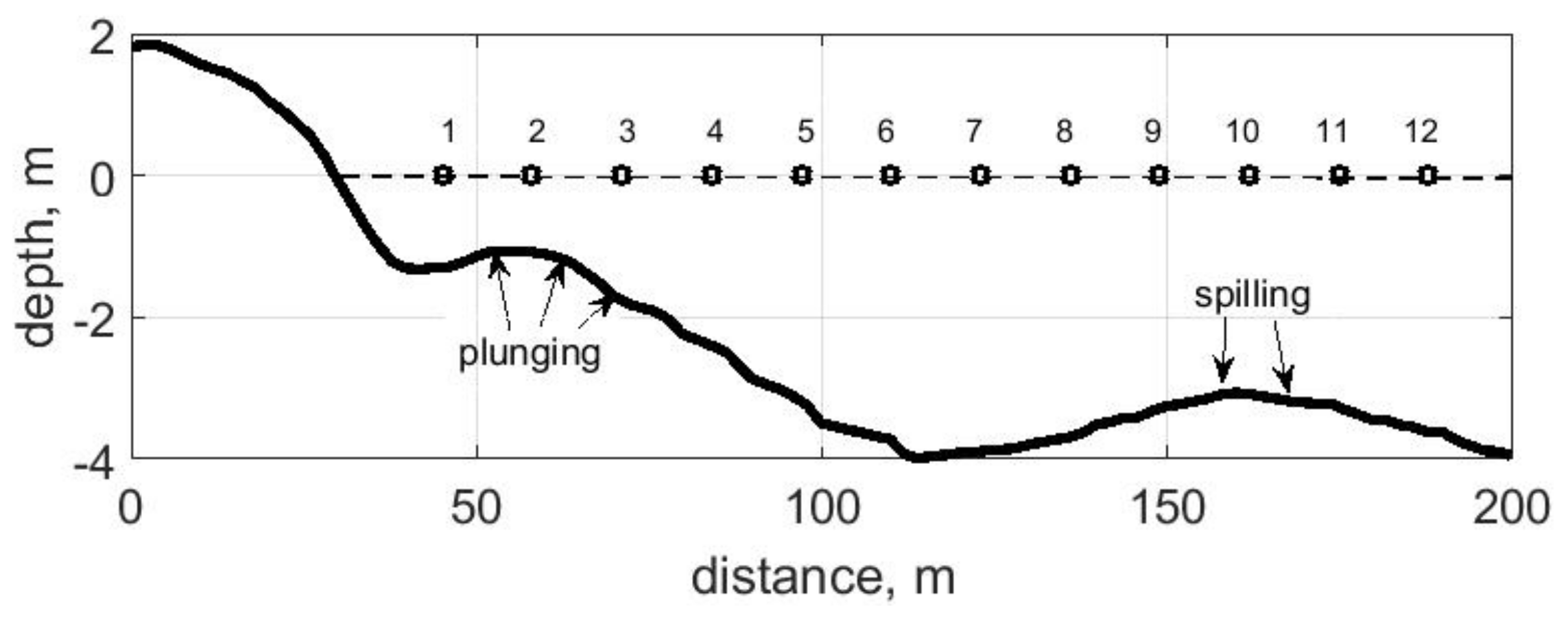
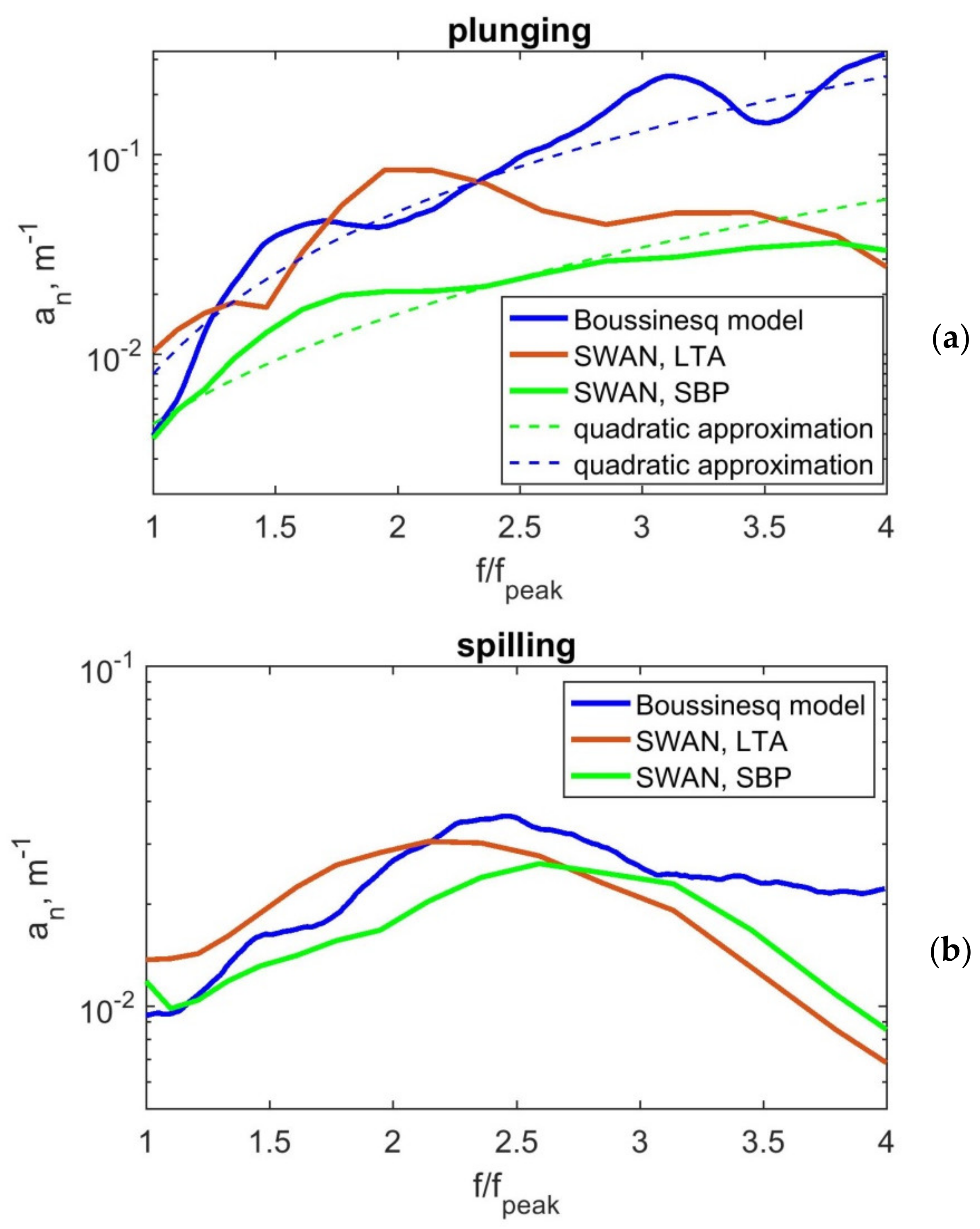
The dissipation coefficient (Equation (1)) calculated for different wave breaking types on the basis of the above-described models is shown in
Figure 3. The frequency dependences of the dissipation coefficient presented in this figure differ but can be qualitatively classified as quadratic and selective. It can be seen that the form of the dissipation coefficient for spilling waves on a qualitative level is in agreement (
Figure 3b). There is some selectivity of dissipation at frequencies of the 2nd and 3rd harmonics. However, since the coefficient itself has small values (in the order of 10
−2), it can be assumed that the dissipation of all harmonics occurs approximately uniformly. As was mentioned in the introduction, this approach is implemented in many wave models. When comparing the dissipation coefficients for spilling and plunging waves, it can be seen that they are different in both models (
Figure 3). Plunging waves dissipate more strongly and have a large dissipation coefficient, especially for higher harmonics. If we consider plunging breaking waves, in general we can say that dissipation occurs approximately according to the quadratic law when using Boussinesq and SPB modeling methods. This is the second way for the modeling of breaking waves suggested in [
4]. For the SPB method, the quadratic dependence is small, while for the Boussinesq model it is significant. The LTA method still gives a frequency-selective dependence of the dissipation coefficient on the frequency of the 2nd harmonic. Taking into account the fact that for SPB the dependence of the dissipation coefficient on the square of the frequency is small, it can also be considered approximately constant (uniform dissipation).
Let us consider the contribution of linear and nonlinear wave transformation processes to wave spectrum shape of differently breaking waves. Note that plunging and spilling breaking waves transform and break over different bottom slopes. We simulate the propagation of waves with the “switching off” of the model terms responsible for (a) the nonlinear triad interactions and (b) the linear transformation of waves. As was mentioned above, in real conditions, linear and nonlinear transformations of waves occur together, and it is impossible to strictly carry out such an artificial separation; however, in modeling, the intensity of manifestation of certain processes in the wave spectra, depending on the conditions of their transformation, can be demonstrated quite clearly.
Figure 4 and
Figure 5 show the results of the influence of the linear and nonlinear transformation of waves breaking by different types on the wave spectra shape. The relative changes in the spectrum (modelled (S
mod) from the initial ones measured in the field experiment (S
exp)) were estimated in points before and after wave breaking during wave propagation to the coast as S
mod/S
exp*Δx, where Δx is the distance of wave propagation between the initial and compared points.
Linear transformation of the spectrum for both wave models occurs approximately in the same way. The greater contribution to the main frequencies occurs where the slope is greater (0.04) and waves are breaking by plunging. At a smaller slope (0.02) and for spilling breaking waves, the contribution is approximately the same in all frequencies.
As already mentioned, the dissipation compensates for the effects of linear and nonlinear transformations of the spectrum [
16]. Since the linear changes for all wave models approximately coincide, we will consider the influence of nonlinear processes on the spectrum change (
Figure 5).
Indeed, it is clearly seen that dissipation occurs to a greater extent where the spectral energy has increased due to nonlinear processes. It can be seen that due to nonlinear processes during plunging breaking, the energy of the main harmonics is transferred to a greater extent to the higher harmonics, and during spilling breaking, mainly to the frequencies of the second harmonic.
The influence of nonlinear energy transfer within the spectrum during wave transformation on the form of the frequency dependence of the dissipation coefficient has been noted in many works. It is assumed that an increase in such transfer leads to a quadratic type of dependence, while a weak transfer leads to frequency independence [
4,
12]. Thus, the differences in the dependences of the dissipation coefficient on frequency for different models are determined mainly by nonlinear changes arising in the simulation of waves.
It is seen that in the LTA method the nonlinear contribution of the second harmonic is significantly higher, which is associated with the method of parametrization of nonlinear triad interactions. In the SPB method, the nonlinear changes for the 2nd and 3rd harmonics are similar to the Boussinesq model. The Boussinesq model gives a too-fast growth of the higher harmonics (for example, 4th), which requires its greater dissipation. An additional factor affecting the significant difference in the dissipation coefficient for plunging waves when simulating using the LTA method may be an inaccurate approximation of the phase shift (biphase) by the empirical formula [
34]:
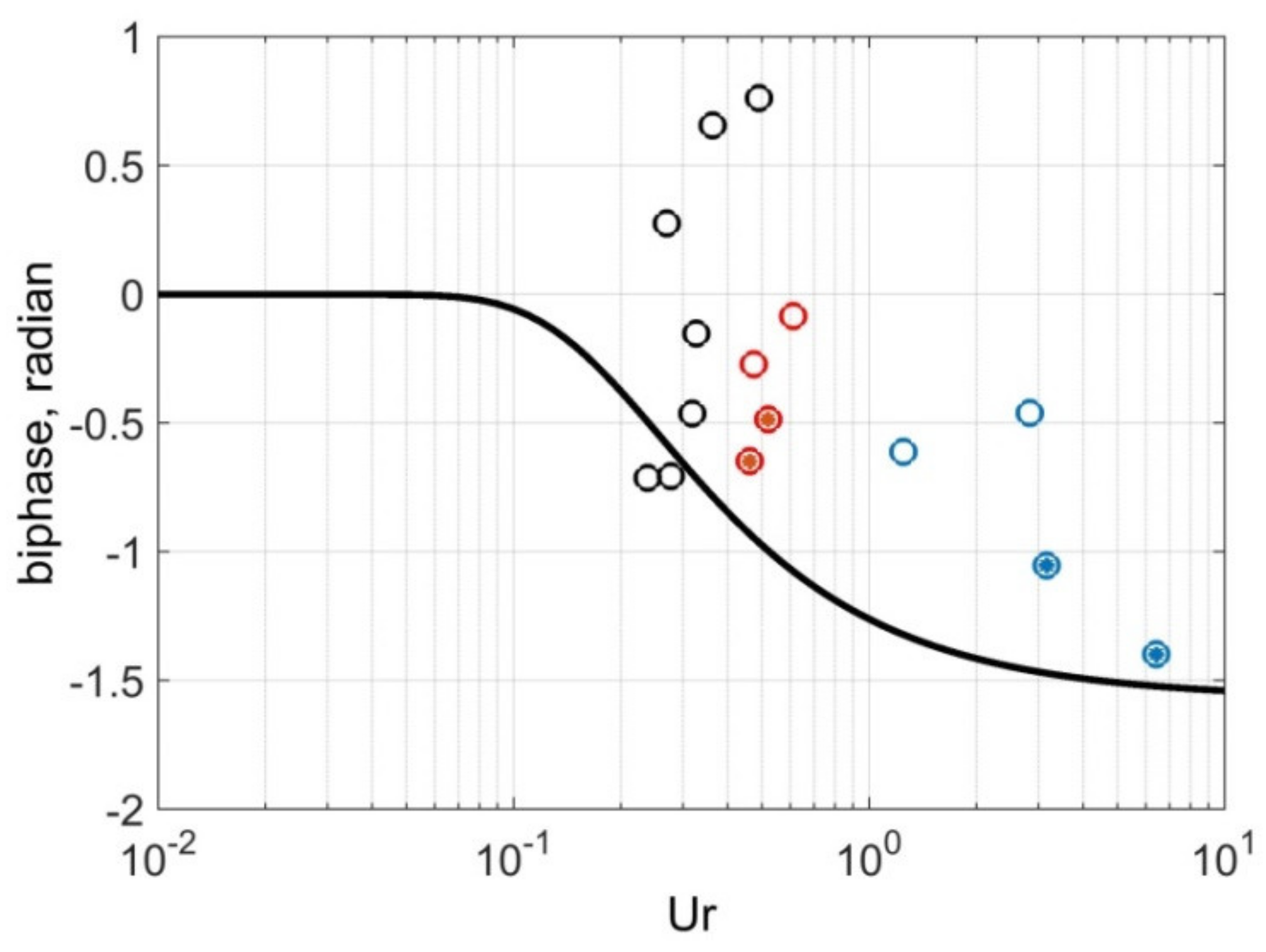
As can be seen from
Figure 6, the biphases obtained from experimental data do not coincide well with this parameterization. The disadvantages of this parameterization of the Ursell number are discussed in more detail in [
24].
The main reason for the inaccuracy of this parametrization is the neglect of visible periodic energy exchange between harmonics and the corresponding fluctuations of biphase (
Figure 7), which arises as a consequence of the detuning in the wavenumber or near-resonance wave interaction, when the doubled wave number of the first harmonic is not equal to the wavenumber of the second harmonic and the amplitudes of the harmonics in the frequency domain are the result of the interference of amplitudes of several wave numbers or free and bound waves [
23,
37]. As can be seen from
Figure 6 and
Figure 7, those biphase values that correspond to the maximum of the second harmonic are significantly outside of the parameterization (see Equation (7)). For spilling breaking waves, the Ursell number is smaller, the deviation is smaller, and the results are similar. The SPB method, which takes into account the wave number detuning, turns out to be closer to the Boussinesq model.
To reduce the discrepancy in modeling, including due to incorrect parameterization, tuning of the model coefficients is widely used. Both SPB and LTA nonlinearity source models have an adjustable proportionality coefficient,
trfac, with default values of 0.05 for LTA and 0.9 for SPB models [
28]. The coefficient for LTA model has been recently adjusted from its previous default value of 0.8 [
27]. The coefficient for 2D applications was calibrated in [
36], resulting in a recommended value of 0.52 for the LTA model. The behavior of the SPB model can be further adjusted by calibrating the parameter
K [
35]:
where
kp is the seaward peak wavenumber computed from the peak frequency, f
p.
For this purpose, the SWAN model uses two coefficients
a and
b, which are related to the broadening of the resonance condition. The default values are recommended as
a = 0.95 and
b = 0.0 (for SPB). A sensitivity study is conducted by modifying
trfac, a and b coefficients. However,
b = −0.75 is recommended for the one-dimensional case. Then,
a = 1, with default values of
b = 0 and
b = −0.5, and
b = −0.75, with the default value of
a = 0.95, are evaluated to calibrate the dissipation coefficient for the SPB method. The results are shown in
Figure 8.
It is visible that
trfac = 0.52 significantly decreases the frequency selectivity of wave energy dissipation for the LTA method. Dependence of the dissipation coefficient on frequency is approximately quadratic and qualitatively differs less than for the SPB method.
Figure 8 also indicates that almost all SPB model parameterizations provide more uniform dissipation coefficients than the LTA model for both plunging and spilling breaking waves. The applicable range of
a and
b coefficients is very narrow in models with “no dissipation”. Model results varied slightly, with modifications to
a and
b coefficients, whereas they were impacted significantly by the modification of
trfac. For the considered data, the results also revealed that the SPB model with
trfac = 0.05 parametrization returned the most homogenous outputs for both spilling and plunging breaking waves, allowing the use of non-frequency-dependent energy dissipation formulations (bulk energy dissipation).
Another interesting finding is obtained for plunging breaking by the modification of the model parameters. Much greater dissipation is obtained around the first harmonic for trfac = 0.05 for both the SPB and LTA models.
4. Conclusions
We studied the necessary dissipation term for waves breaking by different types for modeling wave spectrum through phase-resolving and phase-averaged models with recommended default nonlinear terms. For this, the data from modeling with only linear and nonlinear terms (with switch-off dissipation term) and the data of the field experiment were compared. It was revealed that modeling the dissipation of wave energy during wave breaking in the phase-resolved and phase-averaged models should be carried out taking into account the compensation of nonlinear changes arising from the use of different nonlinear source terms.
It was found that spilling breaking waves have a dissipation coefficient with frequency selectivity at frequencies of the 2nd and 3rd harmonics, regardless of the types of spectral model and nonlinear term. The absence of significant differences is apparently due to the small contribution of nonlinearity to the change in the spectrum, since spilling breaking is characteristic of waves transforming over a gentle slope of the bottom.
For the plunging breaking waves, the quadratic dependence of the dissipation coefficient on the frequency is characteristic for the SPB method and for the Boussinesq model. For the LTA method with default parameters for plunging breaking waves as well as spilling breaking waves, there is a frequency-selective dissipation coefficient at a frequency of the 2nd harmonic. This is due to the insufficient accuracy of modeling non-linear processes by this method, including the inaccuracy of the biphase approximation.
It is possible to improve the accuracy of LTA and SPB methods by tuning the model coefficients. Thus, if parameter trfac = 0.52, LTA and SPB methods will give, on a qualitative level, similar results for quadratic frequency dependence of wave energy dissipation for plunging breaking waves.
The differences found show that, to increase the accuracy, it is also possible to have a different description of the dissipative term for waves breaking by different types. In this work, our goal was not to find the exact form of the dissipative term for improving the models, but to determine whether there are qualitative differences in modeling waves with different types of breaking, which was demonstrated. Therefore, as a further work, we will consider obtaining approximations for the dissipative term for waves breaking by spilling and plunging on the basis of a large array of data from field experiments.