Parasitic Capillary Waves on Small-Amplitude Gravity Waves with a Linear Shear Current
Abstract
1. Introduction
2. Formulation of the Problem
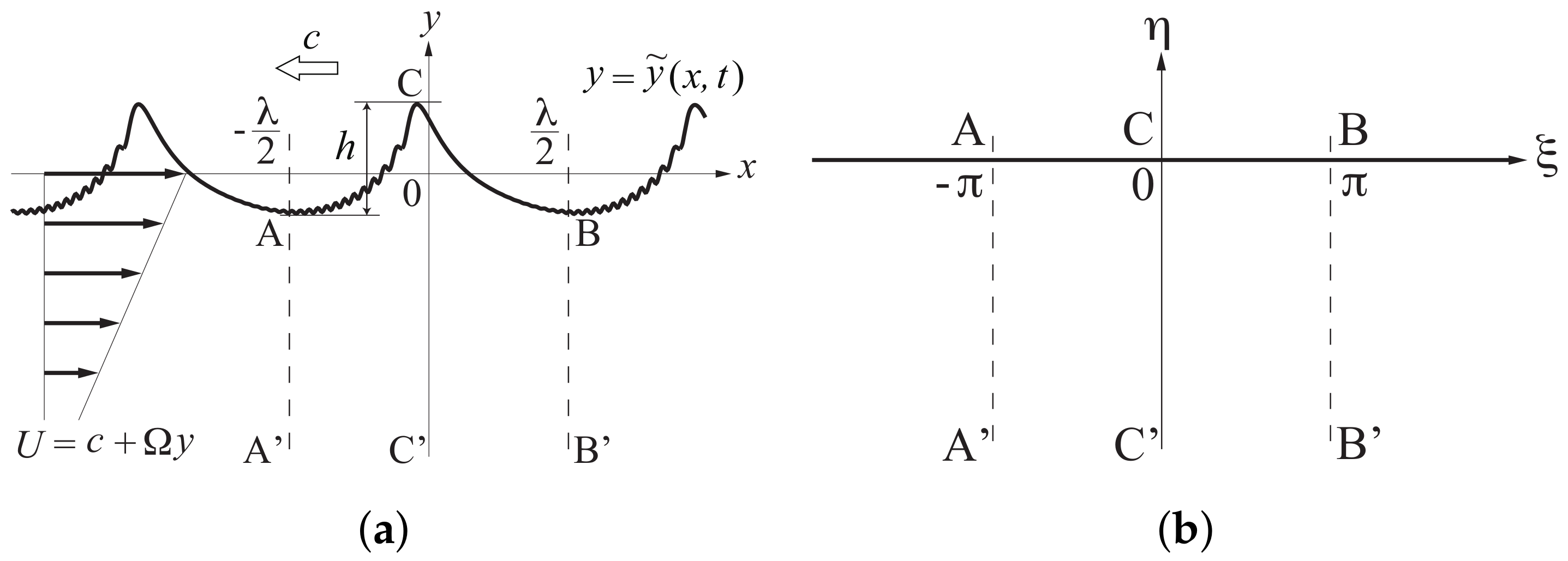
2.1. Formulation in the Physical Plane
2.2. Unsteady Conformal Mapping of the Flow Domain
3. The Method of Computation
4. Numerical Results
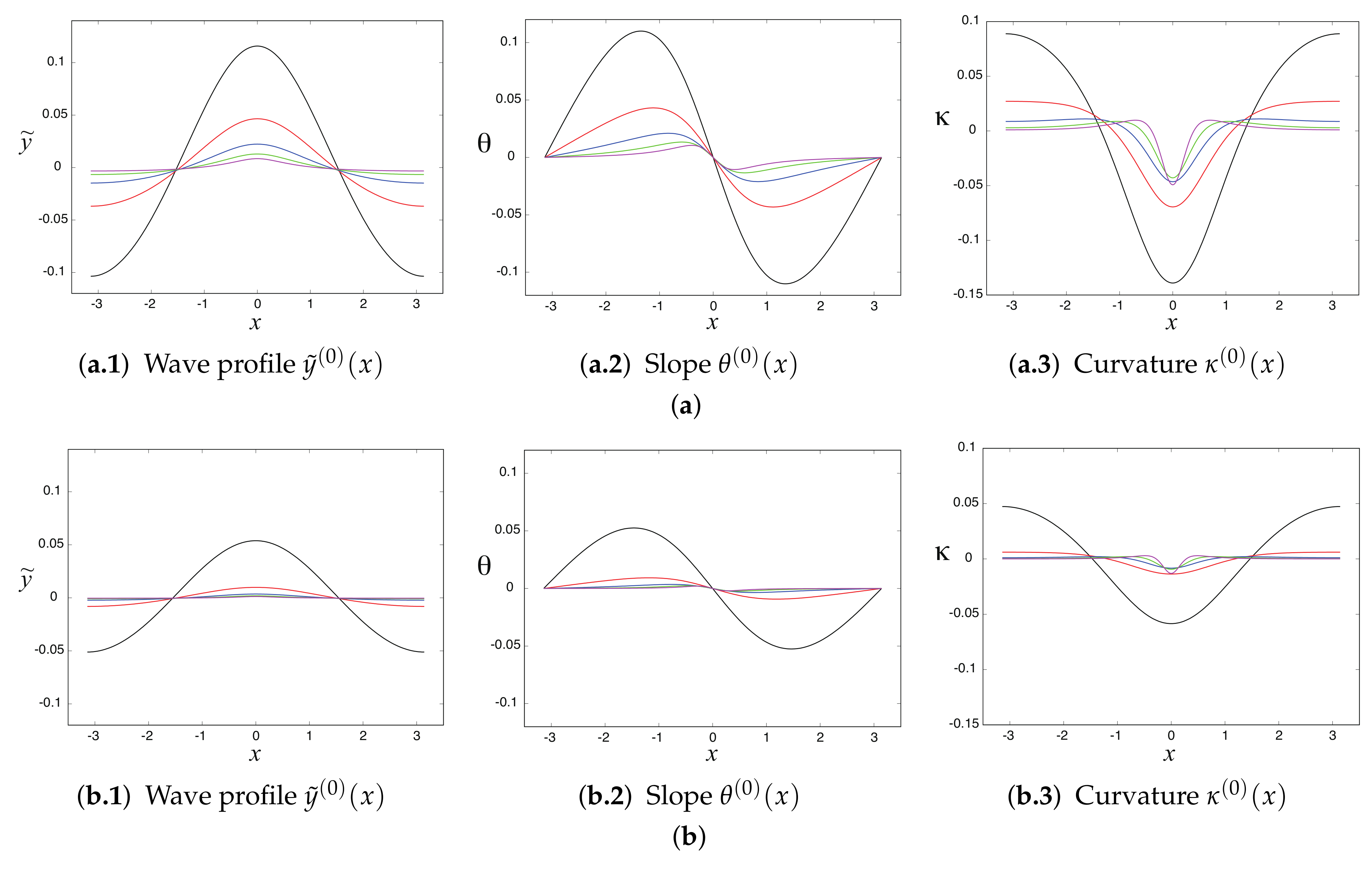
4.1. Initial Values
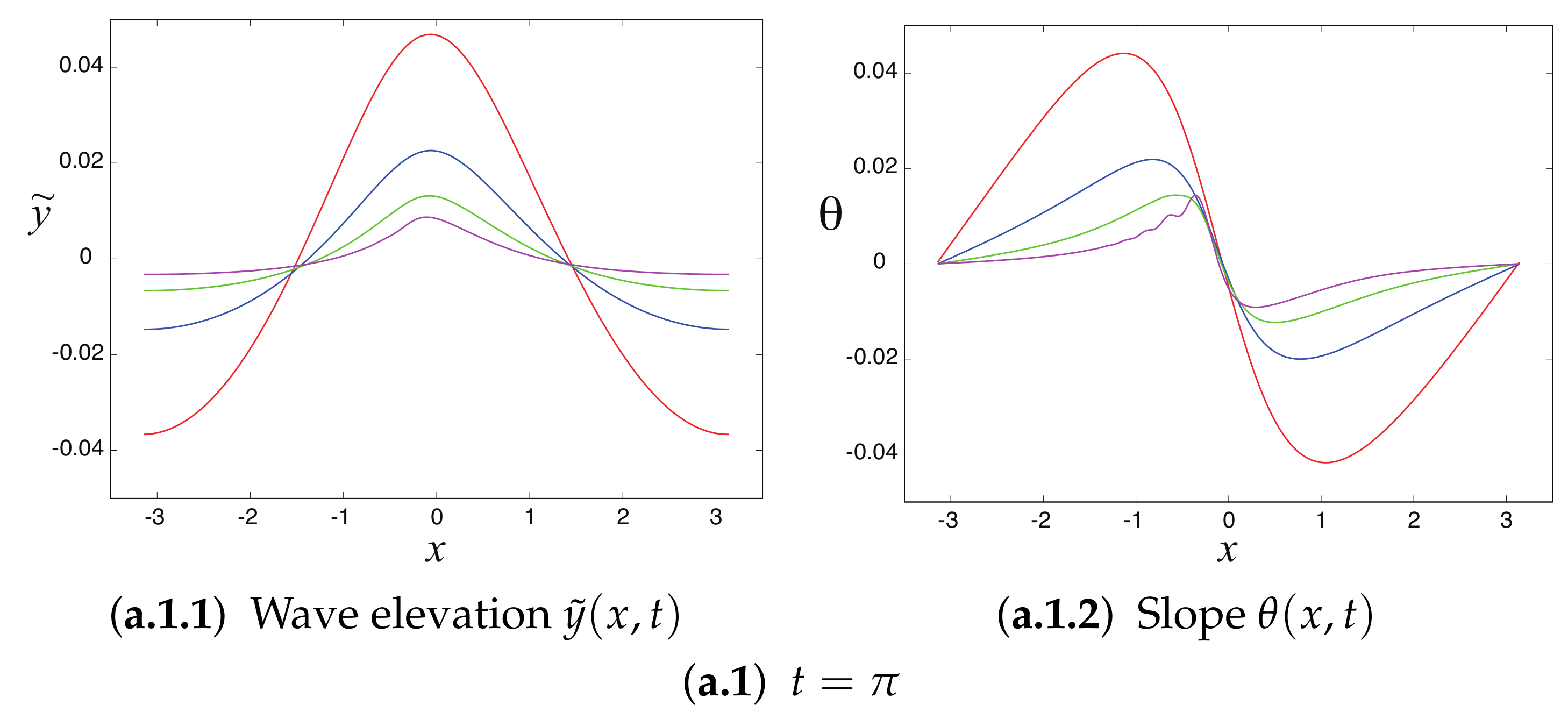
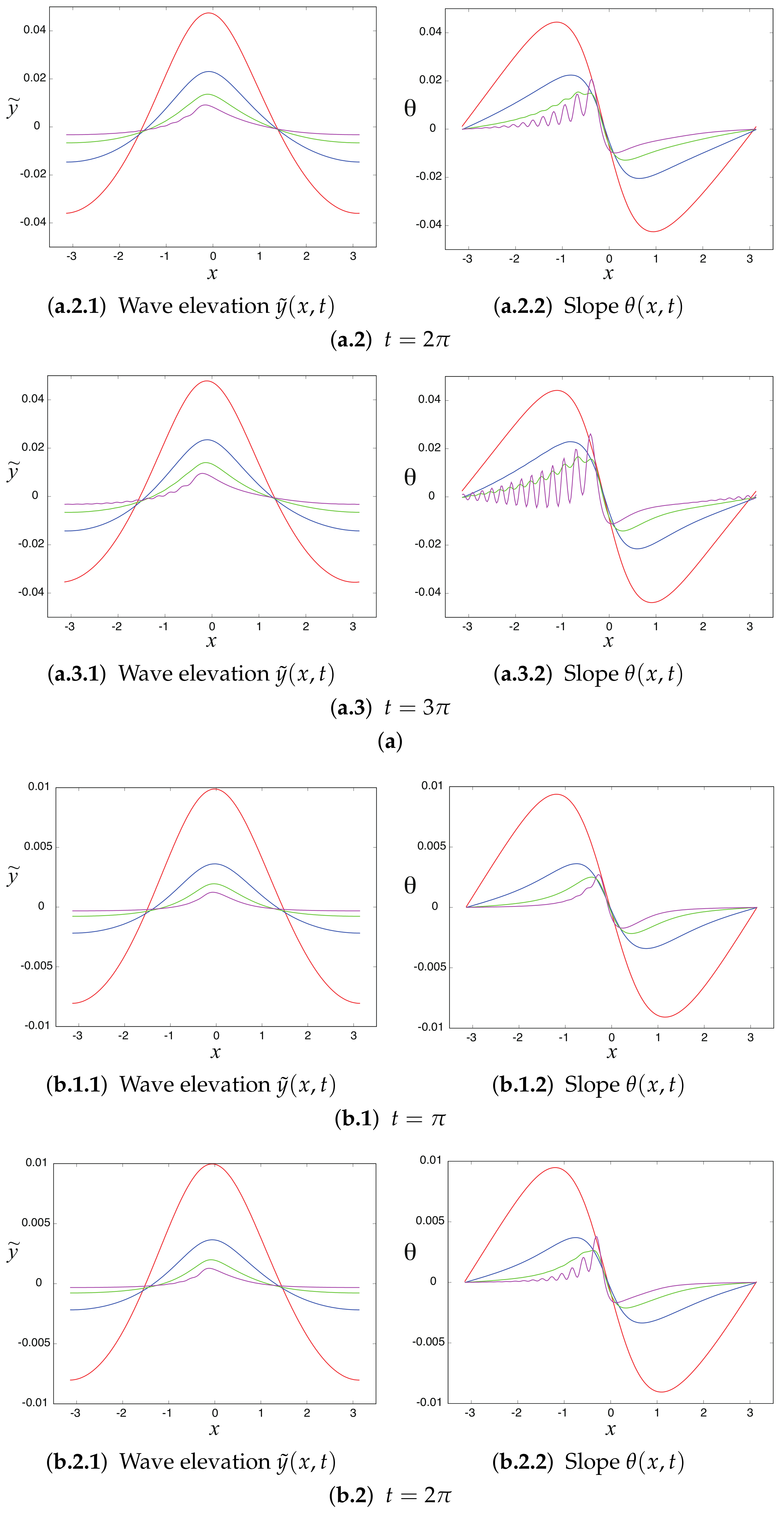
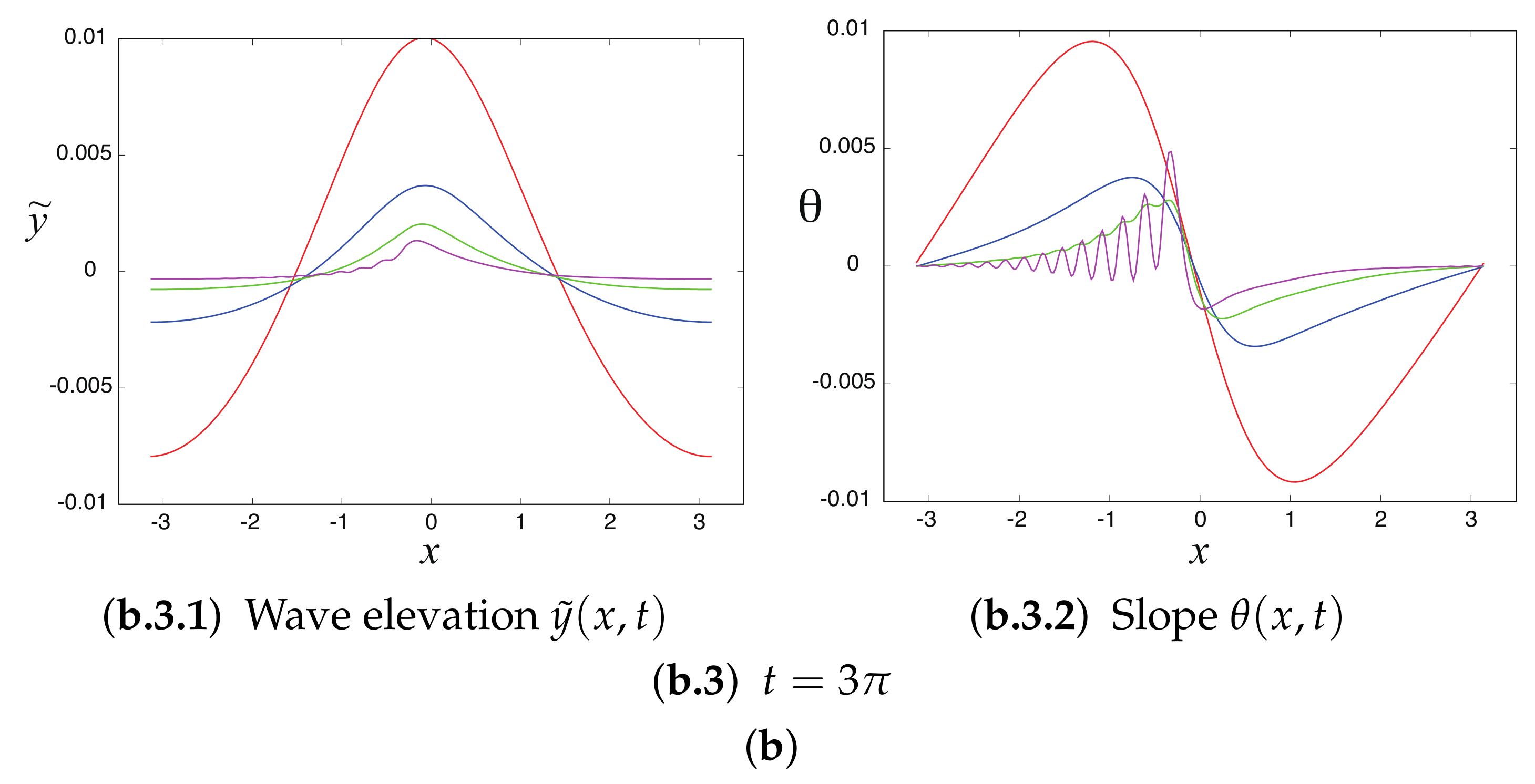
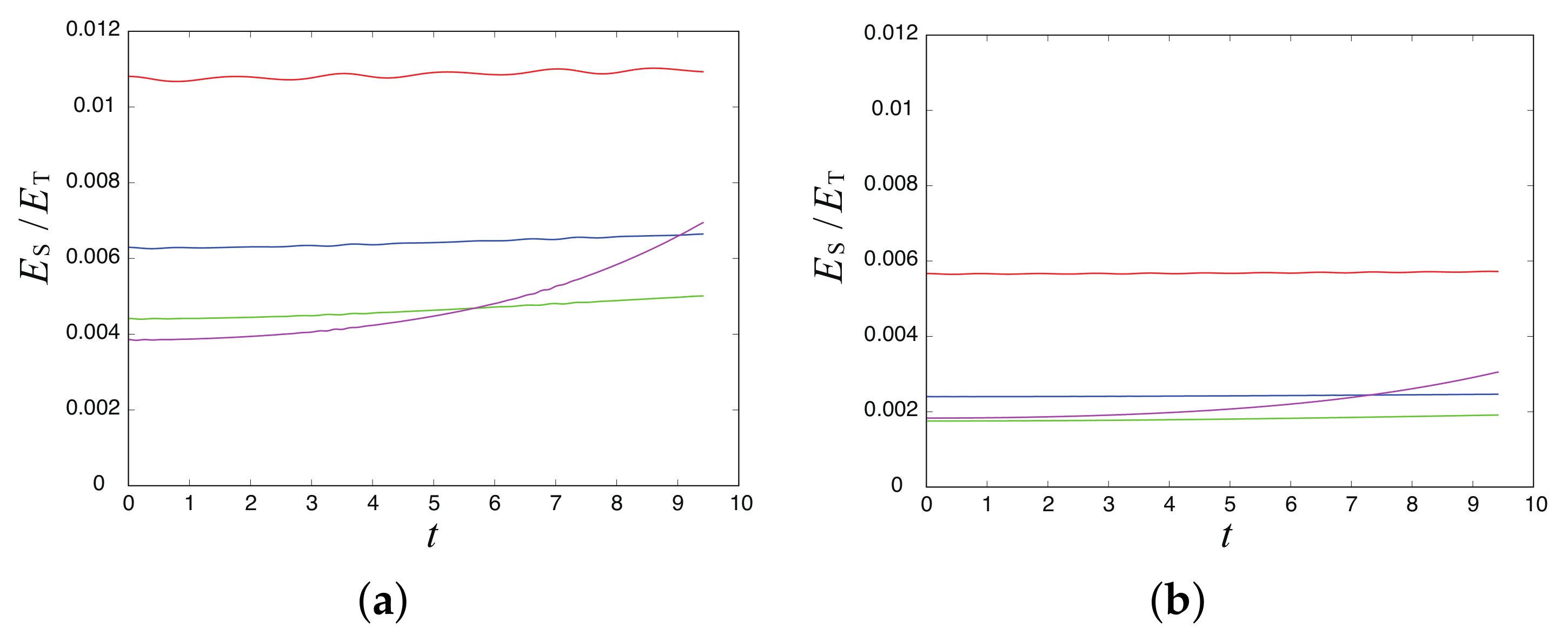
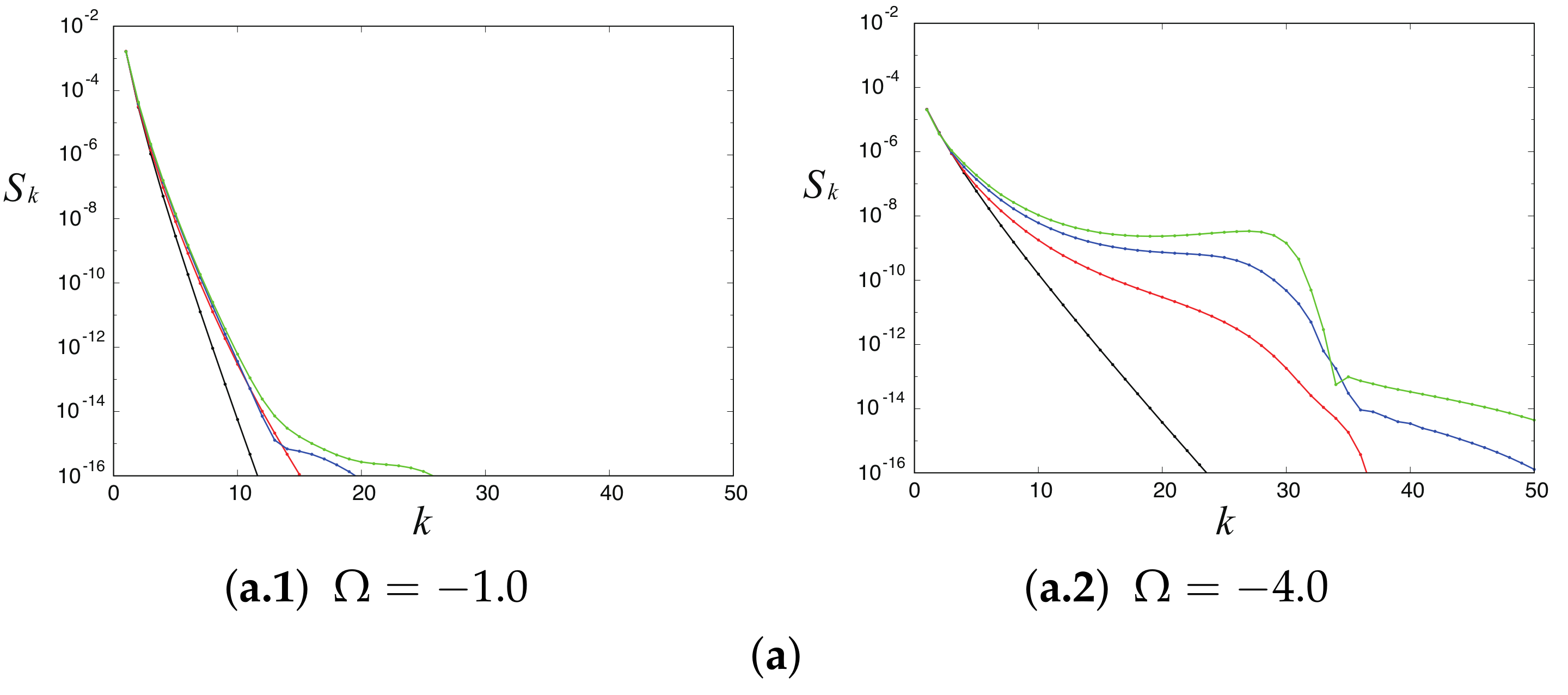
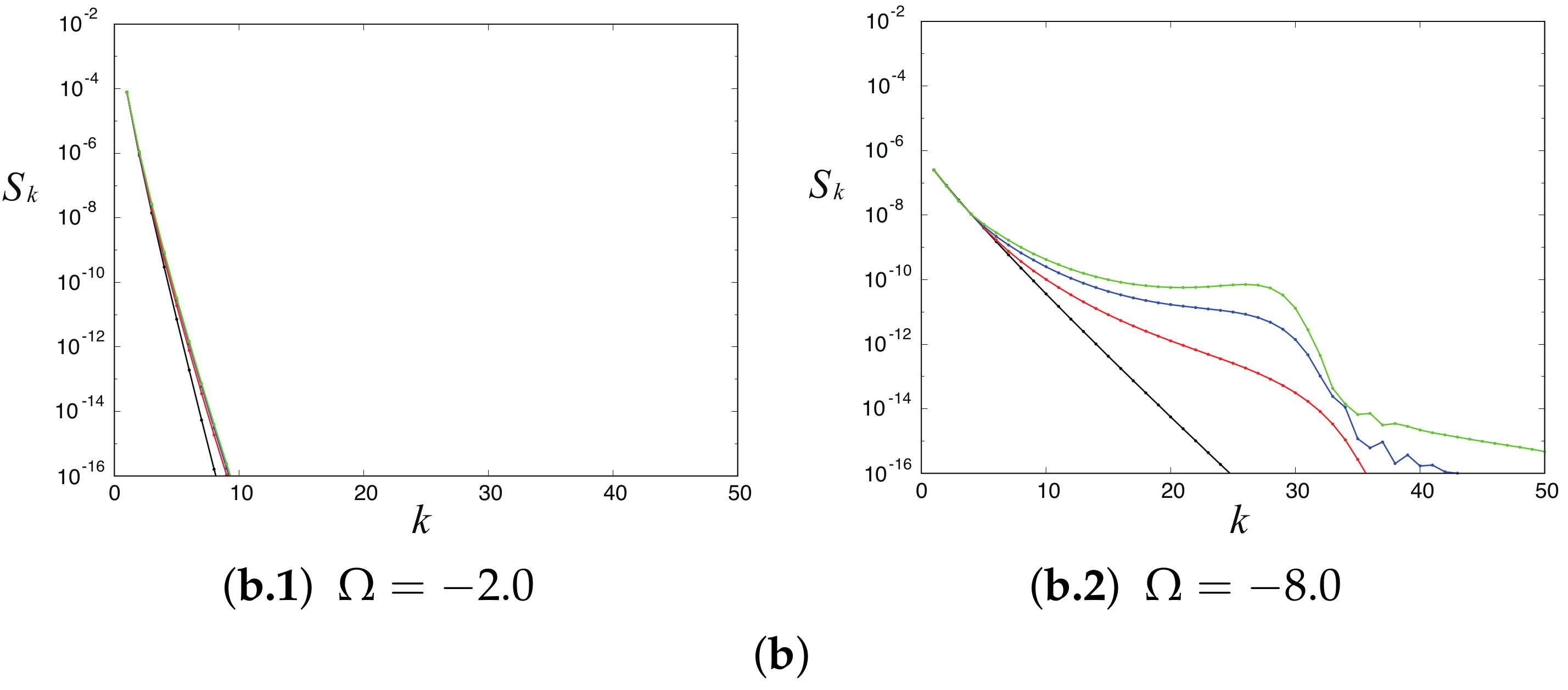
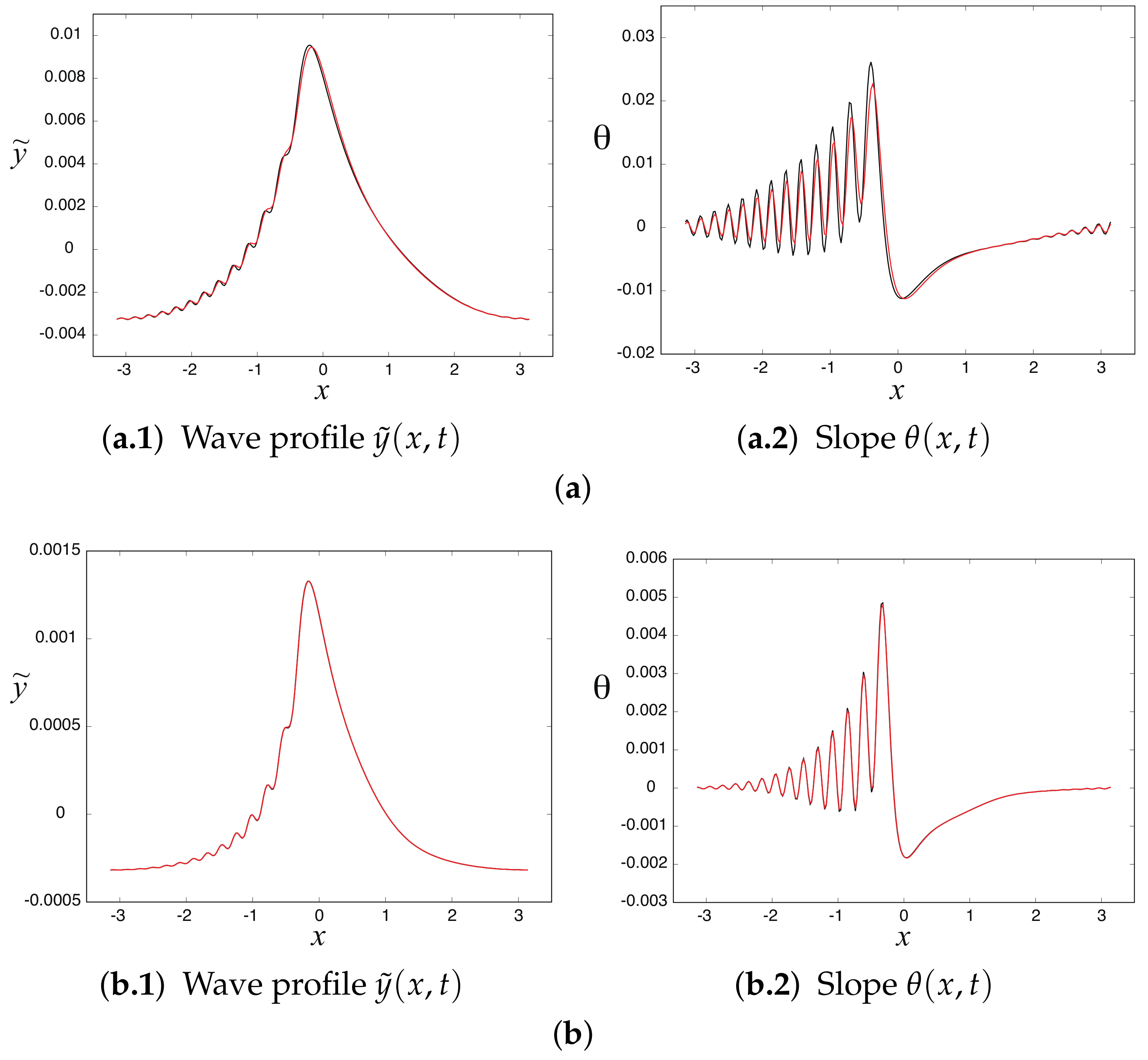
4.2. Generation of Parasitic Capillary Waves
5. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peregrine, D.H. Interaction of water waves and currents. Adv. Appl. Mech. 1976, 16, 9–117. [Google Scholar]
- Perlin, M.; Schultz, W. Capillary effects on surface waves. Annu. Rev. Fluid Mech. 2000, 32, 241–274. [Google Scholar] [CrossRef]
- Cox, C. Measurements of slopes of high-frequency wind waves. J. Mar. Res. 1958, 16, 199–225. [Google Scholar]
- Longuet-Higgins, M. The generation of capillary waves by steep gravity waves. J. Fluid Mech. 1963, 16, 138–159. [Google Scholar] [CrossRef]
- Dommermuth, D. Efficient simulation of short and long-wave interactions with applications to capillary waves. J. Fluids Eng. 1994, 116, 77–82. [Google Scholar] [CrossRef]
- Jiang, L.; Lin, H.-J.; Schultz, W.; Perlin, M. Unsteady ripple generation on steep gravity-capillary waves. J. Fluid Mech. 1999, 386, 281–304. [Google Scholar] [CrossRef][Green Version]
- Murashige, S.; Choi, W. A numerical study on parasitic capillary waves using unsteady conformal mapping. J. Comput. Phys. 2017, 328, 234–257. [Google Scholar] [CrossRef]
- Choi, W. Nonlinear surface waves interacting with a linear shear current. Maths Comput. Simul. 2009, 80, 29–36. [Google Scholar] [CrossRef]
- Murashige, S.; Choi, W. Stability analysis of deep-water waves on a linear shear current using unsteady conformal mapping. J. Fluid Mech. 2020, 885, A41. [Google Scholar] [CrossRef]
- Guo, D.; Tao, B.; Zeng, X. On the dynamics of two-dimensional capillary-gravity solitary waves with a linear shear current. Adv. Math. Phys. 2014, 2014, 480670. [Google Scholar] [CrossRef]
- Fedorov, A.V.; Melville, W.K. Nonlinear gravity-capillary waves with forcing and dissipation. J. Fluid Mech. 1998, 354, 1–42. [Google Scholar] [CrossRef]
| c | |||
|---|---|---|---|
| 0.2 | 0.0 | 1.00604 × 10 | 3.49321 × 10 |
| 0.2 | −1.0 | 6.22553 × 10 | 1.32682 × 10 |
| 0.2 | −2.0 | 4.19196 × 10 | 5.90622 × 10 |
| 0.2 | −3.0 | 3.08239 × 10 | 3.11534 × 10 |
| 0.2 | −4.0 | 2.41766 × 10 | 1.86715 × 10 |
| 0.1 | 0.0 | 1.00138 × 10 | 1.67068 × 10 |
| 0.1 | −2.0 | 4.15398 × 10 | 2.85668 × 10 |
| 0.1 | −4.0 | 2.37640 × 10 | 9.20809 × 10 |
| 0.1 | −6.0 | 1.64103 × 10 | 4.30888 × 10 |
| 0.1 | −8.0 | 1.24961 × 10 | 2.45879 × 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murashige, S.; Choi, W. Parasitic Capillary Waves on Small-Amplitude Gravity Waves with a Linear Shear Current. J. Mar. Sci. Eng. 2021, 9, 1217. https://doi.org/10.3390/jmse9111217
Murashige S, Choi W. Parasitic Capillary Waves on Small-Amplitude Gravity Waves with a Linear Shear Current. Journal of Marine Science and Engineering. 2021; 9(11):1217. https://doi.org/10.3390/jmse9111217
Chicago/Turabian StyleMurashige, Sunao, and Wooyoung Choi. 2021. "Parasitic Capillary Waves on Small-Amplitude Gravity Waves with a Linear Shear Current" Journal of Marine Science and Engineering 9, no. 11: 1217. https://doi.org/10.3390/jmse9111217
APA StyleMurashige, S., & Choi, W. (2021). Parasitic Capillary Waves on Small-Amplitude Gravity Waves with a Linear Shear Current. Journal of Marine Science and Engineering, 9(11), 1217. https://doi.org/10.3390/jmse9111217






