Abstract
Following the 2010 Deepwater Horizon accident of a massive blow-out in the Gulf of Mexico, scientists from government, industry, and academia collaborated to advance oil spill modeling and share best practices in model algorithms, parameterizations, and application protocols. This synergy was greatly enhanced by research funded under the Gulf of Mexico Research Initiative (GoMRI), a 10-year enterprise that allowed unprecedented collection of observations and data products, novel experiments, and international collaborations that focused on the Gulf of Mexico, but resulted in the generation of scientific findings and tools of broader value. Operational oil spill modeling greatly benefited from research during the GoMRI decade. This paper provides a comprehensive synthesis of the related scientific advances, remaining challenges, and future outlook. Two main modeling components are discussed: Ocean circulation and oil spill models, to provide details on all attributes that contribute to the success and limitations of the integrated oil spill forecasts. These forecasts are discussed in tandem with uncertainty factors and methods to mitigate them. The paper focuses on operational aspects of oil spill modeling and forecasting, including examples of international operational center practices, observational needs, communication protocols, and promising new methodologies.
1. Introduction
The Deepwater Horizon (DwH) accident involved the Macondo well (MC 252) blow-out in April 22, 2010 and resulted in a massive oil spill (the largest accidental spill in the world), with about 4.4 millions barrels (0.7 million m3, almost 600,000 tons) released in the Gulf of Mexico (Crone and Tolstoy [1]). In the decade following this incident, many scientific advances have been made in support of operational oil spill modeling, a crucial component of response. This paper provides a synthesis of these advances, focusing on the Gulf of Mexico, but in the context of international best practices. For oceanographic research and development in the Gulf of Mexico, the post-DwH decade has been greatly influenced by the “Gulf of Mexico Research Initiative” (GoMRI1) that funded a broad range of projects under its mission to “improve society’s ability to understand, respond to, and mitigate the impacts of petroleum pollution and related stressors of the marine and coastal ecosystems.” This paper (a) reviews the state of the art of operational modeling before GoMRI; (b) establishes the advances already made and/or now achievable as a result of GoMRI research; and (c) identifies desirable future developments, the opportunities for achieving them, and remaining gaps in the knowledge and technology required.
Operational oil spill modeling is based on predictive numerical models for oceanic circulation, winds, and waves, as well as oil fate and transport, suitably executed to represent the prevailing environmental conditions and oil chemistry characteristics and to obtain forecasts to guide response activities, focusing on the short time period after an oil spill (hours to days). Numerical models use computer simulations to solve complex equations that describe the phenomena of interest and have the advantage that they can be employed for past (hindcast), current (nowcast), and future (forecast) applications. Forecasting ability is essential in case of a spill, providing crucial information for response operations.
Oil spill models are used in multiple ways: To support response decision-making, in planning for spill response, in environmental impact analysis of oil industry infrastructure, and in the assessment of injury to the environment (and economy) after a spill has occurred. The main goal of this paper is to present a comprehensive synthesis of modeling used to support response, focusing on the mechanisms that act on short time scales relevant to operational oil spill modeling.
When applied to computer modeling, the word “operational” can mean multiple things. One definition, sometimes called big “O” Operational (for the capitalization of the word), is used for systems that have met well-defined standards for accuracy, reliability, and availability, so that users can count on them to meet their needs and be available when needed. An example of this is the U.S. National Oceanic and Atmospheric Administration (NOAA) Center for Operational Oceanographic Products and Services (CO-OPS) Operational Forecast Systems2, which operates at many U.S. ports. These systems meet well-specified criteria for accuracy, and are implemented on computer systems with backups and contingency plans so that mariners can count on their results to make critical navigation decisions.
Another way the term operational (with a lowercase “o”) is used is to describe systems that are operating continuously, providing results on a regular basis. Many such systems are operated by academic institutions, and may not meet the robustness and accuracy criteria defined for Operational systems, particularly as they do not have full 24/7 support and reliability. An example of this in the U.S. is the Texas General Land Office (TGLO) Texas Automated Buoy System (TABS) model, operated by Texas A&M University. Such systems are often called “real-time” to distinguish from Operational. As (thankfully) there are not enough major oil spills to justify fully Operational systems specifically to support oil spill modeling, most oil spill modeling systems are designed to use any information available at the time and place of the spill (preferably in real-time), whether or not it is strictly Operational.
When an oil spill occurs, the oil immediately begins to change and move. The oil fate and transport are governed by the environment in which the oil moves. Oil spill models need to have the necessary “drivers”, so they are inextricably linked to oceanographic, atmospheric, wave, and hydrological models, which provide the environment by which the oil is affected. As oil comes into contact with the environment, it can have devastating effects on individual biota and local and regional ecosystems, as well as society and the economy. The goal of oil spill response is to limit these impacts as much as possible, and thus lies on the intersection of the Oil, the Environment, and the Biota (Figure 1). In order to mount an effective response, responders need scientific support about all three of these components. Operational systems used in different countries have related protocols and frameworks. For instance, NOAA in the U.S. employs a framework called “the Five Questions” (Figure 2) to help guide decision-making:
Figure 1.
Spill response works at the intersection of the Oil, the Environment, and the Biota.
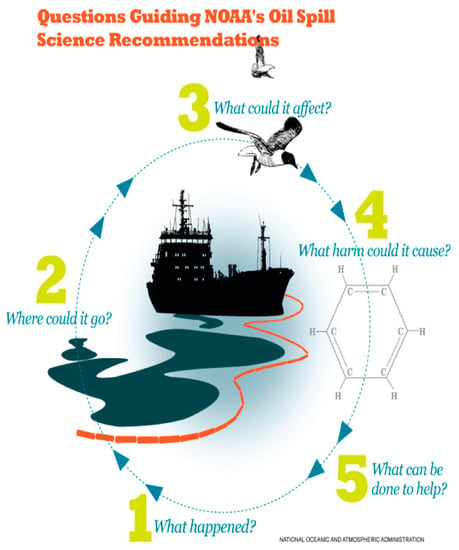
Figure 2.
The five questions guiding the National Oceanic and Atmospheric Administration’s (NOAA’s) scientific support of spill response.
- (1)
- What Happened? In order to begin to plan a response, basic information needs to be available: How much oil was spilled? What type of oil? When was it spilled? Where was it spilled? Is there a continued release?
- (2)
- Where Could Oil Go? Once on the water, the oil will move—responders need to know where it might go in order to understand the potential impacts and know what response actions can be taken.
- (3)
- What Could the Spill Affect? What biota or ecosystems are present in the area where the oil might go?
- (4)
- What Harm Could the Spill Cause? Understanding the harm it could cause is critical for prioritizing response actions.
- (5)
- What Can Be Done to Help? Taking action to reduce the harm.
Within this framework, modeling can be a critical tool to help answer these questions. In response modeling, the primary question addressed is “Where could oil go?”. Oil spill transport models are critical tools for forecasting where the oil might go in order to guide the response. This guidance is critical to understanding what could be affected. Secondarily, oil fate modeling, the modeling of the transformation (“weathering”) of the oil and its ultimate fate, can be critical to understanding the harm the oil could cause, and, finally, modeling can help understand the efficacy and effects of potential response actions.
As oil spill models require the environmental drivers, the fields provided by the ocean, atmospheric, and wave models are critical to modeling in support of response. Reliable circulation modeling is essential, as it has been estimated that most of the uncertainty in oil spill models results from uncertainties in the driving models. It is also critical to keep in mind that the spill responders need a forecast with as much accuracy as possible. Circulation models need to be tuned to provide the best possible forecast of the ocean currents at the specific time and place of the spill in order to get a good forecast of the directions of the oil. For instance, a model that accurately forecasts the size and strength of eddies in a region in the statistical sense may not have a particular eddy in the right place and at the right time, resulting in inaccurate results as to oil transport. Atmospheric and wave models provide important air–sea interaction parameters and fields, while hydrological models support the land–sea interaction needs, especially for spills near regions of river influence. Coupling all these environmental modeling components in an Earth System framework is the desirable methodology for providing comprehensive inputs to the oil spill models.
This paper will discuss the integration of Earth System and oil spill models, as well as their utility under operational conditions. Section 2 presents the state of the practice for operational oil spill modeling, with examples from current, state-of-the-art systems. Section 3 and Section 4 will highlight the separate attributes of Earth System and oil spill models, respectively, including their limitations. Section 5 will discuss uncertainties resulting from these limitations and methods to reduce uncertainty. Section 6 will synthesize the findings and highlight novel steps toward future advances.
2. State of the Practice for Operational Oil Spill Modeling
Oil spill models are used in Planning, Preparedness, and Response operations. Models are traditionally two- or three-dimensional (2-D or 3-D) and time dependent. Models used vary from in-house systems (e.g., Oil-Spill Risk Analysis (OSRA), Canadian Oil Spill Modelling Suite (COSMoS)), open-source code (e.g., General NOAA Operational Modeling Environment (GNOME), OpenDrift, MEDSLICK-II) to commercial models (e.g., Oil Spill Contingency and Response (OSCAR) and OilMap). Oil spill models’ capabilities range from prediction of surface transport (winds, currents, and oil drift) to fully 3-D processes that include oil fate and environmental effects. GoMRI research has benefited all of these types of models through both experimental and theoretical work to better understand various oil fate and transport processes.
2.1. Response Models
Despite the variety of use cases and model authors, most oil spill models share a common framework and methodology. For details, Spaulding [2] provides an overview of the algorithms and common practices of the state of the art as of 2017. The goal of an operational oil spill model is to forecast the “fate and transport” of oil spilled into the ocean or coastal environment (and sometimes rivers or lakes as well) so as to inform an oil spill response. In order to respond, it must be known where oil is likely to go and what its properties may be in the future.
“Fate” modeling involves predicting the chemical and physical changes that the oil undergoes once released into the environment. Oil is a complex mixture of hydrocarbons and it changes, or “weathers”, when exposed to the open environment. This means that some of the components may evaporate into the atmosphere, dissolve into the water column, degrade, etc. The oil remaining may be transformed or form emulsions and have very different properties from those of the originally spilled oil, which affects the toxicity of the oil and the effectiveness of various response strategies.
Often, the most critical piece of response modeling is the transport. When released into the surface waters, spilled oil will be transported by currents, winds, and wave action. The result can be very fast movement covering long distances, and an effective response requires reliable forecasts for where the oil will be in order to deploy resources at the right time and place. The fate of the oil can also be critical to response, particularly for highly volatile products. Evaporation and dispersion into the water column can limit the timescales of the response, but once the timescale has been determined, the major modeling efforts to support the response are focused on the transport.
Due to the large and varying spatial scales and other operational considerations, most spill models use a particle tracking, or Lagrangian element, approach: The oil is represented by individual elements (particles, parcels) that represent a given mass of oil. These elements are transported and transformed within the model, undergoing simulations of the processes affecting the movement and weathering of the spilled oil. As oil in the environment is moved by the winds, waves, and currents, every spill model requires at least wind and current forecasts in order to operate. These fields are usually provided on an Eulerian grid, providing spatially and temporally varying fields of relevant environmental parameters. As oceanographic and atmospheric models necessarily have limited resolution, operational spill models also must apply a method for including diffusion due to sub-grid scale circulations.
In addition to winds and currents, some models may benefit from extra information given by wave forecasts (most models derive wind information from empirical wind wave relations), and oil weathering models require extensive environmental conditions, such as water temperature, salinity, etc. In order to support a wide variety of regions, most operational models are able to ingest these “driver” fields, i.e., winds, currents, and waves, from a wide variety of sources, from hand-entered weather forecasts to full 3-D model output on a variety of model grid types.
In operational use, the modeling process requires these steps (Figure 3):
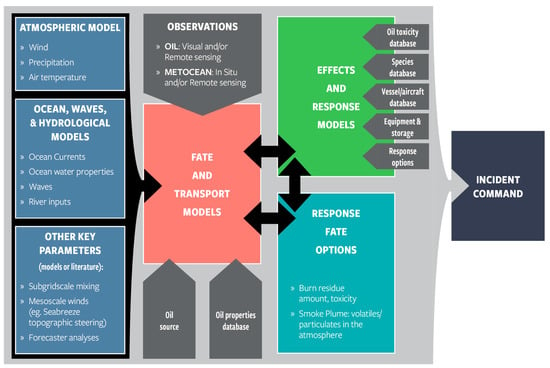
Figure 3.
Schematic of the Operational oil spill modeling process.
- (1)
- Gathering information about the spill: When, where, quantity, and characterization; collecting data from the “drivers”: Circulation models, meteorological models, and weather forecasts;
- (2)
- Evaluating these drivers for suitability for the case at hand;
- (3)
- Configuring the spill model;
- (4)
- Running the model;
- (5)
- Processing the output to present to responders, ideally with an evaluation of uncertainty.
During an oil spill, oil spill modeling forecasts are needed for planning the response actions over the next few days and longer for mobilization of larger assets into position. Trajectories may be needed two or three times a day, depending on the variability in the local conditions, sensitivity of natural resources, the complexity of the oil spill, and the availability of new “driver” information (i.e., updated meteorological and oceanic forecasts) or observations of oil movement. Smaller-scale processes, such as sea breeze and topographical steering, are important considerations in the timing and location of oil reaching the shoreline, but are not generally resolved in operational meteorological models, so human forecasters are used to estimate the potential for occurrence. Coordination between the trajectory analyst and the field observers is important for ground-truthing and updating the spill forecasts. The model results are moved to plots and maps for use by responders and decision-makers to understand the situation at hand and the potential development of the spill. Such maps can identify key risk areas and help responders prioritize response actions in order to minimize environmental and socioeconomic harm.
In addition to the core forecasts of the spill fate and transport, operational modeling may also be used to help evaluate the effectiveness of and provide input for trade-off analysis of response actions. Modeling is also used to guide the injury assessment after a spill, which requires a great deal of detail in observations, field collected data, and experimental results from toxicity and exposure studies. Preliminary modeling of potential injury can also help prioritize and guide response activities.
The results from oil spill models usually include the path of transport, known as the “trajectory”, and the fate of the oil, which are often presented as an “oil budget” delineating what fraction of the original spilled oil is expected to be floating, on the shore, evaporated, etc.
Spill predictions serve a variety of needs; model results need to be clear to their intended users, primarily the people orchestrating the response—typically not experts in oceanography, meteorology, or modeling. Personnel and equipment, such as oil skimmer vessels or protective oil booms, may need to be moved into an area with some lead time, and the trajectory forecasts provide that lead time information. Trajectory uncertainty estimates are typically more important for longer forecast horizons, since model skill tends to diminish over time. Model results should be able to be imported into Geographical Information Systems (GIS) and displayed in a Common Operating Picture (COP) along with other important response information. Trajectory forecasts will be overlaid onto maps, such as Environmental Sensitivity Index maps of natural- and human-use resources, in order to plan and prioritize the response measures. Maps of surfaces of oil locations and forecasts with information on oil location over time and oil state (e.g., thickness, water content, weathering) are used to plan for needs, from personnel response equipment to oil and related response disposal (e.g., sorbent pads). The current and future weathering state of the oil is important, e.g., for providing responders with information related to needed Personal Protective Equipment (PPE) or the increase in oil volume from emulsification of the oil.
2.2. Planning and Preparedness Models
Planning and preparedness for oil spills require estimating where spilled oil from hypothetical oil spills might travel in a region so that response plans can be developed. The model results are used to estimate the type, amount, and best location for response resources in order to mount an effective response. This is often done by running thousands of trajectories over a multiyear period, then statistically examining the results over an area of interest. These analyses provide a way to quantify the variability in both met-ocean conditions and the properties of the spilled oil. These analyses are used to develop response plans, e.g., by determining response equipment needs, such as lengths of oil spill protective boom, amounts of chemical dispersants, and number and type of skimmers. The analyses are also indicative of timing; e.g., how quickly a response may need to be mobilized, such as estimates of how fast oil could reach a bird rookery. The objective is to create response plans to best protect environmental and socio-economic resources that are at risk (e.g., threatened natural resources, such as habitats and individual biota, and economic resources, such as fisheries and infrastructure). This statistical approach to planning is done by various systems, including the SIMAP model from RPS (Rural Planning Services) North America, Ocean Sciences (French et al. [3]), OSCAR model from SINTEF (Aamo et al. [4]), and the Trajectory Analysis Planner (TAP) models from NOAA (Barker and Galt [5]). An overview of the evaluation of risk is given in Boehm and Page [6].
A similar process is used in planning areas for oil industry development. The U.S. Department of the Interior’s Bureau of Ocean Energy Management (BOEM) uses its OSRA model to assess oil-spill risks associated with offshore oil and gas leasing off the U.S. continental coast and Alaska by calculating spill trajectories and contact probabilities. These analyses address the likelihood of spill occurrences, the transport of any spilled oil, and the environmental resources that might be impacted as a result of the spill. OSRA combines the probability of spill occurrence with a statistical description of hypothetical oil spill movement on the ocean surface. OSRA model results are used by BOEM staff for preparation of environmental documents in accordance with the National Environmental Policy Act, by other Federal and State agencies for review of environmental impact statements, environmental assessments, and consultations related to endangered species and essential fish habitats, and by oil industry specialists preparing oil spill response plans.
As an example, this method is described in greater detail here. In order to develop the statistics needed for planning, long time series of environmental information are needed, such as wind fields, ocean circulation model output, and ice in Arctic waters. This requires advanced, accurate ocean circulation fields. Trajectories are run with the results combined into relevant spatial statistics, such as the probability of oil reaching a section of beach, minimal time before shoreline oiling, or potential for contact with sensitive resources. Response modeling is taking the situation at hand and providing predictions of where the oil spill goes and potential environmental impacts and effects, or finding where the oil came from. Planning models evaluate risks from hypothetical spills to biological, physical, and socioeconomic resources that could be exposed to oil from future oil and gas leasing, exploration, or production.
Oil spill trajectory models used for long-term planning require probabilistic estimates of both oil spill contact and likelihood of the initiating event that results in the release of hydrocarbons into the environment. A realistic, objective methodology for estimating oil spill occurrence rates is needed for the long-term planning model’s application. An example is BOEM’s OSRA planning model that is used to help evaluate oil spill risks to biological, physical, and socioeconomic resources that could be exposed to oil from oil and gas leasing, exploration, or development on the U.S. Outer Continental Shelf (OCS). The OSRA model derives its oil spill occurrence rate estimates from worldwide tanker spill data, barge spill data for U.S. waters, and the U.S. OCS platform and pipeline spill data (such as those collected by the Bureau of Safety and Environmental Enforcement; https://www.bsee.gov/stats-facts/offshore-incident-statistics/spills). These spill rates are expressed and normalized in terms of number of spills per volume of crude oil handled, and a Poisson process uses the volume of oil handled as an exposure variable to predict the probability of spill occurrence (Smith et al. [7]). All resulting estimates of spill occurrence rates can be separated by oil spill size class to inform the decision-maker and public of the risk of, e.g., “small” vs. “large” spills. Using long-term hindcast wind and ocean current data, the OSRA model generates hundreds of thousands of trajectories from hypothetical oil spill locations and derives the probability of contact with environmental resources on the U.S. OCS and adjoining coasts. When the trajectory predictions are combined with the occurrence statistics, an estimate of the probability of an oil spill both occurring and contacting the aforementioned resources can be made.
2.3. Model Use Cases: Response Support
Operational oil spill modeling is different from research or planning oil spill modeling in that under operational conditions, responders rely on the trajectory forecasts and hindcasts of the spill in order to determine response resource needs and the potential location of the spill currently and in the future. Modeling centers need to provide information on the oil location and state for responders to use in planning equipment and personnel needs. Worldwide, operational oil spill response centers focusing on modeling exist both in large-scale centers and in individual countries or regions. Industry sponsors ITOPF and Oil Spill Response Limited, with world-wide centers that include modeling, are based in the UK. These centers use a variety of commercial and open-source trajectory models. Individual countries may also have operational centers.
2.3.1. United States
U.S. Federal Operational Response Support
The U.S. National Oceanic and Atmospheric Administration (NOAA)/Office of Response and Restoration (OR&R), under the U.S. Department of Commerce, is designated by statute to provide continuous (“24/7”) scientific support in the event of oil and chemical spills to the Federal On-Scene Commander (usually the U.S. Coast Guard) within U.S. navigable waters.
Along the U.S. borders with Canada and Mexico, joint exercises in transboundary oil spill response occur regularly, with both groups providing oil spill modeling and natural resource information on location and potential oil fate and effects. Personnel are on-call 24/7 for assistance with oil spill science and modeling, with the main modeling center in Seattle, Washington, and regional Scientific Support Coordinators co-located with each U.S. Coast Guard district. OR&R also serves the U.S. military and State Department needs for oil spill response scientific support and modeling worldwide, particularly in countries without specific capabilities for oil spill modeling.
The OR&R supports approximately 150 spill events a year. Most of these are small spills or potential spills that do not result in a release. Oil spills are most common, but the NOAA provides modeling and other support for chemical releases, threats to navigation, and other issues in which its expertise can be helpful. In order to support its mission, the OR&R has been developing and delivering in-house models for over 40 years. The current operational model, the General NOAA Operational Modeling Environment (GNOME), is an oil fate and transport model. It includes scripting capability and a full web-based user interface, and can be run on a remote server or on a local workstation or laptop. It is open source and available on GitHub (https://github.com/NOAA-ORR-ERD). NOAA also develops tools for post-processing and presentation of the results to responders. These tools are specifically designed to meet the ASTM standard for oil spill trajectory results, which includes both the forward trajectory calculation and an uncertainty estimate around the model’s best estimate.
The OR&R’s mission is to provide support to the Incident Command (IC) to help guide response decision-making. In order to support the IC, the OR&R provides a full trajectory analysis, rather than simply model results. These analyses include discussion of the inputs and uncertainties, and provide a narrative explanation of the forecast. Modeling is only one component of these analyses, and can be seen as guiding the final product, rather than being the product. These trajectory analyses are presented to the IC by an NOAA Scientific Support Coordinator (SSC), who can explain the details and answer questions about the analysis.
In order to run GNOME, the core drivers must be available: Shoreline maps, data on currents, winds, oil properties, and parameterizations. The OR&R must be able to support responses to spills in the area of the entire coast and navigable rivers of the United States. There is no single operational model for currents for the US at all relevant spatial scales. While there are Operational meteorological models that cover the entire Continental United States (CONUS) (and globe), they are at resolutions that are not appropriate for smaller spills, and often do not include key physical variables, such as land/sea breeze. To meet its mission, the OR&R takes advantage of every driver model available: Operational models from NOAA and the U.S. Navy, as well as operational models from academic institutions. When necessary, tidal constituent models and an in-house simple steady-state model are used to generate current patterns that can be scaled to tides, river flows, coastal currents, etc.
As every driver model may be served up with different protocols, file formats, etc., the NOAA has built the GNOME Operational Oceanographic Data Server (GOODS3), a publicly available system to provide access to all the models and data sources regularly used for spill response. In the DwH oil spill, there was access to seven different circulation models for the Gulf of Mexico (MacFadyen et al. [8]), but most spills occur where there may be only one or no operational models at an appropriate scale. Additionally key to the NOAA’s process is feedback from field observations. For each modeling cycle, field observers (usually from helicopter overflights) report locations of observed oil. The analyst compares these observations with the model forecasts from the previous cycle. Parameters are adjusted to best match the observations, and a new model run and analyses are produced. This interaction with the responders in the field is critical to providing an accurate and useful product.
U.S. State Example (Texas)
As the state’s lead for oil spill response, the Texas General Land Office (TGLO) Oil Spill Program is responsible for preparedness and response to real and potential releases of oil into Texas coastal waters and over 3300 miles of coastline. Preparedness efforts have been focused on remote sensing and hydrodynamic modeling. The agency funds the operation of the Texas Automated Buoy Systems (TABS), an array of eight in-situ real-time met-ocean observational moorings for the core purpose of modeling oil spill trajectories. The buoys are strategically placed to aid in the decision-making and equipment deployment immediately after a spill.
The TGLO funds continuous operational hydrodynamic and oil spill models that cover the inshore waters of Texas, comprised of the bays, lagoons, estuaries, and tributaries, as well as a Texas–Louisiana shelf model for the offshore waters of the western Gulf of Mexico that forms the basis of the TGLO-funded ocean forecast model. The TGLO Texas–Louisiana shelf (TXLA) model uses surface winds and temperature fluxes from the Global Forecast System (GFS). Circulation and water property information are acquired from the MERCATOR global ocean forecast model. The result is a regionally specific nested high-resolution output designed to provide accurate forecasts for the western Gulf. Boundary conditions for the inshore areas are shared with the Texas Water Development Board (TWDB), which operates an inshore model, providing boundary conditions for bay model operations. Results are provided both to the Regional Ocean Modeling System (ROMS) and to the GNOME oil spill model.
2.3.2. Norway
The Norwegian Meteorological Institute (MET Norway) operates a 24/7 service for providing oil drift and weathering predictions to assist users during an emergency, as well as for training. The users of this service are the Norwegian Coastal Administration and the Norwegian Clean Seas Association for Operating Companies (NOFO), representing all the oil companies (~20) operating on the Norwegian shelf. Despite different formal responsibilities as respectively commercial and governmental bodies, NOFO and the Coastal Administration have a very close cooperation, including a yearly joint exercise where oil (on the order of 50 m3 total) is spilled on the sea to test equipment, logistics, and communication. In case of larger oil spills, forces will be joined, also including voluntary ships and personnel, which sometimes take part in the exercises.
On-duty meteorologists for MET Norway manually test the oil drift system twice per day. The oil drift system consists of the OpenOil model, coupled with the NOAA ADIOS library of oil data, forced by in-house, high-resolution ocean and atmospheric models, as well as with coarser foreign models serving as backup. Despite meteorologists being available for assistance 24/7, the users are also self-served through a web service, where they may initiate simulations through a web interface. Online visualization is provided; however, the users may also import the output directly into their own GIS portals, alongside map layers (e.g., contingency resources and natural habitats). Complementary to the official service, the users will also consult with researchers and model developers at MET Norway, as well as seek independent advice from SINTEF Ocean and their OSCAR modeling system. The developers of the models were also involved in the GoMRI program for experimental and model developments.
2.3.3. Canada
The Canadian Oil Spill Modelling Suite (COSMoS) (Marcotte et al. [9]) is currently in real-time try-outs for proposed operational use. COSMoS is tightly integrated with the Canadian Centre for Meteorological and Environmental Prediction (CCMEP) operational environment and its meteorological and environmental forecasting systems. Modeling research, development, and operations share the same physical infrastructure and computing environment. The proximity of environmental model developers and environmental emergency responders allows for the tailoring of ice, ocean, wave, and atmospheric models to emergency response needs. For example, oceanic forecasting system developers closely follow the development of COSMoS and adjust the forecast product to oil spill needs.
Another advantage of the Canadian operating model is direct access to the best forecast available at any given moment for regions of Canadian interest. The aquatic dispersion model leverages data from the forecasting systems directly from the operational storage units in the native forecasting system’s output format. Furthermore, the aquatic dispersion model has access to the supercomputing infrastructure, which allows it to run quickly with a large number of Lagrangian elements.
Finally, it is possible to archive case studies and to de-archive forecasts from the operational forecasting system easily. This capability allows the CCMEP to develop an aquatic dispersion model validation and verification database, enabling rapid and thorough evaluation of upgrades implemented in COSMoS.
2.3.4. Mediterranean Sea
Operational surface oil spill modeling and forecasting in the Mediterranean Sea started in the early 2000s in support of emergency response organizations, notably the Regional Marine Pollution Emergency Response Centre for the Mediterranean Sea (REMPEC) in the Mediterranean Sea (Carpenter et al. [10]) and the European Maritime Safety Agency (EMSA) at the European level (Girin and Carpenter [11]). The Mediterranean Sea surface oil spill modeling has been recently overviewed by Zodiatis et al. [12] and Cucco and Daniel [13] for the eastern and western Mediterranean, respectively.
In the Mediterranean, the development of surface oil spill forecasting has been tightly connected to the implementation of a complex ocean analysis and prediction system for the Mediterranean Sea (Pinardi et al. [14]) that includes hydrodynamics coupled with surface wave modeling and high-frequency atmospheric forecasts. The regional large-scale, several-kilometer-resolution operational forecasting system is given by the Copernicus Marine Environment Monitoring Service (Le Traon et al. [15]), and several national limited-area models at scales of a few kilometers are nested to provide mesoscale and/or coastal-scale resolved currents and waves in different sub-portions of the basin (Tintoré et al. [16]).
Surface oil spill modeling consists of the numerical solution of an active tracer advection diffusion equation with chemical reaction terms. In the Mediterranean Sea, several surface oil spill numerical models have been developed and used: MOTHY (Daniel [17]), MEDSLIK (Lardner et al. [18]), MEDSLIK-II (De Dominicis et al. [19]), and POSEIDON-OSM (Pollani [20]). These models have been calibrated/validated in several accidents in the Mediterranean Sea—among others, the largest oil spill accident of July of 2006 in Lebanon (Coppini et al. [21]) and the Haven accident in April 1991, offshore the western coasts of Italy (Cucco and Daniel [13]).
The practice of producing oil spill forecasts in the past 20 years demonstrated that uncertainties in surface oil spill forecasting were mainly associated with resolution and quality of forecasts of surface currents, winds, and waves (De Dominicis et al. [22]), the so-called input fields for surface oil spill models. An ensemble forecasting approach to quantify such uncertainties was then developed and implemented (Zodiatis et al. [23]), and this will be discussed in Section 5.
2.3.5. International Industries
ITOPF
The global shipping industry supports ITOPF to provide objective technical advice to all parties during ship-source marine pollution incidents. During ITOPF’s onsite attendance at over 820 marine pollution incidents and involvement in over 320 remote cases since the 1970s, ITOPF has developed a broad depth of experience in operational oil spill modeling. In addition, ITOPF is often called upon to undertake oil spill modeling as part of its support work to governments and industry during exercises and drills for pollution events.
ITOPF currently runs the U.S. government-developed GNOME trajectory model. Met-ocean conditions are derived from publicly available models (U.S. Navy HYCOM, NOAA RTOFS, etc.) usually accessed through the NOAA GOODS system. However, on occasion, ITOPF will seek additional information from modeling providers, such as Meteo-France. The level of modeling that ITOPF carries out varies depending on the case and the amount of incident information available. When little information is known, or sometimes unconfirmed, ITOPF will run a suite of modeling forecasts to account for the degree of uncertainty.
Oil Spill Response Limited (OSRL), United Kingdom
OSRL provides a 24/7/365 response modeling service to its members. An initial forecast is produced within 2 h from notification in the early stages of a mobilization, after which a planning cycle is developed of typically two forecasts per day to adjust for new surveillance information or new weather/ocean forecasts. Early oil spill modeling is focused on surface transport (using OILMAP 2D), aiming to provide a first approximation as to the direction of travel of the spill and some approximate impact calculations. The forecast is presented as a two-page summary, accompanied by a video animation and GIS files. As more information comes to light and/or the incident command needs more advanced information, more sophisticated modeling, including fate of the oil and three-dimensional transport (using the OSCAR model), handles the increasing complexity. Where the early forecasts are templated to deliver a fast service in a recognizable format, the more sophisticated modeling results and presentation are tailored to address specific response questions arising from the incident.
The oil spill models are driven by external ocean and weather models sourced from public sources, usually ocean currents from the U.S. Navy Global HYCOM or Copernicus systems, and surface winds from the U.S. NOAA Global Forecast System (GFS) or Climate Forecast System (CFS). If required, OSRL will initiate custom modeling to create tailored ocean models to improve the accuracy and confidence of the forecasts.
3. Earth System Modeling: Physical Drivers for Oil Spill Modeling
In an operational environment, emergency response is a required procedure. Operational oceanography is a fundamental component of the response, blending ocean measurements and numerical models to provide ocean forecasts. The observational approach includes the systematic and long-term routine measurements of the oceans and their rapid interpretation and dissemination. Ocean forecasting is based on the near-real-time collection of ocean observations that are assimilated into numerical models to provide short-term forecasts (5 to 10 days) (Schiller et al. [24]). It is only recently that operational biogeochemical forecasting systems have been developed by extending existing physical forecasting ocean systems, combining them with atmospheric models and also with biogeochemical models developed either for climate research or for ecological modeling (Ford et al. [25]). Earth system models seek to simulate all relevant aspects of the Earth system and integrate the interactions of atmosphere, ocean, land, ice, and biosphere to estimate the state of the ocean under a wide variety of conditions. Here, we focus on three main physical components (represented by ocean, atmospheric, and wave models) and their relevance as drivers to oil trajectory modeling.
3.1. Ocean Circulation Modeling Component
Ocean models are important in oil spill prediction, as they provide fundamental forcing inputs to oil trajectory models. Several such applications were employed during the DwH oil spill. Examples are the Global Hybrid Coordinate Ocean Model (HYCOM4); Chassignet et al. [26]), the Gulf of Mexico HYCOM (Mariano et al. [27]; Le Hénaff et al. [28]), the South Atlantic Bight–Gulf of Mexico model (Hyun and He [29]), the Real-Time Ocean Forecast System for the North Atlantic Ocean (Mehra and Rivin [30]), the intra-Americas-Sea Nowcast/Forecast System (Ko et al. [31]), and the University of South Florida (USF) West Florida Shelf (WFS) model (Barth et al. [32]). These models had limitations that influenced oil spill predictions, even though they were valuable tools for the immediate response, providing both forcing to the oil spill forecasts and vital information about the prevailing ocean conditions during the leakage period. We will discuss limitations that are still valid today, as well as the recent advances to overcome those limitations, including perspectives on further progress regarding this issue (see review at Fox-Kemper et al. [33]).
Model limitations become sources of errors and uncertainties in forecasts. A more comprehensive discussion on model uncertainty will be presented in Section 5. In terms of errors, we note that their sources in ocean models are different between deterministic processes (such as tides, wind-driven events, and coastal freshwater flows) and instabilities (such as mesoscale eddies, sub-mesoscale eddies, and associated fronts). For deterministic processes, the limitations in ocean model performance are controlled by model resolution, accuracy of model inputs, and ability to represent/parameterize the appropriate physical processes. Continuous improvements in these aspects have greatly advanced the ability to predict instabilities, with certain limitations that can be quantified with suitable observations. Data-assimilative models improve accuracy, but are often subject to limited availability of observations, especially in sub-surface/deep environments; certain important oceanographic parameters (e.g., salinity and currents) are generally under-sampled. Operational needs add another level of complexity in ocean model forecasting. The main aspects of ocean operational modeling in relation to recent advances and respective detected limitations are described below.
3.1.1. Downscaling to High-Resolution Local Models
Operational oceanography requires accurate depiction of a range of phenomena from the estuarine and coastal scale (e.g., land–sea interaction and river plume dynamics) to the shelf scale (e.g., wind and tidally driven flows) and the open sea (e.g., upper ocean structure and mesoscale features, such as eddies and meandering fronts). During the past 10 years, most of the improvements in the representation of these features are the direct outcome of more powerful computing platforms that allow for increased horizontal resolution. We can now perform basin-scale simulations (e.g., North Atlantic and the Gulf of Mexico) with grid spacing on the order of 1 km (sub-mesoscale resolving; Chassignet and Xu [34]; Le Hénaff and Kourafalou [35]; Jacobs et al. [36]) and regional/coastal simulations with grid spacing on the order of 100 m (Capet et al. [37]). The process for implementing downscaled, nested areas requires bringing together a wide range of input information, including bathymetry, river flows, lateral boundary conditions from either the global forecast or another nested forecast, surface fluxes from a global or nested atmospheric forecast, and all satellite and in situ observations. Rapidly addressing an emergency response requires systems in place that can quickly assemble this information and set up a new operational nest region as required. An important downscaling issue arises from the fact that the large-scale solution is unbalanced with respect to the local physics of the embedded model due to the different resolutions, bathymetries, numerical boundary conditions, coarse atmospheric forcing fields, etc. (Kourafalou et al. [38]).
3.1.2. Challenges in Model Inputs
Ocean models rely on information at the air–sea interface, the ocean bottom, lateral influences, and the land–sea interface (initial and boundary conditions). Errors in such inputs pose an additional challenge in model predictions. Atmospheric forcing errors are influential on surface currents, upwelling and downwelling, upper-ocean mixing processes, dense water formation, and set-up and set-down along coasts (including storm surges). Accurate bathymetry information can be lacking in the area of interest (e.g., in coastal domains, estuaries, straits, and islands). Boundary conditions provided by the outer, lower-resolution model may also introduce errors. In addition to possible errors in the solution of the outer, coarser model, the boundary condition methodology can also harm the solution of the nested, finer model (Kourafalou et al. [39]). If the boundary tries to impose information that is strongly in conflict with what the model is attempting to do in the interior, then over-specification error results, often leading to instability or spurious boundary re-circulations. If insufficient information is delivered at the boundary, then under-specification error results, and interior solutions can diverge from observations. Inputs on wave parameters are also important and are often provided by coupling between ocean models and surface wave models. Wilkin and Hunter [40] have shown the contribution of wave parameters on the skill of the ocean simulations in resolving the surface current variability (see more discussion in Section 3.2).
Another challenging input to be properly implemented in ocean models (especially in operational mode) is the freshwater flow from land to the ocean and its distribution along the coastlines. Ocean models typically have represented freshwater flow as input at particular points (river “mouth”) of river discharge (Kourafalou et al. [41]), and the spatial and vertical (thickness) distribution of the outflow transport can be optionally specified (Schiller and Kourafalou [42]). The method employed and the parameterization of related processes can impact output on the circulation and transport in areas of river influence (Kourafalou et al. [41,43]; Schiller and Kourafalou [42]; Tseng et al. [44]). The temporal step of the river input is often very coarse (e.g., monthly discharge rates and even climatological values), introducing additional limitations on the solution of the river plume dynamics. Le Hénaff et al. [45] showed the importance of high-frequency (daily) river input data, even for small discharges, in predicting related environmental impacts in the Northwestern Gulf of Mexico (GoM). Real-time river transport information is difficult to obtain, and this has a strong effect on model outputs of river plumes and associated density fronts and currents along shores. This can be crucial in case of oil transport prediction in a river-dominated area, such as the DwH oil spill incident (Kourafalou and Androulidakis [46]) and oil found around the Taylor Energy platform off the Mississippi Delta (Androulidakis et al. [47]; Hole et al. [48]). Improved inputs on atmospheric and river forcings, in combination with high spatial resolution, resulted in accurate predictions of distinct offshore branches of Mississippi River waters in the Gulf of Mexico (Androulidakis et al. [49]).
3.1.3. Representation of Important Ocean Processes: Sub-Mesoscale Features
Despite the new achievements in ocean models, computational capability limits models from explicitly representing the entire range of scale interactions that control ocean circulation. Because of the turbulent nature of oceanic flows, ocean circulation at a given scale is fundamentally dependent on oceanic motions at scales ranging from global (of order 10,000 km) to dissipative (of order 1 cm). The finite grid resolution of a particular ocean model configuration will constrain the spectrum of scales of motions that are explicitly represented in the model solution. An important limitation in ocean modeling thus involves unresolved physical processes. The effects of unresolved physics must be accounted for, both in the numerical model where they can feed back to larger-scale prediction skill and in the forecast of oil spill trajectories. As shown in detailed measurements around the DwH site by Poje et al. [50], the information content of ocean processes affecting surface material dispersion increases by orders of magnitude with decreasing spatial scale, especially below the radius of deformation. One of the net effects of these processes is enhanced dispersion. If the amount of dispersion is known, then it can be modeled using sub-grid models (Haza et al. [51]).
Mesoscale to sub-mesoscale interactions can also create challenges for modeling, since the overall effect is not completely understood. Sub-mesoscale processes are typically much smaller in scale and have much weaker currents than mesoscale features; however, the effects on surface transport can be stronger than those coming from the mesoscale. For instance, sub-mesoscale processes can cause leakage of material through mesoscale transport barriers (Haza et al. [52]). As shown in several multi-platform experiments (Huguenard et al. [53]; Roth et al. [54]; Rascle et al. [55]; Androulidakis et al. [47]), upper ocean fronts created by coastal freshwater outflows act as barriers to transport, exerting a strong influence on the pathways of flotsam coming from the ocean. These fronts evolve rapidly (on the order of hours) and are exceedingly difficult to represent in the correct location and time in ocean models. Some of these fronts can fold into themselves, forming vortices and eventually sink holes, sucking all surface material within an area one million times larger than the size of the sink hole (D’Asaro et al. [56]).
Velocity structure in the upper meter of the water column has also been identified as particularly important in transport of spilled oil without being well represented in ocean models. On the basis of data from hundreds of drifters near the DwH site, there is indication that wind and wave effects are inadequately represented in ocean models, and that transport modeling can be improved by supplementary fractions of wind (and waves due to Stokes drift) to the modeled fields (Haza et al. [57]). Both under hurricane conditions and near the coastal ocean, the upper ocean shear was found to be much larger than expected or modeled to date (Curcic et al. [58]; Laxague et al. [59]), which affects the transport of droplets of different size/buoyancy in the upper ocean.
3.1.4. Representation of Important Ocean Processes: Deep Ocean Currents
The visible portion of oil at the ocean surface often garners the majority of attention, though another critical component of the correct modeling and prediction of oil spills is the deeper mixing and transport by ocean currents. Because there are many more observations at or near the ocean surface than at depth, data-assimilation approaches (see next section) typically improve skill in the water column near the surface, typically the upper 1000 m or less. The deeper circulation is not well monitored, and therefore predictive skill is often lacking. Furthermore, Morey et al. [60] recently showed that there is a striking discrepancy between leading Gulf of Mexico models and the observations in deep eddy kinetic energy over the Loop Current region: The model’s computed deep eddy kinetic energy is generally less than half of that derived from observations. Real-time in-situ information of the deep ocean is key to validate/calibrate ocean current models and to directly drive oil spill predictions, especially in the case of deep leakages. The paucity of such suitable measurements can be a major limitation for the ability to simulate the fate and effect of oil spills. Reasons for the continued lag on real-time sub-surface measurements are generally related to costs, instrumentation, and operational maintenance. An important technical challenge is the design of an array of sensors to transmit measurements from multiple current profilers at depth and in real time.
The Gulf of Mexico does have some in-situ monitoring systems, but with severe gaps in measurements of sub-surface currents and at the near-bed/bottom-boundary layer. For instance, the effort to implement additional High-Frequency (HF) Radars in the context of the on-going Gulf Research Program sponsored by the National Academies of Sciences, Engineering, and Medicine (NASEM) might improve the available real-time information and the respective numerical simulations about the basin’s surface circulation, but the deeper transports would still remain unknown. Sustained real-time measurements of sub-surface and near-bed currents, and especially deep currents below 1000 m, continue to be an expensive and technically difficult problem to solve worldwide. In the Gulf of Mexico, the Bureau of Safety and Environmental Enforcement (BSEE) mandates that drillers and oil and gas (O&G) operators must monitor ocean currents in real time from near-surface (~30 m) to ~1000 m (NTL No. 2018-G01). Monitoring currents from 1000 m down to the seabed is optional for operators. Very few areas in the Gulf of Mexico have real-time current measurements below 1000 m. Beyond the scientific value, there is an added value for the operator to assert integrity of sub-sea infrastructure in the field (Ogle et al. [61]). Currently, there is not an operator-wide effort to systematically improve the monitoring of sub-surface currents in the Gulf. That fact is striking after the DwH oil spill and the lessons learned about tracking and monitoring sub-surface plumes.
3.1.5. Observational Needs and Data Assimilation
As numerical models move to higher model resolution and more powerful computing platforms are used, new classes of physics become resolved (Barkan et al. [62]). It is becoming increasingly apparent that high-resolution modeling requires high-resolution input data. This is because ocean models effectively generate a large solution space within the physical bounds of the primitive equations of motion and a wide variety of plausible parameterizations of ocean–wave–atmosphere coupling (Shi and Bourassa [63]). Even for known forcing functions and boundary conditions, the solution space is effectively infinite due to the nonlinear nature of the equations. The main distinction between obtaining a physically valid solution and one that corresponds to actual reality is how accurately the initial conditions are constrained by the real-time data. This point was made quantitatively within the context of a state-of-the-art, data-assimilative ocean model (Jacobs et al. [36]).
For instability features, such as mesoscale and sub-mesoscale eddies, the data assimilation process applies a correction to a prior model forecast; this correction is computed based on near-real-time observations. The cycle of assimilation and forecast occurs typically every 24 h. The operational data assimilation process is a statistical minimum squared error variance approach through 3DVar (Smith et al. [64]), and 4DVar approaches are nearing operational use (Smith et al. [65]). Both 3DVar and 4DVar are statistical approaches that require information on error covariances in the background and observations. These covariances often rely on long-term climatological observations (e.g., World Ocean Atlas) that enable the assimilation to constrain numerical models and not drift away from expected conditions. Historical work in mesoscale prediction has determined the vertical structure of temperature, salinity, and pressure so that surface observations can provide sub-surface corrections through the covariances. Typically, there are insufficient observations to determine the expected errors directly, and a number of methods have proposed different functional forms and amplitudes. The high density of observational data collected during GoMRI has led to advances in the covariance representation, an important value of these observations (Jacobs et al. [66]).
To date, data assimilation efforts have targeted mesoscale features and larger, which has been motivated by the resolution of available regular satellite and in-situ observations. By “regular”, we mean that these are the observations that are maintained over time, and we have a reasonable level of confidence that these data will continue to be available in the foreseeable future. Present regular observing systems do not resolve smaller-scale features, and much of the GoMRI work has shown the importance of the sub-mesoscale effects on transport and dispersion (D’Asaro et al. [56]). The sub-mesoscale presents a new challenge in this area, and efforts have begun to represent the vertical structures in sub-mesoscale physics (D’Addezio et al. [67]).
In the cases of GoMRI studies, targeted high-density observations allowed corrections at smaller scales. A change in covariance functions to exploit the high-density data has demonstrated that greater forecast skill can be achieved (Carrier et al. [68]). Surface drifters can provide significant observational coverage over an area of high interest at a relatively low cost (Muscarella et al. [69]; Figure 4). Airborne observations could be used to provide better high-resolution data on currents for model initialization (Rodriguez et al. [70]), while satellites can provide high-resolution data with continuous global coverage (Rodriguez et al. [71]). Observations available to the data assimilation have limitations that reflect on the predictive skill of non-deterministic mesoscale and sub-mesoscale features, and these issues are discussed in Section 5.
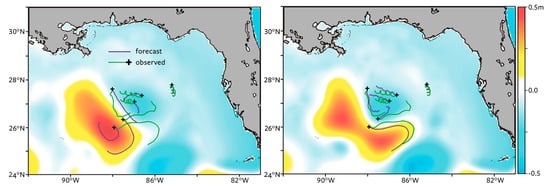
Figure 4.
An example of the improved trajectory forecast when the targeted Grand Lagrangian Deployment (GLAD) drifters are used in the assimilation process (from Carrier et al. [68]).
3.1.6. Operational Issues
Rapidly addressing an emergency response requires that modeling and observational systems are in place to quickly assemble available information and possibly set up a new nested model domain. Rapid solutions are required to provide effective ocean input to oil spill models. Advances have been made to have infrastructure in place to quickly assemble the necessary information and set up a relocatable nested grid over the area of interest. However, there are significant issues that can prevent a fast model implementation to serve a rapid response. The first is the lateral boundary conditions and interactions with the interior solution. As discussed above, the resolution mismatch between the outer boundary condition information and the interior dynamics is an issue. In an operational application, this can produce perturbations that cause the nested interior model to fail. The present approach to this problem is to manually iterate changing boundary locations. This process can be time- and personnel-consuming, as it requires setting up the system manually and, more importantly, scheduling another run into the available operational computer time. Evaluations of the impacts of mismatches in grid spacing of atmospheric and oceanographic models must be integrated in operational response.
A more time-consuming hurdle is to ensure that the nested information is sufficiently accurate to be used in decisions. The validation of a newly implemented nest requires comparisons with available in-situ and satellite observations, which usually takes place with hindcasting simulations. The scarcity of ocean observations requires running a nested system over several months (preferably a year) to ensure that there is a large number of sampled events. During an emergency response, the operational center has to conduct a long cycling hindcast in real time. This rapid implementation has to overcome the hurdle of scheduling operational computer time. Because of these limitations, operational centers often implement and maintain nested forecasts in areas of expected activity and high risk of potential oil spill accidents, which provide the first information during an emergency.
3.2. Meteorological/Wave Model Components
When dealing with a large spill, floating oil can substantially modify the atmosphere–wave–ocean coupling, causing different currents and waves around surface oil, which, in turn, modify the movement of the oil. An idealized numerical experiment (Zheng et al. [72]) showed that the above interactions among oil, wind, and waves substantially influence the oil’s motion in the context of other flows (e.g., strong currents related to eddies).
Oil trajectory forecasting during the DwH oil spill initially relied on available ocean models (see examples in Section 3.1). However, despite some great success from these modeling activities, limitations related to the meteorological and wave effects also became obvious (Liu et al. [73]). For instance, how surface oil modifies air–sea interaction and hence modifies oil transport were not considered. In addition, the wave-induced transport was initially ignored in oil trajectory forecasts during the DwH (Liu et al. [73]). Some models made an adjustment in surface transport due to “wind drift”, which includes an approximation for wave-induced motion based on one specific set of conditions. This was an important process to capture, as shown by Le Hénaff et al. [28]. However, this approach is still a parameterization that does not capture realistic highly variable wave transport (Weber [74]), nor the changes in wave-induced currents due to shoaling. Furthermore, some small-scale features were not captured nearshore, such as sea/land breeze and topographic steering, owing to relatively coarse resolutions in the atmosphere models coupled with ocean and wave models. The improved simulation of these small-scale features is critically important for improving operational oil trajectory forecasts in the near-shore region. When models include these small scales in both the ocean and the atmosphere, the atmosphere’s response to the ocean is substantial, and the impacts of this coupling on currents needs to be further investigated. Shi and Bourassa [63] examined such effects in relation to oil spill modeling and found that the ocean response to these changes in a two-way-coupled model is much faster (near equilibrium is achieved in less than two days based on their experiments) than that seen in coarse resolution models, where these issues could be ignored for a ten-day forecast.
3.3. Coupling of Modeling Systems
It is essential for oil spill models to correctly represent the coupling among ocean, atmosphere, and wave models. Wave-induced transport is very important in shallow water (where mesoscale eddies have less impact) and is responsible for substantial shoreward oil transport because the preferential wave direction is onshore in the coastal zone. However, waves from distant hurricanes cause much greater transport than typical wind-driven waves (see Figure 5). Hurricane-induced ocean waves have a remarkable impact on ocean surface currents because hurricane-induced Stokes drift can produce a cyclonic or anticyclonic rotational flow on the left or right side of the hurricane, respectively. For example, Hurricane Isaac in the Gulf of Mexico making landfall on 29 August 2012 accounted for up to 20% of the average Lagrangian velocity (Curcic et al. [58]).
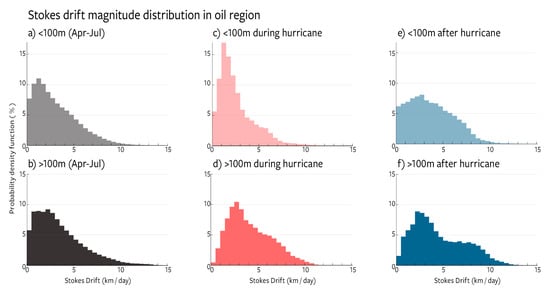
Figure 5.
Distribution of modeled (WaveWatch 3) values of Stokes Drift (km/day) in the region near the Deepwater Horizon oil spill with shallow water (shallower than 100 m) data on the top ((panels (a,c,e)) and deep water (deeper than 100 m) on the bottom (panels (b,d,f)). Panels (a,b) show a long-term average over the period of the oil spill (April–July 2010) for shallow water and deep water, respectively. These distributions peak at slow transport speeds, but the tails are large enough to be of concern for a major oil spill. Panels (c,d) show Stokes drift in shallow and deep water, respectively, when the swell from Hurricane Alex was passing through the region, showing much larger storm-induced transport. Panels (e,f) show transport in shallow and deep water, respectively, during the week following Hurricane Alex, showing that high rates of transport persist after the passage of the storm system. Stokes Drift was computed based on WaveWatch 3 partitioned data (Wind–Sea, Primary Swell, and Secondary Swell wave height, wave period, and wavelength).
The presence of oil slick itself can modify the parameterizations of wind stress and evaporation. Oil reduces the surface friction, which increases wind speed and reduces stress. Horizontal shears in oil coverage, and hence stress, modify vertical motion in the ocean and the atmosphere (Zheng et al. [72], Shi and Bourassa [63]). For the evaporation modification, the oil acts as an impermeable layer through which water vapor cannot pass, leaving only the oil-free portion of the surface available for the evaporation of water. Reducing evaporation reduces the latent heat flux, hence altering the near-surface energy budget in a manner that increases the surface temperature. This may cause a large horizontal surface temperature gradient between water and oil, further modifying the surface winds and the oil movement (Zheng et al. [72]). When both the atmosphere and ocean models are of high resolution in a two-way coupled model, these horizontal surface temperature gradients have a substantial impact in the local atmospheric forcing, further enhancing the impacts of horizontal gradients in currents and winds, and hence further changing the currents and sea surface temperature (SST) (Shi and Bourassa [63]).
Observations (O’Neil et al. [75]) have shown that surface winds respond to SST gradients. Modeling studies (Song et al. [76]) have shown that this response extends into the free atmosphere. One result of such oil spill modeling sensitivity studies was that this response happens very quickly, and that the ocean responds to this change in winds. This response was further found to depend substantially on the parameterization of the atmospheric boundary layer. As an example, the typical boundary layer parameterization used in the Coupled Ocean Atmosphere–Wave–Sediment–Transport (COAWST) modeling system is the improved Mellor–Yamada parameterization (MYNN; Nakanishi and Niino [77]), and the model’s change regarding current due to SST gradients is small, suggesting that this aspect of coupling is weakly important to surface transport. However, Song et al. [76] found that the Grenier–Bretherton (GB) boundary layer parameterization (Grenier and Bretherton [78]) was much more consistent with SST and surface wind observations, although it did not fully capture the observed response. When the GB parameterization was used, the response of the surface currents was larger; Figure 6 shows the differences in responses. This approach indicated that for high-resolution models, the choice of atmospheric boundary-layer parameterization has a substantial impact on the transport in areas with substantial SST gradients. These modifications to currents are dependent on the wind and air temperature, and hence change quickly relative to most ocean features. Nevertheless, the long-term impact is more vigorous surface currents, and, hence, usually more transport of oil.
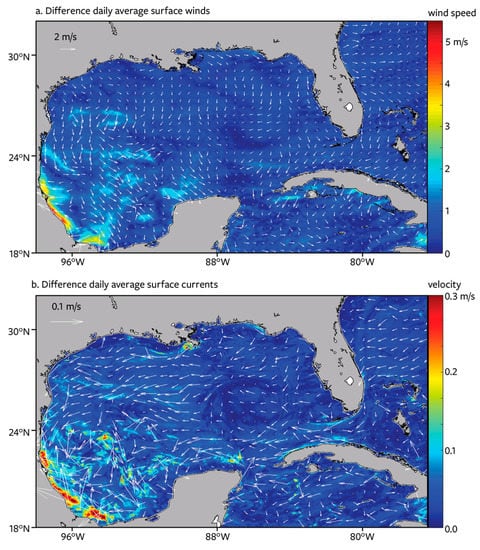
Figure 6.
Differences in daily average surface winds (speed and direction) (upper panel) and daily average surface currents (bottom panel) after four days between Coupled Ocean Atmosphere–Wave–Sediment–Transport (COAWST) with Grenier–Bretherton (GB) atmospheric boundary-layer parameterization and the same model with improved Mellor–Yamada (MYNN) parameterization.
The atmospheric forcing in the Gulf of Mexico in summer and winter is distinct in driving the upper ocean transport. During the summer, the time-mean large-scale atmospheric forcing is weak, the strong sea-breeze circulations greatly affect the coastal regions, and nighttime wind maxima occur over the offshore waters. During the winter, the atmospheric forcing is much stronger and winter storms and/or cold air outbreaks on a time scale of 3–7 days dominate in driving the upper ocean transport (Judt et al. [79]). Addressing such processes requires the use of high-resolution atmosphere and ocean models, which presumably more accurately capture the sea-breeze circulations. Thus, it is critically important to include the coupling among ocean/wave/atmosphere in an oil trajectory forecast model, although there is considerable work needed to be done to validate sea state dependency stress parameterizations, which would benefit from the improved observing system mentioned earlier. Attention should be drawn to the modifications of coupling among model components due to two factors: Differences in resolution of the atmosphere and ocean models, and the presence of oil for future operational oil trajectory forecasting.
An example of a properly downscaled coupled system has been implemented at the U.S. Fleet Numerical Meteorology and Oceanography Center (FNMOC). Initially, this system was the Relocatable ocean forecast system (RELO), based on the Navy Coastal Ocean Model (NCOM) and the Navy Coupled Ocean Data Assimilation (NCODA) system (Rowley and Mask [80]). The Coupled Ocean Atmosphere Prediction System (COAMPS) then advanced to include an atmospheric model, ocean model, and wave models (Allard et al. [81]), while also accounting for river discharges. These nested systems have been running operationally at FNMOC down to resolutions of 300 m on a daily basis. As coastal and nearshore waters and estuarine exchanges are critical for oil spill response, there is an urgent need to advance the development of such high-resolution, integrated operational forecast systems that allow downscaling solutions from the open sea to the shelf, coastal, and estuarine scales. Full coupling with hydrology (representation of the catchment areas, estuaries, and deltas) is very important and currently generally lacking in the operational environment.
4. Oil Spill Modeling
Operational oil spill modeling faces the challenge of providing 24/7 modeling results that must be available quickly, e.g., within 2 h of notification, initially using limited information on the situation and potential errors in the scenario. Error estimates and uncertainties in the forecast area are useful in order for decision-makers to best use this information (e.g., Galt [82]), and the reliability of the information and forecasts should also be provided. This differs from oil spill modeling for planning and preparedness activities, where sophisticated, peer-reviewed, 3-D, time-dependent models use multiple years of environmental data (e.g., winds, ocean currents) to develop statistical probabilities for oil spill trajectories. These predictions can be used for planning for the potential amount of and ideal locations for response equipment and assets, such as oil boom, skimmer vessels, and aircraft. Thus, operational models need to be able to provide quick results, sometimes based on minimal data. In this section, the current state of the art of operational modeling is reviewed, emphasizing advances made during the decade of the GoMRI program and with applications to releases at both the surface and at great depth.
The GoMRI program added a variety of research that improved operational modeling. The scale of this research was from tiny droplets (size distribution, dissolution, complexity) to highly integrated oil spill trajectory, weathering, and fate models. The data from laboratory studies were critical for development and calibration of theoretical models, development of new models of specific processes, and further development in integrated oil spill models. The integrated models rely on physical, chemical, and biological research in order to better predict oil spill release, trajectory, oil fate, and microbial activities on the oil (e.g., French McCay [83,84,85,86]). Integrated trajectory, fate, and effects models rely on a variety of sub-models, including models for well blowout plume dynamics, oil droplet formation, and both subsurface and surface oil fate and effects models. The GoMRI program touched on all of these aspects, focusing on the fate and transport processes that result from a large-scale spill from a well blowout, such as the DwH.
The GoMRI program has supported an extensive portfolio of modeling-related studies (Figure 7), from individual oil droplet scale to full 3-D and time-dependent models for response and planning. GoMRI research has touched on virtually all aspects of oil behavior in the environment, with many of the findings applicable to operational modeling. As the GoMRI research continues to be published, oil spill modeling groups will be able to leverage what was learned to better support oil spill response all over the world.
Figure 7.
Areas of Gulf of Mexico Research Initiative (GoMRI)-funded research on oil spill modeling.
Modeling advances are included from the small scale of computational fluid dynamics (CFD) modeling that lead to better understanding of buoyant subsurface well blowout plumes (e.g., Yang et al. [87], Fabregat et al. [88,89]) and to more operational well blowout models (e.g., the Texas A&M Oil Spill Calculator (TAMOC)). Discussion of advances in modeling for the water column, the mixed layer, and the ocean surface boundary follows.
4.1. Operational Considerations
One of the challenges faced by operational modelers during the DwH oil spill was working with multiple circulation models in the Gulf of Mexico, each of which gave different and, often, conflicting results (MacFadyen et al. [8]). Since that time, work has been done on making better use of multiple driver models—more modeling centers are making their results available via standard protocols, e.g., Integrated Ocean Observing System (IOOS) Coastal Ocean Modeling Testbed, publicly shared data in NetCDF CF standard output, and/or via OPeNDAP protocols. Large data collection centers for operational models, such as the U.S. Coast Guard Search and Rescue Optimal Planning System (SAROPS), actively harvest environmental data from a variety of environmental data sources (Breivik et al. [90]). In addition, as more remote sensing techniques for oil spills become available (Garcia-Pineda [91,92]), operational centers are developing better methods to ingest these data to re-initialize models (Barker and MacFadyen [93]).
Another challenge is locating moving oil that is beneath the surface, either as droplets or heavy oil that sinks to the bottom. Bayesian methods for searching for these subsurface oils are being advanced in the SOSIM model (Jacketti et al. [94]). The SOSIM model has been improved for finding submerged oil, e.g., an oil droplet layer, by including the oceanic density distribution. The model will follow oil droplets on isopycnal surfaces, rather than at a single depth. For sunken oil, e.g., heavy oil on the bottom, the model includes algorithms for following bathymetry on the continental shelf (i.e., the concept of Taylor Columns), using a test case in the Gulf of Mexico (T/B DBL-152). Shipments of heavy oil products, which sink when spilled in freshwater or seawater, are increasing. The combination of both the Bayesian and trajectory methods will be important in improving oil spill trajectory modeling as these heavy products increase in production.
Operational models need to balance fidelity, computational efficiency, and ease of use in order to inform critical decisions, particularly during the early stages of a response. A modest computational burden is desirable to allow execution of the many simulations required to explore the effects of large uncertainty in the flow rate, gas-to-oil ratio, reservoir fluid composition, oil–water interfacial tension, and other parameters. Model results can be compared with the limited and sparse observational data available in the first few days of a response (e.g., water column profiles of dissolved oxygen and fluorescence, location, and the extent of surfacing oil) to somewhat constrain uncertainties, but response decisions will be made with incomplete knowledge. An efficient operational model that can be used by a capable specialist will allow for frequent updates as new data become available.
One of the more consequential response decisions during a subsea release involves the use of subsea dispersant injection (SSDI), and “with and without” simulations of oil fate need to be developed to evaluate environmental trade-offs. Predictions of oil droplet size and the amount of hydrocarbons trapped and degraded in the subsea, floating on the ocean surface, and volatilized to the atmosphere are critical to discussions on environmental, health, and safety trade-offs related to the potential use of SSDI. Initial model predictions can be refined as monitoring data become available, but numerical simulations of a hypothetical deep-water blowout suggest the mitigative effects of SSDI are greatest when the strategy is implemented as soon as possible (French-McCay et al. [95,96]). Response plans in the U.S. Gulf of Mexico envision that SSDI would become operational approximately six days into a loss of well control incident, barring complexities in clearing the working area of debris, so model output will be used to fill many information gaps in the short time when go/no-go decisions must be made. As more observational data become available to constrain uncertainty around key model inputs, such as the sensitivity of oil droplet size to the amount of dispersant applied, subsea models simulating the specifics of the incident can be gradually refined. Observational data will not completely characterize the extent of hydrocarbons dissolved, dispersed, and degraded in the subsea, so gradually refined plume modeling will continue over the duration of the incident.
4.2. Subsea Plumes
A large subsea release of oil and gas, such as the well blowout in the DwH event, results in a momentum- and buoyancy-driven plume spanning an array of complex physical, chemical, and thermodynamic processes (Figure 8). These plumes are energetic systems that drive mixing, dissolution, and oil droplet formation, strongly influencing the resulting fate and transport of the oil and gas. Operational models for subsea releases are limited to integral plume and Lagrangian particle tracking models (e.g., Yapa et al. [97]; Johansen [98]). Integral plume models are appropriate for large releases near the source, where the buoyancy of the released oil and gas entrain seawater, resulting in a strong upward current (Dissanayake et al. [99]). Integral models are efficient because they treat the plume in a cross-sectionally averaged way, reducing the governing dynamics equations to a one-dimensional set of ordinary differential equations along the plume centerline (Bombardelli et al. [100]). Integral models can consider ocean cross-currents and density stratification and will either predict the location of a subsurface intrusion layer or, in shallower releases, track the oil and gas to the sea surface (Dissanayake et al. [99]; Yapa and Zheng [101]; Zheng and Yapa [102]; Johansen [98,103]). For very weak releases or for tracking oil and gas above an intrusion layer, Lagrangian particle tracking can be used at depth similarly to its application in surface spills (Dissanayake et al. [99]).

Figure 8.
Schematic of a deep sea release from a well blow-out.
Integral models have a long history of application in environmental fluid mechanics and have been validated from scales of the laboratory to many kilometers of rise in volcanic eruptions (Turner [104]). Algorithms are also well validated for tracking oil and gas bubbles within the buoyant plume stage and allowing gas bubbles to exit the upstream side of a plume in crossflow (Johansen [98]; Chen and Yapa [105]; Dissanayake et al. [99]). The Texas A&M Oil spill Calculator (TAMOC) provides comprehensive integral plume models for single-phase and multiphase flow in an open-source suite (Dissanayake et al. [99]). Most commercial oil spill models have similar integral plume models, built primarily based on the Clarkson Deep Oil and Gas (CDOG; e.g., Yapa and Zheng [101]) or DeepBlow model algorithms (Johansen [103]).
Most recent model development has been for computational fluid dynamics (CFD) models of the 3-D multiphase plume flow field (Fabregat et al. [88,89,106,107,108]; Fraga and Stoesser [109]; Fraga et al. [110]; Yang et al. [87]). These are predominantly large eddy simulation models, and effective tools have been developed for these models using both an Eulerian and a Lagrangian description of the gas bubbles and oil droplets. These models are valuable to help understand the effects of the Earth’s rotation and the complications of stratified crossflow, providing insight on entrainment coefficients that could be used in integral models. However, these models are too computationally expensive to be deployed operationally in a response, though aspects of the physics investigated with these models could be leveraged for use in response models.
4.2.1. Well Blow-Out Plume Modeling
Well blow-out plume models are of two basic types: A plume in a cross-current and stability-limited plume. Before the DwH oil spill, subsurface well blow-out plume models considered dissolution of the gas phase (Yapa et al. [97]), and some included the growth and effects of natural gas hydrates (Chen and Yapa [111]). The DwH oil spill highlighted the importance of the live oil phase (liquid petroleum with a large fraction of dissolved, gaseous, and light compounds) and the fact that much of the dissolved material sequestered in the ocean originated from the liquid phase at the release. Models have since been developed based on the single-bubble-model approach in which Lagrangian elements of a characteristic gas bubble or oil droplet size are tracked, and the fate calculations are solved for the characteristic particle size and then applied to all particles in the element (Dissanayake et al. [99]). Mass transfer calculations are based on an averaged interfacial mass transfer equation involving the mass transfer coefficient (dependent on the particle hydrodynamics and the molecular diffusion coefficient), the surface area (dependent on the shape), and the chemical potential (the difference between the solubility at the particle–water interface and the concentration in the surrounding fluid). Mass transfer models have been known for decades; hence, the main effort is in calculating the molecular diffusivity and the solubility at the interface, taking into account the real-fluid equations of state at high pressures and extreme temperatures.
Several equations of state are available to models, and recently, emphasis has focused on the Ping–Robinson equation of state with volume translation (Gros et al. [112,113,114]). This cubic equation of state requires knowledge of several thermodynamic properties of the various components of the oil (e.g., critical point properties, acentric factor, heat of solution, etc.) and the estimate of the petroleum fluid composition. TAMOC provides a large database of these properties for typical petroleum compounds, many obtained from the literature, and some estimated by various group-contribution methods (Gros et al. [112]). These complex equations of state are important in the live-oil phase, when many light compounds, including methane, ethane, benzene, and toluene, are dissolving out of the liquid-phase petroleum (Gros et al. [113]). Once the light fraction is dissolved and the composition resembles that of a dead oil (i.e., a produced oil with the gas evolved out), the octanol and water partition coefficient (Kow) can reasonably be used to estimate solubilities without using a sophisticated equation of state. Hence, the equation of state provided in TAMOC is valuable in the integral plume stage of transport and for predicting the mass flux of dissolved hydrocarbons into an intrusion layer, and the simpler Kow model can often be used in the Lagrangian particle tracking phase of the subsurface transport.
4.2.2. Droplet Size
The oil droplet size distribution (DSD) emanating from a blow-out plays an important role in the trajectory and fate of oil. Large droplets (millimeters) rise rapidly to the surface (a few hundred meters per hour), whereas small droplets (less than 100 microns) rise very slowly (Zhao et al. [115]; NRC [116]), on the order of a meter per hour, causing these small droplets to remain at depth and be moved primarily horizontally by ocean currents. In addition, the rate of oil dissolution (Gros et al. [113]) and/or biodegradation (Socolofsky et al. [117], Thrift-Viveros et al. [118]) increase with the water–oil surface area, and the surface-area-to-volume ratio increases as the size of droplets decreases. As response actions, such as dispersant application, can affect droplet size, accurate DSD models are important to response decision-making. Before the DwH spill, most work on DSDs was based on surface wave conditions that were unsuitable to be used as input for plume and 3-D models.
Two major approaches have been pursued to predict the oil DSD. One approach, pioneered in Johansen et al. [119], consists of predicting the d50 (volume median diameter) based on physical arguments and then assuming that the remaining oil DSD fits a lognormal or Rosin–Rammler distribution (Li et al. [120,121]) with a fixed characteristic width. Another approach consists of using a population model (Bandara and Yapa [122], Zhao et al. [123], Nissanka and Yapa [124]) to provide the whole DSD at each distance from the orifice, as done within the VDROPJ model (Zhao et al. [125]) and in the Oildroplets model (Nissanka and Yapa [124]). The VDROPJ model was used to provide the oil DSD to the TAMOC model, providing results that matched the observed oil components in the Gulf of Mexico for the DwH oil spill during a period in June 2010 for which there were numerous measurements for validation (Gros et al. [113]). VDROPJ was also used to predict the combined release of oil and gas without and with dispersant (Zhao et al. [126,127]). As the VDROPJ model uses the jet/plume hydrodynamics (momentum, buoyancy, and energy dissipation rate), it can be used to predict the oil DSD from non-spherical orifices and for non-vertical releases (Zhao et al. [126,127]). When dispersant is applied, tip-streaming occurs, whereby oil sloughs off the oil droplets in strings or “streams” that are microns in thickness, and eventually break into micron-sized droplets (Gopalan and Katz [128]). This results in a bimodal oil DSD, as noted in the experiments of Murphy et al. [129] and Zhao et al. [126,127]; the latter amended the VDROPJ model with a module to capture this mechanism.
In addition, laboratory experiments have been conducted to determine oil droplet breakup and DSD in plumes, including at deep-sea pressures with live oil (oil containing dissolved gas) (Brandvik et al. [130,131]). The ability to make better observations in the field of oil droplets, bubbles, and particulates in the field was made by Davies et al. [132] by using wide-band transmittance with a silhouette camera. These observations allow researchers and response modelers to better calibrate their models for the conditions at hand. In situations where the volumetric flow rate of gas in the release is comparable to that of the liquid oil, churn flow is likely to occur, and it consists of the oil and gas tumbling within the pipe prior to release (Boufadel et al. [133]). In this situation, models for predicting the oil DSD do not exist, but efforts for amending the VDROPJ model for this function are ongoing based on new experimental work.
Applications of the GoMRI Research experimental work on oil DSDs include parameterizations in models (e.g., OSCAR, GNOME), for droplet breakup in waves and oil droplet biodegradation with consumption of dissolved oxygen (Brakstad et al. [134], Thrift-Viveros [117]). For well blow-outs, examples of observational data for predicting the DSD that were obtained from bench to near full scale are discussed in Brandvik et al. [135,136,137] and Johansen et al. [119], including the effects of pressure in the deep ocean (Brandvik et al. [130,131]).
4.3. Processes in the Water Column
As most oils are less dense than water, they usually float to the surface and form a surface film, or “slick”. However, when released at depth, and under turbulent conditions at the surface, oil can spend substantial time in droplet form in the water column, where it undergoes a number of processes.
4.3.1. Dissolution
Dissolution is particularly critical in a deep sea plume, but also plays a key role in the transformation of the oil in the water column and at the surface. As dissolution is a mechanism for making soluble toxic compounds available to biota, this was often omitted in response models, while being included in injury assessment and environmental impact modeling. As being able to answer key questions during a large-scale blow-out about potential effects of response actions is important to decision-makers, dissolution is being included in recent response models.
4.3.2. Degradation
While it has always been assumed that biodegradation was the ultimate fate of oil in the sea, it was generally considered a long-term process, and was often left out of response models. The DwH spill provided an opportunity to study degradation on a large scale, and with new tools available (genomics), it has become clear that under certain conditions, degradation can be a significant process at fairly short timescales. However, most existing models are based on simple decay rates, dependent only on oil composition. Building on this, it is important to consider the colonization of individual droplets by bacteria and the biodegradation of the droplets through biofilm formation, which is highly dependent on surface area and, thus, droplet size. Biodegradation models based on droplet size are making their way into operational models (Brakstad et al. [138,139]; Thrift-Viveros et al. [118]).
4.3.3. Oxygen Demand
During the DwH oil spill, there was a concern related to the potential for oil biodegradation to consume dissolved oxygen in amounts sufficient to create hypoxic or anoxic conditions (Joint Analysis Group [140]; Adcroft et al. [141]). To improve understanding of the evolution of oxygen utilization and the potential for development of subsurface hypoxia or anoxia due to subsurface oil droplet biodegradation, new algorithms are in development. Brakstad et al. [134] shows results of first-generation laboratory measurements of dissolved oxygen consumption during oil biodegradation in hypoxic water. Initial inclusion of simple dissolved oxygen consumption was done in the OSCAR model based on Beegle-Krause et al. [142,143]. As the application of dispersants at depth could influence degradation and, therefore, oxygen demand, these methods could be critical in evaluating response options.
4.3.4. Marine Oil Snow Sedimentation and Flocculent Accumulation (MOSSFA)
In the years following the DwH oil spill, it was discovered that a Marine Oil Snow Sedimentation and Flocculent Accumulation (MOSSFA) event had occurred and continued several months after the DwH oil well had been capped. This MOSSFA event carried a substantial amount (6.9–7.7%) of the spilled oil to the seafloor (Passow et al. [144]; Brooks et al. [145]; Romero et al. [146], Daly et al. [147], Stout et al. [148]; Stout and German [149]; Langenhoff et al. [150]; Passow and Stout [151]). Formation of similar aggregates has also been observed previously when dispersant was applied to oil (Lee et al. [152]), and recent field studies have also confirmed their presence during the IXTOC spill in the southern Gulf of Mexico (Murk et al. [153]) (note that dispersants were not used further north than 25 N). There was also a significant freshet of increased outflow from the Mississippi River during the DwH oil spill that peaked in mid-May (Kourafalou and Androulidakis [46]). The sediment carried in the river water could have led to significant sunken oil (Brakstad et al. [154]). Most research on sunken oil previous to the DwH oil was related to oils heavier than seawater, such as Heavy Fuel Oils (HFOs) (Jacketti et al. [155]). Sedimentation of oil has numerous adverse effects on the ecosystems in the water column and at the sea floor. Therefore, it is important to inform the response community about the possibility of a MOSSFA event for marine oil snow (MOS) or oil-related marine snow (ORMS) aggregate formation.
Operational models (or any oil spill models) have not included this phenomenon of aggregate formation to date, one reason being that this had not been widely observed and studied prior to the DwH oil spill. Formation of marine snow and oil aggregates with the incorporation of mucus from bacteria (transparent exopolymer particles, TEP, and extracellular polymeric substances, EPS) and the mineral particles in the water column is a complex temporally and spatially evolving biogeochemical and physical process. The role of chemical dispersants in the formation and fate of MOS is not clearly understood, but the links have been identified between dispersant addition and possible MOS aggregate formation or MOSSFA events. The models developed using the coagulation theory to study the marine particle size distributions (Jackson, [156]; Jackson and Burd [157]; Burd and Jackson [158]) and oil–mineral aggregates (OMA) (Lee [159]; Khelifa et al. [160,161]; Bandara et al. [162]; Zhao et al. [163]) can be adopted to simulate the formation and behavior of MOS/ORMS. There are only limited numerical modeling studies available in the literature on MOS/ORMS aggregates. They are one-dimensional models that can predict the variation of aggregate size distribution with depth. Lambert and Variano [164] studied the potential to scavenge oil droplets in the water column using the settling marine snow aggregates with collision rate equations. They state that the collision rate is sensitive to local concentration of oil and aggregates, and when the droplets are in the larger size range of the distribution, a greater fraction of the oil volume collides with marine aggregates. Moreover, they suggest further studies on the shear and differential settling mechanism on the collision rate and state that no dominant collision mechanism is present. Dissanayake et al. [165] adopted a stochastic marine snow aggregate formation prediction model (Jokulsdottir and Archer [166]) and applied it to explain the evolution of marine snow aggregate formation during the DwH spill in the Gulf of Mexico. This study identifies the aggregate parameters: The stickiness of particles in the aggregate, the fractal dimension of the aggregates, and the aggregate break-up mechanism play important roles in predicting the aggregate size distributions at different depth levels in the water column and the settling fluxes of oil at the sea bottom. Francis and Passow [167] adopted a mixed-layer particle aggregation model presented in Jackson [168] and Jackson and Lochmann [169] to simulate a large diatom bloom that was observed in the Gulf of Mexico just after the DwH well was capped. The model has been parameterized with field and laboratory data, and they compared the model’s predicted sedimentation rates of oil and organic carbon results with the sediment trap data collected (Yan et al. [170]) near the DwH well site in the months following the spill. Francis and Passow [167] suggested using chlorophyll data as a guide to define phytoplankton concentrations in water.
4.4. Transport
Models for oil transport rely heavily on the driver fields: Ocean currents, surface winds, and surface waves. The transport mechanisms associated with surface oil movement are well known (Venkatesh [171]; Jones et al. [172]; Zelenke et al. [173]; Dagestad et al. [174]). With the continual improvement of environmental forecasting systems, the accuracy of oil spill model trajectories has significantly increased, as they are mainly limited by the forecasts of the underlying surface currents, waves, and winds. Tides are well predicted. However, forecasting winds and currents at the scale required for oil spill modeling remains challenging, particularly in coastal areas where the bathymetry and shoreline may not be well resolved or may change due to anthropogenic modification or large storm events, and where winds are subject to small-scale effects, such as topographic steering and land–sea breeze, which are not resolved by most meteorological models.
4.4.1. Diffusion Parameterizations
There are some limitations in our ability to accurately model oil spills in open environmental conditions: Spill models need to parametrize the diffusion due to sub-grid-scale circulations. Most models use a random walk (or random flight) approach, but determining the appropriate values for the diffusion coefficient is challenging, and isotropic diffusion may not be appropriate at all scales, particularly in regions with fronts and sharp gradients. Using a constant value for a specific coastal area is unlikely to represent the local physics throughout the area. Diffusion estimates based on a forecaster’s understanding of oceanic or estuarine circulation in a particular area based on experience are prone to errors, though these parameterizations can be calibrated during a spill with feedback from observations. Deriving information from ocean forecasting systems (e.g., circulation gradients) might be an alternative, though these coefficients can be much too high for oil spill modeling, as these values are set in order to keep the ocean model stable. The inert tracer release experiment and attempted model by Ledwell et al. [175] inform improvements. More work needs to be done to better capture spatially variable and non-isotropic diffusion. The CARTHE consortium’s field drifter experiments provide a rich dataset that can inform the development of more sophisticated parameterizations of diffusion at the surface.
When modeling concentration and transport of oil in the surface mixed layer, existing operational spill models use simple approaches to vertical mixing near the surface. Recent work considering complications from simplistic difference schemes presented in Visser [176] has been done, notably by Nordam et al. [177,178]. We expect that these approaches will be included in operational models soon.
4.4.2. Calculating Concentration
Modeling chemical concentrations requires the projection of the mass transported by Lagrangian elements onto an Eulerian grid. Several methods exist to calculate gridded concentration (e.g., D’Amours et al. [179]), but the representation depends on the choice of number of elements used and on the desired horizontal or vertical resolution. The Lagrangian elements may have a wide variety of properties, from simple position to sophisticated droplet size distributions and oil properties. Methods that are grid-size independent, such as Thiessen analysis (Galt [82]) or kernel density estimation (NOAA, unpublished), are making their way into operational models.
4.5. Surface Processes
While oil is floating on the surface, it can rapidly spread to form a thin film or slick, is exposed to both the atmosphere and the ocean, and undergoes a number of physical and chemical processes.
4.5.1. Spreading
Near the surface, many transport and weathering algorithms require an estimate of the film thickness or surface area. These estimates are provided by a “spreading” algorithm, most of which are adapted from the original work by Fay [180]. While the processes identified by Fay probably drive much of the initial spreading on calm waters, field-scale observations indicate that the oil on the surface is most often heterogeneously distributed: In patches, streamers, and often windrows. In addition, it has long been observed that the oil spreads out, and is thicker, in the downwind direction. This effect has been quantified by the work of Zeinstra-Helfrich [181], and may make its way into operational models. However, the patchy oil distributions are driven by sub-mesoscale processes, such as Langmuir circulation, fronts, and gyres. Much work has been done by GoMRI researchers on quantifying and better understanding these sub-mesoscale circulations, but this work has not yet made it into parameterizations that can be included in operational models.
4.5.2. Entrainment
One of the major processes in oil spills is “dispersion” or “entrainment”: The process of oil being broken up into tiny droplets that can stay suspended under the surface. For many years, operational models have relied on variations of the classic work by Delvigne and Sweeney [182], but multiple improvements have been made, extending the range of oil types capable of being modeled and including the effects of dispersant application. Johansen et al. [183] and Li et al. [184] have developed complete updated surface entrainment models that have made their way into operations models, with other researchers enhancing understanding of the process for potential future improvements (Zeinstra-Helfrich et al. [185,186]).
4.5.3. Weathering
In the event of a real spill, operational oil spill modeling helps guide response activities. As such, the largest question is the one of “Where is the oil going to go?”, i.e., “drift” or “transport”. However, oil is also weathered in the open environment, and responders need to know how much oil to expect, along with the oil properties, in order to plan a response. In addition, as the oil properties change, the features of the transport are changed, so that these transformations can be an important part of transport modeling as well.
The key processes considered in weathering (fate) modeling are: Evaporation, dissolution, biodegradation, emulsification, spreading, and photooxidation. Often also considered as fate processes (though they are strictly transport) are dispersion (the formation of droplets so small that they stay suspended in the water column) and oil–sediment aggregation (OSA). Evaporation and dissolution are fairly well understood, and are already included in operational models. However, the partitioning between evaporation, dissolution, and dispersion may not be well captured. As an example, a sensitivity analysis was conducted with the NOAA ADIOS2 model (Lehr et al. [187]) with a variety of diesel fuels. The model results showed that under the same conditions, different oils had similar surface persistence, but widely different ratios of evaporated to dispersed oil. Another example is work by Drozd et al. [188,189]. Using a sophisticated evaporation model, they found that the composition of DwH oil collected far from the source had ratios of soluble to insoluble volatile compounds that indicated that the oil had spent significant time underwater, rather than on the surface. Current operational models do not properly capture the partitioning of the oil between evaporation and dispersion/dissolution.
4.5.4. Emulsion Formation
Emulsions are known as a complication to field operations and cleanup operations, and might be a significant parameter in the choice of response options, e.g., mechanical recovery or in-situ burning (Brakstad et al. [138]). Emulsification is the process of small droplets of water mixing with the oil, and can greatly expand the volume of the emulsion, leading to responders needing to clean up more oil-in-water emulsion than the total amount of oil spilled. An emulsion of an oil has very different physical properties from those of the original oil (lower density, higher viscosity, often non-Newtonian) and far larger volume (can be up to 90% water), resulting in different transport and requiring different response equipment.
Operational emulsification models are mostly based on early work by Fay [180], and are known to not capture the process well. Fingas and Fieldhouse [190] summarized emulsion properties in terms of SARA (saturates, aromatics, resins, asphaltenes) composition and oil viscosity. Some models (e.g., SINTEF Oil Weathering Model) can be calibrated to laboratory weathering experiments, giving good results on oils that have been well tested (Daling and Strøm [191] and Daling et al. [192]). There is currently no operational model that can predict emulsification well based on oil chemistry and environmental conditions alone. Current research interests are in being able to predict emulsification through properties of the oil and the environment, as well as the kinetics of emulsion formation, rather than interpolation of laboratory and field data sets.
4.5.5. Photooxidation
Photooxidation has long been considered a secondary effect in the fate of spilled oil, and thus not included in response models (Fingas [193]). However, new work since the DwH spill has indicated that, at least in the conditions during that spill, photooxidation can be rapid, can affect a substantial fraction of the oil (Ward and Overton [194]), and is important in the formation of emulsions. However, the implications of this transformation on parameters important to response are not yet well understood, and thus, it is not included in response models yet.
5. Handling Uncertainty
Operational models cover a range of response needs: Search and rescue, oil and chemical spills, and body (vessel, aircraft) search and recovery. Oil or chemical spills are more common, but search and rescue are the most time-critical. Forecasting oil spill movement, weathering, and assessing hazard from oil spill releases entail an accurate understanding of model uncertainties, encompassing both numerical ocean circulation and oil spill modeling uncertainties. We present recent developments in quantifying uncertainty in ocean circulation and oil spill models that are useful for oil spill forecasting and hazard assessment.
Many government, academic, and private institutions have set up environmental forecasting systems. However, predicting the future is not a certainty. We understand that tides are very predictable, while weather forecasts can have varying reliability. Understanding both the predictions made by numerical models and their potential errors or uncertainties is very important in operational modeling. Uncertainties can also be examined for particular processes reflected in model inputs and/or model parameterizations. For example, Haza et al. [52] examined horizontal dispersion estimates based on drifter data and found that they were affected by drifter position uncertainty.
5.1. Uncertainty in Ocean Circulation Models
Starting from the numerical ocean models, an important note is that the mathematical equations describing the ocean currents are nonlinear so that any initial condition error may amplify with time in a deterministic forecast. A convenient framework to study the uncertainty of the coupled met-ocean forecast is to subdivide the sources of uncertainties into two categories: the internal dynamics and the external forcing (Shukla [195]). Internal dynamics concern errors due to the assumptions from first-principles equations, such as Boussinesq and hydrostatic simplifications, physical parameterizations for unresolved physics, and numerical schemes. External forcing considers initial and boundary conditions, the atmospheric forcing, and the respective air–sea physical parameterizations, the unresolved scales and errors in bathymetry and coastlines, and the lateral seaward and landward boundary conditions.
In ocean numerical modeling and forecasting, the main source of uncertainty will vary according to the location and particular process. Especially for the upper ocean, the uncertainty due to atmospheric forcing is of the same importance as the internal dynamics. The major part of the ocean’s kinetic energy is derived from winds (Ferrari and Wunsh [196]), the model representation of dynamics is limited by vertical resolution, and turbulence closure parameterization must account for effects of surface and internal waves within the density-stratified fluid. In coastal areas, uncertainty in the bathymetry and river outflow rates becomes the primary source. In deep water, the main uncertainty is due to thermocline and mixed layer depth variations, which are due to mesoscale and sub-mesoscale eddy errors in the initial conditions. Additional uncertainties due to the absence of in-situ measurements in the deeper ocean also exist in the contexts of both model evaluation and data assimilation (see Section 5.3).
The problem is then to predict the uncertainty due to a joint probability distribution that is of high dimension because of the many error sources. A range of approaches has been employed, from particle filters to polynomial chaos. The most direct and widely used methods are ensemble and/or super-ensemble predictions (see Section 5.4). The ensemble prediction approach is to provide many realizations due to all the uncertainties associated with internal dynamics and external forcing. Each realization is a separate model run with perturbations across the uncertainties. This process requires consideration of the probability distribution of each error source to ensure that they are properly represented, and many error sources are not simple Gaussian distributions. Again, historical observations are of great value in this problem. At the same time, the ensemble representation of the probability distribution relies on a large ensemble set representing realizations across the multidimensional uncertainty space. This demands large numbers of ensemble members and large computational resources.
In the presence of data assimilation, the statistical effects of observations on the probability distribution are a known Gaussian distribution of errors. In each regular assimilation cycle, observations reduce errors. Bayesian analysis has been used to represent this, and in an ensemble approach, the most direct method is for each ensemble member to assimilate observations. Many approaches to reducing computational requirements have also been employed, and each of these relies on assumptions that neglect some of the error sources.
5.2. Uncertainty in Oil Spill Models
A number of uncertainties in oil spill modeling need to be added to what has been already listed for the ocean current simulations. We can use the same framework and classify the oil spill modeling and forecasting uncertainties as due to internal model dynamics (e.g., oil chemistry, oil spill diffusion, incomplete scenario information early in the response) and external forcing conditions (ocean circulation, wave and wind inputs). For oil spill models, the external forcings are provided from ocean circulation, wave, and atmospheric models (or comprehensive Earth system models; see Section 3), and the related uncertainties from such modeling components or systems will influence oil spill predictions. The uncertainty due to internal oil spill model dynamics encompasses the specific advection–diffusion numerical scheme, the initial oil spill conditions, and the transformation processes related to the specific oil chemical characteristics, i.e., all the active tracer parts of the oil advection–diffusion equations. Owing to this large number of uncertainties and the predictability limits of meteorological and oceanic models, deterministic oil spill forecasting currently has a short predictability limit—perhaps 12 h to a max of 3 days. Ensemble oil spill modeling is necessary to extend the quality of the predictions to the weekly time scales (De Dominicis et al. [19,22,197]). For planning purposes, multiple years of data are used in order to determine the amount of response equipment that could be needed over time and the best locations for storing it.
A standard for oil spill models set by ASTM [198] requires uncertainty estimates (NOAA [199]). Such estimates are critical for providing proper guidance to responders so that resources are well directed, rather than being too focused on only the trajectory provided by a model run itself. Quantifying and presenting the uncertainty in an oil spill trajectory forecast poses many challenges—as all of the drivers of the model (meteorological and oceanic models) and inputs about the spill itself (quantity, location, initial extension area, type of oil) often come with substantial uncertainties that are not well quantified. It is critical that the uncertainty is constrained by integrating observations (of both the oil itself and met-ocean conditions) into each new modeling cycle. A trajectory model that is not calibrated to field conditions has little hope of useful accuracy after the initial days of a spill. In the case of a well blow-out at depth, there are additional challenges, as deep observations are sparse, and the driver models are often less constrained as well. It is also more difficult to present the uncertainty in the results with the extra dimension of depth.
5.3. Using More Observations to Reduce Uncertainty
The GoMRI program has ensured transparency of results and a long-lasting legacy of fostering future research by making all data (from observations and models) and published products from a decade of work publicly accessible through the Gulf of Mexico Research Initiative Information and Data Cooperative (GRIIDC; https://data.gulfresearchinitiative.org/). Even with this big body of work, and combined with additional data, such as from the Gulf of Mexico Coastal Ocean Observing System (GCOOS; https://gcoos.org/), the observations available for data assimilation in the Gulf of Mexico are able to constrain only features larger than a certain scale (Jacobs et al. [36]). These limitations are true in any other ocean region. In a high-resolution model forecast, the larger constrained scales have smaller errors and can provide deterministic prediction. In terms of trajectory forecasts for oil spills, the smaller-scale unconstrained features are the largest source of uncertainty in predictions (Jones et al. [172]; Dagestad et al. [174]).
Targeted observations can change the scale separation of constrained and unconstrained features. In an event of high interest, we know how targeted observations can advance the forecast skill (Carrier et al. [200]). During the DwH oil spill, model forecasts led to decisions without awareness of this information regarding scale separation, and the models revealed a wide range of differing results. Data assimilation, particularly for the subsurface, improved ocean circulation accuracy, which improved the operational oil trajectory predictions. With targeted observations, the constrained regime of the solution will encompass smaller scales, but the remaining separation between constrained and unconstrained variability must be addressed. As an example of the variability, we show a separation of the constrained and unconstrained scales from a 1 km implementation of NCOM (Jacobs et al. [36]; Figure 9). The unconstrained small-scale variability is compared to the standard deviation of an ensemble at 3 km resolution (Wei et al. [201]) to show the correspondence in location. This occurs because the constrained large-scale features modulate the areas of small-scale variability formation. While there are several approaches for generating the uncertainty in the unconstrained field, the transformation of the information into decisions remains to be addressed.
Figure 9.
Model forecasts for 20 March 2016 are shown for the Mixed Layer Depth (MLD) for (a) the full model (Navy Coastal Ocean Model (NCOM)), (b) the unconstrained or uncertainty portion, and (c) the constrained or confident portion of the forecast. (d) A comparison with 32-member ensemble at only 3 km resolution uses the MLD from each ensemble member to compute the standard deviation across the ensemble. The uncertainty features in the two right panels are a result of the larger-scale features modulating the placement and development of the smaller scales.
5.4. Using Ensembles to Reduce Uncertainty
Ensemble modeling has been used operationally for the atmosphere since the early 1990s, and has more recently also been applied to the ocean. Ensemble models typically yield 10 to 50 slightly different fields of winds, currents, or wave conditions, which are valuable for assessing the uncertainty for critical decision-making. Ensemble ocean forecasting started a little over a decade ago for limited areas of the ocean, such as the Gulf of Mexico, the Mediterranean Sea, and the Brazilian Current System (Counillon and Bertino [202], Milliff et al. [203], Pinardi et al. [204], Lima et al. [205]). These initial studies have shown that, given the pervasiveness of the mesoscale eddy field in the ocean, initial condition errors can be amplified in a few weeks, and the external forcing errors are equally important in the initial error growth. The so-called “super-ensembles” are also used, where different forecasting systems are employed. Brassington [206] showed that the evaluation of the ensemble or super-ensemble forecast efficiency (Murphy [207]) also requires a number of sophisticated statistical indices to relate the target variables to the observations.
There are two ways to generate an ensemble of results in a Lagrangian transport model. The simpler way, which could be referred to as a micro-ensemble, is to compute a parallel set of Lagrangian elements, each of which is forced with a perturbed version of the drivers; e.g., the wind or currents are slightly faster or slower or in a slightly different direction from what the forecast provides (Zelenke et al. [173], Lehr et al. [187,208]). The result is essentially a greater diffusion, but structured to match the uncertainty in the underlying drivers. Care must be taken in interpreting these results, as each Lagrangian element sees a different forcing, and thus, concentration information is lost. Analysis of these “uncertainty elements”, however, can help provide an uncertainty bound on the expected trajectory of the oil. Despite the limitations, the approach is computationally and operationally manageable, and has been in use by the NOAA’s Emergency Response division for many years.
A more complex approach to ensemble oil drift modeling can be conducted by performing complete separate simulations for each of the fields of the forcing data. This includes ensemble ocean model simulations that are particularly valuable, as forecasted currents are generally more uncertain than wind and waves (at least away from the coast). A set of even slightly different current fields may yield quite different trajectories with time due to nonlinearities and bifurcation. An alternative to using a single model to produce an ensemble as input in trajectory simulations is the use of the output from several different ocean models. The variation is useful, whether these are deterministic or ensembles. For example, this was done by the NOAA during the operational period of the DwH oil spill. At the time and region of the spill, NOAA had access to multiple peer-reviewed operational ocean circulation models. Note that none of these models were most accurate in any given location or any given time (MacFadyen et al. [8]). The variability among the forecasts of the Loop Current evolution, which has high velocities and chaotic aspects for position and shedding rings (Liu et al. [73]), was especially important during the operational forecasting period.
In addition to the above, a given case can also be simulated with several trajectory models, i.e., a multi-model simulation. Although trajectory models are based on the same or similar principles, several practical choices have to be made when implementing a model. Comparing simulations with different trajectory models (with the same environmental forcing data or different inputs) is therefore a way to assess the sensitivity and robustness of these choices.
Ensemble and super-ensemble oil spill predictions were at the basis of the prototype Mediterranean Decision Support System for Maritime Safety developed in 2010 (Zodiatis et al. [23]). The system was based upon the availability of the large-scale ocean predictions from the Copernicus Marine Environment Monitoring Service (Le Traon et al. [15]) and a wealth of limited areas/nested models with increasing complexity and resolution going toward the coasts (Kourafalou et al. [39]). The super-ensemble approach followed by Zodiatis et al. [23] consisted of using different ocean currents, atmospheric forcing, and different models of oil transformation and advection/diffusion schemes. This is the ultimate system for extending the limit of predictability of oil spill forecasts, but requires access to multiple models in every region in which a spill may occur. Based upon these initial findings and the ensemble and super-ensemble approach, it has been possible to start a proper mapping of the oil spill hazard for the Atlantic Ocean’s coastlines (Sepp- Neves et al. [209,210]). The noticeable result is that, on the basis of ensemble simulations of oil spills from different release points covering the trajectories of maritime transport across the oceans, it is possible to identify the probability distribution function (pdf) for the beached oil and, thus, to inter-compare different hazards with a quantitative method.
For incidents and emergencies, such as “Search and Rescue”, with short timescales and need for rapid response, there is normally not enough time to manually perform such ensemble-model simulations. For search and rescue operations, the U.S. Coast Guard has sponsored the development of the Search and Rescue Optimal Planning System (SAROPS; e.g., Kratzke et al. [211]). The system has four components: (1) Environmental Data Services (EDS), SIMulator (SIM), Search Planner, and Graphical User Interface (GUI). The EDS aggregates and redistributes meteorological and oceanic data from around the globe, providing extensive time series output from multiple ocean and atmospheric models that, in total, cover all the areas of interest to the U.S. Coast Guard and worldwide data for other clients. In addition to drift estimates, data provided by the EDS, such as wave height, cloud cover, sun, and rain, may affect search procedures and survival time. The SIM module includes characteristics of the search object paths and previous searches. This submodel uses Bayesian methods to make forecasts from the environmental information and previous searches. These models together provide recommended search patterns for aircraft.
A pilot system has been developed for automatic on-demand triggering of oil and search-and-rescue simulations with three different trajectory models on three corresponding “nodes” (Belgium, France, and Norway) using a variety of ocean and atmospheric models as input (Noos-Drift EU project5). About 10–15 min after a simulation is requested through a web form, the results are jointly analyzed and visualized in an accompanying WebGIS tool. Such a system requires agreed-upon standards and protocols for machine-to-machine communication and initialization of a simulation request, as well as a common output format. The pilot system is operational and working, and will be extended with more nodes in the future. The first version focuses on the horizontal trajectories, yet with no joint analysis of the differences in oil weathering.
5.5. Communicating Uncertainty
User-Centered Design is critical in testing new outputs for model results that are intended to be consumed by non-modeling-experts, including responders and the general public. During an oil spill incident, scientists need to communicate reliable information to responders and the public daily, ensuring that modeling results are realistic and contain appropriate error estimates. This is key to building and maintaining trust with the public and with other countries that may be affected by a spill of international significance. For instance, predictions by U.S. scientists during the DwH oil spill mattered internationally, and communication with the public eased early worries that the North Atlantic was going to fill up with oil.
However, uncertainty is challenging to understand and difficult to communicate, particularly to the broad public. One relatively simple method is employed by the NOAA in its trajectory analysis products. Figure 10 is an example trajectory from the DwH spill. The outer “uncertainty bound” indicates regions where the model did not forecast oil to go, but where it might go if the meteorological or oceanic forecasts are not quite correct. That bound is computed by examining where the elements with perturbed forcing are moved to.
Figure 10.
Example trajectory map produced by the National Oceanic and Atmospheric Administration (NOAA) for the Deepwater Horizon (DwH) spill. The blue contours indicate the model’s “best estimate” of the location of oil of different concentrations. The line surrounding the larger region is the “uncertainty bound”, indicating a larger area where oil might be found, reflecting the uncertainty in the inputs.
However, as the ability to do full-fledged ensemble modeling is developed, another way to present the results will need to be developed. It is a particularly challenging problem for ensemble oil spill models, as there are many levels of information in the model output—not just the bound of where oil might go, but what the likely concentration might be, and, if oil weathering parameterizations are included, there is additional uncertainty about the state of the oil as well.
Bringing more research and operational oil spill models to better handle uncertainty will require (a) research and development to improve the models’ chemistry, physics, and ocean dynamics; (b) expanding operations to include ensemble modeling in routine operational modeling; and (c) Human-Centered Design to ensure that the response community and the public are able to understand both the basic information about oil spill trajectories and the presentation of the respective uncertainty levels. Though presenting uncertainty in oil spill trajectory models is particularly challenging, there are successes to build upon. An example is the prior art of weather forecasts, in particular for tropical storms, where graphical tools and comments have helped the public’s understanding of the uncertainty in the forecasts.
6. Future Outlook
Current key challenges in operational oil spill modeling were discussed in the previous sections. Going forward, exploring new model developments and methodologies is important to advance oil spill response modeling toward more reliable forecasts under an operational decision support framework. We present suggestions for improvements that are related to both the ocean and oil spill modeling. We include innovative methodologies that are very promising for incorporation into operational systems.
6.1. Improvements in Ocean Models
A seamless modeling approach from the open sea to the shelf and coastal/estuarine environments is important for improved ocean model simulations and forecasts in limited area domains. This is expected to be advantageous for the successful planning and preparedness for a Spill of National Significance (SONS), as well as helpful for moderately sized spills. The majority of oil exploration sites are located in the coastal and shelf ocean, where high-resolution modeling is necessary to resolve processes related to estuary-delta dynamics, river plume dynamics, near-shore wave dynamics, coastal upwelling, etc. To fully alleviate issues with the reliable representation of currents and fronts associated with river plume dynamics (Schiller et al. [212]; Kourafalou and Androulidakis [46]; Soloviev et al. [213]), coupling with estuarine circulation is an important future advancement. Using a representation of estuarine circulation is a promising intermediate step (Verri et al. [214]). The real-time availability of hydrological inputs, either derived from dense and high-quality monitoring of river discharge rates or from numerical simulations at the connected drainage basins, is also important. An example is the NOAA’s National Water Model (NWM) that is providing gridded river flow for models, which fills gaps from river observations. The NOAA-coupled Northern Gulf of Mexico Physical–Biological Model includes the Mississippi River’s flow (Fennel et al. [215]).
The development of unstructured grid models has benefited ocean predictions in complex coastal areas (Herzfeld [216]; Herzfeld et al. [217]). Such models are better suited to resolve coastal details that are critical in case of an oil spill, such as outflows from smaller rivers (e.g., Galt [82]). Sub-grid-scale parameterizations are needed to account for the important physical processes that are not resolved by either the ocean or ocean spill model. Improvements are needed for the representation of bottom boundary layers, which are critical in predicting the movement of sunken oil spills, especially for weathered and heavy oils (Jacketti et al. [155]), spills with extensive oil–marine–snow or oil–mineral aggregate (OMA) formation (e.g., DwH), and spills with buoyant oil leaking from damaged submerged structures (e.g., Taylor Energy) (Warren et al. [218]).
A relocatable ocean circulation model approach is recommended together with permanent, high-resolution ocean models that have the desired accuracy for the processes of interest in areas of high priority. Such models should be, as much as possible, fully integrated met–hydro–wave–ocean models. In recognition that expertise would need to be developed in the operational centers, the focused effort could initially target implementation of a more advanced relocatable system within the high-priority areas, such as the Gulf of Mexico. As capability and expertise within the operational center develops, additional areas could be brought on line.
Advances in the coupling of ocean models with atmospheric and wave models are also needed. Important processes to improve are sea/land breeze, topographic steering, and nearshore small-scale features, which would improve oil spill modeling and forecasting. Seabreeze predictions are particularly important, as these onshore winds can lead to oil beaching. Data assimilation methods need to advance further, especially as high-resolution observations are becoming more readily available. An example of new observations near the ocean surface is the observation of changes in sea surface height by the Surface Water and Ocean Topography (SWOT) mission. Other future missions that would provide basin-wide Doppler coverage are also desired (Rodriguez et al. [70]; Ardhuin et al. [219]; Bourassa et al. [220]). An example of increased availability for observations of deep ocean currents in the Gulf of Mexico is through the Stones Field Public Partnership (Shell—National Academies of Science, Engineering, and Medicine (NAS)/Fugro/Texas A&M/University of Southern Mississippi), which is set to provide real-time current measurements down to ~3000 m depth.
6.2. Improvements in Oil Models
While the greatest sources of uncertainty in operational oil spill modeling are the drivers (source of oil, droplet size distributions, met-ocean forecasts such as winds, waves, and currents), there are a number of avenues for improvements in the oil models themselves. Research done since the DwH oil spill is paving the way for many of these improvements.
6.2.1. More Data: Controlled Oil Release Experiments
A methodology that has shown promising solutions to the limitations of bench and mesoscale observations of oil is the use of field-release experiments that can complement data collection during real spill events. These types of measurements often cannot be made during an incident, as the response actions need to take priority. Field-scale controlled oil release experiments occur rarely, such as when there is a need for confirmation of model development appropriate for a real oil spill. Field experiments are the culmination of laboratory bench and mesoscale experiments and modeling. The results can be used to improve understanding of oil spill processes and modeling. However, there are challenges: After the field measurements are completed, the oil must be cleaned up, but if left long enough to study all processes of interest, cleanup may be impossible (historical spills and mesoscale laboratory studies are used to determine these long-term weathering changes.)
This methodology has been used in Canada, Norway, the UK, and the Netherlands to aid model development and to provide documentation of oil spill cleanup capabilities. A challenge faced is the extensive requirements among various stakeholders for permitting such experiments. For example, an experimental spill on the Norwegian Shelf to obtain observations for model development, test monitoring capabilities, and evaluate safety aspects of response was released during the DeepSpill Experiment (Johansen et al. [221]). The permission process was extensive and was reviewed from multiple viewpoints. The two-day field experiment included three vessels with 42 scientists from SINTEF and the Institute of Marine Research (IMR), operators and observers, and multiple surveillance aircraft. Observers included representatives of the oil companies involved, the Norwegian Pollution Control Authority, an ornithologist from the Norwegian Institute of Nature Research (NINA), and external observers. Recently, a series of field releases of natural gas took place in the Trondheim Fjord and on the Norwegian Shelf, (e.g., Olsen et al. [222]). A key motivator for experimental oil releases is that Norway requires all oil spill response measures to be field-tested. This permission provides scientists and responders with key information related to oil spill response using Norwegian petroleum in realistic local conditions. Canada is in the process of permitting and implementing field experiments through the Multi-Partner Research Initiative (MPRI6). Data collection on oil fate and behavior during real spill events or controlled releases has been successful in defining both the need and working through a stringent approval process for controlled release experiments. Oil release experiments are often combined with requirements for oil response organizations to show their capabilities to clean up oil spills using various techniques, and include research in improving techniques.
6.2.2. Better Parameterizations: Transport
For the most part, oil transport near the ocean surface is fairly straightforward: The oil moves with the ocean currents, and thus, accuracy is governed by the accuracy of the circulation model(s) used. However, there are complications. Considered in oil spill models since their inception (ASCE [223]) is that oil is acted on more or less directly by the wind. This is accommodated by a “windage” parameter, where the oil is moved at a fraction of the wind speed, sometimes with an offset angle to include Ekman effects. While these parameterizations have been effective, the actual “wind drift” is more complicated: The oil is often episodically broken up into droplets pushed beneath the surface, and then transported in the shear layer by Stokes drift and other sub-mesoscale effects (e.g., Langmuir circulation). Recent work has been improving on the simple windage parameterizations (Zeinstra-Helfrich et al. [186]; Hole et al. [48]); these methods are finding their way into operational models. However, in order to fully capture these effects, more needs to be learned about droplet formation at the surface, and better fate parameterizations need to be integrated into the droplet and transport models.
Modeling the transport of oil and dissolved constituents in the upper ocean requires information related to the ocean circulation processes and especially the surface wind forcing. Research remains to be done to understand the surface dispersion of oil, as oil slicks are a continuum of droplets at the surface, just below, and, in some cases, just above in the atmosphere. The waves create the surface mixed layer, and oil is expected to be distributed at variable concentration throughout this layer. Most oil spills are surface oil releases, so these processes are very important for oil spill models. In higher wind conditions, larger waves and stronger winds can lead to aerosolized oil. We focus this discussion vertically, from the air–sea interface into the water column. Breaking waves and bubble bursting can create aerosolized oil droplets, which may be a hazard to oil spill responders (Afshar-Mohajer et al. [224]; Liyana-Arachchi et al. [225]), so there is work to be done to improve our understanding of surface oil processes.
Zhu et al. [226] has improved parameterization of wind drag at low wind speed by modifying Monin–Obukhov Similarity Theory with a new parameterization. Lödise [227] has improved wind drag parameterizations in high winds. The droplet size distribution generated by breaking waves or shear in surface currents has been revisited by Johansen et al. [183] and Li et al. [184], but more complications might arise from surface oil entrainment treated with Sub-Sea Dispersant Injection (SSDI). Daae et al. [228] considered the retention time of dispersant on the droplet from SSDI by modeling different half-lives for dispersant retention of the oil droplets. They found that changing the disassociation time (for the oil droplets and dispersant) modified the surface oil signature. Hypothetically, this could lead to reduced tarball formation when SSDI is used, as there would not be continuous oil slick at the surface. Finally, droplet diffusion algorithm implementations have been advanced to be more accurate (e.g., Visser [176], Nordam et al. [177,178,229]).
6.2.3. Better Parameterizations: Oil Fate
The open sea surface is characterized by highly variable and short-timescale episodic events, such as gravity wave spectra and white capping. However, the currently used models for entrainment (Johansen et al. [183]; Li et al. [184]) cannot capture the complexity of the resulting episodic oil slick and droplet formation. Better models are needed to capture the episodic nature of the sea surface, including the wave spectrum and white capping, as well as the oil entrainment process. In addition to improving entrainment parameterizations, this approach can better distinguish the processes influencing droplets in the subsurface (e.g., dissolution, degradation) and processes at the surface (e.g., evaporation, photooxidation).
6.2.4. Better Parameterizations: Tarball Formation and Photooxidation
Tarballs are the ultimate fate of much of the oil spilled in the open ocean, can form fairly quickly (within days), and can greatly affect the visibility and transport of the oil, but there are no operational models for their formation. They are thought to form with a similar mechanism to that of oil sediment aggregates (OSA), as they generally contain sediments with the weathered oil and may have a diameter from less than 1 mm to 10 s of centimeters (Khelifa and Gamble [230]). Modeling tarball formation combines models of oil breakup into smaller droplets, then coalescence models for oil and particulates, which may be heavier sediments or lighter organic material. The analysis of Harriman et al. [231] of wave-zone tarballs and tar patties showed differences in biodegradation products when exposed to sunlight or kept dark. Sunlight-exposed tarballs showed an accelerated production of water-soluble polar organic compounds.
There has been new and significant fundamental research on the biodegradation and photodegradation of petroleum in the wake of the DwH spill, including work done as part of the GoMRI. Out of this work, some key insights relevant to operational modeling have been uncovered. One of the most important of these is the evidence that, under some conditions, biodegradation and photodegradation can occur quickly enough to compete with other weathering processes known to be important within the first week after an oil spill (Ward et al. [232]). The conventional wisdom in the oil spill response community before 2010, primarily based on science from the T/V Exxon Valdez oil spill, was that photooxidation and biodegradation were slow processes that did not make a significant impact on the fate of floating oil components until after the first week of oil residence time on the surface. This older general approach is reflected in the operational oil fate models used at the time of the DwH and up to the present day. If photodegradation or biodegradation are included at all, they are treated as simple first-order decays. A much more nuanced approach is now possible with the fundamental research that has been conducted since 2010, as outlined below.
The themes in oil degradation research since the DwH spill can be grouped into several major areas. Advances have been made in the application of very high-resolution spectroscopic and chromatographic methods, such as electrospray ion cyclotron resonance mass spectrometry (McKenna et al. [233]; Chen et al. [234]; Zito et al. [235]) and multidimensional gas chromatography (Aeppli et al. [236]; Gros et al. [237]). These are used to identify and quantify weathering products that are not resolved by standard gas chromatography methods, including polar and/or high-weight molecular species that are generated during oxidation in the environment.
Using these new methods, detailed comparisons of the molecular degradation patterns generated by photooxidation and biodegradation have been made, leading to new insights into the molecular degradation pathways (Aeppli et al. [238]; Niles et al. [239]) and relative rates (Bacosa et al. [240]) of both processes; this has opened the door to identifying which process is dominant in field-weathered samples. With better characterization techniques, photooxidation has been established as an important fate mechanism that must be considered during the first week of a spill, particularly under conditions with high UV light exposure (Ward et al. [232], Ray and Tarr [241]). Important advances have also been made in measuring primary biodegradation rates under environmentally relevant conditions, including in seawater mesocosms (McFarlin et al. [242]; Olson et al. [243]) and in ocean floor sediments (Bacosa et al. [244]). Of particular interest is the research by Brakstad et al. [245], which takes into account droplet size distribution as well as other parameters. Some preliminary work has been done to integrate this research into operational oil spill models, including development of a new biodegradation model for the GNOME model, which takes surface area of droplets into account (Thrift-Viveros et al. [118]), but much more work needs to be done in this area. Finally, Daae et al. [228] considered the retention time of dispersant on the droplets from SSDI. Modeling different half-lives for dispersant retention of the oil droplets, they found that the disassociation time for both oil droplets and dispersants modified the surface oil signature.
6.2.5. Better Parameterizations: MOSSFA
Models can be used to predict the formation of marine snow and oil aggregates in the field, but at the same time, many areas still require improvements as well. Defining input parameters for models can be challenging due to the variable nature of the MOSSFA formation events. These parameterizations need further improvements to be included in present operational models for oil spills, as they are currently used only for specific marine snow and oil aggregate formation events. Input from Silhouette camera systems can provide observational data for model input, particularly when automatic particle type detection is included (Davies et al. [132]). Some future improvements suggested in the above-mentioned modeling studies can be listed as modeling the time evolution of oil and marine oil snow (MOS) in the water column, and then coupling the model with a hydrodynamic model that will allow the simulation of oil and MOS advected within a system. Additional research on the factors controlling aggregate fractal structure, stickiness, and disaggregation rates would improve model predictions and comparison with data. Related actions include: Establishing a library of fractal dimensions for phytoplankton aggregates, formed from a variety of different species to generalize the models; allowing for biodegradation of oil in MOS aggregates; defining oil in detail (e.g., pseudo-components); expanding prediction of possibility of blooms and their magnitudes based on the nutrient concentration in the water (nitrate concentration in the case of N-limited surface ocean waters and orthophosphate concentration in the case of P-limited surface ocean waters). In conclusion, we note that the present one-dimensional models can be implemented in 3-D far-field models. Development and integration of simple modules into response models can be done to make predictions of the probability and magnitude of MOSSFA events. In addition, it is important to note that there is also a comparable uncertainty (to MOS/MOSSFA estimation) in many other aspects of oil spill modeling, such as the formation of oil emulsions and tar balls.
In order to improve the outcome of oil spill response, our predictive tools need to keep pace with current research, and our research needs to reach toward answering key questions. The GoMRI program addressed the four basic needs: (1) Understanding oil chemistry and fate of oil in the ocean, (2) improving models and predictive tools in order to best follow the oil in the environment, (3) understanding more of the potential effects of the oil, and (4) new and better understanding of how the oil causes effects in the environment and biota. These pieces, put together, can be leveraged to improve our understanding and predictive ability for working through oil spills in order to have better outcomes for natural, cultural, and human use resources.
6.3. Improvements in Operations
Surprisingly, after years of research and development in environmental driver models (ocean, atmosphere, waves, ice, estuary, etc.), data availability in a timely manner remains an operational challenge. Driver models are run by a number of institutions, and no central server exists for all of them. One solution would be to set up an operational server for models that would either copy over the data from different specialized models on a file system or install and run forecasting systems developed by academia or the public sector. The USCG Search and Rescue System (SAROPS) utilizes a special-purpose system of this sort (O’Donnell et al. [246]), which could be used to inform future systems. The Copernicus System in the EU and the NOAA’s IOOS EDS server and GOODS system are partially filling this need, but are not yet comprehensive nor fully open. This would allow modelers to import data from a single location for spill events and would ease the standardization of data format.
Integration of Plume and Droplet Models
As discussed in Section 4, many improvements have been made to plume and droplet formation models leveraging DwH blow-out observations. These improvements still need to be fully integrated with operational modeling systems and procedures as source models into the larger-scale fate and transport models. As an example, the NOAA has collaborated with Texas A&M University (TAMU) to merge the GNOME and TAMOC models, including new DSD formulations; these improvements will be operational soon. Having accurate source models for a blow-out significantly reduces the uncertainty in oil spill modeling, as it provides a spatial and time evolution of the source. A plume model can also supply responders with critical information about the effects of response actions, such as SSDI, and the likelihood of the presence of dangerous volatile compounds in the surface waters.
6.4. New Methodologies
We discuss new methodologies that should be further developed in the future based on the knowledge gained during the last 10 years (GoMRI period). We focus on methodologies related to Lagrangian approaches, Lagrangian to Eulerian transformation, the use of information theory to analyze Lagrangian point fields, and neural networks using artificial intelligence.
6.4.1. Lagrangian Approaches
New methodologies developed during the GoMRI period, such as expanding Lagrangian methods for circulation and transport (e.g., D’Asaro et al. [56]), are promising for better monitoring and understanding of the Lagrangian nature of the ocean and the relation to the particle simulations used in oil spill models (Hole et al. [48]). Interpretation of such results must also be careful to distinguish between the movements of oil particles associated with different oil types under different environmental conditions.
Lagrangian Coherent Structures (LCS) have been shown to provide additional information for responders, such as identifying boundaries that the oil would not cross or where the greatest change in an oil spill would occur (Allshouse et al. [247] Beegle-Krause et al. [248]). Development of modeling of oil spills using Lagrangian Coherent Structures may be a way for improving oil spill trajectory model “Uncertainty Estimates” (see Section 5). Providing the responders with guidance on where oil may be blocked from traveling would be useful information in determining how to best allocate response options, e.g., pre-spill beach cleanup to remove beach wrack. A related Lagrangian approach (Mezic [249]) was applied on an experimental basis and proved helpful during the Refugio Beach (Santa Barbara, CA, USA) oil spill in 2014.
6.4.2. Lagrangian to Eulerian Transformation of Trajectory Model Point Distributions
Virtually all large-scale oil spill trajectory models use Lagrangian elements to represent the pollutants. These elements vary from representing larger amounts of surface oil (GNOME) to clusters of droplets known as “spillets” with a size distribution (Marine Environmental Modeling Workbench (MEMW), Oil Spill Contingency and Response (OSCAR), Dose-related Risk and Effects Assessment Model (DREAM), OilMap, Spill Impact Model Application Package (SIMAP)). However, in all cases, the models produce information as a collection of individual locations over time, visually represented as “dots on a map”. For response needs and other analyses, it is desirable to obtain the results in an Eulerian framework, i.e., the oil concentration (mass per unit area or volume) over the region of interest, at a scale appropriate to the incident. This transformation, while theoretically straightforward, must be done with care, or the results will be biased and of questionable use. Any method that is based on particle counts over a raster domain or uses defined-size kernel smoothing introduces an extraneous length scale into the analysis that is user-dependent and arbitrary.
There are other options that define the spatial scale of the influence of each particle depending on the local particle density. One such approach is to partition the domain into regions defined as nearest neighbors to the individual particles. The particle mass divided by the area of the neighborhood defined by these “Thiessen Polygons” will provide an Eulerian value that is scaled only on the particle distribution. These same Thiessen Polygons can be used to form a localized smoothing kernel to process the Eulerian data for presentation purposes. A detailed implementation of the method with examples and sample code is given in the technical report (Galt [250]), and the methods are extended to boundary regions using cluster analysis in Galt [251].
Another approach is to use a Kernel Density Estimation (KDE). The typical KDE approaches derive a kernel bandwidth based on analysis of the entire domain. This results in a smooth solution that captures the resolution of the particles at each time step. However, a more robust method can be to use spatial variable bandwidth based on the local density of particles, which can capture the wide variety of spatial scales often present in an oil spill trajectory (Björnham et al. [252]). In addition, if a non-homogeneous kernel is used, then sharp gradients and fronts can be captured as well. This approach is used in the NOAA’s GNOME system. With these algorithms available, older raster-based methods for Lagrangian to Eulerian transformations should be looked on with suspicion.
6.4.3. Using Information Theory to Analyze Lagrangian Point Fields
Many models used to forecast the fate of pollutants use Lagrangian elements, which typically have a mass attribute to represent the pollutant under study. Lagrangian trajectory model output is presented as mapping of the predicted time-dependent locations of the Lagrangian elements. The distribution of elements evolves over time and provides the user with data about expected locations and clustering of the individual elements. These time-dependent mappings represent “information.” This field information can be examined to answer specific questions. For example, (1) “How can one quantitatively understand how much information the model provides?”, (2) “How much does the information degrade over time compared to some objective ‘base level’?”, and (3) “When, or where, should data assimilation be used to restore the ‘information content’ of the model?” For researchers and responders involved in trajectory analysis, these are all important questions.
Lagrangian model output can be represented by a classical Shannon communication channel (Shannon and Weaver [253]). This approach defines an “information entropy” that is bounded between zero and a maximum value dependent only on the number of elements used in the model. It can be shown that the information entropy is linked to dominant physical processes within the Lagrangian model’s geophysical domain. Any dispersive processes (diffusion and non-linear chaos) increase the entropy, and any clustering processes (Lagrangian structures) will decrease the entropy (Galt et al. [254]). As the information entropy approaches the theoretical maximum, the model forecast results lose their dependence on initial conditions, and new input must be assimilated. For basin-wide geophysical models that have developed regional climatologies of the current fields, this new analysis technique may provide considerable insights.
6.4.4. Neural Networks and Artificial Intelligence
High-resolution ocean modeling is a great platform to develop hypotheses and investigate the role of ocean processes for various applications. However, for ocean state forecasting, a recent trend that turned into a main drawback is that too many unconstrained scales of motion are being generated in models, many of which can affect the transport of surface pollutants in unrealistic ways. The data to initialize these large modeled fields are hard to come by, even during bursts of most data-intensive field expeditions (Özgökmen et al. [255]). As such, the avenue of training artificial neural networks for predicting surface material transport on the basis of data alone is a promising, computationally-efficient avenue (Grossi et al. [256]).
6.5. Toward a Comprehensive Approach on Operational Oil Spill Modeling
Oil production and shipping occur all over the world, from inland rivers and lakes to the open ocean. Oil spills pay no attention to international borders, time of year, weather conditions, or holidays. Spills can occur from oil wells, leaking fuel, or leaking cargos. Government and industry need model results to examine potential impacts and response equipment needs for areas proposed for oil production. Governments and industry at the national and local levels need to understand where oil spills could originate from and where they could go in their areas in order to have enough equipment available and realistic scenarios for drills and exercises. Responders need met-ocean forecasts for oil trajectory forecasting in order to be advised about the immediate and near-future conditions in order to allow time for equipment to be moved into place, and to best triage response priorities for the day. Model results are overlaid on Environmental Sensitivity Index (ESI) maps, which show the locations of sensitive areas (e.g., coral reefs), timing of sensitive resources (e.g., occupied bird rookeries), and key areas of human use (e.g., beaches and water intakes). The modeling results, when combined with natural resource information, are an important resource for planning the use of response options for the best outcomes.
Integrated models are key to preparedness and planning for oil spills, including the potential fate and biological effects of the oil spill on natural, human-use, and cultural resources. Models are also used for finding challenging new scenarios to improve response preparedness and planning. Integrated models provide an overview of the development of oil spills and include resource information to assist responders in selecting among response options, e.g., whether or not to apply chemical dispersants. These models also provide a view into the future evolution of oil spills, so that responders can decide whether to use hazing techniques to keep birds away from an area where oil is predicted to arrive. Prediction of oil pathways is largely based on oil spill modeling, which can be performed by a number of institutions, both public and private, and with a variety of different oil spill models. These models need to run on operational modes and they require weather and oceanographic forecasts, usually from operational models as well. In order to provide the best support for spill responders, all operation centers should have access to the best possible models. We envision a future in which all results from operational models are made available via standard protocols to anyone that may need access.
The GoMRI program, over 10 years, touched on oil spill science and modeling from individual droplets to oil slicks and biological effects of oil on wildlife and humans. This large collective focus over such an extensive set of scientific fields with multiple countries involved has set a new benchmark for knowledge in oil spill modeling and assessment. The GoMRI program has been an excellent example of partnership between academia, government, and industry research efforts. The combined scientific results should improve preparedness and understanding of potential impacts with the variety of new models developed. This legacy should be well used by future researchers and responders to improve oil spill modeling and response. The scientific relationships developed through the research consortiums and conference interaction can be called upon to continue the dissemination of the results and to set the stage for future research efforts. The modeling approaches and research scales from droplets to large spills will be useful in answering questions of oil spill science and will lead to improved integrated models.
Author Contributions
Conceptualization, C.H.B., V.H.K. and C.B.-K.; writing—original draft preparation, all authors; writing—review and editing, all authors; visualization, C.H.B., V.H.K., C.B.-K., G.J., M.B. and Y.Z.; supervision, C.H.B. and V.H.K.; funding acquisition, C.H.B. and V.H.K. All authors have read and agreed to the published version of the manuscript.
Funding
Much of the research used for this synthesis and review manuscript was made possible by grants from the Gulf of Mexico Research Initiative (GoMRI). Other national and international grants, too numerous to list, also contributed substantially.
Acknowledgments
Data for the research funded by GoMRI are publicly available through the Gulf of Mexico Research Initiative Information and Data Cooperative (GRIIDC) at https://data.gulfresearchinitiative.org. We thank GoMRI for funding the workshop of international experts that formed the foundation for this manuscript (October 15–17, Washington DC, USA). We acknowledge the graphics help from Woods Hole Oceanographic Institution, Natalie Reniers. We thank 5 anonymous reviewers for supportive remarks and constructive comments.
Conflicts of Interest
The authors declare no conflict of interest.
Disclaimer
The scientific results and conclusions, as well as any views or opinions expressed herein, are those of the author(s) and do not necessarily reflect the views of the NOAA or the Department of Commerce.
References
- Crone, T.J.; Tolstoy, M. Magnitude of the 2010 Gulf of Mexico oil leak. Sci. Express 2010, 330, 634. [Google Scholar] [CrossRef] [PubMed]
- Spaulding, M.L. State of the art review and future directions in oil spill modeling. Mar. Pollut. Bull. 2017, 115, 7–19. [Google Scholar] [CrossRef] [PubMed]
- French, D.P.; Schuttenberg, H.Z.; Isaji, T. Probabilities of Exceeding Thresholds of Concern: Examples from an Evaluation for Florida Power and Light. In Proceedings of the Twenty-Second Arctic and Marine Oil spill Program (AMOP) Technical Seminar, Calgary, AB, Canada, 2–4 June 1999; pp. 243–270. [Google Scholar]
- Aamo, O.E.; Reed, M.; Lewis, A. Regional Contingency Planning Using the OSCAR Oil Spill Contingency and Response Model. In Proceedings of the Twentieth Arctic and Marine Oil Spill Program (AMOP) Technical Seminar, Vancouver, BC, Canada, 11–13 June 1997. [Google Scholar]
- Barker, C.H.; Galt, J.A. Analysis of Methods used in Spill Response Planning: Trajectory Analysis Planner—TAP II. Spill Sci. Technol. Bull. 2000, 6, 145–152. [Google Scholar] [CrossRef]
- Boehm, P.D.; Page, D.S. Exposure Elements in Oil Spill Risk and Natural Resource Damage Assessment: A Review. Hum. Ecol. Risk Assess. Int. J. 2007. [Google Scholar] [CrossRef]
- Smith, R.A.; Slack, J.R.; Wyant, T.; Lanfear, K.J. The Oil Spill Risk Analysis Model of the U.S. Geological Survey. Reston (Virginia): U.S. Geological Survey. In U.S. Geological Survey Professional Paper 1227; The Branch of Distributio: Alexandria, VA, USA, 1982; p. 44. Available online: https://www.boem.gov/Environmental-Stewardship/Environmental-Assessment/Oil-Spill-Modeling/smithetal-pdf.aspx (accessed on 17 August 2020).
- MacFadyen, A.; Watabayashi, G.Y.; Barker, C.H.; Beegle-Krause, C.J. Tactical Modeling of Surface Oil Transport during the Deepwater Horizon Spill Response. In Monitoring and Modeling the Deepwater Horizon Oil Spill; Liu, A., MacFadyen, A., Ji, Z.-G., Weisberg, R.H., Eds.; John Wiley & Sons: Washington, DC, USA, 2011; pp. 167–178. [Google Scholar]
- Marcotte, G.; Bourgouin, P.; Mercier, G.; Gauthier, J.-P.; Pellerin, P.; Smith, G.; Onu, K.; Brown, C.E. Canadian Oil Spill Modelling Suite: An overview. In Proceedings of the 39th Arctic Marine Oil Spill Program Technical Seminar on Environmental Contamination and Response, Halifax, NS, Canada, 7–9 June 2016; pp. 1026–1034. [Google Scholar]
- Carpenter, A.; Donner, P.; Johansson, T. The Role of REMPEC in Prevention of and Response to Pollution from Ships in the Mediterranean Sea. In Oil Pollution in the Mediterranean Sea: Part, I. The Handbook of Environmental Chemistry; Carpenter, A., Kostianoy, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 167–190. [Google Scholar]
- Girin, M.; Carpenter, A. Shipping and Oil Transportation in the Mediterranean Sea. In Oil Pollution in the Mediterranean Sea: Part I; Springer: Berlin/Heidelberg, Germany, 2017; pp. 33–51. [Google Scholar]
- Zodiatis, G.; Coppini, G.; Perivoliotis, L.; Lardner, R.; Alves, T.; Pinardi, N.; Liubartseva, S.; De Dominicis, M.; Bourma, E.; Sepp Neves, A.A. Numerical Modeling of Oil Pollution in the Eastern Mediterranean Sea. In Oil Pollution in the Mediterranean Sea: Part, I. The Handbook of Environmental Chemistry; Carpenter, A., Kostianoy, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 83, pp. 215–254. [Google Scholar]
- Cucco, A.; Daniel, P. Numerical Modeling of Oil Pollution in the Western Mediterranean Sea. In Oil Pollution in the Mediterranean Sea: Part, I. The Handbook of Environmental Chemistry; Carpenter, A., Kostianoy, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 83, pp. 255–271. [Google Scholar]
- Pinardi, N.; Cavaleri, L.; Coppini, G.; De Mey, P.; Fratianni, C.; Huthnance, J.; Lermusiaux, P.E.; Navarra, A.; Preller, R.; Tibaldi, S. From weather to ocean predictions: An historical viewpoint. J. Mar. Res. 2017, 75, 103–159. [Google Scholar] [CrossRef][Green Version]
- Le Traon, P.Y.; Reppucci, A.; Alvarez Fanjul, E.; Aouf, L.; Behrens, A.; Belmonte, M.; Bentamy, A.; Bertino, L.; Brando, V.E.; Kreiner, M.B.; et al. From Observation to Information and Users: The Copernicus Marine Service Perspective. Front. Mar. Sci. 2019, 6, 234. [Google Scholar] [CrossRef]
- Tintorè, J.; Pinardi, N.; Álvarez-Fanjul, E.; Aguiar, E.; Álvarez-Berastegui, D.; Bajo, M.; Balbin, R.; Bozzano, B.; Buongiorno Nardelli, B.; Cardin, V.; et al. Challenges for Sustained Observing and Forecasting Systems in the Mediterranean Sea. Front. Mar. Sci. 2019, 6. [Google Scholar] [CrossRef]
- Daniel, P. Operational forecasting of oil spill drift at Météo-France. Spill Sci. Technol. Bull. 1996, 3, 53–64. [Google Scholar] [CrossRef]
- Lardner, R.W.; Zodiatis, G.; Loizides, L.; Demetropoulos, A. An operational oil-spill model for the Levantine Basin (Eastern Mediterranean Sea). In Proceedings of the International Symposium on Marine Pollution, Monaco, 5–9 October 1998; pp. 511–512. [Google Scholar]
- De Dominicis, M.; Pinardi, N.; Zodiatis, G.; Lardner, R. MEDSLIK-II, a Lagrangian marine surface oil spill model for short-term forecasting—Part 1: Theory. Geosci. Model Dev. 2013, 6, 1851–1869. [Google Scholar] [CrossRef]
- Pollani, A.; Triantafyllou, G.; Petihakis, G.; Nittis, K.; Dounas, C.; Koutitas, C. The Poseidon Operational Tool for the Prediction of Floating Pollutant Transport. Mar. Pollut. Bull. 2001, 43, 270–278. [Google Scholar] [CrossRef]
- Coppini, G.; De Dominicis, M.; Zodiatis, G.; Lardner, R.; Pinardi, N.; Santoleri, R.; Colella, S.; Bignami, F.; Hayes, D.R.; Soloviev, D.; et al. Hindcast of oil-spill pollution during the Lebanon crisis in the Eastern Mediterranean, July–August 2006. Mar. Pollut. Bull. 2011. [Google Scholar] [CrossRef] [PubMed]
- De Dominicis, M.; Bruciaferri, D.; Gerin, R.; Pinardi, N.; Poulain, P.M.; Garreau, P.; Zodiatis, G.; Perivoliotis, L.; Fazioli, L.; Sorgente, R.; et al. A multi-model assessment of the impact of currents, waves and wind in modelling surface drifters and oil spill. Deep-Sea Res. II 2016, 133, 21–38. [Google Scholar] [CrossRef]
- Zodiatis, G.; De Dominicis, M.; Perivoliotis, L.; Radhakrishnan, H.; Georgoudis, E.; Sotillo, M.; Lardner, R.W.; Krokos, G.; Bruciaferri, D.; Clementi, E.; et al. The Mediterranean Decision Support System for Marine Safety dedicated to oil slicks predictions. Deep-Sea Res. II 2016. [Google Scholar] [CrossRef]
- Schiller, A.; Mourre, B.; Drillet, Y.; Brassington, G. An overview of operational oceanography. In New Frontiers in Operational Oceanography; Chassignet, E., Pascual, A., Tintoré, J., Verron, J., Eds.; GODAE Ocean View; The Florida State University Libraries: Tallahassee, FL, USA, 2018; pp. 1–26. [Google Scholar] [CrossRef]
- Ford, D.; Kay, S.; McEwan, R.; Totterdell, I.; Gehlen, M. Marine biogeochemical modelling and data assimilation for operational forecasting, reanalysis and climate research. In New Frontiers in Operational Oceanography; Chassignet, E., Pascual, A., Tintoré, J., Verron, J., Eds.; GODAE Ocean View; The Florida State University Libraries: Tallahassee, FL, USA, 2018; pp. 625–652. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcradt, A.J.; Baraille, R.; Bleck, R. The HYCOM (Hybrid Coordinate Ocean Model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Mariano, A.J.; Kourafalou, V.H.; Srinivasan, A.; Kang, H.; Halliwell, G.R.; Ryan, E.H.; Roffer, M. On the modeling of the 2010 Gulf of Mexico Oil Spill. Dynam. Atmos. Ocean 2011, 52, 322–340. [Google Scholar] [CrossRef]
- Le Hénaff, M.; Kourafalou, V.H.; Paris, C.B.; Helgers, J.; Hogan, P.J.; Srinivasan, A. Surface evolution of the Deepwater Horizon oil spill: Combined effects of circulation and wind induced drift. Environ. Sci. Technol. 2012, 46, 7267–7273. [Google Scholar] [CrossRef]
- Hyun, K.H.; He, R. Coastal upwelling in the South Atlantic Bight: A revisit of the 2003 cold event using long term observations and model hindcast solutions. J. Mar. Syst. 2010, 839, 1–13. [Google Scholar] [CrossRef]
- Mehra, A.; Rivin, I. A real time ocean forecast system for the North Atlantic Ocean. Terr. Atmos. Ocean. Sci. 2010, 21, 211–228. [Google Scholar] [CrossRef]
- Ko, D.S.; Martin, P.J.; Rowley, C.D.; Preller, R.H. A real-time coastal ocean prediction experiment for MREA04. J. Mar. Syst. 2008, 69, 17–28. [Google Scholar] [CrossRef]
- Barth, A.; Alvera-Azcárate, A.; Weisberg, R.H. A nested model study of the Loop Current generated variability and its impact on the West Florida Shelf. J. Geophys. Res. 2008, 113, C05009. [Google Scholar] [CrossRef]
- Fox-Kemper, B.; Adcroft, A.; Böning, C.W.; Chassignet, E.P.; Curchitser, E.; Danabasoglu, G.; Eden, C.; England, M.H.; Gerdes, R.; Greatbatch, R.J.; et al. Challenges and prospects in ocean circulation models. Front. Mar. Sci. 2019, 6, 65. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Xu, X. Impact of horizontal resolution (1/12 to 1/50) on Gulf Stream separation, penetration, and variability. J. Phys. Oceanogr. 2017, 47, 1999–2021. [Google Scholar] [CrossRef]
- Le Hénaff, M.; Kourafalou, V.H. Mississippi waters reaching South Florida reefs under no flood conditions: Synthesis of observing and modeling system findings. Ocean Dyn. 2016, 66, 435–459. [Google Scholar] [CrossRef]
- Jacobs, G.; DAddezio, J.; Bartels, B.; Spence, P. Constrained scales in ocean forecasting. Adv. Space Res. 2019. [Google Scholar] [CrossRef]
- Capet, X.; McWilliams, J.C.; Molemaker, M.J.; Shchepetkin, A.F. Mesoscale to Sub-mesoscale Transition in the California Current System. Part I: Flow Structure, Eddy Flux, and Observational Tests. J. Phys. Oceanogr. 2008, 38, 29–43. [Google Scholar] [CrossRef]
- Kourafalou, V.H.; De Mey, P.; Staneva, J.; Ayoub, N.; Barth, A.; Chao, Y.; Cirano, M.; Fiechter, J.; Herzfeld, M.; Kurapov, A.; et al. Coastal Ocean Forecasting: Science foundation and user benefits. J. Oper. Oceangr. 2015. [Google Scholar] [CrossRef]
- Kourafalou, V.H.; De Mey, P.; Le Hénaff, M.; Charria, G.; Edwards, C.A.; He, R.; Herzfeld, M.; Pasqual, A.; Stanev, E.; Tintoré, J.; et al. Coastal Ocean Forecasting: System integration and validation. J. Oper. Oceangr. 2015. [Google Scholar] [CrossRef]
- Wilkin, J.L.; Hunter, E.J. An assessment of the skill of real-time models of Mid-Atlantic Bight continental shelf circulation. J. Geophys. Res. Ocean. 2013, 118, 2919–2933. [Google Scholar] [CrossRef]
- Kourafalou, V.H.; Oey, L.-Y.; Wang, J.D.; Lee, T.N. The fate of river discharge on the continental shelf. Part I: Modeling the river plume and the inner-shelf coastal current. J. Geophys. Res. 1996, 101, 3415–3434. [Google Scholar] [CrossRef]
- Schiller, R.V.; Kourafalou, V.H. Modeling river plume dynamics with the Hybrid Coordinate Ocean Model. Ocean Model 2010. [Google Scholar] [CrossRef]
- Kourafalou, V.H.; Oey, L.-Y.; Lee, T.N.; Wang, J.D. The fate of river discharge on the continental shelf. Part II: Transport of low-salinity waters under realistic wind and tidal forcing. J. Geophys. Res. 1996, 101, 3435–3455. [Google Scholar] [CrossRef]
- Tseng, Y.-H.; Bryan, F.O.; Whitney, M.M. Impacts of the representation of riverine freshwater input in the Community Earth System Model. Ocean Model 2016, 105, 71–86. [Google Scholar] [CrossRef]
- Le Hénaff, M.; Muller-Karger, F.E.; Kourafalou, V.H.; Otis, D.; Johnson, K.A.; McEachron, L.; Kang, H. Coral Mortality in the Flower Garden Banks of the Gulf of Mexico in July 2016: The Consequence of Cross-Shelf Transport of Flood Waters? Cont. Shelf Res. 2019, 190. [Google Scholar] [CrossRef]
- Kourafalou, V.H.; Androulidakis, Y.S. Influence of Mississippi induced circulation on the Deepwater Horizon Oil Spill transport. J. Geophys. Res. 2013, 118, 1–20. [Google Scholar] [CrossRef]
- Androulidakis, I.; Kourafalou, V.; Özgökmen, T.M.; Garcia-Pineda, O.; Lund, B.; Henaff, M.L.; Hu, C.; Haus, B.K.; Novelli, G.; Guigand, C.; et al. Influence of river induced fronts on hydrocarbon transport: A multi-platform observational study. J. Geophys. Res. Oceans 2018, 123, 3259–3285. [Google Scholar] [CrossRef]
- Hole, L.; Dagestad, K.F.; Röhrs, J.; Wettre, C.; Kourafalou, V.H.; Androulidakis, Y.S.; Le Hénaff, M.; Kang, H.; Garcia, O. Revisiting the DeepWater Horizon spill: High resolution model simulations of effects of oil droplet size distribution and river fronts. J. Mar. Sci. Eng. 2019, 7, 329. [Google Scholar] [CrossRef]
- Androulidakis, Y.S.; Kourafalou, V.H.; Le Hénaff, M.; Kang, H.; Sutton, T.; Chen, S.; Hu, C.; Ntaganou, N. Offshore spreading of Mississippi waters: Pathways and vertical structure under eddy influence. J. Geophys. Res. 2019, 124. [Google Scholar] [CrossRef]
- Poje, A.C.; Özgökmen, T.M.; Lipphart, B., Jr.; Haus, B.; Ryan, E.; Haza, A.; Jacobs, G.; Reniers, A.; Olascoaga, J.; Novelli, G.; et al. Sub-mesoscale dispersion in the vicinity of the Deepwater Horizon spill. Proc. Natl. Acad. Sci. USA 2014, 11135, 12693–12698. [Google Scholar] [CrossRef]
- Haza, A.C.; Özgökmen, T.; Griffa, A.; Garraffo, Z.D.; Piterbarg, L. Parameterization of particle transport at sub-mesoscales in the Gulf Stream region using Lagrangian subgrid scale models. Ocean Model 2012, 42, 31–49. [Google Scholar] [CrossRef]
- Haza, A.C.; Özgökmen, T.; Hogan, P. Impact of sub-mesoscales on surface material distribution in a Gulf of Mexico mesoscale eddy. Ocean Model 2016, 107, 28–47. [Google Scholar] [CrossRef]
- Huguenard, K.; Bogucki, D.J.; Ortiz-Suslow, D.G.; Laxague, N.J.M.; MacMahan, J.H.; Özgökmen, T.M.; Haus, B.K.; Reniers, A.J.H.M.; Hargrove, J.; Soloviev, A.V.; et al. On the nature of the frontal zone of the Chactawhatchee Bay plume in the Gulf of Mexico. J. Geophys. Res. Ocean. 2016, 121, 1322–1345. [Google Scholar] [CrossRef]
- Roth, M.; MacMahan, J.; Reniers, A.; Özgökmen, T.; Woodall, K.; Haus, B. Observations of inner shelf cross-shore surface material transport adjacent to a coastal inlet in the northern Gulf of Mexico. Cont. Shelf Res. 2017, 137, 142–153. [Google Scholar] [CrossRef]
- Rascle, N.; Molemaker, J.; Mari, L.; Nouguier, F.; Chapron, B.; Lund, B.; Mouche, A. Intense deformation field at oceanic front inferred from directional sea surface roughness observations. Geophys. Res. Lett. 2017, 44, 5599–5608. [Google Scholar] [CrossRef]
- D’Asaro, E.; Shcherbina, A.; Klymak, J.; Molemaker, J.; Novelli, G.; Guigand, C.; Haza, A.; Haus, B.; Ryan, E.; Jacobs, G.; et al. Ocean convergence and dispersion of flotsam. Proc. Natl. Acad. Sci. USA 2018, 115, 1162–1167. [Google Scholar]
- Haza, A.C.; Paldor, N.; Özgökmen, T.; Curcic, M.; Chen, S.S.; Jacobs, G. Wind-based estimations of ocean surface currents from massive clusters of drifters in the Gulf of Mexico. J. Geophys. Res. Ocean. 2019, 124, 5844–5869. [Google Scholar] [CrossRef]
- Curcic, M.; Chen, S.; Özgökmen, T.M. Hurricane-induced ocean waves and Stokes drift and their impacts on surface transport and dispersion in the Gulf of Mexico. Geophys. Res. Lett. 2016, 43, 2773–2781. [Google Scholar] [CrossRef]
- Laxague, N.J.M.; Özgökmen, T.M.; Haus, B.K.; Novelli, G.; Shcherbina, A.; Sutherland, P.; Guigand, C.; Lund, B.; Mehta, S.; Alday, M.; et al. Observations of near-surface current shear help describe oceanic oil and plastic transport. Geophys. Res. Letts. 2018, 45, 245–249. [Google Scholar] [CrossRef]
- Morey, S.; Gopalakrishnan, S.; Pallas Sanz, E.; Marcos Azevedo Correia De Souza, J.; Donohue, K.; Perez-Brunius, P.; Dukhovskoy, D.; Chassignet, E.P.; Cornuelle, B.; Bower, A.; et al. Assessment of numerical simulations of deep circulation and variability in the Gulf of Mexico using recent observations. J. Phys. Oceanogr. 2020. [Google Scholar] [CrossRef]
- Ogle, M.T.; Smith, R.; Williams, B.; Schiller, R.; Perry, R.; Leung, P.; DiMarco, S.F.; Howden, S. Four Years of Metocean Support to the Shell Stones Field: From Asset Integrity to Collaborative Research. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2019. [Google Scholar] [CrossRef]
- Barkan, R.; McWilliams, J.C.; Shchepetkin, A.F.; Molemaker, M.J.; Renault, L.; Bracco, A.; Choi, J. Sub-mesoscale dynamics in the northern Gulf of Mexico. Part I: Regional and seasonal characterization and the role of river outflow. J. Phys. Oceanogr. 2017, 47, 2325–2346. [Google Scholar] [CrossRef]
- Shi, Q.; Bourassa, M.A. Coupling Ocean Currents and Waves with Wind Stress over the Gulf Stream. Remote Sens. 2019, 11, 1476. [Google Scholar] [CrossRef]
- Smith, S.; Cummings, J.; Rowley, C.; Chu, P.; Shriver, J.; Helber, R.; Spence, P.; Carroll, S.; Smedstad, O.; Lunde, B. Validation Test Report for the Navy Coupled Ocean Data Assimilation 3D Variational Analysis (NCODA-VAR) System; Version 3.43 Rep.; NRL Report NRL/MR/7320-11-9363; Naval Research Laboratory, Stennis Space Center: Hancock County, MS, USA, 2011. [Google Scholar]
- Smith, S.; Ngodock, H.; Carrier, M.; Shriver, J.; Muscarella, P.; Souopgui, I. Validation and Operational Implementation of the Navy Coastal Ocean Model Four Dimensional Variational Data Assimilation System (NCOM 4DVAR) in the Okinawa Trough. in Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications (Vol. III), Edited; Springer: Berlin/Heidelberg, Germany, 2017; pp. 405–427. [Google Scholar]
- Jacobs, G.A.; Bartels, B.P.; Bogucki, D.J.; Beron-Vera, F.J.; Chen, S.S.; Coelho, E.F.; Curcic, M.; Griffa, A.; Gough, M.; Haus, B.K. Data assimilation considerations for improved ocean predictability during the Gulf of Mexico Grand Lagrangian Deployment (GLAD). Ocean Model 2014, 83, 98–117. [Google Scholar] [CrossRef]
- D’Addezio, J.M.; Jacobs, G.A.; Yaremchuk, M.; Souopgui, I. Sub-mesoscale Eddy Vertical Covariances and Dynamical Constraints from High-Resolution. J. Phys. Oceanogr. 2020, 50, 1087–1115. [Google Scholar] [CrossRef]
- Carrier, M.J.; Ngodock, H.E.; Muscarella, P.; Smith, S. Impact of assimilating surface velocity observations on the model sea surface height using the NCOM-4DVAR. Mon. Weather Rev. 2016, 144, 1051–1068. [Google Scholar] [CrossRef]
- Muscarella, P.; Carrier, M.J.; Ngodock, H.; Smith, S.; Lipphardt, B., Jr.; Kirwan, A., Jr.; Huntley, H.S. Do assimilated drifter velocities improve Lagrangian predictability in an operational ocean model? Mon. Weather Rev. 2015, 143, 1822–1832. [Google Scholar] [CrossRef]
- Rodríguez, E.; Wineteer, A.; Perkovic-Martin, D.; Gál, T.; Stiles, B.W.; Niamsuwan, N.; Rodriguez Monje, R. Estimating Ocean Vector Winds and Currents Using a Ka-Band Pencil-Beam Doppler Scatterometer. Remote Sens. 2018, 10, 576. [Google Scholar] [CrossRef]
- Rodríguez, E.; Bourassa, M.; Chelton, D.; Farrar, J.T.; Long, D.; Perkovic-Martin, D.; Samelson, R. The Winds and Currents Mission Concept. Front. Mar. Sci. 2019, 6, 438. [Google Scholar] [CrossRef]
- Zheng, Y.; Bourassa, M.A.; Hughes, P.J. Influences of sea surface temperature gradients and surface roughness changes on the motion of surface oil: A simple idealized study. J. Appl. Meteor. Clim. 2013, 52, 1561–1575. [Google Scholar] [CrossRef]
- Liu, Y.; MacFadyen, A.; Ji, Z.-G.; Weisberg, R.H. Monitoring and Modeling the Deepwater Horizon Oil Spill: A Record Breaking Enterprise. Geophysical Monograph; American Geophysical Union: Washington, DC, USA, 2011; p. 195. [Google Scholar]
- Weber, J.E. Friction-induced roll motion in short-crested surface gravity waves. J. Phys. Oceanogr. 1985, 15, 936–942. [Google Scholar] [CrossRef][Green Version]
- O’Neil, L.W.; Chelton, D.B.; Esbensen, S.K. Covariability of surface winds and stress responses to sea surface temperature ronts. J. Clim. 2012, 25, 5916–5942. [Google Scholar] [CrossRef]
- Song, Q.; Chelton, D.B.; Esbensen, S.K.; Thum, N.; O’Neill, L.W. Coupling between sea surface temperature and low-level winds in mesoscale numerical models. J. Clim. 2009, 22, 146–164. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. An improved Mellor-Yamada level-3 model with condensation physics: Its design and verification. Bound. Layer. Meteor. 2004, 112, 1–31. [Google Scholar] [CrossRef]
- Grenier, H.; Bretherton, C.S. A moist PBL parameterization for large-scale models and its application to subtropical cloud-topped marine boundary layers. Mon. Weather Rev. 2001, 129, 357–377. [Google Scholar] [CrossRef]
- Judt, F.; Chen, S.S.; Curcic, M. Atmospheric forcing of the upper ocean transport in the Gulf of Mexico from seasonal to diurnal scales. J. Geophys. Res. Ocean. 2016, 121, 4416–4433. [Google Scholar] [CrossRef]
- Rowley, C.; Mask, A. Regional and coastal prediction with the relocatable ocean nowcast/forecast system. Oceanography 2014, 27, 44–55. [Google Scholar] [CrossRef]
- Allard, R.; Rogers, E.; Martin, P.; Jensen, T.; Chu, P.; Campbell, T.; Dykes, J.; Smith, T.; Choi, J.; Gravois, U. The US Navy coupled ocean-wave prediction system. Oceanography 2014, 27, 92–103. [Google Scholar] [CrossRef]
- Galt, J.A. Trajectory Analysis for Oil Spills. J. Adv. Mar. Technol. Conf. 1994, 11, 91–126. [Google Scholar]
- French McCay, D.P.; Jayko, K.; Li, Z.; Horn, M.; Kim, Y.; Isaji, T.; Crowley, D.; Spaulding, M.; Decker, L.; Turner, C.; et al. Technical Reports for Deepwater Horizon Water Column Injury Assessment—WC_TR14: Modeling Oil Fate and Exposure Concentrations in the Deepwater Plume and Cone of Rising Oil Resulting from the Deepwater Horizon Oil Spill. DWH NRDA Water Column Technical Working Group Report. Prepared for National Oceanic and Atmospheric Administration by RPS ASA, South Kingstown, RI, USA, 29 September 2015, Administrative Record no. DWH-AR0285776.pdf. Available online: https://www.doi.gov/deepwaterhorizon/adminrecord (accessed on 28 August 2020).
- French McCay, D.P.; Morandi, A.; McManus, M.C.; Schroeder, M.; Jayko, K.; Rowe, J.J. Technical Reports for Deepwater Horizon Water Column Injury Assessment—WC_TR.09: Vertical Distribution Analysis of Plankton. DWH NRDA Water Column Technical Working Group Report. Prepared for National Oceanic and Atmospheric Administration by RPS ASA, South Kingstown, RI, USA. DWH NRDA Water Column Technical Working Group Report. Prepared for National Oceanic and Atmospheric Administration by RPS ASA, South Kingstown, RI, USA, Administrative Record no. DWH-AR0195958.pdf, DWH-AR0171921.xlsx, DWH-AR0171922.xlsx, 2015b. Available online: https://www.doi.gov/deepwaterhorizon/adminrecord (accessed on 28 August 2020).
- French McCay, D.P.; McManus, M.C.; Balouskus, R.; Rowe, J.J.; Schroeder, M.; Morandi, A.; Bohaboy, E.; Graham, E. Technical Reports for Deepwater Horizon Water Column Injury Assessment: WC_TR.10: Evaluation of Baseline Densities for Calculating Direct Injuries of Aquatic Biota During the Deepwater Horizon Oil Spill. DWH NRDA Water Column Technical Working Group Report. Prepared for National Oceanic and Atmospheric Administration by RPS ASA, South Kingstown, RI, USA, Administrative Record no. DWH-AR0285021.pdf, DWH-AR0285141.xlsx, DWH-AR02851412.xlsx, 2015c. Available online: https://www.doi.gov/deepwaterhorizon/adminrecord (accessed on 28 August 2020).
- French McCay, D.P.; Li, Z.; Horn, M.; Crowley, D.; Spaulding, M.; Mendelsohn, D.; Turner, C. Modeling Oil Fate and Subsurface Exposure Concentrations from the Deepwater Horizon Oil Spill. In Proceedings of the 39th AMOP Technical Seminar on Environmental Contamination and Response, Halifax, NS, Canada, 7–9 June 2016; Volume 39, pp. 115–150. [Google Scholar]
- Yang, D.; Chen, B.; Socolofsky, S.; Chamecki, M.; Meneveau, C. Large-eddy simulation and parameterization of buoyant plume dynamics in stratified flow. J. Fluid Mech. 2016, 794, 798–833. [Google Scholar] [CrossRef]
- Fabregat, A.; Poje, A.; Ozgokmen, T.; Dewar, W.K. Numerical simulations of rotating bubble plumes in stratified environments. J. Geophys. Res. Ocean. 2017, 10, 6795–6813. [Google Scholar] [CrossRef]
- Fabregat, A.; Deremble, B.; Wienders, N.; Stroman, A.; Poje, A.; Ozgokmen, T.; Dewar, W.K. Rotating 2d Point Source Plume Models with Application to Deep Water Horizon. Ocean Model 2017, 119, 118–135. [Google Scholar] [CrossRef]
- Breivik, Ø.; Allen, A.A.; Maisondieu, C.; Olangnon, M. Advances in search and rescue at sea. Ocean Dyn. 2013, 63, 83–88. [Google Scholar] [CrossRef]
- Garcia-Pineda, O.; Staples, G.; Jones, C.E.; Hu, C.; Holt, B.; Kourafalou, V.H.; Haces-Garcia, F. Classification of oil spill by thicknesses using multiple remote sensors. Remote Sens. Environ. 2020, 236. [Google Scholar] [CrossRef]
- Garcia-Pineda, O.; Androulidakis, Y.; Le Henaff, M.; Kourafalou, V.H.; Hole, L.R.; Kang, H.; DiPinto, L. Measuring oil residence time with GPS-drifters, satellites, and Unmanned Aerial Systems (UAS). Mar. Pollut. Bull. 2020, 150, 110644. [Google Scholar] [CrossRef] [PubMed]
- Barker, C.H.; MacFadyen, A. WebGNOME Additions for Remote Sensing Ingestion for Model Initialization. In Interagency Agreement: E19PG00023 between the Bureau of Safety and Environmental Enforcement and the National Oceanic and Atmospheric Administration; Bureau of Safety: Washington, DC, USA; National Oceanic: Silver Spring, MD, USA; Atmospheric Administration: Silver Spring, MD, USA, 2019. [Google Scholar]
- Jacketti, M.; Ji, C.; Englehardt, J.D.; Beegle-Krause, C. Development of the SOSIM Model for Inferential Tracking of Subsurface Oil. In Proceedings of the Arctic and Marine Oil Pollution Conference, Environment and Climate Change Canada, Halifax, NS, Canada, 4–6 June 2019; pp. 485–501. [Google Scholar]
- French-McCay, D.; Horn, M.; Li, Z.; Jayko, K.; Spaulding, M.; Crowley, D.; Mendelsohn, D. Modeling Distribution Fate and Concentrations of Deepwater Horizon Oil in Subsurface Waters of the Gulf of Mexico. Chapter 31. In Oil Spill Environmental Forensics Case Studies; Stout, S., Wang, Z., Eds.; Butterworth-Heinemann: Oxford, UK, 2018; pp. 683–736. ISBN 978-O-12-804434-6. [Google Scholar]
- French-McCay, D.; Crowley, D.; Rowe, J.; Bock, M.; Robinson, H.; Wenning, R.; Walker, A.H.; Joeckel, J.; Parkerton, T. Comparative Risk Assessment of Spill Response Options for a Deepwater Oil Well Blowout: Part, I. Oil Spill Modeling. Mar. Pollut. Bull. 2018, 133, 1001–1015. [Google Scholar] [CrossRef] [PubMed]
- Yapa, P.D.; Dasanayaka, L.K.; Bandara, U.C.; Nakata, K. A model to simulate the transport and fate of gas and hydrates released in deepwater. J. Hydraul. Res. 2010, 48, 559–572. [Google Scholar] [CrossRef]
- Johansen, Ø. Development and verification of deep-water blowout models. Mar. Pollut. Bull. 2003, 47, 360–368. [Google Scholar] [CrossRef]
- Dissanayake, A.L.; Gros, J.; Socolofsky, S.A. Integral models for bubble, droplet, and multiphase plume dynamics in stratification and crossflow. Environ. Fluid Mech. 2018, 18, 1167–1202. [Google Scholar] [CrossRef]
- Bombardelli, F.A.; Buscaglia, G.C.; Rehmann, C.R.; Rincon, L.E.; Garcia, M.H. Modeling and scaling of aeration bubble plumes: A two-phase flow analysis. J. Hydraul. Res. 2007, 45, 617–630. [Google Scholar] [CrossRef]
- Yapa, P.D.; Zheng, L. Simulation of oil spills from underwater accidents I: Model development. J. Hydraul, Res. 1997, 35, 673–687. [Google Scholar] [CrossRef]
- Zheng, L.; Yapa, P.D. Simulation of oil spills from underwater accidents II: Model verification. J. Hydraul. Res. 1998, 36, 117–134. [Google Scholar] [CrossRef]
- Johansen, Ø. DeepBlow—A Lagrangian plume model for deep water blowouts. Spill. Sci. Technol. B 2000, 6, 103–111. [Google Scholar] [CrossRef]
- Turner, J.S. Turbulent entrainment: The development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 1986, 173, 431–471. [Google Scholar] [CrossRef]
- Chen, F.H.; Yapa, P.D. Modeling gas separation from a bent deepwater oil and gas jet/plume. J. Marine Syst. 2004, 45, 189–203. [Google Scholar] [CrossRef]
- Fabregat, A.; Dewar, W.K.; Özgökmen, T.; Poje, A.; Wienders, N. Large eddy simulations of thermal, bubble and hybrid plumes. Ocean Model 2015, 16–28. [Google Scholar] [CrossRef]
- Fabregat, A.; Poje, A.; Özgökmen, T.; Dewar, W.K. Effects of Rotation on Turbulent Buoyant Plumes in Stratified Environments. J. Geophys. Res. 2016. [Google Scholar] [CrossRef]
- Fabregat, A.; Poje, A.; Özgökmen, T.; Dewar, W.K. Dynamics of Multiphase Plumes with Hybrid Buoyancy Sources in Stratified Environments. Phys. Fluids 2016. [Google Scholar] [CrossRef]
- Fraga, B.; Stoesser, T. Influence of bubble size, diffuser width, and flow rate on the integral behavior of bubble plumes. J. Geophys. Res. Ocean. 2016, 121, 3887–3904. [Google Scholar] [CrossRef]
- Fraga, B.; Stoesser, T.; Lai, C.; Socolofsky, S.A. A LES-based Eulerian–Lagrangian approach to predict the dynamics of bubble plumes. Ocean Model. 2016, 97, 27–36. [Google Scholar] [CrossRef]
- Chen, F.H.; Yapa, P.D. Estimating hydrate formation and decomposition of gases released in a deepwater ocean plume. J. Mar. Syst. 2001, 30, 21–32. [Google Scholar] [CrossRef]
- Gros, J.; Reddy, C.M.; Nelson, R.K.; Socolofsky, S.A.; Arey, J.S. Simulating Gas-Liquid-Water Partitioning and Fluid Properties of Petroleum under Pressure: Implications for Deep-Sea Blowouts. Environ. Sci. Technol. 2016, 50, 7397–7408. [Google Scholar] [CrossRef]
- Gros, J.; Socolofsky, S.A.; Dissanayake, A.L.; Jun, I.; Zhao, L.; Boufadel, M.C.; Reddy, C.M.; Arey, J.S. Petroleum dynamics in the sea and influence of subsea dispersant injection during Deepwater Horizon. Proc. Natl. Acad. Sci. USA 2017, 114, 10065–10070. [Google Scholar] [CrossRef]
- Gros, J.; Dissanayake, A.L.; Daniels, M.M.; Barker, C.H.; Lehr, W.; Socolofsky, S.A. Oil spill modeling in deep waters: Estimation of pseudo-component properties for cubic equations of state from distillation data. Mar. Pollut. Bull. 2018, 137, 627–637. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Boufadel, M.C.; Adams, E.E.; Socolofsky, S.; King, T.; Lee, K. Simulation of scenarios of oil droplet formation from the Deepwater Horizon blowout. Mar. Pollut. Bull. 2015, 101, 304–319. [Google Scholar] [CrossRef] [PubMed]
- NRC. The Use of Dispersants in Marine Oil Spill Response; National Academies of Sciences, Engineering, and Medicine (NASEM): Washington, DC, USA; The National Academies Press: Washington, DC, USA, 2019. [Google Scholar] [CrossRef]
- Socolofsky, S.A.; Gros, J.; North, E.; Boufadel, M.C.; Parkerton, T.F.; Adams, E.E. The treatment of biodegradation in models of sub-surface oil spills: A review and sensitivity study. Mar. Pollut. Bull. 2019, 143, 204–219. [Google Scholar] [CrossRef] [PubMed]
- Thrift-Viveros, D.L.; Jones, R.; Boufadel, M. Development of a New Oil Biodegradation Algorithm for NOAA’s Oil Spill Modelling Suite (GNOME/ADIOS). In Proceedings of the Thirty-Eighth AMOP Technical Seminar, Vancouver, BC, Canada, 2–4 June 2015. [Google Scholar]
- Johansen, Ø.; Brandvik, P.J.; Farooq, U. Droplet breakup in subsea oil releases—Part 2: Predictions of droplet size distributions with and without injection of chemical dispersants. Mar. Pollut. Bull. 2013, 73, 327–335. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Miller, J.; Wang, W.; Koley, S.S.; Katz, K. Size Distribution of Droplets Generated by Impinging of Breaking waves on Oil Slicks. J. Geophys. Res. 2017. [Google Scholar] [CrossRef]
- Li, Z.; Spaulding, M.; McCay, D.F.; Crowley, D.; Payne, J.R. Development of a unified oil droplet size distribution model with application to surface breaking waves and subsea blowout releases considering dispersant effects. Mar. Pollut. Bull. 2017, 114, 247–257. [Google Scholar] [CrossRef]
- Bandara, U.C.; Yapa, P.D. Bubble sizes, breakup, and coalescence in deepwater gas/oil plumes. J. Hydraul. Eng. 2011, 137, 729–738. [Google Scholar] [CrossRef]
- Zhao, L.; Boufadel, M.C.; Socolofsky, S.A.; Adams, E.; King, T.; Lee, K. Evolution of droplets in subsea oil and gas blowouts: Development and validation of the numerical model VDROP-J. Mar. Pollut. Bull. 2014, 83, 58–69. [Google Scholar] [CrossRef]
- Nissanka, I.D.; Yapa, P.D. Calculation of oil droplet size distribution in an underwater oil well blowout. J. Hydraul. Res. 2016, 54, 307–320. [Google Scholar] [CrossRef]
- Zhao, L.; Torlapati, J.; Boufadel, M.C.; King, T.; Robinson, B.; Lee, K. VDROP: A comprehensive model for droplet formation of oils and gases in liquids-Incorporation of the interfacial tension and droplet viscosity. Chem. Eng. J. 2014, 253, 93–106. [Google Scholar] [CrossRef]
- Zhao, L.; Boufadel, M.C.; King, T.; Robinson, B.; Gao, F.; Socolofsky, S.A.; Lee, K. Droplet and bubble formation of combined oil and gas releases in subsea blowouts. Mar. Pollut. Bull. 2017, 120. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Gao, F.; Boufadel, M.C.; King, T.; Robinson, B.; Lee, K.; Conmy, R. Oil jet with dispersant: Macro-scale hydrodynamics and tip streaming. AIChE J. 2017, 63, 5222–5234. [Google Scholar] [CrossRef]
- Gopalan, B.; Katz, J. Turbulent shearing of crude oil mixed with dispersants generates long microthreads and microdroplets. Phys. Rev. Lett. 2010, 104, 054501. [Google Scholar] [CrossRef] [PubMed]
- Murphy, D.W.; Xue, X.; Sampath, K.; Katz, J. Crude oil jets in crossflow: Effects of dispersant concentration on plume behavior. J. Geophys. Res. Ocean. 2016, 121, 4264–4281. [Google Scholar] [CrossRef]
- Brandvik, P.J.; Storey, C.; Davies, E.J.; Johansen, Ø. Combined Releases of Oil and Gas Under Pressure: The Influence of Live Oil and Natural Gas on Initial Oil Droplet Formation. Mar. Pollut. Bull. 2019, 140, 485–492. [Google Scholar] [CrossRef] [PubMed]
- Brandvik, P.J.; Storey, C.; Davies, E.J.; Leirvik, F. Quantification of Oil droplets under High Pressure Laboratory Experiments Simulated Deep Water Oil Releases and Subsea Dispersant Injection (SSDI). Mar. Pollut. Bull. 2019, 138, 520–525. [Google Scholar] [CrossRef]
- Davies, E.J.; Brandvik, P.J.; Leirvik, F.; Nepstad, R. The use of wide-band transmittance imaging to size and classify suspended particulate matter in seawater. Mar. Pollut. Bull. 2017, 115, 105–114. [Google Scholar] [CrossRef]
- Boufadel, M.C.; Gao, F.; Zhao, L.; Özgökmen, T.; Miller, R.; King, T.; Robinson, B.; Lee, K.; Leifer, I. Was the Deepwater Horizon well discharge churn flow? Implications on the estimation of the oil discharge and droplet size distribution. Geophys. Res. Lett. 2018, 45, 2396–2403. [Google Scholar] [CrossRef]
- Brakstad, O.G.; Almas, I.K.; Krause, D.F.; Beegle-Krause, C.J. Biotransformation of natural gas and oil in oxygen-reduced seawater. Chemosphere 2020, 182, 555–558. [Google Scholar] [CrossRef]
- Brandvik, P.J.; Johansen, Ø.; Leirvik, F.; Farooq, U.; Daling, P.S. Droplet breakup in subsurface oil releases—Part I: Experimental study of droplet breakup and effectiveness of dispersant injection. Mar. Pollut. Bull. 2013, 73, 319–326. [Google Scholar] [CrossRef]
- Brandvik, P.J.; Davies, E.J.; Johansen, Ø.; Leirvik, F.; Belore, R. Subsea Dispersant Injection—Large-Scale Experiments to Improve Algorithms for Initial Droplet Formation (Modified Weber Scaling); An approach using the Ohmsett facility, NJ, USA and SINTEF Tower Basin in Norway (UNRESTRICTED). Technical Report; SINTEF: Trondheim, Norway, 2017; p. 88. [Google Scholar]
- Brandvik, P.J.; Johansen, Ø.; Leirvik, F.; Krause, D.F.; Daling, P.S. Subsea dispersant injection (SSDI), effectiveness of the different dispersant injection techniques—An experimental approach. Mar. Pollut. Bull. 2018, 136, 385–393. [Google Scholar] [CrossRef] [PubMed]
- Brakstad, O.G.; Nordtug, T.; Throne-Holst, M. Biodegradation of dispersed Macondo oil in seawater at low temperature and different oil droplet sizes. Mar. Pollut. Bull. 2015, 93, 144–152. [Google Scholar] [CrossRef]
- Brakstad, O.G.; Almas, I.K.; Krause, D.F. Biotransformation of natural gas and oil compounds associated with marine oil discharges. Chemosphere 2017, 182, 555–558. [Google Scholar] [CrossRef] [PubMed]
- Deepwater Horizon Incident Joint Information Center (U.S.), Joint Analysis Group; United States, National Ocean Service. Review of Subsurface Dispersed Oil and Oxygen Levels Associated with the Deepwater Horizon MC 252 Spill of National Significance. In NOAA Technical Report NOS OR&R. NOAA; National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 2012; p. 113. [Google Scholar]
- Adcroft, A.; Hallberg, R.; Dunne, J.P.; Samuels, B.L.; Galt, J.A.; Barker, C.H.; Payton, D. Simulations of underwater plumes of dissolved oil in the Gulf of Mexico. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Beegle-Krause, C.; Daae, R.L.; Skancke, J.; Brakstad, O.; Stefanakos, C. Deepwater Wells and the Subsurface Dissolved Oxygen Minimum: A Tale of Two Sides of the Atlantic Ocean. In Proceedings of the Environment Canada’s Arctic and Marine Oil Pollution Conference, Halifax, NS, Canada, 7–9 June 2016. [Google Scholar]
- Beegle-Krause, C.J.; Brakstad, O.G.; Stefanakos, C.; Daae, R.; Pelz, O. Modeled Case Studies of Dissolved Oxygen Reduction During Sub Sea Dispersant Injection in the Event of a Response to an Oil Well Blowout. Mar. Pollut. Bull. 2020, submitted. [Google Scholar]
- Passow, U.; Ziervogel, K.; Asper, V.; Diercks, A. Marine snow formation in the aftermath of the deepwater horizon oil spill in the Gulf of Mexico. Environ. Res. Lett. 2012, 7. [Google Scholar] [CrossRef]
- Brooks, G.R.; Larson, R.A.; Schwing, P.T.; Romero, I.; Moore, C.; Reichart, G.-J.; Jilbert, T.J.; Chanton, J.P.; Hastings, D.W.; Overholt, W.A.; et al. Sedimentation Pulse in the NE Gulf of Mexico following the 2010 DWH Blowout. PLoS ONE 2015, 10, e0132341. [Google Scholar] [CrossRef]
- Romero, I.C.; Toro-Farmer, G.; Diercks, A.-R.; Schwing, P.; Muller-Karger, F.; Murawski, S.; Hollander, D.J. Large-scale deposition of weathered oil in the Gulf of Mexico following a deep-water oil spill. Environ. Pollut. 2017, 228, 179–189. [Google Scholar] [CrossRef]
- Daly, K.L.; Passow, U.; Chanton, J.; Hollander, D. Assessing the impacts of oil-associated marine snow formation and sedimenta- tion during and after the deepwater horizon oil spill. Anthropocene 2016, 13, 18–33. [Google Scholar] [CrossRef]
- Stout, S.A.; Rouhani, S.; Liu, B.; Oehrig, J.; Ricker, R.W.; Baker, G.; Lewis, C. Assessing the footprint and volume of oil deposited in deep-sea sediments following the deepwater horizon oil spill. Mar. Pollut. Bull. 2017, 114, 327–342. [Google Scholar] [CrossRef]
- Stout, S.A.; German, C.R. Characterization and flux of marine oil snow settling toward the seafloor in the northern Gulf of Mexico during the Deepwater Horizon incident: Evidence for input from surface oil and impact on shallow shelf sediments. Mar. Pollut. Bull. 2018, 129, 695–713. [Google Scholar] [CrossRef] [PubMed]
- Langenhoff, A.A.M.; Rahsepar, S.; van Eenennaam, J.S.; Radovic, J.R.; Oldenburg, T.B.P.; Foekema, E.; Murk, A.T.J. Effect of Marine Snow on Microbial Oil Degradation. In Deep Oil Spills—Facts, Fate, and Effects, S.A.; Murawski, D.A., Ainsworth, C.H., Gilbert, S.A., Hollander, D.J., Paris, C.B., Schlüter, M., Wetzel, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 301–311. [Google Scholar]
- Passow, U.; Stout, S.A. Character and sedimentation of “lingering” Macondo oil to the deep-sea after the Deepwater Horizon oil spill. Mar. Chem. 2020, 218, 103733. [Google Scholar] [CrossRef]
- Lee, K.; Wong, C.S.; Cretney, W.J.; Whitney, F.A.; Parsons, T.R.; Lalli, C.M.; Wu, J. Microbial response to crude oil and Corexit 9527: SEAFLUXES enclosure study. Microb. Ecol. 1985, 11, 337–351. [Google Scholar] [CrossRef]
- Murk, A.J.; Hollander, D.J.; Chen, S.; Hu, C.; Liu, Y.; Vonk, S.M.; Schwing, P.T.; Gilbert, S.; Foekema, E.M. A Predictive Strategy for Mapping Locations Where Future MOSSFA Events Are Expected. In Scenarios and Responses to Future Deep Oil Spills; Murawski, A.S., Ainsworth, H.C., Gilbert, S., Hollander, J.D., Paris, B.C., Schlüter, M., Wetzel, L.D., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Brakstad, O.G.; Lewis, A.; Beegle-Krause, C.J. A critical review of marine snow in the context of oil spills and oil spill dispersant treatment with focus on the Deepwater Horizon oil spill. Mar. Pollut. Bull. 2018, 135, 346–356. [Google Scholar] [CrossRef] [PubMed]
- Jacketti, M.; Beegle-Krause, C.J.; Englehardt, J. A Review on the Sinking Mechanisms for Oil and Successful Response Technologies. Mar. Pollut. Bull. 2020, submitted. [Google Scholar]
- Jackson, G.A. Comparing observed changes in particle size spectra with those predicted using coagulation theory. Deep-Sea Res. Part II Top. Stud. Oceanogr. 1995, 42, 159–184. [Google Scholar] [CrossRef]
- Jackson, G.A.; Burd, A.B. Aggregation in the marine environment. Environ. Sci. Technol. 1998, 32, 2805–2814. [Google Scholar] [CrossRef]
- Burd, A.; Jackson, G. Modeling steady state particle size spectra. Environ. Sci. Technol. 2002, 36, 323–327. [Google Scholar] [CrossRef]
- Lee, K. Oil-Particle interactions in aquatic environments: Influence on the transport, fate, effect and remediation of oil spills. Spill Sci. Technol. Bull. 2002, 8, 3–8. [Google Scholar] [CrossRef]
- Khelifa, A.; Stoffyn-Egli, P.; Hill, P.; Lee, K. Characteristics of oil droplets stabilized by mineral particles: Effects of oil type and temperature. Spill Sci. Technol. Bull. 2002, 8, 19–30. [Google Scholar] [CrossRef]
- Khelifa, A.; Stoffyn-Egli, P.; Hill, P.; Lee, K. Effects of salinity and clay type on oil-mineral aggregation. Mar. Environ. Res. 2005, 59, 235–254. [Google Scholar] [CrossRef] [PubMed]
- Bandara, U.C.; Yapa, P.D.; Xie, H. Fate and transport of oil in sediment laden marine waters. J. Hydro-Environ. Res. 2011, 5, 145–156. [Google Scholar] [CrossRef]
- Zhao, L.; Boufadel, M.C.; Geng, X.; Lee, K.; King, T.; Robinson, B.; Fitzpatrick, F. A-drop: A predictive model for the formation of oil particle aggregates (OPAs). Mar. Pollut. Bull. 2016, 106, 245–259. [Google Scholar] [CrossRef]
- Lambert, R.A.; Variano, E.A. Collision of oil droplets with marine aggregates: Effect of droplet size. J. Geophys. Res. Ocean. 2016, 121, 3250–3260. [Google Scholar] [CrossRef]
- Dissanayake, A.L.; Burd, A.B.; Daly, K.L.; Francis, S.; Passow, U. Numerical modeling of the interactions of oil, marine snow, and riverine sediments in the ocean. J. Geophys. Res. Ocean. 2018, 123, 5388–5405. [Google Scholar] [CrossRef]
- Jokulsdottir, T.; Archer, D. A stochastic, lagrangian model of sinking biogenic aggregates in the ocean (slams 1.0): Model formulation, validation and sensitivity. Geosci. Model Dev. 2016, 9, 1455–1476. [Google Scholar] [CrossRef]
- Francis, S.; Passow, U. Transport of dispersed oil compounds to the seafloor by sinking phytoplankton aggregates: A modeling study. Deep-Sea Res. Part I Oceanogr. Res. Pap. 2019, 156, 103192. [Google Scholar] [CrossRef]
- Jackson, G.A. A model of the formation of marine algal flocs by physical coagulation processes. Deep-Sea Res. 1990, 37, 1197–1211. [Google Scholar] [CrossRef]
- Jackson, G.A.; Lochmann, S. Modeling coagulation of algae in marine systems. In Environmental Particles; Buffle, J., van Leeuwen, H.P., Eds.; CRC Press: Boca Raton, FL, USA, 1992; pp. 387–413. [Google Scholar]
- Yan, B.; Passow, U.; Chanton, J.P.; Nöthig, E.-M.; Asper, V.; Sweet, J.; Pitiranggon, M.; Diercks, A.R.; Pak, D. Sustained deposition of contaminants from the deepwater horizon spill. Proc. Natl. Acad. Sci. USA 2016, 113, E3332–E3340. [Google Scholar] [CrossRef]
- Venkatesh, S. The oil spill behaviour model of the canadian atmospheric environment service part 1: Theory and model evaluation. Atmos.-Ocean 1988, 16, 93–108. [Google Scholar] [CrossRef]
- Jones, C.E.; Dagestad, K.-F.; Breivik, Ø.; Holt, B.; Röhrs, J.; Christensen, K.H.; Espeseth, M.; Brekke, C.; Skrunes, S. Measurement and modeling of oil slick transport. J. Geophys. Res. Ocean. 2016, 121, 7759–7775. [Google Scholar] [CrossRef]
- Zelenke, B.; O’Connor, C.; Barker, C.; Beegle-Krause, C.J.; Eclipse, L. General NOAA Operational Modeling Environment (GNOME) Technical Documentation; U.S. Dept. of Commerce: Washington, DC, USA, NOAA Technical Memorandum OR&R; Emergency Response Division; NOAA: Seattle, WA, USA, 2012.
- Dagestad, K.-F.; Röhrs, J.; Breivik, Ø.; Ådlandsvik, B. OpenDrift v1.0: A generic framework for trajectory modelling. Geosci. Model Dev. 2018, 11, 1405–1420. [Google Scholar] [CrossRef]
- Ledwell, J.R.; He, R.R.; Xue, Z.; DiMarco, S.F.; Spencer, L.J.; Chapman, P. Dispersion of a tracer in the deep Gulf of Mexico. J. Geophys. Res. 2016, 1212, 1110–1132. [Google Scholar] [CrossRef]
- Visser, A.W. Using random walk models to simulate vertical distribution of particles in a turbulence water column. Mar. Ecol. Prog. Ser. 1997, 158, 275–280. [Google Scholar] [CrossRef]
- Nordam, T.; Kristiansen, R.; Nepstad, R.; Röhrs, J. Numerical analysis of boundary conditions in a Lagrangian particle model for vertical mixing, transport and surfacing of buoyant particles in the water column. Ocean Model 2019, 136, 107–119. [Google Scholar] [CrossRef]
- Nordam, T.; Nepstad, R.; Litzler, E.; Röhrs, J. On the use of random walk schemes in oil spill modeling. Mar. Pollut. Bull. 2019, 146, 631–638. [Google Scholar] [CrossRef]
- D’Amours, R.; Malo, A.; Flesch, T.; Wilson, J.; Gauthier, J.-P.; Servancks, R. The canadian meteorological centre’s atmospheric transport and dispersion modelling suite. Atmos.-Ocean 2015, 53, 176–199. [Google Scholar] [CrossRef]
- Fay, J.A. Physical Processes in the Spread of Oil on a Water Surface. In Proceedings of the International Oil Spill Conference Proceedings, Washington, DC, USA, 15–17 June 1971; pp. 463–467. [Google Scholar]
- Zeinstra-Helfrich, M.; Koops, W.; Murk, A.J. Predicting the consequence of natural and chemical dispersion for oil slick size over time. J. Geophys. Res. Ocean. 2017, 122, 7312–7324. [Google Scholar] [CrossRef]
- Delvigne, D.A.L.; Sweeney, C. Natural dispersion of oil. Oil Chem. Pollut. 1988, 4, 281–310. [Google Scholar] [CrossRef]
- Johansen, Ø.; Reed, M.; Bodsberg, N. Natural dispersion revisited. Mar. Pollut. Bull. 2015, 93, 20–26. [Google Scholar] [CrossRef]
- Li, Z.; Spaulding, M.L.; McCay, D.F. An algorithm for modeling entrainment and naturally and chemically dispersed oil droplet size distribution under surface breaking wave conditions. Mar. Pollut. Bull. 2017, 119, 145–152. [Google Scholar] [CrossRef] [PubMed]
- Zeinstra-Helfrich, M.; Koops, W.; Dijkstra, K.; Murk, A.J. Quantification of the effect of oil layer thickness on entrainment of surface oil. Mar. Pollut. Bull. 2015, 96, 401–409. [Google Scholar] [CrossRef] [PubMed]
- Zeinstra-Helfrich, M.; Koops, W.; Murk, A.J. How oil properties and layer thickness determine the entrainment of spilled surface oil. Mar. Pollut. Bull. 2016, 110, 184–193. [Google Scholar] [CrossRef] [PubMed]
- Lehr, W.J.; Jones, R.; Evans, M.; Simecek-Beatty, D.; Overstreet, R. Revisions of the ADIOS oil spill model. Environ. Model. Softw. 2002, 17, 191–199. [Google Scholar] [CrossRef]
- Drozd, G.T.; Worton, D.R.; Aeppli, C.; Reddy, C.M.; Zhang, H.; Variano, E.; Goldstein, H. Modeling comprehensive chemical composition of weathered oil following a marine spill to predict ozone and potential secondary aerosol formation and constrain transport pathways. J. Geophys. Res. Oceans 2015, 120, 7300–7315. [Google Scholar] [CrossRef]
- Drozd, G.T.; Worton, D.R.; Aeppli, C.; Reddy, C.M.; Zhang, H.; Variano, E. How Far and How Much? Modeling Oil Weathering Using Comprehensive Composition to Constrain Transport and Pollutant Formation. In Proceedings of the Gulf of Mexico Oil Spill & Ecosystem Science Conference 2016, Tampa, FL, USA, 1–4 February 2016. [Google Scholar]
- Fingas, M.F.; Fieldhouse, B. Water-in-oil-Emulsions. In Handbook of Oil Spill Science & Technology; Wiley: Hoboken, NJ, USA, 2014; Volume 8. [Google Scholar] [CrossRef]
- Daling, P.; Strøm, T. Weathering of Oils at Sea: Model/Field Data Comparisons. Spill Sci. Technol. Bull. 1999, 5, 63–74. [Google Scholar] [CrossRef]
- Daling, P.S.; Singsaas, I.; Reed, M.; Hansen, O. Experiences in dispersant treatment of experimental oil spills. Spill Sci. Technol. Bull. 2002, 7, 201–213. [Google Scholar] [CrossRef]
- Fingas, M. Water-in-oil emulsion formation: A Review of physics and mathematics models. Spill Sci. Technol. Bull. 1995, 2, 55–59. [Google Scholar] [CrossRef]
- Ward, C.P.; Overton, E.B. How the 2010 Deepwater Horizon spill reshaped our understanding of crude oil photochemical weathering at sea: A past, present, and future perspective. Environ. Sci. Process. Impacts. 2020. [Google Scholar] [CrossRef]
- Shukla, J. Predictability. Adv. Geophys. 1985, 28, 126–161. [Google Scholar] [CrossRef]
- Ferrari, R.; Wunsch, C. Ocean circulation kinetic energy: Reservoirs, sources, and sinks. Annu. Rev. Fluid Mech. 2009, 41, 253–282. [Google Scholar] [CrossRef]
- De Dominicis, M.; Falchetti, S.; Trotta, F.; Pinardi, N.; Giacomelli, L.; Napolitano, E.; Fazioli, L.; Sorgente, E.; Haley, P.J.; Lemusiaux, P.; et al. A relocatable ocean model in support of environmental emergencies. Ocean Dyn. 2014. [Google Scholar] [CrossRef]
- ASTM F2067-19. Standard Practice for Development and Use of Oil-Spill Trajectory Models; ASTM International: West Conshohocken, PA, USA, 2019. [Google Scholar]
- NOAA. Standard Practice for Development and Use of Oil-Spill Trajectory Models; ASTM: West Conshohocken, PA, USA; Dept of Commerce/NOAA/OR&R: Seattle, WA, USA, 2000; p. 3.
- Carrier, M.J.; Ngodock, H.; Smith, S.; Jacobs, G.; Muscarella, P.; Özgökmen, T.; Haus, B.; Lipphardt, B. Impact of Assimilating Ocean Velocity Observations Inferred from Lagrangian Drifter Data Using the NCOM-4DVAR. Mon. Weather Rev. 2014, 142, 1509–1524. [Google Scholar] [CrossRef]
- Wei, M.Z.; Rowley, C.; Martin, P.; Barron, C.N.; Jacobs, G. The US Navy’s RELO ensemble prediction system and its performance in the Gulf of Mexico. Q. J. R. Meteor. Soc. 2014, 140, 1129–1149. [Google Scholar] [CrossRef]
- Counillon, F.; Bertino, L. High-resolution ensemble forecasting for the Gulf of Mexico eddies and fronts. Ocean Dyn. 2009, 59, 83–95. [Google Scholar] [CrossRef]
- Milliff, R.F.; Bonazzi, A.; Wikle, C.K.; Pinardi, N.; Berliner, L.M. Ocean ensemble forecasting. Part I: Ensemble Mediterranean winds from a Bayesian hierarchical model. Q. J. R. Meteor. Soc. 2011, 137, 858–878. [Google Scholar] [CrossRef]
- Pinardi, N.; Bonazzi, A.; Dobricic, S.; Milliff, R.F.; Wikle, C.K.; Berliner, L.M. Ocean ensemble forecasting. Part II: Mediterranean Forecast System response. Q. J. R. Meteor. Soc. 2011, 137, 879–893. [Google Scholar] [CrossRef]
- Lima, L.N.; Pezzi, L.P.; Penny, S.G.; Tanajura, C.A.S. An investigation of ocean model uncertainties through ensemble forecast experiments in theSouthwest Atlantic Ocean. J. Geophys. Res. Oceans 2019, 124, 432–452. [Google Scholar] [CrossRef]
- Brassington, G. Forecast Errors, Goodness, and Verification in Ocean Forecasting. J. Mar. Res. 2017, 75, 403–433. [Google Scholar] [CrossRef]
- Murphy, A.H. What is a good forecast? An essay on the nature of goodness in weather forecasting. Weather Forecast. 1993, 8, 281–292. [Google Scholar] [CrossRef]
- Lehr, W.J.; Barker, C.H.; Simecek-Beatty, D.A. New Developments in the Use of Uncertainty in Oil Spill Forecasts. In Proceedings of the Twenty-second AMOP Technical Seminar, Calgary, AB, Canada, 2–4 June 1999. [Google Scholar]
- Sepp Neves, A.A.; Pinardi, N.; Flavio, M. IT-OSRA: Applying ensemble simulations to estimate the oil spill risk associated to operational and accidental oil spills. Ocean Dyn. 2016, 66, 939–954. [Google Scholar] [CrossRef]
- Sepp Neves, A.A.; Pinardi, N.; Navarra, A.; Trotta, F. A General Methodology for Beached Oil Spill Hazard Mapping. Front. Mar. Sci. 2020, 7. [Google Scholar] [CrossRef]
- Kratzke, T.M.; Stone, L.D.; Frost, J.R. Search and Rescue Optimal Planning System. In Proceedings of the 2010 13th International Conference on Information Fusion, Edinburgh, UK, 26–29 July 2010. [Google Scholar]
- Schiller, R.V.; Kourafalou, V.H.; Hogan, P.J.; Walker, N.D. The dynamics of the Mississippi River plume: Impact of topography, wind and offshore forcing on the fate of plume waters. J. Geophys. Res. 2011, 116, C06029. [Google Scholar] [CrossRef]
- Soloviev, A.V.; Matt, S.; Fujimura, A. Three-dimensional dynamics of freshwater lenses in the ocean’s near-surface layer. Oceanography 2015, 28, 142–149. [Google Scholar] [CrossRef]
- Verri, G.; Pinardi, N.; Bryan, F.O.; Tseng, Y.-H.; Coppinia, G.; Clementia, E. A box model to represent estuarine dynamics in mesoscale resolution ocean models. Ocean Model 2020, 148. [Google Scholar] [CrossRef]
- Fennel, K.; Hetland, R. A coupled physical and biological model of the Northern Gulf of Mexico shelf: Model description, validation and analysis of plankton variability. Biogeosciences 2011, 8, 1881–1889. [Google Scholar] [CrossRef]
- Herzfeld, M. The role of numerical implementation on open boundary behaviour in limited area ocean models. Ocean Model 2009, 27, 18–32. [Google Scholar] [CrossRef]
- Herzfeld, M.; Schmidt, M.; Griffies, S.; Liang, Z. Realistic test cases for limited area ocean modelling. Ocean Model 2011, 37, 1–34. [Google Scholar] [CrossRef]
- Warren, C.J.; MacFadyen, A.; Henry, C., Jr. Mapping Oil for the Destroyed Taylor Energy Site in the Gulf of Mexico. In International Oil Spill Conference Proceedings; American Petroleum Institute: Washington, DC, USA, 2014; Volume 1, p. 299931. [Google Scholar]
- Ardhuin, F.; Chapron, B.; Maes, C.; Romeiser, R.; Gommenginger, C.; Cravate, S.; Morrow, R.; Donlon, C.; Bourassa, M. Satellite Doppler observations for the motions of the oceans. Bul. Amer. Meteor. Soc. 2019, 100, ES215–ES219. [Google Scholar] [CrossRef]
- Bourassa, M.A.; Meissner, T.; Cerovecki, I.; Chang, P.; Dong, X.; De Chiara, G.; Donlon, C.; Dukhovskoy, D.S.; Elya, J.; Fore, A.; et al. Remotely Sensed Winds and Wind Stresses for Marine Forecasting and Ocean Model. Front. Mar. Sci. 2019, 6, 443. [Google Scholar] [CrossRef]
- Johansen, Ø.; Jensen, H.V.; Daling, P. Deep Spill JIP. Experimental Discharges of Gas and Oil at Helland Hansen, SINTEF Report No STF66 F00093, 36p. 2000. Available online: https://www.bsee.gov/sites/bsee.gov/files/osrr-oil-spill-response-research//377ab.pdf (accessed on 17 August 2020).
- Olsen, J.E.; Krause, D.F.; Davies, E.J.; Skjetne, P. Observations of Rising Methane Bubbles in Trondheimsfjord and Its Implications to Gas Dissolution. J. Geophys. Res. 2018, 124, 1399–1409. [Google Scholar] [CrossRef]
- ASCE Task Committee on Modeling of Oil Spills. State-of-the-Art Review of Modeling Transport and Fate of Oil Spills. J. Hydraul. Eng. 1996, 122, 594–609. [Google Scholar] [CrossRef]
- Afshar-Mohajer, N.; Li, C.; Rule, A. A laboratory study of particulate and gaseous emissions from crude oil and crude oil-dispersant contaminated seawater due to breaking waves. Atmos. Environ. 2018, 179, 177–186. [Google Scholar] [CrossRef]
- Liyana-Arachchi, T.; Zhang, Z.; Ehrenhauser, F.; Avij, P.; Valsaraj, K.; Hung, F. Bubble bursting as an aerosol generation mechanism during an oil spill in the deep-sea environment: Molecular dynamics simulations of oil alkanes and dispersants in atmospheric air/sal water interfaces. Environ. Sci. Processes Impacts 2014, 16, 53–64. [Google Scholar] [CrossRef]
- Zhu, H.; You, J.; Zhao, H. An experimental investigation of underwater spread of oil spill in a shear flow. Mar. Pollut. Bull. 2017, 116, 156–166. [Google Scholar] [CrossRef]
- Lödise, J.; Özgökomen, T.; Griffa, A.; Berta, M. Vertical structure of ocean currents under high winds from massive arrays of drifters. Ocean Sci. 2019, 15, 1627–1651. [Google Scholar] [CrossRef]
- Daae, R.L.; Skancke, J.; Brandvik, P.J.; Faksness, L.-G. The sensitivity of the surface oil signature to subsurface dispersant injection and weather conditions. Mar. Pollut. Bull. 2018, 127, 175–181. [Google Scholar] [CrossRef]
- Nordam, T.; Lofthus, S.; Brakstad, O. Modelling biodegradation of crude oil components at low temperatures. Chemosphere 2020, 254. [Google Scholar] [CrossRef]
- Khelifa, A.; Gamble, L. Prediction of Tar Ball Formation. In Proceedings of the Twenty-ninth AMOP Technical Seminar, Vancouver, BC, Canada, 6–8 June 2006; pp. 79–90. [Google Scholar]
- Harriman, B.H.; Zito, P.; Podgorski, D.C.; Tarr, M.A.; Suflita, J.M. Impact of Photooxidation and Biodegradation on the Fate of Oil Spilled During the Deepwater Horizon Incident: Advanced Stages of Weathering. Environ. Sci. Technol. 2017, 51, 7412–7421. [Google Scholar] [CrossRef]
- Ward, C.P.; Sharpless, C.M.; Valentine, D.L.; French-McCay, D.P.; Aeppli, C.; White, H.K.; Reddy, C.M. Partial Photochemical Oxidation Was a Dominant Fate of Deepwater Horizon Surface Oil. Environ. Sci. Technol. 2018, 52, 1797–1805. [Google Scholar] [CrossRef]
- McKenna, A.M.; Nelson, R.K.; Reddy, C.M.; Savory, J.J.; Kaiser, N.K.; Fitzsimmons, J.E.; Marshall, A.G.; Rodgers, R.P. Expansion of the Analytical Window for Oil Spill Characterization by Ultrahigh Resolution Mass Spectrometry: Beyond Gas Chromatogr. Environ. Sci. Technol. 2013, 47, 7530–7539. [Google Scholar]
- Chen, H.; Hou, A.; Corilo, Y.E.; Lin, Q.; Lu, J.; Mendelssohn, I.A.; Zhang, R.; Rodgers, R.P.; McKenna, A.M. 4 Years after the Deepwater Horizon Spill: Molecular Transformation of Macondo Well Oil in Louisiana Salt Marsh Sediments Revealed by FT-ICR Mass Spectrometry. Environ. Sci. Technol. 2016, 50, 9061. [Google Scholar] [CrossRef] [PubMed]
- Zito, P.; Podgorski, D.C.; Johnson, J.; Chen, H.; Rodgers, R.P.; Guillemette, F.; Kellerman, A.M.; Spencer, R.G.M.; Tarr, M.A. Molecular-Level Composition and Acute Toxicity of Photosolubilized Petrogenic Carbon. Environ. Sci. Technol. 2019, 53, 8235–8243. [Google Scholar] [CrossRef] [PubMed]
- Aeppli, C.; Swarthout, R.F.; O’Neil, G.W.; Katz, S.D.; Nabi, D.; Ward, C.P.; Nelson, R.K.; Sharpless, C.M.; Reddy, C.M. Oil Weathering after the Deepwater Horizon Disaster Led to the Formation of Oxygenated Residues. Environ. Sci. Technol. 2012, 46, 8799–8807. [Google Scholar] [CrossRef] [PubMed]
- Gros, J.; Reddy, C.M.; Aeppli, C.; Nelson, R.K.; Carmichael, C.A.; Arey, J.S. Resolving Biodegradation Patterns of Persistent Saturated Hydrocarbons in Weathered Oil Samples from the Deepwater Horizon Disaster. Environ. Sci. Technol. 2014, 48, 1628–1637. [Google Scholar] [CrossRef]
- Aeppli, C.; Nelson, R.K.; Carmichael, C.A.; Valentine, D.L.; Reddy, C.M. Biotic and Abiotic Oil Degradation After The Deepwater Horizon Disaster Leads To Formation Of Recalcitrant Oxygenated Hydrocarbons: New Insights Using GC×GC. In Proceedings of the 2014 International Oil Spill Conference, Savannah, GA, USA, 5–8 May 2014; pp. 1087–1098. [Google Scholar]
- Niles, S.F.; Chacón-Patiño, M.L.; Chen, H.; McKenna, A.M.; Blakney, G.T.; Rodgers, R.P.; Marsha, A.G. Molecular-Level Characterization of Oil-Soluble Ketone/Aldehyde Photo-Oxidation Products by Fourier Transform Ion Cyclotron Resonance Mass Spectrometry Reveals Similarity Between Microcosm and Field Samples. Environ. Sci. Technol. 2019, 53, 6887–6894. [Google Scholar] [CrossRef]
- Bacosa, H.P.; Erdner, D.L.; Liu, Z. Differentiating the roles of photooxidation and biodegradation in the weathering of Light Louisiana Sweet crude oil in surface water from the Deepwater Horizon site. Mar. Pollut. Bull. 2015, 95, 265–272. [Google Scholar] [CrossRef]
- Ray, P.Z.; Tarr, M.A. Formation of organic triplets from solar irradiation of petroleum. Mar. Chem. 2015, 168, 135–139. [Google Scholar]
- McFarlin, K.M.; Prince, R.C.; Perkins, R.; Leigh, M.B. Biodegradation of Dispersed Oil in Arctic Seawater at −1 °C. PLoS ONE 2014, 9, e84297. [Google Scholar] [CrossRef]
- Olson, G.M.; Gao, H.; Meyer, B.M.; Miles, M.S.; Overton, E.B. Effect of Corexit 9500A on Mississippi Canyon crude oil weathering patterns using artificial and natural sea water. Heliyon 2017, 3, e00269. [Google Scholar] [CrossRef]
- Bacosa, H.P.; Erdner, D.L.; Rosenheim, B.E.; Shetty, P.; Seitz, K.W.; Baker, B.J.; Liu, Z. Hydrocarbon degradation and response of seafloor sediment bacterial community in the northern Gulf of Mexico to light Louisiana sweet crude oil. ISME J. 2018, 12, 2532–2543. [Google Scholar] [CrossRef] [PubMed]
- Brakstad, O.G.; Daling, P.S.; Faksness, L.-G.; Almås, I.K.; Vang, S.-H.; Syslak, L.; Leirvik, F. Depletion and biodegradation of hydrocarbons in dispersions and emulsions of the Macondo 252 oil generated in an oil-on-seawater mesocosm flume basin. Mar. Pollut. Bull. 2014, 84, 125–134. [Google Scholar] [CrossRef] [PubMed]
- O’Donnell, J. Integration of Coastal Ocean Dyn.Application Radar (CODAR) and Short-Term Predictive System (STPS) Surface Current Estimates into the Search and Rescue Optimal Planning System (SAROPS). Tech. Rep. 2006. [Google Scholar] [CrossRef]
- Allshouse, M.R.; Ivey, G.N.; Xu, J.; Beegle-Krause, C.; Lowe, R.; Jones, N.; Peacock, T. The Impact of Wind on the Lagrangian Structure of Ocean Surface Transport. Environ. Fluid Dyn. 2017, 17, 473–483. [Google Scholar] [CrossRef]
- Beegle-Krause, C.; Peacock, T.; Allshouse, M.R. Exploiting Lagrangian Coherent Structures (LCS) for the Calculations of Oil Spill and Search and Rescue Drift Patterns in the Ocean. In Proceedings of the Arctic and Marine Oil Spill Conference (AMOP). Environment Canada, Banff, AB, Canada, 4–6 October 2011. [Google Scholar]
- Mezic, I.; Loire, S.; Fonoberov, V.A.; Hogan, P. A New Mixing Diagnostic and Gulf Oil Spill Movement. Science 2010, 330, 486–489. [Google Scholar] [CrossRef]
- Galt, J.A. Triangular Tessellation Documentation; Genwest Technical Publications: Edmonds, WA, USA, 2011; Volume 11, p. 48. [Google Scholar]
- Galt, J.A. Triangular Tessellation Documentation Part II—Clustering on Boundaries; Genwest Technical Publications: Edmonds, WA, USA, 2015; Volume 15, p. 23. [Google Scholar]
- Björnham, O.; Brännström, N.; Grahn, H.; Lindgren, P.R.; von Schoenberg, P. Post-processing of results from a particle dispersion model by employing kernel density estimation. In Technical Report No. FOI-R--4135—SE; The Swedish Defence Research Agency: Stockholm, Sweden, 2015; pp. 1650–1942. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; The University of Illinois Press: Urbana, IL, USA; Chicago, IL, USA, 1962; p. 125. [Google Scholar]
- Galt, J.A.; Payton, D.L.; Hanson, R. Analysis of Lagrangian Models Using Information Theory. In Proceedings of the Fortieth AMOP Technical Seminar, Environment and Climate Change Canada, Calgary, AB, Canada, 3–5 October 2017; pp. 694–716. [Google Scholar]
- Özgökmen, T.M.; Boufadel, M.; Carlson, D.; Cousin, C.; Guigand, C.; Haus, B.; Horstmann, J.; Lund, B.; Molemaker, J.; Novelli, G. Technological advances for ocean surface measurements by the Consortium of Advanced Research for Hydrocarbons in the Environment (CARTHE). Mar. Technol. Soc. J. 2018, 52, 71–76. [Google Scholar] [CrossRef]
- Grossi, M.; Kubat, M.; Özgökmen, T. Prediction of particle trajectories using artificial neural networks. Ocean Model 2020. in revision. [Google Scholar]
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).