Reduction of Wave Overtopping and Force Impact at Harbor Quays Due to Very Oblique Waves

Abstract

Physical model experiments were conducted in a wave tank at Flanders Hydraulics Research, Antwerp, Belgium, to characterize the wave overtopping and impact force on vertical quay walls and sloping sea dike (1:2.5) under very oblique wave attack (angle between 45° and 80°). This study was triggered by the scarce scientific literature on the overtopping and force reduction due to very oblique waves since large reduction is expected for both when compared with the perpendicular wave attack. The study aimed to compare the results from the experimental tests with formulas derived from previous experiments and applicable to a Belgian harbor generic case. The influence of storm return walls and crest berm width on top of the dikes has been analyzed in combination with the wave obliqueness. The results indicate significant reduction of the overtopping due to very oblique waves and new reduction coefficients were proposed. When compared with formulas from previous studies the proposed coefficients indicate the best fit for the overtopping reduction. Position of the storm return wall respect to the quay edge rather than its height was found to be more important for preventing wave induced overtopping. The force reduction is up to approximately 50% for the oblique waves with respect to the perpendicular wave impact and reduction coefficients were proposed for two different configurations a sea dike and vertical quay wall, respectively.

1. Introduction

Densely populated coastal zones with very low freeboards are common worldwide (e.g., Belgium, The Netherlands, Vietnam). Often the flood protection is provided in these zones by the sandy beaches, but when it is insufficient or in the case of harbors, the most common solution is storm wall construction. A storm wall is located on top of the crest of a quay or a dike at a certain distance from the seaward edge of the crest, providing additional protection against the overtopping waves. During each overtopping event, the waves runup in form of a bore along its crests before reaching the wall. Usually, this flow is turbulent, and its velocity is decreased along the crest width. Consequently, the distance between the edge of the structure and the storm wall is important because it characterizes the wave impact on the storm wall and overtopping over the storm wall.

Typically, the wave’s angle is assumed to be perpendicular or at an angle lower than 45° with respect to the quay’s normal. However, when the harbor opening is orientated against the main wave direction very oblique waves can approach some of the harbor quays and dikes. There are several formulas proposed for the overtopping computation under oblique wave attack. One of the most widely used is the European Overtopping Manual [1,2] which provides validated formulas to calculate the overtopping discharge for classical configurations (wave angles smaller than 45°). The overtopping is maximum for the perpendicular wave attack on a storm return wall, but for larger wave angles, a reduction factor is applied to account for the overtopping discharge decrease. However, the EurOtop formula suggests keeping the obliqueness reduction factor constant for vertical structures and wave angles larger than 45°. Obviously, the overtopping discharge reduces with the increasing wave angle with respect to the structure normal, but the reduction for very large wave angles has not been fully investigated yet. A similar situation is for the case of the impact force reduction due to the large wave angle, but studies comprehensively analyzing this reduction are not currently available.

The mean wave overtopping is mainly a function of the relative freeboard and the relationship between the overtopping discharge and the freeboard is expressed through, in most of the cases, an exponential formula. Several reduction coefficients are used to account for effects induced by the presence of a berm, a storm return wall, the surface roughness, and the wave obliqueness.

To investigate the overtopping reduction and impact force reduction for oblique waves a physical model was set-up at Flanders Hydraulics Research in Antwerp, Belgium. The present study has three main objectives. Firstly, to investigate overtopping induced by very oblique waves at quay harbors and to propose reliable reduction coefficients for the overtopping calculation. Secondly, to identify the influence on overtopping of a storm return wall placed on the quay at different positions and having variable heights. Thirdly, to evaluate the impact force reduction due wave obliqueness. Although, it was expected that overtopping and impact forces will be reduced at large wave angles (respect to the structure normal), quantification of these reductions is still unclearly defined in previous studies; hence, the necessity of the present study.

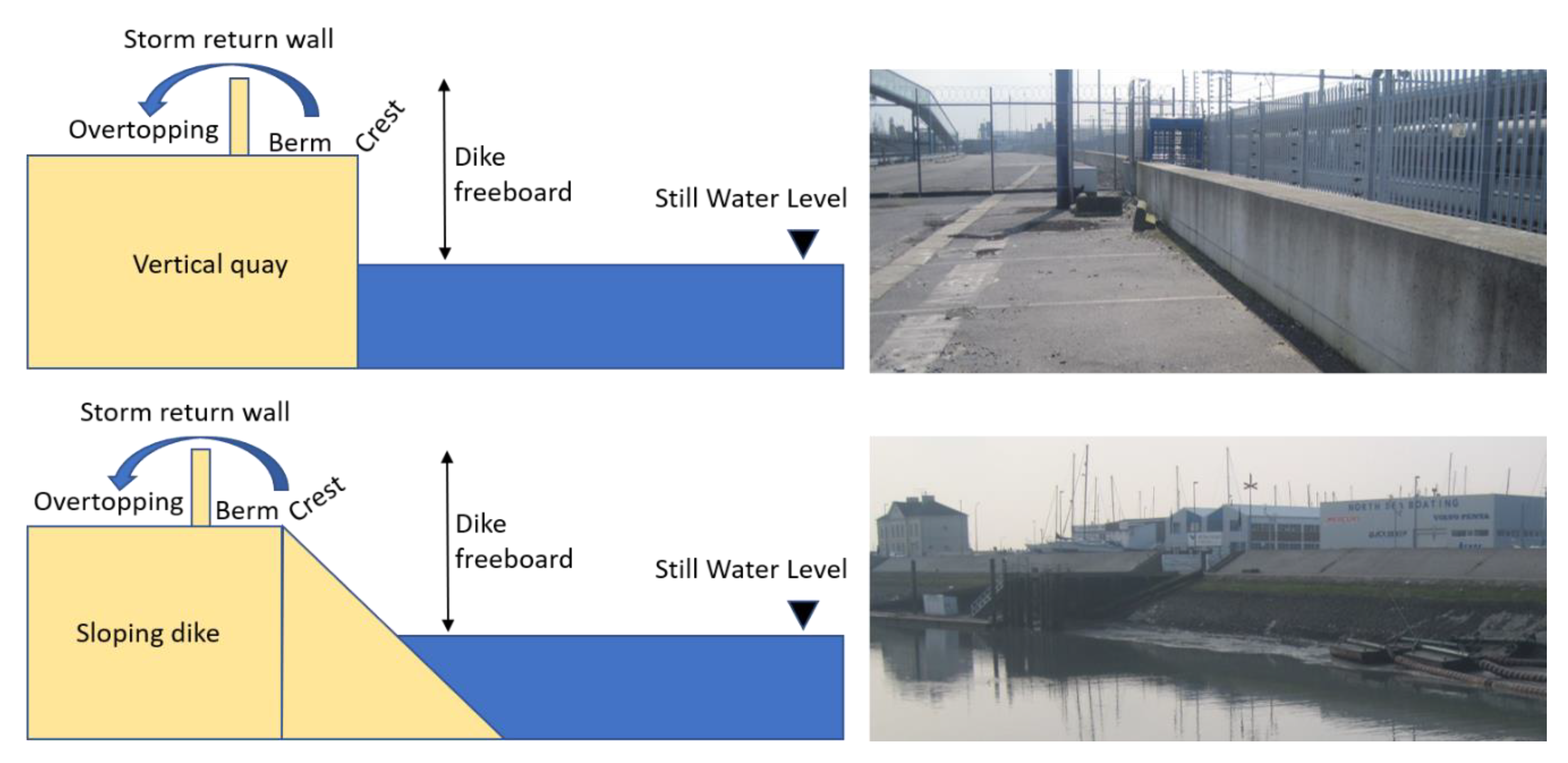
2. Overtopping and Force Reduction

2.1. Vertical Quay

A series of formulations describe the overtopping reduction with the large incident wave angle. Most of the formulas used are presented in [1], but significant contributions are given also in other previous studies [3,4,5]. The overtopping reduction due to very obliques wave angles is usually limited to angles of 45° and for larger wave angles a constant value is proposed.

The most used approach is based on the equations and reduction factors included in the European Overtopping Manual [1] for non-impulsive conditions:

$$\frac{\mathrm{q}}{\sqrt{{\mathrm{gH}}_{\mathrm{m}0}^3}}=0.04\exp \left(-2.6\frac{{\mathrm{R}}_{\mathrm{c}}}{{\mathrm{H}}_{\mathrm{m}0}{\mathsf{\gamma }}_{\mathsf{\beta }}}\right)$$

(1)

where q is the overtopping discharge per meter of width of the structure (m³/s/m), H_m0 is the significant incident wave height, measured at the toe of the structure (m), R_c is the crest freeboard (m), and γ_β is the reduction coefficient that considers the effects of the obliqueness (-).

The coefficient γ_β is expressed in EurOtop as

$${\mathsf{\gamma }}_{\mathsf{\beta }}=1-0.0062\left|\mathsf{\beta }\right|\mathrm{for}:0°\le \mathsf{\beta }\le 45°$$

(2)

For wave angles larger than 45° a constant value of 0.72 is proposed in EurOtop [1].

The formulations contained in the EurOtop manual [1] assume that different regimes of non-breaking, impulsive breaking and broken waves may produce differences in the overtopping. Although the wave loadings on vertical walls due to individual waves are certainly affected by the wave regime, it is not clear if the overtopping is affected in the same way. The overtopping discharge is a mean value where many non-breaking, breaking, and broken waves can contribute in the same wave train. Therefore Goda [3] proposed an equation that is valid for both non-impulsive and impulsive wave conditions:

$$\frac{\mathrm{q}}{\sqrt{{\mathrm{gH}}_{\mathrm{m}0}^3}}=\exp \left[-\left(\mathrm{A}+\mathrm{B}\frac{{\mathrm{R}}_{\mathrm{c}}}{{\mathrm{H}}_{\mathrm{m}0}}\frac{1}{{\mathsf{\gamma }}_{\mathrm{f}}{\mathsf{\gamma }}_{\mathsf{\beta }}^{*}}\right)\right]$$

(3)

The constants A and B can be estimated by:

$$\begin{gathered} A=A_0 tanh\left[b_1 \left(\frac{h_t}{H_{s, toe}}+c_1\right)\right] \\ B=B_0 tanh\left[b_2 \left(\frac{h_t}{H_{s, toe}}+c_2\right)\right] \end{gathered}$$

(4)

where h_t is the water depth at the toe of the dike and H_s,toe is the incident wave height at the toe of the dike. The coefficients b₁, c₁, b₂, and c₂ depend on the foreshore slope as summarized in

Table 1. Optimum coefficient values of empirical formulas for intercept A and gradient coefficient B (after Goda, 2009).

Seabed Slope	Coefficient A			Coefficient B
tan θ	A0	b1	c2	B0	b2	c2
1/10	3.6	1.4	0.1	2.3	0.6	0.8
1/20–1/1000	3.6	1.0	0.6	2.3	0.8	0.6

.

The coefficients $A_0$ and $B_0$ are calculated as a function of the dike slope, $\mathit{cot}{\alpha }_s$, and their value ranges between 0 and 7. The expression for the reduction factor for wave obliqueness has been estimated by Goda [3] as

$${\mathsf{\gamma }}_{\mathsf{\beta }}=1-0.0096\left|\mathsf{\beta }\right|+0.000054\mathsf{\beta }2\mathrm{for}0°\le \mathsf{\beta }\le 80°$$

(5)

2.2. Sloping Dike

Several studies investigate the reduction in overtopping due to oblique waves [6,7], but two formulas from literature were considered due to the similarity with the tests from the present study: EurOtop [1] (6) for non-breaking waves and van der Meer and Bruce [8] (8) which is an adaptation of the EurOtop formula.

$$\frac{\mathrm{q}}{\sqrt{{\mathrm{gH}}_{\mathrm{m}0}^3}}=0.2\exp \left(-2.6\frac{{\mathrm{R}}_{\mathrm{c}}}{{\mathrm{H}}_{\mathrm{m}0}{\mathsf{\gamma }}_{\mathrm{f}}{\mathsf{\gamma }}_{\mathsf{\beta }}}\right)$$

(6)

in which the coefficient γ_β is expressed as

$${\mathsf{\gamma }}_{\mathsf{\beta }}=1-0.0033\left|\mathsf{\beta }\right|\mathrm{for}:0°\le \mathsf{\beta }\le 80°$$

(7)

For wave angles larger than 80° a constant value of 0.736 is proposed.

The formula given by van der Meer and Bruce [8]:

$$\frac{\mathrm{q}}{\sqrt{{\mathrm{gH}}_{\mathrm{m}0}^3}}=0.09\exp {\left(-1.5\frac{{\mathrm{R}}_{\mathrm{c}}}{{\mathrm{H}}_{\mathrm{m}0}{\mathsf{\gamma }}_{\mathrm{f}}{\mathsf{\gamma }}_{\mathsf{\beta }}}\right)}^{1.3}$$

(8)

in which γ_β is identical as in (7).

In all the cases γ_f has been assumed equal to 1 (smooth slope). Van Doorslaer et al. [9] propose a reduction factor γ_{prom_v} to take into account the presence of a storm return wall on the top of the dike. This coefficient considers both the effect of the wall height and position. The values of γ_{prom_v} are calculated for each case based on the approach described in Van Doorslaer et al. [9].

$$\frac{\mathrm{q}}{\sqrt{{\mathrm{gH}}_{\mathrm{m}0}^3}}=0.2\exp \left(-2.3\frac{{\mathrm{R}}_{\mathrm{c}}}{{\mathrm{H}}_{\mathrm{m}0}}\frac{1}{{\mathsf{\gamma }}_{\mathrm{f}}{\mathsf{\gamma }}_{\mathsf{\beta }}{\mathsf{\gamma }}_{\mathrm{prom}\_\mathrm{v}}}\right)$$

(9)

$${\mathsf{\gamma }}_{\mathrm{prom}\_\mathrm{v}}=0.87{\mathsf{\gamma }}_{\mathrm{prom}}{\mathsf{\gamma }}_{\mathrm{v}}$$

(10)

where ${\mathsf{\gamma }}_{\mathrm{prom}}$ and ${\mathsf{\gamma }}_{\mathrm{v}}$ are the individual reduction factors to consider the effects respectively of the promenade and of the storm wall. The promenade reduction factor ${\mathsf{\gamma }}_{\mathrm{prom}}$ is expressed as

$${\mathsf{\gamma }}_{\mathrm{prom}}=1-0.47\mathrm{B}/{\mathrm{L}}_{\mathrm{m}-1,0}$$

(11)

where B is the width of the promenade and L_m−1,0 is the spectral wave length calculated using the spectral period in deep waters T_m−1,0 = m₋₁/m₀.

The reduction factor ${\mathsf{\gamma }}_{\mathrm{v}}$ for the presence of a storm return wall is expressed in Van Doorslaer et al. [9] in function of the wall height (h_wall) and freeboard (R_c) as follows:

$${\mathsf{\gamma }}_{\mathrm{v}}=\{\begin{array}{c}\exp \left(-0.56{\mathrm{h}}_{\mathrm{wall}}/{\mathrm{R}}_{\mathrm{c}}\right)\\ 0.5\end{array}\mathrm{for}\{\begin{array}{c}{\mathrm{h}}_{\mathrm{wall}}/{\mathrm{R}}_{\mathrm{c}}<1.24\\ {\mathrm{h}}_{\mathrm{wall}}/{\mathrm{R}}_{\mathrm{c}}\ge 1.24\end{array}$$

(12)

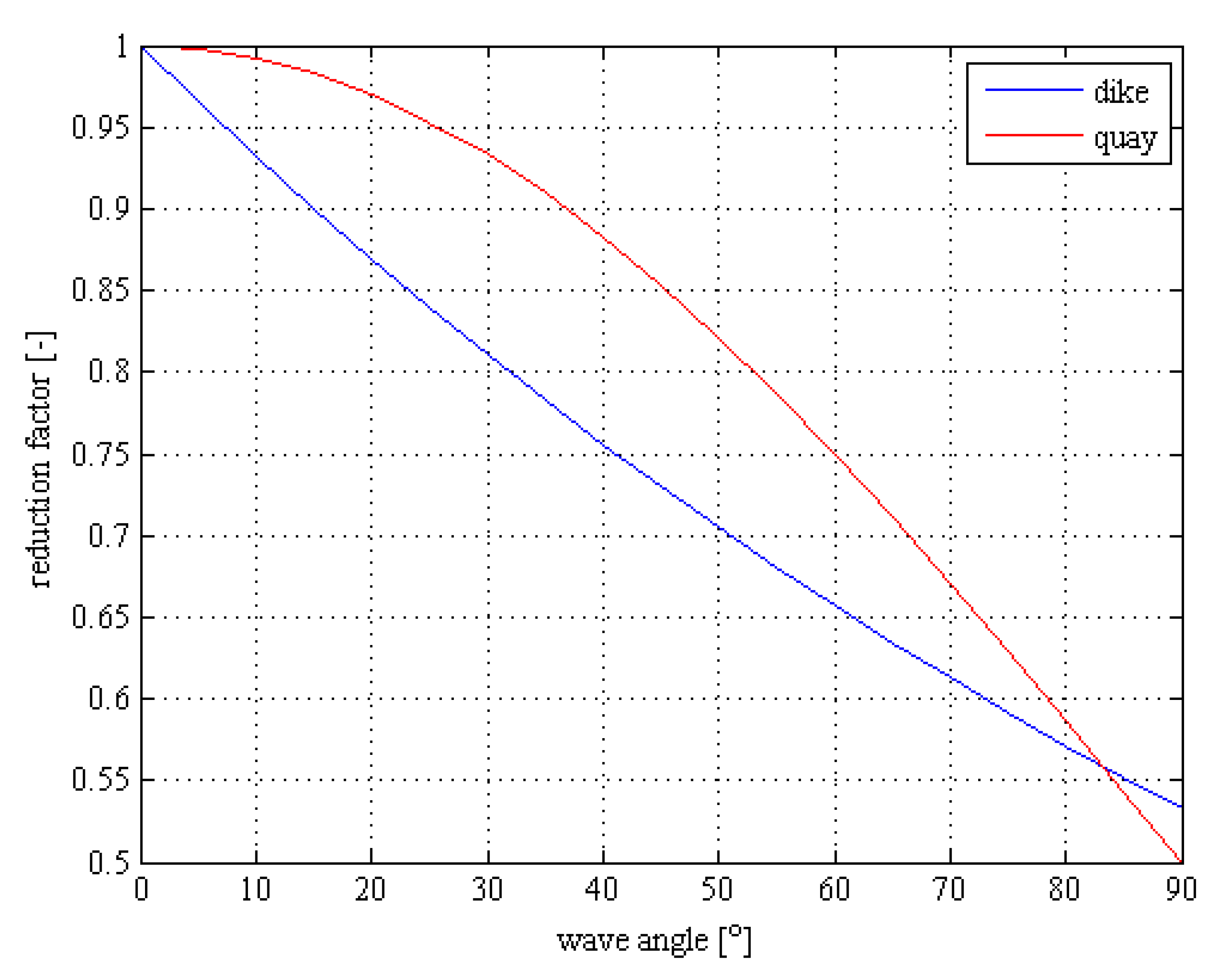
2.3. Force Reduction

There is scarce information regarding the impact forces on a storm wall in case of wave overtopping by oblique waves. However, the study of Van Doorslaer et al. [10] performed at Polytechnic University of Catalonia, Barcelona (UPC), used configurations similar to those tested in the present study. Two structures were tested in the wave flume (scale 1:6): a vertical quay wall and a dike with a smooth slope. The storm wall was 1.20 m high (prototype value) and located at 10.14 m (prototype value) behind the edge of the crest. Three water levels were used resulting in freeboard R_c from the still water level to the top of the storm wall of 3.18 m, 2.22 m, and 1.20 m (prototype values). The irregular waves had a Jonswap wave spectrum (γ = 3.3). The significant wave height H_m0 ranged from 0.78 m to 3.00 m (prototype values); the wave period T_p was either 7.00 s or 10.00 s. The experiments were carried out in two dimensional conditions with perpendicular waves (no wave obliqueness). The authors proposed a new formula to evaluate the wave force on a storm wall, both for quay walls and sea dikes. The formula can be expressed as follows:

$$F_{1/250}=a\rho g{\mathrm{R}}_{\mathrm{c}}^2\exp \left(-\mathrm{b}\frac{{\mathrm{R}}_{\mathrm{c}}}{{\mathrm{H}}_{\mathrm{m}0}}\right)$$

(13)

where F_1/250 is the average force of the highest 1/250 waves. The coefficients a and b (

Table 2. Coefficients a and b in Equation (13) for different geometries (after Van Doorslaer et al. [10]).

Geometry	a	b
Dike	8.31 (0.22)	2.45 (0.07)
Quay	18.27 (0.23)	3.99 (0.06)
All	5.96 (0.23)	2.42 (0.09)

) are derived from a non-linear regression analysis and they are considered as the mean value of normally distributed variables. Under this hypothesis, the relative standard deviation (σ’ = σ/μ) was calculated for each coefficient and is reported in Table 2 between brackets.

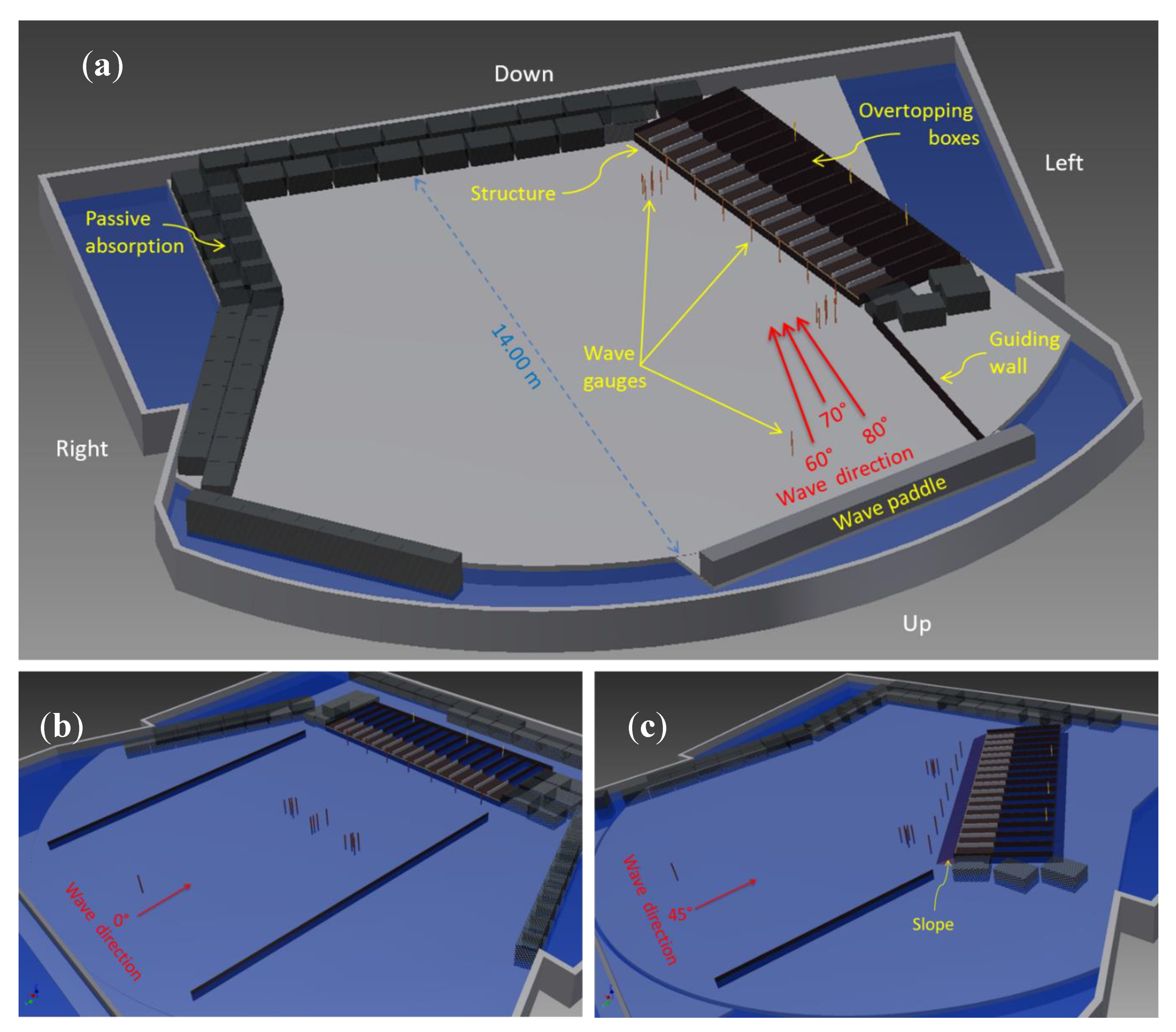
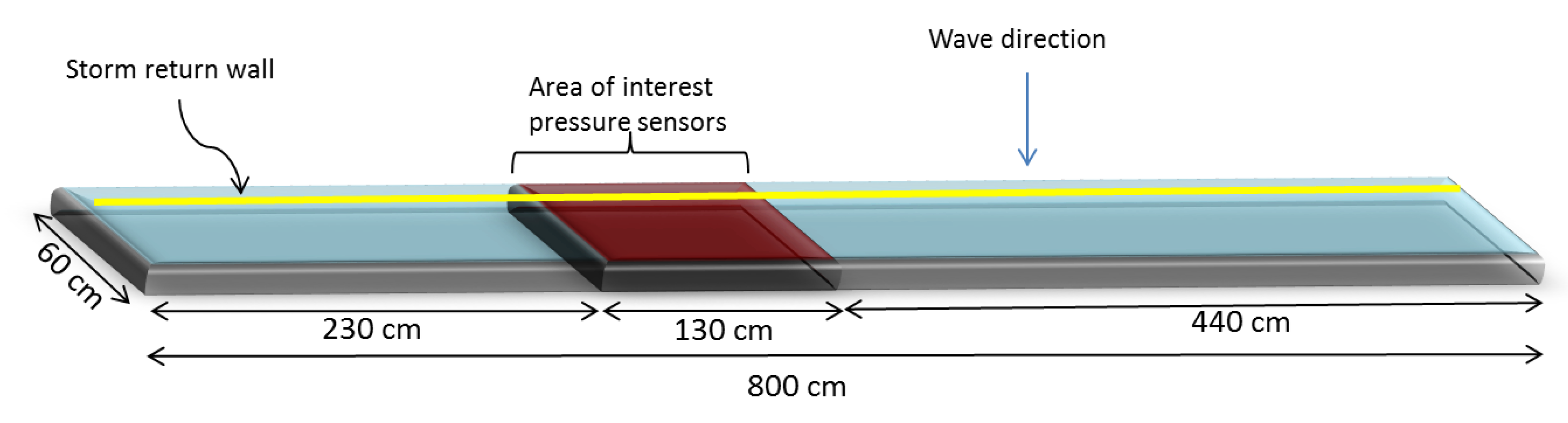
3. Methods and Instrumentation

Investigation of the overtopping reduction required a physical model sufficiently large to observe the alongshore variation and to accommodate the collection of the overtopped volumes, respectively. However, this structure was not firm enough to prevent vibrations which can severely alter the impacting forces measurements. Therefore, it was decided to build two different structures, first one for the overtopping reduction and second one for force reduction due to the wave obliqueness. The structural layout and hydraulic boundary conditions were assumed based on real conditions from the Belgian harbors. However, the model geometries do not represent one specific quay or dike, but they were selected in such way that the results could be extended to other similar structures. The experiments were carried out in the wave tank at FHR (Flanders Hydraulics Research) (dimensions 17.50 m × 12.20 m × 0.45 m), equipped with a piston-type wave generator. The wave generator has a width of 12 m and generates long-crested waves. Both regular and irregular wave patterns can be generated at different angles of wave incidence ranging between −22.5° and 22.5° with respect to the center line of the wave tank.

Two sets of wave directions were used in the experimental campaign conducted at FHR: the first set contains the wave directions 0° and 45°, used to validate the results of the FHR experiments against previous experiments and existing formulas; the second set contains wave directions 60°, 70°, and 80°, used to investigate larger angles. Similar configuration tests from CLASH database [11] were used to compare and validate the tests from the present study.

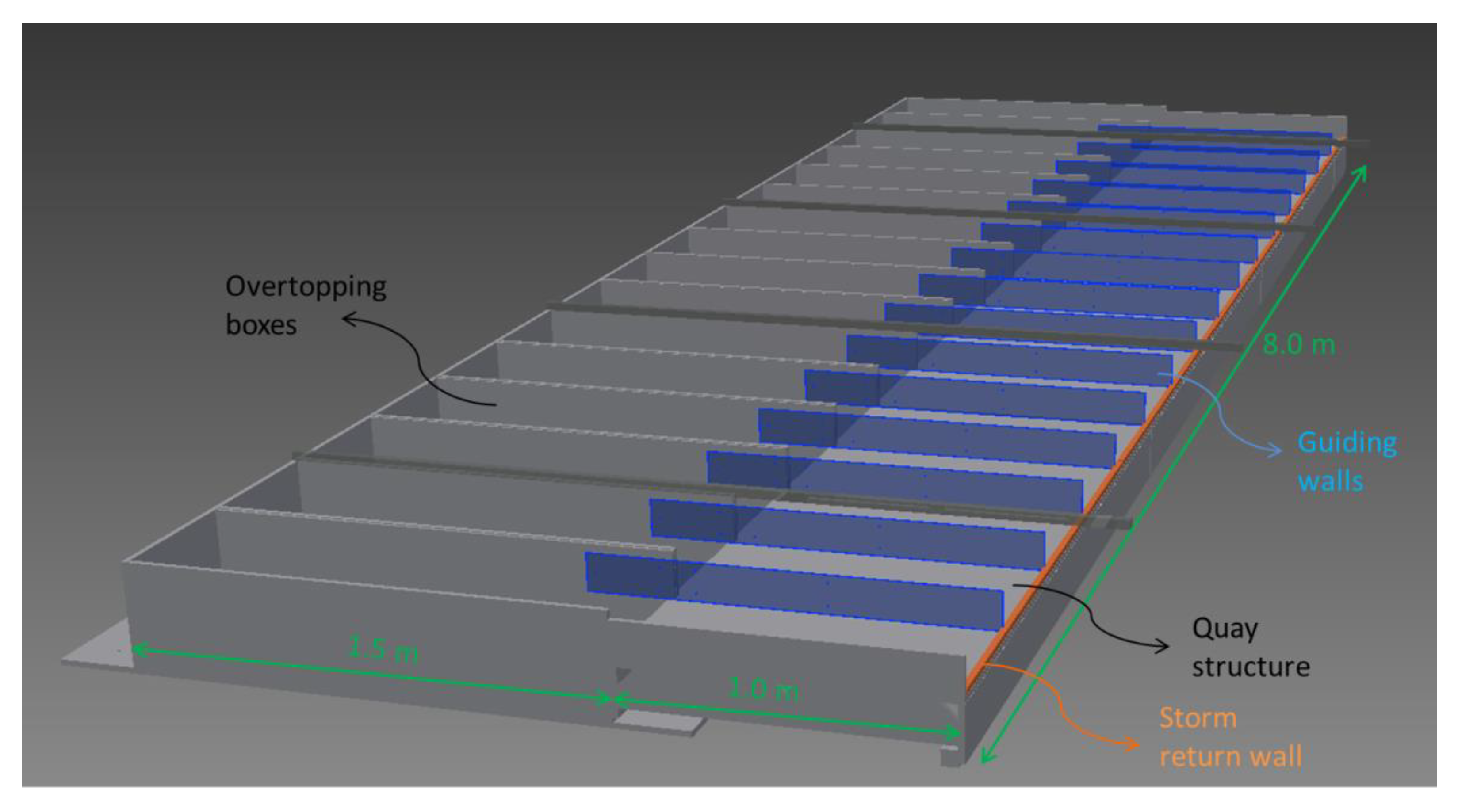
3.1. Model Settings of Overtopping Tests

The first physical model was designed to study very oblique wave attacks and overtopping flows onto vertical quays and sloping dikes with storm return walls (Figure 1).

As the wave height can variate along the structure, a smaller scale was necessary to accommodate a model sufficiently long to record the overtopping variations However, the scale cannot be smaller than 1:50 because some wave height scenarios would be smaller than 3 cm and therefore affected by the surface tension, and thus altering the reproduction of the prototype conditions [12]. Following the above mentioned boundary conditions as well as the Froude’s law a scale of 1:50 was selected as best fitting for the physical model. For vertical walls, tests in large scale flumes and field measurements have demonstrated that results of overtopping discharge in small scale laboratory studies may be securely scaled up to full scale under impulsive and non-impulsive conditions. Only the wind effects are not considered and may cause a significant difference (for further details see [1]). For dikes the evaluation of scale effects is based on the approach of Schüttrumpf and Oumeraci [13]. Calculation of the Reynolds-number and its comparison with the critical value demonstrated that scale effects are negligible. A minimum distance between the wave maker and the structure equal to two wave lengths was kept for every configuration and wave dampers were placed around the basin to absorb the reflected waves. Considering the limitations, it was decided to build a laminated wooden structure of 8 m long and 1 m wide. Attached to this structure, there are 16 boxes (1.5 m long, 0.48 m wide, and 0.18 m deep), built from the same material, designed to collect the overtopping water during the experiment (Figure 2).

Two positions of this structure in the basin were planned. Firstly, the structure was mounted in the central down part of the basin for the 0° wave direction (Figure 3b). Secondly, the structure was moved towards the down left corner to optimize the distance to the wave maker, but also to allow simulation of the wave directions between 45° and 80° just by moving the wave paddle and keep the structure in the same position (Figure 3a,c).

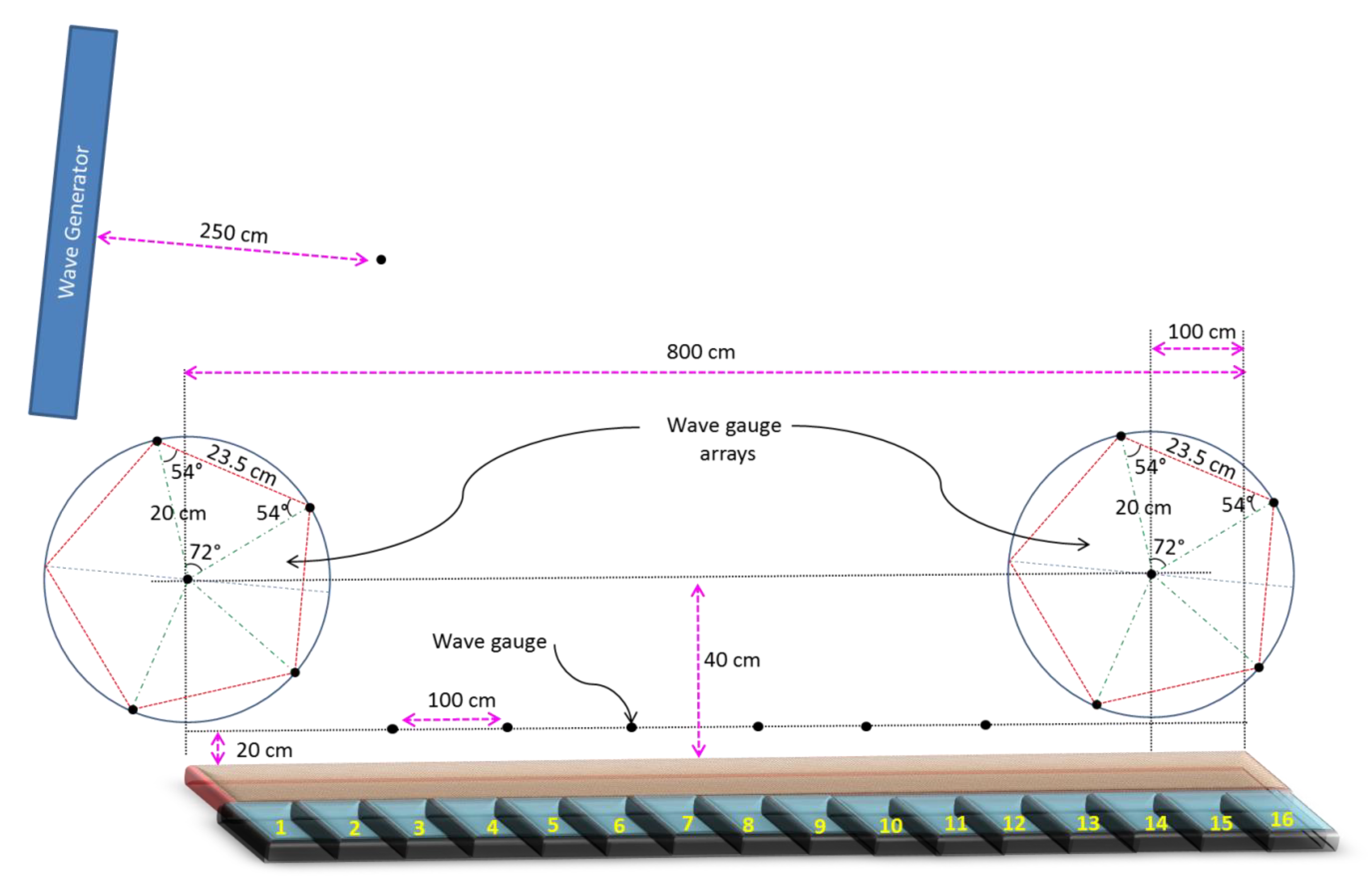
3.1.1. Instrumentation

Resistance type wave gauges (17 in number) were used to measure the wave characteristics (height, period, and direction). One wave gauge is permanently situated in front of the wave maker to verify the generated waves. Two wave gauges arrays were built, each consisting of five wave gauges; these wave gauges are located in such way that a directional spectral analysis can be performed. The incident wave height has been measured using these two 3D-arrays. The WaveLab software (version 3.39, [14]) which utilizes the Baysian Directional spectrum estimation method (BDM) [15], has been used for the analysis. Using this method, the user generally indicates a circular sector around the expected incident and reflected wave direction, so the analysis will be limited to this sector. It is possible to select a very narrow circular sector, excluding from the wave analysis directions too far from the main one. Alternatively, it also possible to select ±90° around the main direction, so the entire 360° will be covered from the analysis. In this study, the analysis for the perpendicular wave case attack used ±30° around the main expected directions (0° for the incident and 180° for the reflected waves respectively). Hence, spurious transversal effects were removed from the results. Differently, for the oblique wave cases, it has been preferred to extend the analysis to the entire 360°, because in such case the main reflected direction can be assumed, but the effects on wave further reflections on the sides of the basin (even though passive absorption was installed) has to be checked. The rest of the six wave gauges were mounted equidistantly, in the proximity of the structure to provide information about the total wave height variation along the structure. This instrument setup was used for all the wave directions, but some minor changes in distances and positions were made for each wave direction (Figure 4). On every overtopping box a mechanical reader for the water level was installed to measure the accumulated volume.

3.1.2. Test Programme

A total of 377 tests were run, covering a wide range of wave conditions and structure configurations (

Table 3. Summary of the test conditions for overtopping reduction.

Total no. of Tests	Used for Analyses	Vertical Quay	Sloping Dike (1 to 2.5)
377	230	191	39
Wave directions	Wave height (Hm0)	Wave period (Tp)	Crest freeboard (Rc)	Storm return wall position
0°, 45°, 60°, 70°, 80°	0.96 to 3.39 m	5.1 to 12.6 s	0 to 2.75 m	0 to 50 m

). The wave angle is defined as the angle between the wave direction and the line normal to the quay structure so that 0° defines perpendicular wave attack. For the majority of the wave angles both the vertical and the sloping dike configurations were used. In all the tests long-crested waves were generated. The water level was varied around the crest level: the defined “dike freeboard” (R_c) can assume negative (i.e., Still Water Level, SWL, above the dike crest) and positive values (SWL below the dike crest). Three different wall heights were used (0 m, 1 m, and 2 m in prototype scale). The wall elevation with respect to the SWL defines the dike freeboard R_c. The berm (distance between the storm return wall and the quay or dike crest) lengths used in the experiments were 0, 5, 25, and 50 m in prototype scale. Tests with no reliable measured wave conditions, zero overtopping, and water volumes exceeding the boxes’ volume, as well as preliminary tests to set-up the model were excluded from further analyses.

The overtopping discharge per each overtopping box and the measured total wave height along the structure were analysed. In most of the tests, the overtopping boxes of both sides (from 0 to 1 m and from 7 ÷ 7.5 to 8 m) were not included in the calculation to avoid errors generated by model boundary effects. The calculation of the mean overtopping discharge starting from the measured overtopping volume follows geometrical rules as

-

For each test the berm length was calculated as a distance between the edge (crest) of the quay (sea dike) and the crown wall.

-

For each angle the projection of the berm length was measured on the wave direction; this is the effective berm length that the wave has to run before reaching the wall.

-

To calculate the mean overtopping for the entire quay some buffer zones at both edges of the structure were skipped (where possible model effects are noticed). For instance, in the case with no crown wall or crown wall on the quay edge, the entire quay length (8 m) was considered excluding the two overtopping boxes situated at the edges of the structure.

-

It was verified on video recordings that the peaks in the overtopping volume were not due to model effects (boundary reflection), but they were due to the wave attack.

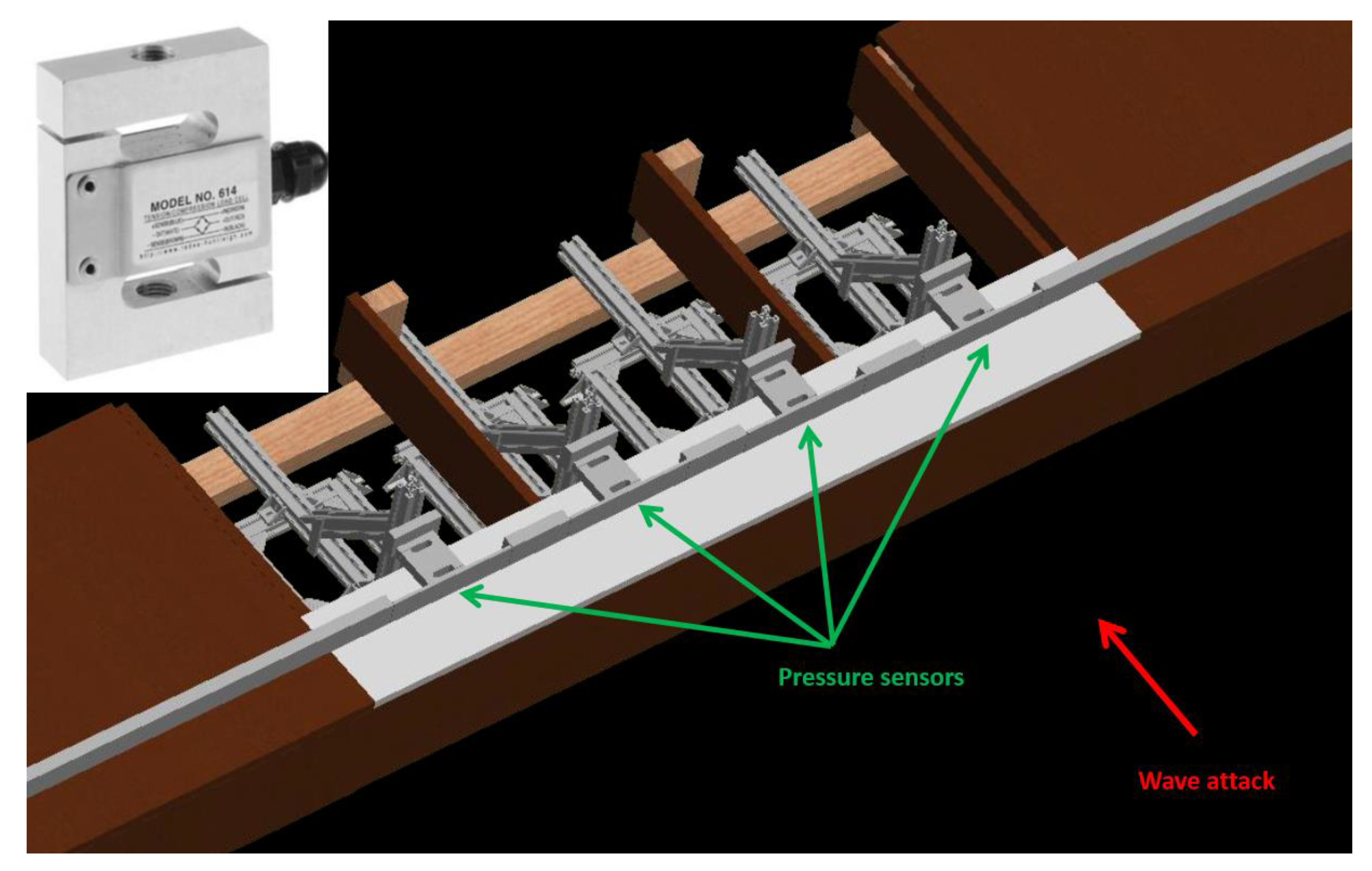
3.2. Model Settings of Force Test

The model built to investigate the reduction of the wave impact forces was very similar with the one for the overtopping reduction with the same 1:50 scale reduction. The structure (Figure 5) had a length of 8 m, a width of 0.6 m, and a height of 0.2 m. Based on the distribution of the largest wave heights and largest overtopping volumes along the structure an area of interest was selected approximately in the structure’s centre, where four force sensors (Tedea Huntleigh, Tension Compression Load Cells, Model 641) were placed to record the time series of the wave forces acting on the storm return wall (Figure 6 and Figure 7). A minimal distance between the wave maker and the structure of two wave lengths was respected for all tests.

Three positions of the structure in the basin were planned. Firstly, the structure was mounted in the central down part of the basin for the 0° wave direction. Secondly, the structure was moved towards the down left corner to optimize the distance to the wave maker and to obtain the angle of 45° without changing the position of the wave paddle. Thirdly, the structure was moved for the 80° wave angle attack (same positions as in Figure 3).

Instrumentation

The wave gauges were installed in a similar position as for the overtopping model and four force sensors were installed to measure the forces acting on the storm return wall at a frequency of 1 kHz (Figure 6 and Figure 7). Forty-four successful tests were performed (

Table 4. Summary of the test conditions for the force reduction.

Total Number of Tests			44
Wave directions	Wave height (Hm0)	Wave period (Tp)	Crest freeboard (Rc)	Storm return wall position
0°, 45°, 80°	1.04 to 4.54 m	10.2 to 12.9 s	0 to 3.0 m	0 to 25 m

).

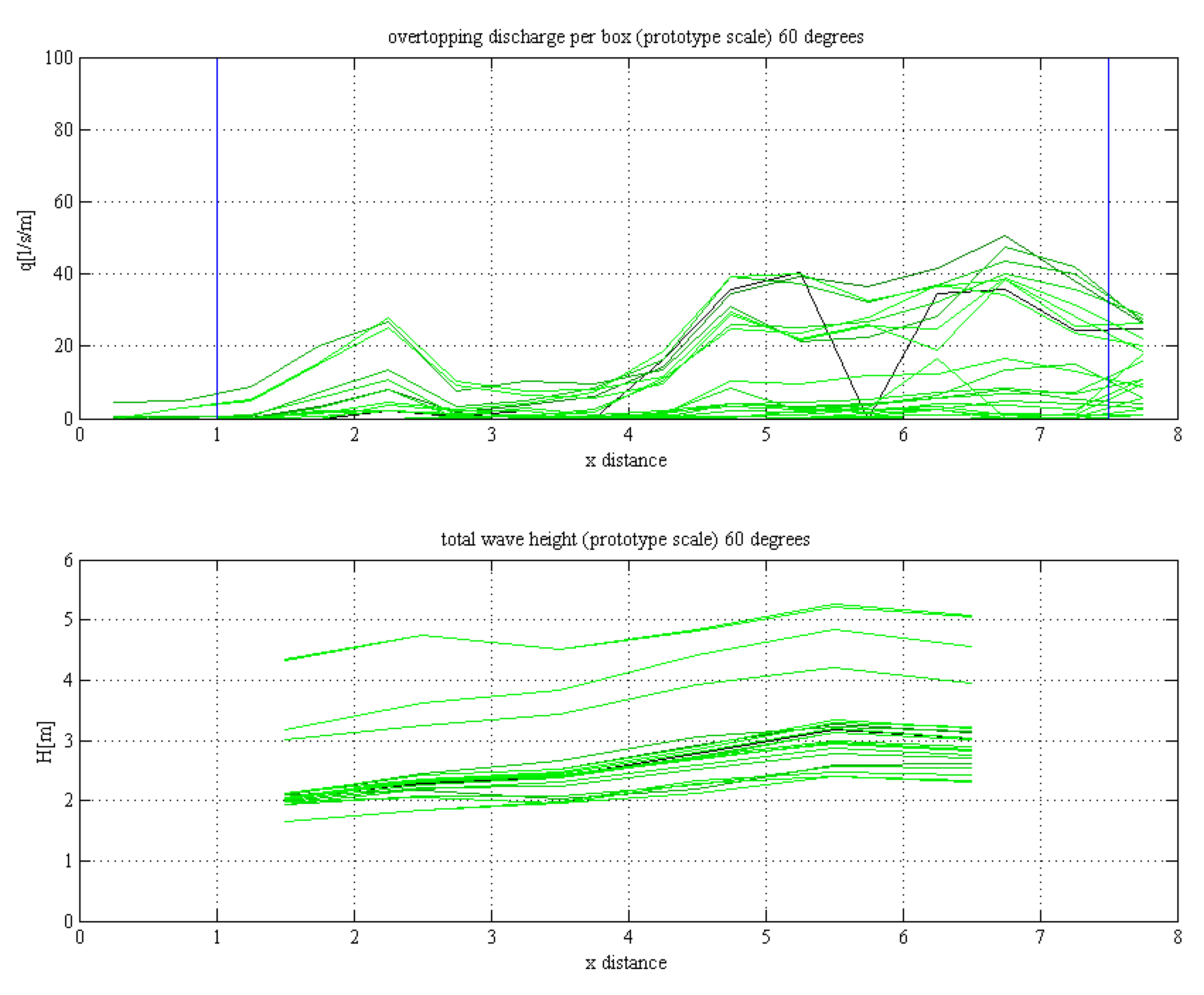
4. Results

4.1. Overtopping Reduction

The measured average wave overtopping has been compared with the predicted values using the existing formulas. A reduction coefficient for each direction has been assessed using the FHR tests results; both mean value and standard deviation of the reduction coefficient were calculated. The distribution of overtopping along the overtopping boxes was analyzed and correlated to the total wave height measured at the toe of the structure. For the analyses of the overtopping reduction due to the obliqueness, only tests without crest berm or with very short crest berm (5 m in prototype) were considered. The influence of long crest berms has been analyzed afterwards.

To cope with the spatial variation, the calculation of the mean overtopping discharge starting from the collected overtopping volume has been done based on a geometrical rule, summarized as follows:

• For each test, the berm length was calculated as a distance between the edge of the quay (sea dike) and the crown wall.
• For each angle, the projection of the berm length along the wave direction was assessed; this represents the effective berm length that the wave has to run before reaching the wall.
• Starting from the first corner of the dike, the projection of the effective berm along the quay gives the minimum distance before which no wave reaches the wall.
• The width considered to calculate the mean overtopping for the entire quay is equal to the quay length minus the calculated distance and some buffer zones at the edge (where possible model effects are noticed).

For incident wave height to be used in the formulas, the one coming from the star array after reflection analysis is employed since the information of the wave gauges placed along the dike only corresponds to total wave height (incident + reflected).

Physical model test results included in the CLASH database [11] similar to the test from the present study were used for comparison. In detail:

-

Sloping dike: only CLASH data with slope between 1:4 and 1:2 with gentle or no foreshore were considered.

-

Vertical quay: only tests with gentle or without foreshore were considered.

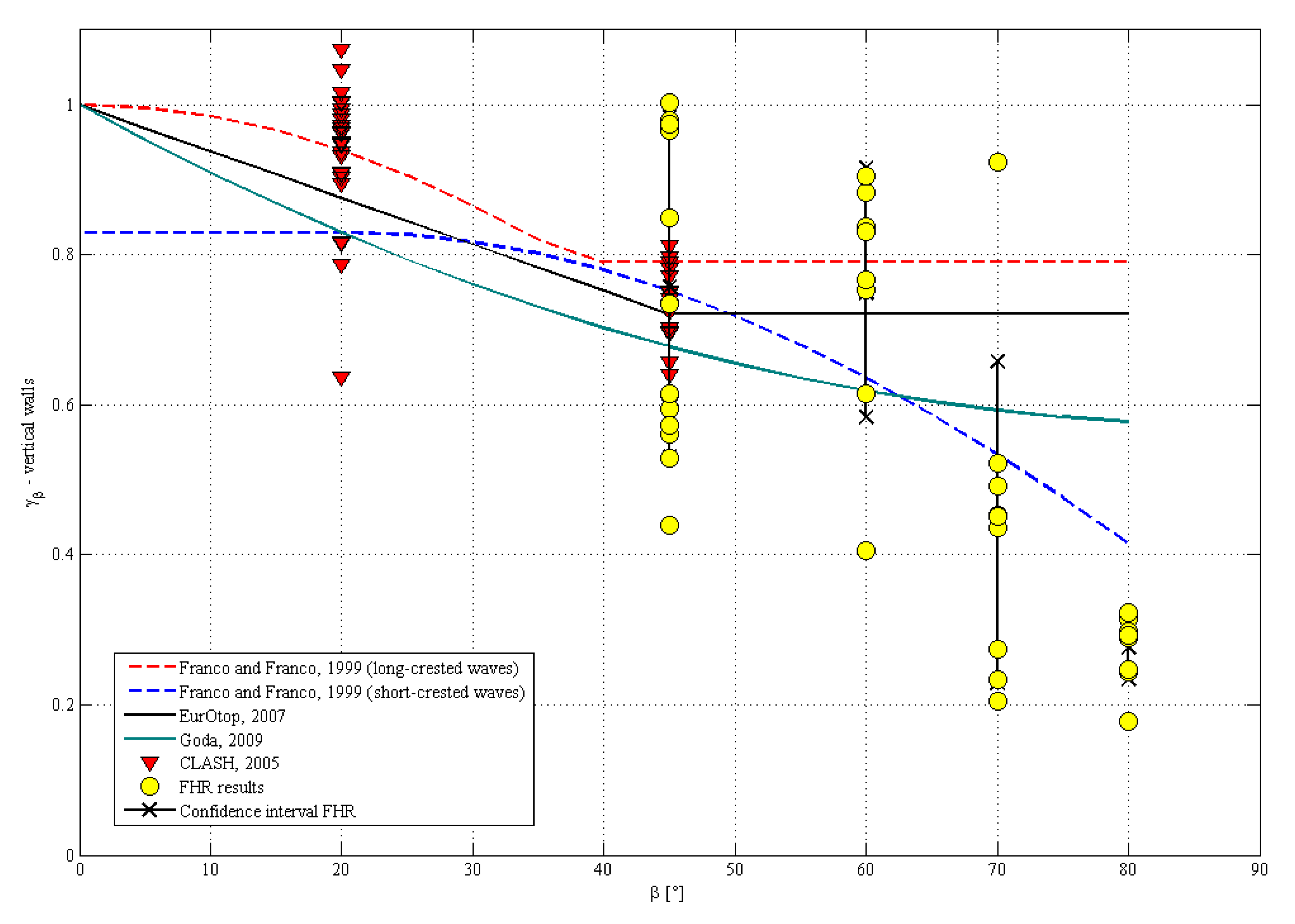
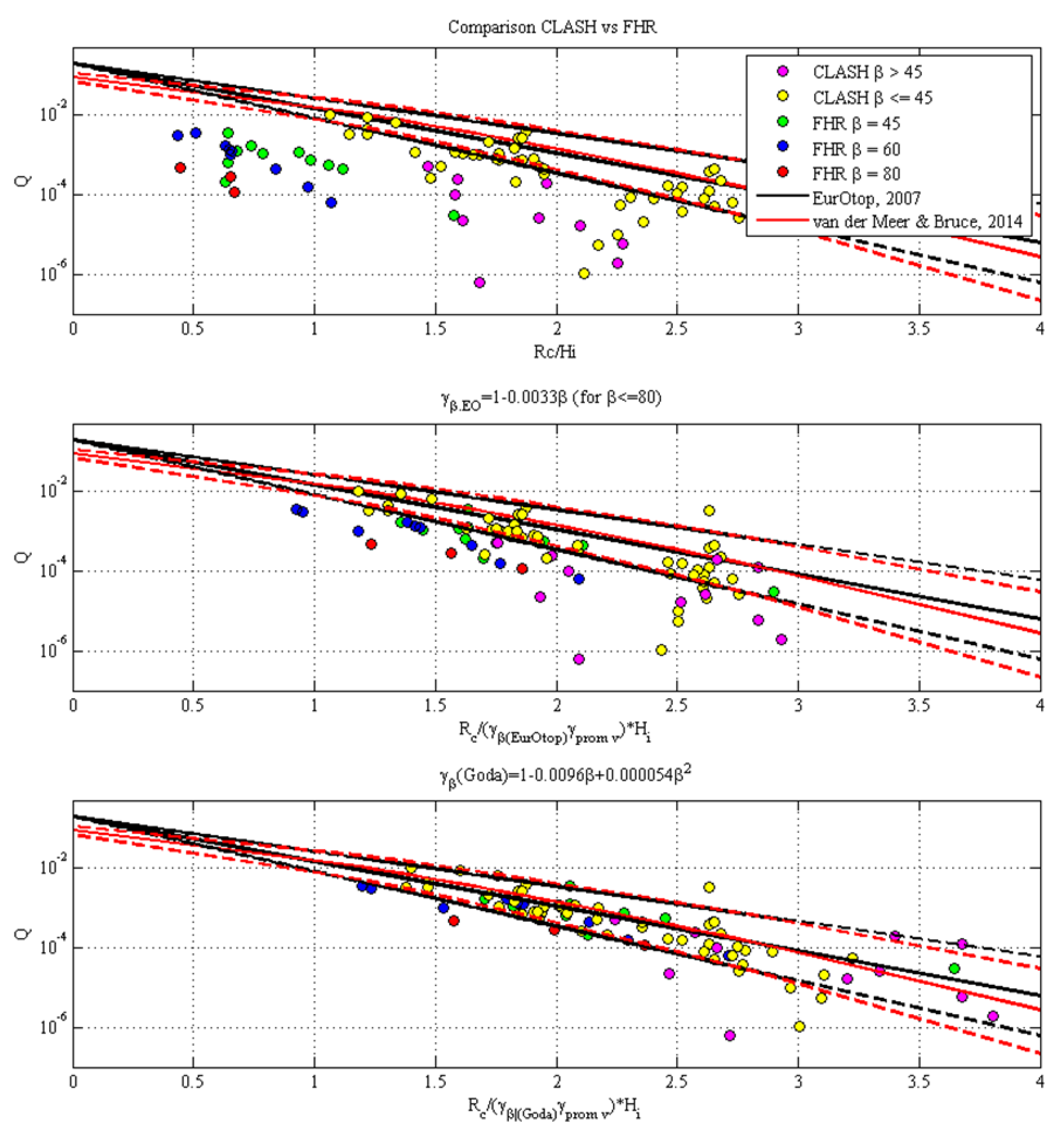
4.1.1. Vertical Quay Wall

The results of the tests indicate a clear decrease in the overtopping volumes with the increase of the wave angle. An increase of the overtopping volumes along the structure was observed for all cases, except for the perpendicular waves. In Figure 8, an example is shown, and the horizontal axis represent the quay extension, from 0 to 8.0 m, where the 0 is taken in the corner of the structure closest to the wave paddle. Each line plotted in every figure represents the results from one model test. The distribution of the wave overtopping along the vertical quay is generally consistent with the distribution of the total wave height at the toe.

However, stem wave formation can play a role in increasing wave height and consequently increasing overtopping along the structure. Research on stem waves along vertical wall with different researchers, ref. [16,17] reveal that the normalized significant stem wave height becomes large as the incident angle of wave become large. It was found also that the wave breaking suppresses the growth of the stem waves. These studies were based on wave tank experiments and on various numerical wave models with regular and irregular waves, but the predictions did not match very well the observations. In the present study the effect of the stem waves was not investigated since just one value of mean discharge along the whole quay was considered in the final analysis, a value measured by the instruments array.

Figure 9 shows the results of the FHR tests in a graph with the measured discharges plotted against the predicted ones, expressed in l/s/m (prototype scale). The plotted data include cases without a crest berm (distance of the wall from the edge of the quay, d_w, equal to 0 m) and with a crest berm (d_w larger than 0 m). The dash–dot lines indicate a prediction of 10 times larger and smaller with respect to the central line (ratio predicted/measured equal to 1:1). The formula overestimates the overtopping discharge for the 70° and 80° directions, while for the 0°, 45°, and 60° directions results are in reasonable agreement or within the above mentioned range.

The effects of the obliqueness on the overtopping discharge were evaluated calculating the reduction coefficient of each case, starting from Equation (14), as follows:

$${\mathsf{\gamma }}_{\mathsf{\beta }}=-2.6\frac{{\mathrm{R}}_{\mathrm{c}}}{{\mathrm{H}}_{\mathrm{m}0}}\frac{1}{\ln \left(\frac{\mathrm{q}}{0.04\sqrt{{\mathrm{gH}}_{\mathrm{m}0}^3}}\right)}$$

(14)

The calculation has been performed both for the FHR data and for the selected CLASH data. Figure 10 shows the variation of the reduction coefficient with the wave angle. The existing formulations were analyzed to calculate the reduction coefficient as function of the wave angle. Despite the scattering of the results (similar scatter can also be noticed in Goda, 2009) a certain trend can be identified.

The tests clearly show that the overtopping discharge is inversely proportional to the wave angle: the larger the wave angle, the smaller the wave overtopping. Different formulas propose constant values for the overtopping volumes for waves larger than 37° (long crested waves, [18], or 45° [1]). Franco and Franco formula [18] for short-crested waves seems to be the closest to FHR results, although the FHR tests were conducted using just long-crested waves. However, the differences due to the “short-crestedness” lie within the scattering of the formula, similar to previous studies [19]. Franco and Franco [18] stated that the directional spreading might allow reducing the freeboard with 30% in respect to cases with only long-crested waves.

The results of the experiments indicate that no formula, among those previously proposed predicts accurately the overtopping reduction. However, it is preferable to use the formula proposed by Goda [3] for large angles due to two main reasons:

(a)

the correction coefficient represents an upper limit (safe approach) for the present cases with very oblique waves, although not excessively high as EurOtop [1]; and

(b)

the expression for γ_β is applicable up to 80°, meanwhile EurOtop [1] indicates a constant value for wave angles larger than 45°.

The mean overtopping discharge is generally expressed by means of an exponential function as follows:

$$\frac{\mathrm{q}}{\sqrt{{\mathrm{gH}}_{\mathrm{m}0}^3}}=\mathrm{Aexp}\left(-\mathrm{B}\frac{{\mathrm{R}}_{\mathrm{c}}}{{\mathrm{H}}_{\mathrm{m}0}{\mathsf{\gamma }}_{\mathsf{\beta }}}\right)$$

(15)

where

• A = 0.040 and B = 2.6 in EurOtop [1],
• A = 0.033 and B = 2.3 in Goda [3], and
• A = 0.116 and B = 3.0 in Franco and Franco [18].

Note that the reduction coefficient γ_β is a function of the A and B coefficients. The differences between Goda [3] and EurOtop [1] can be considered negligible because the values of A and B coefficients are rather similar.

New values for the reduction coefficient are presented here based on the FHR data and it is proposed to be used for similar conditions (Table 3). The resulting values, based on the FHR measurements, including the standard deviation, can be summarized as follows:

• γ_β = 0.76 (σ = 0.23), for β = 45°;
• γ_β = 0.75 (σ = 0.17), for β = 60°;
• γ_β = 0.44 (σ = 0.21), for β = 70°; and
• γ_β = 0.28 (σ = 0.04), for β = 80°.

The calculated gamma value is the mean value for each wave angle. The mean values and standard deviation values were calculated for each wave angle starting from the results of γ_β estimated for each single test. The confidence interval represented in Figure 10 is calculated as ±σ with respect to the mean value. As general approach, the mean value of γ_β has to be used for design purposes. It can be noticed that the difference in the reduction coefficient between 0.72 (calculated value using EurOtop [1]) and 0.28 might cause a difference in the calculated discharge of at least 1 order of magnitude (10 times) in the selected data range.

Figure 11 shows the FHR data, the CLASH data and the EurOtop predictions in term of non-dimensional discharge Q = q/(g·H_m0³)^{^0.5}. Only the FHR cases with the wall on the edge of the quay are plotted in order to avoid misinterpretations due to the effects of the width of the crest berm. Three different plots are shown in Figure 11:

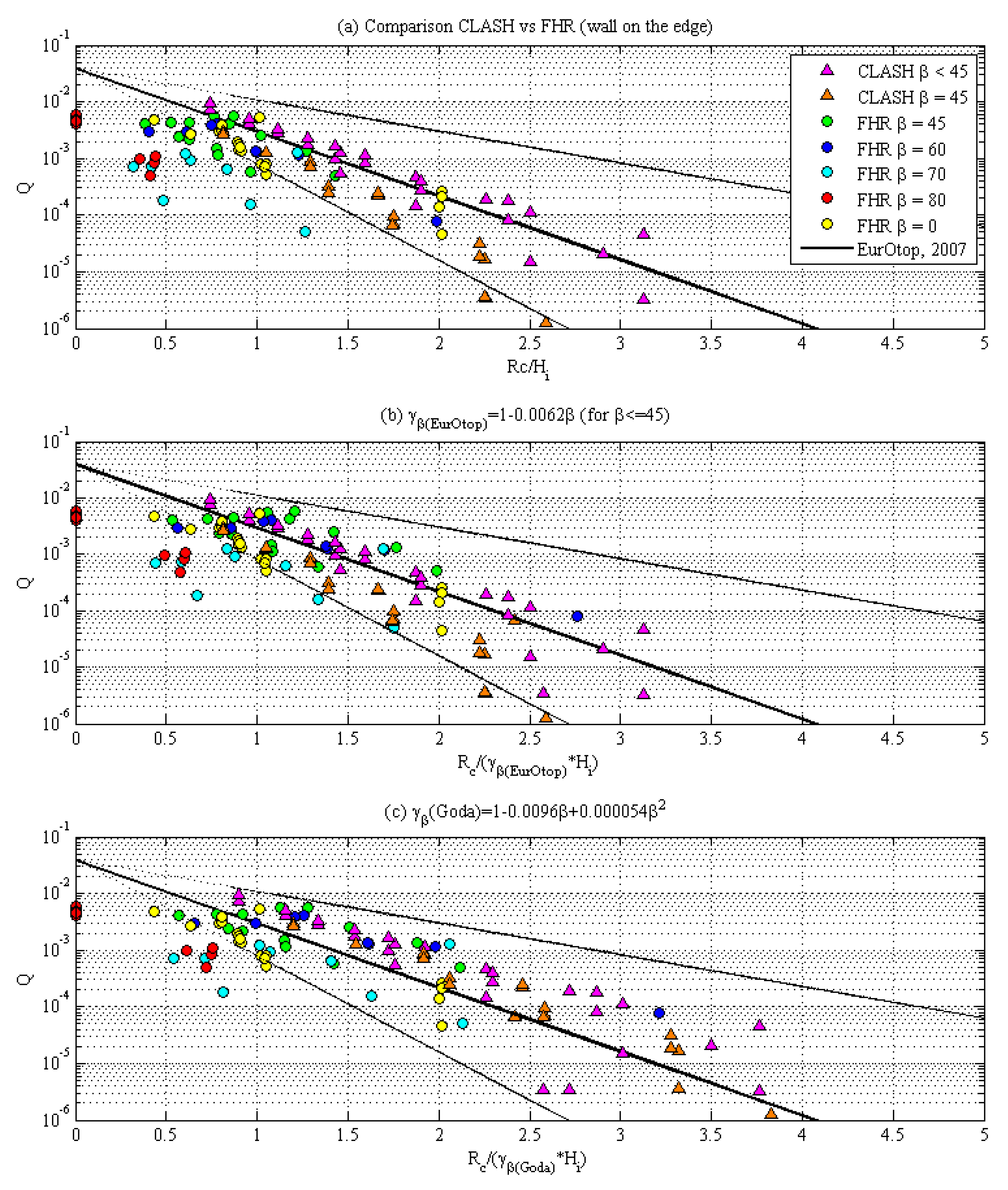
(a)

the values of Q are plotted against the non-dimensional freeboard R_c/H_i;

(b)

the values of Q are plotted against the non-dimensional freeboard R_c/H_iγ_β (EurOtop), where γβ (EurOtop) is the correction coefficient calculated using the EurOtop (2007) formula; and

(c)

(the values of Q are plotted against the non-dimensional freeboard Rc/Hiγβ(Goda), where γβ (Goda) is the correction coefficient calculated using the Goda [3] formula.

The use of Goda [3] formula is improving the wave overtopping prediction in case of oblique wave attack with respect to the EurOtop [1] formula. In most of the cases, especially for very oblique angles, the EurOtop formula seems to overestimate the overtopping, while using Goda correction factors the results are spread around the formula prediction and only few of them are still overestimated.

The analysis on the berm length effects (distance between the seaward edge of the quay and the storm wall) and on the wall height has been carried out. Figure 12 shows the non-dimensional overtopping discharge in function of two different non-dimensional parameters: (i) the ratio between the wall height and the incident wave height, (ii) the ratio between the berm length and 1.56T_p² that can be assumed as the wave length in deep water conditions. The combination of obliqueness, wall height and berm length made it challenging to have a clear view of the phenomena occurring at the structure. Despite the rather wide data scatter, there are clear differences between short or no berm layouts and wide berm layouts. A dependence on the berm length can be detected, the overtopping was reduced when the ratio of the berm length over the wave length was increased and this trend was clearer for larger wave angles. The waves travelled at the dike crest before approaching the storm wall and it was expected that the waves would refract on the berm, and therefore approach the wall with less obliqueness, but still not perpendicular. The distance travelled by the waves to reach the wall was larger for larger angles, so the amount of energy dissipated on the crest might have been larger. The configurations without berm, and with short berm length, 5 m in prototype, show a similar behaviour leading to larger overtopping discharge than the configurations with wider berms (25 m and 50 m in prototype).

4.1.2. Sloping Dike

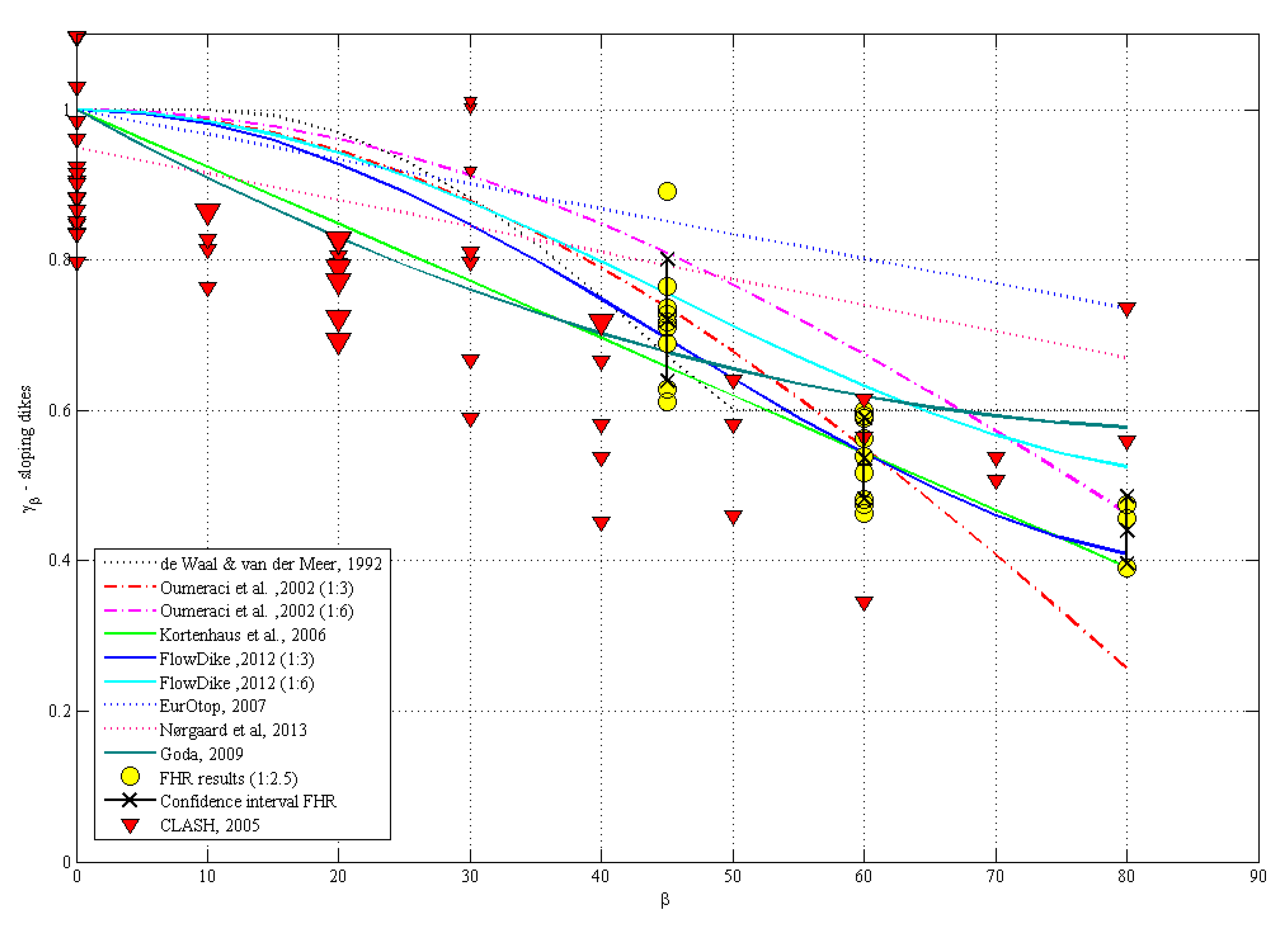
The results of the tests for a sloping dike are similar with those for a vertical quay, indicating the same decrease in the overtopping volumes with the increase of the wave angle. The measured overtopping discharges for FHR data are plotted in Figure 13 against the values predicted using Equations (3) and (4) [3]. As noticed in the previous cases, the formula seems to overestimate the overtopping discharge for very oblique wave attacks.

The effects of the obliqueness on the overtopping discharge were evaluated calculating the reduction coefficient of each case starting from Equation (3) as follows:

$${\mathsf{\gamma }}_{\mathsf{\beta }}=-2.6\frac{{\mathrm{R}}_{\mathrm{c}}}{{\mathrm{H}}_{\mathrm{m}0}{\mathsf{\gamma }}_{\mathrm{prom}\_\mathrm{v}}}\frac{1}{\ln \left(\frac{\mathrm{q}}{0.2\sqrt{{\mathrm{gH}}_{\mathrm{m}0}^3}}\right)}$$

(16)

The calculation has been performed both for the FHR data and for the selected CLASH data. Three different datasets were selected from CLASH (for only non-breaking wave conditions):

• Dataset 030 [20]: 1:2 slope with 1:20 foreshore;
• Dataset 220 [21]: 1:2.5 slope with 1:1000 foreshore; and
• Dataset 222 [21]: it includes data for 1:2.5 and 1:4 slope with 1:1000 foreshore.

Figure 14 shows the variation of the reduction coefficient with the wave angle. The CLASH data are labelled as red triangles whose size is proportional to the slope (e.g., 1:2 larger size than 1:4). Several proposed formulations were analyzed to calculate the reduction coefficient as function of the wave angle. The formulas predictions and the confidence interval for the FHR data are also plotted.

The results display a scattered distribution, but similar scatters can be observed in other studies performed in similar conditions [3,22]. However, a certain trend is visible, and the reduction of the FHR data are in agreement with the reduction of the CLASH data. Figure 15 shows the FHR data, the CLASH data and the EurOtop predictions. Three different plots are depicted:

(a)

the values of Q are plotted against the non-dimensional freeboard R_c/H_i;

(b)

the values of Q are plotted against the non-dimensional freeboard R_c/H_iγ_β(EurOtop)γ_{prom_v}, where γ_β(EurOtop) is the correction coefficient calculated using the EurOtop [1] formula and γ_{prom_v} is the reduction coefficient calculated by means of Van Doorslaer [9]; and

(c)

the values of Q are plotted against the non-dimensional freeboard R_c/H_iγ_β(Goda)γ_{prom_v}, where γ_β(Goda) is the correction coefficient calculated using the Goda [3] formula.

Similar improvement of the wave overtopping prediction, as in the case of a vertical quay when Goda formula is used over EurOtop formula, can be observed for sloping dike cases.

The influence of the geometrical layout is not easily detected due to interreference between three involved parameters: obliqueness, wall height, and berm length. However, the existence of the wall significantly reduces the wave overtopping for all cases. The position of the storm return wall is also important, larger berms leading to a decrease in the overtopping volumes.

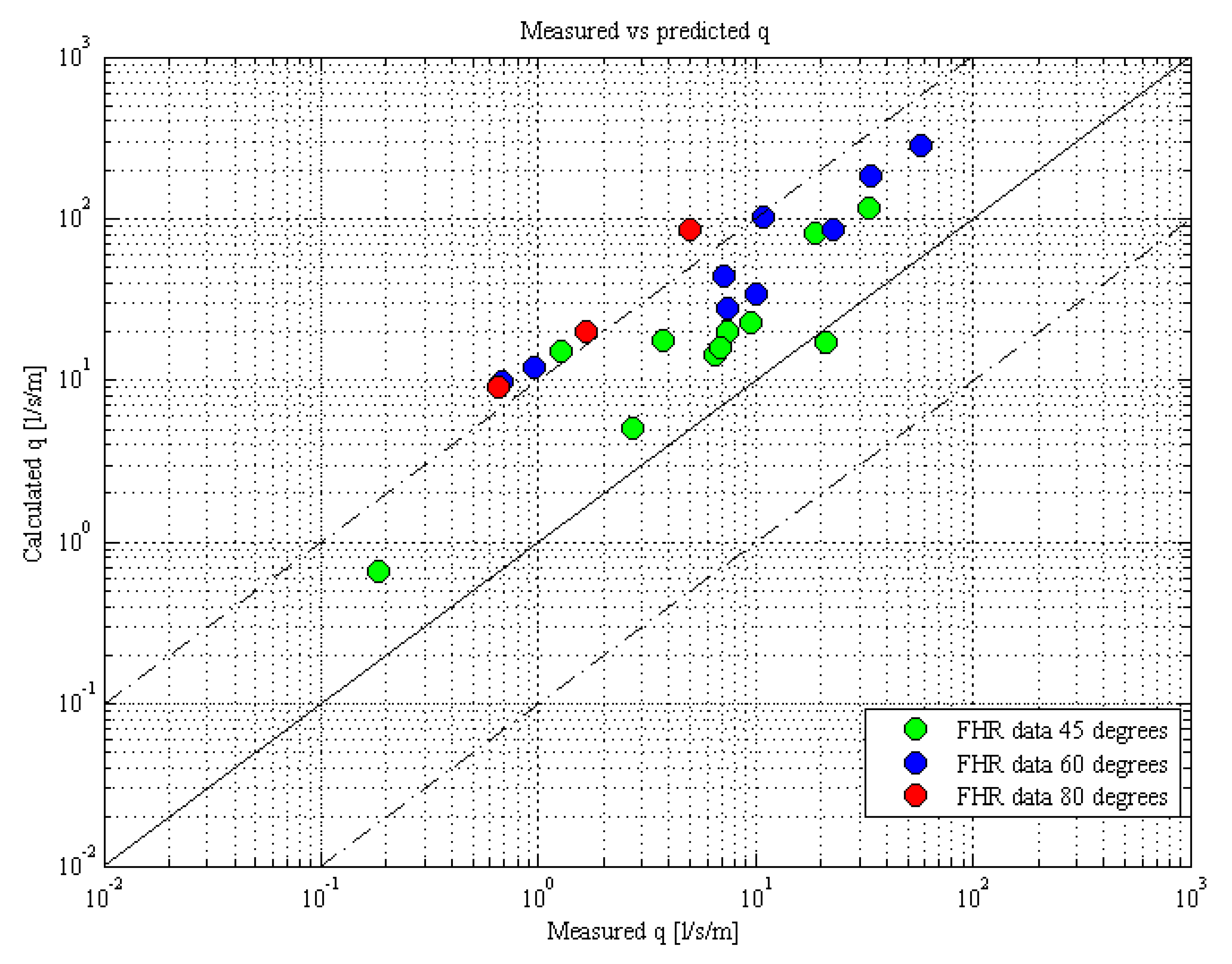
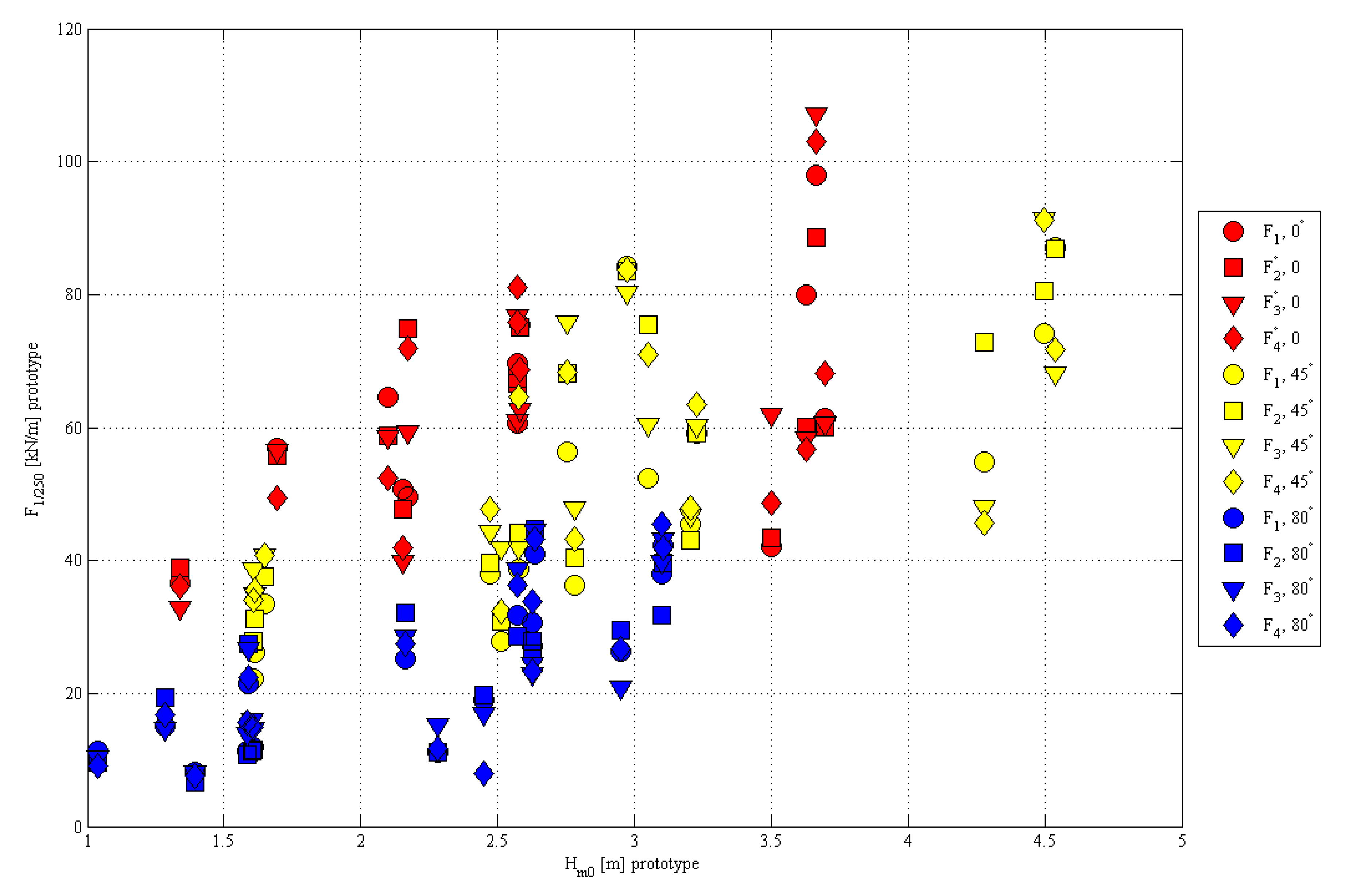
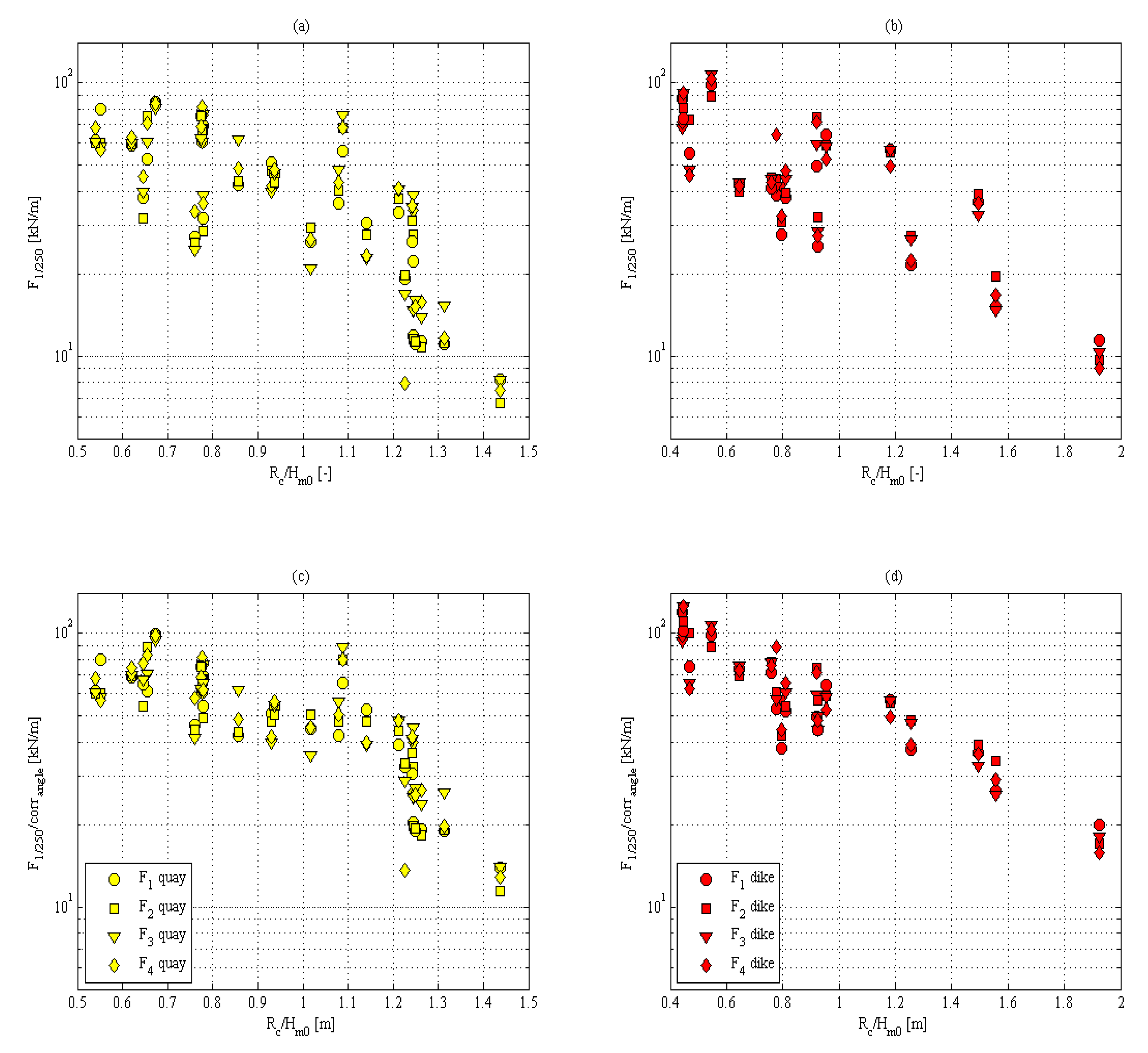
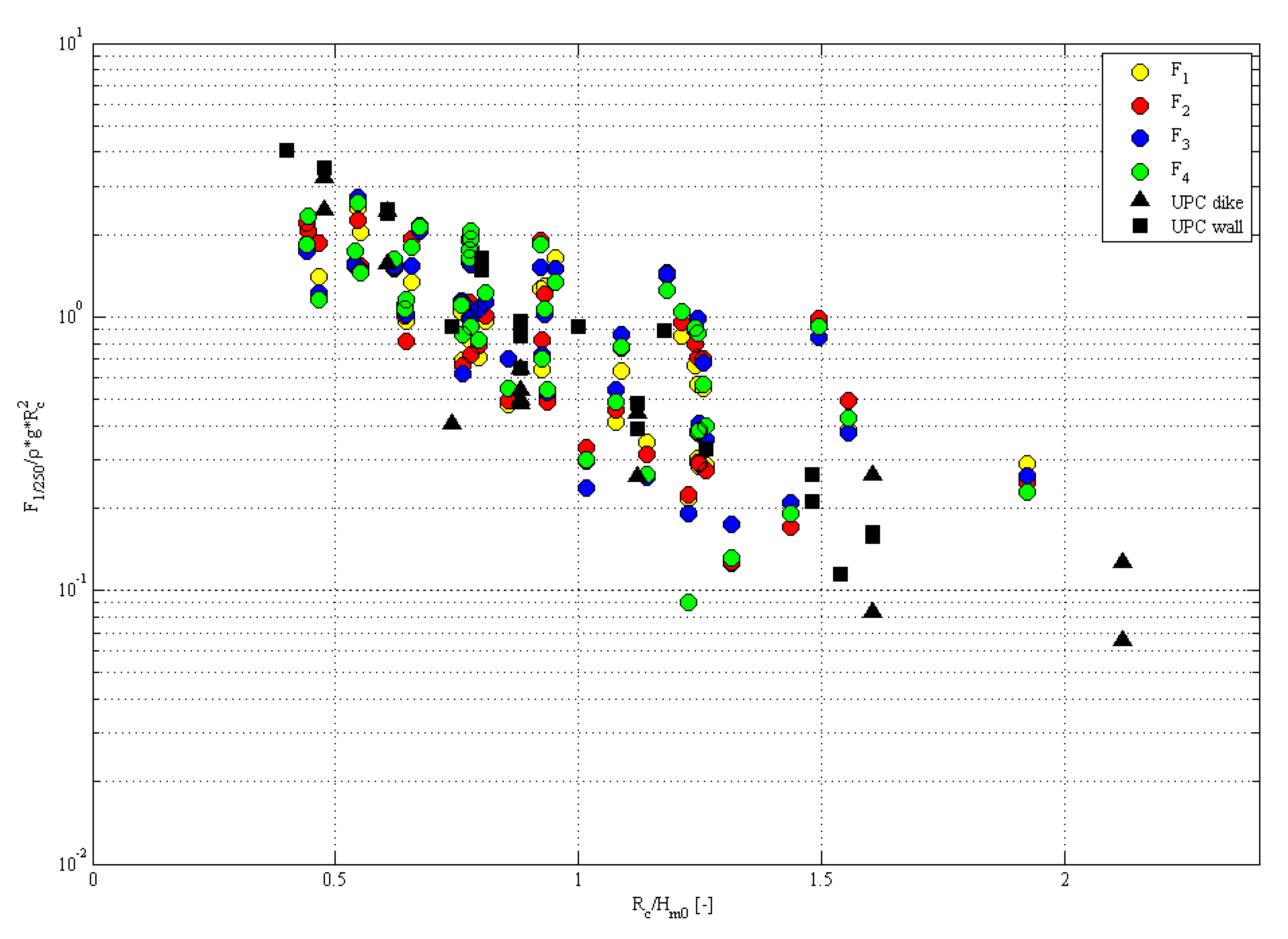
4.2. Force Reduction

The measured forces are plotted in Figure 16 (in prototype scale both vertical quay and sloping dike) in function of the incident significant wave height. The colors indicate the wave angle, respectively red for 0°, yellow for 45°, and blue for 80°. The different shapes indicate the results from each different load cell; this underlines that, despite the waves are long-crested, the forces exerted along the structure have a certain variability. As expected, the forces increase with the wave height. It is clear that the 0° cases result in larger forces than the 45° case, and the 80° cases have the lowest forces. For the same wave height, the very oblique cases present in average a value of the wave force that is almost half of the perpendicular case.

The data were analyzed to define an analytical expression for the reduction factor. This coefficient is the ratio between the force due to an oblique wave attack over the force in case of perpendicular waves reaching the structure. The reduction factor expresses how much the data from cases with oblique attack should be corrected to be in line with a 0° case that present the same hydraulics boundary conditions (except from the obliqueness).

Two different expressions, respectively for quay walls and dikes, were found:

$${\mathsf{\gamma }}_{\mathrm{quay}}=\frac{{\mathrm{F}}_{\mathrm{quay},\mathsf{\beta }>0}}{{\mathrm{F}}_{\mathrm{quay},\mathsf{\beta }=0}}=0.5·\left(1+\cos \mathsf{\beta }\right)$$

(17)

$${\mathsf{\gamma }}_{\mathrm{dike}}=\frac{{\mathrm{F}}_{\mathrm{dike},\mathsf{\beta }>0}}{{\mathrm{F}}_{\mathrm{dike},\mathsf{\beta }=0}}=\exp \left(-0.007\mathsf{\beta }\right)$$

(18)

where β is the wave direction relative to the structure (perpendicular wave direction = 0°, angle expressed in degrees). The variation of the reduction factors as function of the wave angle is depicted in Figure 17. The expression for quay walls is corresponding to the formula for caisson breakwaters proposed by Goda [23].

The two expressions for the reduction factor could certainly be improved if additional data with other wave angles than 45° and 80° were available. However, the new proposed expressions can already be considered as a significant improvement in the prediction. In Figure 18 the measured wave forces are plotted as a function of the relative freeboard. Four figures are reported, two for the dike cases and two for the quay wall cases. In detail:

(a)

measured wave force on the storm wall for the quay wall layout;

(b)

measured wave force on the storm wall for the sea dike layout;

(c)

measured wave force on the storm wall for the quay wall layout, including the correction with the proposed reduction factor for wave obliqueness; and

(d)

measured wave force on the storm wall for the sea dike layout, including the correction with the proposed reduction factor for wave obliqueness.

The scatter in the wave forces is significantly reduced if the wave force is corrected using the reduction factor proposed above. This improvement was also quantified by the relative standard deviation for each case (μ’ = μ/σ): (a) μ’ = 7.9%; (b) μ’ = 7.0%; (c) μ’ = 8.8%; and (d) μ’ = 4.7%.

The analysis of the overall results finally suggests that in case of very oblique wave attack (obliqueness between 70° and 80°), the expected force on the storm wall range between 55% to 65% of the value in case of perpendicular wave attack.

The results of the FHR tests are compared to predictions of the formula proposed by Van Doorslaer et al. [10] for sea dikes, regardless of its range of applicability (e.g., wall position and wall height are different). Figure 19 depicts the variation of the non-dimensional quantity F_1/250/ρgR_c² as function of the relative freeboard, both for FHR and UPC results. A common trend between the two experimental datasets can be noticed, despite of a certain scatter in the FHR results, mainly due to the different wave angles.

Equation (13) was applied to the FHR and UPC data; only FHR cases with 0° were initially considered for comparison, as the UPC data refer to perpendicular wave attack. The results of the are plotted in Figure 20. Generally, Equation (13) underestimates the force for FHR cases probably due to different wall height between UPC data and FHR data, respectively 1.2 m and 2.0 m (in prototype scale). Higher walls would lead to smaller overtopping rates and bigger reflection exerted by the storm wall with consequent higher forces on the same wall.

In the next step, Equation (13) was applied to all FHR data and the results are reported in Figure 21, both without and with, application of the reduction factors (Equations (17) and (18)) for wave obliqueness. Without correction, the prediction showed a large scatter, while the application of the reduction factor reduced significantly the scatter and improved the predictions. Nevertheless, the estimated forces are still slightly smaller than the measured ones and it can be concluded that the correction applied to take into account the wave obliqueness improves the predicted forces.

5. Conclusions

The present study describes the setup and the results of physical model tests carried out at FHR on wave overtopping generated by perpendicular and very oblique waves, based on the generic configurations and conditions at Belgian harbors. A set of different wave angles has been tested: for a vertical quay layout: 0°, 45°, 60°, 70°, and 80° and for the dike layout: 45°, 60°, and 80° were investigated.

The reduction in overtopping discharge has been quantified and the results were compared with similar tests in the CLASH database [11] and with predictions by several semi-empirical formulas and correction factors from literature.

The influences of the storm wall height and the crest berm width were investigated together with the effect of wave obliqueness.

The analysis of the results for the vertical quay and sloping dike layouts leads to the following conclusions:

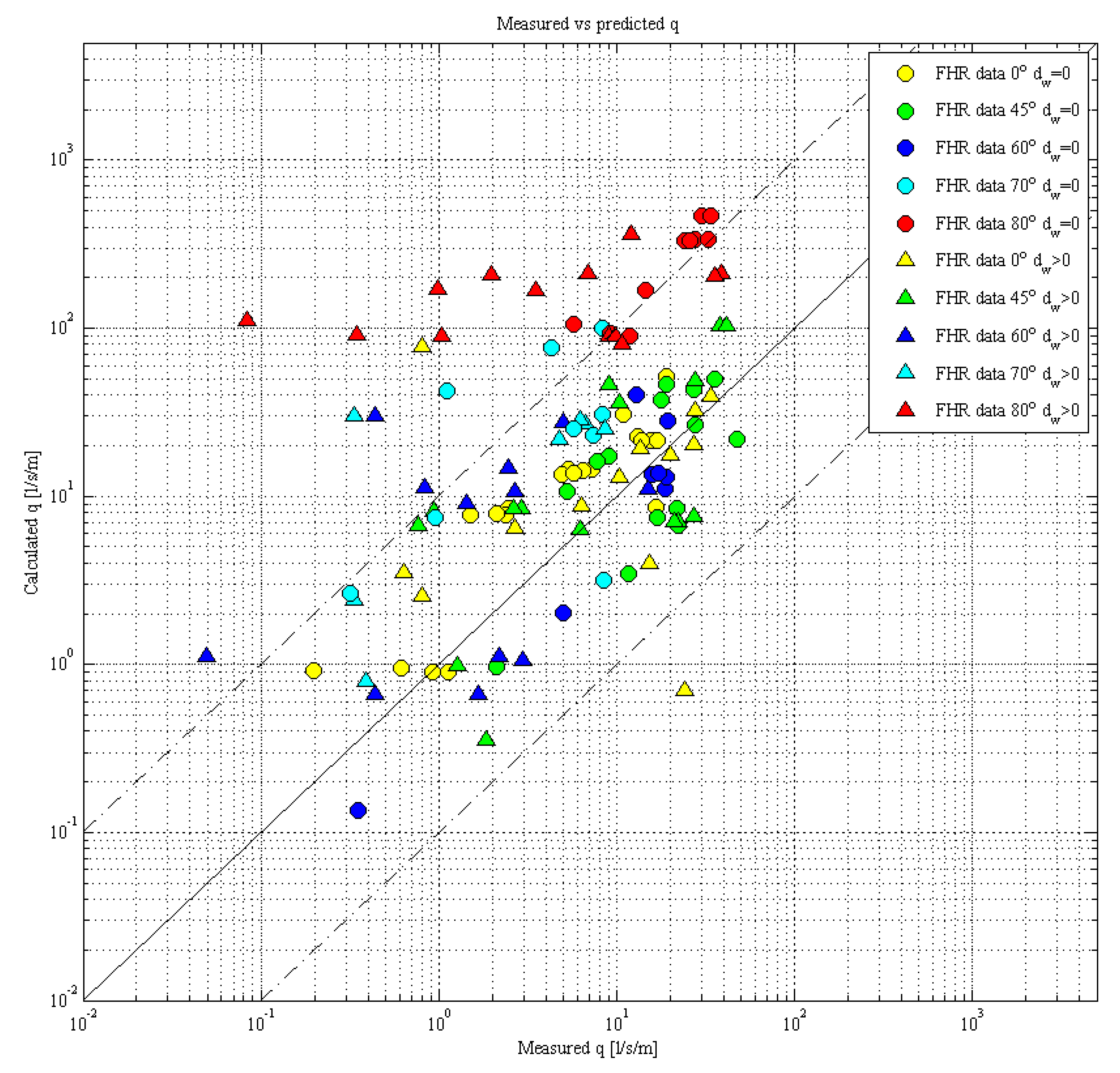
• The EurOtop formula [1] generally overestimates the overtopping discharge for large wave obliqueness.
• The values of the reduction factor γ_β calculated for the vertical quay layout are equal to 0.76, 0.75, 0.44, and 0.28, respectively, for 45°, 60°, 70° and 80°.
• The values of the reduction factor γ_β calculated for the sloping dike layout are equal to 0.72, 0.54 and 0.44 respectively for 45°, 60° and 80°.
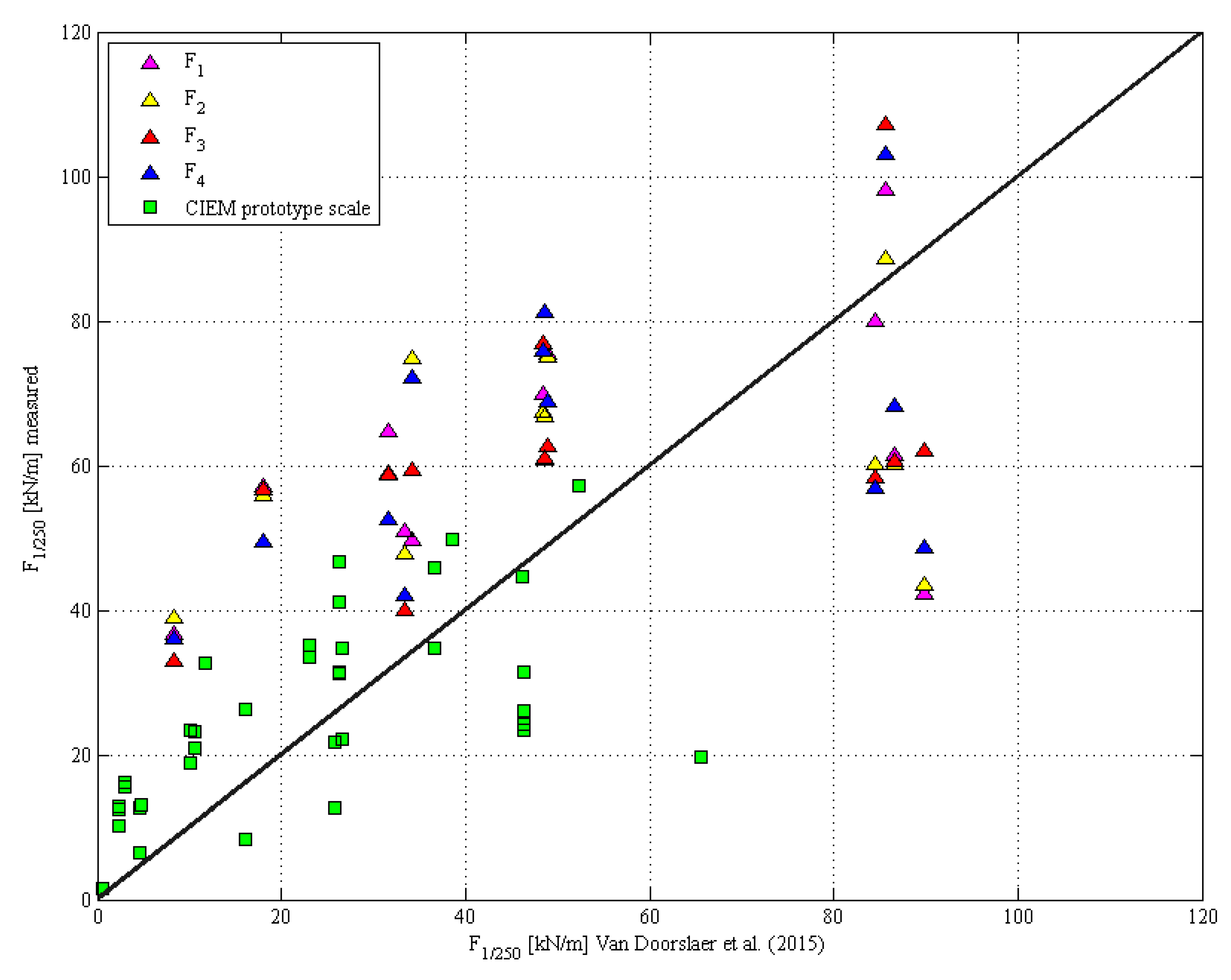
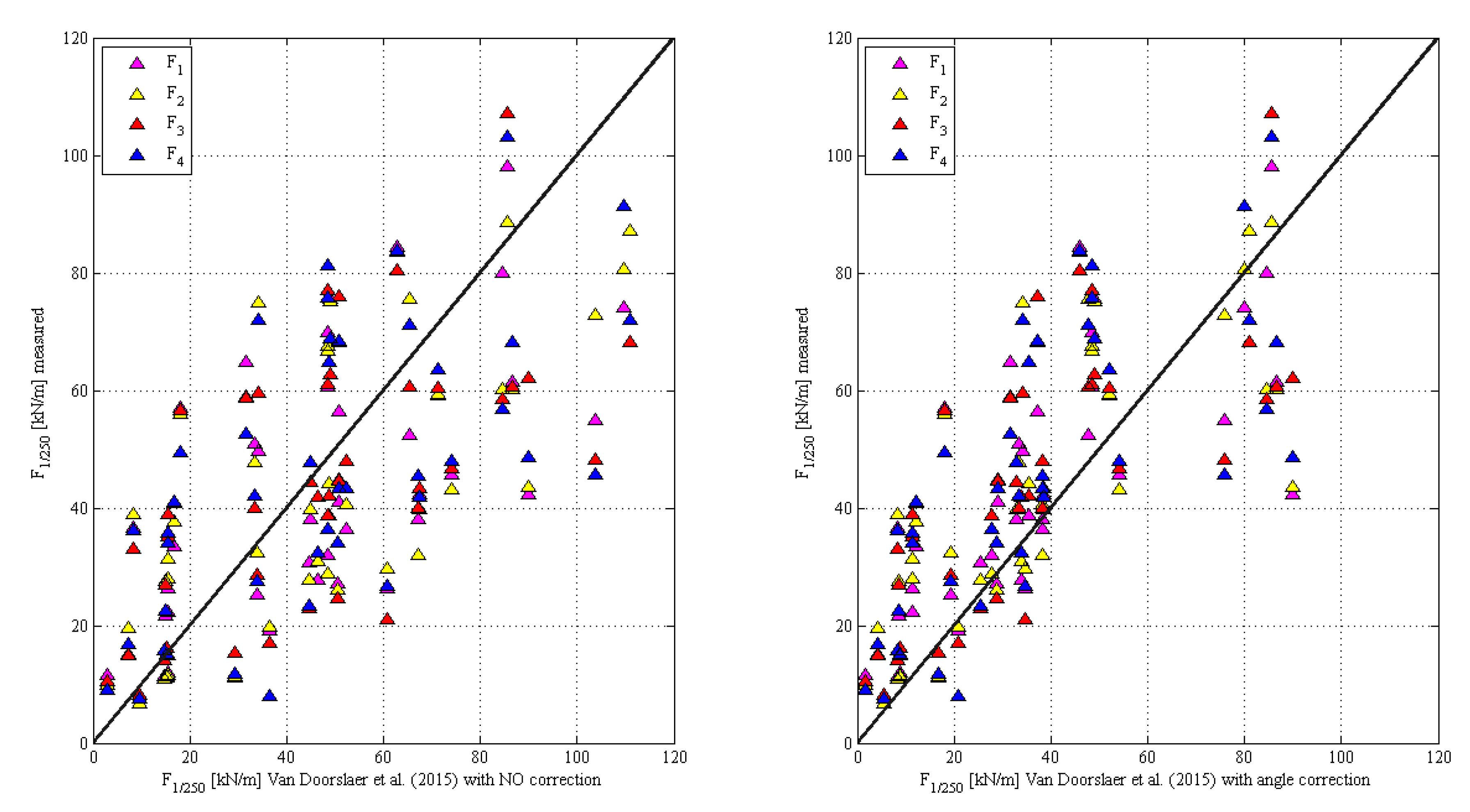
• A rather large scatter is present in the results similar to the results presented in previous studies [3].
• The expression of γ_β presented by Goda [3] is finally proposed as a good compromise between accuracy (in comparison with physical model results) and a certain safety in the design of the storm walls.
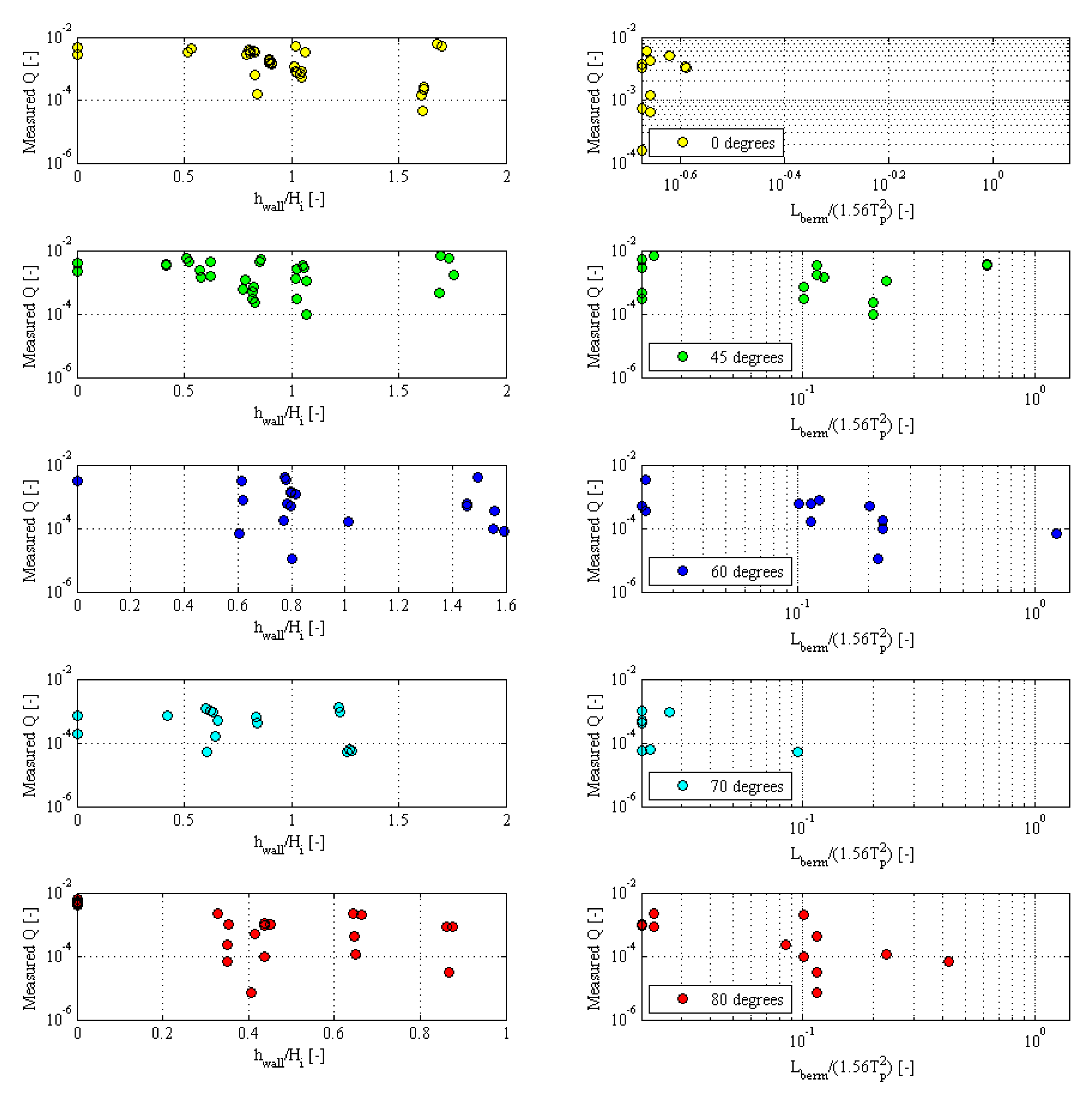
• The high obliqueness combined with long berms on the crest (comparable with the wave length) leads to very low or zero overtopping discharge.
• The berm length (ranging from 0 to 50 m) has a larger influence on the overtopping discharge than the wall height (ranging from 1 to 2 m).

Tests were performed to identify the wave force impact reducing due to wave obliqueness both for sea dike and for quay wall layouts. The wall height was 2.0 m (in prototype scale) and it was located at three different distances from the seaward edge of the main structure (berm).

The results indicate that for high wave obliqueness the force reduction in case of very oblique waves is 0.55–0.65 times the wave forces for similar wave conditions, but for perpendicular wave attack. Two reduction factors were defined, respectively for the sea dike and the vertical quay wall layout as presented in Equations (17) and (18). Finally, the formula of Van Doorslaer et al. [10] was applied, confirming that the use of the above mentioned reduction factors reduces the uncertainties in the wave force predictions due to the effects of the wave obliqueness.

A significant knowledge gap regarding the quantification of overtopping and impact forces reduction due to oblique waves attack was filled by adding valuable data to the scarce existing literature and improving the predicting formulas. These formulas were applied to several specific situations in Belgium [24,25] and they can be used in similar settings worldwide.

Due to the limited amount of available data, the relationship between wave obliqueness and other variables such as wall position has not been analyzed in the present study. Further studies on wave forces on storm walls on top of sea dikes or quay walls should take into account this reduction if the waves are approaching the structure with an angle larger than 45°. Since it was considered limited, the influence of the stem waves formed along the structure on the overtopping were not investigated during this study and further investigation is recommended.