Validation of RANS Modelling for Wave Interactions with Sea Dikes on Shallow Foreshores Using a Large-Scale Experimental Dataset
Abstract
1. Introduction
2. Methods
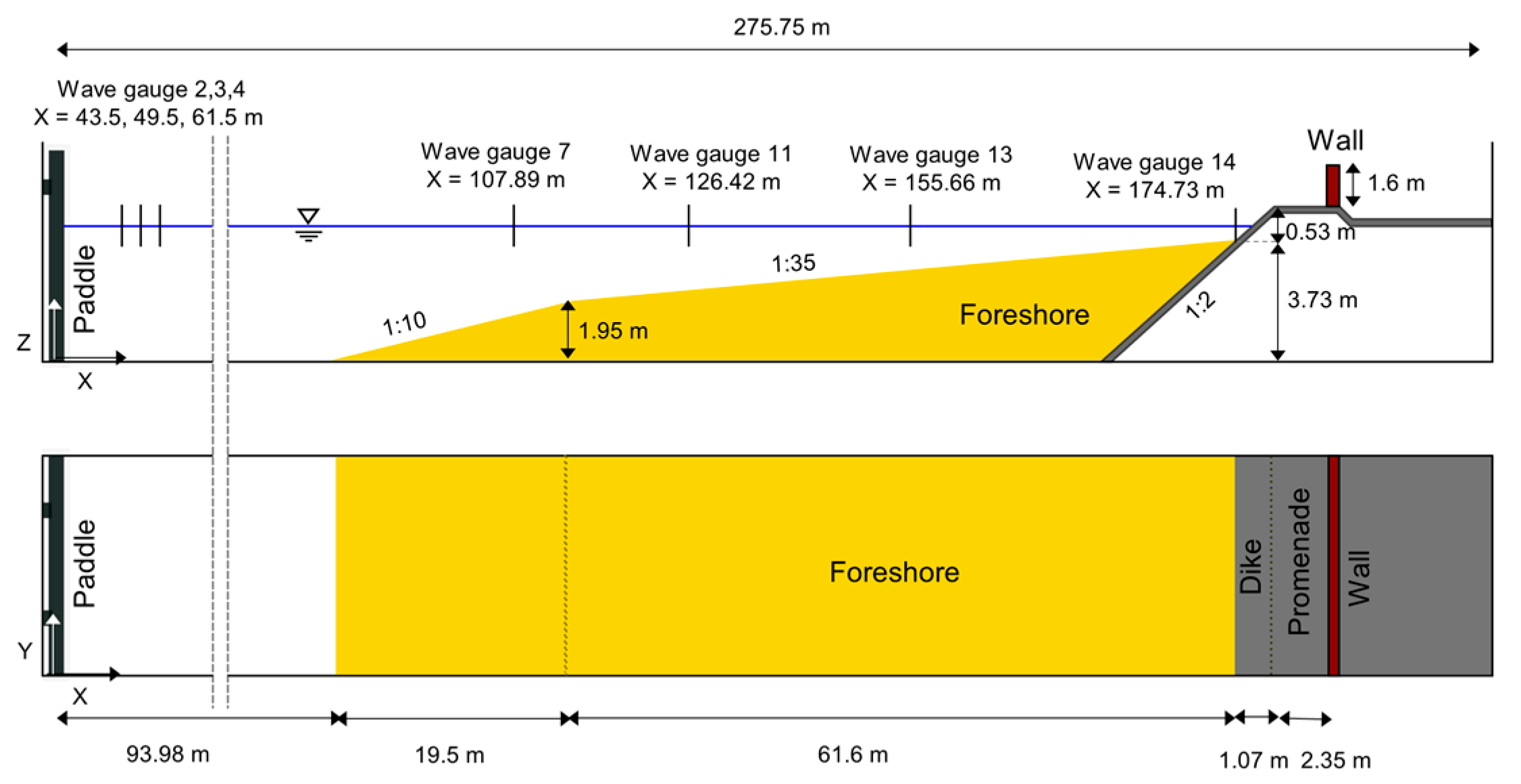
2.1. Large-Scale Laboratory Experiments
2.2. Numerical Model
2.2.1. Model Description
2.2.2. Computational Domain and Mesh
2.2.3. Boundary Conditions
2.2.4. Data Sampling and Processing
2.3. Validation Method
- unnecessarily penalising the numerical model performance for an experimental measurement error. For example, in the experimentally measured and processed time series of p and Fx, often some residual instrumental noise or oscillations persisted during such non-event (or “dry”) times;
- unnecessarily rewarding the model performance towards (almost) perfect agreement. For example, during the time between impacts no water reaches the wall and model performance would be perfect during such times (disregarding measurement noise).
3. Results
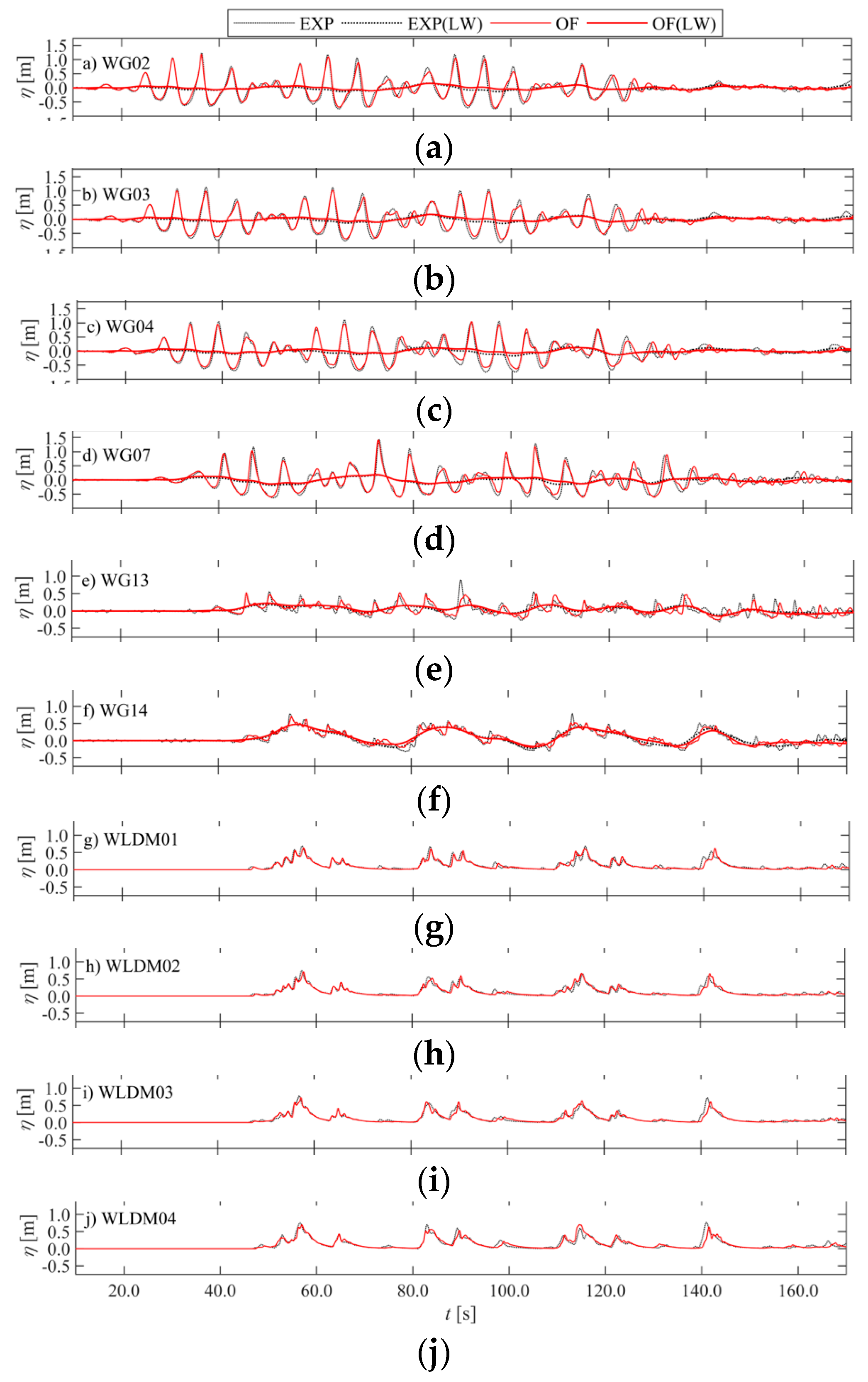
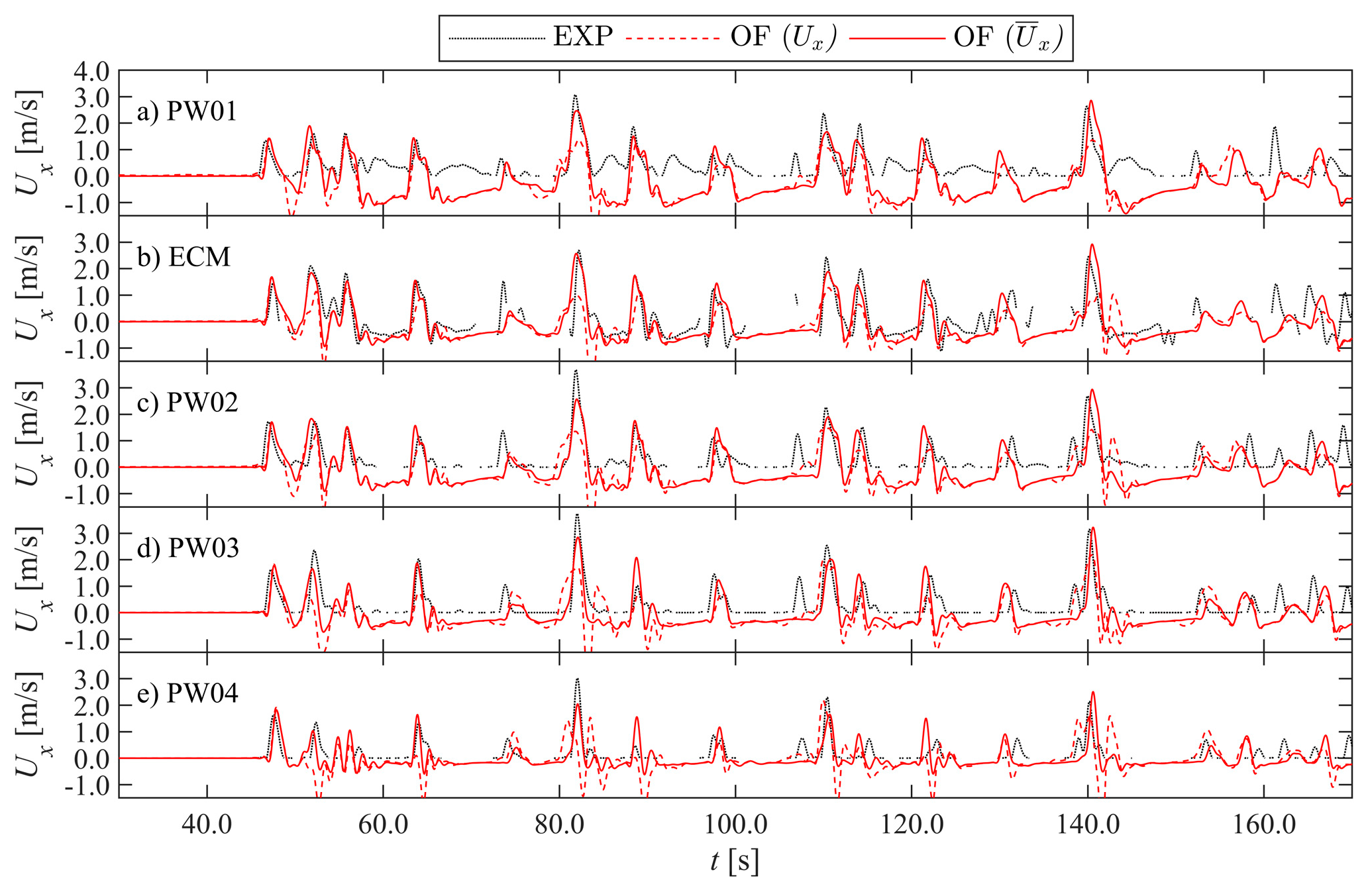
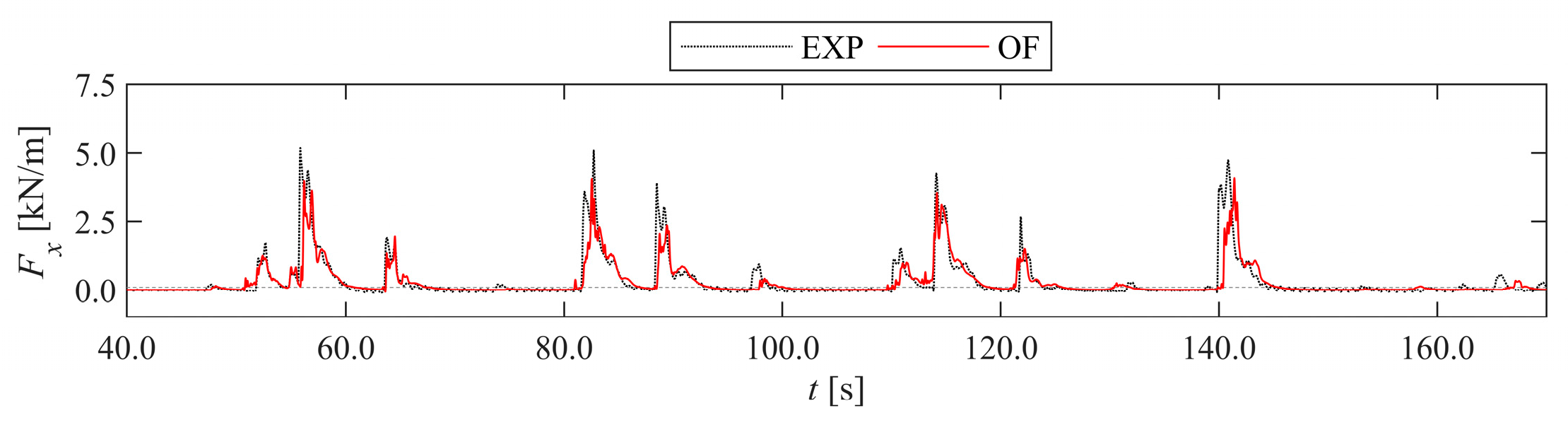
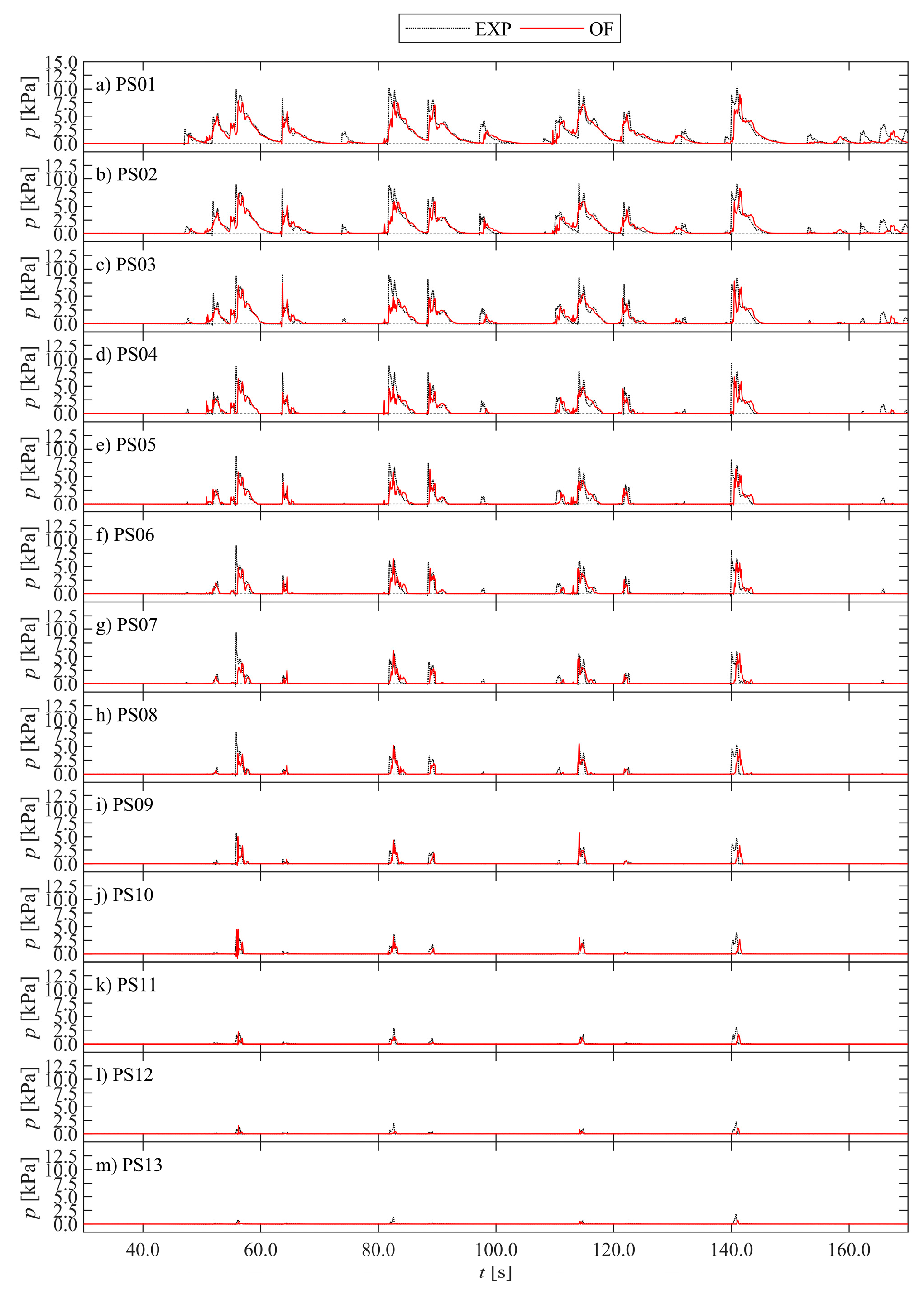
3.1. Time Series
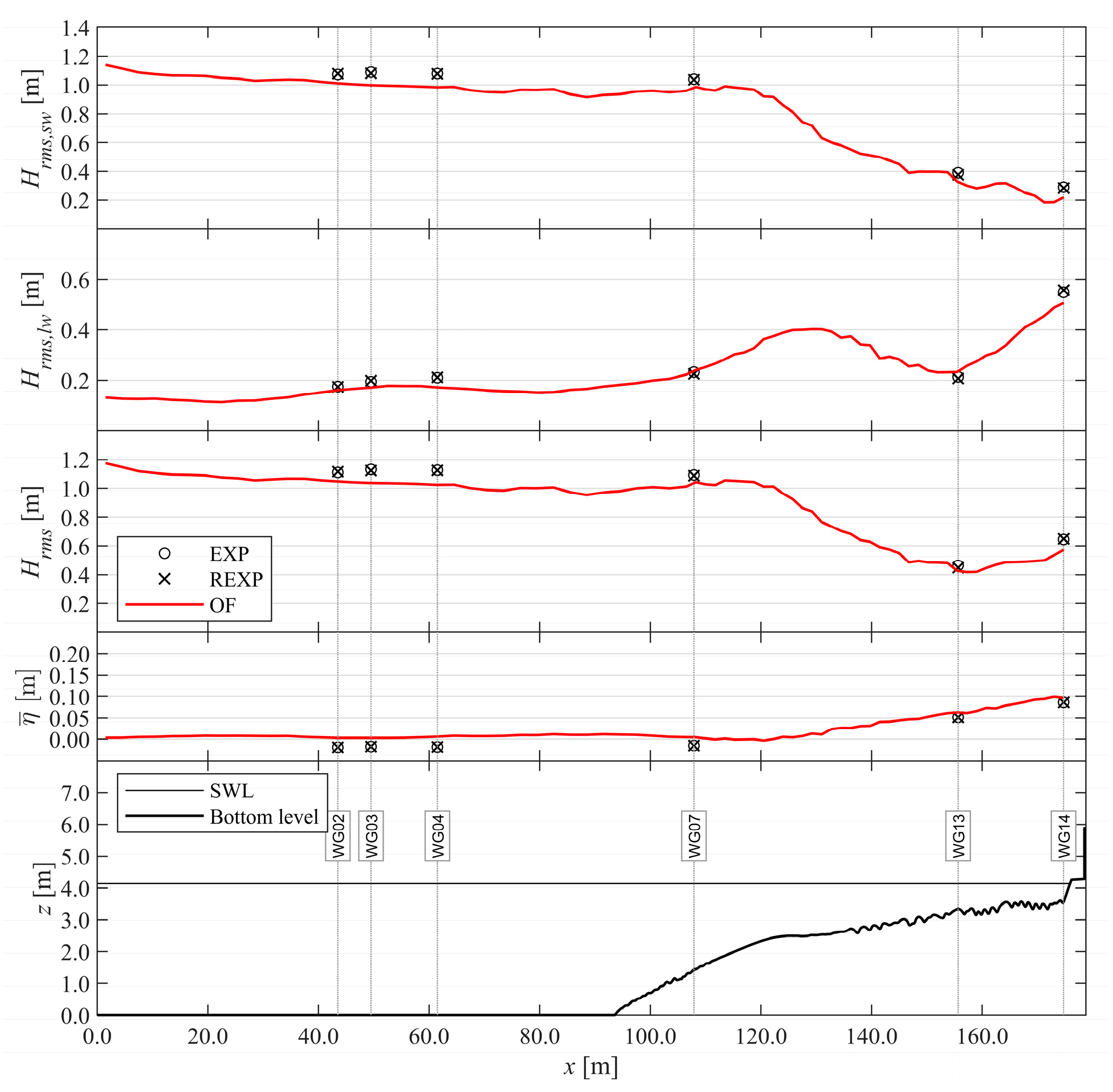
3.2. Wave Characteristics
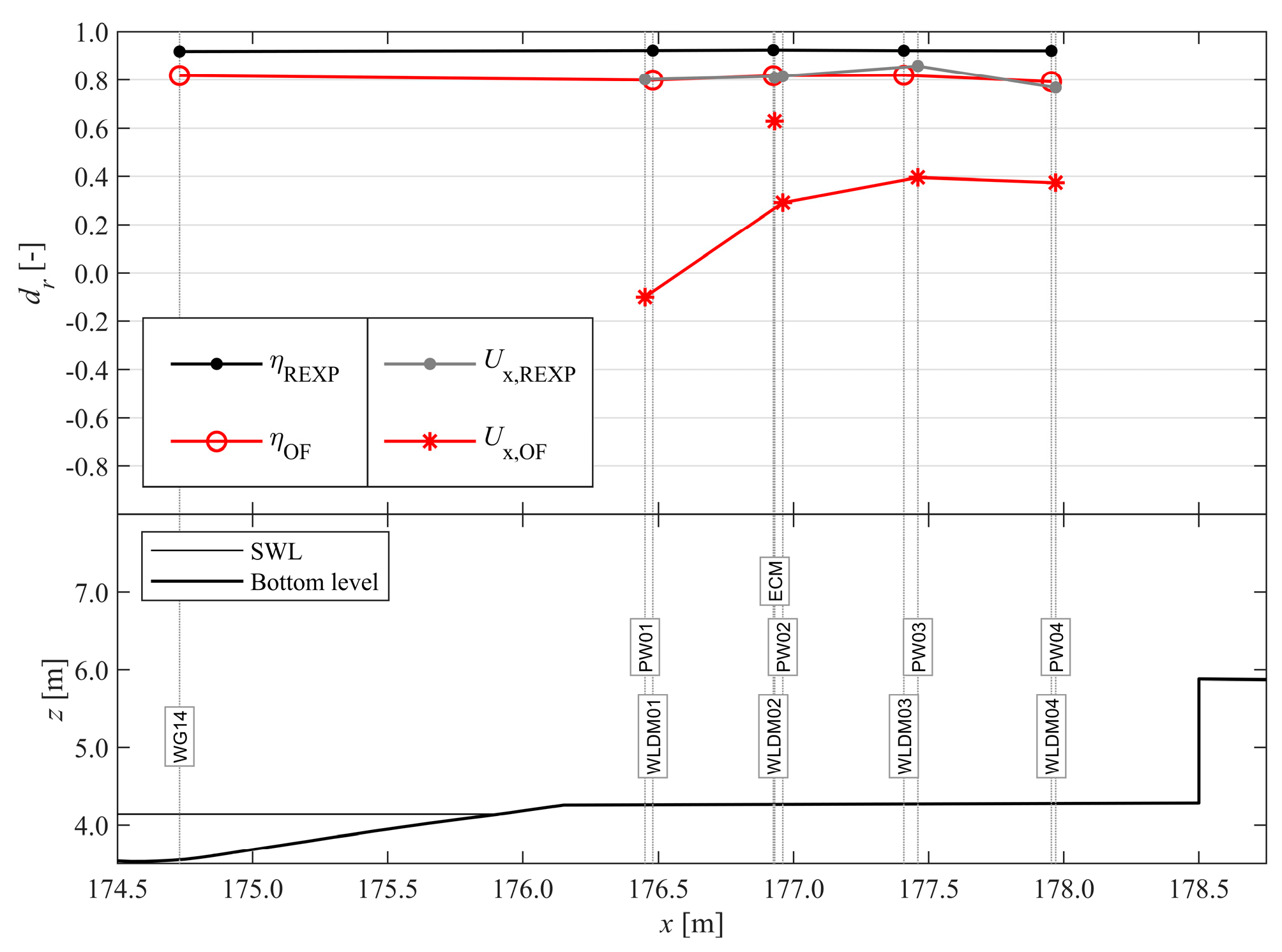
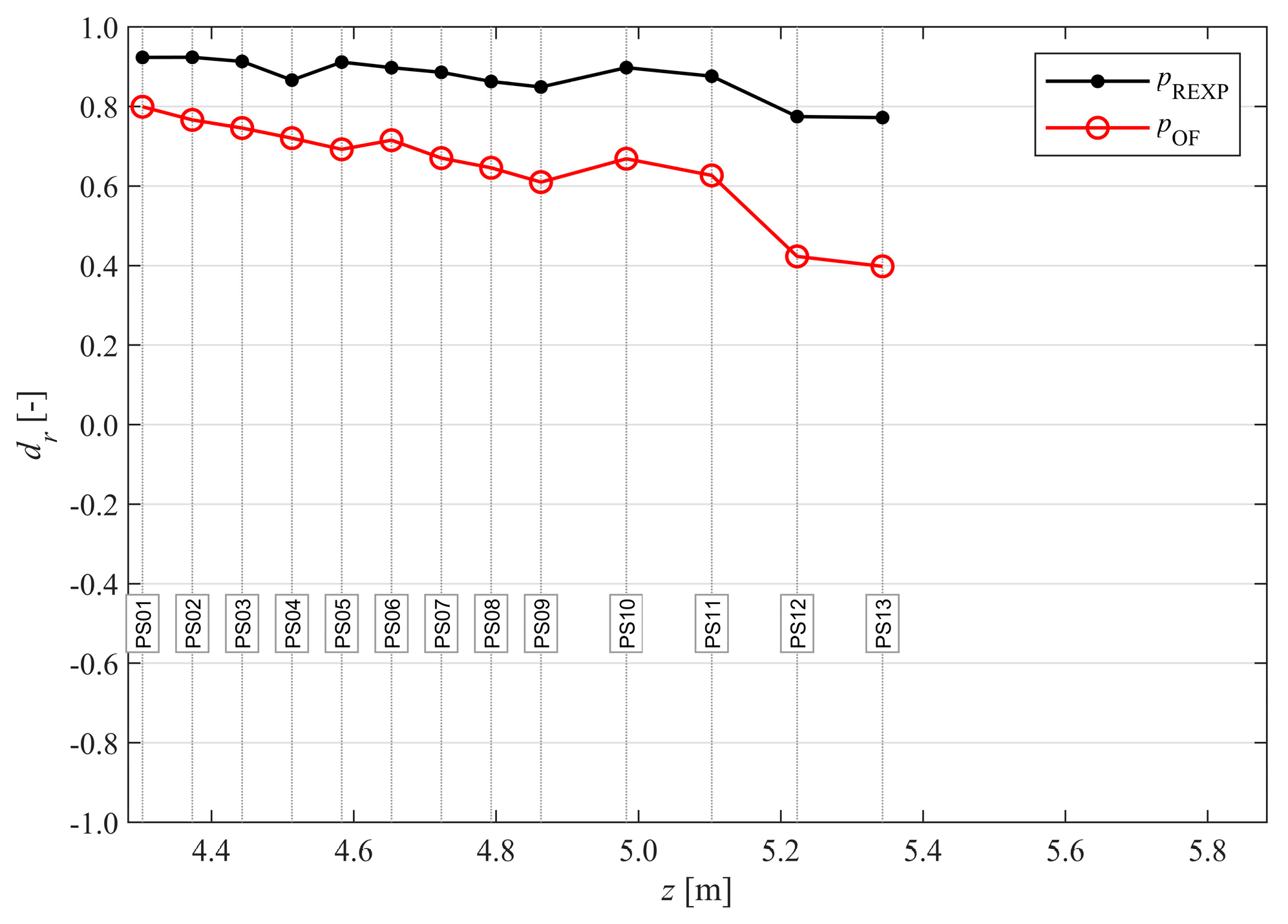
3.3. Model Performance and Pattern Statistics
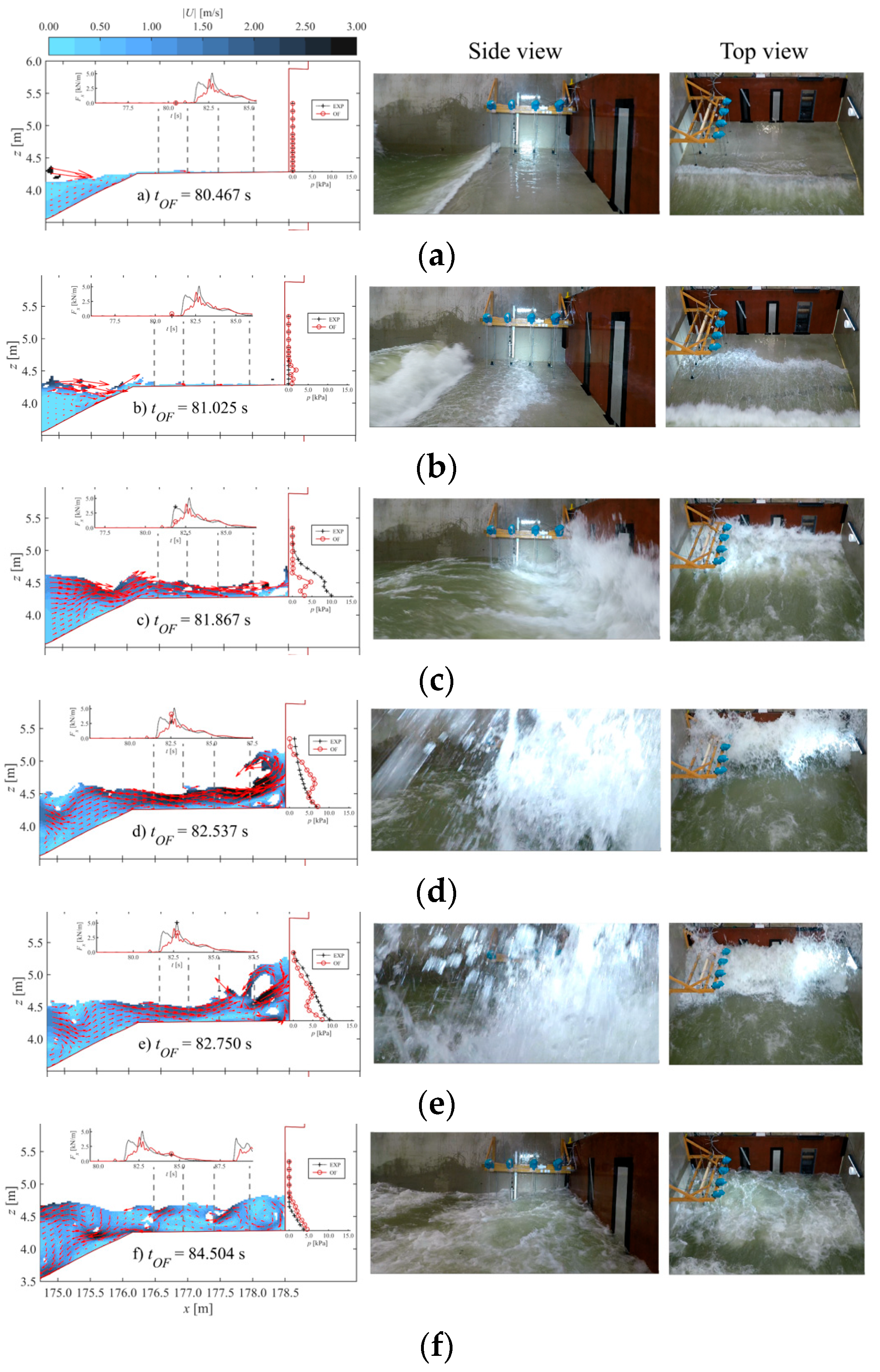
3.4. Bore Interactions and Impact
4. Discussion
4.1. Wave Transformation Processes Until the Dike Toe
4.2. Importance of Differences in Wave Generation Methods
4.3. OF Model Performance for Impacts on a Dike-Mounted Vertical Wall
- 3D effects in EXP (i.e., irregular and oblique wave fronts, wave breaking-induced 3D vortex formation), which are unreproducible by a 2DV RANS model;
- Water-air mixing in bores and air pressure fluctuations in entrained air pockets by overturning wave impacts on the wall, which are both processes not resolved by a multiphase numerical model of two incompressible and immiscible fluids.
- The applied VOF method, which is known to smear the water-air interface over several grid cells and to cause high spurious velocities in the air phase [45]. These limitations may be (partially) overcome by applying the following recent developments:
- o
- An alternative geometric VOF method, isoAdvector, has been developed to obtain a sharper interface [79,80], specifically with applications for marine science and engineering in mind [46]. However, the sharper interface may lead to a larger error in the velocity near the water surface [45] and the method is currently mainly tested and validated for wave propagation, but not yet for wave breaking, overtopping, and wave impact, all processes essential for this study.
- o
- Spurious velocities may be avoided by implementing, e.g., the ghost fluid method [81], although such an implementation is currently not available in any of the open source OpenFOAM versions.
- The turbulence model, which has been carefully chosen as the state-of-the-art (Section 2.2.1), but is still limited by its inherent assumptions.
- Douglas and Nistor [82] have shown that (compared to a dry-bed condition) a bore propagating over a thin layer of water on the bed (i.e., wet-bed condition) can substantially increase the steepness and depth of the bore-front and consequently affect the impact of the bore on the wall. The near-bed resolution of the OF grid along the promenade might not have been able to correctly reproduce wet-bed bore propagation in cases of a very thin layer of water, possibly even modelling a dry-bed bore propagation instead.
- Differences between OF and EXP in the treatment of friction on the bed of the promenade. The no-slip boundary condition and applied wall function in OF modelled a boundary layer, which lowered Ux close to the bed more than was measured in EXP. On average, Ux was underestimated by OF at the measurement locations of the PWs and ECM close to the promenade bed (Figure 5, B* in Table 4 and Figure 13a–c).
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
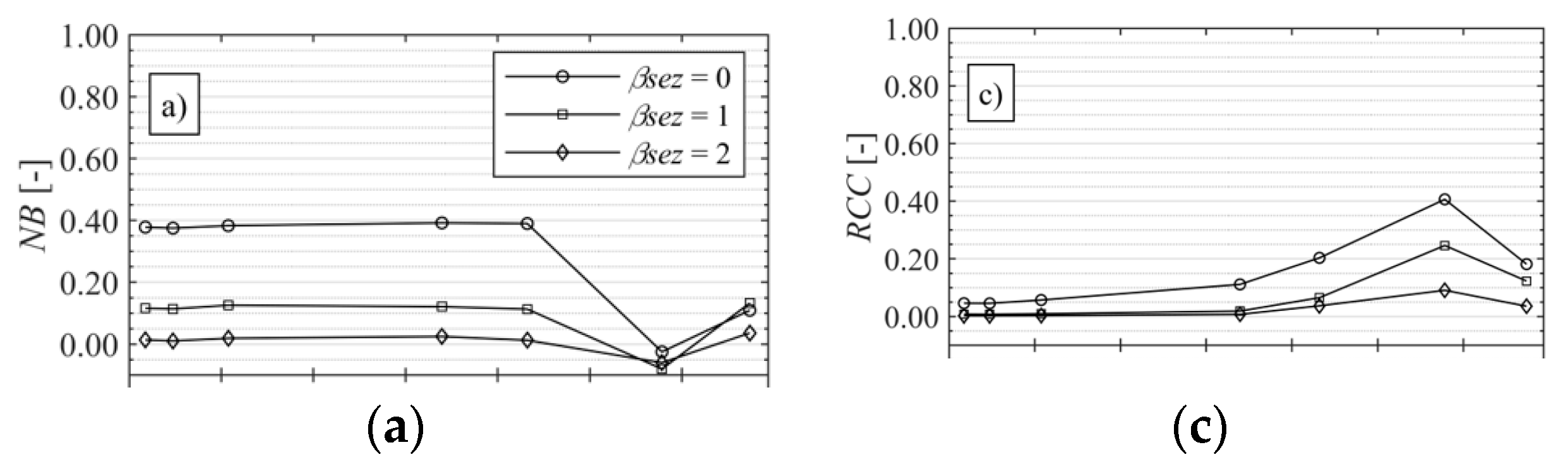
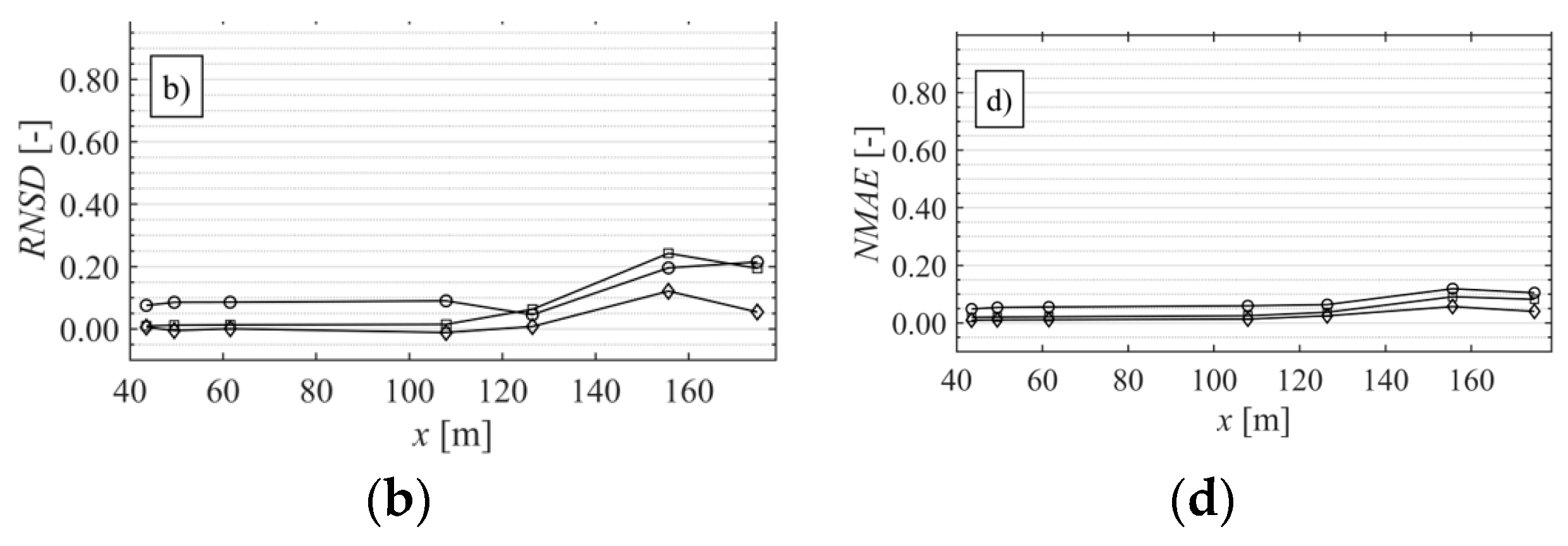
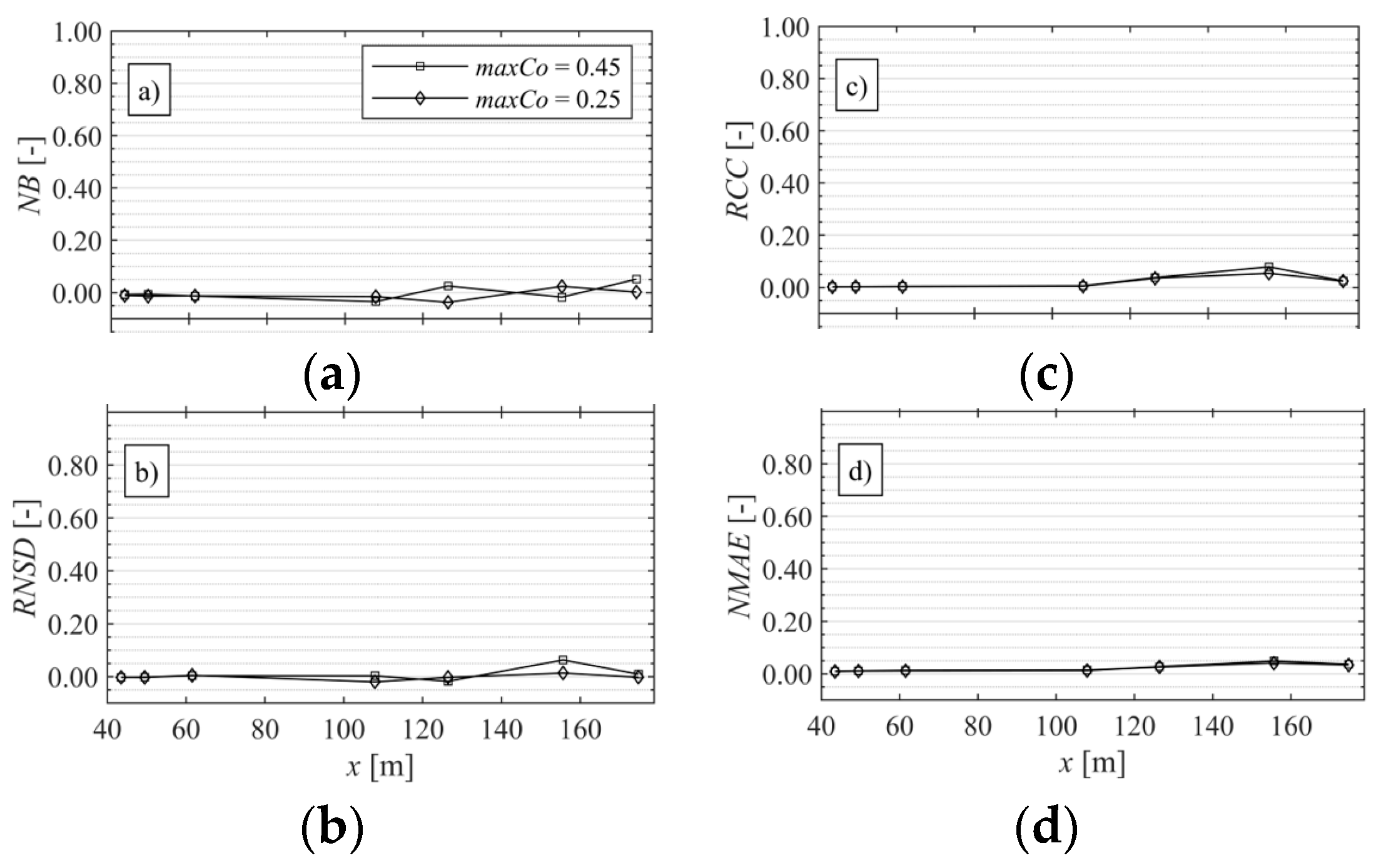
Appendix A. Numerical Convergence Analysis
Appendix A1. Model Convergence Statistics
Appendix A2. Convergence Analyses
References
- IPCC. The Ocean. and Cryosphere in a Changing Climate. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Van Doorslaer, K.; Romano, A.; De Rouck, J.; Kortenhaus, A. Impacts on a storm wall caused by non-breaking waves overtopping a smooth dike slope. Coast. Eng. 2017, 120, 93–111. [Google Scholar] [CrossRef]
- De Finis, S.; Romano, A.; Bellotti, G. Numerical and laboratory analysis of post-overtopping wave impacts on a storm wall for a dike-promenade structure. Coast. Eng. 2020, 155, 103598. [Google Scholar] [CrossRef]
- Chen, X.; Hofland, B.; Uijttewaal, W. Maximum overtopping forces on a dike-mounted wall with a shallow foreshore. Coast. Eng. 2016, 116, 89–102. [Google Scholar] [CrossRef]
- Streicher, M.; Kortenhaus, A.; Gruwez, V.; Hofland, B.; Chen, X.; Hughes, S.; Hirt, M. Prediction of Dynamic and Quasi-static Impacts on Vertical Sea Walls Caused by an Overtopped Bore. Coast. Eng. 2018. [Google Scholar] [CrossRef]
- Gruwez, V.; Vandebeek, I.; Kisacik, D.; Streicher, M.; Verwaest, T.; Kortenhaus, A.; Troch, P. 2D overtopping and impact experiments in shallow foreshore conditions. In Proceedings of the 36th Conference on Coastal Engineering, Baltimore, MD, USA, 30 July–3 August 2018; pp. 1–13. [Google Scholar]
- Xiao, H.; Huang, W.; Tao, J. Numerical modeling of wave overtopping a levee during Hurricane Katrina. Comput. Fluids 2009, 38, 991–996. [Google Scholar] [CrossRef]
- Torres-Freyermuth, A.; Lara, J.L.; Losada, I.J. Numerical modelling of short- and long-wave transformation on a barred beach. Coast. Eng. 2010, 57, 317–330. [Google Scholar] [CrossRef]
- Altomare, C.; Crespo, A.J.C.; Domínguez, J.M.; Gómez-Gesteira, M.; Suzuki, T.; Verwaest, T. Applicability of Smoothed Particle Hydrodynamics for estimation of sea wave impact on coastal structures. Coast. Eng. 2015, 96, 1–12. [Google Scholar] [CrossRef]
- Suzuki, T.; Altomare, C.; Veale, W.; Verwaest, T.; Trouw, K.; Troch, P.; Zijlema, M. Efficient and robust wave overtopping estimation for impermeable coastal structures in shallow foreshores using SWASH. Coast. Eng. 2017, 122, 108–123. [Google Scholar] [CrossRef]
- Altomare, C.; Tagliafierro, B.; Dominguez, J.M.; Suzuki, T.; Viccione, G. Improved relaxation zone method in SPH-based model for coastal engineering applications. Appl. Ocean. Res. 2018, 81, 15–33. [Google Scholar] [CrossRef]
- Violeau, D. Fluid Mechanics and the SPH Method: Theory and Applications; Oxford University Press: New York, NY, USA, 2012; ISBN 978-0-19-965552-6. [Google Scholar]
- Oñate, E.; Celigueta, M.A.; Idelsohn, S.R.; Salazar, F.; Suárez, B. Possibilities of the particle finite element method for fluid–soil–structure interaction problems. Comput. Mech. 2011, 48, 307. [Google Scholar] [CrossRef]
- Didier, E.; Neves, D.R.C.B.; Martins, R.; Neves, M.G. Wave interaction with a vertical wall: SPH numerical and experimental modeling. Ocean. Eng. 2014, 88, 330–341. [Google Scholar] [CrossRef]
- St-Germain, P.; Nistor, I.; Townsend, R.; Shibayama, T. Smoothed-Particle Hydrodynamics Numerical Modeling of Structures Impacted by Tsunami Bores. J. Waterw. Port. Coast. Ocean Eng. 2014, 140, 66–81. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Altomare, C.; Gonzalez-Cao, J.; Lomonaco, P. Towards a more complete tool for coastal engineering: Solitary wave generation, propagation and breaking in an SPH-based model. Coast. Eng. J. 2019, 61, 15–40. [Google Scholar] [CrossRef]
- Subramaniam, S.P.; Scheres, B.; Schilling, M.; Liebisch, S.; Kerpen, N.B.; Schlurmann, T.; Altomare, C.; Schüttrumpf, H. Influence of Convex and Concave Curvatures in a Coastal Dike Line on Wave Run-up. Water 2019, 11, 1333. [Google Scholar] [CrossRef]
- Mokos, A.; Rogers, B.D.; Stansby, P.K. A multi-phase particle shifting algorithm for SPH simulations of violent hydrodynamics with a large number of particles. J. Hydraul. Res. 2017, 55, 143–162. [Google Scholar] [CrossRef]
- Torres-Freyermuth, A.; Losada, I.J.; Lara, J.L. Modeling of surf zone processes on a natural beach using Reynolds-Averaged Navier-Stokes equations. J. Geophys. Res. 2007, 112, C09014. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Simulating coastal engineering processes with OpenFOAM®. Coast. Eng. 2013, 71, 119–134. [Google Scholar] [CrossRef]
- Ingram, D.M.; Gao, F.; Causon, D.M.; Mingham, C.G.; Troch, P. Numerical investigations of wave overtopping at coastal structures. Coast. Eng. 2009, 56, 190–202. [Google Scholar] [CrossRef]
- An, M.H.; Jiang, Q.; Zhang, C.K. Simulation of wave propagation on sloping seadike. In Proceedings of the Proceedings 2013 International Conference on Mechatronic Sciences, Electric Engineering and Computer (MEC), Shengyang, China, 20–22 December 2013; pp. 2505–2509. [Google Scholar]
- Kleefsman, K.M.T.; Fekken, G.; Veldman, A.E.P.; Iwanowski, B.; Buchner, B. A Volume-of-Fluid based simulation method for wave impact problems. J. Comput. Phys. 2005, 206, 363–393. [Google Scholar] [CrossRef]
- Wenneker, I.; Wellens, P.; Gervelas, R. Volume-of-fluid model comflow simulations of wave impacts on a dike. Coast. Eng. Proc. 2011, 1, 17. [Google Scholar] [CrossRef]
- Vanneste, D.F.A.; Altomare, C.; Suzuki, T.; Troch, P.; Verwaest, T. Comparison of numerical models for wave overtopping and impact on a sea wall. Coast. Eng. Proc. 2014, 1, 5. [Google Scholar] [CrossRef]
- Xie, P.; Chu, V.H. The forces of tsunami waves on a vertical wall and on a structure of finite width. Coast. Eng. 2019, 149, 65–80. [Google Scholar] [CrossRef]
- Wemmenhove, R.; Luppes, R.; Veldman, A.E.P.; Bunnik, T. Numerical simulation of hydrodynamic wave loading by a compressible two-phase flow method. Comput. Fluids 2015, 114, 218–231. [Google Scholar] [CrossRef]
- Liu, S.; Gatin, I.; Obhrai, C.; Ong, M.C.; Jasak, H. CFD simulations of violent breaking wave impacts on a vertical wall using a two-phase compressible solver. Coast. Eng. 2019, 154, 103564. [Google Scholar] [CrossRef]
- Streicher, M.; Kortenhaus, A.; Altomare, C.; Gruwez, V.; Hofland, B.; Chen, X.; Marinov, K.; Scheres, B.; Schüttrumpf, H.; Hirt, M.; et al. WALOWA (WAve LOads on WAlls): Large-Scale Experiments in the Delta Flume. In Proceedings of the International Short Course and Conference on Applied Coastal Research (SCACR), Santander, Spain, 3–6 October 2017; pp. 69–80. [Google Scholar]
- Streicher, M.; Kortenhaus, A.; Hughes, S.; Hofland, B.; Suzuki, T.; Altomare, C.; Marinov, K.; Chen, X.; Cappietti, L. Non-Repeatability, Scale- and Model Effects in Laboratory Measurement of Impact Loads Induced by an Overtopped Bore on a Dike Mounted Wall. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering, Glasgow, Scotland, UK, 9–14 June 2019; p. 10. [Google Scholar]
- Kortenhaus, A.; Streicher, M.; Gruwez, V.; Altomare, C.; Hofland, B.; Chen, X.; Marinov, K.; Vanneste, D.; Willems, M.; Suzuki, T.; et al. WALOWA (WAve LOads on WAlls)—Large-scale Experiments in the Delta Flume on Overtopping Wave Loads on Vertical Walls [Dataset]. Zenodo. 2019. Available online: http://doi.org/10.5281/zenodo.2843140 (accessed on 24 May 2019).
- Saponieri, A.; Risio, M.D.; Pasquali, D.; Valentini, N.; Aristodemo, F.; Tripepi, G.; Celli, D.; Streicher, M.; Damiani, L. Beach profile evolution in front of storm seawalls: A physical and numerical study. Coast. Eng. 2018, 70. [Google Scholar] [CrossRef]
- Streicher, M.; Kortenhaus, A.; Gruwez, V.; Suzuki, T.; Altomare, C.; Saponieri, A.; Pasquali, D.; Valentini, N.; Tripepi, G.; Celli, D.; et al. Overtopped wave loads on walls (WALOWA)—Numerical and physical modelling of large-scale experiments in the delta flume. In Proceedings of the Hydralab+ Joint User Meeting, Bucharest, Romania, 22–23 May 2019; pp. 57–67. [Google Scholar]
- Battjes, J.A. Surf similarity. Coast. Eng. Proc. 1974, 1, 26. [Google Scholar] [CrossRef]
- Hofland, B.; Chen, X.; Altomare, C.; Oosterlo, P. Prediction formula for the spectral wave period Tm-1,0 on mildly sloping shallow foreshores. Coast. Eng. 2017, 123, 21–28. [Google Scholar] [CrossRef]
- Mansard, E.P.; Funke, E.R. The measurement of incident and reflected spectra using a least squares method. Coast. Eng. Proc. 1980, 1. [Google Scholar] [CrossRef]
- van Dongeren, A.R.; Battjes, J.; Janssen, T.; van Noorloos, J.; Steenhauer, K.; Steenbergen, G.; Reniers, A. Shoaling and shoreline dissipation of low-frequency waves. J. Geophys. Res. 2007, 112, C02011. [Google Scholar] [CrossRef]
- Cappietti, L.; Simonetti, I.; Esposito, A.; Streicher, M.; Kortenhaus, A.; Scheres, B.; Schuettrumpf, H.; Hirt, M.; Hofland, B.; Chen, X. Large-Scale Experiments of Wave-Overtopping Loads on Walls: Layer Thicknesses and Velocities. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018; p. V07AT06A028. [Google Scholar]
- Streicher, M. Loads Induced by Overtopping Bores on Vertical Walls at the end of Sea Facing Promenades: A Laboratory Study. Ph.D. Thesis, Ghent University, Gent, Belgium, 2019. [Google Scholar]
- Jacobsen, N.G.; van Gent, M.R.A.; Capel, A.; Borsboom, M. Numerical prediction of integrated wave loads on crest walls on top of rubble mound structures. Coast. Eng. 2018, 142, 110–124. [Google Scholar] [CrossRef]
- De Rouck, J.; Trouw, K. Masterplan Kustveiligheid—Evaluatie Toelaatbaar Overtoppingsdebiet; MDK—Afdeling Kust & Flanders Hydraulics Research: Antwerpen, Belgium, 2019. [Google Scholar]
- OpenFOAM Foundation. OpenFOAM: The OpenFOAM Foundation. Available online: https://openfoam.org/ (accessed on 6 August 2019).
- Berberović, E.; van Hinsberg, N.P.; Jakirlić, S.; Roisman, I.V.; Tropea, C. Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution. Phys. Rev. E 2009, 79, 036306. [Google Scholar] [CrossRef] [PubMed]
- Deshpande, S.S.; Anumolu, L.; Trujillo, M.F. Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Disc. 2012, 5, 014016. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R.; Roenby, J. Performance of interFoam on the simulation of progressive waves. Coast. Eng. J. 2019, 0, 1–21. [Google Scholar] [CrossRef]
- Roenby, J.; Larsen, B.E.; Bredmose, H.; Jasak, H. A new volume-of-fluid method in OpenFOAM. In Proceedings of the VII International Conference on Computational Methods in Marine Engineering, Nantes, France, 15–17 May 2017. [Google Scholar]
- Brown, S.A.; Greaves, D.M.; Magar, V.; Conley, D.C. Evaluation of turbulence closure models under spilling and plunging breakers in the surf zone. Coast. Eng. 2016, 114, 177–193. [Google Scholar] [CrossRef]
- Devolder, B.; Troch, P.; Rauwoens, P. Performance of a buoyancy-modified k-ω and k-ω SST turbulence model for simulating wave breaking under regular waves using OpenFOAM®. Coast. Eng. 2018, 138, 49–65. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R. On the over-production of turbulence beneath surface waves in Reynolds-averaged Navier–Stokes models. J. Fluid Mech. 2018, 853, 419–460. [Google Scholar] [CrossRef]
- Martins, K.; Blenkinsopp, C.E.; Almar, R.; Zang, J. The influence of swash-based reflection on surf zone hydrodynamics: A wave-by-wave approach. Coast. Eng. 2017, 122, 27–43. [Google Scholar] [CrossRef]
- Karagiannis, N.; Karambas, T.; Koutatis, C. Wave overtopping numerical simulation using OpenFoam. In Proceedings of the E-Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Raby, A.; Jayaratne, R.; Bredmose, H.; Bullock, G. Individual violent wave-overtopping events: Behaviour and estimation. J. Hydraul. Res. 2019, 1–13. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Realistic wave generation and active wave absorption for Navier–Stokes models: Application to OpenFOAM®. Coast. Eng. 2013, 71, 102–118. [Google Scholar] [CrossRef]
- Higuera, P. phicau/olaFlow: CFD for waves. Zenodo 2018. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsøe, J. A wave generation toolbox for the open-source CFD library: OpenFoam®. Int. J. Numer. Meth. Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Vyzikas, T.; Stagonas, D.; Buldakov, E.; Greaves, D. The evolution of free and bound waves during dispersive focusing in a numerical and physical flume. Coast. Eng. 2018, 132, 95–109. [Google Scholar] [CrossRef]
- Windt, C.; Davidson, J.; Schmitt, P.; Ringwood, J.V. On the Assessment of Numerical Wave Makers in CFD Simulations. J. Mar. Sci. Eng. 2019, 7, 47. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. In Turbulence, Heat and Mass Transfer 4; Begell House: Otterfing, Germany, 2003. [Google Scholar]
- Mayer, S.; Madsen, P.A. Simulation of Breaking Waves in the Surf Zone using a Navier-Stokes Solver. In Coast. Eng.2000; American Society of Civil Engineers: Reston, VA, USA, 2001; pp. 928–941. [Google Scholar]
- Devolder, B.; Rauwoens, P.; Troch, P. Application of a buoyancy-modified k-ω SST turbulence model to simulate wave run-up around a monopile subjected to regular waves using OpenFOAM®. Coast. Eng. 2017, 125, 81–94. [Google Scholar] [CrossRef]
- Larsen, B.E. stabRAS_OF50. 2018. Available online: https://github.com/BjarkeEltardLarsen/StabRAS_OF50 (accessed on 18 September 2018).
- Ting, F.C.K.; Kirby, J.T. Observation of undertow and turbulence in a laboratory surf zone. Coast. Eng. 1994, 24, 51–80. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.L.-F. A numerical study of breaking waves in the surf zone. J. Fluid Mech. 1998, 359, 239–264. [Google Scholar] [CrossRef]
- Xie, Z. Two-phase flow modelling of spilling and plunging breaking waves. Appl. Math. Model. 2013, 37, 3698–3713. [Google Scholar] [CrossRef]
- Gruwez, V.; Altomare, C.; Suzuki, T.; Streicher, M.; Cappietti, L.; Kortenhaus, A.; Troch, P. A CFD inter-model comparison for wave interactions with sea dikes on shallow foreshores. (in press)
- Jacobsen, N.G.; Fredsoe, J.; Jensen, J.H. Formation and development of a breaker bar under regular waves. Part 1: Model description and hydrodynamics. Coast. Eng. 2014, 88, 182–193. [Google Scholar] [CrossRef]
- Juretić, F. cfMesh v1.1.2; Creative Fields Holding Ltd., 2016; Available online: https://sourceforge.net/projects/cfmesh/files/v1.1.2/ (accessed on 24 January 2017).
- OpenCFD OpenFOAM®—Official home of The Open Source Computational Fluid Dynamics (CFD) Toolbox. Available online: http://www.openfoam.com (accessed on 7 August 2019).
- Higuera, P. olaFOAM—Reference Manual. 2016, p. 61. Available online: https://github.com/phicau/olaFlow (accessed on 2 May 2016).
- Spalding, D.B. A Single Formula for the “Law of the Wall”. J. Appl. Mech. 1961, 28, 455–458. [Google Scholar] [CrossRef]
- Kimmoun, O.; Branger, H. A particle image velocimetry investigation on laboratory surf-zone breaking waves over a sloping beach. J. Fluid Mech. 2007, 588, 353–397. [Google Scholar] [CrossRef]
- Lowe, R.J.; Buckley, M.L.; Altomare, C.; Rijnsdorp, D.P.; Yao, Y.; Suzuki, T.; Bricker, J.D. Numerical simulations of surf zone wave dynamics using Smoothed Particle Hydrodynamics. Ocean Model. 2019, 144, 101481. [Google Scholar] [CrossRef]
- Sutherland, J.; Walstra, D.J.R.; Chesher, T.J.; van Rijn, L.C.; Southgate, H.N. Evaluation of coastal area modelling systems at an estuary mouth. Coast. Eng. 2004, 51, 119–142. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]
- van Rijn, L.C.; Walstra, D.J.R.; Grasmeijer, B.; Sutherland, J.; Pan, S.; Sierra, J.P. The predictability of cross-shore bed evolution of sandy beaches at the time scale of storms and seasons using process-based Profile models. Coast. Eng. 2003, 47, 295–327. [Google Scholar] [CrossRef]
- Streicher, M.; Kortenhaus, A.; Marinov, K.; Hirt, M.; Hughes, S.; Hofland, B.; Scheres, B.; Schüttrumpf, H. Classification of bore patterns induced by storm waves overtopping a dike crest and their impact types on dike mounted vertical walls—A large-scale model study. Coast. Eng. J. 2019, 1–19. [Google Scholar] [CrossRef]
- Battjes, J.A.; Bakkenes, H.J.; Janssen, T.T.; van Dongeren, A.R. Shoaling of subharmonic gravity waves. J. Geophys. Res. 2004, 109, C02009. [Google Scholar] [CrossRef]
- Barthel, V.; Mansard, E.P.D.; Sand, S.E.; Vis, F.C. Group bounded long waves in physical models. Ocean Eng. 1983, 10, 261–294. [Google Scholar] [CrossRef]
- Roenby, J.; Bredmose, H.; Jasak, H. A computational method for sharp interface advection. R. Soc. Open Sci. 2016, 3, 160405. [Google Scholar] [CrossRef]
- Roenby, J.; Jasak, H.; Bredmose, H.; Vukčević, V.; Heather, A.; Scheufler, H. isoAdvector. 2019. Available online: https://github.com/isoAdvector/isoAdvector (accessed on 14 October 2019).
- Vukčević, V.; Jasak, H.; Gatin, I. Implementation of the Ghost Fluid Method for free surface flows in polyhedral Finite Volume framework. Comput. Fluids 2017, 153, 1–19. [Google Scholar] [CrossRef]
- Douglas, S.; Nistor, I. On the effect of bed condition on the development of tsunami-induced loading on structures using OpenFOAM. Nat. Hazards 2015, 76, 1335–1356. [Google Scholar] [CrossRef]
- Van der Meer, J.W.; Allsop, N.W.H.; Bruce, T.; De Rouck, J.; Kortenhaus, A.; Pullen, T.; Schüttrumpf, H.; Troch, P.; Zanuttigh, B. Eurotop, Manual on Wave Overtopping of Sea Defences and Related Structures. An Overtopping Manual Largely Based on European Research, but for Worldwide Application, 2nd ed. 2018. Available online: www.overtopping-manual.com (accessed on 26 April 2019).





| TestID [-] | Duration [s] | ho [m] | ht [m] | ht/Hm0,o [-] | Rc [m] | f1 [Hz] | a1 [m] | f2 [Hz] | a2 [m] | βm [-] |
|---|---|---|---|---|---|---|---|---|---|---|
| Bi_02_6 (EXP) & Bi_02_6_R (REXP) | 209 | 4.14 | 0.43 | 0.33 | 0.117 | 0.19 | 0.45 | 0.155 | 0.428 | 0.951 |
| d′r Classification [-] | Rating |
|---|---|
| 0.90–1.00 | Excellent |
| 0.80–0.90 | Very Good |
| 0.70–0.80 | Good |
| 0.50–0.70 | Reasonable/Fair |
| 0.30–0.50 | Poor |
| (−1.00)–0.30 | Bad |
| Location | REXP | OF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B* [-] | σ* [-] | R [-] | dr [-] | B* [-] | σ* [-] | R [-] | dr [-] | d′r [-] | Rating [-] | |
| WG02 | −0.01 | 1.01 | 1.00 | 0.97 | 0.06 | 0.94 | 0.96 | 0.85 | 0.88 | Very Good |
| WG03 | −0.01 | 0.99 | 1.00 | 0.97 | 0.05 | 0.92 | 0.95 | 0.85 | 0.87 | Very Good |
| WG04 | −0.01 | 1.00 | 1.00 | 0.97 | 0.06 | 0.91 | 0.95 | 0.84 | 0.87 | Very Good |
| WG07 | 0.01 | 1.00 | 1.00 | 0.97 | 0.06 | 0.94 | 0.94 | 0.84 | 0.87 | Very Good |
| WG13 | 0.00 | 0.97 | 0.94 | 0.83 | 0.04 | 0.95 | 0.73 | 0.66 | 0.83 | Very Good |
| WG14 | 0.00 | 1.00 | 0.98 | 0.92 | 0.05 | 0.89 | 0.91 | 0.82 | 0.90 | Very Good |
| WLDM01 | −0.02 | 0.99 | 0.99 | 0.92 | −0.08 | 1.00 | 0.89 | 0.80 | 0.88 | Very Good |
| WLDM02 | −0.02 | 1.01 | 0.99 | 0.92 | −0.05 | 1.01 | 0.91 | 0.82 | 0.89 | Very Good |
| WLDM03 | 0.00 | 0.98 | 0.99 | 0.92 | −0.03 | 0.98 | 0.90 | 0.82 | 0.90 | Very Good |
| WLDM04 | 0.01 | 0.97 | 0.98 | 0.92 | −0.00 | 1.00 | 0.87 | 0.79 | 0.87 | Very Good |
| Location | REXP | OF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B* [-] | σ* [-] | R [-] | dr [-] | B* [-] | σ* [-] | R [-] | dr [-] | d′r [-] | Rating [-] | |
| PW01 | 0.02 | 0.96 | 0.91 | 0.80 | −1.24 | 1.55 | 0.58 | −0.10 | 0.10 | Bad |
| ECM | −0.02 | 1.05 | 0.87 | 0.81 | −0.25 | 0.94 | 0.73 | 0.63 | 0.82 | Very Good |
| PW02 | −0.05 | 0.99 | 0.88 | 0.82 | −0.66 | 1.22 | 0.65 | 0.29 | 0.48 | Poor |
| PW03 | −0.02 | 1.00 | 0.92 | 0.86 | −0.57 | 1.06 | 0.68 | 0.40 | 0.54 | Reasonable/Fair |
| PW04 | −0.03 | 1.02 | 0.88 | 0.77 | −0.42 | 0.88 | 0.58 | 0.37 | 0.61 | Reasonable/Fair |
| Location | REXP | OF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B* [-] | σ* [-] | R [-] | dr [-] | B* [-] | σ* [-] | R [-] | dr [-] | d′r [-] | Rating [-] | |
| PS01 | 0.00 | 1.00 | 0.98 | 0.92 | −0.14 | 0.84 | 0.84 | 0.80 | 0.88 | Very Good |
| PS02 | −0.01 | 0.99 | 0.97 | 0.92 | −0.10 | 0.82 | 0.77 | 0.77 | 0.84 | Very Good |
| PS03 | 0.00 | 1.00 | 0.96 | 0.91 | −0.13 | 0.75 | 0.71 | 0.75 | 0.83 | Very Good |
| PS04 | 0.02 | 0.99 | 0.94 | 0.87 | −0.13 | 0.74 | 0.66 | 0.72 | 0.85 | Very Good |
| PS05 | 0.01 | 1.00 | 0.96 | 0.91 | −0.11 | 0.75 | 0.61 | 0.69 | 0.78 | Good |
| PS06 | −0.01 | 0.97 | 0.96 | 0.90 | −0.13 | 0.78 | 0.61 | 0.72 | 0.82 | Very Good |
| PS07 | −0.01 | 0.93 | 0.95 | 0.89 | −0.17 | 0.76 | 0.53 | 0.67 | 0.78 | Good |
| PS08 | −0.05 | 0.86 | 0.94 | 0.86 | −0.20 | 0.74 | 0.46 | 0.65 | 0.78 | Good |
| PS09 | −0.07 | 0.88 | 0.93 | 0.85 | −0.25 | 0.78 | 0.39 | 0.61 | 0.76 | Good |
| PS10 | −0.04 | 0.93 | 0.94 | 0.90 | −0.24 | 0.77 | 0.48 | 0.67 | 0.77 | Good |
| PS11 | −0.04 | 0.91 | 0.94 | 0.88 | −0.33 | 0.57 | 0.37 | 0.63 | 0.75 | Good |
| PS12 | −0.20 | 0.79 | 0.89 | 0.78 | −0.55 | 0.53 | −0.05 | 0.42 | 0.65 | Reasonable/Fair |
| PS13 | −0.15 | 0.57 | 0.92 | 0.77 | −0.59 | 0.33 | 0.12 | 0.40 | 0.63 | Reasonable/Fair |
| LC | 0.00 | 0.97 | 0.90 | 0.90 | −0.12 | 0.74 | 0.73 | 0.76 | 0.85 | Very Good |
| Figure | Description | |
|---|---|---|
| Main Impact 1 | Figure 13a | Pre-impact of small overtopped wave. |
| Figure 13b | Pre-collision of large overtopped bore and small wave reflected from vertical wall. | |
| Figure 13c | Collision of large overtopped bore and reflected small wave. | |
| Figure 13d | Impact on vertical wall of high velocity spray from overturned bore. | |
| Figure 13e | Dynamic impact of overturned bore on vertical wall. | |
| Figure 13f | Quasi-static impact of overturned bore on vertical wall. | |
| Main Impact 2 | Figure 14a | Very small overtopped bore. |
| Figure 14b | Impact of small overtopped bore on vertical wall. | |
| Figure 14c | Impact of large overtopped bore on vertical wall. | |
| Figure 14d | Impact of large overtopped bore on vertical wall, continued. | |
| Figure 14e | Impact of large overtopped bore on vertical wall, continued. | |
| Figure 14f | Return flow of large bore reflected from vertical wall. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gruwez, V.; Altomare, C.; Suzuki, T.; Streicher, M.; Cappietti, L.; Kortenhaus, A.; Troch, P. Validation of RANS Modelling for Wave Interactions with Sea Dikes on Shallow Foreshores Using a Large-Scale Experimental Dataset. J. Mar. Sci. Eng. 2020, 8, 650. https://doi.org/10.3390/jmse8090650
Gruwez V, Altomare C, Suzuki T, Streicher M, Cappietti L, Kortenhaus A, Troch P. Validation of RANS Modelling for Wave Interactions with Sea Dikes on Shallow Foreshores Using a Large-Scale Experimental Dataset. Journal of Marine Science and Engineering. 2020; 8(9):650. https://doi.org/10.3390/jmse8090650
Chicago/Turabian StyleGruwez, Vincent, Corrado Altomare, Tomohiro Suzuki, Maximilian Streicher, Lorenzo Cappietti, Andreas Kortenhaus, and Peter Troch. 2020. "Validation of RANS Modelling for Wave Interactions with Sea Dikes on Shallow Foreshores Using a Large-Scale Experimental Dataset" Journal of Marine Science and Engineering 8, no. 9: 650. https://doi.org/10.3390/jmse8090650
APA StyleGruwez, V., Altomare, C., Suzuki, T., Streicher, M., Cappietti, L., Kortenhaus, A., & Troch, P. (2020). Validation of RANS Modelling for Wave Interactions with Sea Dikes on Shallow Foreshores Using a Large-Scale Experimental Dataset. Journal of Marine Science and Engineering, 8(9), 650. https://doi.org/10.3390/jmse8090650








