1. Introduction
Surfing is a coastal sport practiced in many spots across the Iberian Peninsula. These surfing spots require specific environmental conditions, which produce surfable waves. This includes swell size, swell direction, swell quality (spectral width and peak period), wave-grouping characteristics (number of waves in a set, wave-height distribution within the set and time between sets), wind direction and wind strength [
1]. Surf spots are the specific nearshore locations where surfing occurs and which surfers use regularly and loyally and about which surfers often develop expert local knowledge [
2]. Surfing tourism has increased in popularity as a form of active sport tourism, with surfers bringing economic benefits to a destination [
3].
Although all surf spots are used for the same recreational purpose, each spot is unique given its oceanographic, coastal, social setting and cultural history [
4]. Successful surf spots require good waves. Their definition can be approached from different standpoints, often combining cultural, purely physical elements and the fact that surfers seek different waves according to their surfing skills. Hutt et al. [
5] defined a ranking of the skill level for surfers, grouped in ten categories which are differenced by the peel angle limit (deg) and the minimum and the maximum wave height (m). Hence, different surfing waves attract different surfers to either match or challenge their abilities [
5,
6].
Waves knowledge is central to any attempt to describe surfing spots, more specifically the organization of the waves (swell) and the way they break and peel. When the wind blows over the ocean’s surface, it creates wave energy. Wave characteristics depend on the wind speed and directional constancy, the time the wind is blowing and the extent of the oceanic area affected by the flow. As wave energy travels through the open ocean, it becomes an organized train of waves or swell. Swells present typical wave periods (T), depending on their origin. Ocean swell, also known as ground swell, is the best type for surfing, as it produces non mixed waves with large values of T. Groundswell is generated by storms and the stronger the swell, the larger tend to be the wave periods.. Wind swell is created by wind local winds acting near shore. As a result, it is not as powerful as groundswell and relates to short wave periods. Surfers’ seek well organized wave trains with large wave periods, so ocean swells are preferred over wind and coastal swells. Nevertheless, the perception of swell period for surfing depends on the oceanic basin. For example, in the Mediterranean, local surfers call low periods those smaller than four seconds, medium between four seconds and eight seconds and high periods are those larger than eight seconds. This contrasts with the typical values for the Atlantic, where low periods are those smaller than eight seconds, medium range between 8 s and 13 s and high, larger than 13 s [
7].
When waves approach the shore, they eventually break. Breaking characteristics depend on the shore morphology, wind strength and direction. Offshore winds increase breaking intensity and onshore or cross-shore winds reduce it [
8]. The perfect conditions for surfing are light offshore winds or no wind [
9]. These wind conditions delay wave breaking, causing the wave to break in shallower water and increasing the breaking intensity. Strong offshore winds make waves hard to catch [
10]. When there is no wind, it is called glassy conditions and is regarded as the best condition for surfing in terms of coastal winds.
Furthermore, surfing requires a steep unbroken wave face to create board speed for performing maneuvers, referred as peel [
11]. The peel angle, related to the break angle and the wave obliquity at the breaking depth, determines the speed that the board must adopt to stay ahead of the breaking section of the wave [
12]. A minimum peel angle of 30° is generally required for surfing, large peel angles are generally associated with nonuniform bottom contours [
13].
In the previous paragraphs we described the importance of the characteristics of the wave breaks and the factors influencing them. These factors can be monitored using four parameters: breaking wave height, wave peel angle, wave breaking intensity and wave section length. Wave height–defined as the vertical distance between the trough of a wave and the following crest is perhaps the most important; wave peel angle is defined as the angle between the trail of the broken whitewater and the crest of the unbroken wave as it propagates shoreward. The wave breaking intensity is defined by the orthogonal seabed gradient and it is the dominant variable controlling the wave breaker intensity. The wave section length–defined as the distance between two breaking crests in a wave set–occurs when the wave breaks and, depending on the characteristics of the sections originated, surfers can perform different maneuvers [
14]. According to the values of these parameters, the waves will be useless for surf, adequate for beginners, for intermediate level or for advanced surfers [
5].
The seabed morphology plays an important role in creating wave breakers. Planar beaches with parallel contours do not produce good surfing breaks [
14]. The peel angle is too low for surfing, Waves simply closeout as the crest breaks all at once rather than peeling. Other bathymetric configurations—i.e., sandbar and reef break, see
Section 3 for further description—are needed to cause waves to break along the wave crest rather than all at once. Most surfing spots are near prominent morphologic features which create rough seafloors, such as river mouths, with ebb deltas, coral/rock reefs, points, rock ledges, piers, jetties or beaches where large scale bar/rip features [
15,
16].
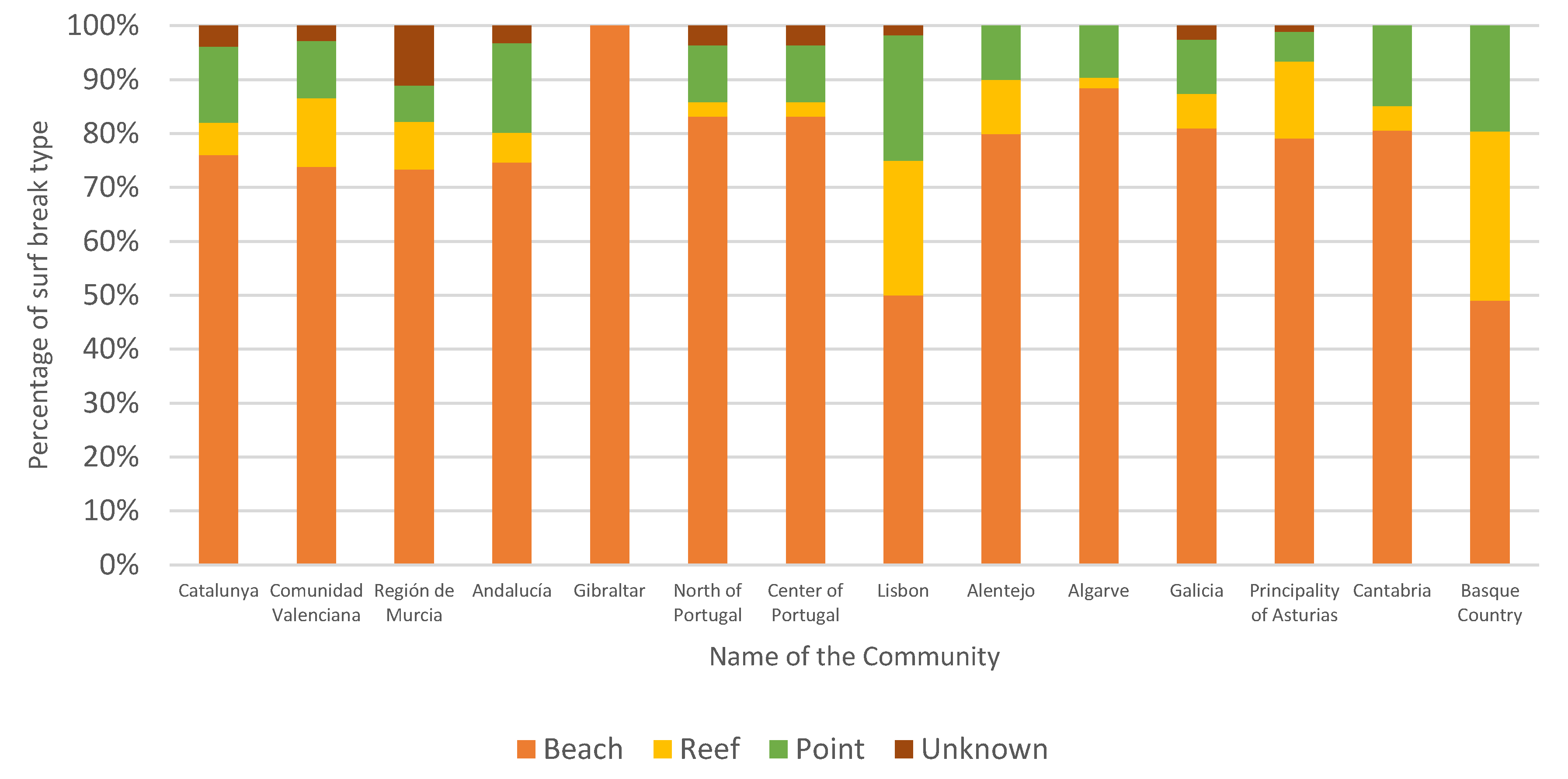
Depending on the characteristics of the seafloor, three different types of surf breaks are defined: beach break, point break and reef break. In beach breaks, the wave breaks on a sand bottom. Wave shape and size will vary depending upon the interaction of the incoming wave field with the underlying sandbar morphology. In a point break, the wave breaks at a rocky point which can be natural or artificial, for example, a dike. In a reef break, the wave breaks on shelves of rocks or coral and are the most consistent in terms of wave shape and peak location.
In this context of fragility of the surf spots—if their environment is modified by the building of a harbor or a jetty—the surfing conditions will also be modified somehow. In order to preserve the surfing resource, it is believed that consideration must be given to the coastal management of these spots because, historically, many surfing breaks have been altered or destroyed by coastal development [
17]. Moreover, as said by Caldwel, M.R. et al. [
18] and Corne, N.P. et al. [
19], coasts—and specifically surf spots—are highly dynamic and often fragile environments, particularly susceptible to local and global environmental threats. Nevertheless, on a global level, some engineers are inspired by natural reefs to not only protect the shore, but also to provide good surfing spots.
Thus, not all surfing breaks are entirely natural. They can be created, modified or destroyed by human activities, such as building seawalls (e.g., Saint Clair, Dunedin, New Zealand), jetties (e.g., Mission Bay jetties, San Diego, California), boating infrastructure (e.g., Manu Bay, Raglan, New Zealand), piers (e.g., Oil Piers, Ventura, California) and beach nourishment (e.g., “The Cove” Sandy Hook, New Jersey). It is not surprising that many existing surfing breaks are unnatural because there are few environments that have not been impacted to some degree by human activity [
20,
21].
As our previous discussion suggests, the determination of the characteristics of existing or potential surfing spots is complex and requires surf quality studies at different scales [
22]. While several global studies are available in the literature [
23,
24,
25] this is not the case for regional and local studies which consider higher resolution and more localized variability, with the exception of [
26,
27]. In this regard, we are not aware of any study which describes the distribution of the number of surfing days per month for each spot in the Iberian Peninsula. In fact, what is known is that it is difficult to have a spot where favorable surfing conditions occur every day of the year–which means that wave, wind, tide and bathymetry conditions would be conducive to surfing. In this study, we pursue the following objectives: (1) to investigate the wave parameters needed to classify surfing days thus obtain wave climate (2) thus, this specific wave climate allows us to assess the dependence on these parameters to know the expected surfing days per year in different surf spots around the Iberian Peninsula. Surf-crafts considered for the study are shortboards and longboards.
The remainder of this paper is organized as follows: study site, data and methods are presented in
Section 2; we present our results at
Section 3, to finish with discussion and conclusions (
Section 4).
2. Study Area, Data and Methods
2.1. Study Area and Data
The study area covers the coast of the Iberian Peninsula, located in the southwest corner of the European continent. The countries which form the peninsula are Spain, Portugal, a small area of France, Andorra and the United Kingdom (Gibraltar). For this study, the Iberian Peninsula coast is divided into 14 regions regarding NUTS2 classification—nomenclature of territorial units for statistics from the European Union, which contains a total of 872 surfing spots, from which we will concentrate on the 46 that can be directly related to available buoy data (see
Section 2.2). Both NUTS2 regions and selected spots are shown in
Figure 1.
The Iberian Peninsula is studied in four main categories: western shore, northern shore, southern shore and southeastern shore-taking as reference the cardinal points. Each main group is formed by territorial subcategories divided in NUTS2. Each NUTS2 region has several specific spots.
This study uses different data sources to study the characteristics of waves. Historical wave data are extracted from 25 buoys managed by
Puertos del Estado (
http://www.puertos.es/es-es/oceanografia/Paginas/portus.aspx.) (Spain) and integrated in the REDCOS network (coastal buoys) and REDEXT network (open ocean buoys) and the Nazaré buoy from the
Instituto Hidrográfico Marinha Portugal (
https://www.hidrografico.pt/boias.) (Portugal) (see
Figure 2 and
Table 1). The buoys from the REDEXT network are characterized by being located offshore in areas with depths over 200 m, to ensure that the measurements are not perturbed by local effects and are representative of large littoral areas. The REDCOS buoys, installed in depths of 100 m more less, complement REDEXT measurements highlighting local conditions in specific areas of interest for harbor activities or for the validation of wave models. Their measurements are conditioned by the shore’s profile and by the effects of the bottom on the surge. The buoy data are quality controlled in origin.
This study analyzed historic wave data recorded between 1982 and 2019 (see again
Table 1 for details). The data were collected hourly in most of the network, except for La Coruña, where data were collected every four hours and Costa Alicante, Costa Málaga and Bilbao–Vizcaya where data were collected every three hours. The variables analyzed in this study were significant wave height
Hm0, maximum wave height
Hmax, peak wave period
Tp and average swell direction
Dmd.
To identify the specific characteristics needed for surfing in the specific surf spots, we make complementary use of information obtained from the Glassy app (The app is no longer in service, but it is possible to download the
apk if needed
https://glassy-pro.es.aptoide.com/app.). This app is made for surfers use and it contains more than 18,000 surf spots around the world. It allows one to store the surfing session. The application was developed thanks to a startup in Valencia (Spain). In this regard the project it was first launched as an app for the mobile phone open to all users. However, nowadays it allows an individual user to log a surfing session experience.
The application provides knowledge on the best conditions for each surf spot (897 across the Iberian Peninsula, including 46 on our database) and we extract from there optimal swell direction (
Osd), optimal wind direction (
Owd), surf break type and bottom type. The app provides access to the forecasted conditions and allows the users to track their sessions, information that we will use for validation purposes (see
Section 2.2 for further explanations).
2.2. Methods
To achieve the objectives described in
Section 1, we combine the two data sources previously introduced (buoy data and Glassy App data) as described in
Figure 3. Our analysis is split in three steps:
Description of the physical characteristics and optimal conditions for each surf spot, using Glassy App Site data (GAS, from now onwards): bottom type, surf break type, optimal wind direction (Owd), optimal swell direction (Osd).
Determination of the probability of occurrence of optimal surf days using buoys dataset (BDS, from now onwards). First, we identify at the buoy scale (macroanalysis) the number of days with
Hm0 > 0.9 m.; second, we combine the previous information with swell direction data and compare it with the optimal swell values (see step 1) to make inference at the surf spot level. This analysis is limited to the 46 surf spots which can be directly linked to one of the 25 available buoys (see
Table A1).
Results from steps 1 and 2 are validated using a citizen science as benchmark data, extracting information (more than 1000.000 hourly observations from the BDS) on real surf sessions from Glassy App Citizen data (GAC, from now onwards). Contrasting how surfers perceived and qualified their experience.
The benchmark is constructed using information from the buoy, attributing
Hm0 and
Dmd registered to the close by surf spots (see
Figure A1). Then days are grouped in surfed days and non-surfed days.
This three steps approach allows us to rank the studied surf spots in the Iberian Peninsula according to the probability of occurrence of good surfing days.
Step 2 is split into buoy level analysis (macro) and surf spot level (micro). The buoy macroanalysis is based on the standard significant wave height (
Hm0) [
28]. As measured and provided by buoy,
Hm0 refers to the height (from the trough to the crest) of the waves following in the third quartile of the empirical wave height distribution. We adopt this variable, originated in the field of navigation, because it is a good proxy of the state of the sea, reflecting the height of the surge that an observer would perceive. However, for the assessment of the actual surfability of the sea, we introduce second parameter, the mean height,
MeanH, informs on the expected height of the surfable waves. It is not directly provided by the BSD, but it is duly approximated using Equation (1), from Breatschneider et al. [
29].
where
is the mean height,
is signficant wave height.
The number of days with
MeanH > 0.5 (~
Hm0 = 0.9) will be considered as surfing days [
30] and we will compute the number of exceedances for each buoy and provide the monthly normal. In this sense, we only use this simple wave height criterion to approach surfed days. That values are taken from BDS.
At the surf spot level or microanalysis, we introduce the surfing waves occurrence probability indicator ( Equation (2)) defined as the ratio of favorable swell observations to the total number of swell observations.
where
cosd is counted optimal swell mean direction,
is counted observations of swell direction and
is the number of counted observations of swell direction.
The indicator is calculated for the surf spots attributable to a nearby buoy (
Table A1). The reason information from the buoys can be attributed to specific spots is the propagation of the free-traveling swell. The storm center is where swell propagation starts to travel from the ocean/sea to the shore. The swell moves away from the generating area (storm center) with circumferential dispersion and radial dispersion. In this respect, waves are just messengers of energy. The further from the storm center the swell travels, the more it expands in both radial and circumferential directions.
In this case, only the swell direction is considered for calculating the SWTOP indicator. It is important to remember that having the necessary swell direction in the surf spot will not necessarily mean having surfable waves, as there are more variables that also play an important role, such as wind direction, peak period or significant wave height.
In Step 3 (
Figure 4), we attempt to validate our results using citizen science data for the 2006–2019 period as a benchmark. All the data registered by citizen sensors correspond to days when there is at least one observation of a surf session. These days are considered surfed days and are pooled to compared them with data from the nearest buoy. Buoys measure the sea state by observing a series of instantaneous elevations of the sea level during a minimum time interval (depending on type of the buoys). This sample is considered representative of the waves at that time. Next, Series of elevations the standard zero crossing and spectral analyses are used to obtain the most representative parameters of the waves.
We derive means and standard deviations for Hm0, maximum wave height (Hmax), peak period (Tp) and mode for mean swell direction (Dmd), which represent the typical values for surfed days. These values are also computed using data for the whole 2006–2019 period for comparison. We do not use wind direction as REDCOST buoys do not collect that variable.
3. Results
In this section, we present an overview of the 872 surf spots characteristics of the Iberian Peninsula, namely: bottom type, surf break type, optimal swell (Osd) and wind direction (Owd). Then the natural frequency of waves is presented for 46 selected surf spots, directly attributable to BDS. Afterwards, validation process is made by using GAC, GAS and BDS for Tarragona’s coast. Finally, we show the frequency of good surfing conditions for the previously 46 selected surf spots. In this section, we see new a contribution to wave climate science thanks to citizen science data and BDS.
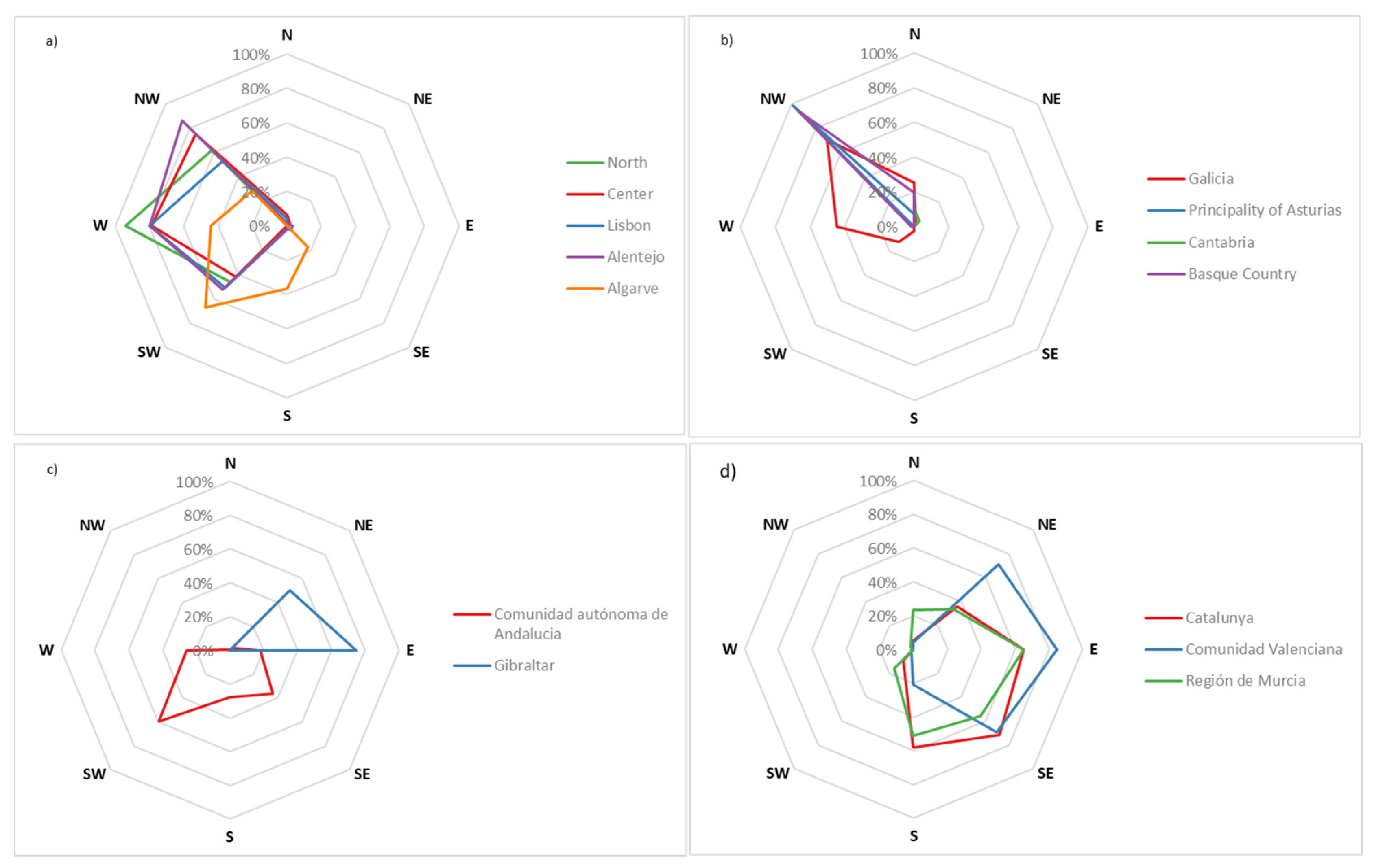
3.1. Optimal Wind and Dmd Conditions for Surfing
We extract optimal swell direction (Osd) and optimal wind direction (Owd) for each surf spot from GAS (
Figure 5 and
Figure 6). The results confirm, as expected, that the location plays an important role in the direction of the necessary Dmd for surfing. The optimal Dmd rotates from W–NW on the western and northern shores to NE–S on the southeastern shore. The two regions in the southern shore, present a larger spread, although dominant directions range from SW to E. Favorable wind direction corresponds to the opposite direction of optimal swell direction. The optimal wind rotates from NE/SW on the western shores to NE–SW in northern shore. For southeastern and southern shores, the optimal wind direction rotates to SW–NE.
3.2. Historical Oceanographic Conditions.
In this section, we present the distribution of the significant wave height using data from 25 from buoys (macroanalysis) attributed to 46 surf spots (microanalysis).
3.2.1. Hm0 Distribution
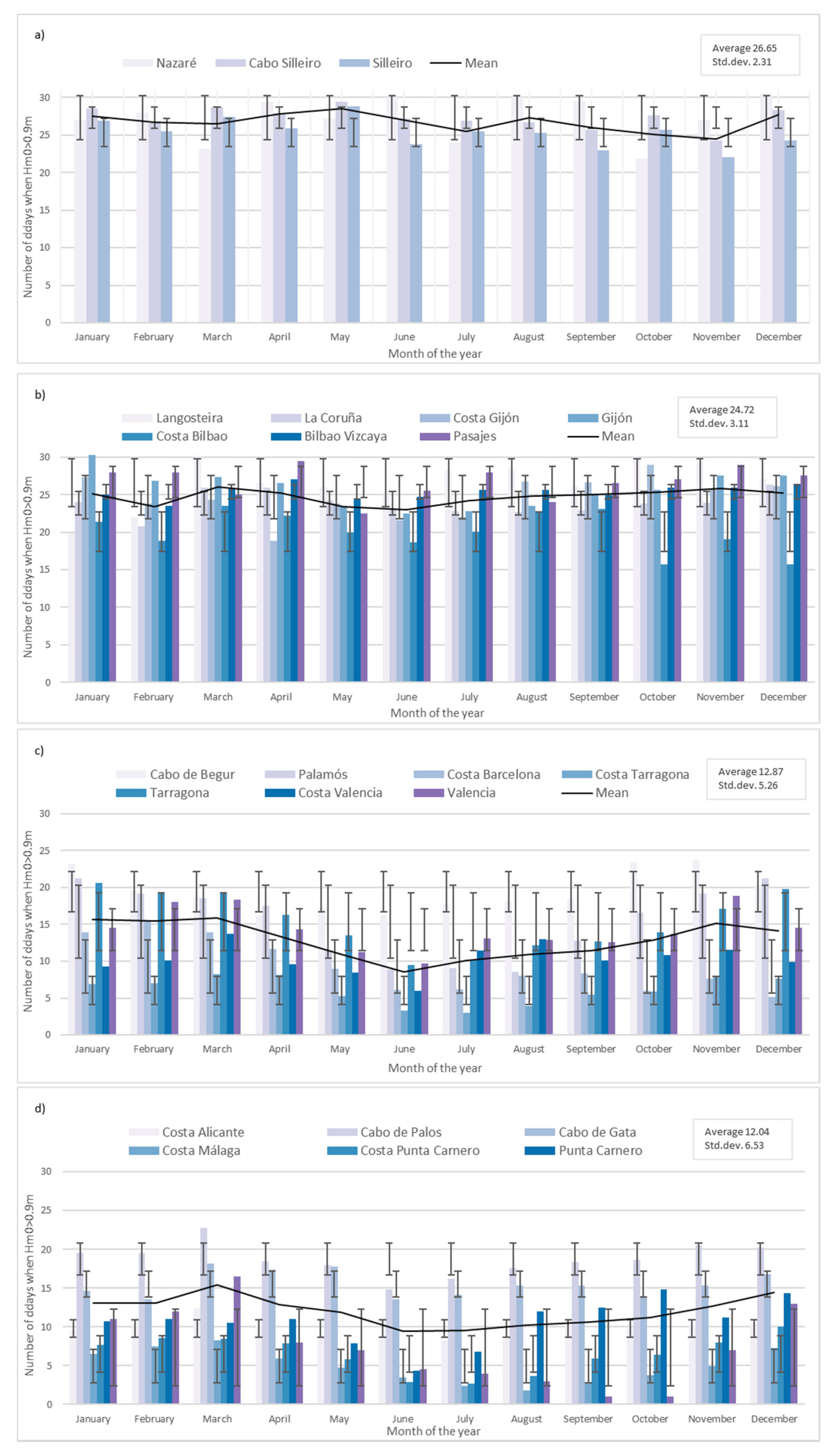
Figure 7 presents the analysis of
Hm0 > 0.9 m. The Atlantic Coast (northern and western shores) is characterized by a larger number of days with significant wave height,
Hm0 > 0.9 m. The mean values, calculated as the arithmetic average of all the spots within a region, of 26.65 days/year (western), 24.72 days/year (northern) nearly double those obtained around the Mediterranean (12.87 days/year, South Eastern; 12.04 days/year southern). In addition, Atlantic spots present smaller seasonality compared to the Mediterranean shore, which presents minimum values in spring and summer and smaller variations across the studied spots (see standard deviations in
Figure 7. Even though these considerations may be biased by the different number of spots on each category, it is worth to mentioning that the smallest monthly value in the Atlantic regions is larger than 15 days, compared to many spots in the Mediterranean that present fewer than 5 days with
Hm0 > 0.9 m during spring and summer months.
Seasonality in wave results is obvious in
Figure 7c and little in
Figure 7d, but interestingly there is no strong seasonality in
Figure 7a,b. These wave results patters can be associated with the swell producing systems. The main generators of surfing wave are low pressures, so atmospheric travel patterns will contribute to wave surfed days patterns. Then, the requirements of having surfing days on Iberian Peninsula’s shore will depend on surf spots location and orientation. Situations of low pressures coming from N, NE, NW, S and SW represent the maximum occurrence of surfed days in the occidental Mediterranean. The swell production systems required for surfing on the northern shore of the peninsula are low pressures coming from N, NE, NW—located commonly in Great Britain. Western shore surfing days require low pressures from W.
3.2.2. SWOP Analysis
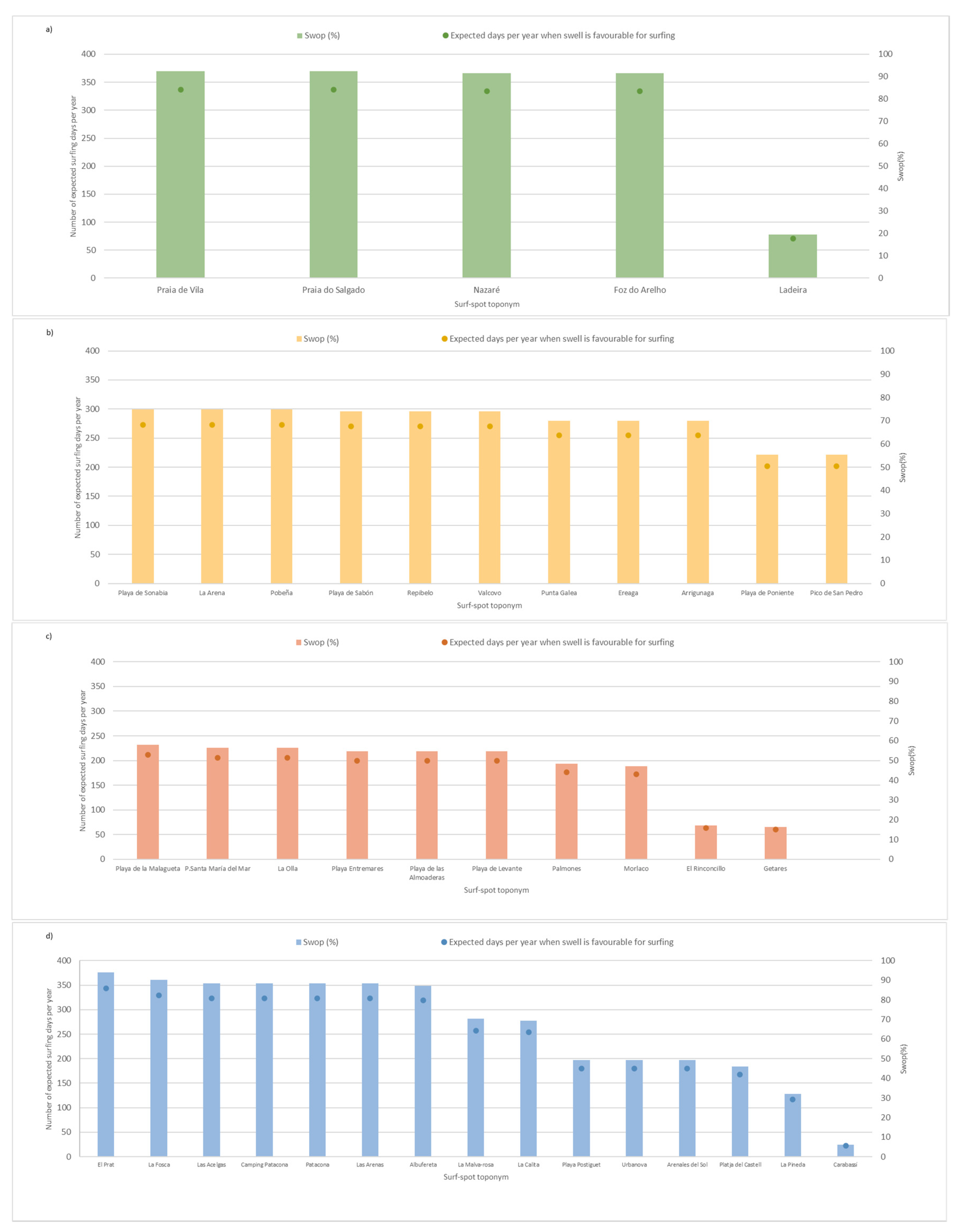
Figure 8 presents the SWOP analysis.
Figure 8a shows the SWOP values the western Shore. As described in
Section 2.2, SWOP values are computed using buoy data and optimal swell directions for each surf spot. Consequently, surf spots attributed to the same buoys and with the same optimal swell direction, i.e., Nazaré, Praia do Salgado, Praia do Sul and Praia da Vila de Nazaré, present the same SWOP value, 92.38% (337 days) corresponding to SW, W or NW swells. For Foz do Arelho and Nazaré, the value is 91.53% (334 days), associated with a W or NW swells. These high values contrast with Ladeira, where SWOP is 19.42% (71 days) of optimal swell.
Figure 8b presents the surf spots on the northern shore with available swell data. The SWOP values oscillate between nearly 75% (273 days) in Playa de Sabón (W and NW swell), Repibleo and Valcovo (SW, W or NW swells) and La Arena and Pobeña (NW swell); 70% (255 favorable days) in Punta Galea Arriguanaga and Eraga (NW swell); and 55% (201 favorable days) in Gijón, Playa Poniente and Pico de San Pedro (NW swell).
Figure 8c presents the SWOP values for southeastern shore. These values are smaller than the ones representing the areas previously presented. The SWOP values oscillate between 57.92% (212 days) in Playa de la Malagueta (E, SE swell), 56.33% (206 days) in Playa Santa Maria del Mar and la Olla (S, SWE swell), 54.67% (200 days) in Playa Entremares, Playa de las Almoaderas and Playa Levante (N, NE, E swell), 48.27% (176 days) in Palmones (SE, S swell), 47.09% (172 days) in Morclaco (SE swell), 17.15% (63 days) in El Rinconcillo (NE, E, SE, S, SW swell) and 16.38% (60 days) in Getares (SE swell).
Figure 8d presents the SWOP values for southern shore. SWOP biggest value for this region is 93.9% (343 days) in El Prat (NE, E, SE, S swell), followed by La Fosca (NE, E, SE, S swell) 90.07% (329 days); 88.4% (323 days) in las Acelgas, la Patacona, Camping la Patacona, Las Arenas (E, SE swell); 87.23% (319 days) in la Albufereta (E, SE, S swell); 70.48% (257 days) in La Malva-rosa; 69.48% (254 days) in La Calita (E, SE swell); 49.34% (180 days) in Playa Postiguet, Urbanova and Arenales del Sol; 46.06% (168 days) in Platja del Castell (SE, S, SW swell) and 32.14% (117 days) in La Pineda (NE, E swell).
The SWOP values in the Iberian Peninsula range from 22 days to 329 days. The lowest value corresponds to Carabassí and the highest one to la Fosca in Palamós. It is important to mention that the SWOP indicator is not the only condition needed for surfing, so maybe the necessary swell direction may be reaching a beach, but the wave height is not enough for surfing. Thanks to SWOP indicator is shown that the expected days when the swell is favorable for surfing varies between the different surf spots.
3.3. Validation Trough Citizen Science Data and BDS
In this section, we present the distribution of Hm0, Hmax, Tp and Dmd for the data from Costa Tarragona’s buoy. This buoy’s data were compared using a Citizens’ Science approach with surfers’ observations which identified and tagged surfing days in the past (2006–2019).
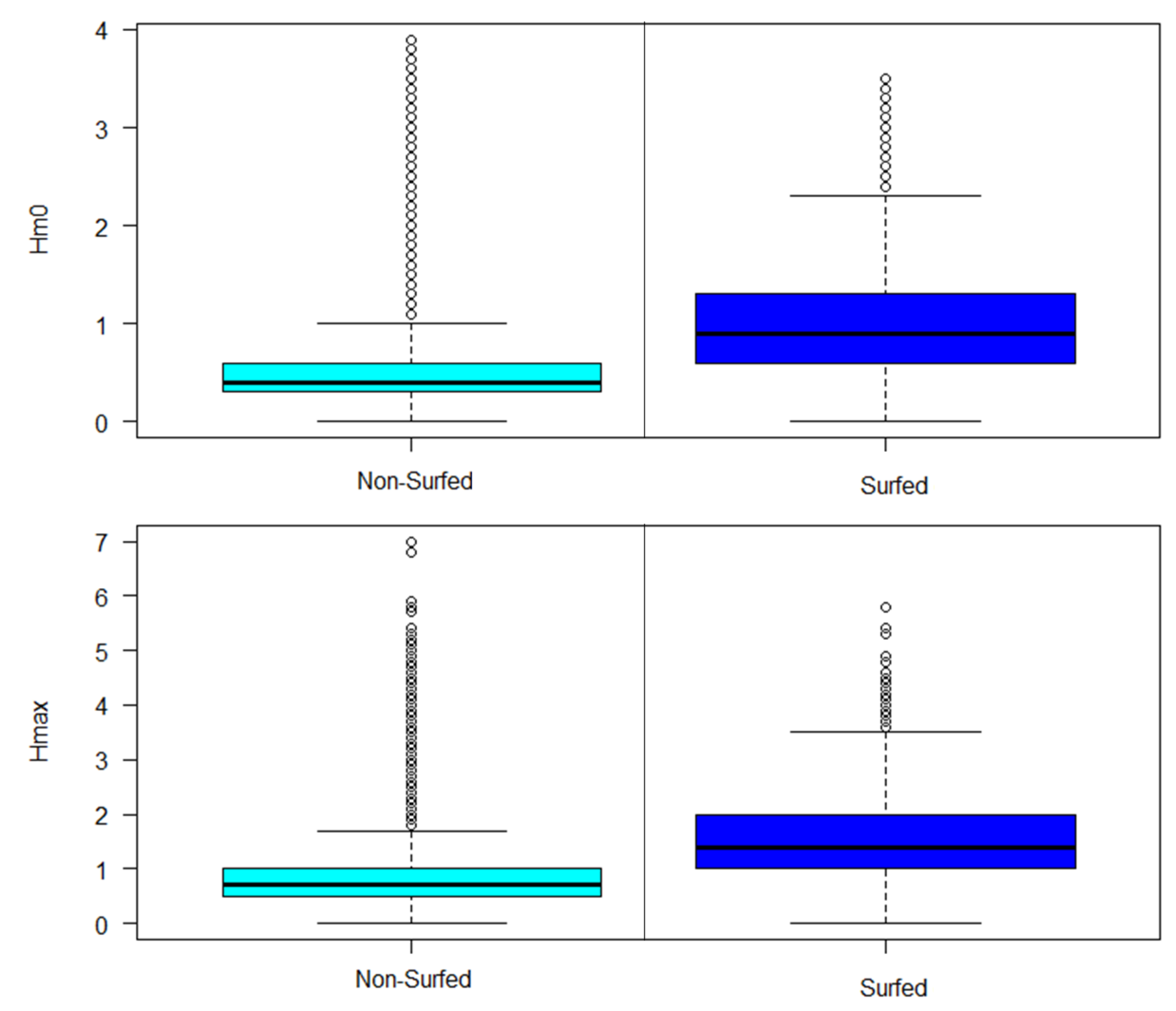
Table 2 provides mean values and their standard deviations of surfed days vs. non-surfed days. They confirm the importance of the parameters shown and how they help in the characterization of a good surfing day. As expected, the values of
Hm0 and
Hmax are larger on surfed days (0.96 m; 1.50 m) than on non-surfed days (0.49 m; 0.77 m). Similarly, the standard deviations are larger for the surfed days, although this is for sure influenced by a smaller sample size. In addition, values of
Tp are larger for the surfed days (6.99 s) in respect with non-surfed days (5.12 s). It is shown that bigger waves, bigger the periods. In addition, we encounter more constant values of swell,
Dmd in surfed days (E observations represent the 67.29% of total observations) in respect with non-surfed days (SE, 50.13%). Results show how swell direction determine surfability of a day.
Figure 9 illustrates the frequency of
Hm0 and
Hmax split on surfed-days and non-surfed days. As expected, general trends of figure show that for surfed days the median is always larger than for non-surfed days for both parameters.
Hmax and
Hm0 distribution are quite similar. These patterns respond to the definition of each parameter [
29]. Boxplots show that the distribution of
Hm0 and
Hmax variables are different for surfed and non-surfed days.
Table 2 shows, significant wave height distribution presents for surfed days values of percentile 25 (0.6 m) higher than for non-surfed days (0.3 m). Median for surfed days (0.9m) is higher than for non-surfed days (0.4 m). The same for percentile 75, surfed days present higher values (1.3 m) than non-surfed days (0.6 m).
Maximum wave height distribution shows that on surfed days values are higher than in non-surfed days. Specifically, for surfed days percentile 25 corresponds to 1 m, the median is 1.4 m, and percentile 75 is 2 m. For non-surfed days values of the boxplot are smaller: lower quartile (0.5 m), mean (0.7 m), and the upper quartile are smaller (1 m). Contrary, maximum values occur on non-surfed days.
Contrary, for Hm0 and Hmax maximum values occur on non-surfed days instead of on surfed days.
For surfed days most of Hm0 values correspond to the ones greater than 0.9 m. Nevertheless, there are some days identified as surfed days in which Hm0 values are smaller than 0.9 m. The reason values of 0 m to 0.4 m exist on surfed days, is explained by the days when, for example, there are no waves in the morning [0 m, 0.9 m] and then in the afternoon the wave height starts to increase [>0.9]. This fact occurs because the Mediterranean shore is characterized to present small values of surfing days per year. In most cases, swells come from generation areas close to the coast so that coming swell do not stay on the surf spots for so long.
We count days as surfed days when citizen science data verify it. The validation process is made in Tarragona’s buoys, so it is normal that in a surfed day appear some hour in which significant wave height is smaller of 0.9. This can be explained by two reasons: (1) the swell did not arrive yet or (2) the swell is not coming anymore. Peak period determines when surfing swell is coming or leaving. this means that the swell is coming when periods tend to be bigger and bigger and thus bigger waves. It happens the other way around when it goes from big periods to smaller periods, this means that surfing waves are probably not coming anymore at that moment. Smaller the period, smaller the wave.
Figure 10 shows the percentage of
Tp distribution on surfed and non-surfed days. General distribution patterns of peak period always show higher periods in surfed days compared with non-surfed days, in exception of maximum values of the peak period in non-surfed days (23.4 s) instead of lower values on non-surfed days (12.6 s). surfed days peak period values are higher for percentile 25, median and percentile 75 (6 s, 6.9 s, 8.1 s) than for non-surfed (4.1 s, 5.1 s, 6.2 s).
Periods > 13 s are identified in non-surfed days, but not in surfing days. This result can probably imply that periods > 13 s relate to bigger waves that citizen data collectors do not try to ride. For periods ≤ 4 it is clear that surfed days present lower values than non-surfed days. These patterns can be explained that probably the day was categorized as surfed day, but big swell did not arrive the entire day. Finally, we see that for surfed days the Tp which fit better are the ones defined as medium (4, 8] and high (8, 13] periods for the Mediterranean. This can be explained because surfing needs high periods, as that way surfers have more time between waves, waves are tidier and do not overlap each other.
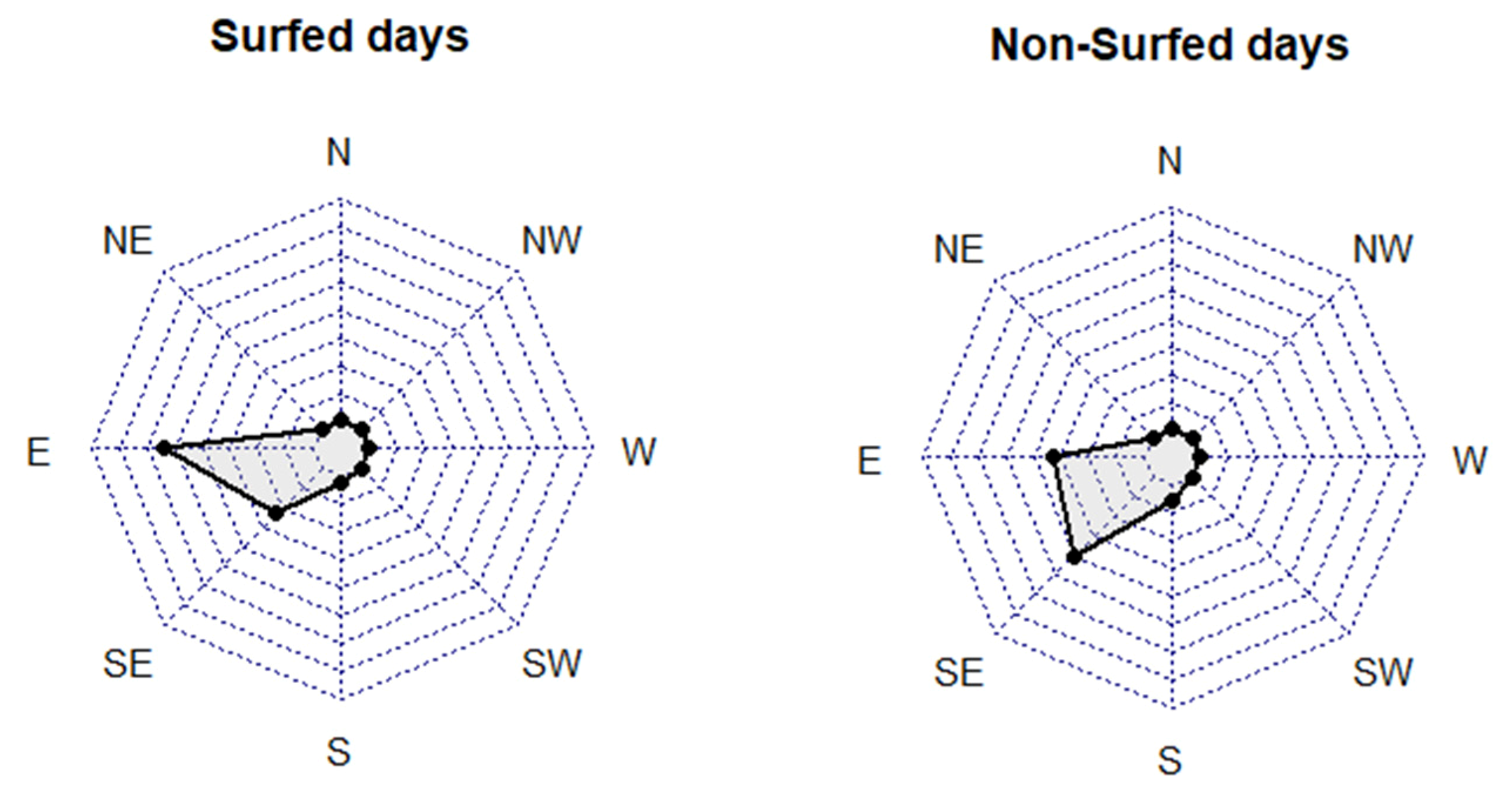
Figure 11 plots
Dmd, distribution by cardinal points for surfed and non-surfed days. The most frequent direction on surfed days is east and southeast. Moreover, surfing is less frequent with south, but still possible. Surfing is also viable with a southwest swell direction, but it is less frequent compared with the other directions mentioned before. Furthermore, in surfed days the
Dmd most relevant is [E]. This range of direction matches with the orientation of the surf spots in Tarragona’s area. The next most common
Dmd is the interval of [SE] which cover the surf spots that are more oriented to the S. From this information it is possible to say that the most common origin of swells in this area will be the swells coming from (1) the east. Then, it is possible to have surfing days when the swell is coming from (2) SE or S. The surfed days on which is identified another
Dmd of these two mentioned would probably be attributed to being those on which the swell is too big (m) and the diffraction does not lose much energy and can arrive to surf spots. Nevertheless, the
Dmd is not directly focused to the surf spot orientation. The graph of non-surfed days allows us to determine that for surfing purposes in the Costa Tarragona area values of E
Dmd fit better than SE
Dmd values. Note that this is studied grouping surf spots and it is possible once they were desegregated, that maybe there is one surf spot which does not fit correctly with E
Dmd values.
The above study shows that with Hm0 values from the buoys, it is possible to consider the monthly distribution of surfing days around the Iberian Peninsula coast with a macroanalysis (buoy-by-buoy). In addition, with swell direction it is possible to convert that macroanalysis into a microanalysis, downscaling buoy data to the surf spots. In this way, it is possible to attribute the surfing waves occurrence probability to the surf spots which are closer to the analyzed buoys.
Afterwards, thanks to the validation process it is possible to know whether surfing days will correspond to periods of observation when: Hm0 is higher than 0.9 m (1) and Dmd corresponds to the Osd on Glassy app (2). The validation process is possible thanks to BDS on the Tarragona coast, GAC and GAS.
Table 3 presents Wilcoxon-Mann–Whitney, nonparametric statistical hypothesis test, used to compare two related samples–surfed days and non-surfed days-results show significance for
Hm0,
Hmax and
Tp with surfed and non-surfed days within 0.95 confidence interval.
3.4. Ranking of Expected Surfing Days Per Year in the Iberian Peninsula
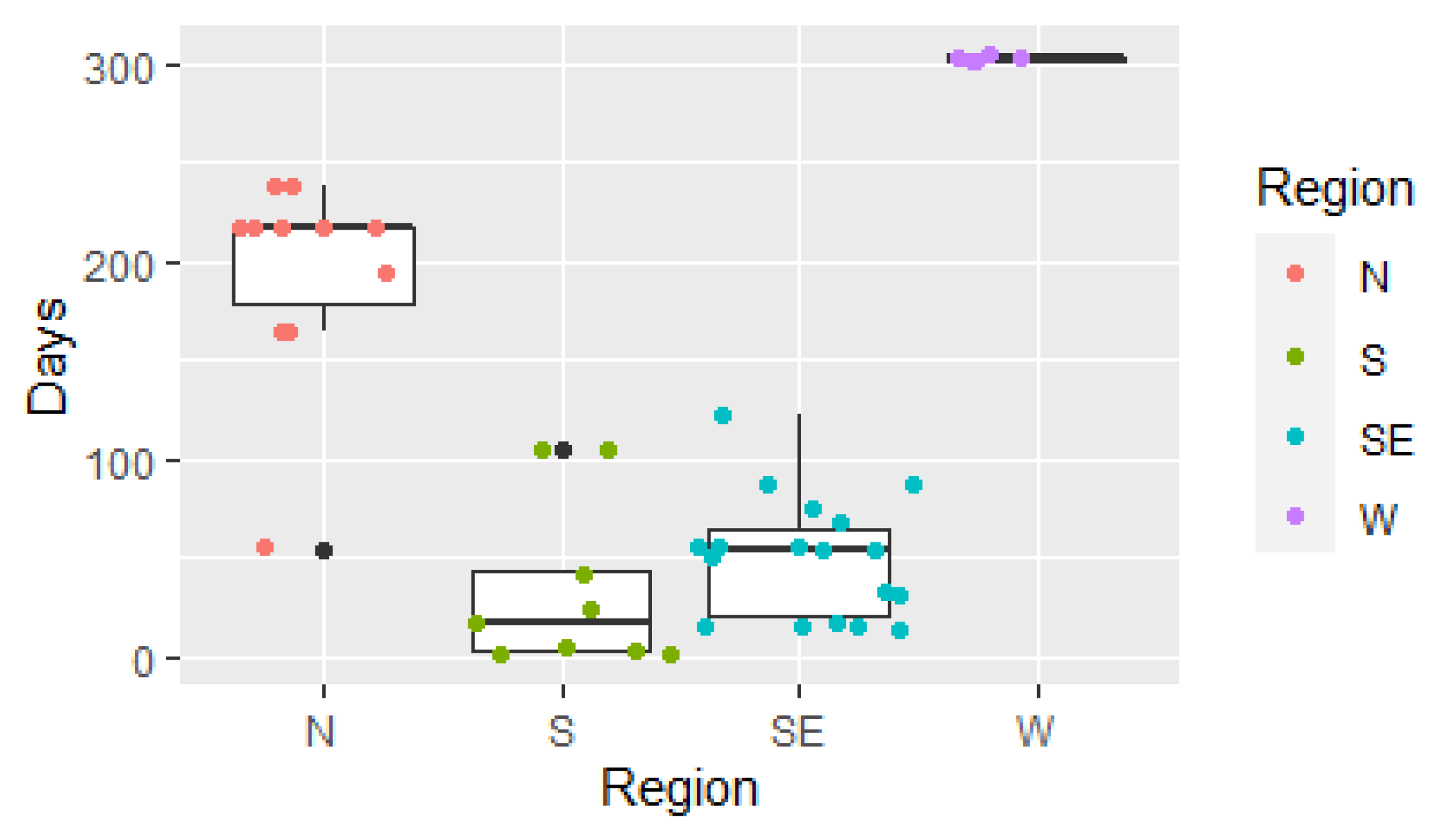
Our previous analyses allow us to rank the surf spots in the Iberian Peninsula according to the expected frequency of surfing days (see
Figure 12 and
Table 4).
Figure 12 shows the distribution of expected surfing days per year for 46 surf spots sorted by regions. Regions with more frequency of expected surfing days are the western shore and northern shore. Shores which present smaller values correspond to southern and southeastern shores. As expected, it is clear that the areas of the Atlantic Ocean present more frequency of surfing days than the shore of the Mediterranean Sea in the Iberian Peninsula. The main results validate the idea that location of surf spots plays an important role in the sense of surfing days frequency. Specifically, following the findings in
Table 4, the top-5 surfing spots are on the western shore (>300 days). Values of [300, 200) correspond to surf spots located on the northern shore, specifically into Langosteira and Costa Bilbao Vizacaya placements. Values of [200, 100) are recognized on the northern shore except for Palamós (123, southeastern shore) and La Olla (105, southern shore). Values of <100 are distributed around the southern and south-eastern shore, highest values of this interval correspond to Cadiz’s surf spots; this can be explained by the special location, in the vicinity of both the Atlantic Ocean and the Mediterranean Sea.
The four extreme cases of low values, of expected surfing days per year are El Rinconcillo (1), Getares (2), Carbassí (3) and Palmones (6). El Rinconcillo, Getares and Palmones are in the same gulf; its geomorphological structure influence waves arrival obstructing waves propagation.
4. Discussion and Conclusions
Buckley, R [
31] explained that waves and snow provide natural resources for adventure tourism and, therefore, these activities are affected by changing weather patterns—and most strikingly by those associated with climate variability and climate change. The global framework for climate services [
32], presents climate services as a way to provide climate information to help individuals and organizations to make informed decisions adapted to the varying and changing climate conditions.
Our research represents an advance in the knowledge of the expected surfing conditions in the Iberian Peninsula through a new methodology which characterizes the number of expected surfing days per year in specific surf spots. Following Butt, T [
33,
34], we attribute buoy wave data to wave height in nearby surf spots, approaching the propagation mechanisms of free-traveling swell and the radial dispersion once the swell reaches shallow water. Our results clearly define how the surfing potential in terms of weather, oceanographic and geomorphologic conditions, is not homogeneous around the Iberian Peninsula’s coast. This has obvious implications in the management of these touristic areas and provides insights into whether the surf activity may be successful. Previous studies by Peñas de Aro, P [
27] identified the distribution of surfing days in Mallorca and the research of Espejo, A [
23,
24,
25] studied the spatial and temporal variability of surfing resources around the world. We agree with them in calculating the expected surfing days for specific surf spots from BDS, we add GAS and GAC in order to validate more directly waves parameters to necessary conditions for surfing.
Espejo, A [
23,
25] found relevant distribution patterns of surfing conditions on a global scale. Conversely, our study makes a special contribution on a local scale to the science thanks to the use of citizen science data. Our validated methodology allows us to know how
Hm0 distribution matches with expected surfing days distribution around the Iberian Peninsula. We find relevant distribution patterns on surfing conditions which vary spatially and temporally. Knowing how they vary seasonally, annually and in the longer term can help decision-making within the surfing tourism industry. Results allow to evidence how climate variations can harm or benefit the activity of surfing. For example, more storms in terms of frequency and intensity on the southern and southeastern shore area will probably harm sun and beach tourism climatological/meteorological requirements. Nevertheless, this fact can produce more frequency of surfing days per year which can be an opportunity for developing this sector. For western and northern shores, the increase of storms associated with strong winds on the shore can possibly contribute to the decrease of perfect conditions for surfing.
Nevertheless, it is also important to defend the preservation of coastal surfing resources as discussed by Martin, S.A [
35] who criticized the “wonderland” in Mentawai Islands in Indonesia. Martin, S.A [
35] and Buckley, R [
31] argue that with better practice, principles of tourism development may allow new more effective foundations for surfing tourist space in pursuit of sustainable tourism development, and in this respect, the present research provides an introduction to creating a climate service for surfing tourism, which can develop the sustainable development needs for surf tourism.
Hritz, N. et al. [
36] highlight the fact that surfing tourism has increased in popularity but has received little attention related to its economic impact. This study is a step towards understanding the surf resources (number of expected surfing days) and helping produce a sustainable economic impact. In this way, the strategies for planning surfing tourism must be different, depending on the location of the surf spots.
Research has explored the advances in climate services in multiple fields but determining the frequency of surfing days around the Iberian Peninsula by attributing data from oceanographic buoys to surf spots has not been done before. Further research could focus on developing a prototype for surf tourism industry translating this historical wave study to tailored wave forecasting. The forecast data and information collected for the future surfing climate services should be transformed into customized products to assist different surfing user communities (tourist destination managers, surf schools, tourist accommodation establishments, particularly surf camps, etc.)