A Wave Input-Reduction Method Incorporating Initiation of Sediment Motion
Abstract
:1. Introduction
- Input reduction, which is based on the principle that the long-term effects of smaller-scale processes can be obtained by applying models of those smaller-scale processes forced with “representative” inputs able to reproduce the aforementioned long-term effects accurately [4].
- Model reduction, in which details of the smaller scale processes are omitted while the model simulation is performed at the scale of interest. The most commonly used acceleration technique of this type in 2-D area models is the morphological acceleration factor (Morfac, [5], which multiplies the bed level change at each time step by this factor, reducing the simulation time while simultaneously predicting the long-term evolution of the morphology.
2. Materials and Methods
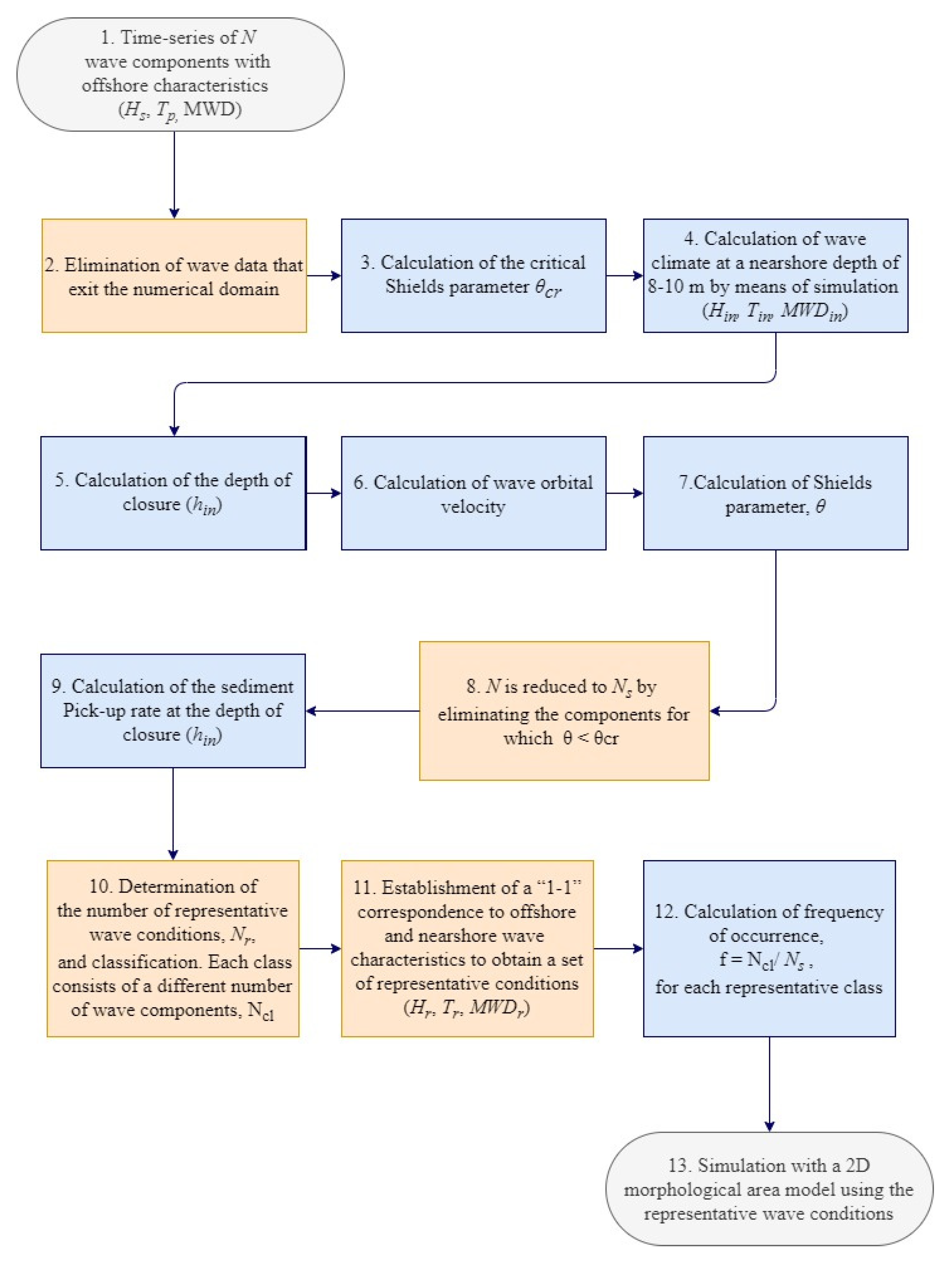
2.1. Proposed Method of Wave Schematization Based on the Sediment Pick-Up Rate
2.1.1. Theoretical Aspects
2.1.2. Layout of the Wave Schematization Method
- Wave characteristic time-series (either by buoy measurements, or hindcast/forecast simulations) are obtained for a desirable time range Ttot on a single point offshore coinciding with the open boundary of the computational domain. The minimum wave characteristics that are required by the input-reduction method are Hs, Tp (or another characteristic wave period) and MWD (mean wave direction).
- The wave time-series are then filtered by disposing of wave data that do not contribute in shaping the bed evolution, namely wave components exiting the computational domain.
- Calculation of the critical Shields parameter θcr through Equation (1).
- Wave characteristics at a characteristic depth (at around h = 8–10 m, set as h = 8 m at the present study) are obtained. For this purpose, either a wave ray model (e.g., [29], a spectral wave model (e.g., [30,31,32], or a mild slope wave model [33,34] can be used. Here we use the parabolic mild slope model with non-linear dispersion characteristics MARIS-PMS. The reason for utilizing this model is the accuracy in prescribing the wave field in mildly sloping beaches due to incorporation of non-linearity and the saving of considerable computational time relatively to the time-dependent formulations of the aforementioned categories of models. After obtaining the wave climate in the nearshore area a “1-1” correspondence between each wave component offshore (Hs, Tp, MWD) and the wave characteristics at the characteristic depth (Hin, Tin, MWDin), is established.
- Calculation of the depth of closure (hin) for the particular time-series through the following equation, which is defined as the seaward limit of the littoral zone [35]:where hin [m] is the depth of closure and [m] is the mean significant wave height at a characteristic depth h = 8–10 m, utilizing the wave characteristics calculated at step 4. The depth of closure was considered for the purpose of this research the critical depth after which no net sediment movement takes places. Consequently this depth will be later set for the calculation of the wave orbital velocity since the larger proportion of sediment transport takes place between hin and the shoreline.
- Calculate the wave orbital velocity signal near the bed through Equation (3) for monochromatic or Equation (4) for spectral waves setting h = hin.
- For each wave component (Hin, Tin, MWDin) the friction factor fw (Equation (9)), the bed shear stress due to waves τb,w (Equation (7)) and ultimately the Shields parameter θ (Equation (10)), are calculated
- If the θ < θcr the wave component is eliminated since it does not contribute in sediment motion. Through the “1-1” correspondence established at step 4, dispose the relative wave condition of the offshore time-series. The total number of wave components offshore N is thus reduced using the criterion of the initiation of motion at a total of Ns (with Ns ≤ N)
- Calculation of the sediment pick-up rate Ein through Equation (11) for each wave component at the depth of closure. Also the cumulative pick-up rate E for the aforementioned wave conditions is determined.
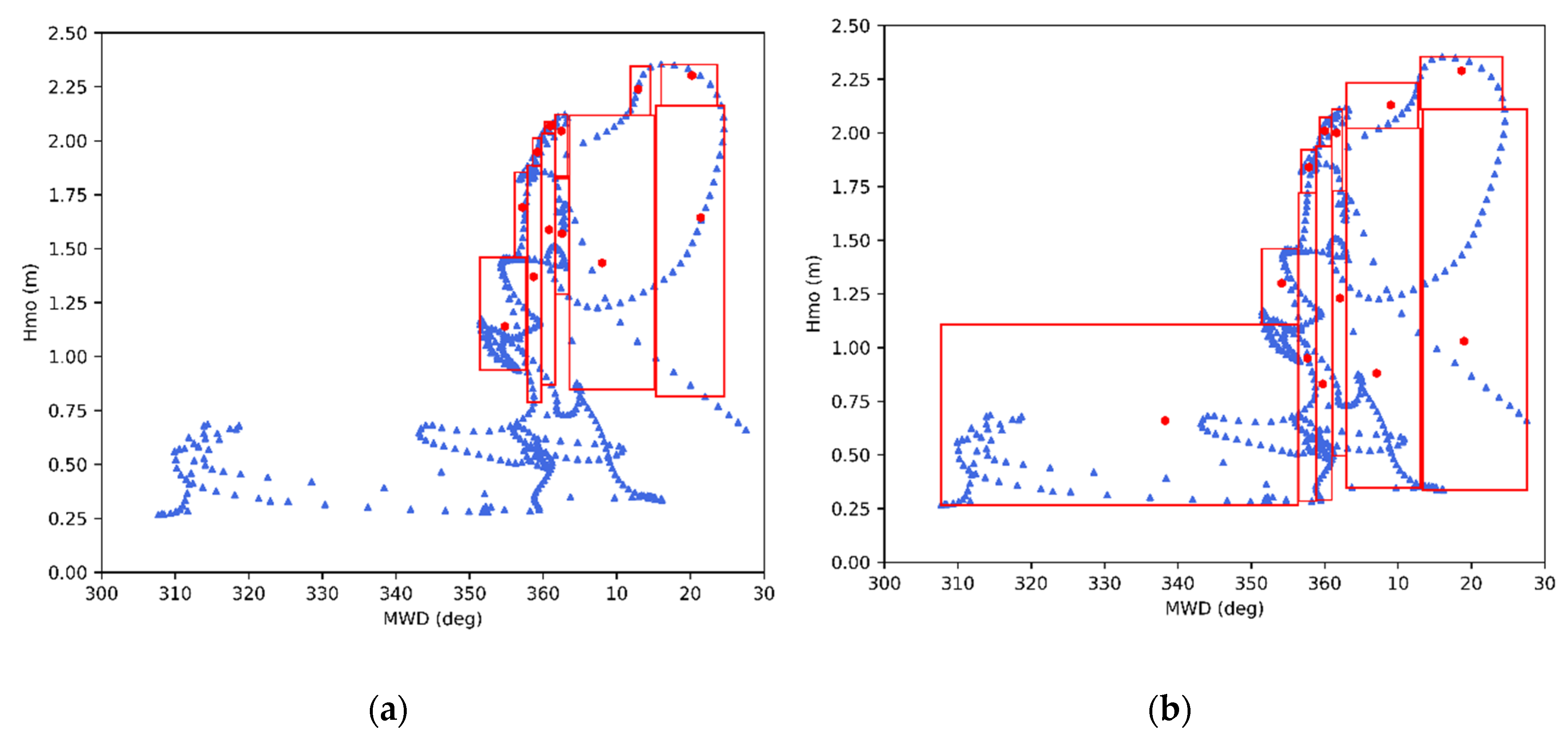
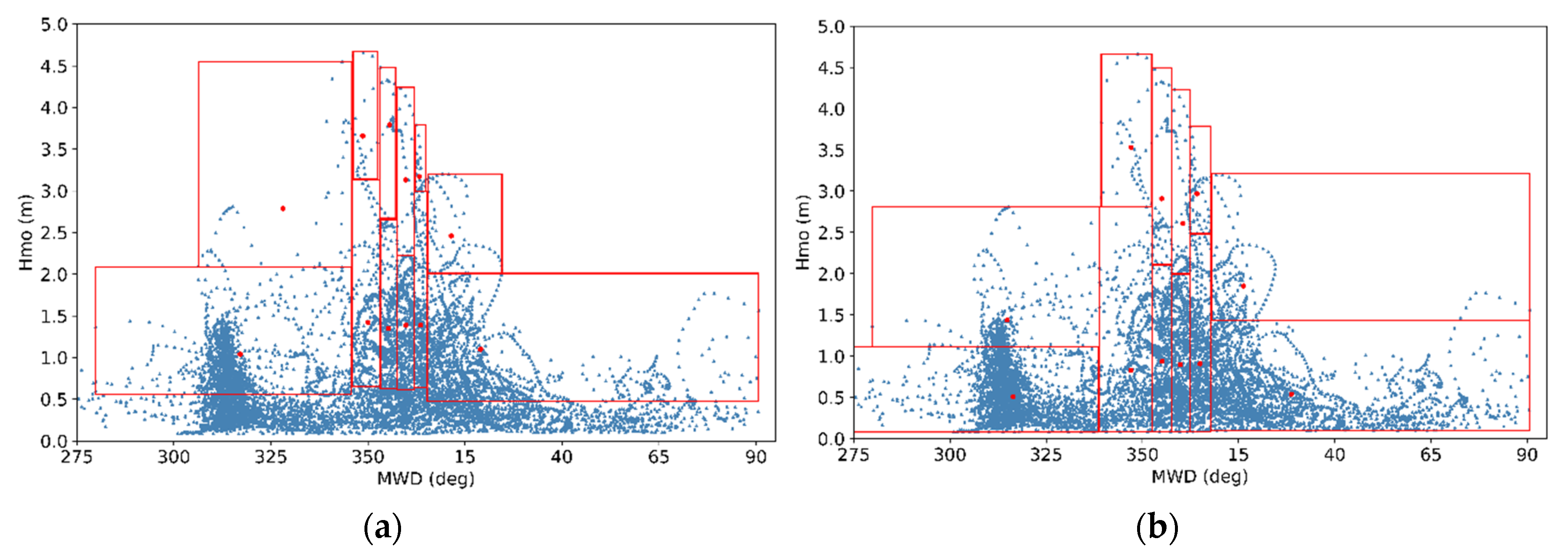
- The number of representative wave conditions Nr that will replace the full wave climate (e.g., 12 representative conditions) are determined. The number of representative conditions is based on discretion, however it is advised that a number between 6 and 30 conditions is chosen for sufficiently accurate model results regarding yearly wave climates [12]. Then, the wave components are divided in classes with respect to wave direction and wave height. The boundaries of each class in both direction and wave heights are determined the same wave as the energy-flux wave schematization method (see Section 2.2 for details). Each representative class is characterized by an equal fraction of the cumulative pick-up rate E (E/Nr) and can be described by a set of wave characteristics (Hr,in, Tr,in, MWDr,in). Thus, it can be derived that each class consists of a different number of wave components, Ncl.
- Utilizing again the “1-1” correspondence of wave characteristics offshore and nearshore, we can obtain a set of representative conditions (Hr, Tr, MWDr) in the offshore wave boundary by considering that the bounding limits of each representative class in the depth of closure coincide with the respective ones in deep water. A small numerical extrapolation error stems from the fact that each representative class in the offshore boundary might not be characterized by exactly equal fraction of sediment pick-up rate, since the pick-up rate was calculated for the corresponding wave conditions at shallower water. However, since the proposed input-reduction method concerns medium to long-term morphological bed changes, this error is considered to have a very small effect in shaping the ultimate bed evolution and thus can be neglected.
- The frequency of occurrence for each representative class is calculated, based on the wave components of each class relatively to the full set of conditions.
- Finally the simulation is executed with a 2D morphological area model using the representative wave conditions as forcing input. The total model run-time Ttot,r is a fraction of the full time series, denoted as , since wave components unable to initiate sediment movement are eliminated in step 8 and have little to no contribution in shaping the bed evolution.
2.2. The Energy Flux Wave Schematization Method (Benchmark Reduction Method)
- Calculation of the wave energy flux for each wave component of a time-series,where [kg/m3] is the water density, [m] is the significant wave height and [m/s] is the wave group celerity in deep water,
- Calculation of the total wave energy flux of the full wave time-series through:
- Division of the wave components in wave direction bins. For a predefined number of directional bins the time series are separated in bins, each consisting of an equal fraction of the total energy flux Further division of the data in wave height bins. Separation is carried out for a predefined number of wave height bins with each bin characterized by an equal fraction of the total energy flux
- A representative wave height for each bin is derived from the mean energy flux of the bin along with a mean energy-flux direction. The representative wave period is then defined as the mean period of the bin.
2.3. Theoretical Background of Numerical Models
2.3.1. The MIKE21 Coupled Model FM Suite
- MIKE21 SW, a 3rd generation spectral wave model based on the conservation of the wave action balance, suited for the propagation and transformation of waves in the coastal zone.
- MIKE21 HD, a depth-averaged hydrodynamic model based on the Reynolds-averaged Navier–Stokes equations of motion (RANS), for the description of the nearshore circulation.
- MIKE21 ST, a sand transport and morphology updating model, used to calculate sediment transport rates and ultimately the morphological bed evolution.
2.3.2. The MARIS-PMS Wave Model
3. Method Implementation
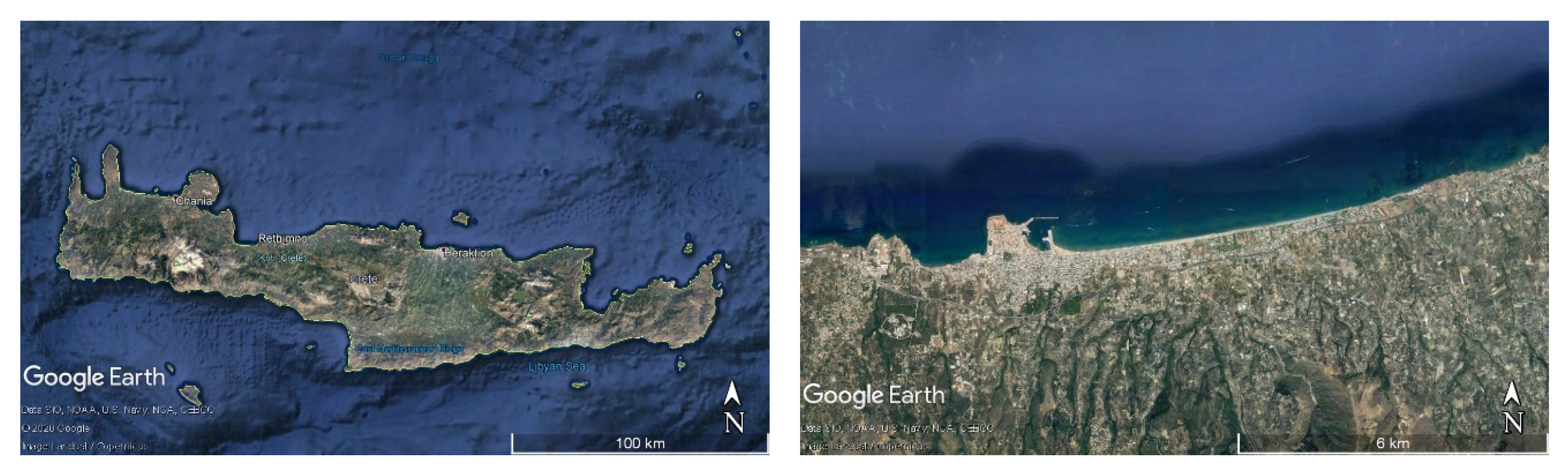
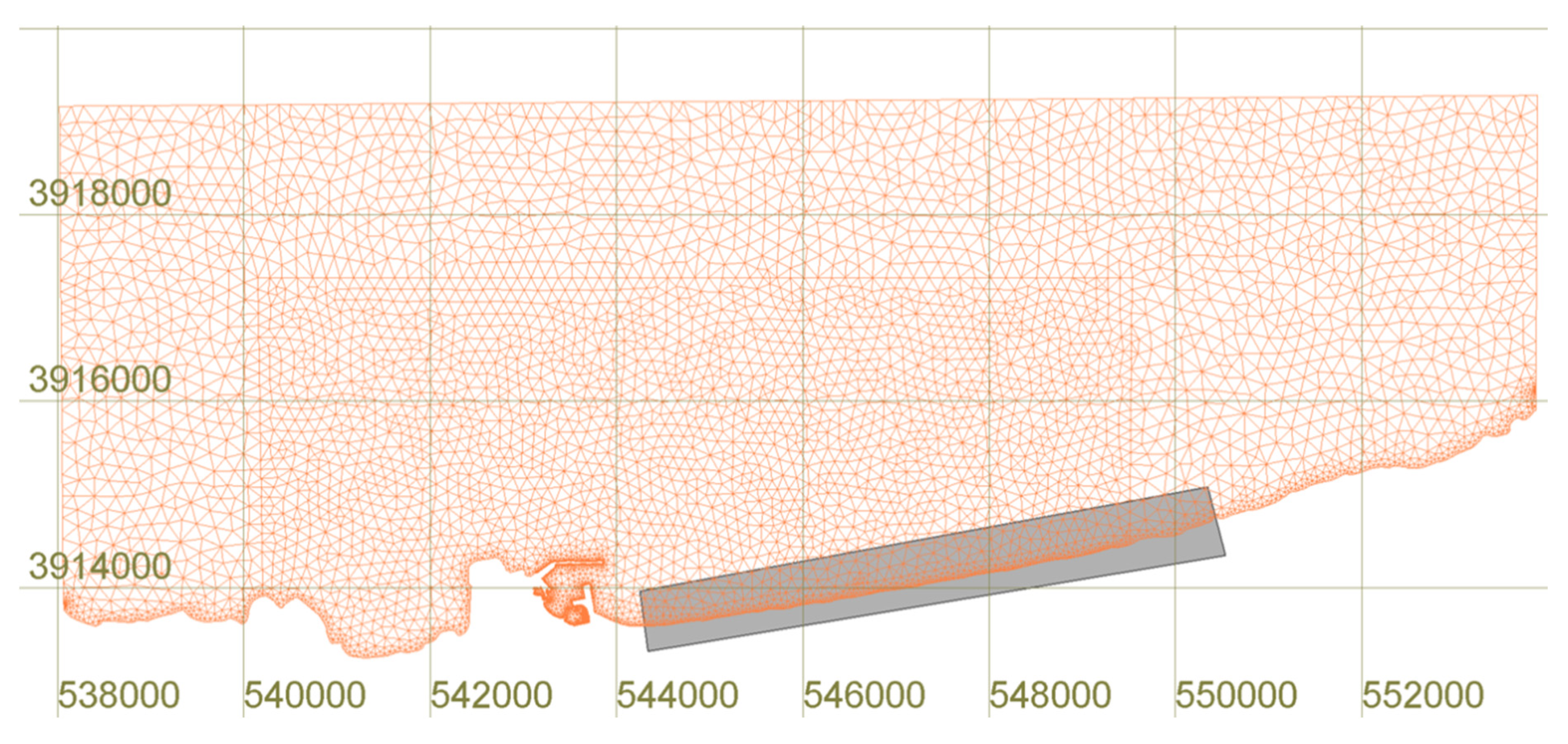
3.1. Study Area
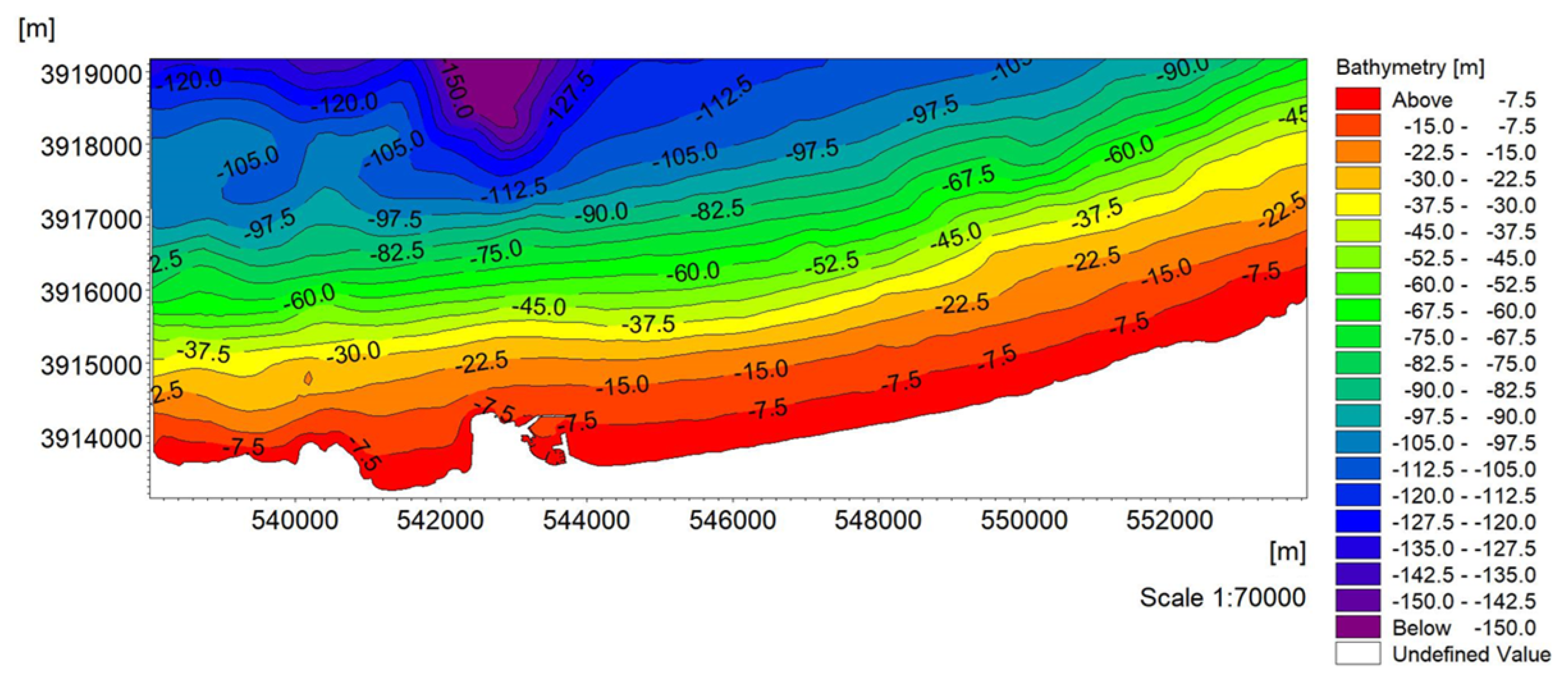
3.2. Mesh Generation
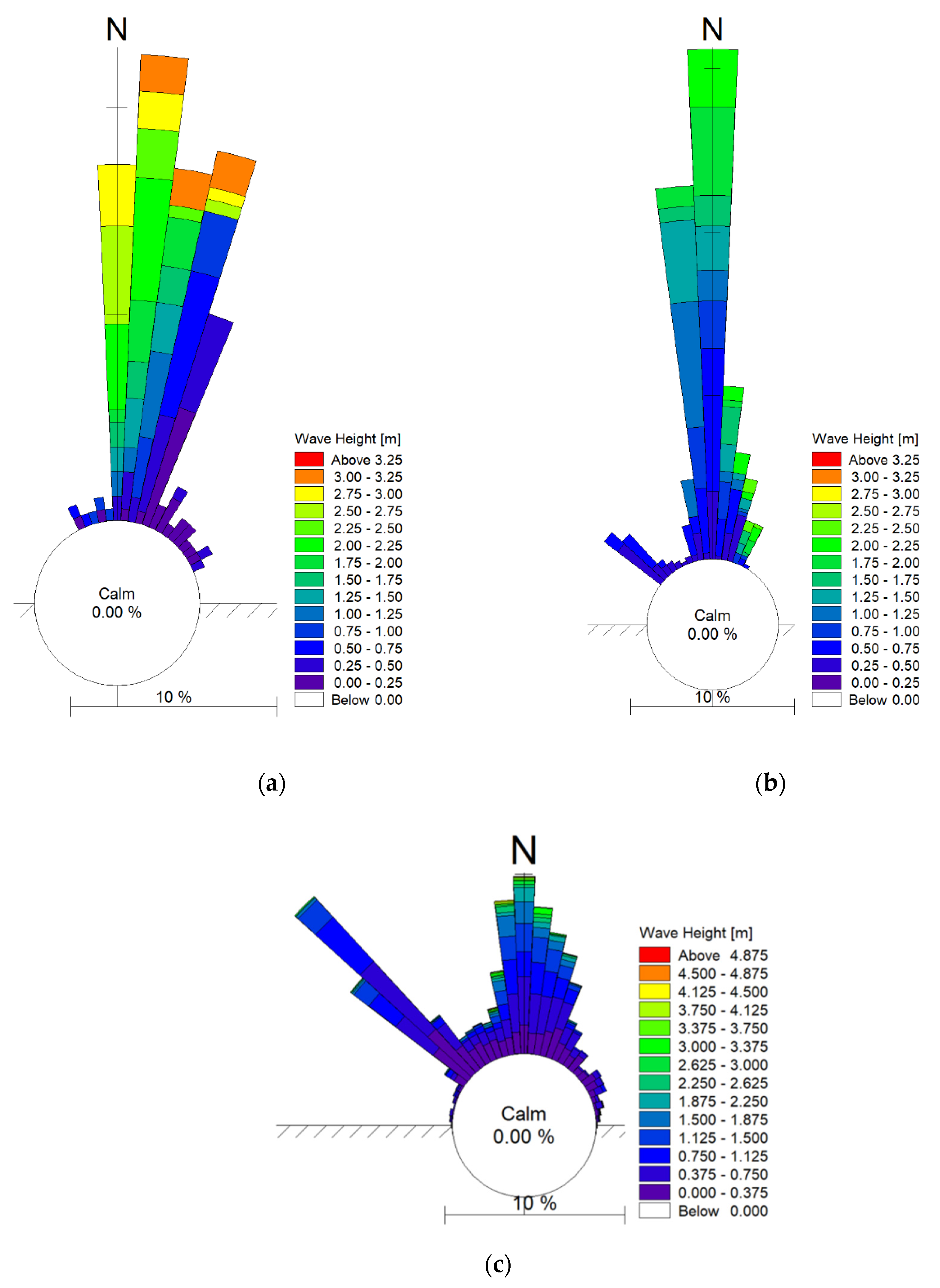
3.3. Offshore Wave Data
- A simulation consisting of the full time series at the offshore boundary, hereafter denoted as Reference simulation
- A simulation using 12 representatives as forcing parameters calculated with the pick-up rate method, hereafter called pick-up rate simulation
- A simulation using 12 representatives calculated with the energy-flux input-reduction method, hereafter denoted as energy-flux simulation, to assess how the pick-up rate method fares against a well-established wave schematization technique.
3.4. Obtained Representative Wave Conditions
4. Results and Discussion
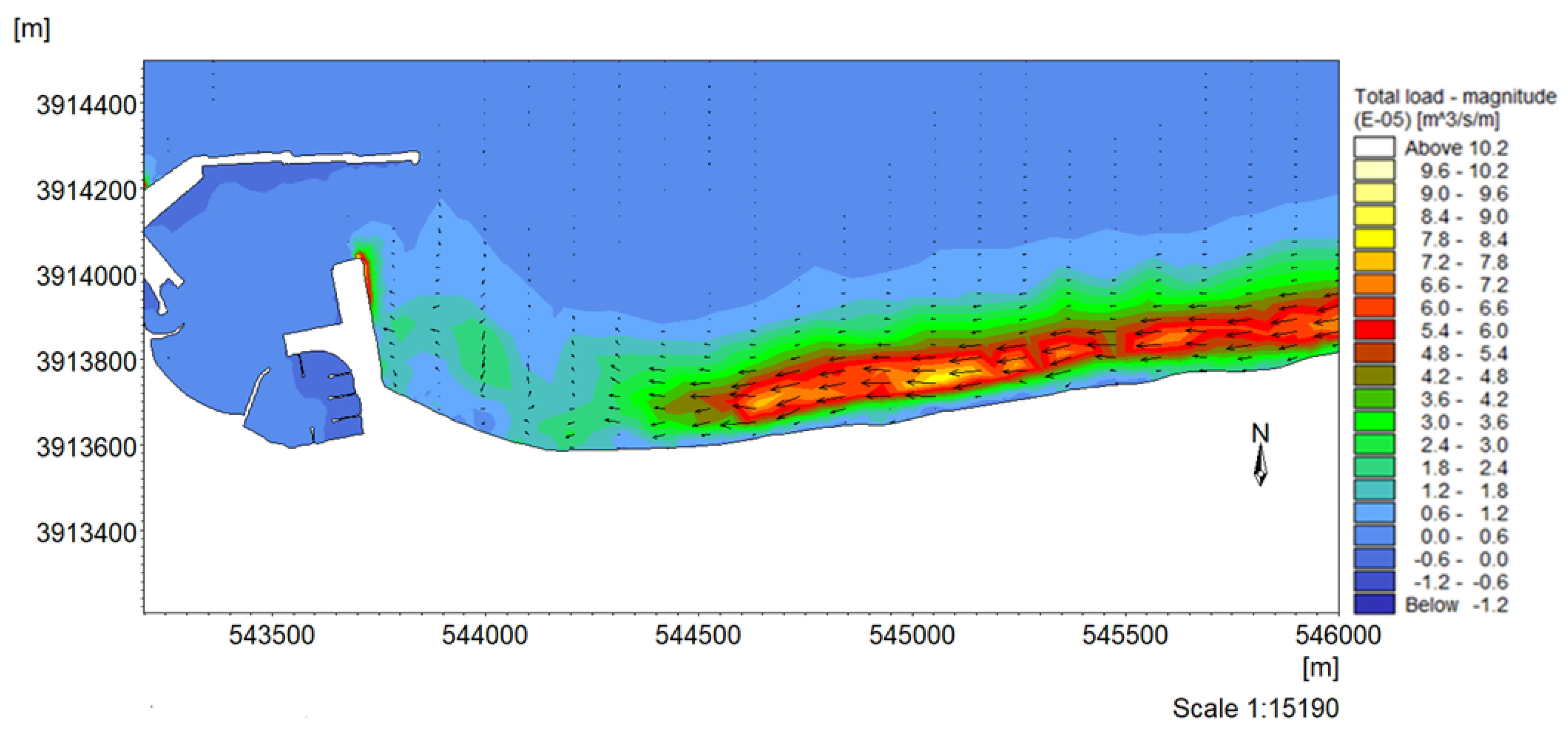
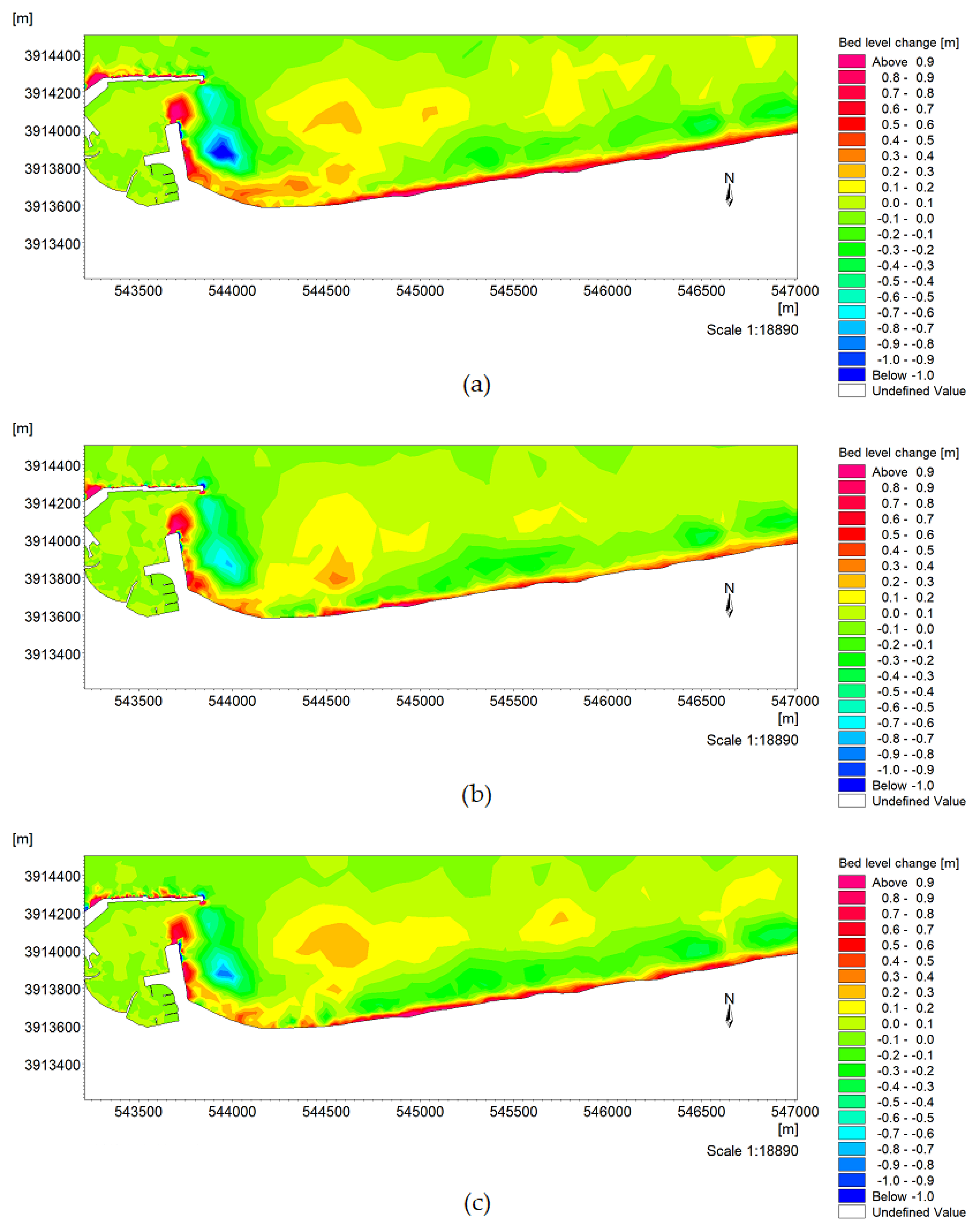
4.1. Morphological Bed Evolution for the Dataset of Seven Days
4.2. Morphological Bed Evolution for the Dataset of 20 Days
4.3. Morphological Bed Evolution for the Dataset of a Year
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Drønen, N.; Kristensen, S.; Taaning, M.; Elfrink, B.; Deigaard, R. Long term modeling of shoreline response to coastal structures. In Proceedings of the Coastal Sediments Conference, Miami, FL, USA, 2–6 May 2011. [Google Scholar]
- Lesser, G.R. An Approach to Medium-Term Coastal Morphological Modelling. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 4 June 2009. [Google Scholar]
- de Vriend, H.J.; Zyserman, J.; Nicholson, J.; Roelvink, J.A.; Péchon, P.; Southgate, H.N. Medium-term 2DH coastal area modelling. Coast. Eng. 1993, 21, 193–224. [Google Scholar] [CrossRef] [Green Version]
- Roelvink, D.; Reniers, A. A Guide to Modeling Coastal Morphology, 1st ed.; Word Scientific: Singapore, 2012; p. 292. [Google Scholar]
- Lesser, G.R.; Roelvink, J.A.; van Kester, J.A.T.M.; Stelling, G.S. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Prasad, R.S.; Svendsen, I.A. Moving shoreline boundary condition for nearshore models. Coast. Eng. 2003, 49, 239–261. [Google Scholar] [CrossRef]
- Casulli, V. A high-resolution wetting and drying algorithm for free surface hydrodynamics. Internat. J. Numer. Methods Fluids 2009, 60, 391–408. [Google Scholar] [CrossRef]
- Copernicus Marine Environment Monitoring Service. Available online: http://marine.copernicus.eu/ (accessed on 19 December 2019).
- ECMWF. Available online: https://www.ecmwf.int/ (accessed on 19 December 2019).
- Walstra, D.J.R.; Hoekstra, R.; Tonnon, P.K.; Ruessink, B.G. Input reduction for long-term morphodynamic simulations in wave-dominated coastal settings. Coast. Eng. 2013, 77, 57–70. [Google Scholar] [CrossRef]
- Brown, J.M.; Davies, A.G. Methods for medium-term prediction of the net sediment transport by waves and currents in complex coastal regions. Cont. Shelf Res. 2009, 29, 1502–1514. [Google Scholar] [CrossRef]
- Benedet, L.; Dobrochinski, J.P.F.; Walstra, D.J.R.; Klein, A.H.F.; Ranasinghe, R. A morphological modeling study to compare different methods of wave climate schematization and evaluate strategies to reduce erosion losses from a beach nourishment project. Coast. Eng. 2016, 112, 69–86. [Google Scholar] [CrossRef]
- Karathanasi, F.E.; Belibassakis, K.A. A cost-effective method for estimating long-term effects of waves on beach erosion with application to Sitia Bay, Crete. Oceanologia 2019, 21, 276–290. [Google Scholar] [CrossRef]
- Roelvink, J.A. Coastal morphodynamic evolution techniques. Coast. Eng. 2006, 53, 277–287. [Google Scholar] [CrossRef]
- Knaapen, M.A.F.; Joustra, R. Morphological acceleration factor: Usability, accuracy and run time reductions. In Proceedings of the XIXth TELEMAC-MASCARET User Conference, Oxford, UK, 18–19 October 2012. [Google Scholar]
- Ranasinghe, R.; Swinkels, C.; Luijendijk, A.; Roelvink, D.; Bosboom, J.; Stive, M.; Walstra, D.J. Morphodynamic upscaling with the MORFAC approach: Dependencies and sensitivities. Coast. Eng. 2011, 58, 806–811. [Google Scholar] [CrossRef]
- van Rijn, L.C. Sediment Pick-up functions. Applications of sediment Pick-up function. J. Hydraul. Eng. 1986, 112, 867–874. [Google Scholar] [CrossRef]
- van Rijn, L.C.; Bisschop, R.; van Rhee, C. Modified Sediment Pick-Up Function. J. Hydraul. Eng. 2019, 145, 060180171–060180176. [Google Scholar] [CrossRef]
- DHI Coupled Model FM (MIKE 21/3 FM). User Guide; DHI: Hørsholm, Denmark, 2017. [Google Scholar]
- Chondros, M.; Metallinos, A.; Karambas, T.; Memos, C.; Papadimitriou, A. Advanced numerical models for simulation of nearshore processes. In Proceedings of the Design and Management of Port, Coastal and Offshore Works Conference, Athens, Greece, 8–11 May 2019. [Google Scholar]
- Soulsby, R.L. Dynamics of Marine Sands: A Manual for Practical Applications, 1st ed.; Thomas Telford: London, UK, 1997; p. 249. [Google Scholar]
- Shields, I.A. Anwendung der Ahnlichkeits-Mechanik und der Turbulenzforschung auf die Geschiebebewegung. Ph.D. Thesis, Technical University of Berlin, Berlin, Germany, 30 June 1936. [Google Scholar]
- Soulsby, R.L.; Whitehouse, R.J. Threshold of sediment motion in coastal environments. In Proceedings of the 13th Australasian Coastal and Ocean Engineering Conference and the 6th Australasian Port and Harbour Conference, Canterbury, UK, 28–30 September 1997. [Google Scholar]
- Soulsby, R.L. Calculating bottom orbital velocity beneath waves. Coast. Eng. 1987, 11, 371–380. [Google Scholar] [CrossRef]
- Soulsby, R.L.; Smallman, J.V. A Direct Method of Calculating Bottom Orbital Velocity under Waves; Technical Report No SR 76; Hydraulics Research Limited: Wallingford, Oxfordshire, UK, February 1986. [Google Scholar]
- Swart, D.H. Offshore Sediment Transport and Equilibrium Beach Profiles. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 18 December 1974. [Google Scholar]
- Nielsen, P. Coastal Bottom Boundary Layers and Sediment Transport, 1st ed.; Advanced Series on Ocean Engineering; World Scientific: Singapore, 1992; Volume 4, p. 340. [Google Scholar]
- van Rijn, L.C. Sediment Pick-Up Functions. J. Hydraul. Eng. 1984, 110, 1494–1502. [Google Scholar] [CrossRef]
- O’Reilly, W.C.; Guza, R.T. Comparison of spectral refraction and refraction-diffraction wave models. J. Waterw. Port Coast. Ocean Eng. 1991, 117, 199–215. [Google Scholar] [CrossRef] [Green Version]
- Tolman, H.L. A Third-Generation Model for Wind Waves on Slowly Varying, Unsteady, and Inhomogeneous Depths and Currents. J. Phys. Oceanogr. 1991, 21, 782–797. [Google Scholar] [CrossRef]
- Benoit, M.; Marcos, F.; Becq, F. Development of a Third Generation Shallow-Water Wave Model with Unstructured Spatial Meshing. In Proceedings of the 25th International Conference on Coastal Engineering, Orlando, FL, USA, 2–6 September 1996. [Google Scholar]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions 1. Model description and validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef] [Green Version]
- Karambas, T.V.; Samaras, A.G. An integrated numerical model for the design of coastal protection structures. J. Mar. Sci. Eng. 2017, 5, 50. [Google Scholar] [CrossRef]
- Chondros, M.K.; Metallinos, A.S.; Memos, C.D.; Karambas, T.V.; Papadimitriou, A.G. Concerted nonlinear mild-slope wave models for enhanced simulation of coastal processes. Appl. Math. Model. 2020. accepted for publication. [Google Scholar]
- Houston, J.R. Beach-Fill Volume Required to Produce Specific Dry Beach Width; Coastal Engineering Technical Note II-32; US Army Corps Engineer Waterways Experiment Station: Vicksburg, MS, USA, March 1995. [Google Scholar]
- Dobrochinski, J.P.H. Wave Climate Reduction and Schematization for Morphological Modeling. Master’s Thesis, Universidade do Vale do Itajaí & Delft University of Technology, Delft, The Netherlands, 2009. [Google Scholar]
- Kaergaard, K.; Mortensen, S.B.; Kristensen, S.E.; Deigaard, R.; Teasdale, R.; Hunt, S. Hybrid shoreline modelling of shoreline protection Schemes, Palm Beach, Queensland, Australia. In Proceedings of the Coastal Engineering Conference, Seoul, Korea, 15–20 June 2014. [Google Scholar]
- Gad, F.-K.; Hatiris, G.-A.; Loukaidi, V.; Dimitriadou, S.; Drakopoulou, P.; Sioulas, A.; Kapsimalis, V. Long-Term Shoreline Displacements and Coastal Morphodynamic Pattern of North Rhodes Island, Greece. Water 2018, 10, 849. [Google Scholar] [CrossRef] [Green Version]
- DHI 21&3 Spectral Wave Module. Scientific Documentation; DHI: Hørsholm, Denmark, 2009. [Google Scholar]
- Komen, G.J.; Cavaleri, L.; Donelan, M.; Hasselmann, K.; Hasselmann, S.; Janssen, P.A.E.M. Dynamics and Modelling of Ocean Waves; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- DHI 21&3 Flow Model FM, Hydrodynamic and Transport Module. Scientific Documentation; DHI: Hørsholm, Denmark, 2009. [Google Scholar]
- DHI 21&3 Flow Model FM, Sand Transport Module. Scientific Documentation; DHI: Hørsholm, Denmark, 2009. [Google Scholar]
- Kirby, J.T.; Dalrymple, R.A. A parabolic equation for the combined refraction diffraction of Stokes waves by mildly varying topography. J. Fluid Mech. 1983, 136, 453–466. [Google Scholar] [CrossRef] [Green Version]
- Dalrymple, R.A.; Kirby, J.T. Models for very wide-angle water waves and wave diffraction. J. Fluid Mech. 1988, 201, 299–322. [Google Scholar] [CrossRef] [Green Version]
- Kirby, J.T. Rational approximations in the parabolic equation method for water waves. Coast. Eng. 1986, 10, 355–378. [Google Scholar] [CrossRef]
- Battjes, J.A.; Janssen, J.P.F.M. Energy Loss and Set-Up Due To Breaking of Random Waves. In Proceedings of the Coastal Engineering Conference, Hamburg, Germany, 27 August–3 September 1979. [Google Scholar]
- Putnam, J.A.; Johson, J.W. The dissipation of wave energy by bottom friction. Eos Trans. Am. Geophys. Union 1949, 30, 67–74. [Google Scholar] [CrossRef]
- Kirby, J.T.; Dalrymple, R.A. An approximate model for nonlinear dispersion in monochromatic wave propagation models. Coast. Eng. 1986, 9, 545–561. [Google Scholar] [CrossRef]
- Svendsen, I.A.; Hansen, J.B. Deformation up to breaking of periodic waves on a beach. In Proceedings of the Coastal Engineering Conference, Honolulu, HI, USA, 11–17 July 1976. [Google Scholar]
- Svendsen, I.A.; Qin, W.; Ebersole, B.A. Modelling waves and currents at the LSTF and other laboratory facilities. Coast. Eng. 2003, 50, 19–45. [Google Scholar] [CrossRef]
- Bell, P.; Williams, J.; Clark, S.; Morris, B.; Vila-Concejo, A. Nested Radar Systems for Remote Coastal Observations. J. Coast. Res. 2006, 39, 483–487. [Google Scholar]
- Svendsen, I.A.; Madsen, P.A.; Buhr Hansen, J. Wave characteristics in the surf zone. In Proceedings of the Coastal Engineering Conference, Hamburg, Germany, 27 August–3 September 1979. [Google Scholar]
- Kraus, N.C.; Larson, M.; Wise, R.A. Depth of Closure in Beach-Fill Design; Coastal Engineering Technical Note II-40; US Army Corps Engineer Waterways Experiment Station: Vicksburg, MS, USA, March 1998. [Google Scholar]
- Google Earth. Image ©2020 Landsat/Coppernicus, Data SIO, NOAA, U.S. Navy, NGA, GEBCO. 2020. [Google Scholar]
- QGIS. Available online: https://qgis.org/ (accessed on 17 December 2019).
- NAVIONICS Chart Viewer. Available online: https://webapp.navionics.com/ (accessed on 9 January 2020).
- Ravdas, M.; Zacharioudaki, A.; Korres, G. Implementation and validation of a new operational wave forecasting system of the Mediterranean Monitoring and Forecasting Centre in the framework of the Copernicus Marine Environment Monitoring Service. Nat. Hazards Earth Syst. Sci. 2018, 18, 2675–2695. [Google Scholar] [CrossRef] [Green Version]
- WAMDI Group. The WAM model—A third generation ocean wave prediction model. J. Phys. Ocean. 1988, 18, 1775–1810. [Google Scholar] [CrossRef] [Green Version]
- Sutherland, J.; Peet, A.H.; Soulsby, R.L. Evaluating the performance of morphological models. Coast. Eng. 2004, 51, 917–939. [Google Scholar] [CrossRef]
- Sutherland, J.; Walstra, D.J.R.; Chesher, T.J.; Van Rijn, L.C.; Southgate, H.N. Evaluation of coastal area modelling systems at an estuary mouth. Coast. Eng. 2004, 51, 119–142. [Google Scholar] [CrossRef] [Green Version]
- van Rijn, L.C.; Wasltra, D.J.R.; Grasmeijer, B.; Sutherland, J.; Pan, S.; Sierra, J.P. The predictability of cross-shore bed evolution of sandy beaches at the time scale of storms and seasons using process-based profile models. Coast. Eng. 2003, 47, 295–327. [Google Scholar] [CrossRef]
- Smit, P.B.; Janssen, T.T. The evolution of inhomogeneous wave statistics through a variable medium. J. Phys. Oceanogr. 2013, 43, 1741–1758. [Google Scholar] [CrossRef] [Green Version]
- Metallinos, A.S.; Chondros, M.K.; Karambas, T.V.; Memos, C.D.; Papadimitriou, A.G. Advanced numerical models for wave disturbance simulation in port basins. In Proceedings of the Design and Management of Port, Coastal and Offshore works Conference, Athens, Greece, 8–11 May 2019. [Google Scholar]
| Class | Pick-up Rate Method Representatives | Energy Flux Method Representatives | ||||||
|---|---|---|---|---|---|---|---|---|
| Hmo (m) | Tp (s) | MWD (°) | Frequency (%) | Hmo (m) | Tp (s) | MWD (°) | Frequency (%) | |
| 1st | 1.78 | 6.96 | 1.30 | 14.94 | 1.23 | 5.87 | 357.57 | 10.84 |
| 2nd | 2.77 | 8.20 | 1.65 | 4.60 | 2.55 | 8.09 | 1.46 | 3.01 |
| 3rd | 2.51 | 7.63 | 2.35 | 5.75 | 2.53 | 7.63 | 2.31 | 3.61 |
| 4th | 2.77 | 8.01 | 2.01 | 4.60 | 2.78 | 8.01 | 1.93 | 2.41 |
| 5th | 2.30 | 7.53 | 3.27 | 8.05 | 1.96 | 7.09 | 3.69 | 6.02 |
| 6th | 2.94 | 8.39 | 3.24 | 3.45 | 2.76 | 8.09 | 2.99 | 3.01 |
| 7th | 1.74 | 6.99 | 4.85 | 19.54 | 1.44 | 6.38 | 5.14 | 10.24 |
| 8th | 2.65 | 8.01 | 4.73 | 4.60 | 2.88 | 8.20 | 5.35 | 2.41 |
| 9th | 1.70 | 7.12 | 8.47 | 18.39 | 1.44 | 6.69 | 8.86 | 10.24 |
| 10th | 3.19 | 8.39 | 8.50 | 2.30 | 2.90 | 8.01 | 8.62 | 2.41 |
| 11th | 1.88 | 6.89 | 12.78 | 10.34 | 0.52 | 4.77 | 21.63 | 43.37 |
| 12th | 3.16 | 7.63 | 12.49 | 3.45 | 3.08 | 7.63 | 14.37 | 2.44 |
| BSS | |
|---|---|
| Excellent | 1.0–0.5 |
| Good | 0.5–0.2 |
| Reasonable/fair | 0.2–0.1 |
| Poor | 0.1–0.0 |
| Bad | <0.0 |
| Pick-Up Rate Method | Energy Flux Method | |
|---|---|---|
| Bias | −0.0054 | −0.0101 |
| MAE(Y,X) | 0.0218 | 0.0233 |
| MSE(Y,X) | 0.0018 | 0.0020 |
| RMSE(Y,X) | 0.0429 | 0.0450 |
| BSS | 0.9300 | 0.9200 |
| Pick-Up Rate Method | Energy Flux Method | |
|---|---|---|
| Bias | −0.0177 | −0.0058 |
| MAE(Y,X) | 0.0633 | 0.0535 |
| MSE(Y,X) | 0.0096 | 0.0066 |
| RMSE(Y,X) | 0.0980 | 0.0813 |
| BSS | 0.8300 | 0.8800 |
| Pick-Up Rate Method | Energy Flux Method | |
|---|---|---|
| Bias | −0.2316 | −0.1441 |
| MAE(Y,X) | 0.2661 | 0.1885 |
| MSE(Y,X) | 0.1070 | 0.0614 |
| RMSE(Y,X) | 0.3272 | 0.2478 |
| BSS | 0.7445 | 0.8535 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadimitriou, A.; Panagopoulos, L.; Chondros, M.; Tsoukala, V. A Wave Input-Reduction Method Incorporating Initiation of Sediment Motion. J. Mar. Sci. Eng. 2020, 8, 597. https://doi.org/10.3390/jmse8080597
Papadimitriou A, Panagopoulos L, Chondros M, Tsoukala V. A Wave Input-Reduction Method Incorporating Initiation of Sediment Motion. Journal of Marine Science and Engineering. 2020; 8(8):597. https://doi.org/10.3390/jmse8080597
Chicago/Turabian StylePapadimitriou, Andreas, Loukianos Panagopoulos, Michalis Chondros, and Vasiliki Tsoukala. 2020. "A Wave Input-Reduction Method Incorporating Initiation of Sediment Motion" Journal of Marine Science and Engineering 8, no. 8: 597. https://doi.org/10.3390/jmse8080597
APA StylePapadimitriou, A., Panagopoulos, L., Chondros, M., & Tsoukala, V. (2020). A Wave Input-Reduction Method Incorporating Initiation of Sediment Motion. Journal of Marine Science and Engineering, 8(8), 597. https://doi.org/10.3390/jmse8080597






