Transformation of Infragravity Waves during Hurricane Overwash
Abstract
:1. Introduction
2. Field Observations
2.1. Study Sites
2.2. Instrumentation
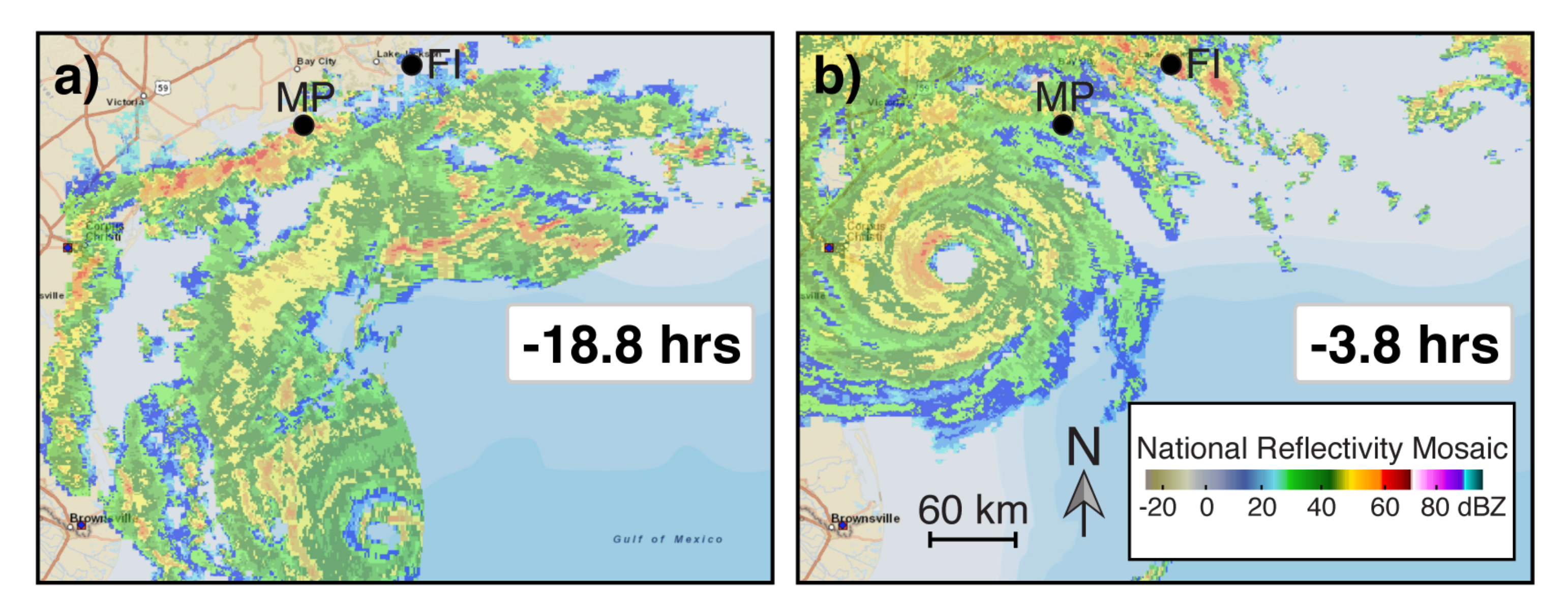
2.3. Overview of Storm Impacts
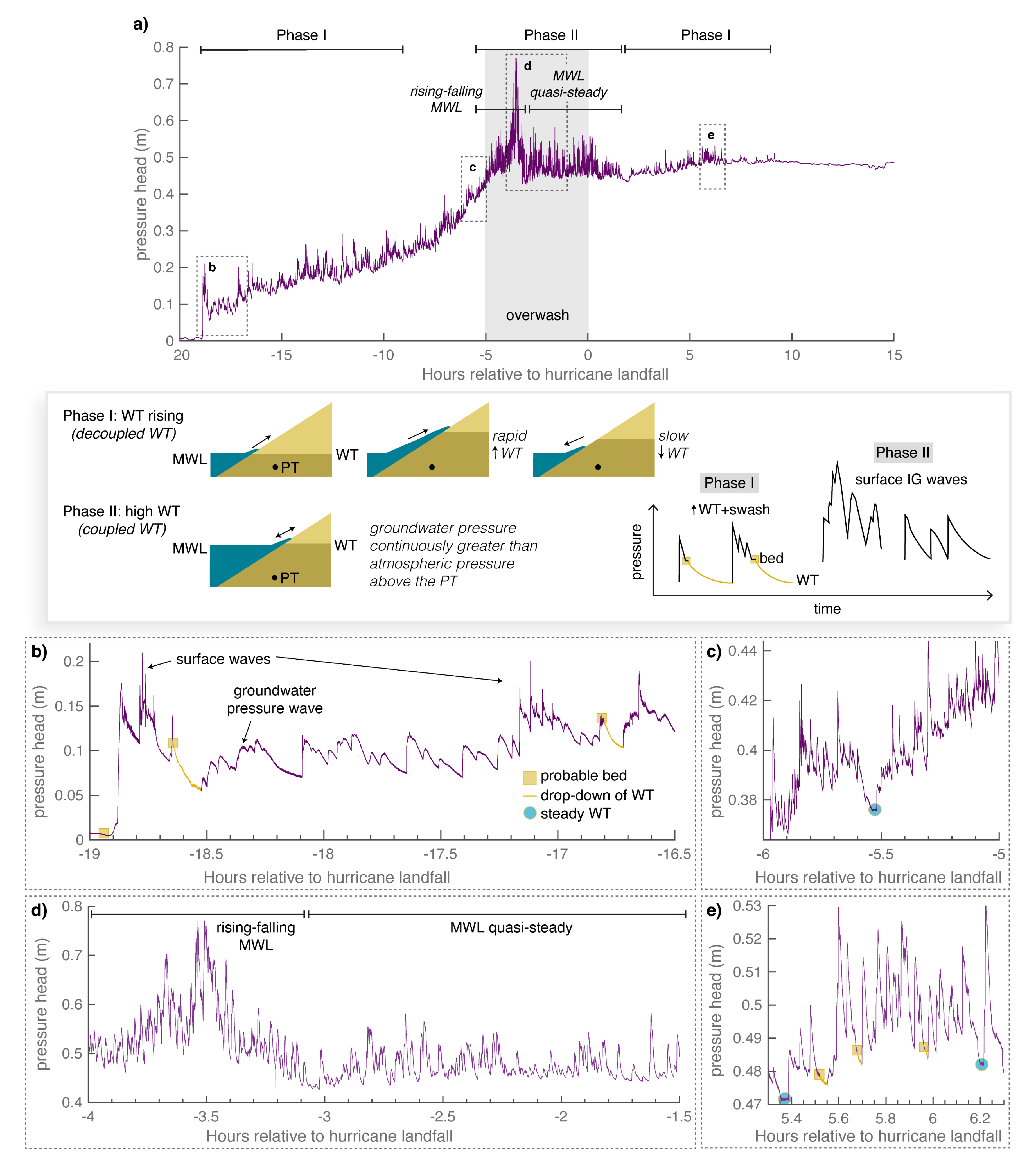
2.4. Groundwater Effects and Bed Level Change at PT-1
3. Methods
3.1. Wave Statistics
3.2. Spectral Estimation
3.3. Multitaper Bispectral Estimation
4. Results
4.1. Surf Zone Wave Fields
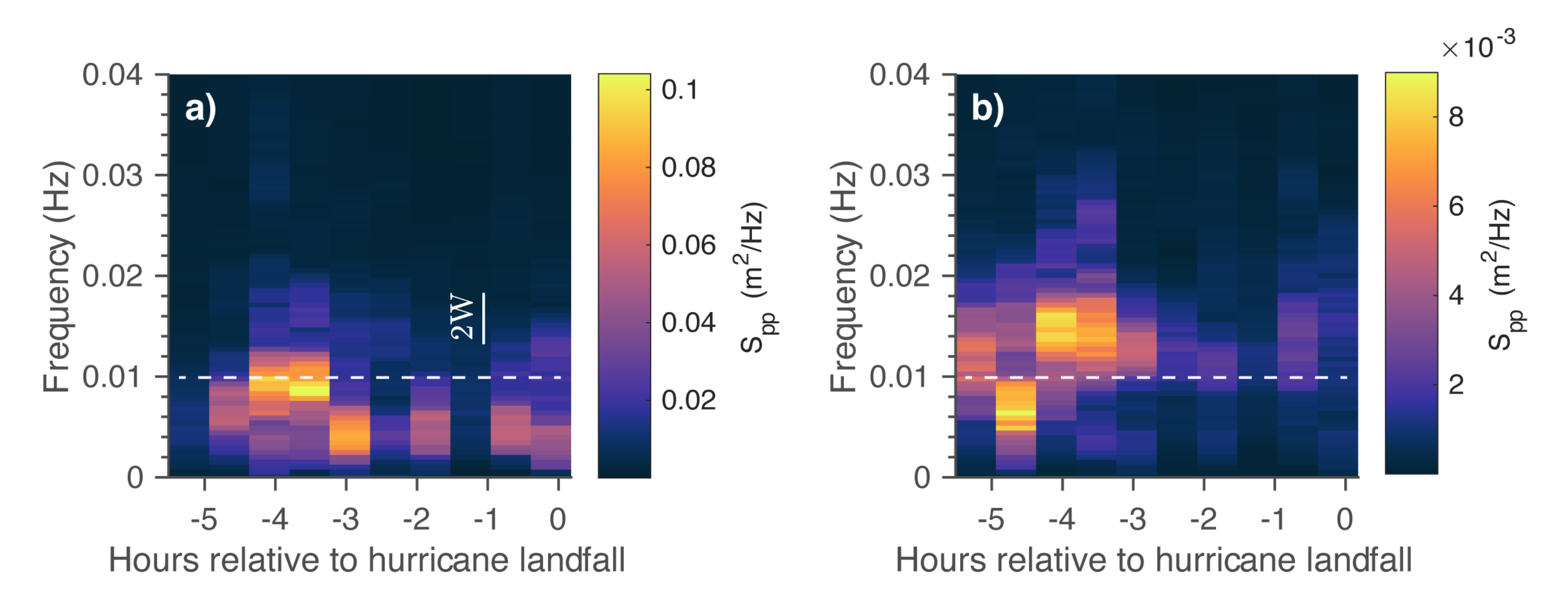
4.2. IG Wave Transformation during Overwash
5. Discussion
5.1. Cross-Barrier Changes in IG Energy during Overwash
5.2. Importance and Origin of VLF Variability
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Zero-Level Bicoherence for the Multitaper Method
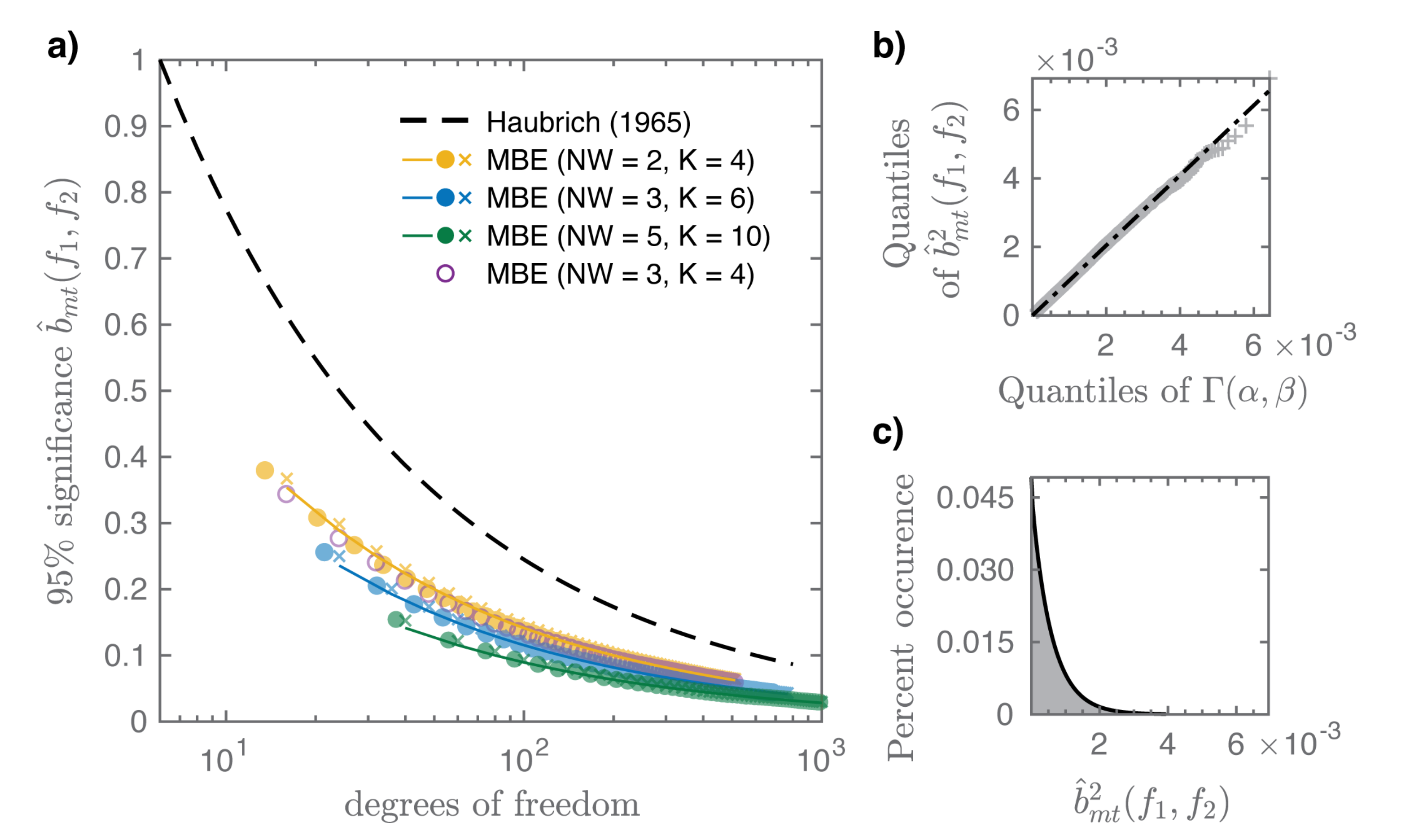
| [95% CL] | [95% CL] | |||
|---|---|---|---|---|
| 2 | 1 | 0.00130 | 0.99 [0.98 1.01] | 0.00135 [0.00133 0.00137] |
| 3 | 1 | 0.00058 | 0.99 [0.97 1.00] | 0.00060 [0.00058 0.00061] |
References
- Sallenger, A.H., Jr. Storm impact scale for barrier islands. J. Coast. Res. 2000, 16, 890–895. [Google Scholar]
- Holland, K.T.; Holman, R.A.; Sallenger, A.H. Estimation of overwash bore velocities using video techniques. In Coastal Sediments; American Society of Civil Engineers: Reston, VA, USA, 1991; pp. 489–497. [Google Scholar]
- Hoekstra, P.; Haaf, M.T.; Buijs, P.; Oost, A.; Breteler, R.K.; van der Giessen, K.; van der Vegt, M. Washover development on mixed-energy, mesotidal barrier island systems. In Proceedings of the Coastal Dynamics 2009: Impacts of Human Activities on Dynamic Coastal Processes; World Scientific: Singapore, 2009; pp. 1–12. [Google Scholar] [CrossRef]
- Matias, A.; Ferreira, Ó.; Vila-Concejo, A.; Morris, B.; Dias, J.A. Short-term morphodynamics of non-storm overwash. Mar. Geol. 2010, 274, 69–84. [Google Scholar] [CrossRef]
- Sherwood, C.R.; Long, J.W.; Dickhudt, P.J.; Dalyander, P.S.; Thompson, D.M.; Plant, N.G. Inundation of a barrier island (Chandeleur Islands, Louisiana, USA) during a hurricane: Observed water-level gradients and modeled seaward sand transport. J. Geophys. Res. Earth Surf. 2014, 119, 1498–1515. [Google Scholar] [CrossRef] [Green Version]
- Engelstad, A.; Ruessink, B.; Wesselman, D.; Hoekstra, P.; Oost, A.; van der Vegt, M. Observations of waves and currents during barrier island inundation. J. Geophys. Res. Ocean. 2017, 122, 3152–3169. [Google Scholar] [CrossRef] [Green Version]
- Lashley, C.H.; Bertin, X.; Roelvink, D.; Arnaud, G. Contribution of Infragravity Waves to Run-up and Overwash in the Pertuis Breton Embayment (France). J. Mar. Sci. Eng. 2019, 7, 205. [Google Scholar] [CrossRef] [Green Version]
- Huntley, D.; Guza, R.; Bowen, A. A universal form for shoreline run-up spectra? J. Geophys. Res. 1977, 82, 2577–2581. [Google Scholar] [CrossRef]
- Guza, R.; Thornton, E.B. Swash oscillations on a natural beach. J. Geophys. Res. Ocean. 1982, 87, 483–491. [Google Scholar] [CrossRef]
- Ruggiero, P.; Holman, R.A.; Beach, R. Wave run-up on a high-energy dissipative beach. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Senechal, N.; Coco, G.; Bryan, K.R.; Holman, R.A. Wave runup during extreme storm conditions. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Hughes, M.G.; Aagaard, T.; Baldock, T.E.; Power, H.E. Spectral signatures for swash on reflective, intermediate and dissipative beaches. Mar. Geol. 2014, 355, 88–97. [Google Scholar] [CrossRef] [Green Version]
- Ruessink, B. Observations of turbulence within a natural surf zone. J. Phys. Oceanogr. 2010, 40, 2696–2712. [Google Scholar] [CrossRef] [Green Version]
- Fiedler, J.W.; Brodie, K.L.; McNinch, J.E.; Guza, R.T. Observations of runup and energy flux on a low-slope beach with high-energy, long-period ocean swell. Geophys. Res. Lett. 2015, 42, 9933–9941. [Google Scholar] [CrossRef] [Green Version]
- Inch, K.; Davidson, M.; Masselink, G.; Russell, P. Observations of nearshore infragravity wave dynamics under high energy swell and wind-wave conditions. Cont. Shelf Res. 2017, 138, 19–31. [Google Scholar] [CrossRef]
- Bertin, X.; Martins, K.; de Bakker, A.; Chataigner, T.; Guérin, T.; Coulombier, T.; de Viron, O. Energy transfers and reflection of infragravity waves at a dissipative beach under storm waves. J. Geophys. Res. Ocean. 2020, 125, e2019JC015714. [Google Scholar] [CrossRef]
- Bertin, X.; Olabarrieta, M. Relevance of infragravity waves in a wave-dominated inlet. J. Geophys. Res. Ocean. 2016, 121, 5418–5435. [Google Scholar] [CrossRef] [Green Version]
- Bertin, X.; Mendes, D.; Martins, K.; Fortunato, A.B.; Lavaud, L. The closure of a shallow tidal inlet promoted by infragravity waves. Geophys. Res. Lett. 2019, 46, 6804–6810. [Google Scholar] [CrossRef]
- Mendes, D.; Fortunato, A.B.; Bertin, X.; Martins, K.; Lavaud, L.; Silva, A.N.; Pires-Silva, A.A.; Coulombier, T.; Pinto, J.P. Importance of infragravity waves in a wave-dominated inlet under storm conditions. Cont. Shelf Res. 2020, 192, 104026. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A.; Van Dongeren, A.; de Vries, J.v.T.; McCall, R.; Lescinski, J. Modelling storm impacts on beaches, dunes and barrier islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- McCall, R.T.; De Vries, J.V.T.; Plant, N.; Van Dongeren, A.; Roelvink, J.; Thompson, D.; Reniers, A. Two-dimensional time dependent hurricane overwash and erosion modeling at Santa Rosa Island. Coast. Eng. 2010, 57, 668–683. [Google Scholar] [CrossRef]
- Baumann, J.; Chaumillon, E.; Bertin, X.; Schneider, J.L.; Guillot, B.; Schmutz, M. Importance of infragravity waves for the generation of washover deposits. Mar. Geol. 2017, 391, 20–35. [Google Scholar] [CrossRef]
- Battjes, J.; Bakkenes, H.; Janssen, T.; Van Dongeren, A. Shoaling of subharmonic gravity waves. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Van Dongeren, A.; Battjes, J.; Janssen, T.; Van Noorloos, J.; Steenhauer, K.; Steenbergen, G.; Reniers, A. Shoaling and shoreline dissipation of low-frequency waves. J. Geophys. Res. Ocean. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- De Bakker, A.; Tissier, M.; Ruessink, B. Shoreline dissipation of infragravity waves. Cont. Shelf Res. 2014, 72, 73–82. [Google Scholar] [CrossRef]
- Henderson, S.M.; Bowen, A. Observations of surf beat forcing and dissipation. J. Geophys. Res. Ocean. 2002, 107, 14. [Google Scholar] [CrossRef]
- Henderson, S.M.; Guza, R.; Elgar, S.; Herbers, T.; Bowen, A. Nonlinear generation and loss of infragravity wave energy. J. Geophys. Res. Ocean. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Thomson, J.; Elgar, S.; Raubenheimer, B.; Herbers, T.; Guza, R. Tidal modulation of infragravity waves via nonlinear energy losses in the surfzone. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Ruju, A.; Lara, J.L.; Losada, I.J. Radiation stress and low-frequency energy balance within the surf zone: A numerical approach. Coast. Eng. 2012, 68, 44–55. [Google Scholar] [CrossRef]
- Guedes, R.; Bryan, K.R.; Coco, G. Observations of wave energy fluxes and swash motions on a low-sloping, dissipative beach. J. Geophys. Res. Ocean. 2013, 118, 3651–3669. [Google Scholar] [CrossRef]
- de Bakker, A.; Herbers, T.; Smit, P.; Tissier, M.; Ruessink, B. Nonlinear infragravity-wave interactions on a gently sloping laboratory beach. J. Phys. Oceanogr. 2015, 45, 589–605. [Google Scholar] [CrossRef] [Green Version]
- De Bakker, A.; Tissier, M.; Ruessink, B. Beach steepness effects on nonlinear infragravity-wave interactions: A numerical study. J. Geophys. Res. Ocean. 2016, 121, 554–570. [Google Scholar] [CrossRef] [Green Version]
- Herbers, T.; Russnogle, N.; Elgar, S. Spectral energy balance of breaking waves within the surf zone. J. Phys. Oceanogr. 2000, 30, 2723–2737. [Google Scholar] [CrossRef]
- Morton, R.A. Texas barriers. In Geology of Holocene Barrier Island Systems; Springer-Verlag: Berlin/Heidelberg, Germany, 1994; pp. 75–114. [Google Scholar]
- Morton, R.A.; Miller, T.L.; Moore, L.J. National Assessment of Shoreline Change: Part 1: Historical Shoreline Changes and Associated Coastal Land Loss along the US Gulf of Mexico; U.S. Geological Survey Open-file Report 2004-1043; U.S. Geological Survey: Reston, VA, USA, 2004.
- Blake, E.; Zelinsky, D. Hurricane Harvey. NOAA, National Hurricane Center Tropical Cyclone Report. 2018. Available online: https://www.nhc.noaa.gov/data/tcr/AL092017_Harvey.pdf (accessed on 25 July 2018).
- USACE; JALBTCX; NOAA; National Ocean Service; Office for Coastal Management (OCM). 2016 USACE NCMP Topobathy Lidar DEM: Gulf Coast (TX); NOAA’s Ocean Service, OCM: Charleston, SC, USA, 2017. [Google Scholar]
- Turner, I.L.; Nielsen, P. Rapid water table fluctuations within the beach face: Implications for swash zone sediment mobility? Coast. Eng. 1997, 32, 45–59. [Google Scholar] [CrossRef]
- Turner, I.L.; Masselink, G. Swash infiltration-exfiltration and sediment transport. J. Geophys. Res. Ocean. 1998, 103, 30813–30824. [Google Scholar] [CrossRef]
- Horn, D.P. Measurements and modelling of beach groundwater flow in the swash-zone: A review. Cont. Shelf Res. 2006, 26, 622–652. [Google Scholar] [CrossRef]
- Sous, D.; Lambert, A.; Rey, V.; Michallet, H. Swash—Groundwater dynamics in a sandy beach laboratory experiment. Coast. Eng. 2013, 80, 122–136. [Google Scholar] [CrossRef]
- Sous, D.; Petitjean, L.; Bouchette, F.; Rey, V.; Meulé, S.; Sabatier, F.; Martins, K. Field evidence of swash groundwater circulation in the microtidal rousty beach, France. Adv. Water Resour. 2016, 97, 144–155. [Google Scholar] [CrossRef] [Green Version]
- Guza, R.; Thornton, E.; Holman, R. Swash on steep and shallow beaches. In Proceedings of the 19th International Conference on Coastal Engineering, Houston, TX, USA, 3–7 September 1984; pp. 708–723. [Google Scholar] [CrossRef]
- Thomson, D.J. Spectrum estimation and harmonic analysis. Proc. IEEE 1982, 70, 1055–1096. [Google Scholar] [CrossRef] [Green Version]
- Raubenheimer, B.; Elgar, S.; Guza, R.T. Estimating Wave Heights from Pressure Measured in Sand Bed. J. Waterw. Port Coast. Ocean. Eng. 1998, 124, 151–154. [Google Scholar] [CrossRef]
- Bronez, T.P. On the performance advantage of multitaper spectral analysis. IEEE Trans. Signal Process. 1992, 40, 2941–2946. [Google Scholar] [CrossRef]
- Rahim, K.J.; Burr, W.S.; Thomson, D.J. Applications of Multitaper Spectral Analysis to Nonstationary Data. R Package Version 1.0-14. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2014. [Google Scholar]
- Collis, W.; White, P.; Hammond, J. Higher-order spectra: The bispectrum and trispectrum. Mech. Syst. Signal Process. 1998, 12, 375–394. [Google Scholar] [CrossRef]
- Elgar, S.; Guza, R. Observations of bispectra of shoaling surface gravity waves. J. Fluid Mech. 1985, 161, 425–448. [Google Scholar] [CrossRef]
- Birkelund, Y.; Hanssen, A.; Powers, E.J. Multitaper estimators of polyspectra. Signal Process. 2003, 83, 545–559. [Google Scholar] [CrossRef]
- Haubrich, R.A. Earth noise, 5 to 500 millicycles per second: 1. Spectral stationarity, normality, and nonlinearity. J. Geophys. Res. Ocean. 1965, 70, 1415–1427. [Google Scholar] [CrossRef]
- Kim, Y.C.; Powers, E.J. Digital Bispectral Analysis and Its Applications to Nonlinear Wave Interactions. IEEE Trans. Plasma Sci. 1979, 7, 120–131. [Google Scholar] [CrossRef]
- Birkelund, Y.; Hanssen, A. Multitaper estimators for bispectra. In Proceedings of the IEEE Signal Processing Workshop on Higher-Order Statistics, Caesarea, Israel, 16 June 1999; pp. 207–211. [Google Scholar]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H., Jr. Empirical parameterization of setup, swash, and runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- Bertin, X.; de Bakker, A.; Van Dongeren, A.; Coco, G.; Andre, G.; Ardhuin, F.; Bonneton, P.; Bouchette, F.; Castelle, B.; Crawford, W.C.; et al. Infragravity waves: From driving mechanisms to impacts. Earth-Sci. Rev. 2018, 177, 774–799. [Google Scholar] [CrossRef] [Green Version]
- Billson, O.; Russell, P.; Davidson, M. Storm Waves at the Shoreline: When and Where Are Infragravity Waves Important? J. Mar. Sci. Eng. 2019, 7, 139. [Google Scholar] [CrossRef] [Green Version]
- Lippmann, T.; Herbers, T.; Thornton, E. Gravity and shear wave contributions to nearshore infragravity motions. J. Phys. Oceanogr. 1999, 29, 231–239. [Google Scholar] [CrossRef]
- Tucker, M. Surf beats: Sea waves of 1 to 5 min. period. Proc. R. Soc. Lond. A 1950, 202, 565–573. [Google Scholar] [CrossRef]
- Guza, R.; Thornton, E.B. Observations of surf beat. J. Geophys. Res. Ocean. 1985, 90, 3161–3172. [Google Scholar] [CrossRef]
- Elgar, S.; Herbers, T.; Guza, R. Reflection of ocean surface gravity waves from a natural beach. J. Phys. Oceanogr. 1994, 24, 1503–1511. [Google Scholar] [CrossRef]
- Sheremet, A.; Guza, R.; Elgar, S.; Herbers, T. Observations of nearshore infragravity waves: Seaward and shoreward propagating components. J. Geophys. Res. Ocean. 2002, 107, 10-1. [Google Scholar] [CrossRef]
- List, J.H. A model for the generation of two-dimensional surf beat. J. Geophys. Res. Ocean. 1992, 97, 5623–5635. [Google Scholar] [CrossRef]
- Masselink, G. Group bound long waves as a source of infragravity energy in the surf zone. Cont. Shelf Res. 1995, 15, 1525–1547. [Google Scholar] [CrossRef]
- Janssen, T.; Battjes, J.; Van Dongeren, A. Long waves induced by short-wave groups over a sloping bottom. J. Geophys. Res. Ocean. 2003, 108. [Google Scholar] [CrossRef]
- Guerin, T.; de Bakker, A.; Bertin, X. On the Bound Wave Phase Lag. Fluids 2019, 4, 152. [Google Scholar] [CrossRef] [Green Version]
- Freilich, M.H.; Guza, R.T.; Whitham, G.B. Nonlinear effects on shoaling surface gravity waves. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1984, 311, 1–41. [Google Scholar] [CrossRef]
- Herbers, T.; Burton, M. Nonlinear shoaling of directionally spread waves on a beach. J. Geophys. Res. Ocean. 1997, 102, 21101–21114. [Google Scholar] [CrossRef]
- Biésel, F. Équations générales au second ordre de la houle irrégulière. La Houille Blanche 1952, 3, 372–376. [Google Scholar] [CrossRef] [Green Version]
- Longuet-Higgins, M.S.; Stewart, R. Radiation stress and mass transport in gravity waves, with application to ‘surf beats’. J. Fluid Mech. 1962, 13, 481–504. [Google Scholar] [CrossRef]
- Hasselmann, K. On the nonlinear energy transfer in a gravity-wave spectrum Part 1. General theory. J. Fluid Mech. 1962, 12, 481–500. [Google Scholar] [CrossRef]
- Masuda, A.; Kuo, Y.Y. A note on the imaginary part of bispectra. Deep. Sea Res. Part A Oceanogr. Res. Pap. 1981, 28, 213–222. [Google Scholar] [CrossRef]
- Oltman-Shay, J.; Howd, P.; Birkemeier, W. Shear instabilities of the mean longshore current: 2. Field observations. J. Geophys. Res. Ocean. 1989, 94, 18031–18042. [Google Scholar] [CrossRef]
- Haller, M.C.; Putrevu, U.; Oltman-Shay, J.; Dalrymple, R.A. Wave group forcing of low frequency surf zone motion. Coast. Eng. J. 1999, 41, 121–136. [Google Scholar] [CrossRef]
- Shi, L.; Olabarrieta, M.; Nolan, D.S.; Warner, J.C. Tropical cyclone rainbands can trigger meteotsunamis. Nat. Commun. 2020, 11, 678. [Google Scholar] [CrossRef]
- Olabarrieta, M.; Valle-Levinson, A.; Martinez, C.J.; Pattiaratchi, C.; Shi, L. Meteotsunamis in the northeastern Gulf of Mexico and their possible link to El Niño Southern Oscillation. Natural Hazards 2017, 88, 1325–1346. [Google Scholar] [CrossRef] [Green Version]
- Tissier, M.; Bonneton, P.; Ruessink, B. Infragravity waves and bore merging. In Proceedings of the Coastal Dynamics 2017, Helsingor, Denmark, 12–16 June 2017; pp. 451–460. [Google Scholar]
- García-Medina, G.; Özkan-Haller, H.; Holman, R.A.; Ruggiero, P. Large runup controls on a gently sloping dissipative beach. J. Geophys. Res. Ocean. 2017, 122, 5998–6010. [Google Scholar] [CrossRef]
- Elgar, S.; Sebert, G. Statistics of bicoherence and biphase. J. Geophys. Res. Ocean. 1989, 94, 10993–10998. [Google Scholar] [CrossRef]
- Elgar, S.; Guza, R.T. Statistics of bicoherence. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1667–1668. [Google Scholar] [CrossRef]
- Birkelund, Y.; Hanssen, A.; Powers, E.J. Multitaper estimation of bicoherence. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Salt Lake City, UT, USA, 7–11 May 2001; Volume 5, pp. 3085–3088. [Google Scholar] [CrossRef] [Green Version]
- Thomson, D.J. Multi-window bispectrum estimates. In Proceedings of the Workshop on Higher-Order Spectral Analysis, Vail, CO, USA, 28–30 June 1989; pp. 19–23. [Google Scholar] [CrossRef]






| Scenario | PT-1 | PT-2 | (% Decrease between PT-1 and PT-2) | ||
|---|---|---|---|---|---|
| h [cm] | Total IG | High-f IG (0.01–0.04 Hz) | Low-f IG (0.003–0.01 Hz) | ||
| Maximum depth | 30 | 52 | 86% | 70–71% | 95–96% |
| Minimum depth | 10 | 40 | 79% | 52–56% | 92–94% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anarde, K.; Figlus, J.; Sous, D.; Tissier, M. Transformation of Infragravity Waves during Hurricane Overwash. J. Mar. Sci. Eng. 2020, 8, 545. https://doi.org/10.3390/jmse8080545
Anarde K, Figlus J, Sous D, Tissier M. Transformation of Infragravity Waves during Hurricane Overwash. Journal of Marine Science and Engineering. 2020; 8(8):545. https://doi.org/10.3390/jmse8080545
Chicago/Turabian StyleAnarde, Katherine, Jens Figlus, Damien Sous, and Marion Tissier. 2020. "Transformation of Infragravity Waves during Hurricane Overwash" Journal of Marine Science and Engineering 8, no. 8: 545. https://doi.org/10.3390/jmse8080545
APA StyleAnarde, K., Figlus, J., Sous, D., & Tissier, M. (2020). Transformation of Infragravity Waves during Hurricane Overwash. Journal of Marine Science and Engineering, 8(8), 545. https://doi.org/10.3390/jmse8080545





