Propagation and Depolarization of a Short Pulse of Light in Sea Water
Abstract
1. Introduction
2. Theoretical Background
2.1. Vector Radiative Transfer Equation
2.2. Basic Mode Approximation
3. Model of Single Scattering of Light in Sea Water
4. Small-Angle Approximation. Scaling Relations
4.1. Distribution of Light Field in a Pulse
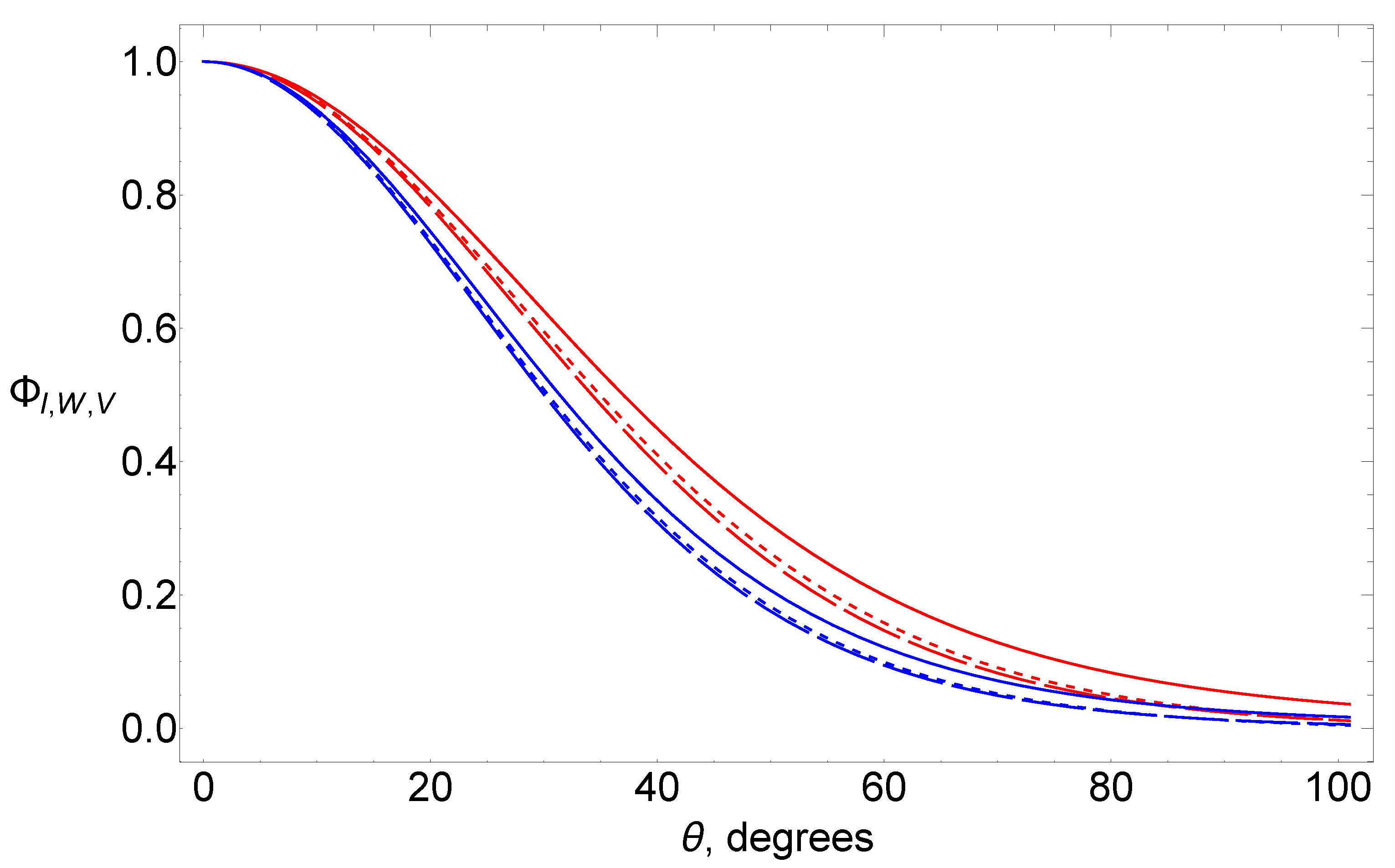
4.2. Degree of Polarization
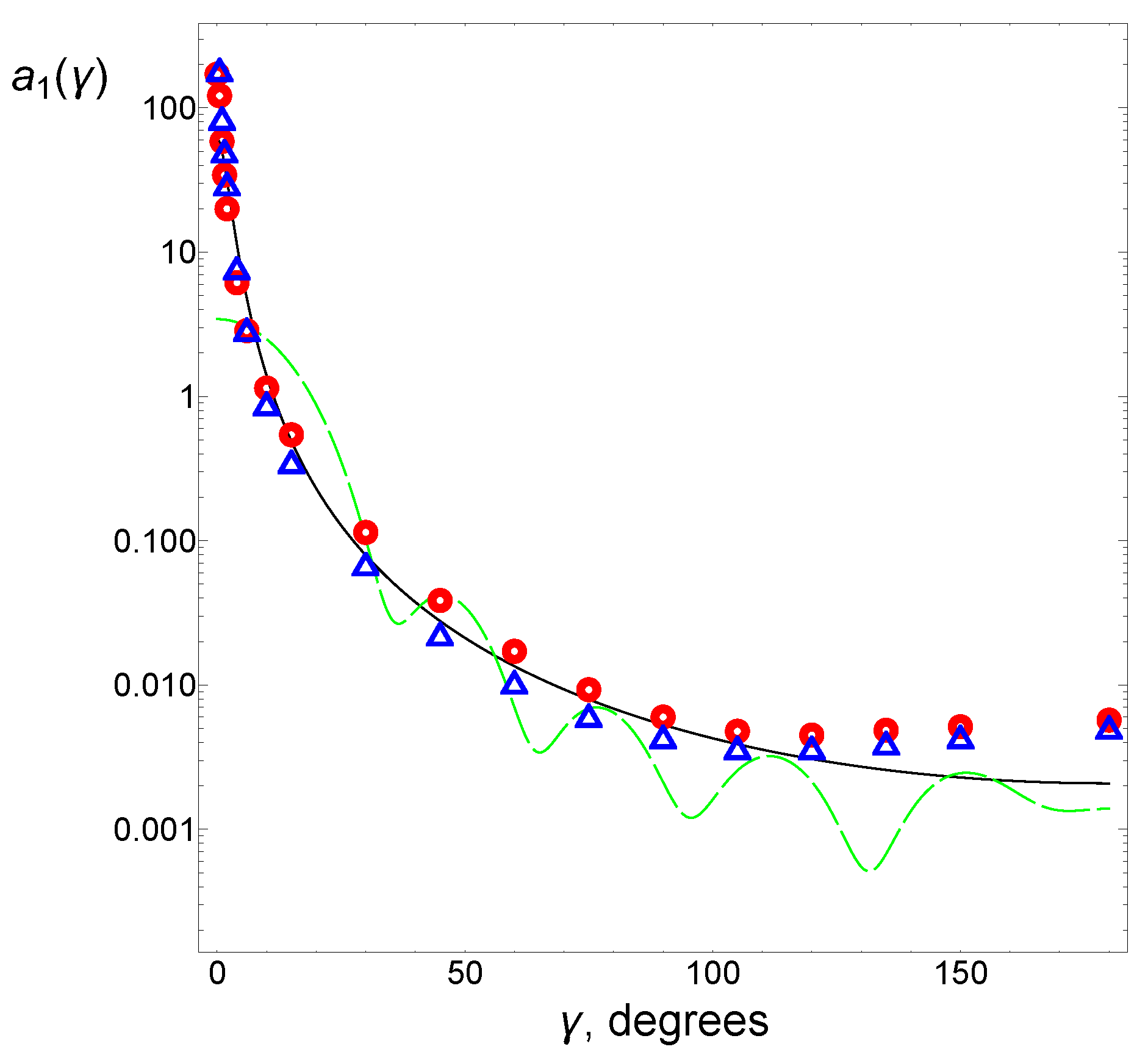
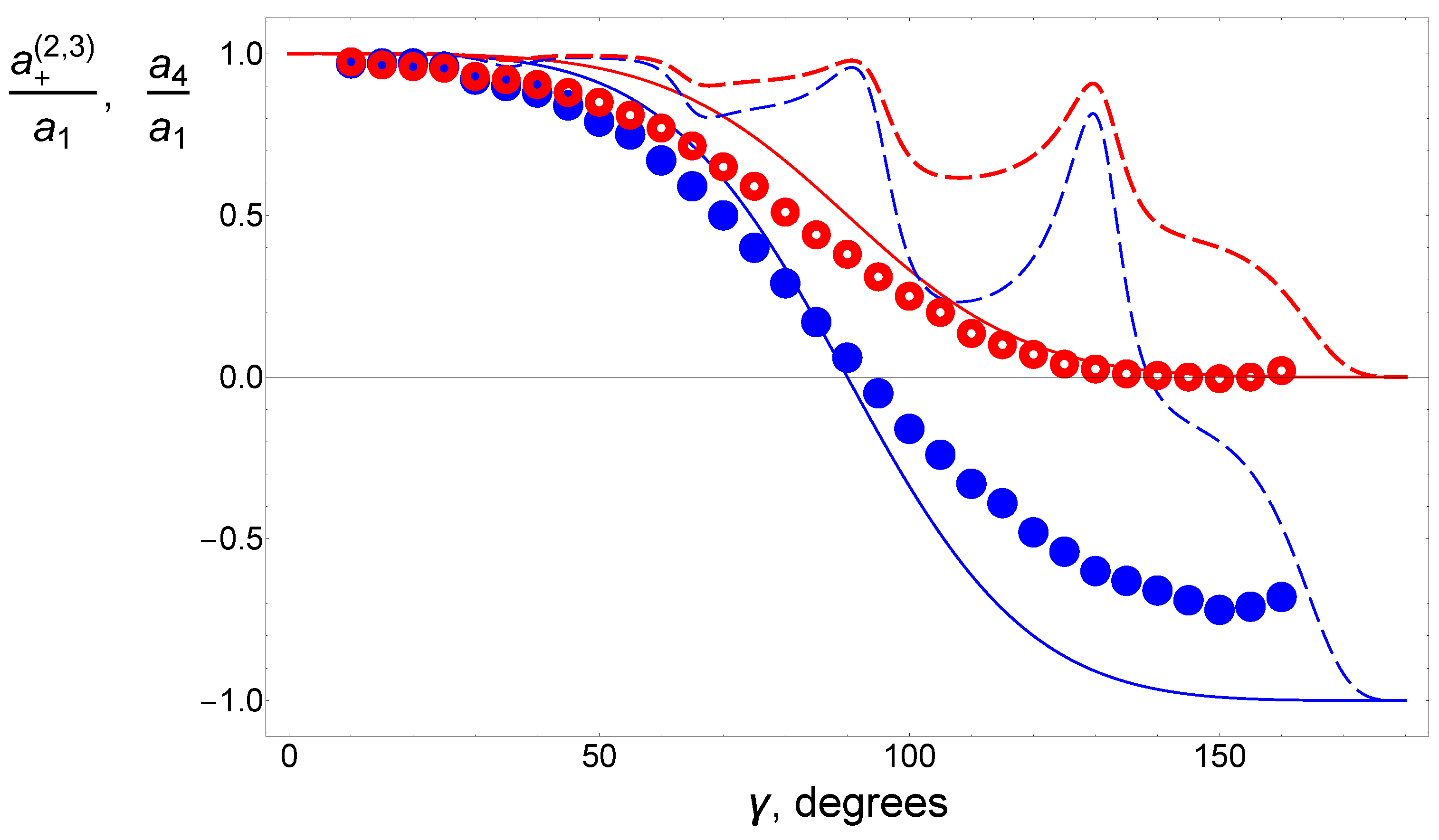
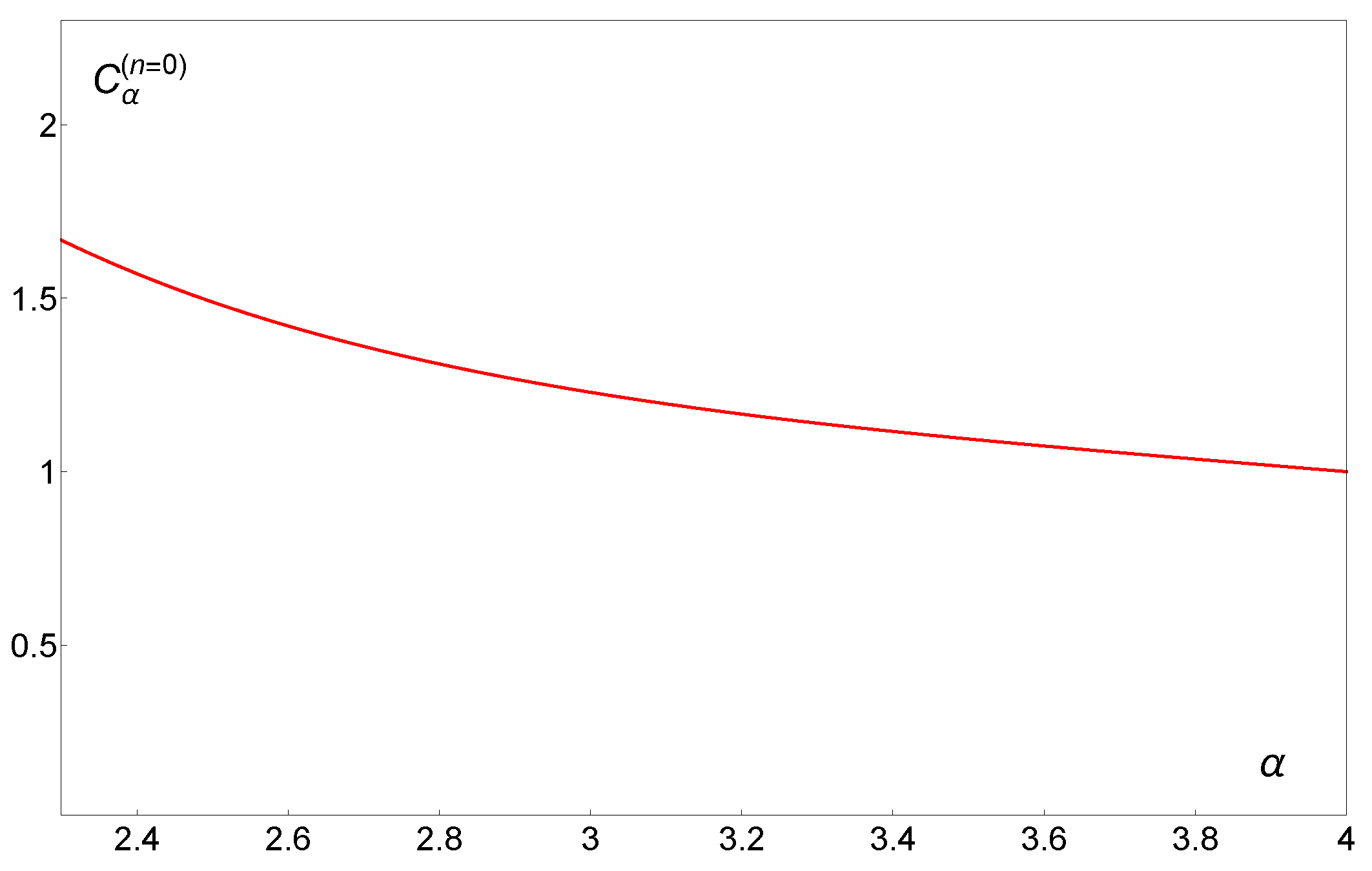
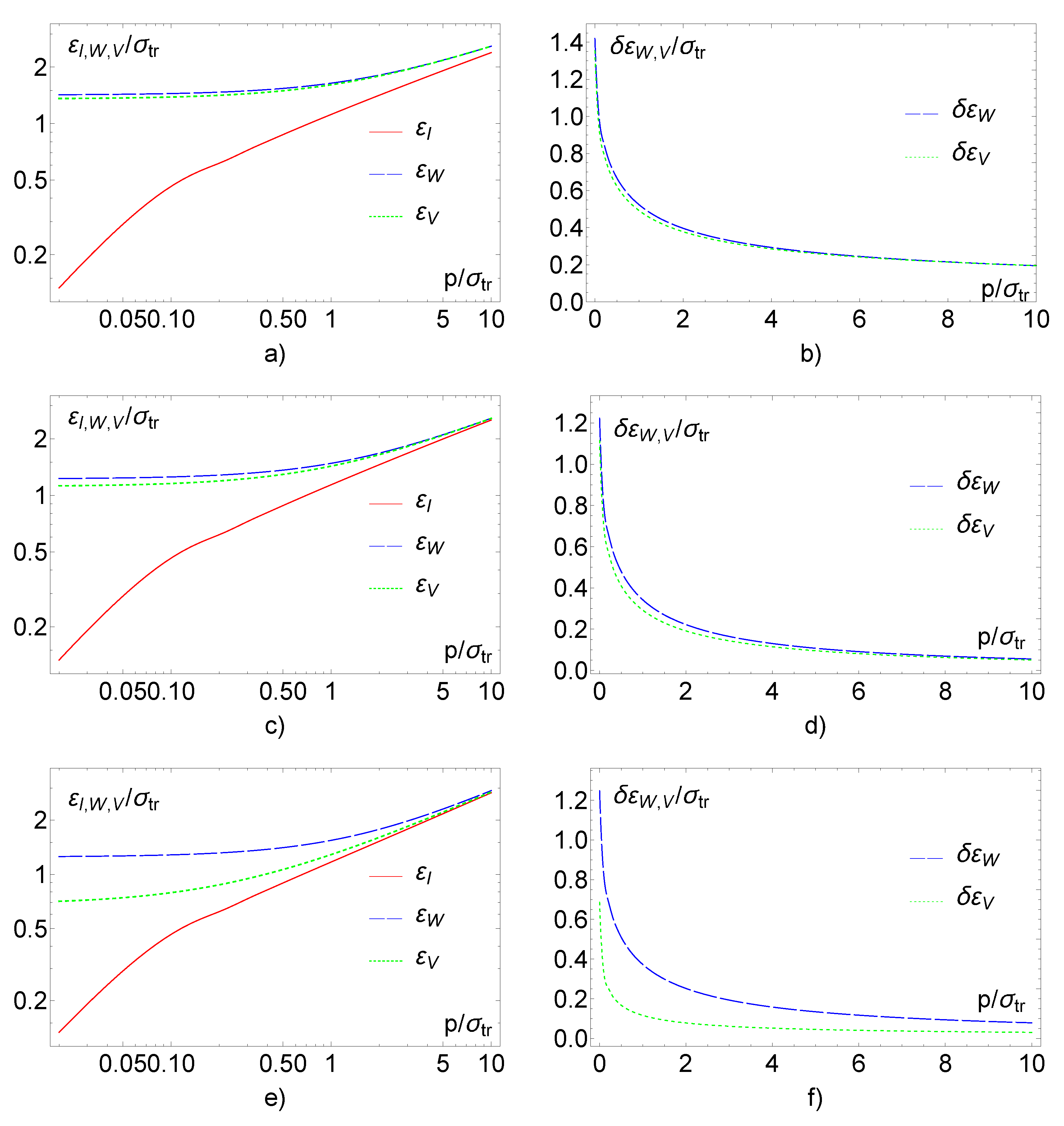
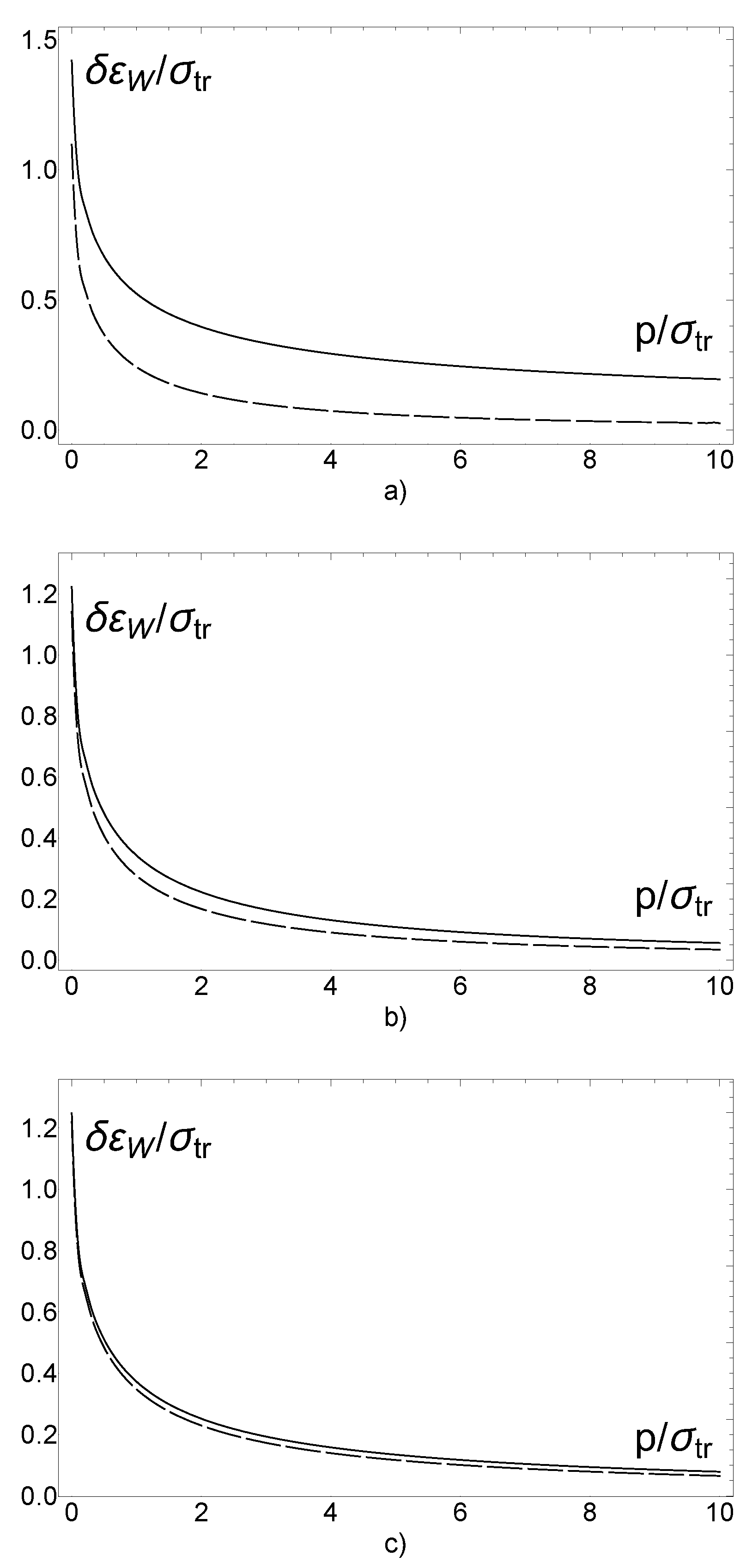
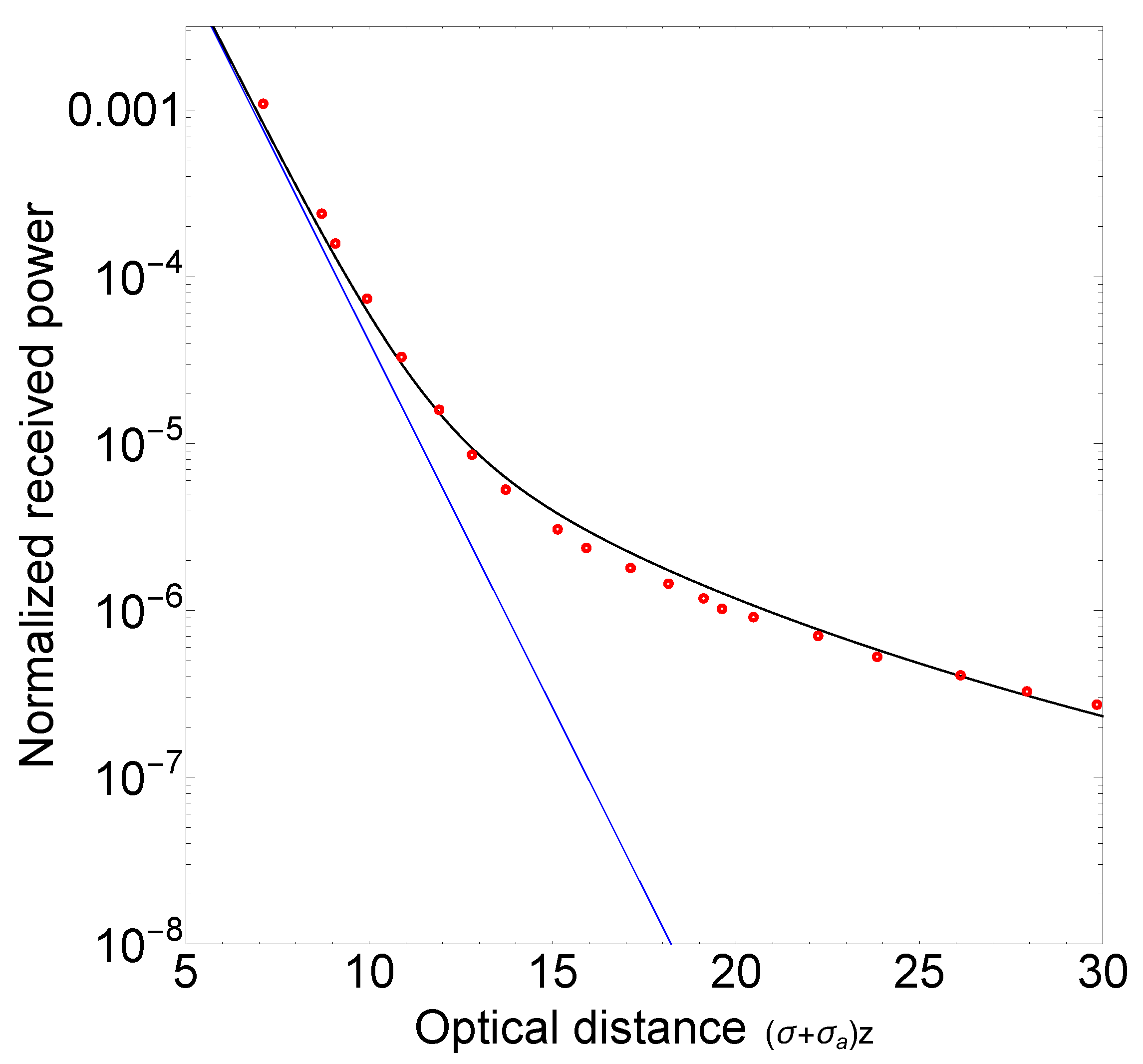
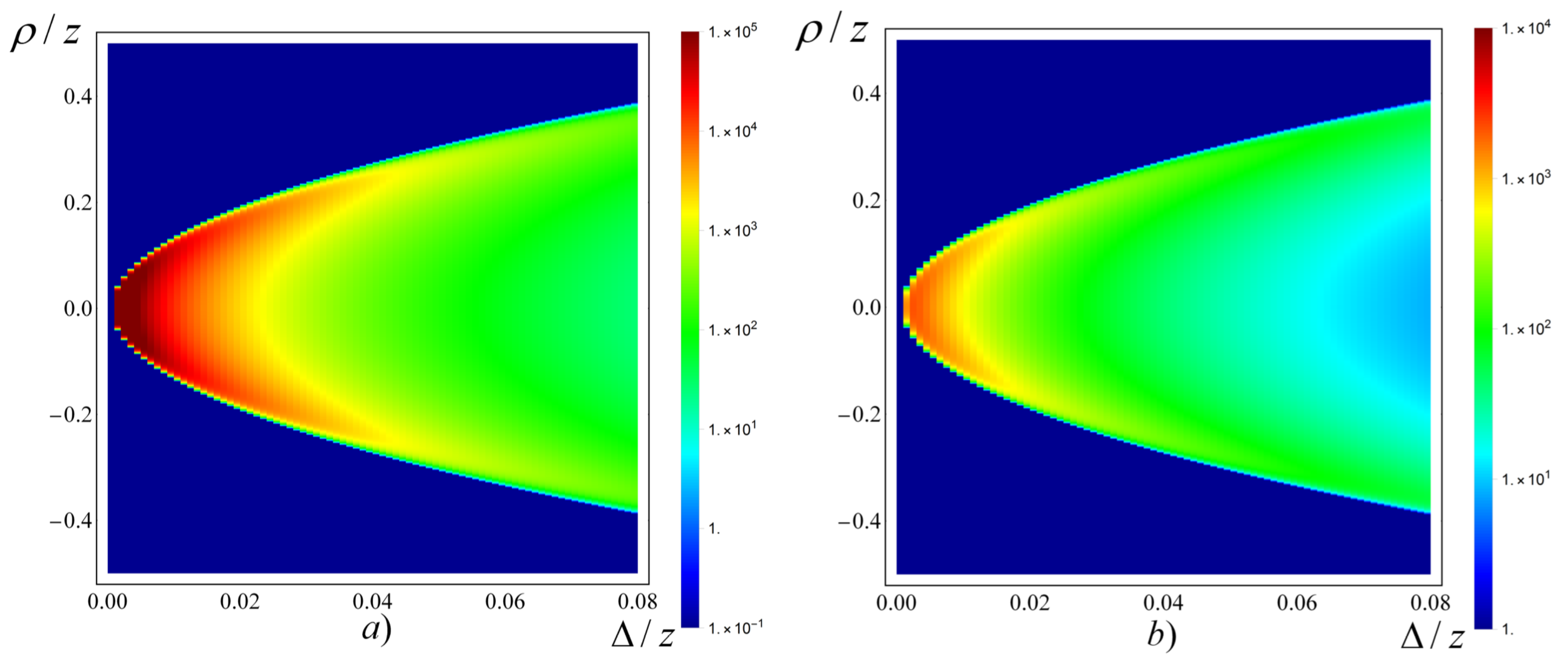
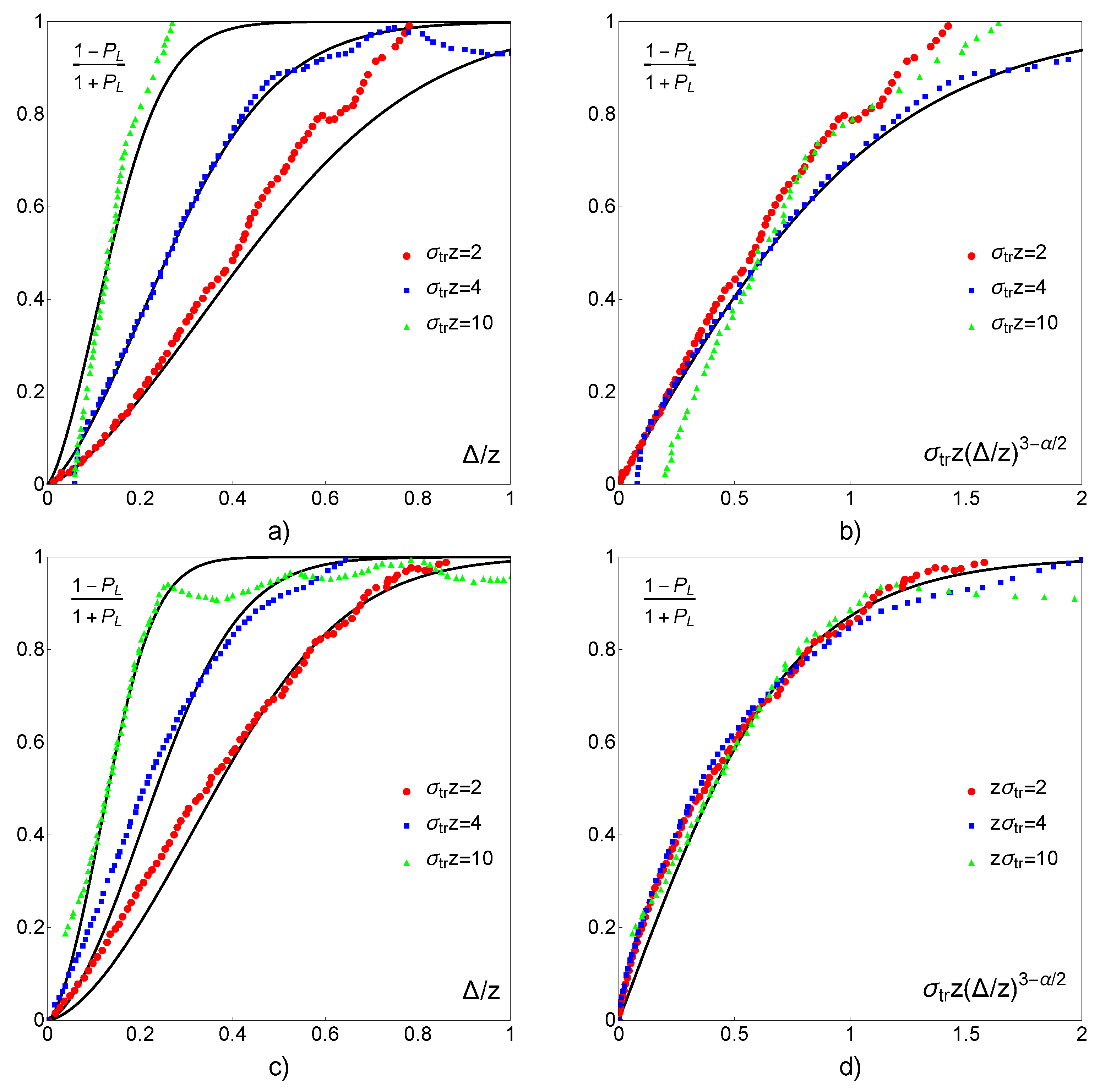
5. Results of Numerical Calculations
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
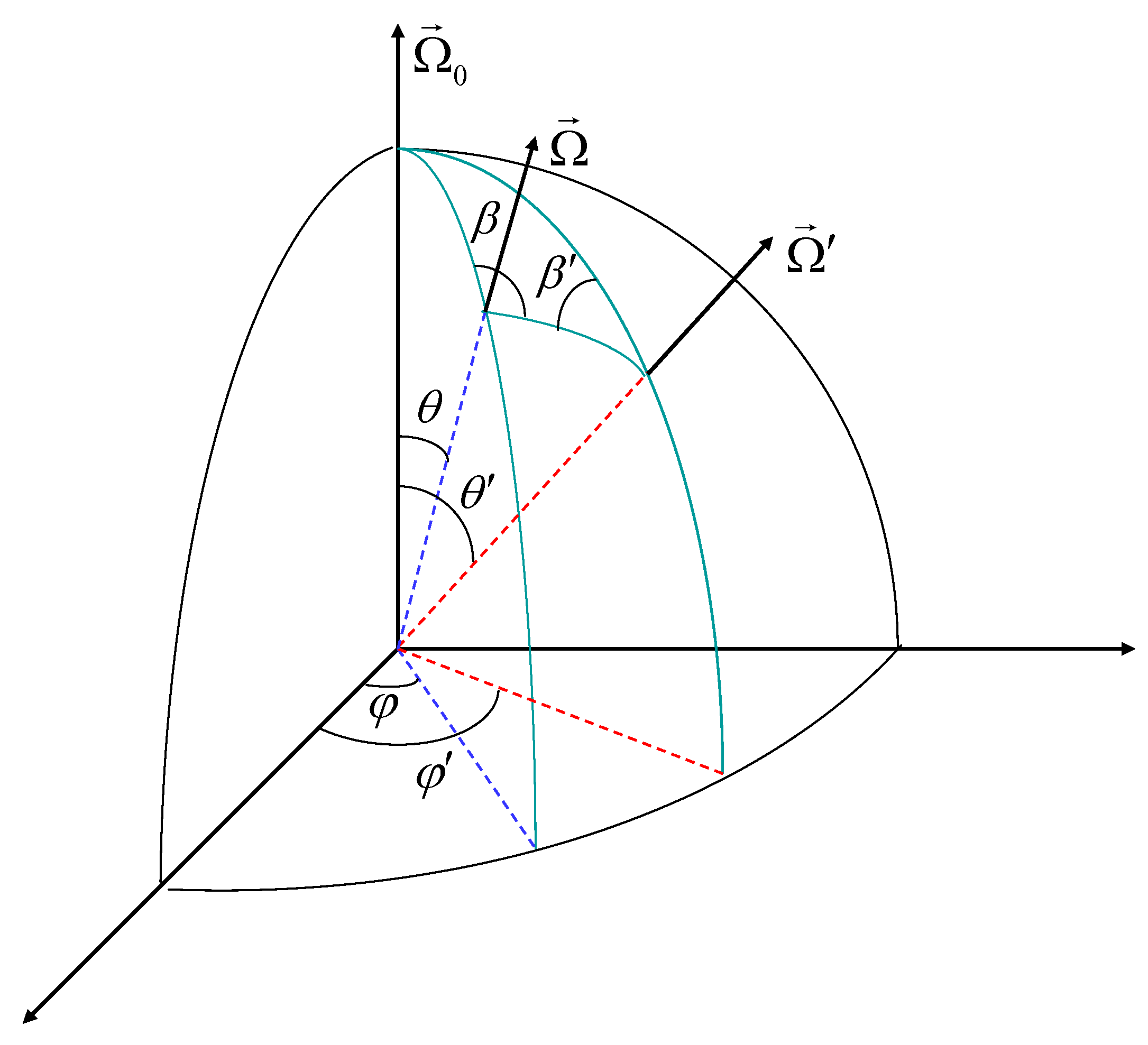
Appendix A. Eigenvalue Problem for the Basic Modes
Appendix B. Generalization to a Narrow Beam
References
- Monin, A.S. (Ed.) Optika Okeana (Oceanic Optics); Nauka: Moscow, Russia, 1983; Volume 2. [Google Scholar]
- Zege, E.P.; Ivanov, A.P.; Katsev, I.L. Image Transfer through a Scattering Medium; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Jaruwatanadilok, S. Underwater wireless optical communication channel modeling and performance evaluation using vector radiative transfer theory. IEEE J. Ser. Areas Commun. 2008, 26, 1620–1627. [Google Scholar] [CrossRef]
- Cochenour, B.M.; Mullen, L.J.; Laux, A.E. Characterization of the beam-spread function for underwater wireless optical communications links. IEEE J. Ocean. Eng. 2008, 33, 513–521. [Google Scholar] [CrossRef]
- Mullen, L.; Alley, D.; Cochenour, B. Investigation of the effect of scattering agent and scattering albedo on modulated light propagation in water. Appl. Opt. 2011, 1396–1404. [Google Scholar] [CrossRef] [PubMed]
- Cochenour, B.; Mullen, L.; Muth, J. Temporal response of the underwater optical channel for high-bandwidth wireless laser communications. IEEE J. Ocean. Eng. 2013, 38, 730–742. [Google Scholar] [CrossRef]
- Cox, W.; Muth, J. Simulating channel losses in an underwater communication system. J. Opt. Soc. Am. 2014, 31, 920–934. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z.; Fu, S.; Zhang, H.; Dong, Y.; Cheng, J. A survey of underwater optical wireless communications. IEEE Commun. Surv. Tutor. 2017, 19, 204–238. [Google Scholar] [CrossRef]
- Sahu, S.K.; Shanmugam, P. A theoretical study on the impact of particle scattering on the channel characteristics of underwater optical communication system. Opt. Commun. 2018, 408, 3–14. [Google Scholar] [CrossRef]
- Luchinin, A.G.; Dolin, L.S. Model of an underwater imaging system with a complexly modulated illumination beam. Izv. Atmos. Ocean. Phys. 2014, 50, 411–419. [Google Scholar] [CrossRef]
- Luchinin, A.G.; Kirillin, M.Y. Temporal and frequency characteristics of a narrow light beam in sea water. Appl. Opt. 2016, 55, 7756–7762. [Google Scholar] [CrossRef]
- Walker, R.E.; McLean, J. Lidar equations for turbid media with pulse stretching. Appl. Opt. 1999, 38, 2384–2397. [Google Scholar] [CrossRef]
- Vasilkov, A.P.; Goldin, Y.A.; Gureev, B.A.; Hoge, F.E.; Swift, R.N.; Wright, C.W. Airborne polarized lidar detection of scattering layers in the ocean. Appl. Opt. 2001, 40, 4353–4364. [Google Scholar] [CrossRef] [PubMed]
- Luchinin, A.G. Theory of underwater lidar with a complex modulated illumination beam. Izv. Atmos. Ocean. Phys. 2012, 48, 663–671. [Google Scholar] [CrossRef]
- Lerner, R.M.; Summers, J.D. Monte-Carlo description of time-resolved and space-resolved multiple forward scatter in natural water. Appl. Opt. 1982, 21, 861–869. [Google Scholar] [CrossRef] [PubMed]
- Zakharov, A.K.; Goldin, Y.A. The Monte Carlo calculation of the structure of narrow non-stationary light beams in sea water up to a large optical depth. Izv. Akad. Nauk SSSR Fiz. Atmos. Okeana 1986, 22, 533–540. [Google Scholar]
- Bruscaglioni, P.; Zaccanti, G.; Wei, Q. Transmission of a pulsed polarized light beam through thick turbid media: Numerical results. Appl. Opt. 1993, 32, 6142–6150. [Google Scholar] [CrossRef]
- McLean, J.; Freeman, J.D.; Walker, R.E. Beam spread function with time dispersion. Appl. Opt. 1998, 37, 4701–4711. [Google Scholar] [CrossRef]
- Ishimaru, A.; Jaruwatanadilok, S.; Kuga, Y. Polarized pulse waves in random duscrete scatterers. Appl. Opt. 2001, 40, 5495–5502. [Google Scholar] [CrossRef]
- Luchinin, A.G. Spatial spectrum of a narrow sine-wave-modulated light beam in an anisotropically scattering medium. Izv. Acad. Sci. USSR Atmos. Ocean. Phys. 1974, 10, 1312–1317. [Google Scholar]
- Ishimaru, A. Wave Propagation and Scattering in Random Media; Institute of Electrical and Electronics Engineers: New York, NY, USA, 1997. [Google Scholar]
- Dolin, L.S. Solution of the radiation transfer equation in a small-angle approximation for a stratified turbid medium with photon path dispersion taken into account. Izv. Acad. Sci. USSR Atmos. Ocean. Phys. 1980, 16, 55–64. [Google Scholar]
- Dolin, L.S. Self-similar approximation in the theory of multiple strongly anisotropic light scattering. Dokl. Akad. Nauk SSSR 1981, 260, 1344–1347, [Sov. Phys. Dokl. 1981, 26, 976–979]. [Google Scholar]
- Dolin, L.S. Passage of a pulsed light signal through an absorbing medium with strongly anisotropic scattering. Izv. Vyss. Uchebnykh Zaved. Radiofiz. 1983, 26, 220–228. [Google Scholar] [CrossRef]
- Remizovich, V.S.; Rogozkin, D.B.; Ryazanov, M.I. Propagation of a narrow modulated light beam in a scattering medium: The effect of fluctuations in path lengths of multiply scattered photons. Radiophys. Quantum Electron. 1982, 25, 639–645. [Google Scholar] [CrossRef]
- Remizovich, V.S.; Rogozkin, D.B.; Ryazanov, M.I. Propagation of an optical signal in matter with large-scale random inhomogeneities with allowance for fluctuations of the photon paths in multiple scattering. Izv. Akad. Nauk SSSR Fiz. Atmos. Okeana 1982, 18, 623–631. [Google Scholar]
- Remizovich, V.S.; Rogozkin, D.B.; Ryazanov, M.I. Propagation of a light-flash signal in a turbid medium. Izv. Acad. Sci. USSR Atmos. Ocean. Phys. 1983, 19, 796–801. [Google Scholar]
- Rogozkin, D.B. Propagation of a light pulse in a medium with strongly anisotropic scattering. Izv. Acad. Sci. USSR Atmos.Ocean. Phys. 1987, 23, 275–281. [Google Scholar]
- van de Hulst, H.C.; Kattawar, G.W. Exact spread function for a pulsed collimated beam in a medium with small-angle scattering. Appl. Opt. 1994, 33, 5820–5829. [Google Scholar] [CrossRef]
- Gorodnichev, E.E.; Rogozkin, D.B. Multiple small-angle scattering of an optical pulse in turbid media: Polarization characteristics. Izv. Atmos. Ocean. Phys. 1997, 33, 74–81. [Google Scholar]
- Gorodnichev, E.E.; Ivliev, S.V.; Kuzovlev, A.I.; Rogozkin, D.B. Depolarization of light in the pulse transmission through the medium with large inhomogeneities. Laser Phys. 2010, 20, 2021–2028. [Google Scholar] [CrossRef]
- Gorodnichev, E.E.; Ivliev, S.V.; Kuzovlev, A.I.; Rogozkin, D.B. Transillumination of highly scattering media by polarized light. Light Scatt. Rev. 2013, 8, 317–362. [Google Scholar]
- Luchinin, A.G.; Dolin, L.S. On dispersive properties of photon density waves in anisotropic scattering medium. Radiophys. Quantum Electron. 2016, 59, 145–152. [Google Scholar] [CrossRef]
- Gorodnichev, E.E.; Kuzovlev, A.I.; Rogozkin, D.B. Small-angle multiple scattering of polarized light in turbid media. Izv. Atmos. Ocean. Phys. 2003, 39, 333–345. [Google Scholar]
- Gorodnichev, E.E.; Kuzovlev, A.I.; Rogozkin, D.B. Multiple scattering of polarized light in turbid media with large particles. Light Scatt. Rev. 2006, 291–338. [Google Scholar] [CrossRef]
- Gorodnichev, E.E.; Kuzovlev, A.I.; Rogozkin, D.B. Multiple scattering of polarized light in a turbid medium. JETP 2007, 104, 319–341. [Google Scholar] [CrossRef]
- Zege, E.P.; Chaykovskaya, L.I. Peculiarities of transfer of polarized radiation in media with highly anisotropic scattering. Zh. Prikl. Spektrosk. 1986, 44, 996–1004. [Google Scholar]
- Gorodnichev, E.E.; Kuzovlev, A.I.; Rogozkin, D.B. Propagation of a narrow beam of polarized light in a random medium with large-scale inhomogeneities. Laser Phys. 2000, 10, 1236–1243. [Google Scholar]
- Gorodnichev, E.E.; Kuzovlev, A.I.; Rogozkin, D.B. Influence of the inhomogeneity properties on the depolarization of multiply scattered light in a turbid medium. In Proceedings of the International Radiation Symposium IRS 2000: Current Problems in Atmospheric Radiation, St Petersberg, Russia, 24–29 July 2001; Smith, W.L., Timofeev, Y.M., Eds.; Deepak: Hampton, VA, USA, 2001; pp. 287–290. [Google Scholar]
- Demos, S.G.; Alfano, R.R. Temporal gating in highly scattering media by the degree of optical polarization. Opt. Lett. 1996, 21, 161–163. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L.V.; Sun, C.-W.; Yang, C.-C. Polarized light propagation through scattering media: Time-resolved Monte Carlo simulations and experiments. J. Biomed. Opt. 2003, 8, 608–617. [Google Scholar] [CrossRef]
- Ni, X.; Xing, Q.; Cai, W.; Alfano, R.R. Time-resolved polarization to extract coded information from early ballistic and snake signals through turbid media. Opt. Lett. 2003, 28, 343–345. [Google Scholar] [CrossRef]
- Horinaka, H.; Hashimoto, K.; Wada, K.; Cho, Y.; Osawa, M. Extraction of quasi-straightforward-propagating photons from diffused light transmitting through a scattering medium by polarization modulation. Opt. Lett. 1995, 20, 1501–1503. [Google Scholar] [CrossRef] [PubMed]
- Gorodnichev, E.E.; Kuzovlev, A.I.; Rogozkin, D.B. Depolarization of light in small-angle multiple scattering in random media. Laser Phys. 1999, 9, 1210–1227. [Google Scholar]
- Gorodnichev, E.E.; Kuzovlev, A.I.; Rogozkin, D.B. Depolarization coefficients of light in multiply scattering media. Phys. Rev. 2014, 90, 043205. [Google Scholar] [CrossRef]
- Reynolds, L.; McCormick, N.J. Approximate two-parameter phase function for light scattering. JOSA 1980, A70, 1206–1212. [Google Scholar] [CrossRef]
- Kopelevich, O.V. Application of data on seawater light scattering for the study of marine particles: A selective review focusing on Russian literature. Geo-Mar. Lett. 2012. [Google Scholar] [CrossRef]
- Hultrin, V.I. Absorption and scattering of light in natural waters. Light Scatt. Rev. 2006, 445–486. [Google Scholar] [CrossRef]
- Voss, K.J.; Fry, E.S. Measurement of the Mueller matrix for ocean water. Appl. Opt. 1984, 23, 4427–4439. [Google Scholar] [CrossRef] [PubMed]
- van de Hulst, H.C. Multiple Light Scattering; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Mishchenko, M.I.; Travis, L.D.; Lacis, A.A. Multiple Scattering of Light by Particles; Cambridge University: Cambridge, UK, 2006. [Google Scholar]
- Kuscer, I.; Ribaric, M. Matrix formalism in the theory of diffusion of light. Opt. Acta 1959, 6, 42–57. [Google Scholar] [CrossRef]
- Zege, E.P.; Chaikovskaya, L.I. Approximate theory of linearly polarized light propagation through a scattering medium. JQSRT 2000, 66, 413–435. [Google Scholar] [CrossRef]
- Case, K.M.; Zweifel, P.F. Linear Transport Theory; Addison-Wesley Publishing Company: Boston, MA, USA, 1967; Chapter 7. [Google Scholar]
- Strohbenh, J.W.; Clifford, S.F. Polarization and angle-of-arrival fluctuatins for a plane wave propagated through a turbulent medium. IEEE Trans. Anten. Propag. 1967, 15, 416–421. [Google Scholar] [CrossRef]
- Tatarskii, V.I. Depolarization of a light beam in a turbulent atmosphere. Izv. Vyssh. Uchebn. Zaved. Radiofiz. 1967, 10, 1762–1763. [Google Scholar]
- Kravtsov, Y.A. “Geometrical” depolarization of light in a turbulent atmosphere. Izv. Vyssh. Uchebn. Zaved. Radiofiz. 1970, 13, 281–284. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media; Pergamon: New York, NY, USA, 1960. [Google Scholar]
- Mobley, C.D.; Gentili, B.; Gordon, H.R.; Jin, Z.; Kattawar, G.W.; Morel, A.; Reinersman, P.; Stamnes, K.; Stavn, R.H. Comparison of numerical models for computing underwater light fields. Appl. Opt. 1993, 32, 7484–7504. [Google Scholar] [CrossRef] [PubMed]
- Laven, P. Simulation of rainbows, coronas, and glories by use of Mie theory. Appl. Opt. 2003, 42, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Kattawar, G.W.; Yang, P.; Zhang, X. A brief review of Muller matrix calculations associated with oceanic particles. Appl. Sci. 2018, 8, 2686. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A. Parameterization of the Mueller matrix of oceanic waters. J. Geophys. Res. 2003, 108, 3175. [Google Scholar] [CrossRef]
- Alexandrov, M.D.; Remizovich, V.S.; Rogozkin, D.B. Multiple light scattering in a two-dimensional medium with large scatterers. J. Opt. Soc. Am. 1993, 10, 2602–2610. [Google Scholar] [CrossRef]
- Marinyuk, V.V.; Rogozkin, D.B.; Sheberstov, S.V. Propagation of a light beam in an absorbing medium with large-scale inhomogeneities. Opt. Spectrosc. 2014, 117, 102–114. [Google Scholar] [CrossRef]
- Bicout, D.; Brosseau, C.; Martinez, A.S.; Schmitt, J.M. Depolarization of multiply scattered waves by spherical diffusers: Influence of the size parameter. Phys. Rev. 1994, 49, 1767–1770. [Google Scholar] [CrossRef]
- Xu, M.; Alfano, R.R. Circular polarization memory of light. Phys. Rev. 2005, 72, 065601. [Google Scholar] [CrossRef]
- Dark, J.; Kim, A.D. Asymptotic theory of circular polarization memory. J. Opt. Soc. Am. 2017, 34, 1642–1650. [Google Scholar] [CrossRef] [PubMed]

| sea water | ||
| 0.315 | 1.15 | |
| 0.313 | 1.12 | |
| aqueous suspension of polystyrene spheres | ||
| m | 0.383 | 1.17 |
| m | 0.294 | 1.23 |
| sea water | ||||
| 0.49 | 0.645 | 0.47 | 0.610 | |
| 0.46 | 0.605 | 0.44 | 0.550 | |
| Henyey-Greenstein phase function/Rayleigh matrix | 0.47 | 1.50 | 0.38 | 1.50 |
| aqueous suspension of polystyrene spheres | ||||
| m | 0.46 | 1.38 | 0.10 | 1.38 |
| m | 0.40 | 1.57 | 0.34 | 1.57 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorodnichev, E.E.; Kondratiev, K.A.; Kuzovlev, A.I.; Rogozkin, D.B. Propagation and Depolarization of a Short Pulse of Light in Sea Water. J. Mar. Sci. Eng. 2020, 8, 371. https://doi.org/10.3390/jmse8050371
Gorodnichev EE, Kondratiev KA, Kuzovlev AI, Rogozkin DB. Propagation and Depolarization of a Short Pulse of Light in Sea Water. Journal of Marine Science and Engineering. 2020; 8(5):371. https://doi.org/10.3390/jmse8050371
Chicago/Turabian StyleGorodnichev, Evgeniy E., Kirill A. Kondratiev, Alexandr I. Kuzovlev, and Dmitrii B. Rogozkin. 2020. "Propagation and Depolarization of a Short Pulse of Light in Sea Water" Journal of Marine Science and Engineering 8, no. 5: 371. https://doi.org/10.3390/jmse8050371
APA StyleGorodnichev, E. E., Kondratiev, K. A., Kuzovlev, A. I., & Rogozkin, D. B. (2020). Propagation and Depolarization of a Short Pulse of Light in Sea Water. Journal of Marine Science and Engineering, 8(5), 371. https://doi.org/10.3390/jmse8050371




