Numerical Study of the Influence of Fishnet Mesh Size on a Floating Platform
Abstract
1. Introduction
2. Description of the Numerical Model
2.1. Governing Equation
2.2. Inflow Boundary Condition
2.3. Free Surface Boundary Condition
2.4. Body Surface Boundary Condition
2.5. Rigid Boundary Condition
2.6. Curvilinear Coordinate System
2.7. Corner Problem between the Free Surface and Body Surface
2.8. Wave Forces on the Body
2.9. Acceleration Potential Method
2.10. Modal Decomposition Method
2.11. Mooring Force
2.12. Wave Forces on Fishnet
2.13. Consideration of Damping Effects
3. Numerical Model Test
4. Results and Discussion
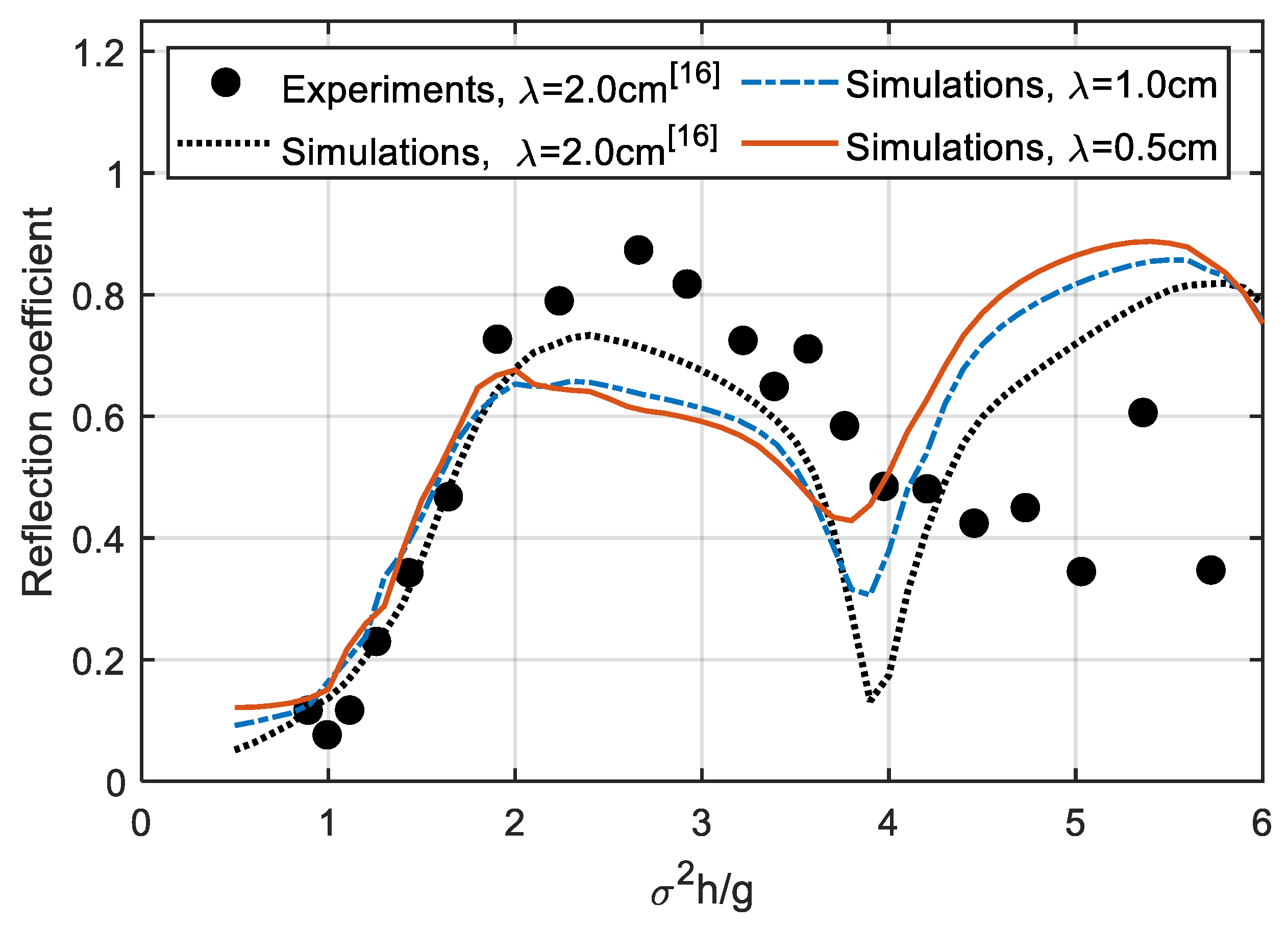
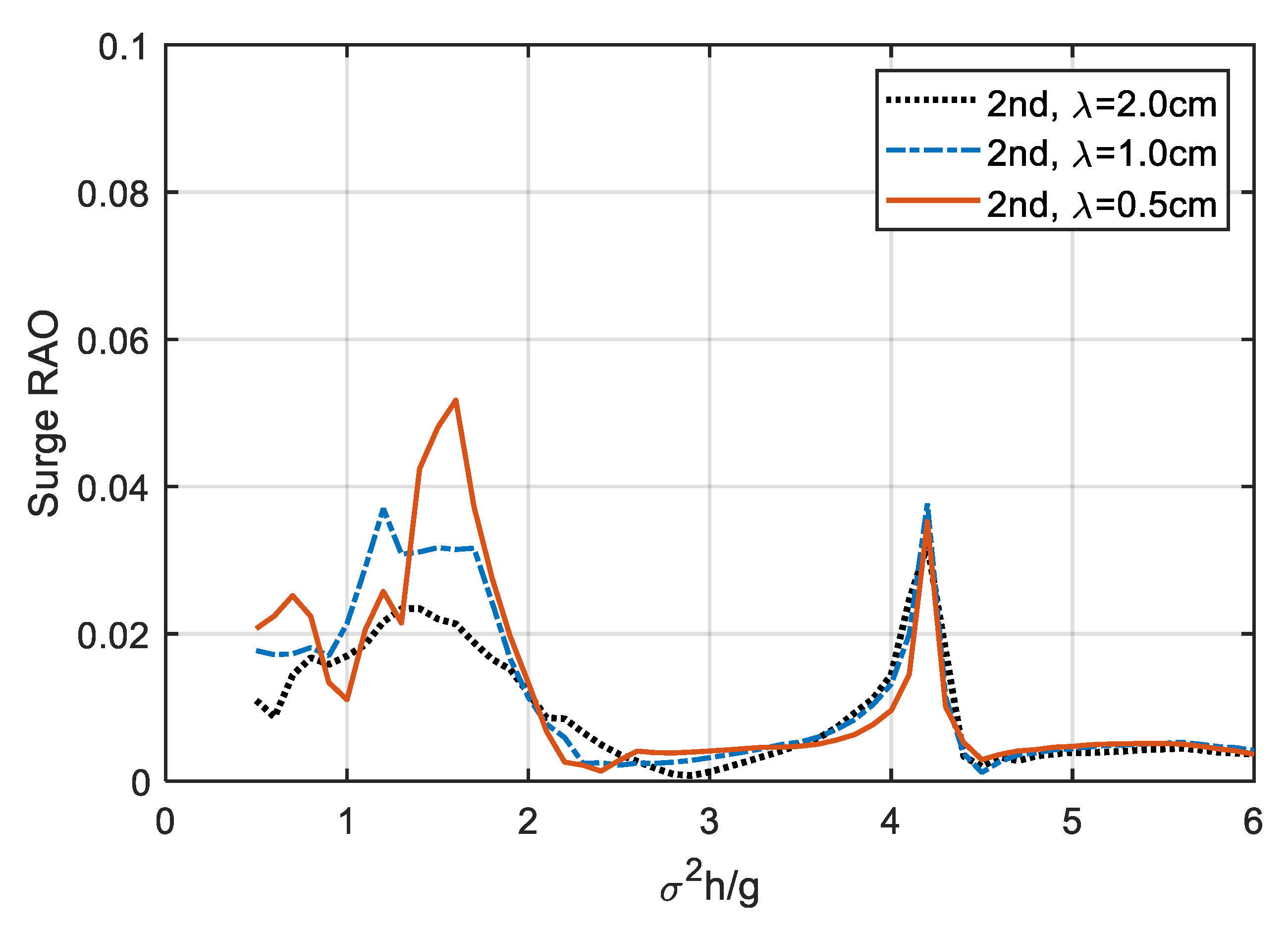
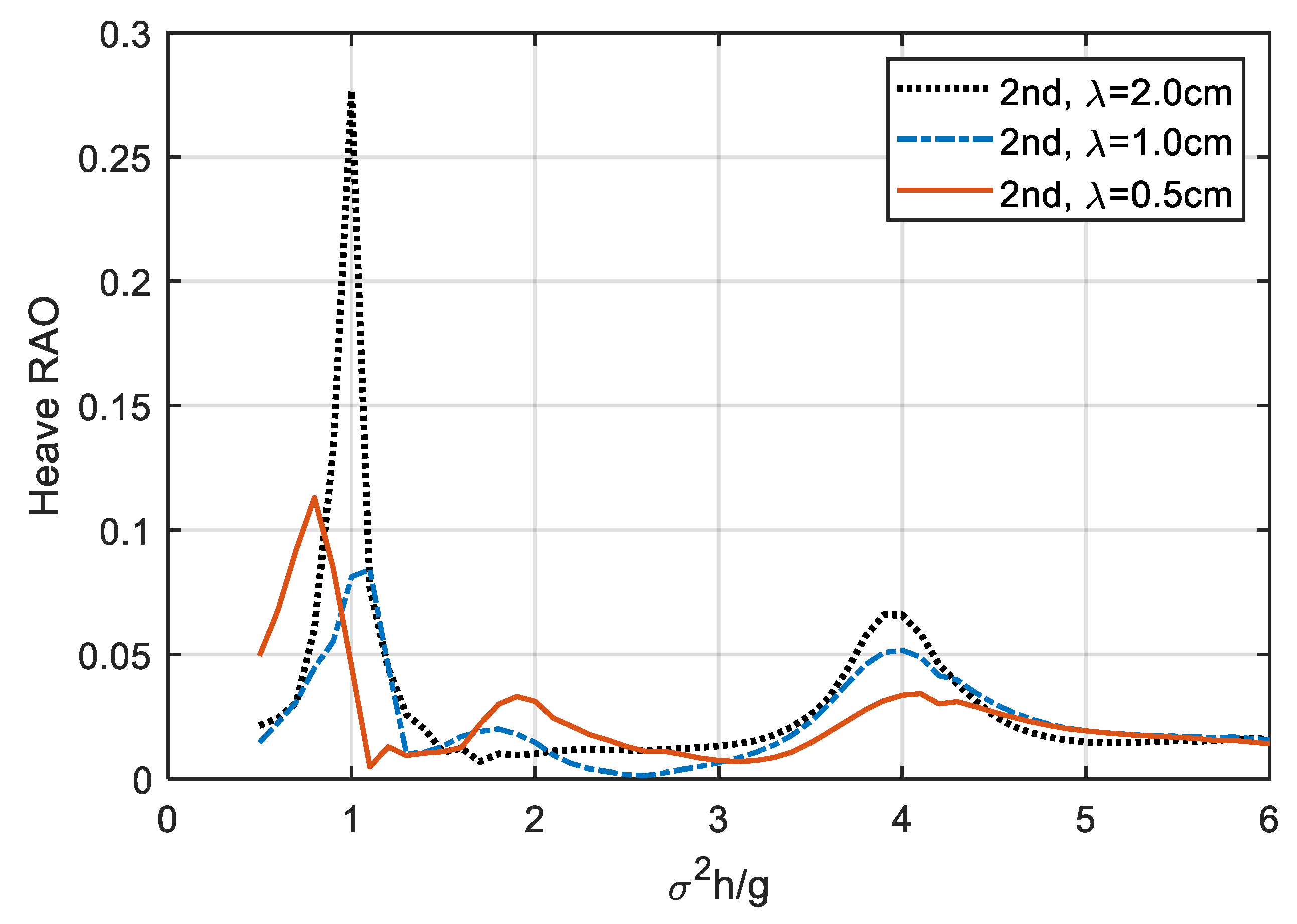
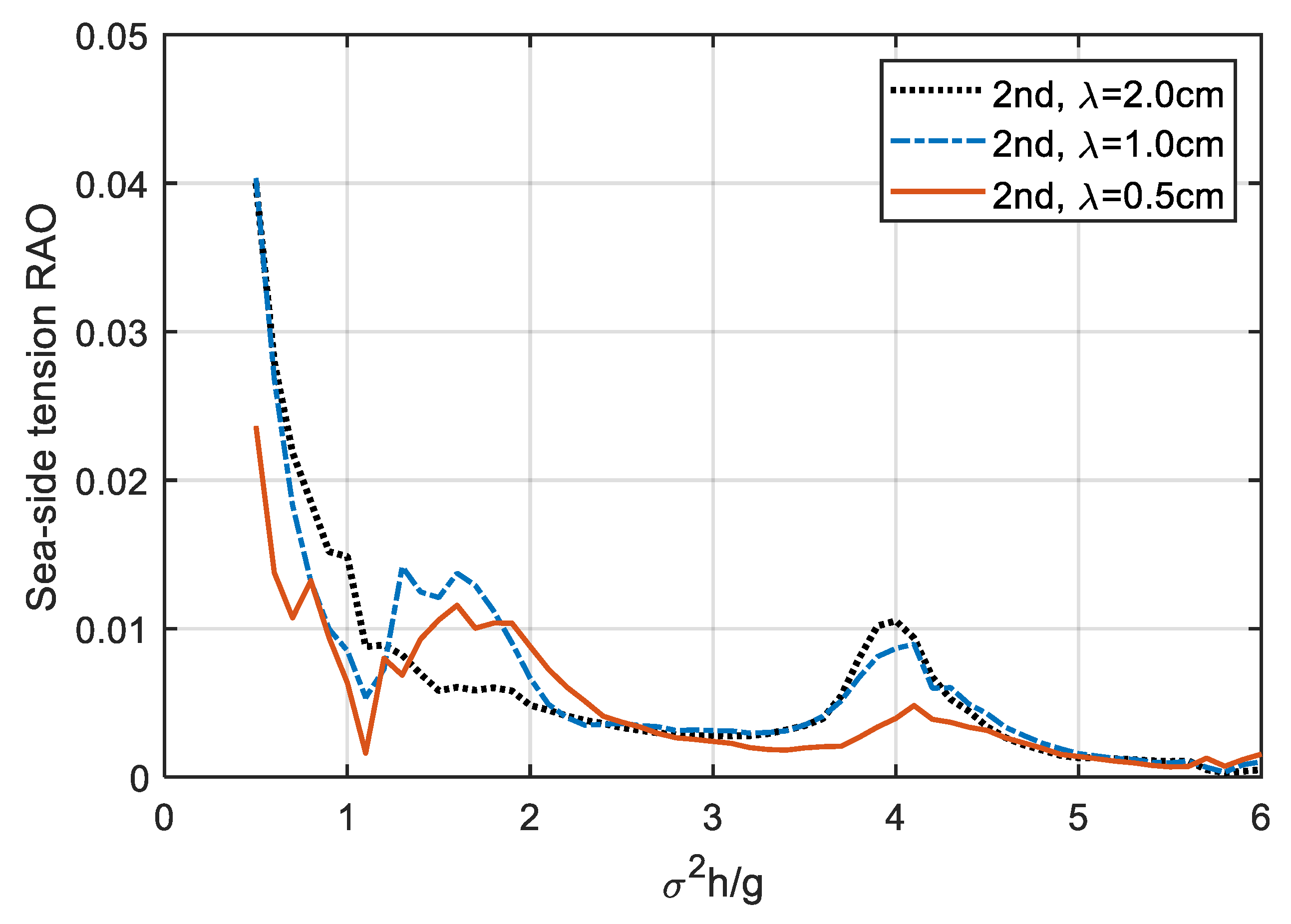
4.1. Frequency-Domain Results
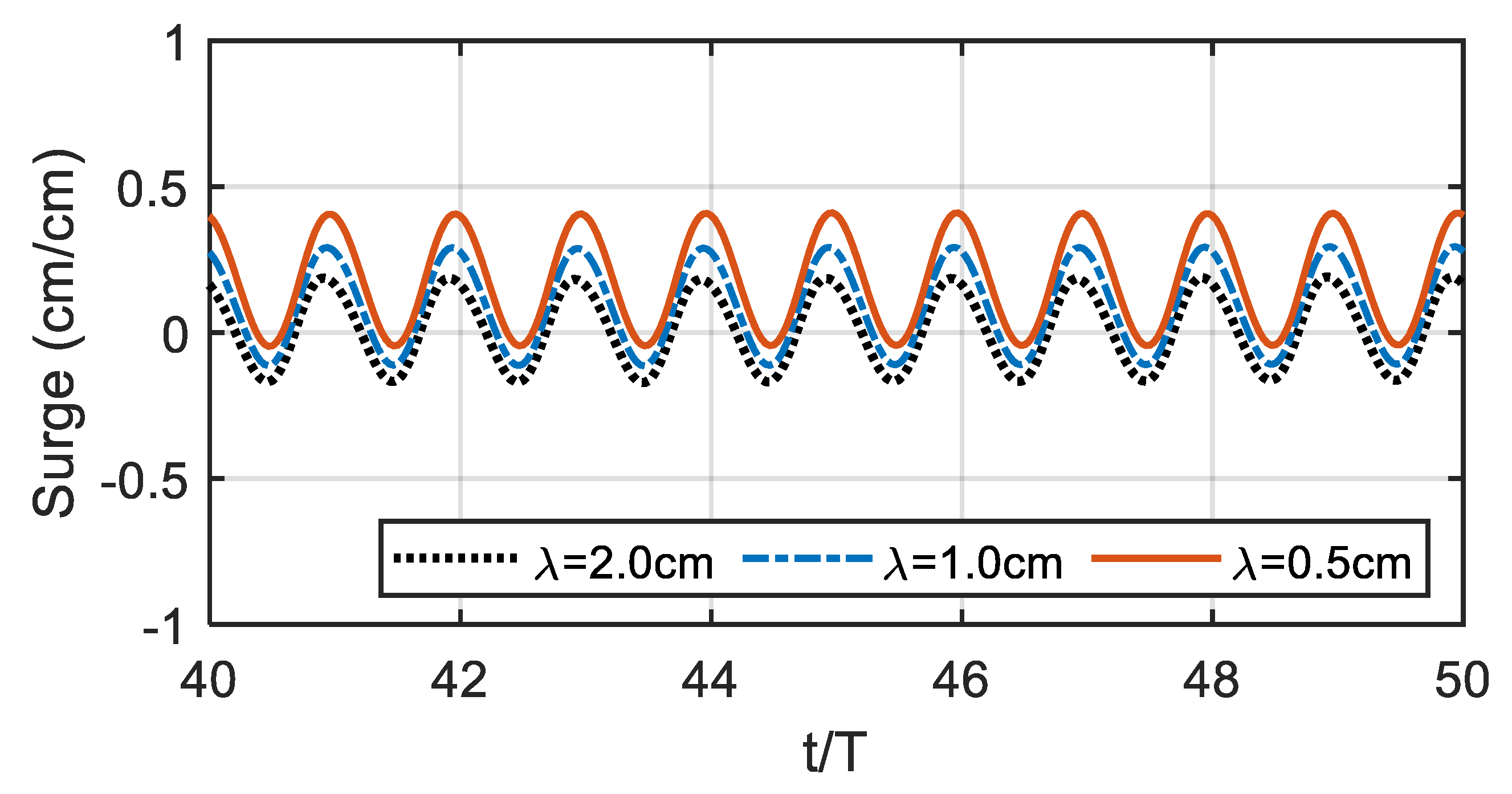
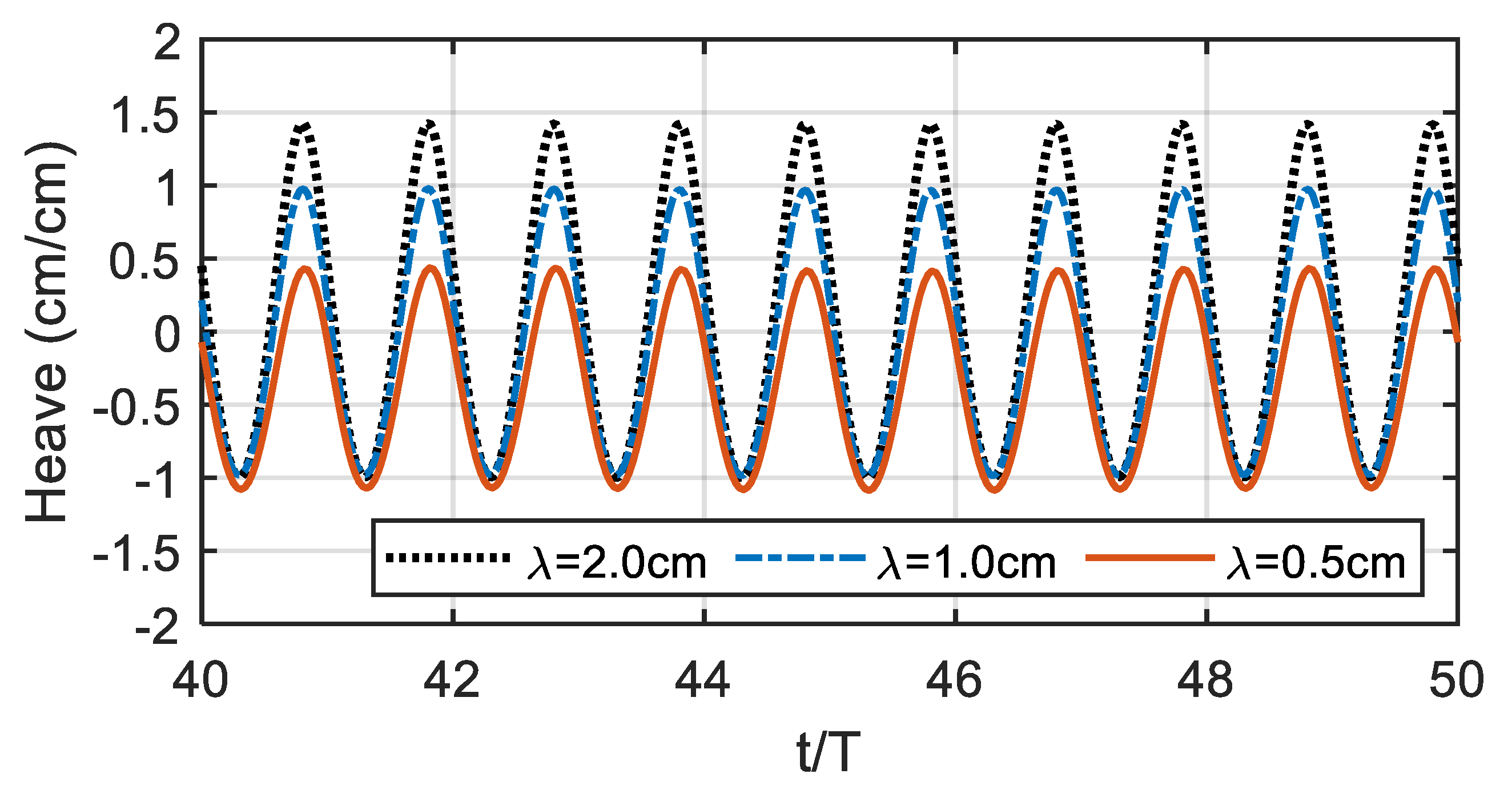
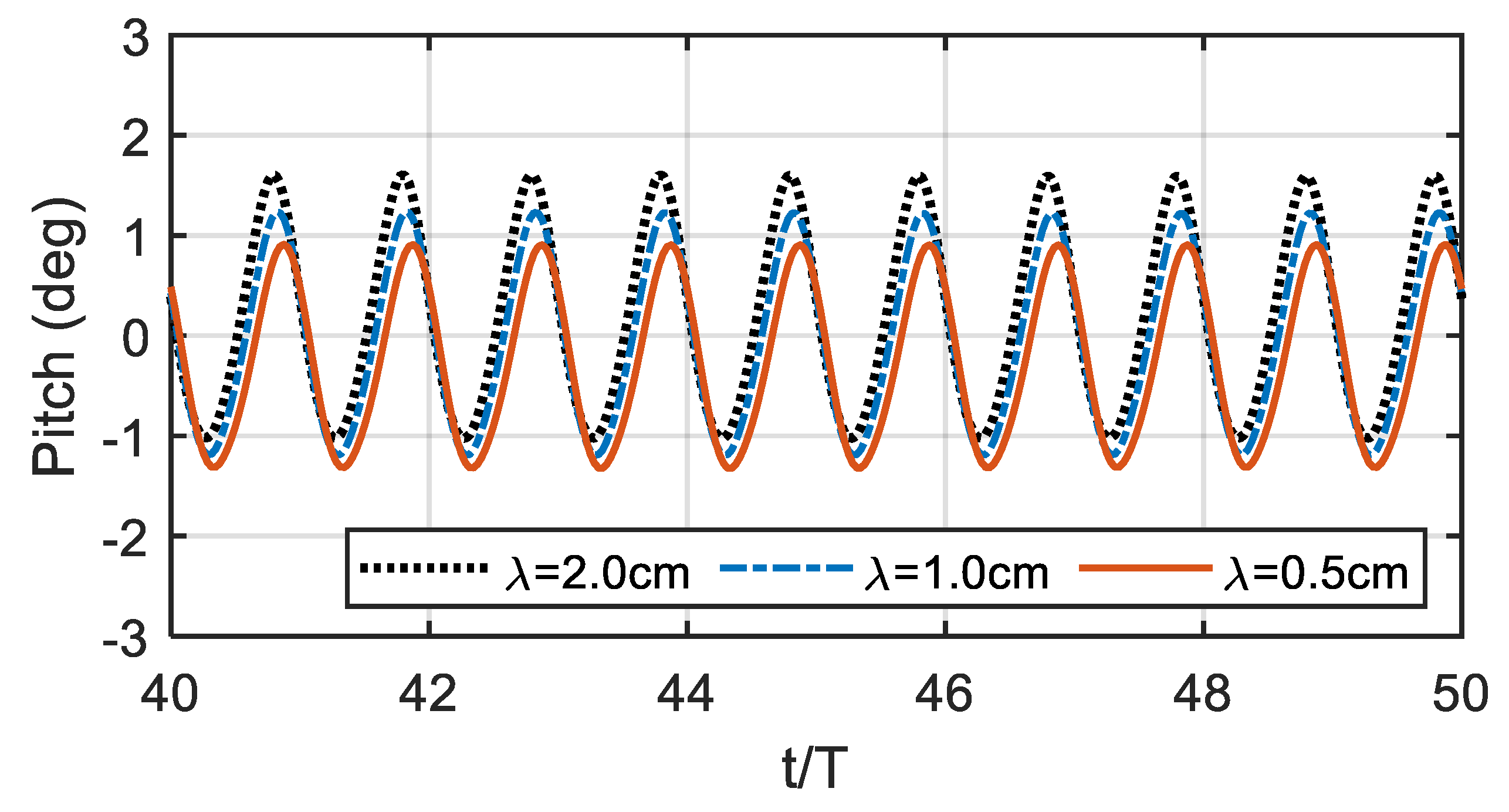
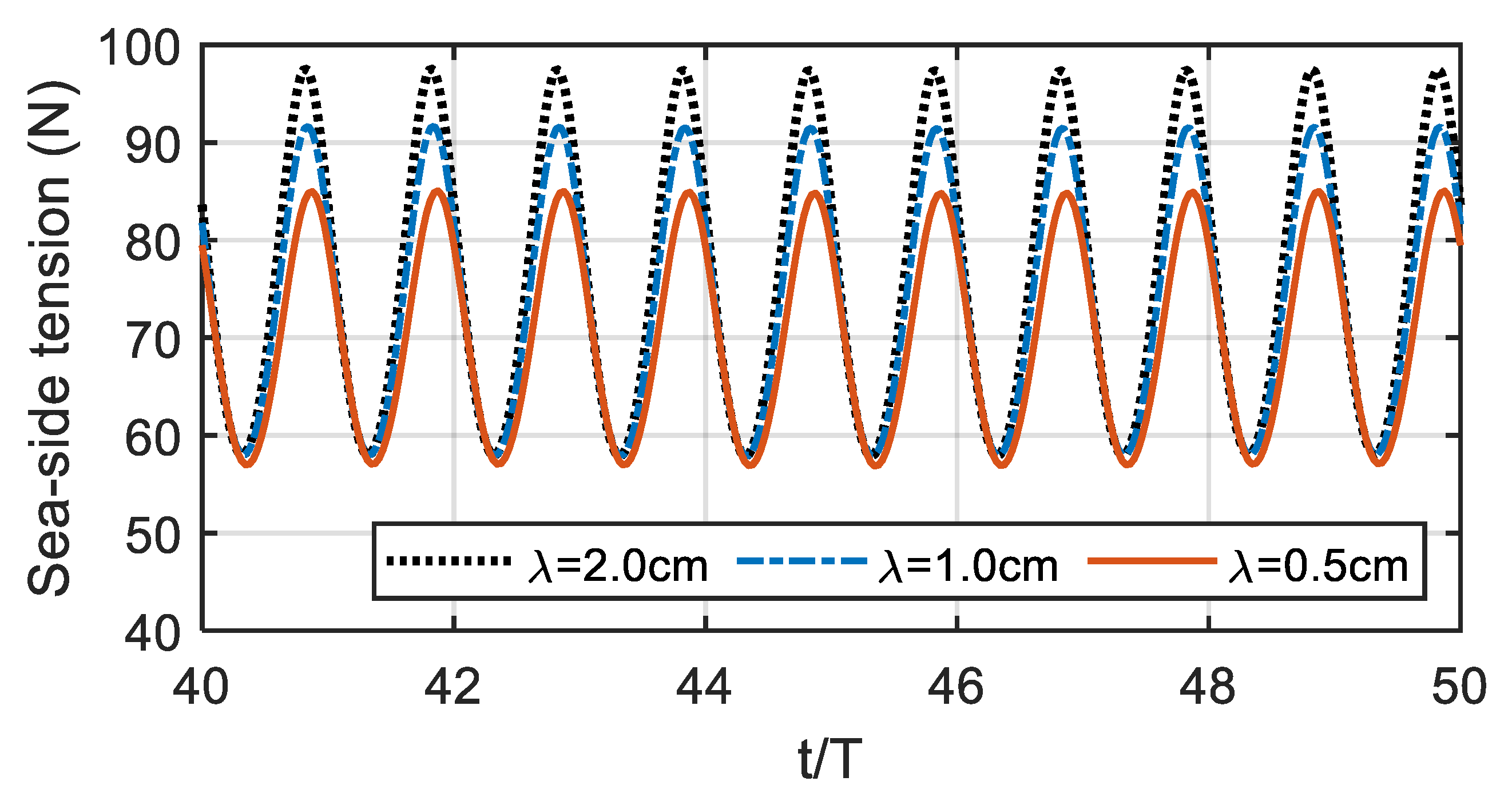
4.2. Time-Domain Results
4.3. Nonlinear Dynamic Properties
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, L.; Collu, M.; Ruzzo, C.; Failla, G.; Abhinav, K.A.; Arena, F. Analysis of the Coupled Dynamics of an Offshore Floating Multi-Purpose Platform: Part A—Rigid Body Analysis. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2019), Glasgow, Scotland, UK, 9–14 June 2019. [Google Scholar]
- Ruzzo, C.; Failla, G.; Arena, F.; Li, L.; Collu, M. Analysis of the Coupled Dynamics of an Offshore Floating Multi-Purpose Platform: Part B—Hydro-Elastic Analysis with Flexible Support Platform. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2019), Glasgow, Scotland, UK, 9–14 June 2019. [Google Scholar]
- Tsukrov, I.; Eroshkin, O.; Fredriksson, D.; Swift, M.; Celikkol, B. Finite element modeling of net panels using a consistent net element. Ocean Eng. 2003, 30, 251–270. [Google Scholar] [CrossRef]
- Fredriksson, D.W.; Swift, M.; Irish, J.D.; Tsukrov, I.; Celikkol, B. Fish cage and mooring system dynamics using physical and numerical models with field measurements. Aquac. Eng. 2003, 27, 117–146. [Google Scholar] [CrossRef]
- Huang, C.-C.; Tang, H.-J.; Liu, J.-Y. Dynamical analysis of net cage structures for marine aquaculture: Numerical simulation and model testing. Aquac. Eng. 2006, 35, 258–270. [Google Scholar] [CrossRef]
- Huang, C.-C.; Tang, H.-J.; Liu, J.-Y. Modeling volume deformation in gravity-type cages with distributed bottom weights or a rigid tube-sinker. Aquac. Eng. 2007, 37, 144–157. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Li, Y.; Dong, G.; Gui, F.-K.; Teng, B. A numerical study on dynamic properties of the gravity cage in combined wave-current flow. Ocean Eng. 2007, 34, 2350–2363. [Google Scholar] [CrossRef]
- Kristiansen, T.; Faltinsen, O.M. Experimental and numerical study of an aquaculture net cage with floater in waves and current. J. Fluids Struct. 2015, 54, 1–26. [Google Scholar] [CrossRef]
- Moe-Føre, H.; Lader, P.F.; Lien, E.; Hopperstad, O.S. Structural response of high solidity net cage models in uniform flow. J. Fluids Struct. 2016, 65, 180–195. [Google Scholar] [CrossRef]
- Cifuentes, C.; Kim, M. Hydrodynamic response of a cage system under waves and currents using a Morison-force model. Ocean Eng. 2017, 141, 283–294. [Google Scholar] [CrossRef]
- Bai, W.; Taylor, R.E. Higher-order boundary element simulation of fully nonlinear wave radiation by oscillating vertical cylinders. Appl. Ocean Res. 2006, 28, 247–265. [Google Scholar] [CrossRef]
- Bai, W.; Taylor, R.E. Numerical simulation of fully nonlinear regular and focused wave diffraction around a vertical cylinder using domain decomposition. Appl. Ocean Res. 2007, 29, 55–71. [Google Scholar] [CrossRef]
- Bai, W.; Taylor, R.E. Fully nonlinear simulation of wave interaction with fixed and floating flared structures. Ocean Eng. 2009, 36, 223–236. [Google Scholar] [CrossRef]
- Boo, S. Linear and nonlinear irregular waves and forces in a numerical wave tank. Ocean Eng. 2002, 29, 475–493. [Google Scholar] [CrossRef]
- Gaeta, M.G.; Segurini, G.; Moreno, A.; Archetti, R. Implementation and Validation of a Potential Model for a Moored Floating Cylinder under Waves. J. Mar. Sci. Eng. 2020, 8, 131. [Google Scholar] [CrossRef]
- Tang, H.-J.; Huang, C.-C.; Chen, W.-M. Dynamics of dual pontoon floating structure for cage aquaculture in a two-dimensional numerical wave tank. J. Fluids Struct. 2011, 27, 918–936. [Google Scholar] [CrossRef]
- Guo, Y.; Mohapatra, S.; Soares, C.G. Review of developments in porous membranes and net-type structures for breakwaters and fish cages. Ocean Eng. 2020, 200, 107027. [Google Scholar] [CrossRef]
- Bi, C.-W.; Zhao, Y.-P.; Dong, G.; Cui, Y.; Gui, F.-K. Experimental and numerical investigation on the damping effect of net cages in waves. J. Fluids Struct. 2015, 55, 122–138. [Google Scholar] [CrossRef]
- Zhou, C.; Xu, L.; Hu, F.; Qu, X. Hydrodynamic characteristics of knotless nylon netting normal to free stream and effect of inclination. Ocean Eng. 2015, 110, 89–97. [Google Scholar] [CrossRef]
- Gansel, L.C.; Plew, D.R.; Endresen, P.C.; Olsen, A.I.; Misimi, E.; Guenther, J. Jensen, Østen Drag of Clean and Fouled Net Panels – Measurements and Parameterization of Fouling. PLoS ONE 2015, 10, e0131051. [Google Scholar] [CrossRef]
- Bi, C.-W.; Zhao, Y.-P.; Dong, G.-H.; Wu, Z.-M.; Zhang, Y.; Xu, T.-J. Drag on and flow through the hydroid-fouled nets in currents. Ocean Eng. 2018, 161, 195–204. [Google Scholar] [CrossRef]
- Koo, W.; Kim, M.-H. Freely floating-body simulation by a 2D fully nonlinear numerical wave tank. Ocean Eng. 2004, 31, 2011–2046. [Google Scholar] [CrossRef]
- Tang, H.-J.; Huang, C.-C. Bragg reflection in a fully nonlinear numerical wave tank based on boundary integral equation method. Ocean Eng. 2008, 35, 1800–1810. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Cokelet, E. The Deformation of Steep Surface Waves on Water: I. a Numerical Method of Computation. Proc. Royal. Soc. Lond. 1976, A350, 1–26. [Google Scholar]
- Cointe, R. Numerical simulation of a wave channel. Eng. Anal. Bound. Elem. 1990, 7, 167–177. [Google Scholar] [CrossRef]
- Tanizawa, K. Long Time Fully Nonlinear Simulation of Floating Body Motions with Artificial Damping Zone. J. Soc. Nav. Arch. Jpn. 1996, 1996, 311–319. [Google Scholar] [CrossRef]
- Grilli, S.; Svendsen, I. Corner problems and global accuracy in the boundary element solution of nonlinear wave flows. Eng. Anal. Bound. Elem. 1990, 7, 178–195. [Google Scholar] [CrossRef]
- Tanizawa, K. A Nonlinear Simulation Method of 3-D Body Motions in Waves (1st Report). J. Soc. Nav. Arch. Jpn. 1995, 1995, 179–191. [Google Scholar] [CrossRef]
- Cao, Y.; Beck, R.F.; Schultz, W.W. Nonlinear Computation of Wave Loads and Motions of Floating Bodies in Incident Waves. In Proceedings of the 9th Workshop on Water Waves and Floating Bodies, Kuju, Oita, Japan, 17–20 April 1994; pp. 33–37. [Google Scholar]
- Yan, S.; Ma, Q. Numerical simulation of fully nonlinear interaction between steep waves and 2D floating bodies using the QALE-FEM method. J. Comput. Phys. 2007, 221, 666–692. [Google Scholar] [CrossRef]
- Vinje, T.; Brevig, P. Nonlinear Ship Motions. In Proceedings of the 3rd International Conference on Numerical Ship Hydrodynamics, Paris, France, 16–19 June 1981; Volume 10. [Google Scholar]
- Wu, G.X.; Eatock Taylor, R. Transient Motion of a Floating Body in Steep Water Waves. In Proceedings of the Eleventh International Workshop on Water Waves and Floating Bodies, Hamburg, Germany, 17–20 March 1996. [Google Scholar]
- Tanizawa, K. The State of the Art on Numerical Wave Tank. In Proceedings of the 4th Osaka Colloquium on Seakeeping Performance of Ships, Osaka, Japan, 17–21 October 2000; pp. 95–114. [Google Scholar]
- Ma, Q.; Yan, S. QALE-FEM for numerical modelling of non-linear interaction between 3D moored floating bodies and steep waves. Int. J. Numer. Methods Eng. 2009, 78, 713–756. [Google Scholar] [CrossRef]
- Brebbia, C.; Walker, S. Dynamic analysis of offshore structures. Appl. Ocean Res. 1981, 3, 205. [Google Scholar] [CrossRef]
- Loland, G. Current Forces On and Flow through Fish Farms, Division of Marine Hydrodynamics; Norwegian Institute of Technology: Trondheim, Norway, 1991; pp. 85–95. [Google Scholar]
- Yamamoto, T.; Yoshida, A.; Ijima, T. Dynamics of elastically moored floating objects. Appl. Ocean Res. 1980, 2, 85–92. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Application to Earthquake Engineering; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Mansard, E.P.D.; Funke, E.R. The Measurement of Incident and Reflected Spectra Using a Least Squares Method. In Proceedings of the 17th Coastal Engineering Conference, ASCE, Sydney, Australia, 23–28 March 1980; pp. 154–172. [Google Scholar]
- Williams, A.; Abul-Azm, A. Dual pontoon floating breakwater. Ocean Eng. 1997, 24, 465–478. [Google Scholar] [CrossRef]
- Williams, A.; Lee, H.; Huang, Z. Floating pontoon breakwaters. Ocean Eng. 2000, 27, 221–240. [Google Scholar] [CrossRef]
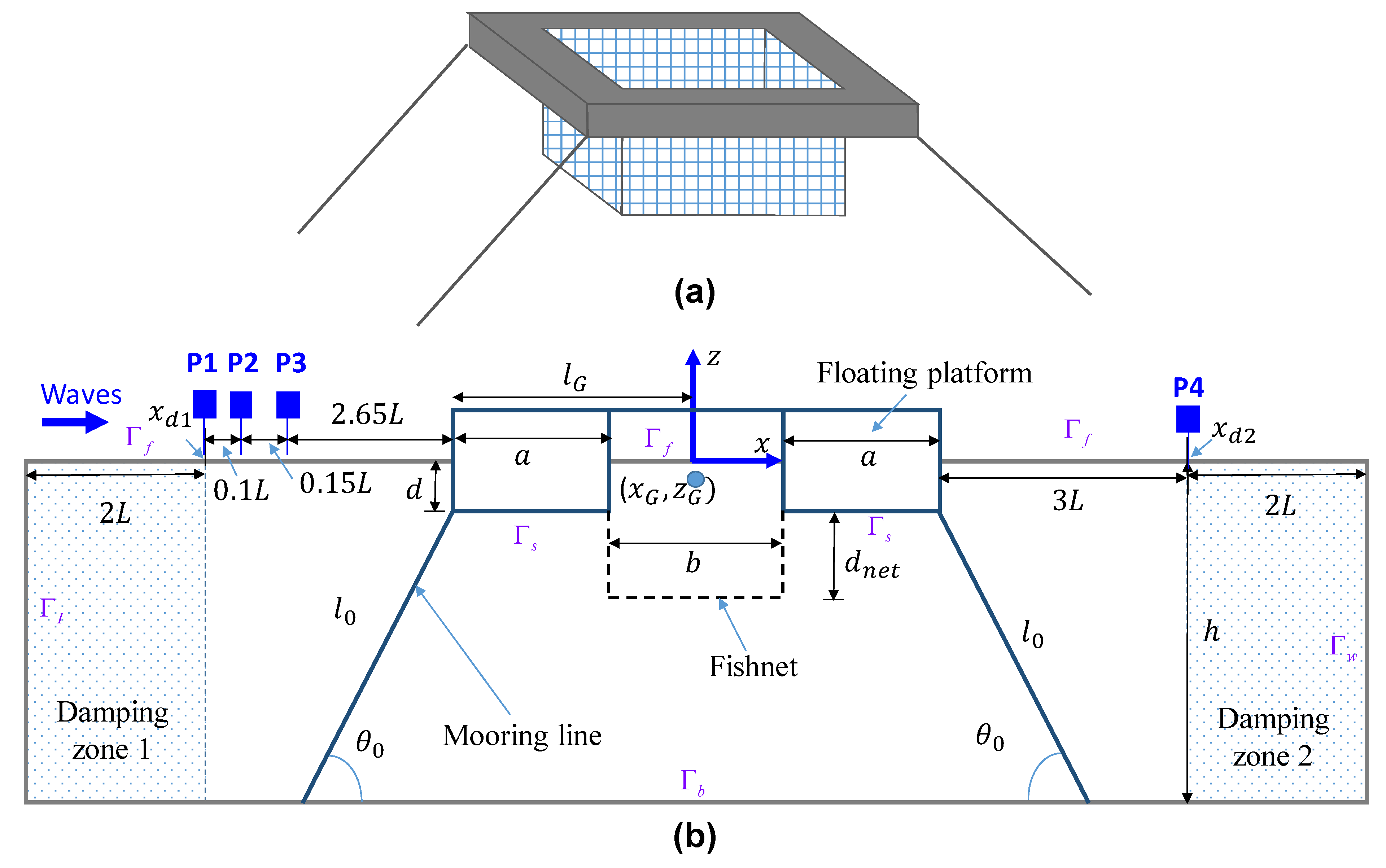
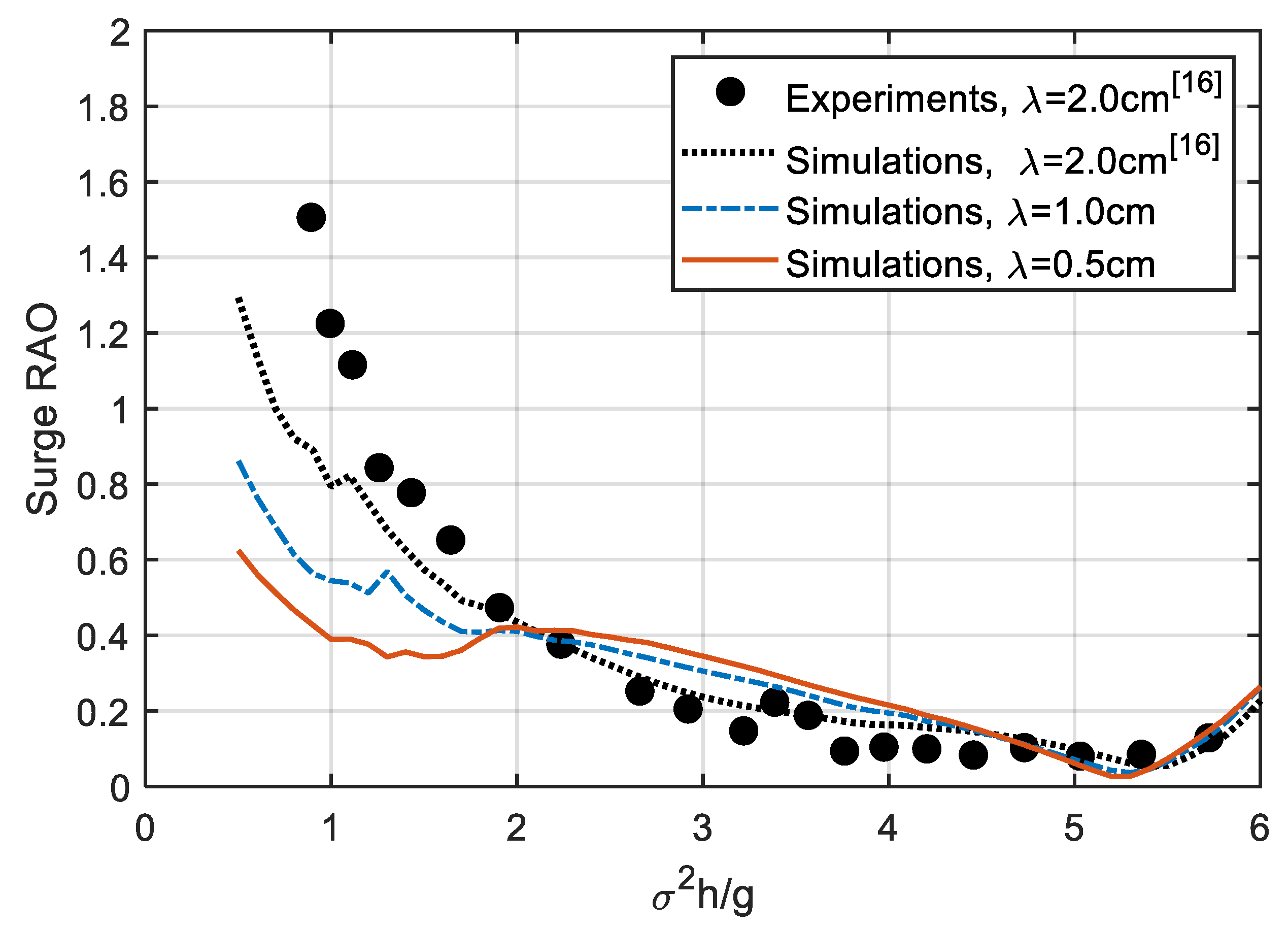

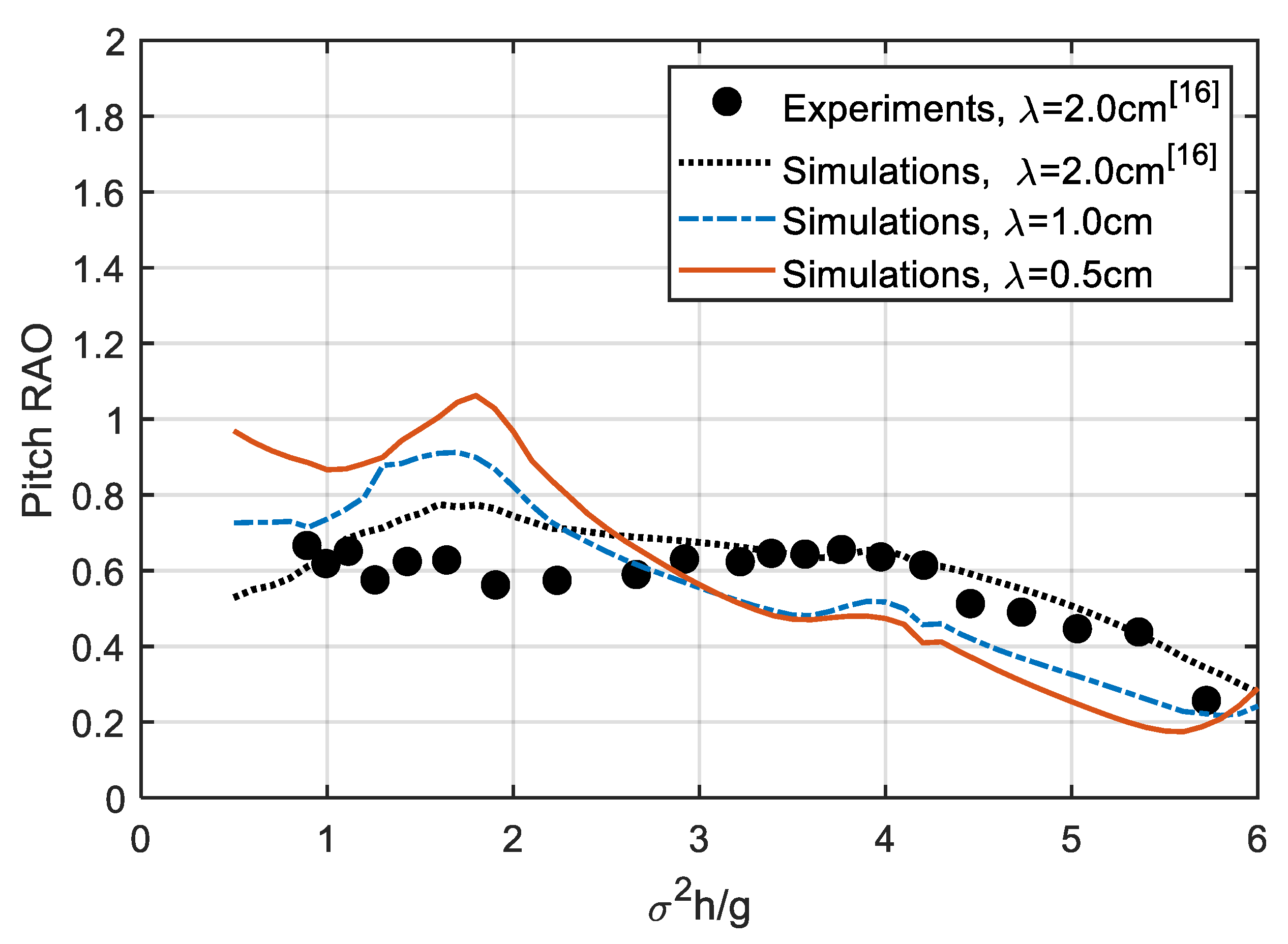
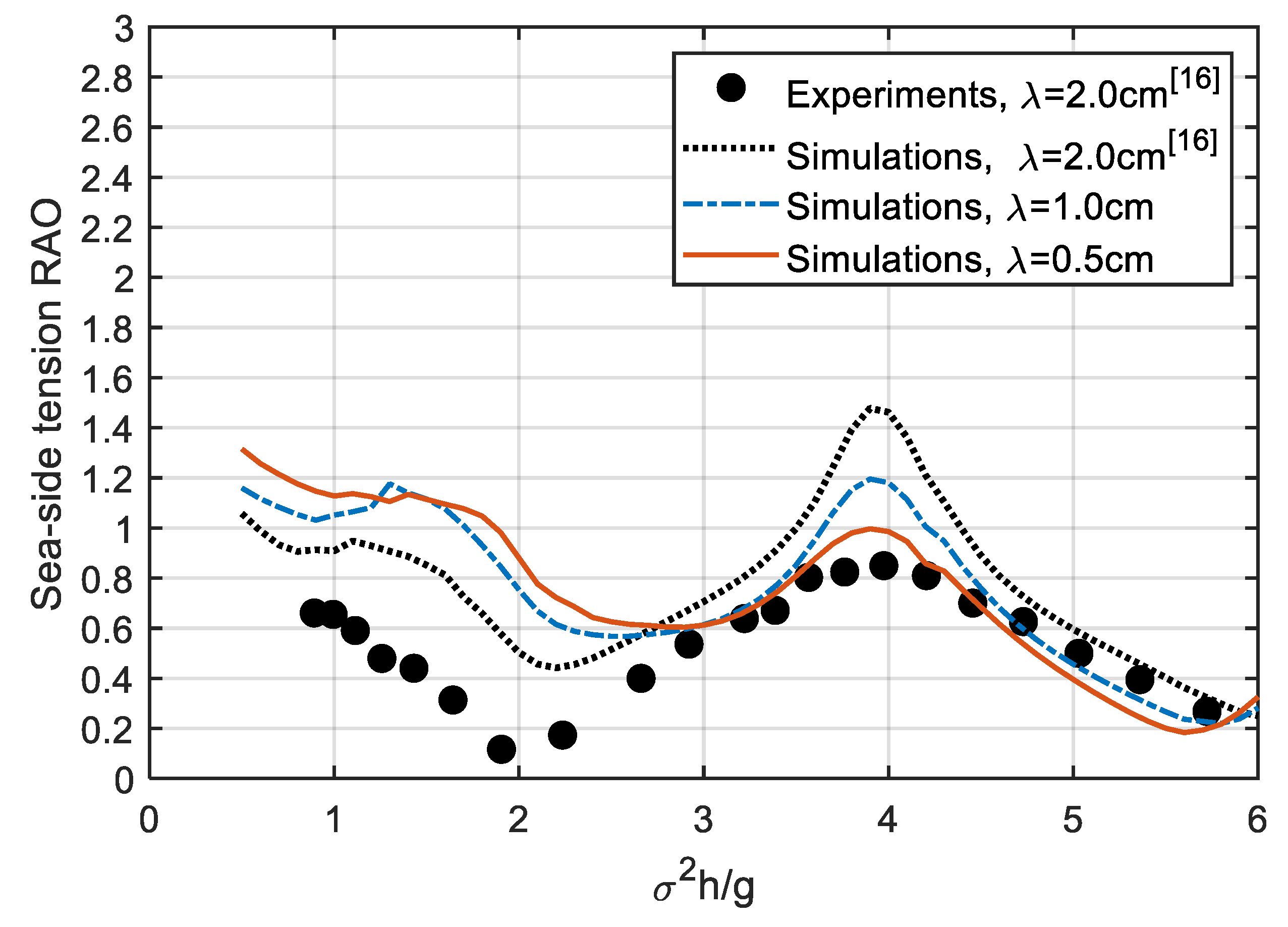


| Specifications | Sizes |
|---|---|
| Wave amplitude (A) | 0.02 m |
| Wave period (T) | 0.73–2.54 s |
| Water depth (h) | 0.80 m |
| Total mass of platform (m) | 62.58 kg |
| Width of platform (a) | 0.25 m |
| Spacing between pontoons (b) | 0.50 m |
| Draft (d) | 0.153 m |
| Pitch moment arm (lG) | 0.50 m |
| Moment of inertia (IG) | 8.93 kg∙m2 |
| Spring constant (K) | 674.93 N/m |
| Mooring angle () | 52° |
| Gravity center (, ) | (0.0 m, −0.0861 m) |
| Net depth () | 0.455 m |
| Twine diameter () | 0.175 cm |
| Specific gravity of net (Nylon) | 1.14 |
| 2.0 | 0.179 | 1.645 | 2.6 |
| 1.0 | 0.365 | 3.361 | 5.4 |
| 0.5 | 0.761 | 7.003 | 11.2 |
| Normalized Parameters | Definition |
|---|---|
| Normalized surge RAO | |
| Normalized heave RAO | |
| Normalized pitch RAO | |
| Normalized tension RAO | |
| Normalized angular frequency |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, H.-J.; Huang, C.-C.; Yang, R.-Y. Numerical Study of the Influence of Fishnet Mesh Size on a Floating Platform. J. Mar. Sci. Eng. 2020, 8, 343. https://doi.org/10.3390/jmse8050343
Tang H-J, Huang C-C, Yang R-Y. Numerical Study of the Influence of Fishnet Mesh Size on a Floating Platform. Journal of Marine Science and Engineering. 2020; 8(5):343. https://doi.org/10.3390/jmse8050343
Chicago/Turabian StyleTang, Hung-Jie, Chai-Cheng Huang, and Ray-Yeng Yang. 2020. "Numerical Study of the Influence of Fishnet Mesh Size on a Floating Platform" Journal of Marine Science and Engineering 8, no. 5: 343. https://doi.org/10.3390/jmse8050343
APA StyleTang, H.-J., Huang, C.-C., & Yang, R.-Y. (2020). Numerical Study of the Influence of Fishnet Mesh Size on a Floating Platform. Journal of Marine Science and Engineering, 8(5), 343. https://doi.org/10.3390/jmse8050343







