Determination of Parameters Describing the Risk Areas of Ships Chaotic Rolling on the Example of LNG Carrier and OSV Vessel
Abstract
1. Introduction
2. Materials and Methods
2.1. Basic Notations
2.2. Regulation for Avoiding Dangerous Situations for Ship Rolling
- Surf-riding and broaching-to,
- Successive high wave attack,
- Synchronous rolling and parametric rolling motions.
2.3. Applied Model of Ship Rolling
3. Results and Discussion
3.1. Considered Ships and Loading Conditions
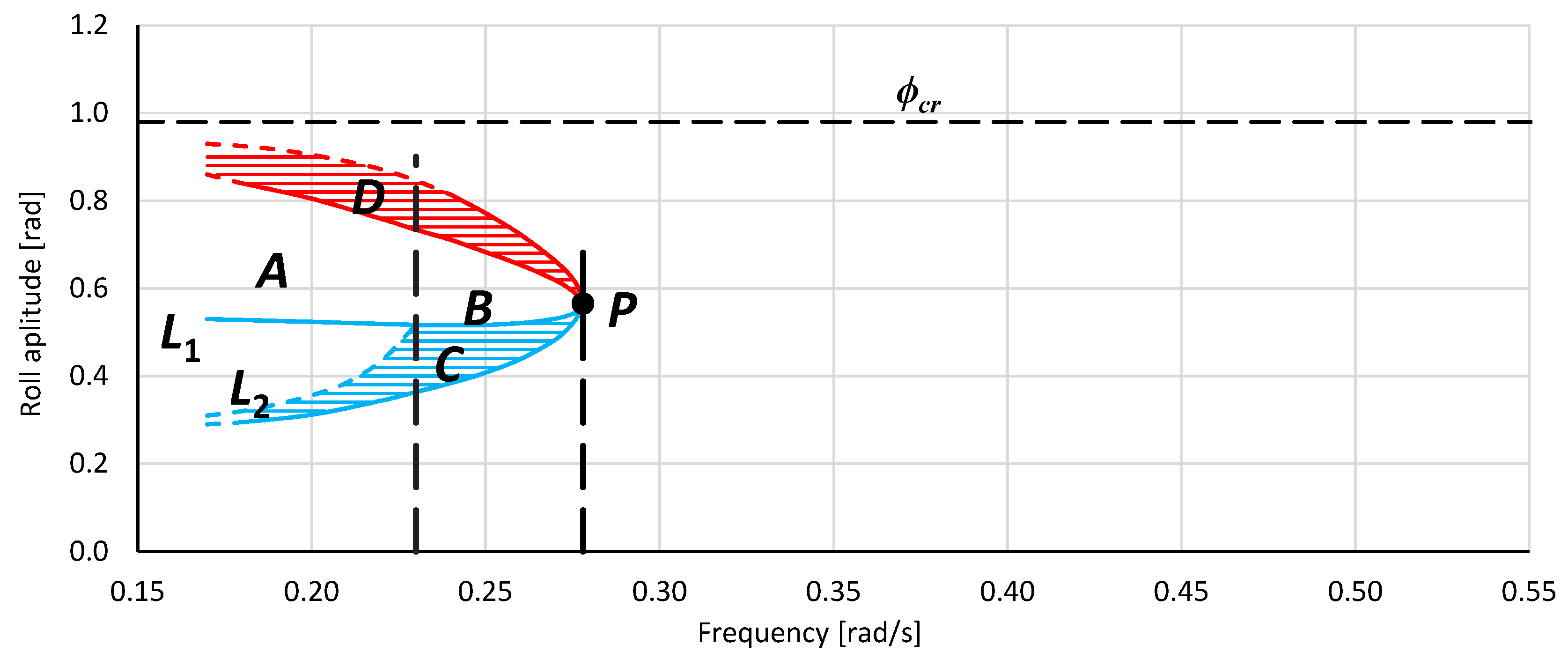
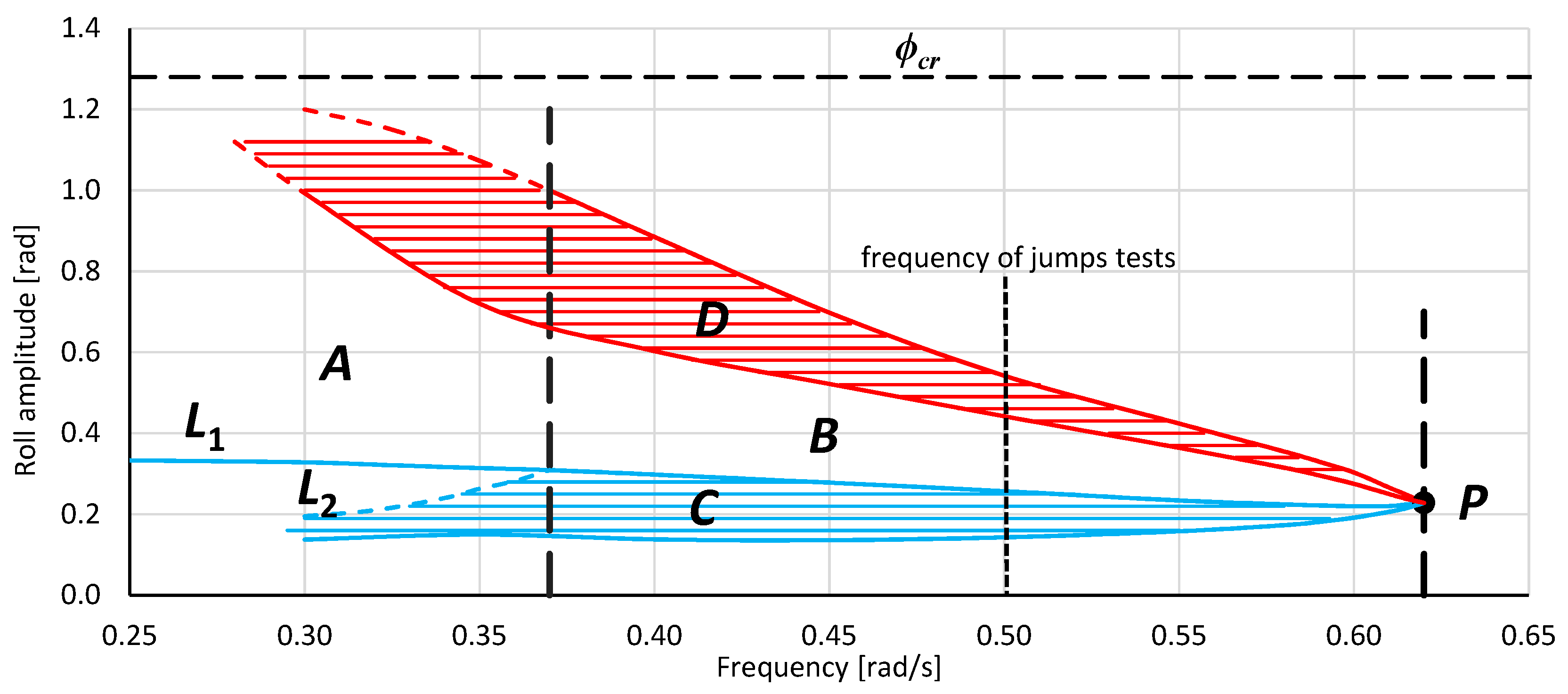
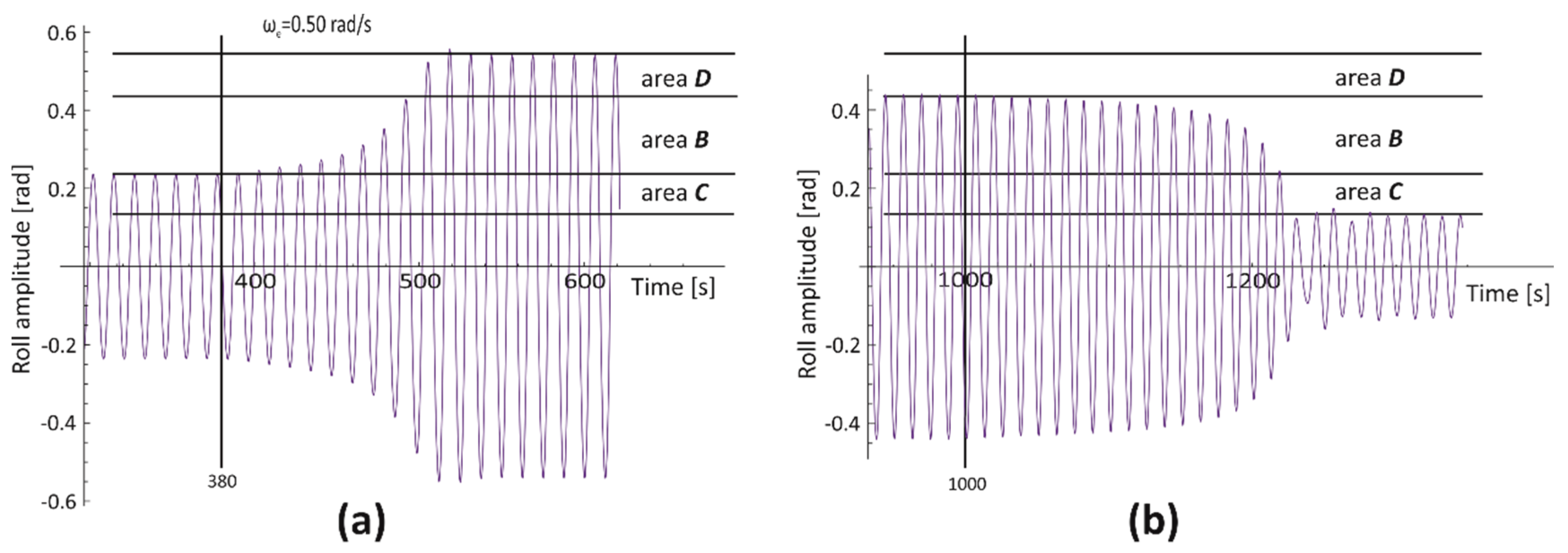
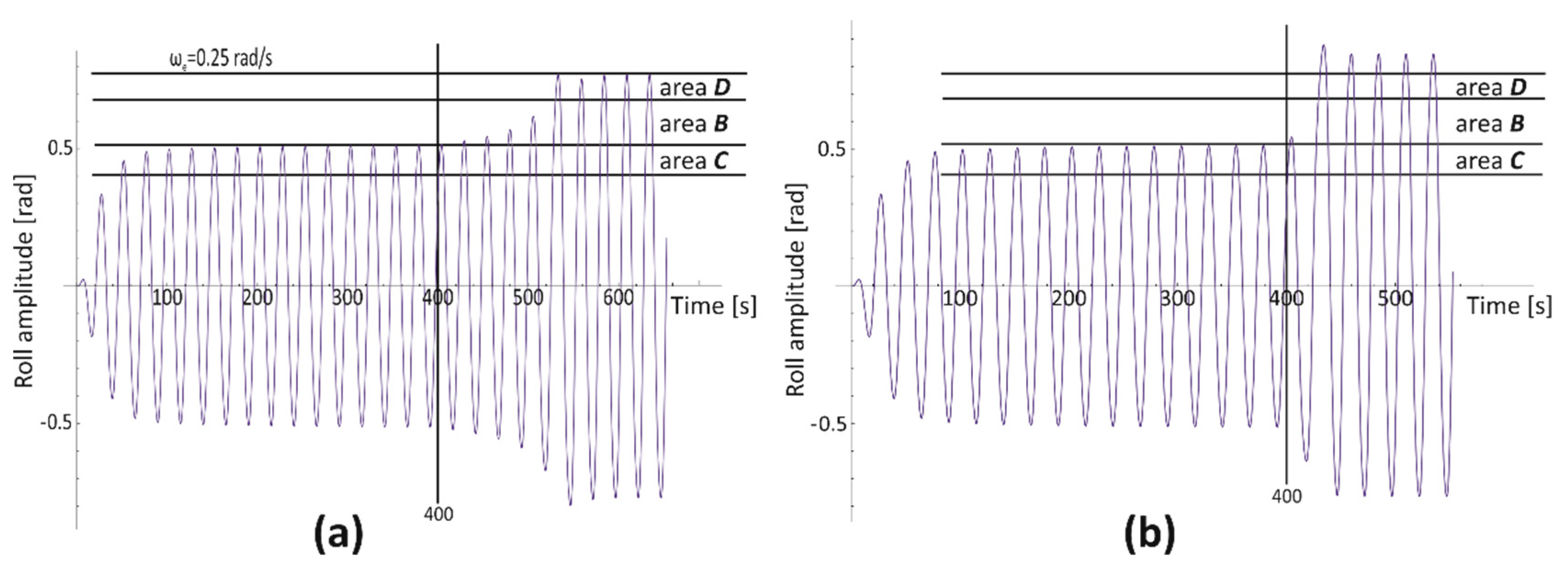
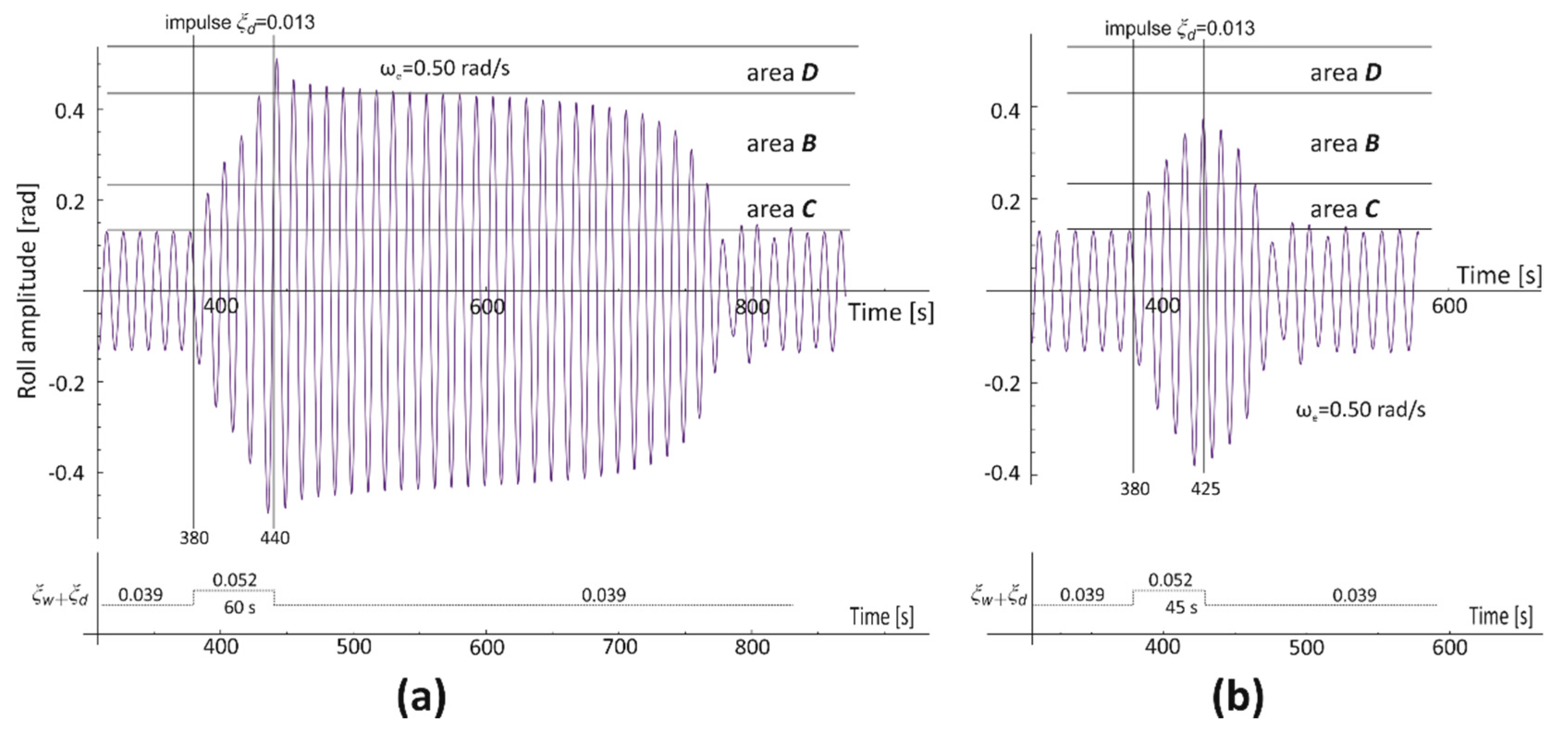
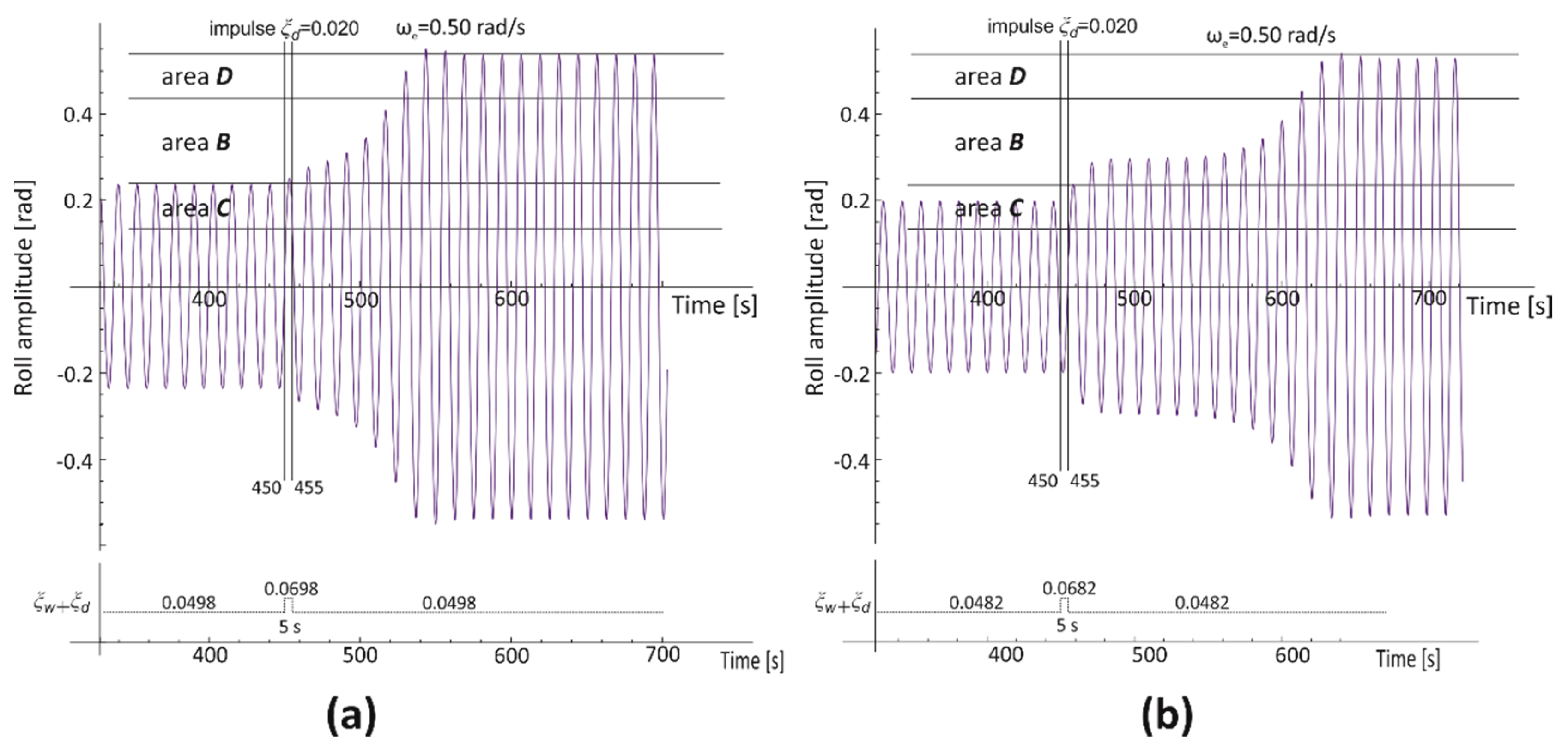
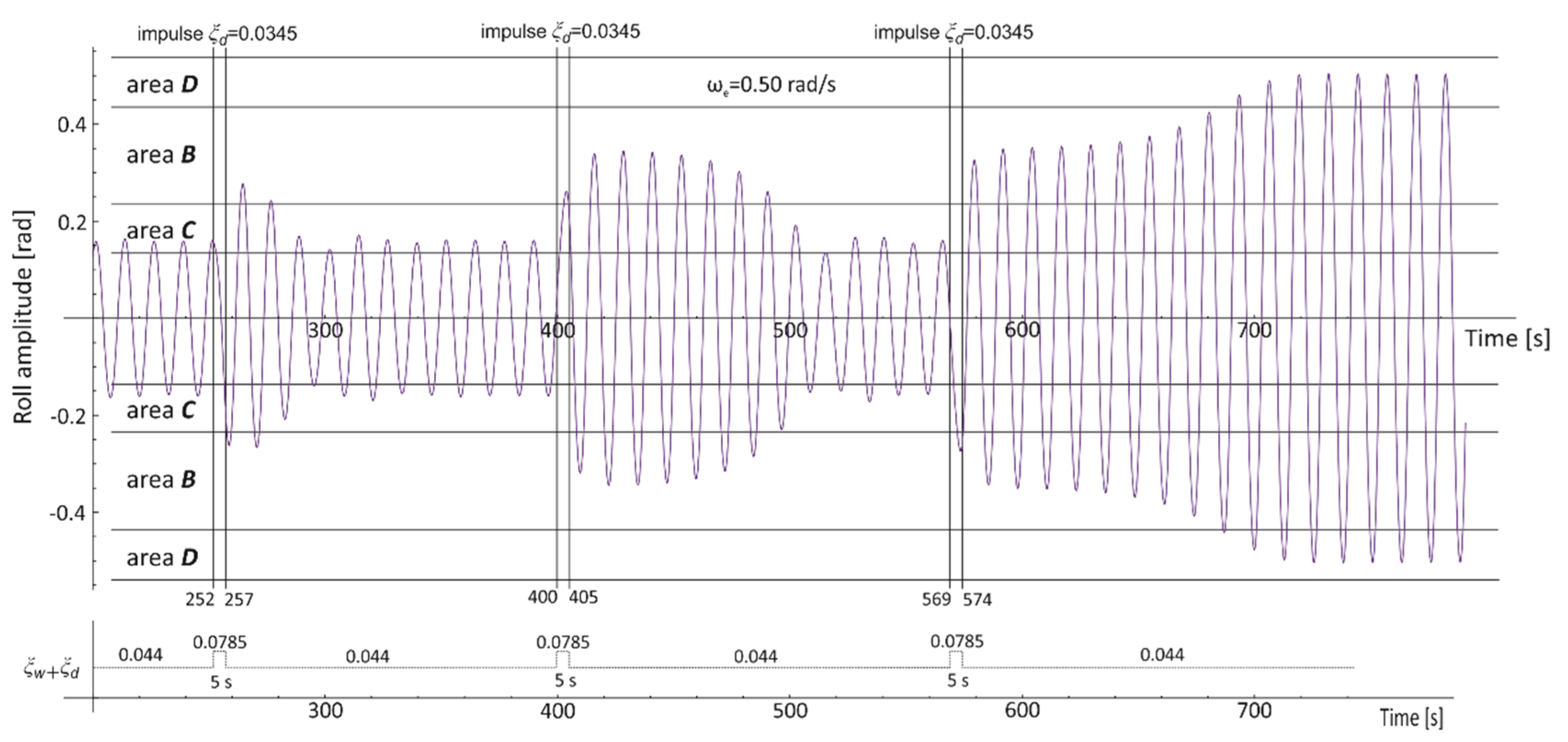
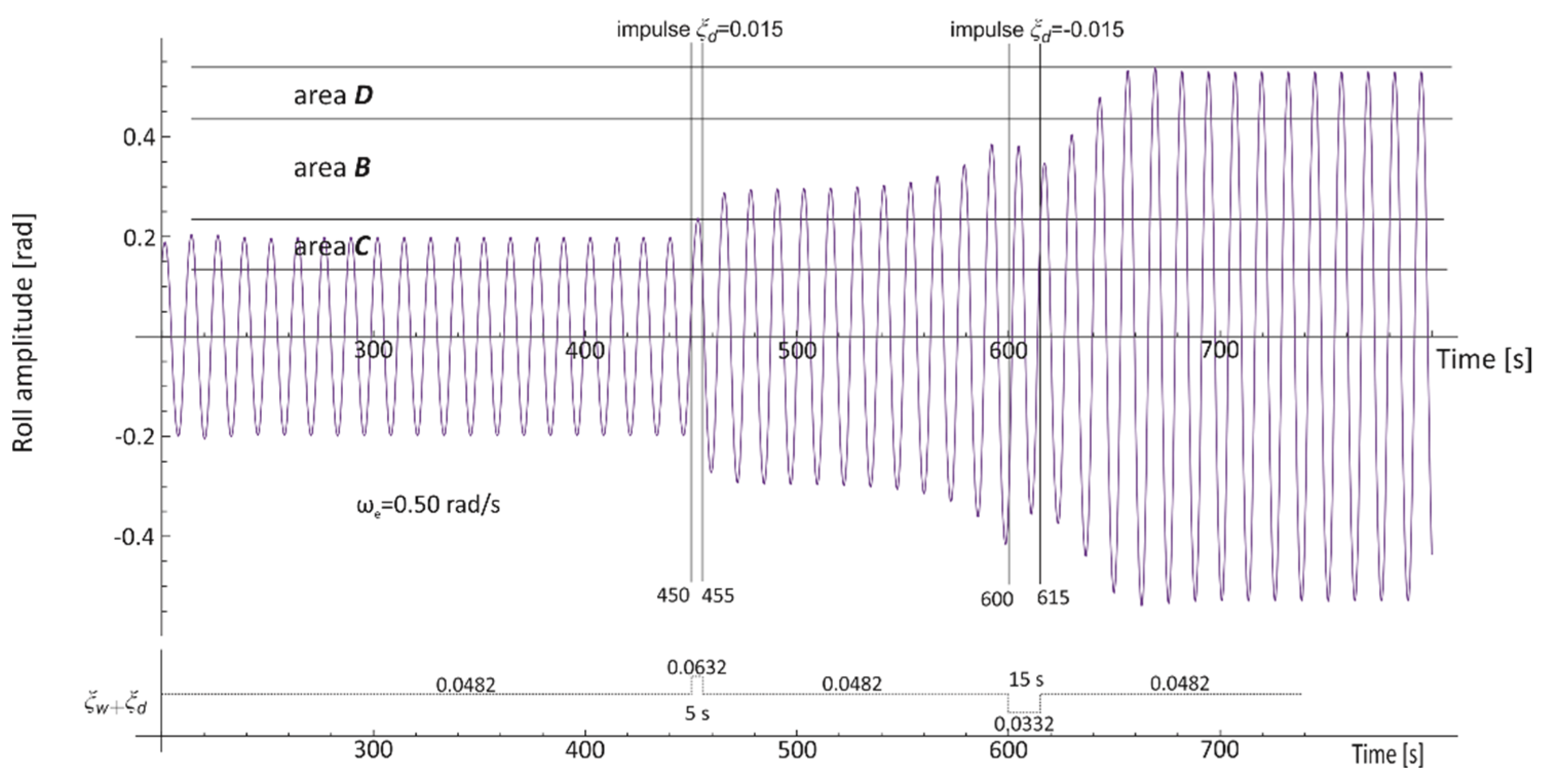
3.2. Areas of Bistability and Unstable Solution of the Mathematical Model of Rolling
- Point P—the bistability origin point—the onset point of bistability areas C and D.
- Areas C and D—rolling bistability areas. In area C, the oscillations are non-resonant, but the energy provided by the excitation moment is big enough for resonant oscillations within the area D. The transitions between the non-resonant and resonant oscillations, and thus between C and D areas, are possible. The lower limit of area C determines the minimum value of the energy (excitation moment) needed for resonant oscillations.
- Areas B and A—areas of an unstable solution of the rolling equation. Areas B and A appear together with the bistability areas C and D and are separated by a dashed vertical line. The difference between areas B and A is indicated in the description of Line L1. The entire border of the area of unstable solutions of the rolling equation is the line of bifurcation.
- Line L1—the maximum amplitude of non-resonant oscillations that can be obtained, at a given frequency, with the smooth increase in the value of excitation (starting from zero value). Inside region A, further increase of the excitation induces bifurcation with jump-up over the critical amplitude ϕcr. Inside region B, further increase of the excitation induces bifurcation with jump-up to the upper limit of area D and next above it.
- Line L2—the maximum amplitude of non-resonant rolling at which it is possible to force, with the use of an additional impulse, a jump-up to the area of resonant oscillations—from line L1 to the upper limit of area D.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- France, W.M.; Levadou, M.; Treakle, T.W.; Paulling, J.R.; Michel, K.; Moore, C. An Investigation of Head-Sea Parametric Rolling and its Influence on Container Lashing Systems. Mar. Technol. 2003, 40, 1–19. [Google Scholar]
- Acanfora, M.; Montewka, J.; Hinz, T.; Matusiak, J. On the estimation of the design loads on container stacks due to excessive acceleration in adverse weather conditions. Mar. Struct. 2017, 53, 105–123. [Google Scholar] [CrossRef]
- Francescutto, A. On the probability of large amplitude rolling and capsizing as a consequence of bifurcations. In Proceedings of the 9th International Conference on Offshore Mechanics and Arctic Engineering OMAE’91, Stavanger, Norway, 23–28 June 1991; pp. 91–96. [Google Scholar]
- Falzarano, J.; Taz Ul Mulk, M. Large Amplitude Rolling Motion of an Ocean Survey Vessel. Mar. Technol. 1994, 31, 278–285. [Google Scholar]
- Contento, G.; Francescutto, A.; Piciullo, M. On the Effectiveness of Constant Coefficients Roll Motion Equation. Ocean Eng. 1996, 23, 597–618. [Google Scholar] [CrossRef]
- Francescutto, A.; Contento, G. Bifurcations in ship rolling, experimental results and parameter identification technique. Ocean Eng. 1999, 26, 1095–1123. [Google Scholar] [CrossRef]
- Wawrzyński, W.; Krata, P. On ship roll resonance frequency. Ocean Eng. 2016, 126, 92–114. [Google Scholar] [CrossRef]
- Wawrzyński, W. Bistability and accompanying phenomena in the 1-DOF mathematical model of rolling. Ocean Eng. 2018, 147, 565–579. [Google Scholar] [CrossRef]
- Liangqiang, Z.; Fangqi, C. Stability and bifurcation analysis for a model of a nonlinear coupled pitch–roll ship. Math. Comput. Simul. 2008, 79, 149–166. [Google Scholar]
- Fossen, T.; Nijmeijer, H. (Eds.) Parametric Resonance in Dynamical Systems; Springer Science Business Media: Berlin, Germany, 2012. [Google Scholar]
- Jordan, D.W.; Smith, P. Nonlinear Ordinary Differential Equations—An Introduction for Scientists and Engineers, 4th ed.; Oxford University: Oxford, UK, 2007. [Google Scholar]
- Brennan, M.J.; Kovacic, I.; Carrella, A.; Waters, T.P. On the jump-up and jump-down frequencies of the Duffing oscillator. J. Sound Vib. 2008, 318, 1250–1261. [Google Scholar] [CrossRef]
- Shin, Y.S.; Belenky, V.L.; Paulling, J.R.; Weems, K.M.; Lin, W.M. Criteria for Parametric Roll of Large Containerships in Longitudinal Seas; SNAME Annual Meeting: Washington, DC, USA, 2004. [Google Scholar]
- Bulian, G. Nonlinear parametric rolling in regular waves—A general procedure for the analytical approximation of the GZ curve and its use in time domain simulation. Ocean. Eng. 2005, 32, 309–330. [Google Scholar] [CrossRef]
- Holden, C.; Galeazzi, R.; Rodriguez, C.; Perez, T.; Fossen, T.; Blanke, M.; Neves, M. Nonlinear container ship model for the study of parametric roll resonance. Model. Identif. Control 2007, 28. [Google Scholar] [CrossRef][Green Version]
- Neves, M.; Rodriguez, C. On unstable ship motions resulting from strong non-linear coupling. Ocean. Eng. 2006, 33, 1853–1883. [Google Scholar] [CrossRef]
- Spyrou, K.; Tigkas, I.; Scanferla, G.; Pallikaropoulos, N.; Themelis, N. Prediction potential of the parametric rolling behaviour of a post-Panamax containership. Ocean. Eng. 2008, 35, 1235–1244. [Google Scholar] [CrossRef]
- Ribeiro e Silva, S.; Guedes Soares, C. Prediction of parametric rolling in waves with a time domain non-linear strip theory model. Ocean. Eng. 2013, 72, 453–469. [Google Scholar] [CrossRef]
- Galeazzi, R.; Holdeny, C.; Blanke, M.; Fossen, T. Stabilisation of Parametric Roll Resonance by Combined Speed and Fin Stabiliser Control. In Proceedings of the Control Conference (ECC), Budapest, Hungary, 23–26 August 2009; pp. 4895–4900. [Google Scholar]
- Stoker, J. Nonlinear Vibrations in Mechanical and Electrical Systems; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Lin, H.; Yim, S.C.S. Chaotic roll motion and capsize of ships under periodic excitation with random noise. Appl. Ocean Res. 1995, 17, 185–204. [Google Scholar] [CrossRef]
- Hu, K.; Ding, Y.; Wang, H. Chaotic roll motions of ships in regular longitudinal waves. J. Mar. Sci. Appl. 2010, 9, 208–212. [Google Scholar] [CrossRef]
- Liu, S.; Yang, Z. Real-time online forecasting model of ship rolling motion based on chaotic online LSSVM. In Proceedings of the IEEE 18th International Conference on Industrial Engineering and Engineering Management, Changchun, China, 3–5 September 2011; pp. 1732–1736. [Google Scholar]
- Shaofang, W.; Yongjun, S.; Xianghong, L.; Shaopu, Y. Dynamical analysis of Mathieu equation with two kinds of van der Pol fractional-order terms. Int. J. Non-Linear Mech. 2016, 84, 130–138. [Google Scholar]
- Kovacic, I. Generalised perturbation techniques for strongly nonlinear oscillators with a positive, zero or negative linear stiffness term. Int. J. Dyn. Control 2015, 3, 137–147. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, M.J. (Eds.) The Duffing Equation: Nonlinear Oscillators and Their Behavior; John Wiley and Sons: Chichester, UK, 2011. [Google Scholar]
- Eric, W. Duffing Differential Equation. From MathWorld—A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/DuffingDifferentialEquation.html (accessed on 20 September 2019).
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Younesian, D.; Askari, H.; Saadatnia, Z.; Yazdi, M.K. Periodic solutions for nonlinear oscillation of a centrifugal governor system using the He’s frequency–amplitude formulation and He’s energy balance method. Nonlinear Sci. Lett. A 2011, 2, 143–148. [Google Scholar]
- Srinil, N.; Zanganeh, H. Modelling of coupled cross-flow/in-line vortex-induced vibrations using double Duffing and van der Pol oscillators. Ocean Eng. 2012, 53, 83–97. [Google Scholar] [CrossRef]
- IMO MSC/Circ. 707 Guidance to the Master for Avoiding Dangerous Situations in Following and Quartering Seas; IMO: London, UK, 1995. [Google Scholar]
- IMO MSC.1/Circ. 1228 Revised Guidance to the Master for Avoiding Dangerous Situations in Adverse Weather and sea Conditions on 11th January 2007; IMO: London, UK, 2007. [Google Scholar]
- Himeno, Y. Prediction of Ship Roll Damping—State of the Art, Report of Dept. of Naval Architecture and Marine Engineering; No. 239; The University of Michigan: Ann Arbor, MI, USA, 1981. [Google Scholar]
- Kawahara, Y.; Maekawa, K.; Ikeda, Y. A Simple Prediction Formula of Roll Damping of Conventional Cargo Ships on the Basis of Ikeda’s Method and Its Limitations. J. Shipp. Ocean Eng. 2012, 2, 201–210. [Google Scholar]
- ITTC Recommended Procedures, Numerical Estimation of Roll Damping; ITTC: Rio de Janeiro, Brazil, 2011.
- Wawrzyński, W. Predykcja składowej tłumienia kołysań bocznych statku dla stępek przechyłowych, porównanie skróconej i pełnej metody Ikedy, Zeszyty Naukowe Akademii Morskiej w Gdyni. Zeszyt 2017, 102, 124–141. [Google Scholar]
- Bassler, C.; Reed, A. A Method to Model Large Amplitude Ship Roll Damping. In Proceedings of the 11th International Ship Stability Workshop, Wageningen, The Netherlands, 21–23 June 2010; pp. 217–224. [Google Scholar]
- IMO. Intact Stability Code; IMO: London, UK, 2008. [Google Scholar]
- Wawrzyński, W. Area of the unstable solution of rolling equation—Jumps of the oscillations amplitude. J. KONES 2018, 25, 489–496. [Google Scholar]
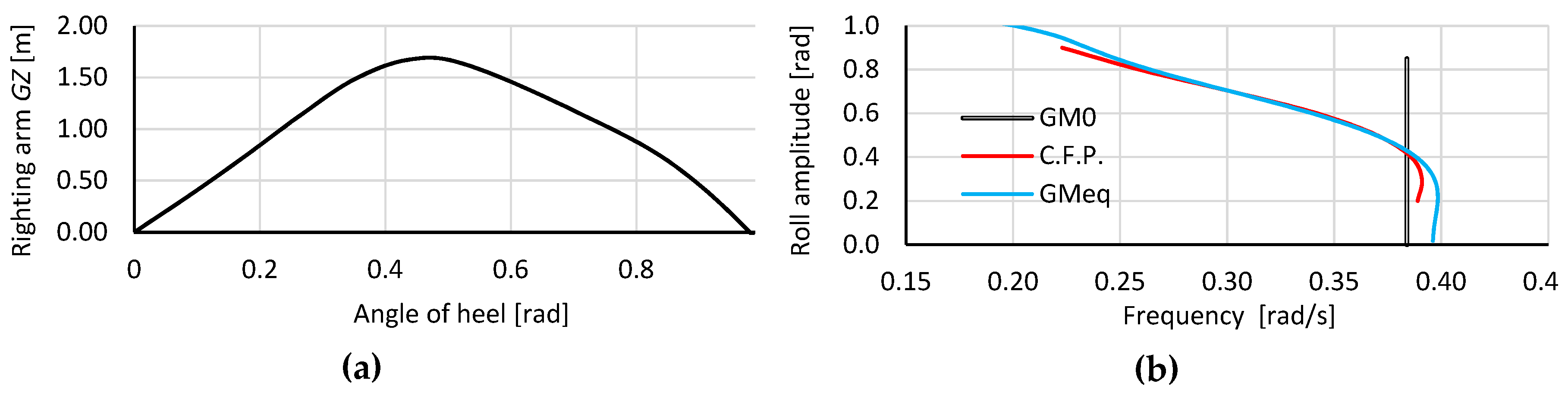

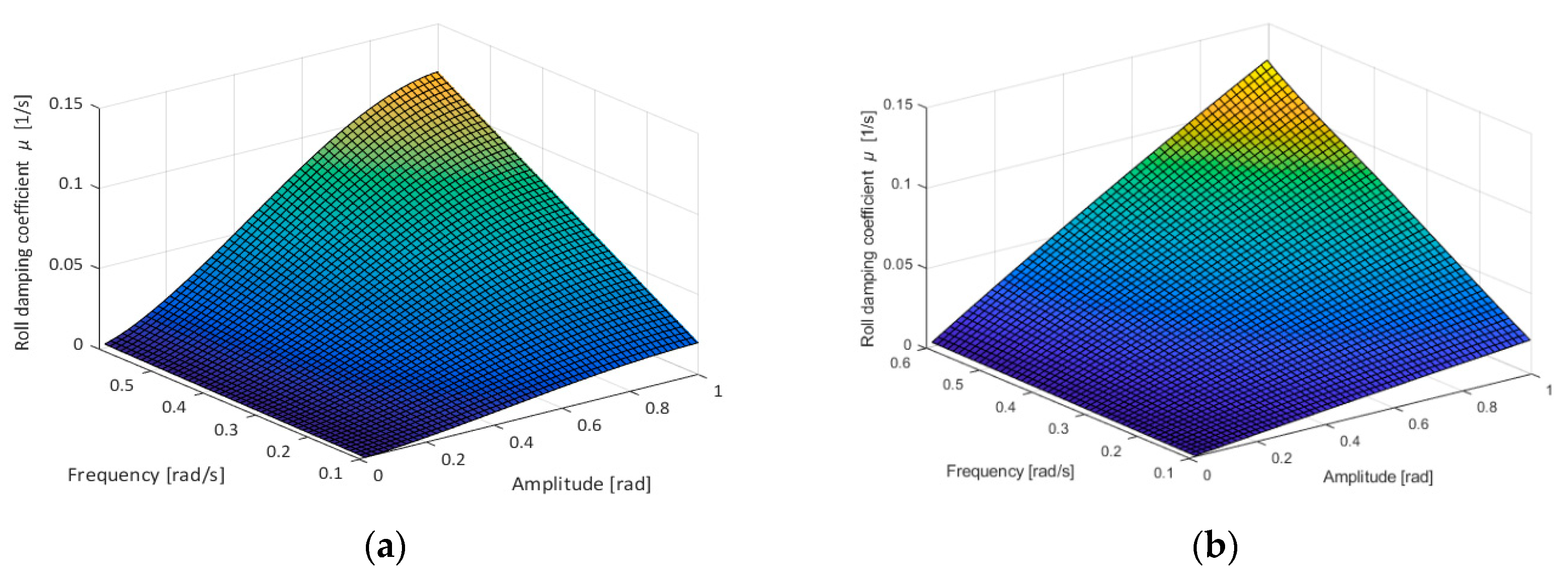
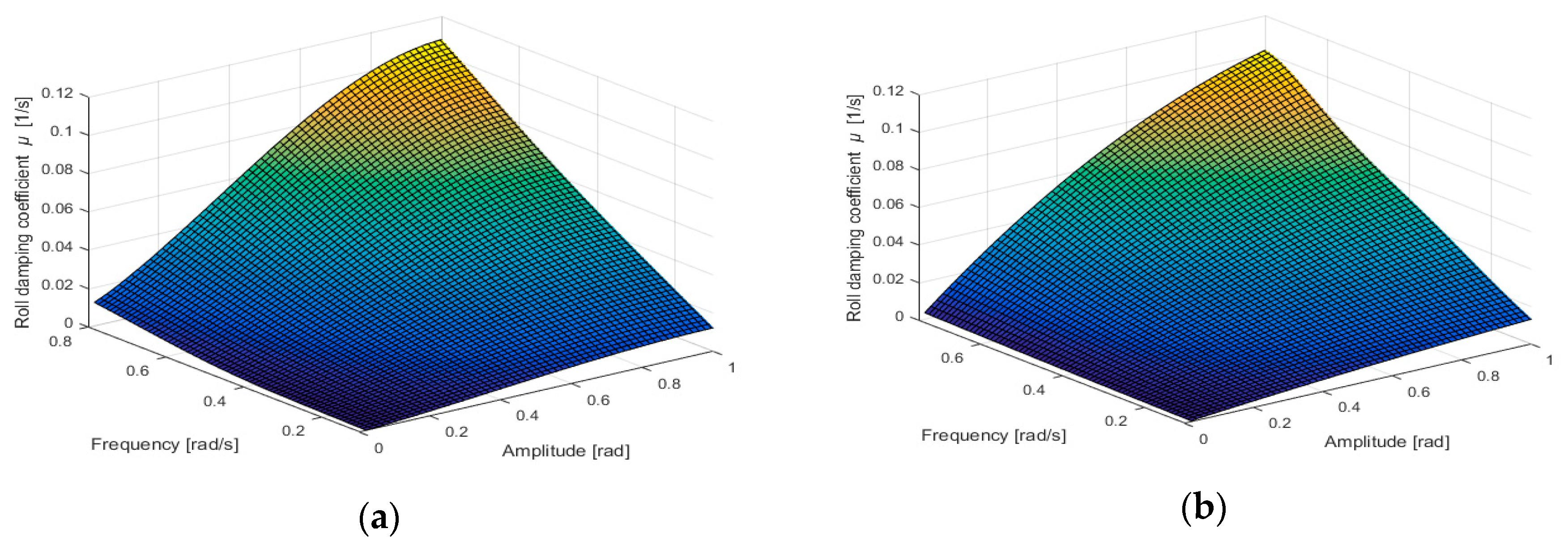
| Type of Vessel | LPP [m] | B [m] | T [m] | GM0 [m] | rx [m] | τ [s] | ωn [rad/s] | |
|---|---|---|---|---|---|---|---|---|
| 1 | LNG carrier | 278.80 | 42.60 | 7.50 | 4.00 | 16.3456 | 16.4 | 0.383 |
| 2 | OSV | 76.20 | 17.00 | 6.10 | 2.50 | 6.8736 | 8.7 | 0.722 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guze, S.; Wawrzynski, W.; Wilczynski, P. Determination of Parameters Describing the Risk Areas of Ships Chaotic Rolling on the Example of LNG Carrier and OSV Vessel. J. Mar. Sci. Eng. 2020, 8, 91. https://doi.org/10.3390/jmse8020091
Guze S, Wawrzynski W, Wilczynski P. Determination of Parameters Describing the Risk Areas of Ships Chaotic Rolling on the Example of LNG Carrier and OSV Vessel. Journal of Marine Science and Engineering. 2020; 8(2):91. https://doi.org/10.3390/jmse8020091
Chicago/Turabian StyleGuze, Sambor, Wojciech Wawrzynski, and Przemyslaw Wilczynski. 2020. "Determination of Parameters Describing the Risk Areas of Ships Chaotic Rolling on the Example of LNG Carrier and OSV Vessel" Journal of Marine Science and Engineering 8, no. 2: 91. https://doi.org/10.3390/jmse8020091
APA StyleGuze, S., Wawrzynski, W., & Wilczynski, P. (2020). Determination of Parameters Describing the Risk Areas of Ships Chaotic Rolling on the Example of LNG Carrier and OSV Vessel. Journal of Marine Science and Engineering, 8(2), 91. https://doi.org/10.3390/jmse8020091





