Embedding of a Blade-Element Analytical Model into the SHYFEM Marine Circulation Code to Predict the Performance of Cross-Flow Turbines
Abstract
1. Introduction
2. Methodology
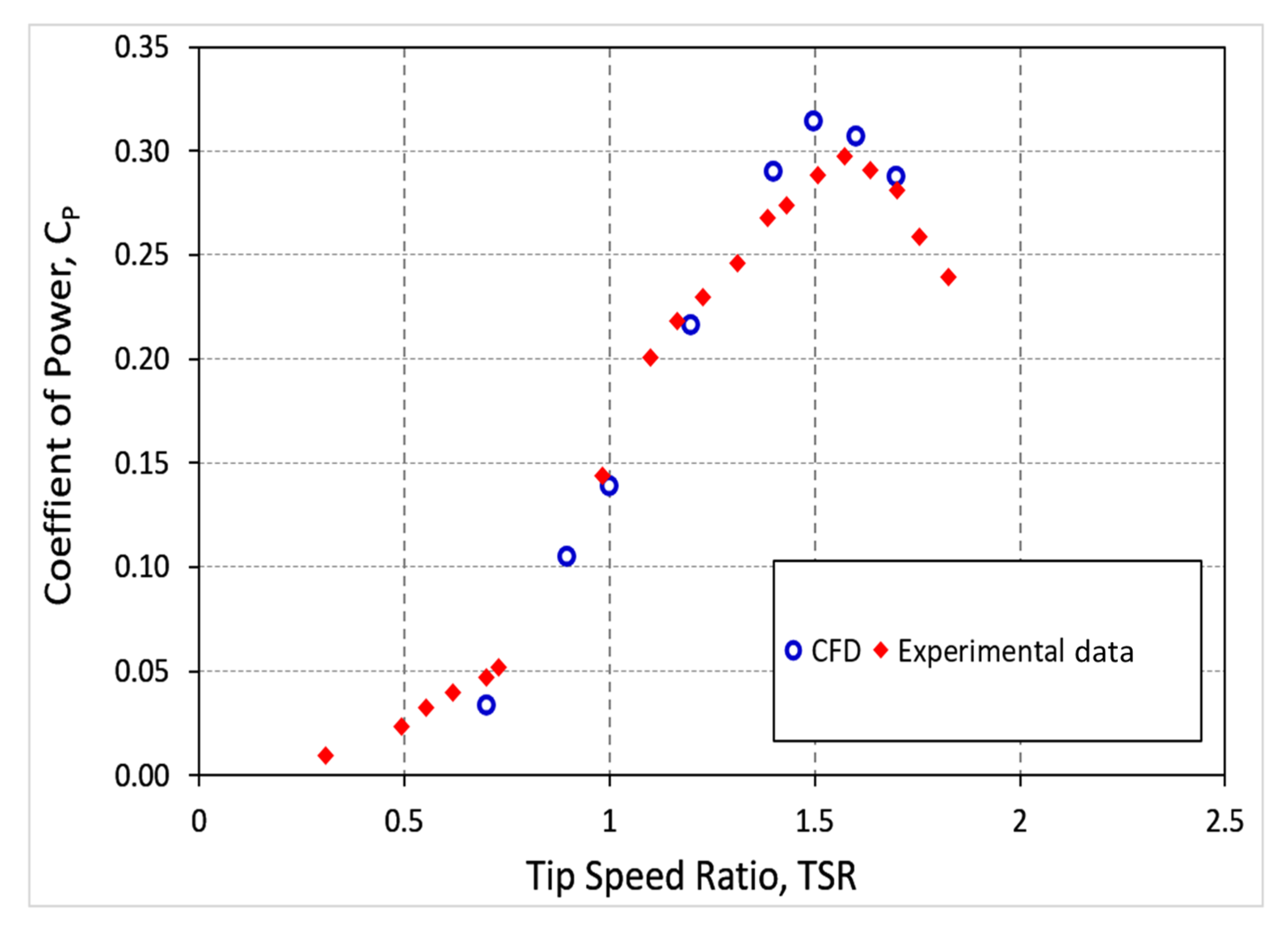
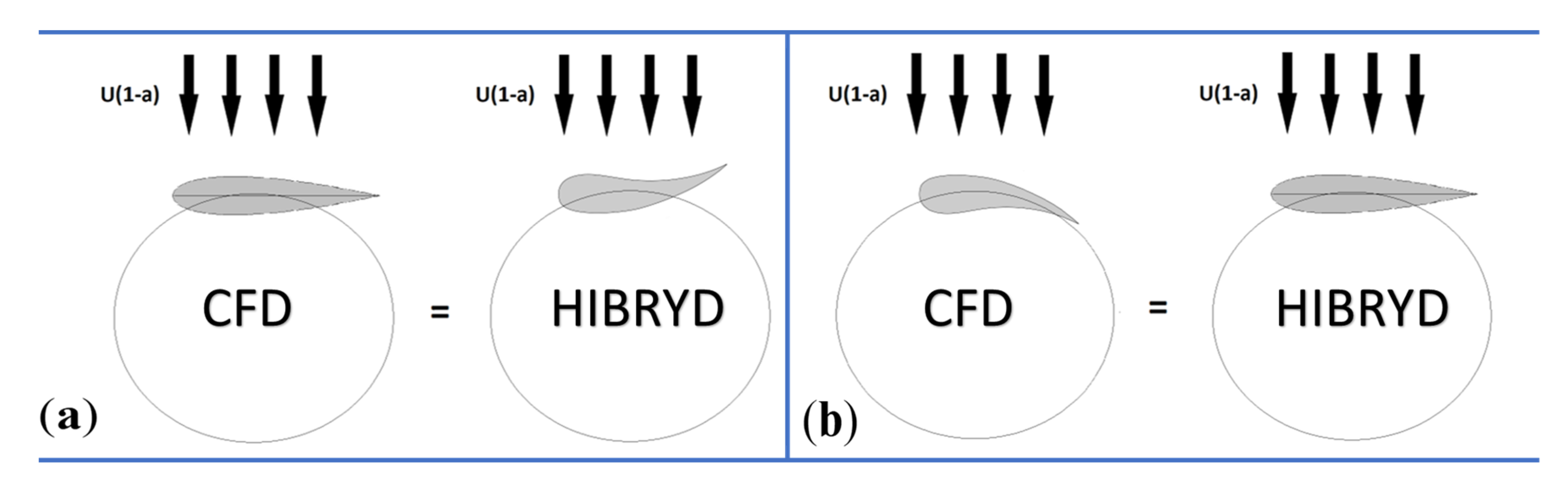
2.1. Preliminary Validation of the ANSYS CFD Model
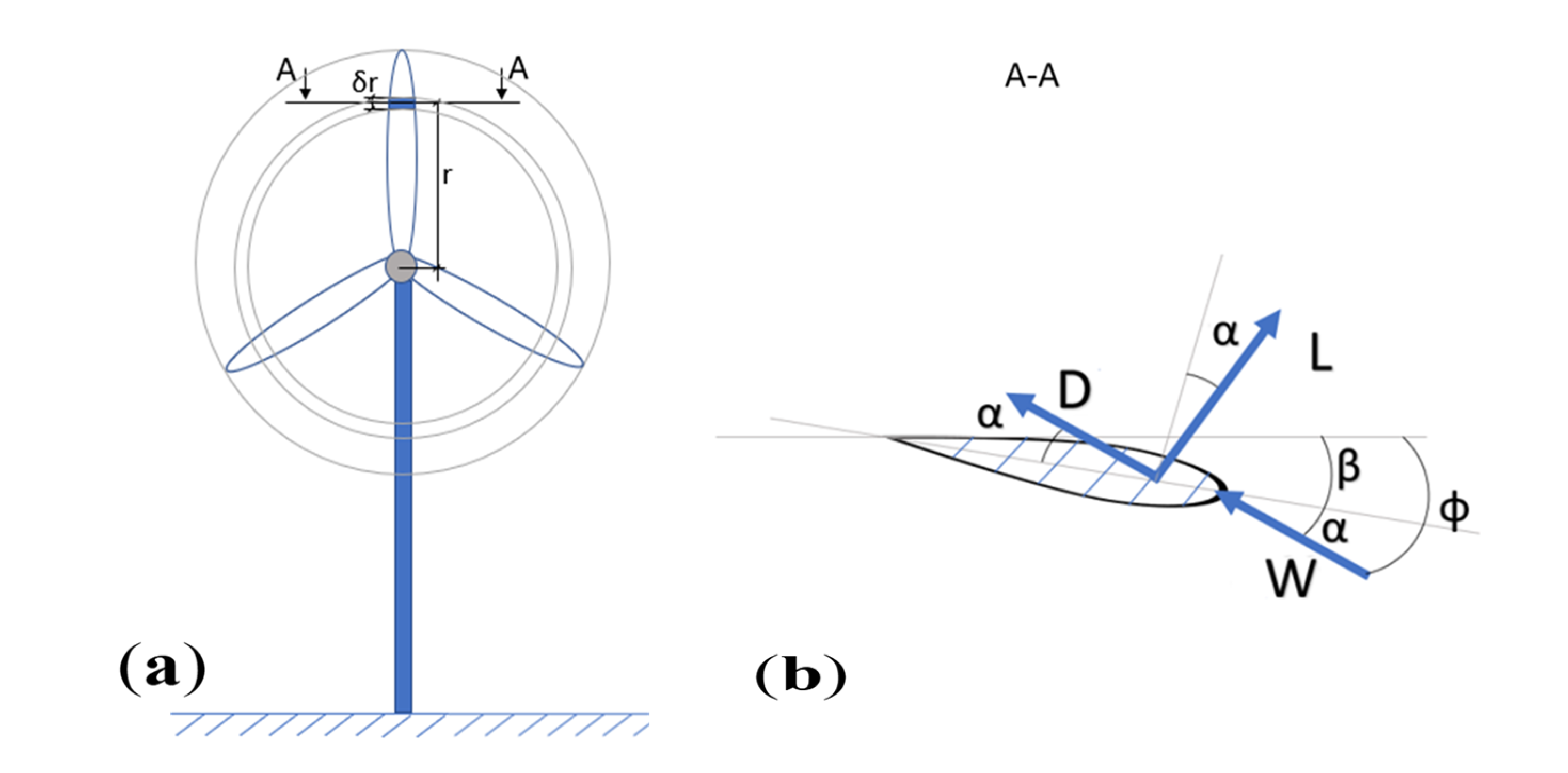
2.2. BEM Theory Basics
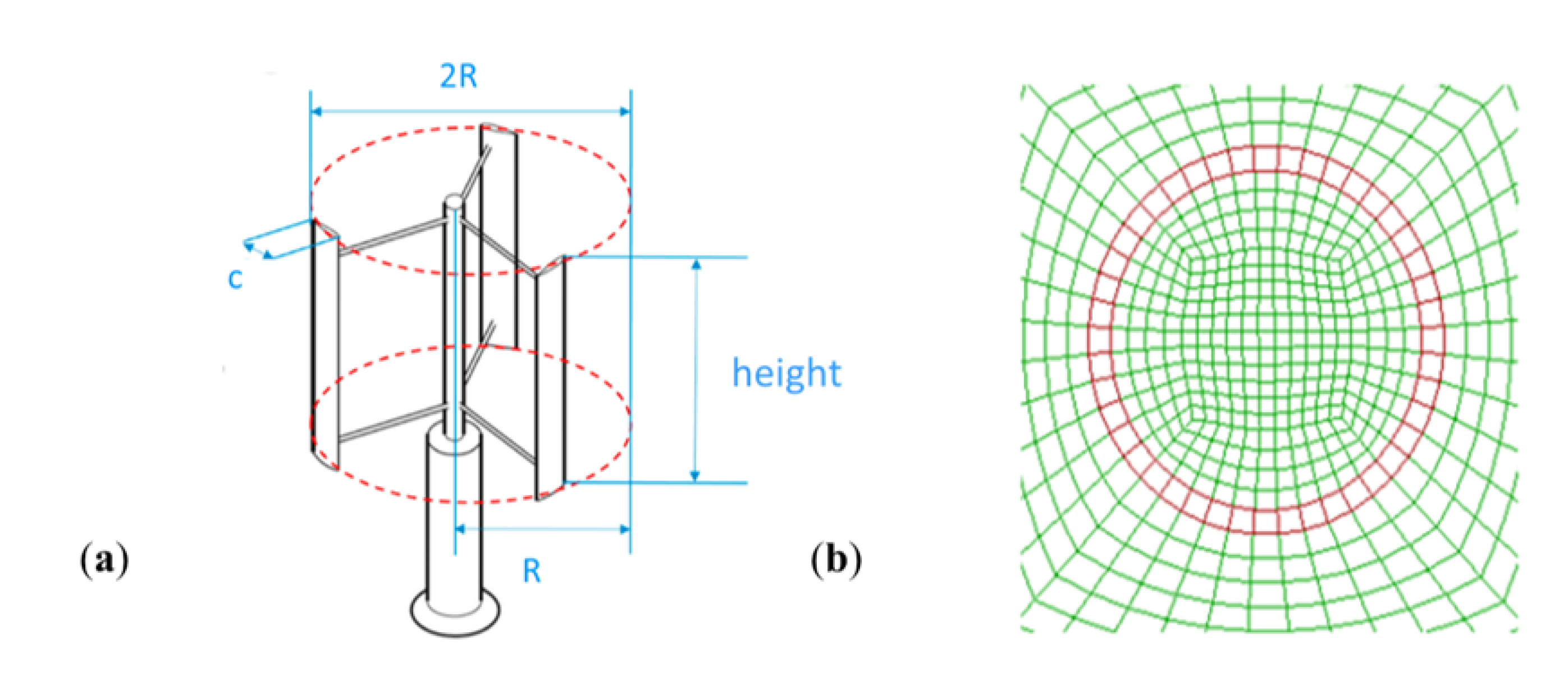
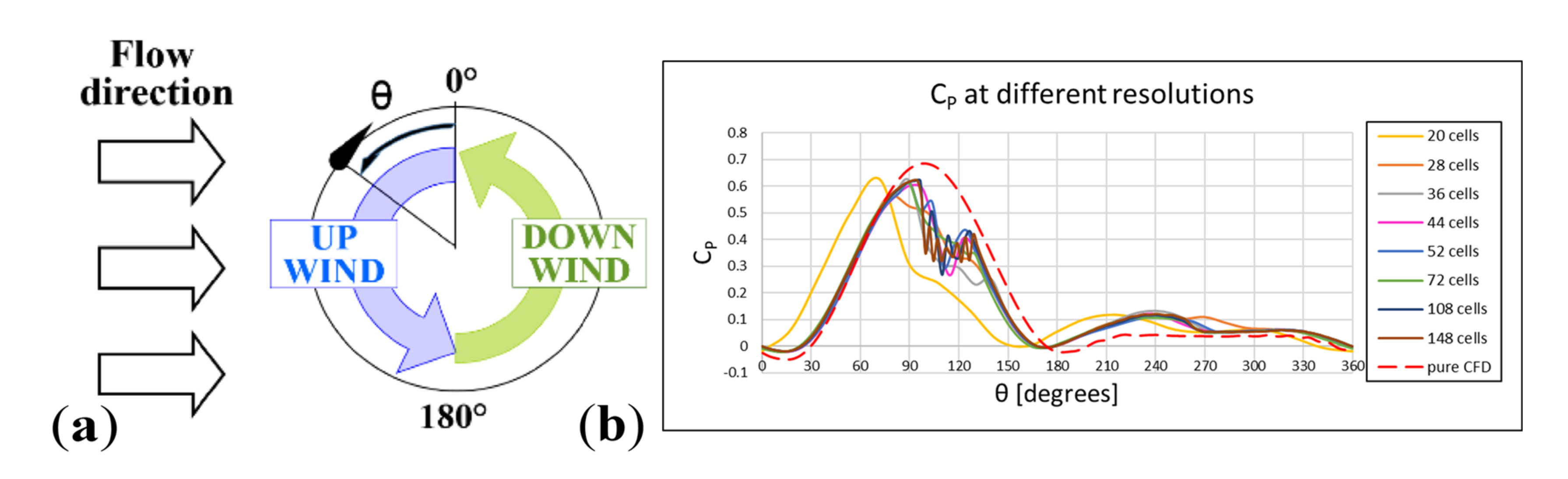
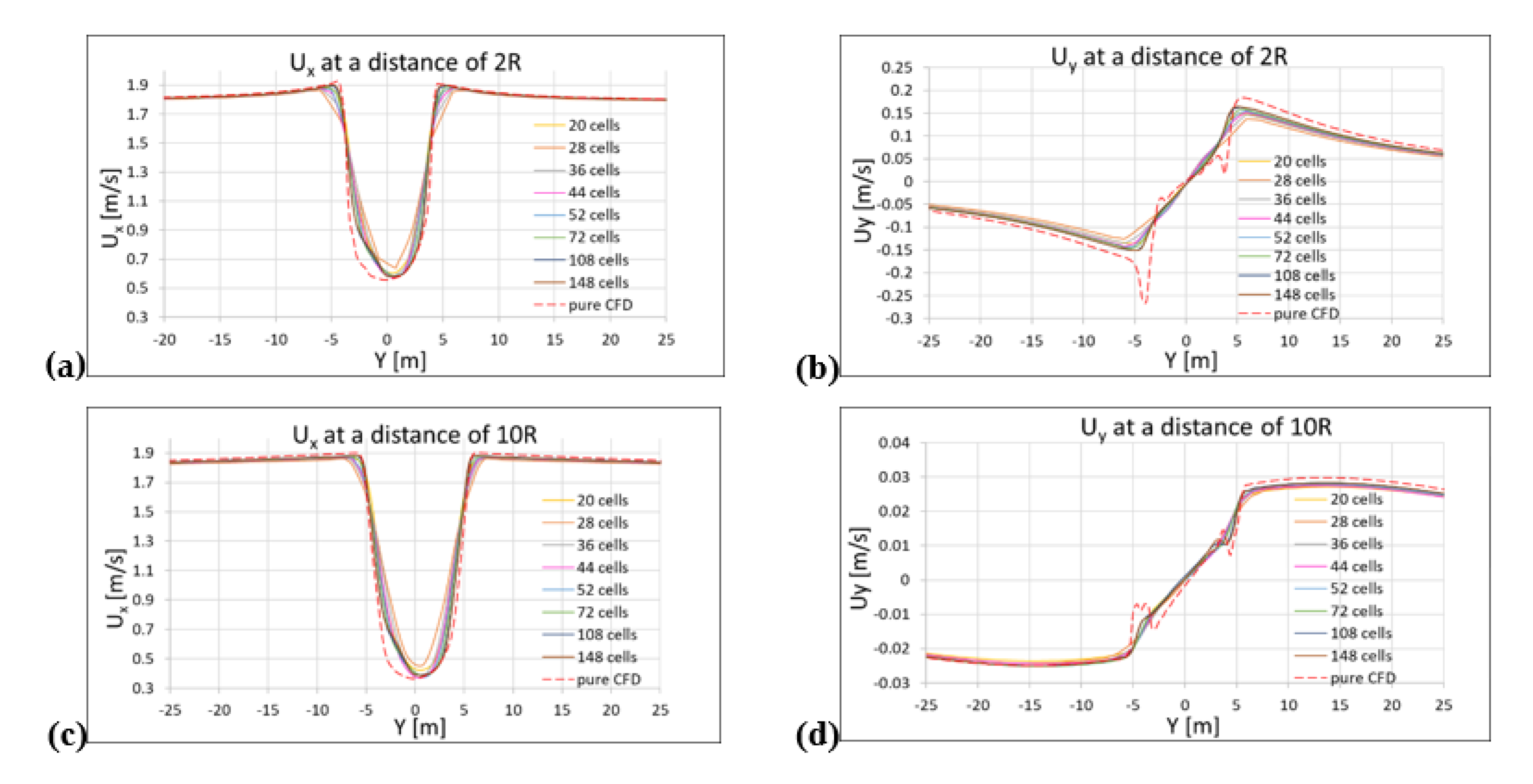
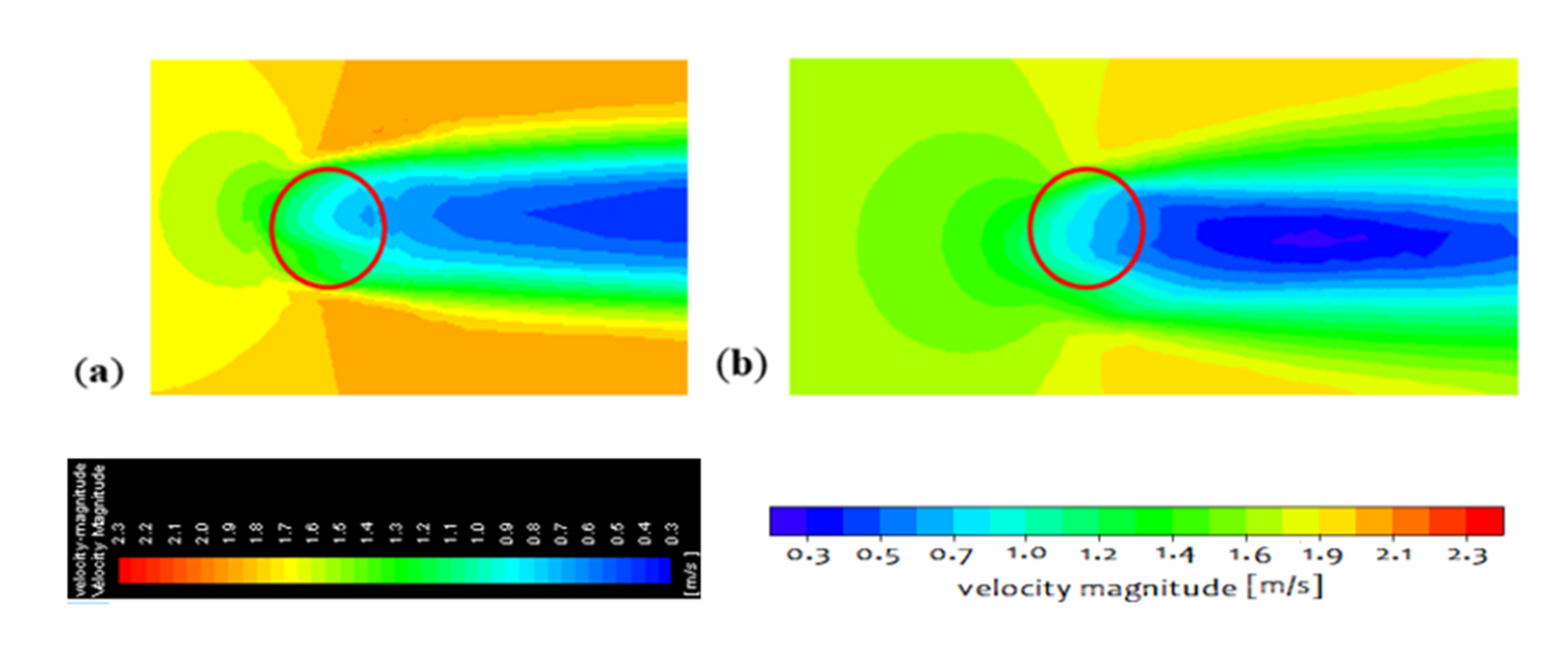
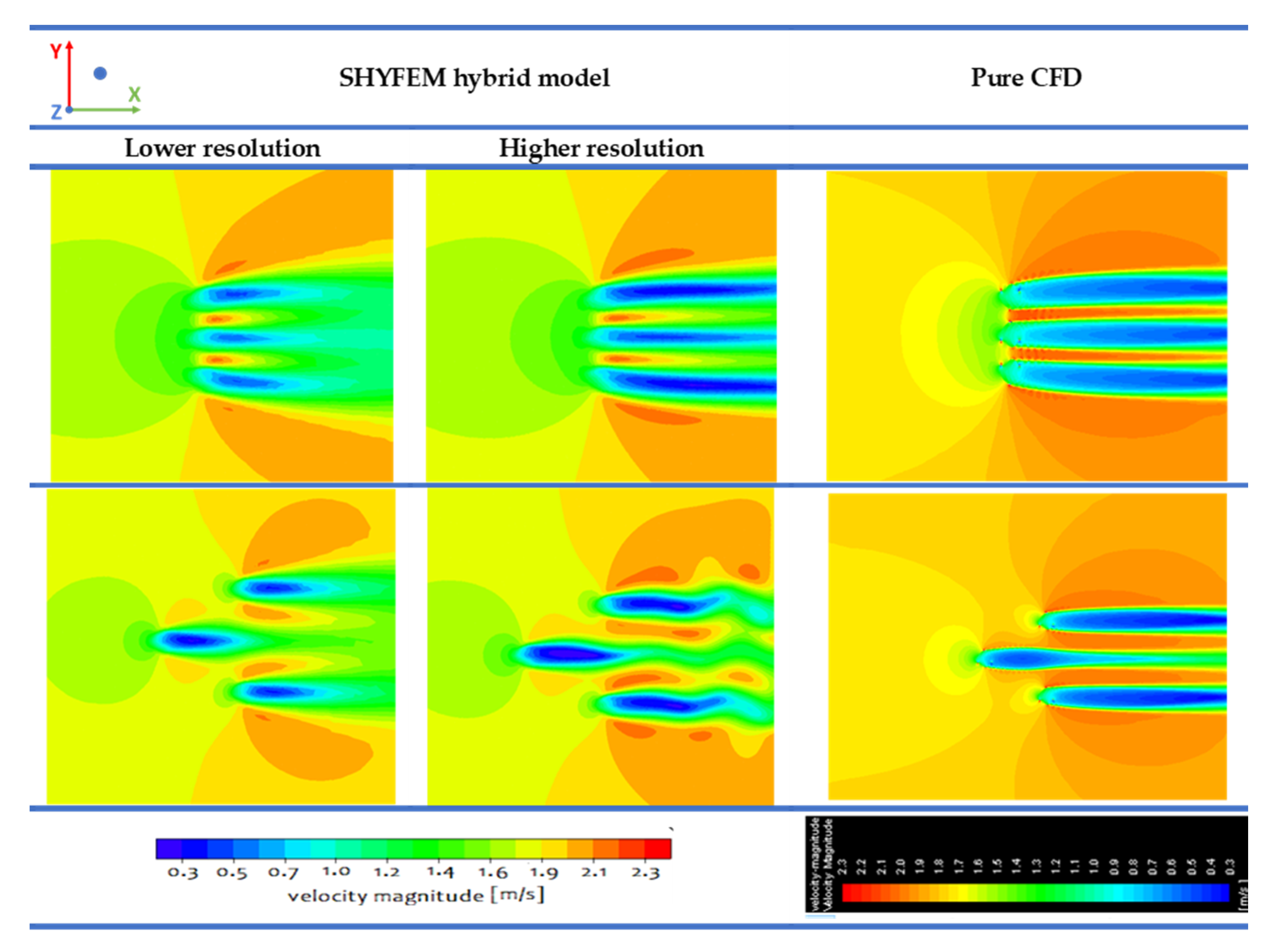
2.3. Grid Effect Analysis With the ANSYS Hybrid Model
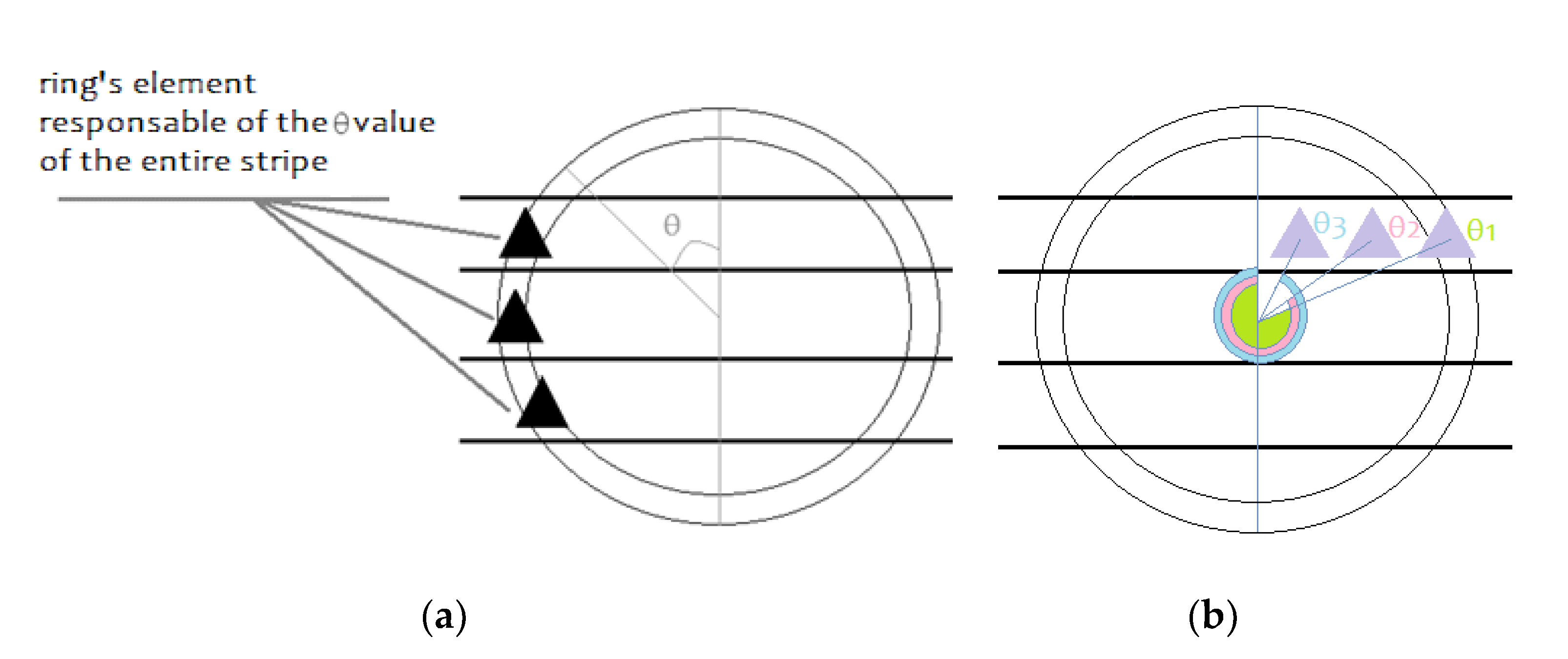
2.4. SHYFEM Grid
2.5. Friction’s Formulation in the SHYFEM Hybrid Model
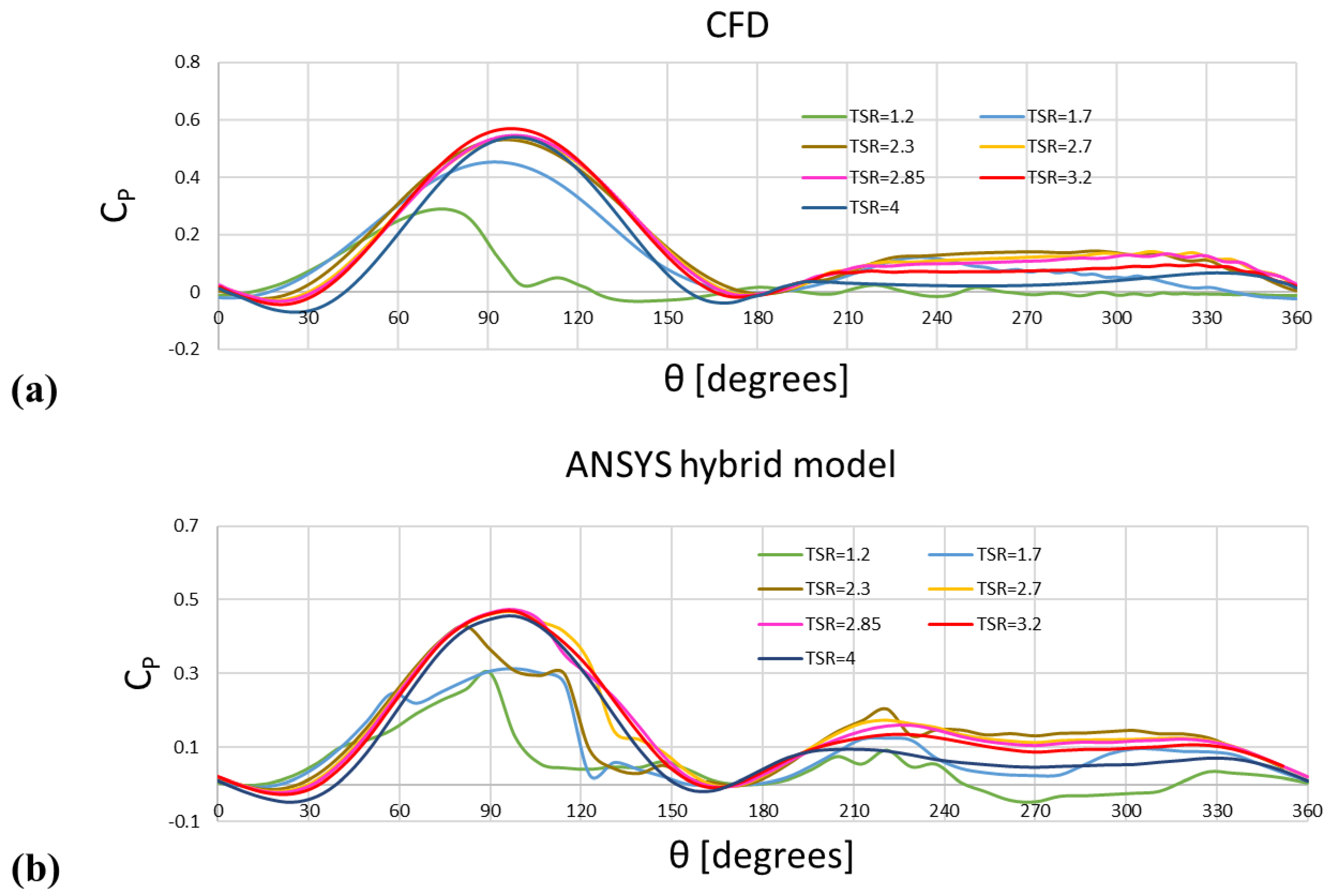
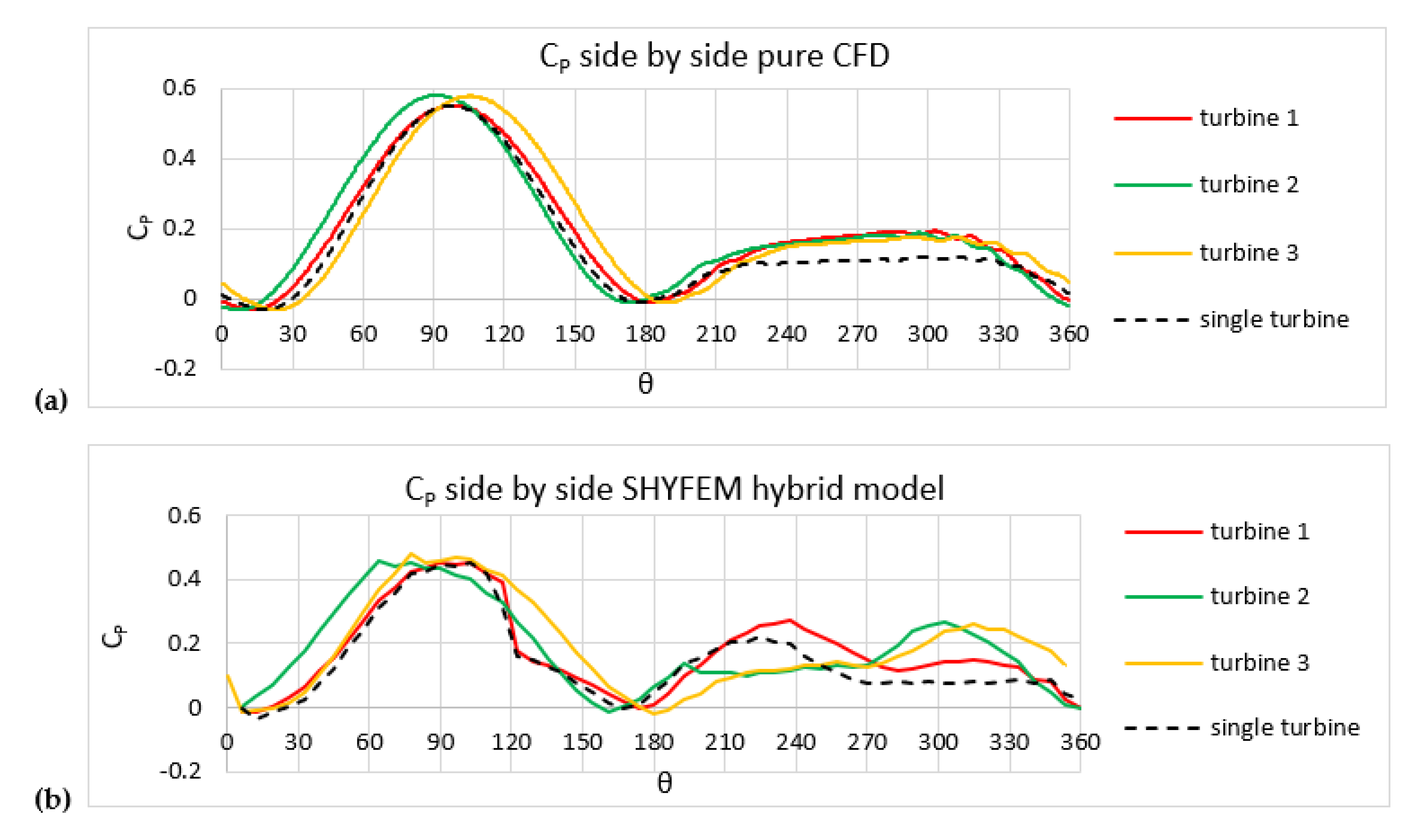
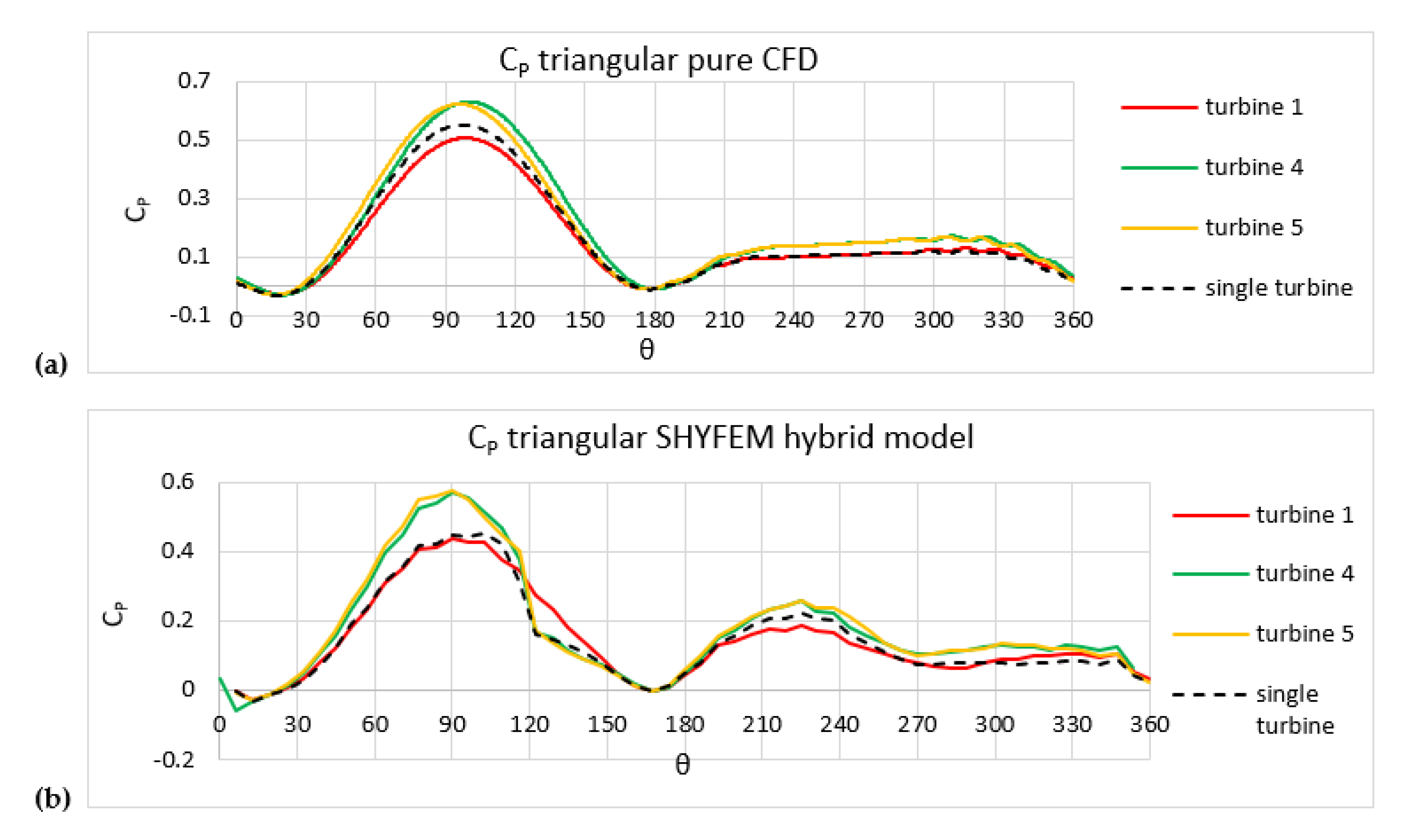
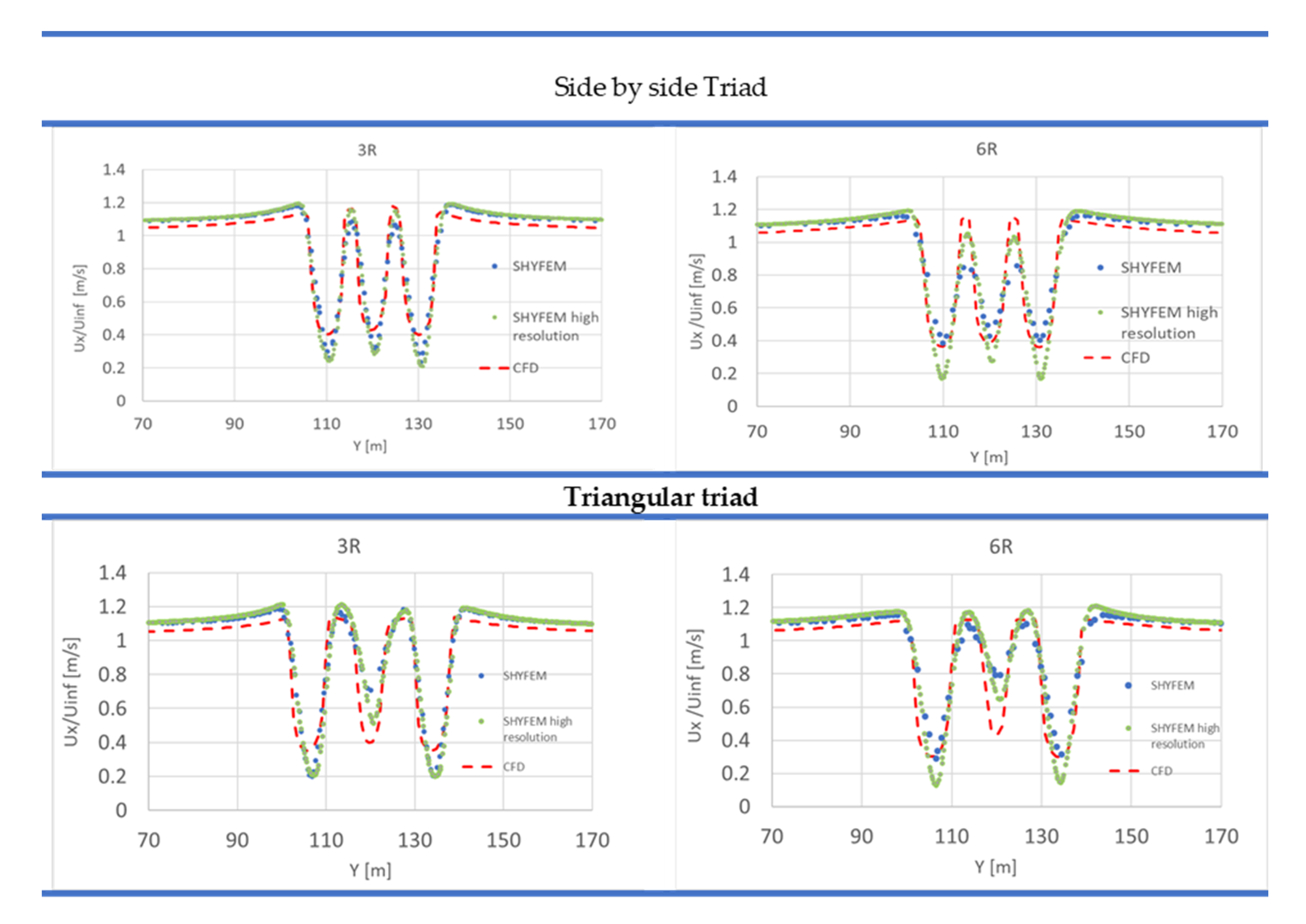
3. Results of the BEM–SHYFEM Hybrid Model
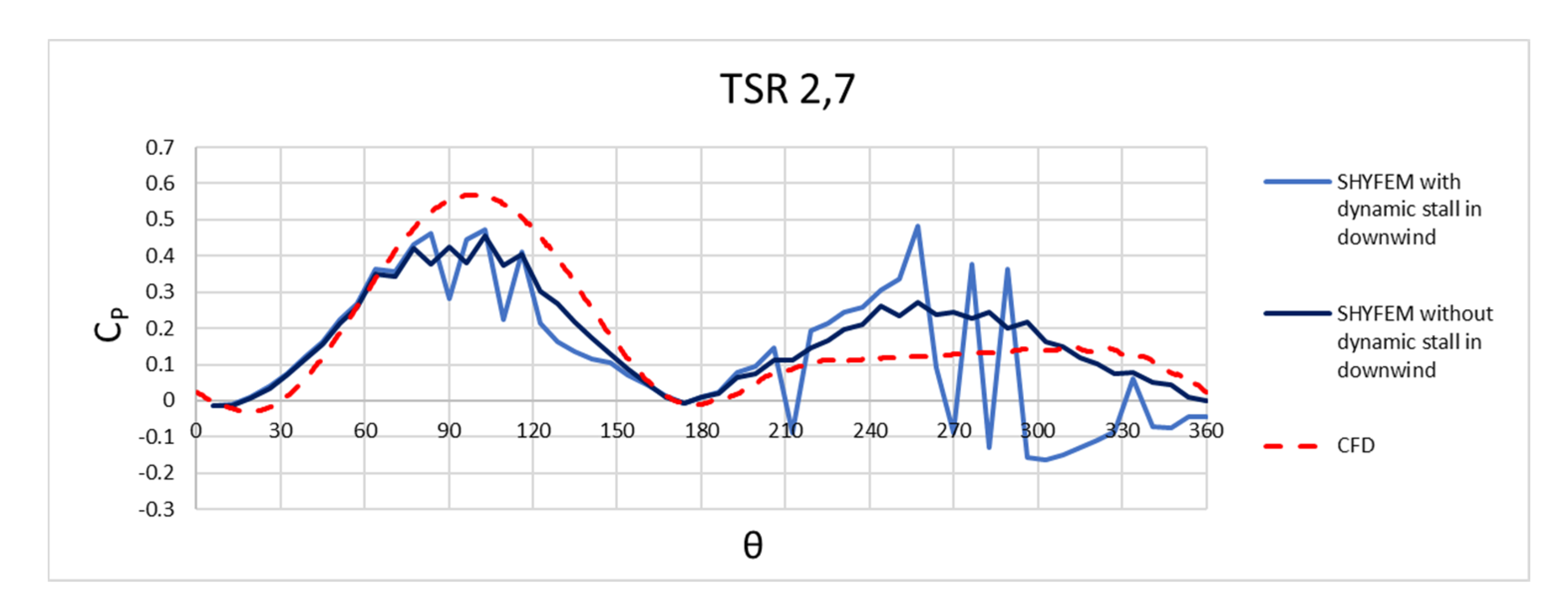
3.1. Behavior of the Single Turbine at Different TSR
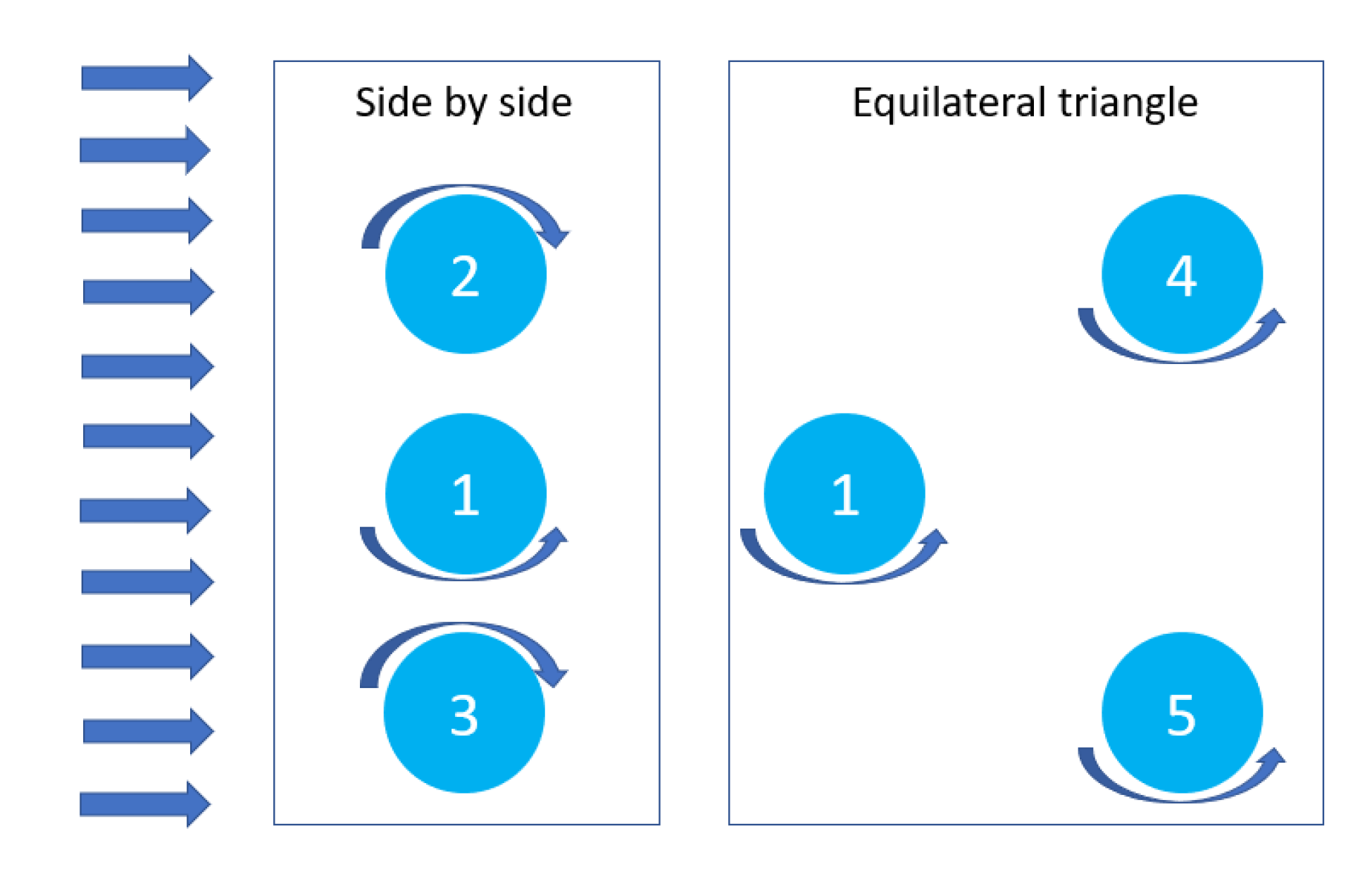
3.2. Application to a Small Turbine’s Cluster
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Coles, D.; Blunden, L.; Bahaj, A.S. Assessment of the energy extraction potential at tidal sites around the Channel Islands. Energy 2017, 124, 171–186. [Google Scholar] [CrossRef]
- Thiebot, J.; du Bois, P.B.; Guillou, S. Numerical modeling of the effect of tidal stream turbines on the hydrodynamics and the sediment transport e Application to the Alderney Race (Raz Blanchard), France. Renew. Energy 2015, 75, 356–365. [Google Scholar] [CrossRef]
- Piano, M.; Ward, S.; Robins, P.; Neill, S.; Lewis, M.; Davies, A.; Powell, B.; Owen, A.W.; Hashemi, R. Characterizing the Tidal Energy Resource of the West Anglesey Demonstration Zone (UK), Using TELEMAC-2D and Field Observations. In Proceedings of the XXII TELEMAC-MASCARET Technical User Conference, Liverpool, UK, 15–16 October 2015; pp. 195–203. [Google Scholar]
- Murray, R.O.; Gallego, A. A modelling study of the tidal stream resource of the Pentland Firth, Scotland. Renew. Energy 2017, 102, 326–340. [Google Scholar] [CrossRef]
- Tidal Devices. Available online: http://www.emec.org.uk/marine-energy/tidal-devices/ (accessed on 5 August 2012).
- Pathway to EMEC. Available online: http://www.emec.org.uk/services/pathway-to-emec/technology-readiness-levels/ (accessed on 30 September 2012).
- European Comission. LCEO Ocean Energy Technology Development Report 2018; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar]
- Ferreira, C.S.; van Bussel, G.J.W.; van Kuik, G. An Analytical Method to Predict the Variation in Performance of a H-Darrieus in Skewed Flow and Its Experimental Validation. In Proceedings of the European Wind Energy Conference (“EWEC”), Athens, Greece, 27 February–2 March 2006. [Google Scholar]
- Orlandi, A.; Collu, M.; Zanforlin, S.; Shires, A. 3D URANS analysis of a vertical axis wind turbine in skewed flows. J. Wind. Eng. Ind. Aerodyn. 2015, 147, 77–84. [Google Scholar] [CrossRef]
- Dabiri, J.O. Potential order-of-magnitude enhancement of wind farm power density via counter-rotating vertical-axis wind turbine arrays. J. Renew. Sustain. Energy 2011, 3, 043104. [Google Scholar] [CrossRef]
- Zanforlin, S.; Nishino, T. Fluid dynamic mechanisms of enhanced power generation by closely spaced vertical axis wind turbines. Renew. Energy 2016, 99, 1213–1226. [Google Scholar] [CrossRef]
- Zanforlin, S. Advantages of vertical axis tidal turbines set in close proximity: A comparative CFD investigation in the English Channel. Ocean Eng. 2018, 156, 358–372. [Google Scholar] [CrossRef]
- Kinzel, M.; Mulligan, Q.; Dabiri, J.O. Energy exchange in an array of vertical-axis wind turbines. J. Turbul. 2012, 13, N38. [Google Scholar] [CrossRef]
- Van Der Molen, J.; Ruardij, P.; Greenwood, N. Potential environmental impact of tidal energy extraction in the Pentland Firth at large spatial scales: Results of a biogeochemical model. Biogeosciences 2016, 13, 2593–2609. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, T. Numerical Models as Enabling Tools for Tidal-Stream Energy Extraction and Environmental Impact Assessment. In Proceedings of the ASME 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016. [Google Scholar]
- Shields, M.A.; Dillon, L.J.; Woolf, D.K.; Ford, A.T. Strategic priorities for assessing ecological impacts of marine renewable energy devices in the Pentland Firth (Scotland, UK). Mar. Policy 2009, 33, 635–642. [Google Scholar] [CrossRef]
- Sudderth, E.A.; Lewis, K.C.; Cumper, J.; Mangar, A.C.; Flynn, D.F.B. Potential Environmental Effects of the Leading Edge Hydrokinetic Energy Technology; U.S. Department of Energy Advanced Research Projects Agency–Energy: Washington, DC, USA, 2017.
- Roche, R.C.; Walker-Springett, K.; Robins, P.; Jones, J.; Veneruso, G.; Whitton, T.A.; Piano, M.; Ward, S.; Duce, C.; Waggitt, J.; et al. Research priorities for assessing potential impacts of emerging marine renewable energy technologies: Insights from developments in Wales (UK). Renew. Energy 2016, 99, 1327–1341. [Google Scholar] [CrossRef]
- Du Feu, R.; Funke, S.; Kramer, S.; Hill, J.; Piggott, M. The trade-off between tidal-turbine array yield and environmental impact: A habitat suitability modelling approach. Renew. Energy 2019, 143, 390–403. [Google Scholar] [CrossRef]
- Ramírez-Mendoza, R.; Murdoch, L.; Jordan, L.; Amoudry, L.; McLelland, S.; Cooke, R.; Thorne, P.; Simmons, S.; Parsons, D.; Vezza, M. Asymmetric effects of a modelled tidal turbine on the flow and seabed. Renew. Energy 2020, 159, 238–249. [Google Scholar] [CrossRef]
- Gillibrand, P.; Walters, R.; McIlvenny, J. Numerical Simulations of the Effects of a Tidal Turbine Array on Near-Bed Velocity and Local Bed Shear Stress. Energies 2016, 9, 852. [Google Scholar] [CrossRef]
- Ramos, V.; Carballo, R.; Ringwood, J.V. Application of the actuator disc theory of Delft3D-FLOW to model far-field hydrodynamic impacts of tidal turbines. Renew. Energy 2019, 139, 1320–1335. [Google Scholar] [CrossRef]
- Haverson, D.; Bacon, J.; Smith, H.C.M.; Venugopal, V.; Qing, X. Modelling the hydrodynamic and morphological impacts of a tidal stream development in Ramsey Sound. Renew. Energy 2018, 126, 876–887. [Google Scholar] [CrossRef]
- Fairley, I.; Masters, I.; Karunarathna, H. The cumulative impact of tidal stream turbine arrays on sediment transport in the Pentland Firth. Renew. Energy 2015, 80, 755–769. [Google Scholar] [CrossRef]
- Robins, P.E.; Neill, S.P.; Lewis, M.J. Impact of tidal-stream arrays in relation to the natural variability of sedimentary processes. Renew. Energy 2014, 72, 311–321. [Google Scholar] [CrossRef]
- Schuchert, P.; Kregting, L.; Pritchard, D.; Savidge, G.; Elsäßer, B. Using coupled hydrodynamic biogeochemical models to predict the effects of tidal turbine arrays on phytoplankton dynamics. J. Mar. Sci. Eng. 2018, 6, 58. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook, 2nd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Thiébot, J.; Guillou, N.; Guillou, S.; Good, A.; Lewis, M. Wake field study of tidal turbines under realistic flow conditions. Renew. Energy 2020, 151, 1196–1208. [Google Scholar] [CrossRef]
- Michelet, N.; Guillou, N.; Chapalain, G.; Thiébot, J.; Guillou, S.; Goward Brown, A.J.; Neill, S. Three-dimensional modelling of turbine wake interactions at a tidal stream energy site. Appl. Ocean Res. 2020, 95, 102009. [Google Scholar] [CrossRef]
- Umgiesser, G.; Canu, D.M.; Cucco, A.; Solidoro, C. A finite element model for the Venice Lagoon. Development, set up, calibration and validation. J. Mar. Syst. 2004, 51, 123–145. [Google Scholar] [CrossRef]
- Bellafiore, D.; McKiver, W.J.; Ferrarin, C.; Umgiesser, G. The importance of modeling nonhydrostatic processes for dense water reproduction in the Southern Adriatic Sea. Ocean Model. 2018, 125, 22–38. [Google Scholar] [CrossRef]
- Umgiesser, G.; Ferrarin, C.; Fivan; Bajo, M. SHYFEM-Model/Shyfem: Stable Release 7.4.1; Version VERS_7_4_1; Zenodo: Meyrin, Switzerland, 2018; Available online: http://doi.org/10.5281/zenodo.1311751 (accessed on 13 July 2018).
- Letizia, S.; Zanforlin, S. Hybrid CFD-source Terms Modelling of a Diffuser-augmented Vertical Axis Wind Turbine. Energy Procedia 2016, 101, 1280–1287. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Porté-Agel, F. A Large-Eddy Simulation Study of Vertical Axis Wind Turbine Wakes in the Atmospheric Boundary Layer. Energies 2016, 9, 366. [Google Scholar] [CrossRef]
- Rocchio, B.; DeLuca, S.; Salvetti, M.; Zanforlin, S. Development of a BEM-CFD tool for Vertical Axis Wind Turbines based on the Actuator Disk Model. Energy Procedia 2018, 148, 1010–1017. [Google Scholar] [CrossRef]
- Mendoza, V.; Chaudhari, A.; Goude, A. Performance and wake comparison of horizontal and vertical axis wind turbines under varying surface roughness conditions. Wind Energy 2019, 22, 458–472. [Google Scholar] [CrossRef]
- Grondeau, M.; Guillou, S.; Mercier, P.; Poizot, E. Wake of a Ducted Vertical Axis Tidal Turbine in Turbulent Flows, LBM Actuator-Line Approach. Energies 2019, 12, 4273. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Porté-Agel, F. Effect of aspect ratio on vertical-axis wind turbine wakes. J. Fluid Mech. 2020, 889. [Google Scholar] [CrossRef]
- ANSYS. Available online: https://www.ansys.com/about-ansys (accessed on 1 June 2018).
- Bravo, R.; Tullis, S.; Ziada, S. Performance Testing of a Small Vertical-Axis Wind Turbine. In Proceedings of the 21st Canadian Congress of Applied Mechanics CANCAM, Toronto, ON, Canada, 3–7 June 2007. [Google Scholar]
- Zanforlin, S.; DeLuca, S. Effects of the Reynolds number and the tip losses on the optimal aspect ratio of straight-bladed Vertical Axis Wind Turbines. Energy 2018, 148, 179–195. [Google Scholar] [CrossRef]
- Coiro, D.; Nicolosi, F.; De Marco, A.; Melone, S.; Montella, F. Flow Curvature Effect on Dynamic Behavior of a Novel Vertical Axis Tidal Current Turbine: Numerical and Experimental Analysis. In Proceedings of the OMAE2005: 24th International Conference on Offshore Mechanics and Arctic Engineering, Halkidiki, Greece, 12–17 June 2005. [Google Scholar] [CrossRef]
- Rocchio, B.; Chicchiero, C.; Salvetti, M.V.; Zanforlin, S. A simple model for deep dynamic stall conditions. Wind. Energy 2020, 23, 915–938. [Google Scholar] [CrossRef]
- Bachant, P.; Wosnik, M. Characterising the near-wake of a cross-flow turbine. J. Turbul. 2015, 16, 392–410. [Google Scholar] [CrossRef]
- Migliore, P.G.; Wolfe, W.P.; Fanucci, J.B. Flow Curvature Effects on Darrieus Turbine Blade Aerodynamics. J. Energy 1980, 4, 49–55. [Google Scholar] [CrossRef]
- Ferrarin, C.; Cucco, A.; Umgiesser, G.; Bellafiore, D.; Amos, C.L. Modelling fluxes of water and sediment between Venice Lagoon and the sea. Cont. Shelf Res. 2010, 30, 904–914. [Google Scholar] [CrossRef][Green Version]
- Ferrarin, C.; Umgiesser, G.; Roland, A.; Bajo, M.; De Pascalis, F.; Ghezzo, M.; Scroccaro, I. Sediment dynamics and budget in a microtidal lagoon—A numerical investigation. Mar. Geol. 2016, 381, 163–174. [Google Scholar] [CrossRef]
- Coles, D.; Blunden, L.; Bahaj, A.S. Experimental validation of the distributed drag method for simulating large marine current turbine arrays using porous fences. Int. J. Mar. Energy 2016, 16, 298–316. [Google Scholar] [CrossRef][Green Version]
- Thiébot, J.; Guillou, S.; Nguyen, V.T. Modelling the effect of large arrays of tidal turbines with depth-averaged Actuator Disks. Ocean Eng. 2016, 126, 265–275. [Google Scholar] [CrossRef]




| Turbulence Model | SST k-ω | |
|---|---|---|
| Solution Methods | Pressure–Velocity Coupling | Scheme SIMPLEC |
| Spatial Discretization | Gradient | Least Squares Cell-Based |
| Pressure | 2nd Order | |
| Momentum | 2nd-Order Upwind | |
| TKE | 2nd-Order Upwind | |
| Specific Dissipation Rate | 2nd-Order Upwind | |
| Transient Formulation | 2nd-Order Implicit | |
| Transient Formulation | Second-Order Implicit | |
| Residuals | 0.0001 | |
| Time Step (idt) | 1 s |
| End Simulation Time (itend) | 1500 s |
| Flow | 1680 m3/s |
| Friction | Ireib 5 czdef 0.02 |
| External Forces | NO |
| (N/m3) | Sources x | Sources y | Total Sources | CP Averaged | |
|---|---|---|---|---|---|
| TSR 1,2 | UDF | 16˙004 | 22˙582 | 38˙586 | 0.16 |
| SHYFEM | 35˙722 | 1˙520 | 37˙242 | 0.19 | |
| TSR 1,7 | UDF | 23˙063 | 33˙330 | 56˙393 | 0.28 |
| SHYFEM | 49˙795 | 3˙425 | 53˙220 | 0.29 | |
| TSR 2,3 | UDF | 29˙681 | 42˙803 | 72˙484 | 0.40 |
| SHYFEM | 65˙200 | 7˙292 | 72˙492 | 0.40 | |
| TSR 2,7 | UDF | 46˙897 | 33˙271 | 80˙168 | 0.45 |
| SHYFEM | 74˙618 | 11˙518 | 86˙136 | 0.43 | |
| TSR 2,85 | UDF | 35˙425 | 46˙865 | 82˙290 | 0.44 |
| SHYFEM | 77˙248 | 12˙946 | 90˙194 | 0.44 | |
| TSR 3,2 | UDF | 36˙857 | 48˙781 | 85˙638 | 0.42 |
| SHYFEM | 84˙372 | 17˙072 | 101˙444 | 0.40 | |
| TSR 4 | UDF | 39˙079 | 51˙375 | 90˙454 | 0.33 |
| SHYFEM | 83˙242 | 18˙737 | 101˙979 | 0.33 |
| % | SHYFEM Hybrid | Pure CFD |
|---|---|---|
| Turbine 1 (side by side) | 17.75 | 17.53 |
| Turbine 1 (triangular) | 0.78 | −5.97 |
| Turbine 2 | 25.62 | 19.76 |
| Turbine 3 | 28.81 | 18.37 |
| Turbine 4 | 21.93 | 20.71 |
| Turbine 5 | 24.95 | 19.37 |
| Side by side triad | 24.06 | 18.55 |
| Triangular triad | 15.89 | 11.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pucci, M.; Bellafiore, D.; Zanforlin, S.; Rocchio, B.; Umgiesser, G. Embedding of a Blade-Element Analytical Model into the SHYFEM Marine Circulation Code to Predict the Performance of Cross-Flow Turbines. J. Mar. Sci. Eng. 2020, 8, 1010. https://doi.org/10.3390/jmse8121010
Pucci M, Bellafiore D, Zanforlin S, Rocchio B, Umgiesser G. Embedding of a Blade-Element Analytical Model into the SHYFEM Marine Circulation Code to Predict the Performance of Cross-Flow Turbines. Journal of Marine Science and Engineering. 2020; 8(12):1010. https://doi.org/10.3390/jmse8121010
Chicago/Turabian StylePucci, Micol, Debora Bellafiore, Stefania Zanforlin, Benedetto Rocchio, and Georg Umgiesser. 2020. "Embedding of a Blade-Element Analytical Model into the SHYFEM Marine Circulation Code to Predict the Performance of Cross-Flow Turbines" Journal of Marine Science and Engineering 8, no. 12: 1010. https://doi.org/10.3390/jmse8121010
APA StylePucci, M., Bellafiore, D., Zanforlin, S., Rocchio, B., & Umgiesser, G. (2020). Embedding of a Blade-Element Analytical Model into the SHYFEM Marine Circulation Code to Predict the Performance of Cross-Flow Turbines. Journal of Marine Science and Engineering, 8(12), 1010. https://doi.org/10.3390/jmse8121010







