Tensile Bending Stresses in Mortar-Grouted Riprap Revetments Due to Wave Loading
Abstract
:1. Introduction
1.1. Motivation
- Flexible revetments: Limited interaction between individual elements of the revetment results in the individual elements resisting wave loading mainly by their weight while the whole revetment can deform by redistribution of the single elements and thereby easily adapt to subsoil settlement. Non-grouted (loose) riprap forms a flexible revetment, see for example [8].
- Revetments with some flexibility: Revetments made of individual elements with high interaction or monolithic revetments that due to their creep behavior can adapt to subsoil settlement to a certain degree while remaining coherent. This type of revetment can resist higher wave loads than fully flexible revetments given the same size of the individual elements or the same revetment thickness, but especially asphalt is subject to fatigue and abrasion [9]. Asphalt revetments or riprap grouted with asphalt are examples of revetments with some flexibility.
- Revetments with no flexibility: These monolithic revetments or revetments made of individual elements with high interaction are too stiff to follow subsoil settlement. It is therefore possible that cavities beneath the revetment are present, resulting in a non-continuous bedding of the revetment. This type of revetment can also resist higher wave loads than fully flexible revetments given the same size of the individual elements or the same revetment thickness, but it is subject to breaking and crack formation. Mortar-grouted riprap revetments are revetments with no flexibility [10].
- For very permeable revetments such as loose riprap the pressure beneath the revetment almost instantaneously adapts to the pressure on the revetment. In case of small amounts of grouting mortar, MGRRs also represent this type of revetment.
- With decreasing permeability of the top layer the load on the top layer is increasingly dominated by the pressure difference on and beneath the top layer. For pattern placed revetments the leakage length, which takes into account the permeability and thickness of both the filter layer and top layer of the revetment, is a measure for the loading of the top layer [15]. In case of high amounts of grouting mortar, MGRRs can qualitatively represent this type of revetment. However, the concept of the leakage length assumes flow in the filter layer parallel to the embankment and can therefore not be applied for MGRRs that are in most cases placed on a geotextile filter layer, because the thickness of a geotextile filter is in the order of a few centimeters and does not allow any significant flow in its plane.
- In the case of a non-permeable top layer, the pressure beneath the revetment adapts to the pressure on the revetment only for time periods of several hours or longer (tides, storms), but not for the time periods of individual waves [9]. This is the case for fully grouted MGRRs and for example for asphalt revetments.
1.2. Modelling Tensile Stresses for Crack Formation Assessment
1.3. Objective and Outline
2. Materials and Methods
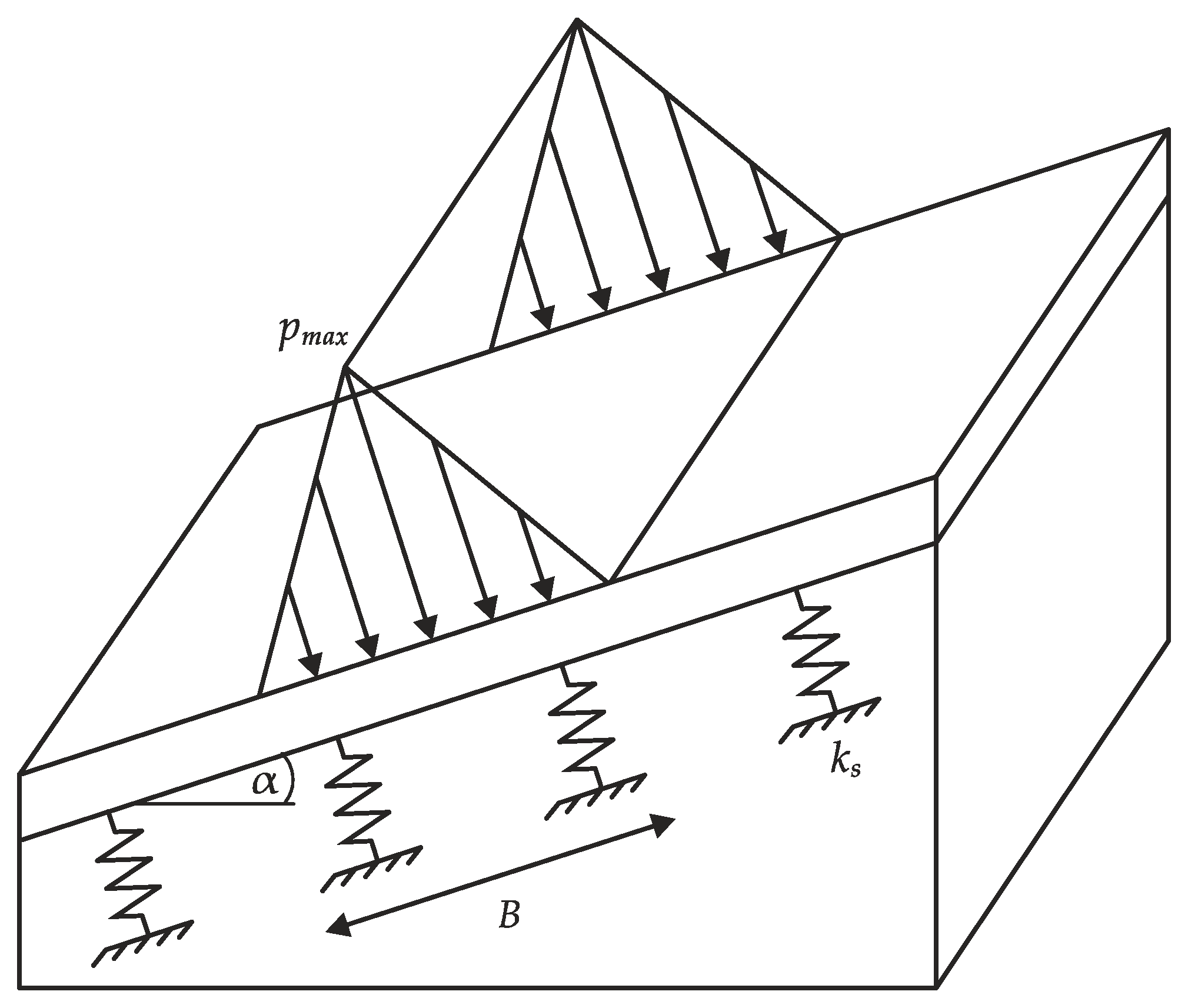
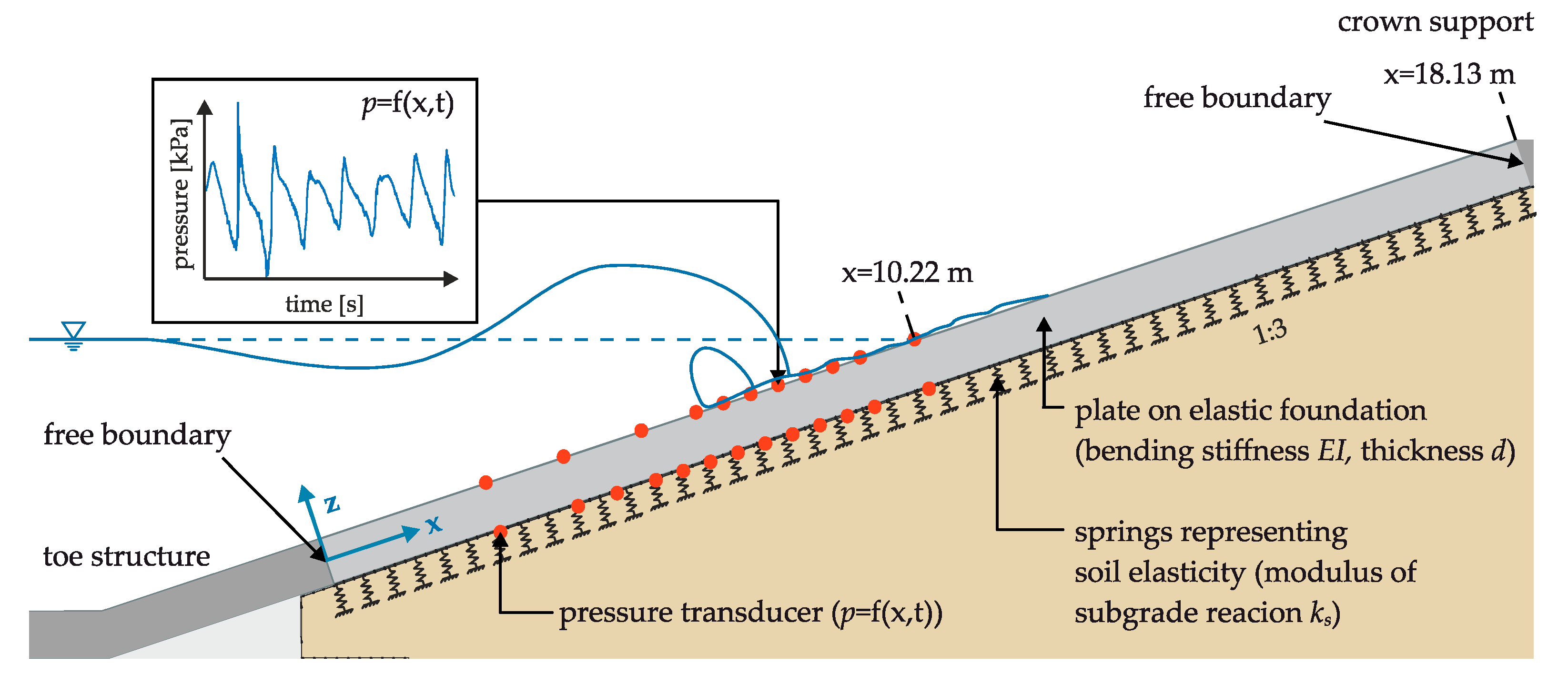
2.1. Plate on an Elastic Foundation Model
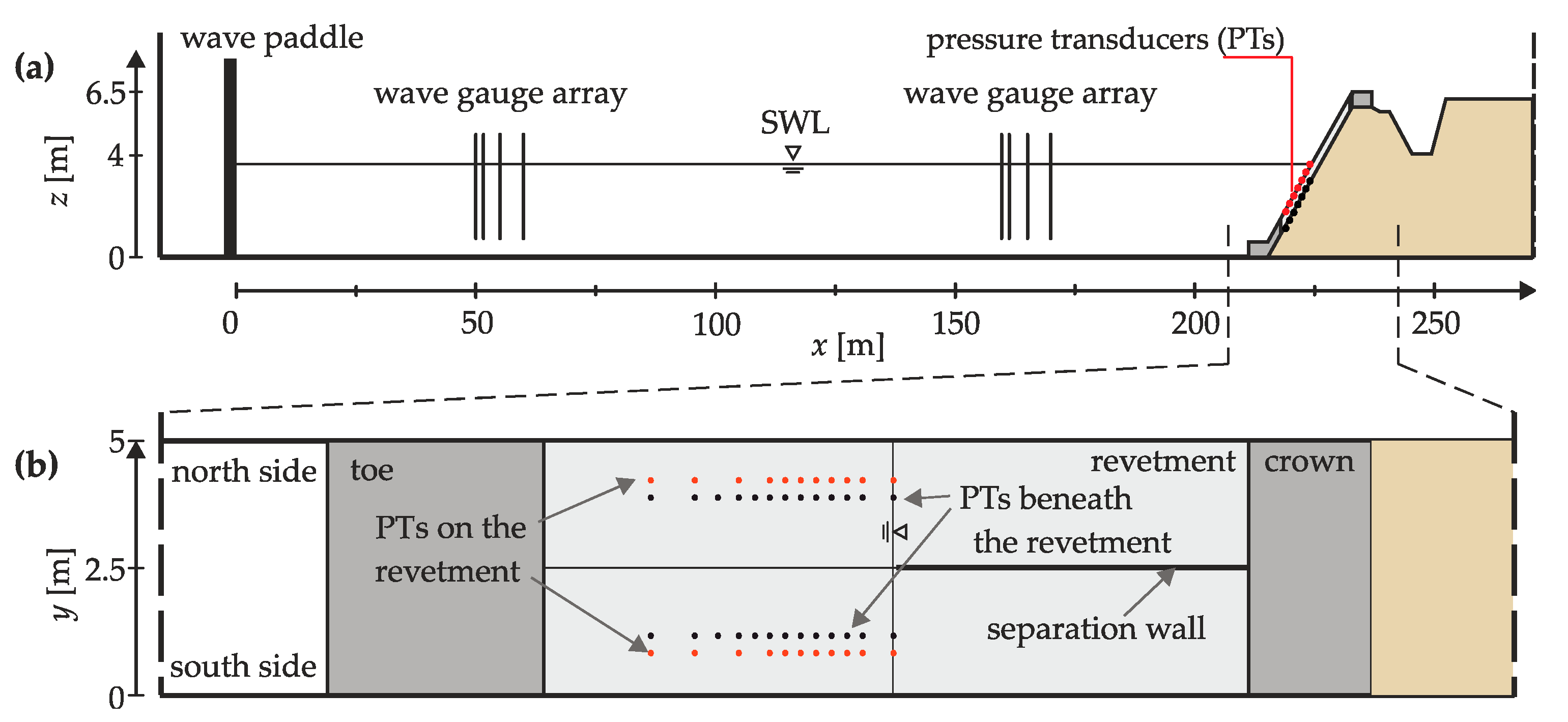
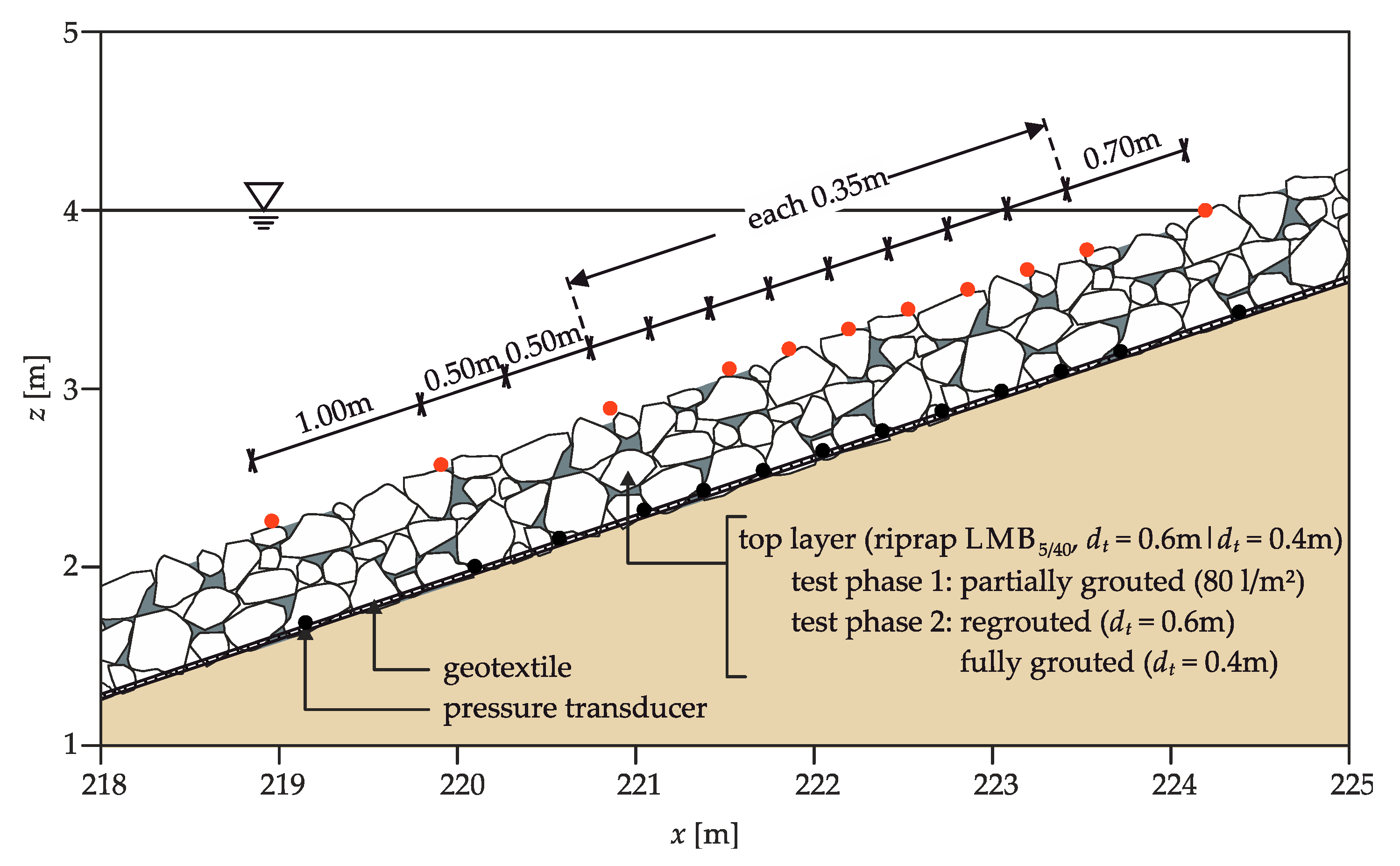
2.2. Full Scale Hydraulic Model Tests
2.3. Boundary Conditions PEF
2.4. Plate on an Elastic Foundation Model
2.4.1. Bending Stiffness
- The materials cannot shift against each other at their interfaces (no slippage).
- Since the behavior of a mortar-grouted riprap is to be described up to the first crack formation, a linear relationship between stress and strain is assumed in the uncracked state according to Hooke’s law.
2.4.2. Modulus of Subgrade Reaction
2.4.3. Parameter Variations
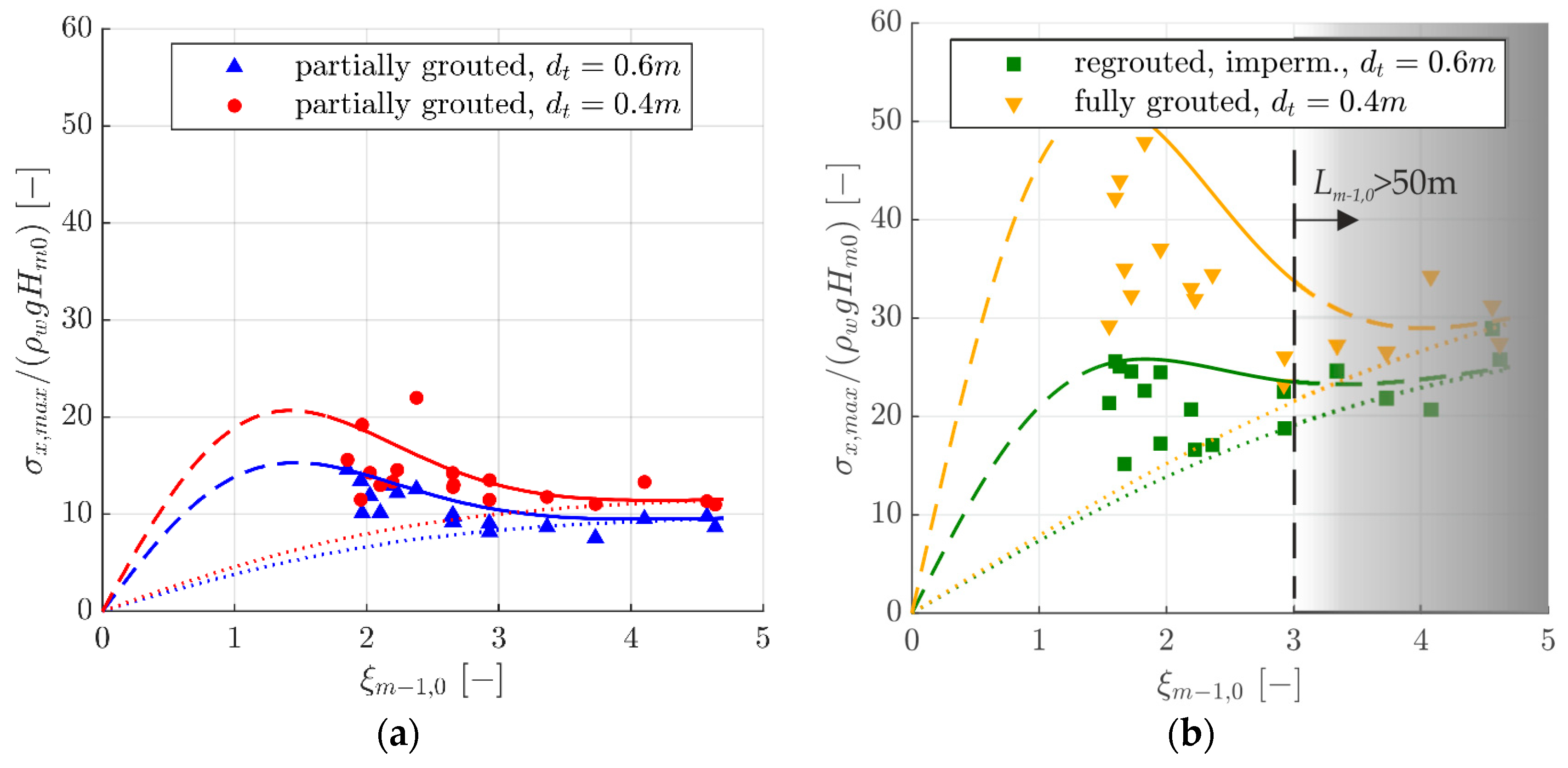
3. Results
3.1. Paramter Combination 1
3.2. Parameter Combination 2
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Introduction
Appendix A.2. Materials, Methods and Results: Riprap


| Compression | Tension | |||||||
|---|---|---|---|---|---|---|---|---|
| Specimen No. | Group | Compressive Strength βD | Modulus of Elasticity EC | Poisson’s Ratio µ | Speci-men No. | Group | Tensile Strength βZ | Modulus of Elasticity ET |
| (N/mm2) | (N/mm2) | (-) | (N/mm2) | (N/mm2) | ||||
| 3 | 1 | 268.3 | 75,385 | 0.218 | 3 | 1 | 13.4 | 64,861 |
| 4 | 1 | 231.2 | 60,951 | 0.223 | 4 | 1 | 10.3 | 40,394 |
| 7 | 1 | 143.4 | 67,475 | 0.200 | 7 | 1 | 8.6 | 52,698 |
| 6 | 2 | 257.0 | 63,331 | 0.247 | 1 | 2 | 8.5 | 77,009 |
| 9 | 2 | 171.4 | 76,771 | 0.268 | 2 | 2 | 11.7 | 69,932 |
| 10 | 2 | 141.6 | 68,686 | 0.213 | 8 | 2 | 11.6 | 53,792 |
| 9 | 2 | 16.2 | 74,870 | |||||
| Mean | 202.2 | 68,767 | 0.228 | Mean | 11.47 | 61,936 | ||
| Coefficient of variation | 0.28 | 0.09 | 0.11 | Coefficient of variation | 0.24 | 0.22 | ||
Appendix A.3. Materials, Methods and Results: Grouting Mortar

| Compression | Tension | |||||
|---|---|---|---|---|---|---|
| Specimen No. | Compressive Strength βD | Modulus of Elasticity EC | Poisson’s Ratio µ | Specimen No. | Tensile Strength βZ | Modulus of Elasticity ET |
| (N/mm2) | (N/mm2) | (-) | (N/mm2) | (N/mm2) | ||
| 1 | 35.6 | 22,532 | 0.061 | 1 | 1.1 | 18,621 |
| 2 | 35.4 | 23,229 | 0.054 | 2 | 1.0 | 17,766 |
| 3 | 33.1 | 22,962 | 0.067 | 3 | 1.0 | 21,329 |
| 4 | 37.8 | 24,287 | 0.066 | 4 | 0.7 | 20,085 |
| 5 | 34.5 | 23,591 | 0.061 | 5 | 1.0 | 19,802 |
| 6 | 31.6 | 23,020 | 0.052 | |||
| Mean | 34.7 | 23,270 | 0.060 | Mean | 0.96 | 19,520 |
| Coefficient of variation | 0.06 | 0.03 | 0.10 | Coefficient of variation | 0.16 | 0.07 |
Appendix A.4. Discussion
References
- CIRIA. The International Levee Handbook; C731: London, UK, 2013; ISBN 978-0-86017-734-0. [Google Scholar]
- EAK. Empfehlungen für die Ausführung von Küstenschutzwerken durch den Ausschuss für Küstenschutzwerke der Deutschen Gesellschaft für Geotechnik e.V. und der Hafenbautechnischen Gesellschaft e.V.; Westholsteinische Verlagsanstalt Boyens & Co.: Heide, Germany, 2007; ISBN 978-3-8042-1056-1. [Google Scholar]
- German Institute for Standardization. Armourstone—Part 1: Specification; Beuth Verlag GmbH: Berlin, Germany, 2002. [Google Scholar]
- Federal Waterways Engineering and Research Institute. Anwendung von Regelbauweisen für Böschungs- und Sohlensicherungen an Binnenwasserstraßen (Application of Standard Construction Methods for Embankment and Bottom Protection on Inland Waterways); Federal Waterways Engineering and Research Institute: Karlsruhe, Germany, 2008. [Google Scholar]
- Federal Waterways Engineering and Research Institute. Use of Cementitious and Bituminous Materials for Grouting Armourstone on Waterways (Anwendung von Hydraulisch Gebundenen Stoffen zum Verguss von Wasserbausteinen an Wasserstraßen, MAV); Federal Waterways Engineering and Research Institute: Karlsruhe, Germany, 2017. [Google Scholar]
- Federal Waterways Engineering and Research Institute. Prüfung von Hydraulisch- und Bitumengebundenen Stoffen zum Verguss von Wasserbausteinen an Wasserstraßen (Testing of Hydraulically and Bitumen-Bonded Materials for Grouting Armourstones on Waterways); Federal Waterways Engineering and Research Institute: Karlsruhe, Germany, 2008. [Google Scholar]
- Federal Waterways Engineering and Research Institute. Grundlagen zur Bemessung von Böschungs- und Sohlensicherungen an Binnenwasserstraßen (Principles for the Design of Embankment and Bottom Protection on Inland Waterways); Federal Waterways Engineering and Research Institute: Karlsruhe, Germany, 2010. [Google Scholar]
- CIRIA; CUR; CETMEF. The Rock Manual. The use of Rock in Hydraulic Engineering, 2nd ed.; C683: London, UK, 2007. [Google Scholar]
- Technical Advisory Committee on Flood Defence. Technisch Rapport Asfalt voor Waterkeren; Rijkswaterstaat, DWW: Delft, The Neterlands, 2002. [Google Scholar]
- Knieß, H.-G.; Köhler, H.-J. Untersuchung gebundener Steinschüttungen auf Flexibilität, Verbundfestigkeit und Wasserdurchlässigkeit. Bull. Fed. Waterw. Eng. Res. Inst. 1984, 55, 113–134. [Google Scholar]
- Alcérreca-Huerta, J.C.; Oumeraci, H. Wave-induced pressures in porous bonded revetments. Part I: Pressures on the revetment. Coast. Eng. 2016, 110, 87–101. [Google Scholar] [CrossRef]
- Alcérreca-Huerta, J.C.; Oumeraci, H. Wave-induced pressures in porous bonded revetments. Part II: Pore pressure just beneath the revetment and in the embankment subsoil. Coast. Eng. 2016, 110, 76–86. [Google Scholar] [CrossRef]
- Liebisch, S. Bonded Porous Revetments—Effect of Porosity on Wave-Induced Loads and Hydraulic Performance: An Experimental Study. Ph.D. Thesis, Technische Universität Carolo-Wilhelmina, Braunschweig, Germany, 2015. [Google Scholar]
- Schiereck, G.J. Introduction to Bed, Bank and Shore Protection; Spon Press: London, UK, 2004; ISBN 0-415-33177-3. [Google Scholar]
- Peters, D.J. Design of Pattern-Placed Revetments. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2017. [Google Scholar]
- De Looff, A.K.; t’Hart, R.; Montauban, K.; van den Ven, M. GOLFKLAP A Model to Determine the Impact of Waves on Dike Structures with an Asphaltic Concrete Layer. In Proceedings of the 30th International Conference, San Diego, CA, USA, 3–8 September 2006; pp. 5106–5116. [Google Scholar]
- ARCADIS. Polyurethane Bonded Aggregate Revetments Design Manual; ARCADIS: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Rijkswaterstraat. The Use of Asphalt in Hydraulic Engineering; Rijkswaterstraat: Utrecht, The Netherlands, 1985. [Google Scholar]
- Oumeraci, H.; Staal, T.; Pfoertner, S.; Ludwigs, G.; Kudella, M. Hydraulic Performance, Wave Loading and Response of Elastocoast Revetments and their Foundation—A Large Scale Model Study; TU Braunschweig—Leichtweiss Institut: Braunschweig, Germany, 2010. [Google Scholar]
- Führböter, A.; Sparboom, U. Shock Pressure Interactions on Prototype Sea Dikes Caused by Breaking Waves. In Proceedings of the SOWAS’88 (Modelling Soil-Water-Structure Interactions), Delft, The Netherlands, 29 September–2 October 1988. [Google Scholar]
- IMS Ingenieurgesellschaft mbH. Werkstoff Elastocoast—Zusammenstellung der Technischen Bemessungsgrundlagen für den Werkstoff Elastocoast; IMS Ingenieurgesellschaft mbH: Hamburg, Germany, 2010. [Google Scholar]
- Losada, I.J.; Lara, J.L.; del Jesus, M. Modeling the interaction of water waves with porous coastal structures. J. Waterw. Port Coast. Ocean Eng. 2016. [Google Scholar] [CrossRef]
- Dankert, J.; Dankert, H. Technische Mechanik. Statik, Festigkeitslehre, Kinematik/Kinetik, 7th ed.; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-8348-1809-6. [Google Scholar]
- Monnet, W.; Dartsch, B.; Wehefritz, K. Colcrete-Beton im Wasserbau; Beton-Verlag: Düsseldorf, Germany, 1980; ISBN 3-7640-0134-8. [Google Scholar]
- Leichtweiß-Institut für Wasserbau. L~davis: Manual for the Data Analysis and Visualization Software of the Leichtweiss Institute; Leichtweiß-Institut für Wasserbau: Braunschweig, Germany, 2007. [Google Scholar]
- Mansard, E.P.D.; Funke, E.R. The Measurement of Incident and Reflected Spectra Using a Least Square Method. In Proceedings of the 17th International Conference on Coastal Engineering (ICCE), Sydney, Australia, 23–28 March 1980; pp. 154–172. [Google Scholar]
- EurOtop. Manual on Wave Overtopping of Sea Defences And Related Structures. An Overtopping Manual Largely Based on European Research, but for Worldwide Application. 2018. Available online: www.overtopping-manual.com (accessed on 11 November 2020).
- Kreyenschulte, M. Wellen-Bauwerks-Interaktion bei Mörtelvergossenen Schüttsteindeckwerken. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2020. [Google Scholar]
- Klein Breteler, M.; van der Werf, I.; Wenneker, I. Kwantificering Golfbelasting en Invloed Lange Golven. Onderzoeksprogramma Kennisleemtes Steenbekledingen; Deltares: Delft, The Netherlands, 2012. [Google Scholar]
- Gross, D.; Hauger, W.; Schröder, J.; Wall, W.A. Technische Mechanik 2—Elastostatik; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 978-3-662-53678-0. [Google Scholar]
- Klotzek, T. Mechanical and Fracture Mechanical Properties of Hydraulically Bonded Revetments. Master’s Thesis, RWTH Aachen University, Aachen, Germany, 2017. Unpublished Work. [Google Scholar]
- Stichting Toegepast Onderzoek Waterbeheer. State of the Art Asfaltdijkbekledingen; Rijkswaterstraat: Utrecht, The Netherlands, 2010. [Google Scholar]
- Ruygrok, P.A. Dimensioneren van Asfaltbekledingen op Golfbelasting, Analyse van de Relatie Tussen Golfbelasting en Rekken; Report CO-347160/17; Grondmechanica: Delft, The Netherlands, 1994. [Google Scholar]
- Richwien, W. Seegang und Bodenmechanik—Geotechnische Versagensmechanismen von Seedeichen. Bull. Fed. Waterw. Eng. Res. Inst. 1989, 66, 139–154. [Google Scholar]
- Witte, H.-H. Druckschlagbelastung durch Wellen in Deterministischer und Stochastischer Betrachtung. Ph.D. Thesis, Technische Universität Carolo-Wilhelmina, Braunschweig, Germany, 1988. [Google Scholar]
- Klein Breteler, M.; Pilarczyk, K.W.; Stoutjesdijk, T. Design of Alternative Revetments. Coast. Eng. Proc. 1998, 1. [Google Scholar] [CrossRef]
- Klein Breteler, M.; Bezuijen, A. Design criteria for Placed Block Revetments. In Dikes and Revetments. Design, Maintanance and Safety Assessment; Pilarczyk, K.W., Ed.; A.A. Balkema: Rotterdam, The Netherlands, 1998; pp. 217–248. ISBN 90 5410 455 4. [Google Scholar]
- Hughes, S.A. Physical Models and Laboratory Techniques in Coastal Engineering; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1993; ISBN 981-02-1540-1. [Google Scholar]
- Führböter, A. Wellenbelastung von Deich- und Deckwerksböschungen; Schiffahrts-Verlag “Hansa”: Hamburg, Germany, 1991. [Google Scholar]
- Oumeraci, H. More than 20 years of experience using the Large Wave Flume (GWK): Selected research projects. Die Küste 2010, 77, 179–239. [Google Scholar]
- EAU. Empfehlungen des Arbeitskreises “Ufereinfassungen”. Häfen und Wasserstraßen; Wilhelm Ernst & Sohn Verl.: Berlin, Germany, 2012. [Google Scholar]
- German Institute for Standardization. Natural Stone Test Method—Determination of Real Density and Apparent Density, and of Total and Open Porosity; Beuth Verlag GmbH: Berlin, Germany, 2007. [Google Scholar]
- German Institute for Standardization. Natural Stone Test Methods—Determination of Static Elastic Modulus; Beuth Verlag GmbH: Berlin, Germany, 2005. [Google Scholar]
- German Institute for Standardization. Concrete, Reinforced and Prestressed Concrete Structures—Part 2: Concrete—Specification, Properties, Production and Conformity—Application Rules for DIN EN 206-1; Beuth Verlag GmbH: Berlin, Germany, 2008. [Google Scholar]
- German Institute for Standardization. Concrete— Specification, Performance, Production and Conformity; German Version EN 206:2013+A1:2016; Beuth Verlag GmbH: Berlin, Germany, 2017. [Google Scholar]
- German Institute for Standardization. Cement—Part 1: Composition, Specifications and Conformity Criteria for Common Cements; German and English Version prEN 197-1:2018 (Draft); Beuth Verlag GmbH: Berlin, Germany, 2018. [Google Scholar]
- German Institute for Standardization. Special Cement—Part 10: Composition, Requirements and Conformity Evaluation for Cement with Low Effective Alkali Content; Beuth Verlag GmbH: Berlin, Germany, 2013. [Google Scholar]
- Hallauer, O. Vergussstoffe für Uferdeckwerke. Bull. Fed. Waterw. Eng. Res. Inst. 1986, 58, 29–69. [Google Scholar]





| Revetment | kp | Width B | Slope Angle Tan (α) | Reference |
|---|---|---|---|---|
| Asphalt | approx. 2–6 * | Hs | 1:3–1:8 | [9,16] |
| Polyurethane bonded revetment | 4 | Hs | 1:3 | [17,21] |
| Riprap fully grouted with asphalt | approx. 2–6 * | Hs | 1:3–1:8 | [18] |
| Partially Grouted | Fully Grouted | |||
|---|---|---|---|---|
| Section | North | South | North | South |
| Configuration Nr. | 1 | 2 | 3 | 4 |
| Top layer thickness dt (m) | 0.6 | 0.4 | 0.6 | 0.4 |
| Amount of mortar vg (L/m2) | 80 | 80 | 80 + 100 | 180 |
| Estimated porosity n before grouting (-) | 0.45 | 0.45 | 0.45 | 0.45 |
| Porosity n after grouting (-) | 0.32 | 0.25 | 0.16 | 0 |
| Pore volume Vp after grouting (L/m2) | 190 | 100 | 90 | 0 |
| Component and Load | Static Modulus of Elasticity Estat,33 (N/mm2) | ||||
|---|---|---|---|---|---|
| Minimum | Mean | Maximum | Standard Deviation | Coefficient of Variation (–) | |
| Riprap (Compression) | 60,951 | 68,767 | 76,771 | 6327 | 0.09 |
| Riprap (Tension) | 40,394 | 61,936 | 77,009 | 13,433 | 0.22 |
| Mortar (Compression) | 22,532 | 23,270 | 24,287 | 606 | 0.03 |
| Mortar (Tension) | 17,766 | 19,520 | 21,329 | 1374 | 0.07 |
| Top Layer Thickness dt (m) | Description | Static Modulus of Elasticity Estat,33 (N/mm2) | Area Share of Components in Cross-Section (–) | Bending Stiffness (MNm2) | ||
|---|---|---|---|---|---|---|
| Riprap | Mortar | aRR | aM | |||
| 0.40 | Fully grouted | 60,000 | 20,000 | 0.55 | 0.45 | 224.00 |
| Partially grouted, vg = 80 L/m2 | 0.20 | 197.33 | ||||
| 0.60 | Regrouted, vg = 80 + 100 L/m2 | 60,000 | 20,000 | 0.55 | 0.29 | 698.40 |
| Partially grouted, vg = 80 L/m2 | 0.13 | 642.00 | ||||
| Soil | ks (MN/m3) | Description | Reference |
|---|---|---|---|
| “Sandy soil“ | 10–20 | Recommendation for soils beneath revetments, wave impact load | [15] |
| “Dense sand“ | 100 | Beneath asphalt revetments, wave impact load | [32] |
| 64 | |||
| “Sand“ | 40–100 * | Beneath asphalt revetments | [9] |
| 35–60 | Beneath asphalt revetments, quasi-static load | [33] | |
| 50–90 | Beneath asphalt revetments, wave impact load |
| Top Layer Thickness dt (m) | Description | Bending Stiffness (MNn2) | Modulus of Subgrade Reaction ks (MN/m3) | Denomination |
|---|---|---|---|---|
| 0.40 | Fully grouted | 224.00 | 50 | Parameter combination 1 |
| Partially grouted, vg = 80 L/m2 | 197.33 | |||
| 0.60 | Regrouted, vg = 80 + 100 L/m2 | 698.40 | ||
| Partially grouted, vg = 80 L/m2 | 642.00 | |||
| 0.40 | Fully grouted | 224.00 | 10 | Parameter combination 2 |
| Partially grouted, vg = 80 L/m2 | 197.33 | |||
| 0.60 | Regrouted, vg = 80 + 100 L/m2 | 698.40 | ||
| Partially grouted, vg = 80 L/m2 | 642.00 |
| dt (m) | Description | c1 | c2 | c3 | c4 | Restriction of Validity * | |
|---|---|---|---|---|---|---|---|
| 0.40 | Fully Grouted | 20 | 0.2 | 30 | 1.8 | Lm−1,0 <50 m | Parameter combination 1 (ks = 50 MN/m3) |
| Partially grouted, vg = 80 L/m2 | 7 | 0.4 | 14 | 1.5 | - | ||
| 0.60 | Regrouted, vg = 80 + 100 L/m2 | 20 | 0.2 | 10 | 1.8 | Lm−1,0 <50 m | |
| Partially grouted, vg = 80 L/m2 | 5 | 0.4 | 8 | 1.5 | - | ||
| 0.40 | Fully grouted | 40 | 0.2 | 50 | 1.8 | Lm−1,0 <50 m | Parameter combination 2 (ks = 10 MN/m3) |
| Partially grouted, vg = 80 L/m2 | 12 | 0.4 | 20 | 1.5 | - | ||
| 0.60 | Regrouted, vg = 80 + 100 L/m2 | 30 | 0.25 | 18 | 1.8 | Lm−1,0 <50 m | |
| Partially grouted, vg = 80 L/m2 | 10 | 0.4 | 14 | 1.5 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kreyenschulte, M.; Schüttrumpf, H. Tensile Bending Stresses in Mortar-Grouted Riprap Revetments Due to Wave Loading. J. Mar. Sci. Eng. 2020, 8, 913. https://doi.org/10.3390/jmse8110913
Kreyenschulte M, Schüttrumpf H. Tensile Bending Stresses in Mortar-Grouted Riprap Revetments Due to Wave Loading. Journal of Marine Science and Engineering. 2020; 8(11):913. https://doi.org/10.3390/jmse8110913
Chicago/Turabian StyleKreyenschulte, Moritz, and Holger Schüttrumpf. 2020. "Tensile Bending Stresses in Mortar-Grouted Riprap Revetments Due to Wave Loading" Journal of Marine Science and Engineering 8, no. 11: 913. https://doi.org/10.3390/jmse8110913
APA StyleKreyenschulte, M., & Schüttrumpf, H. (2020). Tensile Bending Stresses in Mortar-Grouted Riprap Revetments Due to Wave Loading. Journal of Marine Science and Engineering, 8(11), 913. https://doi.org/10.3390/jmse8110913






