Performance of an Array of Oscillating Water Column Devices in Front of a Fixed Vertical Breakwater
Abstract
1. Introduction
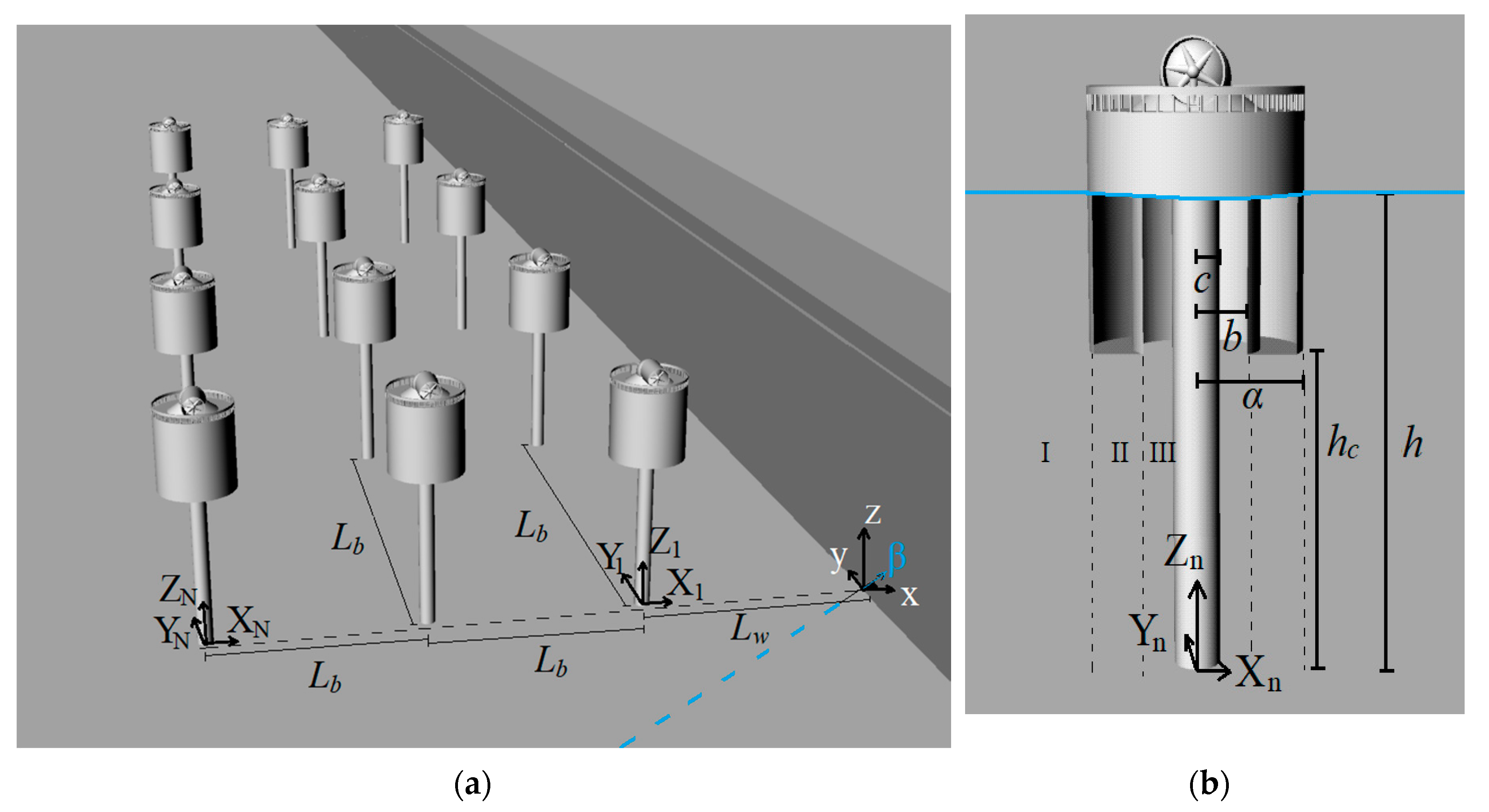
2. Formulation of the Hydrodynamic Problem
- (a)
- on the water free surface:
- (b)
- on the sea bottom:
- (c)
- kinematic condition on the mean device’s wetted surface:
3. Array’s Efficiency
4. Numerical Results
4.1. Test Cases
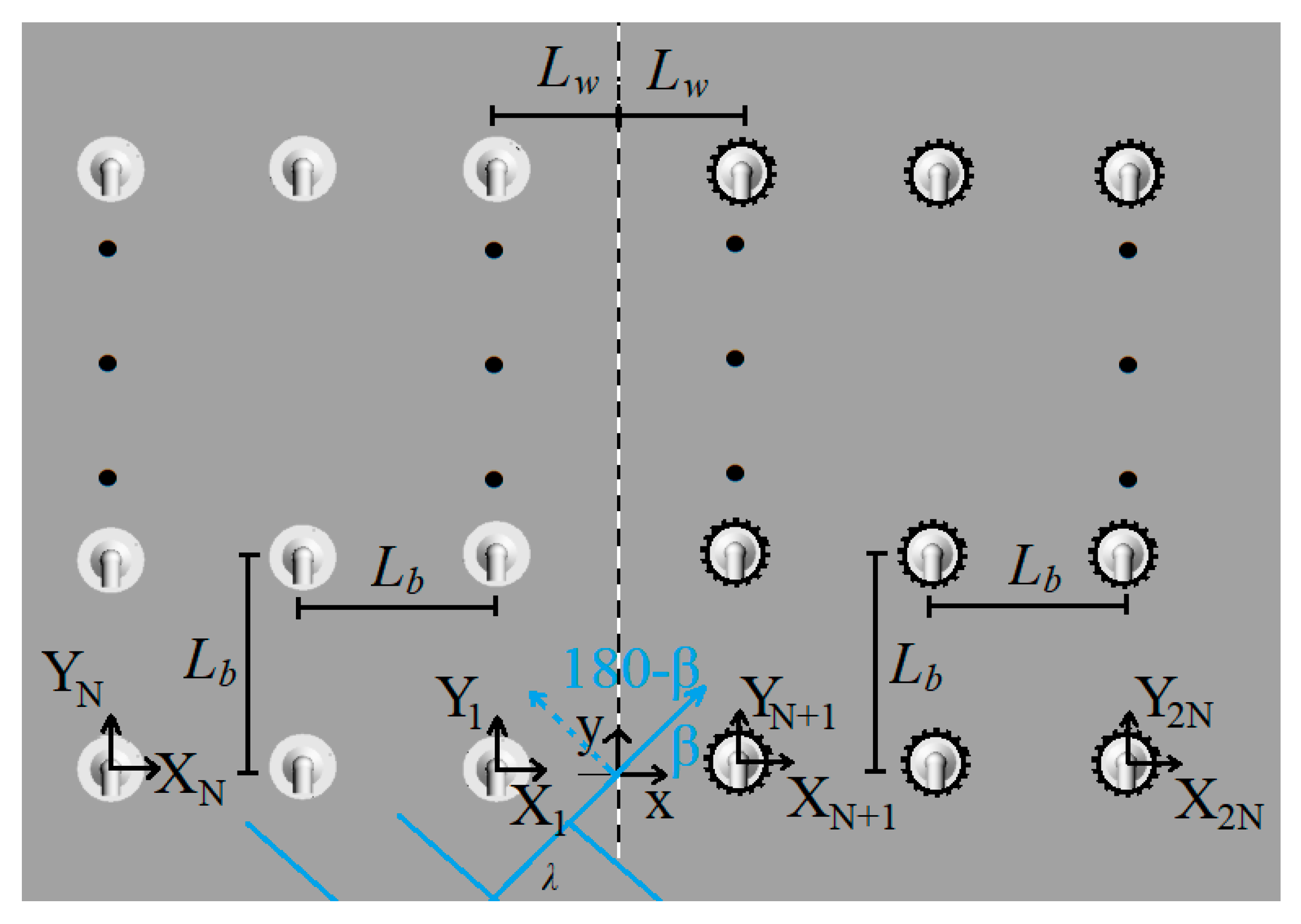
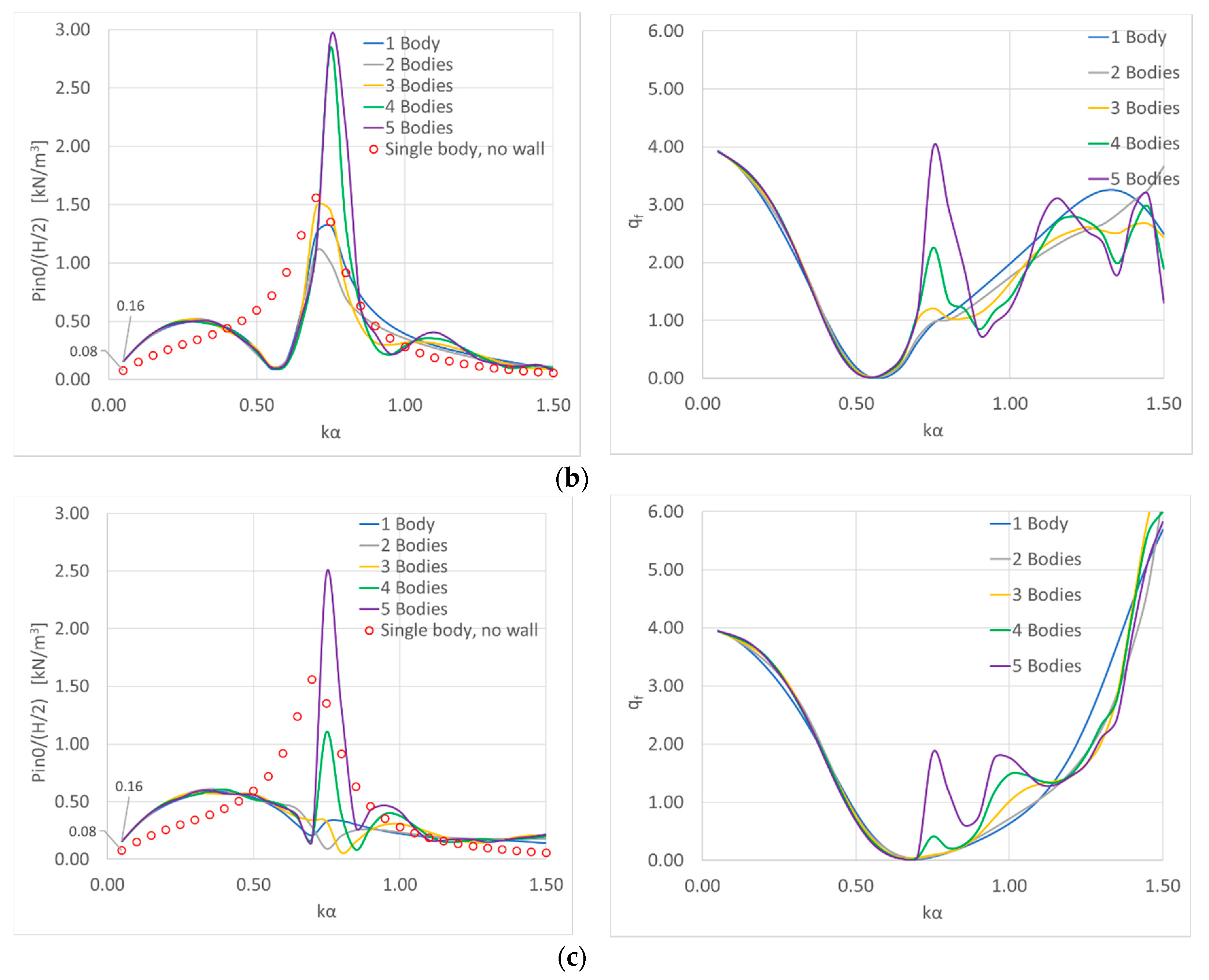
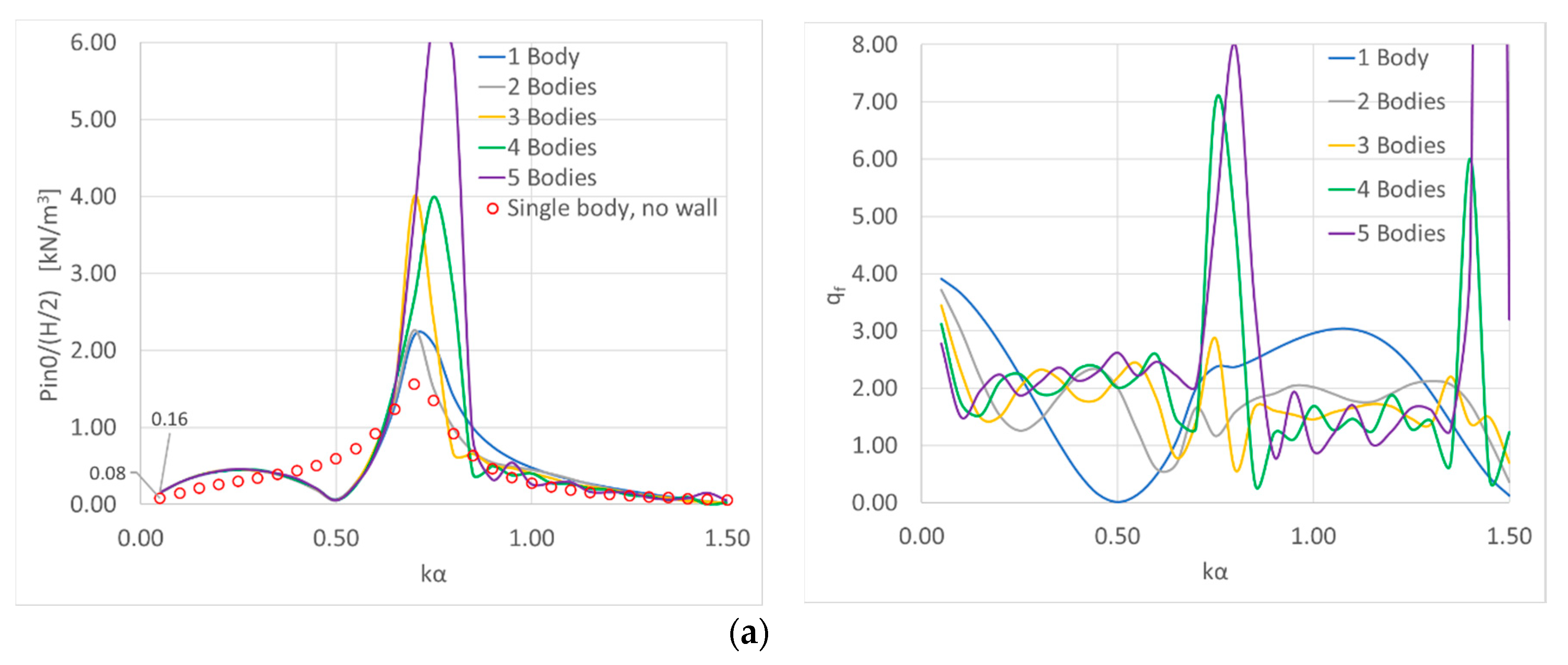
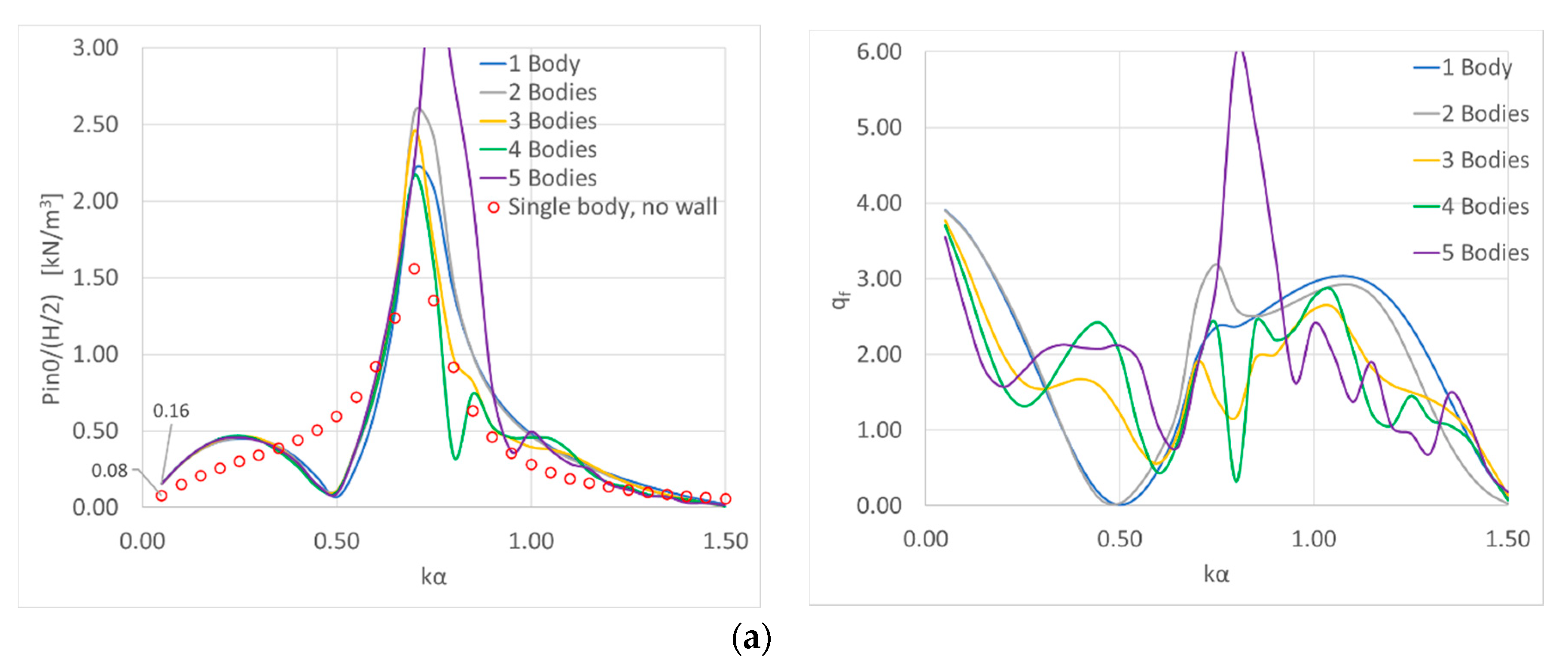
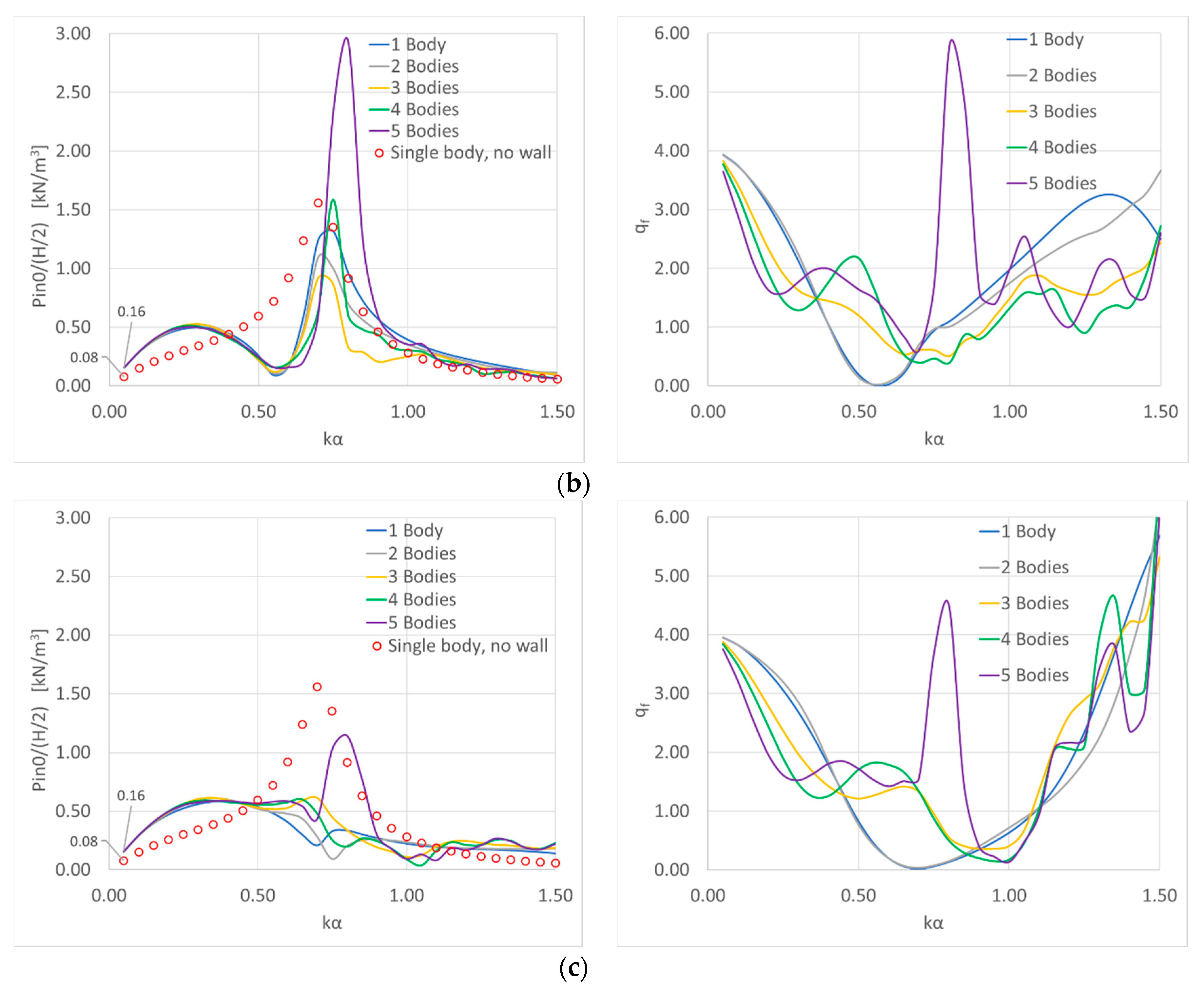
4.2. Effect of the OWCs Orientation to the Breakwater
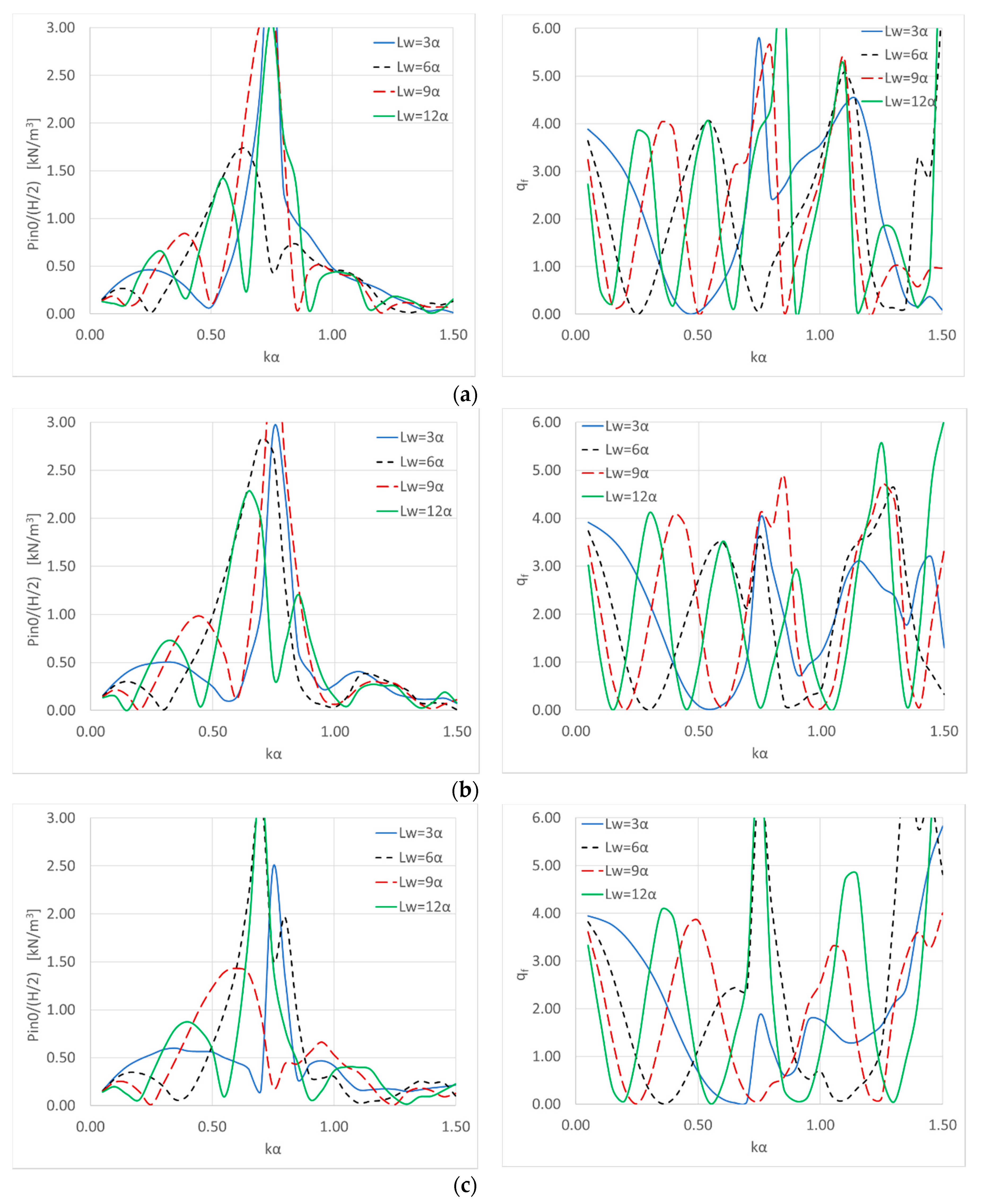
4.3. Effect of the OWCs’ Distance from the Breakwater
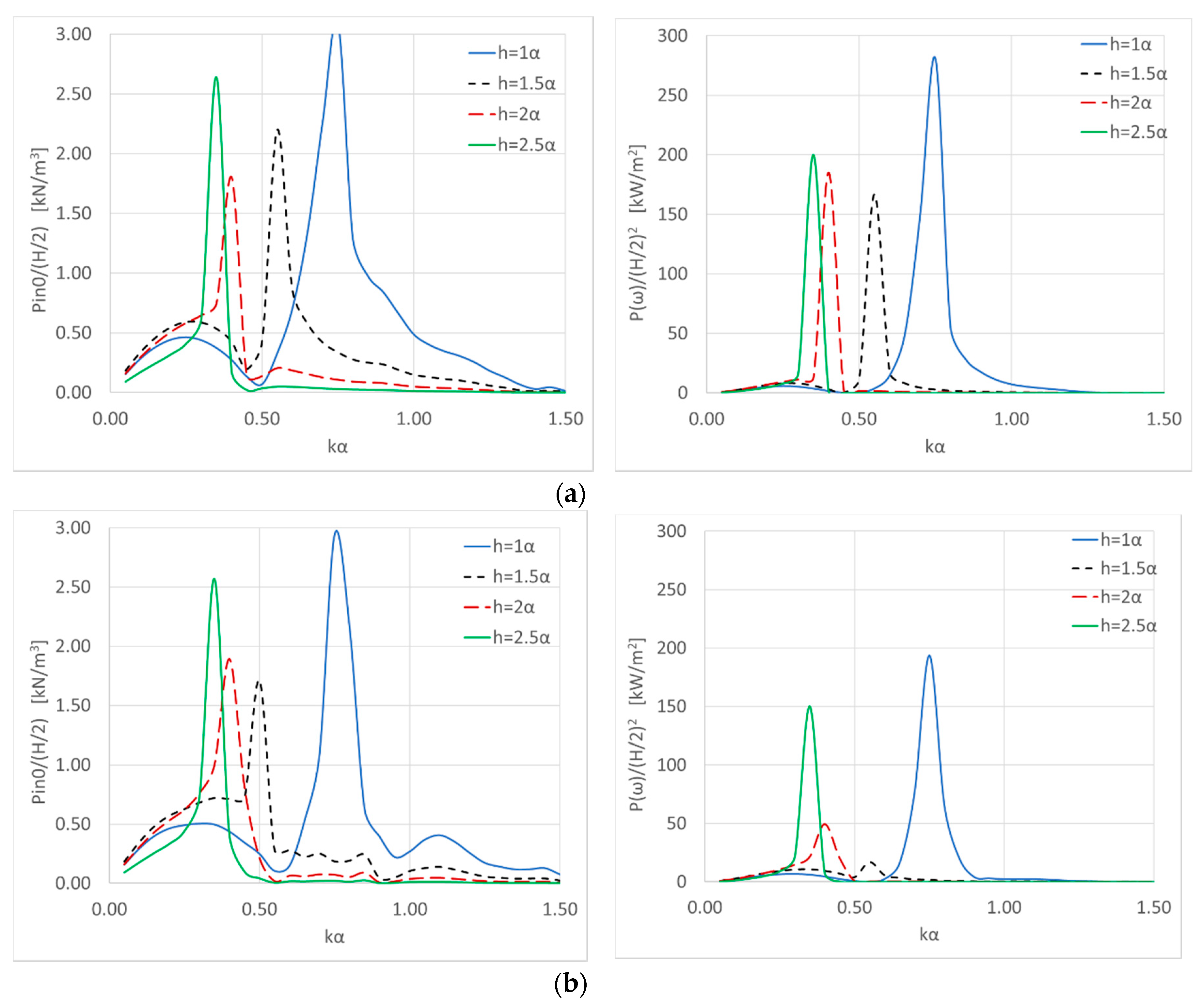
4.4. Effect of the OWCs’ Draught
4.5. Effect of the Distance between the OWCs
5. Conclusions
Funding
Conflicts of Interest
Nomenclature
| N | Number of OWC devices |
| h | Water depth |
| α | OWC outer radius |
| b | OWC inner radius |
| hc | Distance between the bottom of the external torus and the seabed |
| c | Radius of the internal cylindrical body |
| Lw | Distance between the closest to the wall OWC and the vertical wall |
| Lb | Distance between adjacent OWCs |
| β | Wave heading angle |
| ω | Wave frequency |
| H | Wave height |
| λ | Wave length |
| rk,θk,zk | Local co-ordinate system of the k OWC |
| Φ | Time harmonic complex velocity potential |
| Velocity potential of the undisturbed incident harmonic wave | |
| Scattered velocity potential of the q OWC | |
| Diffraction velocity potential of the q OWC | |
| Radiation velocity potential resulting from the inner air pressure in p OWC | |
| Amplitude of the oscillating pressure head in the chamber of the p OWC | |
| g | Gravitational acceleration |
| ρ | Water density |
| Unit normal vector | |
| δq,p | Kronecker’s symbol |
| Mean wetted surface of the q OWC | |
| I | The infinite ring element around the q OWC |
| II | The ring element below the q OWC |
| III | The ring element inside the chamber of the q OWC |
| Time dependent air volume flow | |
| Vertical velocity of the water surface in the OWC | |
| Cross-sectional area of the inner water surface inside the OWC | |
| Diffraction volume flow of the q OWC | |
| Pressure-dependent volume flow of the q OWC | |
| Radiation conductance of the q OWC | |
| Radiation susceptance of the q OWC | |
| Λ | Complex pneumatic admittance (air turbine coefficient) |
| Air turbine coefficient optimum value | |
| Absorbed wave power by each OWC of the array | |
| q-factor term |
Appendix A
References
- Biesheuvel, A.C. Effectiveness of Floating Breakwaters. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar]
- Haggi, A. Report on underwater excavation at the Phoenician Harbour, Atlit, Israel. Int. J. Naut. Archaeol. 2010, 39, 278–285. [Google Scholar] [CrossRef]
- Sadeghi, K.; Abdeh, A.; Al-Dubai, S. An Overview of Construction and Installation of Vertical Breakwaters. Int. J. Innov. Technol. Explor. Eng. 2017, 7, 1–5. [Google Scholar]
- Van der Meer, J.W. Conceptual design of rubble mound breakwaters. Adv. Coast. Ocean Eng. 1995, 1, 221–315. [Google Scholar]
- Goda, Y. Random Seas and Design of Maritime Structures, 2nd ed.; World Scientific Publishing: Singapore, 2000. [Google Scholar]
- Burcharth, H.F.; Lykke-Andersen, T. Overtopping of rubble mound breakwaters with front reservoir. In Proceedings of the 30th International Conference of Coastal Engineering, San Diego, CA, USA, 3–8 September 2006; pp. 4605–4615. [Google Scholar]
- USACE. Coastal Engineering Manual; USACE: Washington, DC, USA, 2002.
- Vicinanza, D.; Lauro, E.D.; Contestabile, P.; Gisonni, C.; Lara, J.L.; Losada, I.J. Review of Innovative Harbor Breakwaters for Wave-Energy Conversion. J. Waterw. Port Coast. Ocean Eng. 2019, 145, 03119001. [Google Scholar] [CrossRef]
- Contestabile, P.; Crispino, G.; Russo, S.; Gisonni, C.; Cascetta, F.; Vicinanza, D. Crown wall modifications as response to wave overtopping under a future sea level scenario: An experimental parametric study for an innovative composite seawall. Appl. Sci. 2020, 10, 2227. [Google Scholar] [CrossRef]
- Lee, B.W.; Park, W.-S. Evaluation of the Hydraulic Performance of a Rear-Parapet Vertical Breakwater under Regular Waves through Hydraulic Experiments. Water 2020, 12, 2428. [Google Scholar] [CrossRef]
- Park, W.S.; Seo, J.; Won, D.; Lee, B.W. Stability assessment formulas for an interlocking caisson breakwater under oblique wave conditions. J. Coast. Res. 2018, 85, 1236–1240. [Google Scholar] [CrossRef]
- Hu, P. Dynamic responses analysis of permeable breakwater subjected to random waves. Adv. Mater. Res. 2015, 1061–1062, 809–812. [Google Scholar]
- Elkotby, M.; Rageh, O.; Sarhan, T.; Ezzeldin, M. Wave transformation behind permeable breakwater. Int. J. Sci. Eng. Res. 2019, 10. [Google Scholar] [CrossRef]
- Yoo, J.; Kim, S.-Y.; Kim, J.-M.; Cho, Y.-S. Experimental Investigation of the Hydraulic Performance of Caisson-Pile Breakwaters. J. Coast. Res. 2010, 263, 444–450. [Google Scholar] [CrossRef]
- Pourteimouri, P.; Hejazi, K. Development of An Integrated Numerical Model for Simulating Wave Interaction with Permeable Submerged Breakwaters Using Extended Navier–Stokes Equations. J. Mar. Sci. Eng. 2020, 8, 87. [Google Scholar] [CrossRef]
- Mellink, B. Numerical and Experimental Research of Wave Interaction with a Porous Breakwater. Master’s Thesis, TU Delft, Delft, The Netherlands, 2012. [Google Scholar]
- Kralli, V.E.; Theodossiou, N.; Karambas, T. Optimal Design of Overtopping Breakwater for Energy Conversion (OBREC) Systems Using the Harmony Search Algorithm. Front. Energy Res. 2019, 7. [Google Scholar] [CrossRef]
- Contestabile, P.; Ferrante, V.; Di Lauro, E.; Vicinanza, D. Prototype overtopping breakwater for wave energy conversion at port of Naples. In Proceedings of the 26th International Ocean and Polar Engineering Conference (ISOPE 2016), Rhodes, Greece, 26 June–2 July 2016; pp. 616–621. [Google Scholar]
- Gravas, A.; Savvidis, Y.; Koutitas, C. Modelling study of wave energy harnessing port structures. Fresenius Environ. Bull. 2012, 21, 3069–3076. [Google Scholar]
- Vicinanza, D.; Margeritini, L.; Kofoed, J.P.; Buccino, M. The SSG wave energy converter: Performance, status and recent developments. Energies 2012, 5, 193–226. [Google Scholar] [CrossRef]
- Cabral, T.; Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F.; Morais, T.; Belga, F.; Cestaro, H. Performance Assessment of a Hybrid Wave Energy Converter Integrated into a Harbor Breakwater. Energies 2020, 13, 236. [Google Scholar] [CrossRef]
- Sarkar, D.; Renzi, E.; Dias, F. Effect of a straight coast on the hydrodynamics and performance of the Oscillating Wave Surge Converter. Ocean Eng. 2015, 105, 25–32. [Google Scholar] [CrossRef]
- Michele, S.; Sammarco, P.; Errico, M. The optimal design of a flap gate array in front of a straight vertical wall: Resonance of the natural modes and enhancement of the existing torque. Ocean Eng. 2016, 118, 152–164. [Google Scholar] [CrossRef]
- Cascajo, R.; Garcia, E.; Quiles, E.; Correcher, A.; Morant, F. Integration of marine wave energy converters into seaports: A case study in port of Valencia. Energies 2019, 12, 787. [Google Scholar] [CrossRef]
- Konispoliatis, D.N.; Mavrakos, S.A.; Katsaounis, G.M. Theoretical evaluation of the hydrodynamic characteristics of arrays of vertical axisymmetric floater of arbitrary shape in front of a vertical breakwater. J. Mar. Sci. Eng. Res. 2020, 8, 62. [Google Scholar] [CrossRef]
- Konispoliatis, D.N.; Mavrakos, S.A. Wave power absorption by arrays of wave energy converters in front of a vertical breakwater: A theoretical study. Energies 2020, 13, 1985. [Google Scholar] [CrossRef]
- Martins-rivas, H.; Mei, C.C. Wave power extraction from an oscillating water column at the tip of a breakwater. J. Fluid Mech. 2009, 626, 395–414. [Google Scholar] [CrossRef]
- Martins-rivas, H.; Mei, C.C. Wave power extraction from an oscillating water column along a straight coast. Ocean Eng. 2009, 36, 426–433. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, Y.; Inglesias, G. Coast/breakwater-integrated OWC: A theoretical model. Mar. Struct. 2019, 66, 121–135. [Google Scholar] [CrossRef]
- Viviano, A.; Naty, S.; Foti, E.; Bruce, T.; Allsop, W.; Vicinanza, D. Large-scale experiments on the behavior of a generalized oscillating water column under random waves. Renew. Energy 2016, 99, 875–887. [Google Scholar] [CrossRef]
- Howe, D.; Nader, J.R. OWC WEC integrated within a breakwater versus isolated: Experimental and numerical theoretical study. Int. J. Mar. Energy 2017, 20, 165–182. [Google Scholar] [CrossRef]
- Naty, S.; Viviano, A.; Foti, E. Wave energy exploitation system integrated in the coastal structure of a Mediterranean port. Sustainability 2016, 8, 1342. [Google Scholar] [CrossRef]
- Naty, S.; Viviano, A.; Foti, E. Feaseability study of a wec integrated in the port of giardini naxos, Italy. In Proceedings of the 35th Conference on Coastal Engineering, Antalya, Turkey, 17–20 November 2016. [Google Scholar]
- Zheng, S.; Antonini, A.; Zhang, Y.; Greaves, D.; Miles, J.; Iglesias, G. Wave power extraction from multiple oscillating water columns along a straight coast. J. Fluid Mech. 2019, 878, 445–480. [Google Scholar] [CrossRef]
- Park, S.; Kim, K.H.; Nam, B.W.; Kim, J.S.; Hong, K. A Study on Effects of Breakwater on Performance of OWC. In Proceedings of the 13th International Society of Offshore and Polar Engineers Symposium, (ISOPE), Jeju, Korea, 14–17 October 2018. [Google Scholar]
- Tsai, C.P.; Ko, C.H.; Chen, Y.C. Investigation on Performance of a Modified Breakwater-Integrated OWC Wave Energy Converter. Sustainability 2018, 10, 643. [Google Scholar] [CrossRef]
- Konispoliatis, D.; Mavrakos, S. Theoretical performance investigation of a vertical cylindrical oscillating water column device in front of a vertical breakwater. J. Ocean Eng. Mar. Energy 2019. [Google Scholar] [CrossRef]
- Konispoliatis, D.; Mavrakos, S.A.; Soukissian, T.H. Array of oscillating water column devices in front of a vertical breakwater in the Mediterranean Sea. In Proceedings of the 12th International Conference on Deregulated Electricity Market Issues in Southern Eastern Europe (DEMSEE 2019), Herakleion, Greece, 19–20 September 2019. [Google Scholar]
- Zhou, Y.; Zhang, C.; Ning, D. Hydrodynamic Investigation of a Concentric Cylindrical OWC Wave Energy Converter. Energies 2018, 11, 985. [Google Scholar] [CrossRef]
- Michele, S.; Renzi, E.; Perez-Collazo, C.; Greaves, D.; Iglesias, G. Power extraction in regular and random waves from an OWC in hybrid wind-wave energy systems. Ocean Eng. 2019, 191, 106519. [Google Scholar] [CrossRef]
- Perez-Collazo, C.; Greaves, D.; Iglesias, G. A Novel Hybrid Wind-Wave Energy Converter for Jacket-Frame Substructures. Energies 2018, 11, 637. [Google Scholar] [CrossRef]
- Qiao, D.; Feng, C.; Ning, D.; Wang, C.; Liang, H.; Li, B. Dynamic response analysis of Jacket platform integrated with oscillating water column device. Front. Energy Res. 2020. [Google Scholar] [CrossRef]
- Falnes, J.; McIver, P. Surface wave interactions with systems of oscillating bodies and pressure distributions. Appl. Ocean Res. 1985, 7, 225–234. [Google Scholar] [CrossRef]
- Yeung, R.W.; Sphaier, S.H. Wave-interference effects on a truncated cylinder in a channel. J. Eng. Math. 1989, 23, 95–117. [Google Scholar] [CrossRef]
- Kokkinowrachos, K.; Mavrakos, S.A.; Asorakos, S. Behaviour of vertical bodies of revolution in waves. Ocean Eng. 1986, 13, 505–538. [Google Scholar] [CrossRef]
- Konispoliatis, D.; Mavrakos, S. Hydrodynamic analysis of an array of interacting free-floating oscillating water column (OWC’s) devices. Ocean Eng. 2016, 111, 179–197. [Google Scholar] [CrossRef]
- Evans, D.V. Wave-power absorption by systems of oscillating surface pressure distributions. J. Fluid Mech. 1982, 114, 481–499. [Google Scholar] [CrossRef]
- Sarmento, A.J.N.A.; Falcao, A.F.O. Wave generation by an oscillating surface-pressure and its application in wave-energy extraction. J. Fluid Mech. 1985, 150, 467–485. [Google Scholar] [CrossRef]
- Evans, D.V.; Porter, R. Efficient calculation of hydrodynamic properties of O.W.C type devices. In Proceedings of the 15th Offshore Mechanics and Arctic Engineering (OMAE 1996), Florence, Italy, 16–20 June 1996; Part B. pp. 123–132. [Google Scholar]
- Mavrakos, S.A.; McIver, P. Comparison of methods for computing hydrodynamic characteristics of arrays of wave power devices. Appl. Ocean Res. 1997, 19, 283–291. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Mavrakos, S.A. User’s Manual for the Software HAMVAB; School of Naval Architecture and Marine Engineering, Laboratory for Floating Structures and Mooring Systems: Athens, Greece, 1995. [Google Scholar]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Silverman, S.; Abramson, H.N. Lateral Sloshing in Moving Containers. The Dynamic Behavior of Liquids in Moving Containers; Abramson, N.H., Ed.; NASA SP-106; NASA: Washington, DC, USA, 1966; p. 13. 467p.
- Loukogeorgaki, E.; Chatjigeorgiou, I.K. Hydrodynamic Performance of an Array of Wave Energy Converters in Front of a Vertical Wall. In Proceedings of the 13th European Wave and Tidal Energy Conference (EWTEC 2019), Napoli, Italy, 1–6 September 2019; p. 1464. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konispoliatis, D.N. Performance of an Array of Oscillating Water Column Devices in Front of a Fixed Vertical Breakwater. J. Mar. Sci. Eng. 2020, 8, 912. https://doi.org/10.3390/jmse8110912
Konispoliatis DN. Performance of an Array of Oscillating Water Column Devices in Front of a Fixed Vertical Breakwater. Journal of Marine Science and Engineering. 2020; 8(11):912. https://doi.org/10.3390/jmse8110912
Chicago/Turabian StyleKonispoliatis, Dimitrios N. 2020. "Performance of an Array of Oscillating Water Column Devices in Front of a Fixed Vertical Breakwater" Journal of Marine Science and Engineering 8, no. 11: 912. https://doi.org/10.3390/jmse8110912
APA StyleKonispoliatis, D. N. (2020). Performance of an Array of Oscillating Water Column Devices in Front of a Fixed Vertical Breakwater. Journal of Marine Science and Engineering, 8(11), 912. https://doi.org/10.3390/jmse8110912




