Sound Field Properties of Non-Cavitating Marine Propellers
Abstract
1. Introduction
1.1. State of the Art
1.2. Contributions of Current Work
2. Methodology
2.1. Boundary Element Method
2.2. Ffowcs Williams-Hawkings Equation
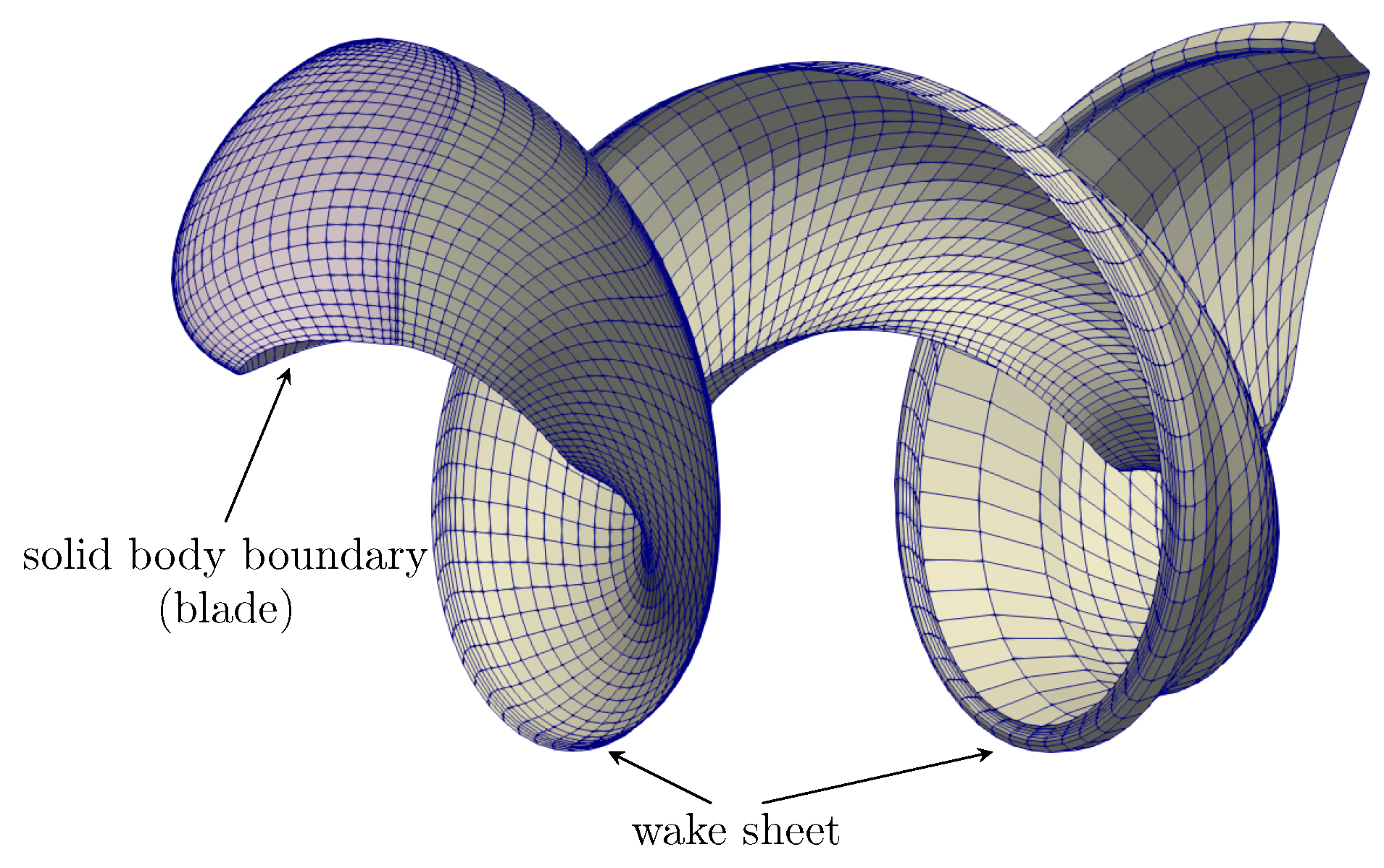
2.3. Formulation of FWH Equation on the Potential Wake Sheet
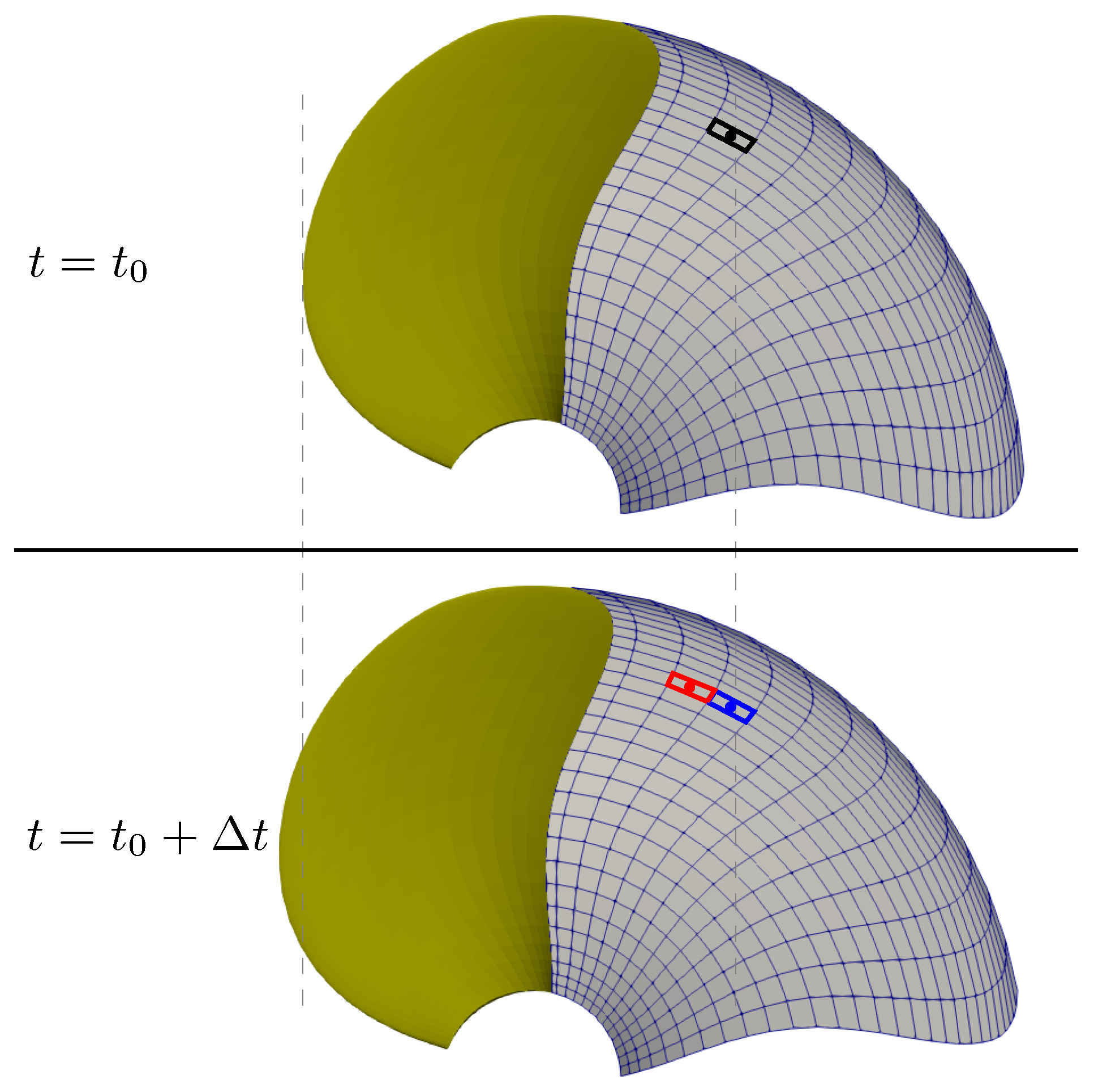
2.3.1. Thickness Terms
2.3.2. Loading Terms
2.4. Coupling of Permeable FWH Approach with BEM
3. Numerical Results
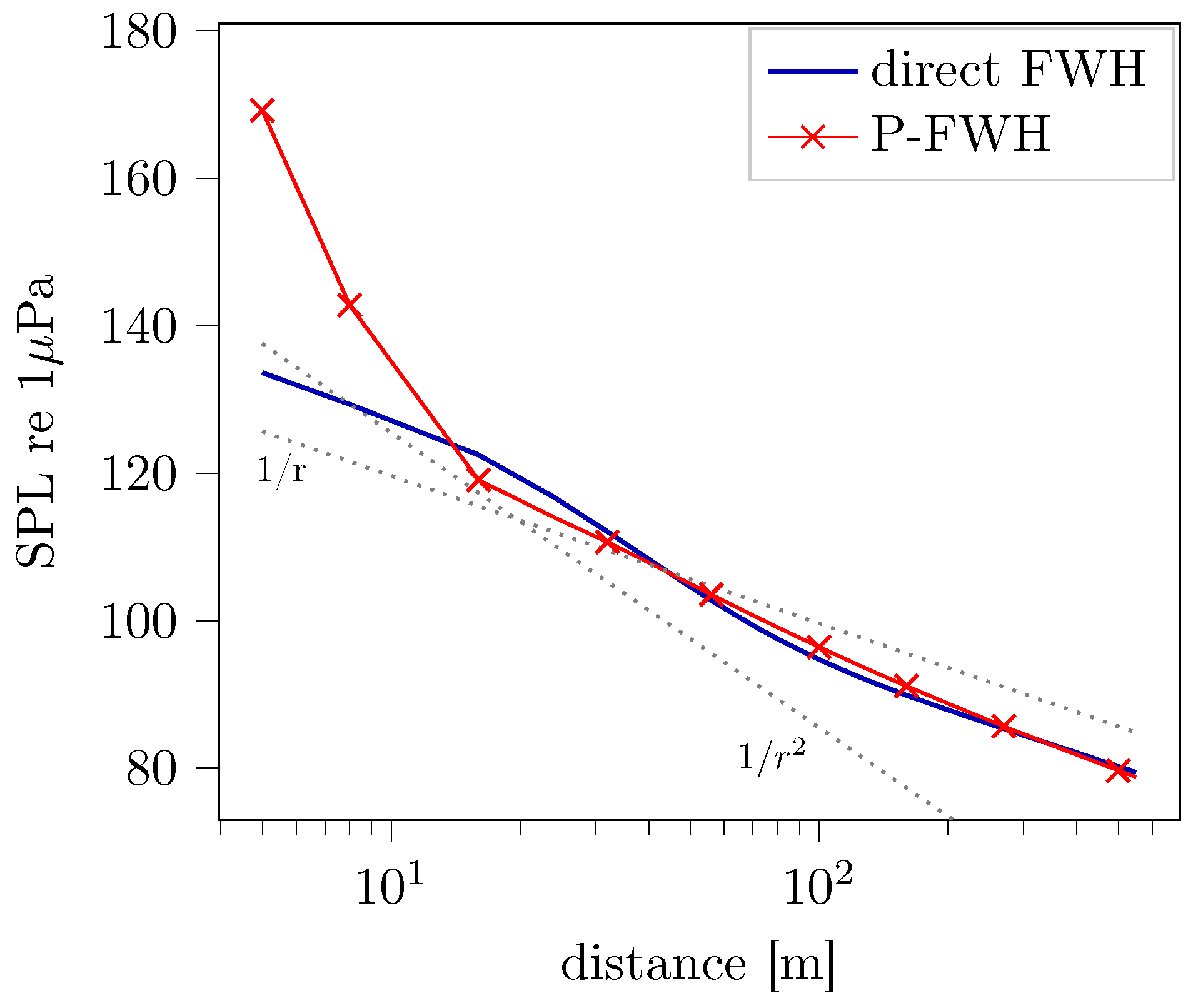
3.1. Open Water Case with the Direct FWH Approach
3.2. Behind-Hull Case with the Direct FWH Approach
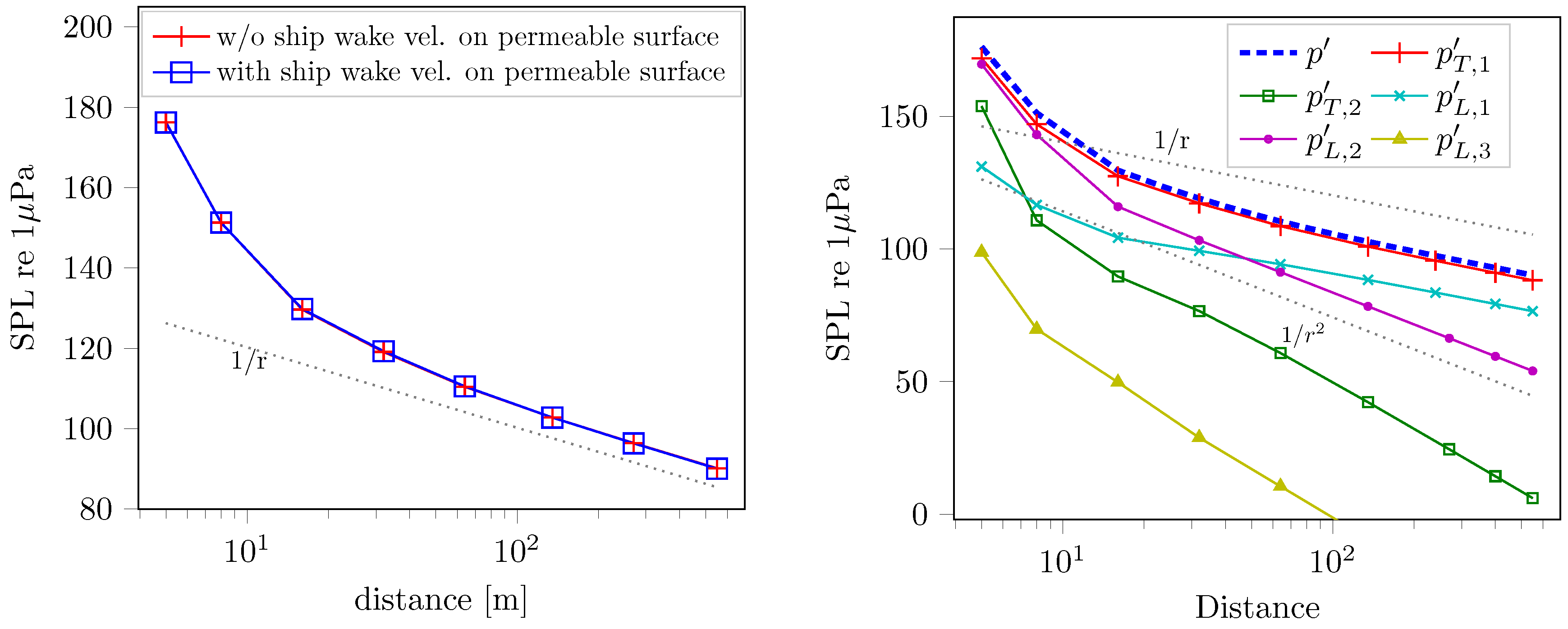
3.3. Behind-Hull Case with the BEM/P-FWH Hybrid Method
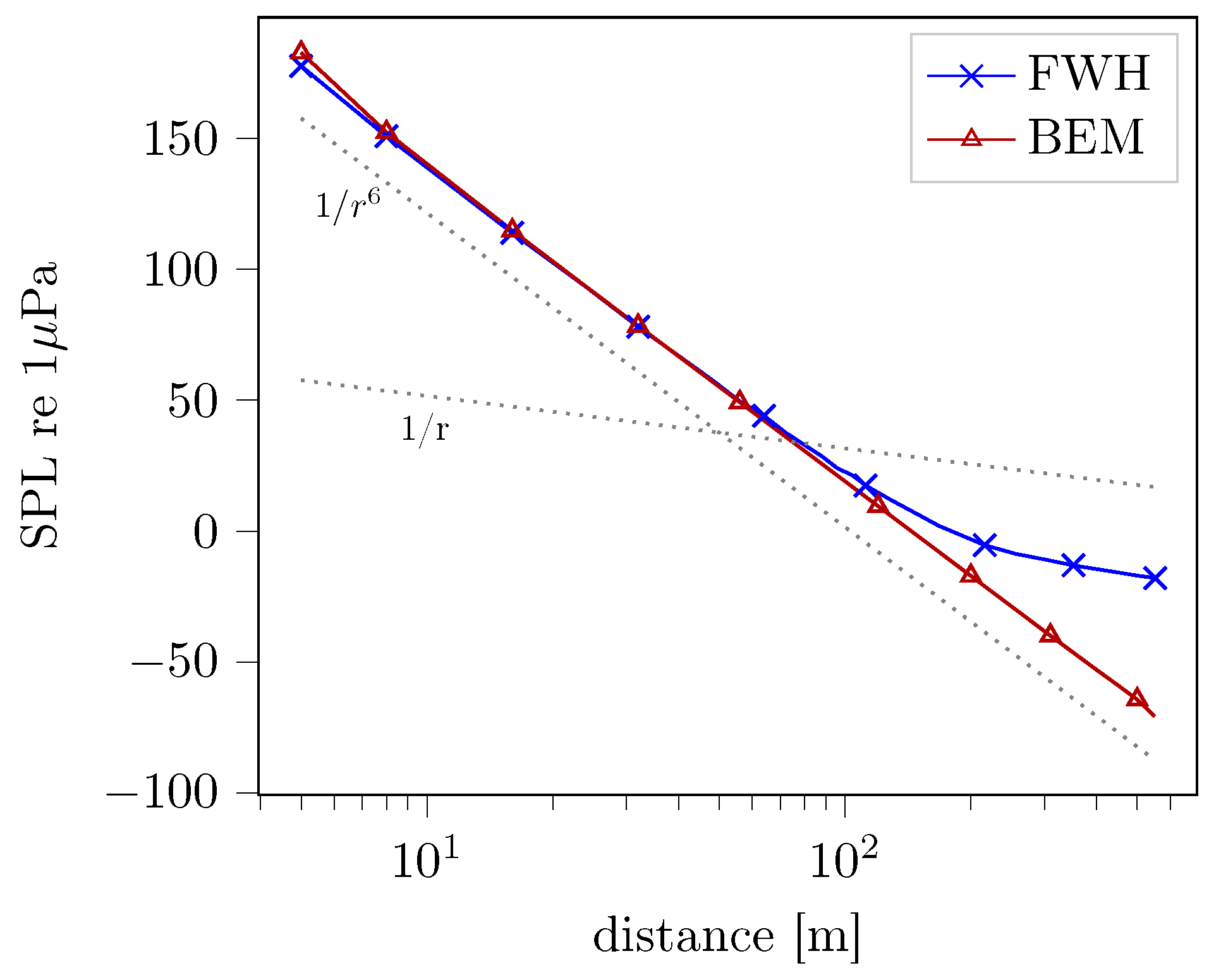
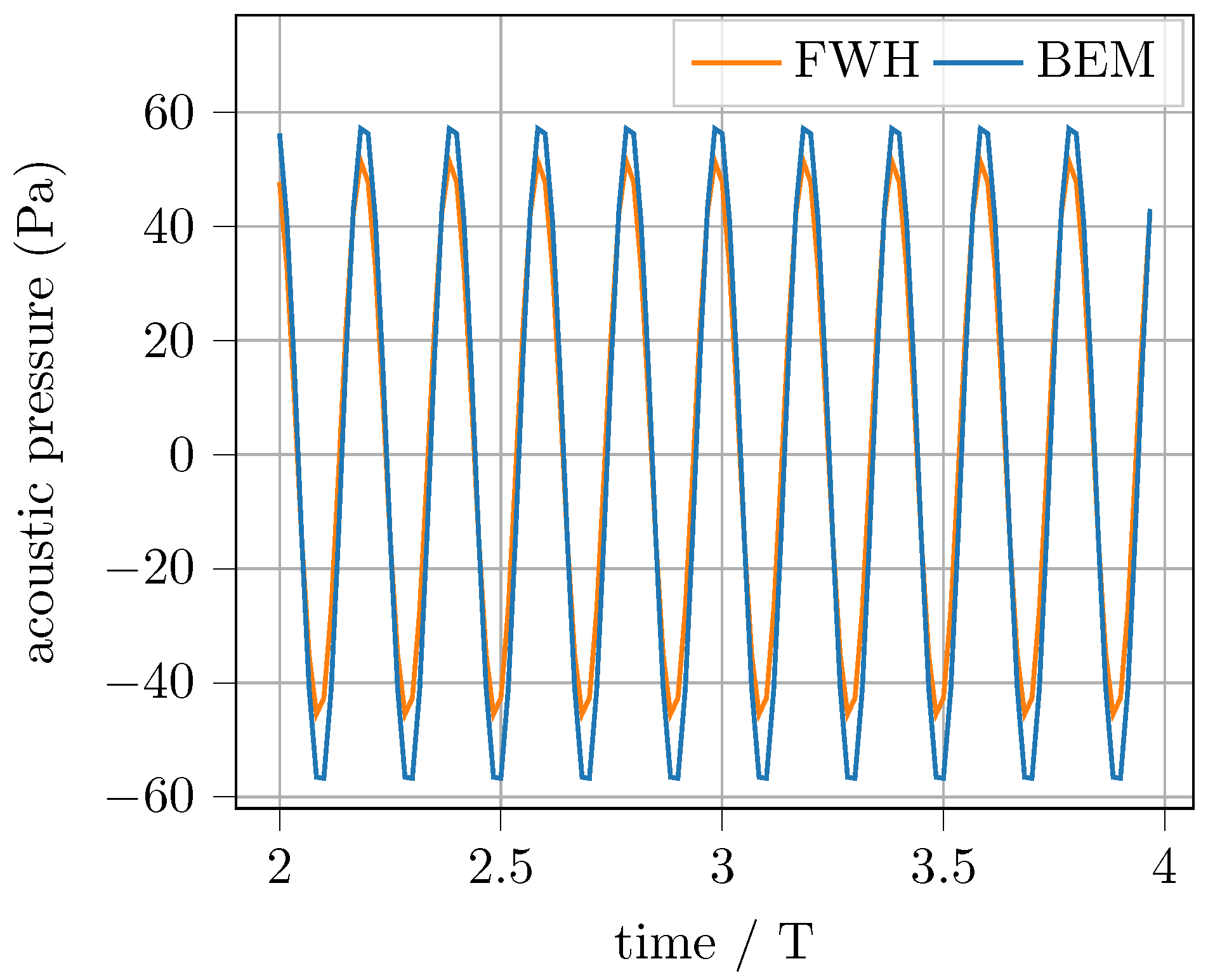
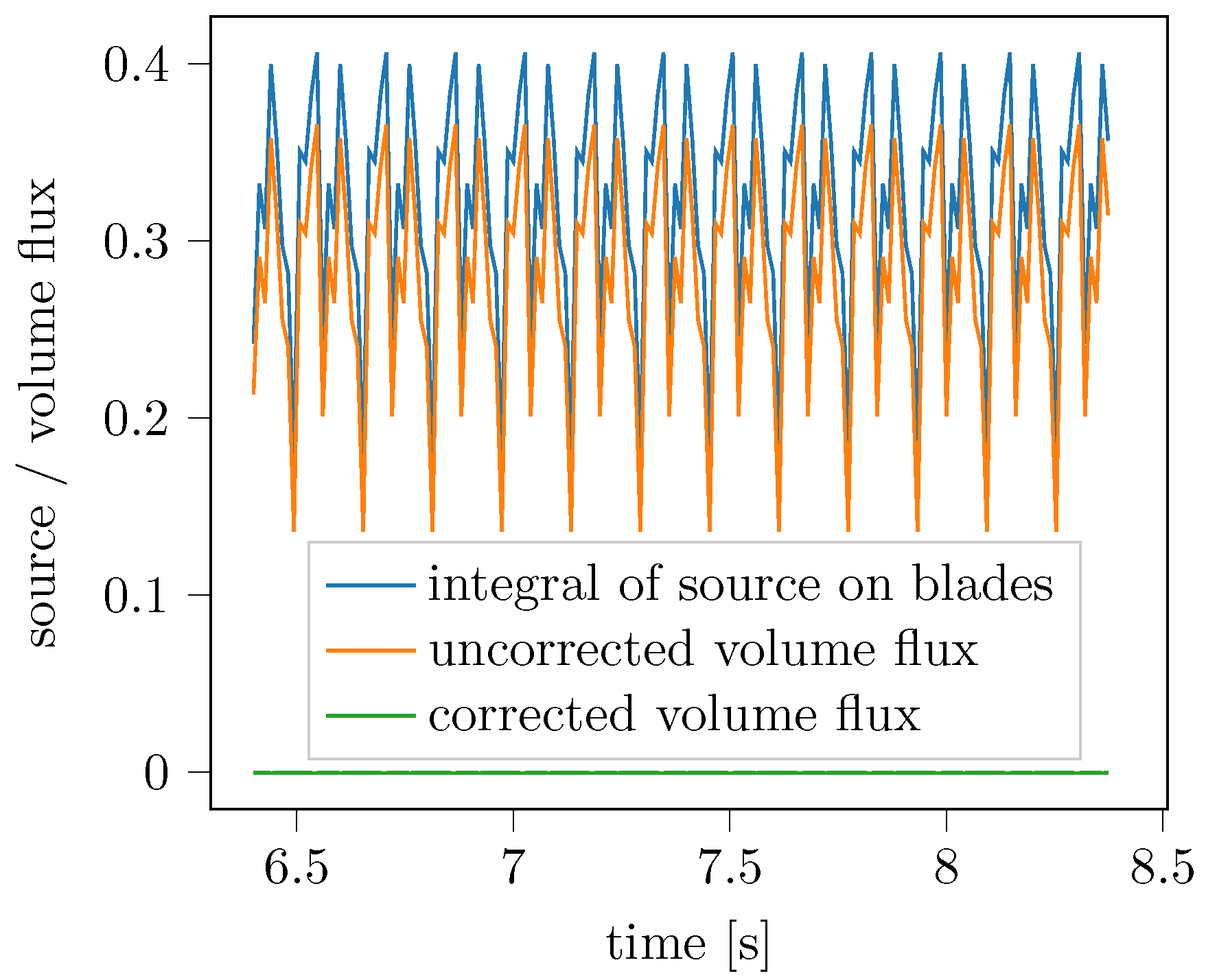
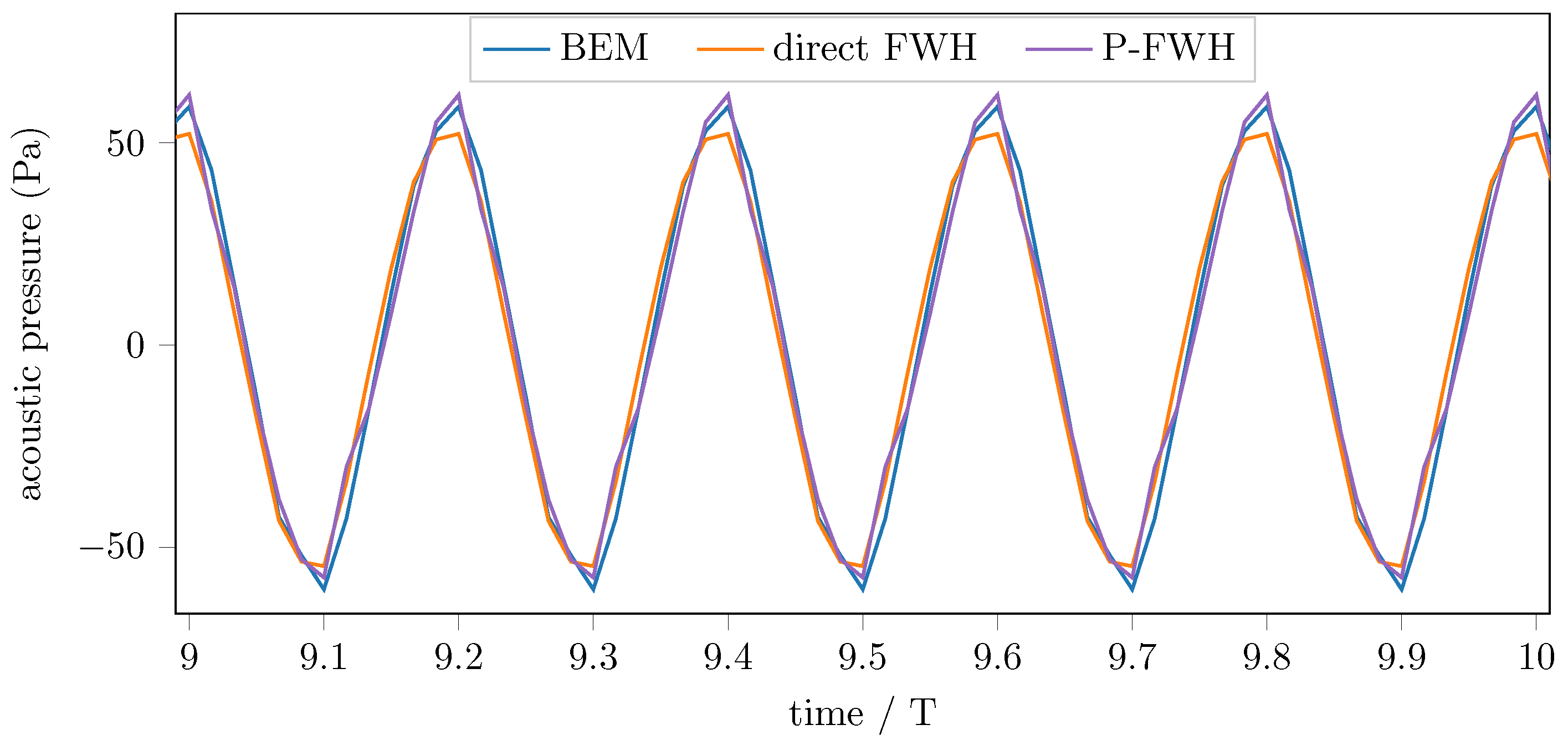
3.4. Verification of the FWH Formulation on the Wake Sheet
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Krasilnikov, V. CFD modeling of hydroacoustic performance of marine propellers: Predicting propeller cavitation. In Proceedings of the 22nd Numerical Towing Tank Symposium, Tomar, Portugal, 29 September–1 October 2019. [Google Scholar]
- European-Commission. Our Oceans, Seas and Coasts. 2019. Available online: https://ec.europa.eu/environment/marine/good-environmental-status/descriptor-11/index_en.htm (accessed on 31 July 2020).
- AQUO Project Consortium. AQUO: Achieve Quieter Oceans by Shipping Noise Footprint Reduction. 2012. Available online: http://www.aquo.eu (accessed on 31 July 2020).
- SONIC Project Consortium. SONIC: Supression of Underwater Noise Induced by Cavitation. 2015. Available online: https://cordis.europa.eu/project/id/314394/results (accessed on 31 August 2020).
- ProNoVi-Consortium. ProNoVi:Analysis Methods and Design Measures for the Reduction of Noise and Vibration Induced by Marine Propellers. 2017. Available online: http://www.pronovi.eu (accessed on 31 July 2020).
- Wang, M.; Freund, J.B.; Lele, S.K. Coputational prediction of flow-generated sound. Annu. Rev. Fluid Mech. 2006, 38, 483–512. [Google Scholar] [CrossRef]
- Williams, J.F.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. Lond. A 1969, 264, 321–342. [Google Scholar]
- Di Francescantonio, P. A new boundary integral formulation for the prediction of sound radiation. J. Sound Vib. 1997, 202, 491–509. [Google Scholar] [CrossRef]
- Farassat, F. Derivation of Formulations 1 and 1A of Farassat; Technical Report NASA/TM-2007-214853; NASA, Langley Research Center: Hampton, VA, USA, 2007.
- Ianniello, S.; Muscari, R.; Di Mascio, A. Ship underwater noise assessment by the Acoustic Analogy part II: Hydroacoustic analysis of a ship scaled model. J. Mar. Sci. Technol. 2014, 19, 52–74. [Google Scholar] [CrossRef]
- Bensow, R.; Liefvendahl, M. An acoustic analogy and scale-resolving flow simulation methodology for the prediction of propeller radiated noise. In Proceedings of the 31th Symposium on Naval Hydrodynamics, Monterey, CA, USA, 11–16 September 2016. [Google Scholar]
- Li, D.Q.; Hallander, J.; Johansson, T. Predicting underwater radiated noise of a full scale ship with model testing and numerical methods. Ocean. Eng. 2018, 161, 121–135. [Google Scholar] [CrossRef]
- Göttsche, U.; Lampe, T.; Scharf, M.; Abdel-Maksoud, M. Evaluation of Underwater Sound Propagation of a Catamaran with Cavitating Propellers. In Proceedings of the 6th International Symposium on Marine Propulsors (SMP’19), Rome, Italy, 26–30 May 2019. [Google Scholar]
- Seol, H.; Suh, J.C.; Lee, S. Development of hybrid method for the prediction of underwater propeller noise. J. Sound Vib. 2005, 288, 345–360. [Google Scholar] [CrossRef]
- Lloyd, T.; Rijpkema, D.; Van Wijngaarden, E. Implementing the Ffowcs Williams-Hawkings acoustic analogy into a viscous CFD solver. In Proceedings of the 17th Numerical Towing Tank Symposium (NuTTS), Marstrand, Sweden, 28–30 September 2014. [Google Scholar]
- Lloyd, T.; Rijpkema, D.; van Wijngaarden, E. Marine propeller acoustic modelling: Comparing CFD results with an acoustic analogy method. In Proceedings of the 4th International Symposium on Marine Propulsors, Austin, TX, USA, 31 May–4 June 2015. [Google Scholar]
- Lloyd, T.P.; Lidtkeb, A.K.; Rijpkemac, D.R.; van Wijngaardenc, E.; Turnockb, S.R.; Humphreyd, V.F. Using the FW-H equation for hydroacoustics of propellers. In Proceedings of the Numerical Towing Tank Symposium (NuTTS), Marstrand, Sweden, 28–30 September 2015. [Google Scholar]
- Lidtke, A.K.; Humphrey, V.F.; Turnock, S.R. Feasibility study into a computational approach for marine propeller noise and cavitation modelling. Ocean. Eng. 2016, 120, 152–159. [Google Scholar] [CrossRef]
- Testa, C.; Procacchia, F.; Greco, L.; Muscari, R. Effectiveness of Boundary Element Method Hydrodynamic Data for Propeller Hydroacoustics. In Proceedings of the A. Yucel Odabasi Colloquium Series 3rd International Meeting-Progress in Propeller Cavitation and its Consequences, İstanbul, Turkey, 15–16 November 2018. [Google Scholar]
- Ianniello, S. The Ffowcs Williams–Hawkings equation for hydroacoustic analysis of rotating blades. Part 1. The rotpole. J. Fluid Mech. 2016, 797, 345–388. [Google Scholar] [CrossRef]
- Liefvendahl, M.; Bensow, R. Simulation-Based Analysis of Flow-Generated Noise from Cylinders with Different Cross-Sections. In Proceedings of the 32nd Symposium on Naval Hydrodynamics, Hamburg, Germany, 5–10 August 2018. [Google Scholar]
- Cianferra, M. Acoustic Analogies and Large-Eddy Simulations of Incompressible and Cavitating Flows Around Bluff Bodies. Ph.D. Thesis, Università degli Studi di Trieste, Trieste, Italy, 2018. [Google Scholar]
- Wang, Y.; Abdel-Maksoud, M.; Song, B. Convergence of different wake alignment methods in a panel code for steady-state flows. J. Mar. Sci. Technol. 2016, 21, 567–578. [Google Scholar] [CrossRef]
- Wang, Y.; Göttsche, U.; Abdel-Maksoud, M.; Krüger, S. Different techniques to simulate tandem propeller with boundary element method. In Proceedings of the 11th Internationa Workshop on Ship and Marine Hydrodynamic, Hamburg, Germany, 22–25 September 2019. [Google Scholar]
- Wang, Y.; Abdel-Maksoud, M.; Song, B. A fast method to realize the pressure Kutta condition in boundary element method for lifting bodies. Ocean. Eng. 2017, 130, 398–406. [Google Scholar] [CrossRef]
- Katz, J.; Plotkin, A. Low-Speed Aerodynamics; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2001; Volume 13. [Google Scholar]
- Bres, G.; Pérot, F.; Freed, D. A Ffowcs Williams-Hawkings solver for Lattice-Boltzmann based computational aeroacoustics. In Proceedings of the 16th AIAA/CEAS Aeroacoustics Conference, Stockholm, Sweden, 7–9 June 2010; p. 3711. [Google Scholar]
- MOERI. MOERI Container Ship (KCS). 2008. Available online: http://www.simman2008.dk/KCS/kcs_geometry.htm (accessed on 14 September 2015).
- Felli, M.; Camussi, R.; Di Felice, F. Mechanisms of evolution of the propeller wake in the transition and far fields. J. Fluid Mech. 2011, 682, 5. [Google Scholar] [CrossRef]
- Muscari, R.; Di Mascio, A.; Verzicco, R. Modeling of vortex dynamics in the wake of a marine propeller. Comput. Fluids 2013, 73, 65–79. [Google Scholar] [CrossRef]
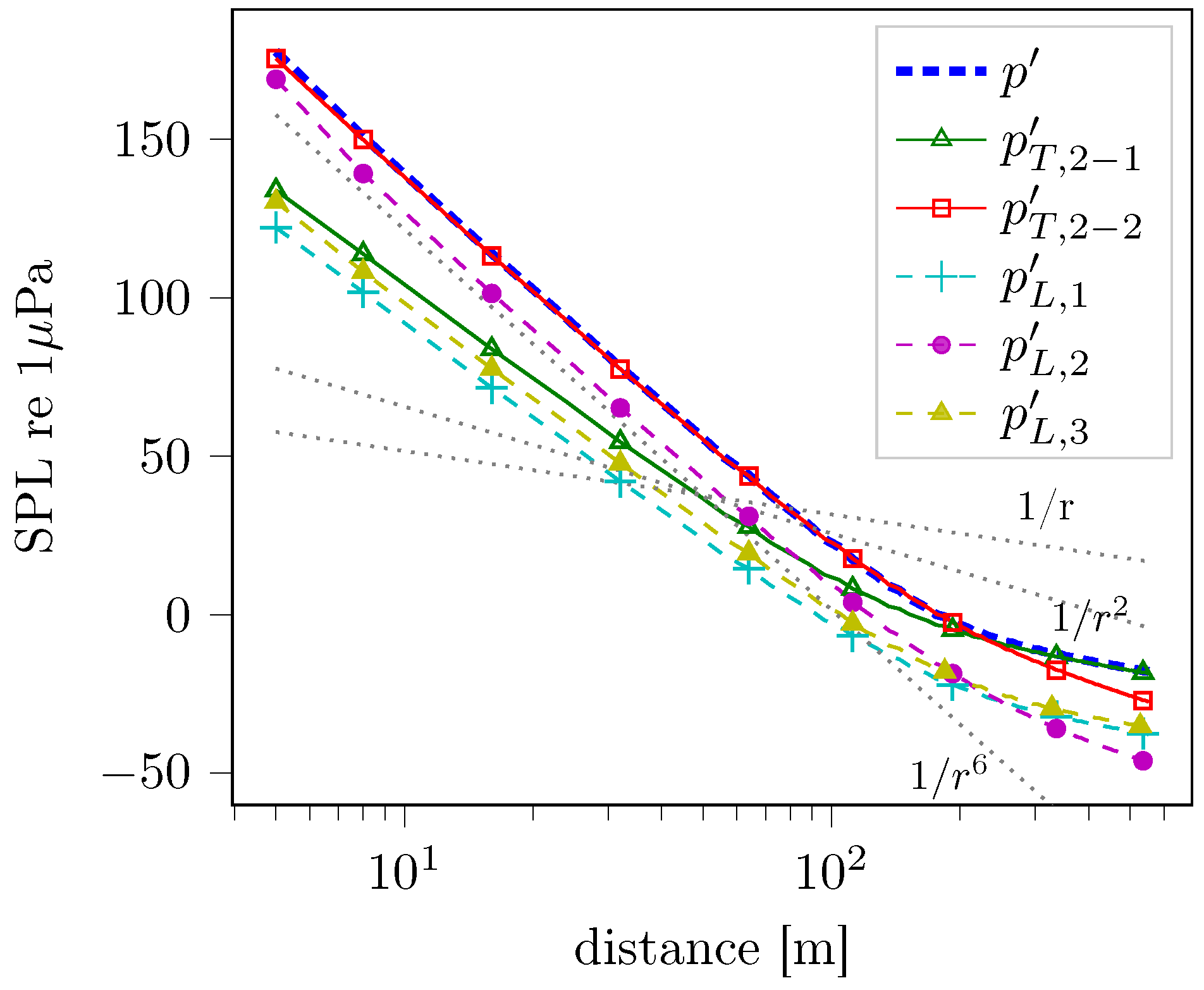
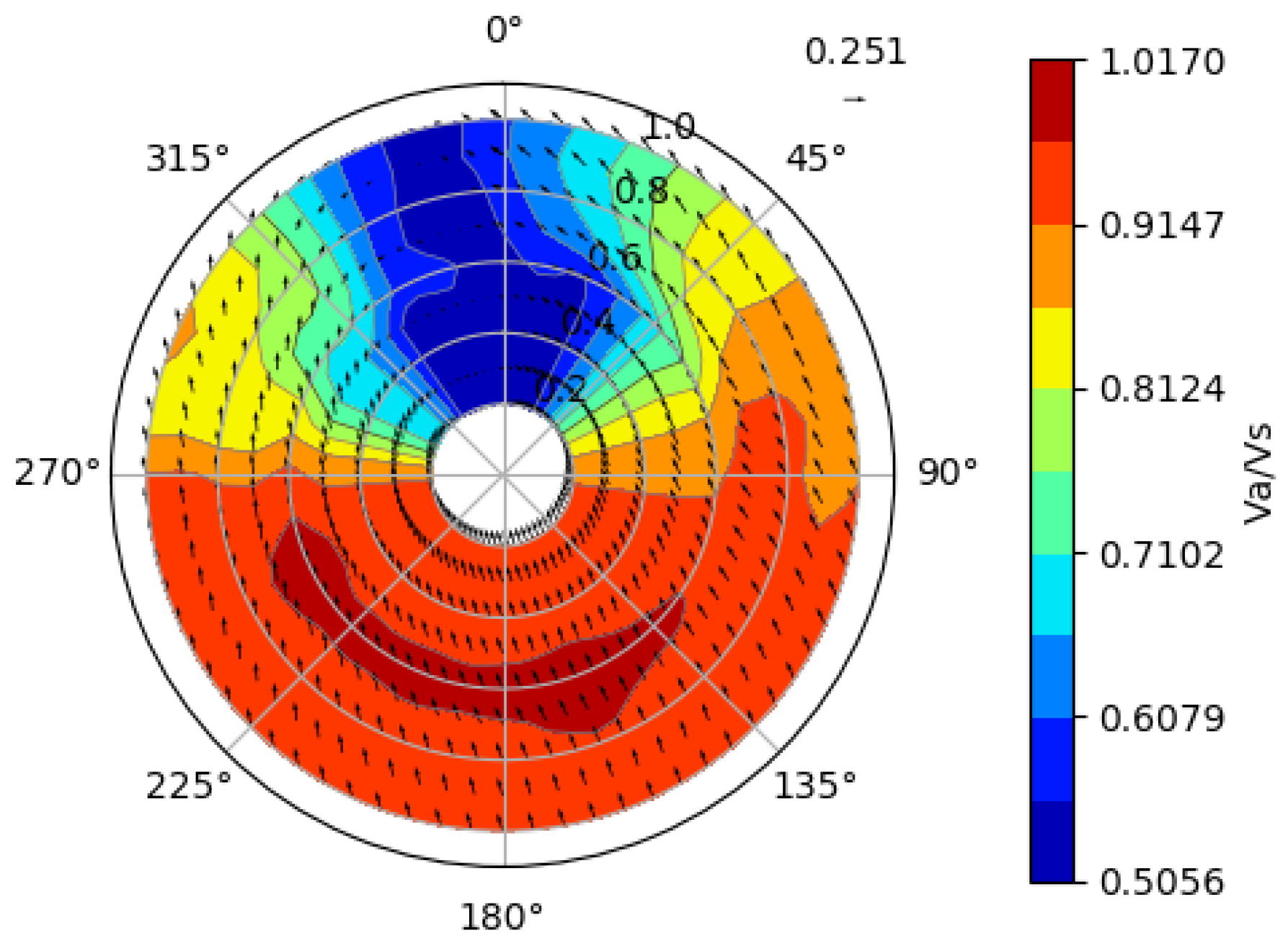
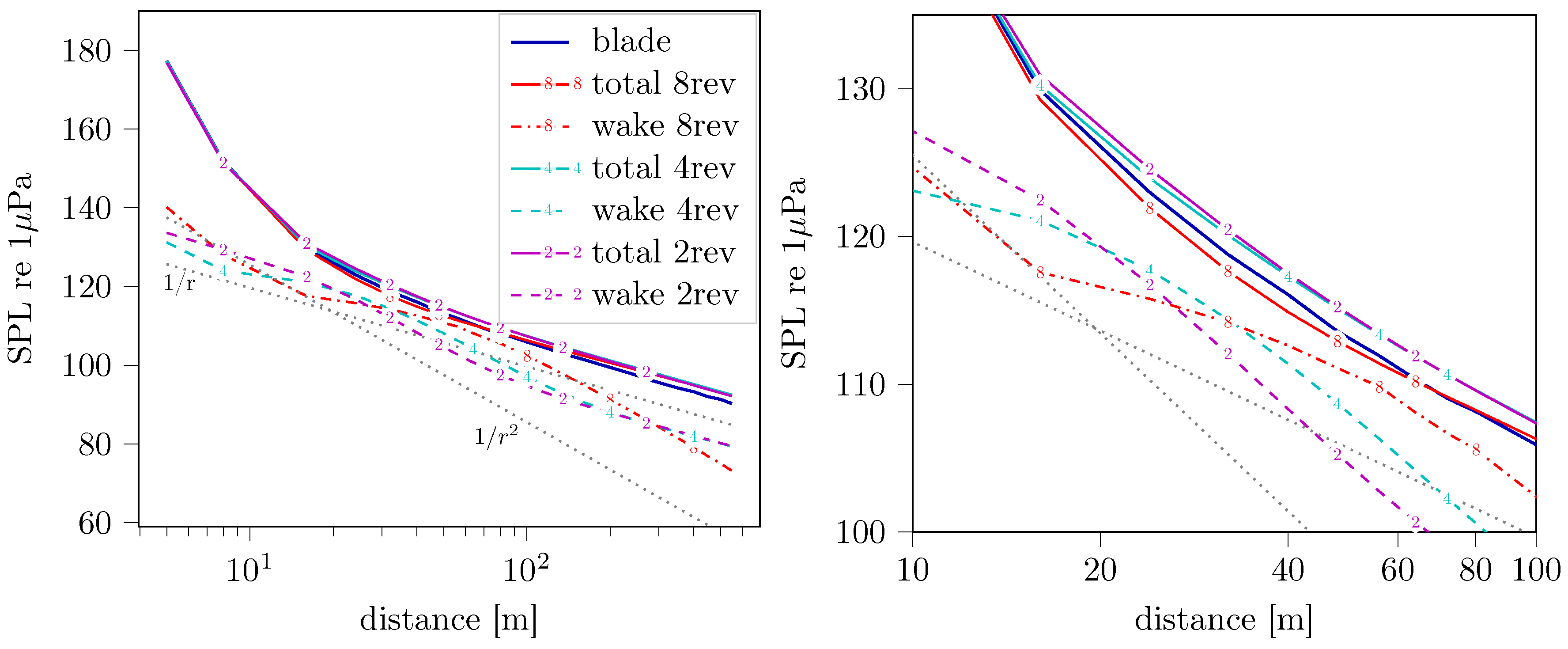
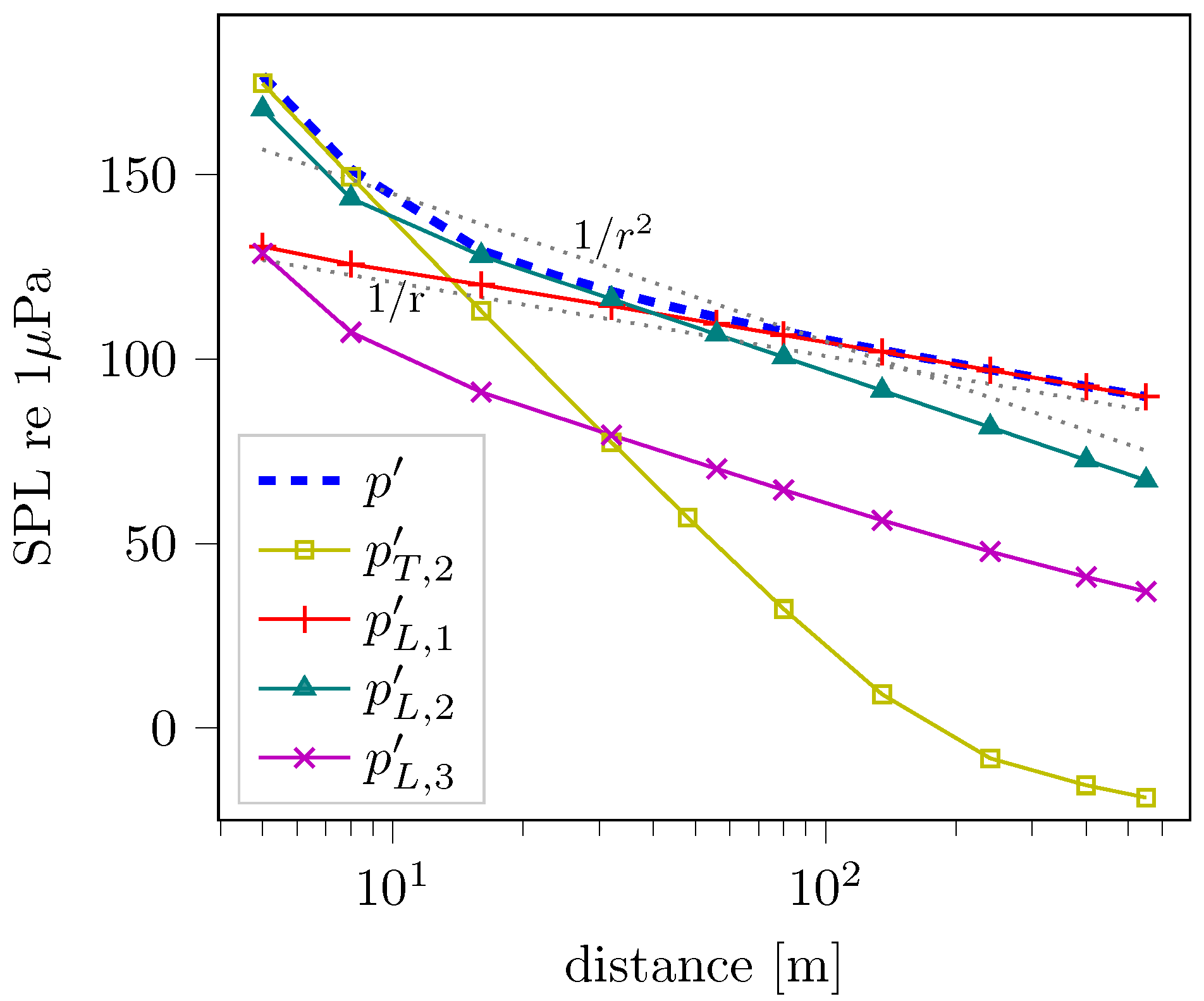
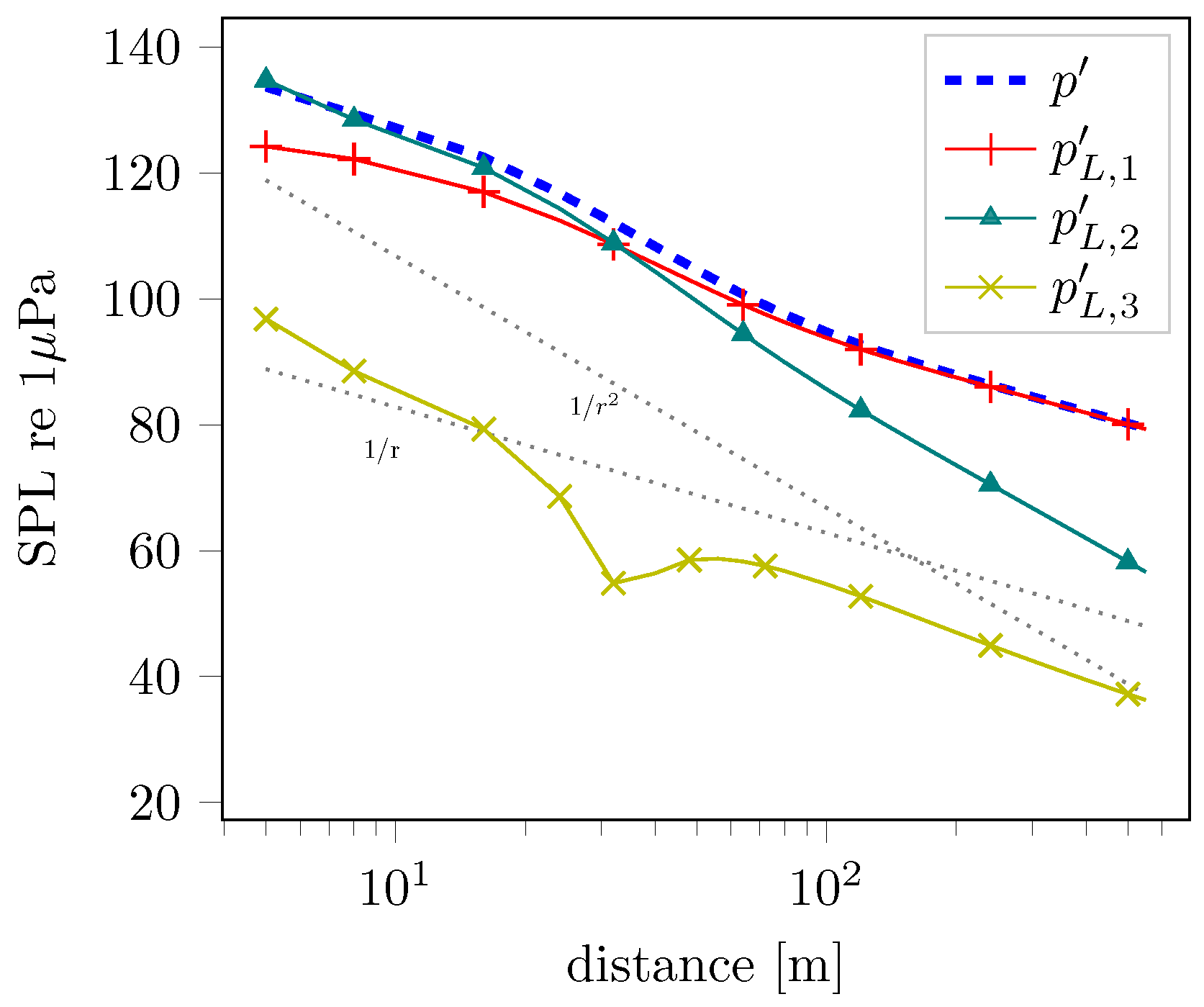
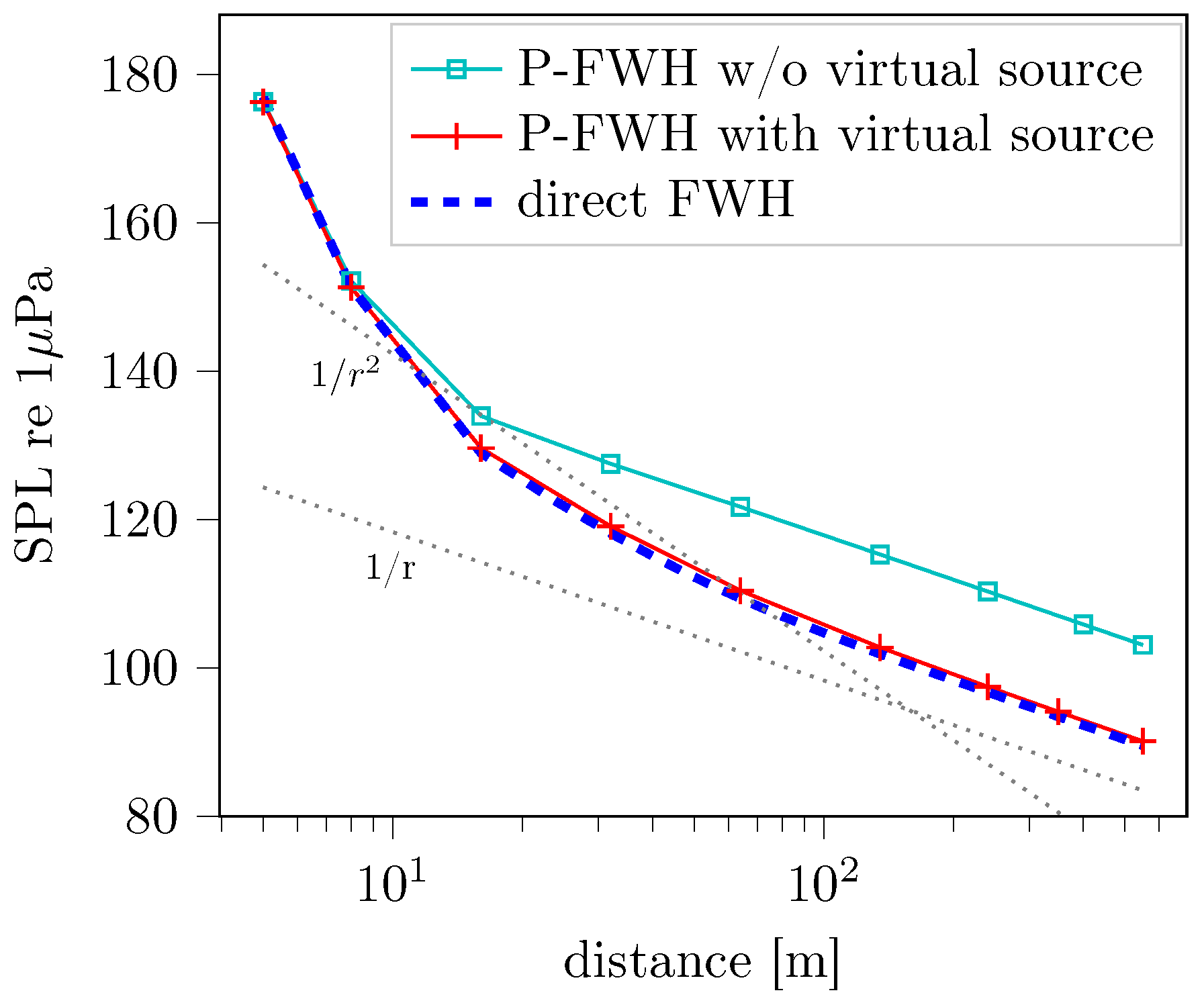
| 1 | to distinguish it from the P-FWH approach, the approach in which the FWH terms are integrated directly on the blade and wake sheet surfaces are denoted as the direct FWH approach in current work, although no direct volume integration is carried out. |



| Parameter | Symbol | Value |
|---|---|---|
| diameter | D | 7.9 m |
| number of blades | Z | 5 |
| designed advance ratio | 0.7 | |
| rotation rate | n | 1.25 s |
| angular speed | 7.85 s | |
| BPF (Blade Pass Frequency) | 6.25 Hz | |
| acoustic wave length for BPF | 240 m |
| Parameters | Basic | Long | Large |
|---|---|---|---|
| front length | 1.5 m | 50 m | 13 m |
| rear length | 21.5 m | 21.5 m | 33 m |
| radius | 0.6D | 0.6D | 2D |
| panel size | 0.5 m | 0.5 m | 2 m |
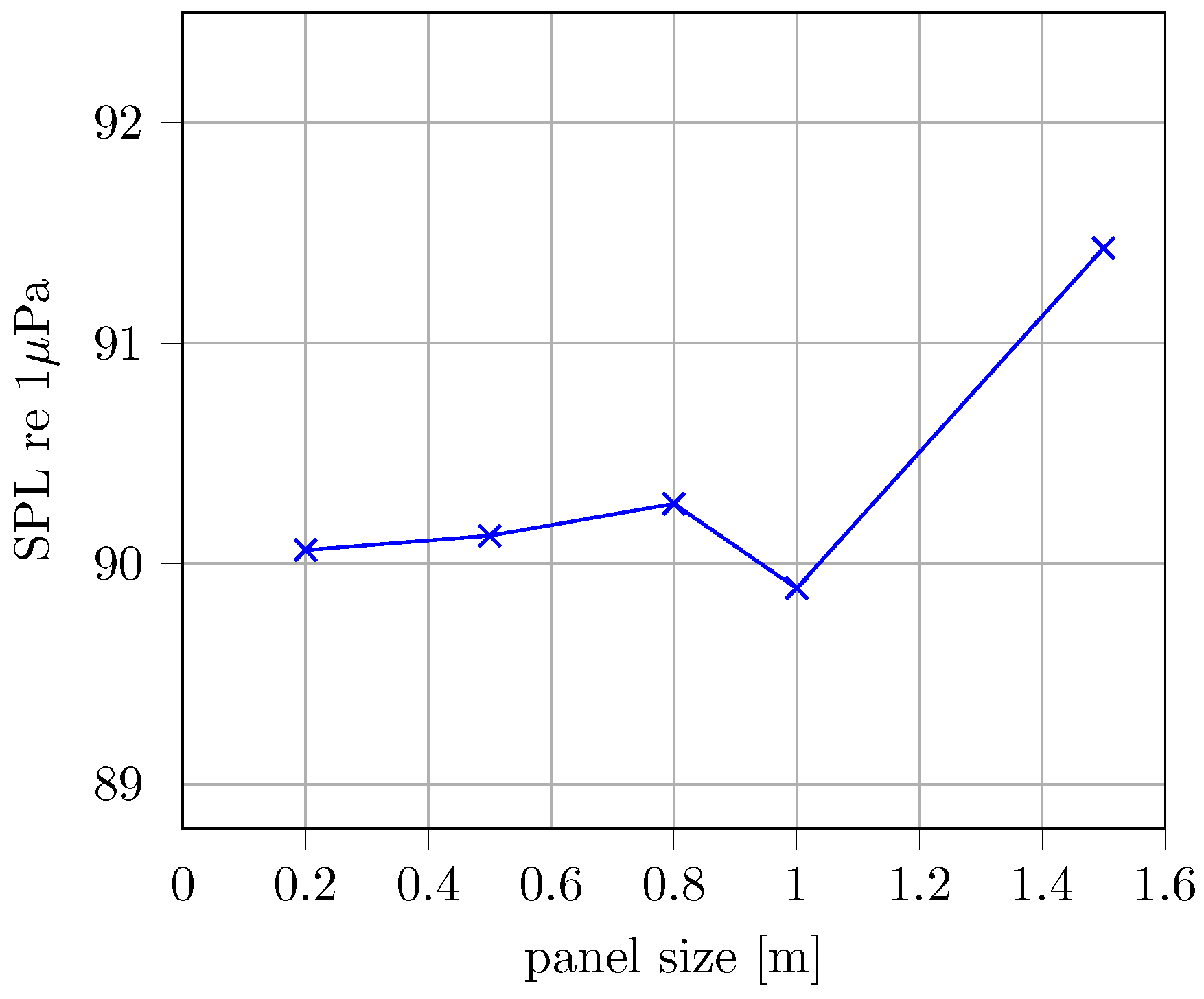
| 1st BPF | 3rd BPF | |||
|---|---|---|---|---|
| Panel Size | 100 m | 550 m | 100 m | 550 m |
| 0.2 m | 105.62 | 90.06 | 102.33 | 87.00 |
| 0.5 m | 105.70 | 90.13 | 102.33 | 87.01 |
| 0.8 m | 105.86 | 90.27 | 102.36 | 87.04 |
| 1.0 m | 105.41 | 89.89 | 102.40 | 87.08 |
| 1.5 m | 108.15 | 91.43 | 105.33 | 89.34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Göttsche, U.; Abdel-Maksoud, M. Sound Field Properties of Non-Cavitating Marine Propellers. J. Mar. Sci. Eng. 2020, 8, 885. https://doi.org/10.3390/jmse8110885
Wang Y, Göttsche U, Abdel-Maksoud M. Sound Field Properties of Non-Cavitating Marine Propellers. Journal of Marine Science and Engineering. 2020; 8(11):885. https://doi.org/10.3390/jmse8110885
Chicago/Turabian StyleWang, Youjiang, Ulf Göttsche, and Moustafa Abdel-Maksoud. 2020. "Sound Field Properties of Non-Cavitating Marine Propellers" Journal of Marine Science and Engineering 8, no. 11: 885. https://doi.org/10.3390/jmse8110885
APA StyleWang, Y., Göttsche, U., & Abdel-Maksoud, M. (2020). Sound Field Properties of Non-Cavitating Marine Propellers. Journal of Marine Science and Engineering, 8(11), 885. https://doi.org/10.3390/jmse8110885






