Theoretical Evaluation of the Hydrodynamic Characteristics of Arrays of Vertical Axisymmetric Floaters of Arbitrary Shape in front of a Vertical Breakwater
Abstract
1. Introduction
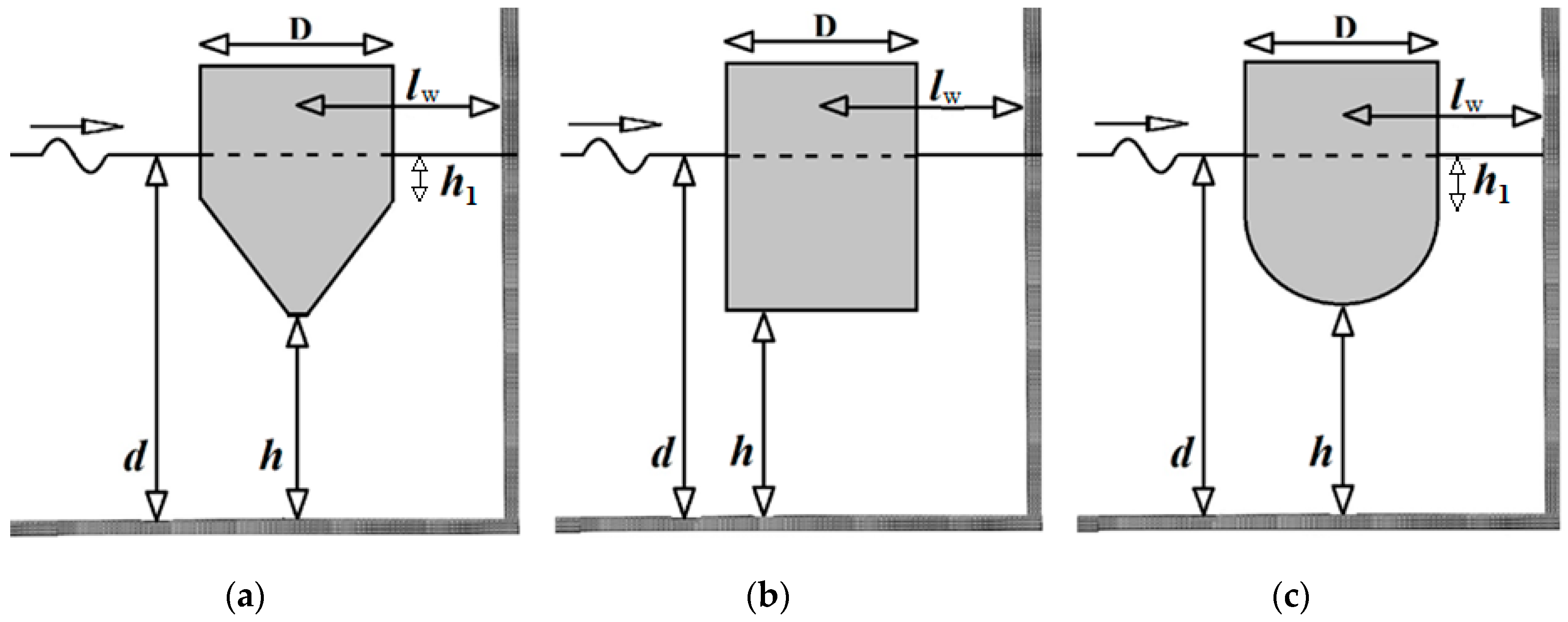
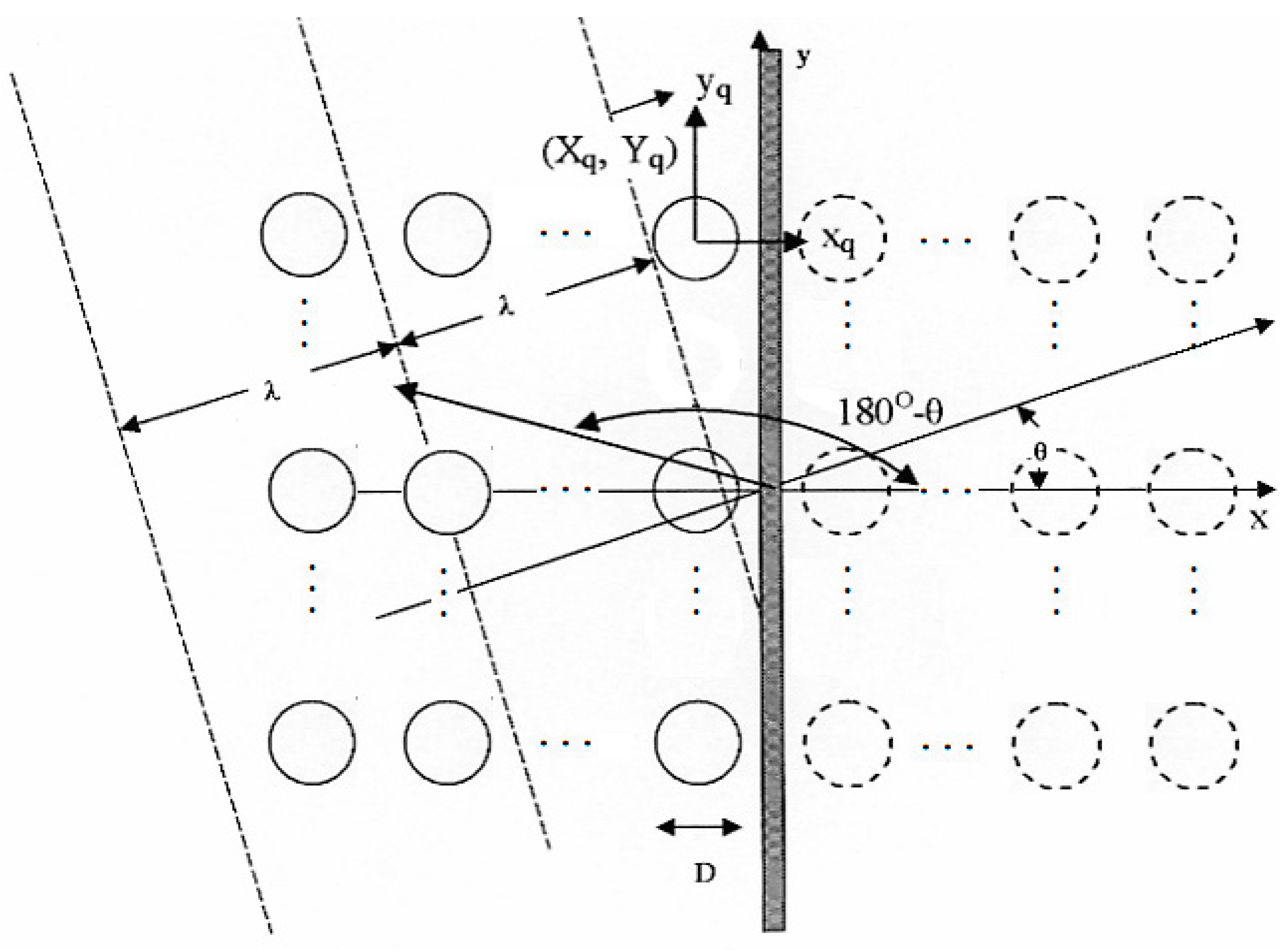
2. Hydrodynamic Formulation
3. Hydrodynamic Reaction Forces
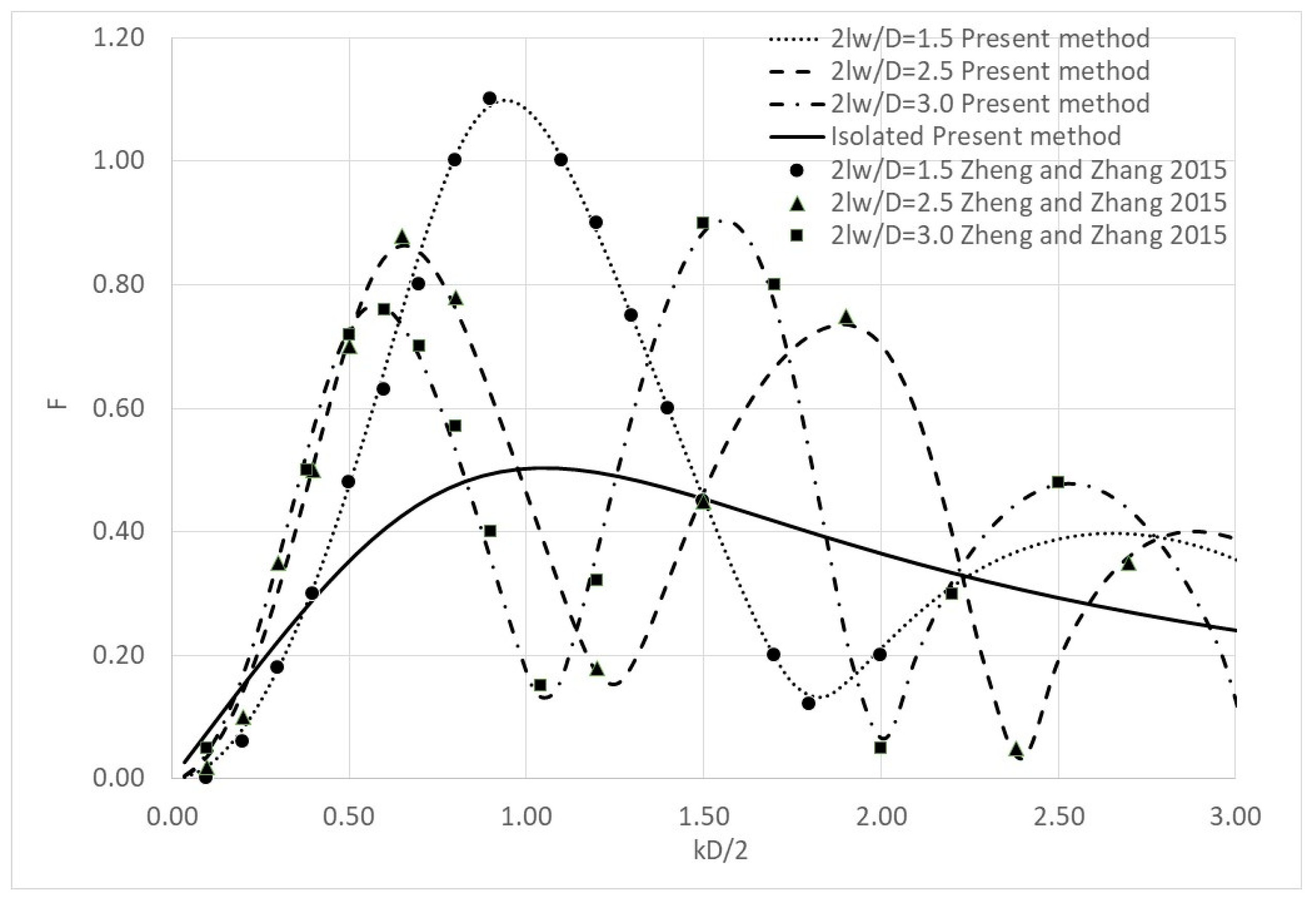
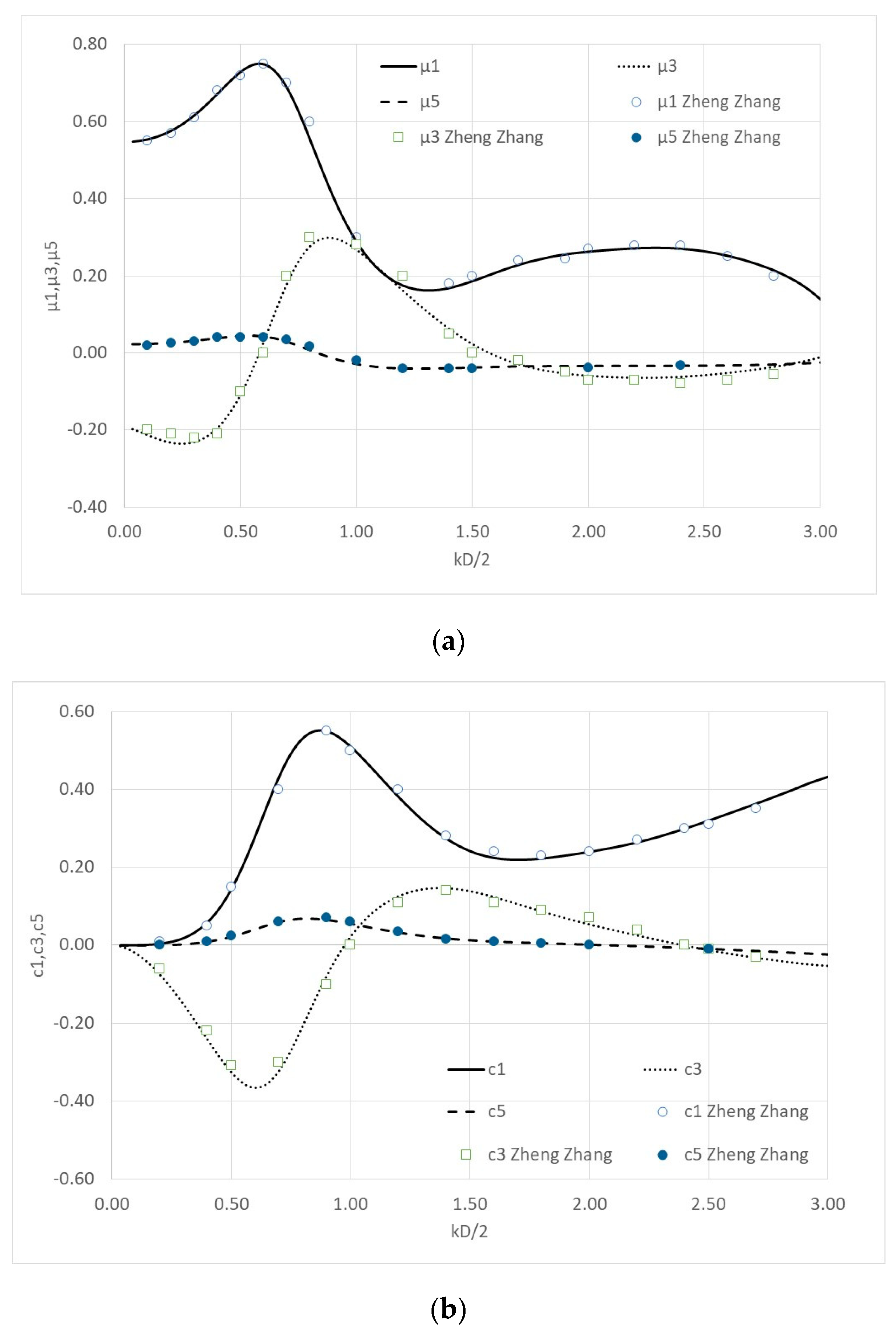
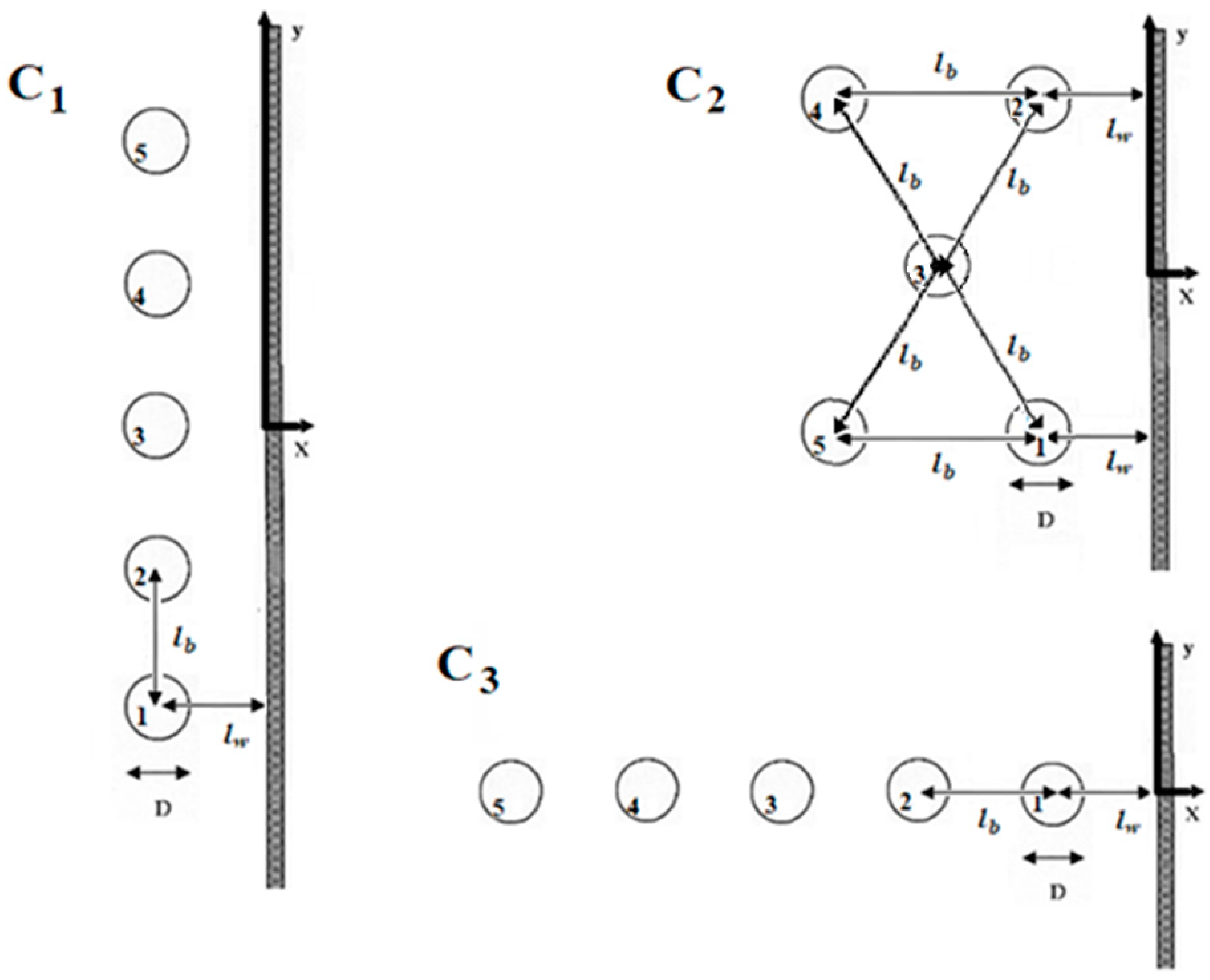
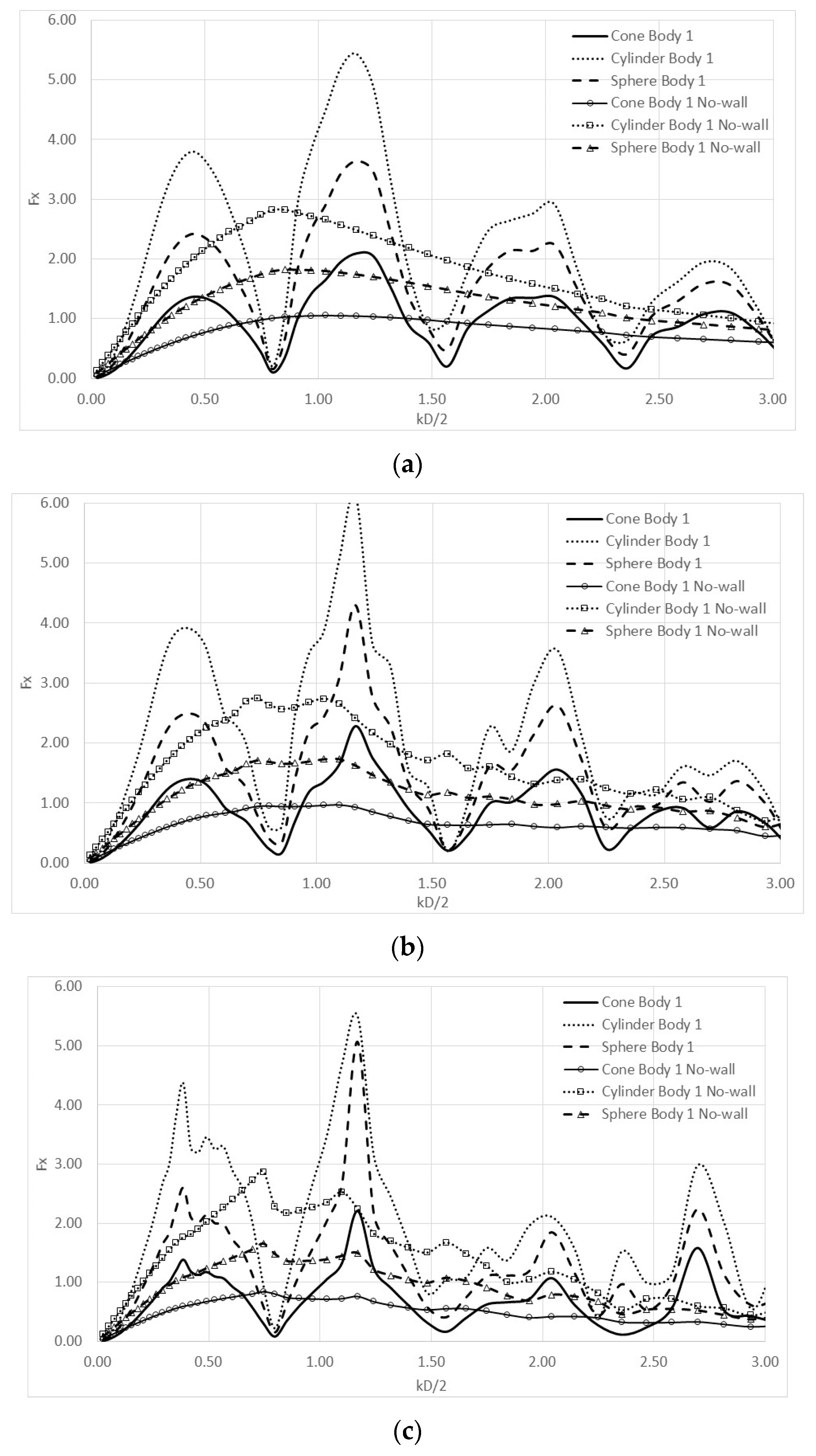
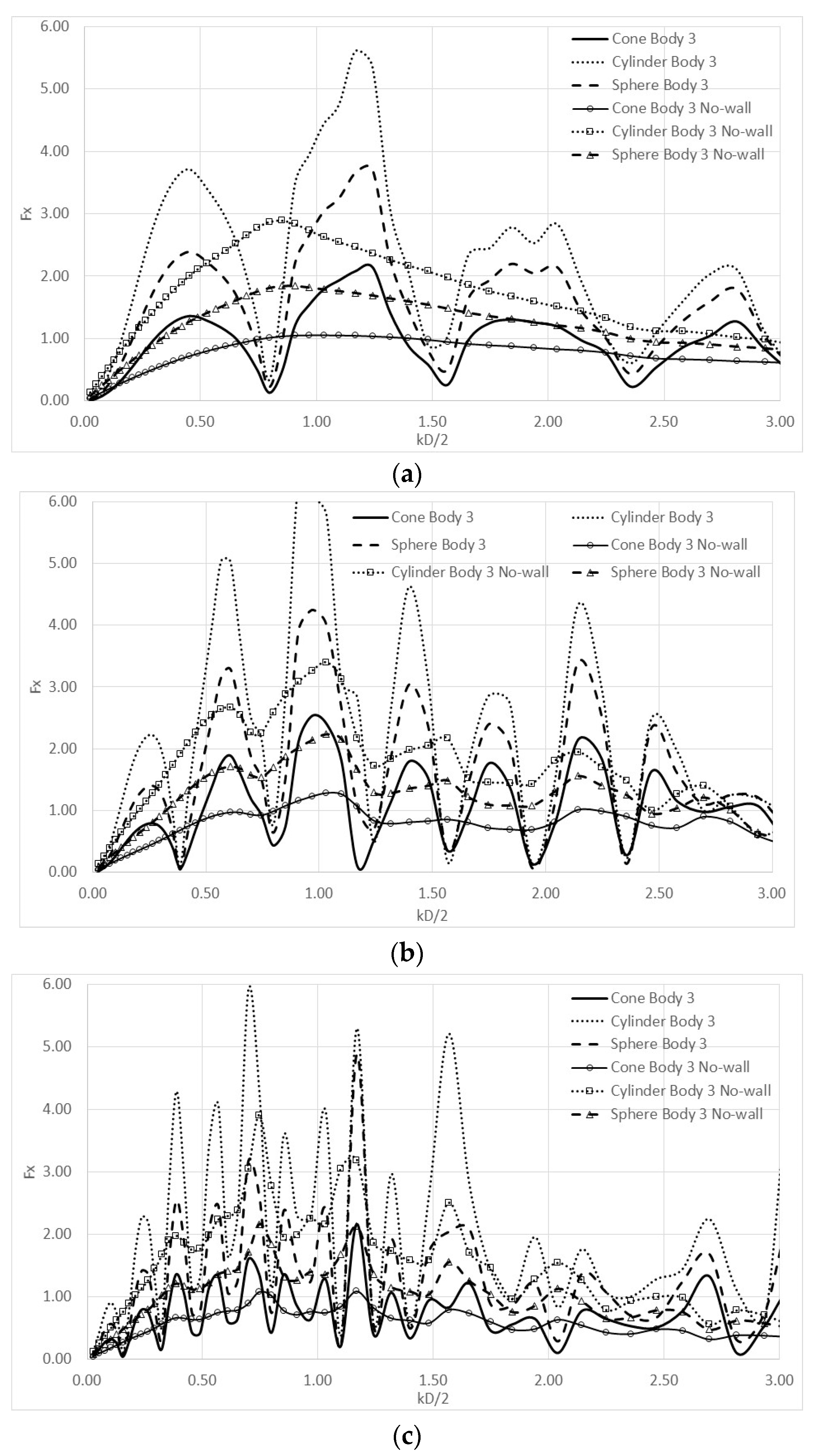
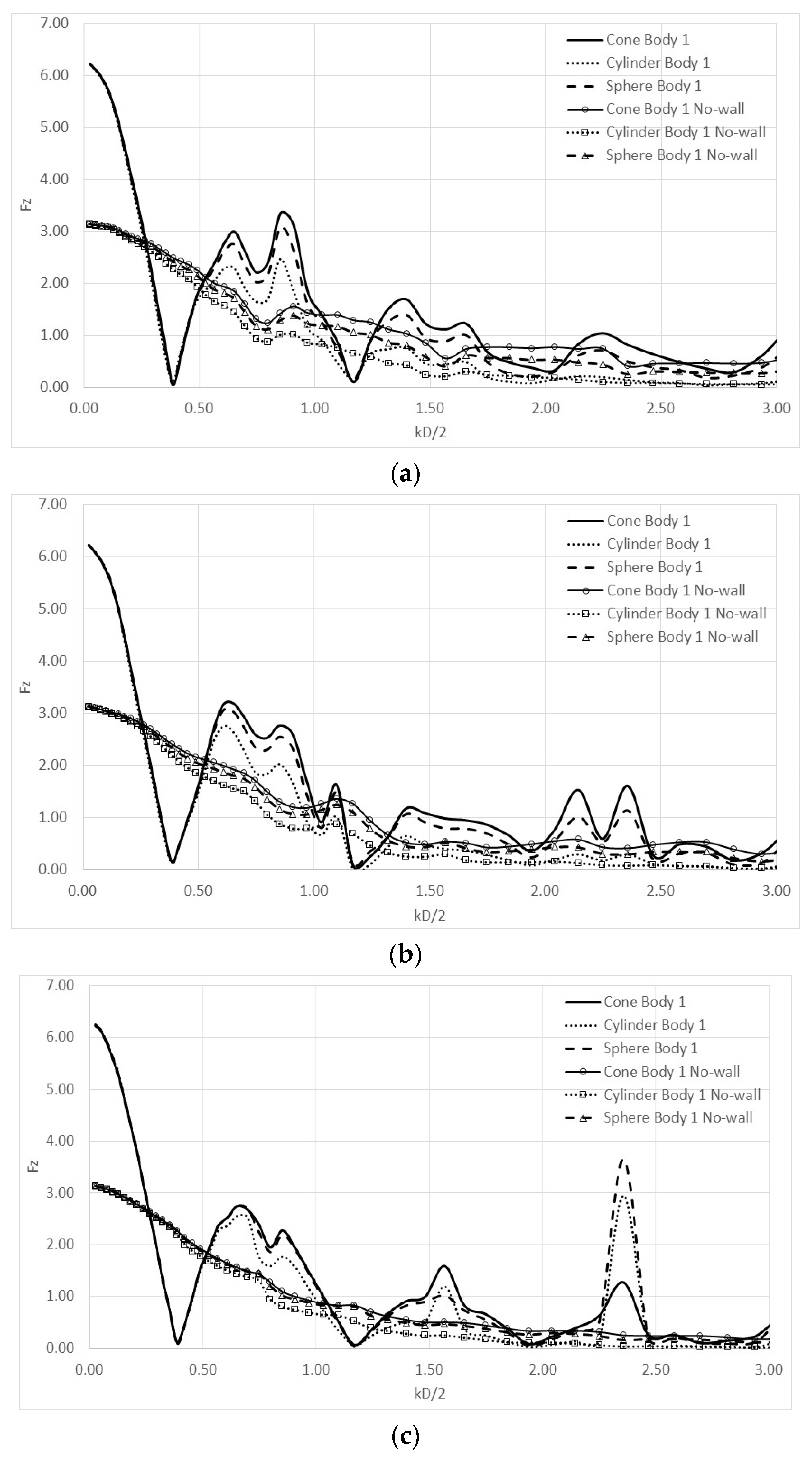
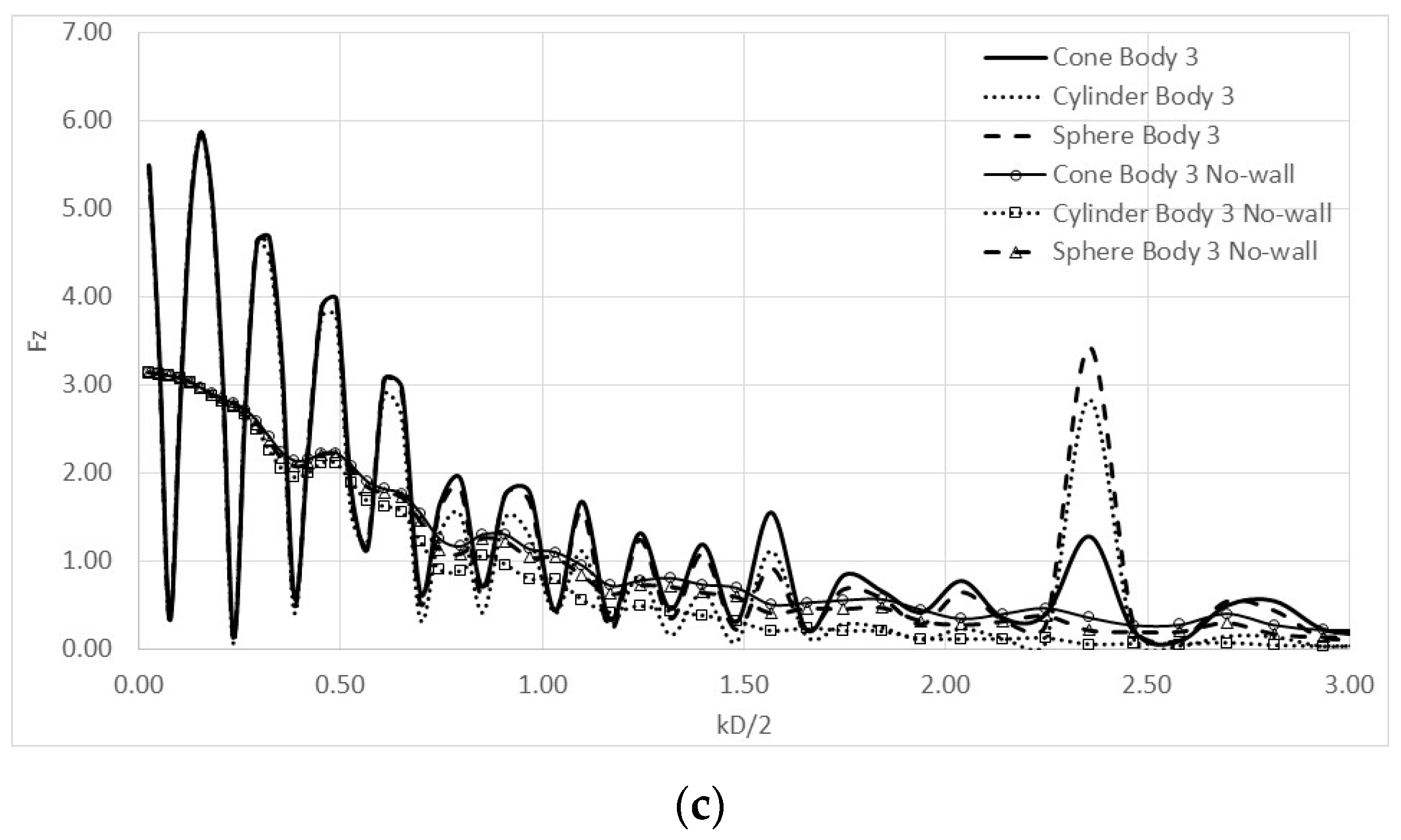
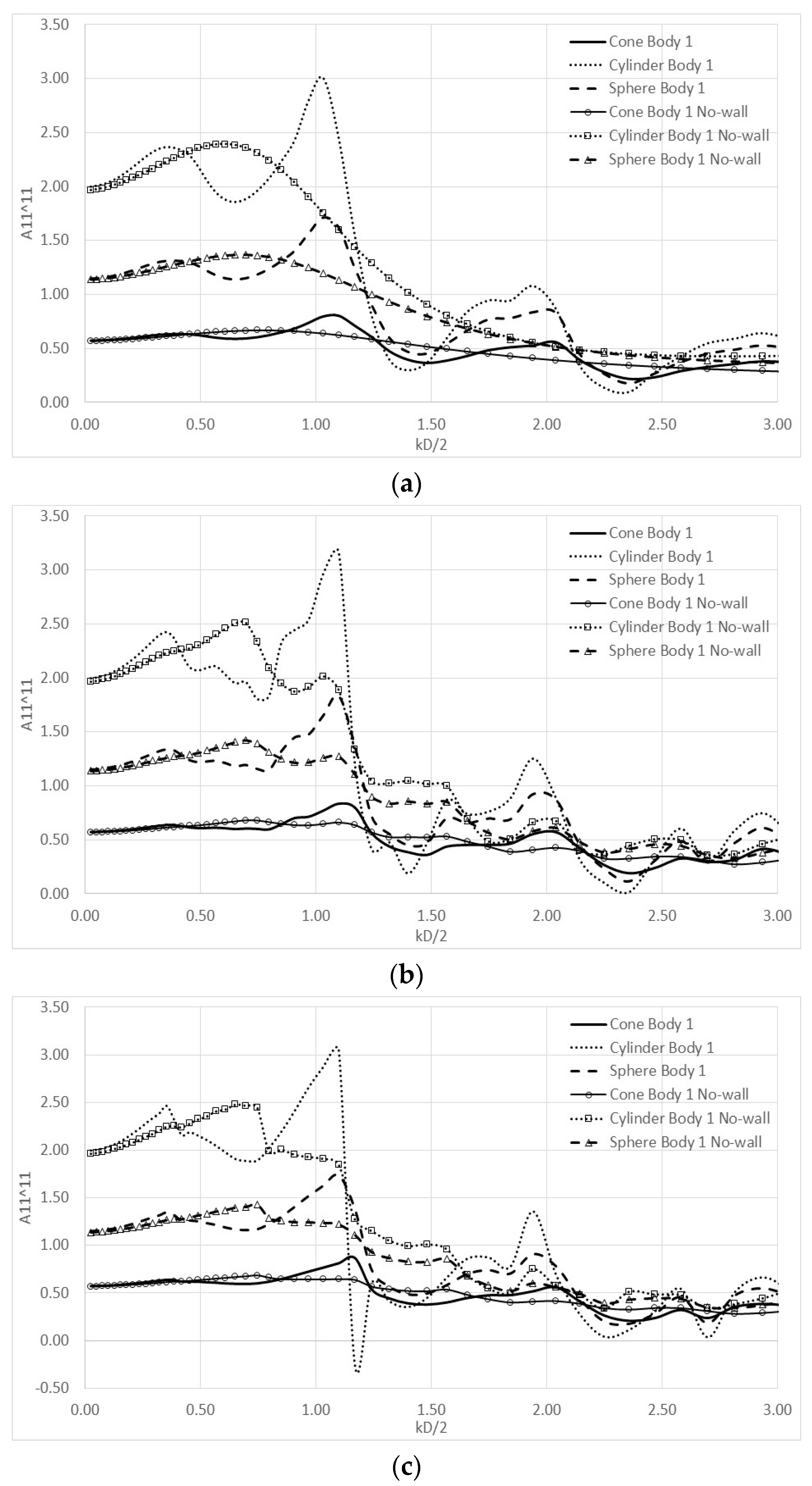
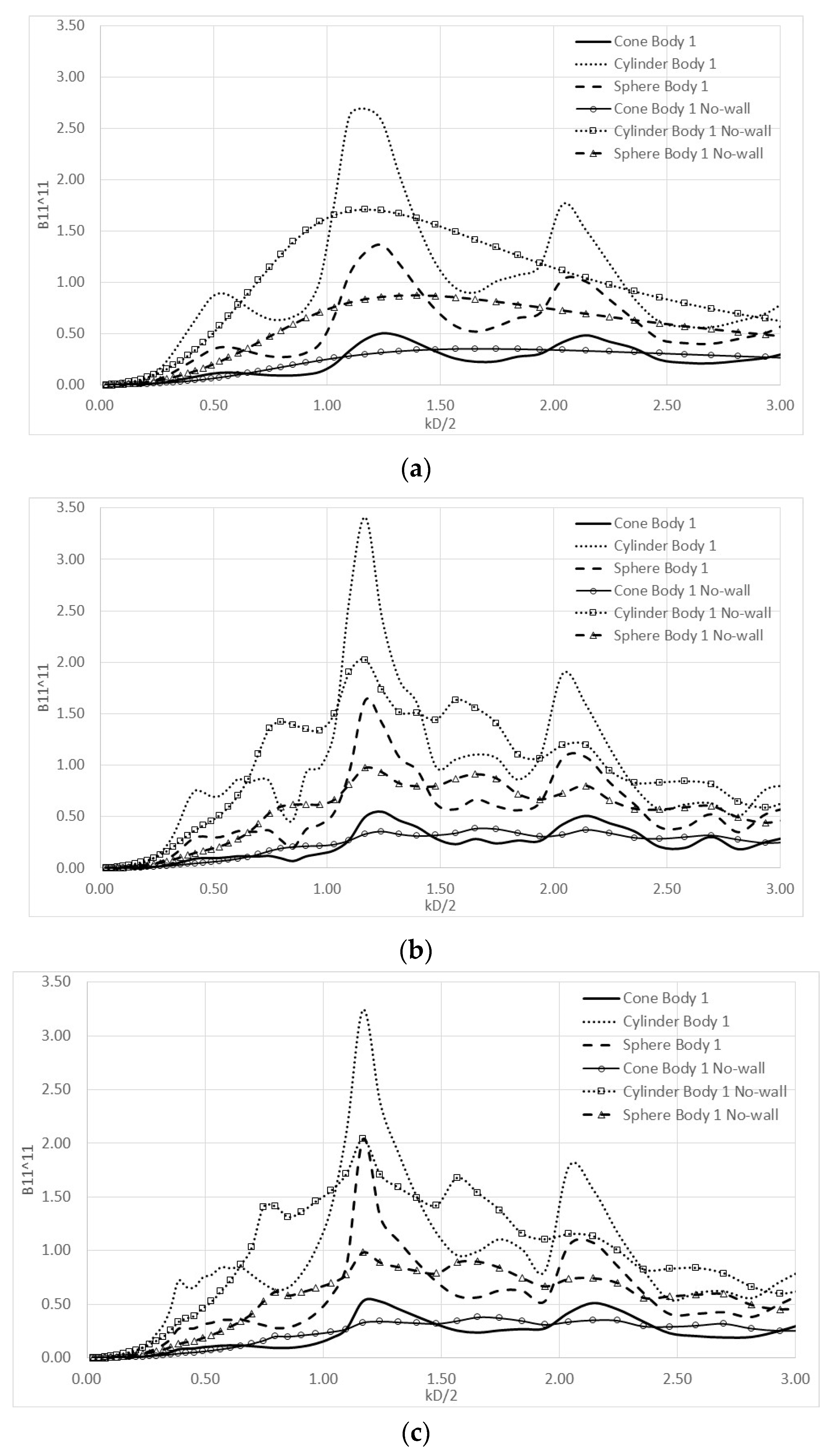
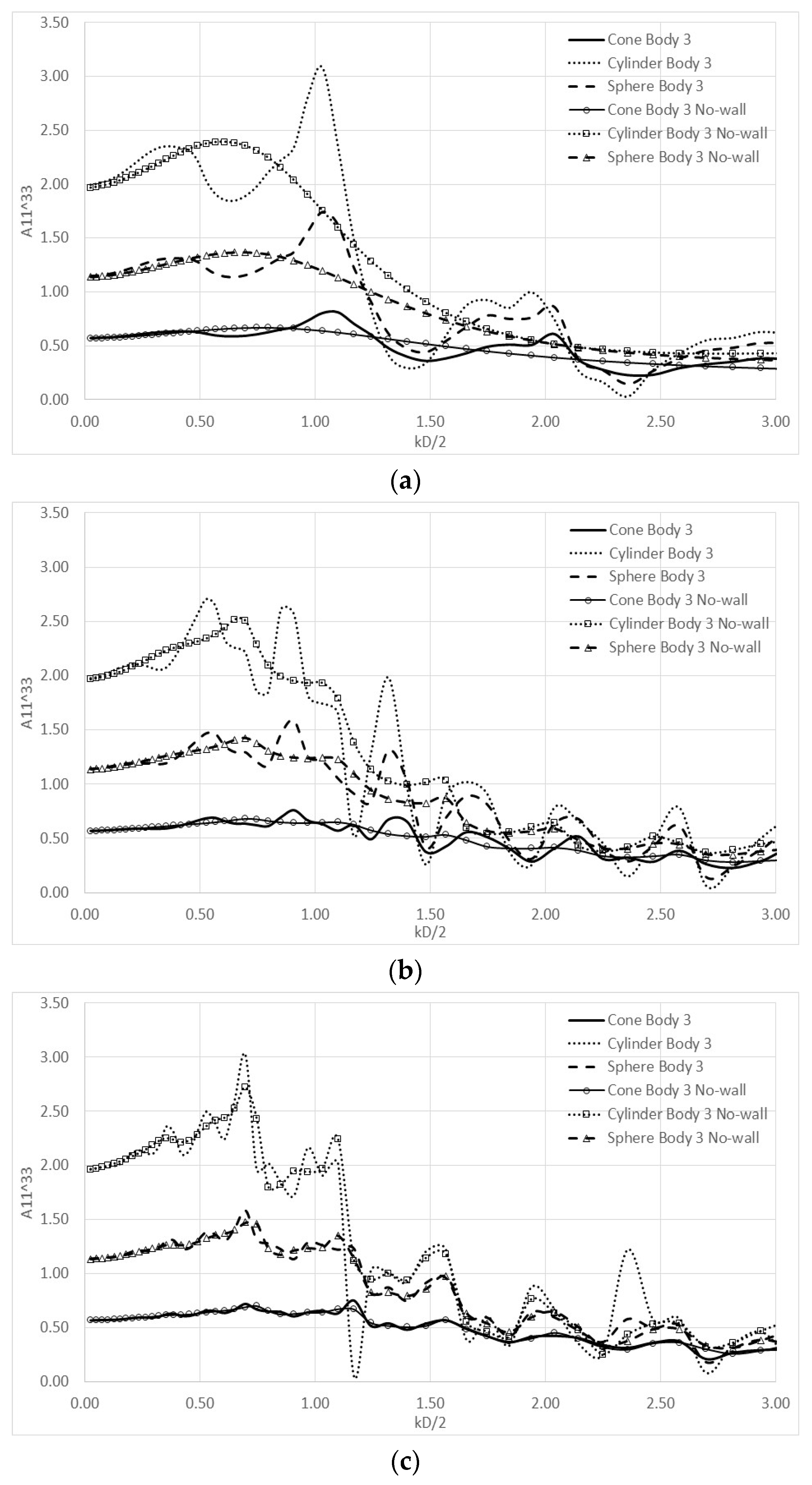
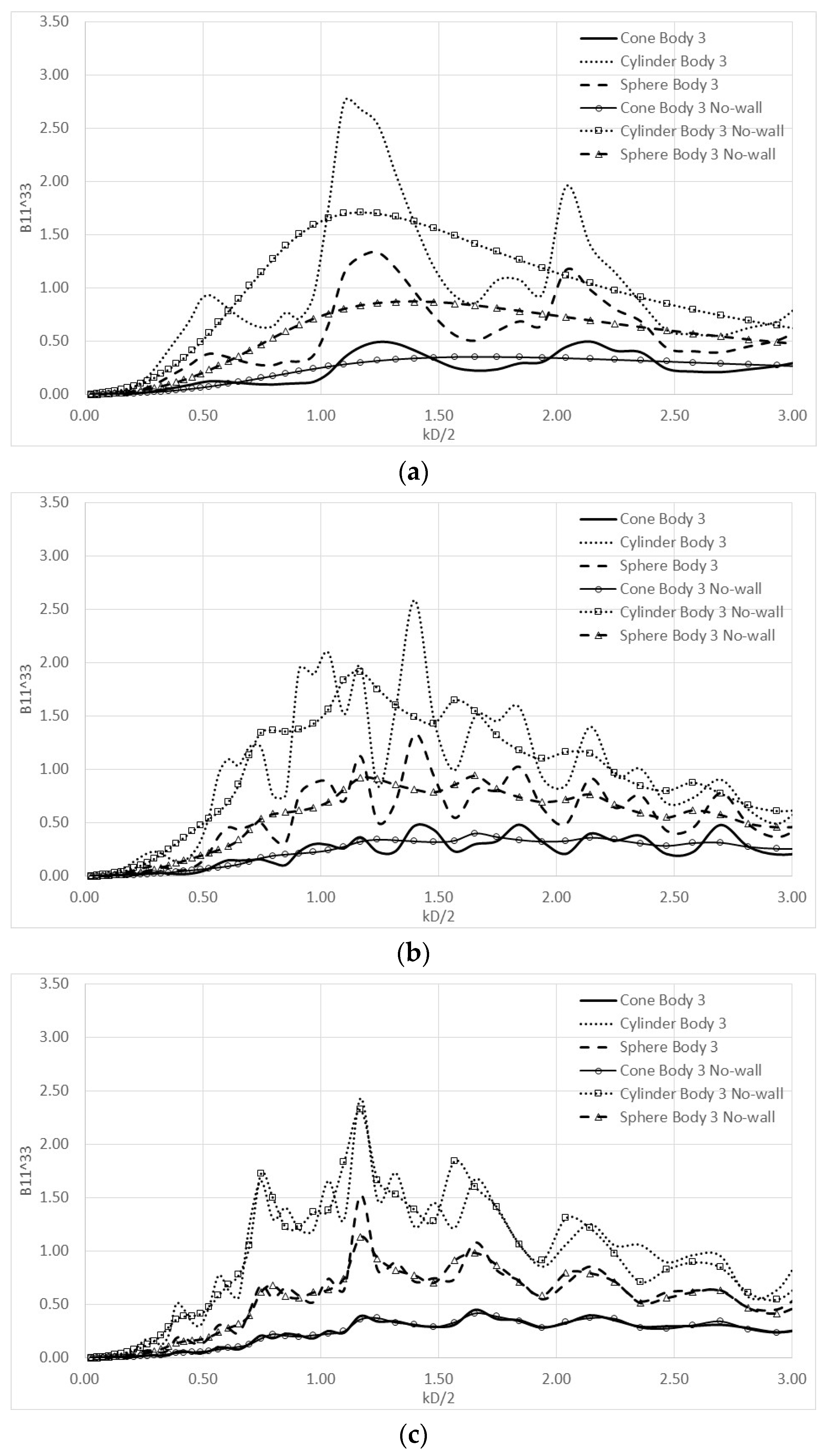
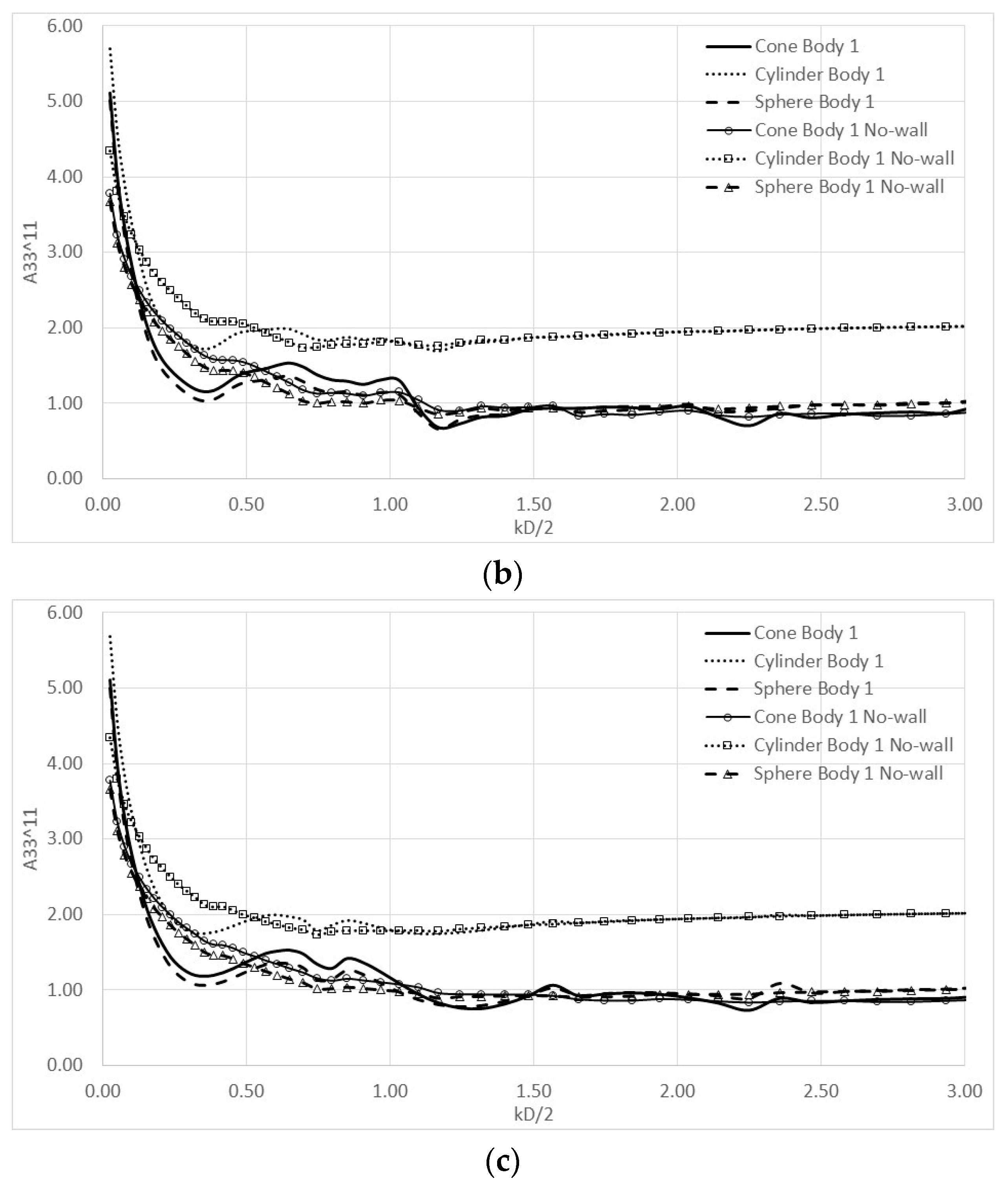
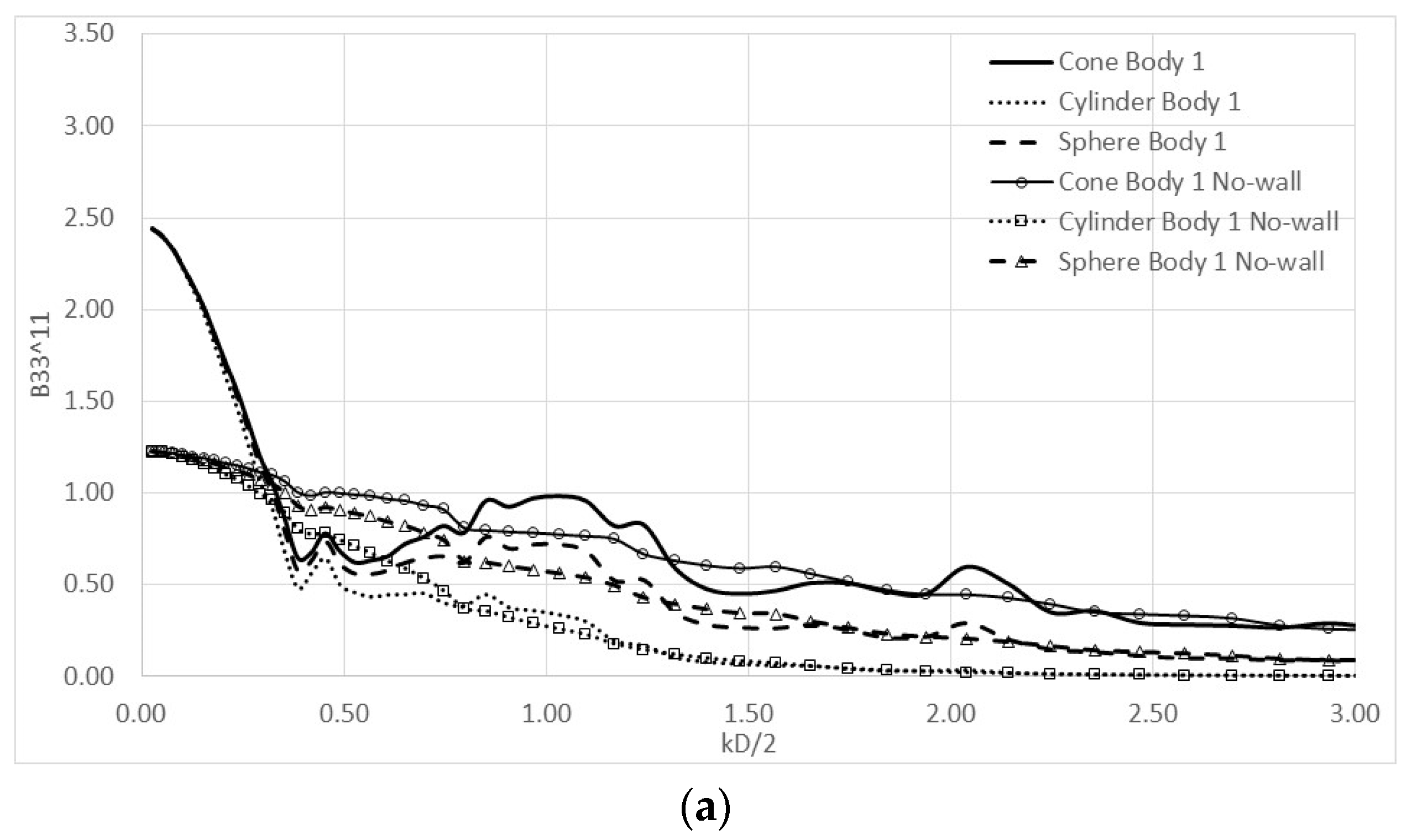
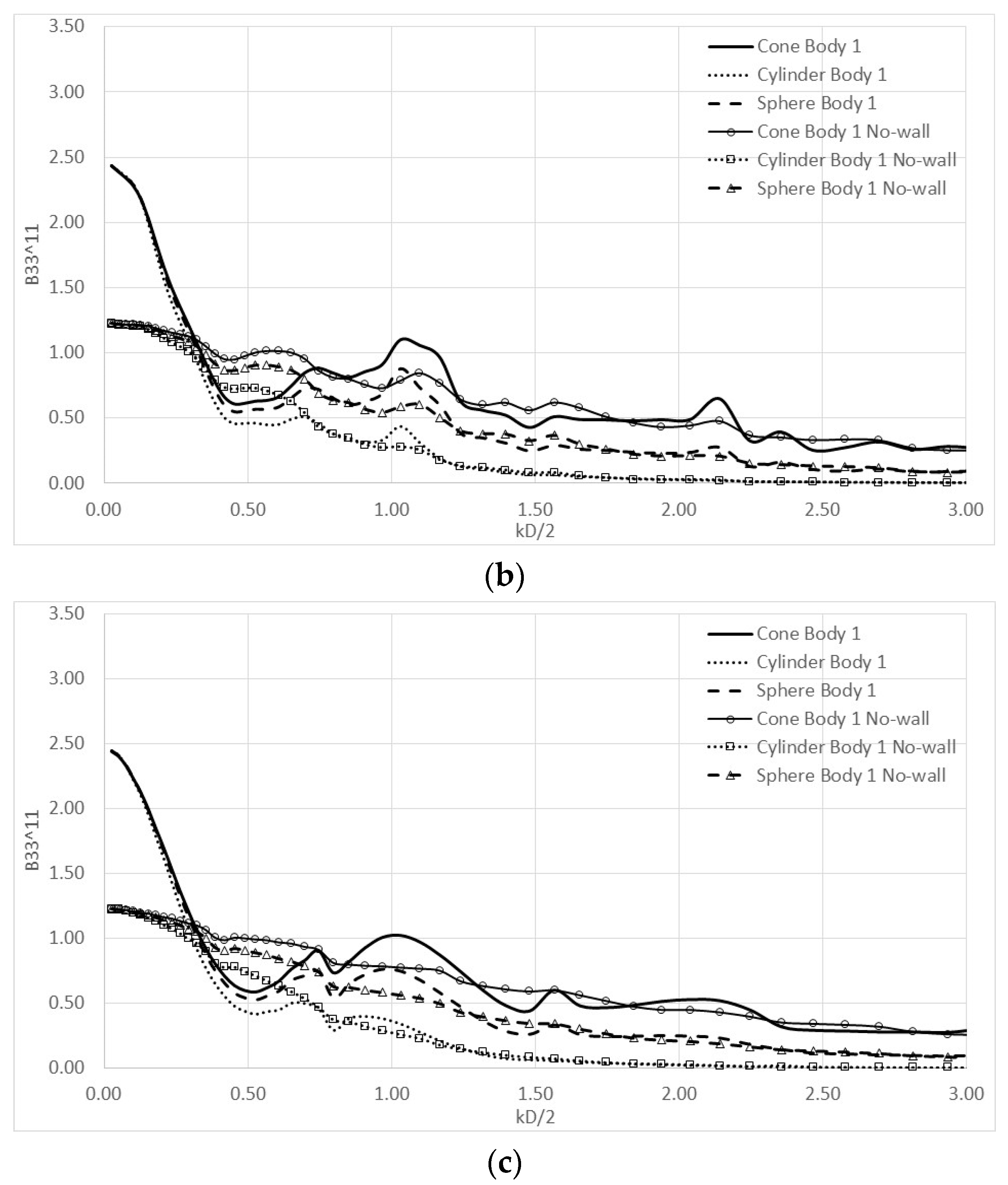
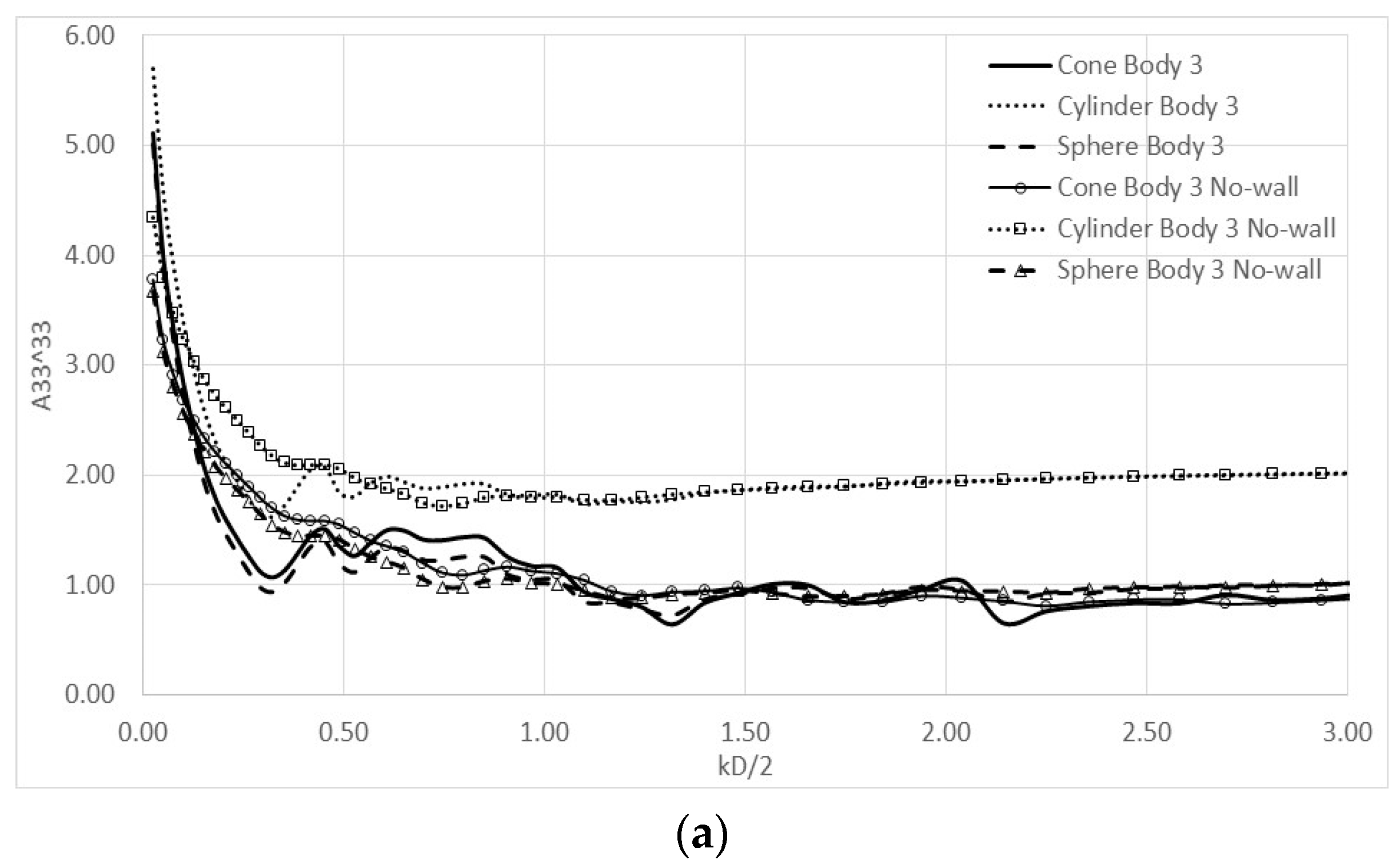
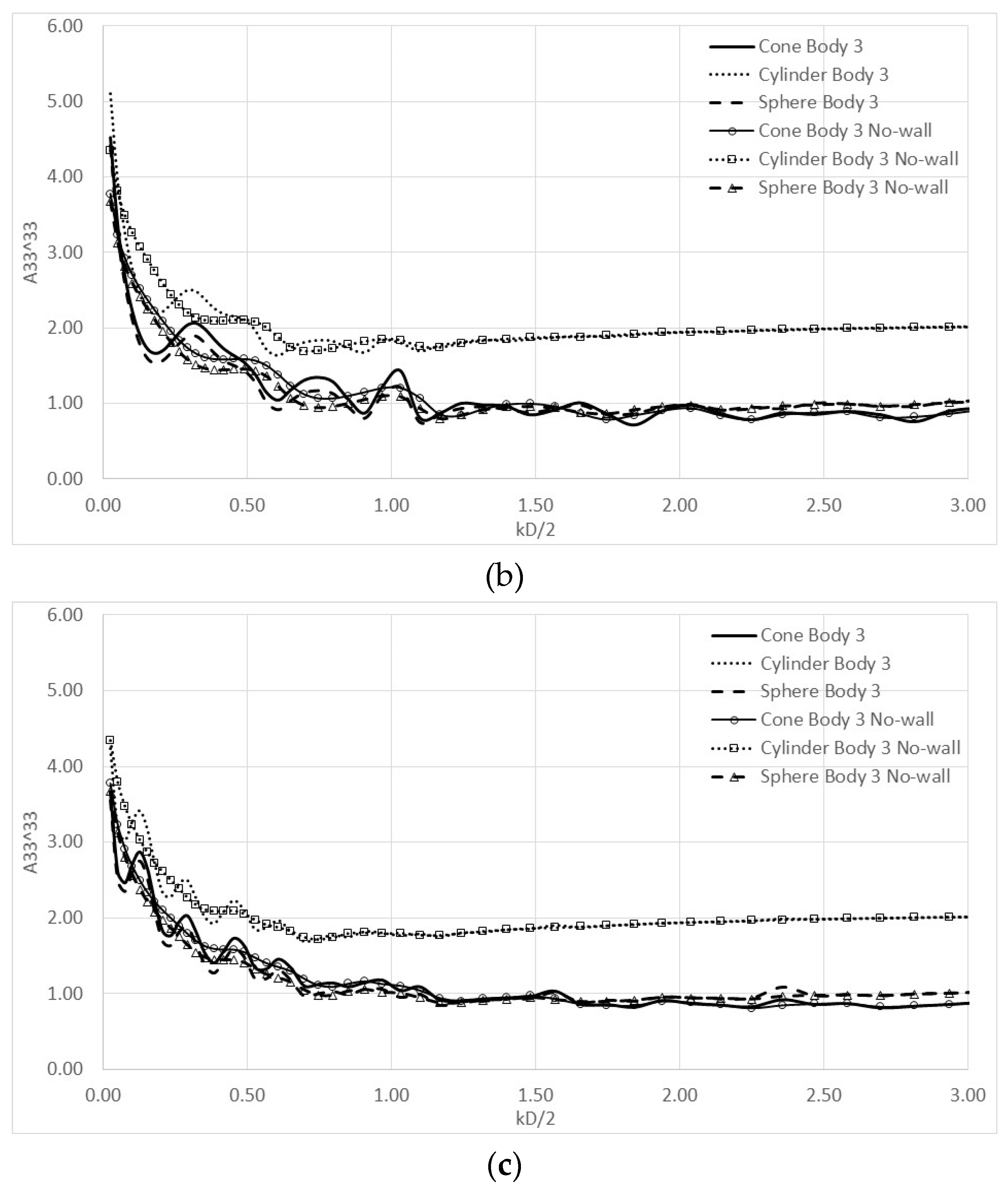
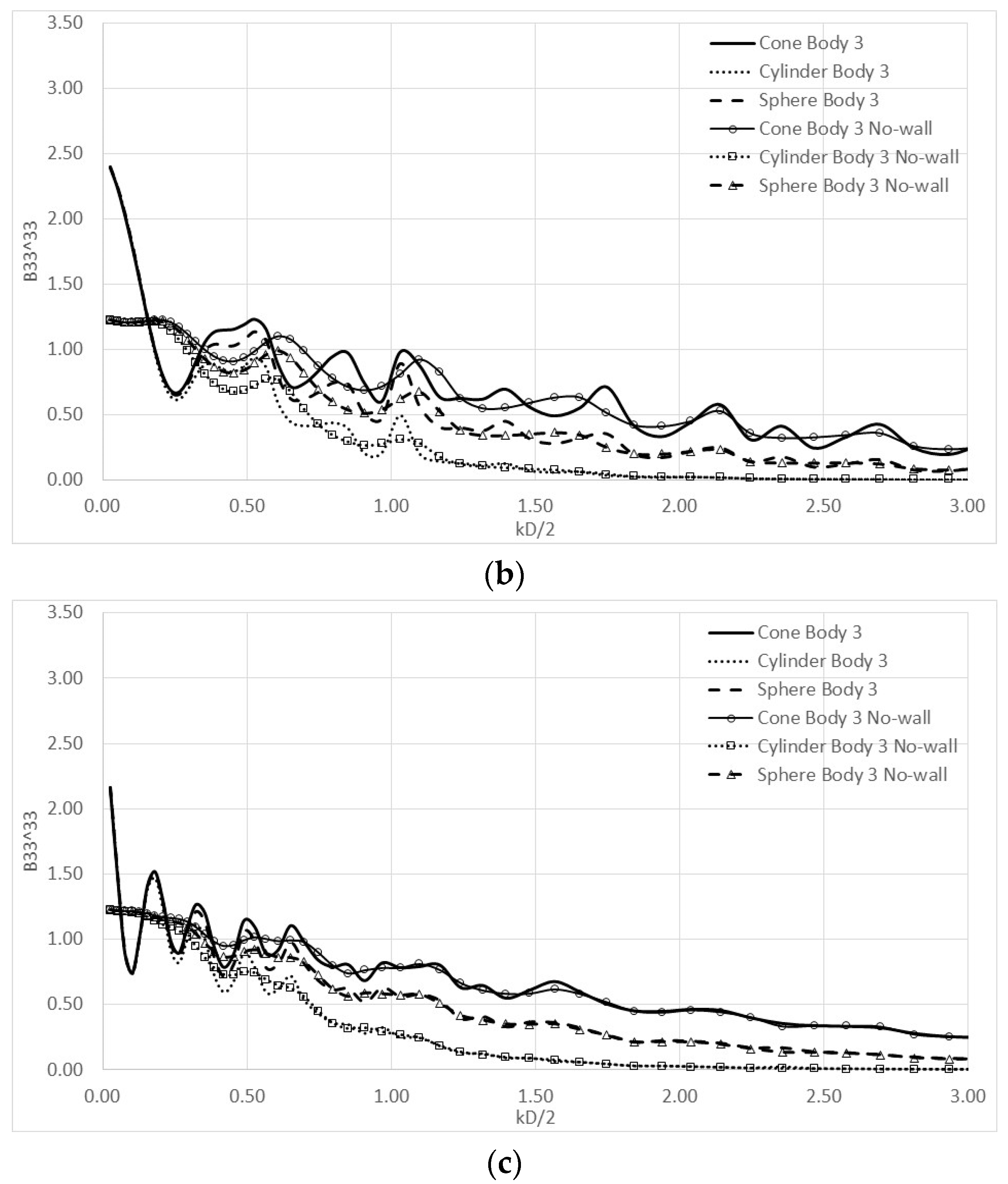
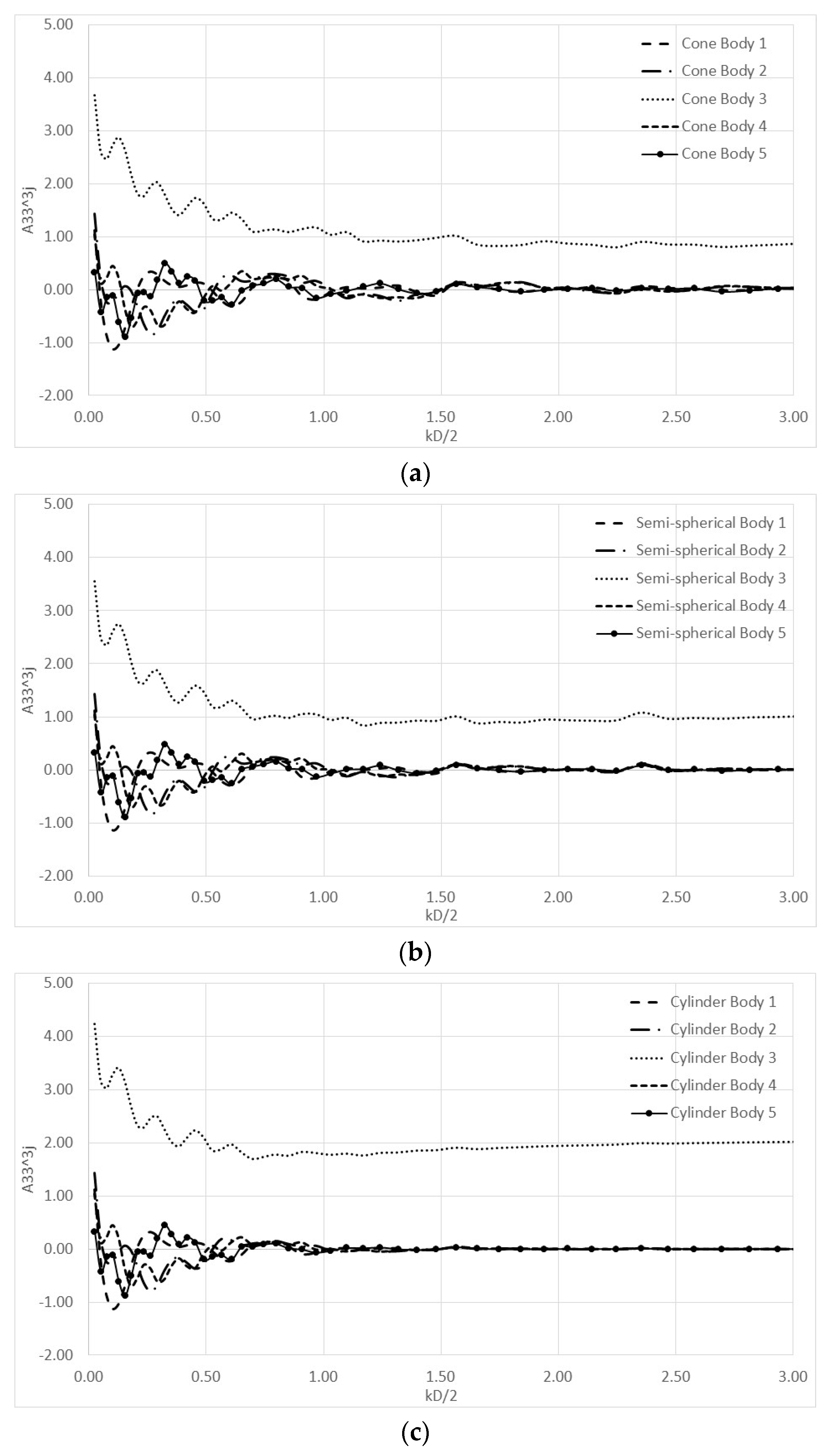
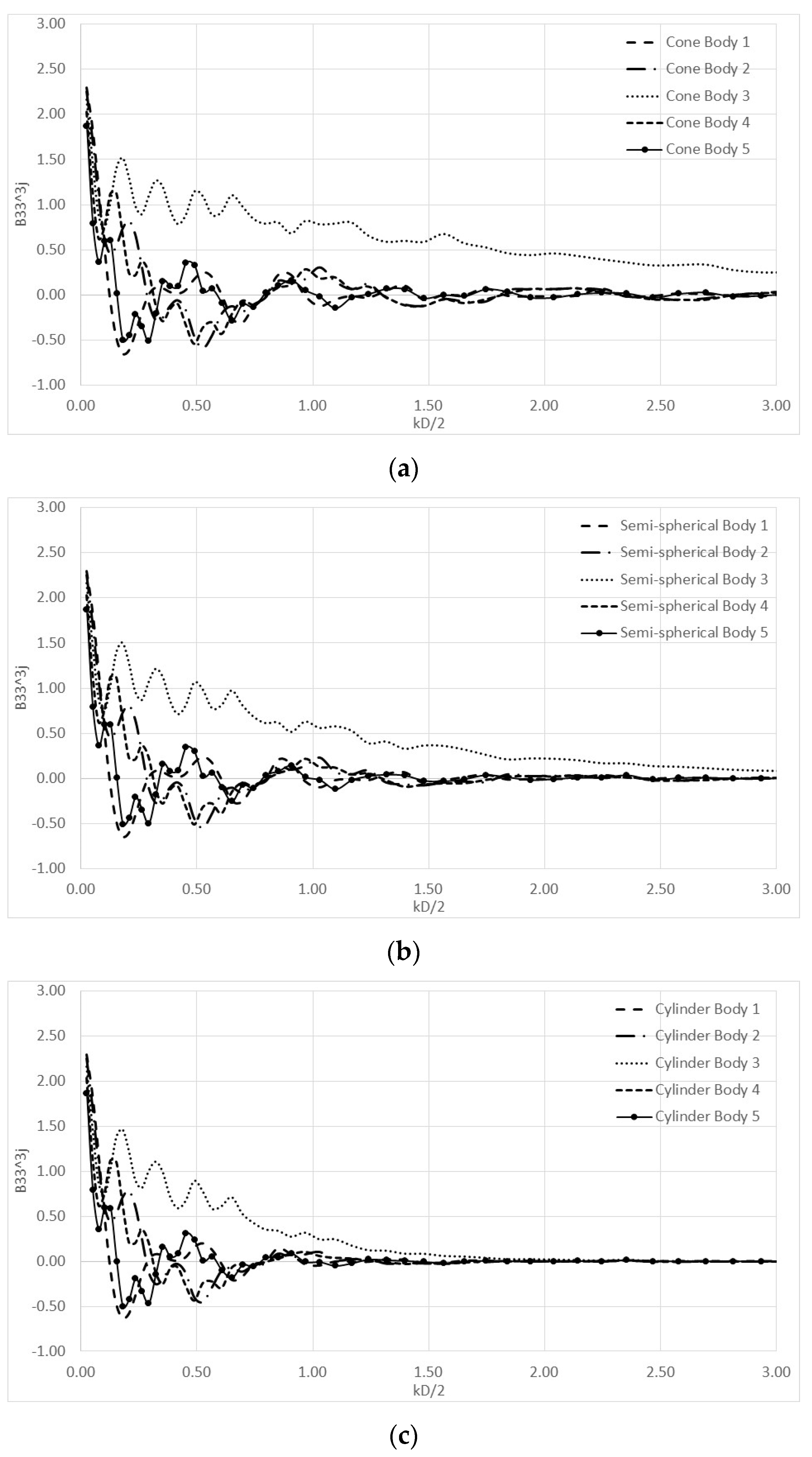
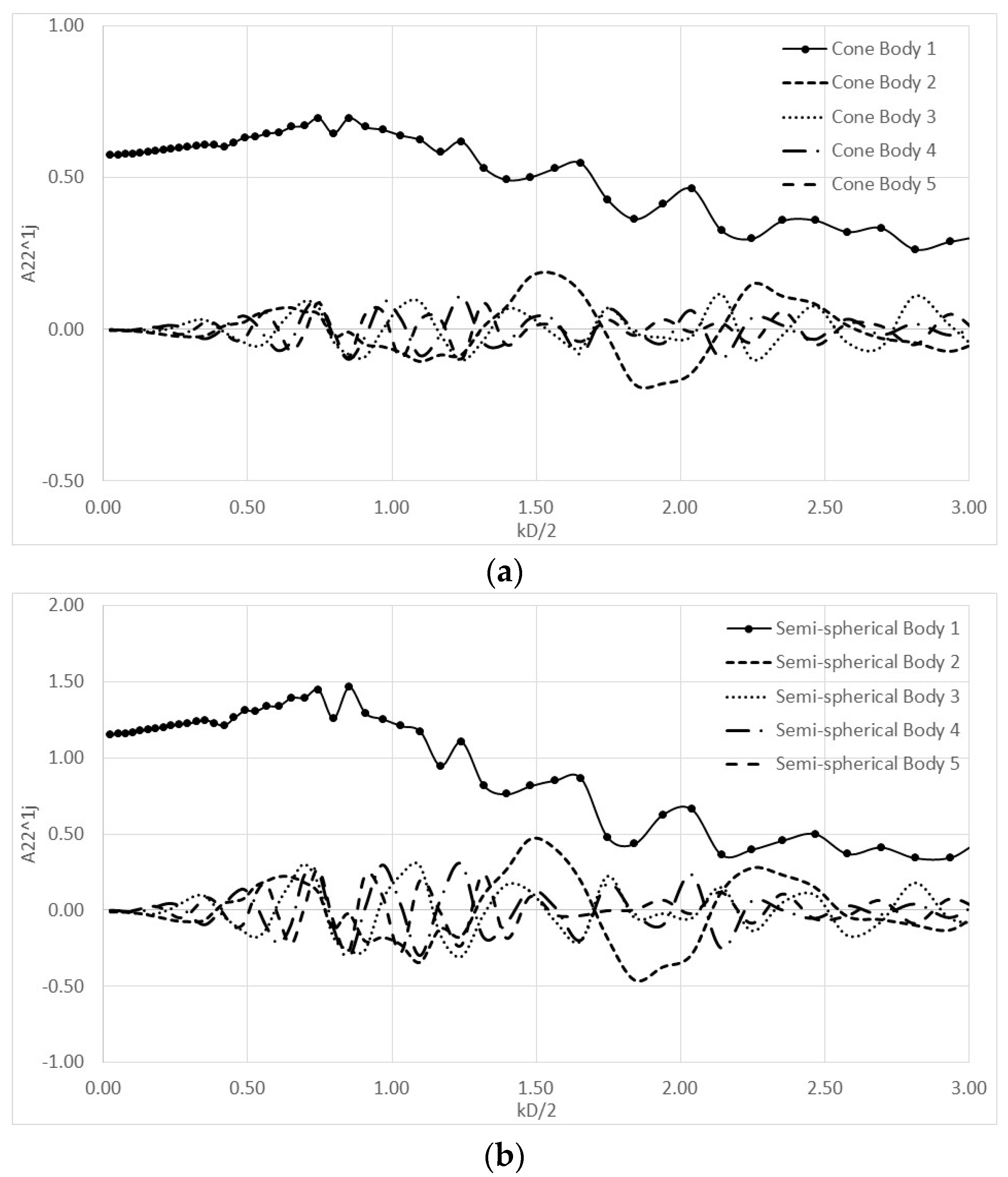
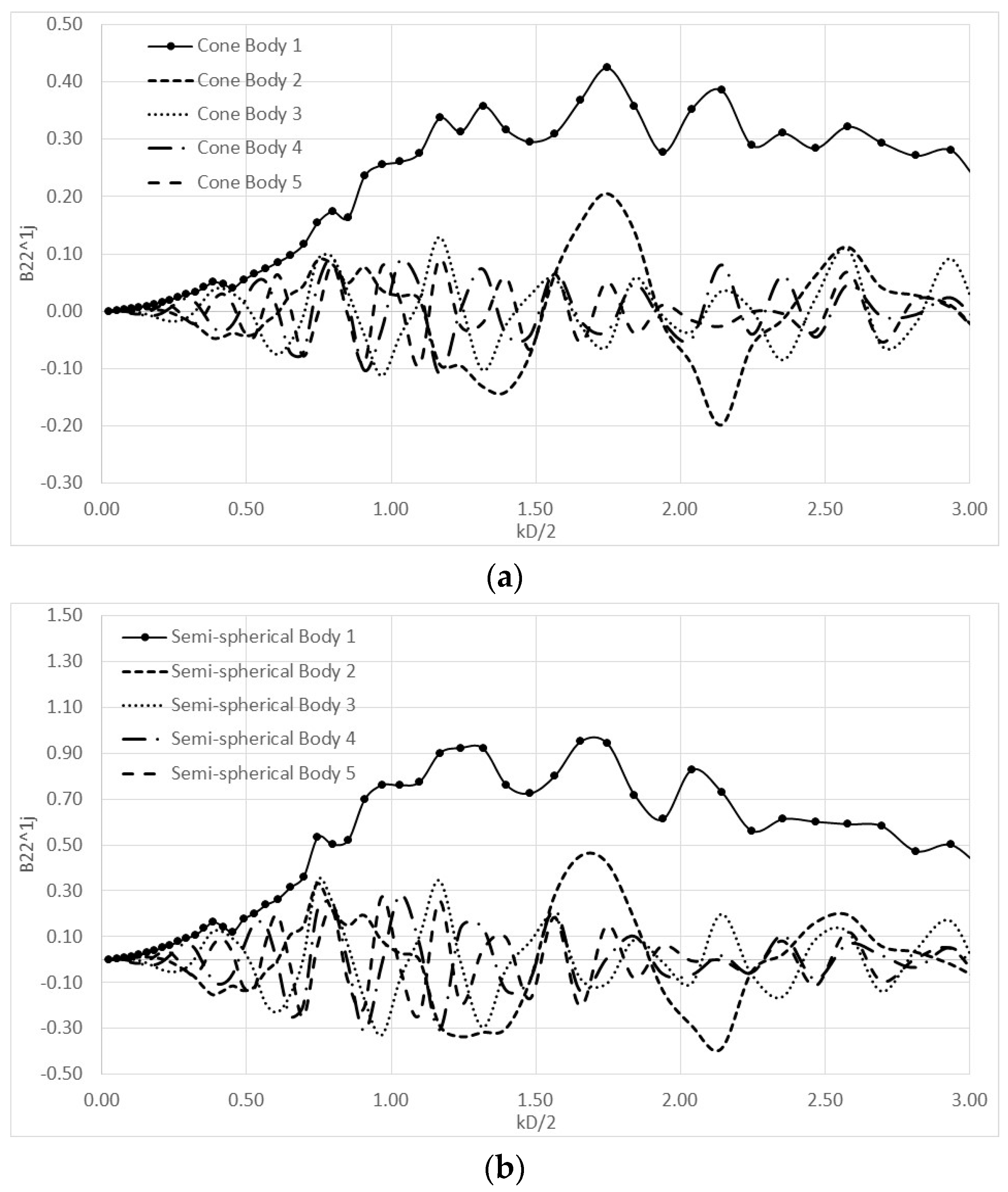
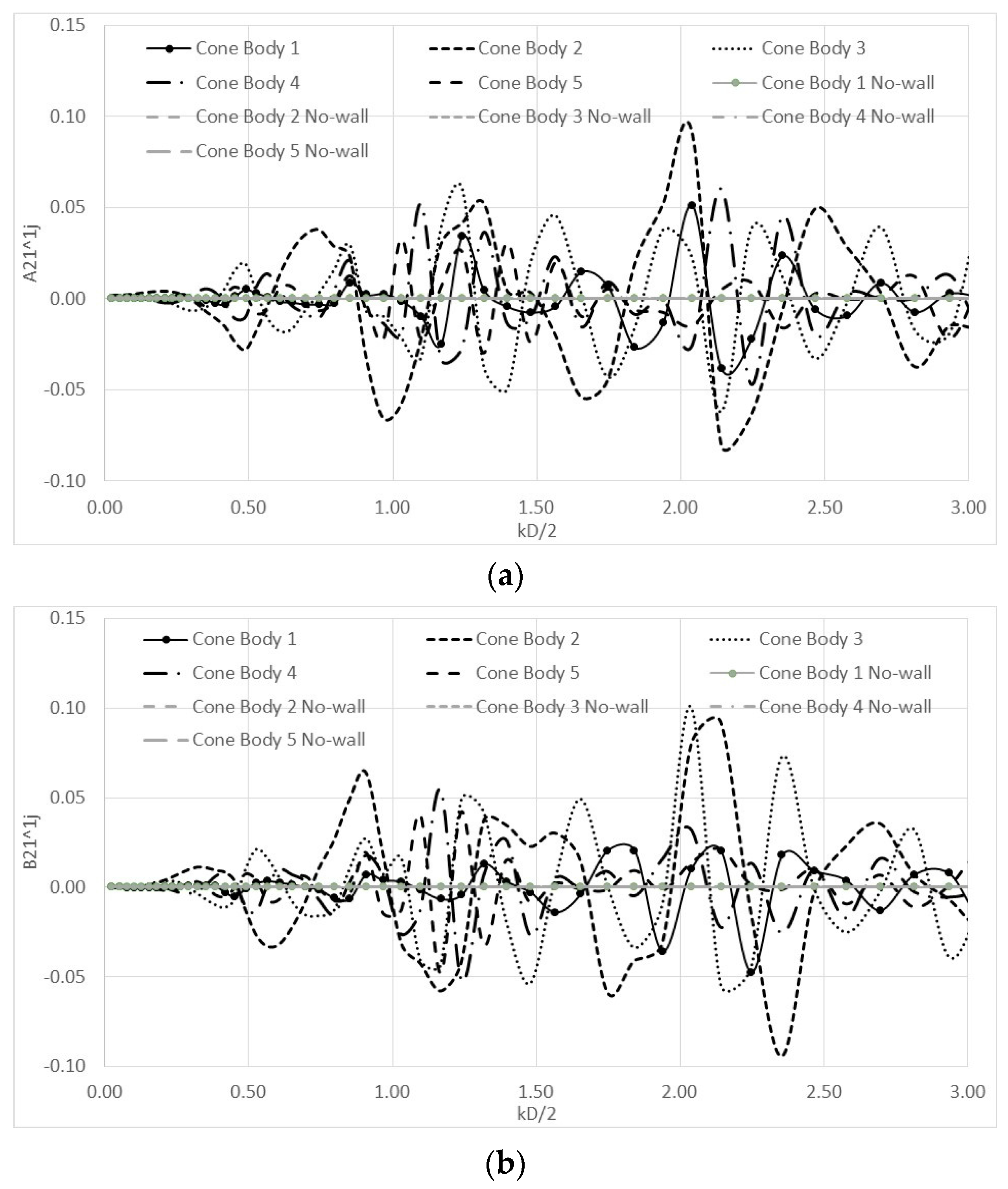
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
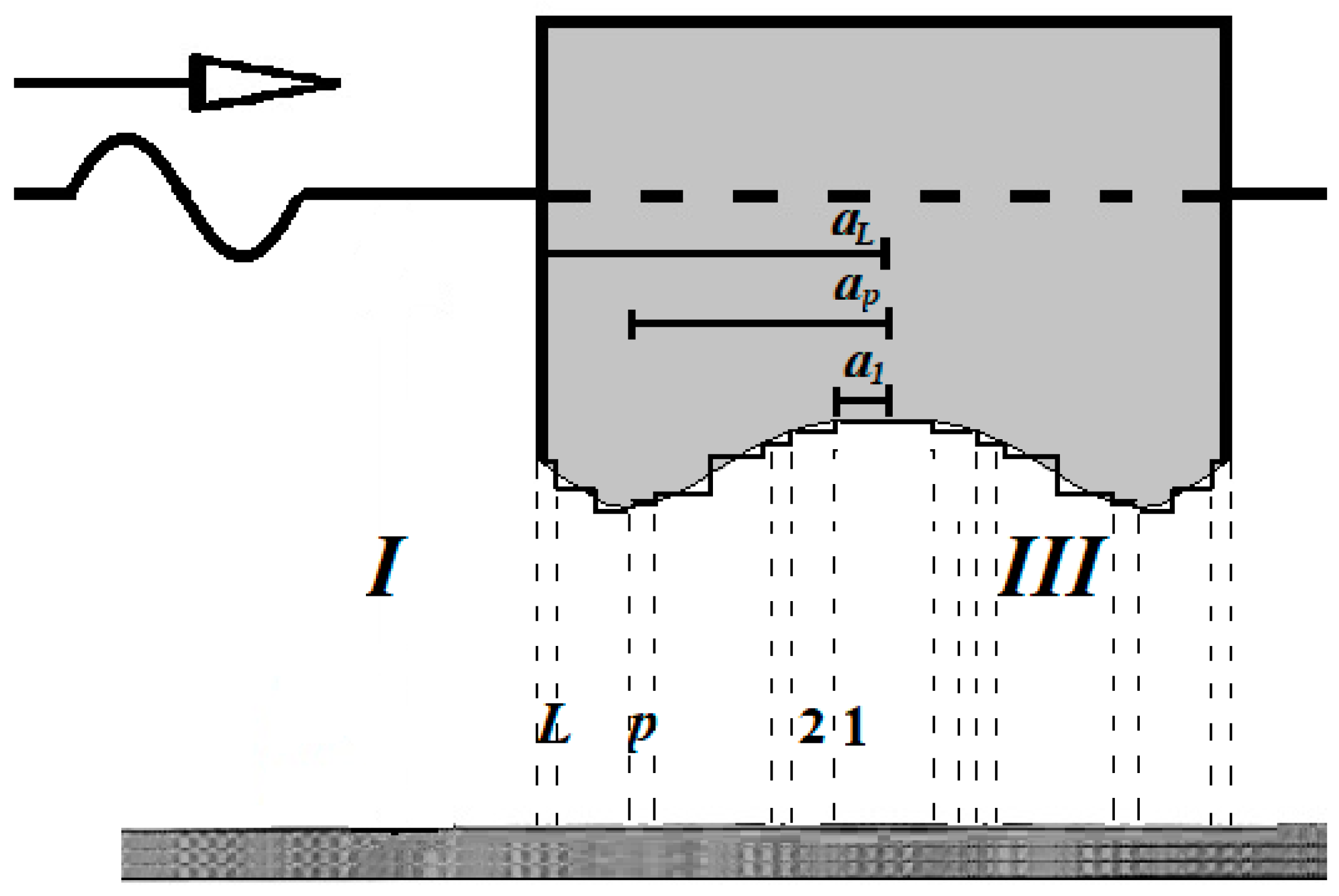
Nomenclature
| N | Number of vertical axisymmetric floaters |
| d | Water depth |
| ω | Wave frequency |
| A | Wave amplitude |
| θ | Angle of wave propagation with respect to the positive x-axis |
| D | Outer diameter of the examined floater |
| h | Distance of the floater’s bottom from the sea bed |
| lW | Distance between the center of the closest to the wall floater and the breakwater |
| lb | Distance between adjacent floaters |
| Potential function describing the fluid flow around the q floater, i.e., | |
| Velocity potential of the undisturbed incident wave | |
| Velocity potential of the scattered wave field around the q floater | |
| Velocity potential of the radiated wave field around the q floater | |
| Diffraction velocity potential around the q floater | |
| The m-th order Bessel function of the first kind | |
| k | Wave number |
| The polar coordinates of the q floater center relative to the origin of the global co-ordinate system | |
| Orthonormal functions | |
| The complex velocity amplitude of q floater’s motion in the j-th direction | |
| I | The infinite ring element around the q floater |
| IIIp | The p-th ring element, p = 1, …, L, below the q floater |
| αp | The radius of the p-th ring element of type III |
| hp | Distance of the upper surface of the p-th ring element of type III from the sea bottom |
| The m-th order Hankel function of first kind | |
| The m-th order modified Bessel function of second kind | |
| The unknown Fourier coefficients | |
| The Neumann’s symbol, p = 1, …, L | |
| The roots of the transcendental equation: | |
| ρ | Sea water density |
| The exciting wave forces on the q floater in the i-th direction | |
| The hydrodynamic reaction forces acting on the q floater in the i-th direction, due to the forced oscillation of the p floater in the j-th direction | |
| The mean wetted surface of the q floater | |
| The generalized normal components | |
| The position vector of a point on the wetted surface with respect to the reference co-ordinate system of q floater | |
| The added mass of the q floater in i-th direction due to the forced oscillation of the p floater in the j-th direction | |
| The damping coefficient of the q floater in i-th direction due to the forced oscillation of the p floater in the j-th direction | |
| bPTO | The PTO damping coefficient |
| Absorbed wave power by the q floater |
Appendix A
| kD/2 | A33^31 | B33^31 | A33^32 | B33^32 | A33^33 | B33^33 | A33^34 | B33^34 | A33^35 | B33^35 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0760 | −0.2360 | 1.1028 | −0.8603 | 1.2179 | 2.4640 | 0.8949 | −0.1510 | 0.3629 | 0.2158 | 0.6327 |
| 0.1805 | −0.0252 | 0.7306 | −0.3496 | −0.6498 | 2.1878 | 1.5191 | −0.5434 | −0.5031 | −0.7096 | 0.6787 |
| 0.2928 | −0.7786 | −0.0826 | 0.2841 | 0.0017 | 2.0292 | 1.0917 | 0.1770 | −0.5122 | −0.6660 | 0.2569 |
| 0.3536 | −0.2798 | −0.2549 | 0.0789 | 0.0752 | 1.5308 | 1.2013 | 0.3457 | 0.1524 | −0.4136 | −0.2889 |
| 0.4894 | −0.3789 | −0.4587 | 0.1129 | 0.1740 | 1.6349 | 1.1434 | −0.2070 | 0.3310 | −0.1616 | −0.5393 |
| 0.5665 | 0.2184 | −0.4510 | −0.2133 | 0.1988 | 1.3301 | 0.8888 | −0.1542 | 0.0658 | −0.0215 | −0.3010 |
| 0.6515 | 0.1568 | −0.1270 | −0.2278 | −0.2506 | 1.3399 | 1.1049 | −0.0274 | −0.2827 | 0.3463 | −0.2111 |
| 0.7459 | 0.2740 | −0.1072 | 0.2078 | −0.1297 | 1.1247 | 0.8422 | 0.1125 | −0.1327 | 0.2257 | −0.1059 |
| 0.8511 | 0.2465 | 0.1522 | 0.1636 | 0.2200 | 1.0931 | 0.8060 | 0.0502 | 0.1023 | 0.1927 | 0.0828 |
| 0.9683 | 0.1613 | 0.1726 | −0.1883 | −0.0104 | 1.1807 | 0.8200 | −0.1564 | 0.0511 | 0.0755 | 0.2864 |
| 1.0984 | −0.1636 | 0.1469 | 0.0456 | −0.0476 | 1.0931 | 0.7917 | −0.0254 | −0.1468 | −0.1188 | 0.1967 |
| 1.3980 | −0.0915 | −0.1084 | −0.0460 | 0.1049 | 0.9388 | 0.6009 | −0.0733 | 0.0654 | −0.1622 | −0.1120 |
| 1.5668 | 0.1309 | −0.0473 | 0.1312 | 0.0015 | 1.0226 | 0.6763 | 0.0959 | 0.0004 | 0.1154 | −0.0474 |
| 1.7476 | 0.0903 | −0.0753 | −0.0075 | 0.0715 | 0.8328 | 0.5286 | 0.0126 | 0.0632 | 0.1197 | −0.0466 |
| 1.9397 | 0.0314 | 0.0606 | −0.0039 | −0.0147 | 0.9211 | 0.4426 | −0.0080 | −0.0302 | 0.0322 | 0.0677 |
| 2.1428 | −0.0420 | 0.0704 | 0.0427 | −0.0067 | 0.8566 | 0.4343 | 0.0330 | 0.0079 | −0.0113 | 0.0764 |
| 2.3564 | 0.0234 | −0.0184 | 0.0627 | −0.0189 | 0.9101 | 0.3617 | 0.0254 | 0.0180 | 0.0049 | −0.0015 |
| 2.8148 | 0.0482 | −0.0051 | −0.0109 | −0.0057 | 0.8368 | 0.2777 | −0.0160 | −0.0170 | 0.0489 | 0.0003 |
| kD/2. | A33^31 | B33^31 | A33^32 | B33^32 | A33^33 | B33^33 | A33^34 | B33^34 | A33^35 | B33^35 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0760 | −0.8635 | 1.2148 | −0.2368 | 1.1000 | 2.3526 | 0.8922 | 0.2178 | 0.6306 | −0.1497 | 0.3611 |
| 0.1805 | −0.3377 | −0.6459 | −0.0255 | 0.7255 | 2.0528 | 1.5033 | −0.7073 | 0.6624 | −0.5302 | −0.5045 |
| 0.2928 | 0.2713 | 0.0112 | −0.7435 | −0.0973 | 1.8795 | 1.0634 | −0.6481 | 0.2397 | 0.1851 | −0.4980 |
| 0.3536 | 0.0697 | 0.0699 | −0.2516 | −0.2337 | 1.3792 | 1.1262 | −0.3762 | −0.2743 | 0.3186 | 0.1590 |
| 0.4894 | 0.1053 | 0.1708 | −0.3529 | −0.4431 | 1.4818 | 1.0611 | −0.1367 | −0.5065 | −0.2121 | 0.2974 |
| 0.5665 | −0.2086 | 0.1730 | 0.2169 | −0.3894 | 1.1993 | 0.7768 | −0.0269 | −0.2731 | −0.1417 | 0.0625 |
| 0.6515 | −0.1809 | −0.2476 | 0.1228 | −0.1022 | 1.1718 | 0.9735 | 0.3082 | −0.1472 | 0.0078 | −0.2533 |
| 0.7459 | 0.1729 | −0.0814 | 0.2182 | −0.0751 | 0.9993 | 0.6822 | 0.1856 | −0.0862 | 0.1099 | −0.1063 |
| 0.8511 | 0.1182 | 0.2058 | 0.1870 | 0.1343 | 0.9866 | 0.6190 | 0.1473 | 0.0605 | 0.0313 | 0.0802 |
| 0.9683 | −0.1454 | −0.0338 | 0.1254 | 0.1400 | 1.0568 | 0.6282 | 0.0262 | 0.2212 | −0.1289 | 0.0170 |
| 1.0984 | 0.0373 | −0.0214 | −0.1192 | 0.0709 | 0.9910 | 0.5761 | −0.0992 | 0.1234 | 0.0071 | −0.1188 |
| 1.3980 | −0.0485 | 0.0664 | −0.0432 | −0.0657 | 0.9364 | 0.3272 | −0.0918 | −0.0885 | −0.0619 | 0.0327 |
| 1.5668 | 0.1177 | −0.0224 | 0.1128 | −0.0457 | 1.0162 | 0.3594 | 0.1023 | −0.0503 | 0.0942 | −0.0324 |
| 1.7476 | −0.0175 | 0.0401 | 0.0557 | −0.0414 | 0.9123 | 0.2609 | 0.0660 | −0.0130 | −0.0058 | 0.0377 |
| 1.9397 | −0.0006 | −0.0068 | 0.0105 | 0.0251 | 0.9558 | 0.2206 | 0.0105 | 0.0300 | −0.0018 | −0.0174 |
| 2.1428 | 0.0254 | 0.0013 | −0.0227 | 0.0273 | 0.9354 | 0.2011 | −0.0070 | 0.0384 | 0.0186 | 0.0096 |
| 2.3564 | 0.1268 | 0.0071 | 0.1106 | 0.0097 | 1.0873 | 0.1657 | 0.0914 | 0.0234 | 0.0862 | 0.0364 |
| 2.8148 | −0.0019 | −0.0036 | 0.0110 | 0.0014 | 0.9984 | 0.0946 | 0.0089 | −0.0001 | −0.0010 | −0.0021 |
| kD/2 | A33^31 | B33^31 | A33^32 | B33^32 | A33^33 | B33^33 | A33^34 | B33^34 | A33^35 | B33^35 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0760 | −0.8664 | 1.2090 | −0.2374 | 1.0945 | 3.0262 | 0.8876 | 0.2201 | 0.6269 | −0.1477 | 0.3583 |
| 0.1805 | −0.3195 | −0.6352 | −0.0257 | 0.7127 | 2.6931 | 1.4694 | −0.6980 | 0.6354 | −0.5085 | −0.5018 |
| 0.2928 | 0.2484 | 0.0224 | −0.6812 | −0.1127 | 2.4978 | 1.0035 | −0.6103 | 0.2122 | 0.1914 | −0.4677 |
| 0.3536 | 0.0568 | 0.0609 | −0.2102 | −0.2000 | 2.0120 | 0.9968 | −0.3184 | −0.2468 | 0.2732 | 0.1608 |
| 0.4894 | 0.0873 | 0.1554 | −0.2938 | −0.3956 | 2.1036 | 0.8971 | −0.0964 | −0.4327 | −0.2007 | 0.2357 |
| 0.5665 | −0.1818 | 0.1275 | 0.1911 | −0.2858 | 1.8794 | 0.5890 | −0.0282 | −0.2209 | −0.1173 | 0.0530 |
| 0.6515 | −0.1067 | −0.2072 | 0.0754 | −0.0699 | 1.8190 | 0.7170 | 0.2225 | −0.0680 | 0.0404 | −0.1837 |
| 0.7459 | 0.1062 | −0.0356 | 0.1313 | −0.0411 | 1.7336 | 0.4294 | 0.1208 | −0.0532 | 0.0868 | −0.0606 |
| 0.8511 | 0.0511 | 0.1419 | 0.0973 | 0.0879 | 1.7539 | 0.3439 | 0.0834 | 0.0306 | 0.0146 | 0.0443 |
| 0.9683 | −0.0712 | −0.0342 | 0.0641 | 0.0800 | 1.8073 | 0.3221 | −0.0093 | 0.1074 | −0.0671 | −0.0080 |
| 1.0984 | 0.0145 | −0.0034 | −0.0436 | 0.0155 | 1.7947 | 0.2482 | −0.0459 | 0.0415 | 0.0196 | −0.0510 |
| 1.3980 | −0.0206 | 0.0164 | −0.0085 | −0.0166 | 1.8519 | 0.0885 | −0.0188 | −0.0268 | −0.0214 | 0.0041 |
| 1.5668 | 0.0423 | −0.0165 | 0.0399 | −0.0211 | 1.9072 | 0.0634 | 0.0316 | −0.0260 | 0.0327 | −0.0210 |
| 1.7476 | −0.0050 | 0.0059 | 0.0115 | −0.0063 | 1.9025 | 0.0426 | 0.0096 | 0.0011 | −0.0027 | 0.0057 |
| 1.9397 | 0.0000 | −0.0007 | 0.0013 | 0.0024 | 1.9347 | 0.0278 | 0.0065 | 0.0063 | 0.0003 | −0.0019 |
| 2.1428 | 0.0027 | 0.0009 | −0.0018 | 0.0020 | 1.9542 | 0.0177 | −0.0010 | 0.0035 | 0.0018 | 0.0017 |
| 2.3564 | 0.0176 | 0.0108 | 0.0168 | 0.0110 | 1.9931 | 0.0212 | 0.0126 | 0.0118 | 0.0125 | 0.0120 |
| 2.8148 | 0.0001 | −0.0002 | 0.0007 | 0.0001 | 2.0082 | 0.0032 | 0.0010 | −0.0003 | 0.0002 | 0.0003 |
Appendix B
| kD/2 | A22^11 | B22^11 | A22^12 | B22^12 | A22^13 | B22^13 | A22^14 | B22^14 | A22^15 | B22^15 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0760 | 2.0240 | 0.0183 | −0.0333 | 0.0156 | −0.0229 | 0.0089 | −0.0208 | 0.0000 | −0.0165 | −0.0084 |
| 0.1805 | 2.0946 | 0.0988 | −0.1033 | 0.0271 | −0.0532 | −0.0743 | 0.0491 | −0.0597 | 0.0608 | 0.0351 |
| 0.2928 | 2.1574 | 0.2369 | −0.1880 | −0.1245 | 0.1852 | −0.0818 | −0.0532 | 0.1774 | −0.0791 | −0.1307 |
| 0.3536 | 2.2015 | 0.3541 | −0.1477 | −0.3186 | 0.2236 | 0.2107 | −0.2359 | −0.0907 | 0.2053 | −0.0131 |
| 0.4894 | 2.3223 | 0.4508 | 0.2054 | −0.3321 | −0.3508 | 0.0840 | 0.3204 | 0.1705 | −0.1637 | −0.3285 |
| 0.5665 | 2.3637 | 0.6022 | 0.4733 | −0.0971 | −0.2355 | −0.5107 | −0.3272 | 0.3323 | 0.3707 | 0.2725 |
| 0.6515 | 2.4707 | 0.8085 | 0.5054 | 0.3262 | 0.5083 | −0.3324 | −0.1108 | −0.6708 | −0.5270 | −0.2038 |
| 0.7459 | 2.3836 | 1.4354 | 0.0344 | 0.9222 | 0.1344 | 0.9514 | 0.3748 | 0.6947 | 0.4932 | 0.3823 |
| 0.8511 | 2.5715 | 1.3667 | −0.0572 | 0.4063 | −0.6186 | 0.0419 | −0.7277 | −0.2513 | −0.5758 | −0.4337 |
| 0.9683 | 1.8682 | 1.6947 | −0.4459 | 0.1238 | 0.3490 | −0.6673 | 0.6573 | 0.1634 | −0.0601 | 0.6370 |
| 1.0984 | 1.8146 | 1.6999 | −0.8365 | −0.2386 | 0.7164 | 0.4411 | −0.7716 | −0.0823 | 0.6550 | −0.3169 |
| 1.3980 | 0.9078 | 1.3463 | 0.5921 | −0.4201 | 0.3349 | −0.0537 | −0.0863 | −0.2994 | −0.4034 | 0.0289 |
| 1.5668 | 0.9926 | 1.4841 | 0.5586 | 0.7083 | −0.2482 | 0.4221 | −0.1401 | 0.4517 | −0.2159 | 0.3162 |
| 1.7476 | 0.2887 | 1.3876 | −0.4381 | 0.5763 | 0.4545 | −0.0133 | 0.2373 | 0.1227 | −0.1345 | 0.1795 |
| 1.9397 | 0.7768 | 1.0233 | −0.5525 | −0.3183 | 0.0166 | 0.0321 | −0.1709 | −0.1282 | 0.0572 | 0.1157 |
| 2.1428 | 0.3299 | 1.0565 | 0.2992 | −0.5280 | 0.0286 | 0.3425 | −0.3123 | −0.1373 | 0.1857 | 0.1297 |
| 2.3564 | 0.4857 | 0.8862 | 0.3346 | 0.1012 | 0.1713 | −0.1660 | −0.0121 | 0.1464 | 0.0771 | 0.1877 |
| 2.8148 | 0.4188 | 0.6489 | −0.1544 | 0.0188 | 0.2062 | 0.1173 | 0.0848 | −0.0616 | −0.1132 | −0.0147 |
Appendix C
| kD/2 | A21^11 | B21^11 | A21^12 | B21^12 | A21^13 | B21^13 | A21^14 | B21^14 | A21^15 | B21^15 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0760 | 0.0000 | 0.0000 | 0.0025 | 0.0001 | 0.0010 | 0.0002 | 0.0005 | 0.0002 | 0.0002 | 0.0002 |
| 0.1805 | 0.0002 | 0.0000 | 0.0044 | 0.0024 | 0.0006 | 0.0027 | −0.0014 | 0.0010 | −0.0010 | −0.0006 |
| 0.2928 | 0.0000 | 0.0006 | 0.0008 | 0.0099 | −0.0062 | −0.0002 | 0.0014 | −0.0034 | 0.0018 | 0.0024 |
| 0.3536 | −0.0007 | 0.0011 | −0.0069 | 0.0110 | −0.0043 | −0.0070 | 0.0056 | 0.0015 | −0.0043 | 0.0006 |
| 0.4894 | 0.0050 | −0.0008 | −0.0276 | −0.0125 | 0.0193 | 0.0097 | −0.0099 | −0.0104 | 0.0026 | 0.0077 |
| 0.5665 | 0.0010 | 0.0035 | −0.0034 | −0.0329 | −0.0107 | 0.0162 | 0.0137 | 0.0009 | −0.0058 | −0.0071 |
| 0.6515 | −0.0020 | 0.0016 | 0.0269 | −0.0224 | −0.0163 | −0.0079 | −0.0038 | 0.0072 | 0.0067 | 0.0043 |
| 0.7459 | −0.0031 | −0.0013 | 0.0381 | 0.0108 | 0.0037 | −0.0160 | −0.0105 | −0.0070 | −0.0065 | −0.0007 |
| 0.8511 | 0.0088 | −0.0066 | 0.0238 | 0.0484 | 0.0299 | 0.0095 | 0.0211 | 0.0023 | 0.0126 | −0.0044 |
| 0.9683 | 0.0025 | 0.0040 | −0.0653 | 0.0189 | −0.0095 | 0.0073 | −0.0134 | 0.0066 | −0.0223 | −0.0142 |
| 1.0984 | −0.0096 | −0.0015 | −0.0223 | −0.0425 | −0.0325 | −0.0407 | 0.0520 | −0.0127 | −0.0220 | 0.0408 |
| 1.3980 | −0.0043 | 0.0033 | 0.0048 | 0.0346 | −0.0497 | −0.0195 | −0.0134 | 0.0265 | 0.0310 | 0.0155 |
| 1.5668 | −0.0041 | −0.0140 | −0.0197 | 0.0303 | 0.0459 | 0.0043 | 0.0232 | 0.0050 | 0.0199 | 0.0026 |
| 1.7476 | 0.0069 | 0.0205 | −0.0447 | −0.0583 | −0.0428 | 0.0014 | 0.0092 | 0.0090 | 0.0054 | −0.0011 |
| 1.9397 | −0.0132 | −0.0358 | 0.0521 | −0.0315 | 0.0380 | −0.0102 | −0.0003 | 0.0157 | −0.0074 | −0.0014 |
| 2.1428 | −0.0384 | 0.0204 | −0.0797 | 0.0922 | −0.0619 | −0.0546 | 0.0604 | −0.0223 | 0.0050 | 0.0217 |
| 2.3564 | 0.0235 | 0.0179 | −0.0055 | −0.0941 | 0.0119 | 0.0728 | 0.0453 | −0.0255 | −0.0161 | −0.0010 |
| 2.8148 | −0.0074 | 0.0071 | −0.0370 | 0.0074 | −0.0170 | 0.0323 | 0.0005 | −0.0024 | 0.0123 | −0.0109 |
Appendix D
References
- McCormick, M.E. Ocean Wave Energy Conversion; Courier Corporation: North Chelmsford, MA, USA, 1981. [Google Scholar]
- Pelc, R.; Fujita, R.M. Renewable energy from the ocean. Mar. Policy 2002, 26, 471–479. [Google Scholar] [CrossRef]
- Falnes, J. A review of wave-energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
- Falcao, A.F.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Aderinto, T.; Li, H. Ocean wave energy converters: Status and Challenges. Energies 2008, 11, 1250. [Google Scholar] [CrossRef]
- Giebhardt, J.; Kracht, P.; Dick, C.; Salcedo, F. Report on Grid Integration and Power Quality Testing; Deliverable 4.3 Final; Marinet: Singapore, 2014. [Google Scholar]
- Magagna, D.; Uihlein, A. Ocean energy development in Europe: Current status and future perspectives. Int. J. Mar. Energy 2015, 11, 84–104. [Google Scholar] [CrossRef]
- Mustapa, M.A.; Yaakob, O.B.; Ahmed, Y.M.M.; Rheem, C.K.; Koh, K.K.; Faizul, A.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energy Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
- Rusu, E. Evaluation of the wave energy conversion in various coastal environments. Energies 2014, 7, 4002–4018. [Google Scholar] [CrossRef]
- Cascajo, R.; Garcia, E.; Quiles, E.; Correcher, A.; Morant, F. Integration of marine wave energy convertres into seaports: A case study in port of Valencia. Energies 2019, 12, 787. [Google Scholar] [CrossRef]
- Mavrakos, S.A.; Katsaounis, G.M.; Nielsen, K.; Lemonis, G. Numerical performance investigation of an array of heaving wave power converters in front of a vertical breakwater. In Proceedings of the 14th International Offshore and Polar Engineering Conference (ISOPE 2004), Toulon, France, 23–28 May 2004. [Google Scholar]
- Mavrakos, S.A.; Katsaounis, G.M.; Kladas, A.; Kimoulakis, N. Numerical and experimental investigation of performance of heaving WECs coupled with DC generators. In Proceedings of the 9th European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011. [Google Scholar]
- Teng, B.; Ning, D.Z. Wave diffraction from a uniform cylinder in front of a vertical wall. Ocean Eng. 2003, 21, 48–52. [Google Scholar]
- Teng, B.; Ning, D.Z.; Zhang, X.T. Wave radiation by a uniform cylinder in front of a vertical wall. Ocean Eng. 2004, 31, 201–224. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, Y. Wave diffraction from a truncated cylinder in front of a vertical wall. Ocean Eng. 2015, 104, 329–343. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, Y. Wave radiation from a truncated cylinder in front of a vertical wall. Ocean Eng. 2016, 111, 602–614. [Google Scholar] [CrossRef]
- Schay, J.; Bhattacharjee, J.; Soares, C. Numerical modelling of a heaving point absorber in front of a vertical wall. In Proceedings of the 32nd International Conference on Ocean, Offshore and Artic Engineering (OMAE 2013), Nantes, France, 9–14 June 2013. [Google Scholar] [CrossRef]
- He, F.; Huang, Z. Using an oscillating water column structure to reduce wave reflection from vertical wall. J. Waterw. Port Coast. Ocean Eng. 2016, 142. [Google Scholar] [CrossRef]
- Martins-rivas, H.; Mei, C.C. Wave power extraction from an oscillating water column at the tip of a breakwater. J. Fluid Mech. 2009, 626, 395–414. [Google Scholar] [CrossRef]
- Martins-rivas, H.; Mei, C.C. Wave power extraction from an oscillating water column along a straight coast. Ocean Eng. 2009, 36, 426–433. [Google Scholar] [CrossRef]
- Howe, D.; Nader, J.R. OWC WEC integrated within a breakwater versus isolated: Experimental and numerical theoretical study. Mar. Energy 2017, 20, 165–182. [Google Scholar] [CrossRef]
- Naty, S.; Viviano, A.; Foti, E. Wave energy exploitation system integrated in the coastal structure of a Mediterranean port. Sustainability 2016, 8, 1342. [Google Scholar] [CrossRef]
- Naty, S.; Viviano, A.; Foti, E. Feasibility study of a WEC integrated in the port of Giardini Naxos, Italy. In Proceedings of the 35th Conference on Coastal Engineering, Antalya, Turkey, 17–20 November 2016. [Google Scholar]
- He, F.; Huang, Z.; Law, A.W.K. Hydrodynamic performance of a rectangular floating breakwater with and without pneumatic chambers: An experimental study. Ocean Eng. 2012, 51, 16–27. [Google Scholar] [CrossRef]
- Zheng, X.; Zeng, Q.; Liu, Z. Hydrodynamic performance of rectangular heaving buoys for an integrated floating breakwater. J. Mar. Sci. Eng. 2019, 7, 239. [Google Scholar] [CrossRef]
- He, F.; Zhang, H.; Zhao, J.; Zheng, S.; Iglesias, G. Hydrodynamic performance of a pile-supported OWC breakwater: An analytical study. Appl. Ocean Res. 2019, 88, 326–340. [Google Scholar] [CrossRef]
- Zhao, X.L.; Ning, D.Z.; Zhang, C.W.; Liu, Y.Y.; Kang, H.G. Analytical study on an oscillating buoy wave energy converter integrated into a fixed box-type breakwater. Math. Probl. Eng. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Zhao, X.L.; Ning, D.Z.; Liang, D.F. Experimental investigation on hydrodynamic performance of a breakwater-integrated WEC system. Ocean Eng. 2019, 171, 25–32. [Google Scholar] [CrossRef]
- Salter, S.; Taylor, J.; Caldwell, N. Power conversion mechanisms for wave energy. J. Eng. Marit. Environ. 2002, 216, 1–27. [Google Scholar] [CrossRef]
- Falnes, J.; Hals, J. Heaving buoys, point absorbers and arrays. Philos. Trans. R. Soc. A 2012, 370, 246. [Google Scholar] [CrossRef] [PubMed]
- Rahmati, M.T.; Aggidis, G.A. Numerical and experimental analysis of the power output of a point absorber wave energy converter in irregular waves. Ocean Eng. 2016, 111, 483–492. [Google Scholar] [CrossRef]
- Tampier, G.; Grueter, L. Hydrodynamic analysis of a heaving wave energy converter. Int. J. Mar. Energy 2017, 19, 304–318. [Google Scholar] [CrossRef]
- Son, D.; Yeung, R. Real time implementation and validation of optimal damping control for a permanent magnet linear generator in wave energy extraction. Appl. Energy 2017, 208, 571–579. [Google Scholar] [CrossRef]
- Gaspar, J.; Calvario, M.; Kamarlouei, M.; Soares, C. Power take-off concept for wave energy converters based on oil-hydraulic transformer units. Renew. Energy 2016, 86, 1232–1246. [Google Scholar] [CrossRef]
- Spring, B.W.; Monkmeyer, P.L. Interaction of plane waves with a row of cylinders. In Proceedings of the 3rd Specialty Conference of Civil Engineering in Oceans ASCE, Newark, DE, USA, 9–12 June 1975; pp. 979–998. [Google Scholar]
- Yeung, R.W.; Sphaier, S.H. Wave-interference effects on a truncated cylinder in a channel. J. Eng. Math. 1989, 23, 95–117. [Google Scholar] [CrossRef]
- Yeung, R.W.; Sphaier, S.H. Wave-interference effects on a floating body in a towing tank. In Proceedings of the 4th International Symposium on Practical Design of Ships and Mobile Units (PRADS), Varna, Bulgaria, 23–28 October 1989. [Google Scholar]
- Mavrakos, S.A. The scattered wave field by vertical cylinders in a narrow tank. In Proceedings of the 4th National Symposium on Theoretical and Applied Mechanics, Xanthi, Greece, 26–29 June 1995; Volume II, pp. 819–829. [Google Scholar]
- Twersky, V. Multiple scattering of radiation by an arbitrary configuration of parallel cylinders. J. Acoust. Soc. Am. 1952, 24, 42. [Google Scholar] [CrossRef]
- Okhusu, M. Hydrodynamic forces on multiple cylinders in waves. In Proceedings of the International Symposium on the Dynamics of Marine Vehicles and Structures in Waves, London, UK, 1–5 April 1974. [Google Scholar]
- Mavrakos, S.A.; Koumoutsakos, P. Hydrodynamic interaction among vertical axisymmetric bodies restrained in waves. Appl. Ocean Res. 1987, 9, 128–140. [Google Scholar] [CrossRef]
- Mavrakos, S.A. Hydrodynamic coefficients for groups of interacting vertical axisymmetric bodies. Ocean Eng. 1991, 18, 485–515. [Google Scholar] [CrossRef]
- Mavrakos, S.A.; McIver, P. Comparison of methods for computing hydrodynamic characteristics of arrays of wave power devices. Appl. Ocean Res. 1997, 19, 283–291. [Google Scholar] [CrossRef]
- Konispoliatis, D.N.; Mavrakos, S.A. Hydrodynamic analysis of an array of interacting free–floating oscillating water column devices. Ocean Eng. 2016, 111, 179–197. [Google Scholar] [CrossRef]
- Kokkinowrachos, K.; Mavrakos, S.; Asorakos, S. Behavior of vertical bodies of revolution in waves. Ocean Eng. 1986, 13, 505–538. [Google Scholar] [CrossRef]
- Newman, J.N. Marine Hydrodynamics; MIT Press: Cambridge, UK, 1977. [Google Scholar]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Loukogeorgaki, E.; Chatjigeorgiou, I. Hydrodynamic performance of an array of wave energy converters in front of a vertical wall. In Proceedings of the 13th European Wave and Tidal Energy Conference (EWTEC), Naples, Italy, 1–6 September 2019. [Google Scholar]
- Nader, J.R.; Zhu, S.P.; Cooper, P.; Steppenbelt, B. A finite element study of the efficiency of arrays of oscillating water column wave energy converters. Ocean Eng. 2012, 43, 72–81. [Google Scholar] [CrossRef]
- Falnes, J. Ocean. Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konispoliatis, D.N.; Mavrakos, S.A.; Katsaounis, G.M. Theoretical Evaluation of the Hydrodynamic Characteristics of Arrays of Vertical Axisymmetric Floaters of Arbitrary Shape in front of a Vertical Breakwater. J. Mar. Sci. Eng. 2020, 8, 62. https://doi.org/10.3390/jmse8010062
Konispoliatis DN, Mavrakos SA, Katsaounis GM. Theoretical Evaluation of the Hydrodynamic Characteristics of Arrays of Vertical Axisymmetric Floaters of Arbitrary Shape in front of a Vertical Breakwater. Journal of Marine Science and Engineering. 2020; 8(1):62. https://doi.org/10.3390/jmse8010062
Chicago/Turabian StyleKonispoliatis, Dimitrios N., Spyridon A. Mavrakos, and Georgios M. Katsaounis. 2020. "Theoretical Evaluation of the Hydrodynamic Characteristics of Arrays of Vertical Axisymmetric Floaters of Arbitrary Shape in front of a Vertical Breakwater" Journal of Marine Science and Engineering 8, no. 1: 62. https://doi.org/10.3390/jmse8010062
APA StyleKonispoliatis, D. N., Mavrakos, S. A., & Katsaounis, G. M. (2020). Theoretical Evaluation of the Hydrodynamic Characteristics of Arrays of Vertical Axisymmetric Floaters of Arbitrary Shape in front of a Vertical Breakwater. Journal of Marine Science and Engineering, 8(1), 62. https://doi.org/10.3390/jmse8010062







