Dynamic Response for a Submerged Floating Offshore Wind Turbine with Different Mooring Configurations
Abstract
1. Introduction
2. Theoretical Calculations for SFOWT
2.1. Equation of Motion in the Time Domain
2.2. Mooring Loads for SFOWT
3. Dynamic Response of SFOWT under Different Mooring Configurations
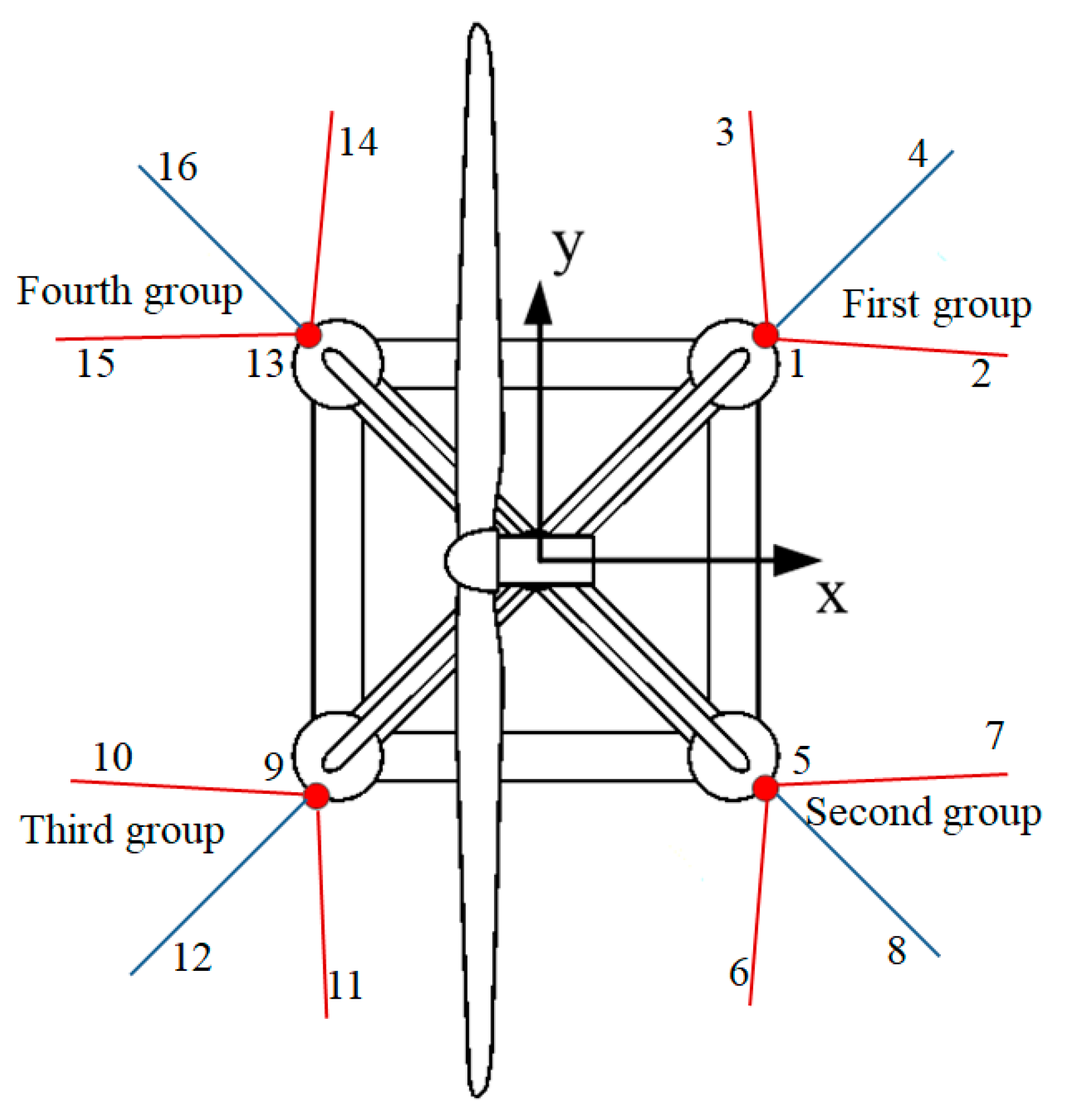
3.1. Structural Form of SFOWT
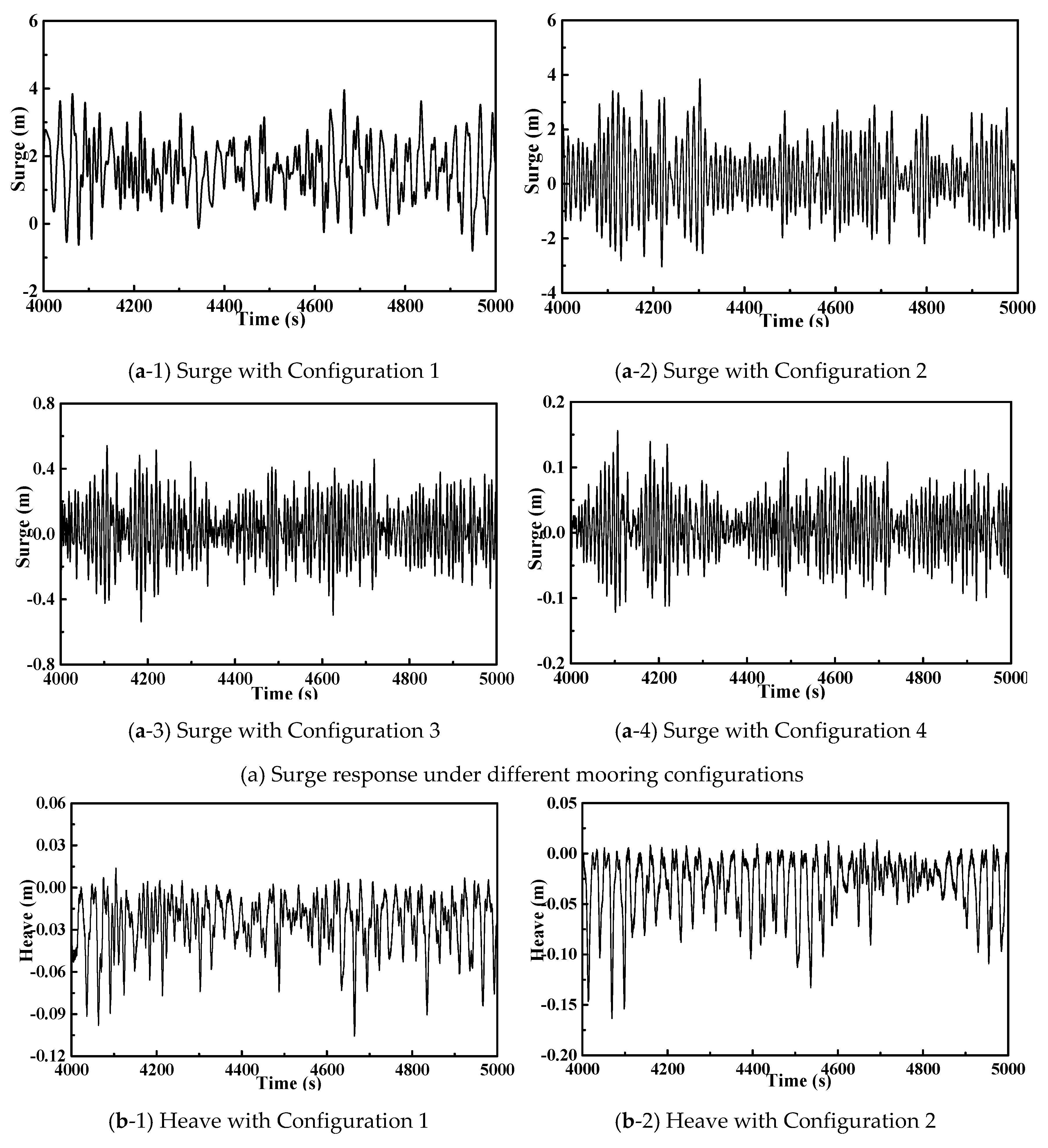
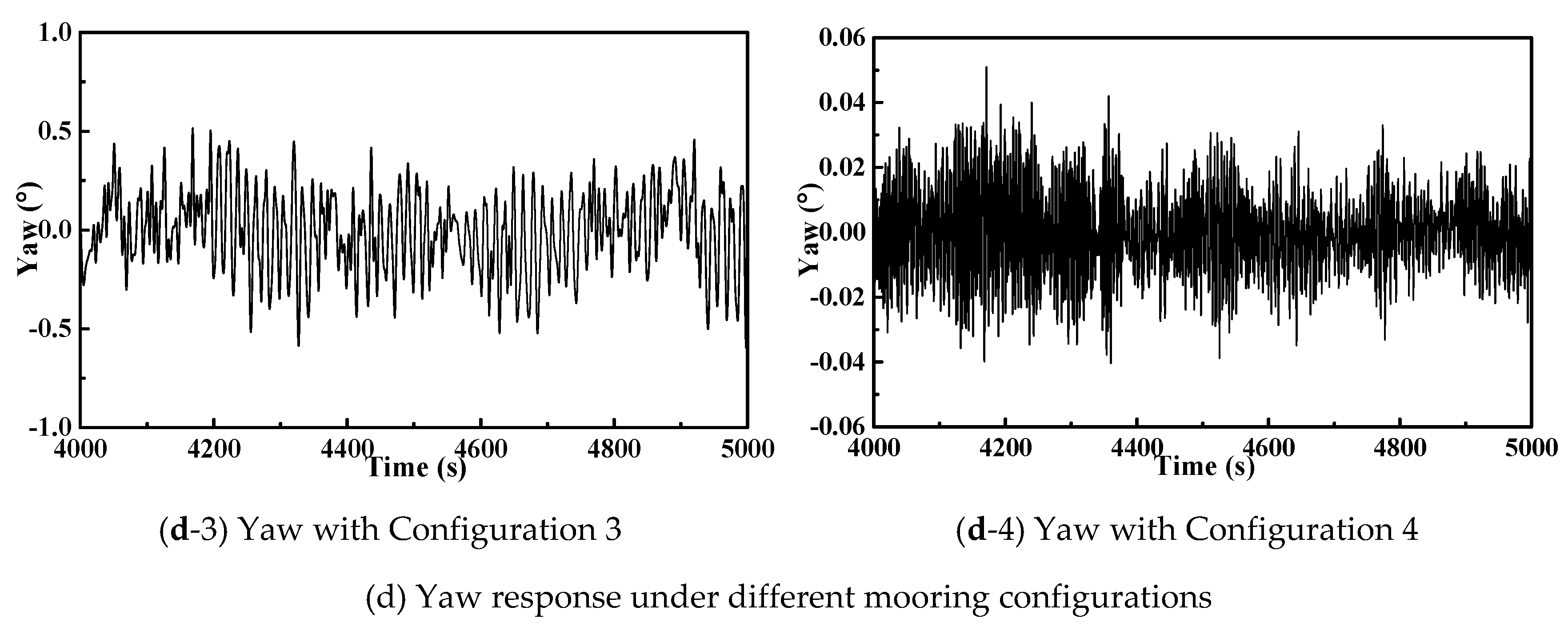
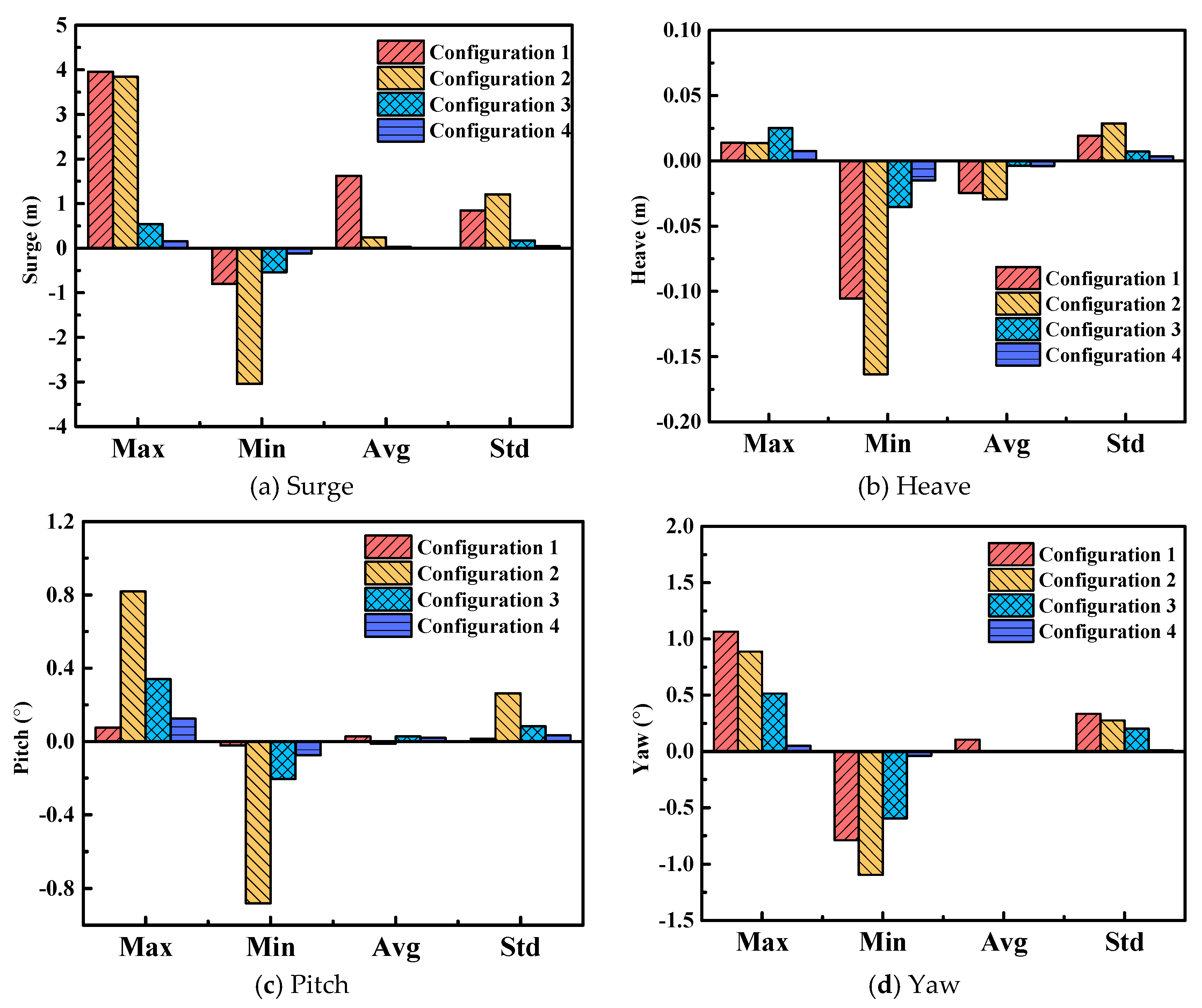
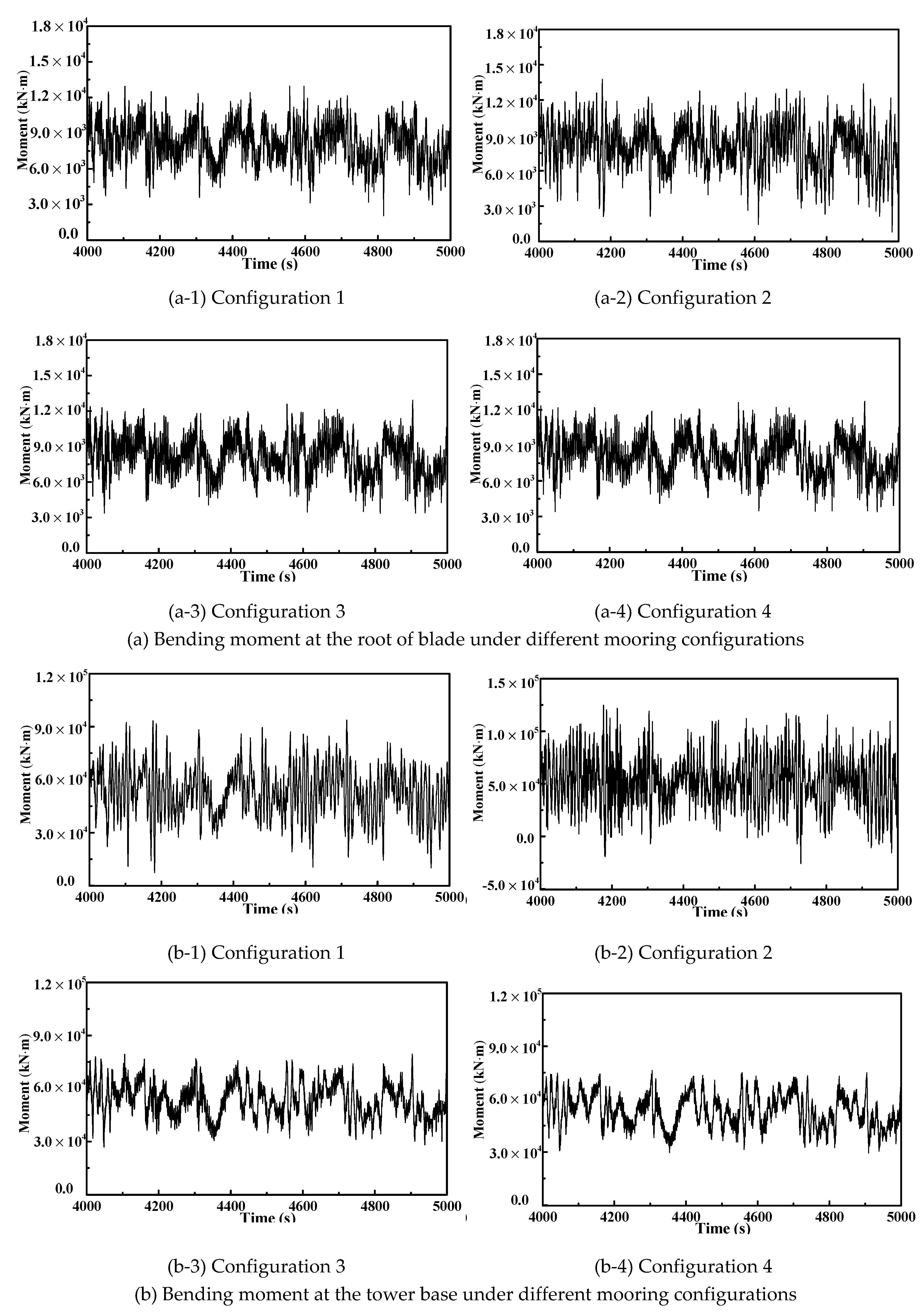
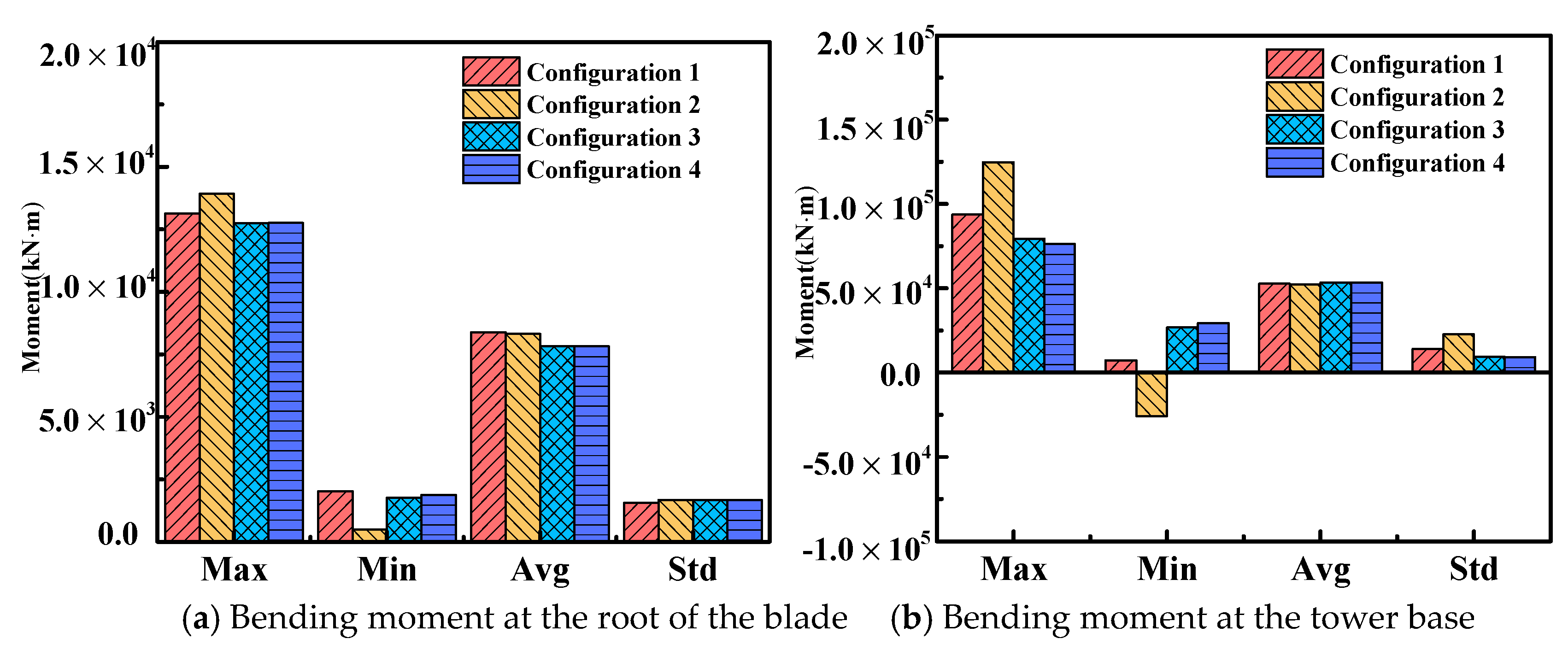
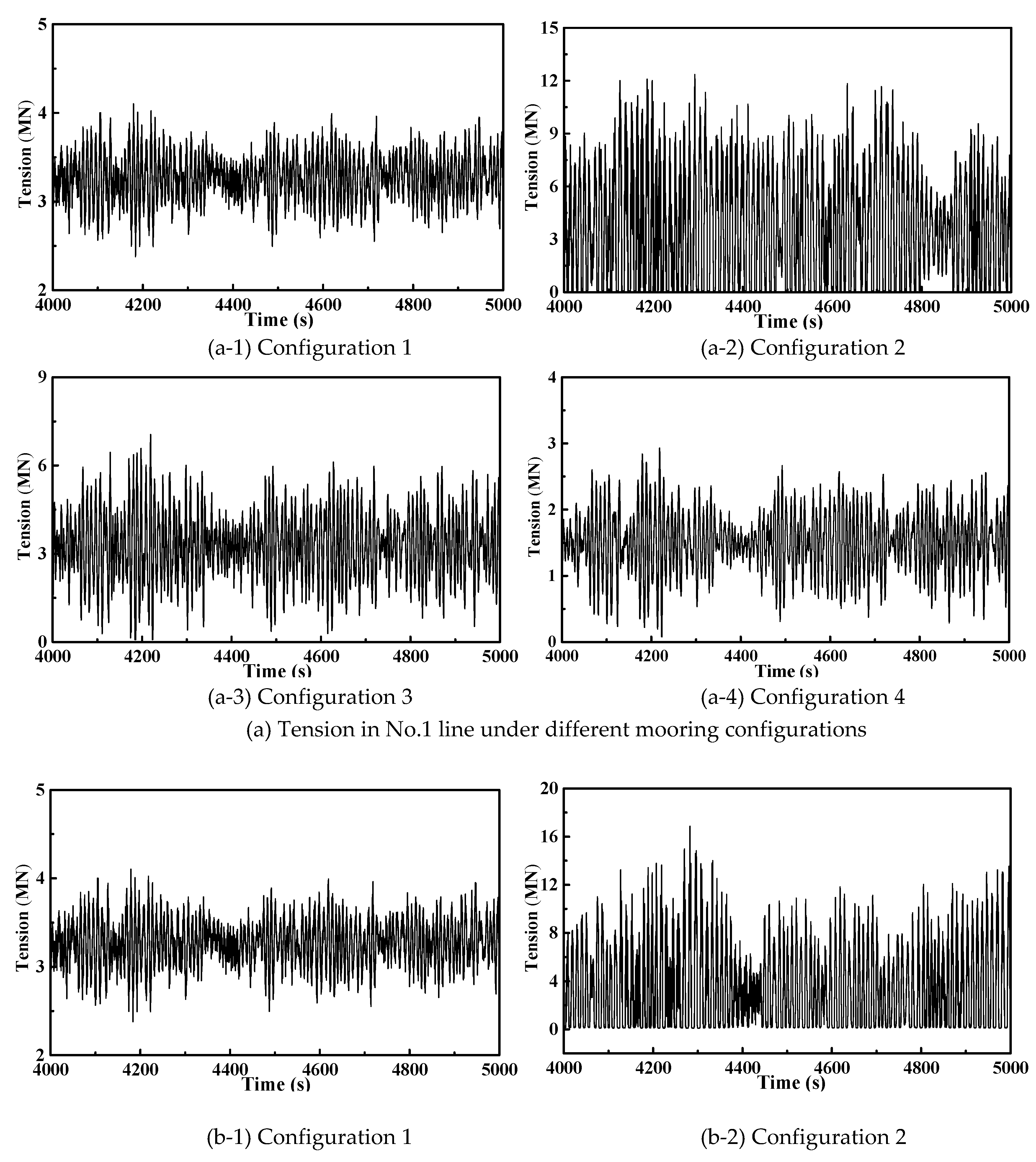
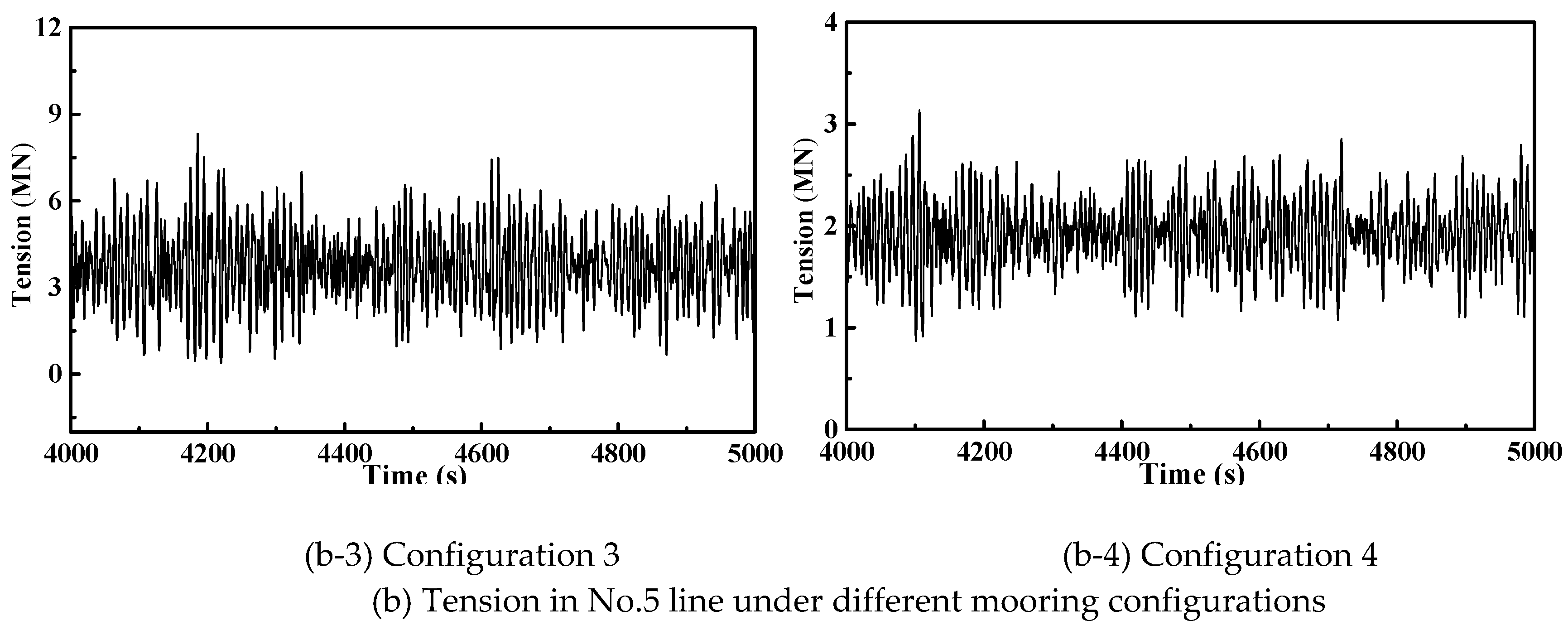
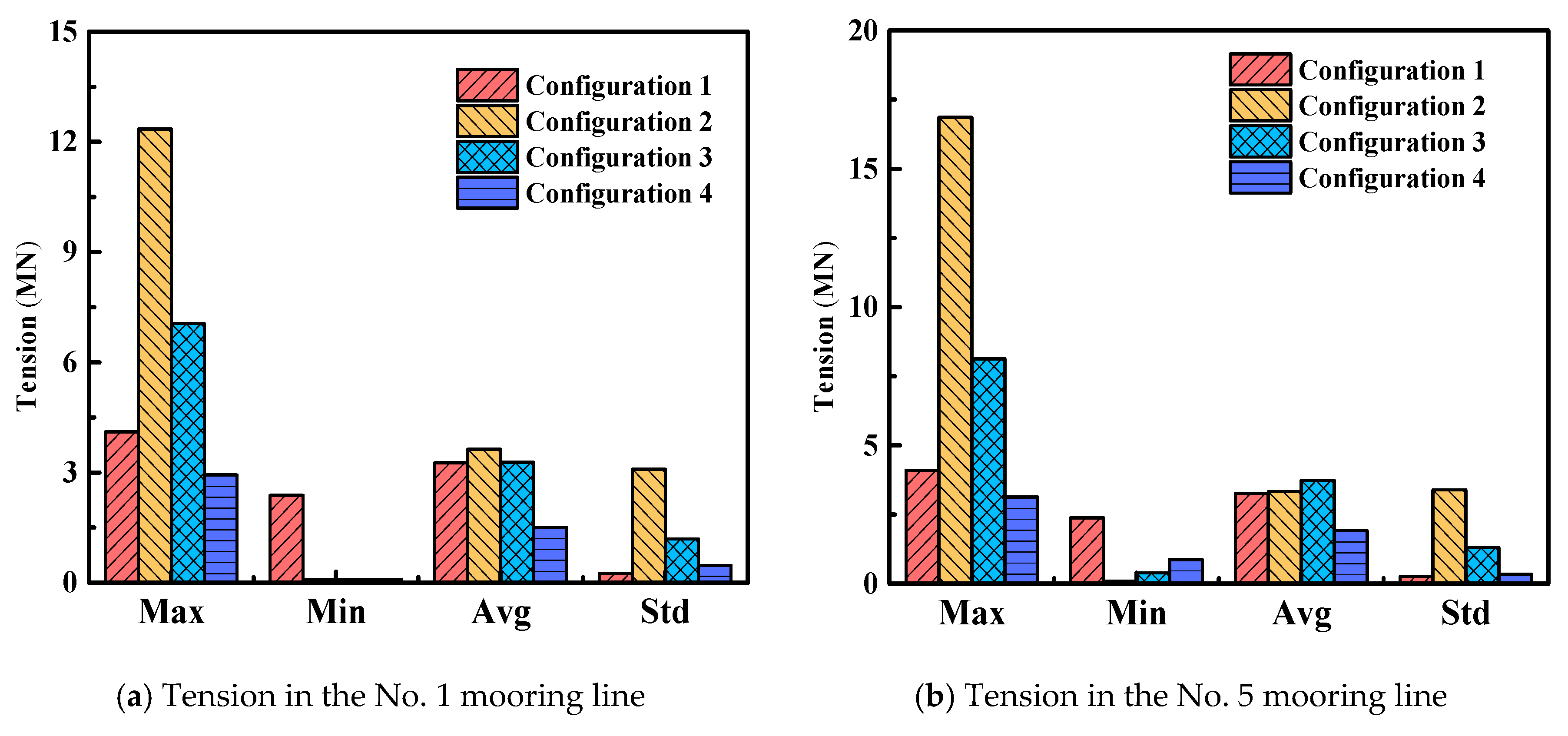
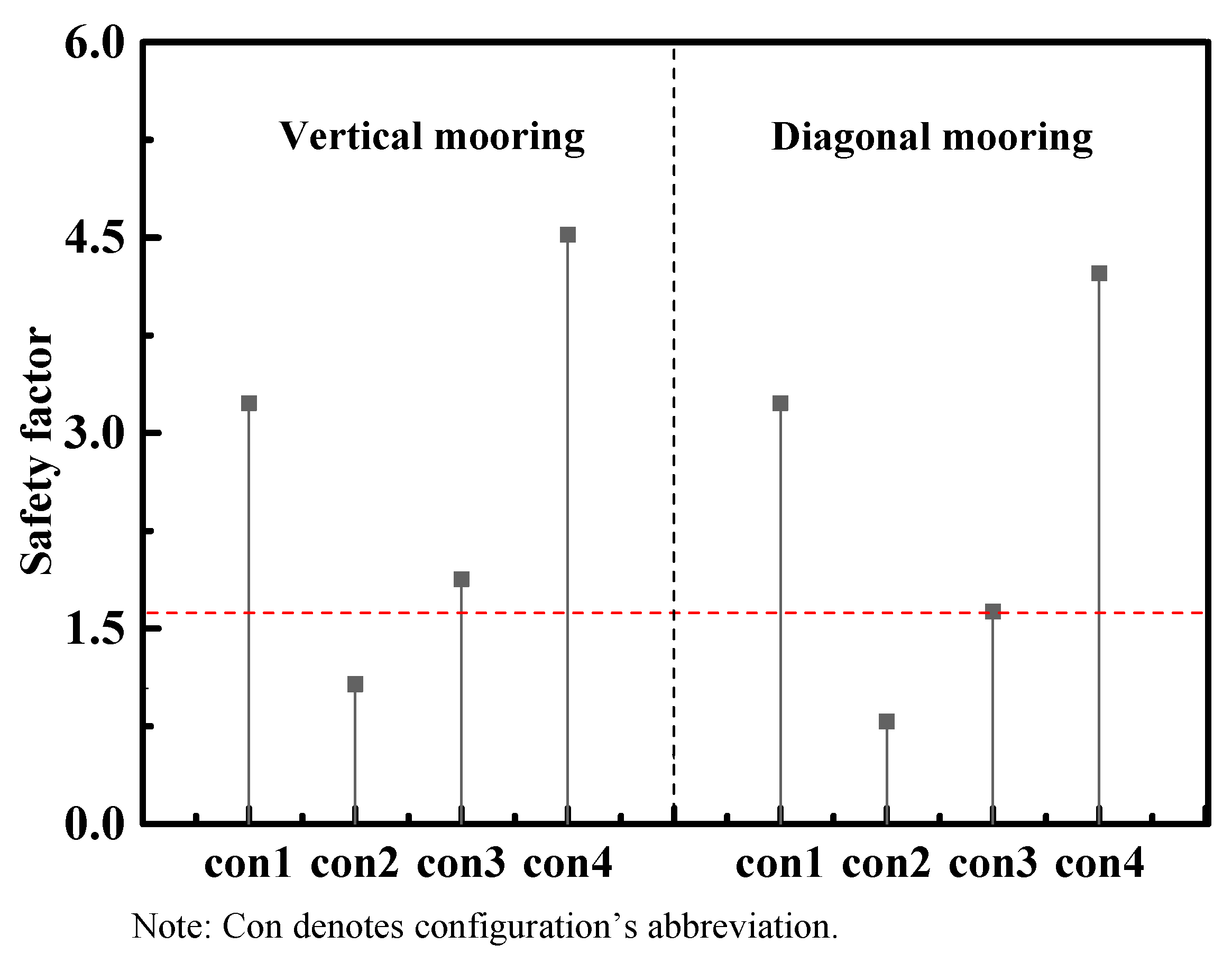
3.2. Dynamic Response
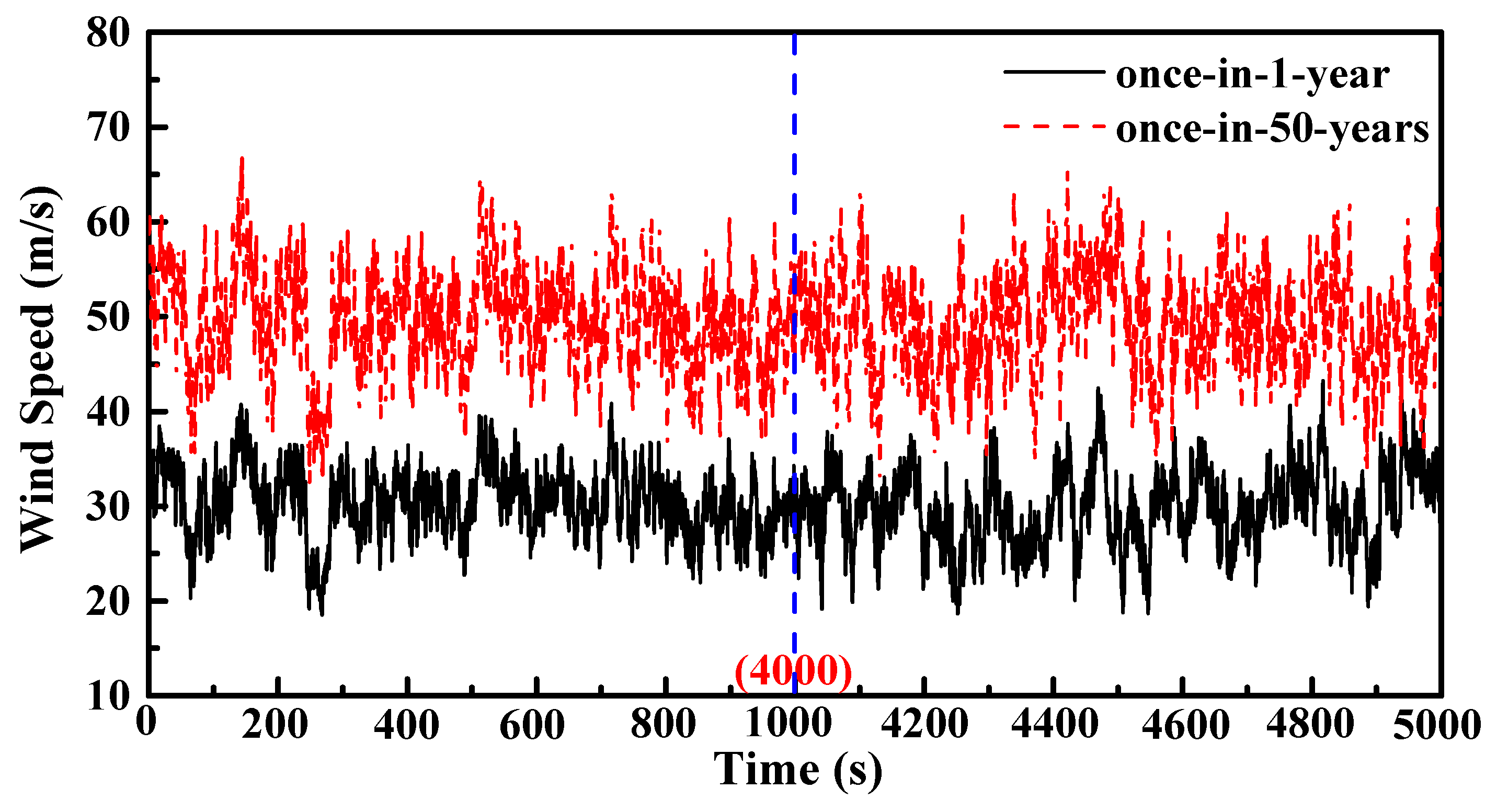
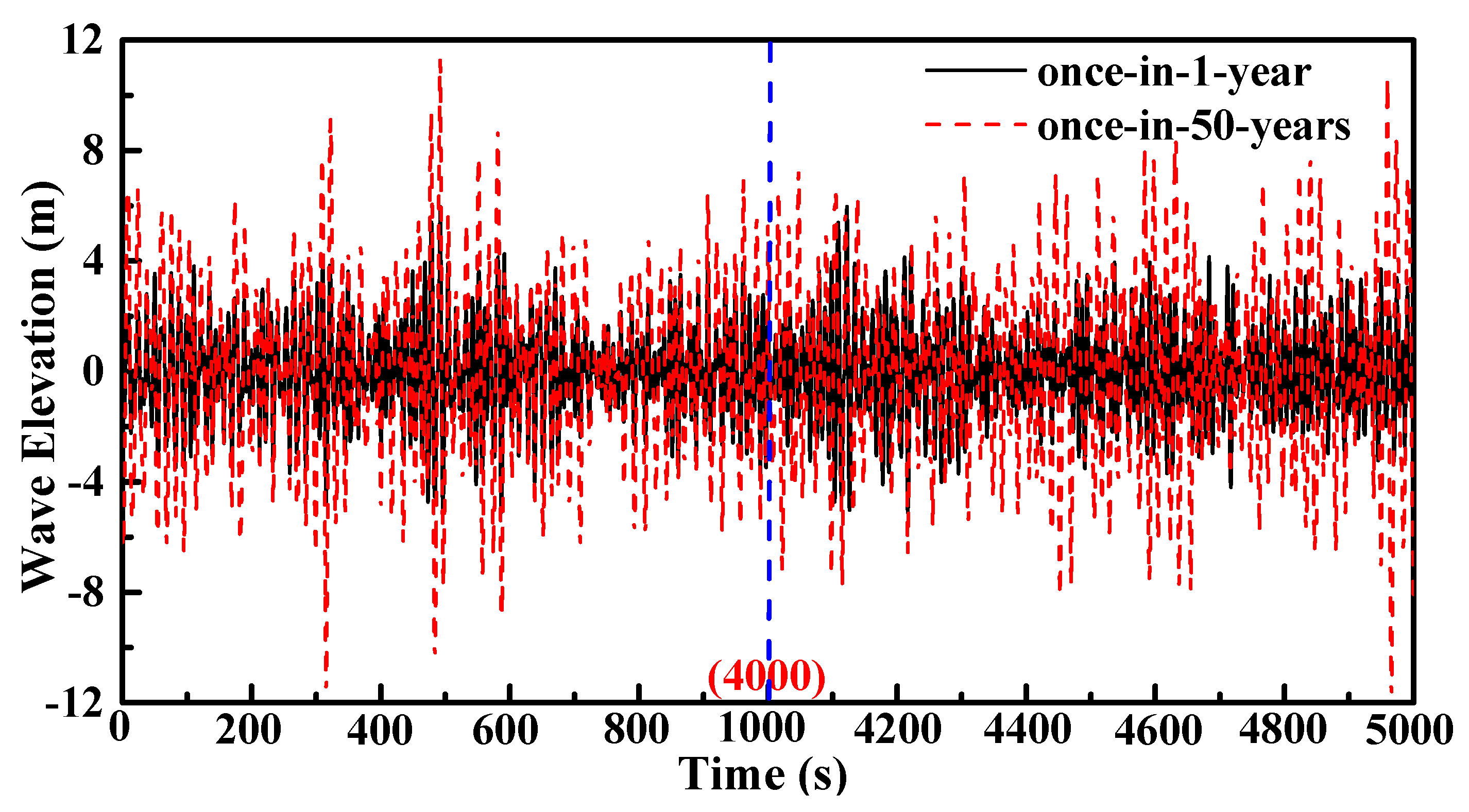
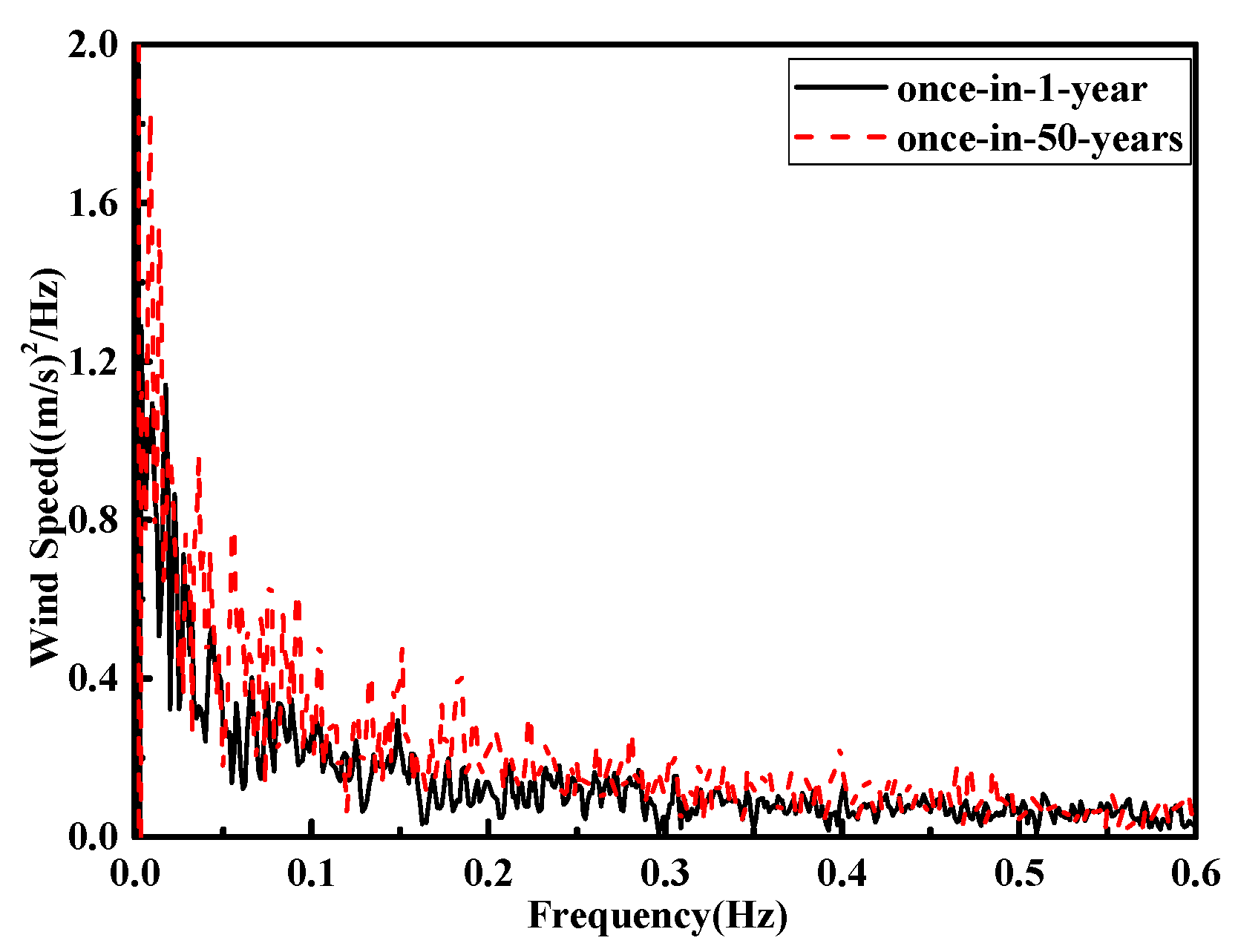
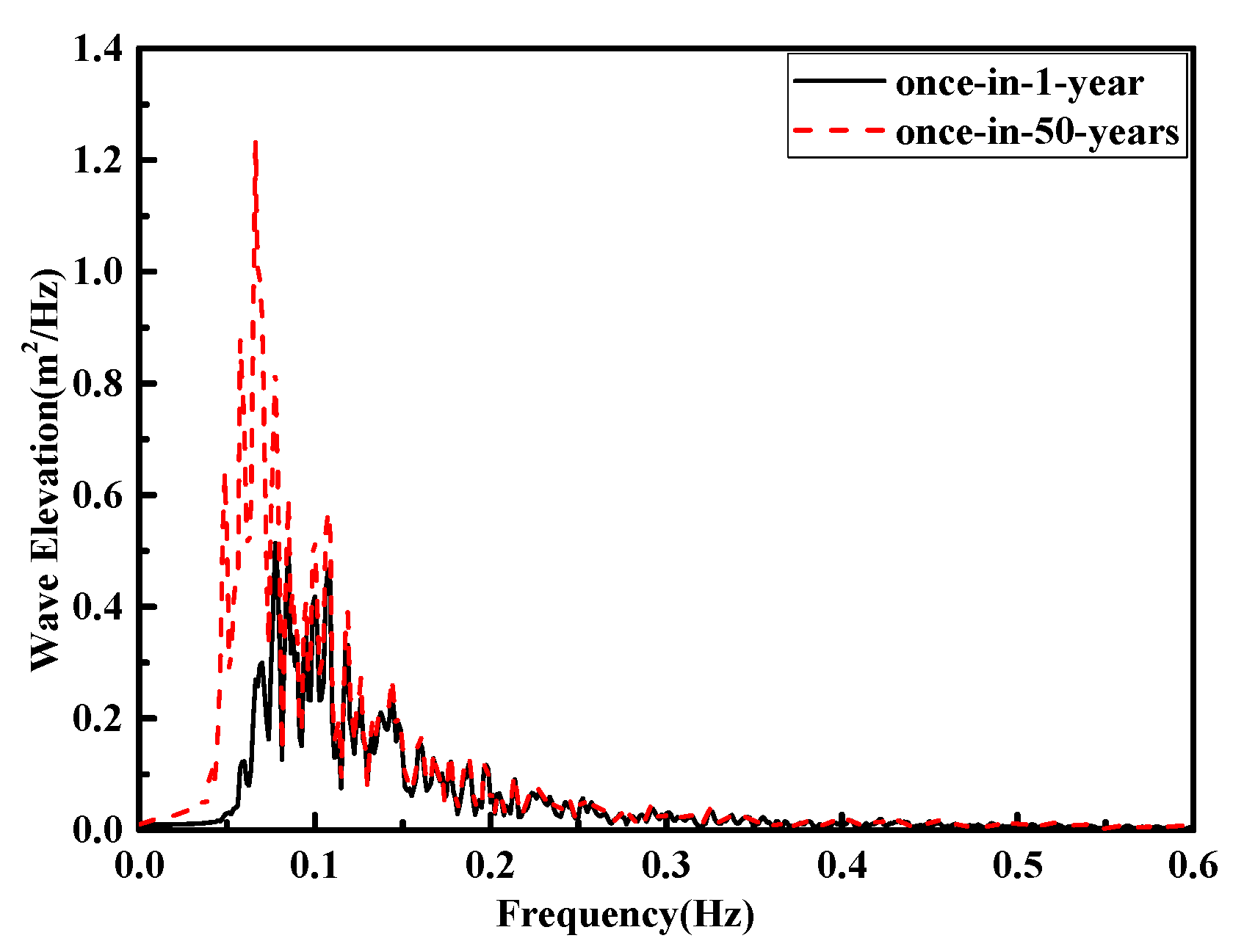
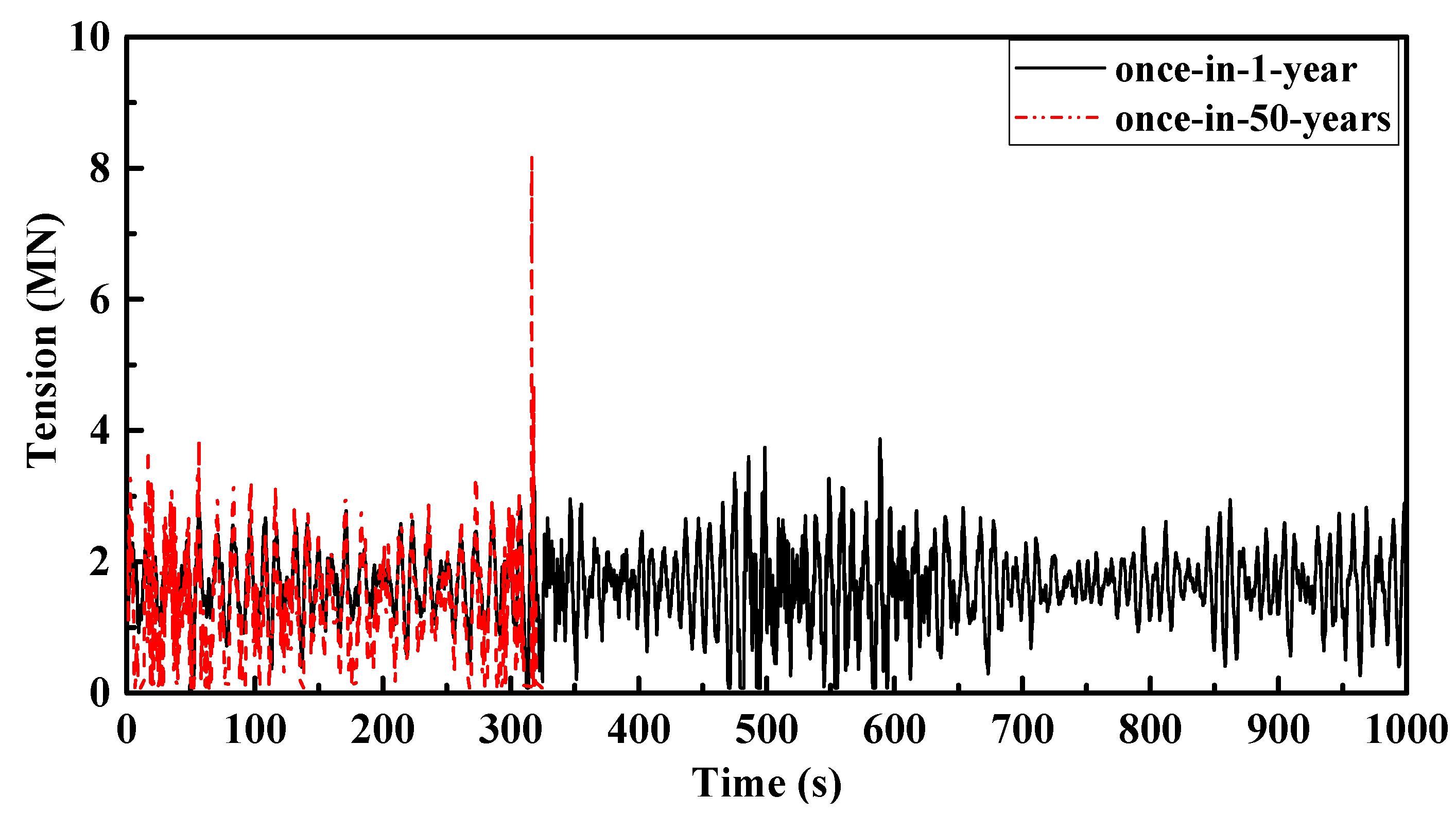
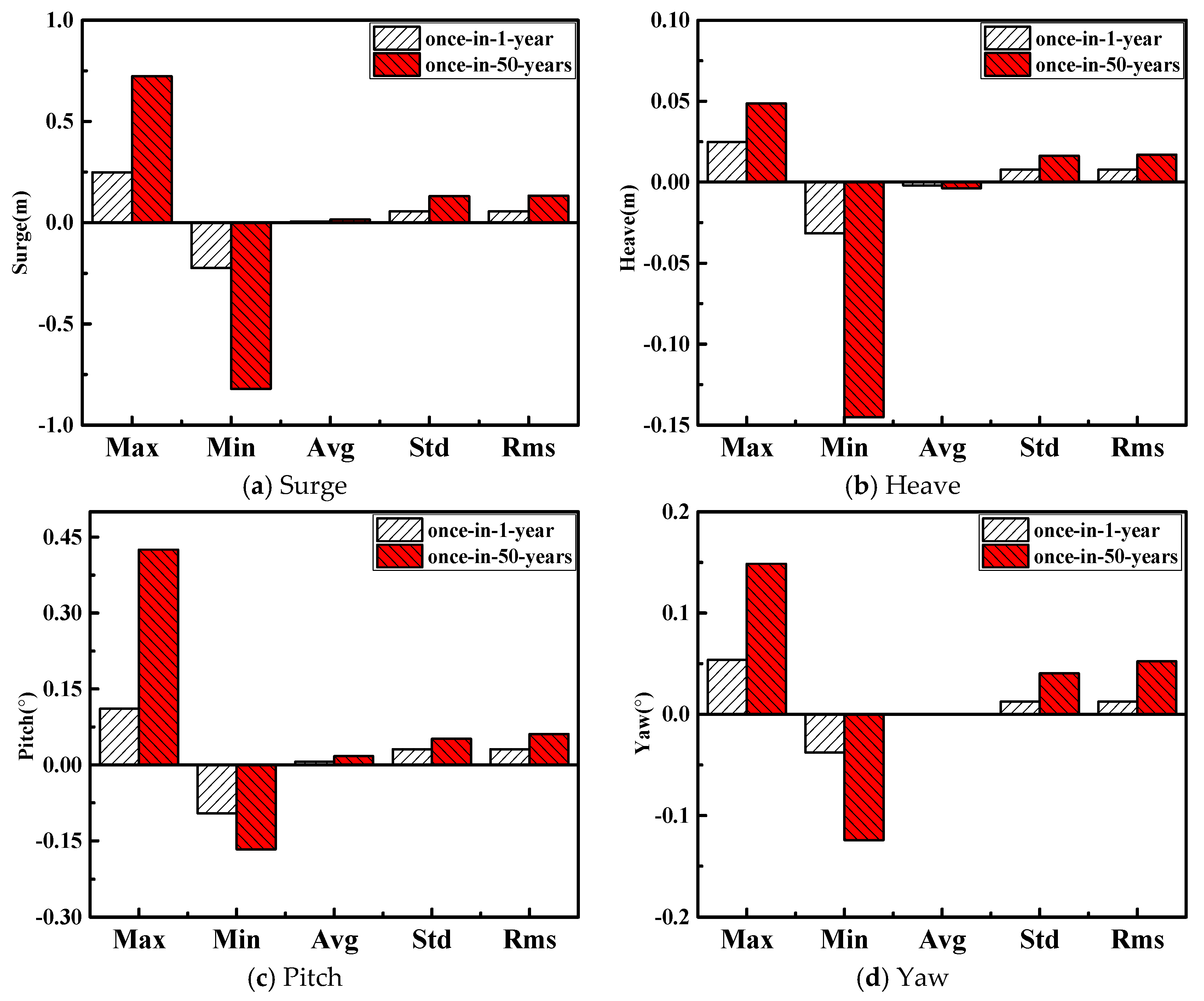
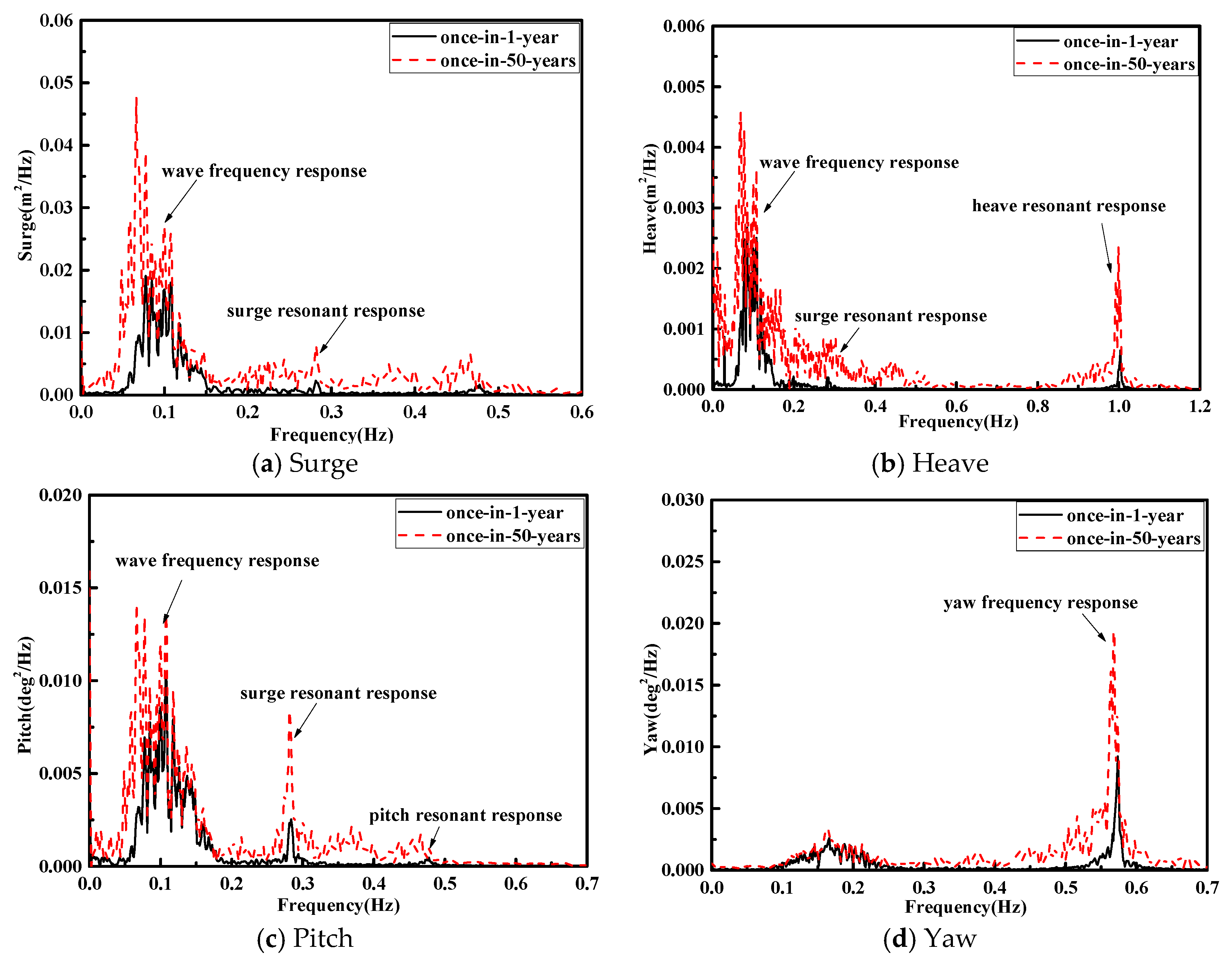
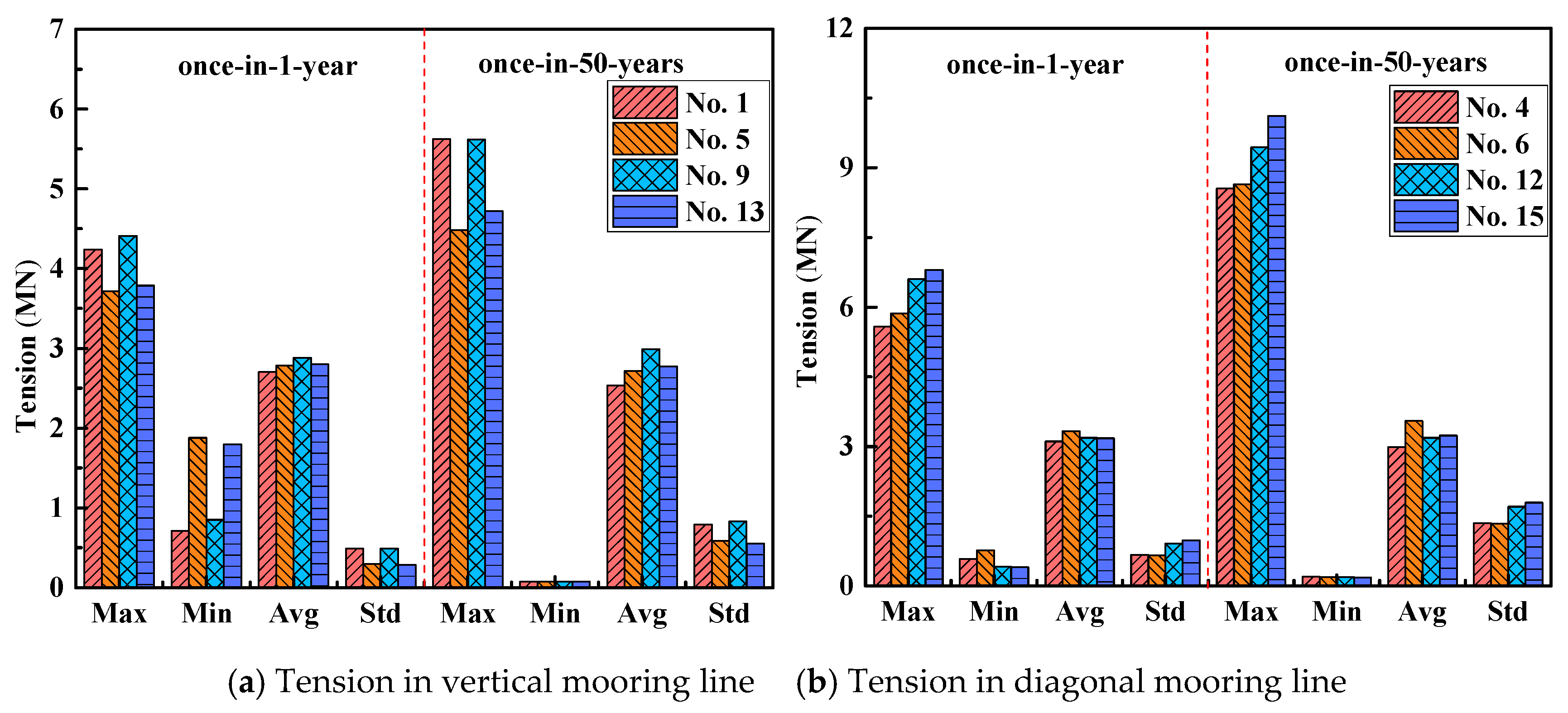
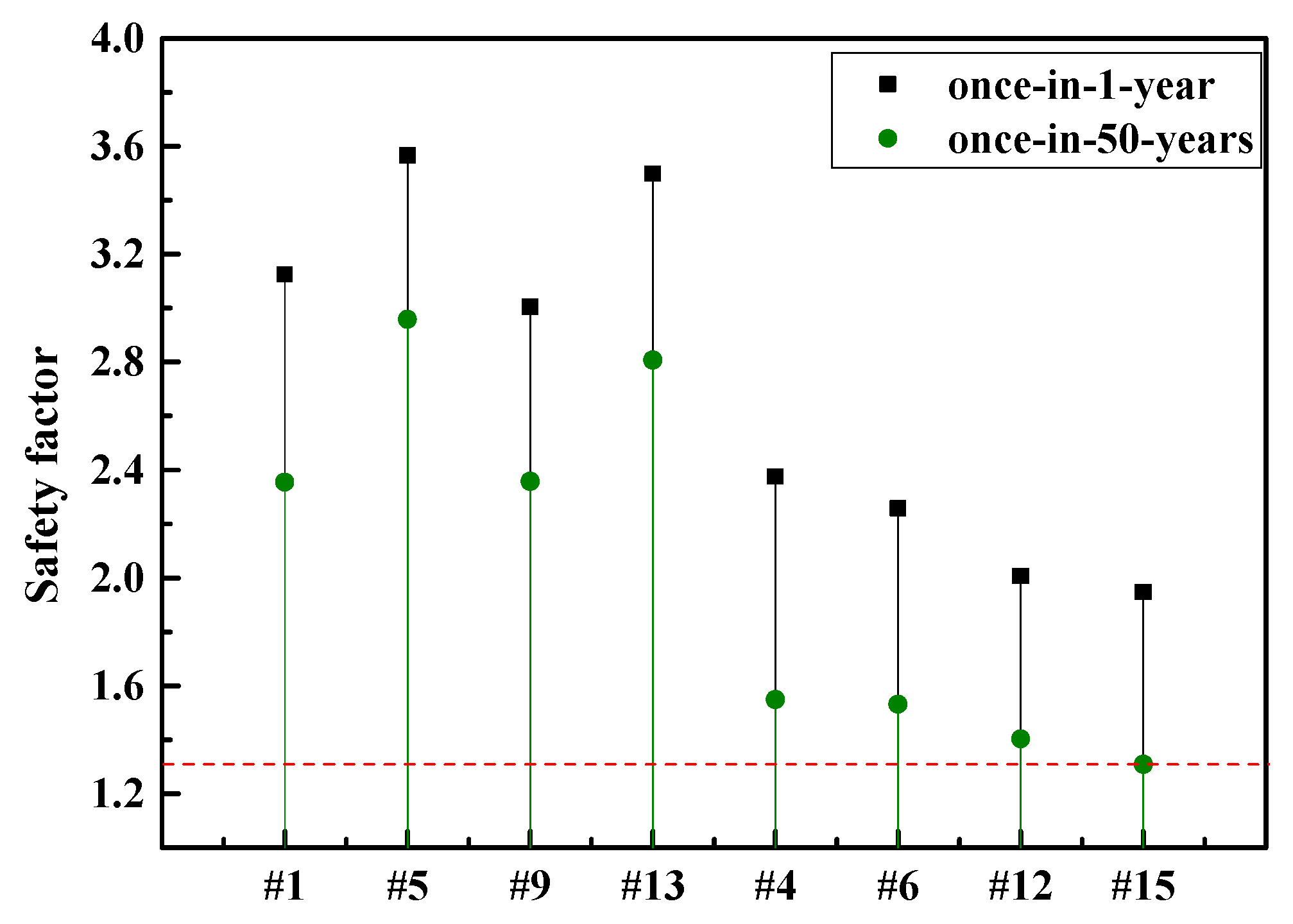
4. Dynamic Response of SFOWT under Extreme Sea-States
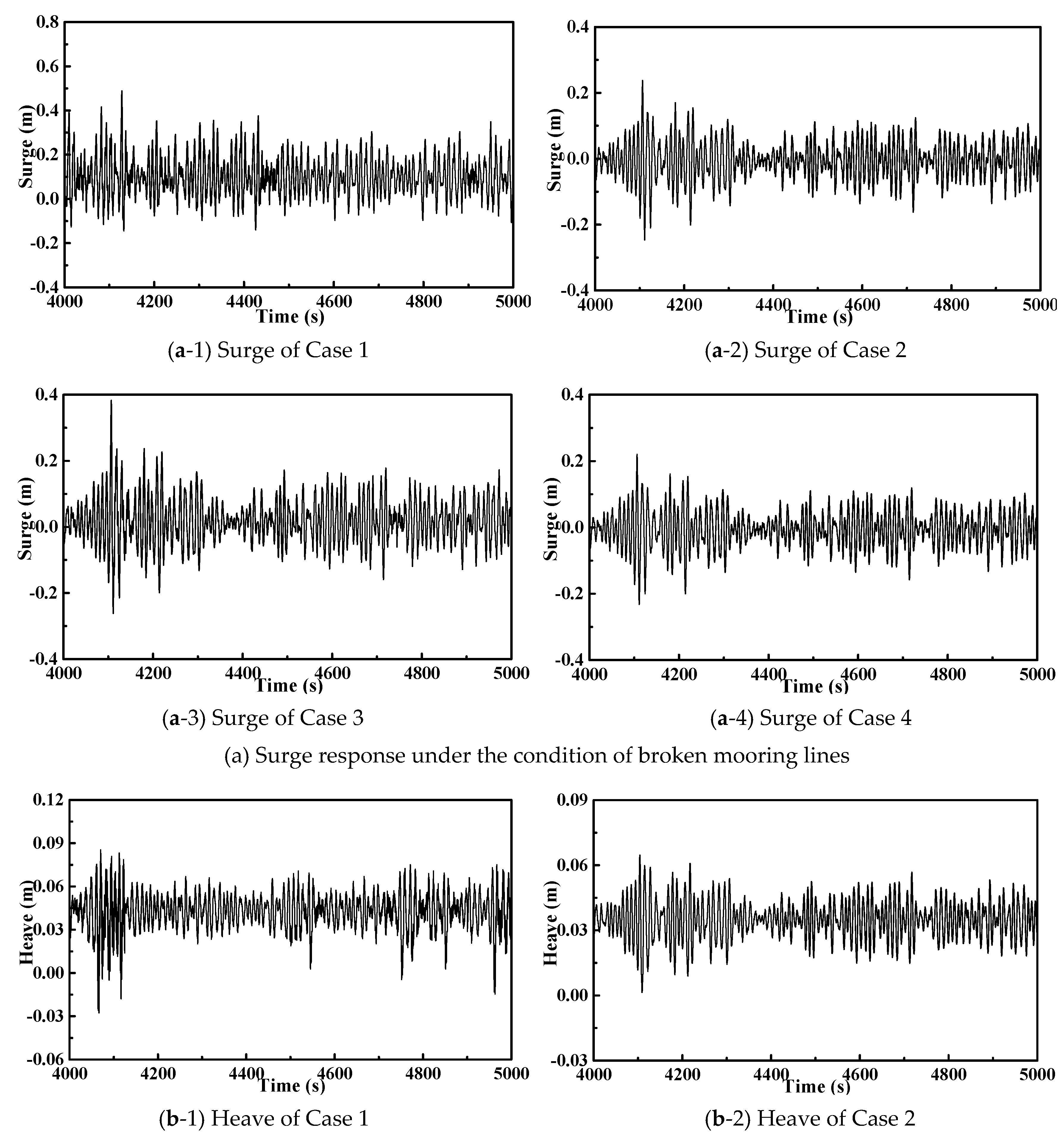
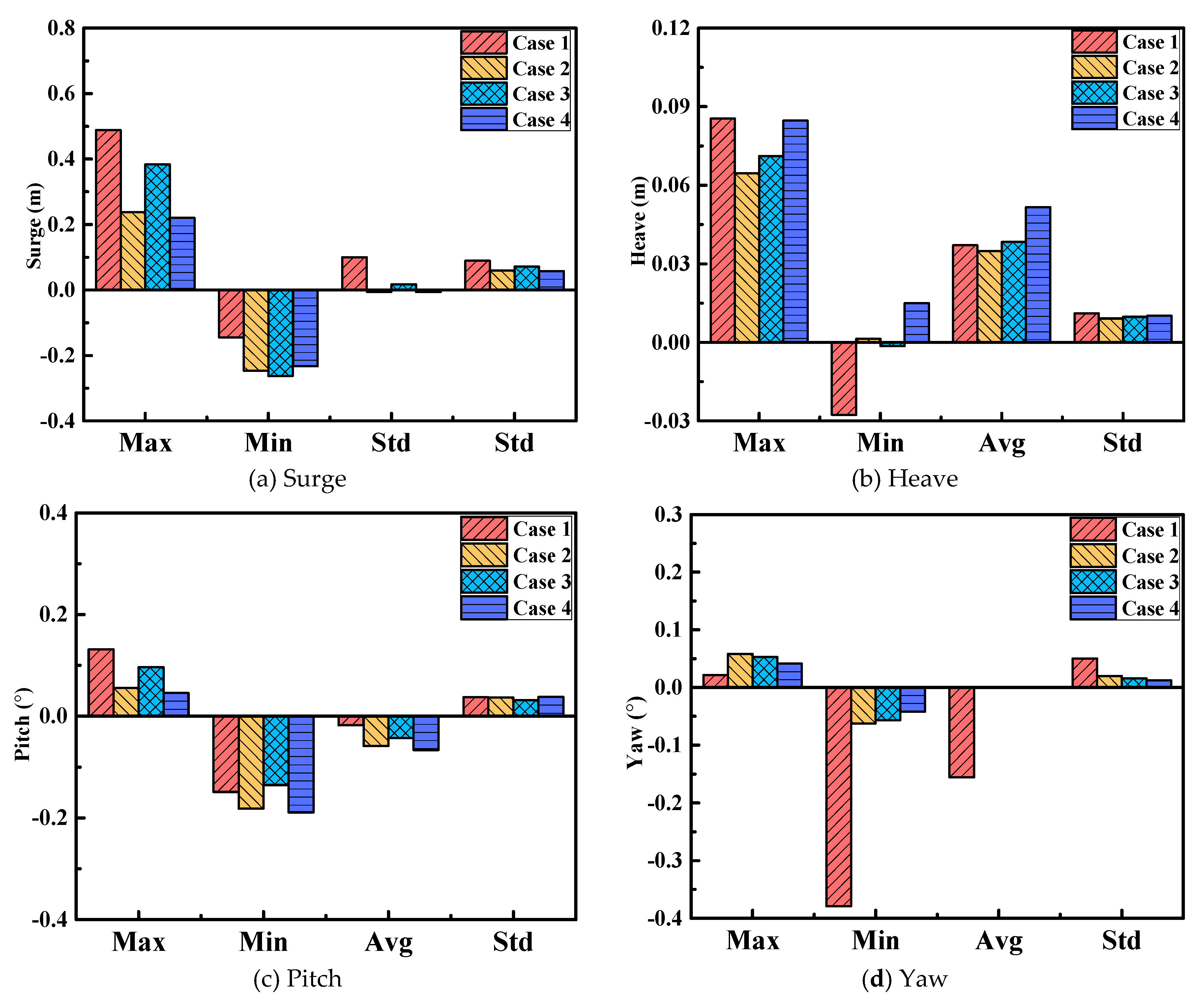
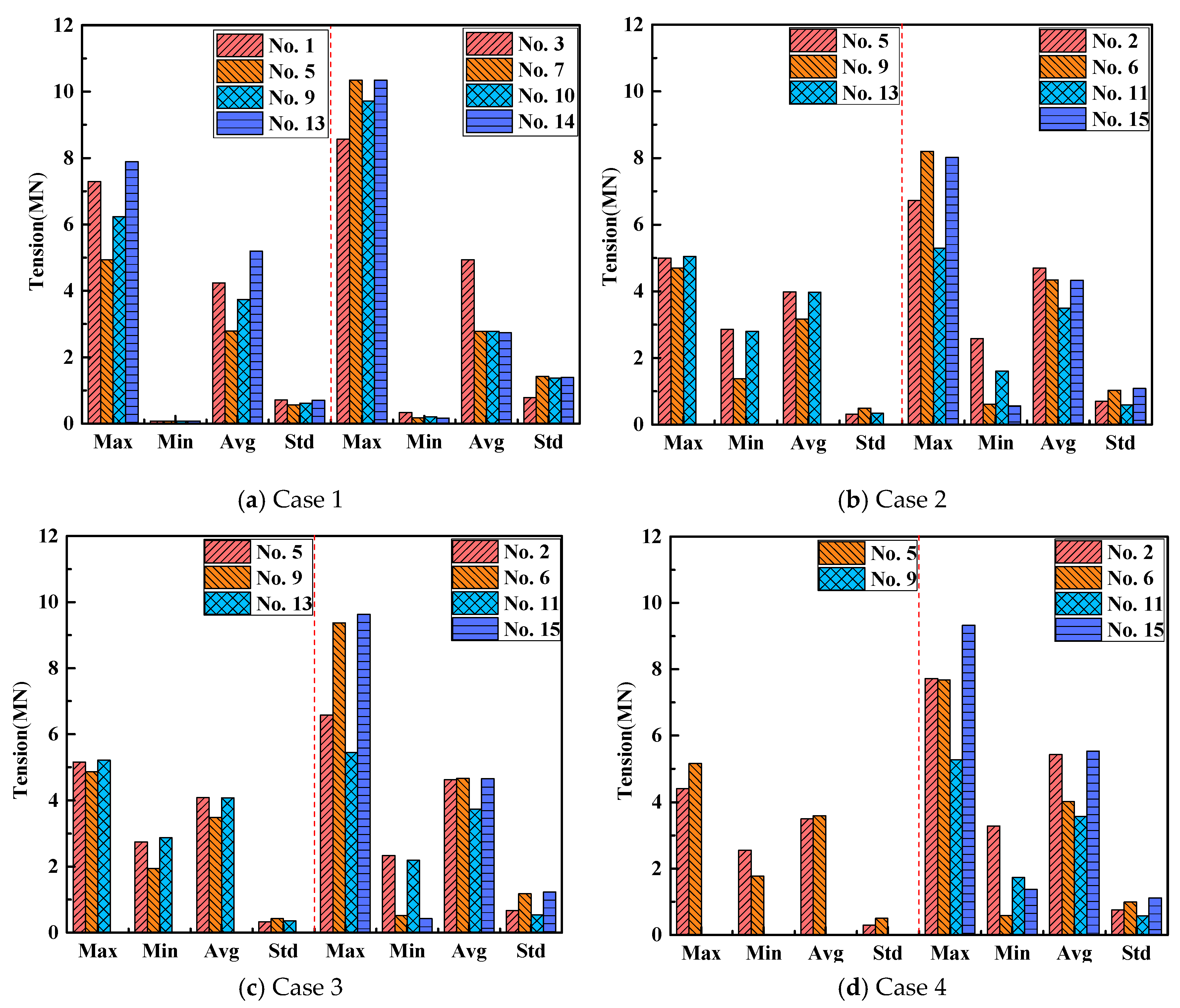
5. Dynamic Response of SFOWT with Broken Mooring Lines
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bachynski, E.E. Design and Dynamic Analysis of Tension Leg Platform Wind Turbines; Norwegian University of Science and Technology: Trondheim, Norway, 2014. [Google Scholar]
- Wen, B.; Tian, X.; Dong, X.; Peng, Z.; Zhang, W. Influences of surge motion on the power and thrust characteristics of an offshore floating wind turbine. Energy 2017, 141, 2054–2068. [Google Scholar] [CrossRef]
- Musial, W.; Butterfield, S.; Boone, A. Feasibility of floating platform systems for wind turbines. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 5 January 2004. [Google Scholar]
- Roddier, D.; Cermelli, C.; Aubault, A.; Weinstein, A. WindFloat: A floating foundation for offshore wind turbines. J. Renew. Sustain. Energy 2010, 2, 033104. [Google Scholar] [CrossRef]
- Hong, S.; Lee, I.; Park, S.H.; Lee, C.; Chun, H.-H.; Lim, H.C. An experimental study of the effect of mooring systems on the dynamics of a spar buoy-type floating offshore wind turbine. Int. J. Nav. Archit. Ocean Eng. 2015, 7, 559–579. [Google Scholar] [CrossRef][Green Version]
- Musial, W.; Butterfield, S.; Ram, B. Energy from offshore wind. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2006. [Google Scholar]
- Stewart, G.M.; Lackner, M.A. The effect of actuator dynamics on active structural control of offshore wind turbines. Eng. Struct. 2011, 33, 1807–1816. [Google Scholar] [CrossRef]
- Arapogianni, A.; Genachte, A.; Ochagavia, R.M.; Vergara, J.P.; Castell, D.; Tsouroukdissian, A.R.; Korbijn, J.; Bolleman, N.C.F.; Huera-Huarte, F.J.; Schuon, F.; et al. Deep Water: The next Step for Offshore Wind Energy; European Wind Energy Association: Belgium, Brussels, 2013. [Google Scholar]
- Bjoska, B.; Hanson, T.; Ruy, R.; Nielsen, F. Dynamic response and control of the hywind demo floating wind turbine. In Proceedings of the European Wind Energy Conference, Warsaw, Poland, 20–23 April 2010. [Google Scholar]
- Weinzettel, J.; Reenaas, M.; Solli, C.; Hertwich, E.G. Life cycle assess of a floating offshore wind turbine. Renew. Energy 2009, 34, 742–747. [Google Scholar] [CrossRef]
- Aubault, A.; Cermelli, C.; Roddier, D. WindFloat: A floating foundation for offshore wind turbines-part III: Structural analysis. In Proceedings of the ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering, Honolulu, HI, USA, 31 May–5 June 2009; American Society of Mechanical Engineers: New York, NY, USA, 2009; pp. 213–220. [Google Scholar]
- Chengxi, L.; Jun, Z. Nonlinear Coupled Dynamics Analysis of A Truss Spar Platform. China Ocean Eng. 2016, 30, 835–850. [Google Scholar]
- Lefebvre, S.; Collu, M. Preliminary design of a floating support structure for 5 MW offshore wind turbine. Ocean Eng. 2012, 40, 15–26. [Google Scholar] [CrossRef]
- Polaris Wind Power Network. The Success Assembly of the First Floating Offshore Wind Power Base in the World. Polaris Wind Power. 2017. Available online: http://news.bjx.com.cn/html/20170207/806667.shtml (accessed on 7 February 2017).
- Coulling, A.J.; Goupee, A.J.; Robertson, A.N.; Jonkman, J.M.; Dagher, H.J. Validation of a FAST semi-submersible floating wind turbine numerical model with DeepCwind test data. J. Renew. Sustain. Energy 2013, 5, 023116. [Google Scholar] [CrossRef]
- Duan, F.; Hu, Z.; Niedzwecki, J.M. Model test investigation of a spar floating wind turbine. Mar. Struct. 2016, 49, 76–96. [Google Scholar] [CrossRef]
- Benassai, G.; Campanile, A.; Piscopo, V.; Scamardella, A. Optimization of Mooring Systems for Floating Offshore Wind Turbines. Coast. Eng. J. 2015, 57, 1550021-1–1550021-9. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Q.; Incecik, A.; Peyrard, C.; Wan, D. Establishing a fully coupled CFD analysis tool for floating offshore wind turbines. Renew. Energy 2017, 112, 280–301. [Google Scholar] [CrossRef]
- Benassai, G.; Campanile, A.; Piscopo, V.; Scamardella, A. Ultimate and accidental limit state design for mooring systems of floating offshore wind turbines. Ocean Eng. 2014, 92, 64–74. [Google Scholar] [CrossRef]
- Yasunori, N.; Yusuke, M. Research and development about the mechanisms of a single point mooring system for offshore wind turbines. Ocean Eng. 2018, 147, 431–446. [Google Scholar]
- Utsunomiya, T.; Yoshida, S.; Ookubo, H.; Sato, I.; Ishida, S. Dynamic analysis of a floating offshore wind turbine under extreme environmental conditions. J. Offshore Mech. Arct. Eng. 2014, 136, 02094. [Google Scholar] [CrossRef]
- Bae, Y.H.; Kim, M.H.; Kim, H.C. Performance changes of a floating offshore wind turbine with broken mooring line. Renew. Energy 2017, 101, 364–375. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Q.; Liu, L.; Tang, Y. Transient response of a SPAR-type floating offshore wind turbine with fractured mooring lines. Renew. Energy 2018, 122, 576–588. [Google Scholar] [CrossRef]
- Ahmed, M.O.; Yenduri, A.; Kurian, V.J. Evaluation of the dynamic responses of truss SPAR platforms for various mooring configurations with damaged lines. Ocean Eng. 2016, 123, 411–421. [Google Scholar] [CrossRef]
- Ding, H.; Han, Y.; Zhang, P. Dynamic analysis of a new type of floating platform for offshore wind turbine. In Proceedings of the 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–2 July 2016. [Google Scholar]
- Han, Y.; Le, C.; Ding, H.; Cheng, Z.; Zhang, P. Stability and dynamic response analysis of a submerged tension leg platform for offshore wind turbines. Ocean Eng. 2017, 129, 68–82. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Ding, H. Study on the coupled dynamic responses of a submerged floating wind turbine under different mooring conditions. Energies 2019, 12, 418. [Google Scholar] [CrossRef]
- Jonkman, J.M. Dynamics of Offshore Floating Wind Turbines-Model Development and Verification. Wind Energy 2009, 12, 459–492. [Google Scholar] [CrossRef]
- Jonkman, B.J. TurbSim User’s Guide: Version 1.50. Available online: https://www.nrel.gov/docs/fy09osti/46198.pdf (accessed on 26 January 2019).
- Det Norske Veritas. SESAM User Manual HydroD; Det Norske Veritas: Oslo, Norway, 2013. [Google Scholar]
- Bae, Y.H.; Kim, M.H. Rotor-floater-tether coupled dynamic analysis including second-order sum-frequency wave loads for a mono-column-TLP-type FOWT (floating offshore wind turbine). Ocean Eng. 2013, 61, 109–122. [Google Scholar] [CrossRef]
- Zhao, Y.S.; Yang, J.M.; He, Y.P. Coupled dynamic response analysis of a multi-column tension-leg-type floating wind turbine. China Ocean Eng. 2016, 30, 505–520. [Google Scholar] [CrossRef]
- Li, Y.; Tang, Y.-G.; Zhu, Q.; Qu, X.-Q.; Wang, B.; Zhang, R.-Y. Effects of second-order wave forces and aerodynamic forces on dynamic responses of a TLP-type floating offshore wind turbine considering the set-down motion. J. Renew. Sustain. Energy 2017, 9, 063302. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009. [Google Scholar]
- DNV. Offshore Standard DNV-OS-J103. Design of Floating Wind Turbine Structures; Det Norske Veritas: Oslo, Norway, 2013. [Google Scholar]
- DNV. DNV-RP-C205 Environmental Conditions and Environmental Loads; Det Norske Veritas: Oslo, Norway, 2010. [Google Scholar]
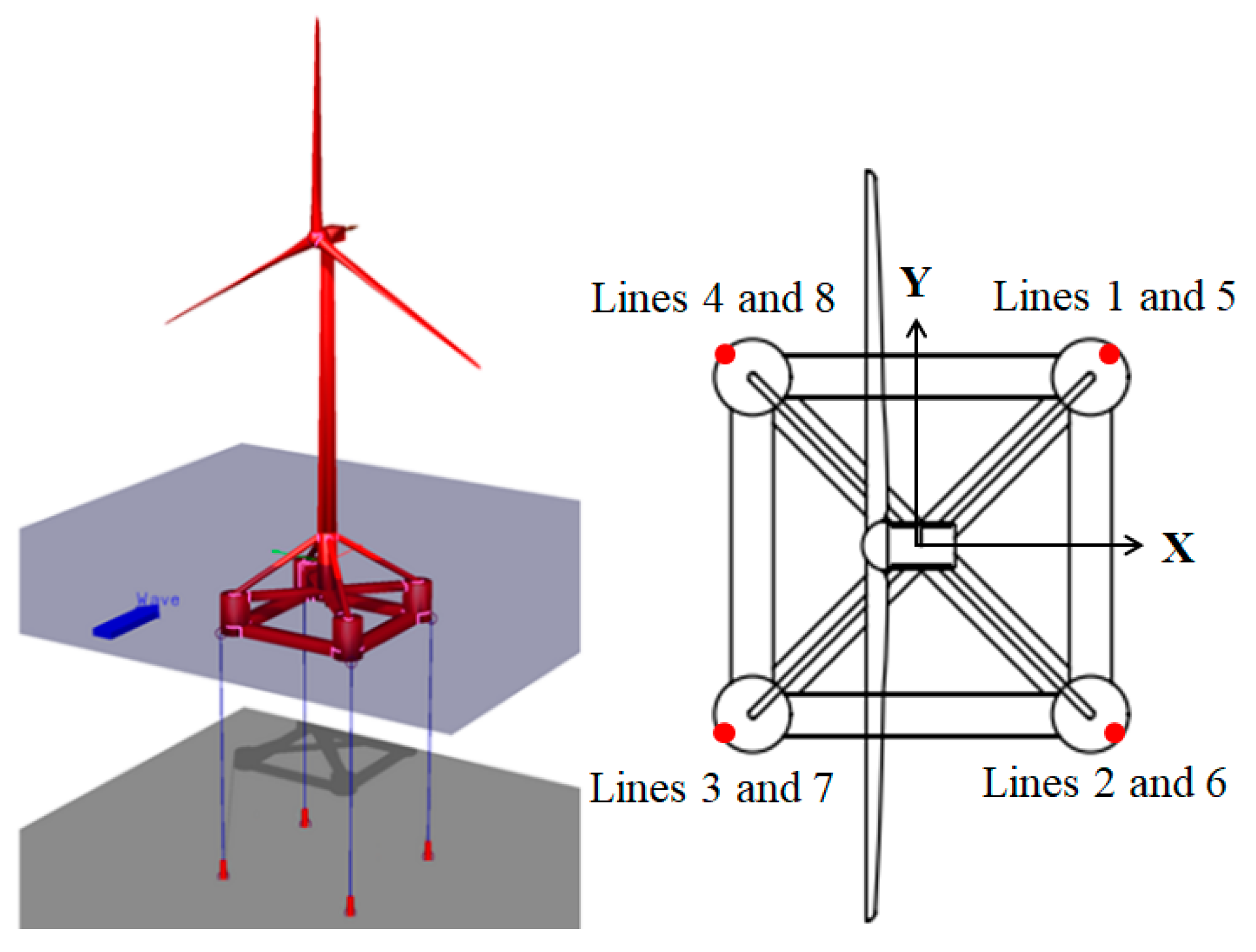




| Parameter | Value |
|---|---|
| Diameter of vertical pontoon | 9 m |
| Height of vertical pontoon | 12 m |
| Distance between vertical pontoons | 40 m |
| Height of column | 20 m |
| Column diameter | 6 m |
| Mass of platform | 2,734,200 kg |
| Mass moment of inertia in roll | 7.818 × 108 kg m2 |
| Mass moment of inertia in pitch | 7.818 × 108 kg m2 |
| Mass moment of inertia in yaw | 1.359 × 109 kg m2 |
| COG of the platform during operation | (0, 0, −16.75 m) |
| Area of water plane during operation | 51.45 m2 |
| Parameter | Value |
|---|---|
| Diameter of mooring line | 0.127 m |
| Mass of per unit length | 116.027 kg/m |
| Breaking strength | 13,249 kN |
| Axial stiffness of mooring line (EA) | 2.47 × 109 N |
| Parameter | Value |
|---|---|
| Rated power | 5 MW |
| Turbine control | Variable speed, collective pitch |
| Rotor diameter | 126 m |
| Hub diameter | 3 m |
| Hub height | 90 m |
| Cut-in, rated, cut-out wind speeds | 3, 11.4, and 25 m/s |
| Mass of impeller | 110,000 kg |
| Mass of nacelle | 240,000 kg |
| Mass of tower | 347,460 kg |
| Centroid coordinates | (−0.2 m, 0, 74 m) |
| State | Analysis Method | Safety Factor |
|---|---|---|
| Normal operation state (NOS) | Dynamic | 1.67 |
| Extreme sea-states | Dynamic | 1.3 |
| Broken mooring lines | Dynamic | 1.0 |
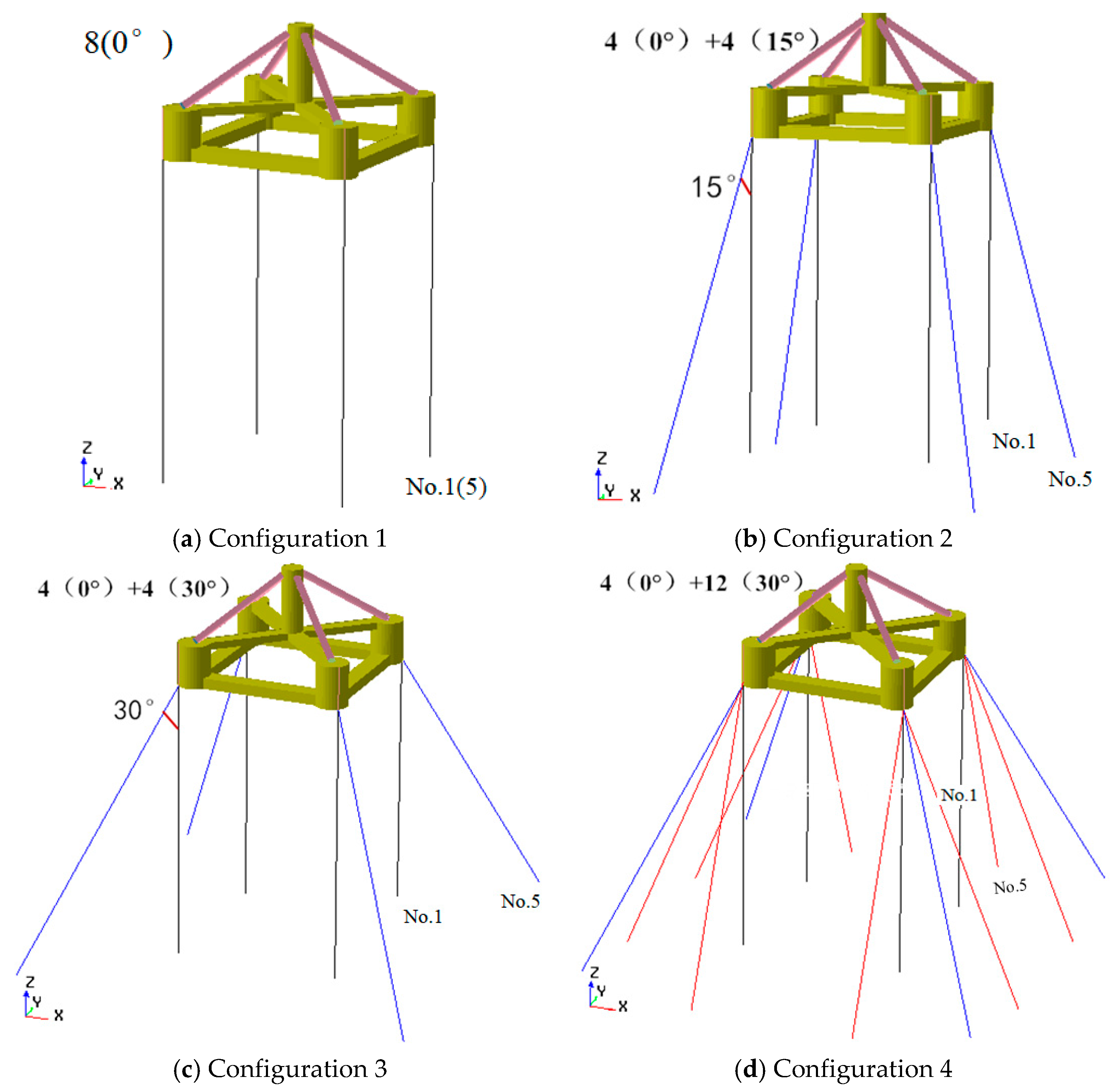
| Mooring Configuration | No. of Vertical Mooring Lines | No. of Diagonal Mooring Lines | Inclination Angle |
|---|---|---|---|
| Configuration 1 | 8 | - | - |
| Configuration 2 | 4 | 4 | 15° |
| Configuration 3 | 4 | 4 | 30° |
| Configuration 4 | 4 | 12 | 30° |
| Mooring Configuration | Pretension in Vertical Lines/kN | Pretension in Diagonal Lines/kN |
|---|---|---|
| Configuration 1 | 3600 | - |
| Configuration 2 | 3600 | 3727 |
| Configuration 3 | 3600 | 4157 |
| Configuration 4 | 1800 | 2078 |
| Extreme Sea-States | Wind Speed (m/s) | Hs (m) | Tp (s) |
|---|---|---|---|
| Once-in-1-year | 30 | 7.1 | 11.9 |
| Once-in-50-years | 49 | 13 | 15.5 |
| Case | Broken Mooring Line |
|---|---|
| Case 1 | No. 15 |
| Case 2 | No. 1 |
| Case 3 | Nos. 1 and 12 |
| Case 4 | Nos. 1 and 13 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Le, C.; Ding, H.; Zhang, P.; Zhang, J. Dynamic Response for a Submerged Floating Offshore Wind Turbine with Different Mooring Configurations. J. Mar. Sci. Eng. 2019, 7, 115. https://doi.org/10.3390/jmse7040115
Li Y, Le C, Ding H, Zhang P, Zhang J. Dynamic Response for a Submerged Floating Offshore Wind Turbine with Different Mooring Configurations. Journal of Marine Science and Engineering. 2019; 7(4):115. https://doi.org/10.3390/jmse7040115
Chicago/Turabian StyleLi, Yane, Conghuan Le, Hongyan Ding, Puyang Zhang, and Jian Zhang. 2019. "Dynamic Response for a Submerged Floating Offshore Wind Turbine with Different Mooring Configurations" Journal of Marine Science and Engineering 7, no. 4: 115. https://doi.org/10.3390/jmse7040115
APA StyleLi, Y., Le, C., Ding, H., Zhang, P., & Zhang, J. (2019). Dynamic Response for a Submerged Floating Offshore Wind Turbine with Different Mooring Configurations. Journal of Marine Science and Engineering, 7(4), 115. https://doi.org/10.3390/jmse7040115






