Effects of Swell on Wave Height Distribution of Energy-Conserved Bimodal Seas
Abstract
1. Introduction
2. Material and Methods
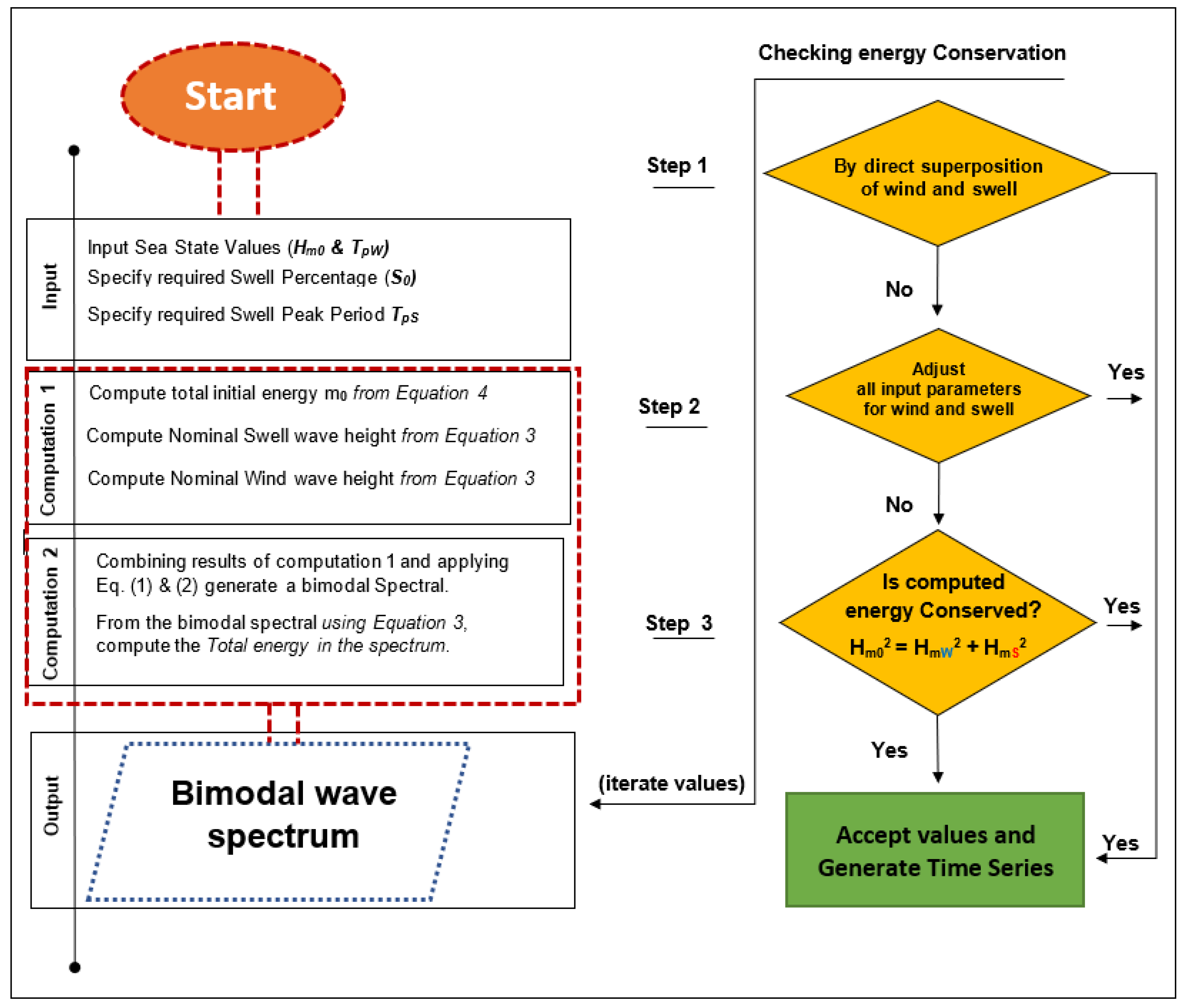
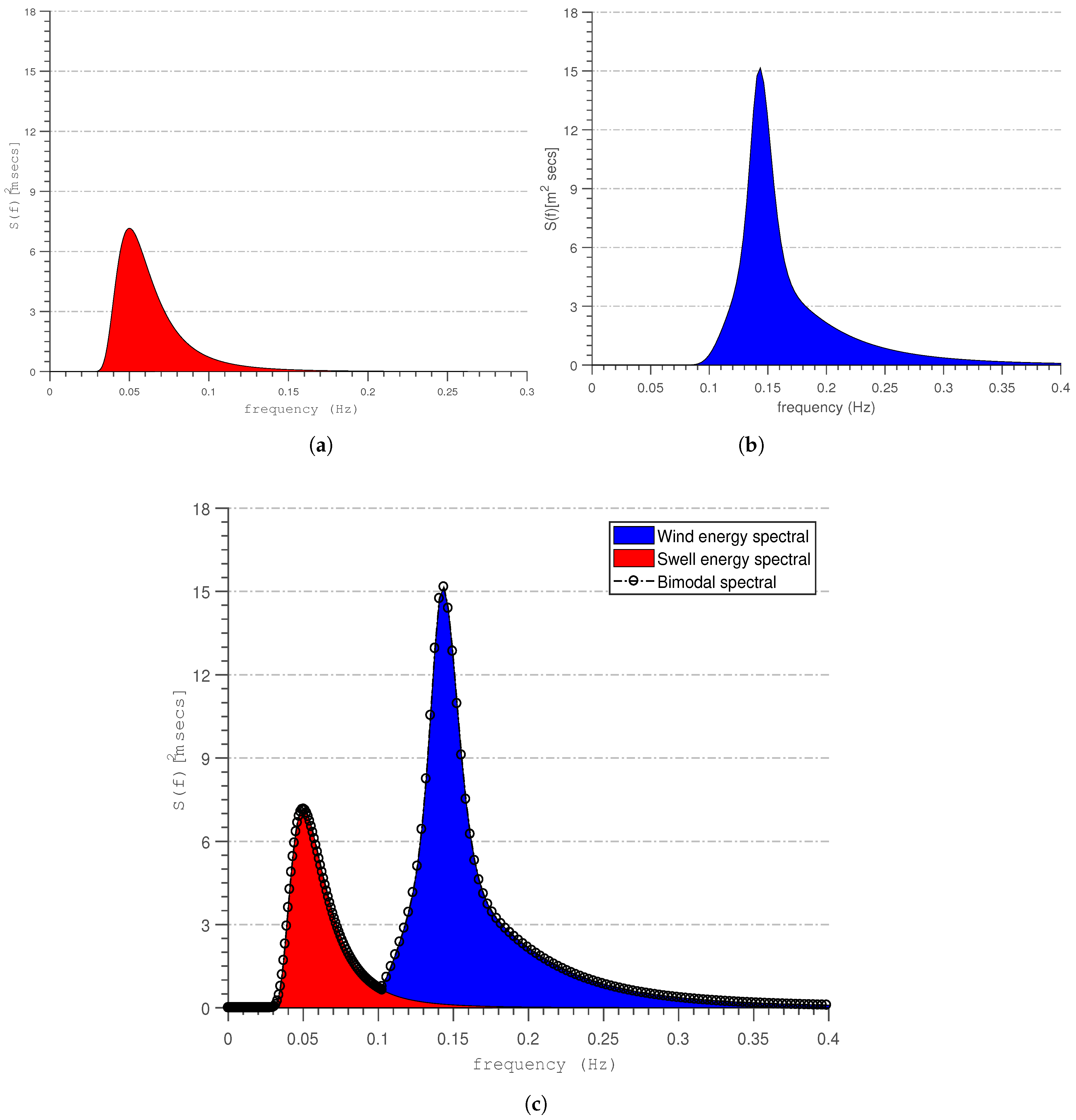
2.1. Development of a Bimodal Spectrum
2.2. Estimation of Total Energy in the Bimodal Spectrum
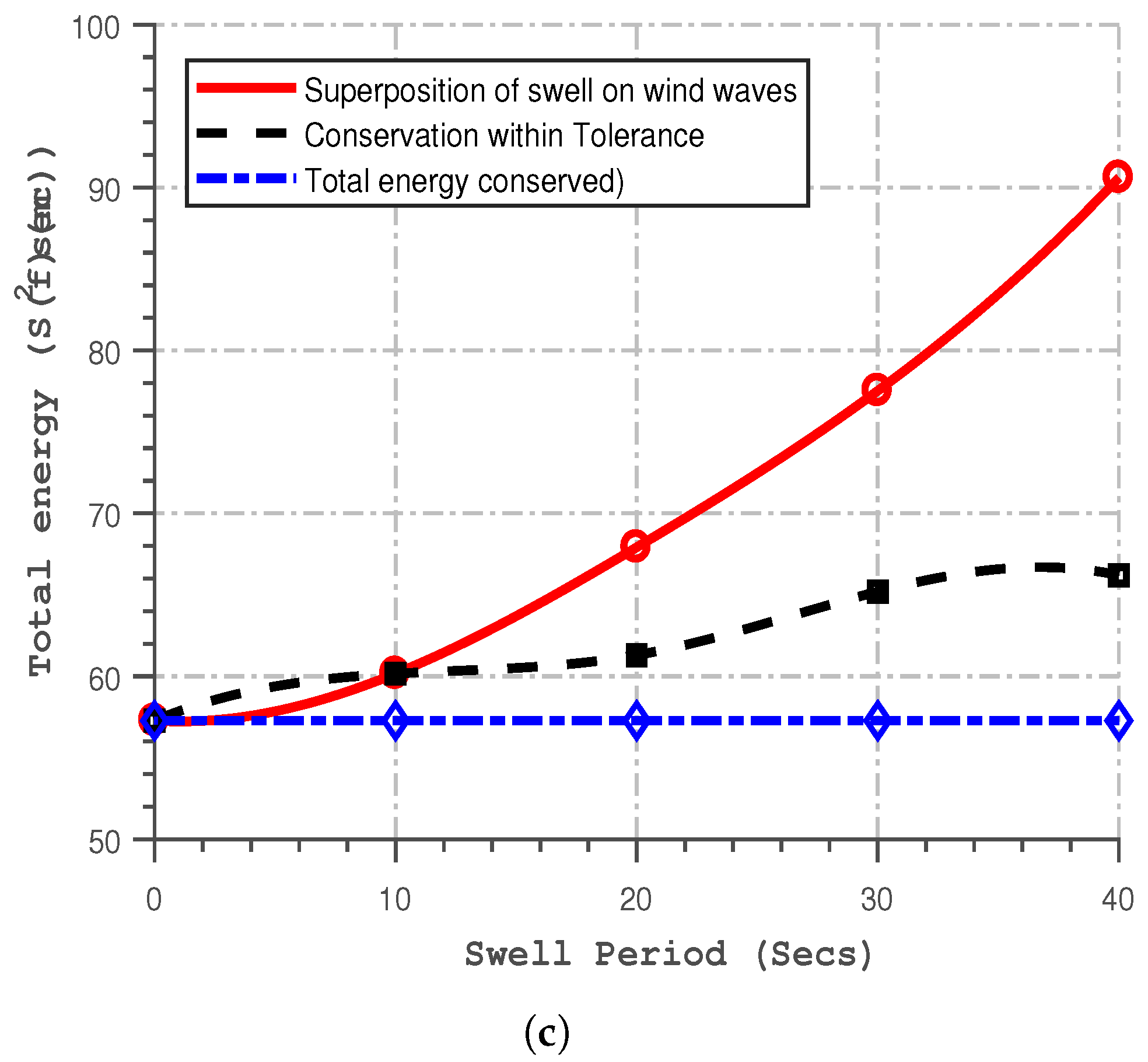
2.3. Ensuring Energy Conservation in the Bimodal Spectrum
2.4. Determination of Kurtosis and Skewness of the Bimodal Spectrum
2.5. Wave Height Extraction Using Numerical Model
3. Results and Discussions
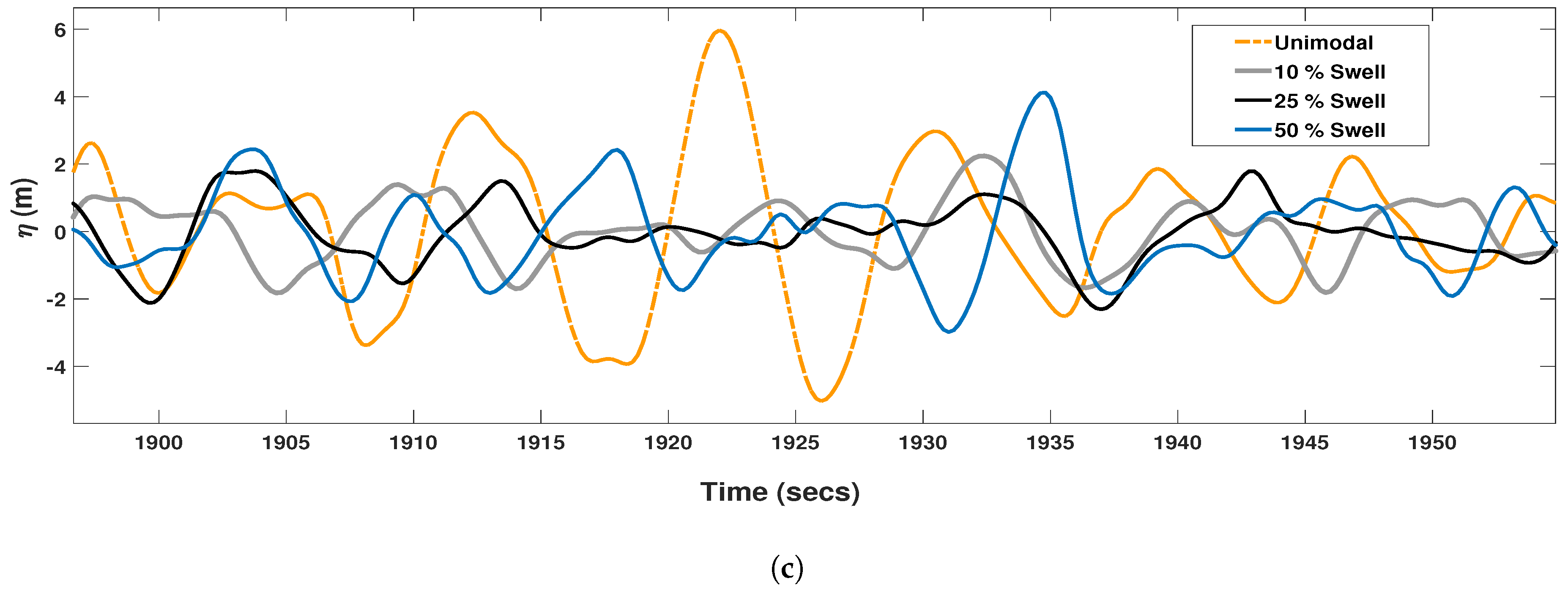
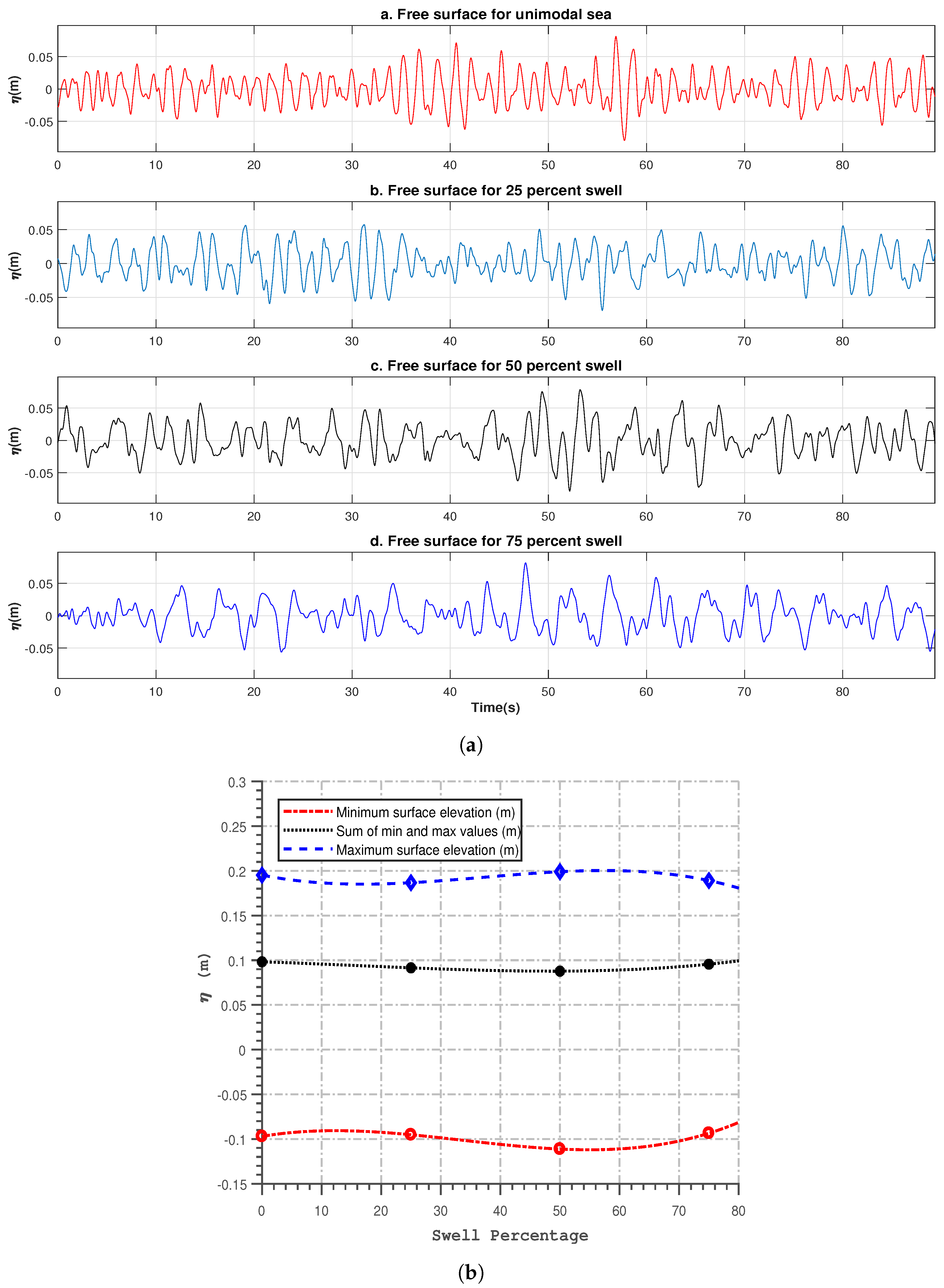
3.1. Analysis of Free Surface From the Energy-Conserved Bimodal Spectrum
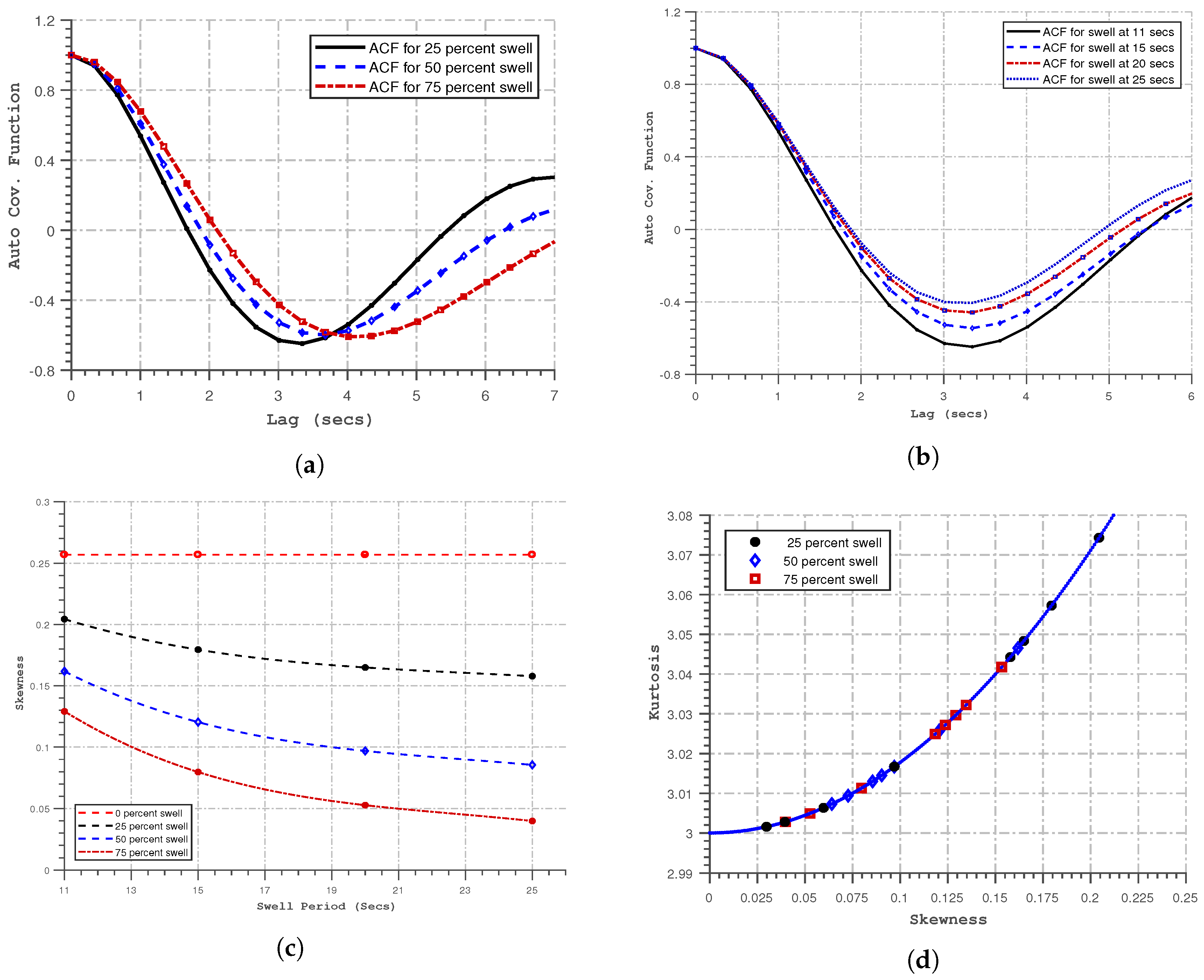
3.2. Analysis of Kurtosis and Skewness
4. Influence of Swell on Wave Height Distribution
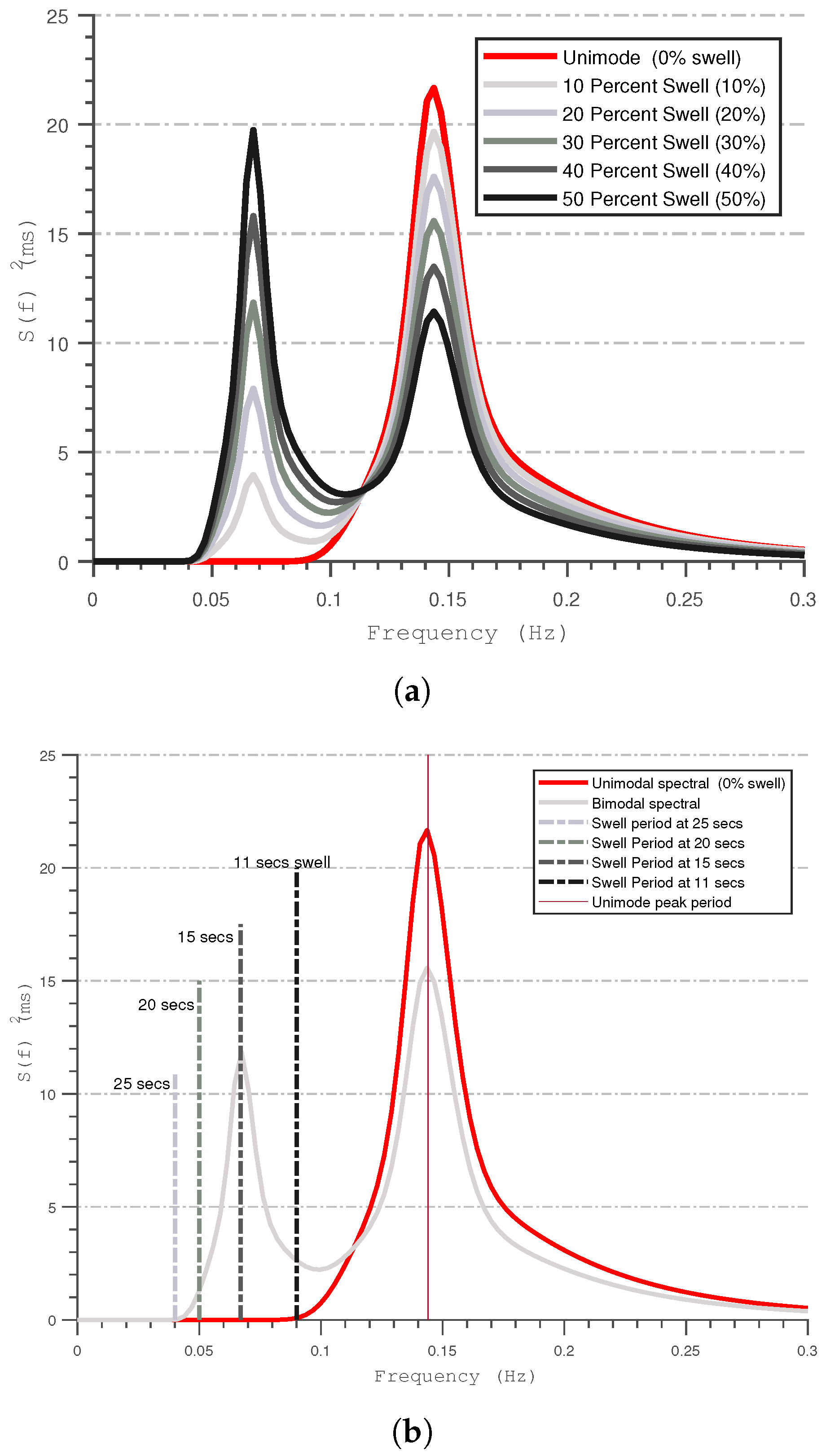
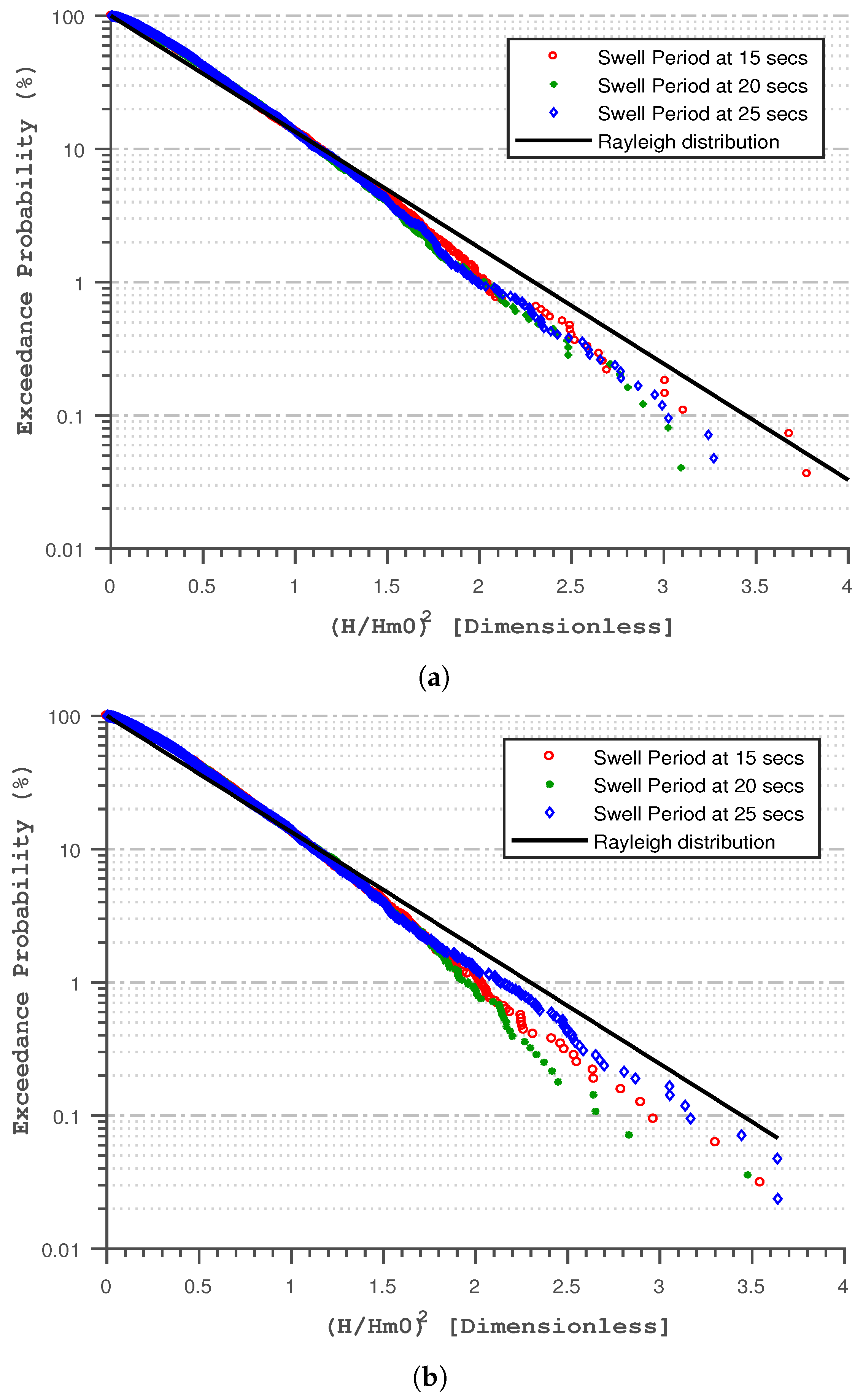
4.1. Influence of Swell Period
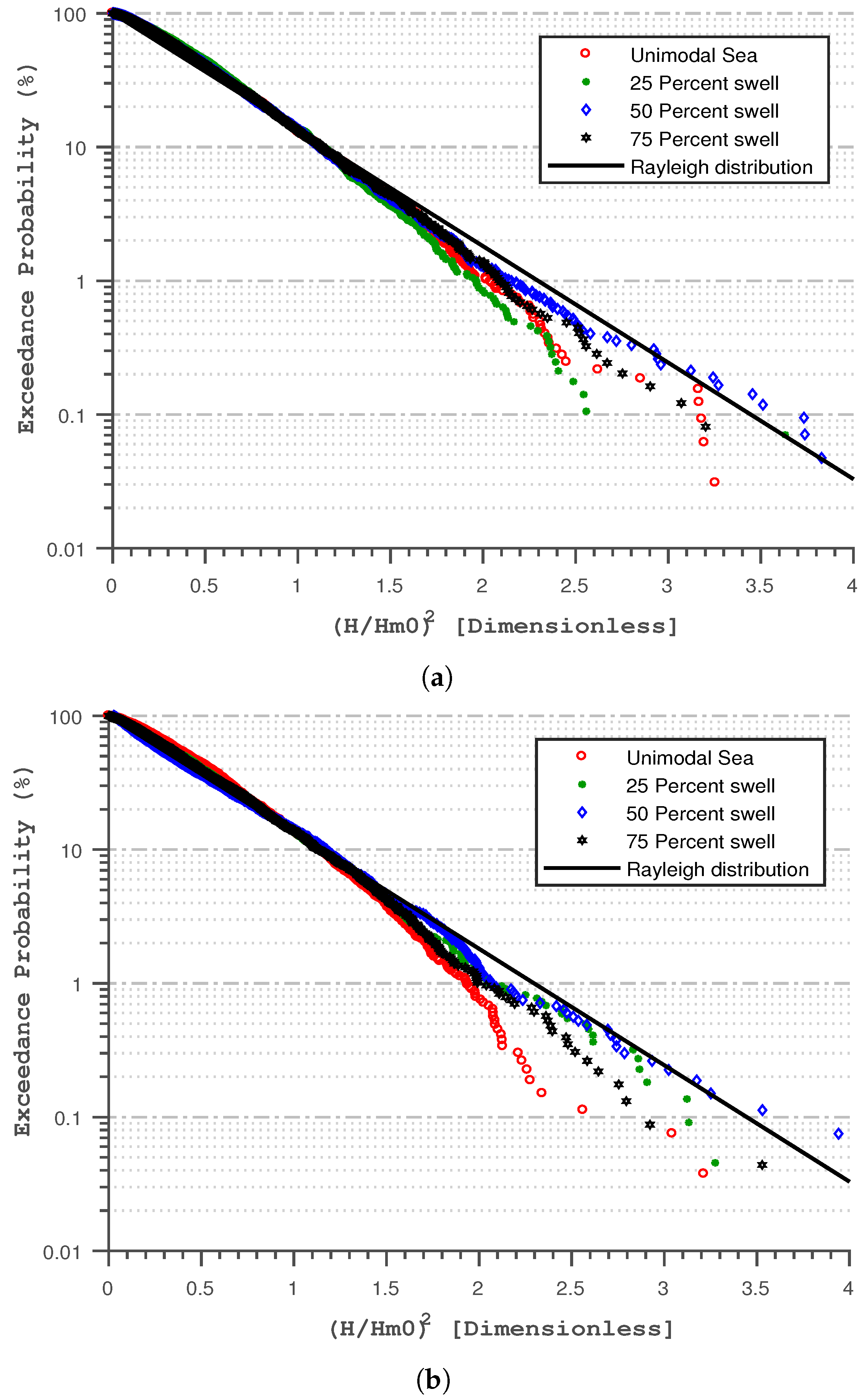
4.2. Influence of Swell Percentages
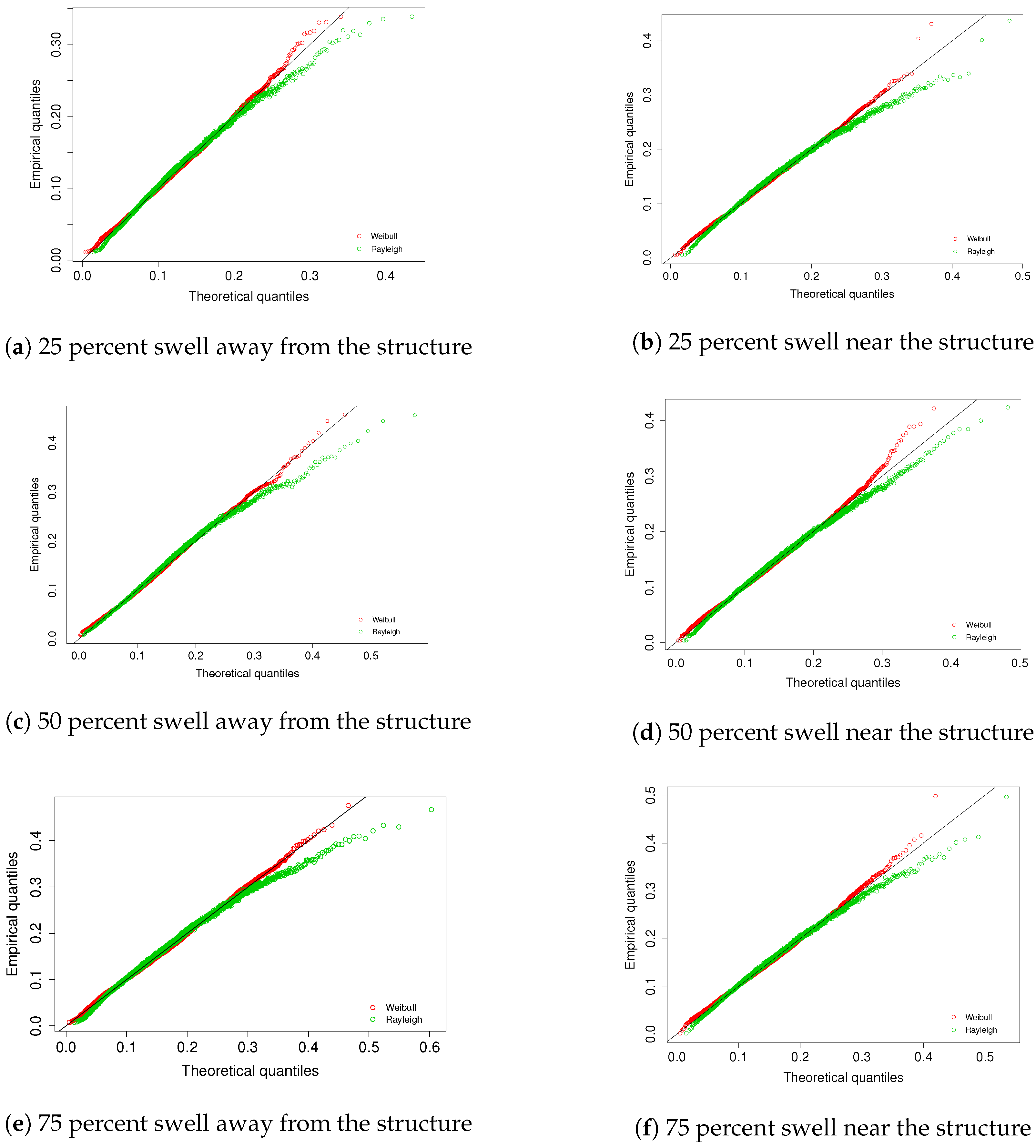
4.3. Patterns of Wave Height Distribution
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ACF | Auto-covariance function |
| FFT | Fast Fourier Transform |
| IHC | The Environmental Hydraulics Institute Cantabria |
| IFFT | Inverse Fast Fourier Transform |
| H | Significant wave height |
| Jonswap | Joint North Sea Wave Project |
| RANS | Reynolds-Averaged Navier Stokes (RANS) |
| Kurtosis | |
| Skewness | |
| SSER | Sea-Swell energy ratio |
| UKCP | United kingdom climate projections |
| VOF | Volume of Fluid |
References
- Jenkins, G.; Murphy, J.; Sexton, D.; Lowe, J.; Jones, P.; Kilsby, C. UK Climate Projections: Briefing Report; Technical Report; Met Office Hadley Centre: Exeter, UK, 2009.
- Hawkes, P.J.; Coates, T.; Jones, R.J. Impacts of Bimodal Seas on Beaches, Hydraulic Research Wallingford; HR Wallingford Report; HR wallingford Lld.: Wallingford, UK, 1998; p. 80. [Google Scholar]
- Forristall, G. On the Statistical Distribution of Wave Heights in a Storm. Geophys. Res. 1978, 83, 2353–2358. [Google Scholar] [CrossRef]
- Guedes Soares, C. Representation of Double-Peaked Sea Wave Spectra. Ocean Eng. 1984, 11, 185–207. [Google Scholar] [CrossRef]
- Tayfun, A.; Fedele, F. Wave-height distributions and nonlinear effects. Ocean Eng. 2007, 34, 1631–1649. [Google Scholar] [CrossRef]
- Arena, F.; Guedes Soares, C. Nonlinear High Wave Groups in Bimodal Sea States. J. Waterw. Port Coast. Ocean Eng. 2009, 135, 69–79. [Google Scholar] [CrossRef]
- Burcharth, H.F. The effect of wave grouping on on-shore structures. Coast. Eng. 1978, 2, 189–199. [Google Scholar] [CrossRef]
- Battjes, J.A.; Groenendijk, H.W. Wave height distributions on shallow foreshores. Coast. Eng. 2000, 40, 161–182. [Google Scholar] [CrossRef]
- Reeve, D.; Chadwick, A.; Fleming, C. Coastal Engineering: Processes, Theory and Design Practice; Spon: London, UK, 2015; 518p. [Google Scholar]
- Longuet-Higgins, M.S. On the statistical distribution of the heights of sea waves. J. Mar. Res. 1952, 11. [Google Scholar] [CrossRef]
- Tayfun, M.A. Distribution of crest-to-trough waveheights. J. Waterw. Ports Coast. 1981, 116, 149–158. [Google Scholar]
- Naess, A. On the distribution of crest-to-trough waveheights. Ocean Eng. 1985, 12, 221–234. [Google Scholar] [CrossRef]
- Vinje, T. The statistical distribution of waveheights in a random seaway. Appl. Ocean Res. 1989, 11, 143–152. [Google Scholar] [CrossRef]
- Boccotti, P. Wave Mechanics for Ocean Engineering; Elsevier Science B.V.: Amsterdam, The Netherlands, 2000; p. 479. [Google Scholar]
- Rodriguez, G.; Guedes Soares, C.; Pacheco, M.; Perez-Martell, E. Wave Height Distribution in Mixed Sea States. Offshore Mech. Arct. Eng. 2002, 124, 34–40. [Google Scholar] [CrossRef]
- Petrova, P.G.; Guedes Soares, C. Wave height distributions in bimodal sea states from offshore basin. Ocean Eng. 2011, 38, 658–672. [Google Scholar] [CrossRef]
- Nørgaard, J.Q.H.; Lykke Andersen, T. Can the Rayleigh distribution be used to determine extreme wave heights in non-breaking swell conditions? Coast. Eng. 2016, 111, 50–59. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.; Bouws, E.; Carlson, H.; Cartwright, D.; Enke, K.; Ewing, J.; Gienapp, H.; Hasselmann, D.; Kruseman, P.; et al. Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP); Deutsches Hydrographisches Institut: Hamburg, Germany, 1973; Volume A8. [Google Scholar]
- Goda, Y. Random Seas and Design of Maritime Structures; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2010; p. 708. [Google Scholar]
- Marthinsen, T.; Winterstein, S. On the skewness of random surface waves. In Proceedings of the 2nd International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 14–19 June 1992; pp. 472–478. [Google Scholar]
- Cavannie, A.; Arhan, M.; Ezraty, R. A statistical relationship between individual heights and periods of storm waves. In Proceedings of the 1st Conference on Behaviour of Offshore Structures, Trondheim, Norway, 2–5 August 1976; pp. 354–360. [Google Scholar]
- Lara, J.L.; Ruju, A.; Losada, I. RANS modelling of long waves induced by a transient wave group on a beach. Proc. R. Soc. A 2011, 467, 1212–1242. [Google Scholar] [CrossRef]
- Ruju, A.; Lara, J.L.; Losada, I.J. Numerical analysis of run-up oscillations under dissipative conditions. Coast. Eng. 2014, 86, 45–56. [Google Scholar] [CrossRef]
- Rychlik, I.; Johannesson, P.; Leadbutter, M. Modelling and Statistical Analysis of Ocean-wave Data Using Transformed Gaussian Processes. Mar. Struct. 1997, 10, 13–47. [Google Scholar] [CrossRef]
- Toffoli, A.; Onorato, M.; Monbaliu, J. Wave statistics in unimodal and bimodal seas from a second-order model. Eur. J. Mech. B/Fluids 2006, 25, 649–661. [Google Scholar] [CrossRef]
- Petrova, P.G.; Guedes Soares, C. Distributions of nonlinear wave amplitudes and heights from laboratory generated following and crossing bimodal seas. Nat. Hazards Earth Syst. Sci. 2014, 14, 1207–1222. [Google Scholar] [CrossRef]
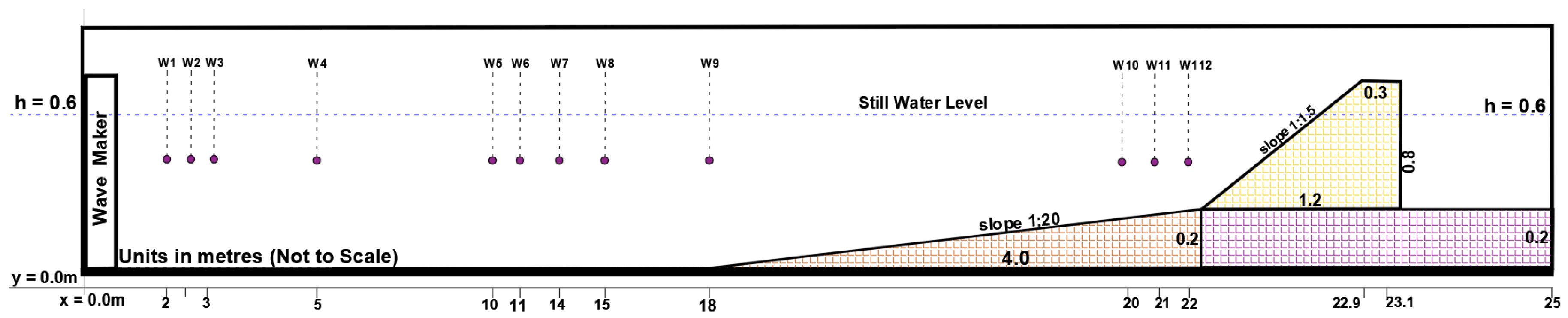
| (m) | (s) | Swell Peak Periods (s) | Swell Percentages | Gamma |
|---|---|---|---|---|
| 1.0 | 7.0 | 15, 20, 25 | 25 | Wind = 3.3; Swell = 2.5 |
| 1.5 | 8.0 | 15, 20, 25 | 50 | Wind = 3.3; Swell = 2.5 |
| 2.0 | 9.0 | 15, 20, 25 | 75 | Wind = 3.3; Swell = 2.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orimoloye, S.; Karunarathna, H.; Reeve, D.E. Effects of Swell on Wave Height Distribution of Energy-Conserved Bimodal Seas. J. Mar. Sci. Eng. 2019, 7, 79. https://doi.org/10.3390/jmse7030079
Orimoloye S, Karunarathna H, Reeve DE. Effects of Swell on Wave Height Distribution of Energy-Conserved Bimodal Seas. Journal of Marine Science and Engineering. 2019; 7(3):79. https://doi.org/10.3390/jmse7030079
Chicago/Turabian StyleOrimoloye, Stephen, Harshinie Karunarathna, and Dominic E. Reeve. 2019. "Effects of Swell on Wave Height Distribution of Energy-Conserved Bimodal Seas" Journal of Marine Science and Engineering 7, no. 3: 79. https://doi.org/10.3390/jmse7030079
APA StyleOrimoloye, S., Karunarathna, H., & Reeve, D. E. (2019). Effects of Swell on Wave Height Distribution of Energy-Conserved Bimodal Seas. Journal of Marine Science and Engineering, 7(3), 79. https://doi.org/10.3390/jmse7030079







