Two-Dimensional Numerical Study of Seabed Response around a Buried Pipeline under Wave and Current Loading
Abstract
1. Introduction
2. Methods
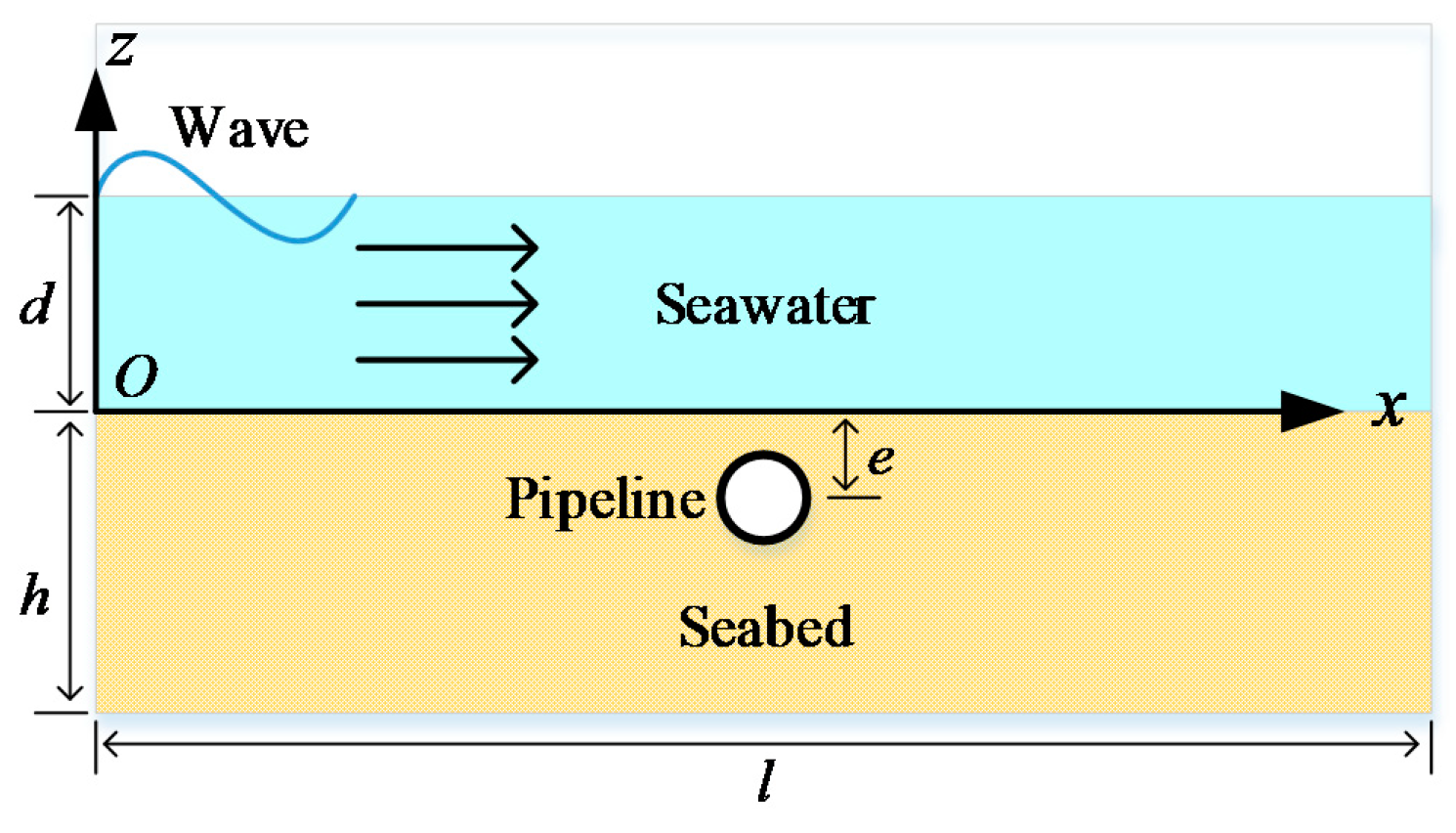
2.1. Wave–Current Model
2.2. Seabed Model
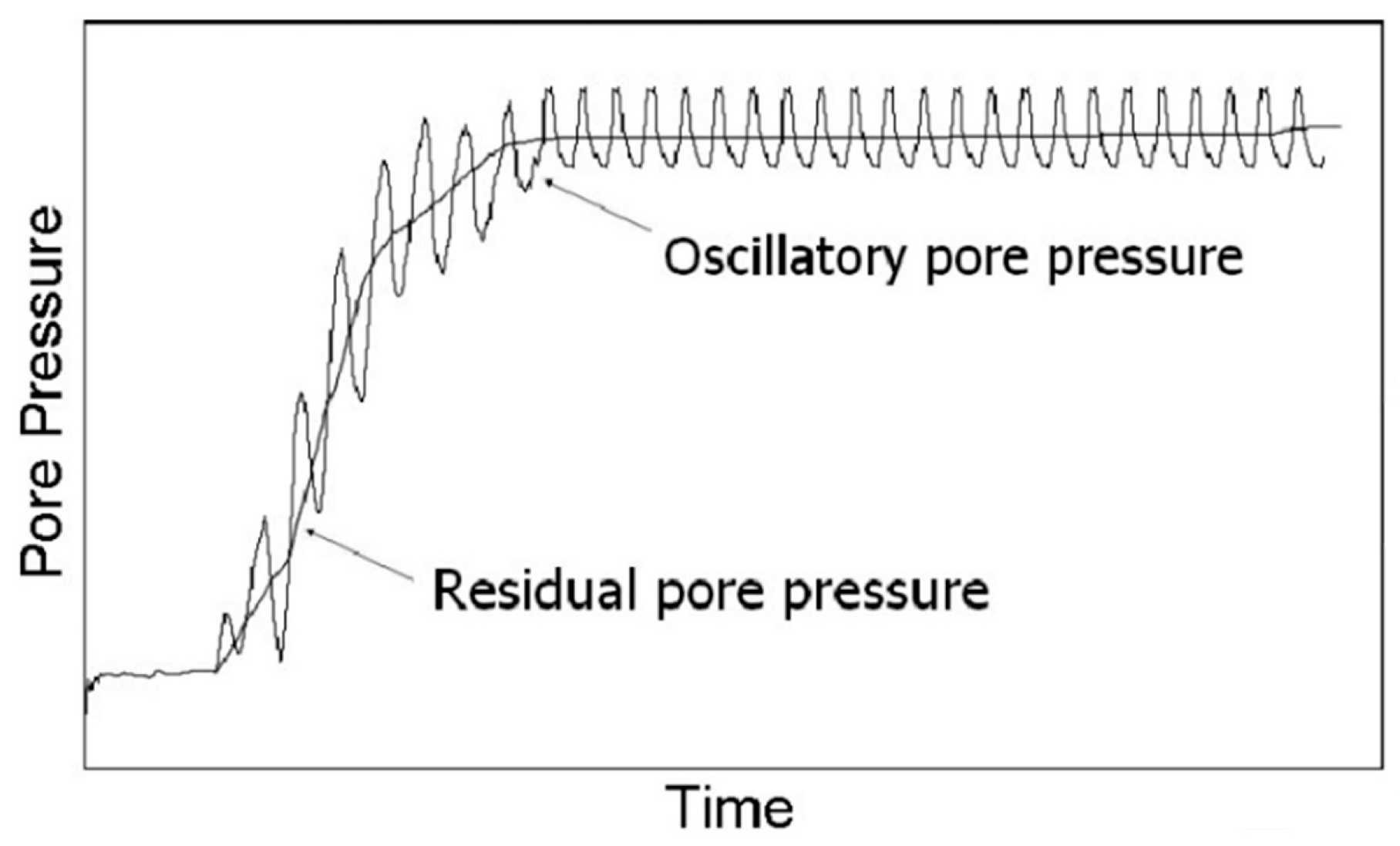
2.2.1. Oscillatory Soil Response
2.2.2. Residual Soil Response
2.3. Boundary Condition
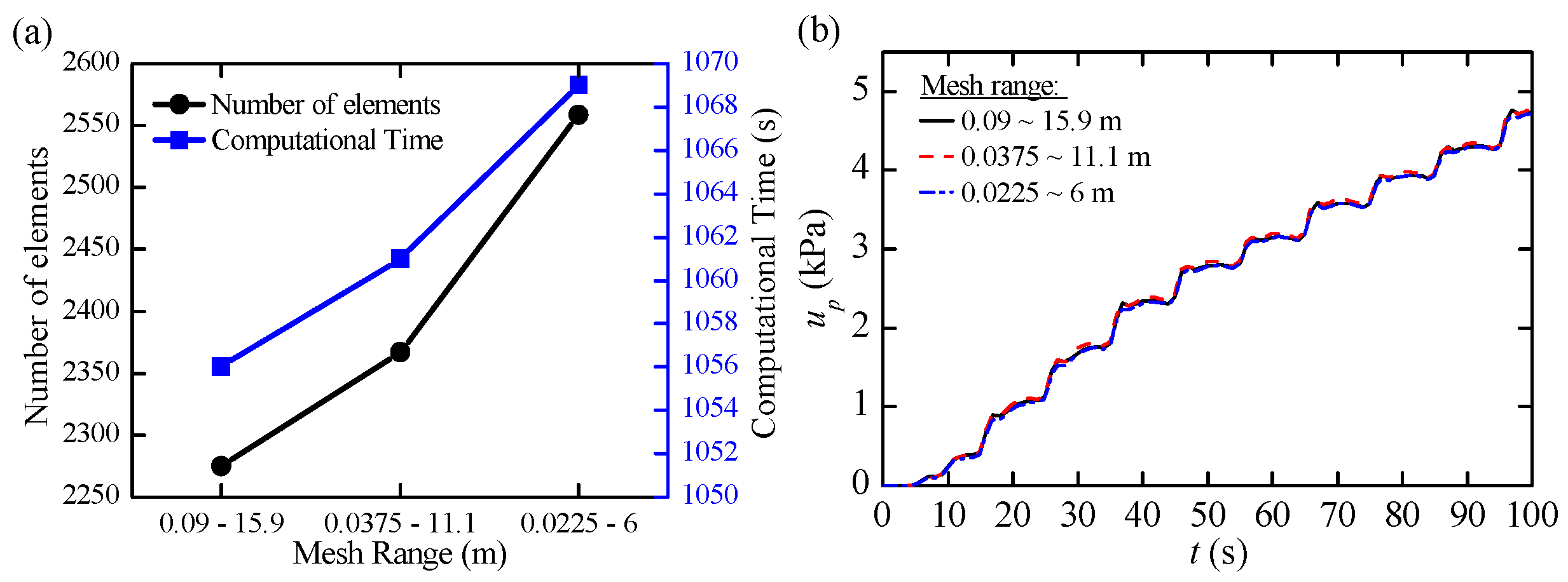
2.4. Numerical Scheme
3. Results and Discussion
3.1. Wave Characteristics
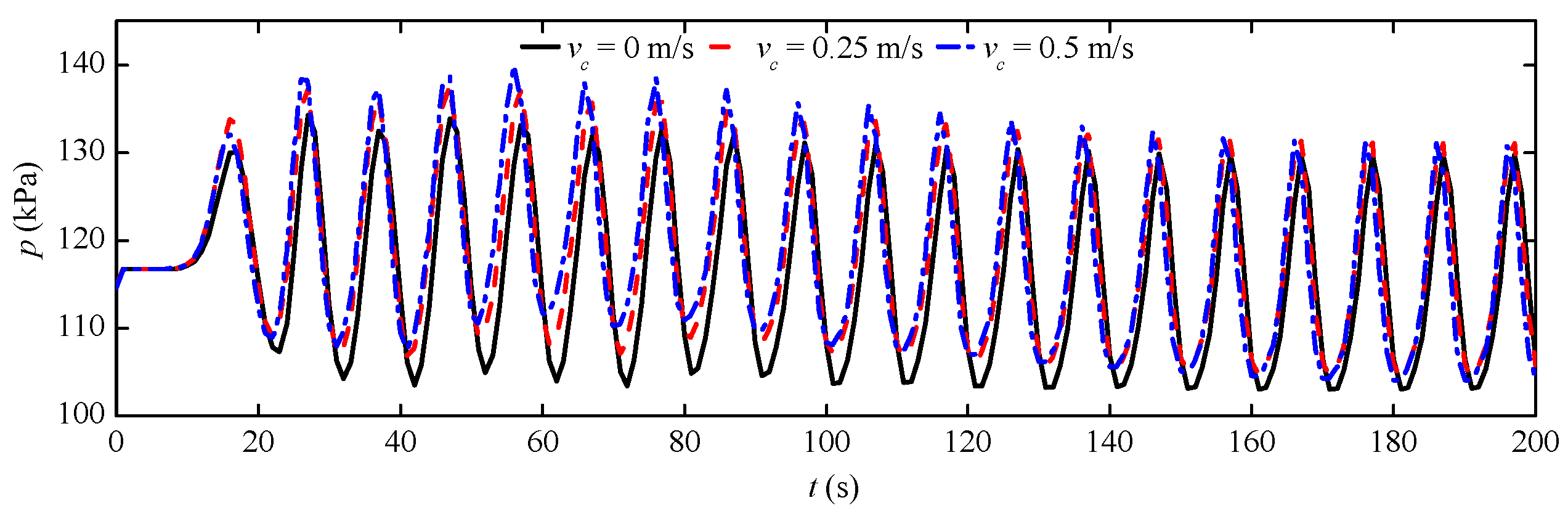
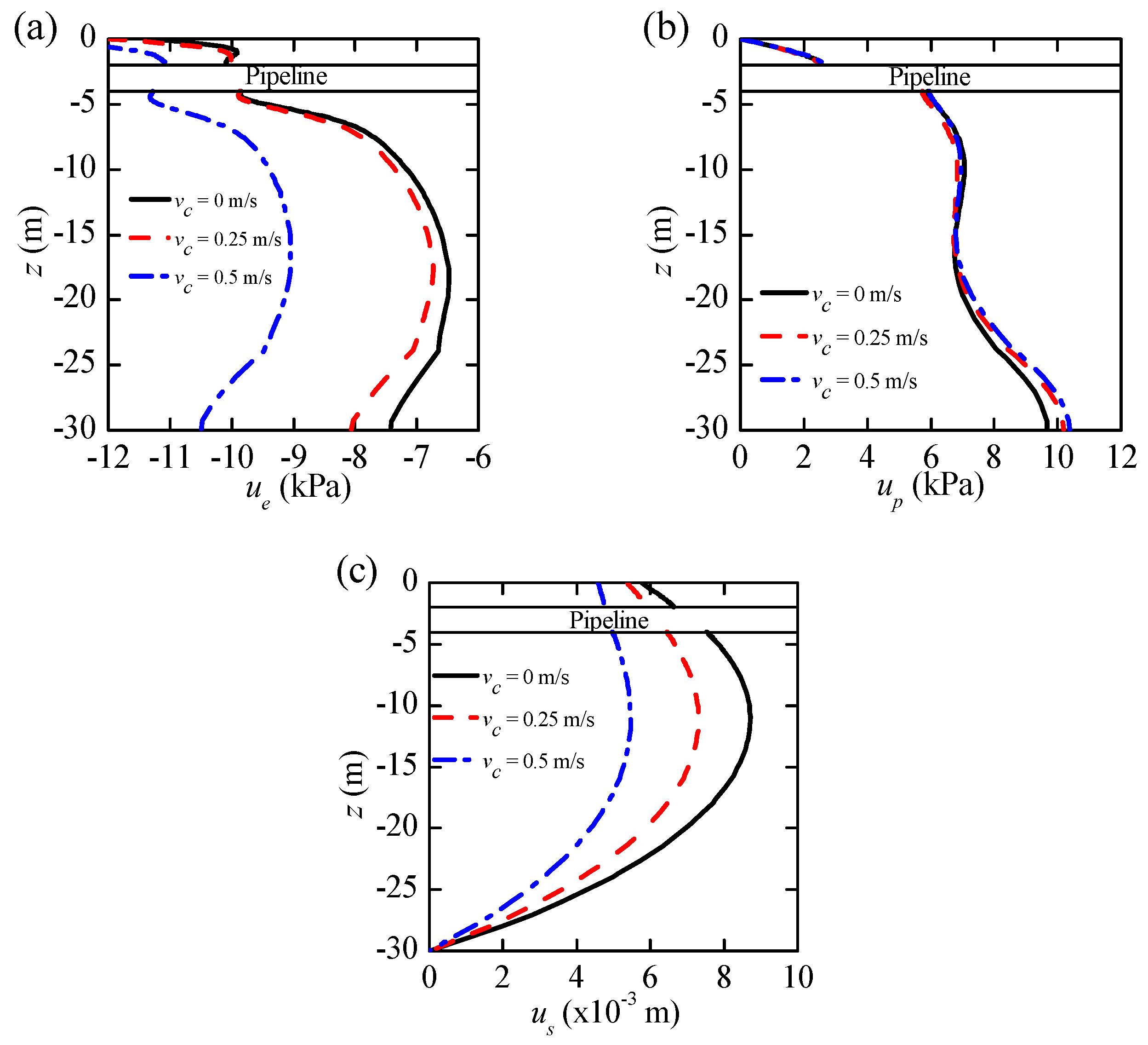
Influence of Current Velocities
3.2. Seabed Characteristics
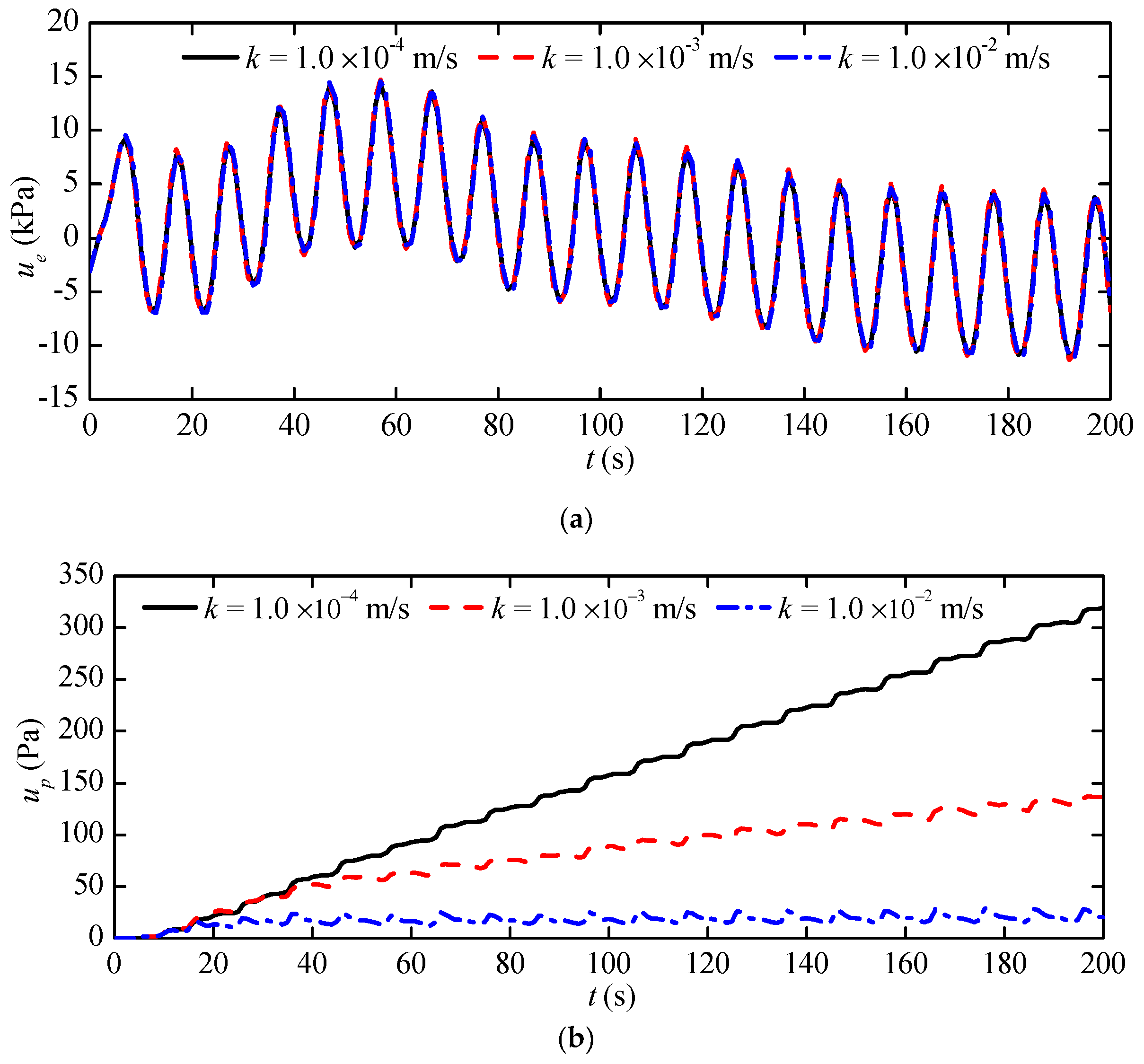
3.2.1. Effects of Soil Permeability
3.2.2. Effects of Shear Modulus
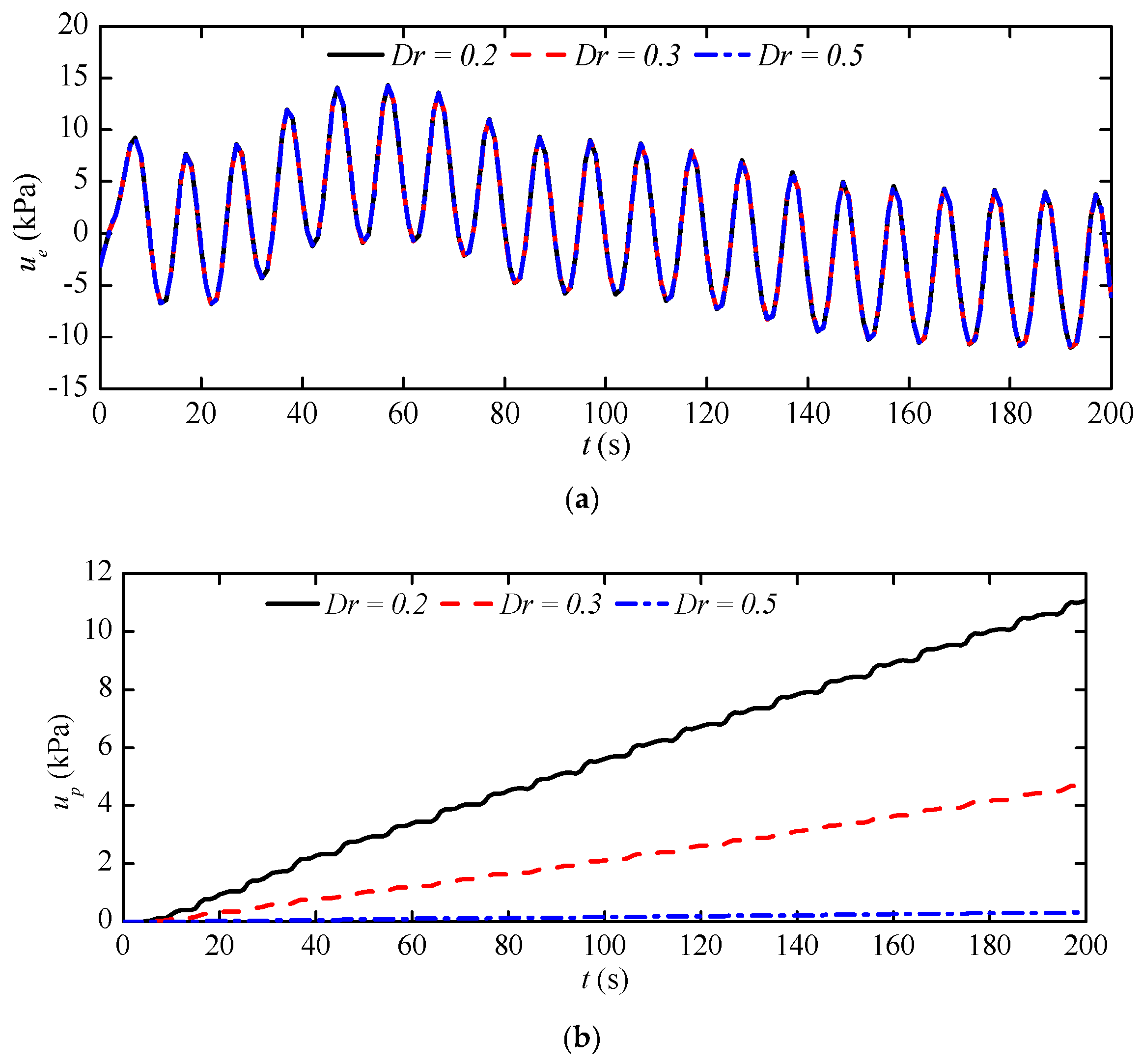
3.2.3. Effects of Relative Density
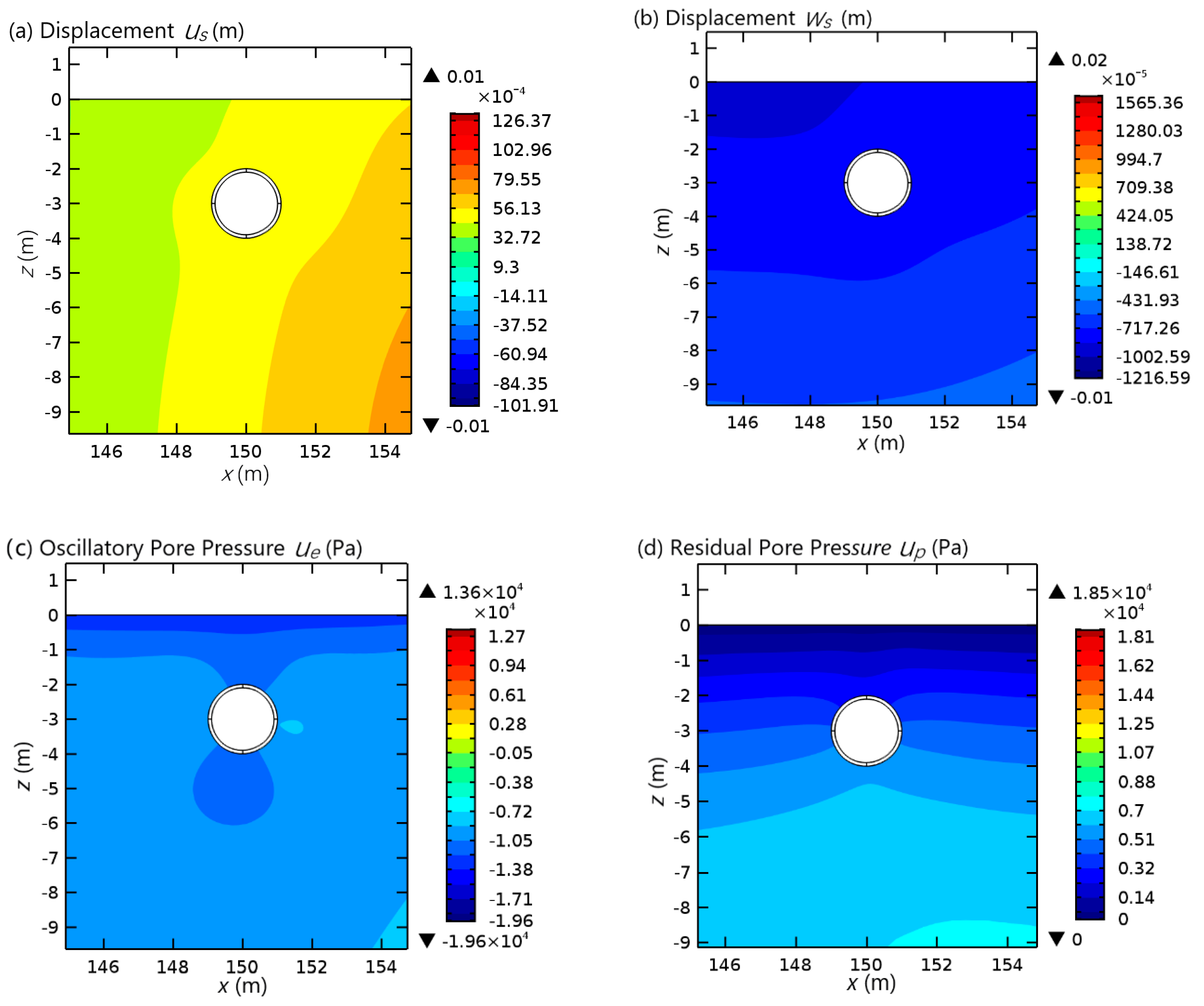
3.3. Around the Vicinity of the Pipeline
4. Conclusions
- (1)
- In the analysis of wave-seabed-structure interaction, the current should be taken into consideration—an increase in the current flow results in an increase in wave pressure. When wave pressure increases, the oscillatory pore pressure tends to increase with increasing current velocity.
- (2)
- Soil permeability governs the seepage of fluid passing through or flowing out of the seabed. Low permeability, i.e., pore fluids cannot dissipate efficiently, resulted in higher residual pore pressure due to the increase in the buildup of excess pore pressure.
- (3)
- Shear modulus has a relationship with Young’s modulus and Poisson’s ratio, which describe the rigidity of the seabed. Keeping the Poisson’s ratio as a constant value, a higher value of shear modulus generates a higher value of Young’s modulus, which represents a denser soil. As presented above, loose sand tends to produce a higher value of residual pore pressure.
- (4)
- Relative density controls the empirical coefficients αr and βr in source term, which affects the generation of residual pore pressure. It concludes that a smaller value of relative density results in a higher value of residual pore pressure. However, there is no visible difference in the oscillatory pore pressure.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Liao, C.; Tong, D.; Chen, L. Pore Pressure Distribution and Momentary Liquefaction in Vicinity of Impermeable Slope-Type Breakwater Head. Appl. Ocean Res. 2018, 78, 290–306. [Google Scholar] [CrossRef]
- Liao, C.; Chen, J.; Zhang, Y. Accumulation of pore water pressure in a homogenous sandy seabed around a rocking mono-pile subjected to wave loads. Ocean Eng. 2019, 173, 810–822. [Google Scholar] [CrossRef]
- Guo, Z.; Jeng, D.S.; Zhao, H.Y.; Guo, W.; Wang, L.Z. Effect of Seepage Flow on Sediment Incipient Motion around a Free Spanning Pipeline. Coast. Eng. 2019, 143, 50–62. [Google Scholar] [CrossRef]
- Chen, W.Y.; Chen, G.X.; Chen, W. Numerical simulation of the non-linear wave-induced dynamic response of anisotropic poro-elastoplastic seabed. Mar. Georesour. Geotechnol. 2018, 1–12. [Google Scholar] [CrossRef]
- Wong, Z.S.; Liao, C.C.; Jeng, D.S.-D. Poro-Elastoplastic Model for Short-Crested Wave-Induced Pore Pressures in a Porous Seabed. Open Civ. Eng. J. 2015, 9, 408–416. [Google Scholar] [CrossRef]
- Zen, K.; Yamazaki, H. Mechanism of wave-induced liquefaction and densification in seabed. Soils Found. 1990, 30, 90–104. [Google Scholar] [CrossRef]
- Jeng, D.-S. Porous Models for Wave-Seabed Interactions; Springer: Berlin/Heidelberg, Germany, 2013; Volume 9783642335, ISBN 978-3-642-33592-1. [Google Scholar]
- Yang, G.; Ye, J. Wave & current-induced progressive liquefaction in loosely deposited seabed. Ocean Eng. 2017, 142, 303–314. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, G.; Xu, C. Stability analysis on a porous seabed under wave and current loadings. Mar. Georesour. Geotechnol. 2017, 35, 710–718. [Google Scholar] [CrossRef]
- Wen, F.; Wang, J.H. Response of Layered Seabed under Wave and Current Loading. J. Coast. Res. 2015, 314, 907–919. [Google Scholar] [CrossRef]
- Ye, J.H.; Jeng, D.-S. Response of Porous Seabed to Nature Loadings: Waves and Currents. J. Eng. Mech. 2012, 138, 601–613. [Google Scholar] [CrossRef]
- Tong, D.; Liao, C.; Chen, J.; Zhang, Q. Numerical Simulation of a Sandy Seabed Response to Water Surface Waves Propogating on Current. J. Mar. Sci. Eng. 2018, 6, 88. [Google Scholar] [CrossRef]
- Zhang, Y.; Jeng, D.S.; Gao, F.P.; Zhang, J.S. An analytical solution for response of a porous seabed to combined wave and current loading. Ocean Eng. 2013, 57, 240–247. [Google Scholar] [CrossRef]
- Liao, C.C.; Jeng, D.-S.; Zhang, L.L. An Analytical Approximation for Dynamic Soil Response of a Porous Seabed due to Combined Wave and Current Loading. J. Coast. Res. 2015, 315, 1120–1128. [Google Scholar] [CrossRef]
- Zhou, X.L.; Wang, J.H.; Zhang, J.; Jeng, D.S. Wave and current induced seabed response around a submarine pipeline in an anisotropic seabed. Ocean Eng. 2014, 75, 112–127. [Google Scholar] [CrossRef]
- Liu, B.; Jeng, D.-S.; Ye, G.L.; Yang, B. Laboratory study for pore pressures in sandy deposit under wave loading. Ocean Eng. 2015, 106, 207–219. [Google Scholar] [CrossRef]
- Gao, F.P.; Yan, S.; Yang, B.; Wu, Y. Ocean Currents-Induced Pipeline Lateral Stability on Sandy Seabed. J. Eng. Mech. 2007, 133, 1086–1092. [Google Scholar] [CrossRef]
- Zhou, C.; Li, G.; Dong, P.; Shi, J.; Xu, J. An experimental study of seabed responses around a marine pipeline under wave and current conditions. Ocean Eng. 2011, 38, 226–234. [Google Scholar] [CrossRef]
- Youssef, B.S.; Tian, Y.; Cassidy, M.J. Centrifuge modelling of an on-bottom pipeline under equivalent wave and current loading. Appl. Ocean Res. 2013, 40, 14–25. [Google Scholar] [CrossRef]
- Sassa, S.; Sekiguchi, H. Wave-induced liquefaction of beds of sand in a centrifuge. Géotechnique 1999, 49, 621–638. [Google Scholar] [CrossRef]
- Yang, B.; Luo, Y.; Jeng, D.; Feng, J.; Huhe, A. Experimental studies on initiation of current-induced movement of mud. Appl. Ocean Res. 2018, 80, 220–227. [Google Scholar] [CrossRef]
- Zhao, H.-Y.; Jeng, D.-S.; Guo, Z.; Zhang, J.-S. Two-Dimensional Model for Pore Pressure Accumulations in the Vicinity of a Buried Pipeline. J. Offshore Mech. Arct. Eng. 2014, 136, 042001. [Google Scholar] [CrossRef]
- Zhao, H.-Y.; Jeng, D.-S. Accumulated pore pressures around submarine pipeline buried in trench layer with partial backfills. J. Eng. Mech. 2016, 142, 04016042. [Google Scholar] [CrossRef]
- Zhou, X.-L.; Zhang, J.; Guo, J.-J.; Wang, J.-H.; Jeng, D.-S. Cnoidal wave induced seabed response around a buried pipeline. Ocean Eng. 2015, 101, 118–130. [Google Scholar] [CrossRef]
- Duan, L.; Liao, C.; Jeng, D.-S.; Chen, L. 2D numerical study of wave and current-induced oscillatory non-cohesive soil liquefaction around a partially buried pipeline in a trench. Ocean Eng. 2017, 135, 39–51. [Google Scholar] [CrossRef]
- Duan, L.; Jeng, D.-S.; Liao, C.; Zhu, B.; Tong, D. Three-dimensional poro-elastic integrated model for wave and current-induced oscillatory soil liquefaction around offshore pipeline. Appl. Ocean Res. 2017, 68, 293–306. [Google Scholar] [CrossRef]
- Benra, F.-K.; Dohmen, H.J.; Pei, J.; Schuster, S.; Wan, B. A Comparison of One-way and Two-Way Coupling Methods for Numerical Analysis of Fluid-Structure Interactions. J. Appl. Math. 2011, 1–16. [Google Scholar] [CrossRef]
- Jones, W.P.; Launder, B.E. The predictions of Laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.L.F. A numerical study of breaking wave in the surf zone. J. Fluid Mech. 1998, 359, 239–264. [Google Scholar] [CrossRef]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Jeng, D.-S. Mechanics of Wave-Seabed-Structure Interactions: Modelling, Processes and Applications; Cambridge University Press: Cambridge, UK, 2018; ISBN 978-1-107-16000-2. [Google Scholar]
- Sumer, B.M.; Kirca, V.S.O.; Fredsøe, J. Experimental Validation of a Mathematical Model Liquefaction Under Waves. Int. J. Offshore Polar Eng. 2012, 22, 133–141. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Paulsen, B.T.; Bredmose, H.; Bingham, H.; Jacobsen, N. Forcing of a bottom-mounted circular cylinder by steep regular water waves at finite depth. J. Fluid Mech. 2014, 755, 1–34. [Google Scholar] [CrossRef]
- COMSOL Inc. COMSOL Multiphysics 5.3 User Guide Manual; COMSOL Inc.: Burlington, MA, USA, 2014. [Google Scholar]
- Das, B.M. Principles of Foundation Engineering; Thomson/Brooks/Cole: Pacific Grove, CA, USA, 2007; ISBN 978-0-495-08246-0. [Google Scholar]
- Das, B.M. Principles of Geotechnical Engineering-SI Version, 7th ed.; Cengage Learning: Boston, MA, USA, 2014; ISBN 978-1-133-10867-2. [Google Scholar]
- Alberello, A.; Pakodzi, C.; Nelli, F.; Bitner-Gregersen, E.M.; Toffoli, A. Threee Dimensional Velocity Field Underneath a Breaking Rogue Wave. In Proceedings of the ASME 2017 36th International Conference Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017; Volume 3A: Structures, Safety and Reliability. p. V03AT02A009. [Google Scholar] [CrossRef]

| Module | Parameter | Notation | Magnitude | Unit |
|---|---|---|---|---|
| Wave | Water Depth | d | 12 | m |
| Wave Height | H | 4 | m | |
| Wave Period | T | 10 | s | |
| Current | Velocity | vc | 0, 0.25, 0.5 | m/s |
| Seabed | Permeability | ks | 1.0 × 10−2, 1.0 × 10−3, 1.0 × 10−4 | m/s |
| Degree of Saturation | Sr | 1 | - | |
| Shear Modulus | G | 5.0 × 106, 1.5 × 107 | N/m2 | |
| Poisson’s Ratio | ν | 0.35 | - | |
| Relative Density | 0.2, 0.3, 0.5 | - | ||
| Porosity | ns | 0.4 | - | |
| Pipeline | Pipe Diameter | D | 2.0 | m |
| Burial Depth | e | 3.0 | m | |
| Young Modulus | EP | 2.09 × 1011 | N/m2 | |
| Shear Modulus | 6.8 × 1010 | N/m2 |
| Type of Soil | Young’s Modulus, E (MPa) | Poisson’s Ratio, v |
|---|---|---|
| Loose sand | 10.5–24.0 | 0.20–0.40 |
| Medium dense sand | 17.25–27.60 | 0.25–0.40 |
| Dense sand | 34.50–55.20 | 0.30–0.45 |
| Silty sand | 10.35–17.25 | 0.20–0.40 |
| Sand and gravel | 69.00–172.50 | 0.15–0.35 |
| Soft clay | 4.1–20.7 | - |
| Medium clay | 20.7–41.4 | 0.20–0.50 |
| Stiff clay | 41.4–96.6 | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foo, C.S.X.; Liao, C.; Chen, J. Two-Dimensional Numerical Study of Seabed Response around a Buried Pipeline under Wave and Current Loading. J. Mar. Sci. Eng. 2019, 7, 66. https://doi.org/10.3390/jmse7030066
Foo CSX, Liao C, Chen J. Two-Dimensional Numerical Study of Seabed Response around a Buried Pipeline under Wave and Current Loading. Journal of Marine Science and Engineering. 2019; 7(3):66. https://doi.org/10.3390/jmse7030066
Chicago/Turabian StyleFoo, Cynthia Su Xin, Chencong Liao, and Jinjian Chen. 2019. "Two-Dimensional Numerical Study of Seabed Response around a Buried Pipeline under Wave and Current Loading" Journal of Marine Science and Engineering 7, no. 3: 66. https://doi.org/10.3390/jmse7030066
APA StyleFoo, C. S. X., Liao, C., & Chen, J. (2019). Two-Dimensional Numerical Study of Seabed Response around a Buried Pipeline under Wave and Current Loading. Journal of Marine Science and Engineering, 7(3), 66. https://doi.org/10.3390/jmse7030066




