Experimental Study and Estimation of Groundwater Fluctuation and Ground Settlement due to Dewatering in a Coastal Shallow Confined Aquifer
Abstract
:1. Introduction
- How are MCA and Aq I hydraulically connected and how does the hydraulic connection affect the responses of groundwater fluctuations and strata deformation?
- What is the correlation between stratum deformation (ground settlement, stratum compression) and groundwater fluctuations?
- How to estimate the hydrogeological parameters of the MCA based on pumping well tests if the MCA is directly connected with the confined aquifer.
- How to predict the ground settlement induced by dewatering in the MCA when the MCA is directly connected with the confined aquifer.
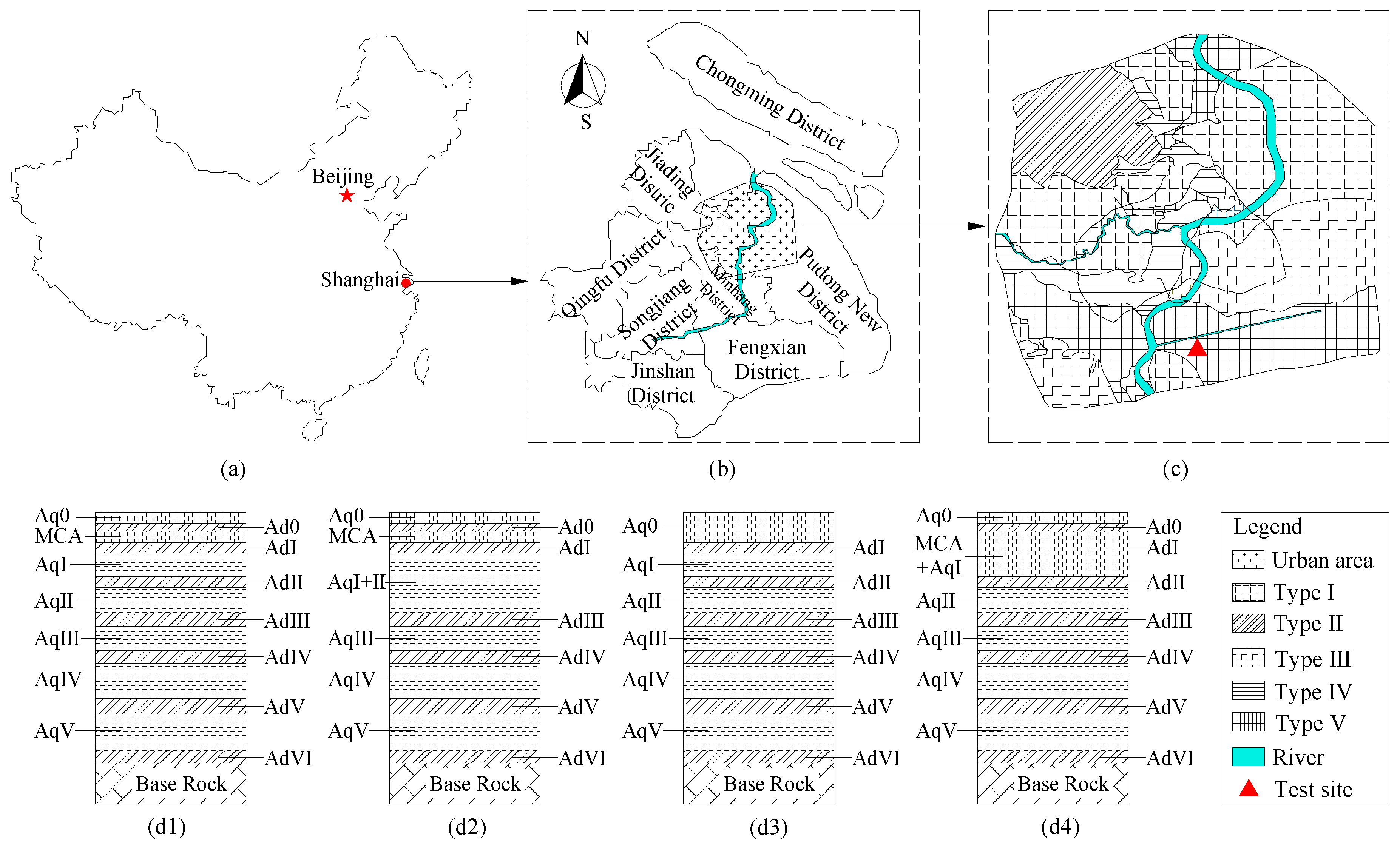
2. Study Area
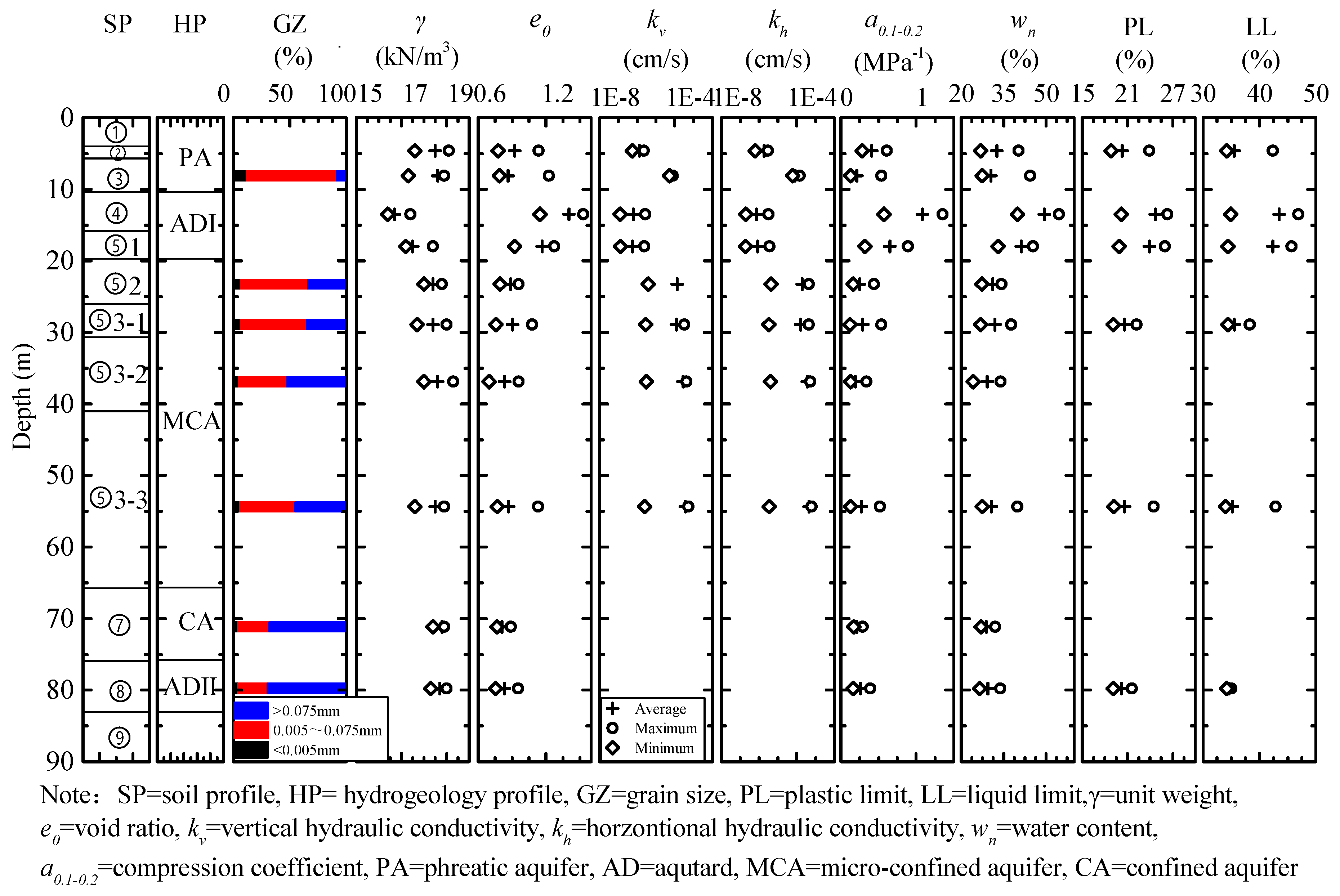
2.1. Engineering Geology
2.2. Hydrogeology
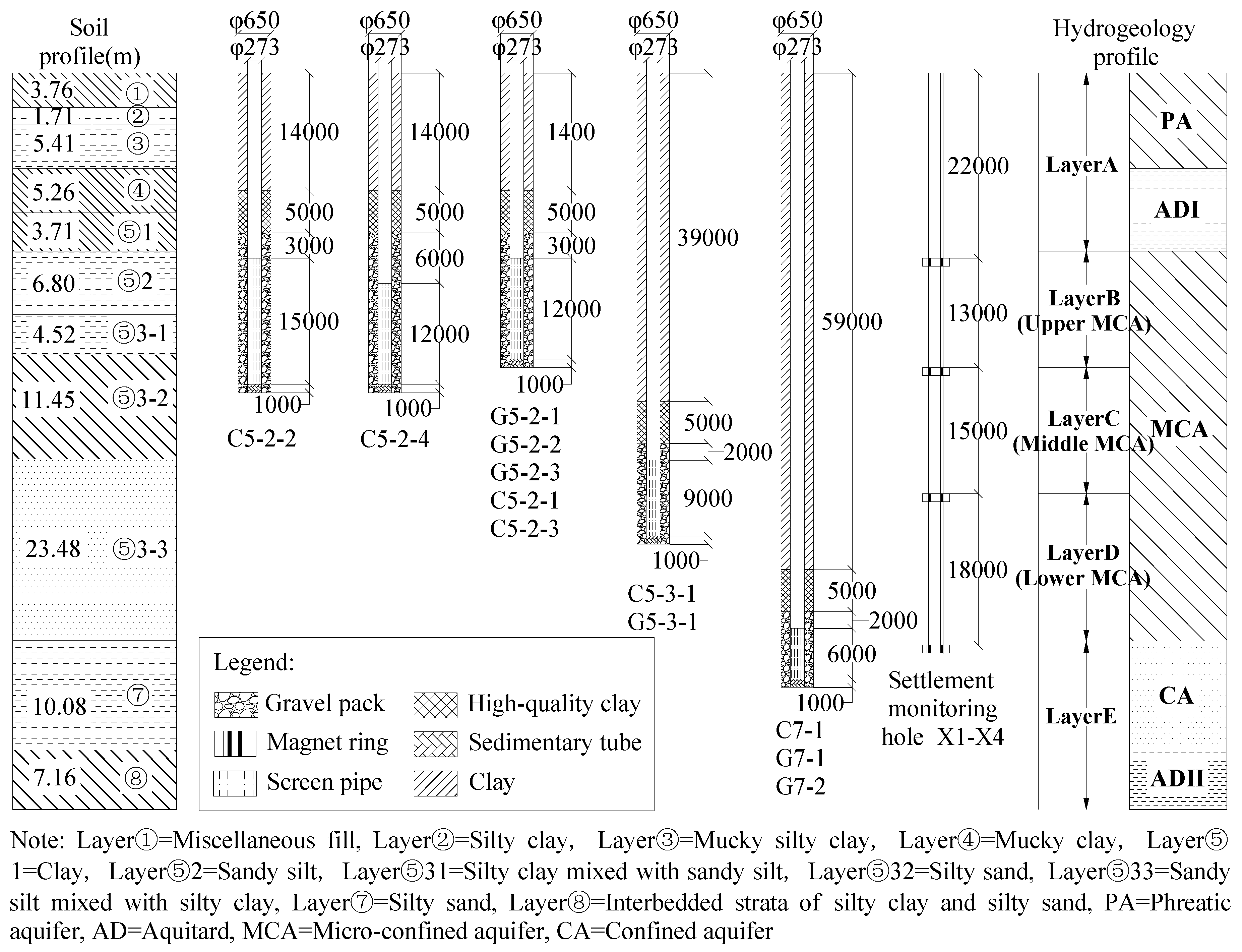
3. Pumping Well Tests
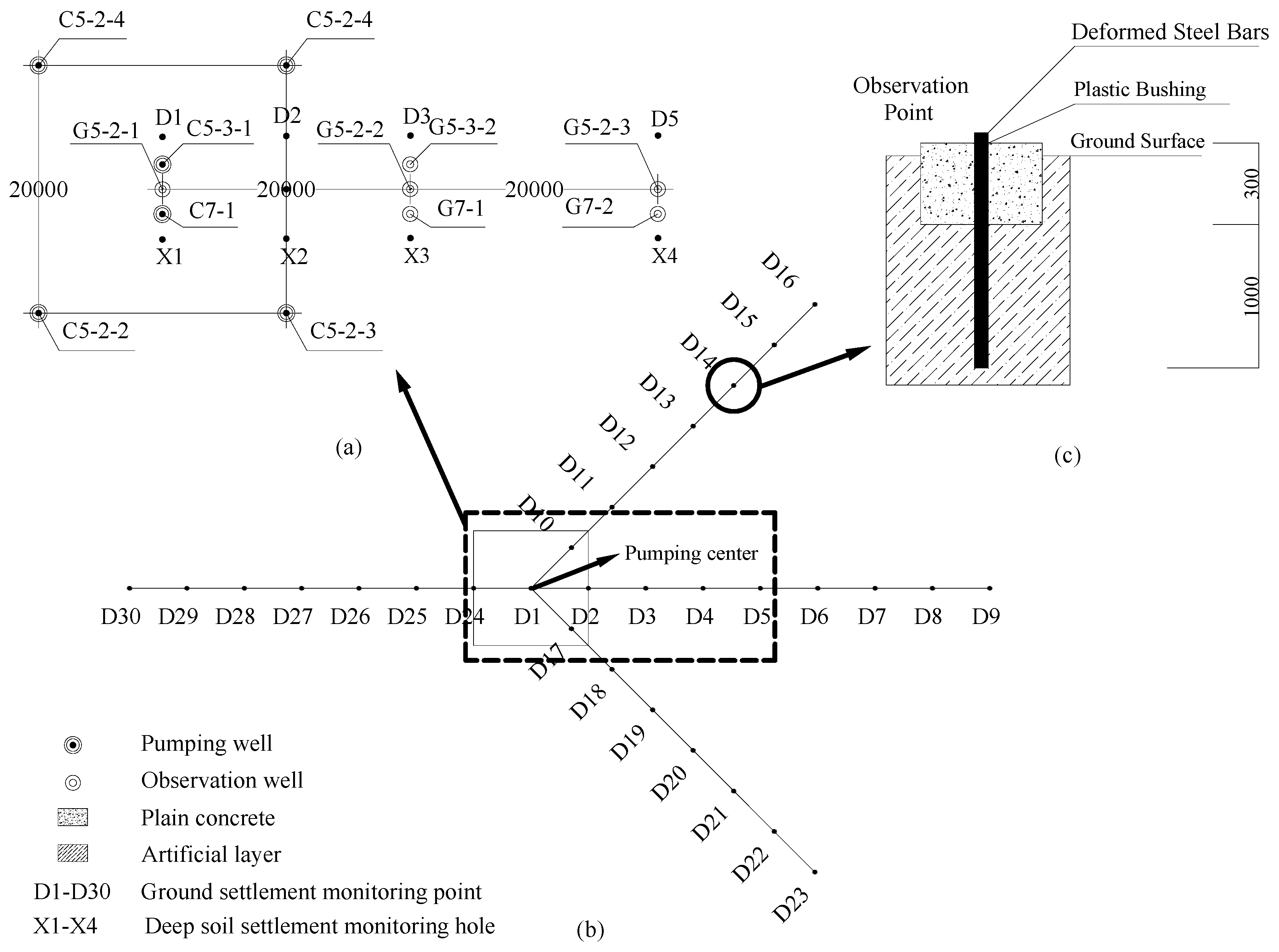
3.1. Well Installation
3.2. Test Scheme
3.3. Stratum Deformation
4. Results and Analysis
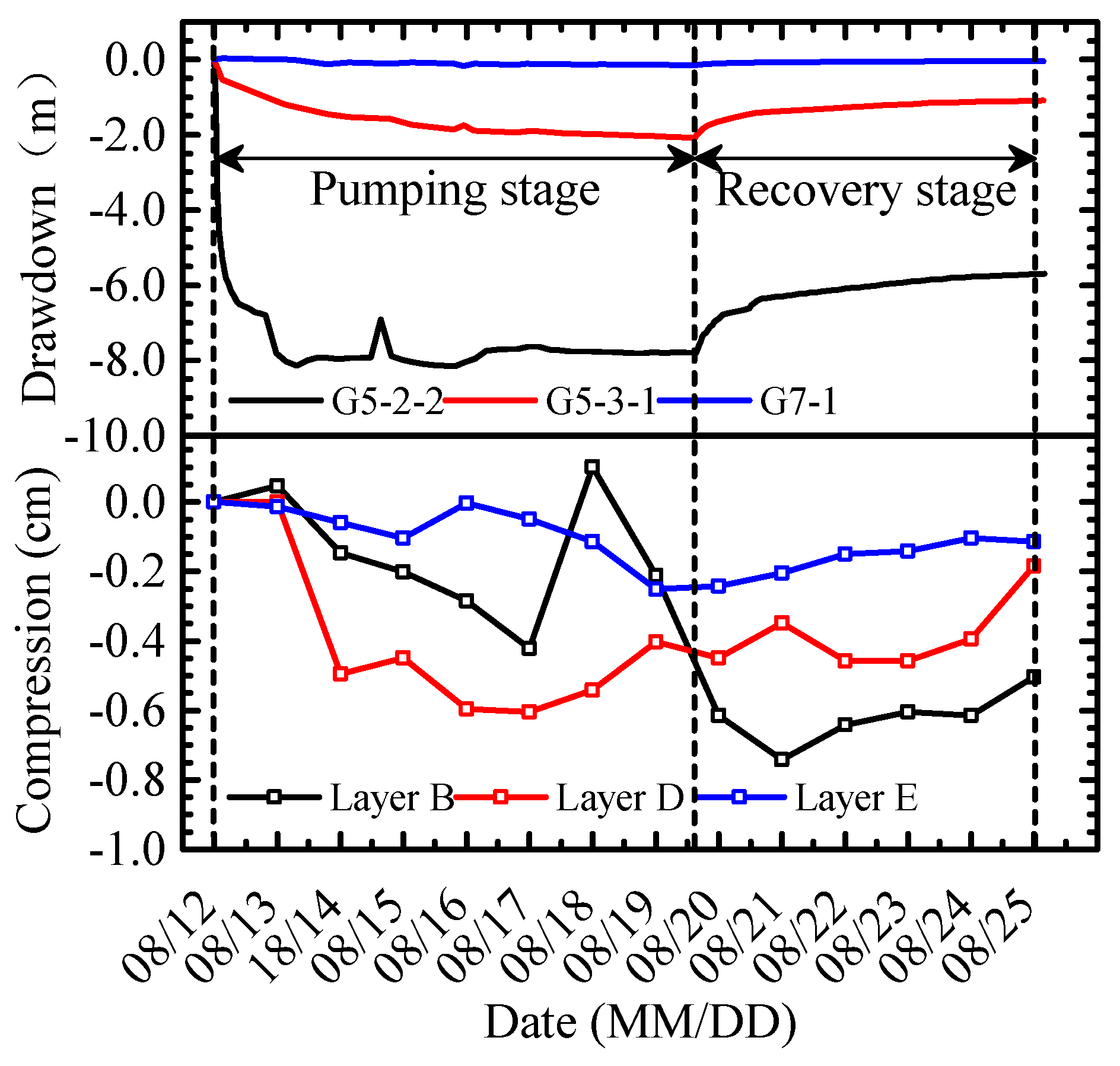
4.1. Responses of Groundwater Level
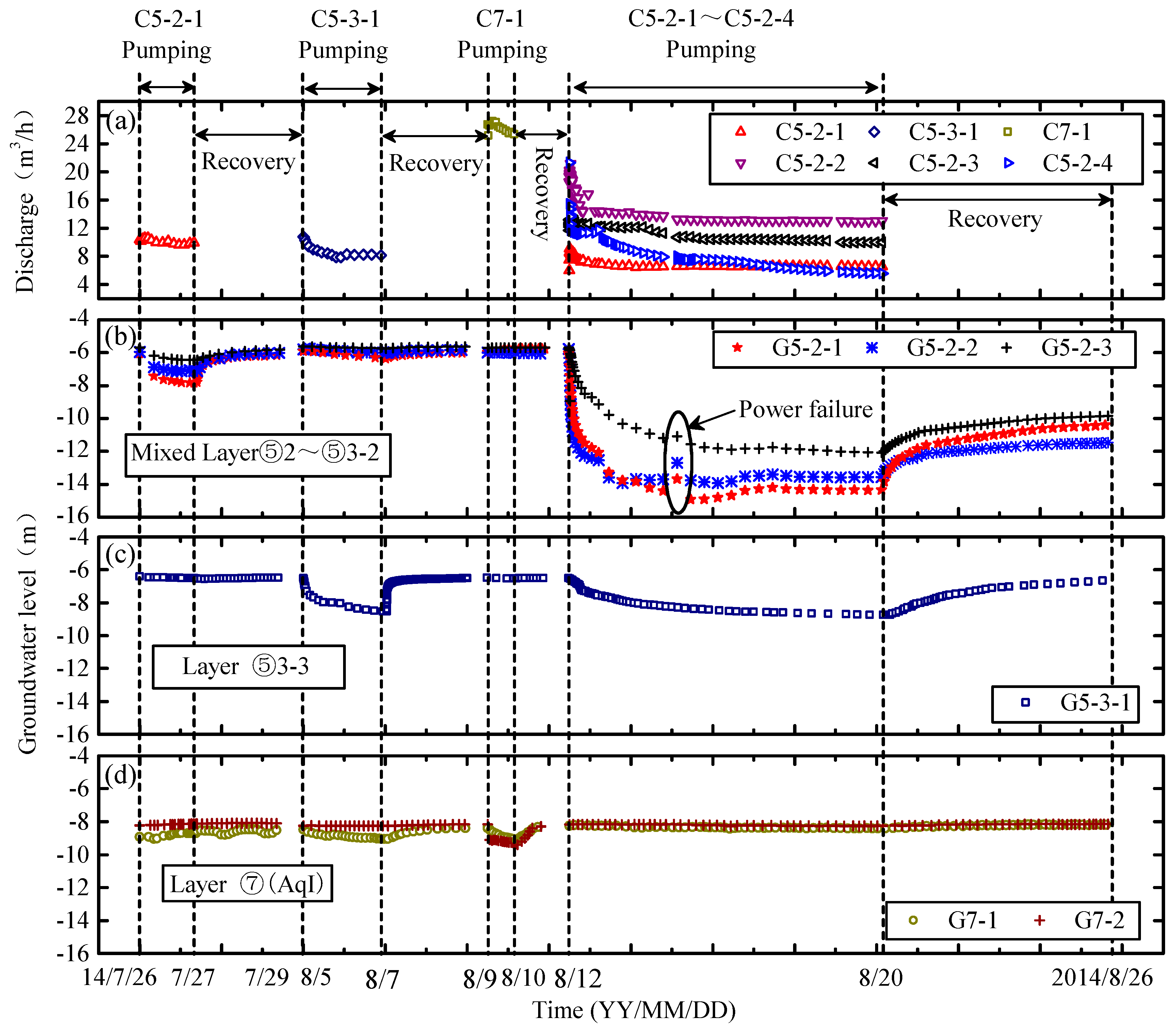
4.1.1. Test Results
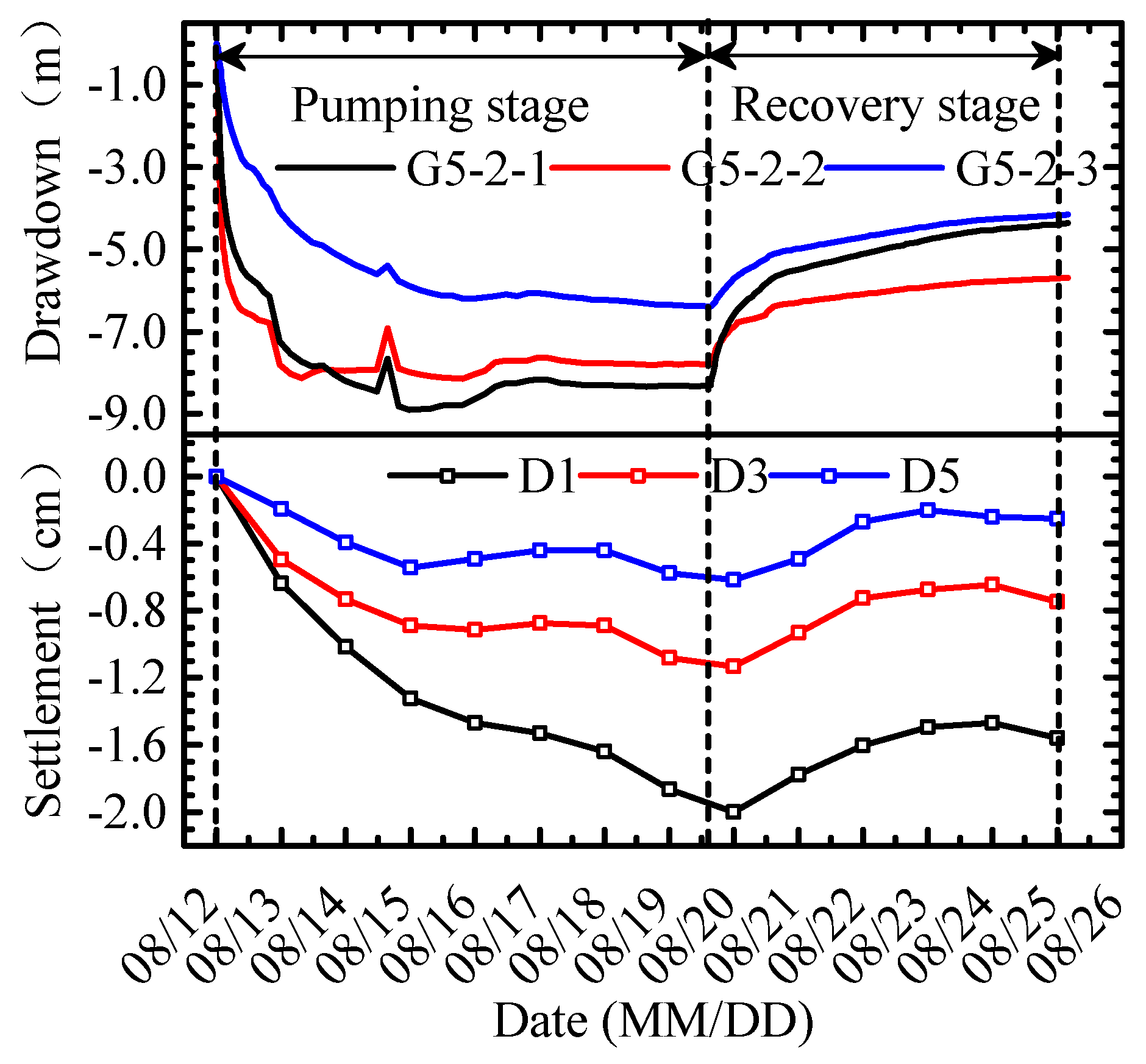
4.1.2. Analyses
4.2. Responses of Ground Settlement
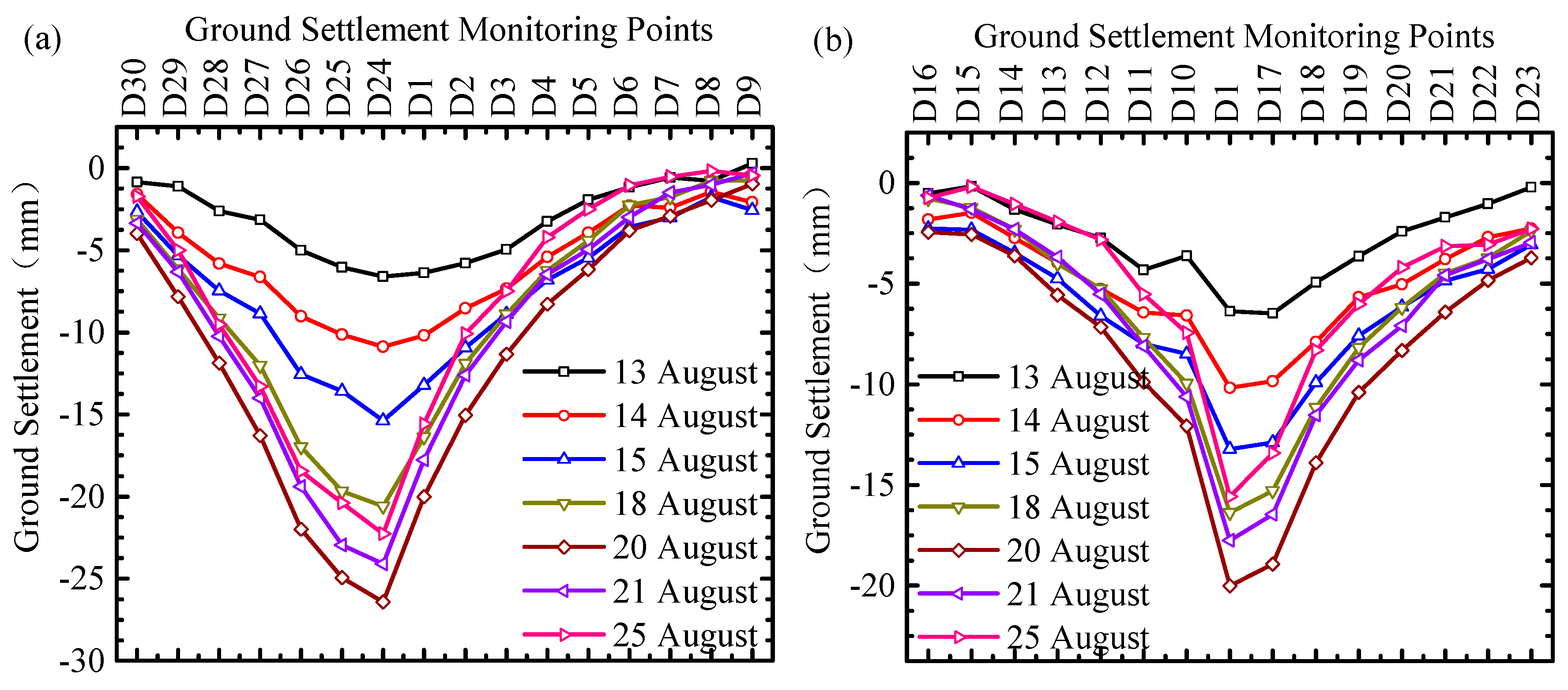
4.2.1. Results
4.2.2. Analyses
4.3. Responses of Deep Soil Deformation
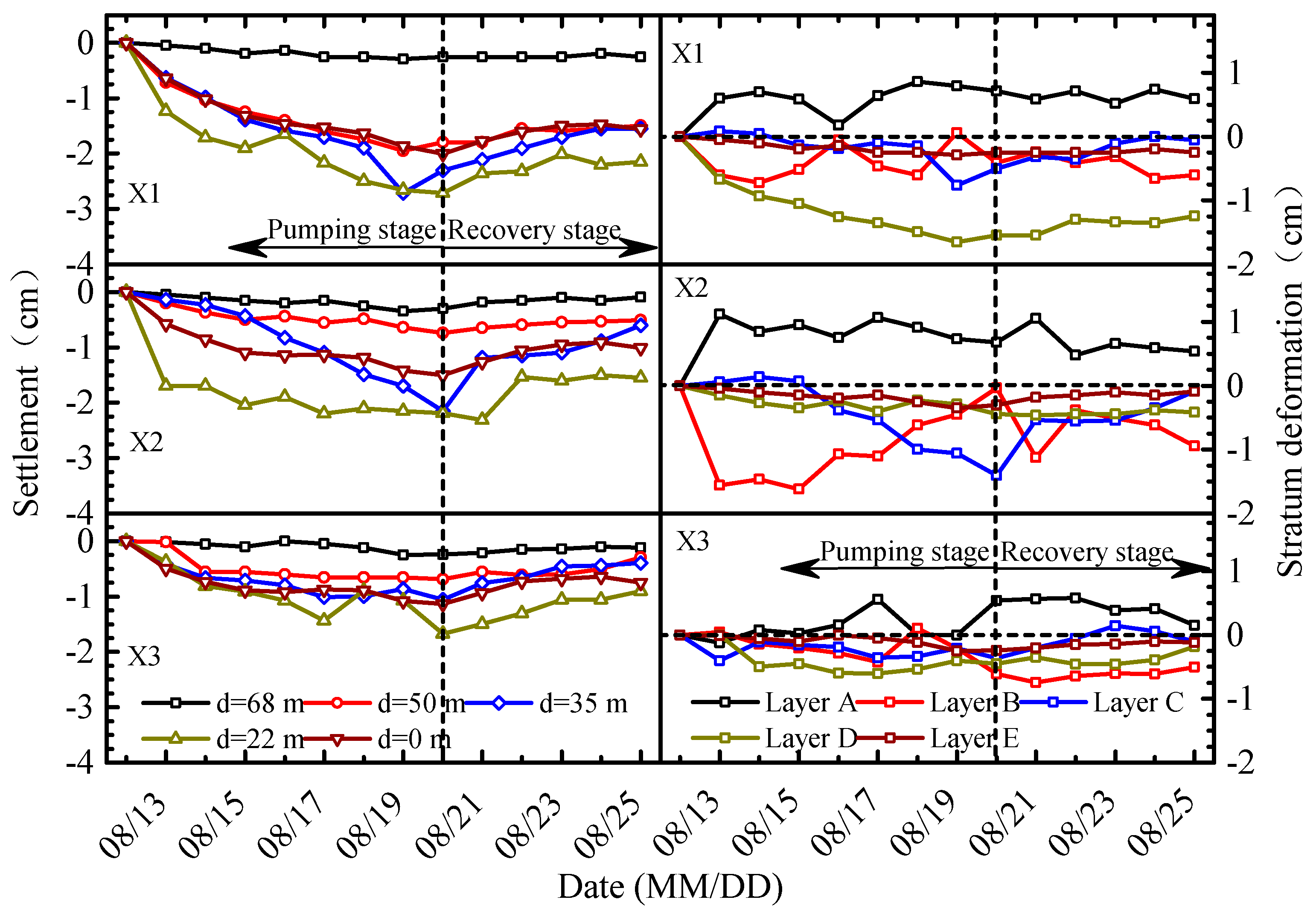
4.3.1. Results
4.3.2. Analyses
5. Back Analysis of Groundwater Fluctuations and Ground Settlement
5.1. Hydrogeological Parameter Estimation Based on Pumping Well Test
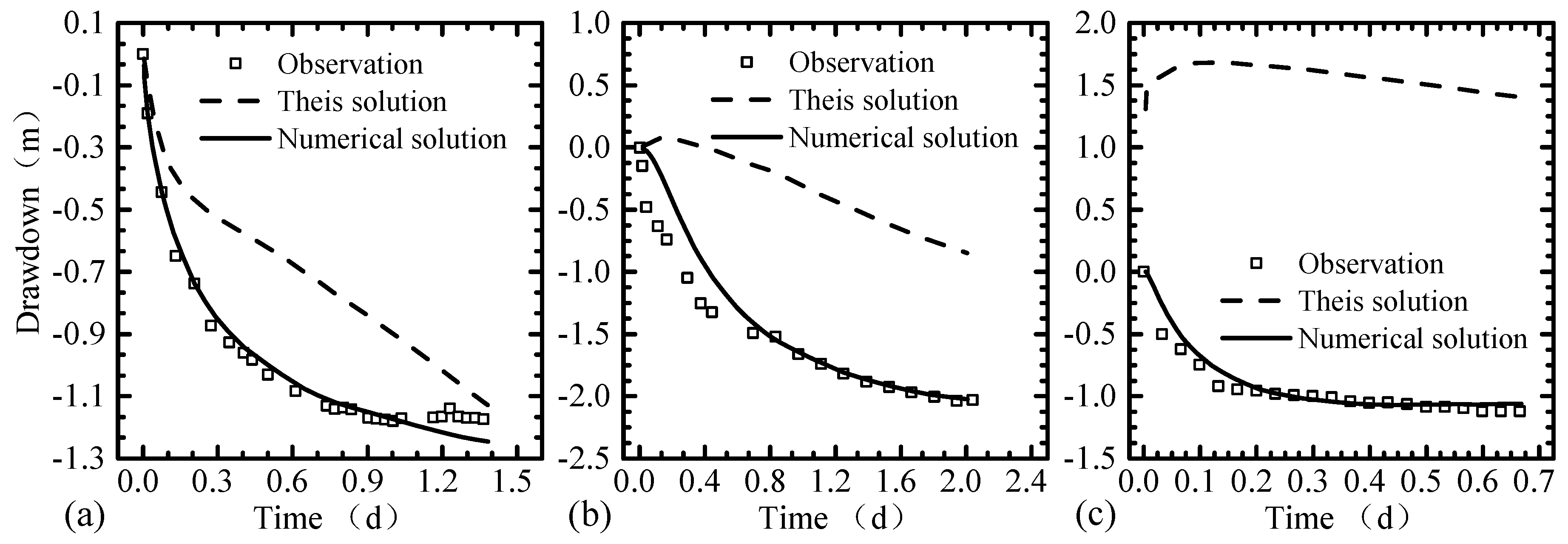
5.1.1. Limitations of the Analytical Methods
5.1.2. Parameter Estimation using Numerical Method
5.1.3. Results and Analyses
5.2. Ground Settlement Prediction Induced by Dewatering
5.2.1. Basic Assumptions
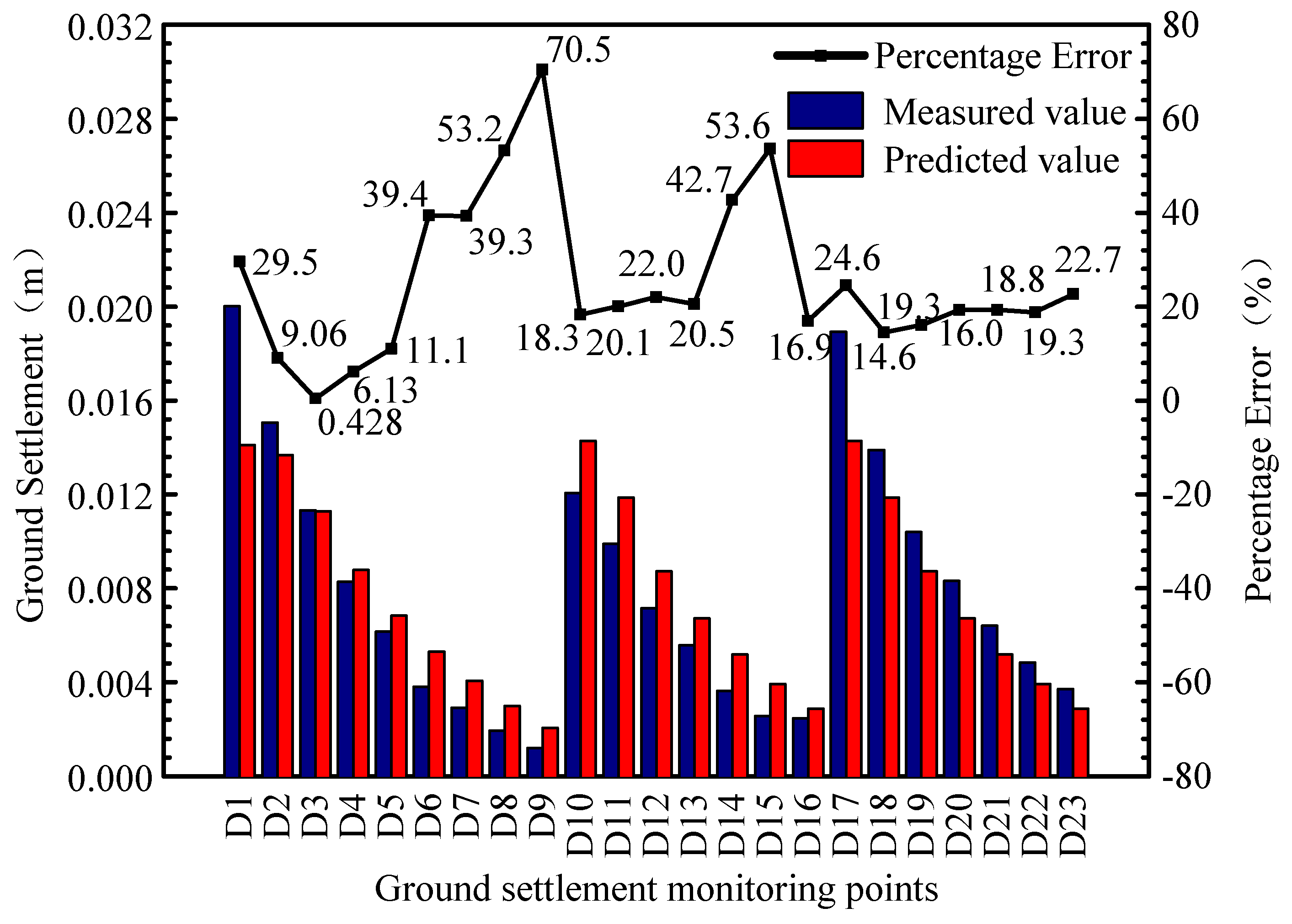
5.2.2. Ground Settlement Prediction Based on Pumping Well Test
5.2.3. Validation and Analyses
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Shanghai Geology Office (SGO). Report on Land Subsidence in Shanghai (1962–1976); SGO: Shanghai, China, 1979. (In Chinese) [Google Scholar]
- The Institute of Hydrogeology and Engineering Geology (IHEG). Hydrogeological map of Shanghai, Hydrogeological in Atlas of China, No. 45; IHEG: Shanghai, China, 1979. (In Chinese) [Google Scholar]
- Chai, J.C.; Shen, S.L.; Zhu, H.H.; Zhang, X.L. Land subsidence due to groundwater drawdown in Shanghai. Géotechnique 2004, 56, 143–147. [Google Scholar] [CrossRef]
- Xu, Y.; Shen, S.; Du, Y. Geological and hydrogeological environment in Shanghai with geohazards to construction and maintenance of infrastructures. Eng. Geol. 2009, 109, 241–254. [Google Scholar] [CrossRef]
- Xu, Y.; Shen, S.; Ma, L.; Sun, W.; Yin, Z. Evaluation of the blocking effect of retaining walls on groundwater seepage in aquifers with different insertion depths. Eng. Geol. 2014, 183, 254–264. [Google Scholar] [CrossRef]
- Shanghai Geology and Minerals Topology Editorial Board (SGMTEB). Shanghai Geology and Minerals Topology (SGMT); Shanghai Academy of Social Science Press: Shanghai, China, 1999. (In Chinese) [Google Scholar]
- Zeng, C.F.; Xue, X.L.; Zheng, G.; Xue, T.Y.; Mei, G.X. Responses of retaining wall and surrounding ground to pre-excavation dewatering in an alternated multi-aquifer-aquitard system. J. Hydrol. 2018, 559, 609–626. [Google Scholar] [CrossRef]
- Zheng, G.; Zeng, C.F.; Xue, X.L. Settlement mechanism of soils induced by local pressure-relief of confined aquifer and parameter analysis. Chin. J. Geotech. Eng. 2014, 36, 802–807. (In Chinese) [Google Scholar]
- Zhang, Y.; Li, M.; Wang, J.; Chen, J.; Zhu, Y. Field tests of pumping-recharge technology for deep confined aquifers and its application to a deep excavation. Eng. Geol. 2017, 228, 249–259. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Chen, J.; Li, M. Numerical study on the responses of groundwater and strata to pumping and recharge in a deep confined aquifer. J. Hydrol. 2017, 548, 342–352. [Google Scholar] [CrossRef]
- Wang, J.; Feng, B.; Liu, Y.; Wu, L.; Zhu, Y.; Zhang, X.; Tang, Y.; Yang, P. Controlling subsidence caused by de-watering in a deep foundation pit. Bull. Eng. Geol. Environ. 2012, 71, 545–555. [Google Scholar] [CrossRef]
- Xu, Y.; Yuan, Y.; Shen, S.; Yin, Z.; Wu, H.; Ma, L. Investigation into subsidence hazards due to groundwater pumping from Aquifer II in Changzhou, China. Nat. Hazards 2015, 78, 281–296. [Google Scholar] [CrossRef]
- Zheng, G.; Dai, X.; Diao, Y.; Zeng, C.F. Experimental and simplified model study of the development of ground settlement under hazards induced by loss of groundwater and sand. Nat. Hazards 2016, 82, 1869–1893. [Google Scholar] [CrossRef]
- Shanghai Geotechnical Engineering Survey and Design Research Institute (SGESDRI). Code for Investigation of Geotechnical Engineering; SGESDRI: Shanghai, China, 2012. (In Chinese) [Google Scholar]
- Zhang, H.; Liu, M. “Feeble confined water” in Shanghai area and related geotechnical engineering problems in foundation excavation. Chin. J. Geotech. Eng. 2005, 27, 944–947. (In Chinese) [Google Scholar]
- Wei, T.Y.; Chen, Z.Y.; Wei, Z.X.; Wang, Z.Q.; Wang, Z.H.; Yin, H.F. The distribution of geochemical trace elements in the Quaternary sedments of the Changjiang River Mouth and the paleo environmental implications. Quat. Sci. 2006, 26, 397–405. (In Chinese) [Google Scholar]
- Wei, Z.X. Quaternary Environmental Evolution in Eastern Yangtze Delta: Coupling of Neotectonic Movement, Paleoclimate and Sea-Level Fluctuation. Ph.D. Thesis, East China Normal University, Shanghai, China, 2003. (In Chinese). [Google Scholar]
- Chen, J.; Wang, J.; Zhang, J.; Zhang, L.; Zhu, Y. Field Tests, Modification, and application of deep soil mixing method in soft clay. J. Geotech. Geoenviron. 2013, 139, 24–34. [Google Scholar] [CrossRef]
- Li, M.; Zhang, Z.; Chen, J.; Wang, J.; Xu, A. Zoned and staged construction of an underground complex in Shanghai soft clay. Tunn. Undergr. Space Technol. 2017, 67, 187–200. [Google Scholar] [CrossRef]
- Shen, S.; Wu, H.; Cui, Y.; Yin, Z. Long-term settlement behaviour of metro tunnels in the soft deposits of Shanghai. Tunn. Undergr. Space Technol. 2014, 40, 309–323. [Google Scholar] [CrossRef]
- Liao, C.; Chen, J.; Zhang, Y. Accumulation of pore water pressure in a homogeneous sandy seabed around a rocking mono-pile subjected to wave loads. Ocean Eng. 2019. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Y.; Li, M.; Wen, S. Novel excavation and construction method of an underground highway tunnel above operating metro tunnels. J. Aerosp. Eng. 2015, 28, A4014003. [Google Scholar] [CrossRef]
- Li, M.G.; Wang, J.H.; Chen, J.J.; Zhang, Z.J. Responses of a Newly Built Metro Line Connected to Deep Excavations in Soft Clay. J. Perform. Constr. Facil. 2017, 31, 04017096. [Google Scholar] [CrossRef]
- Wei, B.; Tan, Y. Performance of an Overexcavated Metro Station and Facilities Nearby. J. Perform. Constr. Facil. 2012, 26, 241–254. [Google Scholar]
- Wu, Y.; Shen, S.; Xu, Y.; Yin, Z. Characteristics of groundwater seepage with cut-off wall in gravel aquifer. I: Field observations. Can. Geotech. J. 2015, 52, 1526–1538. [Google Scholar] [CrossRef]
- Zheng, G.; Cao, J.; Cheng, X.; Ha, D.; Wang, F. Experimental study on the artificial recharge of semiconfined aquifers involved in deep excavation engineering. J. Hydrol. 2018, 557, 868–877. [Google Scholar] [CrossRef]
- Wang, J.; Deng, Y.; Ma, R.; Liu, X.; Guo, Q.; Liu, S.; Shao, Y.; Wu, L.; Zhou, J.; Yang, T.; et al. Model test on partial expansion in stratified subsidence during foundation pit dewatering. J. Hydrol. 2018, 557, 489–508. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Zheng, G.; Xue, X.-L.; Mei, G.-X. Combined recharge: A method to prevent ground settlement induced by redevelopment of recharge wells. J. Hydrol. 2019, 568, 1–11. [Google Scholar] [CrossRef]
- Wu, Y.X.; Shen, S.L.; Yuan, D.J. Characteristics of dewatering induced drawdown curve under blocking effect of retaining wall in aquifer. J. Hydrol. 2016, 539, 554–566. [Google Scholar] [CrossRef]
- Pujades, E.; Vàzquez-Suñé, E.; Carrera, J.; Jurado, A. Dewatering of a deep excavation undertaken in a layered soil. Eng. Geol. 2014, 178, 15–27. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Liu, X.; Yang, T.; Wang, H.; Zhu, Y. Areal subsidence under pumping well–curtain interaction in subway foundation pit dewatering: Conceptual model and numerical simulations. Environ. Earth Sci. 2016, 75, 198. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, J.; Zhang, Y.; Gao, Y. Cause investigation of damages in existing building adjacent to foundation pit in construction. Eng. Fail. Anal. 2018, 83, 117–124. [Google Scholar] [CrossRef]
- Chen, X.Y.; Zhang, L.L.; Chen, L.H.; Li, X.; Liu, D.S. Slope stability analysis based on the Coupled Eulerian-Lagrangian finite element method. Bull. Eng. Geol. Environ. 2019. [Google Scholar] [CrossRef]
- Zheng, G.; Zeng, C.F.; Diao, Y.; Xue, X.L. Test and numerical research on wall deflections induced by pre-excavation dewatering. Comput. Geotech. 2014, 62, 244–256. [Google Scholar] [CrossRef]
- Shen, S.; Xu, Y. Numerical evaluation of land subsidence induced by groundwater pumping in Shanghai. Can. Geotech. J. 2011, 48, 1378–1392. [Google Scholar] [CrossRef]
- Li, M.G.; Chen, J.J.; Wang, J.H.; Zhu, Y.F. Comparative study of construction methods for deep excavations above shield tunnels. Tunn. Undergr. Space Technol. 2018, 71, 329–339. [Google Scholar] [CrossRef]
- Li, M.G.; Xiao, X.; Wang, J.H.; Chen, J.J. Numerical study on responses of an existing metro line to staged deep excavations. Tunn. Undergr. Space Technol. 2019, 85, 268–281. [Google Scholar] [CrossRef]
- Theis, C.V. The relation between the lowering of the Piezometric surface and the rate and duration of discharge of a well using ground-water storage. Eos Trans. Am. Geophys. Union 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Cooper, H.H.; Jacob, C.E. A generalized graphical method for evaluating formation constants and summarizing well-field history. Eos Trans. Am. Geophys. Union 1946, 27, 526–534. [Google Scholar] [CrossRef]
- Hantush, M.S. Nonsteady flow to flowing wells in leaky aquifers. J. Geophys. Res. 1959, 64, 1043–1052. [Google Scholar] [CrossRef]
- Hantush, M.S. Modification of the theory of leaky aquifers. J. Geophys. Res. 1960, 65, 3713–3725. [Google Scholar] [CrossRef]
- Hantush, M.S. Drawdown around Wells of variable discharge. J. Geophys. Res. 1964, 69, 4221–4235. [Google Scholar] [CrossRef]
- Papadopulos, I.S.; Cooper, H.H. Drawdown in a well of large diameter. Water Resour. Res. 1967, 3, 241–244. [Google Scholar] [CrossRef]
- Agarwal, R.G.; Al-Hussainy, R. An Investigation of Wellbore Storage and Skin Effect in Unsteady Liquid Flow: I. Analytical Treatment. Soc. Petroleum Eng. J. 1970, 10, 279–290. [Google Scholar] [CrossRef]
- Wen, Z.; Zhan, H.; Wang, Q.; Liang, X.; Ma, T.; Chen, C. Well hydraulics in pumping tests with exponentially decayed rates of abstraction in confined aquifers. J. Hydrol. 2017, 548, 40–45. [Google Scholar] [CrossRef]
- Wu, Y.X.; Shen, J.S.; Cheng, W.C.; Hino, T. Semi-analytical solution to pumping test data with barrier, wellbore storage, and partial penetration effects. Eng. Geol. 2017, 226, 44–51. [Google Scholar] [CrossRef]
- Shen, S.; Wu, Y.; Xu, Y.; Hino, T.; Wu, H. Evaluation of hydraulic parameters from pumping tests in multi-aquifers with vertical leakage in Tianjin. Comput. Geotech. 2015, 68, 196–207. [Google Scholar] [CrossRef]
- Chen, C.; Jiao, J.J. Numerical simulation of pumping tests in multilayer wells with non-Darcian flow in the wellbore. Groundwater 1999, 37, 465–474. [Google Scholar] [CrossRef]
- Doulgeris, C.; Zissis, T. 3D variable density flow simulation to evaluate pumping schemes in coastal aquifers. Water Resour. Manag. 2014, 28, 4943–4956. [Google Scholar] [CrossRef]
- Calvache, M.L.; Sánchez-Úbeda, J.P.; Duque, C.; López-Chicano, M.; De la Torre, B. Evaluation of analytical methods to study aquifer properties with pumping tests in coastal aquifers with numerical modelling (Motril-Salobreña aquifer). Water Resour. Manag. 2006, 30, 559–575. [Google Scholar] [CrossRef]
- HydroGeoLogic, Inc. MOD-HMS/MODFLOW-SURFACT ver. 4.0 User’s manual. A Comprehensive MODFLOW-Based Hydrologic Modeling System; HydroGeoLogic, Inc.: Herndon, VA, USA, 2008. [Google Scholar]
| Well Type | Well Number | Buried Depth of Well Bottom (m) | Internal Diameter (mm) | External Diameter (mm) | Buried Depth of Well Screen (m) | Pumping/ Monitoring Stratum | |
|---|---|---|---|---|---|---|---|
| Upper | Bottom | ||||||
| Pumping well | C5-2-1 | 35 | 273 | 650 | 20 | 34 | ⑤2~⑤3-2 |
| C5-2-2 | 38 | 273 | 650 | 20 | 37 | ⑤2~⑤3-2 | |
| C5-2-3 | 35 | 273 | 650 | 20 | 34 | ⑤2~⑤3-2 | |
| C5-2-4 | 38 | 273 | 650 | 20 | 37 | ⑤2~⑤3-2 | |
| C5-3-1 | 56 | 273 | 650 | 46 | 55 | ⑤3-3 | |
| C7-1 | 73 | 273 | 650 | 66 | 72 | ⑦ | |
| Monitoring well | G5-2-1 | 35 | 168 | 650 | 22 | 34 | ⑤2~⑤3-2 |
| G5-2-2 | 35 | 168 | 650 | 22 | 34 | ⑤2~⑤3-2 | |
| G5-2-3 | 35 | 168 | 650 | 22 | 34 | ⑤2~⑤3-2 | |
| G5-3-1 | 56 | 168 | 650 | 46 | 55 | ⑤3-3 | |
| G7-1 | 73 | 168 | 650 | 66 | 72 | ⑦ | |
| G7-2 | 73 | 168 | 650 | 66 | 72 | ⑦ | |
| Test Type | Pumping Aquifer | Well Number | sw (m) | t0 | te | tp (min) | tr (min) | Q (m3/h) |
|---|---|---|---|---|---|---|---|---|
| Single- well | ⑤2~⑤3-2 | C5-2-1 | 8.94 | 09:00 26 Jul. | 18:37 27 Jul. | 2017 | 2920 | −9.96 |
| ⑤3-3 | C5-3-1 | 31.21 | 12:00 5 Aug. | 13:00 7 Aug. | 2940 | 2828 | −9.77 | |
| ⑦ | C7-1 | 10.21 | 08:00 9 Aug. | 10:00 10 Aug. | 980 | 1020 | −26.7 | |
| Multi- well | ⑤2~⑤3-2 | C5-2-1 | 10.87 | 12:00 12 Aug. | 15:00 20 Aug. | 10930 | 8120 | −7.28 |
| C5-2-2 | 7.82 | −15.64 | ||||||
| C5-2-3 | 7.63 | −11.68 | ||||||
| C5-2-4 | 9.69 | −10.87 |
| Estimation Method | Theis Method | Numerical Solution | |
|---|---|---|---|
| Layers ⑤2~⑤3-2 | kh (cm/s) | 3.73 × 10−3 | 1.02 × 10−2 |
| kv (cm/s) | 3.73 × 10−3 | 3.58 × 10−3 | |
| S | 4.07 × 10−4 | 8.90×10−4 | |
| Layer ⑤3-3 | kh (cm/s) | 1.68 × 10−3 | 4.51 × 10−4 |
| kv (cm/s) | 1.68 × 10−3 | 1.50 × 10−4 | |
| S | 2.44 × 10−4 | 9.12 × 10−4 | |
| Layer ⑦ | kh (cm/s) | 4.86 × 10−2 | 9.21 × 10−3 |
| kv (cm/s) | 4.86 × 10−2 | 3.84 × 10−3 | |
| S (10−4) | 9.80 × 10−6 | 1.44 × 10−3 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Li, M.-G.; Zhang, L.-L.; Chen, H.; Xia, X.-H.; Chen, J.-J. Experimental Study and Estimation of Groundwater Fluctuation and Ground Settlement due to Dewatering in a Coastal Shallow Confined Aquifer. J. Mar. Sci. Eng. 2019, 7, 58. https://doi.org/10.3390/jmse7030058
Li J, Li M-G, Zhang L-L, Chen H, Xia X-H, Chen J-J. Experimental Study and Estimation of Groundwater Fluctuation and Ground Settlement due to Dewatering in a Coastal Shallow Confined Aquifer. Journal of Marine Science and Engineering. 2019; 7(3):58. https://doi.org/10.3390/jmse7030058
Chicago/Turabian StyleLi, Jiong, Ming-Guang Li, Lu-Lu Zhang, Hui Chen, Xiao-He Xia, and Jin-Jian Chen. 2019. "Experimental Study and Estimation of Groundwater Fluctuation and Ground Settlement due to Dewatering in a Coastal Shallow Confined Aquifer" Journal of Marine Science and Engineering 7, no. 3: 58. https://doi.org/10.3390/jmse7030058
APA StyleLi, J., Li, M.-G., Zhang, L.-L., Chen, H., Xia, X.-H., & Chen, J.-J. (2019). Experimental Study and Estimation of Groundwater Fluctuation and Ground Settlement due to Dewatering in a Coastal Shallow Confined Aquifer. Journal of Marine Science and Engineering, 7(3), 58. https://doi.org/10.3390/jmse7030058





