1. Introduction
In recent decades, aquaculture production has served as an essential source of protein for large parts of the world population. An ever-increasing demand for aquatic products suggests that aquaculture will continue to be one of the fastest-growing sectors for the production of protein-based foods [
1]. An important part of its production is of bivalve origin, i.e., clams, oysters, mussels and other species. As of 2014, more than 16 million tons of bivalve produce were farmed around the world [
1]. Bivalve cultivation continues to play an important role in providing food for the growing world population.
Currently, mussel farming is situated near or inshore, mostly because sheltered sites have less technological requirements. However, these sites can also pose a variety of different problems. These range from navigational issues for marine vessels [
2], nutrient depletion in the wake of mussel farms and undesirable changes in the species assemblage to negative alterations to the benthic environment below the farms due to the mussels’ pseudofaeces and marine litter [
3]. These issues in combination with more and more contested space nearshore have stipulated a push towards offshore developments. The perspective to use larger volumes of high-quality water to decrease the stress on cultured organisms offshore and the chance to create more revenue by offsetting seafood deficits have led to an increasing effort to move mussel farming into open waters [
4].
Aquaculture design is predominantly governed by environmental constraints, and depending on the in situ conditions, different aspects have to be considered in, near or offshore. Especially at offshore sites, high energy is acting on the structures as a result of wave and current conditions. Although hydrodynamic forces acting on fixed and floating structures in such conditions are commonly investigated, existing research related to shellfish aquaculture is generally limited [
5]. The feasibility of moving bivalve-related aquaculture offshore is mainly evaluated in regard to farming techniques that are already in use. Suspended farm systems can be divided into intertidal, raft and long-line cultures. Intertidal farms use lines connected to stakes driven into the intertidal sea bed from which the dropper lines are suspended [
6]. In raft systems, the mussels are grown on ropes which are hung from a moored raft into the water column [
7,
8]. Furthermore, so-called “long-line systems” are a possible candidate to be moved further offshore [
9]. Long-line systems consist of floatation elements that are connected by ropes to form a mussel-bearing backbone. The backbone is kept in place at each end via an anchor warp connected to the mooring systems. The mussels are cultivated on ropes, so called “dropper lines” or “collectors”, and suspended perpendicular from the backbone. The dropper lines are usually spaced evenly along the backbone, with lengths between 5–30 m depending on the water depth and available nutrition. The hydrodynamic forcing on long-line systems has been observed in near-shore conditions to identify the dominant modes of flow-structure interaction and to provide a baseline for designs of future structures [
10]. On this basis, work regarding the physics of offshore bivalve-aquaculture has been presented [
11]. A description of the hydrodynamic implications of large long-line farms based on observations and scaling arguments is available [
12]. A study using a rigid, artificial mussel crop rope constructed from the shells of
Perna canaliculus provides
-values for the towing velocities of 0.05 to 0.40 m/s.
The aim of the study was to determine the influence of the inhalants and exhalents of fluids on the drag [
13]. An investigation regarding the drag coefficients of suspended canopies, i.e., mussel dropper lines, derived from a physical model with circular cylinders as a representation of the dropper lines is available by Plew, D.R. [
14]. Research regarding numerical simulations of suspended bivalve farms is available to a limited extent and mostly details the flow patterns in the wake of farm systems [
15]. A numerical study by Raman-Nair and Colbourne [
16] to quantify the loads induced into long-line systems is the basis for a numerical model of the three-dimensional dynamics of a submerged mussel long-line system presented by the same author [
17]. Further, a flow analysis around mussels is part of the current research activities, however mainly focusing on naturally bedded mussel cultures [
18] or on netted structures in association with biofouling [
19] in contrast to the long-line systems. While observations of long-line systems are available alongside numerical work, to date no laboratory tests are available. However, experimental data are of crucial concern for the calibration of numerical models facilitating the design process. Thus, this work depicts the first detailed examination of the response of a live-mussel long-line to hydrodynamic forcing in laboratory conditions.
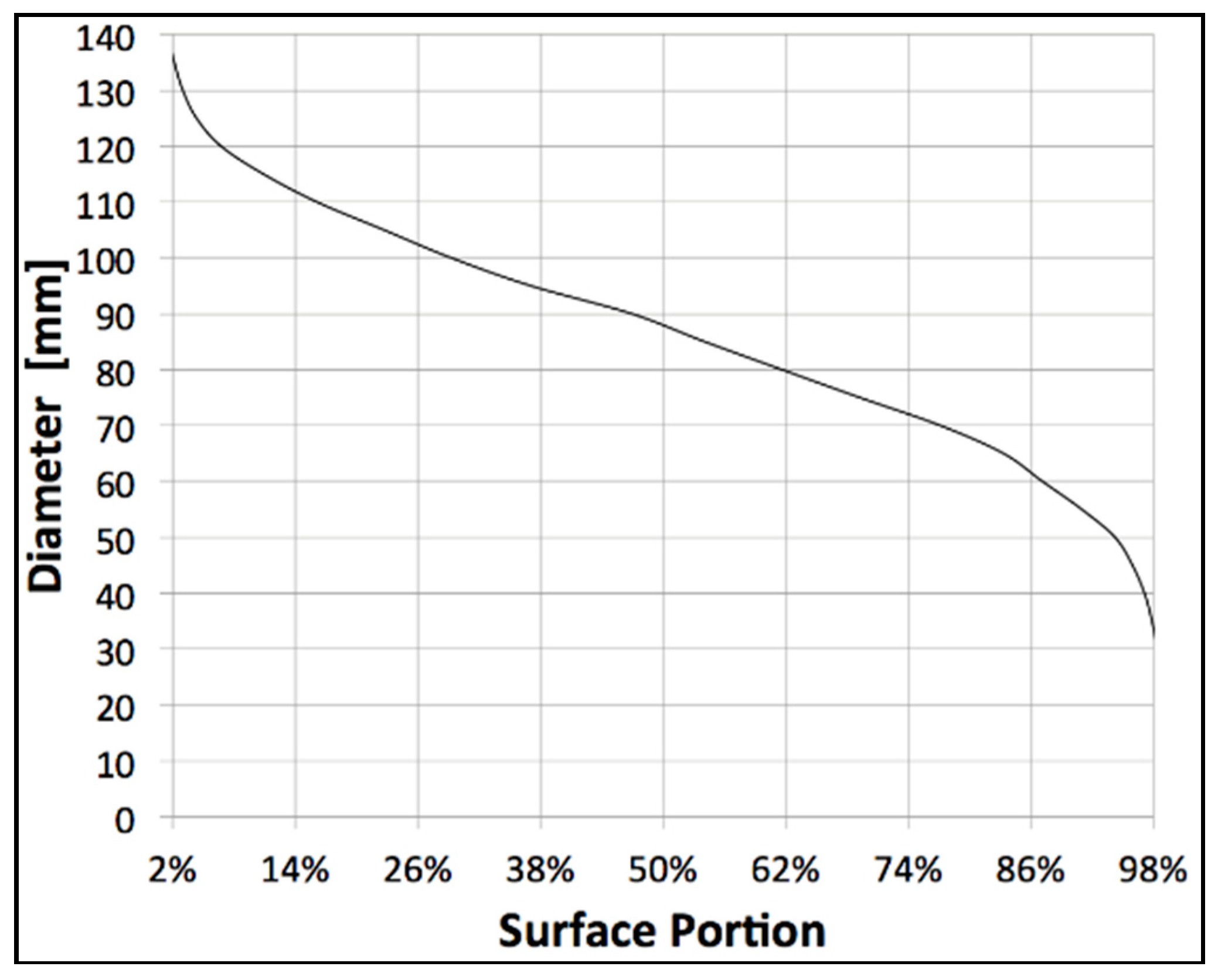
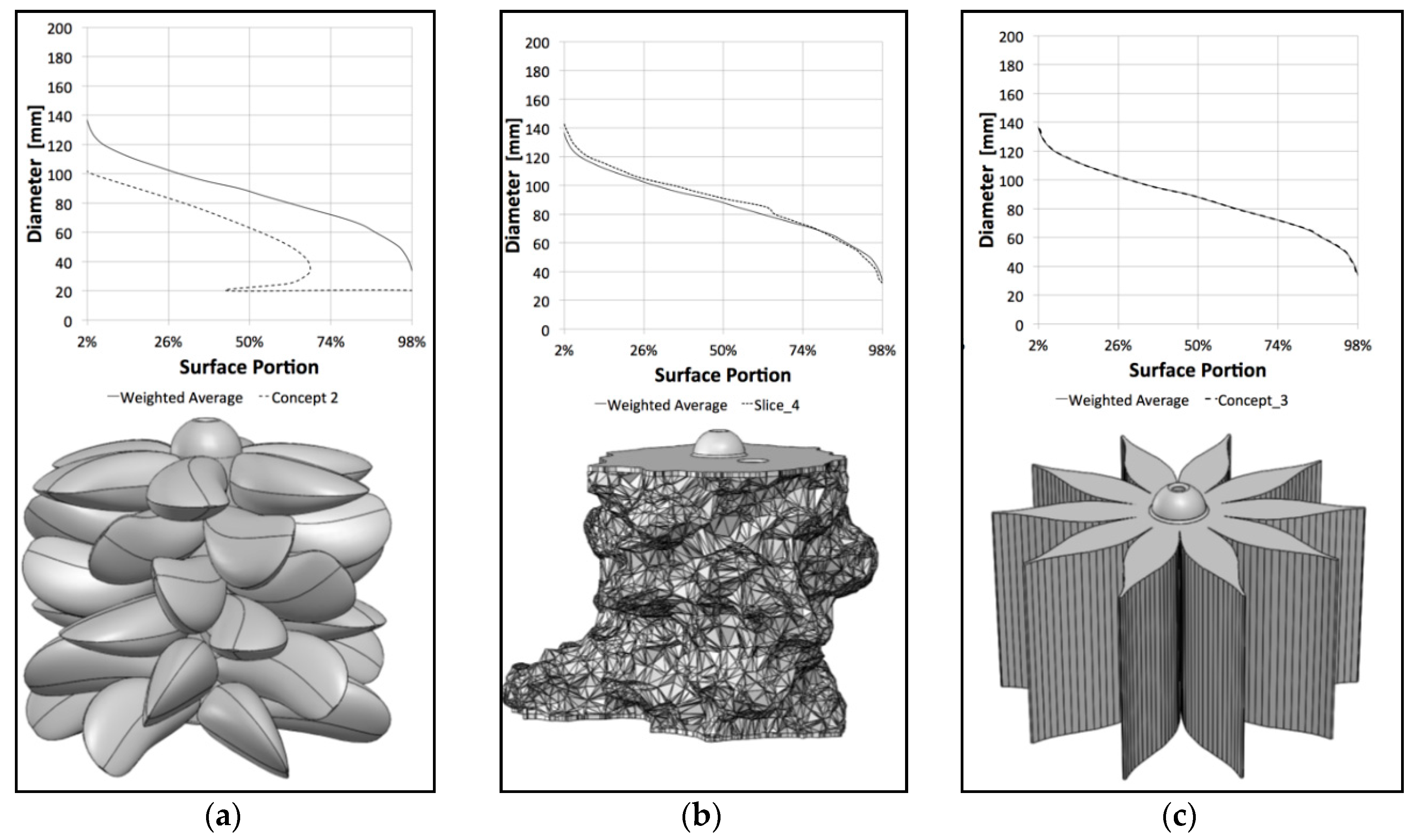
The available literature shows that research gaps concerning the behaviour of suspended long-lines in current and wave conditions exists. Especially the behaviour of dropper lines under waves has received only little attention. A series of physical tests with full-scale blue mussel dropper lines was conducted to evaluate the corresponding drag and inertia characteristics in the future as well as to determine the magnitude of wave and current forces acting on the mussel dropper lines. To that end, a custom-made test rack consisting of aluminium profiles was attached to a traversing carriage located over a wave flume. Three different specimens of live blue mussel (Mytilus edulis) dropper lines were fitted to the test rack. These were tested at various current speeds simulated by the carriage runs to obtain the drag coefficients. Independently, wave tests with varying parameters were conducted to obtain the inertia coefficients. Additionally, surrogate models were created from a digital model based on the 3-D scanned data of the live-mussel dropper lines. The live and surrogate shellfish dropper lines were compared subsequently. The surrogate models were evaluated regarding the statistical mean values of sampled single mussels as well as a surface descriptor. By this means, a number of different surrogates were created and assessed in regard to their fit to the corresponding Abbot–Firestone curve.
2. Materials and Methods
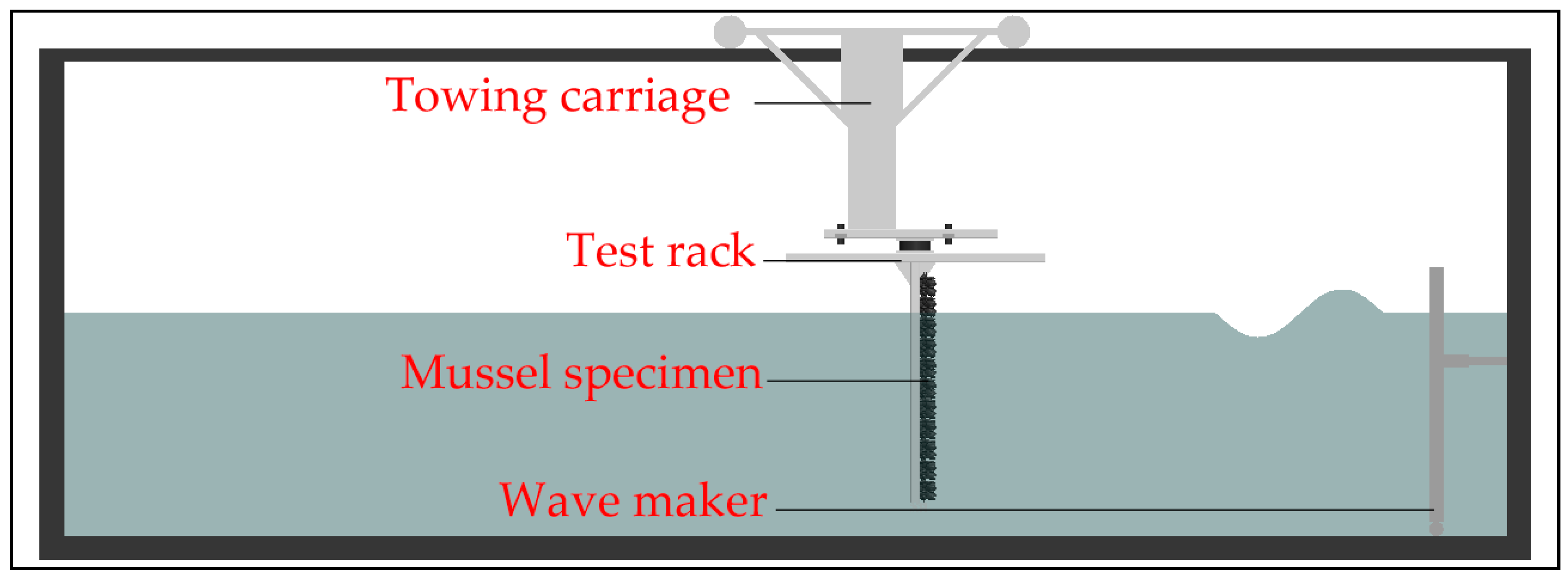
Experiments involving live-mussel specimens were carried out at the medium wave and towing tank “Schneiderberg” (WKS) at the Ludwig-Franzius Institute for Hydraulic, Estuarine and Coastal Engineering of the Leibniz Universität Hannover, Germany. The WKS is 110 m long, is 2.2 m wide and contains up to 1.1 m water with a total depth of 2.0 m. In this facility, regular and irregular waves can be generated up to 0.5 m in wave height. A towing carriage allows for testing at constant velocities of up to 1.5 m/s. A plan and side view of the WKS including the towing carriage and wave maker are outlined in
Figure 1. All data chosen for the current velocities and wave characteristics were related to potential offshore sites, e.g., off the coast of New Zealand or Canada, and scaled down to allow for future experiments with scaled surrogates. A 1:10 scale was selected, and a Froude similarity was applied.
A vertical aluminium beam of 2.52 m length, attached to the carriage, allowed the connection of additional equipment. In this work, a load frame was fixed to the main beam that consists of interconnected aluminium profiles. To ensure a sufficient rigidity, a 1.08 m × 0.72 m aluminium frame, horizontally oriented, was used as the top part of the rack. This frame was braced and reinforced by two 1.0 m-long aluminium profiles on the inside of the frame, running in line with the 1.08 m-long outer profiles. The lower part of the test rack was also assembled with an aluminium frame of 1.00 m × 0.80 m, vertically oriented, and used primarily for the attachment of the live-mussel specimens.
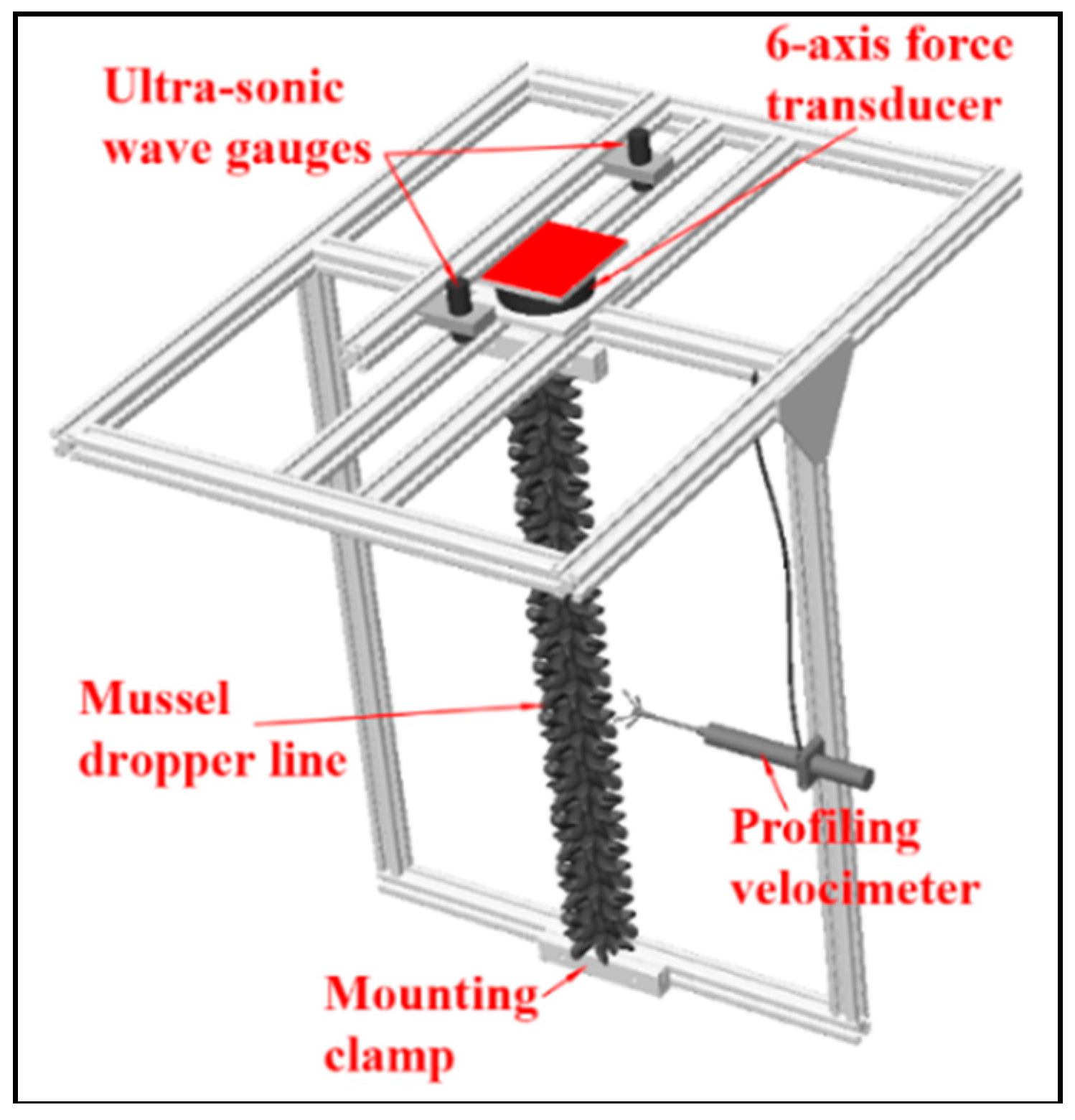
Figure 2 presents schematic sketches of the test rack with the attached measuring equipment. The main beam, not visible in the sketches, is represented by a connecting plate. Custom-made clamps with a coarse interlocking grid were CNC-milled. These allowed for an easy connection of the mussel dropper line to the test rack while also being able to restrict unwanted movements for the test duration. The clamps were attached to the bottom of the lower frame and the interior profiles of the upper frame. This allowed for a horizontal orientation of the mussel dropper lines in a defined distance from the main beam. Four wire connections ran from the outer corners of the upper frame to the bottom of the lower frame to further increase the stability. Further, the wires were tensioned to ensure the stability of the test rack. The test rack, as a whole, provided a structure for mussel droppers with a maximal length of 1.1 m. The carriage speed for drag testing was checked via an incremental rotary encoder (SICK DBV50) with a resolution of 12.5 pulses/mm. The rotary encoder allowed for the exact determination of the associated towing velocity by means of single differentiation over the travelled distance. Testing was conducted in either direction, along-flume; hence the rotary encoder installed on the carriage track was either used as a trailing or guiding encoder, depending on the direction of the test run.
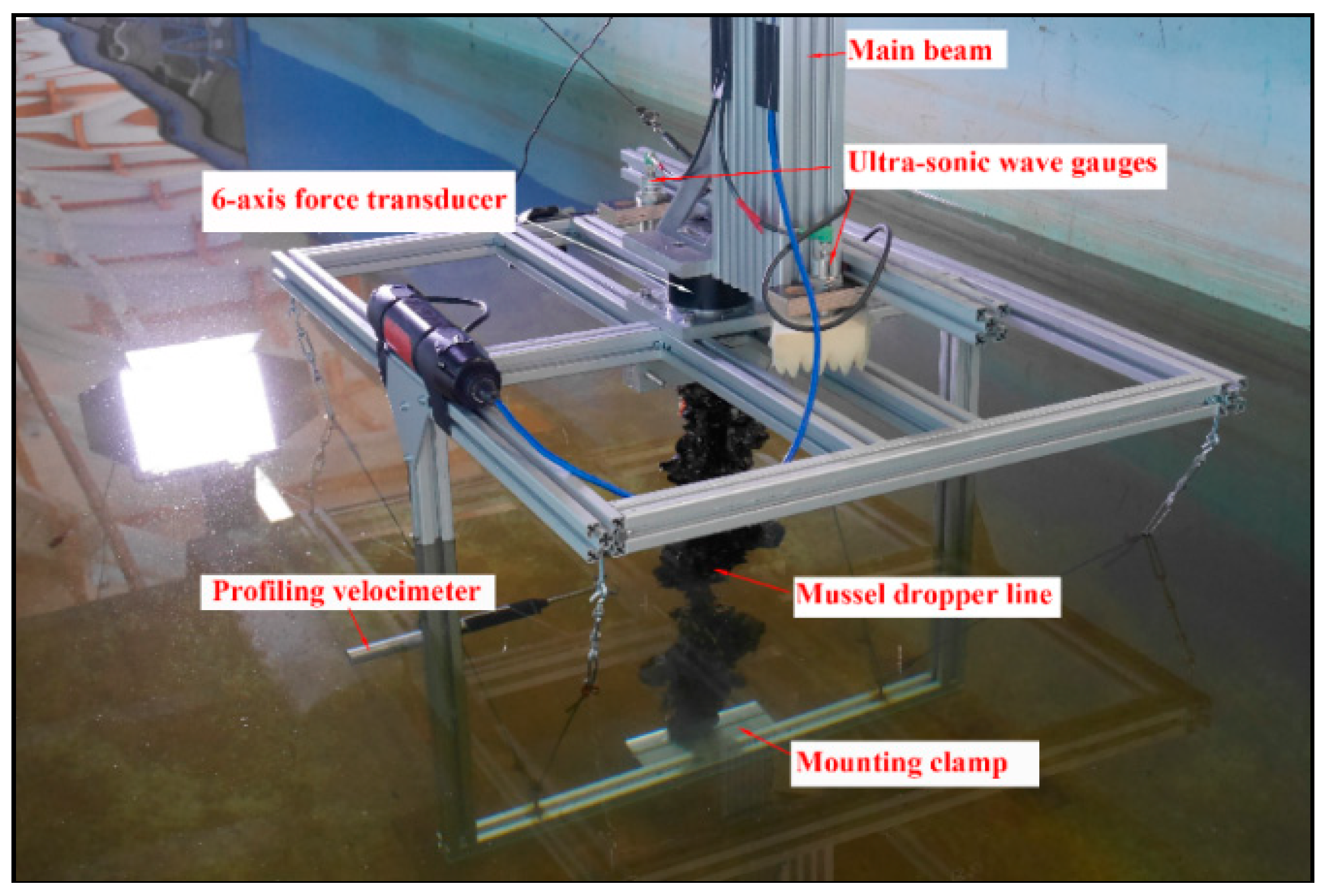
Most importantly, the forces on the mussel dropper lines were of interest when subjected to waves and currents. To obtain this information on the test rack, a six-axis force-transducer (K6D110 ME-Meßsysteme GmbH, 16761 Henningsdorf, Germany) was rigidly attached to the main beam. The K6D110 has a nominal force range of up to 10 kN in x-, y- and z-directions and a nominal torque range of 750 Nm in Mx, My and Mz. Accurate measurements as low as 0.1 kN were possible, based on the specifications by the manufacturer. The x-direction corresponds to a movement from the point of origin along the flume; the y-direction represents the lateral direction, while the z-direction described the direction towards the bottom of the flume. The recorded momentum forces in Mx, My and Mz describe the torques around these axes, respectively. Furthermore, a profiling, acoustic Doppler velocimeter, ADV, (Vectrino Profiler, Nortek, 1351 Rud, Norway) with a maximum sample rate of 100 Hz was attached to the test rack. With the ability to profile three-component velocities over a vertical range of 3 cm and with a resolution of 1 mm, insights into the turbulence dynamics alongside the mussel dropper lines becomes possible. The ADV Profiler was attached in a distance of approximately 0.45 m from the lowest aluminium profile. That approximately corresponds to the midsection of the tested blue mussel dropper lines. Furthermore, measurements of the time-history of the free surface elevation in close vicinity to the dropper line were carried out by ultrasonic wave gauges to obtain information concerning the local wave field. To this end, two locations roughly 0.20 m in front of and behind the dropper line are selected.
All tests were recorded via two sets of cameras. A GoPro Hero4 with a high-definition resolution and a sample rate of 100 fps as well as a Logitech C920 webcam with high-definition resolution and a sample rate of 30 fps were added to the test setup. A linear Field-of-View (FOV) setting for the GoPro Hero4 (Firmware v5.00) was used to correct the convex distortion of the camera. The C920 recorded with a linear FOV as the default setting. The GoPro was installed underwater to the side of the test rack with a slight offset to the dropper line. The offset ensured an unobstructed view on the test specimen. The webcam was installed on the upper frame of the test rack directed at the blue mussel dropper line in the direction of the wave flume. It was fitted to monitor the wake and oscillatory behaviour of the dropper line. During inertia testing, the carriage, as a whole, was positioned in front of a window section of the flume. A tripod holding another Logitech C920 webcam was used. All video files recorded allowed hindsight into the testing conditions and also provided data regarding the motion response of the dropper-lines under different current velocities. The water depth was kept constant at 0.93 m and was recorded together with temperature periodically throughout the testing procedure. The constant water depth allowed for continuous and identical testing conditions.
Figure 3 shows the test rack with the attached measuring equipment and mussel dropper line.
A 3.62 m long dropper line of marketable, adult blue mussels (Mytilus edulis) encrusted with newly seeded spat was selected for testing. The blue mussel was selected due to its wide distributional pattern. Furthermore, blue mussels are prime candidates for aquaculture [
20]. This is mainly due to its ability to withstand wide fluctuations in salinity, desiccation, temperature and oxygen levels [
21]. Blue mussels are found throughout European waters, occupying habitats from Russia to the Bay of Biscay off the French coast. Its zonatial range stretches from the high intertidal to subtidal regions, and its salinity adaptability extends from estuarine areas to fully oceanic seawaters. The blue mussel is euryhaline and proliferates in offshore sea- as well as in brackish-waters down to 4% salinity. Blue mussels are also eurythermal, withstanding freezing conditions for several months. The species is acclimated for a 5–20 °C temperature range, with an upper sustained thermal tolerance limit of about 29 °C for fully grown conditions [
21]. These behavioural characteristics allow for a broad application of the insights gathered into drag and inertia characteristics. The blue mussels used in the drag and inertia tests were obtained from an aquaculture farm located in Kiel, Germany and were transported and stored in a controlled sea water tank with aeration and temperature regulation systems in use. Thus, the survival of the mussels for a prolonged time was possible with no loss of adhesive qualities of the byssus, the bundled filaments secreted by the bivalves. The byssus function was the attachment points to the dropper line and was weakened when subjected to adverse conditions.
The blue mussel dropper line was segmented into three specimens with lengths of 1.03 m to 1.05 m. These were labelled 1 to 3 to distinguish in between testing. The specimens were individually weighed, and their width was measured in steps of 5 cm. This was required to determine the mean diameter of the blue mussel specimens. The volumetric displacement of each specimen was determined by immersing them into a container of known dimensions. The water level was then measured before and after the immersion of the specimen. The extant blue mussel dropper line with a length below 50 cm was treated the same way. Additionally, the length, diameter, displacement and weight of individual blue mussels were also determined. Some mussel individuals were selected randomly to obtain information on the individuals of the encrusted rope.
The mean values for the individual mussels correspond to a mean single mussel length
, a mean single mussel thickness
and a mean single mussel weight
.
Figure 4 depicts a specimen prepared before testing alongside a single mussel evaluated regarding the mean values.
The specimens were inserted into the mounting clamps and tightened. For each specimen tested, several towing and wave tests with varying setups were conducted. However, before each set of experiments, an eigenfrequency test for the test rack itself was carried out with an impact hammer. The impact event was synchronously recorded by the 6-axis force transducer mounted to the load frame. By this means, the eigenfrequencies of the load frame as well as all possible combinations with dropper line specimens were recorded. Upon completion, the drag experiments in the wave tank were carried out with top- and bottom-mounted dropper lines that were towed at velocities of
u1 = 0.25 m/s,
u2 = 0.50 m/s,
u3 = 0.75 m/s and
u4 = 1.00 m/s. The mount at both ends ensures an equal flow velocity for the whole length of the dropper line. Each specimen, though differing in total length, was submerged over a length of
Lwet = 0.80 m. This, in turn, allows the correct determination of the drag coefficient
for a specified length of mussel dropper line. The Reynolds numbers
covered during the tests were determined with the characteristic diameter
, the aforementioned towing velocities
, the kinematic viscosity of the water
ν = 1.004/998,200 m²/s and the constant water temperature of 20 °C and range from 2.0 × 10
4 to 1.1 × 10
5. In between all drag tests, the flow disturbances potentially induced by previous testing settled during a waiting period in order to avoid biased influence. Testing of the first specimen was repeated three times for testing repeatability. In order to gain further information about the force and motion response of the specimen, the towing operation was divided into forward and backward motions such that a single specimen is towed twice yet with a 180° change in direction. For specimens 2 and 3, the repetitions were reduced to one to allow for quicker laboratory tests, as the live mussels lose their cohesive properties when exposed to non-autochthonous conditions over a prolonged period of time [
20]. After the completion of these tests, the setup of the dropper line was changed by loosening the lower clamp, leaving a top-mounted dropper line. As the pretests had revealed that major oscillations of the blue mussel dropper lines in the lateral and longitudinal directions occur at velocities
u > 0.50 m/s, the tested velocities were reduced for the drag tests with the top-mounted specimens. The reduced velocities tested were
u5 = 0.10 m/s,
u1 = 0.25 m/s,
u6 = 0.375 m/s and
u2 = 0.5 m/s.
Figure 5 shows the top-mounted mussel specimen dragged at
u5 = 0.10 m/s,
u1 = 0.25 m/s and
u2 = 0.5 m/s. The progressive lift towards the surface due to the forces acting on the dropper line is visible throughout the three sections.
After completing the towing tests, the carriage was positioned in front of a windowpane in the wall of the flume, which allows a side-view documentation of the motion response of the droppers during wave loading. The distance between the wave maker and carriage is 65 m. Three sets of waves were tested. These are described by their period
T and their targeted wave height
H. Thus, the wave tests were carried out with targeted wave heights
H of 0.1 m, 0.12 m and 0.15 m with corresponding periods
of 1.20 s, 2.4 s and 1.65 s. Each wave test was conducted once for each of the three specimens. The chosen values regarding the wave characteristics were related to potential offshore sites, e.g., off the coast of New Zealand or Canada, and scaled down to allow for future experiments with scaled surrogates. A 1:10 scale was selected, and a Froude similarity was applied. The corresponding Keulegan–Carpenter numbers
ranged from 4.1 to 5.9. In
Table 1, an overview of the wave height, wave period, maximum horizontal and vertical velocity, maximum horizontal and vertical acceleration and wave length is provided according to Stokes 2nd order wave theory for the waves tested in the flume. The tested wave heights are displayed in model
M and full-scale
F according to Froude similitude and a scaling factor of 1:10. The tests were performed for the top- and bottom-mounted configurations to enable comparative studies regarding the commonly investigated cylinders under wave loads as well as the free-swinging systems.
Figure 6 exemplarily shows specimen 3 in waves with a targeted wave height of 0.12 m and a period of 2.4 s in a top-and-bottom-mounted configuration in comparison to a top-mounted only configuration. The latter setup results in an additional oscillatory movement of the blue mussel dropper line. To attain the actual forces acting on the blue mussel dropper line alone, frame-only tests are necessary as a concluding step. Here, all drag and inertia tests with corresponding current velocities and wave sets were carried out without an attached specimen.
In between testing, a 3-D point cloud as a digital copy of the dropper line specimens was acquired by a terrestrial laser scanner in collaboration with the Geodetic Institute of the Leibniz Universität. The acquisition of the 3-D point cloud was carried out without immersing the specimen into the wave flume, as subaquatic scanning is less accurate and difficult to achieve with the current technology. The dropper lines were hung from the laboratory ceiling by a crane. The surrounding area is closed off for foot traffic to minimize specimen movement by unintended air flow. Around the blocked area, three tripods are pre-mounted to allow for an exact positioning of the 3-D laser scanner (Z+F IMAGER® 5010) with a measurement rate of up to 1 million points per second and a horizontal and vertical accuracy of 0.0007° (rms). Furthermore, reference points for the spatial registration were added in the vicinity of the scanning area. The 3-D point clouds from the differently positioned tripods were combined into a 3-D point cloud, with every single point containing information about x-, y-and z-directions as well as intensity.