Abstract
Because of special morphologies and complex runoff–tide interactions, the landward floodtide flows in Yangtze Estuary are observed to spill over from the North to the South Branches, carrying a lot of sediment. To quantitatively clarify the spillover problem, a two-dimensional numerical model using a high-resolution channel-refined unstructured grid is developed for the entire Yangtze Estuary from Datong to river mouths (620 km) and part of the East Sea. The developed model ensures a good description of the river-coast-ocean coupling, the irregular boundaries, and local river regimes in the Yangtze Estuary. In tests, the simulated histories of the tidal level, depth-averaged velocity, and sediment concentration agree well with field data. The spillover of sediment in the Yangtze Estuary is studied using the condition of a spring and a neap tide in dry seasons. For a representative cross-section in the upper reach of the North Branch (QLG), the difference of the cross-sectional sediment flux (CSSF) between floodtide and ebbtide durations is 43.85–11.26 × 104 t/day, accounting for 37.5–34.9% of the landward floodtide CSSF. The mechanics of sediment spillover in Yangtze Estuary are clarified in terms of a successive process comprising the source, transport, and drainage of the spillover sediment.
1. Introduction
The Yangtze Estuary is a large-scale shallow water system characterized by three-level bifurcations (North and South Branches, North and South Channels, North and South Passages) and has four outlets into the East Sea (see in Figure 1 and Figure 2). Significant runoff from the Yangtze River (about 9000 × 108 m3/year) and periodical tides from the ocean meet in the estuary and interact with each other, leading to complicated hydrodynamics and sediment transport. The landward floodtide flow often spills over from the North to the South Branches, carrying a lot of sediment. The estuarine circulations of water and sediment fluxes, characterized by the spillover of water and sediment, play an important role in shaping the morphology of the Yangtze Estuary [1,2,3,4,5].
Figure 1.
The location of the Yangtze Estuary and the study area (a Google Map diagram showing the geographical features of the location). (a) Location; (b) Tidal reaches and estuary.
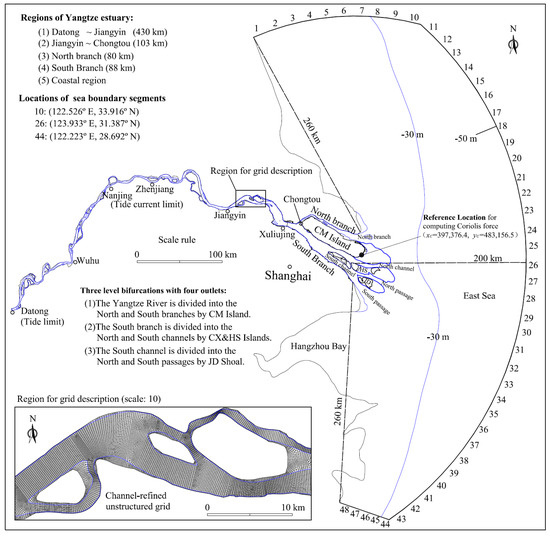
Figure 2.
Description of the bound, the three-level bifurcations and the strong river-coast-sea coupling in Yangtze Estuary (computational domain and grid are also given).
The spillover of water and sediment in the Yangtze Estuary is very complex because of the special morphology and the complex runoff-tide interactions. First, the spillover happens in a three-level branching estuary, where the exchanges of water and sediment are complex between different branches of the branching Yangtze Estuary. Second, the North Branch of the Yangtze Estuary is characterized by a special morphology [5]. The upper reach is narrow and almost orthogonal to the South Branch, preventing upstream inflows from entering during ebbtides. The lower and tail reaches are trumpet-shaped with a wide outlet, in favor of accommodating a great deal of landward tidal flows during floodtides. Third, the river, the coast, and the ocean in the Yangtze Estuary are closely related, where the bidirectional flows inside the estuary evolve gradually into clockwise irregular rotational tidal flows in offshore regions (under the influence of runoff-tide interactions, rapidly varying topographies and complex solid boundaries in coastal areas). As a result, it is difficult to study the spillover problem of water and sediment in the Yangtze Estuary. Moreover, because of limitations of field data and methods (the details will be introduced in the following paragraphs), quantitative studies on the spillover of sediment from the North to the South Branches in the Yangtze Estuary have not been reported. The quantitative knowledge on the spillover of sediment in the Yangtze Estuary is currently quite limited.
On the other hand, surrounded by the most developed regions of China (Shanghai city and Jiangsu Province), the Yangtze Estuary has seen extensive launching of flood-defense, water-resource, reclamation, and navigation projects because of requirements for the development of cities. It is generally necessary to check the reasonability of the designed constructions before launching a project. The influences of a project on the estuarine environment (e.g., the tidal flow, sediment transport, and long-term riverbed evolutions) should also be evaluated to clarify its possible negative side and for corresponding preventions. Under the influence of the spillover of water and sediment, figuring out the aforementioned issues of a project in the branching Yangtze Estuary is challenging. As a result, it is important to have extensive knowledge of the horizontal circulations of water-sediment fluxes in the Yangtze Estuary, which will provide a guide and a support for the design of constructions in real applications.
The tidal flows and sediment transport in the Yangtze Estuary are often studied by analyzing field data using the physical model or adopting the numerical models. However, the knowledge based on the analysis of topographical and hydrological data is often limited by space–time resolutions of the field data of sediment transport. Existing studies of analysis are often only carried out for local reaches or parts of cross-sections in some branches of the Yangtze Estuary, e.g., the sediment transport rate along the streamline of main-flow channels [1,2,6]. Scale models are expensive to build and operate. As an effective and less expensive method, many numerical models have gradually become the most widely used method in studying estuarine hydrodynamics and sediment transport due to continuous improvements in computers and numerical schemes.
Two-dimensional (2D) or three-dimensional (3D) numerical models applied to the Yangtze Estuary should meet the multiple requirements for computational accuracy and efficiency. First, to get a full description of river-coast-ocean coupling, the upstream tidal reach, the entire Yangtze Estuary and part of the East Sea are included in a single model. The computational domain of the entire Yangtze Estuary (from Datong to seaward contours of −4 m) is 84.4 × 108 m2, as shown in Figure 2. Second, the computational grid should be fine enough to describe well the local river regimes in the Yangtze Estuary and simulate the estuarine mesoscale structures and transport process correctly [7,8]. Corresponding to fine grids, a small time step of 1–2 min is often required to ensure the stability and accuracy in simulating the fully unsteady flows and sediment transport. Third, simulations of long-term tidal flows, sediment transport, and riverbed evolution are often required in studies of the morphological dynamics. When the domain of the entire Yangtze Estuary is divided using a high-resolution grid, a huge computational cost is required. These requirements challenge almost all existing 2D or 3D numerical models [9]. As a result, in real applications of the Yangtze Estuary, researchers often have to use coarse grids, establish local models [10,11,12], or adopt simplified methods, such as the method of the morphological scale factor [13,14].
In this paper, an efficient 2D numerical model is developed to simulate the tidal flow, sediment transport, and riverbed evolution in the Yangtze Estuary using a high-resolution channel-refined unstructured grid. The model is then applied to a quantitative study on the mechanics of the spillover of water and sediment in the Yangtze Estuary.
2. Numerical Formulation
The governing equations, computational grids, and numerical schemes of the hydrodynamic model (HDM) and the sediment transport model (STM) are introduced.
2.1. Governing Equations
Depth-averaged 2D shallow water equations (SWEs), with Coriolis terms, are used as the governing equations for the HDM, which are given by
where h(x, y, t) is the water depth, (m); u(x, y, t) and v(x, y, t) are the components of depth-averaged velocity in the horizontally in the x- and y-directions, respectively, (m/s); t is the time, (s); g is the gravitational acceleration, (m/s2); η(x, y, t) is the water level measured from an undisturbed reference water surface, (m); υt is the coefficient of the horizontal eddy viscosity, (m2/s); f is Coriolis factor; nm is Manning’s roughness coefficient, (m−1/3 s); ρ is the water density, (kg/m3); and τsx and τsy are the wind stress in the x- and y-directions, respectively, (N/m2).
The above equations construct a set of equations for u, v and η. Their forms are invariable in the rotating frame of unstructured grids. The wind stress is imposed as per [12,13]. For a given location (x, y) of the Yangtze Estuary, the Coriolis factor f is given by
where Ω (7.29 × 10−5 rad/s) is the angular velocity of rotation of the Earth; ϕ (31.38724°) is the latitude of the reference location (xc, yc) which is shown in Figure 2.
The annual bed-load quantity transported through the outlets of the Yangtze Estuary is about 500–1000 × 104 tons, accounting for 1–2% of the total sediment load [15]. The bed-load transport therefore contributes little to the horizontal circulations of global water–sediment fluxes in the Yangtze Estuary, and is not solved by the present model. The suspended sediment is regarded to be nonuniform and is described by a fraction method. The vertically averaged 2D advection–diffusion equation, with a source term describing sediment exchange between flow and riverbed, is used to describe the transport of nonuniform suspended load:
where k is the index of the sediment fraction, k = 1, 2, …, Ns (Ns is the number of fractions); Ck and S*k = sediment concentration and the sediment-carrying capacity of flows for the kth fraction of the nonuniform suspended load, respectively, kg/m3; wsk = settling velocity of sediment particles for the kth fraction of the suspended load, m/s; α = sediment recovery coefficient, which is set to 1.0 and 0.25, respectively, in case of erosion and deposition [16].
According to particle size and physical/chemical property, the nonuniform sediment is divided into four fractions. The size ranges of fractions 1–4 are, sequentially, 0–0.031, 0.031–0.125, 0.125–0.5, and >0.5 mm. In real applications, researchers often determined the settling velocity (ws) of the fine particles according to field data, experiments or their experience [11,12,17,18,19,20]. In the present model, the ws of fraction 1 is set according to field data in the Yangtze Estuary, while the primitive settling velocity is directly used for other fractions.
Zhang’s formula [21], which is widely used in evaluating the sediment-carrying capacity of flows in real applications, is used in our model and given by
where U is a vertically averaged velocity (); m is an exponent and set to 0.92 in our model; K is sediment-carrying coefficient and determined by calibrations with field data. In the model, Zhang’s formula [21], with the help of the method in [22], is used to determine the fractional sediment-carrying capacities of flows for the nonuniform sediment.
Corresponding to Equation (4), riverbed deformation induced by the transport of the kth fraction of the nonuniform suspended load is described by
where zbk = riverbed deformation caused by the kth fraction sediment, m; ρ′ = dry density of bed materials, kg/m3. The gradation state of the bed materials is also updated using the method of [22].
The coefficient of Manning’s roughness, nm, in the HDM and the coefficient of the sediment-carrying capacity, K, in the STM are determined by calibration tests with field data. Because the Yangtze Estuary is large and includes various regions with different characteristics of flows and sediment transports (e.g., river reach, tidal reach, coast sea area, and sea region), non-constant model parameters are used in different regions.
2.2. Computational Grid and Model Formulation
2.2.1. Computational Grid
The computational domain is divided up by a set of non-overlapping triangles or convex quadrangles. A CD staggered grid of variable arrangement [23] is used. The horizontal velocity components, u and v, are defined at side (cell face) centers, while the water level, η, and the scalar concentration, C, are defined at element centroids. The notations ne, np, and ns are respectively used to denote the number of elements (cells), nodes, and sides of the unstructured grid. For the sake of convenience, the notations associated with the unstructured grid are introduced as follows:
(1) i34(i) is the number of nodes/sides of cell i; j(i,l) is the sides of cell i, where l = 1, 2,…, i34(i); Pi is the area of cell i; (2) i(j,l) are two cells that share side j, where l = 1, 2; δj is the distance between two adjacent cell centroids that are separated by side j; Lj is the length of side j; (3) si,l is a sign function associated with the orientation of the normal velocity defined on side l of cell i. Specifically, si,l = 1/−1 if a positive velocity on side l of cell i corresponds to outflow/inflow (of cell i).
2.2.2. Numerical Discretizations
The adopted HDM uses a θ semi-implicit formulation [24,25,26], while finite-volume and finite-difference methods are combined. Momentum equations are solved within a finite-difference framework and using operator-splitting techniques. The θ semi-implicit method is used to advance the time stepping. Correspondingly, the gradient of the free-surface elevation is discretized into explicit and implicit parts. A point-wise Eulerian-Lagrangian method (ELM), using the multistep backward Euler technique [23,27], is used to solve the advection term. The horizontal diffusion term is discretized using an explicit center-difference method.
When the advection term is solved by the ELM, the velocities are updated at once and are denoted by ubt and vbt. The horizontal momentum equations in the local horizontal x-, y-directions of unstructured grids are then discretized as follows (at side j)
where θ is the implicit factor and Δt the time step; superscripts “n” indicate the n-th time step; for simplicity, the explicitly discretized horizontal diffusion term is not expanded here; the riverbed friction is discretized using ubt and vbt to enhance computation stability. The explicitly discretized horizontal diffusion term is not expanded here for simplicity, and denoted by EX and EY in x- and y-directions, respectively. The η at nodes is regarded as auxiliary variables, which are interpolated from water-level values of neighboring cells.
When explicit terms of the discretized momentum equations are incorporated, the unknowns (free-surface elevation η) emerge. Equation (7a,b) are then transformed into (at side j)
where ; , are the incorporated explicit terms respectively in the horizontal x-, y-directions, , .
To achieve good mass conservation, the depth-integrated continuity equation, Equation (1), is discretized by the finite-volume method, which is given by (at cell i)
where l is the side index of cell i, and l = 1, 2, …, i34(i).
The velocity–pressure coupling is performed by substituting ujn+1 and vjn+1 of Equation (8a,b) into the discrete depth-integrated continuity equation. This substitution results in a wave propagation equation with cell water levels (η) as unknowns. Using the topology relations among the cells, the resulting discrete wave propagation equation is given by (at cell i)
The HDM solves the vertically averaged 2D shallow water equations at three steps. First, all the explicit terms (advection, diffusion, riverbed friction, and the explicit part of free-surface gradients) in momentum equations are explicitly computed to obtain the provisional velocities. Second, the velocity-pressure coupling is performed by substituting the expressions of normal velocity components into the discrete continuity equation, where a wave propagation equation is constructed and solved to obtain new water levels. Third, a back substitution of the new water levels into the momentum equations is performed to get the final velocity field.
For each fraction of nonuniform sediment, one transport equation must be solved. The STM is advanced fully explicitly, and the transport equation is discretized as (for fraction k)
where Δt is the time step for the STM; Cbt is the solution to the advection subequation. The Cbt is calculated using a recently developed finite-volume ELM (FVELM) [28], where mass is conserved and large time steps (for which the Courant-Friedrichs-Lewy number (CFL) can be much greater than 1) are allowed.
For the FVELM, the geometrical computation which is common for each sediment fraction can be reused. When the most time-consuming parts (calculations of trajectories and interpolation weights) are avoided, only a relatively very small computation cost is added for solving each additional sediment fraction. Therefore, the FVELM allows constructing efficient algorithms for solving the transport of a large number of sediment fractions, and this property of the FVELM is defined as the multiscalar property. Benefiting from “allowing large time steps, parallelizable, multiscalar property”, the FVELM is much more efficient than the traditional Eulerian advection schemes in solving the transport of nonuniform sediment with several fractions.
2.3. Parallelization of the Model Code
The HDM and STM can both be well parallelized. In the code of the model, the computation of one time step was implemented as a number of loops. Among these loops, the parallelizable ones were parallelized using loop-based parallelization and the open multiprocessing technique (OpenMP). In this study, a 16-core processor (Intel Xeon E5-2697a v4) and Intel C++ 14.0 formed the hardware and software environment. The runtime speedup, used as an indicator of how much faster the parallel code is than the sequential code, is defined by
where Sp = speedup of a parallel run relative to a sequential run; T1 = runtime of a sequential run using one working core; Tnc = runtime of a parallel run using nc working cores.
3. Model Parameters and Tests
3.1. Computational Grid and Boundary Conditions
To get a full description of the river-coast-ocean coupling, the upstream tidal reach, the entire Yangtze Estuary and part of the East Sea are included in a single model. Station Datong (620 km upstream of the outlets), which is regarded as the tidal limit of the estuary and has routinely collected hydrological field data, was chosen as the upstream boundary. Seaward open boundaries are extended to deep-water (>50 m) regions, where a global tide model (GTM) [29] can provide an accurate history of astronomical tides. The eastern seaward open boundary is located around 124° E, with southern and northern boundaries being at 28.7° N and 33.9° N, respectively.
With three-level bifurcations and tens of islands or shoals, the Yangtze Estuary has complex river regimes [30]. The common resolution of bathymetry graphs, for an accurate description of the local river regimes of the Yangtze Estuary, is listed in Table 1. Coarse computational grids only describe an oversmoothed riverbed and are unable to correctly solve estuarine mesoscale structures [7] and transport process [8]. To ensure a good description of irregular boundaries and local river regimes, a channel-refined unstructured grid is used, whose grid scale (listed in Table 1) is approximately equal to the intervals between two neighboring survey points of the corresponding bathymetry graph. The main-flow channels in tidal reaches are covered by refined structured-like grids, with floodplains and inner islands covered by relatively coarse unstructured grids. There are 199,310 quad cells, and an example of the grid is given in Figure 2 (see Figure S1 for details).

Table 1.
Grid scales of high-resolution unstructured grids in Yangtze Estuary.
At the upstream boundary (see Figure 2), field data of discharges and sediment concentration at Station Datong were used to set the upstream boundary conditions. At downstream boundaries, the seaward open boundary is forced by semidiurnal tides. The time series of the tidal levels at the seaward boundary are predicted by the GTM developed in reference [29]. The seaward boundary is divided into 48 segments (see Figure 2), for each of which the tidal harmonic constants are, respectively, interpolated from a constituent database on a full global grid.
In calibration and validation tests of the HDM and the STM, the computational time step (Δt) is set to 90 s, and is equally divided into 9 sub time steps in the backtracking of the point-wise ELM.
3.2. Calibration and Validation Tests of HDM
Field data of spring neap tides during 6–16 December 2012 were used to calibrate parameters of the model and then validate its accuracy. In the hydrological survey, tidal levels were recorded at 14 fixed gauges from 6 December (the 340th day of 2012) to 16 December. The depth-averaged horizontal velocity was recorded from 8 December at 12:00 to 9 December at 21:00 for neap tides and from 14 December at 7:00 to 15 December at 13:00 for spring tides. Arrangements of the hydrological survey locations are shown in Figure 3. At the upstream boundary, the daily average river discharge at Station Datong gradually reduced from 22,000 to 18,700 m3/s during 6–16 December 2012.
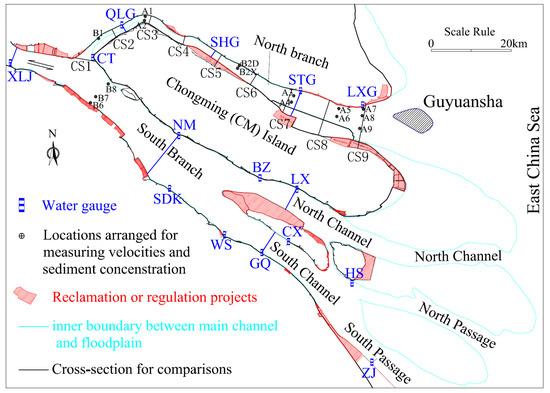
Figure 3.
Arrangements of hydrology survey locations in Yangtze Estuary.
In the simulations, the time step of the HDM is set to 90 s, while nine sub steps are used in the backtracking of the ELM. For a simulation of free-surface flows, the initial condition has a significant effect on the simulation of unsteady flows. In our simulations, the initial condition was determined by a preliminary simulation.
Manning’s roughness coefficient, nm, was calibrated using the spring-tide condition from 14 December at 0:00 to 16 December at 0:00. The inflow discharge was set to 19,000 m3/s. The nm of sub regions was adjusted so that the simulated tide-level histories would agree with field data. The nm was then corrected slightly so that the simulated velocity histories would agree with field data at the same time. The nm was finally calibrated as 0.022–0.021 from Station Datong to Jiangyin, 0.021–0.015 from Station Jiangyin to Xuliujing, and 0.014–0.011 for the North and South Branches. The nm in the North and South Branches was similar to the values reported in previous research [31,32].
Using the aforementioned distribution of nm, the histories of the simulated tidal levels and depth-averaged velocities were shown to agree well with field data. Generally, the mean absolute error in simulated tide levels was less than 0.15 m compared with the field data, while the mean absolute relative error in simulated velocity at survey positions was less than 10%. The accuracy of the model was then verified by simulating a full spring-neap tide process on 6–16 December 2012, and the simulation results are shown in Figure 4 and Figure 5.
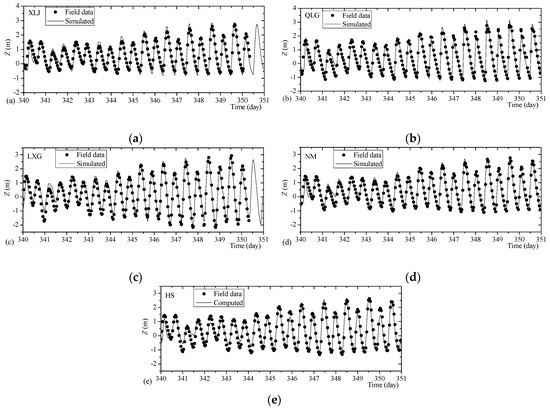
Figure 4.
Comparisons of the simulated tide-level histories and field data. (a) at Station Xuliujing (XLJ), (b) at Station Qinglonggang (QLG), (c) at Station Lianxingang (LZG), (d) at Station Nanmen (NM), (e) at Station Hengsha (HS).
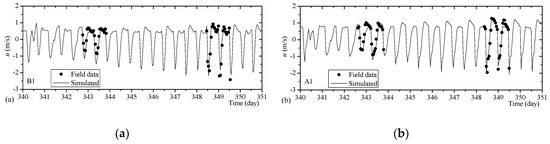

Figure 5.
Comparisons of simulated histories of velocity with field data (negative velocity is landward velocity, which appears during the flood duration). (a) at Survey Point B1, (b) at Survey Point A1, (c) at Survey Point A3, (d) at Survey Point A5, (e) at Survey Point B7.
3.3. Calibration and Validation Tests of STM
The sediment-capacity coefficient, K, is also calibrated using the spring-tide condition from 2012/12/14 0:00 to 2012/12/16 0:00. At the upstream boundary, the river discharge and the sediment concentration are respectively 19,000 m3/s and 0.112 kg/m3. The parameter K is calibrated as 0.11–0.08 from Datong to Jiangyin, 0.07–0.04 from Jiangyin to Xuliujing, 0.05–0.02 for the North and the South Branches. Similar to the calibrated nm, the calibrated K in coast sea regions of the Yangtze Estuary (0.07–0.02) also appears to be smaller than that of inland rivers (0.1–0.2), but approaches the values (about 0.07) reported by [32].
Using the aforementioned distribution of K, the STM is then verified by simulating a full spring neap tide process in the Yangtze Estuary on 6–16 December 2012. The histories of the simulated sediment concentration are generally observed to agree with field data, with minor amplitude errors (see Figure 6). The mean absolute relative errors in simulated sediment concentrations are generally less than 20%.
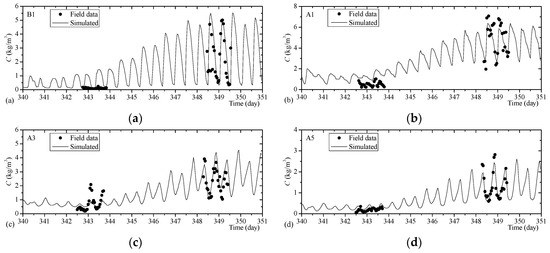
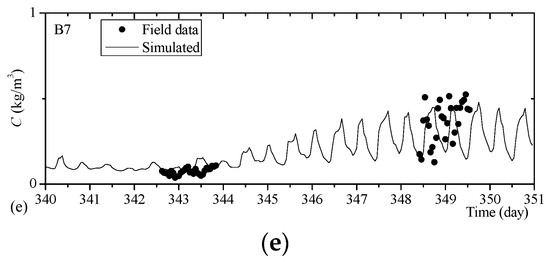
Figure 6.
Comparisons of simulated sediment concentration histories and field data at survey locations. (a) at Survey Point B1, (b) at Survey Point A1, (c) at Survey Point A3, (d) at Survey Point A5, (e) at Survey Point B7.
On the one hand, Zhang’s formula [21], used to evaluate the sediment-carrying capacity, does not involve an incipient velocity (the critical velocity at which sediment particles begin to move from a rest state). Hence, the sediment-carrying capacity calculated by Zhang’s formula [21] is always sensitive to the velocity. In neap-tide periods, the calculated sediment-carrying capacity is closely related to the velocity of the flow, so the history of the simulated depth-averaged sediment concentration closely follows the tidal process. On the other hand, in the survey of field data, the depth-averaged sediment concentration is evaluated by using the measurements at different heights in a vertical line. However, during neap tides, the vertical distribution of sediment concentration is strongly nonuniform, and a great number of the transported sediment gathers in the bottom layers of the flow. The high concentration at bottom layers is often not caught or improperly measured because of the sensibility problem or the inaccurate vertical location of instruments. The vertical distribution of sediment concentration during spring-tide periods is much more uniform than that during neap-tide periods. It is easier to obtain the accurate sediment concentrations which can achieve a good representation of the value of the measured vertical line. This may explain that the data around day 343 (neap-tide periods) is poorly approximated and that around day 349 is fairly well reproduced in Figure 6a–c.
The topographical data of December 2011 and November 2013 are then employed to verify the module of bed evolution, where a simulation of 2-year unsteady flow, nonuniform sediment transport, and fluvial process from 2011/12/1 to 2013/11/30 in the Yangtze Estuary is carried out. During the 731 days, the total quantities of the runoff and the inflow sediment are respectively 17,947 × 108 m3 and 2.854 × 108 tons. The daily river discharge and sediment concentration are imposed at the upstream boundary, while the seaward open boundaries are forced by tide levels of one-hour intervals. The measured topographical data in December 2011 is used to set the initial topography. The elevations of the nodes in the area of reclamations (or regulations) are modified to be consistent with the design, and the cells there are set to be non-erodible. Then, the model steps forward to November 2013 to get the final topography.
The simulated riverbeds at selected cross-sections of the North Branch (see Figure 3) are compared with those measured in November 2013, as shown in Figure 7. Generally, the simulated topographies at most cross-sections agree with field data. The reach, where cross-section CS5 is located, is narrowed by a project named “Xincun Sand regulation” which was launched during 2011–2013. In this reach, the flow is gathered, and the flow intensity is stronger than that in the original wider channel. As a result, the shallow sand is erased by the gathered flow after the time of the simulation. However, on the one hand, the disturbances from the projects of reclamations and regulations, launched in the North Branch during 2011–2013, may not be fully considered in the simulation. On the other hand, the present model does not have a module for simulating bank failures. Due to these disadvantages, the simulated riverbed evolutions at some cross-sections deviate from the field data. The North Branch experienced mild erosion form December 2012 to November 2013 in the simulation, which is consistent with the field. The erosion quantity of sediment is 5128.1 × 104 tons in the simulation, and has an error of +11.1% relative to field data.
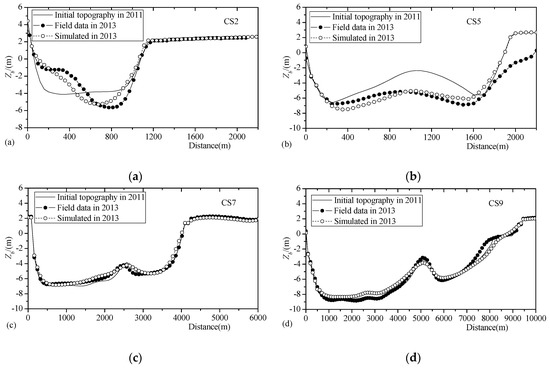
Figure 7.
Comparisons of the simulated riverbed evolutions and field data at cross-sections. (a) at CS2, (b) at CS5, (c) at CS7, (d) at CS9.
3.4. Sensitivity Study of Model Parameters and Coefficients
Generally, the accuracy of a simulation may be sensitive to the variation of model parameters and coefficients, while simulation results vary with respect to them. The spring neap tide process in the Yangtze Estuary on 6–16 December 2012 is also used to perform the sensitivity studies of the main model parameters (e.g., Δt) and coefficients (e.g., nm, and K).
First, the sensitivity study of time steps is performed. On the one hand, the use of a large time step means low time resolution of cell update, which will reduce the accuracy of the simulations of strongly unsteady tidal flows, such as those in the Yangtze Estuary. On the other hand, the ELM used in the current model becomes very dissipative at small time steps, per [27,33,34]. According to the tests of real shallow water systems in [25,26,28], the time step of the current model is suggested to be equal to or larger than 60 s, under a grid of moderate scale. Hence, the model is tested here on gradually reduced time steps which are sequentially 60, 75, 90, 100, and 120 s, to clarify the influence of time steps on the accuracy of solutions. Correspondingly, the number of substeps for the ELM backtracking (Nbt) is, respectively, set to 6, 8, 9, 10, and 12.
Under different time steps, the histories of the simulated tide level, survey-point velocity, and sediment concentration are shown in Figure 8, respectively (taking Station QLG and Survey Point A1 as examples). In a simulation of the adopted spring neap tide process, the mean absolute error in simulated tide levels is calculated to be 0.01–0.02 m, the mean absolute error in simulated survey-point velocities is 0.019–0.035 m/s, and the mean absolute error in simulated survey-point sediment concentrations is 2.8–3.5%, based on the simulated histories using different Δts. Although minor differences are observed in the results of simulations using different time steps, the accuracies of the HDM and the STM are both stable with respect to the time step. The suggested time step (90 s) is revealed to be proper.
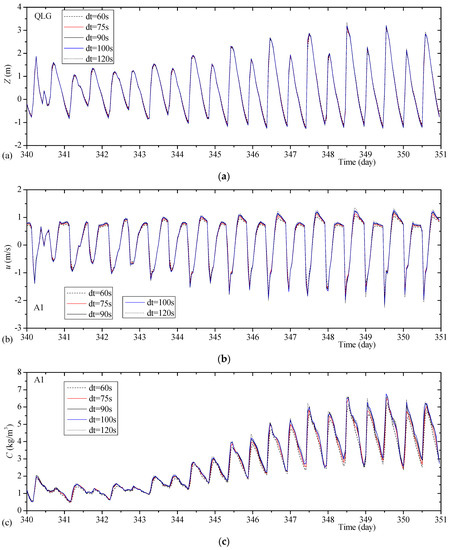
Figure 8.
Comparisons of the simulated histories and field data. (a) Tide-level histories at Station Qinglonggang (QLG), (b) velocity histories at Survey Point A1, and (c) sediment concentration histories at Survey Point A1.
Second, the sensitivity study of the coefficient of Manning’s roughness (nm) is performed by changing the nm in the North and the South Branches which are considered as the most important regions in this case study. The distribution of the nm, obtained by the calibration test, is taken as the reference and is denoted by “original friction (nm)”. The tests, with the nm being reduced (−0.001) and increased (+0.001), are denoted by “nm −0.001” and “nm +0.001”, respectively.
Under different nm, the histories of the simulated tide level and survey-point velocity are, respectively, shown in Figure 9 (taking Station QLG and Survey Point A1 as examples). It is found that the smaller the nm of the North and South Branches are, the stronger the landward floodtide flow in these reaches will be (characterized by higher tidal levels and large velocities). It is obvious that the variation of water levels with respect to the nm is just opposite for the estuary tidal flows and for the inland river flows. The variation of the peak water level in Station QLG is +0.15 m when the nm is reduced by 0.001, and is −0.04 m when the nm is increased by 0.001. The variation of the peak velocity in Survey Point A1 is +0.12 m/s when the nm is reduced by 0.001, and is −0.25 m/s when the nm is increased by 0.001.
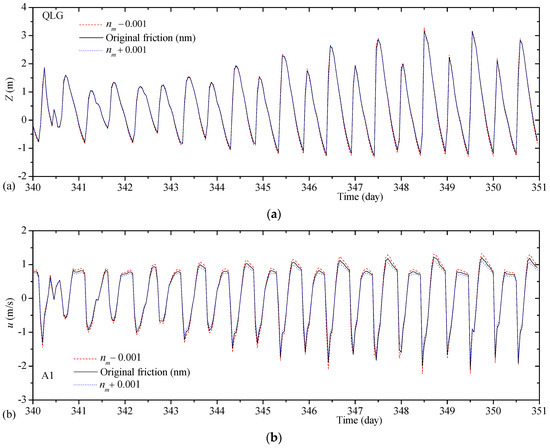
Figure 9.
Comparisons of the simulated histories and field data. (a) Tide-level histories at Station Qinglonggang (QLG) and (b) velocity histories at Survey Point A1.
Third, the sensitivity study of the coefficient of sediment-carrying capacity (K) is performed by changing the K in the North and South Branches, which are considered as the most important regions in this case study. The distribution of the K, obtained by the calibration test, is taken as the reference and is denoted by “original coefficient”. The tests, with the K being reduced (−0.002) and increased (+0.002), are denoted by “K −0.002” and “K +0.002”, respectively.
Under different K, the histories of the simulated sediment concentration are shown in Figure 10 (taking Survey Point A1 as an example). It is found that the simulated sediment concentration increases with respect to K. The variation of the sediment concentration in Survey Point A1 is −0.33 kg/m3 when the K is reduced by 0.002, and is +0.25 kg/m3 when the K is increased by 0.002.
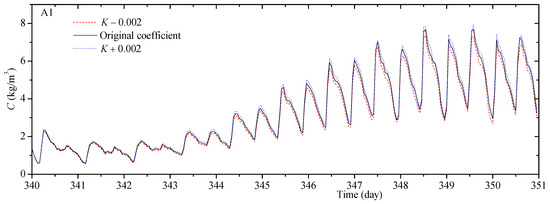
Figure 10.
Comparisons of the histories of the simulated sediment concentration and field data (at Survey Point A1).
3.5. Efficiency Tests of HDM and STM
The computational time step (Δt) is set to 90 s and is equally divided into 9 sub time steps in the backtracking of the point-wise ELM. The 1-day unsteady flow and sediment transport, under an upstream bankfull discharge (45,000 m3/s) and a downstream spring tide, is tested to clarify the speedup property of the modeling system. The total runtime of the HDM and the STM is 1550.7 s in sequential runs, and is reduced to 131.1 s in parallel runs (nc = 16) with a speedup of 11.8. The unsteady flow and sediment transport in 1999 are then tested. It takes the modeling system 12.2 h (using 16 cores) to complete the simulation of a 1-year unsteady flow, sediment transport, and riverbed evolution in the Yangtze Estuary.
4. Results
The mechanics of spillover of water and sediment in the Yangtze Estuary are quantitatively studied by simulating typical tidal processes (e.g., a spring tide or a neap tide).
4.1. Simulation Conditions
Similar to former studies on the spillover of saltwater, the spillover of sediment in the Yangtze Estuary is studied using the condition of a spring and a neap tide in dry seasons, when the sediment spillover in the Yangtze Estuary is considered to be most significant.
At the upstream boundary, the river discharge and sediment concentration are set to 19,000 m3/s and 0.112 kg/m3, respectively. The flow and sediment fluxes at Datong are then respectively calculated to be 16.41 × 108 m3 and 18.39 × 104 tons per day. The seaward boundaries are forced by the tide-level histories of a spring tide and a neap tide, respectively, which leads to two tests of 1-day simulation. Nine cross-sections are arranged to record the histories of the flow rates and the sediment transport rates (see Figure 3). For the sake of convenience, the divisions of North Branch are defined as follows: the upper reach (from the bifurcation of North and South Branches to Station QLG); the middle reach (from Station QLG to SHG); the lower reach (from Station SHG to STG); the tail reach (from Station STG to LXG).
4.2. Horizontal Circulation of Water Flux
The history of the flow rate at cross-sections is integrated over the floodtide and the ebbtide periods to produce the cross-sectional water fluxes (CSWF), as listed in Table 2. According to the simulation results, the reasons for the spillover of water from the North to the South Branches are analyzed in two terms.

Table 2.
Cross-sectional water fluxes (CSWF) at tide stations (unit: ×108 m3/day).
First, the tail reach of the North Branch is trumpet-shaped with a wide mouth, in favor of accommodating a great deal of landward tidal flows during floodtide durations. At the same time, the valid river width of the North Branch decreases from the downstream to the upstream, which is accordingly 5–8 km (tail reach), 3–5 km (lower reach), 1–3 km (middle reach), and 1 km (upper reach). Although the CSWF at QLG is only 22.4–26.0% of that at STG during floodtide durations, the huge landward floodtide discharge at the mouth of the North Branch and the fast shrinking river width together determine that strong flow intensity can be kept in all the lower, middle, and upper reaches. The velocities in the upper, middle, and lower reaches of North Branch are, respectively, observed to be as large as 2.4, 3.0, and 2.5 m/s, during a floodtide period. The landward floodtide tidal flow moves along the North Branch, while the strong flow intensity is maintained. Finally, some pioneer floodtide flows continue to go through the upper reach of North Branch and arrive at the bifurcation, forming the spillover of water. After a short spillover time, the transition between the floodtide and the ebbtide comes, and the spillover of water is ended.
Second, the upper reach of the North Branch is narrow and almost orthogonal to the South Branch (see Figure 3), which prevents upstream inflows from entering during ebbtide durations. As a result, in upper reach of the North Branch, the seaward ebbtide CSWF is smaller than the landward floodtide CSWF. At the same time, in the upper reach of the North Branch, the flow intensity during ebbtide durations (maximum velocity, 1.5 m/s) is sharply decreased relative to that during floodtide durations (maximum velocity, 2.4 m/s). The CSWF difference between the floodtide and the ebbtide durations at QLG of the North Branch is 0.6–0.47 × 108 m3/day, accounting for 24.2–28.8% of the landward floodtide CSWF. The CSWF difference of the North Branch runs downstream along South Branch during ebbtide durations, and a horizontal anticlockwise circulation of water flux is formed.
4.3. Sediment Spillover from North to South Branches
The simulated history of the sediment transport rate at cross-sections is integrated over the floodtide and the ebbtide periods to produce the cross-sectional sediment fluxes (CSSF), as listed in Table 3. According to the simulation results, sediment transport of the North Branch, related closely to its hydrodynamics, is analyzed to clarify the mechanics of the sediment spillover from the North to the South Branches.

Table 3.
Cross-sectional sediment fluxes (CSSF) at tide stations (unit: × 104 t/day).
First, the source of the sediment, which spills over from the North to the South Branches, is recognized. The CSSF results show that there exists a critical position of zero sediment flux (ZSF) in the lower reach of North Branch, where the seaward ebbtide CSSF just counteracts the landward floodtide CSSF in a 1-day runoff-tide process. The ZSF critical position locates about 4 km upstream of STG. Riverbeds in the middle and lower reaches upstream of the ZSF critical position in the North Branch experiences erosions during floodtide durations, corresponding to strong flow intensities there. Sediment concentration of the landward tidal flow is essentially increased during its journey through the erosion reaches of the North Branch. This results in high sediment concentrations of 6–8 kg/m3 in the reach between QLG and SHG of during floodtide duration in field data. The landward floodtide high-concentration flow, going through cross-section QLG, provides sediment input for the upper reach of North Branch, some of which spillovers from the North to the South Branches.
Second, the kinetic energy of flow, used to advance the spillover of sediment in the Yangtze Estuary, is analyzed. During a floodtide period, the landward flow still maintains considerate intensity (flow velocity) in the upper reach of the North Branch, and at the same time, provides enough kinetic energy for carrying and transporting sediment. The landward floodtide sediment-carrying flow goes through the upper reach of the North Branch and towards the bifurcation. In the journey of the landward flow, partial sediment in the flow deposits on the riverbed along the upper reach of the North Branch, due to the gradually reduced flow intensity. The left part of the sediment in the landward flow arrives at the bifurcation and then spills over to the South Branch.
The process of the sediment spillover in the Yangtze Estuary experiences the following stages. After the floodtide period begins, it takes about 5 h to form the high-concentration floodtide flows in the middle North Branch. The high-concentration floodtide flow arrives at QLG at about 6 h after the floodtide, and begins to spill over to the South Branch at about 7 h. After that, the sediment spillover lasts about 3 h. Then, the transition between the flood and the ebbtides comes, and the sediment spillover gradually disappears.
Third, in the upper reach of the North Branch, the CSWF and the flow intensity during ebbtide durations are both sharply reduced relative to those during floodtide durations. The seaward ebbtide CSSF is also much smaller than the landward floodtide CSSF in the upper reach of the North Branch. The CSSF difference between the floodtide and the ebbtide durations at Station QLG is 43.85–11.26 × 104 t/day, accounting for 37.5–34.9% of the landward floodtide CSSF. The CSSF difference of the North Branch is caused by the sediment which spills over from the North to the South Branches. The sediment, arising from the spillover, runs downstream toward the coast along with the ebbtide flow of the South Branch, and a horizontal anticlockwise circulation of sediment flux is formed.
Mechanics of sediment spillover in the Yangtze Estuary can be summarized as a successive process comprising the source, transport, and drainage of the sediment of the spillover.
4.4. Balances of Water and Sediment Fluxes
Using the simulation results (see Video S1 for details), the spatial distributions of water and sediment fluxes in the Yangtze Estuary are sketched, as shown in Figure 11. The horizontal circulations of the water and the sediment fluxes are quantitatively analyzed as follows.
Figure 11.
Sketch of the spatial distributions of water and sediment fluxes in Yangtze Estuary.
For a spring tide, the ebbtide CSWF at the entrance cross-section of the South Branch (SE) comprises three parts. Water flux, which intrudes upstream of cross-section SE from the South Branch during the floodtide duration, returns during the ebbtide duration and contributes to the first part (31.41 × 108 m3/day). Inflow runoff from Datong (16.31 × 108 m3/day) contributes to the second part. The water spillover from the North Branch (0.6 × 108 m3/day) contributes to the third part, accounting for 1.24% of the ebbtide CSWF at cross-section SE. The ebbtide CSSF at the entrance cross-section of the South Branch (SE) also comprises three parts. Sediment flux, which intrudes upstream of cross-section SE from the South Branch during the floodtide duration, returns during the ebbtide duration, and contributes to the first part (85.76 × 104 t/day). Sediment input at Datong is 18.39 × 104 t/day and it evolves to 25.35 × 104 t/day at cross-section XLJ after a long-distance adjustment of erosion and deposition, which contributes to the second part. The sediment spillover from North Branch (30.89 × 104 t/day) contributes to the third part, accounting for 21.75% of the ebbtide CSSF at cross-section SE.
For a neap tide, the water spillover from the North Branch reduces to 0.46 × 108 m3/day, accounting for 1.39% of the CSWF at cross-section SE during the ebbtide duration. At the same time, the sediment spillover from the North Branch reduces to 7.88 × 104 t/day, accounting for 18.46% of the CSSF at cross-section SE during the ebbtide duration.
4.5. Analysis of Spillover on Morphological Dynamics
The riverbed evolution around the bifurcation of the North and the South Branches, which closely relates to the spillover of water and sediment, is qualitatively analyzed, based on the simulation results and the aforementioned spillover mechanics.
When the landward floodtide high-concentration flow goes through the entrance reach of the North Branch, some of the sediment deposits on the riverbed on its landward journey through the upper reach of North Branch and the other part spills over to the South Branch. Overall, for the North Branch, the deposition at the entrance reach will facilitate the shrinkage of its upper reach and further prevent upstream inflows from entering during the ebbtide duration. This conclusion is consistent with field observations and former studies [5,30,35,36,37,38].
The entrance reach from the bifurcation to the QLG in the North Branch has a compound floodplain-channel cross-section (see Figure 3), where riverbed evolution may have the following properties. On the one hand, most of the floodtide flow goes through the main channel, and considerate flow intensity is kept there. As a result, it is not easy for the sediment to deposit in the main channel. On the other hand, according to the simulated velocity field of the floodtide flow, the flow intensity of the floodplain is much weaker than that of the main channel, which implies that widespread sediment deposition may happen there.
The morphological dynamics of the North Branch can be summarized as the entrance reach of North Branch will experience successive sediment deposition (the possible sediment deposition mainly happens in the floodplain), leading to shrinkage of the branch.
5. Discussion
5.1. Calculation of Hydrodynamics in Estuaries
The estuary is a transitional region which connects the inland rivers and coastal regions, and is still often regarded as a shallow water system. In existing studies, the nonhydrostatic models and the SWE models are both widely used to simulate estuarine flows.
Relative to SWE models, 3D nonhydrostatic models can include influences of nonhydrostatic pressures which are significant when the ratio of the vertical scale to horizontal scale of motions of flows is not small. Examples are flows over abruptly changing bed topographies, flows with sharp density gradients, and short-wave motions (e.g., waves in coastal and ocean regions). In these cases, the hydrostatic assumption is no longer valid. A short review of certain kinds of 3D nonhydrostatic models can be found in the authors’ former studies [9]. Generally, for shallow water systems such as estuary regions, the results simulated by an SWE model are quite similar to those by a 3D nonhydrostatic model. Moreover, a 3D nonhydrostatic model (e.g., 10 layers are used in vertical direction) is at least tens of times slower than a 2D SWE model. It may take more than a month to complete a high-resolution simulation of the 2011–2013 process of the flow, sediment transport, and riverbed evolution in the Yangtze Estuary using the current computing technology used in this paper. Without resorting to simplified methods (e.g., local models, morphological scale factors), high-resolution simulations of long-term processes of flow and sediment transport in the entire Yangtze Estuary using a 3D nonhydrostatic model have not yet been reported.
The SWE models, applied to simulations of estuarine flows, include the 2D SWE models [8,10,13,18,19,39,40,41] and the 3D SWE model (e.g., [12,23,24,42,43,44,45]). The two kinds of SWE models both use the hydrostatic assumption. On the one hand, high-resolution simulations of short-term processes of tides (e.g., [39,41]), salinity transport (e.g., [8,40,41,42,43,44]), pollutant transport (e.g., [45]) and sediment concentration fields at selected times (e.g., [46]) in the Yangtze Estuary have been gradually enabled due to continuous improvements in computers in the past two decades. On the other hand, the huge computation cost, brought about by simulations of long-term fluvial processes in the Yangtze Estuary using high-resolution grids and small time steps, still challenges most existing 2D/3D numerical codes. In real applications, most of the simulations of hydrodynamics of the Yangtze Estuary take two steps. First, the seaward open boundaries are forced by the time series of tidal levels which are predicted by a GTM such as in [29]. Second, the hydrodynamics of the estuary are simulated by 2D or 3D SWE models. As a result, simulations of the ocean waves, which may be characterized by strong nonhydrostatic pressures and beyond the estuary regions, are in essence not needed. Hence, the application of time-consuming nonhydrostatic 3D models can be totally avoided.
Following the existing studies using SWE models, we adopted a 2D SWE model to perform the simulation of the flow and sediment transport in the Yangtze Estuary in this paper.
5.2. Calculation of Sediment Transport in Estuaries
SWE models for the free-surface flow and sediment transport may be divided into three kinds, which are the Level-1 (the so-called “coupled” model), Level-2 (decoupled model with timely riverbed update, which is used in this paper), and Level-3 (decoupled model using a morphological scale factor) models. These models are compared as follows.
(1) The Level-1 model
The governing equations of the HDM in a Level-1 model can be regarded as an extended version of the SWEs by inserting additional terms, mainly including the density gradient terms and the terms related to the (zb is riverbed elevation). However, the effects of these additional terms are still open issues. Some researchers [47,48] included both of the two kinds of additional terms in their models. Wu [49] pointed out that the effect of the term, added into the continuity equation, is dominant relative to the effect of other additional terms. This point is supported in Cao et al. [50], where only the enhanced continuity equation is used together with the momentum equations from the original SWEs. Generally, the Level-1 model is mainly used when the flow, sediment transport, and morphological evolution are strongly coupled to each other (the rate of bed deformation being considerable compared to that of flow evolution), such as the dam-break flows on a moveable riverbed.
(2) The Level-3 model
Notable evolutions of estuarine morphology generally take days, months, or even years, which is much slower than the variations of flow and sediment concentration fields. Impacts of short-term morphology evolutions of riverbeds on tidal currents and sediment transport are also minor. Using these facts, an accelerated calculation of bed deformations could be incorporated in sediment models through multiplying the flux of sediment exchange (between the flow and the riverbed) by a morphological scale factor [10,13,14]. This kind of model is called the Level-3 model.
For a Level-3 model, upstream boundary conditions (e.g., river discharges and sediment concentrations) of a given time interval are set with the average data in this time interval (often a month). Monthly averaged data is used to set the upstream boundary conditions, while water levels of two full-period neap-spring tides are imposed at seaward boundaries. As a result, for each month, only the process of two full neap-spring tides is simulated, and the bed deformation is scaled by a morphological scale factor. Obviously, a Level-3 model using a morphological scale factor does not simulate the real process of the flow, sediment transport, and bed evolution in the estuary.
(3) The Level-2 model
On the one hand, in an estuary, the rate of bed deformation is generally much slower than that of flow evolution, so a Level-1 model is not necessary. On the other hand, the Level-3 model does not simulate a real process of flow-sediment-riverbed evolution. In this study, the real hydrological and tidal processes are simulated. At each time step of a simulation, the calculation of hydrodynamics is done first, and the sediment transport is then solved, followed by a timely riverbed update. This kind of model is called the Level-2 model. Obviously, it is simpler than the Level-1 model and is expected to achieve higher accuracy than the widely used Level-3 model.
5.3. Differences between the Spillover of Saltwater and Sediment
A few quantitative studies on the spillover of saltwater from the North to the South Branches have been reported. Gu et al. [51] found that the spillover of saltwater might occur when the upstream runoff was less than 30,000 m3/s and the tidal range at Station QLG was greater than 2 m, and became remarkable when the upstream runoff was less than 20,000 m3/s and the tidal range at Station QLG was greater than 2.5 m. The mechanics and quantitative studies on the spillover of saltwater from the North to the South Branches can be found in [5]. These research results provide references for our study on the spillover of sediment-carrying flow.
It must be pointed that the spillover of sediment in the Yangtze Estuary is quite different from that of saltwater. First, the source for the saltwater spillover is simply from seas, which is uniform at offshore boundaries. As stated in this study, the source for the sediment spillover is produced by the erosion of local riverbed mainly in the middle and upper reaches of the North Branch. Second, salinity can be regarded as a solute whose transport is assumed to fully follow the motion of flows. However, the transport of sediment is quite sensitive to flow intensities. Under weak flow intensity, the heavier particles of sediment will deposit on the riverbed. The flow intensity will determine if and when spillover occurs and its extent. Moreover, the intensity of the sediment spillover is also closely related to the constituents of bed materials. Studies on the sediment spillover are more challenging. This may be one reason that quantitative studies on the sediment spillover in the Yangtze Estuary have not been reported.
According to the aforementioned analysis, a qualified simulation of flow and sediment transport in the Yangtze Estuary (which can reproduce detailed fields of tidal flows and sediment concentration) generally requires a grid resolution higher than that used in the simulation of saltwater transport. High grid resolution is achieved with as few cells as possible by using a channel-refined unstructured grid in this study. Moreover, the semi-implicit method, the ELM, and the FVELM were combined to achieve solve the efficiency problems of the model.
6. Conclusions
To quantitatively clarify the problem of sediment spillover in Yangtze Estuary, a 2D numerical model using a high-resolution channel-refined unstructured grid (200,000 cells) was developed for the entire Yangtze Estuary from Datong to river mouths (620 km) and part of the East Sea. The developed model achieves a good description of the river-coast-ocean coupling, irregular boundaries, and local river regimes in the Yangtze Estuary. The model parameters are calibrated using field data, for which the sensitivity studies are done. In validation tests, the simulated histories of the tidal level, depth-averaged velocity, and sediment concentration agree well with the field data. In efficiency tests, it takes the model 12.2 h (using 16 cores) to complete a simulation of a 1-year unsteady flow, sediment transport, and riverbed evolution in the Yangtze Estuary.
The sediment spillover in the Yangtze Estuary was studied using the conditions of a spring and neap tide in dry seasons. The fluxes of water and sediment at cross-sections are respectively calculated using the simulated histories of flow rates and sediment transport rates. For a representative cross-section in the upper reach of the North Branch (QLG), the difference of the cross-sectional water flux (CSWF) between the floodtide and the ebbtide durations is 0.6–0.47 × 108 m3/day, accounting for 24.2–28.8% of the landward floodtide CSWF. The difference of the cross-sectional sediment flux (CSSF) between the floodtide and the ebbtide durations is 43.85–11.26 × 104 t/day, accounting for 37.5–34.9% of the landward floodtide CSSF.
The mechanics of sediment spillover in the Yangtze Estuary are summarized as a successive process comprising the source, transport, and drainage of the sediment of the spillover.
Supplementary Materials
The following are available online at https://www.mdpi.com/2077-1312/7/11/390/s1, Figure S1: Channel-refined computational grid for numerical model of Yangtze Estuary. Video S1: Process of the spillover of sediment from the North to the South Branches during a full spring tide in Yangtze Estuary.
Author Contributions
Conceptualization: D.H. and Z.J.; methodology: D.H. and Z.J.; software: D.H. and M.W.; validation: D.H., M.W. and Z.J.; formal analysis: D.H., M.W. and Z.J.; investigation: D.H. and Z.J.; resources: S.Y. and Z.J.; data curation: S.Y. and D.H.; writing—original draft preparation: D.H. and Z.J.; writing—review and editing: M.W. and D.H.; visualization: M.W.; supervision: S.Y. and Z.J.; project administration: S.Y. and Z.J.; funding acquisition: D.H., S.Y. and Z.J.
Funding
Financial support from Science and Technology Program of Guizhou Province, China (Grant No. 2017-3005-4), the Fundamental Research Funds for the Central Universities (2017KFYXJJ197), China’s National Natural Science Foundation (51339001, 51779015 and 51479009) are acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- He, S.L.; Sun, J.M. Characteristics of suspended sediment transport in the turbidity maximum of the Changjiang river estuary. Oceanol. Limnol. Sin. 1996, 27, 60–66. (In Chinese) [Google Scholar]
- Li, J.F.; Shi, W.R.; Shen, H.T. Sediment properties and transportation in the turbidity maximum in Changjiang estuary. Geogr. Res. 1994, 13, 51–59. (In Chinese) [Google Scholar]
- Shen, J.; Shen, H.T.; Pan, D.A.; Xiao, C.Y. Analysis of transport mechanism of water and suspended sediment in the turbidity maximum of the Changjiang estuary. Acta Geogr. Sin. 1995, 50, 412–420. (In Chinese) [Google Scholar]
- Shi, Z.; Chen, M.W. Fine sediment transport in turbidity maximum at the north passage of the Changjiang Estuary. J. Sediment Res. 2000, 1, 28–39. (In Chinese) [Google Scholar]
- Wu, H.; Zhu, J.R.; Chen, B.R.; Chen, Y.Z. Quantitative relationship of runoff and tide to saltwater spilling over from the North Branch in the Changjiang Estuary, A numerical study. Estuar. Coast. Shelf Sci. 2006, 69, 125–132. [Google Scholar] [CrossRef]
- Chen, W.; Li, J.F.; Li, Z.H.; Li, Z.H.; Dai, Z.J.; Yan, H.; Xu, M.; Zhao, J.K. The suspended sediment transportation and its mechanism in strong tidal reaches of the North Branch of the Changjiang Estuary. Acta Oceanol. Sin. 2012, 34, 84–91. (In Chinese) [Google Scholar]
- Chen, C.S.; Xue, P.F.; Ding, P.X.; Beardsley, R.C.; Xu, Q.C.; Mao, X.M.; Gao, G.P.; Qi, J.H.; Li, C.Y.; Lin, H.C.; et al. Physical mechanisms for the offshore detachment of the Changjiang Diluted Water in the East China Sea. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Xue, P.F.; Chen, C.S.; Ding, P.X.; Beardsley, R.C.; Lin, H.C.; Ge, J.Z.; Kong, Y.Z. Saltwater intrusion into the Changjiang River, A model-guided mechanism study. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Hu, D.C.; Wang, G.Q.; Zhang, H.W.; Zhong, D.Y. A semi-implicit three-dimensional numerical model for non-hydrostatic pressure free-surface flows on an unstructured, sigma grid. Int. J. Sediment Res. 2013, 28, 77–89. [Google Scholar] [CrossRef]
- Hu, K.L.; Ding, P.X.; Wang, Z.B.; Yang, S.L. A 2D/3D hydrodynamic and sediment transport model for the Yangtze Estuary, China. J. Mar. Syst. 2009, 77, 114–136. [Google Scholar] [CrossRef]
- Shi, Z.; Zhou, H.Q.; Liu, H.; Zhang, Y.C. Two-dimensional horizontal modeling of fine-sediment transport at the South Channel–North Passage of the partially mixed Changjiang River Estuary, China. Environ. Earth Sci. 2010, 61, 1691–1702. [Google Scholar] [CrossRef]
- Zuo, S.H.; Zhang, N.C.; Li, B.; Zhang, Z.; Zhu, Z.X. Numerical simulation of tidal current and erosion and sedimentation in the Yangshan deep-water harbor of Shanghai. Int. J. Sediment Res. 2009, 24, 287–298. [Google Scholar] [CrossRef]
- Kuang, C.P.; Liu, X.; Gu, J.; Guo, Y.K.; Huang, S.C.; Liu, S.G.; Yu, W.W.; Huang, J.; Sun, B. Numerical prediction of medium-term tidal flat evolution in the Yangtze Estuary, impacts of the Three Gorges project. Cont. Shelf Res. 2013, 52, 12–26. [Google Scholar] [CrossRef]
- WL|Delft Hydraulics. Delft3D-FLOW User Manual; Version 3.13; WL|Delft Hydraulics: Delft, The Netherlands, 2006. [Google Scholar]
- Wang, D.Z. Transport of Nonuniform Bedload in the Changjiang Estuary and Its Numerical Simulation. Master’s Thesis, Zhejiang University, Zhejiang, China, 2002. (In Chinese). [Google Scholar]
- Han, Q.W.; He, M.M. The Statistics Theory of Sediment Transport; Chinese Science Press: Beijing, China, 1984. (In Chinese) [Google Scholar]
- Cheng, C.; Huang, H.M.; Liu, C.Y.; Jiang, W.M. Challenges to the representation of suspended sediment transfer using a depth-averaged flux. Earth Surf. Proc. Land. 2016, 41, 1337–1357. [Google Scholar] [CrossRef]
- Dou, X.P.; Li, T.L.; Dou, G.R. Numerical model of total sediment transport in the Yangtze Estuary. China Ocean Eng. 1999, 13, 277–286. [Google Scholar]
- Wan, Y.Y.; Roelvink, D.; Li, W.H.; Qi, D.M.; Gu, F.F. Observation and modeling of the storm-induced fluid mud dynamics in a muddy-estuarine navigational channel. Geomorphology 2014, 217, 23–36. [Google Scholar] [CrossRef]
- Xie, J.; Yan, Y.X. Promoting siltation effects and impacts of Hengsha East. J. Hydrodyn. 2011, 23, 649–659. [Google Scholar] [CrossRef]
- Zhang, R.J.; Xie, J.H. River Sediment Transport; Press of Chinese Hydraulic and Electric Engineering: Beijing, China, 1989. (In Chinese) [Google Scholar]
- Wei, Z.L.; Zhao, L.K.; Fu, X.P. Research on mathematical model for sediment in Yellow River. J. Wuhan Univ. Hydr. Electr. Eng. 1997, 30, 21–25. (In Chinese) [Google Scholar]
- Zhang, Y.L.; Baptista, A.M.; Myers, E.P. A cross-scale model for 3D baroclinic circulation in estuary-plume-shelf systems, I. Formulation and skill assessment. Cont. Shelf Res. 2004, 24, 2187–2214. [Google Scholar] [CrossRef]
- Casulli, V.; Walters, R.A. An unstructured grid, three-dimensional model based on the shallow water equations. Int. J. Numer. Meth. Fluids 2000, 32, 331–348. [Google Scholar] [CrossRef]
- Hu, D.C.; Zhong, D.Y.; Zhang, H.W.; Wang, G.Q. Prediction–correction method for parallelizing implicit 2D hydrodynamic models I scheme. J. Hydraul. Eng. 2015, 141, 04015014. [Google Scholar] [CrossRef]
- Hu, D.C.; Zhong, D.Y.; Zhu, Y.H.; Wang, G.Q. Prediction–correction method for parallelizing implicit 2D hydrodynamic models II application. J. Hydraul. Eng. 2015, 141, 06015008. [Google Scholar] [CrossRef]
- Dimou, K. 3-D Hybrid Eulerian–Lagrangian/Particle Tracking Model for Simulating Mass Transport in Coastal Water Bodies. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1992. [Google Scholar]
- Hu, D.C.; Zhu, Y.H.; Zhong, D.Y.; Qin, H. Two-dimensional finite-volume Eulerian-Lagrangian method on unstructured grid for solving advective transport of passive scalars in free-surface flows. J. Hydraul. Eng. 2017, 143, 04017051. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Andersen, O.B.; Knudsen, P. Integrating non-tidal sea level data from altimetry and tide gauges for coastal sea level prediction. Adv. Space Res. 2012, 50, 1099–1106. [Google Scholar] [CrossRef]
- Wu, S.H.; Cheng, H.Q.; Xu, Y.J.; Li, J.F.; Zheng, S.W.; Xu, W. Riverbed micromorphology of the Yangtze River Estuary, China. Water 2016, 8, 190. [Google Scholar] [CrossRef]
- Cao, Z.Y. A Two-Dimensional Non-Uniform Sediment Numerical Model for the Yangtze Estuary. Ph.D. Thesis, East China Normal University, Shanghai, China, 2003. (In Chinese). [Google Scholar]
- Shi, Y.B.; Lu, H.Y.; Yang, Y.P.; Cao, Y. Prediction of erosion depth under the action of the exceptional flood in the river reach of a tunnel across the Qiantang estuary. Adv. Water Sci. 2008, 19, 685–692. (In Chinese) [Google Scholar]
- Baptista, A.M. Solution of Advection-Dominated Transport by Eulerian–Lagrangian Methods Using the Backwards Method of Characteristics. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1987. [Google Scholar]
- Hu, D.C.; Zhang, H.W.; Zhong, D.Y. Properties of the Eulerian-Lagrangian method using linear interpolators in a three dimensional shallow water model using z-level coordinates. Int. J. Comput. Fluid Dyn. 2009, 23, 271–284. [Google Scholar] [CrossRef]
- Li, Z.H.; Li, M.Z.; Dai, Z.J.; Zhao, F.F.; Li, J.F. Intratidal and neap-spring variations of suspended sediment concentrations and sediment transport processes in the North Branch of the Changjiang Estuary. Acta Oceanol. Sin. 2015, 34, 137–147. [Google Scholar] [CrossRef]
- Liu, H.; He, Q.; Wang, Z.B.; Weltje, G.J.; Zhang, J. Dynamics and spatial variability of near-bottom sediment exchange in the Yangtze Estuary, China. Estuar. Coast. Shelf Sci. 2010, 86, 322–330. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, S.Y.; Hamilton, L.J. Bottom fine sediment boundary layer and transport processes at the mouth of the Changjiang Estuary, China. J. Hydrol. 2006, 327, 276–288. [Google Scholar] [CrossRef]
- Yang, S.L.; Belkinb, I.M.; Belkinac, A.I.; Zhao, Q.Y.; Zhu, J.; Ding, P.X. Delta response to decline in sediment supply from the Yangtze River: Evidence of the recent four decades and expectations for the next half-century. Estuar. Coast. Shelf Sci. 2003, 57, 689–699. [Google Scholar] [CrossRef]
- Tan, Y.; Yang, F.; Xie, D.H. The change of tidal characteristics under the influence of human activities in the Yangtze Estuary. J. Coast. Res. 2016, 75, 163–167. [Google Scholar] [CrossRef]
- Wu, D.; Shao, Y.; Pan, J. Study on activities and concentration of saline group in the South Branch in Yangtze River Estuary. Procedia Eng. 2015, 116, 1085–1094. [Google Scholar]
- Lu, S.; Tong, C.; Lee, D.Y.; Zheng, J.; Shen, J.; Zhang, W.; Yan, Y. Propagation of tidal waves up in Yangtze Estuary during the dry season. J. Geophys. Res. Oceans 2015, 120, 6445–6473. [Google Scholar] [CrossRef]
- Ge, J.Z.; Ding, P.X.; Chen, C.S. Low-salinity plume detachment under non-uniform summer wind off the Changjiang Estuary. Estuar. Coast. Shelf Sci. 2015, 156, 61–70. [Google Scholar] [CrossRef]
- Hou, C.C.; Zhu, J.R. The response time of saltwater intrusion in the Changjiang River to the change of river discharge in dry season. Acta Oceanol. Sin. 2013, 35, 29–35. (In Chinese) [Google Scholar]
- An, Q.; Wu, Y.Q.; Taylor, S.; Zhao, B. Influence of the Three Gorges Project on saltwater intrusion in the Yangtze River Estuary. Environ. Geol. 2009, 56, 1679–1686. [Google Scholar] [CrossRef]
- Zhang, J.X.; Liu, H. Numerical investigation of pollutant transport by tidal flow in the Yangtze Estuary. In Trends in Engineering Mechanics Special Publication; Huang, W., Wang, K., Chen, Q., Eds.; American Society of Civil Engineers: Los Angeles, CA, USA, 2010; pp. 99–110. [Google Scholar]
- Kuang, C.P.; Chen, W.; Gu, J.; He, L.L. Comprehensive analysis on the sediment siltation in the upper reach of the deepwater navigation channel in the Yangtze Estuary. J. Hydrodyn. 2014, 26, 299–308. [Google Scholar] [CrossRef]
- Zhang, S.; Duan, J.; Strelkoff, T. Grain-scale nonequilibrium sediment-transport model for unsteady flow. J. Hydraul. Eng. 2012, 139, 22–36. [Google Scholar] [CrossRef]
- Xia, J.Q.; Lin, B.L.; Falconer, R.A.; Wang, G.Q. Modelling dam-break flows over mobile beds using a 2D coupled approach. Adv. Water Res. 2010, 33, 171–183. [Google Scholar] [CrossRef]
- Wu, W.M. Earthen embankment breaching. J. Hydraul. Eng. 2011, 137, 1549–1564. [Google Scholar]
- Cao, Z.; Pender, G.; Wallis, S.; Carling, P. Computational dam-break hydraulics over erodible sediment bed. J. Hydraul. Eng. 2004, 130, 689–703. [Google Scholar] [CrossRef]
- Gu, Y.; Wu, S.; Yue, Q. Impact of intruded saline water via North Branch of the Yangtze River on water source areas in the estuary area. Yangtze River 2003, 34, 1–16. (In Chinese) [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).