Deciphering the Tsunami Wave Impact and Associated Connection Forces in Open-Girder Coastal Bridges
Abstract
1. Introduction
2. Description of Hydrodynamic Experiments
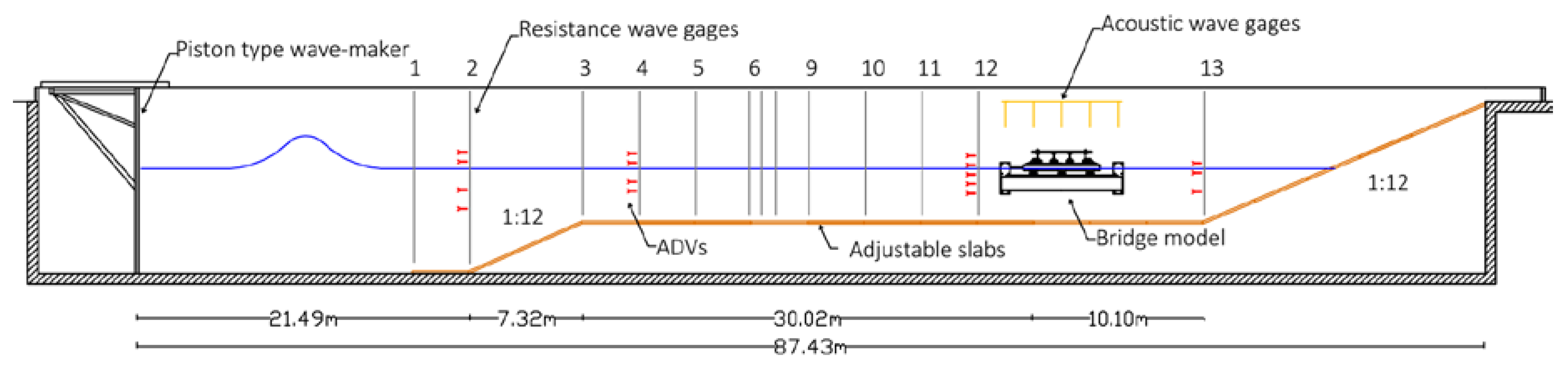
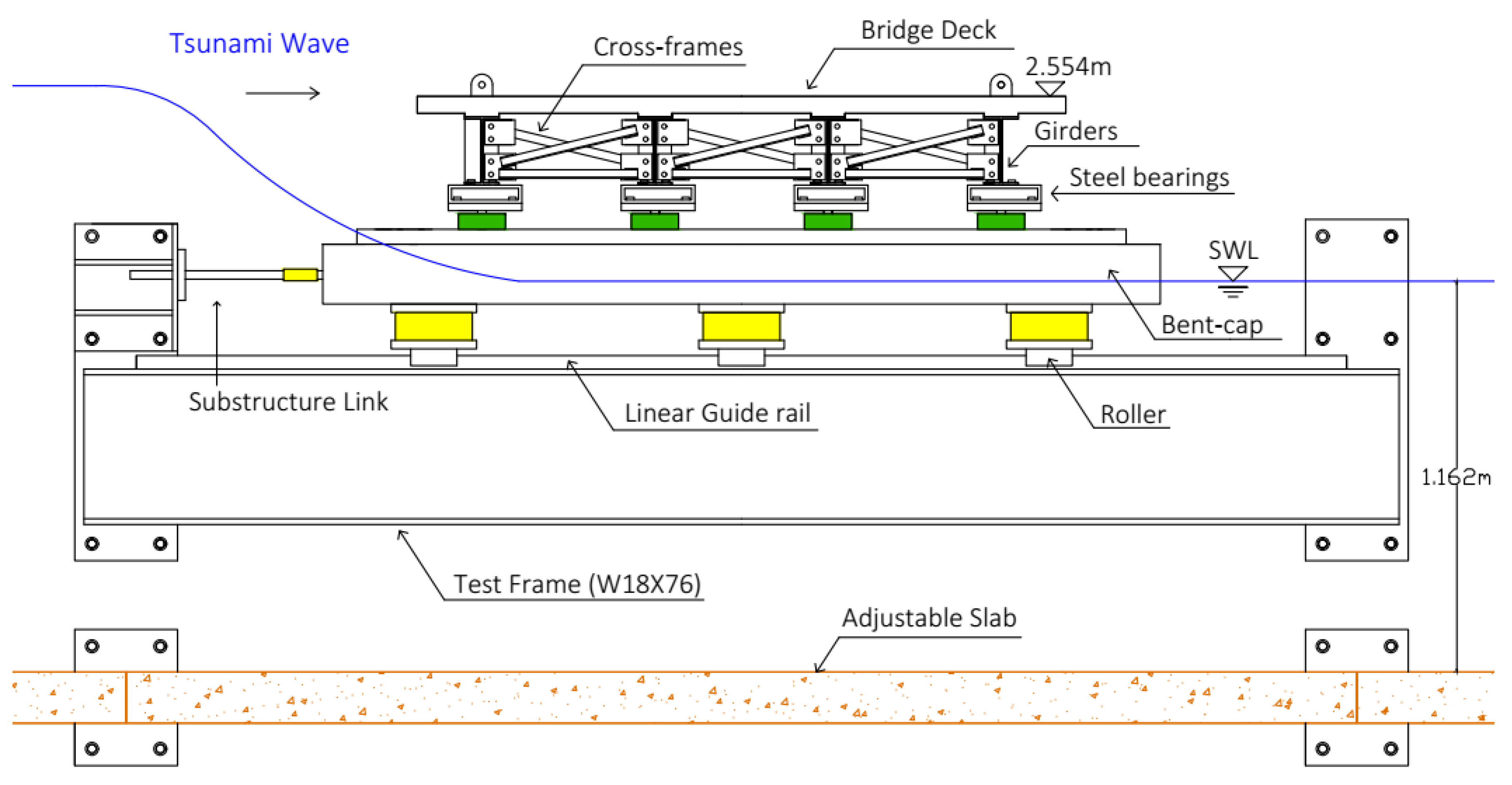
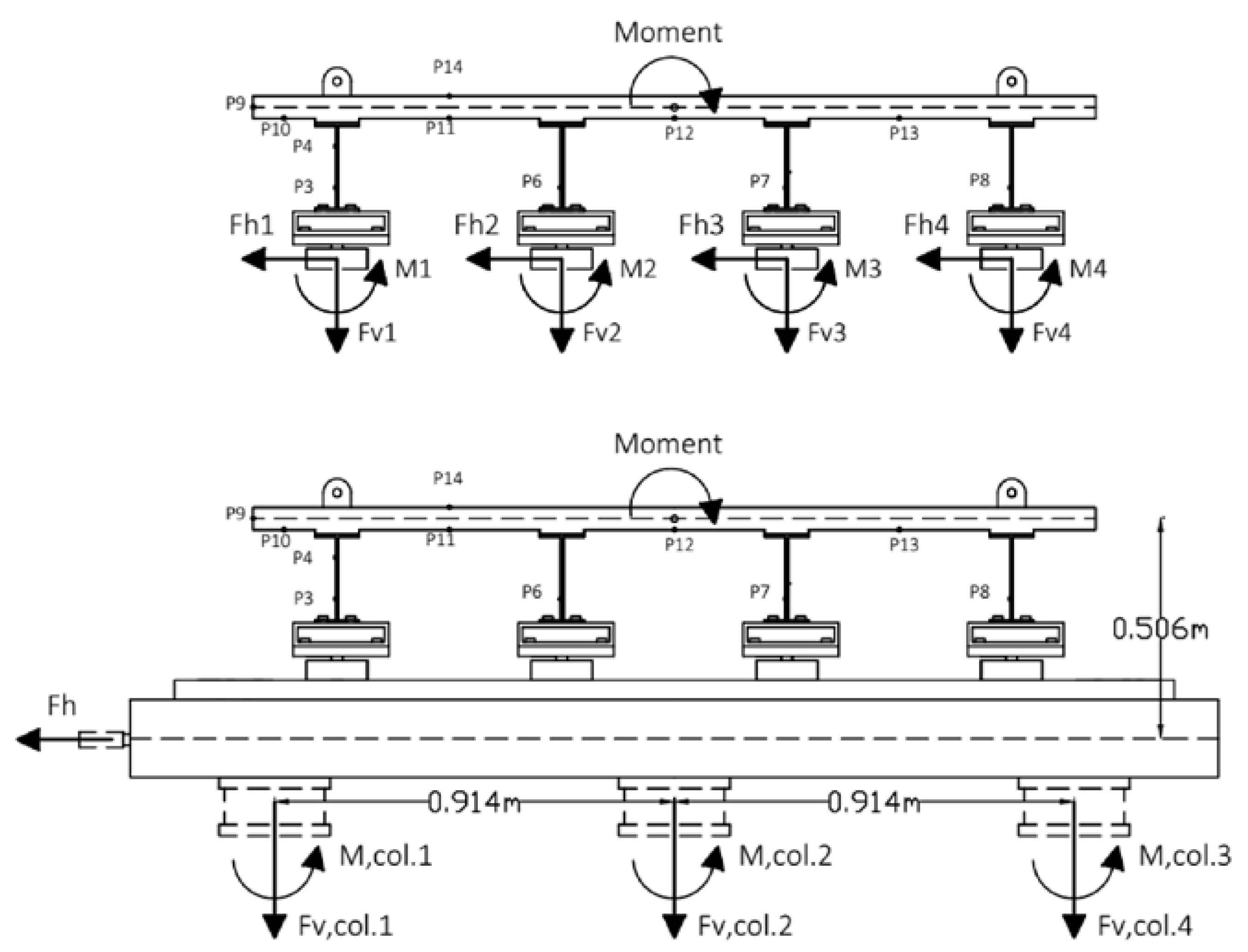
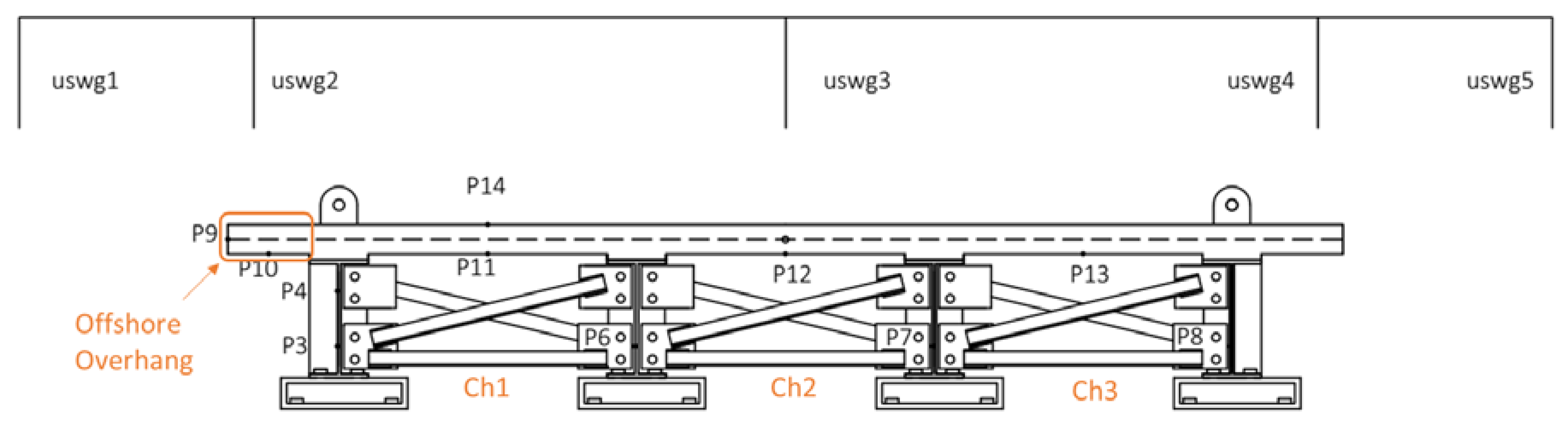
2.1. Experimental Setup
2.2. Testing Program and Instrumentation
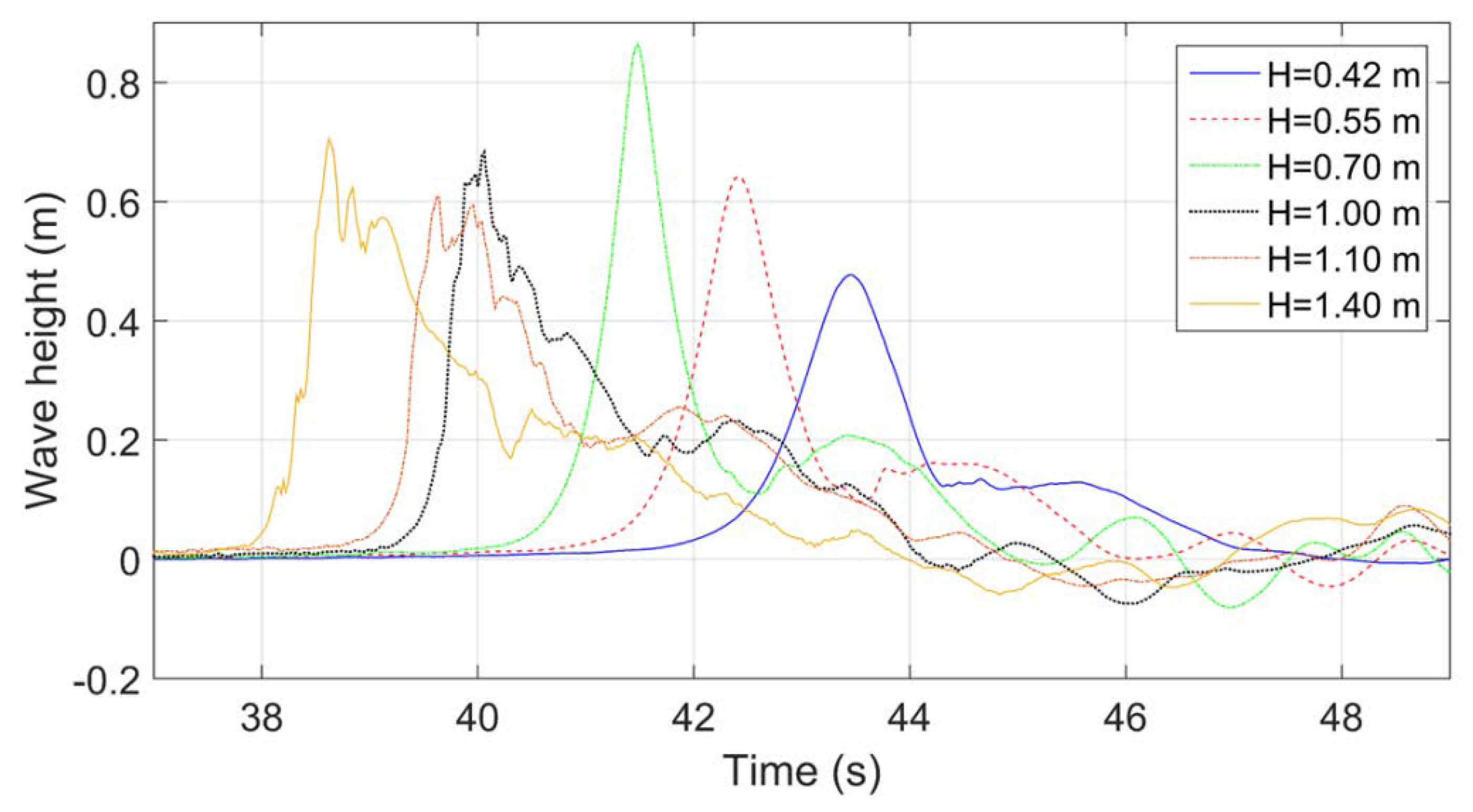
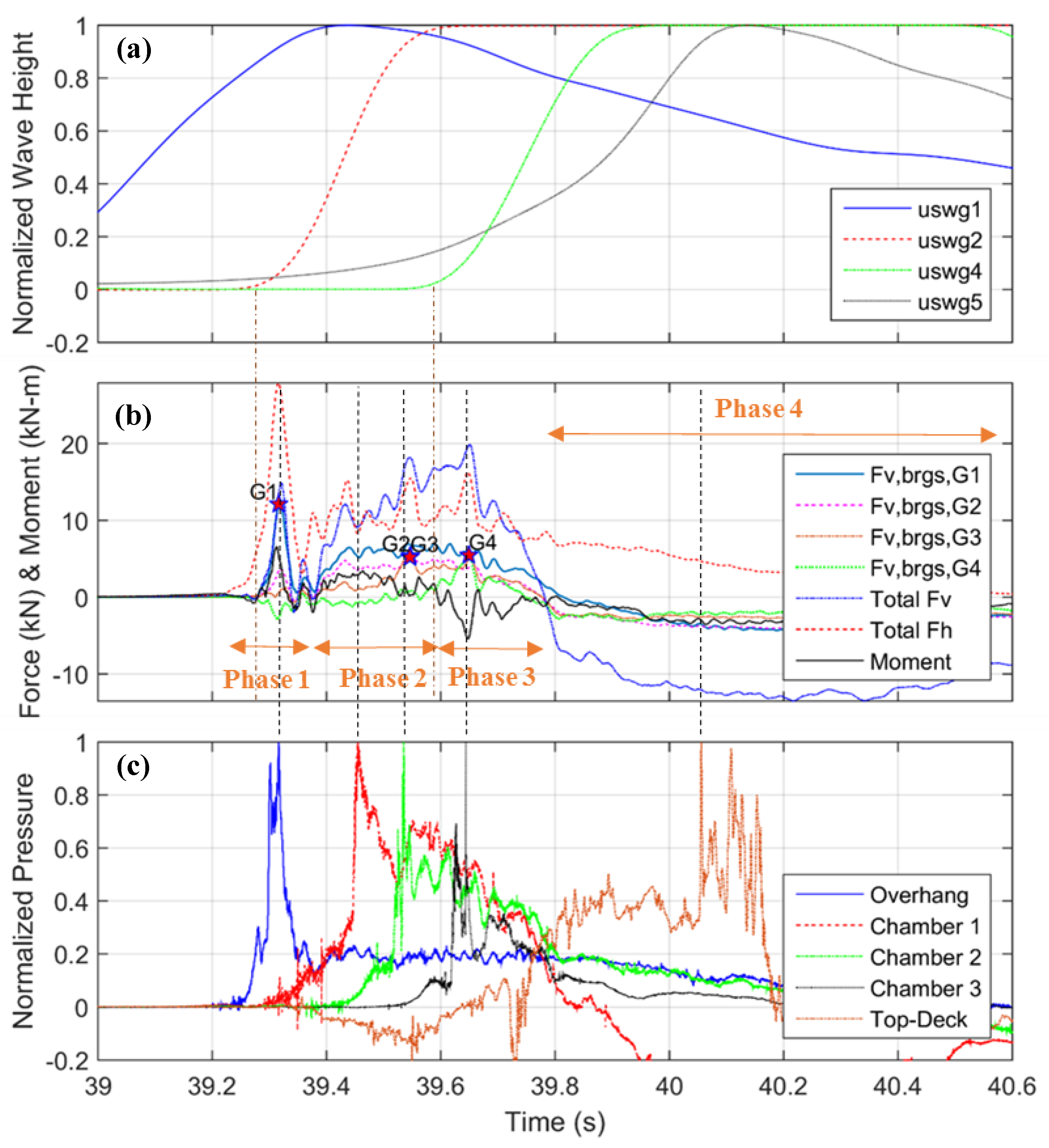
3. Experimental Findings
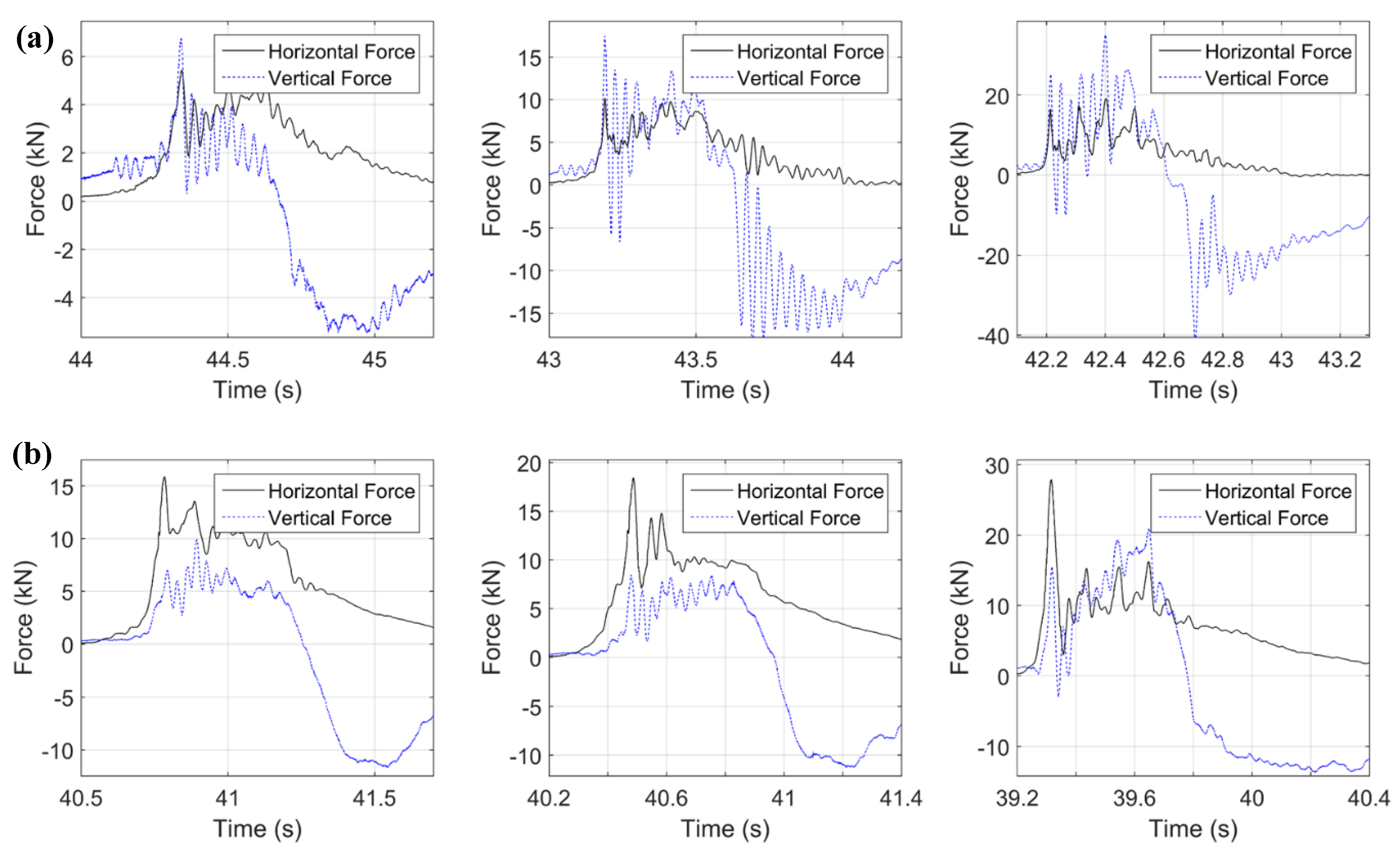
3.1. Total Horizontal and Vertical Forces
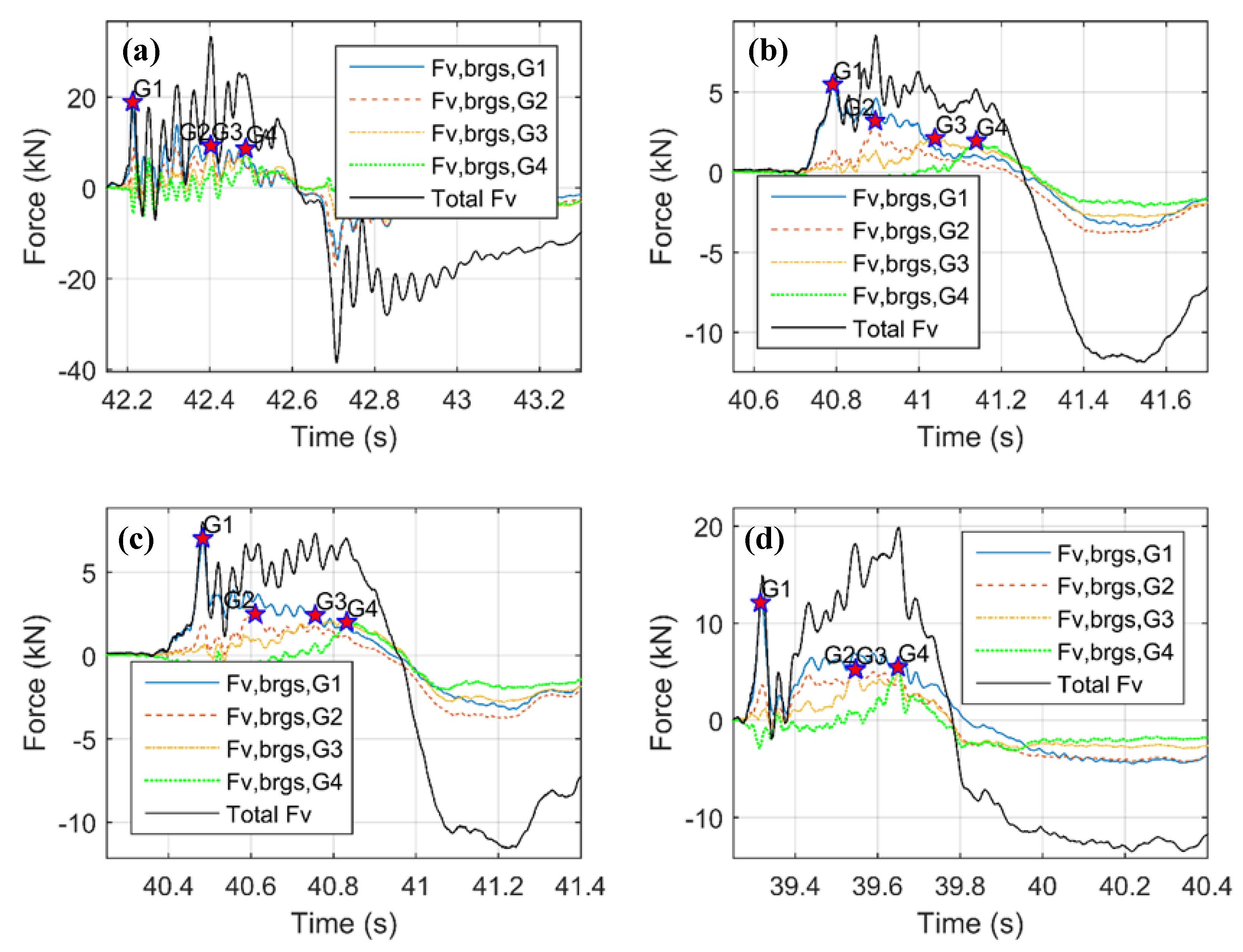
3.2. Vertical Forces in Bearings
- For both solitary waves and bores all bearings are experiencing both uplift and downward forces during the tsunami impact and the flooding process.
- At the initial impact the forces in the offshore (upstream) and onshore (downstream) bearings are out-of-phase, with the offshore bearings witnessing uplift forces and the onshore ones downward forces. At that point in time the offshore steel bearings are taking most of the uplift tsunami force with the bearings of the second offshore girder sharing part of this force. However, as the inundation progresses and the chambers become flooded then all bearing witness uplift forces that are in phase, and are sharing the total uplift force.
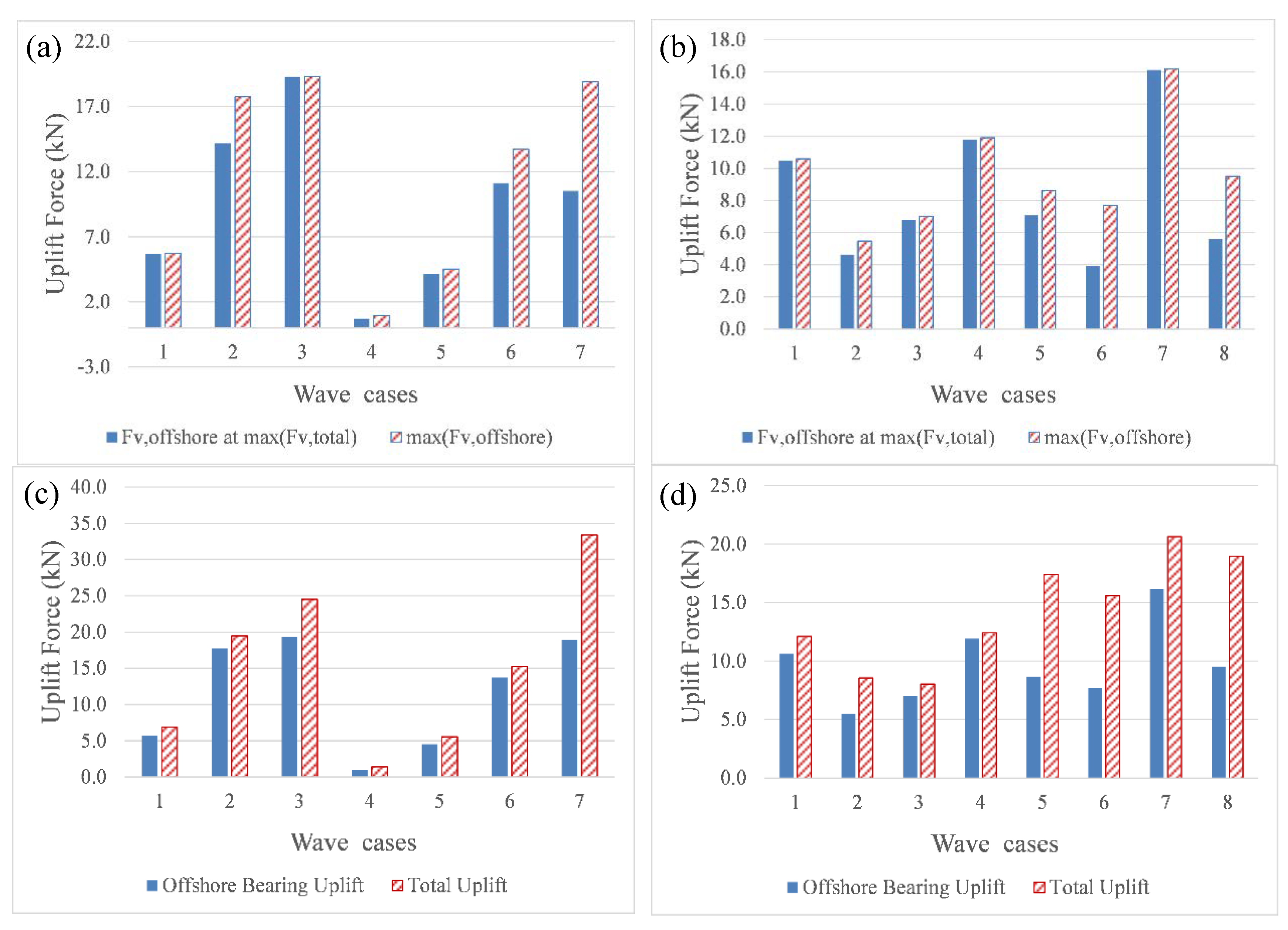
- The offshore bearings have to withstand significantly larger uplift forces than the rest of the bearings for all the tested waves, indicating that the offshore bearings should be designed for larger tsunami demand than the rest of the bearings in order to avoid failure of the bridge.
- The uplift forces in the bearings of the four girders are maximized at different instants (as shown by the red stars in Figure 7), highlighting the transient nature of the inundation process and the influence of the bearing forces by local effects created during the passage of the wave.
- For many wave heights and both wave types the maximum uplift force in the offshore bearings (Fv, brgs, G1) and the maximum total tsunami uplift (maxFv) do not coincide. The former forces are always maximized at the instant of the initial impact, while the latter ones can reach maximum either at the initial impact or later on as the deck flooding progresses. This is a major finding because it implies that the maximum total uplift on the deck might not result in the “worst case” scenario (largest demand) for every bearing.
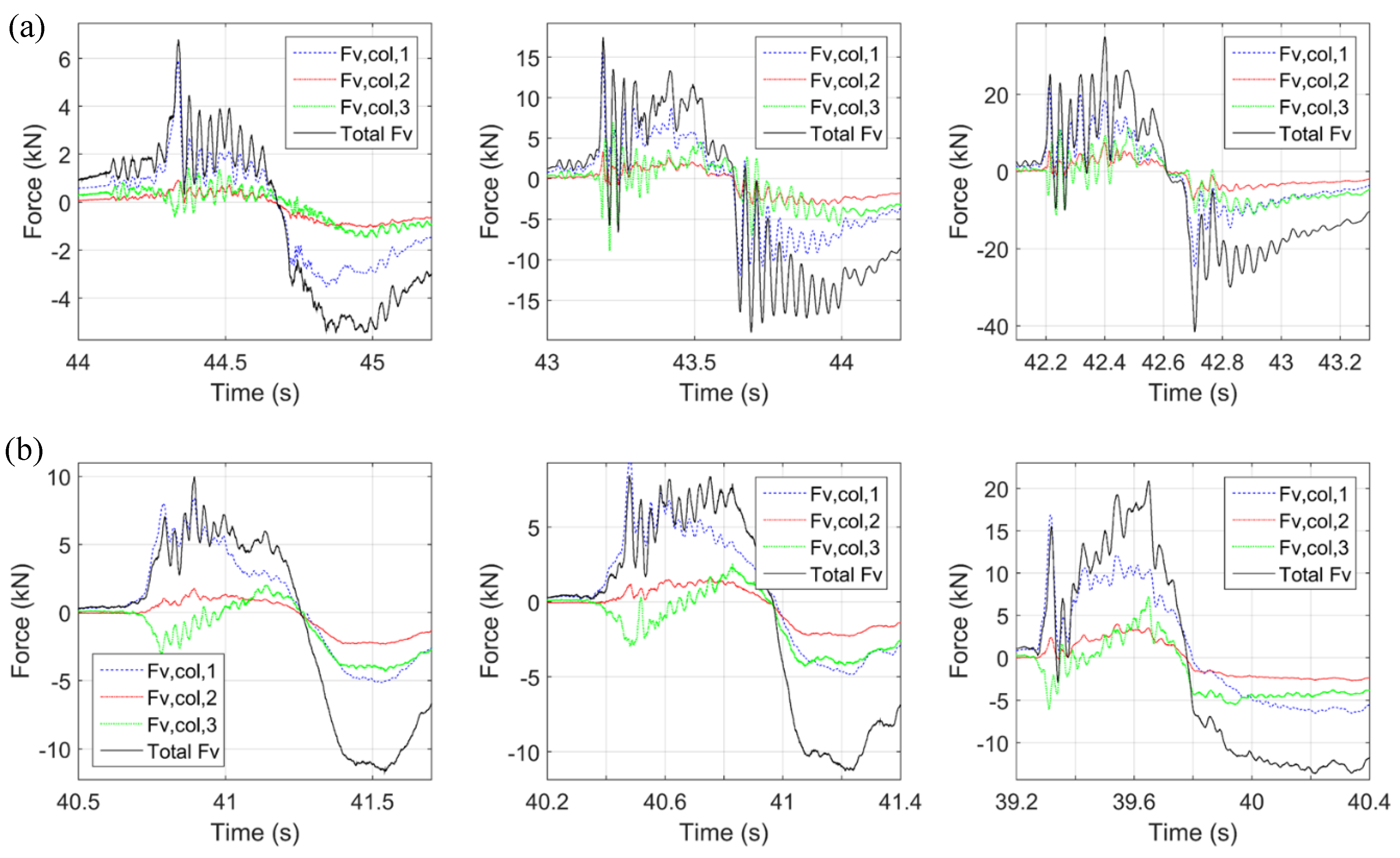
3.3. Vertical Forces in Column-Bent Cap Connections
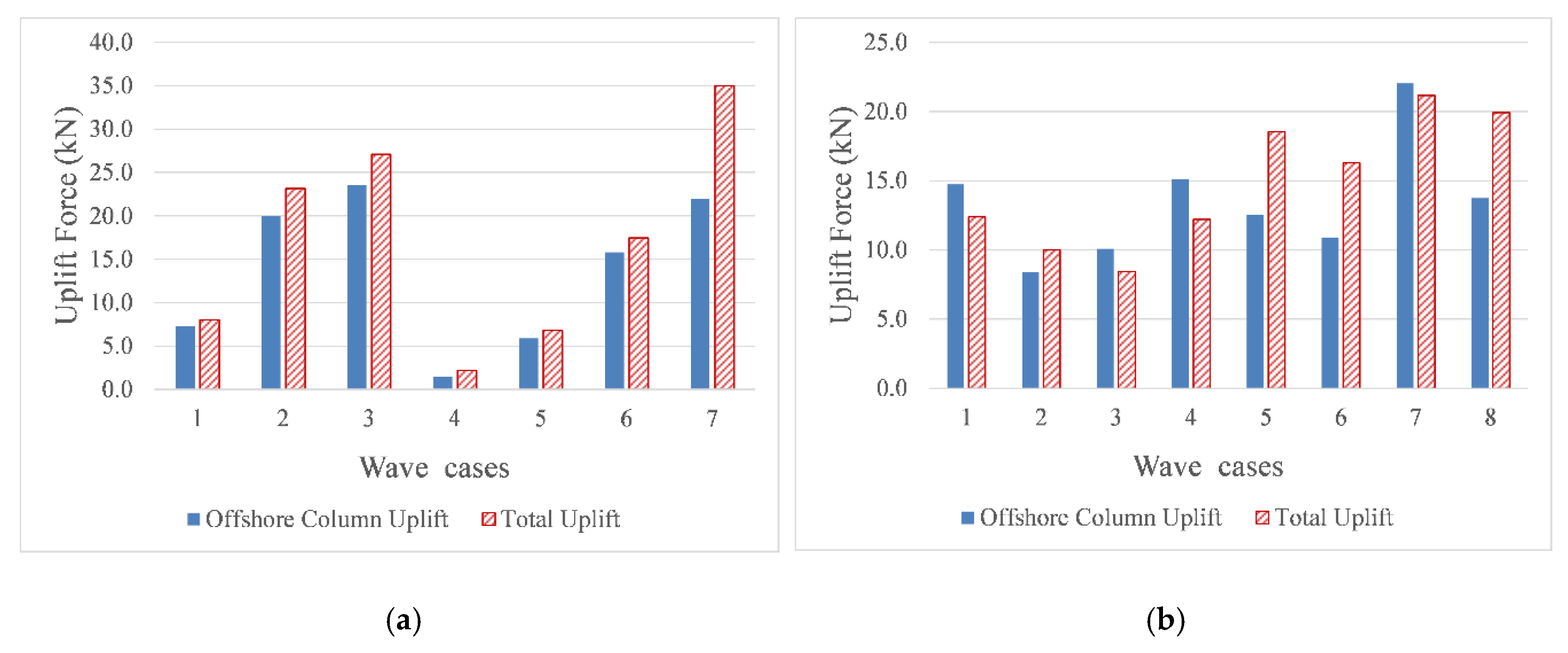
- The offshore column-bent cap connections experience significantly larger uplift than the rest of the connections, while the onshore connections experience larger uplift than the center ones.
- The maximum uplift in the different connections/columns does not occur at the same time, and does not necessarily coincide with the maximum deck uplift. The maximum uplift demand in the offshore connections takes place at the initial impact when the onshore connections witness downward tsunami loading, while the uplift in the rest of the connections is maximized at a later instant of the inundation process.
- The offshore connections/columns have to withstand a large percentage of the total uplift force and for some waves this connection forces is larger than the total applied uplift.
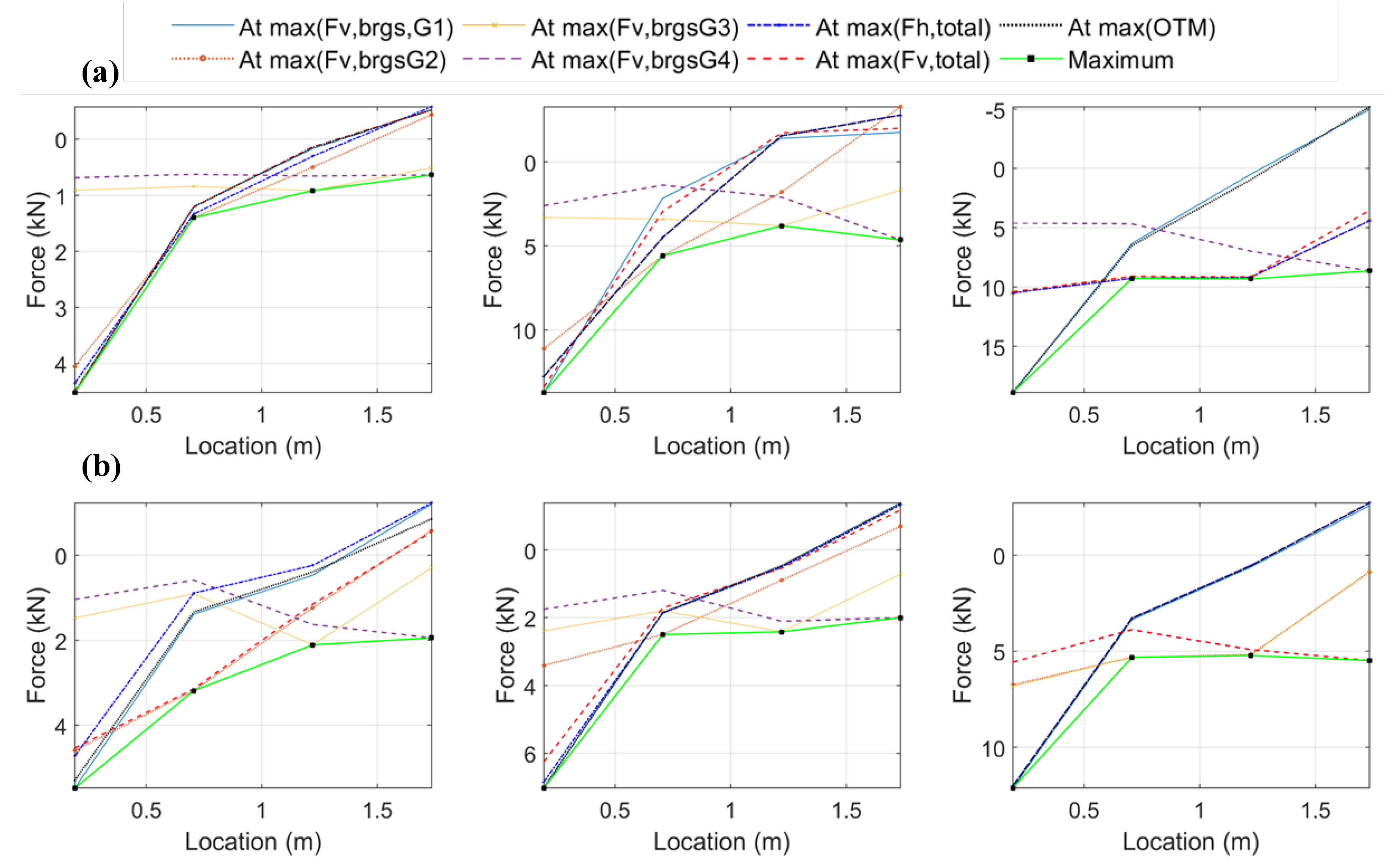
4. Estimation of Bearing and Column Uplift Forces Based on Simplified Approach
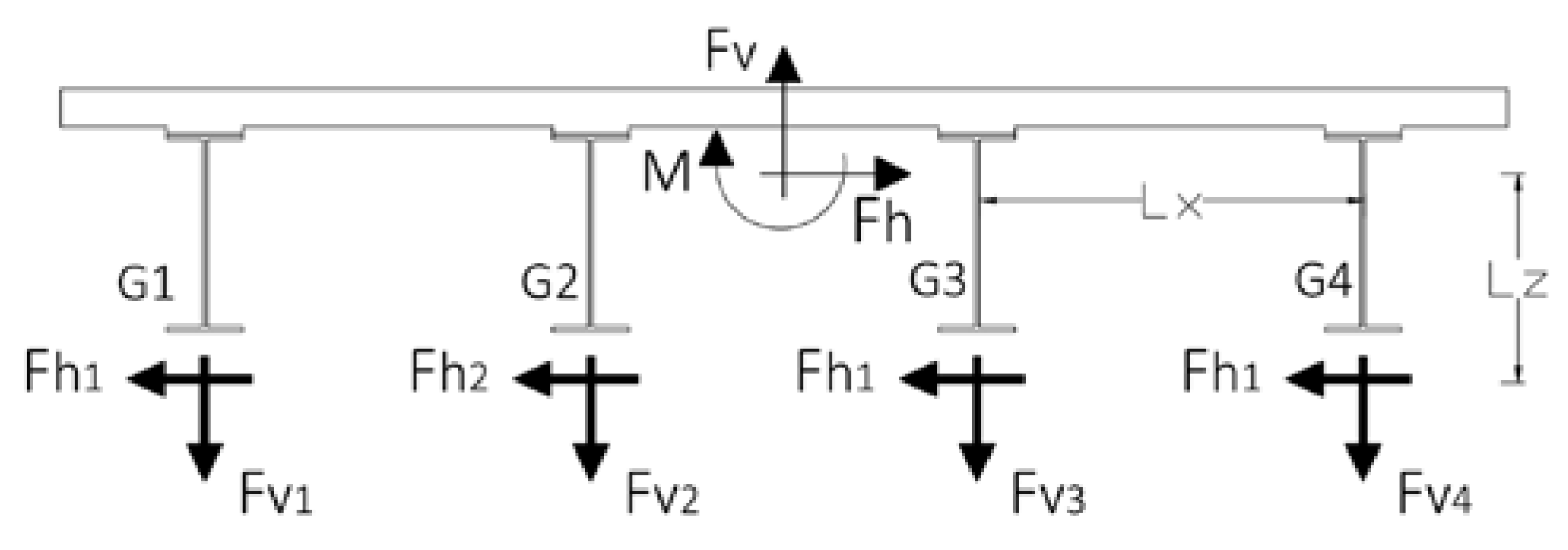
4.1. Application of Maximum Horizontal and Vertical Forces
4.2. Role of Overturning Moment
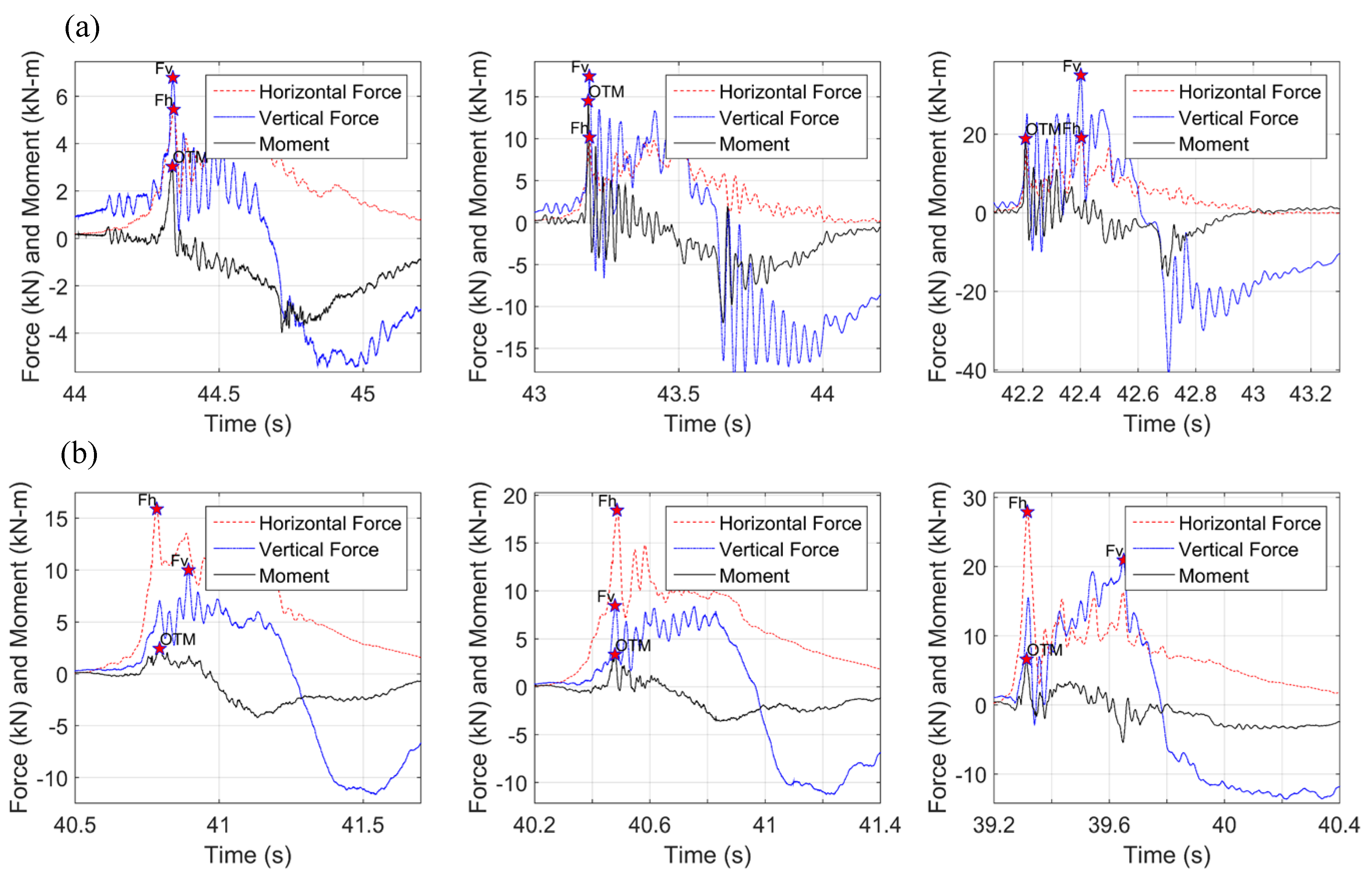
- Significant clockwise moment is generated at the instant of the first impact of the wave on the offshore face of the bridge. This moment is reduced as the wave propagates through the bridge and later on it becomes counter-clockwise.
- Although the forces can be maximized at different instants during the deck flooding, the moment is always maximized at the initial impact of the wave on the offshore girder and overhang for both wave types.
- The maximum overturning moment and maximum bridge uplift do not occur at the same time for many of the tested waves in the experiment. The existence of this significant overturning moment could possibly explain why for the solitary wave of H = 0.70 m although the maximum total uplift force occurs when the wave has flooded all the chambers, the maximum uplift in the offshore bearings occurs at the time of the initial impact.
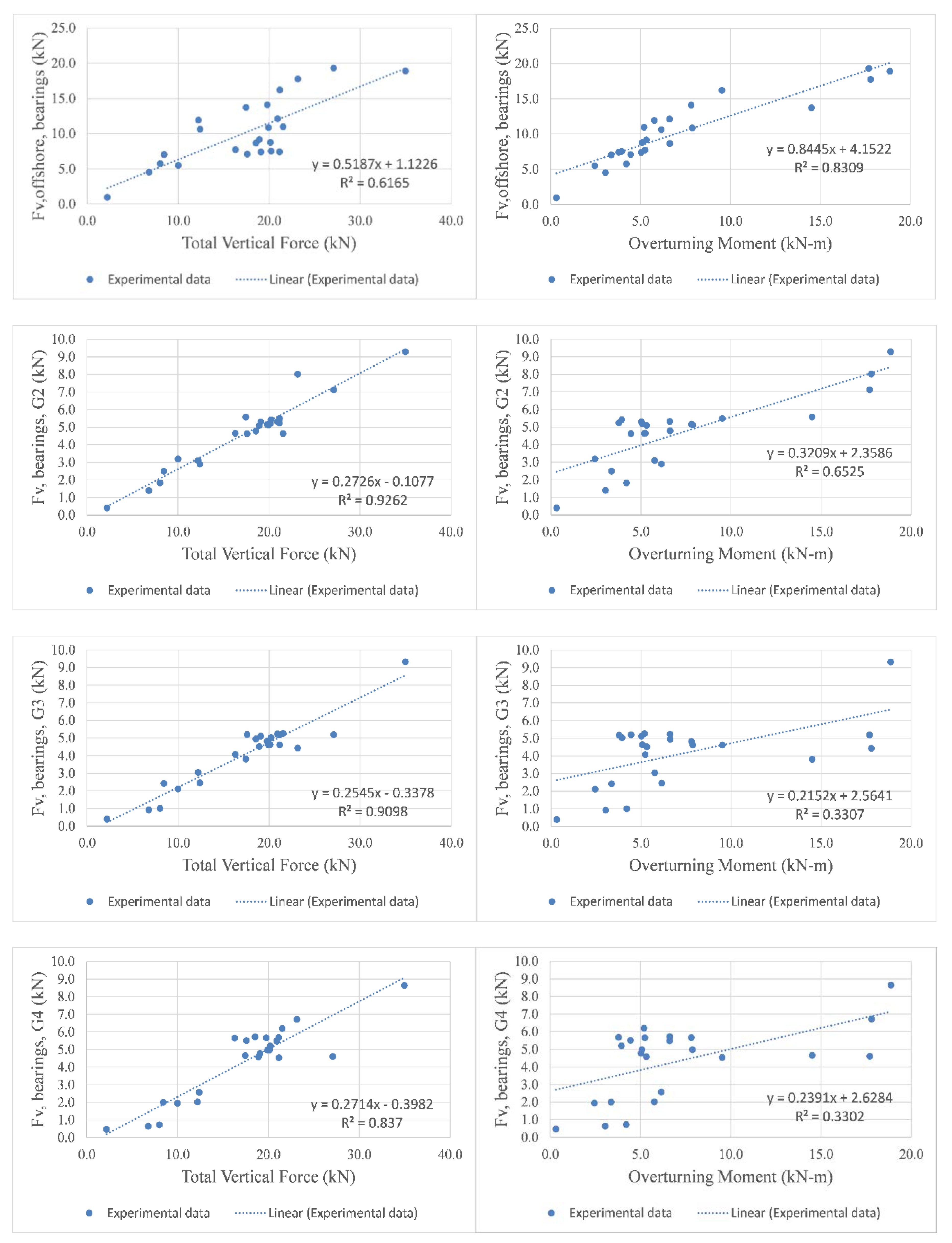
- The offshore bearings do not have a good correlation with the maximum recorded total uplift (R2 = 0.62), and in some cases a larger total uplift gives a smaller uplift in the bearings, which seems counter-intuitive. Instead, the uplift in these bearings is better correlated with the maximum clockwise moment (R2 = 0.83). This is a major finding and it seems to make sense if one considers the observations made in previous sections, according to which the uplift force in the offshore bearings was always maximized at the first impact of the wave on the bridge, while the maximum total uplift on the deck was maximized at different instants of the inundation process depending on the wave height.
- The bearings of the internal girders (G2 and G3) are showing good correlation with the maximum uplift on the deck, with G2 having the best agreement among all bearings (R2 = 0.926). For both of these bearings the correlation with the max clockwise moment is poor, indicating that the moment does not govern tsunami-induced uplift at these locations.
- Generally, as the horizontal distance of the bearings from the offshore face of the bridge increases, the agreement of the individual bearing uplift with the maximum clockwise moment weakens, and for the onshore bearings there is no apparent correlation (R2 = 0.33). The onshore bearings also seem to have a weaker correlation with the maximum total uplift than the bearings of the internal girders, demonstrating that predicting the maximum uplift in these bearings might be more complex than expected.
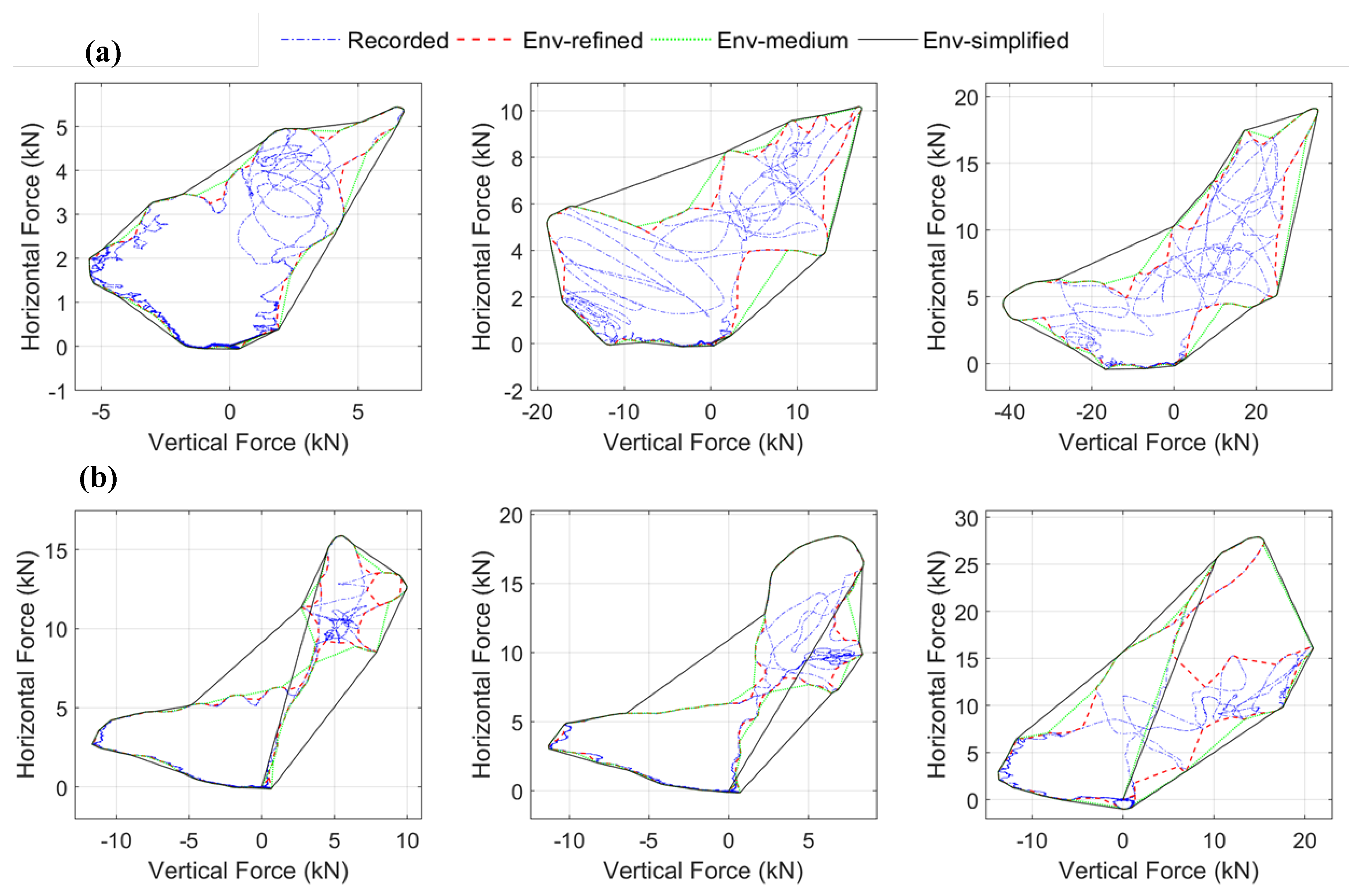
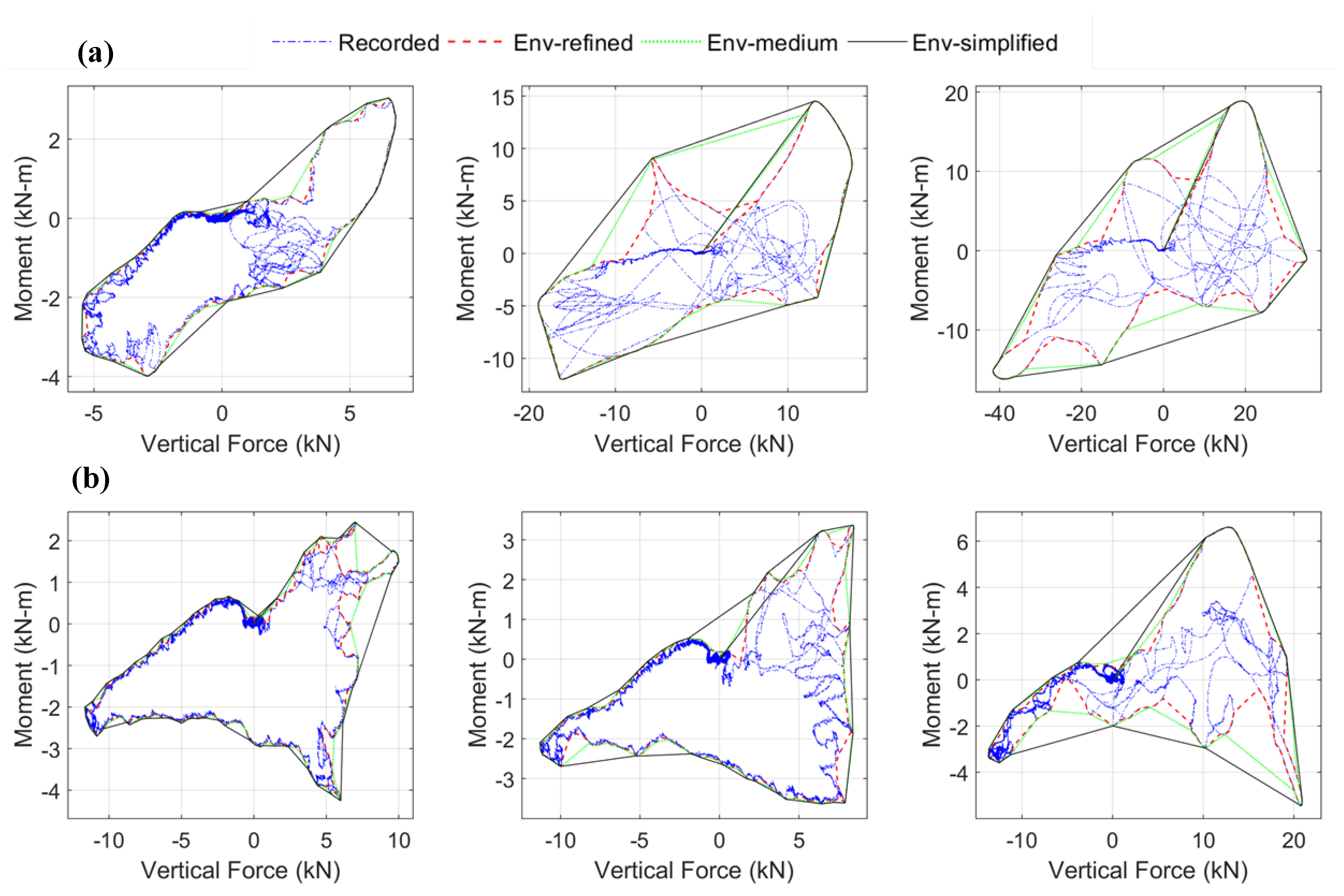
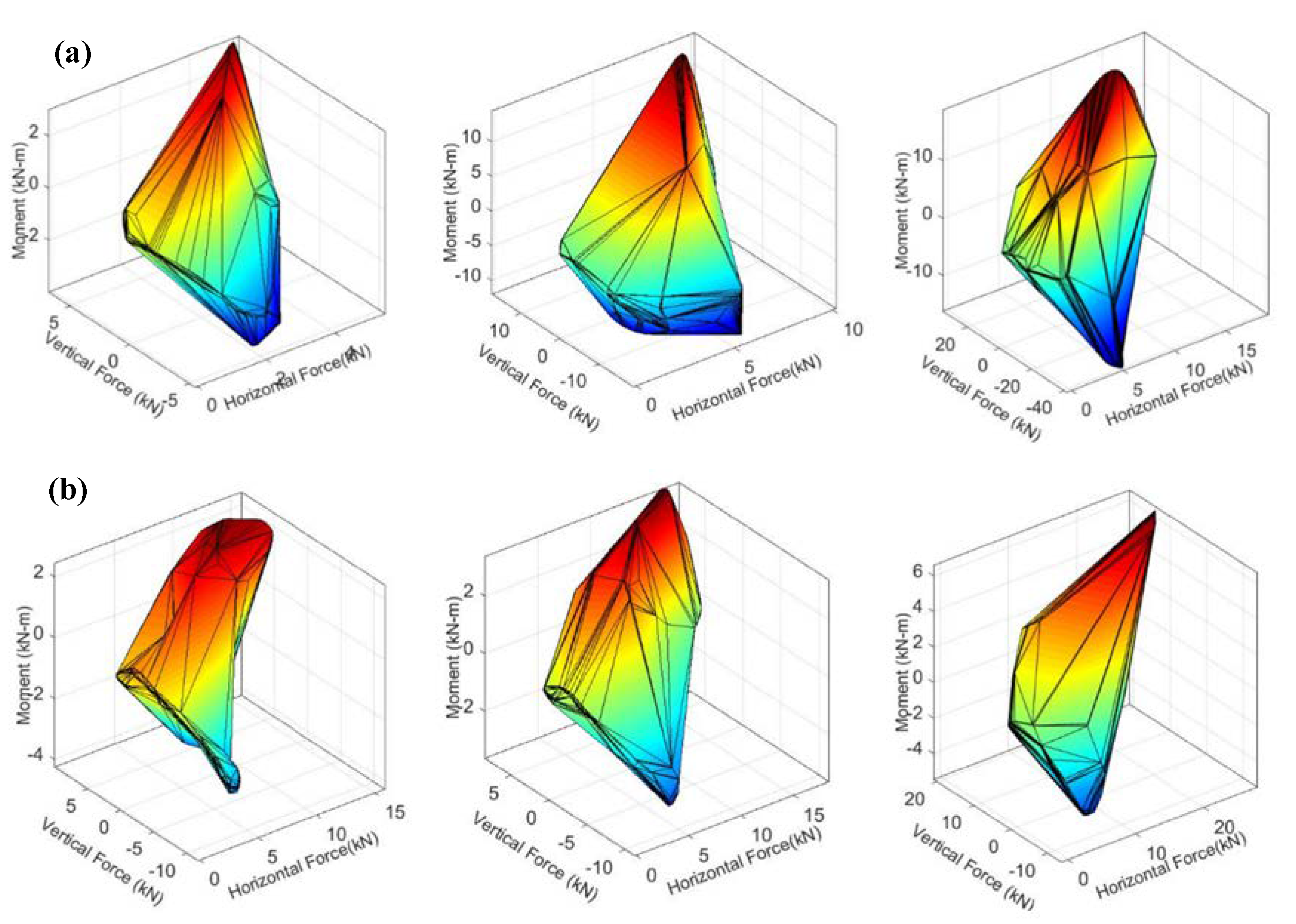
5. Tsunami Demand Diagrams
- For most solitary waves, the maximum horizontal force and maximum uplift force occur at the same time, while for most bores the two maxima do not coincide (Section 3).
- All waves introduce significant clockwise moment (positive value on graph) and simultaneously large uplift loading, however for most wave heights the maxOTM does not take place at the same instant with maxFv. This implies that for the tsunami design of bridges engineers will have to consider several load cases (e.g., maxOTM with corresponding Fv and Fh or maxFv with corresponding OTM and Fh) in order to identify the worst-case scenario for each component.
- For all wave heights a large counter-clockwise moment is generated during the inundation, which was not expected beforehand. In fact, for solitary waves at the instant of the maximum counter-clockwise moment the wave applies a downward vertical load, while for bores this is not true and significant uplift is observed instead.
- The refined envelopes (red color) of Fh versus Fv and OTM versus Fv are quite complex and their shapes have significant differences between waves indicating a dependence on the wave height and wave type. However, as the envelope becomes less refined then similarities start appearing between the different heights. Especially, the simplified envelopes (Env-simplified) of Fh versus Fv and the ones of OTM versus Fv have very similar shapes among different bore heights. This tends to be true for the unbroken solitary waves too but the similarities are not as striking.
- The existence of fundamental differences in the effects introduced on the bridge by the two different wave types, which suggests the need for the development of methodologies that will be able to predict the exact wave type at a particular bridge location.
- The need to consider different load cases/combinations of (Fh, Fv and OTM) and not just maxFh and maxFv as done to date, since it is not a priori known which case will be governing the design of individual structural components of the bridge.
- The possibility to develop simplified 2D demand diagrams (Fh versus Fv, OTM versus Fv) or simplified 3D diagrams (Fh versus Fv versus OTM), which will have the same shape for all bores and a size that will change with the wave height. Once the shape is known then simplified predictive equations could potentially be developed for estimating the magnitude. This approach sounds quite futuristic for the time being; however, it is simpler than trying to predict both the spatial and temporal variation of the applied forces. Such an approach would be less economical but more convenient. Given the uncertainties involved in the tsunami wave breaking and impact on structures, some conservatism in the method that estimates the tsunami-induced loading on the structure might be acceptable.
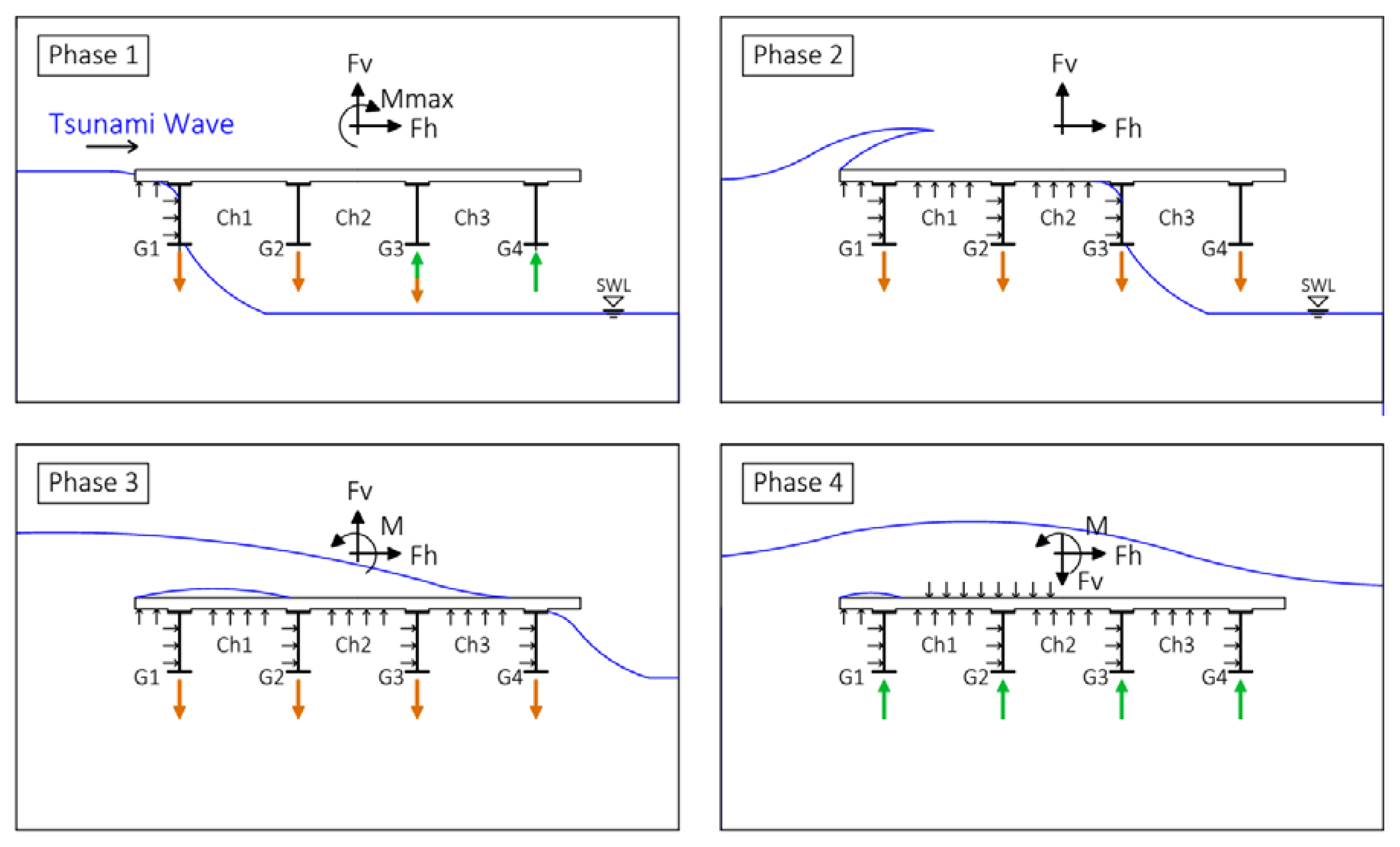
6. Tsunami Inundation Mechanism of Bridges
- Phase 1: This is a short duration phase during which the bridge experiences significant impulsive horizontal and vertical forces and occurs when the wave hits the offshore girder and overhang. This phase produced the maximum horizontal force for all bores and the maximum overturning moment, generating an uplift and a downward force in the offshore and onshore bearings respectively. Due to the simultaneously large uplift force and moment, this phase produces the largest uplift in the offshore bearings meaning that it could be the most catastrophic phase for the offshore structural components (bearings, connections, columns etc.).
- Phase 2: This is a longer duration phase that starts when the wave reaches chamber 1 and finishes when the wave has inundated chamber 2 of the bridge, at which point the uplift force is applied close to the CG of the deck. During this phase the overtopping process begins, with the tip of the wave splashing over the top of the offshore overhang. In this phase, the applied moment is small, however the bridge uplift force is very large and for some wave heights it can actually reach its maximum value. In this phase all bearings are in phase witnessing uplift forces, and the bearings of the interior girders (G2 and G3) are reaching their maximum uplift values for most waves. This phase can also produce the largest horizontal force for solitary waves, however this is not true for bores, the horizontal force of which is reduced significantly since the slamming component is minimized and only the hydrodynamic (drag) component remains.
- Phase 3: This phase occurs when the wave has reached chamber 3. During this phase the tip of the wave starts inundating the offshore side (uswg2) of the top surface of the deck and towards the end of the phase the water reaches the onshore side (uswg4). In this phase the horizontal force is reduced for all wave types, the vertical force is large -can even be at a maximum- and there is a counter-clockwise moment, which generates the largest uplift force in the onshore bearings. Therefore, this phase has to be considered because it is the governing one for the onshore bearings. It must be noted though that this phase is different for bores and solitary waves because the former waves introduce the maximum counter-clockwise moment in this phase, while this is not true for the latter waves.
- Phase 4: This phase occurs after the wave has passed the onshore chamber, the whole top surface of the deck becomes inundated and the overtopping water introduces large downward pressures on the deck (at P14). The slamming downward force on the deck is so high that it exceeds the simultaneously applied uplift force below the deck, consequently introducing compression in all bearings. This phase also produces the maximum counter-clockwise moment for all solitary waves.
7. New Physics-Based Simplified Methodology for Engineering Practice
- Load Case 1: In this case the maximum horizontal force is applied at the mid-height of the offshore girder and the maximum vertical force is applied at the mid-width of the offshore overhang, with the aim to represent Phase 1 of the inundation mechanism and the associated large overturning moment. This load case is expected to give the largest uplift forces in the offshore bearings, columns and connections. The experimental results demonstrated that it is more reasonable to apply the horizontal load at the mid-height of the girder, instead of the mid-height of the bridge or the CG of the deck, since as seen in [23] the recorded pressures histories on the offshore girder at Hgirder/3 and 2Hgirder/3 are simultaneously large in Phase 1, while the pressure on the offshore face of the overhang is maximized much later. It must be clarified though that this is limited only to bridges without barriers (rails) or barriers with perforations that do not have a significant effect on the total horizontal load. This situation might be different for solid barriers and for such a case further investigation is required.
- Load Case 2: In this load case the maximum uplift force is applied at the mid-width of chamber 1, while a reduced horizontal load is simultaneously applied at the mid-height of girder G2. The intent for this load case is to capture the effects associated with phase 2 of the inundation mechanism during which the wave could be reaching either chamber 1 or chamber 2. Therefore, the horizontal load is reduced (Fh = a×maxFh) using a calibrated factor that accounts for the observed trends in the recorded time-histories, which showed that for all bore heights and several solitary wave heights the horizontal load was reduced after the initial impact on the offshore girder. A factor a = 0.85 was seen to give reasonable results, however it must be noted that this number is not intended to be conservative in terms of estimating the horizontal force for all solitary waves, since in the experiments some large solitary waves (e.g., H = 0.70 m) showed continuously large horizontal forces during the whole inundation process, so for such waves a = 1 could be used. This load case will generate a smaller overturning moment than load case 1 and could possibly give a more accurate estimation of the uplift forces in bearings G2.
- Load Case 3: For load case 3 the maximum uplift force is applied at the mid-width of the onshore chamber 3 together with a reduced horizontal load (Fh = b×maxFh). The objective of this load case is to capture the maximum uplift in bearings G3 and G4, which were seen to be governed by the reverse overturning moment for most wave heights. In this study three values of the reduction factor “b” were examined and particularly b = 0, b = 0.5 and b = 0.65. The zero value would mean that the horizontal load is totally neglected leading to a larger counter-clockwise moment than the one generated by the other two values, and a conservative estimation of the uplift load in bearings G3 and G4.
8. Conclusions
- Bores introduce a significant, short-duration impulsive (slamming) force followed by a longer duration lateral force with significantly reduced amplitude. This is not the case for unbroken solitary waves. However, both types of waves apply a distinct short-duration impulsive uplift force when the wave hits the offshore overhang followed by (a) a longer duration uplift force as the chambers of the bridge flooded, and (b) a downward force as the deck is inundated.
- The maximum of the horizontal (Fh) and vertical (Fv) forces did not always occur at the same point of the flooding process nor did they coincide in time for all waves, and in fact the horizontal loading was seen to be reduced to 60% of its maximum value at the instant the uplift force was maximized. This demonstrates the transient nature of the tsunami inundation mechanism and its complexity, as well as the need to predict time-consistent vertical and horizontal forces in order to achieve an economical tsunami bridge design.
- The uplift forces in individual bearings and column-bent connections are maximized at different instants of the flooding and overtopping process and have different magnitudes, with the offshore components having to withstand the majority of the total deck uplift, reaching as high as 91% of maxFv for unbroken solitary waves and 96% for bores, with average values being 78% and 70% for the two wave types respectively. Similarly, for the same wave types, the offshore columns are subject to an average of 82% and 94% of maxFv, while for some wave heights the uplift demand can be up to 124% of maxFv, which seems counter-intuitive.
- The maximum uplift force individual bearings and columns do not necessarily coincide with the maximum applied uplift on the deck. This is a major finding because it indicates that the maximum total uplift on the deck might not result in the “worst case” scenario (largest demand) for every structural component, suggesting that the current approach of using the total tsunami force as the sole measure of tsunami demand might not be sufficient.
- The concurrent application of the maximum total horizontal and maximum uplift loading at the CG is not conservative for most bearing and column connections, in contrast to conventional wisdom. The reason behind this observation is the generation of a significant OTM, which has not been fully understood to date. This moment is always maximized at the initial impact of the wave on the offshore girder and overhang, and together with the concurrently large applied uplift force is causing the significant uplift demand on offshore connections and components.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Unjoh, S. Bridge damage caused by tsunami. Jpn. Assoc. Earthq. Eng. 2007, 6, 6–28. [Google Scholar]
- Maruyama, K.; Tanaka, Y.; Kosa, K.; Hosoda, A.; Arikawa, T.; Mizutani, N.; Nakamura, T. Evaluation of tsunami force acting on bridge girders. In Proceedings of the Thirteenth East Asia-Pacific Conference on Structural Engineering and Construction (EASEC-13), Sapporo, Japan, 11–13 September 2013. Keynote-Lecture. [Google Scholar]
- Kosa, K. Damage analysis of bridges affected by tsunami due to Great East Japan Earthquake. In Proceedings of the Symposium on Engineering Lessons Learned from the 2011 Great East Japan Earthquake, Tokyo, Japan, 1–4 March 2012. [Google Scholar]
- Kasano, H.; Oka, J.; Sakurai, J.; Kodama, N.; Yoda, T. Investigative research on bridges subjected to tsunami disaster in 2011 off the pacific coast of Tohoku earthquake. In Australasian Structural Engineering Conference 2012: The Past, Present and Future of Structural Engineering; Engineers Australia: Barton, Australia, 2012; p. 51. [Google Scholar]
- Kawashima, K. Damage of bridges due to the 2011 great east japan earthquake. In Proceedings of the International Symposium on Engineering Lessons Learned from the 2011 Great East Japan Earthquake, Tokyo, Japan, 1–4 March 2012. [Google Scholar]
- Lau, T.L.; Ohmachi, T.; Inoue, S.; Lukkunaprasit, P. Experimental and numerical modeling of tsunami force on bridge decks. In Tsunami-a Growing Disaster; InTech: London, UK, 2011. [Google Scholar]
- Hayashi, H. Study on tsunami wave force acting on a bridge superstructure. In Proceedings of the 29th US-Japan Bridge Engineering Workshop, Tsukuba, Japan, 11–13 November 2013. [Google Scholar]
- Seiffert, B.; Hayatdavoodi, M.; Ertekin, R.C. Experiments and computations of solitary-wave forces on a coastal-bridge deck. Part I: Flat plate. Coast. Eng. 2014, 88, 194–209. [Google Scholar] [CrossRef]
- Hayatdavoodi, M.; Seiffert, B.; Ertekin, R.C. Experiments and computations of solitary-wave forces on a coastal-bridge deck. Part II: Deck with girders. Coast. Eng. 2014, 88, 210–228. [Google Scholar] [CrossRef]
- Bozorgnia, M.; Lee, J.J.; Raichlen, F. Wave structure interaction: Role of entrapped air on wave impact and uplift forces. Coast. Eng. Proc. 2011, 1, 57. [Google Scholar] [CrossRef]
- Yim, S.C.; Boon-intra, S.; Nimmala, S.B.; Winston, H.M.; Azadbakht, M.; Cheung, K.F. Development of a Guideline for Estimating Tsunami Forces on Bridge Superstructures; Report No. OR-RD-12-03; Oregon Department of Transportation: Salem, OR, USA, 2011. [Google Scholar]
- Kataoka, S.; Kaneko, M. Estimation of wave force acting on bridge superstructures due to the 2011 Tohoku Tsunami. J. Disaster Res. 2013, 8, 605–611. [Google Scholar] [CrossRef]
- Nakao, H.; Zhang, G.; Sumimura, T.; Hoshikuma, J. Numerical assessment of tsunami-induced effect on bridge behavior. In Proceedings of the 29th US-Japan Bridge Engineering Workshop, Tsukuba, Japan, 11–13 November 2013. [Google Scholar]
- Bricker, J.D.; Nakayama, A. Contribution of trapped air deck superelevation, and nearby structures to bridge deck failure during a tsunami. J. Hydraul. Eng. 2014, 140, 05014002. [Google Scholar] [CrossRef]
- Azadbakht, M.; Yim, S.C. Simulation and estimation of tsunami loads on bridge superstructures. J. Waterw. Port Coast. Ocean Eng. 2014, 141, 04014031. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.G. Effect of fluid-structure interaction on connection forces in bridges due to tsunami loads. In Proceedings of the 30th US-Japan Bridge Engineering Workshop, Washington, DC, USA, 21–23 October 2014. [Google Scholar]
- Fu, L.; Kosa, K.; Sasaki, T. Tsunami damage evaluation of utatsu bridge by video and 2-d simulation analyses. J. Struct. Eng. 2013, 59, 428–438. [Google Scholar]
- Kawashima, K.; Buckle, I. Structural performance of bridges in the tohoku-oki earthquake. Earthq. Spectra 2013, 29, S315–S338. [Google Scholar] [CrossRef]
- Araki, S.; Ishino, K.; Deguchi, I. Stability of girder bridge against tsunami fluid force. Coast. Eng. Proc. 2011, 1, 56. [Google Scholar] [CrossRef]
- Rahman, S.; Akib, S.; Shirazi, S.M. Experimental investigation on the stability of bride girder against tsunami forces. Sci. China Technol. Sci. 2014, 57, 2028–2036. [Google Scholar] [CrossRef]
- Maruyama, K.; Hosoda, A.; Tanaka, Y.; Kosa, K.; Arikawa, T.; Mizutani, N. Tsunami force acting on bridge girders. J. JSCE 2017, 5, 157–169. [Google Scholar] [CrossRef]
- Mazinani, I.; Ismail, Z.; Hashim, A.M.; Saba, A. Experimental investigation on tsunami acting on bridges. Int. J. Civ. Archit. Struct. Constr. Eng. 2014, 8, 1040–1043. [Google Scholar]
- Istrati, D. Large-Scale Experiments of Tsunami Inundation of Bridges Including Fluid-Structure-Interaction. Doctoral Dissertation, University of Nevada, Reno, NV, USA, May 2017. [Google Scholar]
- Hoshikuma, J.; Zhang, G.; Nakao, H.; Sumimura, T. Tsunami-induced effects on girder bridges. In Proceedings of the International Symposium for Bridge Earthquake Engineering in Honor of Retirement of Professor Kazuhiko Kawashima, Tokyo, Japan, 15 March 2013. [Google Scholar]
- Martinelli, L.; Lamberti, A.; Gaeta, M.G.; Tirindelli, M.; Alderson, J.; Schimmels, S. Wave loads on exposed jetties: Description of large-scale experiments and preliminary results. In Proceedings of the Conference on Coastal Engineering, Shanghai, China, 30 June–5 July 2010. [Google Scholar]
- Murakami, K.; Sakamoto, Y.; Nonaka, T. Analytical investigation of slab bridge damages caused by tsunami flow. Coast. Eng. Proc. 2012, 1, 42. [Google Scholar] [CrossRef]
- Motley, M.R.; Wong, H.K.; Qin, X.; Winter, A.O.; Eberhard, M.O. Tsunami-induced forces on skewed bridges. J. Waterw. Port Coast. Ocean Eng. 2015, 142, 04015025. [Google Scholar] [CrossRef]
- Wei, Z.; Dalrymple, R.A. Numerical study on mitigating tsunami force on bridges by an SPH model. J. Ocean Eng. Mar. Energy 2016, 2, 365–380. [Google Scholar] [CrossRef]
- Zhu, M.; Elkhetali, I.; Scott, M.H. Validation of opensees for tsunami loading on bridge superstructures. J. Bridge Eng. 2018, 23, 04018015. [Google Scholar] [CrossRef]
- Xu, G.; Cai, C.S.; Hu, P.; Dong, Z. Component level–based assessment of the solitary wave forces on a typical coastal bridge deck and the countermeasure of air venting holes. Pract. Period. Struct. Des. Constr. 2016, 21, 04016012. [Google Scholar] [CrossRef]
- Winter, A.O.; Motley, M.R.; Eberhard, M.O. Tsunami-like wave loading of individual bridge components. J. Bridge Eng. 2017, 23, 04017137. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.G.; Itani, A.; Lomonaco, P.; Yim, S. Large-scale fsi experiments on tsunami-induced forces in bridges. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017. [Google Scholar]
- Douglass, S.L.; Chen, Q.; Olsen, J.M.; Edge, B.L.; Brown, D. Wave Forces on Bridge Decks; Final Report Prepared for U.S.; Department of Transportation and Federal Highway Administration Office of Bridge Technology: Washington, DC, USA, 2006. [Google Scholar]
- McPherson, R.L. Hurricane Induced Wave and Surge Forces on Bridge Decks. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2008. [Google Scholar]
- Bradner, C.; Schumacher, T.; Cox, D.; Higgins, C. Experimental setup for a large-scale bridge superstructure model subjected to waves. J. Waterw. Port Coast. Ocean Eng. 2010, 137, 3–11. [Google Scholar] [CrossRef]
- Hayatdavoodi, M.; Ertekin, R.C. Review of wave loads on coastal bridge decks. Appl. Mech. Rev. 2016, 68, 030802. [Google Scholar] [CrossRef]
- AASHTO. Guide Specifications for Bridges Vulnerable to Coastal Storms; AASHTO: Washington, DC, USA, 2008. [Google Scholar]
- FEMA P-646. Guidelines for Design of Structures for Vertical Evacuation from Tsunamis, 2nd ed.; Federal Emergency Management Agency: Washington, DC, USA, 2012; 174p. [Google Scholar]
- MATLAB User’s Guide Release 2016a; The MathWorks, Inc.: Natick, MA, USA, 2016.




| Water Depth (m) | Nominal Wave Height (m) | Wave Type |
|---|---|---|
| 1.90 | 0.46, 0.52, 0.65 | Unbroken solitary |
| 0.80, 1.00, 1.10, 1.30 | Bore | |
| 2.00 | 0.36, 0.42, 0.52, 0.70 | Unbroken solitary |
| 0.90, 1.00, 1.20, 1.40 | Bore |
| Wave Type | Depth (m) | Wave Case # | Hinput (m) | Hwg12 (m) | Fup, G1/Fup, tot | Fup, G2/Fup, tot | Fup, G3/Fup, tot | Fup, G4/Fup, tot |
|---|---|---|---|---|---|---|---|---|
| Un-broken solitary | 1.90 | 1 | 0.46 | 0.56 | 0.72 | 0.23 | 0.12 | 0.09 |
| 2 | 0.52 | 0.64 | 0.77 | 0.35 | 0.19 | 0.29 | ||
| 3 | 0.65 | 0.87 | 0.71 | 0.26 | 0.19 | 0.17 | ||
| 2.00 | 4 | 0.36 | 0.40 | 0.44 | 0.19 | 0.18 | 0.21 | |
| 5 | 0.42 | 0.48 | 0.67 | 0.21 | 0.14 | 0.09 | ||
| 6 | 0.55 | 0.64 | 0.79 | 0.32 | 0.22 | 0.27 | ||
| 7 | 0.70 | 0.86 | 0.54 | 0.27 | 0.27 | 0.25 | ||
| Bore | 1.90 | 1 | 0.80 | 0.85 | 0.86 | 0.23 | 0.20 | 0.21 |
| 2 | 1.00 | 0.68 | 0.55 | 0.32 | 0.21 | 0.19 | ||
| 3 | 1.10 | 0.61 | 0.83 | 0.30 | 0.29 | 0.24 | ||
| 4 | 1.30 | 0.72 | 0.97 | 0.25 | 0.25 | 0.16 | ||
| 2.00 | 5 | 0.90 | 0.84 | 0.47 | 0.26 | 0.27 | 0.31 | |
| 6 | 1.00 | 0.76 | 0.47 | 0.29 | 0.25 | 0.35 | ||
| 7 | 1.20 | 0.73 | 0.77 | 0.26 | 0.22 | 0.21 | ||
| 8 | 1.40 | 0.75 | 0.48 | 0.26 | 0.25 | 0.27 |
| Wave Type | Hinput (m) | Bearings, G1 | Bearings, G2 | Bearings, G3 | Bearings, G4 | Col. 1 | Col. 2 | Col. 3 |
|---|---|---|---|---|---|---|---|---|
| Un-broken solitary | 0.46 | 0.52 | 1.17 | 1.30 | 0.63 | 0.70 | 2.12 | 0.19 |
| 0.52 | 0.41 | 0.71 | 0.92 | 0.37 | 0.61 | 1.58 | 0.34 | |
| 0.65 | 0.54 | 1.06 | 0.91 | 0.40 | 0.73 | 1.87 | 0.11 | |
| 0.36 | 0.85 | 1.25 | 0.49 | −0.24 | 1.08 | 1.90 | −0.17 | |
| 0.42 | 0.53 | 1.23 | 1.15 | 0.62 | 0.70 | 2.43 | 0.27 | |
| 0.55 | 0.41 | 0.79 | 0.84 | 0.42 | 0.59 | 1.75 | 0.33 | |
| 0.70 | 0.63 | 1.02 | 0.77 | 0.56 | 0.83 | 1.55 | 0.45 | |
| Bore | 0.80 | 0.73 | 1.59 | 0.59 | −0.67 | 0.89 | 2.22 | −1.91 |
| 1.00 | 0.92 | 0.97 | 0.56 | −0.39 | 1.05 | 1.87 | −1.05 | |
| 1.10 | 0.77 | 1.25 | 0.37 | −0.68 | 0.91 | 1.69 | −1.37 | |
| 1.30 | 0.67 | 1.53 | 0.49 | −0.87 | 0.88 | 2.03 | −1.94 | |
| 0.90 | 0.95 | 1.18 | 0.62 | 0.09 | 1.07 | 1.64 | −0.17 | |
| 1.00 | 0.99 | 1.11 | 0.65 | 0.02 | 1.15 | 1.83 | −0.28 | |
| 1.20 | 0.68 | 1.29 | 0.70 | −0.14 | 0.82 | 1.82 | −0.71 | |
| 1.40 | 0.95 | 1.21 | 0.67 | 0.09 | 1.07 | 1.77 | −0.21 |
| Wave Type | Hinput (m) | Brngs, G1 | Brngs, G2 | Brngs, G3 | Brngs, G4 | Col. 1 | Col. 2 | Col. 3 |
|---|---|---|---|---|---|---|---|---|
| Unbroken solitary | 0.46 | 0.93 | 1.61 | 0.51 | −2.66 | 1.01 | 2.12 | −1.36 |
| 0.52 | 0.91 | 1.07 | 0.26 | −0.94 | 1.10 | 1.58 | −0.70 | |
| 0.65 | 0.96 | 1.44 | 0.38 | −1.37 | 1.14 | 1.87 | −1.02 | |
| 0.36 | 1.06 | 1.40 | 0.33 | −0.66 | 1.20 | 1.90 | −0.36 | |
| 0.42 | 0.90 | 1.64 | 0.53 | −2.05 | 0.98 | 2.43 | −0.89 | |
| 0.55 | 0.89 | 1.18 | 0.26 | −0.99 | 1.09 | 1.75 | −0.80 | |
| 0.70 | 1.13 | 1.36 | 0.43 | −0.53 | 1.30 | 1.55 | −0.46 | |
| Bore | 0.80 | 0.98 | 1.89 | 0.23 | −1.69 | 1.12 | 2.22 | −3.24 |
| 1.00 | 1.16 | 1.11 | 0.35 | −1.08 | 1.21 | 1.87 | −1.70 | |
| 1.10 | 0.99 | 1.46 | 0.15 | −1.46 | 1.09 | 1.69 | −2.08 | |
| 1.30 | 0.97 | 1.91 | 0.10 | −2.65 | 1.09 | 2.03 | −3.13 | |
| 0.90 | 1.29 | 1.38 | 0.42 | −0.43 | 1.36 | 1.64 | −0.74 | |
| 1.00 | 1.25 | 1.25 | 0.48 | −0.34 | 1.41 | 1.83 | −0.75 | |
| 1.20 | 0.97 | 1.58 | 0.36 | −1.19 | 1.05 | 1.82 | −1.66 | |
| 1.40 | 1.23 | 1.39 | 0.49 | −0.43 | 1.29 | 1.77 | −0.65 |
| Wave Type | Hinput (m) | Brngs, G1 | Brngs, G2 | Brngs, G3 | Brngs, G4 | Col. 1 | Col. 2 | Col. 3 |
|---|---|---|---|---|---|---|---|---|
| Unbroken solitary | 0.46 | 1.07 | 1.75 | 0.24 | −3.79 | 1.12 | 2.12 | −1.87 |
| 0.52 | 0.94 | 1.10 | 0.21 | −1.03 | 1.06 | 1.58 | −0.62 | |
| 0.65 | 1.13 | 1.59 | 0.18 | −2.07 | 1.19 | 1.87 | −1.17 | |
| 0.36 | 1.46 | 1.72 | 0.01 | −1.49 | 1.47 | 1.90 | −0.82 | |
| 0.42 | 1.10 | 1.84 | 0.22 | −3.40 | 1.12 | 2.43 | −1.45 | |
| 0.55 | 0.95 | 1.23 | 0.20 | −1.16 | 1.03 | 1.75 | −0.67 | |
| 0.70 | 1.49 | 1.61 | 0.19 | −1.32 | 1.53 | 1.55 | −0.92 | |
| Bore | 0.80 | 1.18 | 2.13 | −0.06 | −2.52 | 1.21 | 2.22 | −3.79 |
| 1.00 | 1.56 | 1.34 | 0.00 | −2.19 | 1.46 | 1.87 | −2.76 | |
| 1.10 | 1.21 | 1.67 | −0.06 | −2.22 | 1.22 | 1.69 | −2.58 | |
| 1.30 | 1.08 | 2.05 | −0.05 | −3.29 | 1.20 | 2.03 | −3.80 | |
| 0.90 | 1.85 | 1.72 | 0.09 | −1.28 | 1.68 | 1.64 | −1.36 | |
| 1.00 | 1.88 | 1.60 | 0.08 | −1.20 | 1.76 | 1.83 | −1.39 | |
| 1.20 | 1.22 | 1.83 | 0.06 | −2.10 | 1.21 | 1.82 | −2.29 | |
| 1.40 | 1.84 | 1.76 | 0.10 | −1.51 | 1.67 | 1.77 | −1.42 |
| Wave Type | Hinput (m) | Brngs, G1 | Brngs, G2 | Brngs, G3 | Brngs, G4 | Col. 1 | Col. 2 | Col. 3 |
|---|---|---|---|---|---|---|---|---|
| Unbroken solitary | 0.46 | 0.79 | 1.45 | 0.79 | −1.49 | 0.88 | 2.12 | −0.70 |
| 0.52 | 0.68 | 0.91 | 0.56 | −0.35 | 0.83 | 1.58 | −0.12 | |
| 0.65 | 0.82 | 1.32 | 0.55 | −0.80 | 0.93 | 1.87 | −0.45 | |
| 0.36 | 1.09 | 1.43 | 0.31 | −0.72 | 1.20 | 1.90 | −0.36 | |
| 0.42 | 0.80 | 1.52 | 0.70 | −1.32 | 0.88 | 2.43 | −0.48 | |
| 0.55 | 0.69 | 1.02 | 0.51 | −0.39 | 0.80 | 1.75 | −0.15 | |
| 0.70 | 1.08 | 1.33 | 0.47 | −0.42 | 1.18 | 1.55 | −0.23 | |
| Bore | 0.80 | 0.88 | 1.77 | 0.37 | −1.29 | 0.96 | 2.22 | −2.34 |
| 1.00 | 1.16 | 1.11 | 0.35 | −1.07 | 1.17 | 1.87 | −1.54 | |
| 1.10 | 0.90 | 1.38 | 0.23 | −1.16 | 0.97 | 1.69 | −1.61 | |
| 1.30 | 0.81 | 1.70 | 0.31 | −1.69 | 0.95 | 2.03 | −2.37 | |
| 0.90 | 1.36 | 1.43 | 0.38 | −0.54 | 1.31 | 1.64 | −0.64 | |
| 1.00 | 1.39 | 1.33 | 0.40 | −0.52 | 1.38 | 1.83 | −0.70 | |
| 1.20 | 0.91 | 1.52 | 0.43 | −0.96 | 0.95 | 1.82 | −1.25 | |
| 1.40 | 1.35 | 1.46 | 0.41 | −0.64 | 1.31 | 1.77 | −0.69 |
| Wave Type | Hinput (m) | b = 0 | b = 0.50 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Brg1 | Brg2 | Brg3 | Brg4 | Brg1 | Brg2 | Brg3 | Brg4 | ||
| Unbroken solitary | 0.46 | −0.06 | 0.57 | 2.41 | 5.28 | 0.01 | 0.64 | 2.27 | 4.68 |
| 0.52 | −0.05 | 0.36 | 1.54 | 1.60 | −0.01 | 0.40 | 1.48 | 1.48 | |
| 0.65 | −0.06 | 0.52 | 1.65 | 2.93 | 0.01 | 0.58 | 1.56 | 2.61 | |
| 0.36 | −0.07 | 0.52 | 1.24 | 1.67 | 0.09 | 0.65 | 1.11 | 1.33 | |
| 0.42 | −0.06 | 0.60 | 2.12 | 4.79 | 0.01 | 0.68 | 2.00 | 4.26 | |
| 0.55 | −0.06 | 0.41 | 1.40 | 1.80 | −0.01 | 0.45 | 1.34 | 1.67 | |
| 0.70 | −0.09 | 0.54 | 1.25 | 2.12 | −0.03 | 0.58 | 1.21 | 1.99 | |
| Bore | 0.80 | −0.06 | 0.63 | 1.72 | 2.59 | 0.09 | 0.81 | 1.51 | 1.97 |
| 1.00 | −0.08 | 0.40 | 1.42 | 2.42 | 0.10 | 0.50 | 1.27 | 1.92 | |
| 1.10 | −0.06 | 0.48 | 1.16 | 2.21 | 0.10 | 0.63 | 1.01 | 1.65 | |
| 1.30 | −0.05 | 0.60 | 1.43 | 3.39 | 0.08 | 0.78 | 1.25 | 2.58 | |
| 0.90 | −0.10 | 0.55 | 1.23 | 1.68 | 0.05 | 0.64 | 1.15 | 1.45 | |
| 1.00 | −0.10 | 0.50 | 1.34 | 1.52 | 0.06 | 0.59 | 1.24 | 1.29 | |
| 1.20 | −0.06 | 0.56 | 1.57 | 2.51 | 0.06 | 0.68 | 1.42 | 2.08 | |
| 1.40 | −0.10 | 0.56 | 1.34 | 1.97 | 0.05 | 0.65 | 1.24 | 1.70 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Istrati, D.; Buckle, I.; Lomonaco, P.; Yim, S. Deciphering the Tsunami Wave Impact and Associated Connection Forces in Open-Girder Coastal Bridges. J. Mar. Sci. Eng. 2018, 6, 148. https://doi.org/10.3390/jmse6040148
Istrati D, Buckle I, Lomonaco P, Yim S. Deciphering the Tsunami Wave Impact and Associated Connection Forces in Open-Girder Coastal Bridges. Journal of Marine Science and Engineering. 2018; 6(4):148. https://doi.org/10.3390/jmse6040148
Chicago/Turabian StyleIstrati, Denis, Ian Buckle, Pedro Lomonaco, and Solomon Yim. 2018. "Deciphering the Tsunami Wave Impact and Associated Connection Forces in Open-Girder Coastal Bridges" Journal of Marine Science and Engineering 6, no. 4: 148. https://doi.org/10.3390/jmse6040148
APA StyleIstrati, D., Buckle, I., Lomonaco, P., & Yim, S. (2018). Deciphering the Tsunami Wave Impact and Associated Connection Forces in Open-Girder Coastal Bridges. Journal of Marine Science and Engineering, 6(4), 148. https://doi.org/10.3390/jmse6040148









