Abstract
The effects of large scale tidal energy device (TED) arrays on phytoplankton processes owing to the changes in hydrodynamic flows are unknown. Coupled two-dimensional biogeochemical and hydrodynamic models offer the opportunity to predict potential effects of large scale TED arrays on the local and regional phytoplankton dynamics in coastal and inshore environments. Using MIKE 21 Software by DHI (https://www.dhigroup.com), coupled two-dimensional biogeochemical and hydrodynamic models were developed with simulations including no turbines or an array of 55 turbines with four solar radiation scenarios to assess the temporal and spatial changes of phytoplankton dynamics in an idealised domain. Results suggest that the effect of TEDs on phytoplankton dynamics accounted for up to 25% of the variability in phytoplankton concentrations, most likely associated with an increased residence time in an inshore basin. However, natural variation, such as the intensity of photosynthetically active radiation, had a larger effect on phytoplankton dynamics than an array of TEDs.
1. Introduction
Arrays of tidal energy devices (TEDs) are a potential source of renewable energy that will assist in the effort to reduce carbon dioxide emissions worldwide. They extract kinetic energy from the tides on a strongly cyclical and predictable basis and convert the extracted energy into electricity. Estimates suggest that large arrays of TEDs could provide a significant proportion of the global electricity demand, with an estimated 32 GW in the UK alone [1]. However, it is inevitable that they will have some effect on the ecosystem in the area in which they are deployed. To date, there are only a few isolated TEDs in operation. However, to meet the 2050 targets of reducing carbon emissions by 80% of 1990s level, there are plans to deploy a number of tidal arrays around the British Isles [1]. Arrays are also planned in shallow (up to 50 m depth) coastal and inshore areas around Canada [2] and France [3].
Poorly understood environmental impacts of marine renewables remain one of the main hurdles for consenting and licensing of projects [4]. There are several concerns about the likely environmental effect of large TED arrays along coastal inshore environments. Reviews have discussed the potential local ecological effects [5,6,7,8,9] focusing largely on sediment dynamics [10,11], collision risks with mammals [12,13], fish or seabirds [14,15,16], and changes in larger community structures [17,18]. The installation of a large TED array will change the hydrodynamics of the ambient flow [19,20]. Many sessile and sedentary organisms depend on the flow of the water for availability of nutrients and food and hence changes in the hydrodynamics due to the presence of tidal turbines could potentially reduce the growth and ultimately survival of these organisms [8].
Hydrodynamic forces may also act to modify key predictors of phytoplankton derived primary production, either directly (e.g., transport of phytoplankton to deep water, thus reducing photosynthetically active radiation (PAR) available for photosynthesis) or indirectly (e.g., dilution and transport of nutrients, increased residence time in a basin) and therefore any changes to hydrodynamic conditions may have the potential to modify temporal and spatial patterns of primary production. Primary production supports higher trophic levels and therefore there is a concern that anthropogenic effects which alter primary production may multiply through the food chain in unknown ways.
In most marine ecosystems, the ultimate source of energy for primary production is the sun (photoautotrophic growth) with a key predictor of photoautotrophic growth being the availability of PAR [21]. However, nutrient availability is one of the limiting factors for phytoplankton growth in many marine environments such that, in certain near-shore areas, nutrient availability may be used as a key currency for primary production. The biochemical, biophysical, and ecological processes that regulate phytoplankton derived primary production are complex and a review of these processes is beyond the scope of this manuscript. Nevertheless, the global importance of phytoplankton ensures that the processes resulting in growth, mortality, and nutrient remineralisation are included at a basic level in many numerical modelling studies of marine ecosystems.
As arrays of TEDs are still in the developmental stage, the best approach to determine the potential effects of their deployment is to use numerical modelling. Over the last 40 years, a simplified picture of controls on primary production and the interactions with other core components of the planktonic system has been widely studied using NPZD (Nutrient–Phytoplankton–Zooplankton–Detritus) models [22]. These models predict changes over time in four state variables through a set of differential equations and have proven to be useful in capturing the properties and dynamics of the marine ecosystem at a higher level. The use of more complex models—i.e., models with greater numbers of state variables—has inherent difficulties, including lack of data for model initialisation, verification, and parameterisation [23], which may reduce the value of the model in its ability to answer key ecological questions [24]. NZPD models have been shown to be useful tools in predicting how an ecosystem is likely to change in response to changes in the physical and natural environment [22]. For example, the models have been used to show the consequences of intense aquaculture [25,26,27] and the impact of offshore wind farms [28] and large scale (>100 km) impacts of TED array on primary production using the GETM-ERSEM-BFM model [29] and water quality [30]. However, to date, there are no studies that investigate the possible changes in primary production in near proximity to TED arrays.
This paper addresses the applicability of using coupled hydrodynamic and biogeochemical models to investigate regional scale (up to 30 km) effects of an array of tidal turbines on phytoplankton dynamics in a near coastal, shallow environment. In particular, we use a high resolution, two-dimensional coupled hydrodynamic and biogeochemical NPZD model with two scenarios: no TEDs and an extreme case with an array of 55 TEDs. The model is set in an idealised domain without external sources of nitrogen or freshwater inflow. Four PAR scenarios are used to statistically assess the temporal and spatial changes of phytoplankton dynamics in relation to an array of turbines and solar radiation.
2. Materials and Methods
2.1. Hydrodynamic Model
Hydrodynamic and biogeochemical models were created using MIKE 21 software (DHI Water and Environment software package: www.dhisoftware.com). MIKE 21 FM is a two-dimensional, depth-averaged flexible mesh model using a Reynolds averaged Navier–Stokes equation. For this study, an idealised, relatively shallow, model was used, which was modified from the benchmark test case domain developed in [31,32] with a tidal free surface forcing of a realistic amplitude from the Strangford Lough model [33] that was held uniform along the open boundary. The domain consisted of a high flow velocity channel between the shallow area of the open sea and an enclosed shoaling out basin with some deeper channels of up to 50 m with no river discharge (Table 1; Figure 1). Current speed varied throughout the domain with ~3, ~1.5, and ~0.10 m/s in the channel, mid, and end of the basin respectively (Figure 2). Grid cell sizes ranged from approximately 80 m2 in the channel to 0.02 km2 in the basin and between 0.02 and 4 km2 in the open sea. Temporal resolution was set to 15 min time-steps for the output of hydrodynamic data and simulations were run over a whole year. Two different simulations were run, one with no turbines and one including a setup of an array of 55 tidal turbines in the channel representing an energy extraction scenario of 66 MW (1.2 MW per device) (Figure 1). The layout of the array was chosen to represent as high a number of turbines in the channel as possible (even to the point of an exaggeration). Specifically, 55 turbines were considered because further work in progress removes ‘blocks’ of five to simulate how different layouts affect various biological processes. The layout was chosen to provide reality to the layout of the array by maintaining a navigation channel through the centre of the array. The MIKE 21 software models the effect of turbines on the hydrodynamics as sub-grid structures by calculating a current induced drag and lift force on each individual turbine to capture the increasing resistance imposed by the turbine blades as the flow speed increases where the drag force, FD and lift force, FL, are determined from
where is the density of water, α is a correction factor, CD is the drag coefficient, CL is the lift coefficient, Ae is the effective area of turbine exposed to current, and V is the current speed. Simulated tidal turbines were based on the surface piercing horizontal axis tidal turbine SeaGen currently installed in the Strangford Narrows. The structure consists of a fixed cylindrical pile of 3 m diameter and 30 m height on which two separate 16 m diameter rotor blades on a large cross-arm are mounted. The centroid of the turbine was assumed to be in the middle of the water column.

Table 1.
Dimensions of the model domain.
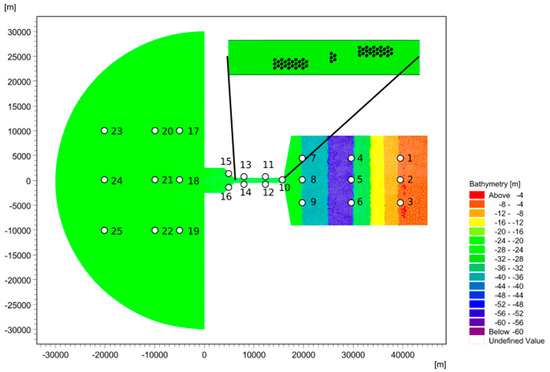
Figure 1.
Idealised model of a channel, the outer coastal zone (on the left) and the basin (on the right). The inset displays the setup of the 55 TEDs in the channel. The depth in the channel and outside the channel is constant at 20 m, while the basin has got some deeper areas of up to 60 m and is shoaling out towards the end. Concentrations of the state variables were recorded at the displayed 25 points, 1–9 in the basin, 10–16 in the channel, and 17–25 outside the channel.
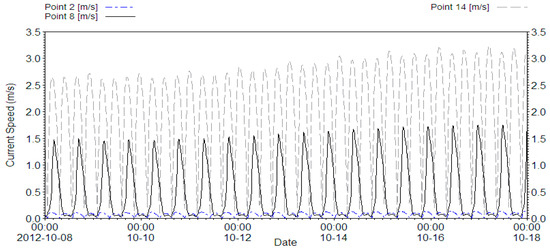
Figure 2.
Current speed (m/s) at points 2 and 8 within the basin and 14 in the channel from the idealised model (see Figure 1 for positions of points).
To assure that the idealised model consisted of a well-mixed body of water, the “h over U cubed criterion” in Equation (3)
where U is the mean tidal flow in m/s (i.e., the mean of maximum current speeds on both flood and ebb tides, ignoring direction) and h the water depth in m, was used. The criterion predicts the location of seasonal tidal mixing fronts in coastal waters separating zones of stratified and well-mixed water columns [34,35]. In shallow regions of relatively fast tidal flows, as in the basin and the channel of the idealized model, the term is relatively small and turbulence generated by shear stress on the bottom reaches the surface and results in mixing throughout the water column, sustaining the non-stratified conditions [35].
2.2. NPZD Model
A NPZD model following [36] was developed in MIKE by DHI ECOLab (Hørsholm, Denmark). A two-dimensional model was chosen, omitting interactions with a sediment layer and sinking of phytoplankton and detritus. Nitrogen is used as the currency across the model [22,36]. Only one generic type of both phytoplankton and zooplankton, are included. The process and growth rates loosely follow Longdill [25] (Table 2). For each grid cell, the time evolution of phytoplankton, nutrient, zooplankton, and detritus concentrations is the sum of advection, diffusion, and biogeochemical processes, which are described as
where N is the growth limiting nutrient nitrogen consisting of pooled concentrations of NO3 and NH4, P represents phytoplankton, Z zooplankton, and D detritus. A schematic model is shown in Figure 3, showing the movement of nutrients from the nutrient pool through the different stages.

Table 2.
State variables, processes, and constants of the two-dimensional NPZD model. “Type” refers to the type of the variable/process. “State” refers to the variables whose concentrations are being calculated at each time t by using auxiliary processes. Concentrations at time t of state variables can be used in auxiliary processes to calculate the concentration at t + 1; “aux” refers to auxiliary processes, which are intermittent processes calculated in order to calculate the concentration of the state variable. Auxiliary processes cannot include circular references, any additional auxiliary process used need to have been defined before. “Const” refers to constant values, which are provided to the model prior to the simulation, such as the half saturation constant. “Forcing” refers to external variables provided to the model, such as a file of PAR concentrations for each time t of the simulation. The depth forcing is provided from the hydrodynamic model for each grid cell and time t of the simulation.
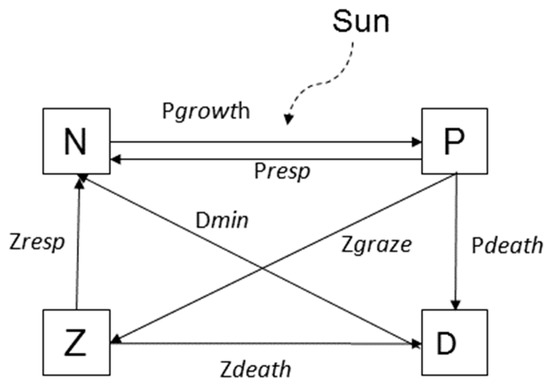
Figure 3.
Schematic NPZD model. State variables N (nutrients), P (phytoplankton), Z (zooplankton), and D (detritus) and the various processes affecting them.
The processes include light and nutrient dependent phytoplankton growth (Pgrowth), mortality (Pdeath), respiration (Presp) and grazing of zooplankton on phytoplankton (Pgraze) (Table 2). Other processes are mortality and excretion of zooplankton (Zdeath and Zexcretion) and mineralization of detritus back into the nutrient pool (Dmineralization) (Table 2). The model includes key aspects of lower level trophic food web dynamics which are widely accepted in the marine ecosystem modelling community, such as Michaelis–Menten kinetics for phytoplankton nutrient uptake and zooplankton grazing and light-dependent growth of phytoplankton. Surface irradiance is modelled as the photosynthetically active radiation (PAR). The depth distribution of PAR is a function of the surface PAR and the light attenuation profile averaged over the water depth. For the two-dimensional hydrodynamic model, concentrations are averaged over the well-mixed water column. Biomass of phytoplankton, zooplankton, and detritus are described as total dry mass calculated using the Redfield ratio [25]. As the model was focused on the effect of an array of tidal turbines and light in a two-dimensional model, neither water and/or ambient temperature nor external or internal sources of nitrogen—such as rivers, fresh-water or sewage input—are included.
2.3. Data and Simulation
The NPZD model was coupled to each of the two hydrodynamic models: with and without an array of TEDs. For photoautotrophic growth four PAR scenarios (A–D) based on PAR surface measurements made between 2004 and 2014 at the Queen’s University Marine Laboratory in Portaferry, Northern Ireland, were conducted for each of the coupled models. No full year of PAR measurements was available, so available data were collated to form four full years to provide annual variation. The resulting PAR records were representative of the strong natural annual variability in light conditions in North West Europe (Figure 4). The models were run over a one-year period from October 1 to September 30. Prior to examination of the PAR scenarios, a four-year spin-up was run using randomly selected solar radiation scenarios to assure a stable running of the system. The NPZD model was driven by initial concentrations of 5, 0.001, 0.001, and 5 of nitrogen, phytoplankton, zooplankton, and detritus without dimensions, respectively, following Fennel and Neumann [36]. In total, eight scenarios were conducted each TED setup—with and without arrays—was run for each PAR (A–D) scenario.
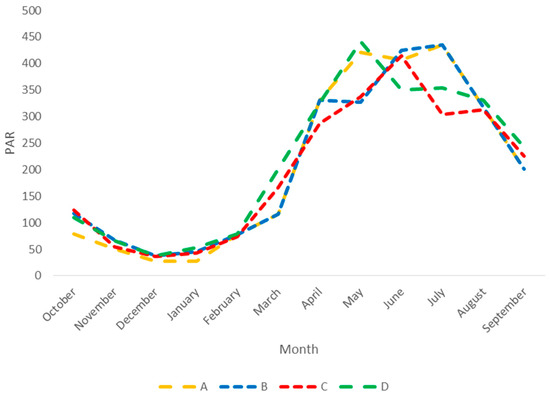
Figure 4.
Average monthly PAR values for the four PAR scenarios collated from measurements made between 2004 and 2014 at the Queen’s University Marine Laboratory in Portaferry, Northern Ireland. NB: PAR in the model are provided at an hourly rate, data not shown.
2.4. Analysis
Changes in residence time in the basin and current speed were calculated from the hydrodynamic model setups with and without TEDs. In particular, due to the very basic shape of the basin, residence time T, number of tidal cycles, was calculated as ‘flushing time’, using the simple equation method Equation (8)
following [37], where V is the mean volume of the basin and Q the quantity of water which is exchanged during a tidal cycle.
To detect shifts in phytoplankton dynamics within the NPZD model only phytoplankton concentrations, which were recorded every 15 min throughout the simulation at 25 sampling stations in the domain, were investigated (Figure 1). While all other concentrations were recorded, they are derived from a simulation based on differential equations and therefore dependent on each other. Daily average concentrations for each of the eight scenarios (two hydrodynamic settings with four PAR scenarios each) were derived from the raw data. Additionally, annual mean and peak/maximum concentrations were calculated. Visual interpretation and basic comparisons, such as time-series graphs, boxplots, and differences between annual average mean and peak values were used in the first instance to investigate the effect of a TED array and any spatial or temporal variability. Linear regression and hierarchical partitioning [38] were conducted to quantify the effects and the relative importance of TEDs in comparison to spatial and temporal effects. However, we omit significance tests and p-values because these significance tests applied to simulated data are not meaningful [39]. All analyses were performed using R; hierarchical partitioning was implemented with the package relaimpo using the included the Lindeman, Merenda, and Gold (LMG) metric [38,40].
3. Results
Average residence time of water in the basin increased by 5%, from 6 days, 13 h, 43 min without turbines to 6 days, 21 h, 48 min with TEDs. Average differences in flow speed over one tidal cycle (12.4 h) varied inside the channel (up to 0.32 m/s) but only by a small (<0.04 m/s) amount in the basin and the open sea (Figure 5). Water flow in the centre of the channel decreased with the introduction of the tidal turbines, while flow speed near the shore of the channel increased.
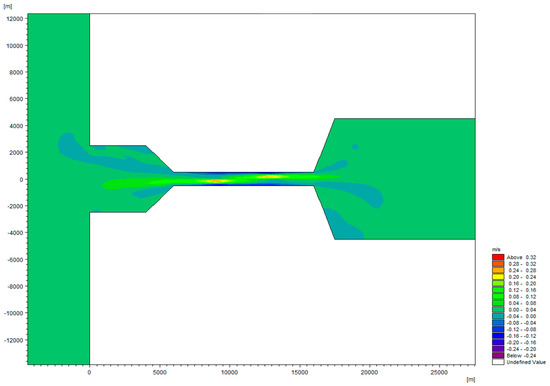
Figure 5.
Differences in current speed between scenarios with and without turbines, i.e., difference between the scenario without TED and scenario with TED in m/s. The values are averaged across one tidal cycle (i.e., 12.4 h). Outside the displayed area changes in current speed were less than 0.004 m/s.
Time series of daily mean concentrations in the basin, channel and open sea (Figure 6) showed stronger variation in phytoplankton concentration between PAR scenarios than TED scenarios. However, for each of the four PAR scenarios, phytoplankton concentrations declined slightly faster and earlier when a TED array was present. Boxplots of mean phytoplankton concentrations in the channel and basin also showed greater variation between PAR than TED scenarios (Figure 7).
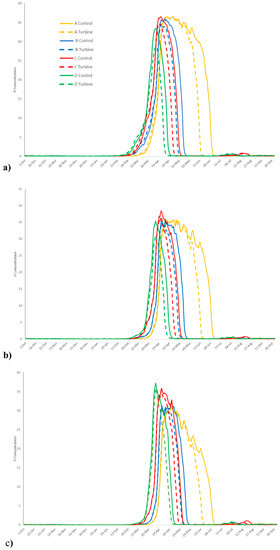
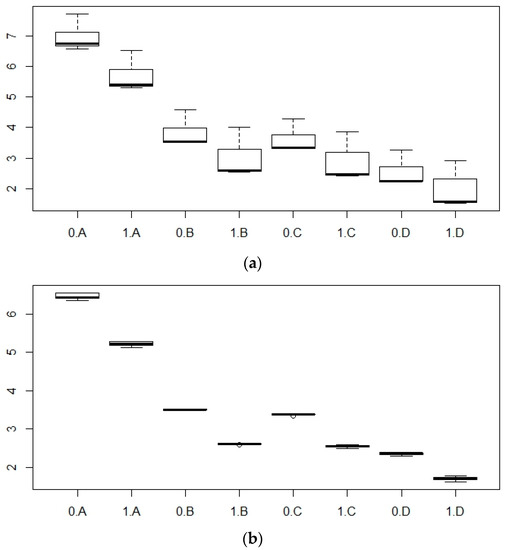
Figure 7.
Boxplots for the mean concentrations of phytoplankton in the basin (a); in the channel (b). A–D refer to the PAR scenarios (as in Figure 4) and 0 and 1 to the scenarios without (0) and with (1) an array of TEDs. 0. A hence refers to PAR scenario A without turbines.
Comparisons between annual mean and peak (maximal) concentrations at each of the 25 sampling points of phytoplankton showed that differences in phytoplankton concentration as a result of natural annual solar radiation were considerably greater than those associated with the presence of the TED array (Table 3). The greatest difference in mean concentrations of phytoplankton between PAR scenarios without TEDs was 4.42 g/m3 and with TEDs 3.72 g/m3, while the greatest observed difference between no TED/TED scenarios for PAR scenario A was 1.28 g/m3. Mean phytoplankton concentrations were generally 18–28% lower in scenarios with TEDs than without, except under PAR scenario C, in which phytoplankton concentration increased in the basin by 3.9%. Peak concentrations were between 0.3% and 13% lower with TEDs across all locations and PAR scenarios.

Linear regression and hierarchical partitioning models for annual mean and maximal concentrations of phytoplankton with PAR, TED scenario and location (basin, channel, open sea) as predictors showed that concentrations and dynamics varied between scenarios (Table 4). PAR was determined to be the most important factor in controlling phytoplankton dynamics, explaining 76% in the variation of mean phytoplankton concentrations but only 13% in variation of maximal peak concentration. TED absence/presence explained only 8% of mean phytoplankton concentration and 6% in variation of peak concentrations. The location—i.e., basin, channel, or open sea—explained only 4% of variation in mean phytoplankton concentrations, but 7% in maximal concentrations. In general, the predictors explained a total of 87% of the differences in phytoplankton mean concentrations, but only 27% of the variation in maximum concentrations (Table 4).

Table 4.
Results of general linear models for mean, max, and cumulative values of phytoplankton and maximal and cumulative values of nitrogen. The variables turbine, location, and radiation year are categorical variables, with the following categories: Turbine: no turbine/turbine; Location: basin/channel/open ocean; and Solar Radiation: A/B/C/D. Residual standard error, multiple R-squared, F, and p-value are not displayed as they are not meaningful in this context [37].
4. Discussion
In the absence of any operational TED arrays, using coupled hydrodynamic and biogeochemical models provides the only approach to investigate possible changes on phytoplankton dynamics as a result of the installation of an array of TEDs. This is especially important at the planning stage. Using an idealised domain, in the near-field (50 m up to 5 km) and local scale (up to 30 km) the model predicted changes in phytoplankton dynamics as a result of the changes in the hydrodynamics owing to the installation of a large array of TEDs. Even for this extreme case of energy extraction, hydrodynamic influences on phytoplankton processes were less than the natural seasonal variation in changes in phytoplankton production. These results therefore indicate that in the absence of a full scale tidal energy array, coupled hydrodynamic and biogeochemical models provide the possibility to detect changes in phytoplankton dynamics because of changes in hydrodynamics.
The results suggest that natural variation in PAR could potentially have a greater impact on primary production than changes in hydrodynamics as a result of the installation of a very large TED array. Primary production generally shows natural annual variability which typically includes phytoplankton cyclical blooms, seasonal shifts, and long-term trends. The underlying mechanisms influencing this variability can vary both spatially and temporally [40,41] and depend on many interacting physical and biological factors, including light conditions, temperature, wind speed, and species composition [42]. For example, a long-term study in the North Sea showed peak chlorophyll a concentrations between 30 and 100 mg/m3, a change of 300% at the same spatial coordinates due to natural variation [42]. However, in addition to natural variation, anthropogenic changes can have a substantial impact on phytoplankton dynamics. Those include increased nutrient loads transported into the sea by rivers (such as fertilizer run-off from agriculture), sewage, aquaculture, and mussel farming sites. The influence of such additions can be exacerbated through slower or less pronounced flushing of coastal areas or inlets after introduction of structures that slow down or prevent water movement, like a large array of TEDs [20]. In the idealised model presented here, residence time increased by 5% under the TED array scenario. In response, a decrease in the average and cumulative phytoplankton concentrations of up to 20% was observed and phytoplankton concentrations decreased more quickly at the end of the spring bloom. In support of this phenomenon, enhanced grazing and growth time for the zooplankton population was observed. Indeed, a slightly faster growth of the zooplankton concentration under the TED scenario was observed in the model (Figure 8). Although the generic state variables and processes applied here are physically and ecologically realistic, to what extent this effect could be observed in natural scenarios—involving multispecies assemblages and complex trophic interactions—remains to be seen.
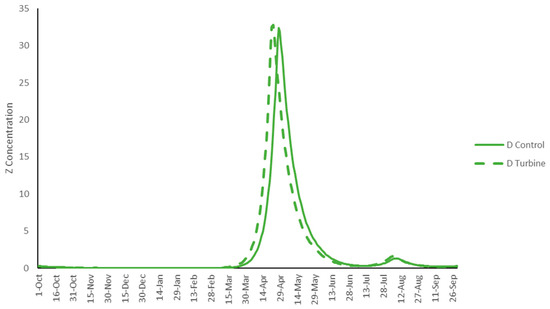
Figure 8.
Annual variation in zooplankton concentration in the basin under PAR scenario D (Figure 4).
This is a first attempt to investigate the effect of TED arrays on a local scale, using a high resolution two-dimensional model. While it could be argued that three-dimensional hydrodynamic models offer a range of additional facilities and the opportunity to include biological effects such as sinking and sediment processes [30], they also demand a high number of parameters. Often environments in which TED arrays are planned are poorly studied and the availability of ecological and biological information is scarce and inadequate. Therefore, the parameterisation of a three-dimensional model would be extremely difficult; the greater the number of unknown parameters the greater the uncertainties in the validation of the model and in the results. Additionally, three-dimensional models with the high spatial resolution as used in this study would lead to high computational costs. One reason to use a three-dimensional model would be if vertical stratification of the water column is likely, as this may strongly regulate phytoplankton dynamics [41]. A decrease in flow speed through the introduction of a TED array might lead to stratified conditions in a previously un-stratified area. However, in shallow (<50 m) coastal regions with relatively fast tidal flows, as in the idealized model of this study or the areas under consideration for the deployment of TED arrays [1], the water column is well mixed, which prevents vertical stratification of the water column [35]. In cases where the environment to be modelled experiences seasonal stratification, or stratification due to freshwater input, this would have to be accounted for in a three-dimensional model. However, in those areas where TED arrays are most likely to be deployed, we consider that a two-dimensional hydrodynamic model is appropriate and as we demonstrate here, this approach can provide significant insight without the added complexity of a fully three-dimensional simulation.
As with any modelling approach, however complex, it is not possible to incorporate all predictors or processes of interest. Each model can only focus on a select number of processes, while others are omitted, combined, or included indirectly. For example, predation could be generalised as a mortality or sink term that removes matter from the system while omitting in-between processes. The modeller has to therefore critically assess the minimal necessary complexity of the model to find a satisfactory solution for the problem that is being solved [22]. In this study, only annual variation in PAR was included as a physical factor, while species composition was reduced to two generic categories of phytoplankton and zooplankton. Including additional state variables or processes would most likely mask the effect of a TED array and would make it more difficult to extract the degree to which the natural and anthropogenic factors contribute to the phytoplankton dynamics.
The present study fills a gap in the investigation of near field, coastal effects of TED arrays on primary production. While recent modelling studies on the possible near-field effects of tidal barrages (e.g., Severn Barrage) showed changes in the concentration of nitrogen and phytoplankton as well as changes in sediment transport, the environmental impacts of a barrage structure cannot be directly compared to an array of individual turbines [6]. Two recent studies by van der Molen et al. [29] and Wang et al. [30] used a three-dimensional modelling approach to predict the possible large scale effects of TED arrays in distances of 100 s of kilometers. However, these models had large grid sizes in the range of 300 m to kilometers rather than <100 m in the areas of interest and therefore precludes the investigation of regional and near-field behaviour of phytoplankton dynamics.
In recent years, much research into tidal turbine technology has focused on the optimal design of the devices and the setup and optimisation of TED arrays [43,44]. These studies have shown that the setup constellation of an array, the number of turbines and relation to other devices will also affect the hydrodynamics. In this study, the structure of the tidal turbine was based on the SeaGen turbine. It is to be expected that the effect of an array of tidal turbines might depend on the particular conditions of the site and community structure of organisms. For example, if the substrate is predominantly soft sediment as for wind farms, increased turbulence arising from the turbine structure may increase turbidity, which decreases light attenuation and ultimately may affect photoautotrophic growth [45]. However, in areas with rocky/boulder substrata, such as the Strangford Narrows [18], enhanced turbidity may not be an issue. Furthermore, while the wake of SeaGen was observable, the background turbulent nature of the Strangford Narrows meant that recovery of any disturbance by the device was fast and only five rotor diameter downstream (80 m) there is already a > 95% wake recovery [46] suggesting that turbidity levels will not be enhanced. The model in this study was parameterised with basic assumptions and concentrations obtained from published literature rather than direct measurements of a particular system, used only one group of phytoplankton and zooplankton, and pooled all forms of nutrients into a single state variable. Despite these simplifications, the changes in hydrodynamics as a result of an array of tidal turbines have been realistically modelled and the approach used here would provide a good indication of changes in NPZD dynamics if applied to a realistic array or parameterised with real (measured) values. All of those components would need investigation for any particular array and location in order to understand their specific impacts on the total environment.
This study demonstrates that coupled hydrodynamic and ecological models can simulate ecological effects of TED arrays on phytoplankton dynamics. Although simplified, these simulated effects are based on the response of well understood ecological processes responding to known physical forcings. Using this approach, the relative impacts of TED arrays can be assessed. A two-dimensional approach offers the opportunity to use a high resolution grid while keeping the computational costs and necessary data input to a minimum. Our simulations show that, in this idealised system, TED arrays have an effect on primary production; however, this effect is relatively small in comparison to effects associated with natural variation. Further investigation is needed to implement a ‘living’ system with realistic parameters and processes. This may include: additional zooplankton and phytoplankton species, a more complex channel with headlands and other features, filter feeders and other organisms settling on the structures and excess nutrient input entering the basin through agricultural run-offs or other sources. These processes will be important in determining the realised effect of increased residence time in inshore loughs as a result of large TED arrays.
Author Contributions
P.S., L.K., D.P., G.S., and B.E. conceived and designed the experiments; P.S. performed the computations; P.S., D.P., and B.E. analyzed the data; P.S., L.K., D.P., G.S., and B.E wrote the paper.
Funding
The research was financially supported by the EPSRC research grant EP/J010065/1.
Conflicts of Interest
The authors declare no conflict of interest
References
- The Crown Estate. UK Wave and Tidal Key Resource Areas Project; The Crown Estate: London, UK, 2012. [Google Scholar]
- Cameron, B.; Farwell, S.; Oldreive, M. Establishing marine renewable energy legislation in Nova Scotia, Canada. In Proceedings of the 11th European Wave & Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Magagna, D.; Uihlein, A.; Silva, M.; Raventos, A. Wave and tidal energy in Europe: Assessing present technologies. In Proceedings of the 11th European Wave & Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Magagna, D.; Monfardini, R.; Uihlein, A. JRC Ocean Energy Status Report: 2016 Edition; EUR 28407 EN; Publications Office of the European Union: Luxembourg City, Luxembourg, 2016. [Google Scholar]
- Boehlert, G.W.; Gill, A.B. Environmental and ecological effects of ocean renewable energy development. A current synthesis. Oceanography 2010, 23, 68–81. [Google Scholar] [CrossRef]
- Kadiri, M.; Ahmadian, R.; Bockelmann-Evans, B.; Rauen, W.; Falconer, R. A review of the potential water quality impacts of tidal renewable energy systems. Renew. Sustain. Energy Rev. 2012, 16, 329–341. [Google Scholar] [CrossRef]
- Maclean, I.M.D.; Inger, R.; Benson, D.; Booth, C.G.; Embling, C.B.; Grecian, W.J.; Heymans, J.J.; Plummer, K.E.; Shackshaft, M.; Sparling, C.E.; et al. Resolving issues with environmental impact assessment of marine renewable energy installations. Front. Mar. Sci. 2014, 1, 75. [Google Scholar] [CrossRef]
- Shields, M.A.; Woolf, D.K.; Grist, E.P.M.; Kerr, S.A.; Jackson, A.C.; Harris, R.E.; Bell, M.C.; Beharie, R.; Want, A.; Osalusi, E.; et al. Marine renewable energy: The ecological implications of altering the hydrodynamics of the marine environment. Ocean Coast. Manag. 2011, 54, 2–9. [Google Scholar] [CrossRef]
- Shields, M.A.; Payne, A.I.L. Marine Renewable Energy Technology and Environmental Interactions; Springer Science and Business Media: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Martin-Short, R.; Hill, J.; Kramer, S.C.; Avdis, A.; Allison, P.A.; Piggott, M.D. Tidal resource extraction in the Pentland Firth, UK: Potential impacts on flow regime and sediment transport in the Inner Sound of Stroma. Renew. Energy 2015, 76, 596–607. [Google Scholar] [CrossRef]
- Neill, S.P.; Litt, E.J.; Couch, S.J.; Davies, A.G. The impact of tidal stream turbines on large-scale sediment dynamics. Renew. Energy 2009, 34, 2803–2812. [Google Scholar] [CrossRef]
- Thompson, D.; Hall, A.J.; Lonergan, M.; McConnell, B.; Northridge, S. Current status of knowledge of effects of offshore renewable energy generation devices on marine mammals and research requirements. In Report to Scottish Government; Scottish Government: Edinburgh, UK, 2013. [Google Scholar]
- Hastie, G.D.; Russell, D.J.F.; Lepper, P.; Elliott, J.; Wilson, B.; Benjamins, S.; Thompson, D. Harbour seals avoid tidal turbine noise: Implications for collision risk. J. Appl. Ecol. 2017, 1–10. [Google Scholar] [CrossRef]
- Hammar, L.; Ehnberg, J. Who should be afraid of a tidal turbine—The good, the bad or the ugly? In Proceedings of the 10th European Wave and Tidal Energy Conference Proceedings, Aalborg, Denmark, 2–5 September 2013. [Google Scholar]
- Hammar, L.; Eggertsen, L.; Andersson, S.; Ehnberg, J.; Arvidsson, R.; Gullstroem, M.; Molander, S. A Probabilistic model for hydrokinetic turbine collision risks: Exploring Impacts on Fish. PLoS ONE 2015, 10, e0117756. [Google Scholar] [CrossRef] [PubMed]
- Williamson, B.; Fraser, S.; Blondel, P.; Bell, P.; Waggitt, J.; Scott, B. Multisensor Acoustic Tracking of Fish and Seabird Behavior Around Tidal Turbine Structures in Scotland. IEEE J. Ocean. Eng. 2017, 42, 948–965. [Google Scholar] [CrossRef]
- Adams, T.P.; Miller, R.G.; Aleynik, D.; Burrows, M.T. Offshore marine renewable energy devices as stepping stones across biogeographical boundaries. J. Appl. Ecol. 2014, 51, 330–338. [Google Scholar] [CrossRef]
- Kregting, L.; Elsäßer, B.; Kennedy, R.; Smyth, D.; O’Carroll, J.; Savidge, G. Do changes in current flow as a result of arrays of tidal turbines have an effect on benthic communities? PLoS ONE 2016, 11, e0161279. [Google Scholar] [CrossRef] [PubMed]
- Couch, S.J.; Bryden, I.G. Large-scale physical response of the tidal system to energy extraction and its significance for informing environmental and ecological impact assessment. In Proceedings of the Oceans 2007-Europe International Conference, Aberdeen, UK, 18–21 June 2007. [Google Scholar]
- Yang, Z.; Wang, T. Assessment of Energy Removal Impacts on Physical Systems: Development of MHK Module and Analysis of Effects on Hydrodynamics. Pacific Northwest National Laboratory. Available online: https://tethys.pnnl.gov/sites/default/files/publications/Development_of_MHK_Module_and_Analysis.pdf (accessed on 22 May 2018).
- Falkowski, P.G.; Raven, J.A. Aquatic Photosynthesis; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Franks, P. NPZ models of plankton dynamics: Their construction, coupling to physics, and application. J. Oceanogr. 2002, 58, 379–387. [Google Scholar] [CrossRef]
- Ji, R.; Davis, C.; Chen, C.; Beardsley, R. Influence of local and external processes on the annual nitrogen cycle and primary productivity on Georges Bank: A 3-D biological-physical modeling study. J. Mar. Syst. 2008, 73, 31–47. [Google Scholar] [CrossRef]
- Hannah, C.; Vezina, A.; John, M.S. The case for marine ecosystem models of intermediate complexity. Prog. Oceanogr. 2010, 84, 121–128. [Google Scholar] [CrossRef]
- Longdill, P. Environmentally Sustainable Aquaculture: An eco-Physical Perspective. Ph.D. Thesis, The University of Waikato, Hamilton, New Zealand, 2007. [Google Scholar]
- Wild-Allen, K.; Herzfeld, M.; Thompson, P.A.; Rosebrock, U.; Parslow, J.; Volkman, J.K. Applied coastal biogeochemical modelling to quantify the environmental impact of fish farm nutrients and inform managers. J. Mar. Syst. 2010, 81, 134–147. [Google Scholar] [CrossRef]
- Wild-Allen, K.; Thompson, P.A.; Volkman, J.K.; Parslow, J. Use of a coastal biogeochemical model to select environmental monitoring sites. J. Mar. Syst. 2011, 88, 120–127. [Google Scholar] [CrossRef]
- Van der Molen, J.; Smith, H.C.M.; Lepper, P.; Limpenny, S.; Rees, J. Predicting the large-scale consequences of offshore wind turbine array development on a North Sea ecosystem. Cont. Shelf Res. 2014, 85, 60–72. [Google Scholar] [CrossRef]
- Van der Molen, J.; Ruardij, P.; Greenwood, N. Potential environmental impact of tidal energy extraction in the Pentland Firth at large spatial scales: Results of a biogeochemical model. Biogeosciences 2016, 13, 2593–2609. [Google Scholar] [CrossRef]
- Wang, T.; Yang, Z.; Copping, A. A modelling study of the potential water quality impacts from in-stream tidal energy extraction. Estuaries Coasts 2015, 38 (Suppl. 1), S173–S186. [Google Scholar] [CrossRef]
- Walkington, I.; Burrows, R. Modelling tidal stream power potential. Appl. Ocean Res. 2009, 31, 239–245. [Google Scholar] [CrossRef]
- Kramer, S.C.; Piggott, M.D.; Hill, J.; Kregting, L.; Pritchard, D.; Elsäßer, B. The modelling of tidal turbine farms using multi-scale, unstructured mesh models. In Proceedings of the 2nd International Conference on Environmental Interactions of Marine Renewable Energy Technologies (EIMR2014), Kirkwall, Orkney, 28 April–02 May 2014. [Google Scholar]
- Kregting, L.; Elsäßer, B. A hydrodynamic framework for Strangford Lough Part 1: Tidal Model. J. Mar. Sci. Eng. 2014, 2, 46–65. [Google Scholar] [CrossRef]
- Simpson, J.S.; Hunter, J.R. Fronts in the Irish Sea. Nature 1974, 250, 404–406. [Google Scholar] [CrossRef]
- Thorpe, S.A. An Introduction to Ocean Turbulence; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Fennel, W.; Neumann, T. Introduction to the Modelling of Marine Ecosystems; Elsevier: New York, NY, USA, 2015. [Google Scholar]
- Herman, J.; Shen, J.; Huang, J. Tidal Flushing Characteristics in Virginia’s Tidal Embayments. In Virginia Coastal Zone Management Program; Virginia Department of Environmental Quality: Richmond, VA, USA, 2007. [Google Scholar]
- Groemping, U. Relative Importance for Linear Regression in R: The package realimpo. J. Stat. Softw. 2006, 17, 1–27. [Google Scholar]
- White, J.W.; Rassweiler, A.; Samhouri, J.F.; Stier, A.C.; White, C. Ecologists should not use statistical significance tests to interpret simulation model results. Oikos 2014, 123, 385–388. [Google Scholar] [CrossRef]
- Lindeman, R.H.; Merenda, P.F.; Gold, R.Z. Introduction to Bivariate and Multivariate Analysis; Scott Foresman: Glenview, IL, USA, 1980. [Google Scholar]
- Cloern, J.E.; Schraga, T.S.; Lopez, C.B.; Knowles, N.; Labiosa, R.G.; Dugdale, R. Climate anomalies generate an exceptional dinoflagellate bloom in San Francisco Bay. Geophys. Res. Lett. 2005, 32, 172–180. [Google Scholar] [CrossRef]
- Philippart, C.J.M.; van Iperen, J.M.; Cadée, G.C.; Zuur, A.F. Long-term field observations on seasonality in chlorophyll-a concentrations in a shallow coastal marine ecosystem, the Wadden Sea. Estuar. Coasts 2010, 33, 286–294. [Google Scholar] [CrossRef]
- Culley, D.M.; Funke, S.W.; Kramer, S.C.; Piggott, M.D. Integration of cost modelling within the micro-siting design optimisation of tidal turbine arrays. Renew. Energy 2016, 85, 215–227. [Google Scholar] [CrossRef]
- Stansby, P.; Stallard, T. Fast optimisation of tidal stream turbine positions for power generation in small arrays with low blockage based on superposition of self-similar far-wake velocity deficit profiles. Renew. Energy 2016, 92, 366–375. [Google Scholar] [CrossRef]
- Vanhellemont, Q.; Ruddick, K. Turbid wakes associated with offshore wind turbines observed with Landsat 8. Remote Sens. Environ. 2014, 145, 105–115. [Google Scholar] [CrossRef]
- Savidge, G.; Ainsworth, D.; Bearhop, S.; Christen, N.; Elsäßer, B.; Fortune, F.; Inger, R.; Kennedy, R.; McRobert, A.; Plummer, K.E.; et al. Strangford Lough and the SeaGen tidal turbine. In Marine Renewable Energy Technology and Environmental Interactions; Shields, M.A., Payne, A.I.L., Eds.; Humanity and the Sea: Dordrecht, The Netherland, 2014; pp. 153–172. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).